Gravitational wave and collider probes of a triplet Higgs sector with a low cutoff

Abstract

We study the scalar triplet extension of the standard model with a low cutoff, preventing large corrections to the quadratic masses that would otherwise worsen the hierarchy problem. We explore the reach of LISA to test the parameter space region of the scalar potential (not yet excluded by Higgs to diphoton measurements) in which the electroweak phase transition is strongly first-order and produces sizeable gravitational waves. We also demonstrate that the collider phenomenology of the model is drastically different from its renormalizable counterpart. We study the reach of the LHC in ongoing searches and project bounds for the HL-LHC. Likewise, we develop a dedicated analysis to test the key but still unexplored signature of pair-production of charged scalars decaying to third-generation quarks: $pp\rightarrow t\overline{b} (\overline{t}b), b\overline{b}$. These results apply straightforwardly to other extensions of the Higgs sector such as the 2HDM/MSSM.

1 Introduction

Hyperchargeless triplet scalars $\Phi$ arise in a variety of models of new physics. They include

(i) :

theories of grand unification (GUT), where scalar multiplets, often transforming in the adjoint representation of the GUT group, break spontaneously the GUT symmetry. A simple example is the $\mathbf {24}$ in SU(5), which decomposes as $(1,1)_0+(1,\mathbf {3})_0+\cdots$ under the Standard Model (SM) gauge group $SU(3)_c\times SU(2)_L\times U(1)_Y$, therefore delivering a scalar triplet. Likewise, the $\mathbf {45}$ representation of SO(10) contains the $\mathbf {24}$ of SU(5) and therefore a SM triplet as well.

(ii) :

Supersymmetric (SUSY) models. As a matter of fact, the triplet extension of the MSSM is one of the simplest options to alleviate the little hierarchy problem [1, 2].

(iii) :

Composite Higgs models (CHM). The scalar sector of most CHMs is non minimal. It includes a hyperchargeless triplet in one of the two simplest cosets admitting an UV completion à la QCD in four dimensions, viz. SU(5) / SO(5) [3, 4]. Moreover, models based on $SO(7)/G_2$ [5] provide exactly one triplet in addition to the Higgs boson.

Therefore, the phenomenology of such triplet is not dictated by the renormalizable Lagrangian. The latter has to be instead supplemented with effective operators encoding the effects of the heavier resonances (SUSY partners, composite states, etc.), which can modify drastically the dynamics of $\Phi$. To demonstrate this, we will work under the assumption that the triplet does not get a (custodial symmetry breaking) vacuum expectation value (VEV). This limit can be naturally enforced assuming the triplet is a CP-odd scalar and CP is conserved in the Higgs sector. At the renormalizable level, the Lagrangian becomes accidentally $\mathbb {Z}_2$ symmetric, i.e. $\Phi \rightarrow -\Phi$, making the neutral component of the triplet a potential dark matter candidate. The charged components are in turn long-lived. The corresponding phenomenology has been studied in Refs. [6,7,8]. However, the effective operators make all components decay promptly even if the cutoff is $f\sim$ several TeV at which new resonances are out of the reach of current facilities. A much larger cutoff would introduce too large corrections also to the triplet mass, worsening the hierarchy problem.¹ In this article, we study probes of current and future colliders to this more natural version of the inert triplet model (ITM).

The extended Higgs sector modifies also the electroweak (EW) phase transition (EWPT). Thus, we extend previous studies in this respect [10, 11] computing the reach of future detectors for gravitational waves that originate in the production, evolution and eventual collisions of bubbles of vacuum in a first-order phase transition. The paper is organized as follows. We introduce the model in Sect. 2. We discuss the dynamics of the EWPT in Sect. 3. We explore collider signatures in Sect. 4. In Sect. 5 we propose an LHC analysis that has not been yet worked out experimentally for probing the key channel $pp\rightarrow t\overline{b} (\overline{t}b), b\overline{b}$. We study signal and background and provide prospects for the HL-LHC, namely the LHC running at a center of mass energy (c.m.e) $\sqrt{s} = 13$ TeV with integrated luminosity $\mathcal {L} = 3$ $\hbox {ab}^{-1}$. We conclude in Sect. 6.

2 Model

The Lagrangian of the CP-odd scalar triplet when it is assumed embedded in an UV theory, takes the form:

$$\begin{aligned} L =&\,\frac{1}{2}|D_\mu \Phi |^2 {-}\bigg \lbrace \frac{1}{2}\mu _\Phi ^2|\Phi |^2 {+} \frac{1}{2}\lambda _{H\Phi }|H|^2 |\Phi |^2 + \frac{1}{4}\lambda _\Phi |\Phi |^4\bigg \rbrace \nonumber \\&+ \frac{1}{f}\bigg \lbrace \text {i}\,\overline{q_L^i}\bigg [c^u_{ij}(\tilde{H}\Phi ) u^j_R + c^d_{ij}(H\Phi )d_R^j\bigg ] + \text {h.c.}\bigg \rbrace , \end{aligned}$$

(1)

where $H=(h^+, h_0 = (h+v)/\sqrt{2})$ and $\Phi = (\phi ^+, -\phi ^0, \phi ^-)$. We will assume flavour diagonal couplings: $c^{u(d)}_{ij}\sim c y_{u(d)}\delta _{ij}$ with c a constant and y Yukawa. We will comment on departures from this assumption in the conclusions. The relevant parameter is therefore the ratio c / f. The product $\tilde{H}\Phi$ $(H\Phi )$ stands for the doublet in the $SU(2)_L\times U(1)_Y$ decomposition $\mathbf {2}_{-(+)1/2}\times \mathbf {3}_0 = \mathbf {2}_{-(+)1/2} + \mathbf {4}_{-(+)1/2}$. Explicitly:

$$\begin{aligned} \tilde{H}\Phi = \bigg (\begin{array}{c} \phi _0 h_0^* - \sqrt{2}\phi ^+ h^- \\ \phi _0 h^- - \sqrt{2} \phi ^- h_0^* \end{array}\bigg ), \end{aligned}$$

(2)

and analogously for $H\Phi$ upon the replacement $h_0^*\rightarrow h^+$ and $h^- \rightarrow -h_0$. Therefore, in the unitary gauge after EWSB, we obtain:

$$\begin{aligned} L&\supset \dfrac{v}{\sqrt{2}}\frac{c}{f}\bigg \lbrace \text {i}y^t\phi _0 \overline{t}\gamma _5 t - \text {i}y^b\phi _0 \overline{b}\gamma _5 b \end{aligned}$$

(3)

$$\begin{aligned}&\quad \times \bigg [-\sqrt{2} \text {i} \phi ^- \overline{b}(y^t P_R + y^b P_L )t + \text {h.c.}\bigg ]\bigg \rbrace , \end{aligned}$$

(4)

with $v\sim 246$ GeV and the sum extends to the first and second families of quarks, that we will denote collectively by q. Couplings to the leptons could be also present. We neglect them in this analysis.

Fig. 1

Exotic decay widths of the different heavy particles in our model for $f = 1$ TeV

$\phi ^{0(\pm )}$ can decay into SM quarks. Likewise, for $m_t> m_\Phi$, the top quark can decay into the triplet and a bottom quark. ($m_t$ stands for the top quark mass, whereas $m_\Phi$ is the physical mass of $\Phi$; at tree level $m_\Phi ^2 = \mu _\Phi ^2 + \lambda _{H\Phi }v^2/2$.) The following relations hold:

$$\begin{aligned} \Gamma \left( \phi _0 \rightarrow q \overline{q}\right)&= \frac{3 y_q^2 v^2}{16\pi }\frac{c^2}{f^2} m_\phi \sqrt{ 1 - \frac{4 m_q^2}{m_\phi ^2}}, \end{aligned}$$

(5)

$$\begin{aligned} \Gamma \left( \phi ^+ \rightarrow q \overline{q^\prime } \right)&= \frac{3 (y_q^2 + y_{q^\prime }^2) v^2}{16 \pi }\frac{c^2}{ f^2} m_\phi \left[ 1-\frac{m_q^2}{m_\phi ^2}\right] ^2, \end{aligned}$$

(6)

$$\begin{aligned} \Gamma \left( t \rightarrow \phi ^+ b\right)&= \frac{(y_b^2 + y_t^2) v^2}{32 \pi }\frac{c^2}{ f^2} m_t \left[ 1 - \frac{m_\phi ^2}{m_t^2}\right] ^2. \end{aligned}$$

(7)

In the second equation we are assuming $m_q \gg m_{q^\prime }$, which is normally the case if the former is an up quark and the later a down quark. Note that decays into the light quarks are dominant if channels involving the top quark are kinematically closed. Partial widths as a function of $m_\Phi$ are depicted in Fig. 1.

Note also that, had we assumed a CP violating trilinear term in the potential, $\sim \kappa \Phi H^2$, this term would induce a VEV for the triplet, $v^\prime \sim \kappa v^2/m_\Phi ^2$. The triplet could also decay into the Higgs degrees of freedom, the corresponding width scaling as $\Gamma \sim (v^\prime /v^2)^2 m_\Phi ^3$. Given that $v^\prime$ modifies the $\rho$ parameter, it is bounded to be $v^\prime \lesssim$ GeV [12]. Therefore, the corresponding decay would still be subdominant with respect to those suppressed by v / f even for $f\sim 10$ TeV.

This setup can be easily accommodated in a SUSY framework. The minimal model consists of the MSSM extended with a supermultiplet $\Sigma$ with quantum numbers $(1, \mathbf {3})_0$; see Ref. [13]. The most general and renormalizable superpotential is the MSSM superpotential extended by

$$\begin{aligned} \Delta W = \mu H_1 H_2 + \lambda H_1 \Sigma H_2 + \frac{1}{2}\mu _\Sigma \text {tr} \Sigma ^2, \end{aligned}$$

(8)

with $H_1$ and $H_2$ the two doublet superfields. Likewise, the extra soft-breaking Lagrangian reads

$$\begin{aligned} L_{\text {SB}} = m_4^2 \text {tr} \Sigma ^\dagger \Sigma + \bigg [B_\Sigma \text {tr}\Sigma ^2 + \lambda A_\lambda H_1\Sigma H_2 + \text {h.c.}\bigg ]. \end{aligned}$$

(9)

In the limit $\lambda \rightarrow 0$, $\lambda \mu _\Sigma \rightarrow \text {finite}$, the fermionic partner in $\Sigma$ decouples and the model is approximately inert with

$$\begin{aligned} \mu _\Phi ^2&\sim m_4^2 + \mu _\Sigma ^2 + B_\Sigma \mu _\Sigma , \end{aligned}$$

(10)

$$\begin{aligned} \kappa _{\Phi }&\sim -\sqrt{2}\lambda \mu _\Sigma . \end{aligned}$$

(11)

In the previous expression, $\kappa _{\Phi }$ stands for the trilinear coupling in $\kappa _\Phi \Phi H H_{2}$. (With a slight abuse of notation, we are denoting here by $H_2$ the scalar component of this superfield.) After integrating $H_2$ out, we get

$$\begin{aligned} \lambda _{H\Phi } \sim \dfrac{(\lambda \mu _{\Sigma })^2}{m_2^2}, \quad \frac{c^{u(d)}}{f}\sim y_2^{u(d)}\frac{\lambda \mu _\Sigma }{m_2^2}, \end{aligned}$$

(12)

with $m_2$ the mass of $H_2$ and $y_2^{u(d)}$ its Yukawa couplings.

The Lagrangian above can also arise naturally in CHMs, in which both H and $\Phi$ are pNGBs originated in the (approximate) symmetry breaking pattern $\mathcal {G}\rightarrow \mathcal {H}$ at a scale f at which a new strong sector confines. The smallest realization of this setup relies on $SO(7)\rightarrow G_2$. The global symmetry is only approximate because it is explicitly broken by loops of SM gauge bosons, as well as by linear mixings between the left- and right-handed top quark fields and composite operators $\mathcal {O}_{L,R}$. The latter transform in representations of SO(7). If $\mathcal {O}_L\sim \mathbf {35}$ and $\mathcal {O}_R\sim 1$, one obtains the Lagrangian [14]

$$\begin{aligned} L \sim y_u\overline{q_L} \tilde{H} \bigg [1 + \frac{\gamma }{f}\Phi + \mathcal {O}(1/f^2)\bigg ]u_R, \end{aligned}$$

(13)

and similarly for other quarks. $\gamma$ parametrises the degree of mixing of $q_L$ with the two doublets in the $\mathbf {35}$. (Under $G_2$, $\mathbf {35} = 1+\mathbf {7}+\mathbf {27}$, whereas $\mathbf {7} =(\mathbf {2},\mathbf {2})+(\mathbf {3},1)$ and $\mathbf {27} =(1,1)+(\mathbf {2},\mathbf {2})+(\mathbf {3},\mathbf {3})+(\mathbf {4},\mathbf {2} )+(\mathbf {5},1)$ under the custodial symmetry group $SU(2)_L\times SU(2)_R$.)

The elementary ITM can also get 1 / f corrections provided it is extended with new vector-like quarks with quantum numbers $(\mathbf {3},\mathbf {3})_{-2/3\,(1/3)}$, $(\mathbf {3},\mathbf {2})_{-1/6}$; and/or with scalar doublets with quantum numbers $(1,\mathbf {2})_{1/2}$. The effective operator in Eq. 1 is then generated after integrating the heavy modes at the mass scale $M\sim f$; see Fig. 2. This list exhausts the possible tree-level weakly-coupled UV completions of the ITM that fit into our phenomenological framework.

LEP operated at $\sqrt{s} = 209$ GeV, excluding $\Phi$ masses below $\sim 100$ GeV. (This limit is however slightly model dependent; other sources of new physics could weaken it to even $\sim 75$ GeV [15].) We will therefore restrict our analysis to the mass range $100< m_\Phi < 500$ GeV.

Fig. 2

Generation of the effective operator in Eq. 1 after integrating out a heavy scalar with with quantum numbers $(1, \mathbf {2})_{1/2}$ (left), a heavy vector-like quark $\sim (\mathbf {3},\mathbf {3})_{{-2/3}\, (1/3)}$ (center) or $\sim (\mathbf {3},\mathbf {2})_{-1/6}$ (right) at a mass scale $M\sim f$. From left to right and top to bottom, the different fields are: $q_L$, $t_R$, H, $\Phi$

Table 1 Comparison of tree-level obtained parameters ($^0$) versus the ones computed at one loop for different values of the three inputs

3 The electroweak phase transition

The new scalar potential modifies the EWPT, which in the SM is a cross over. In the region of the parameter space where it is first order and strong, gravitational waves can be produced via nucleation and eventual collision of bubbles of symmetry-breaking vacuum. In order to explore this phenomenology, we study the evolution of the one-loop effective potential at finite temperature:

$$\begin{aligned} V = V_{\text {tree}} + \Delta V_\text {CW} + \Delta V_T~ + C. \end{aligned}$$

(14)

C is a constant fixed so that V vanishes at the origin of the field space. $V_{\text {tree}}$ stands for the tree-level potential. $V_\text {CW}$ is the one-loop correction at zero temperature in $\overline{\text {MS}}$ and Landau gauge, namely

$$\begin{aligned} \Delta V_\text {CW}&= \frac{1}{64 \pi ^2} \sum _i (\pm ) n_i m_i^4 \bigg [ \log {\frac{m_i^2}{v^2}} - c_i \bigg ], \end{aligned}$$

(15)

where i runs over all bosons ($+$) and fermions $(-)$. The factor $n_i$ denotes de number of degrees of freedom of the field i, while $c_i$ is 5 / 6 for gauge bosons and 3 / 2 otherwise. The field-dependent masses squared of the spectator fields are

$$\begin{aligned} m_W^2&= \frac{1}{4} g^2 (h^2 + 4 \phi _0^2), \end{aligned}$$

(16)

$$\begin{aligned} m_Z^2&= \frac{1}{4} (g^2 + g'^2) h^2, \end{aligned}$$

(17)

$$\begin{aligned} m_{G^{0, \pm }}^2&= -\mu _H^2 + \lambda _H h^2 + \frac{1}{2}\lambda _{H\Phi } \phi _0^2, \end{aligned}$$

(18)

$$\begin{aligned} m_{\phi ^\pm }^2&= \mu _\Phi ^2+\frac{1}{2}\lambda _{H\Phi }h^2+\lambda _\Phi \phi _0^2, \end{aligned}$$

(19)

$$\begin{aligned} m_t^2&= \frac{1}{2} y_t^2 h^2. \end{aligned}$$

(20)

In addition, we have two more field dependent masses squared, $m_1^2$ and $m_2^2$, given by the eigenvalues of the mixing matrix

$$\begin{aligned} \mathcal {M}^2=\bigg [\begin{array}{cc} -\mu _H^2 + 3 \lambda _H h^2 + \frac{1}{2} \lambda _{H\Phi } \phi _0^2~ &{} \lambda _{H\Phi } h \phi _0\\ \lambda _{H\Phi } h \phi _0 &{} \mu _\Phi ^2 + 3 \lambda _\Phi \phi _0^2 + \frac{1}{2} \lambda _{H\Phi } h^2. \end{array}\bigg ] \end{aligned}$$

(21)

Finally, the finite temperature corrections read

$$\begin{aligned} \Delta V_{T} =&\, \frac{T^4}{2\pi ^2}\sum _i (\pm )n_i \int _0^\infty y^2 \log {\bigg [1\mp e^{-\sqrt{\frac{m_i^2}{T^2}+y^2}}\bigg ]}. \end{aligned}$$

(22)

As input parameters, we take $m_\Phi$, $\lambda _{H\Phi }$ and $\lambda _\Phi$. The remaining three parameters in the tree level potential are numerically obtained after requiring $V_\text {tree} + \Delta V_\text {CW}$ to have a extreme at $\langle h\rangle = v, \langle \phi _0\rangle = 0$, at which the physical Higgs and $\Phi$ masses are $m_h \sim 125$ GeV and $m_\Phi$, respectively. In other words:

$$\begin{aligned} \frac{\partial V}{\partial h} = 0~, \quad \frac{\partial ^2 V}{\partial h^2} = m_h^2~, \quad \frac{\partial ^2 V}{\partial \phi _0^2} = m_\Phi ^2. \end{aligned}$$

(23)

At tree level, (v, 0) is guaranteed to be an extreme provided $\lambda _{\Phi }, \lambda _{H\Phi }>0$ and $\mu _\Phi ^2 > -1/2 v^2 \lambda _{H\Phi }$. A comparison between tree and loop level values of $\mu _H$, $\mu _\Phi$ and $\lambda _H$ in a set of benchmark inputs can be seen in Table 1.

Fig. 3

Evolution of the VEV with the temperature for the parameter space point $m_\Phi = 120$ GeV, $\lambda _{h\Phi }=1.1$, $\lambda _\Phi =1.1$. At high temperatures, the EW symmetry is restored. It is spontaneously broken to $(\langle h\rangle ,\langle \phi _0\rangle ) \sim (0, 10)$ GeV at $T\sim 160$ GeV, evolving until $T_n\sim 85$ GeV at which the step $(0, 120)\rightarrow (220,0)$ GeV takes place. This latter transition is clearly strong; $\langle h\rangle /T_n > 1$. The shape of the potential at $T_n$ is also shown

Fig. 4

Same as Fig. 3 but for the parameter space point $m_\Phi =460$ GeV, $\lambda _{H\Phi }=4.9$, $\lambda _\Phi =0.1$. The EWPT proceeds in one step at $T_n = 115$ GeV in this case. $\langle \phi _0\rangle$ vanishes for all values of T

At high temperatures, the EW symmetry is restored. For certain values of the model parameters, the transition between $\langle h\rangle = 0\rightarrow \langle h \rangle = v_n$ is not smooth as in the SM, but rather first order. One example is given in Fig. 3. In this case, the EWPT proceeds in two steps. An example of a first-order EWPT in one step is shown in Fig. 4. We will denote by $T_n$ the nucleation temperature, namely the temperature at which the Higgs first order phase transition takes place. This is determined by the condition $S_3/T_n \sim 100$, where $S_3$ stands for the action of the thermal transition between vacua [16, 17].

In the region enclosed by the dashed green line in the plane ($\lambda _{H\Phi }, m_\Phi )$ of Fig. 5, $v_n/T_n > 1$; i.e. the phase transition is said to be strong. The nature of the strongest phase transition (one or two steps) is also labelled. The way we performed the scan is as follows: We varied $m_\Phi$ in the range [100, 500] GeV in steps of 20 GeV. We varied $\lambda _{H\Phi }$ in the range [0.1, 10] in steps of 0.1. For each pair $(m_\Phi , \lambda _{H\Phi })$, we found the value of $\lambda _\Phi$ in $[0.1, 0.3, \ldots , 10]$ maximizing $v_n/T_n$. The points with smallest value of $\lambda _{H\Phi }$ are interpolated using straight lines. Likewise for those with largest value of this coupling. The resulting lines are further smoothed according to the bezier method using Gnuplot.

Fig. 5

The region in the plane $(m_\Phi , \lambda _{h\Phi })$ where the EWPT is strongly first order is enclosed by the two dashed green lines, each one labeling the structure of the phase transition (1- or 2-step). The sub-regions above the dotted lines can be tested at LISA. The area enclosed by the solid (dashed) orange line is (could be) excluded at the 95 % CL by current (future) measurements of the Higgs to photon width

Note that at $T > 0$, the triplet squared term reads $\sim \mu ^2_\Phi + T^2$, which can not be negative for any value of $\mu ^2_\Phi > 0$. Therefore, the 2-step EWPT can only occur if the triplet minimum is present at $T=0$. Moreover, for a fixed $m_\Phi$, there is a minimum $\lambda _{H\Phi }$ below which $\mu ^2_\Phi$ is not negative. Likewise, there is a maximum value of the coupling above which the potential at the triplet minimum, $V(0, \langle \phi _0\rangle )\sim -|\mu _\Phi |^4/\lambda _\Phi$, is deeper than the Higgs one, the theory being therefore unstable. Altogether, they explain the bounded shape of the figure above.

It is also well known that strong first order phase transition, resulting from non-standard Higgs sectors, produce gravitational waves [18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47]. They are roughly characterized by the normalized latent heat of the phase transition

$$\begin{aligned} \alpha \sim \frac{\epsilon (T_n)}{35 T_n^4}; \end{aligned}$$

(24)

(with $\epsilon (T_n)$ the latent heat at $T_n$), and by the inverse duration time of the phase transition,

$$\begin{aligned} \frac{\beta }{H} \sim T_n \frac{d}{dT}\frac{S_3}{T}\sim T_n\frac{\Delta (S_3/T)}{\Delta T}. \end{aligned}$$

(25)

We computed these quantities using CosmoTransitions [48]. $\Delta (S_3/T)$ is estimated finding the two values of T for which $S_3/T = 100, 200$ GeV, respectively. (Therefore, $\Delta (S/T) = 100$ GeV.) We warn that, due to the rapid growth of $S_3/T$ with T, the linear estimation of the derivative can be sensibly overestimated. Given that small values of $\beta /H$ give rise to stronger gravitational waves, our results are conservative. The region of the parameter space that we estimate it can be tested by the future gravitational wave observatory LISA lies above the dotted green line in Fig. 5. The points in this are lead to $\alpha , \beta$ within the region “C1” of Ref. [21] for $T_n = 100$ GeV. (The bubble velocity is close to unity in good approximation. Also, we have neglected the effect that sounds waves might be not “long-lasting”, what could weaken the gravitational wave signal [49].)

Large values of $\lambda _{H\Phi }$ can be also probed in the $h\rightarrow \gamma \gamma$ channel. Indeed, the width of the later in this case reads

$$\begin{aligned} \Gamma (h\rightarrow \gamma \gamma ) = \frac{\alpha ^2 m_h^3}{1024 \pi ^3}\bigg \lbrace&\frac{2}{v}\bigg [A_1(\tau _W) + \frac{4}{3}A_{1/2}(\tau _t)\bigg ] \nonumber \\&+\lambda _{H\Phi }\frac{v}{m_\Phi ^2}A_0(\tau _\Phi )\bigg \rbrace ^2, \end{aligned}$$

(26)

with $\alpha$ the electromagnetic constant and $\tau _i = 4m_i^2/m_h^2$. The last ATLAS+CMS combined measurement of the Higgs decay into photons was provided in Ref. [50], $\Gamma (h\rightarrow \gamma \gamma )/\Gamma (h\rightarrow \gamma \gamma )_{ \text {SM}} = 1.14^{+0.19}_{-0.18}$. The region in the plane $(m_\Phi , \lambda _{H\Phi })$ that is consequently excluded at the 95 % CL is enclosed by the solid orange line in Fig. 5. The expectation at the HL-LHC is that ratios outside the range $1.0\pm 0.1$ will be excluded [51]. The corresponding region is enclosed by the dashed orange line. It is clear that, if departures from the SM prediction on the Higgs to diphoton rate are not observed, only one-step EWPT (i.e. single peak signatures) could be detected by LISA.

Finally, let us very briefly comment on the possibility of EW baryogenesis [52,53,54,55]. In our scenario, CP is violated spontaneously during the second transition in the two-step case, when both h and $\phi _0$ change VEV and therefore the top mass acquires a CP violating phase. In related models [56] (see also Refs. [32, 57, 58]), EW baryogenesis has been shown successful provided $c\Delta v/f \gtrsim 0.1$, with $\Delta v$ the change in VEV during the EWPT. In our case, $\Delta v$ can be easily $\gtrsim 100$ GeV (see Fig. 3) and therefore $c \Delta v/f \gtrsim 0.1$ for $c/f\sim 1$ $\hbox {TeV}^{-1}$.

A small explicit CP violating potential $\Delta V/T_n^4 \gg \text {H}/T_n\sim 10^{-16}$, with the Hubble scale $\text {H}$, is only needed to avoid domain wall problems [56]. In our setup, this can be triggered by a small CP-violating term in the potential, $\sim \kappa \Phi H^2$. At leading order in $\kappa$, it reflects in the (finite-temperature) potential as $V\sim \kappa T^3/(4\pi )^2$. Avoiding domain walls then implies $\kappa \gtrsim 10^{-12}$ GeV.

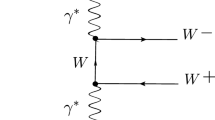
Let us show that this amount of CP violation evades easily neutron and electron dipole moment (EDM) constraints. Indeed, the neutron EDM arises mainly from the running of the diagram on the right panel of Fig. 6. It gives [59]

$$\begin{aligned} \bigg |\frac{d_n}{e}\bigg |\sim 20 ~\text {MeV} \frac{g_3^3}{(4\pi )^4}\frac{y_t^2 v^2}{m_t^2 m_\Phi ^2} \frac{c\kappa }{f} h(m_t^2/m_h^2), \end{aligned}$$

(27)

with $g_3$ the QCD coupling at the scale $\sim 1$ GeV, and

$$\begin{aligned} h(z) =z^2 \int _0^1 dx \int _0^1 dy \frac{x^3 y^3 (1-x)}{[zx(1-xy) + (1-x)(1-y)]^2}. \end{aligned}$$

(28)

For the values of c / f and $\kappa$ stated previously we obtain $|d_n|\sim 10^{-38}$ e cm, much smaller than the current 90 % CL bound $2.9\times \sim 10^{-26}$ e cm [60].

Fig. 6

Main contribution to the electron (left) and neutron (right) EDMs in the scalar triplet extension of the SM with a low cutoff

Fig. 7

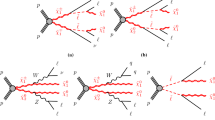
Representative diagrams of the main $\Phi$ production mechanisms at pp colliders. Left) Pair production via EW currents. Middle-left) Single production via gluon fusion. Middle-right) Production in association with $t\overline{b}$ ($\overline{t}b$). Right) Production from the decay of a top quark

An electron EDM will be generated mainly via two-loop diagrams as that depicted in the left panel of Fig. 6. Using the expressions of Ref. [61], we find that the value of the electron EDM in our case reads

$$\begin{aligned} \frac{d}{e} \sim \frac{\alpha v^2 c}{6\pi ^3 m_t f} y_t \frac{\kappa y_e}{m_\Phi ^2} \bigg [f(m_t^2/m_h^2) + g(m_t^2/m_h^2)\bigg ], \end{aligned}$$

(29)

with

$$\begin{aligned} f(z)&= \frac{1}{2}z\int _0^1 \frac{1-2x(1-x)}{x(1-x)-z}\log {\frac{x(1-x)}{z}} dx, \end{aligned}$$

(30)

$$\begin{aligned} g(z)&=\frac{1}{2}z\int _0^1 \frac{1}{x(1-x) -z}\log {\frac{x(1-x)}{z}}dx. \end{aligned}$$

(31)

We obtain $|d_e|\sim 10^{-42}$ e cm, much smaller than the latest measurement by ACME [62], $d < 1.1\times 10^{-29}$ e cm.

Regarding c / f, more stringent bounds could be set at colliders. We dedicate next section to this point.

Fig. 8

Cross section of the different production modes for $\Phi$ at pp colliders of different c.m.e. The coupling c / f is set to $1\mathrm {TeV}^{-1}$. The production cross section of $\phi _0$ via gluon fusion was rescaled from Ref. [63], at $\sqrt{s}=13$ TeV. To obtain the cross sections for other c.m.e., we have computed the corresponding ratio in MadGraph, by using the Higgs EFT of the ggHFullLoop model. This ratio turns out to be a good approximation of the ratio in the full theory; see Ref. [64]

4 Collider signatures

The scalar triplet can be produced at pp colliders in a variety of ways; see Fig. 7. The corresponding cross sections at $\sqrt{s} = 8, 13$ TeV are given in Fig. 8. For completeness, we also provide numbers for 27 and 100 TeV center-of-mass energy.

The triplet can be singly produced in $q\overline{q}$ initiated processes. The Yukawa suppression, together with the 1 / f factor, makes the production cross section in this channel very small, though. Still, $\phi _0$ can be singly produced in gluon fusion. In the regime $m_\Phi < 2 m_t$, the most constraining searches are those looking for single production of $b\overline{b}$ resonances. The most up-to-date such analysis was recently released by CMS; see Ref. [66]. It is based on 35.9 $\hbox {fb}^{-1}$ of integrated luminosity collected at $\sqrt{s} = 13$ TeV. The region of the plane $(m_\Phi , c/f)$ that is excluded by this analysis is enclosed by the solid blue line in Fig. 9. It is expected that they become a factor of $\sqrt{3\,\text {fb}/35.9\,\text {ab}}\sim 9$ stronger at the HL-LHC. The projected bound on the plane is enclosed by the dashed blue line in the same figure. For $m_\Phi > 2m_t$, $\phi _0$ decays mostly into $t\overline{t}$. There are however no resonant searches for invariant masses below 500 GeV, neither at $\sqrt{s}=8$ TeV nor $\sqrt{s}=13$ TeV.

Moreover, the scalar triplet can be produced in association with top and bottom quarks, namely $pp\rightarrow \phi ^{+} t \overline{b}$. For $m_\Phi > m_t$, the most updated and constraining search is the ATLAS study of Ref. [67], which uses 36.1 $\hbox {fb}^{-1}$ of LHC data collected at 13 TeV. It combines both the semi- and di-leptonic channels. The limits on $\sigma (pp\rightarrow tb\phi ^\pm )\times \mathcal {B}(\phi ^\pm \rightarrow tb)$ translate into the bounded region delimited by the green solid line in Fig. 9. A naive rescaling with the luminosity enhancement suggests that cross sections a factor of $\sim 0.1$ smaller can be tested at the HL-LHC. Translated to the plane $(m_\Phi , c/f)$, the corresponding bound is given by the region enclosed by the dashed line of the same colour.

In addition, for $m_t > m_\Phi$, the triplet can be also produced in the decay of the top quark. Current searches for $t\overline{t}$ production with $t\rightarrow \phi ^\pm b, \phi ^\pm \rightarrow jj$ have been carried out in CMS at $\sqrt{s}=8$ TeV with an integrated luminosity of $\mathcal {L} = 19.7$ $\hbox {fb}^{-1}$ [65]. This latter reference sets an upper bound on this rare top decay of $\mathcal {B}(t\rightarrow \phi ^\pm b, \phi ^\pm \rightarrow j j)<$ 1–2 % for $m_\Phi \sim$ 100–160 GeV. Using Eq. 5, this constraint translates into the region enclosed by the solid red line in Fig. 9. The projected bound at the HL-LHC is depicted, too.

Finally, irrespectively of the value of c / f, the scalar triplets can be always pair-produced via EW charged currents (CC), $pp\rightarrow W^{\pm (*)}\rightarrow \phi ^\pm \phi _0$, as well as via neutral currents (NC), $pp\rightarrow Z/\gamma \rightarrow \phi ^+\phi ^-$. (Note that $\phi _0$ does not interact with the Z boson and therefore it can not be pair-produced via NCs.) For $m_\Phi < m_t$, the new charged and neutral scalars decay mainly into $q'\overline{q}$ and $b\overline{b}$, respectively. Searches for pair-produced dijet resonances might therefore be sensitive to this regime. The most constraining such search is the CMS analysis presented in Ref. [68]. At this mass scale, each pair of quarks is very collimated and manifests as a single jet. The experimental analysis uses boosted techniques, including jet grooming to remove QCD radiation. The analysis considers $\mathcal {L} = 35.9$ $\hbox {fb}^{-1}$ at 13 TeV of c.m.e. The current limits on the total cross section range from $\sim 170$ pb (100 GeV) to $\sim 20$ pb (170 GeV). Therefore, the parameter space of our model is not constrained. Furthermore, a naive rescaling with the larger luminosity shows that this analysis will not be even constraining at the HL-LHC.

Fig. 9

Current (solid) and future (dashed) bounds on the parameter space $(m_\Phi , c/f)$. The red region to the left comes from LHC searches for rare top decays, $t\rightarrow b\phi ^\pm , \phi ^\pm \rightarrow$ jets; see Ref. [65]. The upper blue region comes from LHC searches for single production of $\phi ^0\rightarrow b\overline{b}$ via gluon fusion; see Ref. [66]. The green region to the right comes from LHC searches for single production of $\phi ^\pm$ in association with a top and a bottom quark; see Ref. [67]. The middle vertical orange band is the region that could be tested using our dedicated analysis

For $m_t<m_\Phi <2m_t$, the NC process gives rise to the final state $t\overline{b}, \overline{t}b$. The latest analysis exploring this channel for masses below 500 GeV was performed by CMS at $\sqrt{s} = 8$ TeV; see Ref. [69]. Unfortunately, the corresponding limits range from $\sim 2.5$ pb (250 GeV) to $\sim 0.5$ pb (500 GeV). No region in our parameter space can be even constrained at the HL-LHC. Likewise, the CC gives $t\overline{b}(\overline{t}b), b\overline{b}$. To the best of our knowledge, there is however no dedicated search for pair produced resonances decaying to these final states. Being this channel c / f independent, we perform a signal and background simulation of this process in Sect. 5.

For $m_\Phi > 2m_t$, the NCs still give resonant $t\overline{b}, b\overline{t}$. The CC channel instead results in $t\overline{t}, t\overline{b} (b\overline{t})$. Once more, no dedicated analysis exists for this final state. (The lack of analyses sensitivity to similar final states has been also recently pointed out in Ref. [70] in the context of composite dark sectors.) However, in comparison to this one, the $t\overline{b}(b\overline{t}),b\overline{b}$ analysis is much cleaner. Furthermore, it probes the mass range where the 2-step EWPT, and therefore EW baryogenesis, can occur.

5 LHC sensitivity

EW pair production of $t\overline{b} (\overline{t}b), b\overline{b}$ resonances occurs naturally in broadly-studied models, such as the 2HDM. Moreover, the cross section is independent of scalar to fermion couplings, provided the former decay promptly. It is therefore surprising that no experimental search has explored this channel at the LHC yet.

A plausible explanation is that the majority of these analyses are based on the 2HDM of the MSSM. In that case, one Higgs doublet gives mass to the up fermions, while the second gives mass to the down fermions. The physical charged components then couple to the top and bottom quarks with effective $c/f \sim (y_t\cot {\beta } + y_b\tan {\beta })/v$, with $\tan {\beta }$ the ratio of the two doublet VEVs. Therefore, $c/f \geqslant 2\sqrt{y_b y_t}/v\sim 1$ $\hbox {TeV}^{-1}$, the inequality being saturated at $\tan {\beta } = \sqrt{y_t/y_b}\sim 1.3$. As it can be seen in Fig. 9, this value is at the reach of $b\overline{b}$ resonant searches. Therefore, there is a priori no need for further analyses. The situation in our model and in other versions of the 2HDM is very different, though, because the coupling of the new scalars to the SM fermions can be (and typically is) very small. In the composite Higgs scenario, the effective scalar-fermion coupling can also be small, i.e. $c/f \lesssim 1~\text {TeV}^{-1}$, according to Eq. 13 for natural values of $0 < \gamma \le 1$.

Fig. 10

Normalized distribution of $m_{\phi _0,\mathrm {rec}}$ in the main background (dashed black) and in the signal for $m_\Phi = 185$ GeV (solid red) and $m_\Phi = 310$ GeV (solid blue)

With the aim of filling this gap, we perform a dedicated analysis for the process $pp\rightarrow \phi ^\pm \phi _0\rightarrow t\overline{b} (\overline{t}b), b\overline{b}$. We generate the hard processes for signal and background using MadGraph v5 [71] and shower them to a fully hadronised final state using Pythia v8 [72]. No parton-level cuts are applied. The main backgrounds are $t\overline{t}+\text {jets}$, $t\overline{t} b\overline{b}$, $t(\overline{t})+3b$ and $W + 4b$.

Table 2 Top) Effective cross section in fb for the signal (for $m_\Phi = 185$ GeV) and the backgrounds after each cut (1 – 5), as described in the text. Bottom) Effective cross section in fb after all cuts, including cut 6, for different signals and for the total background. The sensitivity at the HL-LHC is also shown

Fig. 11

Same as Fig. 10 but for $p_T$ of the reconstructed $\phi ^0$

Fig. 12

Current (solid) and futute (dashed) bounds on the plane $(m_\Phi , c)$ for $\lambda _{H\Phi } = 0.1c$ (left), $\lambda _{H\Phi } = c$ (center) and $\lambda _{H\Phi }=10c$ (right) and $f=1$ TeV

At the reconstruction level, a lepton is considered isolated if the hadronic energy deposit within a cone of size $R = 0.3$ is smaller than 10 % of the lepton candidate’s $p_T$. Jets are defined by the anti-$k_t$ algorithm with $R=0.4$. The following cuts are imposed:

• 1. Exactly one isolated lepton with $|y| < 2.5$ and $p_T > 15$ GeV;

• 2. At least four jets, with $p_T > 30$ GeV.

The longitudinal component of the missing neutrino is reconstructed using the requirement $m_W^2 = (p_l+p_\nu )^2$, with $m_W$ the mass of the W boson. The neutrino and lepton four-momenta, $p_\nu$ and $p_l$, are then added to the jet wich gives a total invariant mass closest to the top quark mass. After this,

• 3. The invariant mass of this top is required to be within 50 GeV of the top mass;

• 4. Three b-tagged jets are to be found among the jets not coming from the leptonic top.

• 5. We require the reconstructed masses of $\phi _0$ and $\phi ^\pm$ to be similar, i.e. $|m_{\phi _0,\mathrm {rec}} - m_{\phi ^\pm ,\mathrm {rec}}| \le 50$ GeV.

To decide which b-tagged jet is assigned to $\phi ^\pm$ and which two are assigned to $\phi _0$, we compute all possible combinations and choose the one resulting in the minimum difference between $m_{\phi _0,\mathrm {rec}}$ and $m_{\phi ^\pm ,\mathrm {rec}}$. The normalized distribution of this former variable in the main background ($t\overline{t}$+jets) and in the signal for $m_\Phi = 185$ GeV and $m_\Phi =310$ GeV is depicted in Fig. 10. In Fig. 11, we also show the normalized distribution of the $p_T$ of the reconstructed $\phi ^0$. However, cutting on this variable is costly in cross section, but would allow to improve the ratio of signal over background further.

Finally,

• 6. We reconstruct the resonances $\phi _0$ and $\phi ^{\pm }$ in the mass window of $\pm 30$ and $\pm 40$ GeV, respectively. As shown in Fig. 10 the experimental width of the resonances depends on their masses, thus, the central value of the mass window in the $(m_{\phi _0,\mathrm {rec}}, m_{\phi ^\pm ,\mathrm {rec}})$ plane has to be optimised for each $m_\Phi$ separately.

The cut-flow for the signal and the relevant backgrounds is given in Table 2. The sensitivity estimates are conservative, as the reconstruction relies on fairly inclusive cuts using large mass windows. Further, it is likely that some of the background was counted twice, as b-quarks from the parton shower in $t\bar{t}$ and from the matrix element in $t\bar{t} b\bar{b}$ are both contributing to the total background. Thus, we expect that the sensitivity can be improved further using a combination of multi-variate techniques [73,74,75] and high-$p_T$ final states [76].

We estimate the sensitivity at the HL-LHC as $\mathcal {S} = s/\sqrt{s+b}$, with s and b the number of signal and background events after all cuts, respectively. It ranges from 2.7 to 7.3 for $m_\Phi$ between 185 and 340 GeV. Thus, at the LHC ($\sqrt{s}=13$ TeV) we can probe the entire mass interval with $3000~\mathrm {fb}^{-1}$. The corresponding region in the plane $(m_\Phi , c/f)$ is therefore a vertical band, the one enclosed by the dashed orange line in Fig. 9.

6 Conclusions

Natural scalar extensions of the SM must have a low cutoff f preventing large corrections to the scalar masses. However, such models are usually studied neglecting 1 / f terms. Basing on the real triplet extension of the SM, we have highlighted that, if these terms are taken into account, the phenomenology can be drastically different. In particular, the only renormalizable interaction allowing the new scalars to decay is so suppressed by the measurement of the $\rho$ parameter, that decays mediated by effective operators dominate.

We have studied the reach of current LHC analyses. We have found that, despite being f independent, searches for EW pair-produced charged scalars decaying to third generation quarks are absent. This is particularly surprising given that such signals appear in a plethora of new physics models, including the 2HDM/MSSM. Therefore, we have developed a dedicated analysis to probe the cleanest of these channels: $pp\rightarrow \phi ^\pm \phi _0\rightarrow t\overline{b} (\overline{t} b), b\overline{b}$. We have shown that the whole range of masses $\sim 185$–340 GeV can be tested at the HL-LHC.

For this analysis, we have neglected new scalar couplings to the leptons. Under the sort of Minimal Flavour Violation [77] assumed after Eq. 1, explicitly reproduced in concrete models as shown in Eq. 13, the only relevant lepton would be the tau. Still, the decay of $\phi ^0$ into $\tau ^+\tau ^-$ would involve only a $\sim m_\tau ^2/(m_b^2 N_c)\sim 5\,\%$ of its width; our results being effectively unaffected. If couplings to the leptons are accidentally larger, the scalar could be better seen elsewhere; see Ref. [78].

We also stress that, had he assume flavour-violating couplings $c_{ij}^{u(d)}$, they would give rise to a plethora of signals in meson decays [79]. They could be also seen in top decays as in the singlet extension of the Higgs sector [80].

On another front, we have studied the reach of the future gravitational wave observatory LISA to the gravitational waves produced in the EWPT for certain region of the parameter space of the model. In particular, we have demonstrated that regions not yet excluded by Higgs to diphoton measurements will be testable. In this region, the EWPT proceeds mainly in one step, and therefore only one signal peak might be expected.

Finally, it is worth mentioning that in concrete models c and $\lambda _{H\Phi }$ related; normally $\lambda _{H\Phi }\propto c$. This is evident for example in CHMs, in which the former (latter) is induced by integrating out heavier resonances at tree level (one loop). To exhaust this point, we plot in Fig. 12 the current and future bounds on the plane $(m_{\Phi }, c)$ considering all collider searches and gravitational wave signatures for different simple assumptions on the relation $\lambda _{H\Phi } = \lambda _{H\Phi }(c)$.

Appendix A: Loop functions

In our case, $2m_\Phi > m_h$, and therefore

$$\begin{aligned} A_0(x)&= -x^2 \bigg [x^{-1} - f(x^{-1})\bigg ]~,\nonumber \\ A_{1/2}(x)&= 2 x^2 \bigg [x^{-1} + (x^{-1} - 1)f(x^{-1})\bigg ]~,\nonumber \\ A_1(x)&= -x^2 \bigg [ 2 x^{-2} + 3 x^{-1} + 3(2 x^{-1} -1)f(x^{-1}) \bigg ]~ \end{aligned}$$

(A1)

with

$$\begin{aligned} f(x) = \arcsin ^2{\sqrt{x}}~. \end{aligned}$$

(A2)