1 Introduction

Although direct evidence of New Physics (NP) has not been explored at the high-energy collider experiments, there are some interesting tensions in B-physics data. The two B factories Belle [1,2,3] and BaBar [4, 5] as well as LHCb [6,7,8] have reported several anomalies in the \(R_{\mathrm{D}^{(*)}}\) and \(R_{\mathrm{J}/\Psi }\) observables in various semileptonic B meson decays mediated via \(b\rightarrow c\) charged current interactions. These anomalies show a large tension between the experimental measurements and their corresponding Standard Model (SM) predictions, which indicates Lepton Flavor Universality (LFU) violation and may imply possible hints of NP. In the case of the ratios

$$\begin{aligned} R_{\mathrm{D}^{(*)}} = \frac{\mathrm{Br}\left( B\rightarrow D^{(*)} \tau {\bar{\nu }}_{\tau }\right) }{\mathrm{Br}\left( B\rightarrow D^{(*)}l {\bar{\nu }}_{l} \right) }, \end{aligned}$$
(1)

with \( l= e,\mu \), the latest experimental average values for them reported by the Heavy Flavor Average Group (HFAG) are [9]

$$\begin{aligned} R^\mathrm{Exp.}_\mathrm{D}= & {} 0.407\pm 0.039 \pm 0.024 ,\nonumber \\ R^\mathrm{Exp.}_{\mathrm{D}^{*}}= & {} 0.304\pm 0.013 \pm 0.007 , \end{aligned}$$
(2)

which deviate from the SM predictions [10, 11]

$$\begin{aligned} R^\mathrm{SM}_\mathrm{D}= & {} 0.297\pm 0.017,\nonumber \\ R^\mathrm{SM}_{\mathrm{D}^{*}}= & {} 0.252\pm 0.003, \end{aligned}$$
(3)

at \(1.9\sigma \) and \(3.3\sigma \) level, respectively. For the ratio \(R_{\mathrm{J}/\Psi }\), LHCb recently reported the new measurement [8]

$$\begin{aligned} R_{\mathrm{J}/\Psi }=\frac{\mathrm{Br}\left( B^{+}\rightarrow J/\Psi \tau ^{+}\nu _{\tau }\right) }{\mathrm{Br} \left( B^{+} \rightarrow J/\Psi \mu ^{+}\mu _{\tau } \right) }=0.71\pm 0.17\pm 0.18,\nonumber \\ \end{aligned}$$
(4)

which lies within \(2\sigma \) deviation range from the central values currently predicted in the SM, 0.25–0.28 [8, 12, 13], although the errors are too large at present to draw a definitive conclusion.

In order to investigate the possible NP effects implied by the \(R_{\mathrm{D}^{(*)}}\) anomalies, much theoretical work has been done looking for the reasonable explanation in various specific NP models, among which was the solution of adding a single vector leptoquark (LQ) transforming as (3, 3, 2 / 3) under the SM gauge group [14]. The scalar LQ (3, 1, −1/3) also can explain the \(R_{\mathrm{D}^{(*)}}\) anomalies [15]. But this scalar LQ can couple to a diquark state too and therefore it potentially leads to proton decay. One may impose the requirement that this coupling vanish, but such a scenario is not easily realized within Grand Unified Theories. Combining the constraints from the experimental measurements of \(R_{\mathrm{D}^{(*)}}\) anomalies and the contributions of a vector LQ to the \( B\rightarrow D^{(*)}\tau {\bar{\nu }}_{\tau } \) decays, the two best-fit solutions, denoted as \( R_\mathrm{A} \) and \( R_\mathrm{B}\), for the Wilson coefficients are given in Ref. [16]. The NP effects of \(R_{\mathrm{D}^{(*)}}\) anomalies on other semileptonic \( \Lambda _{b}\rightarrow \Lambda _{c}l {\bar{\nu }}_{l}\) and \( B\rightarrow J/\Psi l{\bar{\nu }}_{l} \) decays which are also induced by the \(b\rightarrow cl{\bar{\nu }}_{l}\) transition at quark level have been researched extensively (for instance, see Refs. [17,18,19,20,21,22,23] and [13, 24,25,26]).

Other particularly interesting decays to study are the semileptonic decays of the \(B_q^{*}\) mesons, the vector ground states of the \((b{\bar{q}})\) system [27]. In this case, the same NP effects should also contribute to the semileptonic decays \({\bar{B}}^{*}_\mathrm{d,s}\rightarrow P \tau {\bar{\nu }}_{\tau }(P=D,D_\mathrm{s},\pi ,K)\), which are induced by the \(b\rightarrow (u,c)\tau {\bar{\nu }}_{\tau }\) transition at quark level. Encouragingly, the \(e^{+}e^{-}\) colliders [28] revisited the high luminosities of themselves and the LHC has a high rate of \(b {\bar{b}}\) pairs, which already makes the sensitivities to branching fractions achieve the level of \( 10^{-10}\) [29]. In additional, the annual integrated luminosity of the Belle-II is expected to reach about \( 13 ab^{-1}\). This makes the study of \(B^{*}\) decays experimentally accessible for investigation.

Some research has been done about the \(B^{*}\) weak decays in the SM [30,31,32,33,34,35,36,37,38] and the NP scenarios for \({\bar{B}}^{*}\rightarrow P\tau {\bar{\nu }}_{\tau }\) decays in a model-independent framework [39]. Motivated by the fact that a vector LQ can well explain the \(R_{\mathrm{D}^{(*)}}\) anomalies on the \(b\rightarrow (u,c)\tau {\bar{\nu }}_{\tau }\) transitions, we further investigate the NP contributions of the vector LQ, which depend on both the couplings between the vector LQ and quarks (leptons) and the mass of the mediated vector LQ. The vectors \(B^{*}\) themselves are interesting since their purely leptonic decays are not chirally suppressed [32]. Using the best-fit values for the Wilson coefficients resulting by comparing with the \(R_{\mathrm{D}^{(*)}}\) anomalies of experimental measurements and the form factors computed in the Bauer–Stech–Wirbel (BSW) model, we investigate several \(q^2\) dependent observables, such as the differential branching fraction \( \mathrm{dBr}/\mathrm{d}q^2\), the ratio of the differential branching fractions \(R^{*}_\mathrm{P}(q^{2})\), the lepton forward–backward asymmetry \( A_\mathrm{FB}(q^{2})\) and the lepton polarization asymmetry \( P_{\tau }(q^2)\), and we test their sensitivity to NP effects.

Our paper is organized as follows. In Sect. 2, we briefly introduce the SM extended by a vector LQ \( U_{3}(3,3,2/3) \) and its contributions to the \({\bar{B}}^{*}\rightarrow P\tau {\bar{\nu }}_{\tau }\) decays. In Sect. 3, we give the helicity amplitudes and introduce several observables for the semileptonic \({\bar{B}}^{*}\rightarrow P\tau {\bar{\nu }}_{\tau }\) decays. In Sect. 4, the numerical results and discussions of the NP effects of the vector LQ to the several observables are reported in detail. Finally, we give the conclusions in Sect. 5.

2 The contribution of the vector LQ \( U_{3}(3,3,2/3) \)

In [14] the SM was extended by a vector \( \text {SU}(2)_{\text {L}}\) triplet LQ generating purely left-handed currents with quarks and leptons which can successfully resolve the \(R_{\mathrm{D}^{(*)}}\) anomalies. The vector triplet \( U^\mu _{3} \) having the charge arrangement (3, 3, 2 / 3) under the SM gauge group couples to a leptoquark current with (V–A) structure:

$$\begin{aligned} {\mathcal {L}}= g_{ij}{\bar{Q}}_{i}\gamma ^{\mu }\tau ^{A}U^{A}_{3\mu }L_{j}+\mathrm{h.c.}, \end{aligned}$$
(5)

where the \( \tau ^{A} (A=1,2,3)\) are the Pauli matrices in the \( \text {SU}(2)_\mathrm{L} \) space, and \( Q_{i} \) and \( L_{j} \) (\(i,j=1,2,3\) is for the generation) indicate the left-handed quarks and leptons \( \text {SU}(2)_\mathrm{L} \) doublets, respectively. For simplicity, \( g_{ij} \) is real and it is defined as the couplings of the \( Q=2/3 \) component of the triplet, \( U^{2/3}_{3\mu } \), to \( {\bar{d}}_{Li} \) and \( l_{Lj} \). Expanding other \( \mathrm{SU}(2)_\mathrm{L} \) components \( U^{5/3}_{3\mu } \) and \( U^{-1/3}_{3\mu } \), the Lagrangian in Eq.  (5) is written in mass basis changes to the eigencharge state:

$$\begin{aligned} {\mathcal {L}}_{U3}= & {} U^{2/3}_{3\mu }\big [\left( {\mathcal {V}} g{\mathcal {U}}\right) _{ij}{\bar{u}}_{i}\gamma ^{\mu } P_\mathrm{L}\nu _{j}-g_{ij}{\bar{d}}_{i}\gamma ^{\mu }P_\mathrm{L}l_{j}\big ] \nonumber \\&+ U^{5/3}_{3\mu }\left( \sqrt{2}{\mathcal {V}}g \right) _{ij}{\bar{u}}_{i}\gamma ^{\mu }P_\mathrm{L}l{j}\nonumber \\&+ U^{-1/3}_{3\mu }\left( \sqrt{2}g{\mathcal {U}} \right) _{ij}{\bar{d}}_{i}\gamma ^{\mu }P_\mathrm{L}\nu _{j}+\mathrm{h.c.}, \end{aligned}$$
(6)

where \( {\mathcal {V}}\) denotes the Cabibbo–Kobayashi–Maskawa (CKM) matrix and \( {\mathcal {U}} \) denotes the Pontecorvo–Maki–Nakagawa–Sakata (PMNS) matrix.

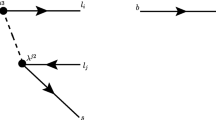
The semileptonic decay \( b\rightarrow c \tau {\bar{\nu }}_{\tau } \) proceeds via exchange of the vector multiplet \( U^\mu _{3} \) at tree level. Combining the SM contribution and the LQ correction, the effective weak Hamiltonian is written as [14]

$$\begin{aligned} H_\mathrm{eff}= \frac{G_\mathrm{F}V_\mathrm{cb}}{\sqrt{2}}\left( 1+V_\mathrm{L} \right) {\bar{c}}\gamma _{\mu }\left( 1-\gamma _{5} \right) b{\bar{\tau }}\gamma ^{\mu }\left( 1-\gamma _{5} \right) \nu _{\tau },\nonumber \\ \end{aligned}$$
(7)

where \(V_\mathrm{L}\) represents the effective NP couplings (Wilson coefficients). At the matching scale \( \mu =M_\mathrm{U} \), it is written as

$$\begin{aligned} V_\mathrm{L}=\dfrac{\sqrt{2}g^{*}_{b\tau }({\mathcal {V}}g)_{c\tau }}{2G_\mathrm{F}V_\mathrm{cb}M^{2}_\mathrm{U}}. \end{aligned}$$
(8)

Direct searches for LQs have pushed the model-independent lower limits on their masses up to a TeV scale. Taking into account the constraints on the vector LQ mass by the CMS collaboration [40, 41], in our numerical results we assume that the mass of the vector LQ \(M_\mathrm{U}\) is 1 TeV. The vector LQ \( U^\mu _{3} \) could explain the \(R_{\mathrm{D}^{(*)}}\) and \(R_{\mathrm{K}^{(*)}}\) simultaneously [14]. Fitting to the measurement results of \(R_{\mathrm{D}^{(*)}}\) and using the accompanying acceptable \( q^{2} \) spectra, two best-fit solutions, \( R_\mathrm{A} \) and \( R_\mathrm{B} \), result in this scenario [16]:

$$\begin{aligned} g^{*}_{b\tau }({\mathcal {V}}g)_{c\tau }= {\left\{ \begin{array}{ll} \quad 0.18 \pm 0.04 \quad \left( R_\mathrm{A}\right) ,\\ -2.88\pm 0.04 \quad \left( R_\mathrm{B}\right) , \end{array}\right. } \end{aligned}$$

where we take \( M_\mathrm{U}=1\,\, \mathrm{TeV} \) as a benchmark in the calculation. Corresponding to the best-fit solutions \( R_\mathrm{A} \) and \( R_\mathrm{B} \) cases, the numerical results of the effective coefficients \( 1+V_\mathrm{L}\) are given, respectively, as

$$\begin{aligned} 1+V_\mathrm{L}= {\left\{ \begin{array}{ll} \quad 1.133\pm 0.030 \quad (R_\mathrm{A})\\ -1.135\pm 0.030 \quad (R_\mathrm{B}), \end{array}\right. } \end{aligned}$$

one can notice that \( 1+V_\mathrm{L} \) have almost the same absolute values for the two solutions \( R_\mathrm{A} \) and \( R_\mathrm{B} \). This is the key to explaining the phenomenon that the NP contributions in \( R_\mathrm{A} \) and \( R_\mathrm{B} \) overlap in our figure.

3 Helicity amplitudes and observables for \({\bar{B}}^{*}\rightarrow Pl{\bar{\nu }}_{l}\) decays

The hadronic helicity amplitudes of the \({\bar{B}}^{*}\rightarrow Pl{\bar{\nu }}_{l}\) decays \(H_{\lambda _{\mathrm{B}^{*}}\lambda _{\mathrm{W}^{*}}}\) are defined as [38, 39]

$$\begin{aligned}&H_{\lambda _{\mathrm{B}^{*}}\lambda _{\mathrm{W}^{*}}}(q^2) \nonumber \\&\quad = {\bar{\epsilon }}^{*\mu }(\lambda _{\mathrm{W}^{*}}) \langle P(p_\mathrm{P})\vert {\bar{p}}\gamma _{\mu }(1-\gamma _{5})b\vert {\bar{B}}^{*}(p_{\mathrm{B}^{*}}, \lambda _{\mathrm{B}^{*}})\rangle , \end{aligned}$$
(9)

where \(\lambda _{\mathrm{B}^{*}}=0,\pm \) and \(\lambda _{\mathrm{W}^{*}}=t,0,\pm \) are the helicity states of \(B^{*}\) and virtual \(W^{*}\), respectively. \({\bar{\epsilon }}^{*\mu }(\lambda _{\mathrm{W}^{*}})\) are the four polarization vectors of virtual \(W^{*}\). This describes the decay of three helicity states of the \(B^{*}\) meson into a pesudo-scalar P meson and the four helicity states of virtual \(W^{*}\).

The matrix elements of the vector and the axial-vector currents for the \(B^{*}\rightarrow P\) transition can be written in terms of the form factors \(V(q^2)\) and \(A_{0,1,2}(q^2)\):

$$\begin{aligned}&\langle P(p_\mathrm{P})\vert {\bar{p}}\gamma _{\mu }b\vert {\bar{\mathrm{B}}}^{*}(\epsilon , p_{\mathrm{B}^{*}})\rangle \nonumber \\&\quad = -\dfrac{2iV(q^2)}{m_{\mathrm{B}^{*}}+m_\mathrm{P}}\varepsilon _{\mu \nu \rho \sigma }\epsilon ^{\nu }p^{\rho }_\mathrm{P} p^{\sigma }_{\mathrm{B}^{*}}, \end{aligned}$$
(10)
$$\begin{aligned}&\langle P(p_\mathrm{P})\vert {\bar{p}}\gamma _{\mu }\gamma _{5}b\vert {\bar{B}}^{*}(\epsilon , p_{\mathrm{B}^{*}})\rangle \nonumber \\&\quad = 2m_{\mathrm{B}^{*}}A_{0}(q^2)\dfrac{\epsilon \cdot q}{q^2}q_{\mu }+(m_{\mathrm{B}^{*}}\nonumber \\&\qquad +m_\mathrm{P})A_{1}(q^2) \left( \epsilon _{\mu }-\dfrac{\epsilon \cdot q}{q^2}q_{\mu }\right) \nonumber \\&\qquad +A_{2}(q^2)\dfrac{\epsilon \cdot q}{m_{\mathrm{B}^{*}}+m_\mathrm{P}}\left[ \phantom {\left. -\dfrac{m^2_{\mathrm{B}^{*}} -m^2_\mathrm{P}}{q^2}q_{\mu }\right] ,} (p_{\mathrm{B}^{*}}+p_\mathrm{P})_{\mu }\right. \nonumber \\&\qquad \left. -\dfrac{m^2_{\mathrm{B}^{*}} -m^2_\mathrm{P}}{q^2}q_{\mu }\right] , \end{aligned}$$
(11)

where we use the sign convention \(\epsilon _{0123}=-1\).

In the rest frame of the \(B^{*}\) meson with a daughter P meson moving in the positive z direction, the momenta of the particles \(B^{*}\), P and the virtual \(W^{*}\) could be written, respectively, as

$$\begin{aligned} p^{\mu }_{\mathrm{B}^{*}}= & {} \left( m_{\mathrm{B}^{*}},0,0,0 \right) ,\quad p^{\mu }_\mathrm{P}= \left( E_{P},0,0,\vert \vec {p}\vert \right) , \nonumber \\ q^{\mu }= & {} \left( q^{0},0,0,-\vert \vec {p}\vert \right) , \end{aligned}$$
(12)

where \(q^0= m_{\mathrm{B}^{*}}-E_\mathrm{P}=(m^2_{\mathrm{B}^{*}}-m^2_\mathrm{P}+q^2)/2m_{\mathrm{B}^{*}}\) and \(\vert \vec {p}\vert =\lambda ^{1/2}(m^2_{\mathrm{B}^{*}}, m^{2}_\mathrm{P},q^2)/2m_{\mathrm{B}^{*}}\) with function \(\lambda (a,b,c)=a^2+b^2+c^2-2(ab+bc+ca)\) and \(q^2\) being the momentum transfer squared bounded at \(m^{2}_{l}\le q^2\le (m_{\mathrm{B}^{*}}-m_\mathrm{P})^2\). For the four polarization vectors of the virtual \(W^{*}, {\bar{\epsilon }}^{\mu }(\lambda _{\mathrm{W}^{*}}=t,0,\pm )\), one can conveniently choose [42, 43]

$$\begin{aligned} {\bar{\epsilon }}^{\mu }(t)= & {} \dfrac{1}{\sqrt{q^2}} \left( q_{0},0,0,-\vert \vec {p}\vert \right) ,\nonumber \\ {\bar{\epsilon }}^{\mu }(0)= & {} \dfrac{1}{\sqrt{q^2}}\left( \vert \vec {p}\vert ,0,0,-q_{0}\right) ,\nonumber \\ {\bar{\epsilon }}^{\mu }(\pm )= & {} \dfrac{1}{\sqrt{2}} \left( 0,\pm 1,-i,0 \right) , \end{aligned}$$
(13)

and the polarization vectors of initial \(B^{*}\) meson could be written as

$$\begin{aligned} \epsilon ^{\mu }(0)= (0,0,0,1),\quad \epsilon ^{\mu }(\pm )= \dfrac{1}{\sqrt{2}}(0,\mp 1-i,0). \end{aligned}$$
(14)

Contracting the \(B^{*}\) and \(W^{*}\) polarization vectors given by the above equations and the hadronic matrix elements given by Eqs. (10) and (11), four non-vanishing helicity amplitudes are obtained:

$$\begin{aligned}&H_{0t}(q^2)=\dfrac{2m_{\mathrm{B}^{*}}\vert \vec {p}\vert }{\sqrt{q^2}}A_{0}(q^2), \end{aligned}$$
(15)
$$\begin{aligned}&H_{00}(q^2)= \dfrac{1}{2m_{\mathrm{B}^{*}}\sqrt{q^2}}[(m_{\mathrm{B}^{*}}{+}m_\mathrm{P})(m^2_{\mathrm{B}^{*}}{-}m^2_\mathrm{P}+q^2) A_{1}(q^2)\nonumber \\&\qquad \qquad \quad \,\,+\frac{4m^2_{\mathrm{B}^{*}}\vert \vec {p}\vert ^2}{m_{\mathrm{B}^{*}}+m_\mathrm{P}}A_{2}(q^2)], \end{aligned}$$
(16)
$$\begin{aligned}&H_{\pm \mp }(q^2)= -(m_{\mathrm{B}^{*}}+m_\mathrm{P}) A_{1}(q^2)\mp \frac{2m_{\mathrm{B}^{*}}\vert \vec {p}\vert }{m_{\mathrm{B}^{*}}+m_\mathrm{P}}V(q^2).\nonumber \\ \end{aligned}$$
(17)

The leptonic helicity amplitudes are defined as:

$$\begin{aligned} h_{\lambda _{l},\lambda _{{\bar{\nu }}_{l}}}= \frac{1}{2}{\bar{u}}_{l}(\lambda _{l})\gamma ^{\mu } (1-\gamma _{5})v_{{\bar{\nu }}_{l}}{\bar{\epsilon }}_{\mu }(\lambda _{\mathrm{W}^{*}}), \end{aligned}$$
(18)

where \(\lambda _{\mathrm{W}^{*}}=\lambda _{l}-\lambda _{{\bar{\nu }}_{l}}\). In the l–\({\bar{\nu }}_{l}\) center-of-mass frame, the four-momenta of lepton and antineutrino pair are given as

$$\begin{aligned}&p^{\mu }_{l}=(E_{l},\vert \vec {p}_{l}\vert \sin \theta ,0,\vert \vec {p}_{l}\vert \cos \theta ),\nonumber \\&\quad p^{\mu }_{\nu _{l}}=(\vert \vec {p}_{l}\vert ,-\vert \vec {p}_{l}\vert \sin \theta ,0,-\vert \vec {p}_{l} \vert \cos \theta ), \end{aligned}$$
(19)

where \(E_{l}=(q^2+m^{2}_{l})/2\sqrt{q^2}\), \(\vert \vec {p}_{l}\vert =(q^2-m^{2}_{l})/2\sqrt{q^2}\), and \(\theta \) is the angle between the P and l three-momenta. In this frame, the polarization vector \({\bar{\epsilon }}^{\mu }\) takes the form

$$\begin{aligned}&{\bar{\epsilon }}^{\mu }(t)=(1,0,0,0), \quad {\bar{\epsilon }}^{\mu }(0)=(0,0,0,1), \nonumber \\&{\bar{\epsilon }}^{\mu }(\pm ) =\frac{1}{\sqrt{2}}(0,\mp 1,-i,0). \end{aligned}$$
(20)

Taking the exact forms of the spinors and polarization vectors, two non-vanishing contributions are obtained,

$$\begin{aligned}&\vert h_{-\frac{1}{2},\frac{1}{2}}\vert ^2 = 8(q^2-m^{2}_{l}), \end{aligned}$$
(21)
$$\begin{aligned}&\vert h_{\frac{1}{2},\frac{1}{2}}\vert ^2 = 8\dfrac{m^{2}_{l}}{2q^2}(q^2-m^{2}_{l}), \end{aligned}$$
(22)

where the cases \(\lambda _{l}=-1/2\) and 1 / 2 are referred to as the non-flip and flip transitions, respectively. The double differential decay rates with a given leptonic helicity state \((\lambda _{l}=\pm \frac{1}{2})\) can be written as

$$\begin{aligned} \dfrac{\mathrm{d}^{2}\Gamma [\lambda _{l}=-\frac{1}{2}]}{\mathrm{d}q^2\mathrm{d}\cos \theta }= & {} \dfrac{G^{2}_\mathrm{F}\vert V_\mathrm{pb}\vert ^2\vert \vec {p}\vert }{ 256\pi ^3 m^{2}_{\mathrm{B}^{*}}}\frac{1}{3}q^2\left( 1-\dfrac{m^{2}_{l}}{q^2}\right) ^2 \nonumber \\&\times \left\{ \vert 1+V_\mathrm{L}\vert ^2[(1-\cos \theta )^2H^{2}_{-+}\right. \nonumber \\&\left. +(1+\cos \theta )^2H^{2}_{+-} +2\sin ^2\theta H^{2}_{00}]\right\} , \end{aligned}$$
(23)
$$\begin{aligned} \dfrac{\mathrm{d}^{2}\Gamma [\lambda _{l}=\frac{1}{2}]}{\mathrm{d}q^2\mathrm{d}\cos \theta }= & {} \dfrac{G^{2}_\mathrm{F}\vert V_\mathrm{pb}\vert ^2\vert \vec {p}\vert }{ 256\pi ^3 m^{2}_{\mathrm{B}^{*}}}\frac{1}{3}q^2\left( 1-\dfrac{m^{2}_{l}}{q^2}\right) ^2 \dfrac{m^{2}_{l}}{q^2}\nonumber \\&\times \left\{ (\vert 1+V_\mathrm{L}\vert ^2)[\sin ^2\theta (H^{2}_{+-}+H^{2}_{-+})\right. \nonumber \\&\left. +2( H_{0t}-\cos \theta H_{00})^2]\right\} . \end{aligned}$$
(24)

The differential decay rate \(\mathrm{d}\Gamma /\mathrm{d}q^2\) and \(\mathrm{d}\mathrm{Br}/\mathrm{d}q^2\), \(R^{*}_\mathrm{P}(q^2)\), \(A_\mathrm{FB}(q^2)\) and \(P_{\tau }(q^2)\) can be written as

$$\begin{aligned}&\mathrm{d}\mathrm{Br}/\mathrm{d}q^2= \dfrac{\mathrm{d}\Gamma / \mathrm{d}q^2}{\Gamma _\mathrm{tot}}, \end{aligned}$$
(25)
$$\begin{aligned}&R^{*}_\mathrm{P}(q^2)\equiv \dfrac{\mathrm{d}\Gamma ({\bar{B}}^{*}\rightarrow P{\tau {\bar{\nu }}}_{\tau })/\mathrm{d}q^2}{\mathrm{d}\Gamma ({\bar{B}}^{*}\rightarrow Pl{\bar{\nu }}_{l})/\mathrm{d}q^2}, \end{aligned}$$
(26)
$$\begin{aligned}&\mathrm{d}\Gamma /\mathrm{d}q^2=\dfrac{G^{2}_\mathrm{F}\vert V_\mathrm{pb}\vert ^2\vert \vec {p}\vert }{ 96\pi ^3 m^{2}_{\mathrm{B}^{*}}}\frac{1}{3}q^2\left( 1-\dfrac{m^{2}_{l}}{q^2}\right) ^2 \nonumber \\&\qquad \times \left\{ (\vert 1+V_\mathrm{L}\vert ^2)[(H^{2}_{+-}+H^{2}_{-+}+H^2_{00}) \left( 1+\dfrac{m^{2}_{l}}{q^2}\right) \right. \nonumber \\&\qquad \left. +\dfrac{3m^{2}_{l}}{2q^2}H^2_{0t}]\right\} ,A_\mathrm{FB}(q^2)\nonumber \\&\quad =\dfrac{\displaystyle \int ^{0}_{-1}\mathrm{d}\cos \theta (\mathrm{d}^2\Gamma /\mathrm{d}q^2 \mathrm{d}\cos \theta )- \int ^{1}_{0}\mathrm{d}\cos \theta (\mathrm{d}^2\Gamma /\mathrm{d}q^2 \mathrm{d}\cos \theta )}{\mathrm{d}\Gamma / \mathrm{d}q^2},\nonumber \\ \end{aligned}$$
(27)
$$\begin{aligned}&P_{\tau }(q^2)= \dfrac{\mathrm{d}\Gamma [\lambda _{l}=1/2]/\mathrm{d}q^2-\mathrm{d}\Gamma [\lambda _{l}=-1/2]/\mathrm{d}q^2}{ \mathrm{d}\Gamma [\lambda _{l}=1/2]/\mathrm{d}q^2+\mathrm{d}\Gamma [\lambda _{l}=-1/2]/\mathrm{d}q^2}.\nonumber \\ \end{aligned}$$
(28)

4 Results and discussions

Firstly, we have to clarify the values of the input parameters relative to the numerical calculations in Table 1 before we present our numerical results. Among these the Fermi coupling constant \(G_\mathrm{F}\) and the masses of the mesons and leptons are taken from PDG [44], while we use the CKM matrix elements from Ref. [45].

When we estimate the branching fractions of the \({\bar{B}}^{*}\rightarrow P\tau {\bar{\nu }}_{\tau }\) decays, the total decay widths (or lifetimes) of \({\bar{B}}^{*}\) are indispensable but have not been measured by experiments until now. According to the fact that the electromagnetic process \(B^{*}\rightarrow B\gamma \) dominates the decays of the \(B^{*}\) meson, we take the approximation \(\Gamma _\mathrm{tot}(B^{*}) \simeq \Gamma (B^{*}\rightarrow B\gamma )\) and adopt the most recent results [46, 47],

$$\begin{aligned} \Gamma _\mathrm{tot}(B^{*+})\simeq & {} \Gamma (B^{*+}\rightarrow B^{+}\gamma )=(468^{+73}_{-75}) ~\mathrm{eV}, \end{aligned}$$
(29)
$$\begin{aligned} \Gamma _\mathrm{tot}(B^{*0})\simeq & {} \Gamma (B^{*0}\rightarrow B^{0}\gamma )=(148\pm 20)~\mathrm{eV}, \end{aligned}$$
(30)
$$\begin{aligned} \Gamma _\mathrm{tot}(B_{s}^{*0})\simeq & {} \Gamma (B_\mathrm{s}^{*0}\rightarrow B_\mathrm{s}^{0}\gamma )=(68\pm 17) ~\mathrm{eV}. \end{aligned}$$
(31)

The next important input parameters are the form factors. They are calculated in Ref. [39] in the BSW model [48, 49] and are shown in Table 2. In our numerical results, \(10\%\) uncertainties for the form factors and the \(1\sigma \) level range of the central values of the CKM matrix elements \(V_\mathrm{pb}(p=u,c)\), the total decay widths of \(B^{*}\), and the NP parameters \(V_\mathrm{L}\) are considered. We employ the model of [48, 49] where monopole-type form factors have been assumed for the \(q^2\) dependence,

Table 1 Input parameters of the SM used in our numerical analysis [44, 45]
Full size table
Table 2 Input parameters of the form factors used in our numerical analysis [39]
Full size table
$$\begin{aligned} A_{0}(q^2)\simeq & {} \dfrac{A_{0}(0)}{1-q^2/m^2_{\mathrm{B}_\mathrm{q}(0^{-})}}, \quad A_{1}(q^2) \simeq \dfrac{A_{1}(0)}{1-q^2/m^2_{\mathrm{B}_\mathrm{q}(1^{+})}}, \nonumber \\ A_{2}(q^2)\simeq & {} \dfrac{A_{2}(0)}{1-q^2/m^2_{\mathrm{B}_\mathrm{q}(1^{+})}}, \quad V(q^2) \simeq \dfrac{V(0)}{1-q^2/m^2_{\mathrm{B}_\mathrm{q}(1^{-})}},\nonumber \\ \end{aligned}$$
(32)

where \(m_{\mathrm{B}_\mathrm{q}}(J^{P})\) are the pole masses of the states of \(B_\mathrm{q}\) with quantum numbers of \(J^{P}\) (J and P are the quantum numbers of total angular momenta and parity, respectively). The values of these masses can easily be found in Table 1 of Ref. [48].

Fig. 1
figure 1

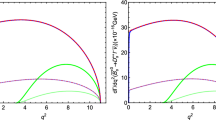
The \(\mathrm{d}\mathrm{Br}/\mathrm{d}q^2\) and \(R^{*}_\mathrm{P}(q^2)\) observables of the transitions \({\bar{B}}^{*0}\rightarrow D^+\tau ^{-}{\bar{\nu }}_{\tau }\) (a, e), \({\bar{B}}^{*0}_{s} \rightarrow D_{s}^+\tau ^{-}{\bar{\nu }}_{\tau }\) (b, f), \({\bar{B}}^{*0}\rightarrow \pi ^+\tau ^{-}{\bar{\nu }}_{\tau }\) (c, g) and \({\bar{B}}^{*0}_\mathrm{s}\rightarrow K^+\tau ^{-}{\bar{\nu }}_{\tau }\) (d, h) in the SM and vector LQ scenarios. The band widths represent theoretical uncertainty of \(B^{*}\) decay widths, form factors, \(V_\mathrm{pb}(p=u,c)\) and NP parameters

Full size image
Fig. 2
figure 2

The \( A_\mathrm{FB}(q^{2})\) and \(P_{\tau }(q^2)\) observables of the transitions \({\bar{B}}^{*0}\rightarrow D^+\tau ^{-}{\bar{\nu }}_{\tau }\) (a, e), \({\bar{B}}^{*0}_\mathrm{s} \rightarrow D_\mathrm{s}^+\tau ^{-}{\bar{\nu }}_{\tau }\) (b, f), \({\bar{B}}^{*0}\rightarrow \pi ^+\tau ^{-}{\bar{\nu }}_{\tau }\) (c, g) and \({\bar{B}}^{*0}_\mathrm{s}\rightarrow K^+\tau ^{-}{\bar{\nu }}_{\tau }\) (d, h) in the SM

Full size image

After introducing theoretical formulas and the input parameters, we present our numerical results and discuss NP effects of vector LQ on the \(\mathrm{dBr}/\mathrm{d}q^2\), \(R^{*}_\mathrm{P}(q^2)\), \(A_\mathrm{FB}(q^2)\) and \(P_{\tau }(q^2)\) combining with the limits of the \(R_{ \mathrm{D}^{(*)}}\) anomalies experimental measurements to the parameter space of the coupling for vector-type interactions.

The numerical results of \(\mathrm{dBr}/\mathrm{d}q^2\) and \(R^{*}_\mathrm{P}(q^2)\) of the \({\bar{B}}^{*0}\rightarrow D^+\tau ^{-}{\bar{\nu }}_{\tau }\), \({\bar{B}}_\mathrm{s}^{*0}\rightarrow D_\mathrm{s}^+\tau ^{-} {\bar{\nu }}_{\tau }\), \({\bar{B}}^{*0}\rightarrow \pi ^+\tau ^{-}{\bar{\nu }}_{\tau }\) and the \({\bar{B}}^{*0}_\mathrm{s}\rightarrow K^+\tau ^{-}{\bar{\nu }}_{\tau }\) transitions in the SM and vector LQ scenarios are displayed in Fig. 1a–h, respectively. The gray bands represent the SM predictions for \(\mathrm{dBr}/\mathrm{d}q^2\) and \(R^{*}_\mathrm{P}(q^2)\), whereas the green and pink bands represent the contributions of the vector LQ in \( R_\mathrm{A} \) and \( R_\mathrm{B} \) cases, respectively. From Fig. 1, we can find that the NP contributions to \(\mathrm{dBr}/\mathrm{d}q^2\) of these decays are significant and have large deviations from the relative SM predictions. The values of \(\mathrm{dBr}/\mathrm{d}q^2\) are all enhanced by about \( 28\% \) both in the \( R_\mathrm{A} \) and the \( R_\mathrm{B}\) cases for all the reasonable \(q^2\) space compared with the SM predictions only a left-handed vector-type interaction having been included. We also observe the feature that the green and pink bands overlap completely, which can be explained by the same absolute value of the coefficient \(1+V_\mathrm{L}\) in \(R_\mathrm{A}\) and \(R_\mathrm{B}\) cases in Sect. 2. Similarly, the NP effects on \(R^{*}_\mathrm{P}(q^2)\) are also prominent and the green and the pink bands overlap for the same reason. Different from \(\mathrm{dBr}/\mathrm{d}q^2\), the numerical values of \(R^{*}_\mathrm{P}(q^2)\) are increased with ascending values of \(q^2\). We think that these two observables could be detected at the high-energy collider experiments in the future. Especially \(R^{*}_\mathrm{P}(q^2)\) will sustain the NP hints of \(R_{\mathrm{D}^{(*)}}\) anomalies once it could be detected and further identify the possible existence of NP.

Since the effective coefficient \(1+V_\mathrm{L}\) identically vanishes from the ratios in \(A_\mathrm{FB}(q^2)\) and \(P_{\tau }(q^2)\), the LQ contribution is indistinguishable from the SM one, making these observables nonsensitive to NP. In Fig. 2, we only present the SM predictions for \(A_\mathrm{FB}(q^2)\) and \(P_{\tau }(q^2)\).

5 Summary and conclusion

The anomalies in the \( R_{\mathrm{D}^{(*)}} \) and \( R_{\mathrm{J}/\psi } \) observables in the B-decays have generally attracted physicists’ attention and much work has been done to explain these deviations. One effective way is adding a single vector LQ \( U_{3}(3,3,2/3)\) to the SM which can couple to quarks and leptons. In order to further explore the NP effects of the vector LQ, we study its contributions to the transitions \({\bar{B}}^{*}_{\mathrm{d,s}}\rightarrow P \tau {\bar{\nu }}_{\tau }(P=D,D_\mathrm{s},\pi ,K)\) which are described by \(b\rightarrow (u,c)\tau {\bar{\nu }}_{\tau }\) at tree level. Studying these modes can be complementary to the \(B\rightarrow D^{(*)}\tau \nu _{\tau }\) decays. Furthermore, accurate measurements of the \({\bar{B}}^{*}\) semileptonic decays’ branching fraction and a more precise calculation of the form factors for the hadron matrix elements are crucial to determine the CKM matrix elements.

Using the best-fit solutions for the Wilson coefficients resulting from \( R_{\mathrm{D}^{(*)}} \) anomalies appearing in experimental measurements and the form factors estimated in the BSW model, we investigate the NP effects of the vector LQ in several observables of the decays \({\bar{B}}^ {*}\rightarrow P \tau {\bar{\nu }}_{\tau }\) such as the differential branching fraction \(\mathrm{dBr}/\mathrm{d}q^2\), the ratio of the differential branching fractions \(R^{*}_\mathrm{P}(q^2)\), the lepton forward–backward asymmetry \( A_\mathrm{FB}(q^{2})\) and the lepton polarization asymmetry \(P_{\tau }(q^2)\). From the numerical results, we can conclude that the NP contributions of the vector LQ to \(\mathrm{dBr}/\mathrm{d}q^2\) and \(R^{*}_\mathrm{P}(q^2)\) are significant and have large deviations from the corresponding SM predictions, while the \( A_\mathrm{FB}(q^{2})\) and \(P_{\tau }(q^2)\) are not sensitive to the vector LQ. Although there is no direct evidence for the existence of NP, both theoretical and experimental researches of \({\bar{B}}^{*}\rightarrow P \tau {\bar{\nu }}_{\tau }\) decays are important for the sake of understanding \(R_{\mathrm{D}^{(*)}}\) and \( R_{\mathrm{J}/\Psi } \) anomalies. Once these two observables are detected at the high-energy collider in the future, we can consider them to be a continuity of \(R_{\mathrm{D}^{(*)}}\) anomalies, which may further identify the existence of NP. All the distinct features of these observables will be helpful to distinguish the different NP models. In additional, more precise measurement of the branching fraction of decays \({\bar{B}}^ {*}\rightarrow P \tau {\bar{\nu }}_{\tau }\) and more precise calculations of the form factors for \({\bar{B}}^{*}\rightarrow P \) one may determine the CKM matrix elements \( \vert V_\mathrm{cb}\vert \) and \( \vert V_\mathrm{ub}\vert \) more accurately.