Investigation on the New Physics effects of the vector leptoquark on semileptonic $\bar{B}^*\rightarrow V \tau ^-\bar{\nu _{\tau }}$ decays

Abstract

In recent years, the experimental results about the ratio of the branching ratios $R_{D^{(*)}}$ and $R_{K^{(*)}}$, which are in the semileptonic $b\rightarrow c l \bar{\nu }_{l}$ and $b\rightarrow s l^+l^-$ decays, have been observed to deviate from the Standard Model prediction by $1.4\sigma$, $2.5\sigma$, $2.4\sigma$ and $2.2\sigma$ respectively. Motivated by these anomalies and by the abundant $B^*$ data samples, we investigate possible New Physics effects of the vector leptoquark in the semileptonic decay $\bar{B}^*_{u,d,s,c} \rightarrow V \tau ^-\bar{\nu }_{\tau }$ ($V=D^*_{u,d,s},J/\psi$). which is induced by $b\rightarrow c \tau ^-\bar{\nu }_{\tau }$ at the quark level. Using the best fit solutions for the new operator Wilson coefficients and the relevant form factors which are obtained in the light-front quark model, we find that (i) the contributions of the vector leptoquark to $d{\varGamma }^{(L)}/dq^2(\bar{B}^*_{u,d,s,c} \rightarrow V \tau ^-\bar{\nu }_{\tau })$ and $R^{*(L)}_{V}(q^2)$ to be significant; (ii) the two best fit solutions in the vector leptoquark are indistinguishable from each other and give similar amounts of enhancements to these two observables; (iii) both two cases of the vector leptoquark give nearly same results as those of the Standard Model for $A_{FB}^{\tau }(q^2)$ , $P_{\tau }(q^2)$ and $F_{L}^{*V}(q^2)$. We hope that the numerical results in this work will be tested in the future high energy experiments.

1 Introduction

The imprints of New Physics (NP) beyond the standard model (SM) can be tested via both the direct approach and the indirect approach. Though no direct evidences about NP beyond the SM have been found in the high-energy collider experiments, there are some interesting indirect hints of NP in the semileptonic B meson decays via both the neutral current process $b \rightarrow s l^+ l^-$ and charged current process $b \rightarrow c l \bar{\nu }_{l}$. Over the past few decades, many intriguing hints of NP have been observed in the form of lepton flavour universality (LFU) observables for semileptonic B decays and some anomalies in these decay processes have also been observed, which indicate $(1-3\sigma )$ deviations from the SM predictions. The SM predictions and the corresponding experimental values of various lepton nonuniversality (LNU) observables with their deviations are listed in the Table 1.

Table 1 List of the measured LNU observables

Unlike the branching fractions which are largely affected by the uncertainties that originate from the Cabibbo Kobayashi Maskawa (CKM) matrix element and the hadronic from factors, all the observables which are presented in the Table 1 are ratio of the branching fraction and the reliance of these observables on the CKM matrix element exactly cancels each other out.

The uncertainties due to the form factors can also be largely reduced in these ratios, resulting the prediction with high accuracy. Hence, the clear disagreements between the experimental measurements and the SM predictions strongly indicate possible NP. Therefore, the lepton flavor universality violation (LFUV) will be considered to be the most powerful tools to probe NP beyond the SM. The observed $R_{D^{(*)}}$ and $R_{K^{(*)}}$ anomalies, if confirmed by future more precise data, will be clear signs for NP beyond the SM, and have already attracted lots of many theoretical studies [24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49]. For a recent review, the readers are referred to Refs. [50,51,52] and relevant references. In this paper we will pay our attention to the possible NP solutions with a single vector leptoquark (LQ) scenario [53]. As discussed in the Ref. [53], the $R_{K^{(*)}}$, $R_{D^{(*)}}$ and the angular observable $P_5'$ of $\bar{B}\rightarrow \bar{K}^{*}\mu ^+\mu ^-$ decay process have been addressed by one vector LQ transforming as $({3}, {3},\frac{2}{3})$ under the SM gauge group. At the same time those anomalies can also be explained by adding to the SM one TeV-scale scalar LQ transforming as $(3,1,-\frac{1}{3})$ under the SM gauge group  [54]. After considering the constraints from both the experimental results of $R_{D^{(*)}}$ anomalies and the contributions of a vector LQ to the $B \rightarrow D^{(*)}\tau \bar{\nu }_{\tau }$ process, two best-fit solutions which are denoted as $R_A$ and $R_B$ are found for the operator coefficients and given in the Ref. [55]. Furthermore, many theoretical works have been done based about the NP effects of $R_{D^{(*)}}$ anomalies on the $\Lambda _b \rightarrow \Lambda _c \tau \bar{\nu }_{\tau }$ [30, 56, 58,59,60,61,62], $B_s\rightarrow D_s^{(*)}(K^{(*)})\tau \bar{\nu }_{\tau }$ [27, 28, 63, 64], $\Xi _b\rightarrow \Xi _c \tau \bar{\nu }_{\tau }$ [32, 33, 57] $B_c \rightarrow \eta _c(J/\psi ) \tau \bar{\nu }_{\tau }$ [65, 66], $\bar{B}^* \rightarrow P \tau \bar{\nu }_{\tau }$ [67,68,69].

In addition to B meson, the $B^*$ meson with the vector ground state of $b\bar{q}$ system and with quantum number of $n^{2s+1}L_J=1^3S_1$ and $J^P=1^{-1}$ [70,71,72,73] can decay $\bar{B}^*\rightarrow V l \bar{\nu }_l(V=D^*_{u,d,s},J/\Psi )$ which are induced by the $b\rightarrow c l \bar{\nu }_l$ transitions at quark level. Therefore, in this case, the corresponding NP effects might also contribute to the semileptonic $B^*$ decays as well. In addition, because the $B^*$ meson is an unstable particle and $m_{B_q^*}-m_{B_q}\le \mathrm 50MeV<m_{\pi }$, so it cannot decay via strong interaction [74]. The $B^*$ meson decay is mainly dominated by the radiative process $\bar{B}^* \rightarrow \bar{B}\gamma$ and the $B^*$ semileptonic decay modes $\bar{B}^*\rightarrow V l \bar{\nu }_l$ which are considered in this work are very rare. Though there is no corresponding experimental information about $B^*$ due to the limited center of mass energy, we hope that the running LHC and upcoming SuperKEKB/Belle-II experiment will make it possible for the $B^*$ weak decays in the future.

Recently, some interesting theoretical research for the $B^*$ weak decays have been done within the SM and the NP scenarios [65, 75,76,77,78,79,80]. Motivated by these facts that a vector LQ can explain the anomalies in the $b\rightarrow c (u)l \bar{\nu }_l$ and $b \rightarrow s l^+l^-$ processes , in this work we will pay our attention to the contributions of the vector LQ for $\bar{B}^*\rightarrow V l \bar{\nu }_l (V=D^*_{u,d,s},J/\Psi )$. Using the best fit solutions for the Wilson coefficients of the new operator by the current data of meson decays and the relevant form factors resulted in the light-front quark model, we will investigate the contribution of vector LQ to some $q^2$ dependent observables, such as the differential branching fraction $dBr^{(L)}/dq^2$, the ratio of the branching fraction $R^{*(L)}_{V}(q^2)$, the lepton forward-backward asymmetry $A_{FB}^l(q^2)$, the longitudinal polarization fraction of the daughter meson $F_L^{*V}(q^2)$ and the lepton spin asymmetry $P_{\tau }(q^2)$.

The layout of the paper is as follows. In Sect. 2, we briefly introduce the SM extended by adding a vector LQ $U_3(3,3,2/3)$ that generate left handed current with quarks and leptons and the contribution to the $\bar{B}^*\rightarrow V \tau \bar{\nu }_{\tau }$ processes. Theoretical framework for $\bar{B}^*\rightarrow V l \bar{\nu }_l$ are presented in Sect. 3. The helicity amplitudes and all definitions of physical observables for the semileptonic $\bar{B}^*\rightarrow V \tau \bar{\nu }_{\tau }$ are also shown in the section. Section 4 is devoted to the numerical results and discussions about the NP effects of the vector LQ to some observable. Finally, we will present a brief summary of our results and main conclusions in Sect. 5.

2 Review of the vector Leptoquark model

We start with the most relevant effective Hamiltonian for the quark level transition $b\rightarrow c \tau \bar{\nu }_{\tau }$ containing both the SM and the possible NP operators [81,82,83,84]

$$\begin{aligned} \mathscr {H}_{eff}= & {} \frac{4G_F}{\sqrt{2}} V_{cb} \Bigg [ \left( 1 + {V_L} \right) \mathscr {O}_{V_L} + {V_R} \mathscr {O}_{V_R} + {S_L} \mathscr {O}_{S_L}\\&+ {S_R} \mathscr {O}_{S_R} + {T} \mathscr {O}_{T} \Bigg ]+ \mathrm{h.c.}, \end{aligned}$$

where $G_F$ is the Fermi coupling constant, $V_{cb}$ is the CKM matrix element. We note that the NP coupling parameters ${V_L}$, ${V_R}$, ${S_L}$, ${S_R}$ and T characterizing the NP contributions coming from the new vector, scalar and tensor NP operators are associated with left handed neutrino and these NP coupling parameters are all zero in the SM. In our paper, we mainly focus on a study of the vector type interaction with the NP coupling parameter $V_L$. The Fermionic operators $\mathscr {O}_{V_L}$, $\mathscr {O}_{V_R}$, $\mathscr {O}_{S_L}$, $\mathscr {O}_{S_R}$ and $\mathscr {O}_{T}$ are defined as,

$$\begin{aligned} \mathscr {O}_{V_L}&= \left( \bar{c} \gamma ^{\mu } b_L \right) \left( \bar{\tau }_L \gamma _{\mu } \nu _{\tau \,L} \right) ,\quad \mathscr {O}_{V_R} = \left( \bar{c} \gamma _{\mu } b_R \right) \left( \bar{\tau }_L \gamma _{\mu } \nu _{l\,L} \right) , \\ \mathscr {O}_{S_L}&= \left( \bar{c} b_L \right) \left( \bar{\tau }_R \nu _{\tau \,L} \right) ,\quad \mathscr {O}_{S_R} = \left( \bar{c} b_R \right) \left( \bar{\tau }_R \nu _{\tau \,L} \right) , \\ \mathscr {O}_{T}&= \left( \bar{c} \sigma ^{\mu \nu } b_L \right) \left( \bar{\tau }_R \sigma _{\mu \nu } \nu _{\tau \,L} \right) . \end{aligned}$$

Here, $\sigma _{\mu \nu }=i[\gamma _{\mu },\gamma _{\nu }]/2$. $(b,\tau ,\nu _{\tau })_{L,R}=P_{L,R}(b,\tau ,\nu _{\tau })$ are the chiral quark (lepton) field with $P_{L,R}=(1\mp \gamma _5)/2$ as the projection operators.

One simple way to obtain a new physics contribution to $b \rightarrow c l \nu _l$ is to use a LQ which couples to the second- and third-generation fermions.

In the Ref. [53], the SM was extended by a vector $SU(2)_L$ triplet LQ generating purely left handed currents with quarks and leptons. The vector triplet $U_3$, which transforms under the SM gauge group $(\mathbf{3},\mathbf{3},\frac{2}{3})$, couples to a leptoquark current with $V-A$ structure and the coupling can be written as

$$\begin{aligned} \mathscr {L}_U=g_{ij}\bar{O}_i \gamma _{\mu }\tau ^{A}U_{3\mu }^{A}L_j+\mathrm{H.c.}, \end{aligned}$$

(1)

where $i,j=1,2,3$ are generation indices; the $Q_i(L_i)$ is the left handed quark and lepton doublets, respectively. The $\tau ^A(A=1,2,3)$ are the Pauli matrices in the $SU(2)_L$ space. For simplicity, we take the constraint that couplings $g_{ij}$ are real and it is defined as the couplings of the $Q=2/3$ component of the triplet $U_{3\mu }^{2/3}$ to $\bar{d}_{Li}$ and $l_{Lj}$. Expending other $SU(2)_L$ components $U_{3\mu }^{5/3}$ and $U^{-1/3}_{3\mu }$ and with the CKM matrix V from the left or Pontecorvo Maki Nakagawa Sakata (PMNS) matrix $\mathscr {U}$ from the right [85, 86], the Lagrangian in the Eq. (1) can be written as

$$\begin{aligned} \mathscr {L}_{U_3}&= U_{3\mu }^{(2/3)}\big [( Vg\mathscr {U})_{ij}\bar{u}_i\gamma ^\mu P_L\nu _j-g_{ij}\bar{d}_i\gamma ^\mu P_L\ell _j\big ]\,\nonumber \\&\quad +U_{3\mu }^{(5/3)}(\sqrt{2}Vg)_{ij}\bar{u}_i\gamma ^\mu P_L\ell _j\,\nonumber \\&\quad +U_{3\mu }^{(-1/3)}(\sqrt{2}g\mathscr {U})_{ij}\bar{d}_i\gamma ^\mu P_L\nu _j+\mathrm{H.c.}, \end{aligned}$$

(2)

here we will assume that the neutrinos is massless and the PMNS matrix can be rotated away via field redefinitions.

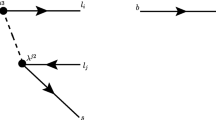
The semileptonic decay $b\rightarrow c \tau \bar{\nu }_{\tau }$ can also be mediated via exchange of the vector multiplet $U^{\mu }_3$ at tree level. The resulting effective weak Hamiltonian including the SM contribution and LQ correction can be written as [53]

$$\begin{aligned} H_{eff}=\frac{G_FV_{cb}}{\sqrt{2}}(1+V_L)\bar{c}\gamma _{\mu }(1-\gamma _5)b\bar{\tau }\gamma ^{\mu }(1-\gamma _5)\nu _{\tau }, \end{aligned}$$

(3)

we can find that the vector LQ only generates (V-A) couplings and the corresponding NP coupling parameter from the vector LQ model can be written as

$$\begin{aligned} V_L=\frac{\sqrt{2}}{4G_FV_{cb}}\frac{g_{b\tau }^*({V}g)_{c\tau }}{M_{U}^2}. \end{aligned}$$

(4)

The lower limits on the masses of the LQs in the model independent have been pushed to a TeV scale by the direct searches about the LQs. In our numerical results, after taking into account the constraints on the vector LQ mass by CMS collaboration [87, 88], the mass of the vector LQ $M_U$ is hypothesized to be 1TeV. It should be noted that in this model the vector LQ could explain the $R_{D^{(*)}}$ and $R_{K^{(*)}}$ simultaneously, as shown in Ref. [53]. From the results of $\chi ^2$ fits to the measured ratios $R_{D^{(*)}}$ and acceptable $q^2$ spectra done in Ref. [55], we learn that at $1\sigma$ we have the following two best fit solution

$$\begin{aligned} g_{b\tau }^*({V}g)_{c\tau }=&\Bigg \{ \begin{array}{ll} 0.18\pm 0.04 &{}\quad R_A\\ -2.88\pm 0.04 &{}\quad R_B \end{array} \Bigg . , \end{aligned}$$

(5)

and for the two best fit solution cases, the coefficients $1+V_L$ can be got and rewritten as

$$\begin{aligned} 1+V_L=&\Bigg \{ \begin{array}{ll} 1.133\pm 0.030 &{}\quad \mathrm{for} R_A\\ -1.135\pm 0.030&{}\quad \mathrm{for} R_B \end{array} \Bigg . , \end{aligned}$$

(6)

although the fit results $R_A$ and $R_B$ are quite different, the coefficients $1+V_L$ they induced have nearly same absolute values for two solutions. Currently, it is very hard for us to differentiate these two solutions, and this is the key to explaining the phenomenon that NP contributions in $R_A$ and $R_B$ overlap each other in our figure which are shown in Sect. 4.

3 Theoretical framework for $\bar{B}^*\rightarrow V l \bar{\nu }_l$

From Eq. (3), we can get the amplitude of $\bar{B}^*\rightarrow V l \bar{\nu }_l$ and it can be expressed as the product of the hadronic matrix element and leptonic current. The square of the matrix element can be written as the product of leptonic ($L_{\mu \nu }$) and hadronic ($H^{\mu \nu }$) tensors. So the square amplitude can be written as

$$\begin{aligned}&|M(\bar{B}^*\rightarrow V l \bar{\nu }_l )|^2=\frac{G_F^2}{2}|V_{cb}|^2L_{\mu \nu }H^{\mu \nu } \nonumber \\&\quad =\frac{G_F^2}{2}|V_{cb}|^2 \sum _{m,m',n,n'}L(m,n)H(m',n')g_{mm'}g_{nn'}. \end{aligned}$$

(7)

It should be noted that the polarization vector of the off-shell particle $W^*(\bar{\varepsilon }^{\mu }(m))$ satisfies the orthonormality and completeness relations

$$\begin{aligned}&\bar{\varepsilon }^{*\mu }(m)\bar{\varepsilon }_{\mu }(m')=g_{mm'} \end{aligned}$$

(8)

$$\begin{aligned}&\sum _{mm'}\bar{\varepsilon }^{*\mu }(m) \bar{\varepsilon }^{\nu }(m')g_{mm'}= g^{\mu \nu } \end{aligned}$$

(9)

where $g_{mm'}=diag(+,-,-,-)$ and $m,m'=\pm ,0,t$ represent the transverse, longitudinal and time-like polarization components. So it is noted that $L(m,n)=L^{\mu \nu }\bar{\varepsilon }_{\mu }(m)\bar{\varepsilon }_{\nu }^*(n)$ and $H(m,n)=H^{\mu \nu }\bar{\varepsilon }_{\mu }^*(m)\bar{\varepsilon }_{\nu }(n)$ are both lorentz invariant and can be evaluated independent in specific reference frames. For convenience, we will calculate H(m, n) and L(m,n) in the $B^*$ meson rest frame and the virtual $W^*$ rest frame, respectively [79].

3.1 The helicity amplitudes of $\bar{B}^*\rightarrow V l \bar{\nu }_l$ decays

For hadronic part, the helicity amplitudes $H_{\lambda _{W^*}\lambda _{B^*}\lambda _{V}}$ of $\bar{B}^*\rightarrow V l \bar{\nu }_l$ decays are defined as [80]

$$\begin{aligned} H_{\lambda _{W^*}\lambda _{B^*}\lambda _{V}}(q^2)= & {} \langle V(p_V,\lambda _{V})|\bar{c}\gamma _{\mu }(1 -\gamma _5)b|\bar{B}^*(p_{B^*},\lambda _{B^*}) \rangle \bar{\varepsilon }^{*\mu }(\lambda _{W^*}) \end{aligned}$$

which can describe the decay of $B^*$ meson into a vector V meson and a virtual $W^*$. Both parent meson $B^*$ and daughter meson V have three helicity states $\lambda _{B^*(V)}=0,\pm$, but $W^*$ has four helicity states $\lambda _{W^*}=t,0,\pm$. Then the hadronic matrix elements $\langle V(p_V,\lambda _{V})|\bar{c}\gamma _{\mu }(1 -\gamma _5)b|\bar{B}^*(p_{B^*},\lambda _{B^*}) \rangle$ can be parameterized in terms of various form factors  [89, 90].

$$\begin{aligned}&\langle V(\varepsilon _2, p_{V})|\bar{c}\gamma _{\mu } b|\bar{B}^*(\varepsilon _1, p_{B^*})\rangle \nonumber \\&\quad = (\varepsilon _1 \cdot \varepsilon _2^{*})\left[ -P_{\mu }\,V_1(q^2)+q_{\mu }\,V_2(q^2)\right] \nonumber \\&\qquad +\frac{(\varepsilon _1 \cdot q)(\varepsilon _2^{*}\cdot q)}{m_{B^*}^2-m_{V}^2}\left[ P_{\mu }\,V_3(q^2)-q_{\mu }\,V_4(q^2)\right] \nonumber \\&\qquad -(\varepsilon _1 \cdot q)\,\varepsilon _{2\mu }^* \,V_5(q^2)+(\varepsilon _2^* \cdot q)\,\varepsilon _{1\mu }\,V_6(q^2),\nonumber \\&\langle V(\varepsilon _2, p_V)|\bar{c} \gamma _{5} \gamma _{\mu } b|\bar{B}^*(\varepsilon _1, p_{B^*})\rangle \nonumber \\&\quad = -i\varepsilon _{\mu \nu \alpha \beta }\varepsilon _1^{\alpha }\varepsilon _2^{*\beta }\left[ P^{\nu }\,A_1(q^2)-q^{\nu }\,A_2(q^2)\right] \nonumber \\&\qquad -\frac{i\varepsilon _2^{*}\cdot q}{m_{B^*}^2-m_{V}^2}\varepsilon _{\mu \nu \alpha \beta }\varepsilon _1^{\nu }P^{\alpha }q^{\beta }\,A_3(q^2) \nonumber \\&\qquad +\frac{i\varepsilon _1\cdot q}{m_{B^*}^2-m_{V}^2}\varepsilon _{\mu \nu \alpha \beta }\varepsilon _2^{*\nu } P^{\alpha }q^{\beta }A_4(q^2) \end{aligned}$$

(10)

here we will use sign convention $\varepsilon _{0123=-1}$.

In the rest frame of $B^*$ meson, we will consider the daughter vector meson V to move along $+z$ direction. The momenta of the mesons $B^*$, V and virtual $W^*$ are written as

$$\begin{aligned} p_{B^*}^{\mu }= & {} (m_{B^*},0,0,0),\nonumber \\ p_{V}^{\mu }= & {} (E_{V},0,0,|\mathbf {p}|),\nonumber \\ q^{\mu }= & {} (q^0,0,0,-|\mathbf {p}|), \end{aligned}$$

(11)

where $q^0$ and $\mathbf {p}$ are the energy and momentum of the virtual $W^*$. Besides, $q^0=m_{B^*}-E_V=(m_{B^*}^2-m_V^2+q^2)/(2m_{B^*})$, $|\mathbf {p}|=\lambda ^{1/2}(m_{B^*}^2,m_{V}^2,q^2)/2m_{B^*}$, with $\lambda (a,b,c)\equiv a^2+b^2+c^2-2(ab+bc+ca)$ and $m_l^2\le q^2 \le (m_{B^*}-m_V)^2$. The polarization vectors of the mesons $B^*$ and V can be written as

$$\begin{aligned} \varepsilon _1^{\mu }(0)= & {} (0,0,0,1), \nonumber \\ \varepsilon _1^{\mu }(\pm )= & {} \frac{1}{\sqrt{2}}(0,\mp 1,-i,0);\nonumber \\ \varepsilon _2^{\mu }(0)= & {} \frac{1}{m_{V}}(|\mathbf {p}|,0,0,E_{V}), \nonumber \\ \varepsilon _2^{\mu }(\pm )= & {} \frac{1}{\sqrt{2}}(0,\mp 1,-i,0). \end{aligned}$$

(12)

The polarization vectors of $W^*$ boson, are conveniently chosen as following

$$\begin{aligned} \bar{\varepsilon }^{\mu }(t)= & {} \frac{1}{\sqrt{q^2}}(q^0,0,0,-|\mathbf {p}|),\nonumber \\ \bar{\varepsilon }^{\mu }(0)= & {} \frac{1}{\sqrt{q^2}}(|\mathbf {p}|,0,0,-q^0),\nonumber \\ \bar{\varepsilon }^{\mu }(\pm )= & {} \frac{1}{\sqrt{2}}(0,\pm 1,-i,0), \end{aligned}$$

(13)

In the $l-\bar{\nu }_l$ center of mass frame (virtual $W^*$ rest frame), the four-momenta of l and $\bar{\nu }_l$ pair can be expressed as

$$\begin{aligned} p_l^{\mu }= & {} (E_{l}, |\mathbf {p}_{l}|\sin \theta _l,0,|\mathbf {p}_{l}|\cos \theta _l),\nonumber \\ \quad p_{\nu _l}^{\mu }= & {} (|\mathbf {p}_{l}|, -|\mathbf {p}_{l}|\sin \theta _l,0,-|\mathbf {p}_{l}|\cos \theta _l), \end{aligned}$$

(14)

with $E_{l}=(q^2+m_{l}^2)/2\sqrt{q^2}$, $|\mathbf {p}_{l}|=(q^2-m_{l}^2)/2\sqrt{q^2}$, and $\theta _l$ is the angle between V and l three-momenta. At the same time, in this frame, the polarization vectors of $W^*$ boson are written in the form

$$\begin{aligned} \bar{\varepsilon }^{\mu }(t)= & {} (1,0,0,0),\nonumber \\ \bar{\varepsilon }^{\mu }(0)= & {} (0,0,0,1),\nonumber \\ \bar{\varepsilon }^{\mu }(\pm )= & {} \frac{1}{\sqrt{2}}(0,\mp 1,-i,0). \end{aligned}$$

(15)

In the $B^*$ meson rest frame, after contracting above hadronic matrix elements with the polarization vectors, the non-vanishing helicity amplitudes can obtained and written as

$$\begin{aligned} H_{0++}(q^2)= & {} -\frac{m_{B^*}^2-m_{V}^2}{\sqrt{q^2}}A_1(q^2)+\sqrt{q^2}A_2(q^2)+\frac{2m_{B^*}|\mathbf {p}|}{\sqrt{q^2}}V_1(q^2),\nonumber \\ H_{t++}(q^2)= & {} -\frac{2m_{B^*}|\mathbf {p}|}{\sqrt{q^2}}A_1(q^2)+\frac{m_{B^*}^2-m_{V}^2}{\sqrt{q^2}}V_1(q^2)-\sqrt{q^2}V_2(q^2),\nonumber \\ H_{-+0}(q^2)= & {} -\frac{m_{B^*}^2+3m_{V}^2-q^2}{2m_{V}}A_1(q^2)+\frac{(m_{B^*}^2-m_{V}^2-q^2)}{2m_{V}}A_2(q^2)\nonumber \\&-\frac{2m_{B^*}^2|\mathbf {p}|^2}{m_{V}(m_{B^*}^2-m_{V}^2)}A_3(q^2) -\frac{m_{B^*}|\mathbf {p}|}{m_{V}}V_6(q^2),\nonumber \\ H_{0--}(q^2)= & {} \frac{m_{B^*}^2-m_{V}^2}{\sqrt{q^2}}A_1(q^2)-\sqrt{q^2}A_2(q^2)+\frac{2m_{B^*}|\mathbf {p}|}{\sqrt{q^2}}V_1(q^2),\nonumber \\ H_{t--}(q^2)= & {} \frac{2m_{B^*}|\mathbf {p}|}{\sqrt{q^2}}A_1(q^2)+\frac{m_{B^*}^2-m_{V}^2}{\sqrt{q^2}}V_1(q^2) -\sqrt{q^2}V_2(q^2),\nonumber \\ H_{+-0}(q^2)= & {} \frac{m_{B^*}^2+3m_{V}^2-q^2}{2m_{V}}A_1(q^2)-\frac{(m_{B^*}^2-m_{V}^2-q^2) }{2m_{V}}A_2(q^2)\nonumber \\&+\frac{2m_{B^*}^2|\mathbf {p}|^2}{m_{V}(m_{B^*}^2-m_{V}^2)}A_3(q^2) -\frac{m_{B^*}|\mathbf {p}|}{m_{V}}V_6(q^2),\nonumber \\ H_{+0+}(q^2)= & {} \frac{3m_{B^*}^2+m_{V}^2-q^2}{2m_{B^*}}A_1(q^2) -\frac{(m_{B^*}^2-m_{V}^2+q^2)}{2m_{B^*}}A_2(q^2)\nonumber \\&+\frac{2m_{B^*}|\mathbf {p}|^2}{m_{B^*}^2-m_{V}^2}A_4(q^2)-|\mathbf {p}|V_5(q^2),\nonumber \\ H_{-0-}(q^2)= & {} -\frac{3m_{B^*}^2+m_{V}^2-q^2}{2m_{B^*}}A_1(q^2) +\frac{(m_{B^*}^2-m_{V}^2+q^2)}{2m_{B^*}}A_2(q^2)\nonumber \\&-\frac{2m_{B^*}|\mathbf {p}|^2}{m_{B^*}^2-m_{V}^2}A_4(q^2)-|\mathbf {p}|V_5(q^2),\nonumber \\ H_{000}(q^2)= & {} \frac{|\mathbf {p}|(m_{B^*}^2+m_{V}^2-q^2)}{\sqrt{q^2}m_{V}}V_1(q^2) +\frac{2m_{B^*}^2|\mathbf {p}|^3}{\sqrt{q^2}m_{V}(m_{B^*}^2-m_{V}^2)}V_3(q^2)\nonumber \\&-\frac{|\mathbf {p}|(m_{B^*}^2-m_{V}^2-q^2)}{2\sqrt{q^2}m_{V}}V_5(q^2) +\frac{|\mathbf {p}|(m_{B^*}^2-m_{V}^2+q^2)}{2\sqrt{q^2}m_{V}}V_6(q^2),\nonumber \\ H_{t00}(q^2)= & {} \frac{(m_{B^*}^2-m_{V}^2)(m_{B^*}^2+m_{V}^2-q^2)}{2\sqrt{q^2}m_{B^*}m_{V}}V_1(q^2)\nonumber \\&-\frac{\sqrt{q^2}(m_{B^*}^2+m_{V}^2-q^2)}{2m_{B^*}m_{V}}V_2(q^2)\nonumber \\&+\frac{m_{B^*}|\mathbf {p}|^2}{\sqrt{q^2}m_{V}}V_3(q^2) -\frac{m_{B^*}|\mathbf {p}|^2\sqrt{q^2}}{m_{V}(m_{B^*}^2-m_{V}^2)}V_4(q^2)\nonumber \\&-\frac{m_{B^*}|\mathbf {p}|^2}{\sqrt{q^2}m_{V}}V_5(q^2) +\frac{m_{B^*}|\mathbf {p}|^2}{\sqrt{q^2}m_{V}}V_6(q^2). \end{aligned}$$

(16)

Moreover, the leptonic helicity amplitudes $h_{\lambda _l,\lambda _{\bar{\nu }_l}}=\frac{1}{2}\bar{u}_l(\lambda _l)\gamma ^{\mu }(1-\gamma _5)\nu _{\bar{\nu }_l}\bar{\varepsilon }_{\mu }(\lambda _{W^*})$ with $\lambda _{W^*}=\lambda _l-\lambda _{\bar{\nu }_l}$ After considering exact expressions of the spinors and polarization vectors of $W^*$ listed in Eq. (15), one can obtain the following non-vanishing results

$$\begin{aligned} \begin{aligned} |h_{-\frac{1}{2},\frac{1}{2}}|^2&= 8(q^2-m_\ell ^2), \\ |h_{\frac{1}{2},\frac{1}{2}}|^2&= 8\frac{m_\ell ^2}{2q^2}(q^2-m_\ell ^2), \end{aligned} \end{aligned}$$

(17)

with the cases $\lambda _l=-1/2$ and 1/2 are referred to as the non-flip and flip transitions, respectively.

3.2 Decay distribution and other observables of $\bar{B}^*\rightarrow V l \bar{\nu }_l$decays

In the presence of NP, the differential angular decay distribution for $\bar{B}^{*} \rightarrow V l \bar{\nu }_l$ decay can be expressed as

$$\begin{aligned} \frac{d^2 \mathrm \varGamma }{dq^2d\cos \theta _l}=\frac{G_F^2|V_{cb}|^2}{(2\pi )^3}\,\frac{|\mathbf {p}|}{8m_{B^*}^2}\, \frac{1}{3}(1-\frac{m_\ell ^2}{q^2})L_{\mu \nu }H^{\mu \nu }, \end{aligned}$$

(18)

furthermore, we can obtain the differential angular decay distribution for leptonic helicity state $\lambda _l=\frac{1}{2}$ and $\lambda _l=-\frac{1}{2}$

$$\begin{aligned} \frac{d^2 {\varGamma }^{\lambda _{\ell }=-1/2}}{dq^2d\cos \theta _l}= & {} \frac{G_F^2|V_{cb}|^2|\mathbf {p}|}{256\pi ^3m_{B^*}^2}\, \frac{1}{3}q^2(1-\frac{m_\ell ^2}{q^2})^2\,\nonumber \\&\times |1+V_L|^2 \Big [(1-\text {cos}\,\theta _l)^2(H_{+0+}^2+H_{+-0}^2)\nonumber \\&+(1+\text {cos}\,\theta _l)^2(H_{-0-}^2+H_{-+0}^2)\nonumber \\&+2\text {sin}^2\,\theta _l(H_{0++}^2+H_{0--}^2+H_{000}^2)\Big ] ;\nonumber \\ \frac{d^2 \mathrm \varGamma ^{\lambda _{\ell }=1/2}}{dq^2d\cos \theta _l}= & {} \frac{G_F^2|V_{cb}|^2|\mathbf {p}|}{256\pi ^3m_{B^*}^2}\, \frac{1}{3}q^2(1-\frac{m_\ell ^2}{q^2})^2\,\frac{m_{\ell }^2}{q^2} |1+V_L|^2\,\nonumber \\&\times \Big [\text {sin}^2\,\theta _l(H_{+0+}^2+H_{+-0}^2+H_{-0-}^2+H_{-+0}^2)\nonumber \\&+2(H_{t++}-\text {cos}\,\theta _l\,H_{0++})^2\nonumber \\&+2(H_{t--}-\text {cos}\,\theta _l\,H_{0--})^2\nonumber \\&+2(H_{t00}-\text {cos}\,\theta _l\,H_{000})^2\Big ]. \end{aligned}$$

(19)

We can determine the differential decay rate $d {\varGamma }/dq^2$ by performing the $cos\theta _l$ integration and summing over the lepton helicity

$$\begin{aligned} \frac{d \varGamma }{dq^2}&=\frac{G_F^2|V_{cb}|^2|\mathbf {p}|}{288\pi ^3m_{B^*}^2}\, q^2\,(1-\frac{m_\ell ^2}{q^2})^2\, |1+V_L|\nonumber \\&\quad \times \bigg [\frac{3m_{\ell }^2}{2q^2}(H_{t++}^2+H_{t--}^2+H_{t00}^2)\nonumber \\&\quad +(H_{+0+}^2+H_{+-0}^2+H_{-0-}^2+H_{-+0}^2\nonumber \\&\quad +H_{000}^2+H_{0--}^2+H_{0++}^2)(1+\frac{m_{\ell }^2}{2q^2})\bigg ], \end{aligned}$$

(20)

After picking out $H_{t00}^2$, $H_{+-0}^2$,$H_{-+0}^2$, and $H_{000}^2$ from Eq. (20). one can get the longitudinal differential decay rate $d \varGamma ^L/dq^2$.

Besides the differential decay branching fraction $dBr/dq^2$, other interesting observables are also investigated in this work and they are $R_V^{*(L)}(q^2)$, $A_{FB}^l(q^2)$, $P_l(q^2)$ and $F_L^{*V}(q^2)$

$$\begin{aligned} R^{*(L)}_{V}(q^2)&\equiv \frac{d{\varGamma }^{(L)}(\bar{B}^*\rightarrow V \tau ^-\bar{\nu }_\tau )/dq^2}{d \varGamma ^{(L)}(\bar{B}^*\rightarrow V\ell ^{\prime -}\bar{\nu }_{\ell ^{\prime }})/dq^2},(\ell = e , \mu ) \end{aligned}$$

(21)

$$\begin{aligned} A_{\text {FB}}^l(q^2)&= \bigg ( \int _{-1}^0 d \cos \theta _l \frac{d^2 \varGamma }{d q^2 d \cos \theta _l}\nonumber \\&\quad - \int _0^1 d \cos \theta _l \frac{d^2 \varGamma }{d q^2 d \cos \theta _l} \bigg ) \Big / \frac{d {\varGamma }}{d q^2}. \end{aligned}$$

(22)

$$\begin{aligned} P_l(q^2)&=\frac{d{\varGamma }^{\lambda _\ell =-1/2}/dq^2-d{\varGamma }^{\lambda _\ell =1/2}/dq^2}{{d {\varGamma }}/{d q^2}}, \end{aligned}$$

(23)

$$\begin{aligned} F_{\mathrm{L}}^{*V}(q^2)&=\frac{d{\varGamma }^{L}(\bar{B}^*\rightarrow V \tau ^-\bar{\nu }_\tau )/dq^2}{{d {\varGamma }}/{d q^2}}, \end{aligned}$$

(24)

and before taking the ratio we integrate the numerator and denominator over $q^2$ separately to obtain the average values of these observables $\langle R_\mathrm{V}^{*(L)}\rangle$, $\langle A_\mathrm{FB}^{l}\rangle$, $\langle P_\mathrm{l}\rangle$, and $\langle F_\mathrm{L}^{*V}\rangle$.

4 Numerical results and discussion

4.1 Input parameters

In this section, we shall present the numerical results of the SM prediction and NP contribution of vector LQ on the aforementioned observables, to see if the effects are large enough to cause obvious deviations from the SM predictions. Firstly, we collect all the input parameters relative to the numerical calculations in the Table 2.

When we evaluate the branching fractions of the $\bar{B}^*\rightarrow V l \bar{\nu }_l$, in addition to aforementioned input parameters, the lifetimes of $B^*_{u,d,s,c}$ are also indispensable. However, there is no references about theoretical or experimental information on these lifetime until now. We impose the fact that the electromagnetic process $B^*\rightarrow B\gamma$ dominates the decays of $B^*$ meson. So in our calculation, we will take the approximation $\varGamma _\mathrm{tot}(B^*) \simeq \varGamma (B^* \rightarrow B \gamma )$. The decay width of $\varGamma (B^* \rightarrow B \gamma )$ in the light front quark model is given by Ref. [80] and the result is in agreement with the ones obtained based on different theoretical models [92,93,94,95,96,97]. And we use the following results,

$$\begin{aligned} \varGamma _\mathrm{{tot}}(B^{*+})\simeq & {} \varGamma (B^{*+}\rightarrow B^+ \gamma )=(349\pm {18})\,\mathrm{eV},\nonumber \\ \varGamma _\mathrm{{tot}}(B^{*0})\simeq & {} \varGamma (B^{*0}\rightarrow B^0 \gamma )=(116\pm 6)\,\mathrm{eV},\nonumber \\ \varGamma _\mathrm{{tot}}(B^{*0}_s)\simeq & {} \varGamma (B^{*0}_s\rightarrow B^0_s \gamma )=(84^{+11}_{-9})\,\mathrm{eV},\nonumber \\ \varGamma _\mathrm{{tot}}(B^{*+}_c)\simeq & {} \varGamma (B^{*+}_c\rightarrow B^+_c \gamma )=(49^{+28}_{-21})\,\mathrm{eV}. \end{aligned}$$

(25)

From Eq. (25), it is clear to find that $\varGamma _\mathrm{{tot}}(B^{*+}) \simeq 3 \varGamma _\mathrm{{tot}}(B^{*0})$, $\varGamma _\mathrm{{tot}}(B^{*+}) \simeq 4 \varGamma _\mathrm{{tot}}(B^{*0}_s)$, $\varGamma _\mathrm{{tot}}(B^{*+}) \simeq 7 \varGamma _\mathrm{{tot}}(B^{*+}_c)$.

Table 2 Input parameters used in our numerical analyses

Besides, it is universally acknowledged that the form factors are indispensable input parameters for the branching fraction. And they are calculated in Refs. [80, 98] in the covariant light-front quark model (CLFQM) [99,100,101]. We will use the values evaluated in the CLFQM and the $q^2$ dependence of the form factors can be parameterized and reproduced by three parameters and have the following form

$$\begin{aligned} F(q^2)=\frac{F(0)}{1-a\,\frac{q^2}{m^2_{B^*}}+b\,\left( \frac{q^2}{m^2_{B^*}}\right) ^2}, \end{aligned}$$

(26)

where $F=V_{1-6}$ and $A_{1-4}$ listed in Eq. (10), the values of the parameters F(0), a and b can be found in Table 3. In our numerical calculations, the $1\sigma$ level range of the CKM $V_{cb}$ is considered.

Table 3 The input parameters of the form factors for $\bar{B}^* \rightarrow D^*$, $\bar{B}^*_s \rightarrow D^*_s$ and $\bar{B}^*_c \rightarrow J/\psi$ transitions within the CLFQM used in our numerical analysis [80, 98]

4.2 SM prediction for $\bar{B}^*\rightarrow V l \bar{\nu }_l$

Employing the framework displayed in Sects. 2 and 3, we now give the SM predictions for the branching fraction $\mathscr {B}(\bar{B}^*\rightarrow V l \bar{\nu }_l)$ and other interesting observables. And we present the SM values of above observables in the Table 4. From the table, it is clear to find that the decay branching fractions are observed to be larger for the lighter lepton modes as compared to the result at $l=\tau$, and same phenomenon arises in $P_l$ and $F_{L}^{*V}$. Especially, for $P_l$, the result for lighter lepton modes are much larger than the ones of $\tau$ mode. The forward-backward asymmetries $A^l_{FB}$ for light leptons are negative, but one of the $\tau$ mode is positive.

The values of various observables for both $\bar{B}^{*-} \rightarrow D^{*0} l \bar{\nu }_l$ and $\bar{B}^{*0} \rightarrow D^{*+}l \bar{\nu }_l$ are very close except decay branching fractions $\mathscr {B}^{(L)}$. One can found that for $\bar{B}^*\rightarrow V \tau \bar{\nu }_{\tau }$ processes, the $F_L^{D^*(D^{*+}_s,J/\Psi )}$ is in the range 20–25%. And this implies that the transverse polarization dominate $\bar{B}^*\rightarrow V \tau \bar{\nu }_{\tau }$ decay. It is obviously different from $\bar{B} \rightarrow V \tau \bar{\nu }_{\tau }$ decay that is dominated by the longitudinal polarization state.

Table 4 The SM central values prediction for branching fractions Br, the lepton polarization fraction $\langle P_{ l}\rangle$, the hadron polarization fraction $\langle F_\mathrm{L}^{*V}\rangle$, the forward-backward asymmetry $\langle A_\mathrm{FB}^{l}\rangle$ and the ratio of branching ratio $\langle R_\mathrm{V}^{*(L)}\rangle$ for $\bar{B}^*\rightarrow V l \bar{\nu }_l$decays, and previous bounds are listed for comparison

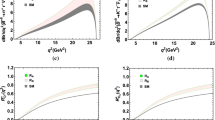
The Figs. 1, 2, 3, 4, and 5 present the SM prediction for $q^2$ variation of various observables in the reasonable kinematic range for $\bar{B}^{*} \rightarrow V l^-\bar{\nu }_l (V=D^*,D^*_s, J/\Psi )$.

In these figures, we have compare the distributions of the each observable and the red (dot dash), blue (solid) and green (solid) lines indicate the e, $\mu$ and $\tau$ mode, respectively. Noted that for above four decay processes the variation of these observables are similar to each other, and in order to avoid repetition we will only illustrate $\bar{B}^{*-} \rightarrow D^{*0} l^- \bar{\nu }_l$ in detail, and the same analyses can be made for the following text.

Fig. 1

The $d{ \varGamma ^{(L)}}/dq^2$ as a function of $q^2$ for $\bar{B}^{*} \rightarrow V l^-\bar{\nu }_l$ in the SM. The red (dot dash ), blue (solid), and green (solid) lines indicate the e, $\mu$ and $\tau$ mode, respectively. The corresponding undertint represent the longitudinal differential decay rate $d{\varGamma ^L}/dq^2$. And the same in Figs. 2, 3, 4, 5

Fig. 2

The forward-backward asymmetry $\mathrm A_{FB}^l(q^2)$ as a function of $q^2$ for $\bar{B}^{*} \rightarrow V l^-\bar{\nu }_l$ in the SM

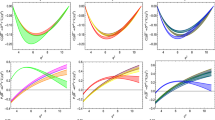
As seen from the first two-dimensional plots of these figures, it is easy to distinct the distribution for both lighter leptons and $\tau$ lepton final state. However, we have observed the feature that the e mode and $\mu$ mode overlap completely except at a large recoil range. One can see that for $\mu$ mode, the $d\mathrm{\varGamma ^{(L)}}/dq^2$ changes to zero quickly at the largest recoil range. Besides, the $d{ \varGamma ^{(L)}}/dq^2$ for e and $\mu$ is maximum when $q^2 \approx 4~ {\mathrm{GeV}}^2$, whereas, for $\tau$mode, the $d{ \varGamma ^{(L)}}/dq^2$ is maximum when $q^2 \approx 8~ {\mathrm{GeV}}^2$ and approaches zero at $q^2_\mathrm{min}$ and $q^2_\mathrm{max}$. At the same time, one can find for e mode, at the largest recoil range, the results of $d\mathrm{\varGamma ^{(L)}}/dq^2(\bar{B}^{*0}_s \rightarrow D^{*+}_s e^- \bar{\nu }_e)$ and $d{ \varGamma ^{(L)}}/dq^2(\bar{B}^{*-}_c \rightarrow J/\Psi e^- \bar{\nu }_e)$ are both smaller than the result of $d\mathrm{\varGamma ^{(L)}}/dq^2(\bar{B}^{*-} \rightarrow D^{*0}_s e^- \bar{\nu }_e)$. For the forward-backward asymmetry shown in Fig. 2, at zero recoil $q^2_\mathrm{max}=(m_{\bar{B}^*}-m_\mathrm{V})^2$, all the $A_{FB}$ are 0. $A_{FB}^e$ is negative over the all $q^2$ region and $A_{FB}^{\mu }$ changes to 0.5 quickly when $q^2=m_{\mu }^2$. Furthermore, there is a zero-crossing point when $q^2\approx 0.5~{\mathrm{GeV}}^2$ for $\mu$ mode and $q^2\approx 9 ~{\mathrm{GeV}}^2$ $\tau$ mode, respectively.

Fig. 3

The lepton polarization fraction $\mathrm{P}_{l}(q^2)$ as a function of $q^2$ for $\bar{B}^{*} \rightarrow V l^-\bar{\nu }_l$ in the SM

Fig. 4

The hadron polarization fraction $\mathrm{F}_{L}^{*V}(q^2)$ as a function of $q^2$ for $\bar{B}^{*} \rightarrow V l^-\bar{\nu }_l$ in the SM

Fig. 5

The ratio of branching ratio $\mathrm{R}_{V}^{*(L)}(q^2)$ as a function of $q^2$ for $\bar{B}^{*} \rightarrow V l^-\bar{\nu }_l$ in the SM and the corresponding undertint represent the longitudinal observable $\mathrm{R}_{V}^{*L}(q^2)$

For the lepton polarization fraction ${ P}_l$ displayed in Fig. 3, we observe that all the $P_e$ is +1 in the whole $q^2$ region, besides, the $P_{\mu }$ changes to -0.3 quickly when $q^2=m_{\mu }^2$. The result of the $\tau$ mode that is quite different from lighter lepton modes and $P_{\tau }$ is great increasing with $q^2$ over the all $q^2$ region. Besides, there is a zero-crossing point when $q^2\approx 5{\mathrm{GeV}}^2$. From the Fig. 4, one can see that all the $F_L^{V}$ are great increasing with $q^2$ over the entire $q^2$ range and around 0.335 at zero recoil $q_\mathrm{max}^2=(m_{B^*}-m_V)^2$ for $\bar{B}^{*} \rightarrow V l^-\bar{\nu }_l (V=D^*,D^*_s, J/\Psi )$. Especially, for $\tau$ mode, $F_L^{V}$ shows an almost positive slope over the entire $q^2$ region. It is clear to find that at $q_\mathrm{min}$ for the lighter lepton modes, $F_L^{D^{*0}(D^{*+})}$ is around 0.22 and $F_L^{D_s^{*+}(J/\Psi )}$ is around 0.17. However, for $\tau$ mode, when at $q_\mathrm{min}=m_{\tau }^2$, $F_L^{D^{*0}(D^{*+})}\rightarrow 0.25$ and $F_L^{D_s^{*+}(J/\Psi )} \rightarrow 0.23$, respectively.

For the ratio of branching fraction $\mathrm{R}_{V}^{*(L)}$ presented in Fig. 5, it is also increasing with $q^2$ over the all $q^2$ region and the longitudinal observable $\mathrm{R}_{V}^{*L}$ has a slightly smaller result than $\mathrm{R}_{V}^{*}$ for $\bar{B}^{*} \rightarrow V l^-\bar{\nu }_l$.

Fig. 6

The $q^2$ dependence of various observables for the $\bar{B}^{*-} \rightarrow D^{*0} \tau ^-\bar{\nu }_{\tau }$ decay mode in the SM and vector LQ scenarios. The band widths represent the uncertainties from the decay widths of $B^*$, $V_{cb}$ and NP parameters in the vector LQ scenario

Then using the limits of the $R_{D^{(*)}}$ anomalies experimental measurements to the parameter space of the coupling, we will present the discussions about the NP contributions of the vector LQ on the aforementioned observables. We have considered the uncertainty of NP parameters displayed in Eq. (5) and $V_{cb}$, and the mass of LQ is taken as $M_U=1\mathrm Tev$ when we calculate all the observables for $\bar{B}^{*} \rightarrow V \tau ^-\bar{\nu }_{\tau }$.

For simplicity, we only present the predictions for the observables of $\bar{B}^{*-} \rightarrow D^{*0} \tau ^-\bar{\nu }_{\tau }$ both in SM and vector LQ scenarios and the results are displayed in Fig. 6. In this figure, the gray bands represent the SM predictions for various observables, whereas the red and green bands represent the contributions of the vector LQ in $R_A$ and $R_B$ scenarios, respectively. From the figure, one can see that the NP contribution to $d{ \varGamma ^{(L)}}/dq^2(\bar{B}^{*-} \rightarrow D^{*0} \tau ^-\bar{\nu }_{\tau })$ and $R^{*(L)}_{D^{*0}}$ is prominent and have large deviations from the corresponding SM prediction. After comparing to the SM prediction, we can find that the result of the $d{ \varGamma ^{(L)}}/dq^2(\bar{B}^{*-} \rightarrow D^{*0} \tau ^-\bar{\nu }_{\tau })$ is enhanced by about $30\%$ both in $R_A$ and $R_B$ scenarios in the reasonable $q^2$ range. From the figure, we can also find that the another obvious feature that it is hard to differentiate $R_A$ and $R_B$ scenarios. In order to explain this phenomenon, from Eq. (3) we have noted that vector LQ contributions only generates V-A couplings. Though the results $R_A$ and $R_B$ are quite different, the coefficient |$1+V_L$| has nearly same result for two scenarios. Different from the contribution of vector LQ to $d{ \varGamma ^{(L)}}/dq^2$, the result of $R_{D^{*0}}^{*(L)}(q^2)$ is the rising trend with the increasing $q^2$. The red and green band are overlapped due to the same reason for $R_A$ and $R_B$ scenarios. Besides, the deviation of $R_{D^{*0}}^{*(L)}(q^2)$ from relevant SM prediction is very significant, especially at zero recoil $q^2_\mathrm{max}$. These two observables have been hoped to detected on the high energy collider in the future. Especially, the ratio of branching fraction $\mathrm{R}_{V}^{*(L)}(q^2)$ will support the NP signal of $R_{D^{(*)}}$ anomalies once it is detected.

Finally, we show the contributions of SM and vector LQ to $A_{FB}(q^2)$ and $P_{\tau }(q^2)$ as well as $F_{L}^{D^{*0}}(q^2)$ of $\bar{B}^{*-} \rightarrow D^{*0} \tau ^-\bar{\nu }_{\tau }$ decay. From the Fig. 6, one can find there is one obvious feature, i.e., the LQ contribution is indistinguishable from the SM prediction. The every only line in $A_{FB}(q^2)$ and $P_{\tau }(q^2)$ as well as $F_{L}^{D^{*0}}(q^2)$ dedicates the contributions coming from either SM prediction or vector LQ scenario. Since the factor $(1+V_L)^2$ appears both in the numerator and denominator of the expressions which describe these observables simultaneously and the NP dependency cancels in the ratios. One can see that the results of $P_{\tau }$ and $F_L^{D^{*0}}$ are both great increasing with $q^2$ and achieve the maximum at zero recoil $q^2_\mathrm{max}$. Besides, the $F_L^{D^{*0}}$ rises in a straight line with a slope of about 1. However, $A_{FB}^{\tau }$ descendent tendency with the increasing of $q^2$. As a consequence, all the three observables are insensitive to the contribution of the vector LQ scenarios and have nearly same behaviour as that in the SM. Similar conclusions can be made for $\bar{B}^{*0} \rightarrow D^{*+} \tau ^-\bar{\nu }_{\tau }$, $\bar{B}^{*0}_s \rightarrow D^{*+}_s \tau ^-\bar{\nu }_{\tau }$ and $\bar{B}^{*-}_c \rightarrow J/\Psi \tau ^-\bar{\nu }_{\tau }$ decay processes as well.

5 Summary

The deviations of $R_{D^{(*)}(K^{(*)})}$, $R_{J/\Psi }$ and $F_L^{D^*}$ between the experimental measurements and relevant SM predictions imply that NP may appear in the B meson decay processes.

In this paper, motivated by above anomalies as well as the abundant $B^*$ data samples at high-luminosity heavy-flavor experiments in the future, we have investigated the effect in the semileptonic $\bar{B}^*_{u,d,s,c} \rightarrow V \tau ^- \bar{\nu }_{\tau }$ decays which is induced by the $b\rightarrow c \tau \bar{\nu }_{\tau }$ quark level transition as $B\rightarrow D^{(*)} \tau \bar{\nu }_{\tau }$ decays in vector LQ model.

In this work, the helicity amplitudes are studied in detail by using the form factors of $\bar{B}^*\rightarrow V$ transitions in the covariant light front quark model. Besides the SM prediction of different observables such as branching fraction $Br^{(L)}$, ratio $\langle R_{V}^{*(L)}\rangle$, forward-backward asymmetry $\langle A_{FB}\rangle$, lepton polarization fraction $\langle P_l\rangle$ and hadron polarization fraction $\langle F_L^{*V}\rangle$ are presented in Table 4.

We have also discussed the $q^2$ distributions of these observables in SM as well as $R_A$ and $R_B$ cases of the vector LQ model. Using the best-fit solutions for the NP coupling parameters from $R_{D^{(*)}}$ anomalies in the experimental measurements, the results of those observables for SM and vector LQ model are displayed in Fig. 6.

It is clear to find that all the $d{ \varGamma }^{(L)}/dq^2$ and $R_{V}^{*(L)}$ are both sensitive to the NP effects of the vector LQ and they have significant deviations from the relevant SM predictions. Besides, one can see that the red and green band are overlapped for $R_A$ and $R_B$ cases due to the coefficient $|1+V_L|$ has nearly same result for two scenarios. In the reasonable $q^2$ range, the result of the $d{ \varGamma }^{(L)}/dq^2$ is enhanced by about $30\%$ both in two cases. Furthermore, the deviation of $R_{V}^{*(L)}$ from corresponding SM prediction ia very significant, especially at zero recoil. So the contributions of vector LQ to this two observables are prominent and they are hoped to be measured on high energy collider in the future. Nevertheless, for $A_{FB}(q^2)$, $P_{\tau }(q^2)$ and $F_L^{V}(q^2)$ we do not see any deviation from the SM prediction, and the NP effects of the vector LQ on these three observables are cancelled.

Unlike B meson decays that have been investigated both experimentally and theoretically in the last few years, $B^*$ meson is an unstable particle, it can not decay by strong interaction, decays which has similar quark level transition are less studied.

In the near future, more data about $B^*$ will be obtained by the running LHC and upcoming SuperKEKB/Belle-II experiment, and we hope the results in this paper will play an important role in probing the hints of possible NP.