1 Introduction

The attempt to modify the general relativity theory has a long history and has begun almost simultaneously as the general relativity inception [1]. There are almost three categories to deal with the general relativity modifications, all are inspiring and have been remained in the mainstream of the physics research and have even become the fundamental idea for many other theoretical proposals. These categories are; assuming higher dimensions, generalizing the Hilbert–Einstein action to an arbitrary function of Ricci scalar (f(R) theories) and assuming nontrivial interaction between gravity and matter (non-minimal coupling).

Assuming higher dimensions which mostly includes new spatial dimension(s) is one of the most interesting ideas and although it has begun from the beautiful works of Kaluza (1921) [2] and Klein (1926) [3], one may find new version of it in pioneering and modern theories of the string theory, the M theory, the brane models and so on. On the other hand, adding spatial dimension(s) to our usual four dimensional space-time, immediately results in some new terms in the Einstein–Hilbert action which are known as Lovelock terms [4]. Of course, one is free to keep these new terms or accept the 4-dimensional Hilbert–Einstein Lagrangian form to outspread in higher dimensions. Disregarding the perspective one chooses to consider the higher dimensional theories, one can accommodate more ideas into the theory of gravity.

The other two modifications of the general theory of relativity (f(R) models and non-minimal coupling between mater and gravity) are somehow connected since one can make the additional scalar degree of freedom of the f(R) model to appear in the form of Brans–Dicke non-minimal coupling theory or even Einstein–Hilbert theory using conformal transformations [5].

Here, we do not aim to discuss the pros and cons of the above competitive theories. It is also out of the scope of the present work to reopen the old dispute about the physical equivalence of the conformally related Einstein and Jordan frames [6]. Instead, we focus on a typical form of Higgs-Inflation model and try to analyze it through the dynamical system approach.

It is of much interest to unify standard model Higgs field as the only available scalar degree of freedom in particle physics [7,8,9] with inflaton scalar field as the most attractive solution for many cosmological dilemmas [10,11,12]. One may even be tempted to unify the standard model symmetry breaking to the emergence of the inflation process. Unfortunately, the former idea has a serious barrier to overcome; although the symmetry breaking mechanism is suitable enough to be an inflationary candidate, both the vacuum energy level and the self coupling constant values have to be much far from the corresponding parameters in the standard model of fields and particles [13,14,15,16,17]. In this regard, the energy level in which the Higgs mechanism triggers the symmetry breaking lies considerably lower than any inflationary scenario. In spite of the above disappointing fact, there are some nontrivial models to deal with the problem [18]. The first and the most well-known idea among others has been unifying the Higgs and the inflaton field through a non-minimal interaction with curvature [17, 19,20,21]. We denote this non-minimal Higgs inflation scenario as the “original Higgs inflation” throughout the paper. Although the energy gap between Higgs symmetry breaking and inflation remains irreconcilably large in the original Higgs inflation model, but the theory becomes more economic since one is not required to infix a new scalar degree of freedom in the delicate structure of the standard model of fields and particles, and if this is not yet enough, the next advantage is preventing the electroweak vacuum to decay as a metastable local minimum; The quantum corrections which are the consequence of assuming non-minimal interaction between the Higgs field and the curvature compensates the running of the self coupling, preventing the model from developing another vacuum with lower energy than the electroweak vacuum. Existence of a new stable vacuum makes the higher electroweak vacuum metastable [22,23,24,25], which means that the universe which is supported by such metastable vacuum finally decays by penetrating to the lower minimum through the quantum true vacuum bubble creation [26, 27]. One may propose increasing the lifetime of the metastable electroweak vacuum to exceed the lifetime of the universe as a quick remedy for the problem, but this proposition arises another question; why our universe has chosen the metastable minimum instead of the stable one during the inflation [28]? The Higgs inflation resolves the problem by adding quantum corrections to the running of the self coupling constant in the right way [23]. This hypothesis does not require any new constraint on the reheating and preheating processes [29, 30] since it is enough for the inflaton field to settle in a less than the GUT energy scale after the inflation [31,32,33]. This is the simplest resolution, although it seems very sensitive to yet unknown interactions. There also exist some ideas which require the standard model to be revised [34]. A very close idea is assuming inflaton as a new field which interacts with the standard Higgs field [35].

Here, we try to employ the powerful dynamical system tools to provide a wider view from inflationary and pre/post-inflationary dynamic. In some parts, we look back to the original equations to resolve technical stiffness and modify the proposed dynamical system calculations. This is important because our analysis is not restricted to slow-roll conditions and therefore gives a panorama of what has been previously considered in a much tighter frame. We also keep the kinetic term and by this promote the scalar field from an auxiliary one to a physical one and break the explicit duality relation between the Higgs-Inflation and the Starobinsky f(R) model [10, 36, 37]. It is interesting to follow the pre-inflationary behavior of the variables where it seems that de Sitter attractor pulls inward the phantom trajectories [38,39,40,41]. Following observations that implied the idea of slight shift of the cosmological equation of state into the phantom region (\(w<-1\)), some pioneering researches showed the capability of scalar-tensor theories to yield late time attractive property of the de Sitter expansion for the phantom trajectories [42,43,44,45,46] which are partly inline with the current research. Phantom crossing at present epoch was investigated numerically by Motohashi et al. [45, 46] Although we will keep the mentioned surveys as the cornerstones for our work and even dedicate one section to compare their approaches with ours in more details, what makes this paper taste differently, besides trying to deliver exact results, is that we have shown that for a phantom originated path, the de Sitter trajectory may behave as a partial attractor which ends in an oscillatory phase. This bestows the entire procedure the possibility of being an inflationary scenario. All the above propositions will be supported by analytical and numerical calculations and the corresponding plots.

The outline of the paper is as follows; first, in the next section, we introduce a more general Lagrangian which is able to provide the Higgs-Inflation scenario. We start from writing the Friedmann equations and derive the corresponding equation of state. In Sect. 3, we introduce a suitable set of dynamical variables and find the dynamical equations. To see the consequences of the proposed dynamical structure, we have wait until Sect.  4, where by fixing the model to its final form we close the equations with respect to the variables. Section  5 contains a detailed discussion about the oscillatory phase. Having the appropriate dynamical variables and equations, in Sect.  6, we proceed by finding fixed points and eigenvalues and anticipating the flow behavior. In Sect. 7, we explain the mathematical results in a physical perspective where we focus on crossing the phantom borders toward de Sitter attractor. In Sect.  8, we transform back to the original variables (\(\phi \) and \({\dot{\phi }}\)), in order to compare our results with those of others. Section  9 is devoted to comparison between our results and some pre-existing works. Finally, in the last section, we summarize the methods and the achievements of the present work.

2 \(f(R,\phi )\) as a generalized gravity theory

Since we intend to analyze the Higgs-Inflation model, the generalized Lagrangian may be written as [47]

$$\begin{aligned} {\mathcal {L}}=\frac{{\mathcal {F}}(\phi )}{2}R-g^{\mu \nu }\partial _\mu \phi \partial _\nu \phi - {\mathcal {G}}(\phi ). \end{aligned}$$
(1)

For the Friedmann–Robertson–Walker universe, the equations of motion will be as follows [47, 48]

$$\begin{aligned} 3(H^2 {\mathcal {F}}+H\dot{{\mathcal {F}}})=\frac{1}{2}\dot{\phi }^2+{\mathcal {G}} \end{aligned}$$
(2)

and

$$\begin{aligned} \ddot{{\mathcal {F}}}-H\dot{{\mathcal {F}}} +2{\dot{H}}{\mathcal {F}}=-\dot{\phi }^2, \end{aligned}$$
(3)

in which dots denote time derivative. It is common to extract the following continuity equation from (2) and (3) or alternatively derive from direct variation of the action with respect to \(\phi \). [49, 50]

$$\begin{aligned} \ddot{\phi }+3 H \dot{\phi }+ {\mathcal {G}},_{\phi }-3 {\mathcal {F}},_{\phi }(2H^2+{\dot{H}})=0. \end{aligned}$$
(4)

In order to cast the above relations in the form of cosmological thermodynamics, we assume an effective perfect fluid in the spatially flat FLRW background;

$$\begin{aligned} a\propto t^{\frac{2}{3(1+w_{eff})}}, \end{aligned}$$
(5)

or equivalently

$$\begin{aligned} w_{eff}=-1-\frac{2}{3}\frac{{\dot{H}}}{H^2}. \end{aligned}$$
(6)

On the other hand, for any fluid to satisfy the conservation law (\(\dot{\rho }+3H(\rho +p)=0\)) in a FLRW metric it is required that

$$\begin{aligned} \rho = 3 C H^2 \;\; \text{ and } \;\; (\rho +p)=-2 C {\dot{H}}, \end{aligned}$$
(7)

for any arbitrary constant \(C_i\) for the fluid i. The additive property of isotropic pressures and homogeneous energy density allows one to write

$$\begin{aligned} \rho _{eff}=3 C H^2 \end{aligned}$$
(8)

and

$$\begin{aligned} \rho _{eff}+p_{eff}=-2 C {\dot{H}}, \end{aligned}$$
(9)

or equivalently

$$\begin{aligned} H^2=\frac{\rho _{eff}}{3 C}\;\; \text{ and } \;\; {\dot{H}}=-\frac{\rho _{eff}+p_{eff}}{2 C}, \end{aligned}$$
(10)

We want to build two relations that include the Friedmann equations (2) and (3) while containing the effective pressure and density definitions in a correct manner. To do this, we add up Eqs. (8) and (9) to the Friedmann equations (2) and (3) to obtain

$$\begin{aligned} 3(H^2 {\mathcal {F}}+H\dot{{\mathcal {F}}})+\rho _{eff} =\frac{1}{2}\dot{\phi }^2+{\mathcal {G}}+3 C H^2 \end{aligned}$$
(11)

and

$$\begin{aligned} \ddot{{\mathcal {F}}}-H\dot{{\mathcal {F}}}+2{\dot{H}}{\mathcal {F}}-2 C {\dot{H}}=-\dot{\phi }^2+\rho _{eff}+p_{eff}. \end{aligned}$$
(12)

By this, one congregates the equations truthfully, but one elaboration is still needed. The above manner of collecting the relations alters the freedom in C, because, one expects by setting \({\mathcal {F}}=1\) to recover minimal gravity-scalar theory with \(\rho _{eff}={\mathcal {G}}+\frac{1}{2}\dot{\phi }^2\) and \(\rho _{eff}+p_{eff}=\dot{\phi }^2\), therefore, C has to be normalized to unity. The final relations for effective density and pressure become

$$\begin{aligned} \rho _{eff}= & {} \frac{1}{2}\dot{\phi }^2+{\mathcal {G}} +3H^2(1-{\mathcal {F}})-3H{\dot{F}}, \end{aligned}$$
(13)
$$\begin{aligned} p_{eff}= & {} \frac{1}{2}\dot{\phi }^2-{\mathcal {G}} +\ddot{{\mathcal {F}}}+2H\dot{{\mathcal {F}}} -(1-{\mathcal {F}})(3H^2+2{\dot{H}}).\nonumber \\ \end{aligned}$$
(14)

Therefore, we have a consistent set of equations for the model in the Jordan frame from which we obtain the dynamical results. In the next section, we will apply the dynamical system method to understand how the system evolves under these equations.

3 Dynamical system approach

We choose the following dynamical variables

$$\begin{aligned} \chi _1\equiv \frac{\dot{\phi }^2}{6 {\mathcal {F}} H^2 }, \end{aligned}$$
(15)
$$\begin{aligned} \chi _2\equiv \frac{{\mathcal {G}}}{3 {\mathcal {F}} H^2 }, \end{aligned}$$
(16)

and

$$\begin{aligned} \chi _3\equiv -\frac{\dot{{\mathcal {F}}}}{{\mathcal {F}} H}. \end{aligned}$$
(17)

According to the Eq. (2), this set of variables obey the following constraint

$$\begin{aligned} \chi _1+\chi _2+\chi _3=1. \end{aligned}$$
(18)

The above algebraic equation lets us eliminate one of the variables in favor of the other two. But before doing this, let us proceed by writing the dynamical equations as

$$\begin{aligned} \frac{d \chi _1}{d N}= & {} \frac{\dot{\phi }\ddot{\phi }}{3{\mathcal {F}} H^3 }-2\chi _1(\frac{{\dot{H}}}{H^2})+\chi _1\chi _3\nonumber \\= & {} -6 \chi _1+\chi _3 (\chi _1-2)-\frac{{\dot{H}}}{H^2}(\chi _3+2\chi _1) -\frac{\dot{{\mathcal {G}}}}{3 {\mathcal {F}}H^3},\end{aligned}$$
(19)
$$\begin{aligned} \frac{d \chi _2}{d N}= & {} \frac{\dot{{\mathcal {G}}}}{3{\mathcal {F}} H^3}-2\chi _2(\frac{{\dot{H}}}{H^2})+\chi _2 \chi _3 \end{aligned}$$
(20)

and

$$\begin{aligned} \frac{d \chi _3}{d N}= & {} -\frac{\ddot{{\mathcal {F}}}}{{\mathcal {F}}H^2}-\chi _3 (\frac{{\dot{H}}}{H^2})\nonumber \\&+\,\chi _3 ^2=6\chi _1+\chi _3+\frac{{\dot{H}}}{H^2}(2-\chi _3)+\chi _3 ^2. \end{aligned}$$
(21)

where \(N=\ln {a}\) is the e-folding. Although the choice of the variables seems similar to [51] but as we will see, the required calculations are very different since in this case the second derivative of the Lagrangian with respect to R is equal to zero. To derive the right hand side of (19) and (21), we use (3) and (4) to obtain

$$\begin{aligned} \frac{\dot{\phi }\ddot{\phi }}{3{\mathcal {F}} H^3 }=-\frac{\dot{{\mathcal {G}}}}{3{\mathcal {F}} H^3}-6 \chi _1-\chi _3(2+\frac{{\dot{H}}}{H^2}) \end{aligned}$$
(22)

and

$$\begin{aligned} \frac{\ddot{{\mathcal {F}}}}{{\mathcal {F}}H^2}=-6 \chi _1-\chi _3-2(\frac{{\dot{H}}}{H^2}). \end{aligned}$$
(23)

Our set of equations seems not closed because of the appearance of the terms \(\frac{\dot{{\mathcal {G}}}}{3{\mathcal {F}} H^3}\) and \(\frac{{\dot{H}}}{H^2}\) in the equations which can not be recasted in terms of \(\chi _1...\chi _3\) at this stage. Of course, one may differentiate (18) to find a new equation in order to find \({\dot{H}}/H^2\) in terms of \(\chi _1...\chi _3\)

$$\begin{aligned} \frac{d \chi _1}{d N}+\frac{d \chi _2}{d N}+\frac{d \chi _3}{d N}=0. \end{aligned}$$
(24)

This new equation leads to

$$\begin{aligned} \frac{d \chi _1}{d N}+\frac{d \chi _2}{d N}+\frac{d \chi _3}{d N}=(\chi _3-\frac{2 {\dot{H}}}{H^2})(\chi _1+\chi _2+\chi _3-1)=0, \nonumber \\ \end{aligned}$$
(25)

Unfortunately, (25) can not be used for recasting \({\dot{H}}/H^2\) in terms of \(\chi _i\)’s, since (25) is always valid regardless of the \({\dot{H}}/H^2\) value. In the next section, we will prove that \({\dot{H}}/H^2\) and \(\frac{\dot{{\mathcal {G}}}}{3{\mathcal {F}} H^3}\) are not new degrees of freedom and can be redefined in terms of \(\chi _1\), \(\chi _2\) and \(\chi _3\) for the model considered in the present work.

4 Higgs-inflation: the unitary case

Unifying the Higgs and the inflaton field normally starts from considering the following non-minimal Lagrangian [23]

$$\begin{aligned} {\mathcal {L}}= \frac{M_p ^2}{2} R+\xi H^{\dagger }H R - \partial _\mu H^{\dagger } \partial ^{\mu }H-{\lambda }(H^{\dagger }H-\nu ^2)^2, \nonumber \\ \end{aligned}$$
(26)

where H stands for the standard model Higgs doublet. We choose to work in the unitary gauge \(H=h/\sqrt{2}\) [33, 37] and assume \(h\gg \nu \) for the infant universe. Then (26) simplifies as

$$\begin{aligned} {\mathcal {L}}\approx \frac{R}{2}\left( {M_p ^2}+\xi h^2\right) -\frac{1}{2}\partial _\mu h\partial ^{\mu }h-\frac{\lambda }{4}h^4. \end{aligned}$$
(27)

In a Friedmann–Robertson–Walker background metric, the above Lagrangian is used to build the inflationary model, by writing down the dynamical equations and using the method described in the previous section.First of all, let us look how the \(\frac{\dot{{\mathcal {G}}}}{3{\mathcal {F}} H^3}\) term appears in this model while one can define

$$\begin{aligned} {\mathcal {F}}(\phi )\equiv {M_p ^2}+\xi \phi ^2 \end{aligned}$$
(28)

and

$$\begin{aligned} {\mathcal {G}}(\phi )\equiv \frac{\lambda }{4}\phi ^4, \end{aligned}$$
(29)

where for convenience, we have renamed the Higgs scalar degree of freedom by the real field \(\phi \), (\(h\rightarrow \phi \)). Then one obtains

$$\begin{aligned} \frac{\dot{{\mathcal {G}}}}{3{\mathcal {F}} H^3}=-\frac{\lambda \dot{\phi }\phi ^3}{144 \xi H^3\left( {M_p ^2}+\xi \phi ^2\right) }=-48\xi \frac{\chi _1 \chi _2}{\chi _3}. \end{aligned}$$
(30)

Therefore, our system of equations become closed and we can write them as

$$\begin{aligned} \frac{d \chi _1}{d N}= & {} -6 \chi _1+\chi _3 (\chi _1-2)-\frac{{\dot{H}}}{H^2}(\chi _3+2\chi _1)+48\xi \frac{\chi _1 \chi _2}{\chi _3}, \end{aligned}$$
(31)
$$\begin{aligned} \frac{d \chi _2}{d N}= & {} -48\xi \frac{\chi _1 \chi _2}{\chi _3}-2\chi _2(\frac{{\dot{H}}}{H^2})+\chi _2 \chi _3, \end{aligned}$$
(32)
$$\begin{aligned} \frac{d \chi _3}{d N}= & {} 6\chi _1+\chi _3+\frac{{\dot{H}}}{H^2}(2-\chi _3)+\chi _3 ^2 \end{aligned}$$
(33)

One may argue that \({\dot{H}}/{H^2}\) needs to be considered as a new dynamical variable, but here, we prove that \({\dot{H}}/{H^2}\) is not a new degree of freedom. We start by calculating \(\frac{\ddot{{\mathcal {F}}}}{{\mathcal {F}}H^2}\) for the Lagrangian (27).

$$\begin{aligned}&\frac{\ddot{{\mathcal {F}}}}{{\mathcal {F}}H^2}=\frac{2\xi (\dot{\phi }^2+\phi \ddot{\phi })}{{\mathcal {F}}H^2}\nonumber \\&\quad =12\xi \chi _1+\frac{2\xi \phi }{{\mathcal {F}}H^2}\left( -3H\dot{\phi }-{\mathcal {G}},_\phi +3 {\mathcal {F}},_\phi (2H^2+{\dot{H}}) \right) \nonumber \\&quad =12 \xi \chi _1+\frac{2\xi \phi }{{\mathcal {F}}H^2}\left( -3 H \dot{\phi }-\lambda \phi ^3+6\xi \phi (2 H^2+{\dot{H}}) \right) \nonumber \\&\quad =12 \xi \chi _1+3{\chi _3}-24 \xi \chi _2+\frac{\chi _3 ^2}{2 \chi _1}(2+\frac{{\dot{H}}}{H^2}). \end{aligned}$$
(34)

Although the original equations are well-defined for \(\dot{\phi }=0\) where \(\dot{\phi }\) cancels out from the \(\chi _3 ^2 / 2 \chi _1\) fraction, in the framework of dynamical systems, \(\chi _1\) appears in the denominator and we have to be cautious about \(\chi _1\) reaching 0. One can avoid possible ambiguities by considering to the original relations, as we will do in this section. To be more clear \(\chi _1=0\) means \(\dot{\phi }=0\) which indicates the return point for the scalar field oscillations. Using the above equation in (23) yields

$$\begin{aligned} \frac{{\dot{H}}}{H^2}=-\frac{2 \left( 4 \hbox {} \chi _1 (\chi _3-6 \xi {\chi }_2)+6 (2 \xi +1) {\chi }_1^2+{\chi }_3^2\right) }{4 {\chi }_1+{\chi }_3^2}, \end{aligned}$$
(35)

which means that our dynamical equations are closed. For the pure f(R) models in the absence of matter sources there is an elegant way to reduce the equations to one first-order equation for H as a function of R in the Jordan frame [52]. But considering the field kinetic term, it is not possible for us to transform the equations to the matter free f(R) gravity, although, we still have a chance to eliminate one of the variables thanks to (18). Eliminating \(\chi _3\) is more reasonable since \(\chi _1=0\) requires \(\dot{\phi }=0\) and \(\chi _2=0\) requires \(\phi =0\) while \(\chi _3=0\) happens to be true for both mentioned conditions separately or together which makes the analysis more complicated. In this regard, the ultimate equations will be

$$\begin{aligned} \begin{aligned} \frac{d \chi _1}{d N}&=-\chi _1 \left( \chi _2 \left( \frac{48 \xi }{\chi _1+\chi _2-1}+1\right) +\chi _1+\frac{{\dot{H}}}{H^2}+3\right) \\&\quad +\,(\chi _2-1) (\frac{{\dot{H}}}{H^2}+2), \end{aligned} \end{aligned}$$
(36)

and

$$\begin{aligned} \frac{d \chi _2}{d N}=\chi _2 \left( \chi _1 \left( \frac{48 \xi }{\chi _1+\chi _2-1}-1\right) -\chi _2-2 \frac{{\dot{H}}}{H^2}+1\right) , \nonumber \\ \end{aligned}$$
(37)

in which \({\dot{H}}/H^2\) can be replaced by

$$\begin{aligned} \frac{{\dot{H}}}{H^2}{=}-\frac{2 \left( 3 \chi _1^2 (1+4 \xi )-2 \chi _1 (12\xi \chi _2 +\chi _2-1)+(\chi _2-1)^2\right) }{\chi _1^2+2 \chi _1 (\chi _2+1)+(\chi _2-1)^2}. \nonumber \\ \end{aligned}$$
(38)

It should be pointed out that the point \((\chi _1+\chi _2)^2+1- 2(\chi _2-\chi _1)=0\) (vanishing denominator) leads to a finite value for \({\dot{H}}/H^2\). Since our choice of variables requires \(\chi _1,\chi _2 \ge 0\), the only condition in which the denominator vanishes is \(\chi _1=0\) and \(\chi _2=1\). But this point is also the root of the numerator. In fact, this ambiguity is not essential and has appeared as a result of our definitions and calculations, as we have mentioned earlier. To see this, let us get back to (35) and write it as

$$\begin{aligned} \frac{{\dot{H}}}{H^2}= & {} -\frac{2 \left( 4 {\chi }_1 ({\chi }_3-6 \xi {\chi }_2)+6 (2 \xi +1) {\chi }_1^2+{\chi }_3^2\right) }{4 {\chi }_1+{\chi }_3^2}\nonumber \\= & {} -2\frac{(4(\chi _3-6\xi \chi _2)+6\chi _1(2\xi +1)+\frac{\chi _3 ^2}{\chi _1}}{4+\frac{\chi _3 ^2}{\chi _1}}. \end{aligned}$$
(39)

We know from the definitions of dynamical variables that

$$\begin{aligned} \frac{\chi _3 ^2}{\chi _1}=\frac{24 \xi ^2 \phi ^2}{{\mathcal {F}}}=\frac{24 \xi ^2 \phi ^2}{{M}_p ^2+\xi \phi ^2}. \end{aligned}$$
(40)

If we substitute the above relation in (39) and evaluate it for \(\chi _1=\chi _3=0\) and \(\chi _2=1\), the result is

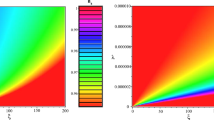
$$\begin{aligned} \frac{{\dot{H}}}{H^2}(\chi _1=0,\chi _2=1,\chi _3=0)=-2\frac{-24\xi +\frac{24 \xi ^2 \phi ^2}{{M}_p ^2+\xi \phi ^2}}{4+\frac{24 \xi ^2 \phi ^2}{{M}_p ^2+\xi \phi ^2}}. \nonumber \\ \end{aligned}$$
(41)

For conformal case (\(\xi =-1/6\)) this always leads to \(-2\). Although for any other choices of \(\xi \) the \({\dot{H}}/H^2\) ratio is a function of \(\phi \), if we limit \(\xi \) to be a positive integer, then \({\dot{H}}/H^2\) at the discussed point also becomes a positive (phantom-like) value which asymptotically vanishes for larger \(\phi \)’s (\(\xi \phi ^2 \gg M_p ^2\)). In Fig. 1, this property has been demonstrated in two different scale: Fig. 1a shows that the de Sitter path appears as an attractor for incoming trajectories. This plot does not have enough resolution to magnify \((\chi _1=0,\chi _2=1)\) point. Figure 1b has an enough resolution and one can recognize the essential role of the point \((\chi _1=0,\chi _2=1)\) which is the return point of oscillations. The former sub-figure contains only one complete oscillation in order to help readers to follow the subject of the current discussion. Several oscillations phase diagram has been plotted in another plot (Fig. 9). From (32) we infer that for \({\dot{H}}/H^2>0\), \(\chi _2\) remains a decreasing function of time at this point and therefore the inward trajectories are pushed to meet the other fixed point at (\(\chi _1=1,\chi _2=0\); Fig. 1). The latter point is a representative of Higgs field minimum since \(\phi \) appears fourth power in \(\chi _2\) definition. To reach the potential minimum, the trajectory needs to cross out the phantom boundary which is defined by

$$\begin{aligned} \chi _2= & {} 12 \chi _1 \xi +\chi _1+1\\&+\sqrt{\chi _1 \left( 72\xi ^2 \chi _1+6 (\chi _1+2) \xi -\chi _1\right) }. \end{aligned}$$

The very important result is that every time the potential is around its minimum, the equation of state is like matter dominated stage and one can demand for the (p)reheating to operate. We know that the preheating is more effective whenever the inflaton crosses its minimum due to the parametric resonance phenomenon. Moreover, our numerical calculations confirm that the mentioned flipping between phantom and ordinary regions gives \({\bar{w}}\approx 1/3\) (where the bar means average over e-folds) which is another support for being in an oscillatory phase (Figs. 2, 3).

5 An oscillatory fate; the vindication of an inflationary scenario

The requirement that the original Higgs inflation model should be followed by a transient oscillatory era after the inflationary period is an old and well-known practice. On the other hand, there have been suggestions that there might be phantom crossings before reaching the de Sitter destiny of the late universe [42, 43, 45, 46]. In this regard, it does not seem likely to reconcile these two different ideas in a manner that a phantom originated path reaches a de Sitter partial attractor where enough inflationary e-folds are accomplished before falling into an oscillatory phase. Figure 7 demonstrates the complete evolution of \(\chi _1\) and \(\chi _2\) in which the motion stars from phantom era and after approximately 1000 e-folding ends in an oscillatory phase. The evolution of \(w_{eff}\) for this simulation has been plotted in Fig. 6 where one can recognize the smooth phantom crossing, the de Sitter inflationary period and the oscillatory ultimate from the plots. It is already known that phantom originated trajectories may exhibit many oscillations around the de Sitter boundary, flipping between phantom and ordinary equations of state, while these oscillations never provide an end to the de Sitter main trajectory [45, 46]. Therefore, one may exclude any inflationary hypothesis which has a phantom origin since it seems impossible to find a required end of de Sitter expansion for them. In other words, Higgs inflation like other inflationary scenarios must possess an ordinary (non-phantom) initial condition. Here, we intend to show that this conclusion is not generally true and at least for the original Higgs inflation scenario, a phantom origin can evolve to an ordinary inflation with a desired oscillatory end. Numerical simulations also confirm this behavior (Figs. 2, 3, 5, 6) and one can recognize the \(w_{eff}\) evolution from phantom region to de Sitter expansion and follow its way towards \(\bar{w_{eff}}=1/3\) during ultimate oscillations around vacuum (Figs. 3, 6). The entire scenario has been plotted in Fig. 6 where one can follow the history from a phantom-like pre-inflationary start point to a quasi de Sitter partial attractor which ends at an oscillatory phase. We have already shown that for a typical f(R) inflationary theory, the post-inflationary oscillations occur around \(R=0\) which in FLRW background \(R=6{\dot{H}}+12 H^2\) can be written as \({\dot{H}}/H^2=-2\) or equivalently \(w_{eff}=1/3\) [53,54,55]. Of course, being in the Jordan frame makes the oscillatory interpretation slightly weird but one can easily infer that during an oscillation the point \((\chi _1=0,\chi _2=1)\) marks the return point of the Higgs field where \(\dot{\phi }\) vanishes and \((\chi _1=1,\chi _2=0)\) indicates the central point of the Higgs potential. Without assuming higher powers of Ricci scalar in the Lagrangian, one may not expect the system to exhibit explicit oscillations around \(R=0\) which is the overall behavior of an extra scalar degree of freedom (scalaron) in f(R) theories. In Sect. 8, we will see that such oscillations around \(R=0\) exist and become quasi sinusoidal as they lose their energy due to expansion (Fig. 10). We also see that the oscillations occur around the Higgs field minimum. Therefore, we witness a twofold oscillation. As we have stated earlier, numerical calculations confirm that \(w_{eff}\) shows flattering behavior around the average 1 / 3 value (see Fig. 3). Any complete oscillation needs to meet the minimum at \(\phi =0\) \((\chi _1=1,\chi _2=0)\) as well as the return point \(\dot{\phi }=0\) at \((\chi _1=0,\chi _2=1)\). In other words, our choice of variables restrict the minimum of the \(\chi _1\) and \(\chi _2\) oscillatory amplitude to be unity. It may seem weird that in an expanding universe \(\chi _1\) and \(\chi _2\) oscillations do not decay out and asymptotically reach a unit amplitude. But one has to remember that \(\chi _1\) and \(\chi _2\) have nontrivial relations with R, \(\phi \) and \(\dot{\phi }\) and as we will show, \(\phi \) and \(\dot{\phi }\) oscillations continue to decay with time even when \(\chi _1\) and \(\chi _2\) oscillate with an approximately constant amplitude (Fig. 11).

6 Fixed points and their behavior

Having the Eqs. (36) and (37), one is able to find the fixed points. Equating these equations to zero, one obtains four fixed points

$$\begin{aligned} P_1: \chi _1= & {} 0,\;\chi _2=0, \end{aligned}$$
(42)
$$\begin{aligned} P_2: \chi _1= & {} 0,\;\chi _2=5, \end{aligned}$$
(43)
$$\begin{aligned} P_3: \chi _1= & {} 1+12\xi + 12\sqrt{\xi \left( \xi +\frac{1}{6}\right) },\; \chi _2=0, \end{aligned}$$
(44)

and

$$\begin{aligned} P_4: \chi _1=1+12\xi - 12\sqrt{\xi \left( \xi +\frac{1}{6}\right) },\; \chi _2=0. \end{aligned}$$
(45)

One can construct the following Jacobian

$$\begin{aligned} J\equiv \begin{pmatrix} \partial _{\chi _1}\left( \frac{d\chi _1}{dN}\right) &{}\partial _{\chi _2} \left( \frac{d\chi _1}{dN}\right) \\ \partial _{\chi _1}\left( \frac{d\chi _2}{dN}\right) &{} \partial _{\chi _2} \left( \frac{d\chi _2}{dN}\right) \end{pmatrix} \end{aligned}$$
(46)

and find the corresponding eigenvalues at each fixed point \(P_i\) as below [56]

$$\begin{aligned} J(\chi _1(P_i),\chi _2(P_i)) \begin{pmatrix} \chi _1(P_i)\\ \chi _2(P_i) \end{pmatrix} =\lambda \begin{pmatrix} \chi _1(P_i)\\ \chi _2(P_i) \end{pmatrix}. \end{aligned}$$
(47)

The above linearization recipe yields

$$\begin{aligned}&P_1: \lambda _1=-1,\;\lambda _2=5, \end{aligned}$$
(48)
$$\begin{aligned}&P_2:\lambda _1=-5,\;\lambda _2=4, \end{aligned}$$
(49)
$$\begin{aligned}&P_3: \lambda _1=-12 \sqrt{\xi \left( \xi +\frac{1}{6}\right) }-12 \xi ,\;\nonumber \\&\lambda _2=36 \sqrt{\xi \left( \xi +\frac{1}{6}\right) }+36 \xi +6, \end{aligned}$$
(50)

and

$$\begin{aligned} \begin{aligned}&P_4: \lambda _1=12 \sqrt{\xi \left( \xi +\frac{1}{6}\right) }-12 \xi ,\;\\&\quad \lambda _2=-36 \sqrt{\xi \left( \xi +\frac{1}{6}\right) }+36 \xi +6. \end{aligned} \end{aligned}$$
(51)

The above results show that the fixed points \(P_1\) and \(P_2\) are always saddle points (unstable). The two remaining points \(P_3\) and \(P_4\) coincide for minimal coupling (\(\xi =0\)) and for non-minimal conformal gravity \(\xi =-1/6\), the \(P_3/P_4\) splitting may be interpreted as the breaking of the conformal gravity symmetry. Here, an elaboration is in order; our analysis involves the Higgs-inflaton in high energy regime where \(\phi ^2\gg \nu ^2\). In this regard, in our approach, the calculations become less accurate near the \(\chi _2=0\) axis, although, the oscillatory behavior can be present. This, of course, is not an important weakness, since we are mostly interested in pre-inflationary and inflationary phases and the primary post-inflationary oscillations where for all of them the high energy conditions govern the universe. The point \(P_1\) plays the role of the unstable local maximum in the Mexican hat scenario. That is the reason why the origin (\(\chi _1=0,\chi _2=0\)) in \(\chi _1-\chi _2\) phase portrait is unreachable by the trajectories. In fact this point represents the \(\phi =0\) and \(\dot{\phi }=0\) unstable point.

7 Where does the inflation happen?

Since we ignore the electroweak vacuum energy in our high energy regime, the fixed point \((\chi _1=0, \chi _2=0)\) does not develop any constant density to cause exponential expansion. This is not important since we already know that symmetry breaking models can not provide effective inflation for the standard model energy scale, mostly because the self-coupling must be much smaller during inflation to explain why the primordial gravitational waves have no considerable footprint on the CMB. This means that although we use terms like Higgs-inflation to reconcile the standard model and inflation, but it does not mean that symmetry breaking and inflation happen coincidentally. In fact, in such scenarios the inflation is realized by assuming a very high energy initial condition in which the potential imitates a power law potential. In our approach, the above fact has been taken into account by using the \(\phi ^2\gg \nu ^2\) regime which enables us to keep only the quadratic potential term throughout the calculations. To find the appropriate region for de Sitter expansion, we solve \({\dot{H}}/H^2=0\), to find

$$\begin{aligned} \frac{{\dot{H}}}{H^2}= & {} 0\Longrightarrow \chi _2=\pm \sqrt{\chi _1 \left( 72\xi ^2 \chi _1+6 (\chi _1+2) \xi -\chi _1\right) }\nonumber \\&+\,12 \chi _1 \xi +\chi _1+1. \end{aligned}$$
(52)

Since the choice of the variables requires \(\chi _1\ge 0\) and \(\chi _2\ge 0\) for the Higgs-Inflation model, the two solutions in (52) represent the boundaries of \(w<-1\) and \(w>-1\) regions respectively (Figs. 4, 5). In an ordinary quintessence or inflationary model (minimal scalar field theory), the phantom realization necessitates ghost fields i.e. negative kinetic energy. Now, one can infer that for non-minimal Higgs-inflation scenario, the phantom conditions might be realized without having ghost. To discuss this more clearly, let us analyze Eq. (52) for \(\xi \gg 1\) which is, in fact, the condition to have an effective inflation. In this regime, the solutions are approximated as

$$\begin{aligned} \chi _2=1+\frac{\chi _1}{2}\;\; and\;\; \chi _2=1+24\xi \chi _1, \end{aligned}$$
(53)

which represent two lines in the first quadrant of the \(\chi _1-\chi _2\) phase portrait. For all the points between these lines w is smaller than \(-1\) which corresponds to phantom energy domination while outside them \(w>-1\) . For large \(\xi \), the line \(\chi _2=1+24\xi \chi _1\) almost matches with the adjacent flow curves.The other line (\(\chi _2=1+\frac{\chi _1}{2}\)) exhibits a constant 1 / 2 slope. The more interesting fact is that the field flow moves from the ordinary region toward the \(w<-1\) area crossing the \(\chi _2=1+\frac{\chi _1}{2}\) line. One has to note that since there is no fixed point for de Sitter expansion, the inflation happens when the field flow asymptotically moves near one of the two \(w=-1\) boundaries. Besides the numerical portrait, it is easy to prove that the field flow could not move tangential to \(\chi _2=1+\frac{\chi _1}{2}\), a simple explanation will be derived from

$$\begin{aligned} \frac{d \chi _1}{d N}_{_{(\chi _2=\chi _1/2)}}=\frac{\chi _1 \left( -9 \chi _1^2-96 \xi \chi _1 +4\right) }{6 \chi _1-4}, \end{aligned}$$
(54)

and

$$\begin{aligned} \frac{d \chi _2}{d N}_{_{(\chi _2=\chi _1/2)}}=\frac{\chi _1 (3 \chi _1 (-3 \chi _1+64 \xi +12)-20)}{12 \chi _1-8}, \end{aligned}$$
(55)

which lead to

$$\begin{aligned} \frac{d \chi _2}{d \chi _1}_{_{(\chi _2=\chi _1/2)}}=\frac{9 \chi _1^2-12 \chi _1 (16 \xi +3)+20}{2 \left( 9 \chi _1^2+96\xi \chi _1 -4\right) }. \end{aligned}$$
(56)

In this case, the slope of the flow asymptotically becomes 1 / 2 when \(\chi _1=2\chi _2\rightarrow \infty \). It means that we may expect de Sitter expansion there. If we take into account the term linear in \(\chi _1\), then the slope is slightly less than 1 / 2 which means that all trajectories which start from \(w>-1\) ultimately cross the phantom boundary. In a same manner, we can check the field behavior near the other border line (\(\chi _2=1+24\xi \chi _1\)). Since we restricted ourselves to \(\xi \gg 1\) and \(\chi _2>1\), i.e. above the fixed point \((\chi _1=0,\; \chi _2=1)\), one obtains

$$\begin{aligned}&\frac{d \chi _1}{d N}_{_{(\chi _2=24\xi \chi _1)}}\nonumber \\&\quad =\chi _1 (2 \chi _1^3 (12 \xi -1) (24 \xi +1) (120 \xi -1)\nonumber \\&\qquad +192 \chi _1^2 \xi (1-54 \xi )\nonumber \\&\qquad -(24 \xi \chi _1 +\chi _1)^4+2 \chi _1 (60 \xi -1)+1)\nonumber \\&\qquad /{(24 \xi \chi _1 +\chi _1-1) \left( (24 \xi \chi _1 +\chi _1)^2+\chi _1 (2-48 \xi )+1\right) }\nonumber \\&\quad \approx -24 \xi \chi _2^2 \end{aligned}$$
(57)

and

$$\begin{aligned}&\frac{d \chi _2}{d N}_{_{(\chi _2=24\xi \chi _1)}}= 24 \xi \chi _1 (12\chi _1^3 (24 \xi +1) \left( 288 \xi ^2+1\right) \nonumber \\&\qquad -2 \chi _1^2 (72 \xi (72 \xi -1)+1)\nonumber \\&\qquad -(24 \xi \chi _1 +\chi _1) ^4+\chi _1 (432 \xi -4)-5)\nonumber \\&\quad /{(24 \xi \chi _1 +\chi _1-1) \left( (24 \xi \chi _1 +\chi _1)^2+\chi _1 (2-48 \xi )+1\right) }\nonumber \\&\quad \approx -576 \xi ^2\chi _1^2. \end{aligned}$$
(58)

It is straightforward to find that

$$\begin{aligned} \frac{d \chi _2}{d \chi _1}_{_{(\chi _2=24\xi \chi _1)}}\approx 24 \xi \,{(\xi \gg 1\; and\; \chi _2>1)}. \end{aligned}$$
(59)

From a mathematical point of view, this de Sitter line appears as an attractor for all the phantom trajectories. Of course, the viability of having a successful inflation also depends on having enough e-folds which means the trajectories must have a sufficient asymptotic motion before reaching the oscillatory phase. It is important that the field flow reaches a region that violates the inflationary conditions and put an end to the inflationary period. It is obvious that for our choice of independent variables i.e. \(\chi _1\equiv \dot{\phi }^2/6{\mathcal {F}}H^2\) and \(\chi _2\equiv \lambda \phi ^4/12{\mathcal {F}}H^2\), the oscillations lie in the \(\chi _1>0\) & \(\chi _2>0\) quadrant and always meet the return point at \(\chi _1=0 \) and \(\chi _2=1\). As it was stated earlier, the mentioned return point is near the de Sitter partial attractors but not part of it since as we have already shown, \({\dot{H}}/H^2>0\) at this point. One has to note that the horizon exit must happen in \(w_{eff}\gtrapprox -1\) region to support the observed spectral index on the CMB. Therefore the horizon exit happens before entering the phantom era or just after leaving it.

Fig. 1
figure 1

a The thick line indicates \(\chi _2= +\sqrt{\chi _1 \left( 72\xi ^2 \chi _1+6 (\chi _1+2) \xi -\chi _1\right) }+12 \chi _1 \xi +\chi _1+1\). We have mentioned that this curve corresponds to the \(w_{eff}=-1\) boundary. As the calculations show, the field flow asymptotically becomes tangent to this line. This graph confirms the de Sitter as a transient attractor path for phantoms. b The smaller scales of \(\chi _1\) and \(\chi _2\) phase portrait with more resolution in numerical calculations reveals more details. The flows depart from the de Sitter line which ends at \((\chi _1=0,\chi _2=1)\) entering ordinary region then passing the local maximum at \(\phi =0\) \((\chi _2=0)\). Afterwards, another oscillation begins conducting the trajectory towards the return point \((\chi _1=0,\chi _2=1)\). In simulations one can achieve more oscillations by cascading several numerical calculations, assuming the higher derivatives or approximating the vicinity of extrema. Without the (p)reheating outgoing energy channel, we do not expect the oscillations to imitate the early universe behavior completely, although it is enough for our purpose to distinguish oscillatory phase at the end of the de Sitter expansion

Full size image
Fig. 2
figure 2

The red trajectory shows a typical path to realize the inflation. One may interpret the semi-spiral trajectories as oscillations around the potential minimum. In the absence of matter and (p)reheating after the inflation, the simulation deviates from the standard early universe models but mathematically, one observes phantom crossings during the oscillatory phase

Full size image
Fig. 3
figure 3

Both plots above are results of the numerical calculation with \(\xi =100000\), \(\chi _1(0)=100\) and \(\chi _2(0)=100\) such that the implied steps pushes out the field from the vicinity of the \((\chi _1=0,\chi _2=1)\) point and the numerical calculation successfully conducts the first oscillation. a One complete oscillation has been plotted; One has to note that the motion starts from \(\chi _1(0)=100\) and \(\chi _2(0)=100\) but the starting part has been ignored to obtain a more clear picture. b The evolution of \(w_{eff}\) has been plotted. As one expects for an oscillatory phase, the time average (e-folds average) of \(w_{eff}\) is positive and according to the numerical integration over a period it is approximately equal to 1 / 3. The dominance of the positive \(w_{eff}\) area with respect to the negative area is obvious

Full size image
Fig. 4
figure 4

Demonstrating the phantom boundaries in some different regions and scales. The blue curve corresponds to \(\chi _2=-\sqrt{\chi _1 \left( 72\xi ^2 \chi _1+6 (\chi _1+2) \xi -\chi _1\right) }+12 \chi _1 \xi +\chi _1+1\) and the orange curve to \(\chi _2=\sqrt{\chi _1 \left( 72\xi ^2 \chi _1+6 (\chi _1+2) \xi -\chi _1\right) }+12 \chi _1 \xi +\chi _1+1\) which are the roots of \({\dot{H}}=0\). As we have discussed in the text, although the point \((\chi _1=0,\chi _2=1)\) is a branching point for the above curves but since it makes \(\frac{{\dot{H}}}{H^2}\) ambiguous, it requires an independent treatment. This care is also required at the vicinity of this point

Full size image
Fig. 5
figure 5

These two plots show the phase portrait of the dynamical variables \(\chi _{1,2}\) at two different scales. The Phantom and ordinary regions have been indicated by colors

Full size image

Note 1; Without considering the electroweak vacuum expectation value, the potential minimum becomes negative since the central local maximum is zero (\(V(\phi =0)=0\)). This Point, of course, reduces the level of generality for the calculations and the plotted simulations. But since we are interested in high energy behavior of the field dynamics and concentrate on the effect of non trivial kinetic energy, all the discussions remain valid with very good accuracy.

Note 2; In our model, we expect the big bang singularity (if any) to occur at \(\chi _1=\chi _2=0\), since at BB, \(a\rightarrow 0\) and \(H\rightarrow \infty \). Numerical results (especially Fig. 1) show that \(\chi _1=\chi _2=0\) is an unstable fixed point and the behavior of trajectories is more consistent with a bouncing universe. This point is essentially unreachable in our approach since it requires \(\chi _1=\chi _2=\chi _3=0\) which is in contradiction to the \(\chi _1+\chi _2+\chi _3=1\) constraint. The repelling characteristic of the \(\chi _1=\chi _2=0\) point physically stems from tachyonic instability at the origin (Fig. 6).

Fig. 6
figure 6

Both the above plots have been taken from one numerical simulation but for different ranges of N. This simulation has been initiated with \(\chi _1(N=0)=1\) and \(\chi _2(N=0)=100\) with \(\xi =400\), \(M_p=1\) and \(\lambda =1\). This set of initial conditions along with the parameters choice corresponds to \(w_{eff}[N=0]\approx -127\). a The phantom energy exponentially increases toward de Sitter (\(w_{eff}=-1\)). This part of the simulation confirms that de Sitter is a transient attractor path for phantom originated trajectories. As one recognizes, the deeper in the phantom region, the faster (less e-folds) motion toward de Sitter attractor. b \(w_{eff}\) asymptotically approaches the de Sitter expansion for enough e-folds before encountering the oscillations. As it is shown in Fig. 3 the average \(w_{eff}\) for each complete oscillation is about 1 / 3

Full size image

8 Return to the original variables

So far we have discussed how a trajectory may move from phantom region to the de Sitter asymptote and then start oscillating. Our analysis has exploited the dynamical system method and the standard rules of this method. Particularly, we have found ‘sink’, ‘source’ and ‘saddle’ points according to the dynamical system terminology and used their behavior as the corner stones for our conclusions. In this section, we will concrete the previous results by delivering supportive numerical analysis and corresponding plots. of course, the dynamical variables \(\chi _1\) and \(\chi _2\) are the best choice for testifying the previous analysis through numerical simulation. Figure 7 shows the behavior of \(\chi _1\) and \(\chi _2\) for the entire proposed scenario: The both initiate from large values inside the phantom region (\(\chi _1(N=0)=100,\chi _2(N=0)=10\)) and after some quasi-static e-folds start oscillating. The amplitude of the oscillations for both \(\chi _1\) and \(\chi _2\) converge toward unity as has been previously discussed. In order to obtain more physical insight about the oscillations, one may analyze the \(\phi \), \(\dot{\phi }\) and Ricci scalar behavior. To achieve the above, first we have to recast the mentioned parameters in terms of the dynamical variables \(\chi _1\) and \(\chi _2\). Using (40) one infers

$$\begin{aligned} \phi ^2=\frac{{M_p} ^2 {\chi _3}^2}{\xi (24 \xi \chi _1-{\chi _3}^2)}=\frac{{M_p}^2 (1-\chi _1-\chi _2)^2}{\xi \left( 24\xi \chi _1-(1-\chi _1-\chi _2)^2\right) }, \nonumber \\ \end{aligned}$$
(60)

where in the last stage we have used \(\chi _1+\chi _2+\chi _3=1\). Plotting the result shows how the field \(\phi \) decreases with time and one can see that \(\phi \) tend to decay with the cosmic expansion. It would be constructive to see the \({\dot{\phi }}\) behavior. To do this, one may start from

$$\begin{aligned} \frac{\chi _1}{\chi _2}=\frac{4 {\dot{\phi }}^2}{\lambda \phi ^4}. \end{aligned}$$
(61)

The above relation in combination with (60) straightforwardly yields

$$\begin{aligned} {\dot{\phi }}^2= & {} \frac{\lambda \chi _1}{4\chi _2}\left( \frac{{M_p}^2 (1-\chi _1-\chi _2)^2}{\xi \left( 24\xi \chi _1 -(1-\chi _1-\chi _2)^2\right) }\right) ^2, \end{aligned}$$
(62)

which has been plotted with respect to e-folds in Fig. 8. It would be constructive to cancel out the time (e-fold) dependency between \(\chi _1\) and \(\chi _2\) to see their implicit behavior with respect to each other. Figure 9 demonstrates this immediate relation which is in complete accord with Figs. 1 and 2 in which only one of the oscillations has been shown. One has to note that all the spins in Fig. 9 is the sequence of one curve and we have deliberately cut the smaller oscillations to respect the plot resolution. One obviously recognizes that all the oscillations pass through the potential minimum at \((\chi _1=1,\chi _2=0)\) \((\phi =0)\) and the return point at \((\chi _1=0,\chi _2=1)\) \(({\dot{\phi }}=0)\). It is also worth to see the \(w_eff\) behavior. One has note that in each simulation in order to clarifying one part of the trajectory history, we have chosen different initial condition and the situation is almost the same about the \(\xi \) parameter. The main idea is to devoted more numerical resolution to the part which is under analysis. For example to focus on the oscillatory phase the initial conditions should be selected in manner that the oscillation starts shortly after the onset of the oscillation which optimizes the resolution and the calculation time. One can also proceed to find Hubble Parameter and Ricci scalar dynamics. From the definition (15) one readily infers

$$\begin{aligned} H^2=\frac{\dot{\phi }^2}{6 {\mathcal {F}}\chi _1}=\frac{\dot{\phi }^2}{6(M_p ^2+\xi \phi ^2)\chi _1}. \end{aligned}$$
(63)

Since we have already derived \(\phi ^2\) and \({\dot{\phi }} ^2\) in terms of \(\chi _{1,2}\) (60 and 62), the above relation can be written as bellow

$$\begin{aligned} H^2=\frac{\lambda M_{P}^2 (1-\chi _1 -\chi _2)^4}{576\xi ^3 \chi _1\chi _2 \left( 24 \xi \chi _1-(1-\chi _1 -\chi _2)^2\right) }. \end{aligned}$$
(64)

From the above relation in combination with (38) one can derive a relation for \({\dot{H}}\) as bellow

$$\begin{aligned} \begin{array}{l@{}l} {\dot{H}}= \frac{\lambda M_p ^2(1-\chi _1-\chi _2)^4\left( (1-\chi _2)^2+3(1+4\xi ) \chi _1^2+2(1-\chi _2-12\xi \chi _2) \right) }{288\xi ^3\chi _1\chi _2\left( \chi _1 ^2+(1-\chi _2)^2+2\chi _1(1+\chi _2)(1-\chi _1-\chi _2)^2-24\xi \chi _1\right) } \end{array} \end{aligned}$$
(65)

and using \(R=12 H^2+6{\dot{H}}\) one ultimately obtains

$$\begin{aligned} \begin{array}{l@{}l} R=\frac{M_P ^2 \lambda (1+6\xi )(\chi _1 - 2 \chi _2)(1-\chi _1 - 2 \chi _2)^4}{24\xi ^3\chi _2 \left( (1-\chi _1 - 2 \chi _2)^2-24\xi \chi _1\right) \left( \chi _1 ^2+ (\chi _2-1)^2+2\chi _1(1+\chi _2)\right) }. \end{array} \end{aligned}$$
(66)

The last relation can be consider as the extractive of all the research analysis since it has interconnectedly employed all the definitions and assumptions of the proposed scenario. In other words, any mistake or deviation must be amplified in calculating the Ricci scalar. Figure 10 shows the result of calculating the Ricci scalar. One easily recognize two facts: first R is oscillating around \(R=0\). Second: the oscillations imitate a damping sinusoidal as time passes. Both the above results are in complete accord with the analysis of the scalar-tensor inflationary models in low energy limit ([53,54,55]).

As it has already been stated all the oscillations have to pass through the point \((\chi _1=1,\chi _2=0)\) and the return point \((\chi _1=0,\chi _2=1)\). In this regard, the trajectories wrap around the \(\chi _2=1-\chi _1\) line segment (Fig. 9). As the oscillations lose their energy, the trajectories become closer to the \(\chi _2=1-\chi _1\) line segment but never reach it. That is because moving on the \(\chi _2=1-\chi _1\) line segment means that \(\chi _3\) vanishes constantly throughout the path and according to \(\chi _3\) definition, it means \(\phi \) or \({\dot{\phi }}\) or both must be zero. In other words, the deviation from the \(\chi _2=1-\chi _1\) line segment is determined by the \(\chi _3\) value which in general, only vanishes for the \((\chi _1=1,\chi _2=0)\) and \((\chi _1=0,\chi _2=1)\) points. As one can infer from the numerical calculations and plots particularly Fig. 8, around the potential central point, \({\dot{\phi }}\) is still much smaller than \(\phi \) and \(\chi _3\) remains near unit unless for very close vicinity when \(\phi \) becomes vanishingly small (Figs. 9, 11). That is why the trajectory has a pyriform.

Fig. 7
figure 7

Both the above plots have been initiated from \(\chi _1=1\), \(\chi _2=100\) with \(\xi =400\), \(M_p\)=1 and \(\lambda =1\). a The deeper in the phantom region the faster motion toward the de Sitter attractor. Both variables then demonstrate very slow motion near the point \((\chi _1=0,\chi _2=1)\). b Oscillatory behavior appears after approximately 1000 e-folds. Both the \(\chi _1\) and \(\chi _2\) oscillations tend to reach unit amplitude, asymptotically

Full size image
Fig. 8
figure 8

The typical behavior of \(\phi ^2\) and \(\dot{\phi }^2\). One has to note that before the onset of the oscillations, \(\dot{\phi }\) is approximately constant which implies \(\ddot{\phi }\approx 0\). This is in complete accord with slow-roll approximation. \(\dot{\phi }\) increases rather gradually when \(\phi \) reaches the minimum but it decreases more abruptly as \(\phi \) leaves the minimum towards the return point. This phenomena stems from the dissipative characteristic of the oscillations and results in decaying amplitude

Full size image
Fig. 9
figure 9

Numerical simulation for \(\chi _1(N=0)=100\) and \(\chi _2(N=0)=100\) initial conditions with \(\xi =100\), \(M_p\)=1 and \(\lambda =1\). The above initial conditions guarantee the smallness of de Sitter expansion and provide the simulation to have more resolution on the oscillations. One has to note that all the spiral trajectory is one curve in the \(3.3585<N<3.4500\) interval. All the oscillations contain the potential central point at \(\phi =0\) \((\chi _1=1,\chi _2=0)\) and the return point \(\dot{\phi }=0\) \((\chi _1=0,\chi _2=1)\)

Full size image
Fig. 10
figure 10

The evolution of Ricci scalar during the oscillatory period. The oscillations tend to be damping sinusoidal for smaller amplitudes

Full size image
Fig. 11
figure 11

From top to down: \(\chi _{1,2}\), \(\phi ^2\), \(\dot{\phi }^2\) and Ricci scalar. The initial conditions are \(\chi _1(N=0)=100\), \(\chi _2(N=0)=100\) with \(\xi =1000\), \(M_p=1\) and \(\lambda =1\). This set of initial conditions has been chosen such that the de Sitter expansion has ignorable e-fold duration. By this, the numerical simulation leads to more resolution on the oscillations. To have more clear perspective, the range of the e-folds N has been chosen in an interval where the amplitudes of oscillations are comparable

Full size image

9 Comparison with some pioneering researches

The idea that scalar-tensor gravity modifications may realize the smooth phantom crossing without the necessity of ghosts originated from an inspiring research published in 2000 [42]. The main motivation to hypothesize such an idea stemmed from finding a justification for the clues of the late time (low redshift) phantom behavior of the dominant constituent of the energy of the universe. As a late time universe idea, the authors have tried to establish the conditions that scalar–tensor theories respect the post-Newtonian solar system and cosmological tests. In the more detailed paper [43] by recasting the dynamical equations through the redshift z and considering the solar system measurement and the dust-like perturbations in longitudinal gauge and adiabatic scale, the authors have provided general conditions for constructing such late time scalar–tensor models. Although we employ the same idea about the smooth phantom crossing capability of scalar–tensor models, we mostly concentrate on early time, high energy and particularly the original Higgs inflation theory. Therefore, the constraints we have respected also stem from the standard model of fields and particles as well as the inflationary footprints on the CMB. A very interesting point explored in [43] is that while the vanishing of \({\mathcal {G}}(\phi )\) (see Eq. 1) is excluded due to the singular behavior at low redshift (\(z<0.66\)), the constancy of \({\mathcal {G}}\) is also ruled out because of producing singularity for larger redshifts (although it works well for \(z\le 2\)). It seems that for obtaining a non-singular behavior which satisfies the phantom behavior in low redshifts, the potential has to possess implicit redshift (time) dependency (\({\mathcal {G}}(\phi (t))\)). The mentioned results for small redshifts have been generally based on the viability of small z expansion of the cosmic scale parameters. We can not use redshift functionality in our work since this method loses its applicability beyond the last scattering surface. But the Higgs inflation automatically admits the required conditions and remains well-defined in all energy intervals of our interest. There is another work about phantom crossing in scalar–tensor theories which raises more interests with respect to our research. The 2011 paper [45, 46] has proposed the idea of late time oscillations around de Sitter attractor. The authors have analyzed their proposal by perturbing the equations around de Sitter fixed point concluding that the oscillations may be separated to decaying and oscillatory parts and the latter may lead to several phantom crossings. The above idea has assumed the de Sitter stability and they have also mentioned that this is not a general behavior. Our research, at first glance, may demonstrate a sort of periodic phantom-passing motion as has already been predicted by [45, 46]. Although, the present research exploits the smooth phantom crossing (Figs. 5, 6), The difference between our results and phantom crossings due to oscillations around de Sitter boundary is that we are finding an oscillatory regime after a transient de Sitter phase which can be an appropriate condition for (p)reheating. Our claim is supported in two ways: analytically, we have shown that the trajectories, finally, leave de Sitter partial asymptote towards the Higgs field minimum outside the phantom region and begin to oscillate. Numerically, the time average of \(w_{eff}\) during this post-inflationary stage is approximately 1 / 3 which is an indicator of the oscillatory phase. As it has been mentioned earlier, \(\chi _1=0\) and \(\chi _2=1\) marks the return point of the scalar field oscillations which qualitatively resembles bounded oscillation under viral conditions. Therefore, we recognize an oscillatory phase which one expects to proceed by (p)reheating and this is why our approach may become suitable for an early universe possibility of phantom crossing. Moreover, the oscillations also show flipping between phantom and ordinary regions crossing the de Sitter boundary, but as has been stated earlier, this is not a bounce around the de Sitter attractor since the oscillations contain the scalar field minimum and \(\bar{w_{eff}\approx 1/3}\) during the oscillations. The other difference between this research and the late time studies is that for late time approaches it is necessary to add a matter (or radiation) term to the Lagrangian and let the classical evolution of the cosmic perfect fluid govern the scene. Instead, the matter source in pre-inflationary and inflationary phase is usually ignored. In fact, this has been the original reason to hypothesize more complicated quantum procedures for (p)reheating [29, 30].

10 Conclusion

We managed to reduce the dynamical equations of the original Higgs-Inflation scenario to two first order, coupled equations. The supportive numerical calculations have been delivered in the form of elusive two dimensional phase portrait plots. We then used the dynamical system approach to analyze the original Higgs-Inflation scenario in a broader scope. This mathematical tool lets us to be more accurate and extend the analysis to pre-inflationary and post-inflationary periods, where one can not use the slow-roll approximation. We included the kinetic term in our calculation. By this, we have followed two goals; first considering how the kinetic term breaks the auxiliary field relation between Higgs-Inflation and the Starobinsky model and second, although one expects the kinetic term to be trivially small during inflation, but if this smallness appears as a kind of attractor path, the picture becomes more compelling. This is indeed the case in our survey; the inflationary period emerges as an attractor which makes the process more natural. Perhaps, the more interesting achievement is that this de Sitter partial attractor pulls inward the phantom trajectories. The phantom trajectories which are trapped by de Sitter attraction may evolve a very smooth and familiar path after leaving the de Sitter attractor path which is an indication of the oscillations around the minimum, where the reheating or preheating processes take place. Therefore, one may talk about phantom region as the birthplace for the universes like what we live in. If one combines the results of this research with the fact that our universe is probably falling into a phantom era [57,58,59,60,61,62,63], then it is appealing to talk about the birth and the fate of the universe both in phantom era. This revives the cyclic universe hypothesis in an astonishing manner [64].