Shadow of the regular Bardeen black holes and comparison of the motion of photons and neutrinos

Abstract

The aim of the present research is the analysis of the photon motion in the regular spacetimes arising as solutions of the Einstein gravity coupled with a non-linear electrodynamics (NED). The photons no longer follow the null geodesic of the background spacetime, but the null geodesics of an effective geometry where the electromagnetic non-linearity is directly reflected in addition to the spacetime geometry. Motion of photons is compared to the motion of neutrinos that are not directly affected by the non-linearities of a non-Maxwellian electromagnetic field, and follow null geodesics of the background spacetime. We determine shadows of the regular Bardeen black holes, representing a special solution of the general relativity coupled with NED related to a magnetic charge, both for photons and neutrinos, and compare them to the shadow of the related Reissner–Nordstrom black holes. We demonstrate that the direct NED effects give clear signature of the presence of the regular black holes, on the level going up to $20\%$ that is detectable by recent observational techniques. We also demonstrate strong influence of the NED effects on deflection angle of photons moving in the Bardeen spacetimes, and on the time delay of the motion of photons and neutrinos in vicinity of the black hole horizon.

1 Introduction

In recent years, the Reissner–Nordstrom (RN) black holes are frequently studied in the astrophysical context. In its standard form governed by the Einstein–Maxwell theory with an electric charge as the source of the electromagnetic field, they are often applied as a model explaining the GRBs [38, 40, 56] – of course, there is a criticism of the strong electric field paradigm [37] implying that existence of stable astrophysical black holes with a significant electric charge seems to be improbable. However, this argument is not relevant in the case of dyonic black holes carrying magnetic charge, as in the field of such black holes the vanishing of charge due to accretion of oppositely electrically charged matter is irrelevant. If the magnetic charge is influencing only uncharged matter through the accordingly modified spacetime geometry, its role is the same as of the electric charge [30, 46].

The interest in the RN black hole geometry occurs also due to the solutions with a tidal charge that arise in the multi-dimensional braneworld Randall – Sundrum approach [21] – possible astrophysical consequences of tidally charged black holes or naked singularities can be found in [1, 16, 31, 32, 49, 54]). We recall that the braneworld tidal charge reflects curvature of the additional dimension in the braneworld models, being formally equivalent to the electric charge squired in the standard models; however, the tidal charge may take both positive and negative values, and currently there are no strong observational constraints on the tidal charge value, contrary to the case of the electric charge. Of course, the tidal charge is not interacting with the electric (magnetic) charges, but it can influence the photon motion, modifying accordingly the optical effect in vicinity of the black hole [41, 42, 54], or the oscillatory motion of Keplerian disks orbiting tidally charged black holes [49, 51]. Further, the RN black holes could be mimicked also by the phantom fields [23], or by the Horndeski gravity [7].

Any form of the RN black hole solutions can be reflected in the shape of its shadow, if the black hole stands between a shining source and a distant observer. It was suggested to apply the RN (or more general) black hole model with a tidal charge for the black hole at the Galactic Center, in particular to consider the gravitational lensing for such an object [4, 13,14,15, 41, 42, 48, 63, 65]. The BH shadows were studied also in the case of more complex rotating spacetimes, starting from the pure Kerr BH spacetime [12], or its extension to the Kerr naked singularity spacetimes [8, 29, 45, 50, 52], the Kerr-NUT spacetime [28] or Kerr-de Sitter spacetime [2, 20, 26, 27, 33, 47, 55, 62], or rotating regular black hole spacetimes [3].

On the other hand, theories predicting so called regular black holes (and related “no-horizon” strong gravity objects), lacking any physical singularity with diverging curvature of the spacetime, attracted strong attention in recent years. There is several such theories, e.g., those of the non-commutative gravity [10, 58], but strongest attention is devoted to the models based on the standard general relativity combined with a non-linear electrodynamics (NED), where a variety of approaches to the NED has been developed and discussed. For the first time, the regular black holes were proposed in connection to magnetic charges by Bardeen [11]. Later their substance has been reflected in detailed studies of their relation to NED [5, 6, 9, 17,18,19, 39, 43, 53, 57, 59, 60]. Generic regular NED black holes were introduced in [25, 61]. Along with the static and spherically symmetric non-rotating solutions, generalizations to the rotating spacetimes were derived and studied extensively [34, 59]. It is thus of crucial importance to look for clear observational signatures of the regular black holes.

Clearly, the most relevant signatures of the NED regular black holes are related to the fact that the motion of uncharged matter, e.g., in Keplerian disks, is related purely to the spacetime geometry of these regular black holes, while motion of photons is not, being related to some effective geometry modified by the NED effects additional to those reflected in the structure of the spacetime. It is thus natural to test this effective geometry – first in the simplest, but very significant and in principle measurable effects on the extension of the black hole shadow.

We start our study concentrating attention on the Bardeen spacetimes, where both the magnetic and electric charges could be introduced, but mainly the case of the magnetic charge could be relevant [18]. We compare the effective-geometry predicted regular black hole shadow related to the photon motion, to the shadow related to the neutrinos considered as massless particles that is determined by the spacetime structure purely; for completeness, we make comparison also to the shadow related to the RN black holes with the same value of the magnetic (electric) charge as those of the regular Bardeen black hole. We demonstrate that the differences are quite significant.

For comparison we consider also the notion of the deflection angle, and the related issue of the time delay of photons and (massless) neutrinos, or general uncharged ultra-relativistic particles, while they are crossing the strong gravity region of a regular Bardeen black hole. We again demonstrate possibility of effects giving clear signatures of NED effects in the regular black hole backgrounds. We consider also a simple situation where both the source and the observer are located oppositely to the BH at the same distance from the BH centre, e.g., on an radiating ring, and determine the time necessary for properly chosen photon and neutrino to reach the observer, if they are radiated simultaneously. There will be a difference of the time interval of the photon and the neutrino, both due to the different trajectory and different metric coefficients of the regular and effective spacetimes. The time difference could be quite significant even for the stellar-mass black holes, and very large for the super-massive black holes, as the time delay dimensional factor is linear in the black hole mass parameter.

2 Geometry and effective geometry

The regular spacetimes can be derived from the Einstein gravitational theory coupled to a non-linear electrodynamics; the corresponding action of the combined theory reads

$$\begin{aligned} S = \frac{1}{16\pi }\int \mathrm {d}x^4\sqrt{-g}\left[ R-{\mathcal {L}}(F)\right] \end{aligned}$$

(1)

where $F\equiv F_{\alpha \beta }F^{\alpha \beta }$ and the electromagnetic tensor is related to the vector potential due to the relation $F_{\alpha \beta }=\partial _\alpha A_\beta - \partial _\beta A_\alpha$. In 1968, Bardeen [11] for the first time proposed black hole solution regular at $r=0$ where the standard black hole spacetimes have a physical singularity. The Bardeen spacetime metric has the line element taking the form

$$\begin{aligned} \mathrm {d}s^2 = -f(r)\mathrm {d}t^2 + \frac{1}{f(r)}\mathrm {d}r^2 + r^2\mathrm {d}\theta ^2 + r^2\sin ^2\theta \mathrm {d}\phi ^2, \end{aligned}$$

(2)

with

$$\begin{aligned} f(r)=1-\frac{2M r^2}{(r^2+q_m^2)^{3/2}}. \end{aligned}$$

(3)

This solution is parametrised by the mass parameter M, and the magnetic charge $q_m$. Later Ayón-Beato and García [5] have found out that the Bardeen spacetime is a solution of the Einstein gravitational equations coupled to the NED represented by the action (1) where the non-linear electromagnetic Lagrangian is given by the formula

$$\begin{aligned} {\mathcal {L}}(F)=\frac{6}{s q_m^2}\left( \frac{\sqrt{q_m^2 F /2}}{1+\sqrt{q_m^2 F/2}}\right) ^{5/2}, \end{aligned}$$

(4)

with $s\equiv q_m/2M$.

In the parametric space of the specific magnetic charge $q_m/M$, the Bardeen spacetimes can be separated into three classes corresponding to different behaviour of the circular geodesics of the spacetime geometry, especially to their stability. Detailed discussion of the circular geodesics of the Bardeen spacetimes can be found in [53] – here we concentrate on the reflection of the three classes of the Bardeen spacetimes in the character of the circular null geodesics.

• Bardeen black hole spacetimes – specific charge $q_m/M<0.7698$. In the black hole spacetimes there is only one unstable null circular geodesic located above the outer horizon, and no null circular geodesic located under the inner horizon.

• Bardeen no-horizon spacetimes containing null circular geodesics – $0.7698<q_m/M<0.8586$. There exists an inner stable null circular geodesic and an outer unstable null circular geodesics in such spacetimes.

• Bardeen no-horizon spacetimes having no null circular geodesics – $q_m/M>0.8586$. In such spacetimes a finite maximum of the deflection angle exists for geodesics approaching the centre of the spacetime [43].

In the following, we directly use the results of the previous works [43, 53] for our recent study.

Due to the non-linearity of the electromagnetic field, photons do not follow null geodesics of the Bardeen spacetime. Novello have shown that the photon trajectory is governed by an effective geometry directly reflecting non-linear electrodynamic effects [17, 22]. In the Appendix, we present an alternative derivation of the effective geometry, using the short-wave approximation; this method leads to the same results as the Novello approach.

The effective geometry corresponding to the Bardeen spacetime geometry reads

$$\begin{aligned} \mathrm {d}\tilde{s}^2=-\frac{f(r)}{{\mathcal {L}}_F}\mathrm {d}t^2 +\frac{1}{{\mathcal {L}}_F f(r)}\mathrm {d}r^2 + \frac{r^2}{\Phi }\mathrm {d}\theta ^2 + \frac{r^2}{\Phi }\mathrm {d}\phi ^2, \end{aligned}$$

(5)

where

$$\begin{aligned}&{\mathcal {L}}_F\equiv \frac{\mathrm {d}{\mathcal {L}}(F)}{\mathrm {d}F},\quad \text {and}\quad {\mathcal {L}}_FF\equiv \frac{\mathrm {d}^2 {\mathcal {L}}(F)}{\mathrm {d}F^2}, \end{aligned}$$

(6)

$$\begin{aligned}&\Phi = {\mathcal {L}}_F + 2{\mathcal {L}}_{FF} F \end{aligned}$$

(7)

and

$$\begin{aligned} F=\frac{q_m^2}{2 r^4}. \end{aligned}$$

(8)

Confronting the effective Bardeen geometry and the spacetime Bardeen geometry, we see immediately that the pseudo-singularities determined by vanishing (diverging) of the metric coefficients are located at the same radii, corresponding to the black hole horizons, and governed by vanishing of the lapse function $f(r;M,q_m)$.

In the case of the linear (Maxwellian) electrodynamics, the Lagrangian of the electromagnetic field reads

$$\begin{aligned} {\mathcal {L}}(F)=F \end{aligned}$$

(9)

and the corresponding static, spherically symmetric spacetime metric is described by the Reissner–Nordström (RN) geometry. The related space-time interval reads

$$\begin{aligned} \mathrm {d}s_{RN}^2 = -f_{RN}(r)\mathrm {d}t^2 + \frac{1}{f_{RN}(r)}\mathrm {d}r^2 + r^2\mathrm {d}\theta ^2 + r^2\sin ^2\theta \mathrm {d}\phi ^2 \end{aligned}$$

(10)

where

$$\begin{aligned} f_{RN}(r)=1-\frac{2M}{r}+\frac{q_e^2}{r^2}. \end{aligned}$$

(11)

M is again the mass parameter of the spacetime while $q_e$ denotes the electric charge of the electromagnetic field of the RN background [35]. Of course, we could consider also the so called dyonic RN spacetimes where both electric and magnetic charges are present ($q_e^2 \rightarrow q_e^2+q_m^2$) [46]. In the Einstein–Maxwellian theory, all zero mass particles, including photons, follow null geodesics of the RN spacetime.

3 Equations of motion

In the regular black hole backgrounds with charges related to a NED, the motion of photons is not governed by the spacetime geometry, but by an effective geometry directly reflecting the non-linearities of the electrodynamics, as shown here in the Appendix. Of course, motion of the other uncharged particles is determined solely by the spacetime geometry. As we would like to test the complete effects of the NED under consideration, we have to study both the motion of photons governed also by the direct non-linear interaction with the black hole charges, and of the other uncharged particles, here assumed to be simply neutrinos (as they could be effectively considered as zero-mass particles, but we can consider any kind of extremely relativistic uncharged particles) that are influenced by the charge parameter only through its influence on the spacetime structure. Therefore, we first summarise the equations of motion of the mass-less particles in the Bardeen spacetime geometry, and in the related Bardeen effective geometry, presenting their derivation in the Appendix.

3.1 Motion governed by the spacetime geometry

The uncharged particles (e.g. neutrinos whose motion could be very close to the photon motion in the vacuum spacetime) are not affected by the electromagnetic field non-linearities and follow geodesics (null geodesics) of the Bardeen spacetime. Let the contravariant components of test particle 4-momentum vector are denoted as $k^\mu$, and the corresponding covariant components as $k_\mu$. Due to the Bardeen spacetime stationarity and spherical (axial) symmetry there are two constants of motion: $E=-k_t$ is the covariant energy, and $L_z=k_\phi$ is the azimuthal angular momentum. One can define the impact parameter due to the standard relation $l\equiv L_z/E$. The corresponding equations of motion for the spacetime geometry then can be expressed in the form

$$\begin{aligned} (k^r)^2= & {} 1 - f(r)(l^2+q)/r^2, \end{aligned}$$

(12)

$$\begin{aligned} (k^\theta )^2= & {} \frac{1}{r^4}(q-l^2{\mathrm {ctg}}^2\theta ),\end{aligned}$$

(13)

$$\begin{aligned} k^\phi= & {} \frac{l}{r^2\sin ^2\theta },\end{aligned}$$

(14)

$$\begin{aligned} k^t= & {} \frac{1}{f(r)}, \end{aligned}$$

(15)

where the motion constant q is associated with the separation constant corresponding to the total angular momentum related to the spherical symmetry of the spacetime, and is introduced in such a way that it vanishes for the motion in the equatorial plane; the lapse function f(r) corresponds to the Bardeen geometry. In the case of the motion in the Reissner–Nördström spacetimes, we replace the function f(r) by the lapse function $f_{RN}(r)$.

3.2 Motion governed by the effective geometry

The photons move along the null geodesics of the effective geometry (5). Let us stress that the effective metric rises and lowers indexes of the photon 4-momentum only. The effective geometry is again static and spherically symmetric and therefore posses again three constants of motion – two of the motion constants are related to the stationarity of the geometry, energy $\tilde{E}=-\tilde{k}_t$, and axial symmetry of the geometry, axial angular momentum $\tilde{L}_z=\tilde{k}_\phi$. Here we also introduce the impact parameter $\tilde{l}=\tilde{L}_z/\tilde{E}$. The equations of motion of photons in the effective geometry take the form

$$\begin{aligned} (k^r)^2= & {} {\mathcal {L}}_F^2\left( 1-\frac{\Phi }{{\mathcal {L}}_F}f(r) (\tilde{l}^2+\tilde{q})/r^2\right) ,\end{aligned}$$

(16)

$$\begin{aligned} (k^\theta )^2= & {} \frac{1}{r^4}(\tilde{q}-\tilde{l}^2{\mathrm {cot}}^2\theta ),\end{aligned}$$

(17)

$$\begin{aligned} k^\phi= & {} \frac{\Phi }{r^2\sin ^2\theta }\tilde{l},\end{aligned}$$

(18)

$$\begin{aligned} k^t= & {} \frac{{\mathcal {L}}_F}{f(r)}, \end{aligned}$$

(19)

where again the impact parameter $\tilde{q}$ is associated with total angular momentum of the photon in the same way as in the spacetime geometry. In the case of Reissner–Nordstrom spacetime the effective geometry coincides with the spacetime geometry.

4 Circular orbits and the black hole shadows

The circular motion in the Bardeen spacetimes was studied in [43, 53], for both the black hole and no-horizon cases; for the Reissner–Nördström spacetimes, both black hole and naked singularity cases were studied in [48]. We can thus directly use the results of these works, concentrating attention on the motion in the effective geometry.

We can recall that the separation between the Reissner–Nördström black holes and naked singularities corresponds to the specific charge $q_{RN}/M=1$. The circular null geodesics exist in the Reissner–Nördström spacetimes with specific charge $q_{RN}/M\le \sqrt{9/8}$ – there is one unstable circular null geodesic for the black hole spacetimes with $q\le 1$, and an inner stable, and outer unstable circular geodesic in naked singularity spacetimes with $q \in (1< q < \sqrt{9/8})$. In Reissner–Nördström naked singularity spacetimes with $q > \sqrt{9/8}$ no circular null geodesics exist [48].

The separation of the black-hole and no-horizon Bardeen spacetimes corresponds to the specific magnetic charge $q_m/M=0.7698$. The circular null geodesics exist in the Bardeen spacetimes with specific charge $q_m/M \le 0.85865$, and for Bardeen ho-horizon spacetimes with $q_m/M \in [0.7698, 0.85865]$, even two circular null geodesics exist, the inner being stable, the outer being unstable [53]. No circular null geodesics exist in the no-horizon spacetimes with $q_m/M > 0.85865$.

4.1 Circular null geodesics of the effective geometry and the spacetime geometry

Here we treat the conditions governing the circular geodesics motion in both the effective geometry and the spacetime geometry of the Bardeen solution of the combined Einstein gravity and the assumed NED. The circular orbits must simultaneously satisfy the following conditions

$$\begin{aligned} k^r=0 \quad \text {and}\quad \frac{\mathrm {d}k^r}{\mathrm {d}\lambda }=0. \end{aligned}$$

(20)

By making derivative of Eq. (16), we obtain a differential equation for $k^r$ in the form

$$\begin{aligned} \frac{\mathrm {d}k^r}{\mathrm {d}\lambda }= & {} \frac{1}{2}\left[ L_{FF}F'\left( L_F-\frac{\Phi f}{r^2}l^2\right) \right. \nonumber \\&\left. +\,L_F\left( L_{FF}F'-( (\Phi ' f + \Phi f')r^2-2r\Phi f)\frac{l^2}{r^4} \right) \right] .\nonumber \\ \end{aligned}$$

(21)

Using the particular case of the Eqs. (16) and (21), we obtain conditions (20) in the form

$$\begin{aligned} 0= & {} L_F-\frac{\Phi f}{r^2}l^2 \end{aligned}$$

(22)

$$\begin{aligned} 0= & {} L_{FF}F'-( (\Phi ' f + \Phi f')r^2-2r\Phi f)\frac{l^2}{r^4}. \end{aligned}$$

(23)

Finally, the radial coordinate of the photon circular orbit is determined by equation

$$\begin{aligned} 0=L_{FF}F'-( (\Phi ' f + \Phi f')r^2-2r\Phi f)\frac{L_F}{\Phi f r^2} \end{aligned}$$

(24)

and the corresponding impact parameter of the circular photon orbit, governing the shadow of the Bardeen black hole determined by the formula

$$\begin{aligned} l^2=\frac{L_F r^2}{\Phi f}. \end{aligned}$$

(25)

The radius of the circular photon orbits, in dependence on the specific charge of the Bardeen spacetime, is given in Fig. 1, while the corresponding impact parameter of photons on the circular orbits, in dependence on the specific charge, is given in Fig. 2.

Other neutral test massless (or strongly ultra-relativistic) particles are not directly affected by the electromagnetic non-linearity and follow the null geodesics of Bardeen spacetime. Radius of their circular orbit is determined by the equations

$$\begin{aligned} f' r^2-2 f r=0, \end{aligned}$$

(26)

while the corresponding impact parameter of the circular orbit is determined by

$$\begin{aligned} l^2=\frac{r^2}{f}. \end{aligned}$$

(27)

We assume these particles are massless neutrinos, $\nu$, and give again the dependence of the radius and impact parameter of the circular orbit on the specific charge of the Bardeen spacetime in Figs. 1 and 2. In the case of the Reissner–Nördström spacetimes both the motion of photons and neutrinos is governed by the spacetime geometry. To find the radius and impact parameter of the circular null geodesics of the Reissner–Nördström spacetimes, we replace f(r) by $f_{RN}(r)$ in the corresponding relations of the spacetime null geodesics. Their dependence on the specific charge of the Reissner–Nördström spacetime is again presented in Figs. 1 and 2, where we assume that the specific charges of the Bardeen and Reissner–Nördström spacetimes are equally valued – we thus assume positive charges satisfying the relation $q_m = q_{RN} = q$.

Fig. 1

The loci of circular orbits in $r-q$ plot (r-the radial coordinate and q-the magnetic charge parameter) of photons in effective Bardeen geometry ($\gamma$) and neutrinos ($\nu$) in Bardeen spacetime. Curve $\chi$ represents loci of the Bardeen spacetime horizons. Curve $\chi _{RN}$ represents loci of the Reissner–Nordstrom spacetime horizons. Note that from the spacetime interval (5) it follows that horizons of $g_{\mu \nu }$ and $\tilde{g}_{\mu \nu }$ coincide

Fig. 2

Plots of photon ($\gamma$), neutrino ($\nu$) circular orbit impact parameters $l_C$ (it determines the radius of the BH shadow) as functions of magnetic charge parameter $q_m$ in effective-Bardeen and Bardeen spacetimes. For comparison with the NED case we constructed the plot of $l_C$ for the case of null geodesics in Reissner–Nördström spacetime where we set the specific charge $q_{RN}=q_m=q$ (curve $\gamma _{RN}$). In the RN spacetimes, there are three distinct regions – the first one with $q_m\le 1$ for black hole spacetimes, demonstrates one photon orbit impact parameter for given magnetic charge, the second one with $1<q_m \le 3/(2\sqrt{2})$ for naked singularity spacetimes, demonstrates two photon orbit impact parameters for any given magnetic charge, and the third one of the particular naked singularity spacetimes with $q_m > 3/(2\sqrt{2})$ demonstrates no circular photon orbit

There is a clear distinction between the circular orbits of neutrinos and photons. There are two neutrino circular orbits for a given specific charge q from the interval $q \in [0.7698, 0.85865]$. For $q<0.7698$, there is only one neutrino circular orbit. In the case of the photon circular orbits in the effective geometry, there is no such limit. The photon circular orbits (governed by the effective geometry) thus exist in all the Bardeen spacetimes, contrary to the circular null geodesics of the spacetime, relevant for the other ultra-relativistic particles.

There is another interesting feature that occurs in the case of the photon circular orbits – the existence of identical photon orbit radius for two different values of the specific charge parameter q. The common radii are located between the radii $r_{cph1}=2.32506$ (when the specific charge $q_{cph1}=1.07663$), and $r_{cph2}=3.0$ (see Fig. 1). The values of $r_{cph1}$ and $q_{cph1}$ are found from the conditions

$$\begin{aligned} \frac{\mathrm {d}r}{\mathrm {d}q}=-\frac{\partial H/\partial q}{\partial H/\partial r}=0 \end{aligned}$$

(28)

and

$$\begin{aligned} H(r,q)=0. \end{aligned}$$

(29)

The last condition is the implicit formula for the curve representing $r-q$ loci of the photon circular orbits, and H introduced here is defined by the relation

$$\begin{aligned} H(r,q)\equiv L_{FF}F'-( (\Phi ' f + \Phi f')r^2-2r\Phi f)\frac{L_F}{\Phi f r^2}. \end{aligned}$$

(30)

We will discuss the observational consequences in the next subsections, concentrating on the shadows of the black hole and on the dependence of the deflection angle on the impact parameter of the photons and neutrinos. Note that the black hole shadow is in fact determined by the limiting value of the impact parameter corresponding to an infinite value of the deflection angle.

4.2 Shadow of the Bardeen BHs

The shadow of the black hole is directly related to the impact parameter of the photon circular orbit. Generally, we consider an observer located at an inclination angle $\theta _o$. The image of a source on the observer photographic plate is determined by two angles on the observer sky, the angles $\alpha$ and $\beta$ giving the angular coordinates related to the photon (neutrino) impact parameters l and q via formulas [12]

$$\begin{aligned} \alpha =l/\sin \theta _o\quad \text {and}\quad \beta ^2 = q - \cos ^2\theta _o \frac{l^2}{\sin ^2\theta _o}. \end{aligned}$$

(31)

The black hole shadow is then governed by the impact parameters of the photon (neutrino) circular orbit. Therefore, the shadow of the black hole corresponds to the area within the circle of the radius

$$\begin{aligned} R_c\equiv \sqrt{\alpha ^2_c(\varphi )+\beta ^2_c(\varphi )}=\sqrt{l^2_c(\varphi )+q_c(\varphi )}=l_c(\pi /2), \end{aligned}$$

(32)

where index “c” denotes the photon circular orbit parameters and $\varphi \equiv \tan ^{-1}(\beta /\alpha )$. In Fig. 3, the shadows of the Bardeen black hole are constructed for the photons and for the neutrinos that are governed by the null geodesics of effective geometry of the Bardeen spacetime (photons) and by the Bardeen spacetime geometry (neutrinos). Of course, recent observational techniques enable measurements of the shadows related to photons; predictions of the effective Bardeen geometry could be then compared to those related to the Schwarzschild black hole of the same mass, or the RN black hole carrying also the same magnetic charge.

Fig. 3

The shadow of the Bardeen black hole constructed for the null geodesics of effective geometry of the Bardeen spacetime (black), and the Bardeen spacetime geometry (gray). The value of the specific magnetic charge parameter is taken $q_m=0.1$

One can see directly that the radius of the photon shadow governed by the effective geometry is significantly lower in comparison to the radius of the neutrino shadow governed by the spacetime geometry. The difference is of the order of $20\%$, as can be seen from Fig. 3, being thus on the level close to the precision of measurements of the super-massive Galaxy centre black hole shadow by the Event Horizon Telescope [24, 64]. For possible relative comparisons see Fig. 4 where the relative difference is given also in relation to the radius of the shadow related to the Schwarzschild black hole of given mass. Notice that the dimension of the shadow related to the Bardeen black hole effective geometry is significantly smaller than the Schwarzschild shadow radius for all values of $q_m$; the limit of $q_{m} \rightarrow 0$ does not correspond to the Schwarzschild value (note that even in the Minkowski spacetime with charge described by the NED, circular photon orbits exist). On the other hand, the Bardeen spacetime geometry shadow radius and the RN black hole shadow radius are comparable to the Schwarzschild one for small values of $q_m$, but decreases significantly for values of $q_m/M > 0.5$.

Fig. 4

The plots of relative differences between black hole shadow areas $A_i\equiv \pi l_i^2$ where index i stands for Schw-Schwarzschild, B Bardeen, NLB non-linear Bardeen, RN Reissner–Nördström . Curve 1: $|A_{NLB}-A_{B}|/A_B$, curve 2: $|A_{NLB}-A_{Schw}|/A_{Schw}$, curve 3: $|A_{B}-A_{Schw}|/A_{Schw}$, curve 4: $|A_{RN}-A_{Schw}|/A_{Schw}$

Table 1 The apparent angular diameter of two astrophysical blackholes, designated Sgr A* and M87, is given for three models of spacetime, Schwarzschild, and R–N and eff-Bardeen with charge parameter $q=0.1$

It is instructive to calculate the actual angular diameter $\theta _{BH}$ of particular astrophysical black holes for effective Bardeen geometry and the related RN geometry. Recently, two black holes are in the focus of the Event Horizon Telescope, namely, the Galaxy Sgr A* and M87 central supermassive black holes [24, 64]. In Table 1 we present their angular diameter calculated for the case of Schwarzschild, R–N and Bardeen spacetimes, using the standard formula

$$\begin{aligned} \theta _{BH}\simeq \sin ^{-1}\left( \frac{l_{ph}}{d} \frac{G M}{c^2}\right) , \end{aligned}$$

(33)

taking the mass M and distance d values of the Sgr A*, M87 black holes from [24, 64] and assuming the magnetic charge value of $q_m = 0.1 M$. Comparing the results presented in Figs. 2 and 4, we can see that the same relation of the black hole angular diameter predicted by the effective Bardeen geometry to the Schwarzschild case holds for wide range of the magnetic charge $0<q_{m}<0.4$. Such a distinction is in the range of precision of the Event Horizon Telescope.

4.3 Deflection angle

The physically very important scattering effects of photons and neutrinos on the Bardeen background can be represented by the deflection angle that is governed again by the effective geometry in the photon case,and by the spacetime geometry in the neutrino case. Usually, in the spherically symmetric black hole (and even naked singularity) backgrounds, the deflection angle increases with decreasing impact parameter, and it diverges while the impact parameter is approaching the value corresponding to the impact parameter of the null geodesic. However, in the special class of the no-horizon Bardeen spacetime geometry having no circular null geodesic, the deflection angle increases with decreasing impact parameter up to a maximum value, and with continuing decreasing impact parameter it starts to decrease – this effect could be reflected by a creation of so called ghost images of Keplerian disks, as shown in [43].

The deflection angle is represented by variation of the azimuthal coordinate $\phi$ while the photon (neutrino) goes from infinity back to infinity. For the photons and neutrinos (having a given impact parameter l) the deflection angle is thus determined by the following formulas

$$\begin{aligned} \Delta \phi _{\gamma }=\int {\frac{\Phi }{L_F}}\frac{l\mathrm {d}r}{r^2\sqrt{1-\frac{\Phi }{L_F}f\frac{l^2}{r^2}}} \end{aligned}$$

(34)

and

$$\begin{aligned} \Delta \phi _{\nu }=\int {\frac{l\mathrm {d}r}{r^2\sqrt{1-f\frac{l^2}{r^2}}}}. \end{aligned}$$

(35)

We compare the dependence of the deflection angles $\Delta \phi$ of photons and neutrinos on the impact parameter for typical values of specific Bardeen spacetime charge in Fig. 5. The impact parameter is decreased from value $l=10$ down to $l=(1+10^{-6})l_{ph}$.

Fig. 5

The comparison of $\Delta \phi$ among photons-in-Bardeen ($\gamma$), neutrinos-in-Bardeen ($\nu$), and photons-in-RN ($\gamma _{RN}$). The spacetime magnetic charge parameter $q_m=0.5$ (top), 0.8, and 1.0 (bottom) and $r_i=r_o=100$. In case of RN spacetime we put $q_e=q_m$

The deflection angle profiles diverge at the value of $l=l_c$. The magnitude of the impact parameter corresponding to the circular orbit is higher for neutrinos than for photons as long as $q_m \le 0.85865$. For this case there exist an impact parameter $l_i$ such that $\Delta \phi _\gamma (l_i)=\Delta \phi _\nu (l_i)$. The value of this special impact parameter $l_i$ decreases with increasing value of the charge parameter $q_m$. For the values of the charge parameter $q_m > 0.85865$, there is no neutrino circular orbit (and the ghost images can occur), but there is still the photon circular orbit and divergence of the photon deflection angle. Therefore, the ghost images are forbidden for photon images on the Keplerian disks, being allowed only for the neutrino images. Such a qualitative difference could be again a clear signature of the existence of strongly charged no-horizon Bardeen spacetimes.

5 Time-delays

The other observationally relevant quantity is time delay of the income of a photon and neutrino signal from some distant event. These delays could be relevant for example in the case of the gravitational lensing phenomena.

Fig. 6

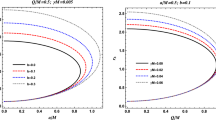
Three illustrative examples of time delay curves for neutrinos ($\nu$), photons-in-Bardeen ($\gamma$), and photons-in-RN ($\gamma _{RN}$) as functions of impact parameter l. The plots are constructed for three representative values of magnetic charge parameter $q=0.5$ (top), 0.8, and 1.0 (bottom)

The formulas of the time delay for photons and neutrinos read

$$\begin{aligned} \Delta t_\gamma = \int \frac{\mathrm {d}r}{f\sqrt{1-\frac{\Phi }{L_F}\frac{f}{r^2}l^2}} \end{aligned}$$

(36)

and

$$\begin{aligned} \Delta t_\nu = \int \frac{\mathrm {d}r}{f\sqrt{1-\frac{f}{r^2}l^2}} \end{aligned}$$

(37)

The estimate of the time delay can be obtained in a simple way demonstrated in Fig. 6, where we compare the time-delays between the neutrino motion governed by the Bardeen spacetime geometry, and the photon motion governed by the effective Bardeen geometry, defined by same impact parameter. The results can be summarized in the following way, using the classification of the Bardeen spacetimes.

The specific charge parameter $q_m/M$ of the Bardeen spacetimes is divided into three regions according to the behaviour of the null circular geodesics of the spacetime geometry, and generally of the properties of circular orbits, giving thus three classes of the Bardeen spacetimes [53]. We thus discuss the time delay effects separately for each of these classes.

• Starting with $q_m/M>0.8586$, the Bardeen no-horizon spacetimes having no neutrino circular orbit. We picked value $q_m/M=1.0$. There is a value of impact parameter $l_i$ where time-delay curves intersect, i.e., where is $\Delta t_\gamma (l_i)=\Delta t_\nu (l_i)$. The time-delay for a fixed impact parameter $l>l_i$ is longer for neutrinos than for photons and for $l<l_i$ the situation is inverse. This behaviour could be a very specific signature of this class of the Bardeen spacetimes.

• In the case of Bardeen no-horizon spacetimes containing two null circular geodesics, $0.7698<q_m/M<0.8586$, we set $q_m/M=0.8$. There is no intersection between the curves $\gamma$ and $\nu$. The neutrino time delay is always larger than the photon time delay.

• In the Bardeen black hole case with an unstable null circular geodesic, $q_m/M<0.7698$, we set $q_m/M=0.5$. There is no intersection between curves $\gamma$ and $\nu$. The neutrino time delay is always larger than the photon time delay.

Let us consider another physically relevant situation, corresponding to self-irradiation of a radiating ring, both due to photons and neutrinos (or any ultra-relativistic particles), by an exceptional radiation event. Assuming planar motion in the equatorial plane, let both, neutrino and photon be emitted from the location $(r,\pi )=(r_0,0)$. We tune the impact parameters $l_\gamma$ and $l_\nu$ (in general $l_\gamma \ne l_\nu$) in such a way that both photon and neutrino will arrive to the location $(r,\phi )=(r_0,\pi )$. We determine the time-delays of both, neutrino and photon, for three representative values of the specific magnetic charge parameter $q_m/M=0.5$, 0.8, and 1.0.

We assume both the direct an indirect irradiation, and compare them. The results are presented in the Table 2. The corresponding geodesics are plotted in Figs. 7 and 8.

Table 2 Time-delays of neutrinos and photons emitter from $(r,\phi )=(100,0)$ and arriving to $(r,\phi )=(100,\pi )$ and to $(r,\phi )=(100,3\pi )$ for three representative values of magnetic charge parameter $q=0.5$, 0.8, and 1.0

Fig. 7

Illustrative examples of geodesics of neutrinos ($\nu$, dashed) in Bardeen, photons ($\gamma$, solid-black) in effective-Bardeen, and photons ($\gamma _{RN}$, solid-red) in RN geometries for three representative values of magnetic charge parameter $q_m=0.5$, 0.8, and 1.0. The impact parameters for the geodesics are presented in Table 2

Fig. 8

Illustrative examples of geodesics of neutrinos ($\nu$, dashed) in Bardeen and photons ($\gamma$, solid-black) in effective-Bardeen, and photons in RN ($\gamma _{RN}$, solid-red) geometries for two representative values of magnetic charge parameter $q=0.5$, 0.8. The corresponding impact parameters are presented in Table 3

We can see that the time delay effect can be quite large and easily observable. The time delay of the direct irradiation is almost twice the indirect irradiation, although the photons and neutrinos are orbiting the black hole ones in the case of the indirect irradiation, however, they are orbiting closer to the black hole in comparison with perihelion of the direct trajectory. Clearly, the time delay of the irradiation can be also a significant distinguishing effect (Table 4).

6 Conclusion

We have studied the simplest phenomena that could give a clear signature of the relevance of NED in the black hole (or no-horizon) spacetimes determined by the Einstein gravity combined with the version of NED governing the Bardeen spacetimes with a magnetic charge, demonstrating clearly that these could give clear signatures of the presence of regular Bardeen black holes (or strong gravity no-horizon objects).

Table 3 List of impact parameters $l_i$ ($i=(\gamma ,\nu ,{\gamma }RN)$) for geodesics connecting observer and emitter at $r=100$ separated by azimuthal angle $\phi =\pi$ of particular spacetime

Table 4 The impact parameters of null geodesics for two representative values of magnetic charge parameter $q_m$, presented in Fig. 8

We have determined shadows of the regular Bardeen black holes by studying the photon motion in the effective geometry governed by the spacetime geometry and the Lagrangian of the NED. Critical impact parameters for photon geodesics separate capture and scattering regions and these parameters characterise shadow sizes (radii). We demonstrate explicitly that the shadows of the black holes have to be by about $20\%$ smaller in comparison with what can be expected due to the standard spacetime geometry effect, measurable by other massless particles. Similar signatures have been found also in the case of the deflection angle. Moreover, we have shown that the direct effect of the NED represented by the effective Bardeen geometry excludes existence of the ghost photon images predicted in the special no-horizon Bardeen spacetimes with no circular null geodesics of the spacetime geometry [43] – thus the ghost images could be relevant only for the neutrino images of the Keplerian disks, or due to highly ultra-relativistic particles.

Assuming that a regular black hole is located in the Galactic Center, and in the centres of other galaxies (e.g., M87), one can use the results obtained in the present paper to analyse future observational data obtained with advanced observational facilities as the Event Horizon Telescope [24].

Finally, we have demonstrated that the relative time delay effects related to the motion of photons and neutrinos (or general ultra-relativistic particles) in strong gravity regions of the Bardeen spacetimes can be also efficient signatures of the relevance of the NED effect in the Bardeen spacetimes.

In the future research we plan to illustrate the NED phenomena in direct or indirect images of the Keplerian disks, and in the related profiled spectral lines. Extension to the studies of other NED regular black holes is also planed.

Appendices

Appendices

Effective geometry of the Bardeen spacetime: derivation

The equations of motion of photons that are determined by the effective geometry follow from the Bianchi identities for the Faraday tensor $F_{\alpha \beta }$, which in the case of NED read

$$\begin{aligned}&\left( L_F F^{\mu \nu }\right) _{;\nu }=0, \end{aligned}$$

(38)

$$\begin{aligned}&F_{\mu \nu ;\lambda }+F_{\lambda \mu ;\nu }+F_{\nu \lambda ;\mu }=0, \end{aligned}$$

(39)

where is $F\equiv F_{\mu \nu }F^{\mu \nu }$ and $L_F\equiv \mathrm {d}L/\mathrm {d}F$. In order to derive the equations of motion of photons in the framework of non-linear electrodynamics, we will employ short-wave approximation assuming that the Faraday tensor of locally plane waves takes the expansion form [44]

$$\begin{aligned} F_{\mu \nu }=\left[ a_{\mu \nu }+\frac{\epsilon }{i}b_{\mu \nu } +\left( \frac{\epsilon }{i}\right) ^2 c_{\mu \nu }+\cdots \right] \exp \left( \frac{i}{\epsilon }S\right) \end{aligned}$$

(40)

where $S/\epsilon$ is the wave phase which can be arbitrarily large, taking small values of $\epsilon$, relative to the wave amplitude $a_{\mu \nu }+\frac{\epsilon }{i}b_{\mu \nu }+\left( \frac{\epsilon }{i}\right) ^2 c_{\mu \nu }+\cdots$. Inserting solution (40) into equations of motion of electromagnetic field (38) and (39), one gets

$$\begin{aligned} L_{F,\nu }F^{\mu \nu }+L_F F^{\mu \nu }_{\phantom {\mu \nu };\nu }=0, \end{aligned}$$

(41)

where

$$\begin{aligned} L_{F,\nu }= & {} L_{FF}F_{,\nu }=2L_{FF}F^{\alpha \beta }F_{\alpha \beta ;\nu }\nonumber \\= & {} 2L_{FF}F^{\alpha \beta }\left( \frac{i}{\epsilon }S_{\nu }F_{\alpha \beta }+b_{\alpha \beta ;\nu }\exp (i S/\epsilon )+\cdots \right) \nonumber \\ \end{aligned}$$

(42)

and

$$\begin{aligned} F^{\mu \nu }_{\phantom {\mu \nu };\nu }=\frac{i}{\epsilon }S_{,\nu }F^{\mu \nu } + \exp (i S/\epsilon )\left( a^{\mu \nu }_{\phantom {\mu \nu };\nu } +\frac{\epsilon }{i}b^{\mu \nu }_{\phantom {\mu \nu };\nu } +\dots \right) . \end{aligned}$$

(43)

Putting last two formulas into Eq. (41), we arrive to equation

$$\begin{aligned}&2L_{FF}F S_\nu F^{\mu \nu } + L_F S_\nu F^{\mu \nu }=0\nonumber \\&\quad \Rightarrow \quad F^{\mu \nu } k_\nu = -\frac{2L_{FF}}{L_F}F F^{\mu \nu }k_\nu \end{aligned}$$

(44)

where the wave vector

$$\begin{aligned} k_\nu \equiv - S_{,\nu }=-\frac{\partial S}{\partial x^\nu }. \end{aligned}$$

(45)

was introduced.

From the Bianchi identity (39), we obtain for the terms of the order $i/\epsilon$ the equation

$$\begin{aligned} F_{\mu \nu }k_\lambda +F_{\lambda \mu }k_\nu +F_{\nu \lambda }k_\mu =0, \end{aligned}$$

(46)

and by multiplying it by $F^{\mu \nu }k^\lambda$, we obtain

$$\begin{aligned} F k_{\lambda } k^{\lambda } + 2k_{\nu }F_{\lambda \mu }k^{\lambda }F^{\mu \nu }=0. \end{aligned}$$

(47)

Using formula (44) for $F^{\mu \nu }k_\nu$ in the last equation, we arrive to equation

$$\begin{aligned} g^{\lambda \nu }k_{\lambda }k_\nu - 4\frac{L_{FF}}{L_F}F^\lambda _{\phantom {\lambda }\mu } F^{\mu \nu }k_{\lambda }k_{\nu }=0 \end{aligned}$$

(48)

which can be rearranged to read

$$\begin{aligned} \left( g^{\lambda \nu } - \frac{4L_{FF}}{L_F}F^\lambda _{\phantom {\lambda }\mu }F^{\mu \nu }\right) k_{\lambda }k_{\nu }=0. \end{aligned}$$

(49)

This is the equation governing the behaviour of photons in spacetimes representing the solutions of GR combined with non-linear electrodynamics. Clearly, this is the standard normalized condition of null geodesics related to metric modified by the electrodynamic terms. The photons then move along the null geodesics of the effective geometry defined by the relation

$$\begin{aligned} \tilde{g}^{\lambda \nu }=g^{\lambda \nu } - \frac{4L_{FF}}{L_F}F^\lambda _{\phantom {\lambda }\mu }F^{\mu \nu }. \end{aligned}$$

(50)

Recall that Novello have used the Hadamard method to obtain the equations of the electromagnetic field propagation. The wavefront is represented by the discontinuity surface $\Sigma$ in the electromagnetic field. According to the Hadamard method, the field is continuous at the surface $\Sigma$, but its first derivative is discontinuous there [18, 36]. The resulting equations obtained by the Novello method coincide with the equations obtained here.

In the particular case of Bardeen geometry, where Faraday tensor reads

$$\begin{aligned} F_{\mu \nu }=\delta ^{\theta }_{[\mu }\delta ^{\phi }_{\nu ]}q_m\sin \theta , \end{aligned}$$

(51)

the effective geometry non-zero components are

$$\begin{aligned} \tilde{g}^{tt}= & {} L_F g^{tt}, \end{aligned}$$

(52)

$$\begin{aligned} \tilde{g}^{rr}= & {} L_F g^{rr},\end{aligned}$$

(53)

$$\begin{aligned} \tilde{g}^{\theta \theta }= & {} \Phi g^{\theta \theta },\end{aligned}$$

(54)

$$\begin{aligned} \tilde{g}^{\phi \phi }= & {} \Phi g^{\phi \phi }, \end{aligned}$$

(55)

and

$$\begin{aligned} \tilde{g}_{tt}= & {} \frac{g_{tt}}{L_F},\end{aligned}$$

(56)

$$\begin{aligned} \tilde{g}_{rr}= & {} \frac{g_{rr}}{L_F},\end{aligned}$$

(57)

$$\begin{aligned} \tilde{g}_{\theta \theta }= & {} \frac{g_{\theta \theta }}{\Phi },\end{aligned}$$

(58)

$$\begin{aligned} \tilde{g}_{\phi \phi }= & {} \frac{g_{\phi \phi }}{\Phi } \end{aligned}$$

(59)

where is

$$\begin{aligned} F=\frac{q_m^2}{2r^4}. \end{aligned}$$

(60)

and

$$\begin{aligned} \Phi \equiv L_F + 2L_{FF}F. \end{aligned}$$

(61)

Equations of photon motion in the effective geometry of the Bardeen spacetimes

The effective geometry of the Bardeen spacetime is spherically symmetric and static, similarly to the spacetime geometry. Here we present the derivation of equations of photon motion in the effective Bardeen geometry noting that the derivation of equations of motion in the Bardeen geometry is analogous; recall that the motion in the Bardeen spacetimes has been studied in [43, 53]. Starting from the null vector normalisation condition in the effective geometry we obtain the equation

$$\begin{aligned} 0=-\frac{{\mathcal {L}}_F}{f(r)}\tilde{E}^2 + \frac{1}{f(r){\mathcal {L}}_F}\left( k^r\right) ^2 + \frac{\Phi }{r^2}\left( k_\theta \right) ^2 + \frac{\Phi }{r^2\sin ^2\theta }\tilde{L}_z^2. \end{aligned}$$

(62)

We can clearly separate the equation into radial and latitudinal parts

$$\begin{aligned} \frac{{\mathcal {L}}_F}{f(r)}\frac{r^2}{\Phi }\tilde{E}^2-\frac{r^2}{f(r){\mathcal {L}}_F\Phi } \left( k^r\right) ^2=\left( k_\theta \right) ^2+\frac{1}{\sin ^2\theta }\tilde{L}_z^2=K, \end{aligned}$$

(63)

where K is the separation constant. The equations of motion read

$$\begin{aligned} \left( k^r\right) ^2={\mathcal {L}}_F^2\left( 1-\frac{\Phi }{{\mathcal {L}}_F} f(r) K /r^2\right) \end{aligned}$$

(64)

and

$$\begin{aligned} \left( k^\theta \right) ^2=\frac{1}{r^4}\left( K-\frac{\tilde{l}^2}{\sin ^2\theta } \right) . \end{aligned}$$

(65)

It is convenient to introduce a new constant $\tilde{q}$ by formula

$$\begin{aligned} K=\tilde{q}+\tilde{l}^2. \end{aligned}$$

(66)

This new constant is constructed in such a way that it implies $\tilde{q}=0$ for the motion in the equatorial plane ($\theta =\pi /2$). Using this new constant, equations of motion will take the final form

$$\begin{aligned} (k^r)^2= & {} {\mathcal {L}}_F^2\left( 1-\frac{\Phi }{{\mathcal {L}}_F} f(r) (\tilde{q}+\tilde{l}^2) /r^2\right) , \end{aligned}$$

(67)

$$\begin{aligned} (k^\theta )^2= & {} \frac{1}{r^4}(\tilde{q}-\tilde{l}^2\mathrm {cot}^2\theta ),\end{aligned}$$

(68)

$$\begin{aligned} k^\phi= & {} \frac{\Phi }{r^2\sin ^2\theta }\tilde{l},\end{aligned}$$

(69)

$$\begin{aligned} k^{t}= & {} \frac{{\mathcal {L}}_F}{f(r)}. \end{aligned}$$

(70)