1 Introduction

Over the past few decades, extensive research has been conducted in order to understand the formation of large scale structures in the universe. More recently, a number of surveys such as the Sloan Digital Sky Survey (SDSS) and the Two-Degree Field (2dF) have have been used to measure the redshifts of millions of galaxies and plot the three-dimensional distribution of matter in the universe. It has been found that smoothing the distribution on the largest scales (larger than several hundred Mpc scales) displays a homogeneous distribution of matter, in accordance with the assumptions that the universe in the large scale is homogeneous and isotropic. At smaller scales, however, there exists density fluctuations; over-dense and under-dense regions like clusters and voids which increase at smaller smoothing scales. In terms of density fluctuation amplitude, the rms is over order unity on average \(\sim \) 10 Mpc scales. Noting that in the past two decades, the cold dark matter (CDM) and dark energy ideas have also contributed into the standard theoretical models of galaxy formations.

A fundamental assumption in structure formation is that it started to grow from weak density fluctuations in the early universe, then, amplified by gravity and eventually turned into the current structure formation. Measurements of the cosmic microwave background (CMB) by the WMAP satellite in combination with the 2dFGRS confirm the assumptions and allow an accurate determination of the geometry and matter content of the Universe about 380000 years after the Big Bang [1,2,3,4].

The perturbation models can in general be divide into scalar, vector and tensor perturbations, based on how they transform under spatial rotations and local time shifts. Based on these, one then study the evolution of small perturbations of homogeneous metric and matter fields. Scalar perturbation models have been widely studied in fourth order gravity mainly in the metric formalism [5,6,7,8,9,10,11,12,13,14]. These models originally developed for General relativity by Bardeen [15] and then expanded in the \(1+3\) covariant approach [16,17,18,19,20,21,22,23,24,25,26,27,28,29]. Many attempts have been implemented to numerically compute the matter power spectrum and its numerical analysis for classes of modified gravity theories, rather solving the full set of field equations [30,31,32,33]. Modifications to the linear order Einstein equations are thus introduced in terms of general functions of scale and time. In general, all studies have proved that the perturbation’s growth depends on the scale. While in General Relativity the evolution of dust matter is scale-independent [18], the numerical investigation of perturbation theories shows that the matter perturbation growth is scale - dependent [34, 35].

Perturbations in scalar-tensor theories have been considered from different approaches, for example: the reconstruction problem was addressed in [36], the density contrast evolution was studied in [20,21,22,23,24,25,26,27,28,29, 37, 38] and the second order perturbations were presented in [39]. In all these approaches the gravitational instability is a fundamental assumption. That is, the early universe has been almost perfectly smooth, with the exception of tiny density deviations with respect to the global cosmic background density and the accompanying tiny velocity perturbations from the general Hubble expansion. The minor density deviations vary from location to location. At one place the density will be slightly higher than the average global density, while a few Mega parsecs further the density may have a slightly smaller value than the average. The observed fluctuations in the temperature of the CMBR are a reflection of these density perturbations, such that the primordial density perturbations have been in the order of \(10^{-5}\). Noting that the origin of this density perturbation field has as yet not been fully understood. The most plausible theory is that the density perturbations are as a result of quantum fluctuations in the very early Universe which during the inflationary phase expanded to macroscopic proportions.

In this work, we consider scalar metric perturbation. We also assume that the matter is made up of a single real scalar field. In the case of General Theory of Relativity that the field equations are extremely coupled and nonlinear, the perturbation become more complicated in which analytical solutions of the governing field equations are impossible to solve or give little understanding about the behaviour of the system. Our novel approach to this problem is to utilise phase space and stability analysis as a fascinating technique to study the dynamics of the system. We apply the technique in the Brans–Dicke (BD) theory as an alternative to General Relativity.

Noting that the gravitational constant in Brans Dicke theory is non-constant. It dependents on the scalar field where its contribution to the Lagrangian density is through its own kinetic term. The evolution of the scalar field as a source term affects the matter distribution in the universe. This in turn makes the gravitational constant dependent of the matter field as well. This provides a manifestation of the Mach’s principle as interpreted by Dicke. (see [40] for a recent review). The authors in [41,42,43] have extensively studies different formulation of Brans Dicke theories and their applications in modern cosmology

The authors in [44] have already studied the evolution of the density contrast for Jordan-Fierz–Brans–Dicke theories in a Friedmann–Lemaitre–Robertson–Walker Universe. Following their work , we are going to investigate the density perturbation of the model based on the phase plane analysis. In particular, we focus on the late time stable solutions and give a qualitative description of the model. This has been done by using proper transformations in which the complicated equations become simplified. In general, there are two approach to examine the stability analysis of the model by simultaneously solving the dynamical system and best fitting the stability parameters with the observational data.

1-we find the critical points and their eigenvalues in terms of parameters of the model, find the stability conditions for each critical point and then constrain the parameters with observation.

2-We first constrain the model parameters and initial conditions with observation. Then find the critical points and eigenvalues for the best fitted parameters and investigate the stability of the model [41, 45].

This approach is more appropriate for complex systems that finding the critical points and eigenvalues in terms of model parameters is difficult. This is the approach we followed in this paper

Our work is organized as follows: In Sect. 2, Brans–Dicke theory has been extracted from Scalar-tensor theories of gravity, we summarize the background field equations of BD theories in both Jordan and Einstein frame. In Sect. 3 following [44], we implement the metric perturbation and drive the perturbed equations. In Sect. 4, we best fit our model with the observational data. In Sect. 6, phase space analysis of the model is discussed. The perturbed second order, coupled and nonlinear equations are transformed into simple ones by introducing new dynamical variables. The stability of the model and attractor solutions are discussed. Section is devoted to discuss the solution in more details. We further derive equation of state parameter in terms of the best fitted stability and model parameters and test the model against observational data. Section 7 is the summary.

2 Extracting Brans–Dicke theory from Scalar-tensor theories of gravity

Scalar-tensor theories are usually formulated in two different frameworks; the Jordan Frame (JF) or the Einstein Frame (EF). The former defines lengths and times as would be measured by ordinary laboratory apparatus so that all observables (time, redshift, among others) have their standard interpretation. Also, the metric is minimally coupled to matter and the scalar field is coupled with the Ricci curvature. Here, we start with the scalar-tensor action in Jordan Frame (JF) [36] as,

$$\begin{aligned} S&={1\over 16\pi G_*} \int d^4x \sqrt{-g} \Bigl (F(\Phi )~R - Z(\Phi )~g^{\mu \nu } \partial _{\mu }\Phi \partial _{\nu }\Phi \ \nonumber \\&\quad - 2U(\Phi ) \Bigr ) + S_m[\psi _m; g_{\mu \nu }]\ , \end{aligned}$$
(1)

where \(G_*\) denotes the bare gravitational coupling constant, R the scalar curvature of \(g_{\mu \nu }\), and g its determinant. The variation of action (1) gives,

$$\begin{aligned}&F(\Phi ) \left( R_{\mu \nu }-{1\over 2}g_{\mu \nu }R\right) \nonumber \\&\quad = 8\pi G_* T_{\mu \nu } + Z(\Phi ) \left( \partial _\mu \Phi \partial _\nu \Phi - {1\over 2}g_{\mu \nu } (\partial _\alpha \Phi )^2\right) \nonumber \\&\qquad +\nabla _\mu \partial _\nu F(\Phi ) - g_{\mu \nu }\Box F(\Phi ) - g_{\mu \nu } U(\Phi )\ ,\nonumber \\&2Z(\Phi )~\Box \Phi = -{dF\over d\Phi }\,R - {dZ\over d\Phi }\,(\partial _\alpha \Phi )^2 + 2 {dU\over d\Phi }\ , \end{aligned}$$
(2)
$$\begin{aligned}&\nabla _\mu T^\mu _\nu = 0\ , \end{aligned}$$
(3)

In the Brans–Dicke theory \(F(\Phi ) = \Phi \) and \(Z(\Phi ) = \omega /\Phi \) and \( 2ZF+3(dF/d\Phi )^2=2\omega + 3\). Thus the field equations become,

$$\begin{aligned}&3H^2=\frac{8\pi G_*\rho }{\Phi }-3H\frac{\dot{\Phi }}{\Phi } +\frac{\omega }{2}\frac{\dot{\Phi }^{2}}{\Phi ^{2}}-\frac{U(\Phi )}{\Phi }, \end{aligned}$$
(4)
$$\begin{aligned}&\dot{H}=-\frac{4\pi G_*(\rho +P)}{\Phi }+H\frac{\dot{\Phi }}{2\Phi } -\frac{\omega }{2}\frac{\dot{\Phi }^{2}}{\Phi ^{2}}-\frac{\ddot{\Phi }}{2\Phi } \end{aligned}$$
(5)
$$\begin{aligned}&\ddot{\Phi }+3H\dot{\Phi }=\frac{(3\dot{H}+2H^{2})}{\Phi }+\frac{\omega }{2}\frac{\dot{\Phi }^{2}}{\Phi ^{3}}-\frac{1}{\Phi }\frac{dU(\Phi )}{ d\Phi } \end{aligned}$$
(6)
$$\begin{aligned}&\dot{\rho }+3H(\rho +P)=0. \end{aligned}$$
(7)

While the above equations are in Jordan frame (JF), it is usually more transparent to analyze the equations and the mathematical consistency of the solutions in the Einstein frame (EF). This is achieved by conformal transformation of the metric and a redefinition of the scalar field. Let us call \(g^*_{\mu \nu }\) and \(\varphi \) the new metric and scalar field, and redefine

$$\begin{aligned} g^*_{\mu \nu }\equiv & {} F(\Phi )~g_{\mu \nu }\ , \end{aligned}$$
(8)
$$\begin{aligned} \left( {d\varphi \over d\Phi }\right) ^2\equiv & {} {3\over 4}\left( {d\ln F(\Phi )\over d\Phi }\right) ^2 + {Z(\Phi )\over 2F(\Phi )}\, \end{aligned}$$
(9)
$$\begin{aligned} A(\varphi )\equiv & {} F^{-1/2}(\Phi )\ ,\end{aligned}$$
(10)
$$\begin{aligned} 2V(\varphi )\equiv & {} U(\Phi )~F^{-2}(\Phi )\ . \end{aligned}$$
(11)

Action (1) then takes the form

$$\begin{aligned} S&={1\over 4\pi G_*} \int d^4x \sqrt{-g_*} \left( {R^*\over 4} - {1\over 2} g_*^{\mu \nu } \partial _{\mu }\varphi \partial _{\nu }\varphi - V(\varphi ) \right) \nonumber \\&\quad + S_m[\psi _m; A^2(\varphi )~g^*_{\mu \nu }]\ , \end{aligned}$$
(12)

where \(g_*\) is the determinant of \(g^*_{\mu \nu }\), \(g_*^{\mu \nu }\) its inverse, and \(R^*\) its scalar curvature. Note that the first term looks like the action of general relativity, but that matter is now explicitly coupled to the scalar field \(\varphi \) through the conformal factor \(A^2(\varphi )\). The field equations deriving from action (12) take the simple form

$$\begin{aligned}&R^*_{\mu \nu } - {1\over 2} R^* g^*_{\mu \nu } = 8\pi G_* T^*_{\mu \nu }+ 2 \partial _\mu \varphi \partial _\nu \varphi \nonumber \\&\quad -g^*_{\mu \nu }(g_*^{\alpha \beta } \partial _\alpha \varphi \partial _\beta \varphi ) - 2 V(\varphi ) g^*_{\mu \nu }\ , \end{aligned}$$
(13)
$$\begin{aligned}&\Box ^*\varphi = -4\pi G_*\alpha (\varphi )~T_* +dV(\varphi )/d\varphi \ , \end{aligned}$$
(14)
$$\begin{aligned}&\nabla ^*_\mu T^\mu _{*\nu } = \alpha (\varphi )~T_* \partial _\nu \varphi \ , \end{aligned}$$
(15)

where, quantities referring to the Einstein frame will always have an asterisk and \(\alpha (\varphi ) \equiv {d \ln A \over d\varphi }\) is the coupling strength of the scalar field to matter sources. In Brans–Dicke theory, using Eqs. (9)–(11) and by considering constant value for \(\omega \), it will be as, \(\alpha ^{2}=({2\omega _+3})^{-1}\). Note that, \(T_* \equiv g^*_{\mu \nu }T_*^{\mu \nu }\) is the trace of the matter energy-momentum tensor \(T_*^{\mu \nu } \equiv (2/\sqrt{-g_*})~\delta S_m/\delta g^*_{\mu \nu }\) in EF units. From its definition, one can deduce the relation \(T^*_{\mu \nu } = A^2(\varphi )~T_{\mu \nu }\) with its JF counterpart.

$$\begin{aligned} T_{\mu \nu }&= (\rho +p) u_{\mu } u_{\nu } + p g_{\mu \nu } =A^{-2}~T^*_{\mu \nu }~ \\ \nonumber&=A^{-2}\left( (\rho _*+p_*) u^*_{\mu } u^*_{\nu } + p_* g^*_{\mu \nu }\right) \ , \end{aligned}$$
(16)

Using Eqs. (8), (10) and (16), it can be concluded that \(\rho _*=A^{4}\rho \) and \(P_*=A^{4}P\), where in Brans–Dicke theory , \(A=e^{\alpha \varphi }\). Also, from Eqs. (8) and (10), \(ds^{2} = A^{2} ds^{2}_{*}\), where \(ds^{2}=-dt^{2}+a(t)^{2}dl^2\) and \(ds_{*}^{2}=-dt_{*}^{2}+a(t_{*})^{2}dl^2\) are the JF and EF metrics respectively. This relation indicates that, \(dt=A(\varphi )dt_{*}\) and \(a(t)=A(\varphi )a_{*}(t_{*})\). Thus, for Brans–Dicke the field equations in EF become

$$\begin{aligned}&3H^{2}_{*} = 8 \pi G_{*}\rho _*+\dot{\varphi }^{2}+2V(\varphi ) \end{aligned}$$
(17)
$$\begin{aligned}&\dot{H_{*}} = -4\pi G_{*}(\rho _*+P_{*})-\dot{\varphi }^{2} \end{aligned}$$
(18)
$$\begin{aligned}&\ddot{\varphi }+3H_{*}\dot{\varphi }+\frac{d V(\varphi )}{d\varphi } = -4\pi G_{*}\alpha (\rho _*-3P_{*}) \end{aligned}$$
(19)

Here, dot denotes derivative respect to \(t_{*}\). We Also can derive the equations by replacing the physical time \(t_{*}\) with the conformal time \(\eta _{*}\). Since, \(d\eta =\frac{dt}{a}\) and \(d\eta _{*}=\frac{dt_{*}}{a_{*}}\), thus,\(\mathcal {H}=\frac{dlna}{d\eta }=aH\) and \(\mathcal {H_{*}}=\frac{dlna_{*}}{d\eta _{*}}=a_{*}H_*\). We also have

$$\begin{aligned} \mathcal {H}_*=\frac{a'_*}{a_*}=\mathcal {H}-\frac{d ln (A)}{ d\varphi }\,\varphi =\mathcal {H}-\alpha \varphi ^{'}, \end{aligned}$$
(20)

where prime denotes derivative respect to conformal time \(\eta \). The conformal time \(\eta \) is the same in both frames \(\eta _{*}\equiv \eta \). Thus, the field equations for Brans–Dicke theory in EF will be

$$\begin{aligned}&3\mathcal {H}_*^2 -\varphi '^2\,=\,2\tilde{\rho _*} +2V(\varphi ) a_{*}^2, \end{aligned}$$
(21)
$$\begin{aligned}&\mathcal {H}_*^2-\mathcal {H}_*'-\varphi '^2\,=\, \tilde{\rho _*}(1+c_s^2), \end{aligned}$$
(22)
$$\begin{aligned}&\varphi ''+2\mathcal {H}_*\varphi '+a_{*}^{2}\frac{dV}{d\varphi } \,=\,- \tilde{\rho _*}(1-3c_s^2)\alpha , \end{aligned}$$
(23)
$$\begin{aligned}&\frac{\rho _*'}{\rho _*}=-3\mathcal {H}_*(1+c_s^2)+\alpha (1-3c_s^2)\varphi ', \end{aligned}$$
(24)

where, \(c^{2}_{s}=\frac{P_*}{\rho _*}\) and \(\tilde{\rho _*}=4\pi G_{*}\rho _*a_{*}^{2}\).

3 Perturbations in BD theories

We begin with the field equations for the action (12). The field equations obtained from action, neglecting the potential, are,

$$\begin{aligned} G^{*}_{\mu \nu }+[-g_{*}^{\alpha \beta }\nabla ^{*}_\alpha \varphi \nabla ^{*}_\beta \varphi ]g^{*}_{\mu \nu }+2\nabla ^{*}_\mu \varphi \nabla ^{*}_\nu \varphi =-8\pi G_{*} T^{*}_{\mu \nu }, \nonumber \\ \end{aligned}$$
(25)

From now on, let us drop the notation (*) for EF quantities. Up to the first order perturbation, the equations of the gravitational field in BD theories (25), the scalar field Eq. (14) and the conservation Eq. (3) respectively become

$$\begin{aligned}&\delta G^\mu _\nu -\nabla _\alpha \varphi \nabla _\beta \varphi \delta ^\mu _\nu (\delta g^{\alpha \beta })+2\nabla _\alpha \varphi \nabla _\nu \varphi (\delta g^{\mu \alpha })\nonumber \\&\qquad +\,2\left( -\delta ^\mu _\nu g^{\alpha \beta }\nabla _\beta \varphi \nabla _\alpha +g^{\alpha \mu }\nabla _\nu \varphi \nabla _\alpha +\nabla ^\mu \varphi \nabla _\nu \right) \delta \varphi \nonumber \\&\quad =-8\pi G\, \delta T^\mu _\nu . \end{aligned}$$
(26)
$$\begin{aligned}&\delta g^{\alpha \beta }\nabla _\alpha \nabla _\beta \varphi +g^{\alpha \beta }\left( \delta \varphi _{,\alpha \beta }-\delta \Gamma ^\gamma _{\beta \alpha }\varphi _{,\gamma }-\Gamma ^\gamma _{\beta \alpha }\delta \varphi _{,\gamma }\right) \nonumber \\&\quad \,=\,-4\pi G\alpha \delta T, \end{aligned}$$
(27)
$$\begin{aligned}&\partial _\mu \delta T^\mu _\nu +\delta \Gamma ^\mu _{\alpha \mu }T^\alpha _\nu +\Gamma ^\mu _{\alpha \mu }\delta T^\alpha _\nu -\delta \Gamma ^\alpha _{\mu \nu }T^\mu _\alpha -\Gamma ^\alpha _{\mu \nu }\delta T^\mu _\alpha \nonumber \\&\quad \,=\,\alpha \delta T \partial _\nu \varphi +\alpha T\partial _\nu \delta \varphi , \end{aligned}$$
(28)

Let us consider the scalar perturbations of the flat FLRW metric in the longitudinal gauge

$$\begin{aligned} \mathrm{d}s^2\,=\,a^2(\eta )[(1+2\Phi )\mathrm{d}\eta ^2-(1-2\Psi )(\mathrm{d}r^2+r^2\mathrm{d}\Omega _{2}^2)], \nonumber \\ \end{aligned}$$
(29)

where \(\Phi \equiv \Phi (\eta ,\vec {x})\) and \(\Psi \equiv \Psi (\eta ,\vec {x})\) are the Bardeen’s potentials [15, 46] and \(\eta \) is the conformal time. We also assume adiabatic perturbations and barotropic fluids where the perturbed stress-energy tensor can be expressed as

$$\begin{aligned} \delta T^{0}_{\;\;0}\,= & {} \,\delta \rho = \rho _{0} \delta ,\;\; \delta T^{i}_{\;\;j}\,=\, -\delta P \delta ^{i}_{\;\;j} = -c_s^2 \delta ^{i}_{\;\;j}\rho _{0}\delta ,\nonumber \\ \delta T^{0}_{\;\;i}\,= & {} \,-\delta T^{i}_{\;\;0}\,=-\,(1 + c_s^2)\rho _{0}\partial _{i}v, \end{aligned}$$
(30)

where \(\rho \) is the perturbed energy density of the cosmological fluid, \(\delta \) is the density contrast and v is the potential for velocity perturbations. In the following, we also assume that both perturbed and unperturbed matter obey the same equation of state.

Using the perturbed metric (29), the perturbed adiabatic and barotropic stress-energy tensor (30) and also assuming that the background equations hold, considering the (ij) components which yields \(\partial (\Phi -\Psi )=0\) and indicates that both scalar potentials are equal as in GR. We finally yield the following set of equations in Fourier space:

$$\begin{aligned}&3\mathcal {H}\Phi '+(k^2+3\mathcal {H}^2-\varphi '^2)\Phi +\varphi '\delta \varphi ' =-\tilde{\rho }\delta , \end{aligned}$$
(31)
$$\begin{aligned}&\Phi ''+3\mathcal {H}\Phi '+(\mathcal {H}^2+2\mathcal {H}'+\varphi '^2)\Phi -\varphi '\delta \varphi ' =\tilde{\rho }c_s^2\delta , \end{aligned}$$
(32)
$$\begin{aligned}&\Phi '+\mathcal {H}\Phi -\varphi '\delta \varphi =-\tilde{\rho }(1+c_s^2)v, \end{aligned}$$
(33)
$$\begin{aligned}&4\varphi '\Phi '+2(\varphi ''+2\mathcal {H}\varphi ')\Phi -\delta \varphi ''-2\mathcal {H}\delta \varphi ' - k^2 \delta \varphi \nonumber \\&\quad \,=\,(1-3c_s^2)\alpha \tilde{\rho }\delta , \end{aligned}$$
(34)
$$\begin{aligned}&3\Phi '-\frac{\delta '}{1+c_s^2}+k^2v=-\frac{1-3c_s^2}{1+c_s^2}\alpha \,\delta \varphi ', \end{aligned}$$
(35)
$$\begin{aligned}&\Phi +v'+\left( 1-3c_s^2\right) \left( \mathcal {H}+\alpha \varphi '\right) v+\frac{c_s^2}{1+c_s^2}\delta \nonumber \\&\quad \,=\,-\frac{1-3c_s^2}{1+c_s^2}\alpha \,\delta \varphi , \end{aligned}$$
(36)

where \(\prime \) means derivative with respect to the conformal time.

4 Constraining the cosmological parameters

The Eqs. (31)–(36) describe the general linear perturbations for the model. The differential equations are second order, nonlinear and coupled in a large number of variables and are impossible to solve them analytically. Our purpose in this section is first to simplify these perturbed equations without losing the generality by converting the second order equations to the first order ones. This makes the equations simpler to solve numerically and and prepare them for phase space analysis in the next section.

The phase space is in particular useful in visualizing the behavior of the dynamical systems and studying the stability of the system.

To simplify these equations, let us introduce a new set of variables as:

$$\begin{aligned} \chi _{1}&=\frac{\Phi '}{\Phi \mathcal {H}} \ \ \chi _{2}=\frac{k}{\mathcal {H}}\ \ \chi _{3}=\frac{\varphi ^{'}}{\mathcal {H}} \ \ \chi _{4}=\frac{\delta \varphi ^{'}}{\Phi \mathcal {H}} \ \ \nonumber \\ \chi _{5}&=\frac{\tilde{\rho }}{\mathcal {H}^{2}} \ \ \chi _{6}=\frac{\delta }{\Phi } \ \ \chi _{7}=\frac{\delta \varphi }{\Phi } \ \ \chi _{8}=\frac{\delta \varphi ''}{\Phi \mathcal { H}^{2}}. \end{aligned}$$
(37)

One then can rewrite the Eqs. (31)–(36) for the autonomous equations of motion as

$$\begin{aligned} \frac{d\chi _{1}}{dN}= & {} \zeta _{2}-\chi _{1}^{2}-\chi _{1}\zeta _{1} \end{aligned}$$
(38)
$$\begin{aligned} \frac{d\chi _{2}}{dN}= & {} -\zeta _{1}\chi _{2}\end{aligned}$$
(39)
$$\begin{aligned} \frac{d\chi _{3}}{dN}= & {} \zeta _{3}-\zeta _{1}\chi _{3}\end{aligned}$$
(40)
$$\begin{aligned} \frac{d\chi _{4}}{dN}= & {} \chi _{8}-\chi _{4}\chi _{1}-\zeta _{1}\chi _{4}\end{aligned}$$
(41)
$$\begin{aligned} \frac{d\chi _{5}}{dN}= & {} -\chi _{5}{(1+3c_{s}^{2})+\alpha (1-3c_{s}^{2})\chi _{3}}-2\zeta _{1}\chi _{5}\end{aligned}$$
(42)
$$\begin{aligned} \frac{d\chi _{6}}{dN}= & {} \zeta _{6}-\zeta _{1}\chi _{6}\end{aligned}$$
(43)
$$\begin{aligned} \frac{d\chi _{7}}{dN}= & {} \chi _{4}-\chi _{7}\chi _{1}\end{aligned}$$
(44)
$$\begin{aligned} \frac{d\chi _{8}}{dN}= & {} -\chi _{8}\chi _{1}-2\zeta _{1}\chi _{8} \end{aligned}$$
(45)

where \(N = ln (a)\) such that \(\frac{d}{dN}=\frac{1}{\mathcal {H}}\frac{d}{d\eta }\) and the new parameters \({\zeta _{1}..\zeta _{6}}\) are given by:

$$\begin{aligned} \zeta _{1}= & {} \frac{\mathcal {H}'}{\mathcal {H}^{2}} \ \ \zeta _{2}=\frac{\Phi ''}{\Phi \mathcal {H}^{2}} \ \ \zeta _{3}=\frac{\varphi ''}{\mathcal {H}^{2}} \ \ \end{aligned}$$
(46)
$$\begin{aligned} \zeta _{4}= & {} \frac{\nu }{\Phi \mathcal {H}} \ \ \zeta _{5}=\frac{\nu ^{'}}{\Phi \mathcal {H}} \ \ \zeta _{6}=\frac{\delta ^{'}}{\Phi \mathcal {H}}. \ \ \end{aligned}$$
(47)

From Eqs. (31)–(36), we can obtain the above parameters in terms of the new variables. By dividing both sides of Eqs. (32) and (34) by \(\Phi \mathcal {H}^{2}\) and using new variables (37), the parameters \(\zeta _{2}\) and \(\zeta _{3}\) become

$$\begin{aligned} \zeta _{2}= & {} -1-2\zeta _{1}-3\chi _{1}-\chi _{3}^{2}+\chi _{3}\chi _{4}+c_s^2\chi _{5}\chi _{6} \end{aligned}$$
(48)
$$\begin{aligned} \zeta _{3}= & {} \frac{1}{2}(1-3c_s^2)\alpha \chi _{5}\chi _{6}{+}\frac{1}{2}\chi _{2}^{2}\chi _{7}{+}\chi _{4}{-}\chi _{3}-2\chi _{3}\chi _{1}{+}\frac{1}{2}\chi _{8}\nonumber \\ \end{aligned}$$
(49)

Also, by dividing both sides of Eqs. (33), (36) and (35) by \(\Phi \mathcal {H}\) and using new variables (37), the parameters \(\zeta _{4}\), \(\zeta _{5}\) and \(\zeta _{6}\) change to

$$\begin{aligned} \zeta _{4}= & {} -\frac{\chi _{2}^{2}}{k^2}(1+\chi _{1}-\chi _{3}\chi _{7})/(1+c_s^2)\chi _{5}) \end{aligned}$$
(50)
$$\begin{aligned} \zeta _{5}= & {} \frac{\chi _{2}}{k}\Big [-1-\frac{k^2}{\chi _{2}^{2}}(1-3c_s^2)(1+\alpha \chi _{3})\zeta _{4}\nonumber \\&-\,\frac{c_s^2}{1+c_s^2}\chi _{6}- \frac{(1-3c_s^2)\chi _{7}}{(1+c_s^2)}\Big ] \end{aligned}$$
(51)
$$\begin{aligned} \zeta _{6}= & {} 3(1+c_s^2)\chi _{1}+(1+c_s^2)k^2\zeta _{4}+(1-3c_s^2)\alpha \chi _{4} \end{aligned}$$
(52)

Next, we derive the parameter \(\zeta _{1}\) in terms of new variables and the other parameters. To do this, we first take derivative of Eq. (33) with respect to \(\eta \):

$$\begin{aligned}&\Phi ''+\mathcal {H}'\Phi +\mathcal {H}\Phi '-\varphi ''\delta \varphi -\varphi '\delta \varphi '\nonumber \\&\quad =-\tilde{\rho }'(1+c_{s}^{2})\upsilon -\tilde{\rho }(1+c_{s}^{2})\upsilon ' \end{aligned}$$
(53)

Then, dividing both sides of (53) by \(\Phi \mathcal {H}^{2}\) results

$$\begin{aligned}&\zeta _{2}+\zeta _{1}+\chi _{1}-\zeta _{3}\chi _{7}-\chi _{3}\chi _{4}\nonumber \\&\quad =-\frac{(1+c_s^2)}{\mathcal {H}}(\tilde{\rho }'\zeta _{4}+\tilde{\rho }\zeta _{5}) \end{aligned}$$
(54)

Note that \(\tilde{\rho }=4\pi Ga^{2}\rho \), thus \(\tilde{\rho }'=\tilde{\rho }\frac{\rho '}{\rho }+2\mathcal {H}\tilde{\rho }\). Using this relation and Eq. (24), the Eq. (54) can be rewritten as

$$\begin{aligned}&\zeta _{2}+\zeta _{1}+\chi _{1}-\zeta _{3}\chi _{7}-\chi _{3}\chi _{4}\nonumber \\&\quad =(1+c_s^2)k^{2}\frac{\chi _{5}}{\chi _{2}^{2}}\Big [(1+\alpha +3c_s^2(1-\alpha ))\zeta _{4}-\frac{\chi _{2}}{k}\zeta _{5}\Big ] \end{aligned}$$
(55)

Combining the above equation with Eq. (48), parameter \(\zeta _{1}\) becomes

$$\begin{aligned}&\zeta _{1}=-1-2\chi _{1}-\chi _{3}^{2}+c_s^2\chi _{5}\chi _{6}-\zeta _{3}\chi _{7}\nonumber \\&\quad +(1+c_s^2)k^{2}\frac{\chi _{5}}{\chi _{2}^{2}}\Big [(1+\alpha +3c_s^2(1-\alpha ))\zeta _{4}-\frac{\chi _{2}}{k}\zeta _{5}\Big ] \end{aligned}$$
(56)

By substituting (48)–(56) into the Eqs. (38)–(45), we obtain a complete set of equations that describe the behavior of the system in terms of new variables. Also by dividing both sides of (31) by \(\Phi \mathcal {H}^{2}\) and some calculation, one can obtain a constrain as

$$\begin{aligned} 3\chi _{1}+\chi _{2}^{2}+3-\chi _{3}^{2}+\chi _{3}\chi _{4}=-\chi _{5}\chi _{6} \end{aligned}$$
(57)

that reduces the number of independent equations to seven. Noting that in the new system of equations the parameter k is replaced by \(\chi _{2}\mathcal {H}\).

Next we are planning to best fit the parameters \(H_0\) and \(\alpha \) in the system of Eqs. (38)–(45) by using observational data. The SNe Ia observations measure the apparent magnitude m of a supernova that is related to the distance modulus \(\mu \) and luminosity distance \(d_L\) of the supernova by

$$\begin{aligned} \mu (z)\equiv m(z )-M=5\log _{10}(d_{L}(z )/Mpc)+25 \end{aligned}$$
(58)

where M is the absolute magnitude of the supernova. In flat FRW cosmology, the luminosity distance is given by

$$\begin{aligned} d_{L}(z )=(1+z )\int _{0}^{z }\frac{dz}{(H(z)}, \end{aligned}$$
(59)

The (59) can be expressed by two new differential equations as

$$\begin{aligned} \frac{d({d_L}(z))}{dN}&=-\left( {d_L}(z)+\frac{e^{2N}}{H(z)}\right) \end{aligned}$$
(60)
$$\begin{aligned} \frac{d(H(z))}{dN}&=H(z)\left( \frac{\dot{H}}{H^{2}}\right) =H(z)\left( \zeta _{1}-1\right) . \end{aligned}$$
(61)

We have a system of Eqs. (38)–(45) plus the above two differential equations for luminosity, (60)–(61) that has to be solves simultaneously. We assumed that the universe is in mater dominated state where \(c_{s}^{2} = 0\). We constrain the model parameters \(H_0\) and \(\alpha \) and initial conditions of the dynamical variables and luminosity differential equations with the observational data, using Supernova Type Ia observational data.

We conduct the \(\chi ^{2}\) goodness of fit that given by

$$\begin{aligned} \chi _{SNe}^{2}(\alpha ,H_{0})=\sum _{i=1}^{557}\frac{[\mu _{i}^{the}(z _{i}|\alpha , H_{0})-\mu _{i}^{obs}]^{2}}{\sigma _{i}^{2}}, \end{aligned}$$
(62)

where the sum is over the distance modulus of 557 Type Ia supernovae (SNeIa) sample ([47, 48]).

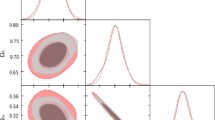
In Fig. 1-RHS, the green, red and blue regions show the confidence region for the constraint on the parameters \(\alpha \) and \(H_{0}\) at the 68.3 %, 95.4 % and 99.7 % confidence levels. A 3-dim of the likelihood is also shown in the Fig. 1-LHS.

Fig. 1
figure 1

The confidence region in 2-dim and 3-dim for the best fitted \(\alpha \) and \(H_0\) parameters

Full size image

In the following section we use the best fitted value of \(H_0\) and \(\alpha \) to conduct the stability analysis in the phase space for our model.

5 Phase space analysis

In stability analysis, and in the context of autonomous dynamical systems, the fixed points ( or critical points) are the exact constant solutions that describe the asymptotic behavior of the system. This can be done by simultaneously solving Eqs.  (38)–(45) such that \(\chi _1^\prime =0,\ldots , \chi _8^\prime =0\) . As mentioned, imposing the constraint reduces the number of independent equations to seven. Employing stability analysis procedure, we find thirteen critical points given in Table 1.

Table 1 Critical points for the perturbed system
Full size table

Here, we used the best fit value of \(\alpha =3.35\) and \(H_0\). Substituting linear perturbations \(\chi _1^\prime \rightarrow \chi _1^\prime + \delta \chi _1^\prime , \ldots , \chi _7^\prime \rightarrow \chi _7^\prime + \delta \chi _7^\prime \) about the critical points into the set of Eqs. (38)–(45), yields thirteen eigenvalues \(\lambda _i\)(i = 1,13) as follows:

Stability requires the real part of the eigenvalues to be negative. As can be seen, in our model all of the elements of \(Ev_{10}\) is negative so this critical point \(P_{10}\) is stable. Also the \(3^{th}\) and \(4^{th}\) elements of the eigenvalue \(Ev_{10}\) is complex with negative real part. This indicates that the nature of this point is stable focus and the trajectories are spiralling in towards the attractor.

In Fig. 2, the dynamical variables \(\chi _1\), . . . , \(\chi _8\) for the best fitted value of parameters \(\alpha =3.35\) and \(h_0=0705\) are plotted in 3-dim phase space. As can be seen, by small perturbation, the system start to oscillate and asymptotically approaches the stable state of attractor.

Fig. 2
figure 2

Attractor behavior and small fluctuation in dynamics of the system in three dimensions for best value of \(\alpha \) and \(H_0\)

Full size image

In Fig. 3, the 1-dim plots of the dynamical variables are given with respect to the redshift z for both best fitted and arbitrary initial conditions.The graphs show that the solutions are independent of the initial conditions. This is because, in the infinite time limit, the system approaches the attractor, independent of the initial conditions.

Fig. 3
figure 3

dynamical behavior and of new variables for best values of \(\alpha \) and different initial conditions

Full size image

In Fig. 4, the solutions are sketched only for the best fitted model parameters and initial conditions. It shows that the system oscillates while approaching the attractor state ( the critical point \(P_{10}\)) in equilibrium. As can be seen in the graphs, over the course of time the oscillation decays, becomes less visible and accordingly the trajectory of the dynamical system approaches the focus closer and closer, as if spiralling into the critical point. Note that the attractor behavior reveals more as the system approaches the critical point. Asymptotically, the small perturbation eventually settles down and system approaches the attractor.

Fig. 4
figure 4

Dynamical behavior of new variables for best values of \(\alpha \) and best fitted initial conditions

Full size image

6 Discussion

In the last section by applying the phase space approach and using variables, \(\{\chi _{1},\chi _{2}, \ldots , \chi _{8}\}\), we converted the set of coupled second order differential equations to first order equations and studied the stability of the model. The new variables are given in terms of original variables \(( \mathcal {H}, \Phi , \varphi , \delta , \upsilon ,\tilde{\rho }, k )\) and their first and second derivatives. As discussed, in stability analysis, we study the dynamics of these new variables instead of the original ones. In fact, one can simply show that the system whose oscillations determined by the initial conditions are:

$$\begin{aligned}&\frac{d\Phi }{dN}=\Phi \chi _{1} \end{aligned}$$
(63)
$$\begin{aligned}&\frac{d\varphi }{dN}=\chi _{3}\end{aligned}$$
(64)
$$\begin{aligned}&\frac{d\delta }{dN}=\Phi \zeta _{3}\end{aligned}$$
(65)
$$\begin{aligned}&\frac{d\upsilon }{dN}=\Phi \zeta _{5} \end{aligned}$$
(66)

On the other hand, in phase space analysis, we plotted the new variables with respect to the redshift (Figs. 2, 3, 4). Noting that the trajectories of these variables are for the best fitted values of \(\alpha \) and initial conditions. As explained, the trajectories are independent of the initial conditions as expected in phase space approach. By perturbing these variables, the system begins oscillating while the trajectories are departed from each other for different initial conditions. Eventually after a long time, where the system converges to the attractor at equilibrium, all the trajectories emerges to a unique final stable state.

Note that non of the variables (\(\chi _{1},\chi _{2}, ..., \chi _{8}\) ) are observable. So we need to test our model against cosmological parameters that are directly or indirectly observable. For this purpose we sketch the equation of state parameter, \(w_{eff}\) that in matter dominated universe vanishes and its current value in an accelerating universe is about \(-0.82\). Fig. 5 shows the EoS parameter for the best fitted values of \(\alpha \) and initial conditions. As can be seen the parameter vanished in the matter dominated era and is equal to \(-0.82\) today which is within the range of observation.The graph also shows that, by perturbing the system, the parameter socialites and in near future approaches \(-1\), i.e. the universe will be in \(\Lambda CDM\) phase.

Fig. 5
figure 5

The evolution of EoS parameter against redshift: for best fitted \(\alpha \)

Full size image

7 Conclusion

This paper is devoted to study the conventional metric perturbation in the Brans–Dicke thoery using the phase space algorithm. in practice, we integrated two different perturbation model; the standard metric perturbation and the perturbation based on phase space analysis of the newly constructed variables from the original geometric, matter and other fields. The conventional scalar perturbation in the metric introduces the scalar field, \(\Phi \), that together with the brans-Dicke scalar field \(\varphi \), the matter density \(\rho \) and Hubble parameter constitute the model that can potentially explain the large scale structure of the universe.

In phase space formalism, the newly constructed variables are used to manifest the attractor characteristic of the model. It is shown that the scalar perturbation of \(\Phi \), \(\delta \), \(\upsilon \) and \(\varphi \), strongly depend on the initial conditions while the newly constructed variables are independent of them. By infinitesimal perturbation of these new variables, the solutions approach the same state corresponding to the attractor state. Noting that for those initial conditions largely different from the one that create the attractor point, the solutions will be represented as an oscillation with large amplitude while for the initial conditions close to the one that create attractor point, the oscillation is with small amplitude.

In standard metric perturbation, the complexity and nonlinearity of equations in addition to exceeding the number of unknown parameter’s, and increasing the sensitivity of the solutions to the initial conditions make it difficult to to interpret the large scale structure of the universe. However, its application in phase space creates a novel mechanism that simplifies both the complexity of the problem and system analysis. here, we also study the stability of the system and visualise the behaviour of the dynamical variable. More importantly, by fitting the parameters of the model, we supported our result with observational data. Though, non of the original variables in metric perturbation or newly constructed variables in phase space are directly or indirectly observable, the EoS parameter resulted from model fitting is in good match with observational data. Also It is important to note that while phase space analysis provides a qualitative description of the model, the fitting algorithm create some quantitative variables compatible with observation.