1 Introduction

The idea of the membrane paradigm was started by Damour [1] and then developed further by Thorne et al. [2, 3]. Later, the membrane paradigm has been applied to various field theories by following a more systematic action-based derivation proposed by Parikh and Wilczek in [4]. In the membrane paradigm, the observer at infinity sees that the black hole is equivalent with a thin fluid membrane living just outside the black hole’s event horizon, and hence the black hole can be replaced by the fluid membrane. The membrane paradigm was originally proposed to study astrophysical black holes [5,6,7]. Realizing the membrane fluid could provide the long wavelength description of the strongly coupled quantum field theory at a finite temperature, researchers take a new interest in the membrane paradigm in the context of gauge/gravity duality [8,9,10,11]. In [10], the low frequency limit of the boundary theory transport coefficients could be expressed in terms of geometric quantities evaluated at the horizon by identifying the currents in the boundary theory with radially independent quantities in bulk. In the presence of momentum dissipation, the DC conductivity can also be calculated in a similar way [12,13,14,15] since there appeared to exist the radially independent zero mode of some current in bulk. Recently, Donos and Gauntlett obtained the DC thermoelectric conductivity in Einstein–Maxwell theory [16] by solving a system of Stokes equations on the black hole horizon for a charged fluid.

The nonlinear electrodynamics (NLED) is an effective model of electromagnetic fields and reduces to Maxwell electrodynamics at the weak field limit. NLED is interesting per se, for example some models give finite self-energy of charged particles and can remove singularity at the classical level. Two famous NLED are Heisenberg–Euler effective Lagrangian [17] and Born–Infeld electrodynamics [18]. On the other hand, it is well-known that the Maxwell action enjoys the conformal invariance in four dimensions. A natural extension of the Maxwell action in \(\left( d+1\right) \)-dimensional spacetime that is the conformally invariant is the action of a power-law Maxwell field [19]:

$$\begin{aligned} S=\int d^{d+1}x\sqrt{-g}s^{p}\equiv \int d^{d+1}x\sqrt{-g}{\mathcal {L}}\left( s\right) , \end{aligned}$$
(1)

where we define a nontrivial scalar

$$\begin{aligned} s=-\frac{1}{4}F^{ab}F_{ab}\text {;} \end{aligned}$$
(2)

\(F_{ab}=\partial _{a}A_{b}-\partial _{b}A_{a}\) is the electromagnetic field tensor, and \(A_{a}\) is the electromagnetic potential. The action (1) is conformally invariant provided \(p=\left( d+1\right) /4.\) When \(d=3\), the action (1) recovers the standard Maxwell action. However, we don’t confine ourselves to \(p=\left( d+1\right) /4\) in our paper. Instead, we shall consider a more general case from now on, in which p is an arbitrary positive integer. Coupling the power-law Maxwell field to gravity, various charged black holes were derived in a number of papers [19,20,21,22,23,24,25] . In the framework of gauge/gravity duality, holographic superconductors [26, 27], action/complexity conjecture [28], and the DC conductivity in the massive gravity [29] were studied in presence of a power-law Maxwell field.

This paper is a follow-up paper of our previous paper [30]. In [30], we used the method of [10] to compute the DC conductivities of an conserved current dual to a probe nonlinear electrodynamics field in a general neutral and static black brane background. However, our previous paper dealt, primarily, with a NLED Lagrangian that would reduce to the Maxwell-Chern-Simons Lagrangian for small fields. Clearly, the power-law Maxwell field with \(p\ne 1\) does not belong to this class of NLED models and would have some different predictions for the DC conductivities in the boundary theory. For example, when the charge density and magnetic field in the boundary theory vanish, the DC conductivities are zero for \(p\ne 1\) in this paper while they are not in [30].

In this paper, we will consider a neutral and static black brane background with a probe power-law Maxwell field and the dual theory. The aim of this paper is to find an expression for the holographic DC conductivity of the dual conserved current and investigate the properties of the boundary theory, e.g the possible phases and the magnetotransport. Note that in the probe limit, the properties of magnetotransport have been investigated in holographic Dirac–Born–Infeld models [31]. Later in [32], the backreaction effects of matter fields on the Dirac–Born–Infeld models was considered.

The remainder of our paper is organized as follows: In Sect. 2, we briefly review the membrane paradigm for a power-law Maxwell field. The holographic DC conductivity of the dual conserved current is studied in Sect. 3. In Sect. 4, we conclude with a brief discussion of our results. We use convention that the Minkowski metric has signature of the metric \(\left( -+++\right) \,\)in this paper.

2 Membrane paradigm

In [30], the electromagnetic membrane properties have been examined for a general NLED model via the method of [4]. In this section, we first give a quick review of the membrane paradigm in the framework of a power-law Maxwell field. In membrane paradigm, a time-like hypersurface, namely the stretched horizon, is put just outside the black hole horizon. The stretched horizon is composed of a family of fiducial observers with world lines \(U^{a}\) and possesses a spacelike outward pointing normal vector \(n_{a}\). The stretched horizon is denoted by \({\mathcal {S}}\). To derive the Euler–Lagrange equations from the action restricted to the spacetime outside the stretched horizon \(S_{\text {out}}\), it is necessary to add a surface term \(S_{\text {surf}}\) to \(S_{\text {out}}\) to exactly cancel all the boundary terms. As a result, we can rewrite the total action \(S_{\text {tot}}\) as

$$\begin{aligned} S_{\text {tot}}=\left( S_{\text {out}}+S_{\text {surf}}\right) +\left( S_{\text {in}}-S_{\text {surf}}\right) . \end{aligned}$$
(3)

Outside \({\mathcal {S}}\), the action is just \(S_{\text {out}}+S_{\text {surf}}\), whose variation \(\delta S_{\text {out}}+\delta S_{\text {surf}}=0\) would give the correct equations of motion.

For a power-law Maxwell field \(A_{a}\), the external action in a \(\left( d+1\right) \)-dimensional spacetime is given by the action (1) . To cancel the boundary contribution on the stretched horizon from the action (1) , we add a surface term \(S_{\text {surf}}\)

$$\begin{aligned} S_{\text {surf}}=\int \limits _{{\mathcal {S}}}d^{3}x\sqrt{\left| h\right| }j_{\text {s}}^{a}A_{a}, \end{aligned}$$
(4)

where \(h_{ab}=g_{ab}-n_{a}n_{b}\) is the induced metric on \({\mathcal {S}}\); we define

$$\begin{aligned} j_{\text {s}}^{a}=G^{ab}n_{b}, \end{aligned}$$
(5)

and

$$\begin{aligned} G^{ab}=-\frac{\partial {\mathcal {L}}\left( s\right) }{\partial F_{ab}} =ps^{p-1}F^{ab}. \end{aligned}$$
(6)

Note that \(j_{\text {s}}^{a}\) can be interpreted as the membrane current on the stretched horizon since \(n_{a}j_{\text {s}}^{a}=0\). From \(j_{\text {s}}^{a}\), we can define the surface electric charge density \(\rho =-j_{\text {s}}^{a}U_{a}\) and the current density \({\mathbf {j}}_{\text {s}}^{a}=j_{\text {s}}^{a}-\sigma U^{a}\), respectively.

To be generic, we consider a \(\left( d+1\right) \)-dimensional black brane with the metric of the form

$$\begin{aligned} ds^{2}&=g_{ab}dx^{a}dx^{b}=g_{rr}\left( r\right) dr^{2}+g_{\mu \nu }\left( r\right) dx^{\mu }dx^{\nu }\nonumber \\&=-g_{tt}\left( r\right) dt^{2}+g_{rr}\left( r\right) dr^{2} +g_{zz}\left( r\right) \delta _{AB}dx^{A}dx^{B}, \end{aligned}$$
(7)

where indices \(\left\{ a,b\right\} \) run over the \(\left( d+1\right) \)-dimensional bulk space, \(\left\{ \mu ,\nu \right\} \) over d-dimensional constant-r slice, and \(\left\{ A,B\right\} \) over spatial coordinates. Moreover, \(g_{tt}\left( r\right) \) and \(g^{rr}\left( r\right) \) are assumed to have a simple zero at the event horizon \(r=r_{+}\). Therefore, it can show that the corresponding Hawking temperature is given by

$$\begin{aligned} T=\frac{\sqrt{g_{tt}^{\prime }\left( r_{h}\right) g^{rr\prime }\left( r_{h}\right) }}{4\pi }. \end{aligned}$$
(8)

If the stretched horizon is located at \(r=r_{0}\) with \(r_{0}-r_{h}\ll r_{h}\), the vector fields \(n_{a}\) and \(U_{a}\) on the stretched horizon become

$$\begin{aligned} n_{a}=\sqrt{g_{rr}\left( r_{0}\right) }\delta _{ar}\text { and }U_{a} =-\sqrt{g_{tt}\left( r_{0}\right) }\delta _{at}. \end{aligned}$$
(9)

Via Eq. (5) , we find that the membrane current reduces to

$$\begin{aligned} j_{\text {s}}^{\mu }=\sqrt{g_{rr}\left( r_{0}\right) }G^{\mu r}. \end{aligned}$$
(10)

It showed in [30] that, on the stretched horizon, the NLED field strength has

$$\begin{aligned} F^{rA}\left( r_{0}\right) =-\sqrt{\frac{g_{tt}\left( r_{0}\right) }{g_{rr}\left( r_{0}\right) }}F^{tA}\left( r_{0}\right) \text {.} \end{aligned}$$
(11)

We then use Eqs. (6), (10) and (11) to rewrite \(j_{\text {s}}^{A}\) as

$$\begin{aligned} j_{\text {s}}^{A}=ps^{p-1}\left( r_{0}\right) E^{A}, \end{aligned}$$
(12)

where the electric field measured by the fiducial observers on the stretched horizon is

$$\begin{aligned} E^{a}=F^{ta}\left( r_{0}\right) \sqrt{g_{tt}\left( r_{0}\right) }, \end{aligned}$$
(13)

and s on the stretched horizon becomes

$$\begin{aligned} s\left( r_{0}\right) =\frac{1}{2}\left[ E^{r}E_{r}-\frac{F^{AB}\left( r_{0}\right) F_{AB}\left( r_{0}\right) }{2}\right] . \end{aligned}$$
(14)

From Eq. (12) , we can read that the diagonal components of the conductivities of the stretched horizon are

$$\begin{aligned} \sigma _{s}^{AA}\equiv \sigma _{s}=ps^{p-1}\left( r_{0}\right) \text {,} \end{aligned}$$
(15)

and the Hall components are zero. These fields also increase the black hole’s entropy S in accord with the Joule-heating relation [3]:

$$\begin{aligned} T\frac{dS}{dt}=\alpha ^{2}\int \limits _{{\mathcal {S}}}dA\sum _{B}j_{\text {s}} ^{B}E^{B}=\alpha ^{2}\int \limits _{{\mathcal {S}}}dA\sigma _{s}\sum _{B}\left( E^{B}\right) ^{2}, \end{aligned}$$
(16)

where \(\alpha =\sqrt{g_{tt}\left( r_{0}\right) }\) is the renormalized factor [3].

3 DC conductivity from gauge/gravity duality

In this section, we calculate the holographic DC conductivity of a power-law Maxwell field in the probe limit. For simplicity, we assume that the background is a \(\left( d+1\right) \)-dimensional black brane with the metric (7) , which is uncharged with trivial background configuration of the power-law Maxwell field. From the AdS/CFT duality, the U\(\left( 1\right) \) gauge symmetry of the power-law Maxwell field corresponds to a global symmetry in the corresponding boundary theory, which means that the power-law Maxwell field is dual to a conserved current \({\mathcal {J}}^{\mu }\) in the boundary theory. We can define AC conductivities for \({\mathcal {J}}^{\mu }\):

$$\begin{aligned} \left\langle {\mathcal {J}}^{A}\left( k_{\mu }\right) \right\rangle =\sigma ^{AB}\left( k_{\mu }\right) F_{Bt}\left( r\rightarrow \infty \right) , \end{aligned}$$
(17)

in the boundary theory, which lives at \(r\rightarrow \infty \). In the long wavelength and low frequency limit, the AC conductivities just become the DC conductivities:

$$\begin{aligned} \sigma _{D}^{AB}=\lim _{\omega \rightarrow 0}\lim _{\vec {k}\rightarrow 0}\sigma ^{AB}\left( k_{\mu }\right) . \end{aligned}$$
(18)

We can compute the expectation value of the current \({\mathcal {J}}^{\mu }\) for the boundary theory by [30]

$$\begin{aligned} \left\langle {\mathcal {J}}^{\mu }\right\rangle =\Pi ^{A}\equiv \frac{\partial {\mathcal {L}}\left( s\right) }{\partial \left( \partial _{r}A_{\mu }\right) }|_{r\rightarrow \infty }=-\sqrt{-g}G^{r\mu }|_{r\rightarrow \infty }, \end{aligned}$$
(19)

where \(\Pi ^{\mu }\) is the conjugate momentum of the field \(A_{\mu }\) with respect to r-foliation. When \(\mu =t\), one hence has

$$\begin{aligned} \rho =\left\langle {\mathcal {J}}^{t}\right\rangle =-\sqrt{-g}G^{rt} |_{r\rightarrow \infty }, \end{aligned}$$
(20)

where \(\rho \) can be interpreted as the charge density in the dual field theory.

Identifying the currents in the boundary theory with radially independent quantities in the bulk, authors of [10] showed that the membrane paradigm fluid on the stretched horizon determined the low frequency limit of conductivities of a conserved current in the boundary theory, which was dual to a Maxwell field in bulk. Later, the method of [10] was extended to the NLED case in [30]. In particular, it showed there that, in the long wavelength and low frequency limit, i.e. \(\omega \rightarrow 0\) and \(\vec {k}\rightarrow 0\) with \(F_{\rho \sigma }\) and \(\Pi ^{\eta }\) fixed, the following quantities did not evolve in the radial direction:

$$\begin{aligned} \partial _{r}\Pi ^{\mu }=0\text { and }\partial _{r}F_{\mu \nu }=0. \end{aligned}$$
(21)

On the horizon, we have

$$\begin{aligned} \Pi ^{A}\left( r_{h}\right) =\sqrt{-g}\frac{j_{\text {s}}^{A}}{\sqrt{g_{rr}\left( r_{h}\right) }}=g_{zz}^{\frac{d-3}{2}}\left( r_{h}\right) {\mathcal {L}}^{\prime }\left( s\right) |_{r=r_{h}}F_{At},\nonumber \\ \end{aligned}$$
(22)

where we take the limit \(r_{0}\rightarrow r_{h}\). Here, s on the horizon becomes

$$\begin{aligned} s\left( r_{h}\right) =\frac{1}{2}\left[ \eta F^{rt}\left( r_{h}\right) ^{2}-\frac{B^{2}}{g_{zz}^{2}\left( r_{h}\right) }\right] , \end{aligned}$$
(23)

where we define

$$\begin{aligned} \eta \equiv g_{rr}\left( r_{h}\right) g_{tt}\left( r_{h}\right) \text { and }B^{2}\equiv \frac{1}{2}\sum \limits _{A,B}F_{AB}^{2}. \end{aligned}$$
(24)

For \(d=2\) and 3, the magnetic field is a scalar and a vector, respectively, and B can be treated as the magnitude of the magnetic field in the boundary theory. To express \(F^{rt}\left( r_{h}\right) \) in terms of quantities in the boundary theory, we can use the following formula

$$\begin{aligned} \Pi ^{t}\left( r_{h}\right) =\Pi ^{t}\left( r\rightarrow \infty \right) =\rho . \end{aligned}$$
(25)

On the boundary, we have that, in the zero momentum limit,

$$\begin{aligned} \left\langle {\mathcal {J}}^{A}\right\rangle= & {} \Pi ^{A}\left( r\rightarrow \infty \right) \nonumber \\= & {} \Pi ^{A}\left( r_{h}\right) =g_{zz}^{\frac{d-3}{2}}\left( r_{h}\right) {\mathcal {L}}^{\prime }\left( s\right) |_{r=r_{h}}F_{At}. \end{aligned}$$
(26)

From Eq. (26) , we can read that the diagonal components of the DC conductivities in the boundary theory:

$$\begin{aligned} \sigma _{D}^{AA}\equiv & {} \sigma _{D}\left( {\tilde{\rho }},{\tilde{B}}\right) \nonumber \\= & {} -\frac{g_{zz}^{\frac{d-3}{2}}\left( r_{h}\right) p}{2^{p-1}}\tilde{B}^{2p-2}\frac{{\tilde{\rho }}/{\tilde{B}}^{2p-1}}{x\left( {\tilde{\rho }}/\tilde{B}^{2p-1}\right) }\text {,} \end{aligned}$$
(27)

where, for later convenience, we define

$$\begin{aligned} {\tilde{\rho }}\equiv \frac{2^{p-1}\rho }{g_{zz}^{\frac{d-1}{2}}\left( r_{h}\right) p} \quad \text { and } \quad {\tilde{B}}\equiv \frac{B}{g_{zz}\left( r_{h}\right) }\ge 0\text {,} \end{aligned}$$
(28)

and \(x\left( y\right) \) is the inverse of the function \(y\left( x\right) =-x\left( x^{2}-1\right) ^{p-1}\). Note that the Hall components vanish. The value of \(\sigma _{D}\) in the limit of \({\tilde{B}}\rightarrow 0\) depends on the value of p:

$$\begin{aligned} \sigma _{D}=1\text {, for }p=1\text {, and }\sigma _{D}\left( \tilde{\rho },0\right) =0\text {, otherwise. } \end{aligned}$$
(29)

When \(d=3\) and \(p=1\), Eq. (27) reproduces the well-known result in the Maxwell case [3]

$$\begin{aligned} \sigma _{D}=1\text {.} \end{aligned}$$
(30)

For \(p\ne 1\), the DC conductivity \(\sigma _{D}\) is zero in the absence of the magnetic field and charge density in the boundary theory, which is consistent with Eq. (44) with \(q=0\) in [29].

In the long wavelength and low frequency limit with \(\omega \rightarrow 0\) and \(\vec {k}\rightarrow 0\), we keep \(F_{\mu \nu }\) and \(\Pi ^{\mu }\) fixed and neglect higher \(\mu \)-derivatives. This means that \(F_{\mu \nu }\) and \(\rho \) are constant and homogeneous on the boundary. In this limit, one can relate the DC conductivity \(\sigma _{D}\) in the boundary theory to \(\sigma _{s}\) of the stretched horizon as

$$\begin{aligned} \sigma _{s}=g_{zz}^{\frac{d-3}{2}}\left( r_{h}\right) \sigma _{D}, \end{aligned}$$
(31)

which is also constant and homogeneous on the stretched horizon. Therefore in the long wavelength and low frequency limit, the rate of the black hole’s entropy S becomes

$$\begin{aligned} T\frac{dS}{dt}=g_{zz}^{\frac{d-3}{2}}\left( r_{h}\right) \sigma _{D} \int \limits _{{\mathcal {S}}}\alpha ^{2}\sum _{B}\left( E^{B}\right) ^{2}dA. \end{aligned}$$
(32)

The second law of black hole mechanics implies that the DC conductivity \(\sigma _{D}\) in the boundary theory is non-negative and real.

It is interesting to note that the function \(x\left( y\right) \) is usually a multivalued function, which indicates that there might exist more than one phase and possible phase transitions. For later convenience, we define

$$\begin{aligned} {\tilde{\sigma }}_{D}=\frac{2^{p-1}\sigma _{D}}{pg_{zz}^{\frac{d-3}{2}}\left( r_{h}\right) }. \end{aligned}$$
(33)
Fig. 1
figure 1

Plots of \(y\left( x\right) \) and \(x\left( y\right) \) for \(p=2\)

Full size image

3.1 Even positive integer p

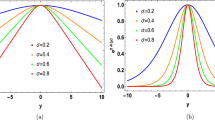
We plot \(y\left( x\right) =-x\left( x^{2}-1\right) ^{p-1}\) for \(p=2\) in Fig. 1a. In fact, \(y\left( x\right) \) and hence \(\sigma _{D}\) in all the cases of p being even positive integer show very similar behavior as in that of \(p=2\). So for concreteness, we shall focus on the case of \(p=2\). Bearing in mind that \(\sigma _{D}\) is non-negative and real, Eq. (27) shows that the green segment of \(y\left( x\right) \) in Fig. 1a is unphysical. Therefore, we only need to consider the blue and red segments to find the inverse function of \(y\left( x\right) \), which is plotted in Fig. 1b. As shown in Fig. 1b, there is a discontinuity at \(y=0\) for \(x\left( y\right) \), which, as will be shown later, indicates possible phase transitions at \(y=0\). Using \(x\left( y\right) \) in Fig. 1b, we plot \({\tilde{\sigma }}_{D}\) versus \({\tilde{\rho }}\) and \({\tilde{B}}\) in Fig. 2. It shows in Fig. 2 that \({\tilde{\sigma }}_{D}\) is continuos everywhere but the derivative \(\partial _{{\tilde{\rho }}}{\tilde{\sigma }}_{D}\) changes the sign at \({\tilde{\rho }}=0\). These observations imply that there might exist two phases for \({\tilde{\rho }}>0\) and \({\tilde{\rho }}<0\), respectively, and a continuous phase transition could occur at \({\tilde{\rho }}=0\).

Since \(x\left( 0\right) =1\), Eq. (27) shows that the DC conductivity \(\sigma _{D}\) vanishes at zero charge density, which implies that the main contribution to \(\sigma _{D}\) is from momentum relaxation for the charge carriers in the system. As shown in Fig. 2, \(\sigma _{D}\) increases with increasing \(\left| \rho \right| \) at constant B, which is a feature similar to the Drude metal. For the Drude metal, a larger charge density provides more available mobile charge carriers to efficiently transport charge. At constant \(\rho \), \(\sigma _{D}\) decreases with increasing B, which means a positive magneto-resistance.

3.2 Odd positive integer p

Since all the cases with an odd positive integer p share very similar behavior, we shall focus on the case of \(p=3\) here. The function \(y\left( x\right) =-x\left( x^{2}-1\right) ^{p-1}\) for \(p=3\) is shown in Fig. 3a. Unlike the \(p=2\) case, \(x/y\le 0\) and hence \({\tilde{\sigma }}_{D}\) is non-negative for all points on \(y\left( x\right) \) in the \(p=3\) case. So the physical inverse function of \(y\left( x\right) \) is plotted in Fig. 3b. As shown in Fig. 3b, the function \(x\left( y\right) \) has a single value for \(y^{2}>y_{c}^{2}\) and three values for \(y^{2}\le y_{c}\). Here we define \(y_{c}=\frac{16}{25\sqrt{5}}\). In Fig. 3b, \(x\left( y\right) \) can be divided into 5 single-valued segments: blue, orange, green, red, and purple ones, and each segment corresponds to a possible phase in the boundary theory. In fact, we have five possible phases: the blue phase exists for \({\tilde{\rho }}/\tilde{B}^{5}\ge 0\); the orange phase exists for \(y_{c}\ge {\tilde{\rho }}/{\tilde{B}}^{5}\ge 0\); the green phase exists for \(y_{c}\ge {\tilde{\rho }}/{\tilde{B}} ^{5}\ge -y_{c}\); the red phase exists for \(0\ge {\tilde{\rho }}/{\tilde{B}}^{5} \ge -y_{c}\); the purple phase exists for \({\tilde{\rho }}/{\tilde{B}}^{5}\le 0\). We plot \({\tilde{\sigma }}_{D}\) versus \({\tilde{\rho }}\) and \({\tilde{B}}\) for the five phases in Fig. 4. One can see that in the region \(y_{c}>\left| {\tilde{\rho }}/{\tilde{B}}^{5}\right| >0\), three values of \({\tilde{\sigma }}_{D}\) are allowed for fixed values of \({\tilde{\rho }}\) and \({\tilde{B}}\). It means that \({\tilde{\sigma }}_{D}\) can jump from one value to another. Since the value of \({\tilde{\sigma }}_{D}\) changes discontinuously, it is acceptable to consider this transition as a first order phase transition. On the other hand, the transitions occurring at \({\tilde{\rho }}=0\) and \(\left| {\tilde{\rho }}/{\tilde{B}}^{5}\right| =y_{c}\) can be regarded as continuous phase transitions. To determine the stable phases and the transition points, one needs to find the thermodynamic potential in a specific boundary theory, which, however, is beyond the scope of this paper.

Fig. 2
figure 2

Plot of \({\tilde{\sigma }}_{D}\) versus \({\tilde{\rho }}\) and \({\tilde{B}}\) for \(p=2\). A continuous phase transition could occur at \({\tilde{\rho }}=0\), where \(\partial _{{\tilde{\rho }}}{\tilde{\sigma }}_{D}\) changes the sign

Full size image

For the blue, orange, red, and purple phases, the behavior of the DC conductivity \(\sigma _{D}\) is similar to that in the \(p=2\) case, i.e. \(\sigma _{D}=0\) at zero charge density, \(\sigma _{D}\) increases with increasing \(\left| \rho \right| \) at constant B, and \(\sigma _{D}\) decreases with increasing B at constant \(\rho \). However, the green phase has some interesting features:

  • Charge conjugation symmetric contribution. At zero charge density, \(\sigma _{D}\) has a non-zero value, if \({\tilde{B}}\ne 0\),

    $$\begin{aligned} \sigma _{D}\left( 0,{\tilde{B}}\right) =\frac{g_{zz}^{\frac{d-3}{2}}\left( r_{h}\right) p}{2^{p-1}}{\tilde{B}}^{2p-2}, \end{aligned}$$
    (34)

    which can be interpreted by a incoherent contribution due to intrinsic current relaxation and independent of the charge density. This contribution is also known as the charge conjugation symmetric contribution [33, 34].

  • Negative magneto-resistance. We plot \({\tilde{\sigma }}_{D}\) versus \({\tilde{B}}\) for \({\tilde{\rho }}=0\), 0.1, 0.3, 0.5, and 0.7 in Fig. 5a. Figures 4 and 5a show that \(\partial {\tilde{\sigma }}_{D}/\partial {\tilde{B}}>0\), which gives a negative magneto-resistance at given temperature and charge density.

  • Mott-like behavior. We plot \({\tilde{\sigma }}_{D}\) versus \({\tilde{\rho }}\) for \({\tilde{B}}=0.7\), 0.8, 0.9, 0.95, and 1 in Fig. 5b. Therefore we can see from Figs. 4 and 5b that \(\partial {\tilde{\sigma }}_{D}/\partial \rho <0\) for the green phase. This can be explained by the electronic traffic jam: strong enough e-e interactions prevent the available mobile charge carriers to efficiently transport charges [35]. Note that a class of holographic models for Mott insulators, whose gravity dual contained NLED, was studied in [35].

Fig. 3
figure 3

Plots of y(x) and x(y) for \(p=3\)

Full size image
Fig. 4
figure 4

Plot of \({\tilde{\sigma }}_{D}\) versus \({\tilde{\rho }}\) and \({\tilde{B}}\) for \(p=3\). Five possible phases are represented by different colors. In the region \(y_{c}>\left| {\tilde{\rho }}/{\tilde{B}}^{5}\right| >0\), jumping from one value of \({\tilde{\sigma }}_{D}\) to another can be considered as a first order phase transition. Continuous phase transitions could occur at \({\tilde{\rho }}=0\) and \(\left| {\tilde{\rho }}/{\tilde{B}}^{5}\right| =y_{c} \)

Full size image

3.3 Temperature dependence of DC conductivity

To discuss the temperature dependence of the DC conductivity, we can express \(\sigma _{D}\) in terms of \(\rho \) and B:

$$\begin{aligned} \sigma _{D}=-\frac{p\rho }{B}x^{-1}\left( \frac{2^{p-1}\rho }{B^{2p-1}} g_{zz}^{\frac{4p-1-d}{2}}\left( r_{h}\right) \right) . \end{aligned}$$
(35)

When \(d=4p-1\), the power-law Maxwell field action (1) is conformally invariant. In this case, the DC conductivity \(\sigma _{D}\) is independent of the geometric quantities evaluated at the horizon, especially the Hawking temperature T of the black brane. So the DC conductivity \(\sigma _{D}\) does not depend on the temperature of the boundary theory when the power-law Maxwell field in bulk is conformally invariant. In fact, the dual conserved current is also scale invariant. For this scale invariant current at finite temperature, all nonzero temperatures should be equivalent since there is no other scale with which to compare the temperature.

For \(d\ne 4p-1\), we can now discuss the temperature dependence of the DC conductivity by relating \(r_{h}\) to the Hawking temperature T. To have a simple expression of \(r_{h}\) in terms of T, we consider the Schwarzschild AdS black brane

$$\begin{aligned} ds^{2}= & {} -\left( r^{2}-r_{h}^{3}/r\right) dt^{2}\nonumber \\&+\frac{dr^{2}}{\left( r^{2}-r_{h}^{3}/r\right) }+r^{2}\delta _{AB}dx^{A}dx^{B}, \end{aligned}$$
(36)

where we take the AdS radius \(L=1\). The corresponding Hawking temperature is just given by

$$\begin{aligned} T=\frac{3r_{h}}{4\pi }\text {.} \end{aligned}$$
(37)

Since \(x\left( y\right) \) behaves differently for small y depending on whether p is an even or odd integer, it will be convenient to consider these two cases separately.

Fig. 5
figure 5

Plots of \({\tilde{\sigma }}_{D}\) versus \({\tilde{B}}\) and \({\tilde{\rho }}\), respectively, for the green phase in the case of \(p=3\)

Full size image
Table 1 Sign of \(\partial \sigma _{D}/\partial T\) in all cases
Full size table
Fig. 6
figure 6

Plot of \(\sigma _{D}\) versus T for \(d=4\) and 10 in the case of \(p=2\). Here the values of \(\rho \) and B are fixed with \(\rho /B^{3}>0\), which means the blue phase

Full size image

When p is even, one has that \(x^{2}\left( y\right) \sim 1\) for \(y\ll 1\). In the case with \(\rho =0\) and nonzero B, one has \(\sigma _{D}=0\). In the case with nonzero B and \(\rho \), one has that, when \(d>4p-1\),

$$\begin{aligned} \sigma _{D}\sim \rho ^{\frac{2p-2}{2p-1}}T^{\frac{d+1-4p}{2p-1}}\text { for small }T\text {, and }\sigma _{D}\sim \frac{\left| \rho \right| }{B}\text { for large }T\text {,} \end{aligned}$$
(38)

and when \(d<4p-1\)

$$\begin{aligned} \sigma _{D}\sim \frac{\left| \rho \right| }{B}\text { for small }T\text {, and }\sigma _{D}\sim \rho ^{\frac{2p-2}{2p-1}}T^{\frac{d+1-4p}{2p-1}}\text { for large }T\text {.} \end{aligned}$$
(39)

Figure 1b shows that \(x\left( y\right) \) is a monotonically decreasing function of y. From Eq. (35), we find that \(\partial \sigma _{D}/\partial T\) \(<0\) for \(d<4p-1\) and \(\partial \sigma _{D}/\partial T\) \(>0\) for \(d>4p-1\). If we define a metal and an insulator for \(\partial \sigma _{D}/\partial T<0\) and \(\partial \sigma _{D}/\partial T\) \(>0\), respectively, one has a metal for \(d<4p-1\) and an insulator for \(d>4p-1\). The results are summarized in Table 1. For fixed values of \(\rho \) and B with \(\rho /B^{3}>0\), we plot \(\sigma _{D}\) versus T for \(d=4\) and 10 in the case of \(p=2\) in Fig. 6.

Fig. 7
figure 7

Plot of \(\sigma _{D}\) versus T for \(d=4\) and 12 in the case of \(p=3\). Here the values of \(\rho \) and B are fixed with \(\rho /B^{3}>0\), for which the blue, orange and green phases could exist

Full size image

When p is odd, one has for \(y\ll 1\) that \(x\left( y\right) \sim 1\) in the purple and red phases; \(x\left( y\right) \sim -1\) in the blue and orange phases; \(x\left( y\right) \sim -y\) in the green phase. In the case with \(\rho =0\) and nonzero B, we find that

$$\begin{aligned}&\sigma _{D}=\frac{pB^{2p-2}}{2^{p-1}}\nonumber \\&\left( \frac{4\pi T}{3}\right) ^{d-4p+1}\text { in the green phase, and }\sigma _{D}= 0\text { otherwise.}\nonumber \\ \end{aligned}$$
(40)

From the monotonicity of x(y), we can also determine whether each phase is a metal or an insulator. The results are summarized in Table 1. In Fig. 7, we plot \(\sigma _{D}\) versus T for \(d=4\) and 12 in the case of \(p=3\). In Fig. 7, we fix the values of \(\rho \) and B with \(\rho /B^{3}>0\), for which only the blue, orange and green phases exist. When \(d=4\), Fig. 7a shows that there are three values for \(\sigma _{D}\) for \(T<T_{c}\), and jumping from one value to another could represent a first order phase transition. Specially, if the system jumps from the blue phase to the orange one or vice versa, one would have a first order metal-insulator transition. A similar behavior applies to \(\sigma _{D}\) for \(T>T_{c}\) in Fig. 7b, where \(d=12\).

4 Discussion and conclusion

In this paper, we extended the method of [10] to study the electrical transport behavior of some boundary field theory in the presence of a power-law Maxwell gauge field. In particular, we first calculated the conductivities of the stretched horizon of some general static and neutral black brane in the framework of the membrane paradigm. Since the conjugate momentum of the power-law Maxwell field encoded the information about the conductivities both on the stretched horizon and in the boundary theory and, in the zero momentum limit, did not evolve in the radial direction, we obtained the DC conductivity of the dual conserved current in the boundary theory. We also found that the DC conductivity could be expressed in terms of the electromagnetic quantities and the temperature of the boundary theory.

In the context of the membrane paradigm, we found that the second law of black-hole mechanics required that the DC conductivities of the stretched horizon and in the boundary theory are real and non-negative. Imposing \(\sigma _{D}\ge 0\), we showed that, when p was an even integer, there might be two phases in the boundary theory, and a continuous phase transition could occur at \({\tilde{\rho }}=0\). When p was an odd integer, there might be five phases in the boundary theory, and the transitions among them could be considered as first order phase transitions. Specifically, it showed that the green phase possessed a charge conjugation symmetric contribution, a negative magneto-resistance and Mott-like behavior. We also discussed the temperature dependence of the DC conductivity. We found that the DC conductivity \(\sigma _{D}\) was independent of the temperature of the boundary theory when \(d=4p-1\). Note that the power-law Maxwell field action is conformally invariant for \(d=4p-1\).

Finally, we discuss the assumption and limitation of our calculations. First, we assumed that the black brane background was neutral, and hence there was no background charge density in the boundary theory. Since the low frequency behavior of the conductivities depends crucially on whether there is a background charge density [12], investigating the behavior of the DC conductivity in a boundary theory dual to a charged power-law Maxwell field black hole is certainly interesting. Second, we assumed that the power-law Maxwell field was a probe field and neglected the backreaction on the bulk spacetime metric. One would like to study the effects of backreaction on the bulk spacetime metric and DC conductivity in the boundary theory. Third, we carried out our calculations in the zero momentum limit, in which the conjugate momentum did not evolve along the radial direction in bulk, and the electromagnetic quantities \(\rho \) and B were time independent and homogeneous in the boundary theory.