1 Introduction

Among modifications of Einstein’s general relativity (GR), extensions to the Einstein–Hilbert action with second order curvature terms are of particular interest, which may arise from the full, but still lacking, quantum theory of gravity [1]. The Chern–Simons (CS) modified gravity [2,3,4,5,6] belongs to such extensions of GR, which has physical roots in particle physics and string theory. In particle physics, the CS modification or the Pontryagin term \(^{\star }RR\) is known to be related to the chiral current anomaly that caused by spacetime curvature [7, 8], which may also serve as a possible candidate that sources the baryon asymmetry of the Universe [9] through gravi-leptogenesis [10]. In string theory, the CS modification emerges as an anomaly-canceling term through the Green–Schwarz mechanism [11]. More interestingly, the CS extension to GR may provide us insights into the physics of possible parity-violations in gravitation, that includes effects like amplitude birefringent gravitational waves [5, 12, 13], different gravito-magnetic (GM) sectors [12,13,14], and etc.. Therefore, experimental tests of the CS modified gravity and the resulted constraints are of importance.

The CS modified gravity is considered as an effective theory, that the ultra-violet modifications to gravitation and their possible observable effects are to be studied in more fundamental and sophisticated theories such as string theory or loop quantum gravity. Theoretical studies had shown that in CS modified gravity the Lorentz symmetry can be satisfied [5, 15, 16], and, up to now, experimental constraints on CS gravity are mainly from astrophysical observations and Solar system tests. Of course, it is natural to expect that stronger bounds on CS gravity might come from particle physics because of the connections between these theories. In this work, we will focus on the tests, with orbiting gradiometers, of the non-dynamical formulation of the CS modified gravity [5], where the coupling field or the deformation parameter \(\theta \) is externally prescribed (one notices that the arbitrariness in \(\theta \) could not be completely removed in the dynamical formulation due to the different choices of the potential \(V(\theta )\)). The first constraint [14] on the time derivative of the coupling scalar \({\dot{\theta }}\) and the corresponding mass scale \(M_{CS}\sim 1/{\dot{\theta }}\) of the non-dynamical CS gravity was obtained based on the observations from the LAGEOS I, II [17, 18] and the Gravity Probe-B [19] missions, which had set \(M_{CS} \ge 10^{-13}\ \mathrm{eV}\) and \({\dot{\theta }} \le 10^{6} \ \mathrm{m}\), and a stronger bounds \(M_{CS}\ge 4.7\times 10^{-10}\ \mathrm{eV}\) and \({\dot{\theta }} \le 0.4\times 10^{3} \ \mathrm{m}\) (been revised in [20]) was obtained based on the data from double binary pulsars [21].

Theoretical studies of testing relativistic gravitational theories with orbiting gravity gradiometers in space were firstly carried out in 1980s [22,23,24], and such measurement schemes could be naturally incorporated into future satellite gradiometry missions or missions that carrying high sensitive gradiometer as one of the key payloads. For the baseline design of high sensitive gravity gradiometers in micro-gravity or zero-g environment in space, such as electrostatic or superconducting ones, one generally has pairs of proof masses aligned along each of the measurement axes, and a combinations of strategies of proof mass disturbances isolation, proof mass position sensing and control is employed, see [25,26,27,28] for reviews. The proof masses are generally enclosed within sensor cages or housings, vacuum maintenances and other shielding devices, and, with such setup, fluctuations forces subjected to proof masses are to be reduced or isolated as much as possible. The relative motions or accelerations between the “free-falling” proof masses (with respect to certain noise level) in space will give rise to measurements of the tidal matrix from spacetime curvature \(R_{0i0}^{\ \ \ \ j}\) along certain orbits (for Newtonian limits, \(R_{0i0}^{\ \ \ \ j}\) reduces to \(\partial _i\partial _j U\) with U the Newtonian gravitational potential). For electrostatic and superconducting gradiometers, the difference between the compensating forces that restoring the proof masses to their nominal positions can be used as the direct readouts of the tidal accelerations. The GOCE satellite, launched in March 2009, carried an electrostatic gravity gradiometer containing six proof masses in three pairs to map out the geopotential of Earth, whose sensitive had reached \(10\ \mathrm{mE/Hz}^{1/2}\) in the frequency band of \(5\sim 100\ \mathrm{mHz}\) [27]. With the continuous advances, the multi-axis superconducting gravity gradiometer under the development could reach the sensitivity about \(10^{-2}\ \mathrm{mE/Hz}^{1/2}\) in the band around \(1\ \mathrm{mHz}\) in space [25, 29]. As an alternative optical readout method, the relative motions between proof masses as integrations of tidal accelerations can also be precisely measured by onboard laser interferometersFootnote 1. The LISA PathFinder (LPF) mission [30, 31], which can be view as a demonstration of an one dimensional optical gradiometer with the resolution of the onboard laser interferometer better than \(9\ \mathrm{pm}/\sqrt{\mathrm{Hz}}\) in the mHz band, had even reached the noise floor of \(10^{-3}\)–\(10^{-4} \ \mathrm{mE/Hz}^{1/2}\). Tests of relativistic gravitational theories including the CS modified gravity with satellite gradiometry now becomes more and more feasible, and for CS gravity a preliminary measurement scheme had been studied in [32, 33]. It was firstly noticed by Mashhoon and Theiss [22, 34,35,36] that along orbit motions relativistic secular tidal effects that growing with time may exist (known as the Mashhoon–Theiss anomaly), which would greatly improve the measurement accuracy of relativistic tidal components. Recently, the physical mechanism behind such secular tidal effects had been studied and explained in [37, 38]. From the post-Newtonian (PN) point of view, the difference between the relativistic precession of the local free-falling frame (or the parallel transported measurement axes) and the orbit plane with respect to the sidereal frame will produce modulations of Newtonian tidal forces along certain axes and then gives rise to periodic secular tidal signals [37, 39]. Back to the tests of the CS modified gravity, in the far field expansion of the non-dynamical theory, the CS gravity will add modifications to the GM sector of GR [12, 13], and therefore will give rise to new secular tidal effects that could be read out precisely along certain measurement axes of an orbiting gradiometer. In this work, we derive, at the PN level, the new secular tidal tensor from the non-dynamical CS modified gravity under the local Earth pointing frame along a relativistic polar and nearly circular orbit. For (possible) future experiments, we give the estimations of the bound on the characteristic mass scale \(M_{CS}\) that could be drawn from such a measurement scheme.

2 Models and settings

The action of the non-dynamical CS modified gravity is given by

$$\begin{aligned} S =\frac{1}{16\pi G}\int d^{4}x\sqrt{-g}\left( R+\frac{1}{4}\theta \ ^{\star }RR\right) , \end{aligned}$$
(1)

for clarity the Natural units \(c=h=1\) are adopted hereafter and in the end the SI units will be recovered. In the non-dynamical theory with the canonical coupling [5], the scalar \(\theta \) is an externally prescribed and spatially isotropic function that proportional to the coordinate time. The field equation reads

$$\begin{aligned} R_{\mu \nu }-\frac{1}{2}g_{\mu \nu }R+ C_{\mu \nu }=8\pi G T_{\mu \nu }, \end{aligned}$$
(2)

where

$$\begin{aligned} C^{\mu \nu }=\nabla _{\rho }\theta \epsilon ^{\rho \lambda \sigma (\mu }\nabla _{\sigma }R_{\ \ \lambda }^{\nu )}+\frac{1}{2}\nabla _{\rho }\nabla _{\lambda } \theta \epsilon ^{\sigma \delta \lambda (\mu }R_{\ \ \ \ \delta \sigma }^{\nu )\rho }. \end{aligned}$$

The introduction of the new scalar degree of freedom gives rise to a new constraint

$$\begin{aligned} \nabla _{\nu }C^{\nu \mu }=-\frac{1}{8}\nabla ^{\mu }\theta (^{\star }RR)=0. \end{aligned}$$

If the constraint is satisfied, the Bianchi identities and the equations of motion for matter fields \(\nabla _{\nu }T^{\nu \mu }=0\) are recovered, which ranks the non-dynamical CS modified gravity a metric theory [40, 41].

In this work, we model Earth as an ideal uniform and rotating spherical body with total mass M and angular momentum \(\mathbf {J}\). The geocentric inertial coordinates system \(\{t,\ x^i\}\) is defined as follows, that one of its bases \(\frac{\partial }{\partial x^3}\) is parallel to the direction of \(\mathbf {J}\) and the coordinate time t is measured in asymptotically flat regions. For an orbiting proof mass or satellite, we have the PN order relations

$$\begin{aligned} v^2\sim \frac{GM}{r}\sim {\mathscr {O}}(\epsilon ^2),\quad \frac{GJv}{r^2}\sim {\mathscr {O}}(\epsilon ^4), \end{aligned}$$
(3)

where \(\mathbf {v}\) is the 3-velocity, \(r=\sqrt{\sum _{i=1}^3(x^i)^2}\) and for low (with altitude below \(2000\ \mathrm{km}\)) and medium (altitude between \(2000\ \mathrm{km}\) and a geostationary orbit) Earth orbits \(\epsilon =\frac{M}{r}\) is about \(10^{-5}\)–\(10^{-6}\). Up to the required order, the metric field outside the ideal Earth model can be expanded as

$$\begin{aligned} g_{\mu \nu }= \left( \begin{array}{llll} -1+\frac{2GM}{r}-\frac{2G^2M^{2}}{r^{2}} &{} \left( \frac{2G x^{2}}{r^{3}}+\frac{6G x^{1}x^{3}}{r^{5}M_{CS}}\right) J &{} \left( -\frac{2 Gx^{1}}{r^{3}}+\frac{6G x^{2}x^{3}}{r^{5}M_{CS}}\right) J &{} -\frac{2G[(x^{1})^{2}+(x^{2})^{2}-2(x^{3})^{2}]}{r^{5}M_{CS}}J\\ \\ \left( \frac{2G x^{2}}{r^{3}}+\frac{6G x^{1}x^{3}}{r^{5}M_{CS}}\right) J &{} 1+\frac{2G M}{r} &{} 0 &{} 0\\ \\ \left( -\frac{ 2Gx^{1}}{r^{3}}+\frac{6 Gx^{2}x^{3}}{r^{5}M_{CS}}\right) J &{} 0 &{} 1+\frac{2G M}{r} &{} 0\\ \\ -\frac{2G[(x^{1})^{2}+(x^{2})^{2}-2(x^{3})^{2}]}{r^{5}M_{CS}}J &{} 0 &{} 0 &{} 1+\frac{2G M}{r} \end{array}\right) , \end{aligned}$$
(4)

where the mass scale \(M_{CS}\) of the CS modified gravity reads

$$\begin{aligned} M_{CS}\equiv \frac{2}{{\dot{\theta }}}. \end{aligned}$$
(5)

As mentioned, the non-dynamical CS modified gravity differs from GR only in the GM sector.

3 Reference orbit and local tetrad

Being a metric theory, motions of free-falling masses or satellites in CS modified gravity satisfy the geodesic equation. According to the general choices of orbits for satellite gradiometry missions (like GOCE [27]), we choose the reference orbit followed by the mass center of the gradiometer to be a polar and circular one with the relativistic precession caused by the GM effect

$$\begin{aligned} x^1= & {} a \cos \varPsi \cos {\dot{\varOmega }}\tau , \end{aligned}$$
(6)
$$\begin{aligned} x^2= & {} a \cos \varPsi \sin {\dot{\varOmega }}\tau , \end{aligned}$$
(7)
$$\begin{aligned} x^2= & {} a\sin \varPsi . \end{aligned}$$
(8)

Here a denotes the orbit radius, \(\varPsi =\omega \tau \) the true anomaly, \(\omega \) is the mean angular frequency with respect to the proper time \(\tau \) along the orbit and \(\varOmega \) is the longitude of ascending node with initial value \(\varOmega (0)=0\). The precession rate of the node \({\dot{\varOmega }}={\dot{\varOmega }}_{GR}+{\dot{\varOmega }}_{CS}\), where the Lense–Thirring precession rate \({\dot{\varOmega }}_{GR}=\frac{2GJ}{a^3}\) [42] and the correction from the non-dynamical CS modified gravity had been worked out in [14] as

$$\begin{aligned} {\dot{\varOmega }}_{CS}=\varPi _{CS}{\dot{\varOmega }}_{GR}=15\frac{a^2}{ R^2}j_2\left( \frac{R}{a}\frac{4}{\chi }\right) y_1\left( \frac{4}{\chi }\right) { \dot{\varOmega }}_{GR}, \end{aligned}$$
(9)

where R is the averaged radius of Earth, \(j_l(x)\) and \(y_l(x)\) are spherical Bessel functions of the first and second kind, and \(\chi \) was a new PN parameter introduced in [12, 13] which can be related to the mass scale as \(\chi =\frac{4}{a M_{CS}}\). For polar circular orbit, the GM force in CS modified gravity generated by spherical sources [14] will also change slightly the orbital eccentricity to \(e\sim \chi {\mathscr {O}}(\epsilon ^2)\), which is too small to be relevant to secular tidal effects at the PN level. Therefore, in this work the small eccentricity is ignored, and its effects together with other orbital perturbations in satellite gradiometry, such as those from geopotential harmonics, can be found in [27, 43].

For satellite gradiometry missions, spacecraft attitudes are generally chosen to follow the Earth pointing orientation (like GOCE [27]). Then, we define the local free-falling Earth pointing frame by the tetrad \(\{E_{(a)}^{\ \ \ \mu }\}\) attached to the mass center of the orbiting gradiometer. We set \(E_{(0)}^{\ \ \ \mu }=\tau ^{\mu }\) with \(\tau ^{\mu }\) the 4-velocity of the mass center, \(E_{(1)}^{\ \ \ \mu }\) is parallel to the 3-velocity \(\mathbf {v}\) in space, \(E_{(2)}^{\ \ \ \mu }\) along the radial direction and \(E_{(3)}^{\ \ \ \mu }\) is transverse to the orbit plane. For the existence of the geodetic and frame-dragging precession of the local frame [44], we solve for the spatial bases \(\{E_{(i)}^{\ \ \ \mu }\}\) in the following three steps. First, in the geocentric coordinates system, we solve for the precession of the local inertial frame (Fermi-shifted frame) along the orbit given in Eqs. (7), (8). Second, with respect to the local inertial frame, we rotate \(\{E_{(i)}^{\ \ \ \mu }\}\) with an initial angular velocity to make it an Earth pointing triad. At last, since the local frame is moving along the orbit, we need to perform the boost Lorentz transformations of the bases \(\{E_{(i)}^{\ \ \ \mu }\}\) with respect to the 4-velocity \(\tau ^{\mu }\). The general time scales or periods of frame-dragging precessions in Earth orbit are about \(\frac{c^2a^3}{GJ}\sim 10^7\ \mathrm{years}\), which is extremely long compared with general mission lifetimes. Then, following the above three steps and within the short time limit \(\frac{\tau }{a}\ll \frac{a^2}{GJ}\), the tetrad can be worked out up to the PN level as

$$\begin{aligned} E_{(0)}^{\ \ \ \mu }= & {} \left( \begin{array}{c} 1+\frac{a^2\omega ^2}{2}+\frac{GM}{a}\\ - \ a\omega \sin \varPsi \\ 0\\ a\omega \cos \varPsi \end{array}\right) . \end{aligned}$$
(10)
$$\begin{aligned} E_{(1)}^{\ \ \ \mu }= & {} \left( \begin{array}{c} a\omega \\ -\ \left( 1+\frac{a^2\omega ^2}{a}-\frac{GM}{a}\right) \sin \varPsi \\ -\frac{(1+\varDelta _{CS})GJ\varPsi \sin \varPsi }{2a^3\omega }\\ \left( 1+\frac{a^2\omega ^2}{a}-\frac{GM}{a}\right) \cos \varPsi \end{array}\right) , \end{aligned}$$
(11)
$$\begin{aligned} E_{(2)}^{\ \ \ \mu }= & {} \left( \begin{array}{c} 0\\ \left( 1-\frac{GM}{a}\right) \cos \varPsi \\ \frac{(1+\varDelta _{CS})GJ(\varPsi \cos \varPsi -3\sin \varPsi )}{2a^3\omega }\\ \left( 1-\frac{GM}{a}\right) \sin \varPsi \end{array}\right) , \end{aligned}$$
(12)
$$\begin{aligned} E_{(3)}^{\ \ \ \mu }= & {} \left( \begin{array}{c} 0\\ \frac{(1+\varDelta _{CS})GJ(3\sin 2\varPsi -2\varPsi )}{4a^3\omega }\\ 1-\frac{GM}{a}\\ \frac{3(1+\varDelta _{CS})GJ\sin ^2\varPsi }{2a^3\omega } \end{array}\right) , \end{aligned}$$
(13)

where the correction to the precessions of the bases from the non-dynamical CS modified gravity reads [14]

$$\begin{aligned} \varDelta _{CS}=15\frac{a^2}{R^2}j_2\left( \frac{R}{a}\frac{4}{ \chi }\right) \left[ y_1\left( \frac{4}{\chi }\right) +\frac{4}{\chi }y_0\left( \frac{4}{\chi }\right) \right] . \end{aligned}$$
(14)

4 Secular gradient observables

We introduce the position difference vector \(Z^{\mu }\) between the pair of two adjacent free-falling proof masses of certain measurement axis in the orbiting gradiometer. Generally \(|Z|\sim 10^{-1}\ \mathrm{m}\), which is much shorter compared with the orbital radius \(a\sim 10^{7}\ \mathrm{m}\), therefore the relative motion between the test masses can be obtained by integrating the geodesic deviation equation along the reference orbit

$$\begin{aligned} \tau ^{\rho }\nabla _{\rho }\tau ^{\lambda }\nabla _{\lambda }Z^{ \mu }+R_{\rho \nu \lambda }^{ \mu }\tau ^{\rho }\tau ^{\lambda }Z^{\nu }=0. \end{aligned}$$
(15)

In the local frame \(\{E_{(a)}^{\ \ \ \mu }\}\), the above geodesic deviation equation can be expanded as

$$\begin{aligned} \frac{d^{2}}{d\tau ^{2}}Z^{(a)}= & {} -2\gamma _{\ \ \ (b)(0)}^{(a)}\frac{d}{d\tau }Z^{(b)}\nonumber \\&- \ \left( \frac{d}{d\tau }\gamma _{\ \ \ (b)(0)}^{(a)}+\gamma _{\ \ \ (b)(0)}^{(c)}\gamma _{\ \ \ (c)(0)}^{(a)}\right) Z^{(b)}\nonumber \\&- \ K_{(b)}^{\ \ (a)}Z^{(b)}. \end{aligned}$$
(16)

where \(Z^{(a)}E_{(a)}^{\ \ \ \mu }=Z^{\mu }\), \(\gamma _{\ \ \ (b)(c)}^{(a)}=E^{(a)\nu }\nabla _{\mu }E_{(b)\nu }E_{(c)}^{\ \ \ \mu }\) are the Ricci rotation coefficients [45]. The first line of the right hand side of the above equation is the relativistic analogue of the Coriolis force, the second line contains the inertial tidal forces and the last line is the tidal force from the spacetime curvature, where the tidal matrix from curvature is defined by

$$\begin{aligned} K_{\nu }^{\ \ \mu }= & {} R_{\rho \nu \lambda }^{\ \ \ \ \ \ \mu }\tau ^{\rho }\tau ^{\lambda }. \end{aligned}$$
(17)

For electrostatic and superconducting gradiometers, the motions of test masses are suppressed by compensating forces. Then the total tidal tensor \(T_{(a)(b)}\) affecting the gradiometer will be

$$\begin{aligned} T_{(a)(b)}=-\frac{d}{d\tau }\gamma _{(a)(b)(0)}-\gamma _{(a)(c)(0)}\gamma _{\ \ \ (b)(0)}^{(c)}-K_{(a)(b)}. \end{aligned}$$
(18)

After straightforward but tedious algebraic manipulations and leaving out all the terms beyond \(\frac{1}{a^{2}}{\mathscr {O}}(\epsilon ^{4})\) and \(\frac{1}{a^{2}}\varPsi {\mathscr {O}}(\epsilon ^{4})\), we work out, to the PN level, the tidal tensors in the local free-falling Earth pointing frame along the reference orbit. For the tidal tensor \(K_{(a)(b)}\), as expected we have \(K_{(a)(0)}=0\), and the Newtonian part

$$\begin{aligned} K_{(i)(j)}^N=\left( \begin{array}{lll} \frac{GM}{a^3} &{} 0 &{} 0 \\ 0 &{} -\frac{2G M}{a^3} &{} 0 \\ 0 &{} 0 &{} \frac{GM}{a^3} \\ \end{array} \right) \end{aligned}$$
(19)

which agrees exactly with the classical Newtonian tidal tensor \(\partial _i\partial _j \frac{GM}{r}\) evaluated in such Earth-pointing frame. The PN part may be divided into the tidal tensor \(K_{(i)(j)}^{GR}\) from GR and the new tensor \(K_{(i)(j)}^{CS}\) from the CS modification, which, within the short time limit \(\frac{\tau }{a}\ll \frac{a^2}{GJ}\), can be worked out as

$$\begin{aligned} K_{(i)(j)}^{GR}= & {} \left( \begin{array}{c@{\quad }c@{\quad }c} -\frac{3 G^2M^2}{a^4} &{} 0 &{} \frac{3G J \omega \cos \varPsi }{a^3} \\ \\ 0 &{} -\frac{3 GM (a^3 \omega ^2-2G M)}{a^4} &{} -\frac{9 GJ (GM \varPsi \cos \varPsi +(2 \omega ^2 a^3+GM) \sin \varPsi )}{2 a^6 \omega } \\ \\ \frac{3 GJ \omega \cos \varPsi }{a^3} &{} -\frac{9 GJ (GM \varPsi \cos \varPsi + (2 \omega ^2 a^3+GM ) \sin \varPsi )}{2 a^6 \omega } &{} \frac{3G M (a^3 \omega ^2-GM)}{a^4} \\ \end{array} \right) , \end{aligned}$$
(20)
$$\begin{aligned} K_{(i)(j)}^{CS}= & {} \left( \begin{array}{c@{\quad }c@{\quad }c} 0 &{} 0 &{} 0 \\ \\ 0 &{}0 &{} \frac{3 G^2J M (\varPsi (\varDelta _{CS} -4 \varPi _{CS}) \cos \varPsi -3 \varDelta _{CS} \sin \varPsi )}{2 a^6 \omega } \\ \\ 0 &{} \frac{3 G^2J M (\varPsi (\varDelta _{CS}-4 \varPi _{CS}) \cos \varPsi -3 \varDelta _{CS} \sin \varPsi )}{2 a^6 \omega } &{} 0 \\ \end{array} \right) , \end{aligned}$$
(21)

here \(K_{(i)(j)}^{GR}\) agrees exactly with the former result derived in [37]. Due to the relativistic precessions of the free-falling local frame and the orbit plane, the modulations of Newtonian tidal tensor given in Eq. (19) produces secular terms in the \(K_{(2)(3)}\) and \(K_{(3)(2)}\) components, which are the expected secular gradient observables appeared along polar and nearly circular orbits. Finally, with the tidal tensor from inertial forces in Eq. (18) been worked out, the total tidal tensor \(T_{(i)(j)}\) turns out to be

$$\begin{aligned} T_{(i)(j)}=\left( \begin{array}{ccc} - \ a^{2}\omega ^{4}+\frac{4GM\omega ^{2}}{a}-\omega ^{2} &{} 0&{} -\frac{GJ(\varDelta _{CS}-3)\omega \cos \varPsi }{a^{3}}\\ +\frac{GM}{a^{3}}-\frac{3G^2M^{2}}{a^{4}}\\ \\ 0 &{} \frac{7G^2M^{2}}{a^{4}}-\frac{\omega ^{2}GM}{a}-\frac{2GM}{a^{3}}-\omega ^{2} &{} \frac{3G^2JM\varPsi (\varDelta _{CS}-4\varPi _{CS}-3)\cos \varPsi }{2a^{6}\omega }\\ &{} &{} -\frac{GJ (2(\varDelta _{CS}+9)\omega ^{2}a^{3}+9GM(\varDelta _{CS}+1) )\sin \varPsi }{2a^{6}\omega }\\ \\ \frac{3GJ(\varDelta _{CS}+1)\omega \cos \varPsi }{a^{3}} &{} \frac{3G^2JM\varPsi (\varDelta _{CS}-4\varPi _{CS}-3)\cos \varPsi }{2a^{6}\omega } &{} -\frac{3G^2M^{2}}{a^{4}}+\frac{3\omega ^{2}GM}{a}+\frac{GM}{a^{3}}\\ &{} -\frac{GJ((2(3\varDelta _{CS}+9)\omega ^{2}a^{3}+9GM(\varDelta _{CS}+1) )\sin \varPsi )}{2a^{6}\omega } &{} \end{array}\right) . \end{aligned}$$
(22)

5 Conclusions

In conclusion, how the new secular gradient components given in Eq. (21) can be measured by an orbiting 3-axis gradiometer is discussed, and the expected constraints on the mass scale of the non-dynamical CS gravity set by the proposed measurement scheme is given. Following [23, 32, 46], we orient two of the three gradiometer axes 45 degrees above and below the orbital plane and difference their outputs to reject the Newtonian and PN gravitoelectric terms and therefore measure only the GM gradient terms. In the local frame \(\{E_{(a)}^{\ \ \ \mu }\}\), the three axes of the gradiometer are oriented as

$$\begin{aligned} \hat{{\mathbf {n}}} = \left( \begin{array}{l} \sin \phi \\ -\cos \phi \\ 0 \end{array}\right) ,\quad \hat{{\mathbf {p}}} = \frac{1}{\sqrt{2}}\left( \begin{array}{l} \cos \phi \\ \sin \phi \\ -1 \end{array}\right) ,\quad \hat{{\mathbf {q}}} = \frac{1}{\sqrt{2}}\left( \begin{array}{l} \cos \phi \\ \sin \phi \\ 1 \end{array}\right) , \end{aligned}$$

see Fig. (1) for the illustration. The difference between the readouts in the \(\hat{{\mathbf {p}}}\) and \(\hat{{\mathbf {q}}}\) axes turns out to be

$$\begin{aligned}&\frac{1}{2}(T_{\hat{{\mathbf {p}}}\hat{{\mathbf {p}}}}-T_{\hat{{\mathbf {q}}}\hat{{\mathbf {q}}}})\nonumber \\&\quad =\boxed {-\frac{3G^2J\sin \phi M\varPsi (\varDelta _{CS}-4\varPi _{CS})\cos \varPsi }{2a^{6}\omega }} \nonumber \\&\qquad +\frac{9G^2J\sin \phi M\varPsi \cos \varPsi }{2a^{6}\omega }\nonumber \\&\qquad +\frac{GJ\sin \phi \sin \varPsi (2a^{3}(2\varDelta _{CS}+9)\omega ^{2}+9GM(\varDelta _{CS}+1) )}{2a^{6}\omega }\nonumber \\&\qquad -\frac{GJ(\varDelta _{CS}+3)\omega \cos \phi \cos \varPsi }{a^{3}}. \end{aligned}$$
(23)

The boxed term is the secular gradient signal \(s^{CS}\) to be measured, which is from the non-dynamical CS modifications and grows linearly with time within the mission lifetime. Such combinations of readouts can be obtained without really re-orientating the gradiometer axes according to Fig. 1 in mission operations, but can be derived in the post data procession by combining the cross-track readouts of multi-axis gradiometers (like in GOCE [27]). As \(M_{CS}\rightarrow \infty \) or \(\chi \rightarrow 0\) we have \(\varPi _{CS}\rightarrow 0\) and \(\varDelta _{CS}\rightarrow 0\), the above combined readout will then reduce to the GM gradient terms from GR as expected [37]. The magnitudes of these GR gradient terms, especially for the secular one to the right of the boxed signal, are suppose to be very large compared with that of the CS secular signal \(s^{CS}\). In the low energy regime or the weak field limit, GR had passed many stringent tests [41]. From the PN point of view, the weak field limits of general metric theories of gravity [40] can be described by ten standard PN parameters (CS gravity and the related parameter not included), which, confronted with modern experiments, have been constrained to agree precisely with the values predicted by GR, see [41] for details. Therefore the relative large tidal gradient terms from GR in Eq. (23) can be treated as from a well-test theory, and are to be modeled by GR in post data analysis. The CS gradient signal \(s^{CS}\) and the new parameter \(\chi \) or \(M_{CS}\) is then to be fitted out in the residuals or measured as the deviations from the prediction of GR. Similar strategy has been used in fitting the signals from the non-dynamical CS gravity in the data of the LAGEOS I, II missions and the Gravity Probe B mission [14]. Errors in such combination \(\frac{1}{2}(T_{\hat{{\mathbf {p}}}\hat{{\mathbf {p}}}}-T_{\hat{{\mathbf {q}}}\hat{{\mathbf {q}}}})\) may also arise from misalignments and mispointings of the gradiometer axes, and the related analysis and possible solutions are discussed in [46].

Fig. 1
figure 1

The axes of the gradiometer are oriented as follows, \(\hat{{\mathbf {p}}}\) and \(\hat{{\mathbf {q}}}\) are symmetric with respect to the \(E_{(1)}^{\ \ \ \mu }-E_{(2)}^{\ \ \ \mu }\) plane, and \(\hat{{\mathbf {n}}}\) is orthogonal to the \(\hat{{\mathbf {p}}}-\hat{{\mathbf {q}}}\) plane. The angle between \(\hat{{\mathbf {n}}}\) and \(- \ E_{(2)}^{\ \ \ \mu }\) is \(\phi \)

Full size image

Recovering the SI units, we have

$$\begin{aligned} s^{CS}=-\frac{3G^2J M\varPsi (\varDelta _{CS}-4\varPi _{CS})\sin \phi \cos \varPsi }{2c^2a^{6}\omega }. \end{aligned}$$

Form previous experiments [14, 20, 21], the new PN parameter \(\chi =4\hbar c/a M_{CS}\) had already been constrained to be a small quantity \(\chi \le 10^{-4}\). \(\varPi _{CS}\) and \(\varDelta _{CS}\) can then be expanded as

$$\begin{aligned} \varPi _{CS}= & {} {\mathscr {O}}(\chi ^2),\\ \varDelta _{CS}= & {} \frac{15 a^3 \chi \cos \left( \frac{4}{\chi }\right) \sin \left( \frac{4 R}{a \chi }\right) }{4 R^3}+{\mathscr {O}}(\chi ^2). \end{aligned}$$

Therefore, one has

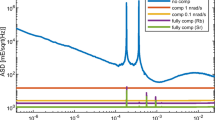
$$\begin{aligned} s^{CS}&=-\frac{45G^2\cos \left( \frac{4}{\chi }\right) \sin \left( \frac{4 R}{a \chi }\right) \chi J M\varPsi \sin \phi \cos \varPsi }{8c^2a^{3}R^3\omega }\\&\quad +{\mathscr {O}}(\chi ^2). \end{aligned}$$

To give the estimation, we assume the orbital altitude to be \(500\ \mathrm{km}\) and the mission life time about one year. After one year’s accumulation, the total orbital cycle N in \(s^{CS}\) will be \(3.5\times 10^4\), and the secular signal will reach about \(4.3\chi \ \mathrm{mE}\). With proper data analysis methods employed, the total signal-to-noise ratio can be further amplified by a factor of the square root of the total cycles \(\sqrt{N}\). Therefore, for superconducting gradiometers with potential sensitivity better than \(10^{-2}\ \mathrm{mE}/\sqrt{\mathrm{Hz}}\) in low frequency band near \(0.1\ \mathrm{mHz}\) [29], a rather strong constraint on the CS mass scale of the non-dynamical theory may in principle be obtained as

$$\begin{aligned} M_{CS}\ge 10^{-7}\ \mathrm{eV}\quad \text {and} \quad {\dot{\theta }} \le 1\ \mathrm{m}. \end{aligned}$$

For future gradiometers with optical readout\(^1\) based on similar measurement schemes and techniques from the LPF mission, an even stronger bound may be expected

$$\begin{aligned} M_{CS} \ge 10^{-6} {-} 10^{-5}\ \mathrm{eV} \quad \text {and} \quad {\dot{\theta }} \le 10^{-1}{-} 10^{-2} \ \mathrm{m}. \end{aligned}$$

Therefore, to conclude, the proposed experiment could naturally be incorporated into future missions that carrying high-sensitive gradiometers as key payloads, which in principle would improve the current constraints of the CS modified gravity and add potential scientific objectives to such satellite gradiometry missions.