An extension of the SM based on effective Peccei–Quinn Symmetry

Abstract

Peccei–Quinn (PQ) mechanism based on a chiral global U(1) symmetry is considered to be a simple and elegant solution for strong CP problem. The fact that the mechanism could be experimentally examined through the axion search makes it much more interesting and recently it causes a lot of attention again. However, it is also known that the mechanism is annoyed by two serious problems, that is, a domain wall problem and goodness of global symmetry. Any global symmetry is considered not to be exact due to the quantum effect of gravity. In this paper, we consider a solution to these problems, in which quark mass hierarchy and mixing, neutrino mass generation and existence of dark matter are closely related. In our solution, PQ symmetry is assumed to be induced through symmetry breaking at an intermediate scale of a local U(1) symmetry, and a global U(1) symmetry which plays a role of Froggatt–Nielsen symmetry . In the lepton sector, a remnant of the PQ symmetry controls neutrino mass generation and dark matter existence.

1 Introduction

Strong CP problem is one of serious problems in the standard model (SM), which is suggested by an experimental bound of the electric dipole moment of a neutron [1,2,3]. The bound requires fine tuning of $O(10^{-10})$ for a parameter $\theta$ in QCD. Invisible axion scenario based on a chiral global symmetry, which is called Peccei–Quinn (PQ) symmetry [4,5,6,7], is known to give a simple and elegant solution to it [8,9,10,11]. Since it predicts the existence of a light and very weakly interacting pseudoscalar, this solution could be examined experimentally. Moreover, it is known to present a good candidate for cold dark matter (DM) under a suitable condition [12,13,14]. Its experimental search is proceeding now.

On the other hand, the scenario has two fatal problems generally. The first one is known as a domain wall problem [15]. Although PQ symmetry is explicitly broken to its discrete subgroup $Z_N$ through the QCD instanton effect, this $Z_N$ is also spontaneously broken to its subgroup when the PQ symmetry is spontaneously broken by a vacuum expectation value (VEV) of scalar fields and quark condensates. This brings about N degenerate vacua due to the spontaneous breaking of the $Z_N$ symmetry, where each vacuum is separated by topological defects called domain wall and N is called the domain wall number. Since the energy density of the domain walls dominates cosmological energy density of the Universe inevitably, the Universe is over-closed contradicting to the observations. It is known that the domain wall problem could be escaped for a non-degenerate vacuum which has $N=1$ [16,17,18,19], even if the cosmological inflation occurs before the PQ symmetry breaking. The KSVZ model is known to be such a representative example [8, 9].

The second one is related to the goodness of the PQ symmetry. The PQ symmetry is global symmetry, which is used to be considered to be broken by the gravitational effect [20, 21].¹ If this breaking effect due to the gravity is larger than the QCD instanton effect, the PQ mechanism cannot solve the strong CP problem. In order to escape this dangerous situation, such symmetry breaking operators caused by the gravity should be forbidden up to dimension ten [25,26,27,28]. There, the PQ symmetry is considered to be realized as the accidental symmetry induced by some gauge symmetry or discrete symmetry, which satisfies such a constraint on its goodness. In such a direction, several works have been done by now [29,30,31,32,33,34,35,36,37].

In this paper, we propose a model which can escape these two problems in axion models. Although the SM has been confirmed by the discovery of the Higgs scalar [38, 39], it cannot explain several experimental and observational data such as quark mass hierarchy and CKM mixing, neutrino masses and their large mixing [40], and also the existence of DM [41, 42]. In the present model construction, we take account of these problems also.² For this purpose, we impose $U(1)_g\times U(1)_{FN}$ on the model, where $U(1)_g$ is the gauge symmetry but $U(1)_{FN}$ is the global symmetry whose charge is flavor dependent. Then, the latter could play a role of Froggatt–Nielsen symmetry [56]. This symmetry is assumed to be spontaneously broken to the PQ symmetry $U(1)_{PQ}$ at some intermediate scale. We require that $U(1)_g$ guarantees the goodness of $U(1)_{PQ}$ to be kept up to a consistent level required by the strong CP problem. After the spontaneous breaking of $U(1)_{PQ}$, both a non-degenerate QCD vacuum and Yukawa couplings with desirable flavor structure are induced in a quark sector [55]. In a leptonic sector, the scotogenic model [57] which connects the neutrino mass generation and the existence of DM is brought about as a low energy effective model. Since the model has a DM candidate other than the axion, a condition on the decay constant of the axion can be weakened.

The remaining parts are organized as follows. In the next section, we present our model by fixing the symmetry $U(1)_g\times U(1)_{FN}$ and the field contents in the model. We discuss features of the model such as the symmetry breaking, the domain wall number, the goodness of the PQ symmetry and so on. In Sect. 3, phenomenological features of this model are discussed, such as quark mass hierarchy and CKM mixing, neutrino mass generation, leptogenesis, DM abundance and so on. We summarize the paper in Sect. 4.

2 A model with $U(1)_g\times U(1)_{FN}$

We start presenting a brief review of the QCD vacuum degeneracy in the PQ mechanism [1,2,3]. If the $U(1)_{PQ}[SU(3)_c]^2$ anomaly takes a value N for the PQ charge assignment of colored contents in the model, the $U(1)_{PQ}$ transformation of the colored fermions shifts a parameter ${\bar{\theta }}$ as [4, 5]

$$\begin{aligned} {\bar{\theta }} \rightarrow {\bar{\theta }} +2\pi N, \end{aligned}$$

(1)

where ${\bar{\theta }}$ is a coefficient of an effective term $\frac{{\bar{\theta }}}{32\pi ^2}F^a_{\mu \nu }{\tilde{F}}^{a\mu \nu }$ induced by instantons and it is defined as ${\bar{\theta }}=\theta + \mathrm{arg}(\mathrm{det}~\mathcal{M})$ where $\mathcal{M}$ stands for a quark mass matrix. If the PQ symmetry is spontaneously broken by a VEV of a scalar field S, ${\bar{\theta }}$ behaves as a dynamical variable corresponding to a pseudo Nambu-Goldstone boson associated with this breaking, which is called axion a [6,7,8,9,10,11]. Since a period of ${\bar{\theta }}$ is $2\pi$ and potential for ${\bar{\theta }}$ can be represented by using a QCD scale $\Lambda _\mathrm{QCD}$ as

$$\begin{aligned} V({\bar{\theta }})=\Lambda _\mathrm{QCD}^4(1-\cos {\bar{\theta }}), \end{aligned}$$

(2)

this potential for ${\bar{\theta }}$ has |N|-fold degenerate minima. The axion a is fixed as $a\equiv |\langle S\rangle |\frac{{\bar{\theta }}}{|N|}$ which is defined at a region $[0,2\pi )$. This requires that the axion decay constant $f_a$ should be defined as $f_a|N|=|\langle S\rangle |$.

Each degenerate vacuum is separated by potential barriers called the domain wall [15]. It can be identified with a topological defect which is produced through the spontaneous breaking of $Z_{|N|}$. As addressed in the introduction, |N| is called the domain wall number and it is written as $N_{DW}$ for the definiteness in the following part. In the $N_{DW}=1$ case, the walls are produced although the vacuum is unique. They have a string at its boundary which is generated due to the breaking of $U(1)_{PQ}$. This type of domain walls can quickly disappear as studied in [58]. On the other hand, in the $N_{DW}\ge 2$ case, each string has $N_{DW}$ domain walls and they generate complex networks of strings and walls. Since these networks are stable, they dominate the energy density of the Universe to over-close it. Thus, if inflation does not occur after the $U(1)_{PQ}$ breaking, the present Universe cannot be realized unless $N_{DW}=1$ is satisfied. Inflation could make the present Universe to be covered with a unique vacuum if inflation occurs after the PQ symmetry breaking. Thus, low scale inflation could give a solution in the $N_{DW}\ge 2$ case. However, we focus on the $N_{DW}=1$ case in the present study.

Here two points on the domain wall problem should be remarked. First, the non-degenerate vacuum can be realized even for the case with $N\not =\pm 1$. As an interesting example, we may consider a case with $N=\pm 2$ where the VEV of the scalar does not break $Z_2$ spontaneously. Since two vacua could be identified each other by this unbroken $Z_2$ symmetry, $N_{DW}=1$ is realized just as in the $N=\pm 1$ case. Second, we should notice that there are two estimations for the axion relic density by taking account of the decay of domain walls in the $N_{DW}=1$ case [59,60,61,62], which give different conclusions. One of them suggests that the domain wall problem might not be solved even in the $N_{DW}=1$ case unless the axion decay constant is less than a certain limit. Another one claims that the axion produced through the domain wall decay is subdominant in comparison with the one due to axion misalignment. In the following discussion, we assume that the axion energy density coming from the domain wall decay is subdominant and $N_{DW}=1$ could be a solution for the strong CP problem.

Now, we try to construct a model so as to escape the domain wall problem by $N_{DW}=1$ [54, 55] and to guarantee the goodness of global symmetry at the required level by gauge symmetry. A framework to keep the goodness of the PQ symmetry has been proposed in [25,26,27,28]. We would like to follow a similar scenario to it.

Table 1 The $U(1)_g\times U(1)_{FN}$ charge of the color triplet fermions $Q_{L,R}^{(i)}$ and the SM singlet complex scalars $\sigma$ and S. The charge $X_{PQ}$ of $U(1)_\mathrm{PQ}$ is defined as $X_{PQ}=X_g+X_{FN}$ where $X_g$ and $X_{FN}$ are the charges of $U(1)_g$ and $U(1)_{FN}$, respectively. Parity of $Z_2$ which remains after the $U(1)_{PQ}$ breaking by $\langle S\rangle$ is also listed

We impose $U(1)_g\times U(1)_{FN}$ on the model above an intermediate scale and introduce new fields with the charge of this symmetry. They are two SM singlet complex scalars $\sigma , ~S$, and also six types of color triplet fermions $Q_{L,R}^{(i)}~(i=1 \sim 3)$, which are assumed to have no charge of $SU(2)_L\times U(1)_Y$ and their subscripts L and R represent their chirality. The $U(1)_g\times U(1)_{FN}$ charges of these fields are given in Table 1. In this charge assignment, each VEV of $\sigma$ and S induces the symmetry breaking

$$\begin{aligned} U(1)_g\times U(1)_{FN}\quad {\mathop {\longrightarrow }\limits ^{\langle \sigma \rangle }}\quad U(1)_{PQ}\quad {\mathop {\longrightarrow }\limits ^{\langle S\rangle }}\quad Z_2, \end{aligned}$$

(3)

where we assume $\langle \sigma \rangle >\langle S\rangle$. The $U(1)_{PQ}$ charge $X_{PQ}$ is defined as a linear combination $X_{PQ}=X_g+X_{FN}$ where $X_g$ and $X_{FN}$ are the charges of $U(1)_g$ and $U(1)_{FN}$, respectively. As we find it later, this $Z_2$ is not broken through quark condensate either.

We have to address various anomalies associated to the introduction of new fields, first of all. All of the gauge anomaly for $[SU(3)_c]^3$, $U(1)_g[SU(3)_c]^2$ and $[U(1)_g]^3$ are easily found to cancel within these field contents. On the other hand, the QCD anomaly $U(1)_{FN}[SU(3)_c]^2$ for $U(1)_{FN}$ does not cancel but it is calculated as $N=-2$ in this extra fermion sector. Since $U(1)_{PQ}$ plays its role as the global symmetry after the first step of the symmetry breaking in Eq. (3) and $U(1)_{PQ}[SU(3)_c]^2$ anomaly takes the same value as $U(1)_{FN}[SU(3)_c]^2$, the strong CP problem is expected to be solved by the PQ mechanism based on an axion caused in the spontaneous symmetry breaking of $U(1)_{PQ}$ due to a VEV of S. In order to escape the domain wall problem, the total anomaly including the contribution from the quark sector should be $N=\pm 1$ or $\pm 2$.³ This suggests that the corresponding anomaly of the quark sector should take a value among 0, 1, 3 and 4. As we will see it later, this value is closely related to the quark mass hierarchy and the CKM mixing. Three examples (i) $\sim$ (iii) of the charge assignment for the quark sector is presented in Table 2. In these cases, $N_{DW}=1$ can be realized.

Next, we move to the problem on the goodness of this $U(1)_{PQ}$ and the mass generation of the extra colored fermions. It is easy to see that a lowest order term in the potential of $\sigma$ and S, which is $U(1)_g$ invariant but $U(1)_{FN}$ violating, is

$$\begin{aligned} \frac{g}{M_\mathrm{pl}^7}\sigma ^{*2} S^9 +\mathrm{h.c.}, \end{aligned}$$

(4)

where g is a constant and $U(1)_{FN}$ violation is considered to be induced by the gravitational effect so that the operator is suppressed by the Planck mass $M_\mathrm{pl}$. If the PQ mechanism works well in this model, the contribution to the axion mass from Eq. (4) should be less than the one coming from the potential (2) due to the QCD instanton effect [25,26,27,28]. Since the latter is given as $m_a^2=\frac{m_\pi ^2f_\pi ^2}{f_a^2}$ [6, 7], this condition gives a constraint on $\langle \sigma \rangle$ such as

$$\begin{aligned} \langle \sigma \rangle ~{^<_\sim }~ 6\times 10^{12} \left( \frac{10^{11}~\mathrm{GeV}}{\langle S\rangle }\right) ^{\frac{9}{2}}~\mathrm{GeV}. \end{aligned}$$

(5)

It should be consistent with our assumption for the symmetry breaking pattern (3) within the astrophysical and cosmological constraint on the axion decay constant which is $10^9~\mathrm{GeV}< f_a <10^{12}~\mathrm{GeV}$ [1,2,3]. It requires that the VEV of S should satisfy

$$\begin{aligned} 10^9~\mathrm{GeV}~{^<_\sim }~\langle S\rangle ~{^<_\sim }~2\times 10^{11}~\mathrm{GeV}, \end{aligned}$$

(6)

for the $N_{DW}=1$ case. It suggests that the axion seems to be difficult to be a dominant component of the DM since $f_a$ has to be rather small in this scenario. From these discussions, we find that the axion in this model is characterized by a lower mass bound such as $m_a~{^>_\sim }~6\times 10^{-5}$ eV and a coupling with photon such as $g_{a\gamma \gamma }=\frac{m_a}{\mathrm{eV}} \frac{2.0}{10^{10}{\mathrm{GeV}}}(\frac{E}{N}-1.92)$ [63] where $\frac{E}{N}=-\frac{58}{3}$ for (i), $\frac{34}{3}$ for (ii), and 6 for (iii).

Table 2 Examples of the $U(1)_{FN}$ charge assignment for quarks which have no domain wall problem. Quarks are assumed to have no $U(1)_g$ charge. N represents a value of the QCD anomaly in each case, which realizes $N_{DW}=1$ by combining with the one from the extra colored fermions given in Table 1

The extra colored fields can get their mass only through the VEVs of $\sigma$ and S. It is crucial for the consistency of the model what scale of mass they can have. The following operators are invariant under $U(1)_g\times U(1)_{FN}$,

$$\begin{aligned} \sigma {\bar{Q}}_{L}^{(1)}Q_{R}^{(1)}, \qquad \sigma \bar{Q}_{L}^{(2)}Q_{R}^{(2)}. \end{aligned}$$

(7)

On the other hand, $\frac{S^{*2}}{M_*}\bar{Q}_L^{(3)}Q_R^{(3)}$ could be generated as a $U(1)_{PQ}$ invariant operator after the $U(1)_g\times U(1)_{FN}$ breaking at $\langle \sigma \rangle =M_*$. These operators give masses to these extra colored fermions through $\langle \sigma \rangle$ and $\langle S\rangle$. However, since they have no hypercharge, they cannot couple with ordinary quarks and then they have no decay modes so as to be stable.⁴ If they are in thermal equilibrium during the history of the Universe, we have to note that several contradictions such as the existence of fractionally charged hadrons and their over-abundant contribution to the energy density could appear [63]. The strongest constraint on their abundance comes from the search of fractionally charged particles, which requires $\frac{n_{Q^{(3)}}}{n_b}~{^<_\sim }~10^{-20}$ for the abundance of the lightest extra colored fermion $n_{Q^{(3)}}$ and the abundance of the ordinary nucleons $n_b$ [64]. This constraint could be satisfied even if $Q^{(3)}$ is in the thermal equilibrium as long as reheating temperature is assumed to be much lower than the mass of $Q^{(3)}$. Since $U(1)_g\times U(1)_{FN}$ is assumed not to be restored after the reheating, these extra colored fermions are not produced in the thermal bath through the reheating process and the model can escape this problem. In fact, we can confirm that the $Q^{(3)}$ mass of $O\left( \frac{\langle S\rangle }{M_*}\right) ^2M_*$ derived by an O(1) coupling could satisfy the above constraint for the parameters used in the following study and the reheating temperature such as $T_R=10^8$ GeV. Such a low reheating temperature could cause a problem if we consider thermal leptogenesis due to the decay of thermal right-handed neutrinos. We will come back this point later.

Now, we couple this model with the SM including the lepton sector. Since the axion could not be a dominant component of DM in this scenario as discussed above, we need to prepare a candidate for the DM. For this purpose, the leptonic sector is extended by an additional doublet scalar $\eta$ and three right-handed neutrinos $N_i$ so as to realize the scotogenic model [57, 65,66,67,68,69,70,71,72]. An example of the $U(1)_g\times U(1)_{FN}$ charge assignment for the leptonic sector is shown in Table 3. After the symmetry breaking due to $\langle \sigma \rangle$, $U(1)_{PQ}$ invariant operators are considered to be generated in both Yukawa couplings and scalar potential of an effective theory at energy regions below $\langle \sigma \rangle$. An interesting point is that nonrenormalizable Yukawa couplings are controlled by the $U(1)_{PQ}$ charge of each quark and lepton [51,52,53, 55]. In fact, if we define

$$\begin{aligned} n^u_{ij}= & {} \frac{1}{2}(X_{u_{R_j}}-X_{q_{L_i}}), \quad n^d_{ij}=\frac{1}{2}(X_{d_{R_j}}-X_{q_{L_i}}), \nonumber \\ n^N_{ij}= & {} \frac{1}{2}(X_{N_{R_i}}+X_{N_{R_j}}), \nonumber \\ n^\nu _{ij}= & {} \frac{1}{2}(X_{N_{R_j}}-X_{\ell _{L_i}}-1), \quad n^e_{ij}=\frac{1}{2}(X_{e_{R_j}}-X_{\ell _{L_i}}), \end{aligned}$$

(8)

quark Yukawa couplings are written as

$$\begin{aligned} -\mathcal{L}_y^q= & {} \sum _{i=1,j}^3\left[ y^u_{ij}\left( \frac{S}{M_*} \right) ^{|n^u_{ij}|}{\bar{q}}_{L_i}\phi u_{R_j}\right. \nonumber \\&\left. +y^d_{ij}\left( \frac{S}{M_*}\right) ^{|n^d_{ij}|} {\bar{q}}_{L_i}{\tilde{\phi }} d_{R_j} \right] , \end{aligned}$$

(9)

Table 3 The $U(1)_{FN}$ charge assignment for leptons, right-handed neutrinos, the Higgs doublet $\phi$ and an additional doublet scalar $\eta$. These are assumed to have no $U(1)_g$ charge

where ${\tilde{\phi }}=i\tau _2\phi ^*$ and $M_*=\langle \sigma \rangle$. On the other hand, Yukawa couplings relevant to the neutrino mass generation are written as

$$\begin{aligned} -\mathcal{L}_y^\ell= & {} \sum _{i,j=1}^3\left[ h_{ij}^\nu \left( \frac{S}{M_*}\right) ^{|n^\nu _{ij}|}{\bar{\ell }}_{L_i}\eta N_{R_j} \right. \nonumber \\&+h_{ij}^e\left( \frac{S}{M_*}\right) ^{|n^e_{ij}|} {\bar{\ell }}_{L_i}{\tilde{\phi }} e_{R_j} \nonumber \\&+ \left. h_{ij}^N\left( \frac{S}{M_*}\right) ^{|n_{ij}^N|} M_*{\bar{N}}^c_{R_i}N_{R_j} +\mathrm{h.c.}\right] . \end{aligned}$$

(10)

The third term related to the mass of right-handed neutrinos should satisfy $|n_{ij}^N|\ge 2$, since the renormalizable one is forbidden by $U(1)_g\times U(1)_{FN}$. In these formulas (9) and (10), S should be replaced by $S^*$ for $n^f_{ij}<0$. The scalar potential at energy regions lower than $\langle \sigma \rangle$ is written as

$$\begin{aligned} V_1= & {} m_S^2S^\dagger S+\kappa _1(S^\dagger S)^2+\kappa _2(S^\dagger S)(\phi ^\dagger \phi ) +\kappa _3(S^\dagger S)(\eta ^\dagger \eta ) \nonumber \\&+\,m_\eta ^2\eta ^\dagger \eta +m_\phi ^2\phi ^\dagger \phi +\lambda _1(\phi ^\dagger \phi )^2 +\lambda _2(\eta ^\dagger \eta )^2\nonumber \\&+\,\lambda _3(\phi ^\dagger \phi )(\eta ^\dagger \eta ) +\lambda _4(\phi ^\dagger \eta )(\eta ^\dagger \phi ) \nonumber \\&+\,\frac{\lambda _5}{2}\left[ \frac{S}{M_*}(\eta ^\dagger \phi )^2 ~+\mathrm{h.c.}\right] , \end{aligned}$$

(11)

where $\lambda _5$ is taken to be real. On the other hand, the scalar potential for the light scalars $\phi$ and $\eta$ after S gets the VEV can be expressed as

$$\begin{aligned} V_2= & {} {\tilde{m}}_\eta ^2\eta ^\dagger \eta +\tilde{m}_\phi ^2\phi ^\dagger \phi +{\tilde{\lambda }}_1(\phi ^\dagger \phi )^2 +{\tilde{\lambda }}_2(\eta ^\dagger \eta )^2 \nonumber \\&+\,{\tilde{\lambda }}_3(\phi ^\dagger \phi )(\eta ^\dagger \eta ) +\lambda _4(\phi ^\dagger \eta )(\eta ^\dagger \phi )\nonumber \\&+\,\frac{{\tilde{\lambda }}_5}{2}\left[ (\eta ^\dagger \phi )^2 ~+\mathrm{h.c.}\right] , \end{aligned}$$

(12)

which is found to coincide with the scalar potential of the scotogenic model.

In Eqs. (11) and (12), scalar masses and couplings are shifted from the ones at higher energy regions because of the symmetry breaking effect by $\sigma$ and S, respectively [54]. The shift of the parameters in (11) can be summarized as

$$\begin{aligned} \kappa _1= & {} {\bar{\kappa }}_1-\frac{\xi _S^2}{4\xi _\sigma }, \quad \kappa _2={\bar{\kappa }}_2-\frac{\xi _S\xi _\phi }{2\xi _\sigma }, \quad \kappa _3={\bar{\kappa }}_3-\frac{\xi _S\xi _\eta }{2\xi _\sigma }, \nonumber \\ \lambda _1= & {} {\bar{\lambda }}_1-\frac{\xi _\phi ^2}{4\xi _\sigma }, \quad \lambda _2={\bar{\lambda }}_2-\frac{\xi _\eta ^2}{4\xi _\sigma }, \quad \lambda _3={\bar{\lambda }}_3-\frac{\xi _\phi \xi _\eta }{2\xi _\sigma }, \nonumber \\ m_S^2= & {} {\bar{m}}_S^2+\xi _S\langle \sigma \rangle ^2, \quad m_\phi ^2={\bar{m}}_\phi ^2+\xi _\phi \langle \sigma \rangle ^2,\nonumber \\ m_\eta ^2= & {} {\bar{m}}_\eta ^2+\xi _\eta \langle \sigma \rangle ^2, \end{aligned}$$

(13)

where the over-lined parameters correspond to the ones before the symmetry breaking and $\xi _\rho ~(\rho =\sigma ,S,\phi ,\eta )$ represents a coupling constant for an operator $(\rho ^\dagger \rho )(\sigma ^\dagger \sigma )$ in the potential at energy scales larger than $\langle \sigma \rangle$. The shift of parameters in (12) can be given as

$$\begin{aligned} {\tilde{\lambda }}_1= & {} \lambda _1-\frac{\kappa _2^2}{4\kappa _1}, \quad {\tilde{\lambda }}_2=\lambda _2-\frac{\kappa _3^2}{4\kappa _1}, \quad {\tilde{\lambda }}_3=\lambda _3-\frac{\kappa _2\kappa _3}{2\kappa _1}, \nonumber \\ {\tilde{\lambda }}_5= & {} \lambda _5\frac{\langle S\rangle }{M_*}, \quad {\tilde{m}}_\phi ^2= m_\phi ^2+\kappa _2\langle S\rangle ^2, \nonumber \\ {\tilde{m}}_\eta ^2= & {} m_\eta ^2+\kappa _3\langle S\rangle ^2. \end{aligned}$$

(14)

The parameters in Eq. (14) should satisfy the conditions for which a vacuum defined in $V_2$ is stable. They are written as

$$\begin{aligned} {\tilde{\lambda }}_{1,2}>0,\quad {\tilde{\lambda }}_3>-2\sqrt{{\tilde{\lambda }}_1{\tilde{\lambda }}_2},\quad {\tilde{\lambda }}_3+\lambda _4-|{\tilde{\lambda }}_5| >-2 \sqrt{{\tilde{\lambda }}_1{\tilde{\lambda }}_2}. \end{aligned}$$

(15)

In Eqs. (9), (10) and (11), the lowest dimension operators invariant under $U(1)_{PQ}$ are listed. There could be $U(1)_{FN}$ violating contributions to them which are induced by the gravity effect. However, since they are suppressed by a factor $\frac{\sigma \sigma ^*}{M_\mathrm{pl}^2}$ at least, their effect can be safely neglected under the condition (5). These formulas show that Yukawa couplings for the quarks and the leptons have a suppression by powers of $\frac{|\langle S\rangle |}{M_*}$ after the PQ symmetry breaking due to $\langle S\rangle$. Neutrino Yukawa couplings in the leptonic sector are also found to be reduced to the ones in the scotogenic model. Moreover, the coupling ${\tilde{\lambda }}_5$ in Eq. (12) could be small so as to cause a small mass difference between the neutral components of the extra doublet scalar $\eta$. One should note that it is a crucial element of the neutrino mass generation in the original scotogenic model.

3 Phenomenological features of the model

3.1 Quark mass hierarchy and CKM mixing

After the PQ symmetry breaking due to $\langle S\rangle$, Eq. (9) induces Yukawa couplings for quarks with a suppression factor $\epsilon ^{|n^f_{ij}|}$ where $\epsilon =\frac{|\langle S\rangle |}{M_*}$ and $n^f_{ij}$ is determined by the PQ charge of quarks just like the Froggatt–Nielsen mechanism [51,52,53, 55].⁵ Elements of quark mass matrices derived from these are represented as

$$\begin{aligned} m^f_{ij}=y^f_{ij}\epsilon ^{|n^f_{ij}|}\langle \phi \rangle , \end{aligned}$$

(16)

where a superscript f stands for up and down sector and then $f=u, d$. If we define the quark mass eigenstates as ${\tilde{f}}_L=U^ff_L$ and ${\tilde{f}}_R=V^ff_R$ by using the unitary matrices $U^f$ and $V^f$, they satisfy the condition

$$\begin{aligned} \left( U^{f\dagger }\right) _{\alpha i}y^f_{ij}\epsilon ^{|n^f_{ij}|}V^{f}_{j\beta } =\frac{m_\alpha ^f}{\langle \phi \rangle }~\delta _{\alpha \beta }, \end{aligned}$$

(17)

where $m^f_\alpha$ represents a mass eigenvalue in the f-sector. The CKM matrix is expressed as $U_{CKM}=U^{u\dagger }U^d$. If we use the PQ charge of quarks given in Table 2, the quark mass matrices defined by ${\bar{u}}_L\mathcal{M}_uu_R$ and ${\bar{d}}_L\mathcal{M}_dd_R$ can be written for each example as

$$\begin{aligned} \mathrm{(i)}\, \mathcal{M}_u= & {} \left( \begin{array}{ccc} y_{11}^u~\epsilon ^4 &{}\quad y_{12}^u~\epsilon ^3 &{}\quad y_{13}^u~\epsilon ^2 \\ y_{21}^u~\epsilon ^3 &{}\quad y_{22}^u~\epsilon ^2 &{}\quad y_{23}^u~\epsilon \\ y_{31}^u~\epsilon ^2 &{}\quad y_{32}^u~\epsilon &{}\quad y_{33}^u \\ \end{array}\right) \langle \phi \rangle , \nonumber \\ \mathcal{M}_d= & {} \left( \begin{array}{ccc} y_{11}^d~\epsilon ^3 &{}\quad y_{12}^d~\epsilon ^2 &{}\quad y_{13}^d~\epsilon ^3 \\ y_{21}^d~\epsilon ^4 &{}\quad y_{22}^d~\epsilon ^3 &{}\quad y_{23}^d~\epsilon ^2 \\ y_{31}^d~\epsilon ^5 &{}\quad y_{32}^d~\epsilon ^4 &{}\quad y_{33}^d~\epsilon \\ \end{array}\right) \langle {\tilde{\phi }}\rangle , \nonumber \\ \mathrm{(ii)}\, \mathcal{M}_u= & {} \left( \begin{array}{ccc} y_{11}^u~\epsilon ^4 &{}\quad y_{12}^u~\epsilon ^2 &{}\quad y_{13}^u~\epsilon ^4 \\ y_{21}^u~\epsilon ^7 &{}\quad y_{22}^u~\epsilon &{}\quad y_{23}^u~\epsilon \\ y_{31}^u~\epsilon ^8 &{}\quad y_{32}^u~\epsilon ^2 &{}\quad y_{33}^u \\ \end{array}\right) \langle \phi \rangle , \nonumber \\ \mathcal{M}_d= & {} \left( \begin{array}{ccc} y_{11}^d~\epsilon ^6 &{}\quad y_{12}^d~\epsilon ^5 &{}\quad y_{13}^d~\epsilon ^5 \\ y_{21}^d~\epsilon ^3 &{}\quad y_{22}^d~\epsilon ^2 &{}\quad y_{23}^d~\epsilon ^2 \\ y_{31}^d~\epsilon ^2 &{}\quad y_{32}^d~\epsilon &{}\quad y_{33}^d~\epsilon \\ \end{array}\right) \langle {\tilde{\phi }}\rangle , \nonumber \\ \mathrm{(iii)}\, \mathcal{M}_u= & {} \left( \begin{array}{ccc} y_{11}^u~\epsilon ^4 &{}\quad y_{12}^u~\epsilon ^2 &{}\quad y_{13}^u~\epsilon ^4 \\ y_{21}^u~\epsilon ^7 &{}\quad y_{22}^u~\epsilon &{}\quad y_{23}^u~\epsilon \\ y_{31}^u~\epsilon ^8 &{}\quad y_{32}^u~\epsilon ^2 &{}\quad y_{33}^u \\ \end{array}\right) \langle \phi \rangle , \nonumber \\ \mathcal{M}_d= & {} \left( \begin{array}{ccc} y_{11}^d~\epsilon ^5 &{}\quad y_{12}^d~\epsilon ^5 &{}\quad y_{13}^d~\epsilon ^5 \\ y_{21}^d~\epsilon ^2 &{}\quad y_{22}^d~\epsilon ^2 &{}\quad y_{23}^d~\epsilon ^2 \\ y_{31}^d~\epsilon &{}\quad y_{32}^d~\epsilon &{}\quad y_{33}^d~\epsilon \\ \end{array}\right) \langle {\tilde{\phi }}\rangle . \end{aligned}$$

(18)

While flavor dependent PQ charge of quarks brings about these mass matrices, it can also cause flavor changing neutral processes with the axion emission [51,52,53, 73], which are severely constrained through experiments. The strongest constraint on $f_a$ due to such processes is known to come from $K^\pm \rightarrow \pi ^\pm a$, whose experimental bound is given as $\mathrm{Br}(K^\pm \rightarrow \pi ^\pm a)< 7.3\times 10^{-11}$ [85]. Since the axion a is introduced in the effective theory through the replacement $S=\langle S\rangle e^{i\frac{a}{f_a}}$, Eq. (9) gives the axion-quark interaction terms

$$\begin{aligned} in^u_{ij}m^u_{ij}~\frac{a}{f_a}~{\bar{u}}_{Li}u_{Rj}+ in^d_{ij}m^d_{ij}~\frac{a}{f_a}~{\bar{d}}_{Li}d_{Rj}+\mathrm{h.c.}, \end{aligned}$$

(19)

where $m^f_{ij}$ is given in Eq. (16). If we focus our attention to the down-sector and use the quark mass eigenstates defined above, the corresponding terms in Eq. (19) can be rewritten as

$$\begin{aligned}&i\frac{\langle \phi \rangle }{f_a}\left[ \left( U^{d\dagger }\right) _{\alpha i} n^u_{ij}y^d_{ij}\epsilon ^{n^u_{ij}}V^{d}_{j\beta }\right. \nonumber \\&\qquad \left. -\left( V^{d\dagger }\right) _{\alpha i}n^u_{ij}y^{*d}_{ji}\epsilon ^{n^u_{ij}} U^{d}_{i\beta }\right] a~{\bar{d}}_\alpha d_\beta \nonumber \\&\qquad +i\frac{\langle \phi \rangle }{f_a}\left[ \left( U^{d\dagger }\right) _{\alpha i} n^u_{ij}y^d_{ij}\epsilon ^{n^u_{ij}}V^{d}_{j\beta }\right. \nonumber \\&\qquad \left. +\left( V^{d\dagger }\right) _{\alpha i}n^u_{ij}y^{*d}_{ji} \epsilon ^{n^u_{ij}}U^{d}_{i\beta }\right] a~{\bar{d}}_\alpha \gamma _5 d_{\beta } \nonumber \\&\quad \equiv iS_{\alpha \beta }~a~{\bar{d}}_\alpha d_\beta + iA_{\alpha \beta }~a~{\bar{d}}_\alpha \gamma _5 d_\beta . \end{aligned}$$

(20)

If we apply Eqs. (8) and (17) to Eq. (20), the coupling constants $S_{\alpha \beta }$ and $A_{\alpha \beta }$ are found to be expressed as

$$\begin{aligned} S_{\alpha \beta }=\frac{m_\alpha -m_\beta }{2f_a}X_{\alpha \beta }^+, \qquad A_{\alpha \beta }=\frac{m_\alpha +m_\beta }{2f_a}X_{\alpha \beta }^-, \end{aligned}$$

where $X_{\alpha \beta }^\pm$ is defined by

$$\begin{aligned} X_{\alpha \beta }^\pm= & {} \left( V^{d\dagger }\right) _{\alpha i}X(d_{Ri})\left( V^{d}\right) _{i\beta }\nonumber \\&\pm \left( U^{d\dagger }\right) _{\alpha i}X(d_{Li})\left( U^{d}\right) _{i\beta }. \end{aligned}$$

(21)

Since the decay width of $K^+ \rightarrow \pi ^+ a$ can be estimated by using this $X_{\alpha \beta }^\pm$ as [51,52,53, 86]

$$\begin{aligned} \Gamma =\frac{|X_{ds}^+|^2}{128\pi }\frac{m_K^3}{f_a^2} \left( 1-\frac{m_\pi ^2}{m_K^2}\right) ^3, \end{aligned}$$

(22)

we obtain the strong constraint on $f_a$ by applying the experimental bound to this formula as

$$\begin{aligned} f_a> 2.4\times 10^{11}~ |X_{ds}^+|~ \mathrm{GeV}. \end{aligned}$$

(23)

Since the condition (6) should be satisfied, Eq. (23) requires $|X_{ds}^+|<1$. The PQ charge of quarks is required not only to reproduce the quark mass eigenvalues and the CKM mixing but also to satisfy this constraint.

We examine these issues in the examples shown in Table 2. Since these realize $N_{DM}=1$, the axion decay constant $f_a$ satisfies $f_a=|\langle S\rangle |$. In order to study the features of the examples quantitatively, we need to fix a value of $\epsilon$ and coupling constants $y_{ij}^f$. Needless to say, the validity of the scenario is determined through how good predictions can be derived for less number of independent coupling constants $y_{ij}^f$ without serious fine tuning. The results obtained in each example are ordered for a typical parameter set. In this analysis, the CP phase of $y_{ij}^f$ is not taken into account, for simplicity.

In the example (i), we assume $\epsilon =0.08$ and the coupling constants $y_{ij}^f$ are fixed as

$$\begin{aligned} y_{11}^u= & {} y_{23}^u=y_{32}^u=y_{33}^u=1,\quad y_{13}^u=y_{22}^u=y_{31}^u=0.1,\\ y_{12}^u= & {} y_{21}^u=0.7, \\ y_{21}^d= & {} y_{22}^d=y_{31}^d=y_{32}^d=1, \quad y_{11}^d=y_{13}^d=y_{23}^d=0.1,\\ y_{12}^d= & {} 0.022, \quad y_{33}^d=0.3, \end{aligned}$$

where the number of independent parameters can be identified as six. For this parameter set, the quark mass eigenvalues and the CKM matrix are obtained as

$$\begin{aligned}&\begin{array}{lll} m_u\simeq 2.6~\mathrm{MeV}, &{}\quad m_c\simeq 1.1~\mathrm{GeV}, &{}\quad m_t\simeq 174~\mathrm{GeV}, \\ m_d\simeq 6.7~\mathrm{MeV}, &{}\quad m_s\simeq 92~\mathrm{MeV}, &{}\quad m_b\simeq 4.2~\mathrm{GeV}, \end{array}\\&\quad V_\mathrm{CKM}\simeq \left( \begin{array}{ccc} 0.97 &{}\quad -0.23 &{}\quad -0.0052 \\ 0.23 &{}\quad 0.97 &{}\quad -0.018 \\ 0.0092 &{}\quad 0.017 &{}\quad 1.0 \\ \end{array}\right) . \end{aligned}$$

In this case, Eq. (23) requires $f_a> 1.7\times 10^{11}$ GeV.

In the example (ii), $\epsilon =0.07$ is assumed and $y_{ij}^f$ are fixed as

$$\begin{aligned} y_{11}^u= & {} y_{13}^u=y_{21}^u=y_{31}^u=y_{32}^u=y_{33}^u=1,\nonumber \\ y_{22}^u= & {} y_{23}^u=0.1, \quad y_{12}^u=0.32, \\ y_{11}^d= & {} y_{21}^d=y_{31}^d=1, \quad y_{22}^d=0.1, \quad y_{23}^d=-0.03,\nonumber \\ y_{32}^d= & {} y_{33}^d=0.26.\quad y_{12}^d= y_{13}^d=60, \end{aligned}$$

where the number of independent parameters can be identified as seven. For this parameter set, we obtain

$$\begin{aligned}&\begin{array}{lll} m_u\simeq 4.0~\mathrm{MeV}, &{}\quad m_c\simeq 1.3~\mathrm{GeV}, &{}\quad m_t\simeq 174~\mathrm{GeV}, \\ m_d\simeq 3.9~\mathrm{MeV}, &{}\quad m_s \simeq 93~\mathrm{MeV}, &{}\quad m_b\simeq 4.6~\mathrm{GeV}, \end{array}\\&\quad V_\mathrm{CKM}\simeq \left( \begin{array}{ccc} 0.97 &{}\quad 0.24 &{}\quad 0.0042 \\ -0.24 &{}\quad 0.97 &{}\quad -0.0056 \\ -0.0054 &{}\quad 0.0043 &{}\quad 1.0 \\ \end{array}\right) . \end{aligned}$$

Eq. (23) requires $f_a> 2.2\times 10^{11}$ GeV.

In the example (iii), we assume the same values for $\epsilon$ and $y^u_{ij}$ as the ones in the example (ii), and the coupling constants $y^d_{ij}$ are taken as

$$\begin{aligned} y_{11}^d= & {} y_{21}^d=y_{31}^d=\epsilon , \quad y_{22}^d=0.1, \quad y_{23}^d=-0.03, \\ y_{32}^d= & {} y_{33}^d=0.26.\quad y_{12}^d= y_{13}^d=60. \end{aligned}$$

Since $\mathcal{M}_u$ and $\mathcal{M}_d$ take the same form as the ones of the example (ii), both the quark mass eigenvalues and the CKM matrix take the same values as the ones in the example (ii). The number of independent parameters used here can be identified as eight. The bound on $f_a$ is estimated as $f_a> 1.3\times 10^{10}$ GeV, which is one order of magnitude smaller than the previous two examples.

These examples show that the constraint on $f_a$ coming from the flavor dependent PQ charge assignment is much stronger than the astrophysical constraint as suggested in [51,52,53]. However, it can be consistent with the cosmological upper bound of $f_a$ even if the realization of realistic values for the quark mass eigenvalues and the CKM mixing is imposed. On the other hand, the consistency of this constraint with the upper bound of $f_a$ imposed by the goodness of the PQ symmetry could depend largely on the PQ charge assignment. In fact, although the consistency is complete in the example (iii), the situation is marginal in the examples (i) and (ii). In the example (iii), the scenario is found to work well even if serious fine tuning of the coupling constants $y_{ij}^f$ is not adopted. The obtained results seem to reproduce the data listed in [40] rather well although the number of independent parameters are smaller than the number of physical observables in the quark sector.

3.2 Leptonic sector

In this model, the neutrino mass generation is forbidden at a tree-level by $U(1)_{PQ}$ even after the breaking of $U(1)_{g}\times U(1)_{FN}$, since $\eta$ is assumed to have no VEV, However, since both the right-handed neutrino masses and the mass difference between the neutral components of $\eta$ are induced after the breaking of $U(1)_{PQ}$ as found form Eqs. (10) and (12), small neutrino masses are generated radiatively in the same way as the original scotogenic model through a one-loop diagram which is shown in Fig. 1. If we apply the PQ charge given in Table 3 to Eq. (10), the Dirac mass matrix for charged leptons which is defined by ${\bar{e}}_L\mathcal{M}_e e_R$ and the Majorana mass matrix $\mathcal{M}_N$ for right-handed neutrinos $N_{R_i}$ are expressed as

$$\begin{aligned} \mathcal{M}_e= & {} \left( \begin{array}{ccc} h_{11}^e~\epsilon ^5 &{}\quad h_{12}^e~\epsilon ^4 &{}\quad h_{13}^e~\epsilon ^4 \\ h_{21}^e~\epsilon ^3 &{}\quad h_{22}^e~\epsilon ^2 &{} \quad h_{23}^e~\epsilon ^2 \\ h_{31}^e~\epsilon ^3 &{}\quad h_{32}^e~\epsilon ^2 &{}\quad h_{33}^e~\epsilon ^2 \\ \end{array}\right) \langle {\tilde{\phi }}\rangle ,\nonumber \\ \mathcal{M}_N= & {} \left( \begin{array}{ccc} h_{11}^N~\epsilon ^3 &{}\quad h_{12}^N\epsilon ^2 &{}\quad h_{13}^N~\epsilon ^3 \\ h_{12}^N\epsilon ^2 &{}\quad h_{22}^N~\epsilon ^3 &{}\quad h_{23}^N~\epsilon ^2 \\ h_{13}^N~\epsilon ^3 &{} \quad h_{23}^N~\epsilon ^2 &{} \quad h_{33}^N\epsilon ^3 \\ \end{array}\right) M_*. \end{aligned}$$

(24)

In the mass matrix $\mathcal{M}_N$, we take into account that the allowed operators start from nonrenormalizable ones.

Fig. 1

The one-loop diagram for the neutrino mass generation, in which $\eta _R$ and $\eta _I$ are a real and an imaginary part of the neutral component of $\eta$, respectively

This right-handed neutrino mass matrix $\mathcal{M}_N$ suggests that three mass eigenvalues tend to take the same order values. If we assume the values of the Yukawa coupling constants $h_{ij}^N$ appropriately, the eigenvalues of $\mathcal{M}_N$ can be fixed, for example, as⁶

$$\begin{aligned} M_1\simeq & {} 1.0\times 10^8~\mathrm{GeV}, \qquad M_2\simeq 4.2\times 10^8~\mathrm{GeV},\nonumber \\ M_3\simeq & {} 1.9\times 10^9~\mathrm{GeV}, \end{aligned}$$

(25)

where we assume $M_*=10^{12}$ GeV. The neutrino mass generated through a one-loop diagram can be approximately written as

$$\begin{aligned} (\mathcal{M}_\nu )_{ij}=\sum _{k=1}^3 {\tilde{h}}_{ik}^\nu {\tilde{h}}_{j k}^\nu \Lambda _k, \qquad \Lambda _k\simeq \frac{{\tilde{\lambda }}_5\langle \phi \rangle ^2}{8\pi ^2M_k} \ln \frac{M_k^2}{{\bar{M}}_\eta ^2}, \end{aligned}$$

(26)

where we use $M_{\eta _{R,I}}^2\gg |M_{\eta _R}^2-M_{\eta _I}^2|$, which is noted in the previous part. $M_k$ is a mass eigenvalue of the right-handed neutrino and ${\bar{M}}_\eta ^2=\tilde{m}_\eta ^2+\left( {\tilde{\lambda }}_3+\lambda _4\right) \langle \phi \rangle ^2$. In this formula, ${\tilde{h}}_{ij}^\nu$ and ${\tilde{\lambda }}_5$ are defined by using $\epsilon$ as $\tilde{h}_{ij}^\nu =h_{ij}^\nu \epsilon ^{|n_{ij}^\nu |}$ and ${\tilde{\lambda }}_5=\lambda _5\epsilon$.

Here, it may be useful to note that the present $\mathcal{M}_\nu$ has the interesting flavor structure consistent with tri-bimaximal mixing if $\mathcal{M}_N$ is diagonal. In fact, if the effective neutrino Yukawa coupling constants defined above satisfy the relation

$$\begin{aligned} {\tilde{h}}_{1j}^\nu= & {} 0, \quad {\tilde{h}}_{2j}^\nu = {\tilde{h}}_{3j}^\nu \equiv h_j \quad (j=1,2);\nonumber \\ {\tilde{h}}_{13}^\nu= & {} {\tilde{h}}_{23}^\nu =-{\tilde{h}}_{33}^\nu \equiv h_3, \end{aligned}$$

(27)

$\mathcal{M}_\nu$ is found to be diagonalized by a tri-bimaximal MNS matrix [70, 87]. The mass eigenvalues are derived as

$$\begin{aligned} m_{\nu _1}= & {} 0, \qquad m_{\nu _2}= 3|h_3|^2\Lambda _3, \nonumber \\ m_{\nu _3}= & {} 2\left[ |h_1|^4\Lambda _1^2+|h_2|^4\Lambda _2^2\right. \nonumber \\&\left. +2|h_1|^2|h_2|^2\Lambda _1\Lambda _2\cos 2(\theta _1-\theta _2) \right] ^{1/2}, \end{aligned}$$

(28)

where $\theta _j=\mathrm{arg}(h_j)$. On the other hand, if we note that the neutrino Yukawa interactions in Eq. (10) take the form

$$\begin{aligned} \eta ^0~({\bar{\nu }}_{L1}, {\bar{\nu }}_{L2}, \bar{\nu }_{L3})\left( \begin{array}{ccc} h_{11}^\nu ~\epsilon ^4 &{}\quad h_{12}^\nu ~\epsilon ^3 &{}\quad h_{13}^\nu ~\epsilon ^2 \\ h_{21}^\nu ~\epsilon ^2 &{}\quad h_{22}^\nu ~\epsilon &{}\quad h_{23}^\nu \\ h_{31}^\nu ~\epsilon ^2 &{}\quad h_{32}^\nu ~\epsilon &{}\quad h_{33}^\nu \\ \end{array}\right) \left( \begin{array}{c} N_{R1}\\ N_{R2} \\ N_{R3}\\ \end{array}\right) , \nonumber \\ \end{aligned}$$

(29)

the above relation (27) among the effective coupling constants ${\tilde{h}}^\nu _{ij}$ is found to be realized just by assuming the same relation for $h_{ij}^\nu$ without changing the suppression structure due to $\epsilon$. This means that the present PQ charge assignment is consistent with the tri-bimaximal flavor structure approximately. However, unfortunately, the present right-handed neutrino mass matrix $\mathcal{M}_N$ is not diagonal. Although this flavor structure is lost after $\mathcal{M}_N$ is diagonalized, this knowledge can be useful to find suitable neutrino Yukawa couplings $h_{ij}^\nu$ referring to the previous study in [71, 72].

In order to see the resulting flavor structure in the leptonic sector, we take $\epsilon =0.07$, ${\tilde{m}}_\eta =1$ TeV, and ${\tilde{\lambda }}_5=5.4\times 10^{-3}$ which corresponds to $\lambda _5\simeq 0.08$. The charged lepton coupling constants $h_{ij}^e$ and the neutrino Yukawa coupling constants $h_{ij}^\nu$ are fixed as

$$\begin{aligned} h_{11}^e= & {} h_{21}^e=h_{31}^e=1,\quad h_{32}^e=h_{33}^e=1.47, \nonumber \\ h_{12}^e= & {} 0.82,\quad h_{22}^e=0.17, \nonumber \\ h_{13}^e= & {} 0.4,\quad h_{23}^e=0.02, \nonumber \\ h_{11}^\nu= & {} h_{12}^\nu =1, \quad h_{13}^\nu =0.6, \nonumber \\ h_{21}^\nu= & {} h_{31}^\nu =6.5\times 10^{-3}, \quad h_{22}^\nu =0.23, \nonumber \\ h_{32}^\nu= & {} 0.184, \quad h_{23}^\nu =0, \quad h_{33}^\nu =7.0\times 10^{-3}. \end{aligned}$$

(30)

For this parameter set, we can obtain

$$\begin{aligned}&\begin{array}{lll} m_{\nu _1}\simeq 0~\mathrm{MeV}, &{} m_{\nu _2}\simeq 8.5\times 10^{-3}~\mathrm{eV}, &{} m_{\nu _3}\simeq 5.2\times 10^{-2}~\mathrm{eV}, \\ m_e=0.51~\mathrm{MeV}, &{} m_\mu =106~\mathrm{MeV}, &{} m_\tau =1.78~\mathrm{GeV}, \end{array}\\&\quad V_\mathrm{MNS}\simeq \left( \begin{array}{ccc} 0.87 &{}\quad -0.46 &{}\quad -0.14 \\ -0.29 &{}\quad 0.74 &{}\quad 0.60 \\ 0.38 &{}\quad -0.48 &{}\quad 0.78 \\ \end{array}\right) . \end{aligned}$$

The squared mass differences required by the neutrino oscillation data could be explained by these values. The MNS matrix is shifted from the tri-bimaximal mixing and $V_{e3}$ takes a favorable value. Although the Yukawa coupling constants have to be tuned within the similar order, the required tuning is not serious one. The suppression due to the PQ symmetry can be considered to work rather well in the leptonic sector also.

Here, we should comment on a reason why ${\tilde{h}}_{i1}^\nu$ is fixed at the small values of $O(10^{-4})$. It is not for the neutrino mass generation but for the thermal leptogenesis [88]. As is known generally and found also from the present neutrino mass formula (28), the neutrino masses required by the neutrino oscillation data could be derived by two right-handed neutrinos only. It means that the mass and the neutrino Yukawa couplings of a remaining right-handed neutrino could be free from the neutrino oscillation data as long as its contribution to the neutrino mass is negligible. As found from Eq. (28), such a situation can be realized for $|h_1|^2\Lambda _1 \ll |h_2|^2\Lambda _2$ in the present parameter setting. This is good for the thermal leptogenesis since an appropriately small neutrino Yukawa coupling constant $\tilde{h}_{i1}^\nu$ makes both effective out-of-equilibrium decay of $N_{R_1}$ and sufficient thermal production of the right-handed neutrino $N_{R_1}$ possible.

3.3 Leptogenesis and DM abundance

In this part, we proceed to the study of other phenomenological subjects such as leptogenesis and DM abundance. Our main interest is what kind of results are obtained for these problems if we use the parameters assumed in the previous discussion. Since the present model is defined even at larger scales than the PQ symmetry breaking scale, we can also examine the consistency of the used value for $\epsilon$ with the assumed symmetry breaking pattern in (3).

Fig. 2

Left panel: example points in the $({\tilde{\lambda }}_3, \lambda _4)$ plane are plotted by the crosses, at which the $\eta _R$ relics can explain the DM abundance $\Omega h^2=0.12$. ${\tilde{m}}_\eta ^2=1$ TeV and ${\tilde{\lambda }}_5=5.4\times 10^{-3}$ are assumed. The region above each line fixed by a listed value of ${\tilde{\lambda }}_2$ satisfies the last condition for the vacuum stability in (15). Right panel: a cut-off scale $\Lambda$ as a function of ${\tilde{\lambda }}_2$, which is fixed as a value at $M_Z$. Each line is plotted for four points marked by the crosses in the left panel where $\Omega h^2=0.12$ is satisfied

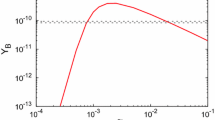
First, we discuss the leptogenesis in this model. If we use the parameters assumed in the leptonic sector, we can estimate baryon number asymmetry expected from the out-of-equilibrium decay of the thermal $N_1$ by solving the Boltzmann equation as done in [71, 72]. The previous analysis in the similar model [54, 55] shows that the required baryon number asymmetry could be generated for $M_1~{^>_\sim }~ 10^8$ GeV. Since this value of $M_1$ is somewhat smaller than the Davidson-Ibarra bound [89] in the ordinary thermal leptogenesis [90], the reheating temperature could take a lower value than the usually assumed one to yield the thermal $N_{R_1}$. This is crucial in the present model to forbid the thermal production of the extra colored fields $Q_{L,R}^{(i)}$ which cause dangerous relics as discussed in the previous part. If we assume the reheating temperature as $T_R \simeq M_1$, we find $Y_B\sim 5\times 10^{-10}$ for the parameters given in (25) and (30), where $Y_B$ is defined as $Y_B\equiv \frac{n_B}{s}$ by using the baryon number density $n_B$ and the entropy density s. In this calculation, we assume a maximal CP phase in the CP violation parameter $\varepsilon _1$ for the $N_{R_1}$ decay [90] and an initial condition $Y_{N_1}(T_R)=0$ at the reheating temperature $T_R$.⁷ Upper bound of the number density of the extra colored fermions $Q_{L,R}^{(i)}$ might be estimated at $T_R$ by assuming that they are in the thermal equilibrium. We find that the previously mentioned bound for $\frac{n_{Q^{(i)}}}{n_B}$ imposed by the search for the fractionally charged particles could be satisfied for $Q^{(3)}$, which has the smallest mass of $O(\epsilon ^2 M_*)$ among the extra colored fermions. Thus, the leptogenesis could be evaded from the dangerous relic problem consistently.

Next, we address the DM abundance in this model. As mentioned before, the axion cannot be a dominant component of the DM in this scenario since the upper bound of the decay constant required by the goodness of the PQ symmetry is too small. However, the model has another DM candidate, that is, the lightest neutral component of $\eta$ which is stable because of $Z_2$ odd parity. Its relic abundance is known to be controlled by the parameters ${\tilde{\lambda }}_3$ and $\lambda _4$ in Eq. (12) since the coannihilation among the components of $\eta$ is effective in case of ${\tilde{m}}_\eta =O(1)$ TeV [71, 72]. In the left panel of Fig. 2, we plot typical points in the $({\tilde{\lambda }}_3, \lambda _4)$ plane, where the required DM abundance $\Omega _\mathrm{DM}h^2=0.12$ is realized by the relics of $\eta _R$. In this calculation, we use ${\tilde{m}}_\eta =1$ TeV and ${\tilde{\lambda }}_5=5.4\times 10^{-3}$ which are assumed in the previous part. In this panel, we take into account the condition $\lambda _4<0$ which is necessary for a neutral component of $\eta$ is lighter than the charged ones. If we use the tree level Higgs mass formula $m_{h^0}^2=4{\tilde{\lambda }}_1\langle \phi \rangle ^2$, we find ${\tilde{\lambda }}_1\simeq 0.13$ for $m_{h^0}=125$ GeV. This allows us to plot the last one in the stability condition (15) as a straight line in the same plane for a fixed ${\tilde{\lambda }}_2$. The points contained in the region above a straight line satisfy this condition for a fixed ${\tilde{\lambda }}_2$. Although the required DM abundance can be obtained for negative values of ${\tilde{\lambda }}_3$, such cases contradict with the condition for ${\tilde{\lambda }}_3$ given in Eq. (15). The figure shows that ${\tilde{\lambda }}_3$ and/or $|\lambda _4|$ should take rather large values to realize the required DM abundance. Since they are used as the initial values at the weak scale, RG evolution of the scalar quartic couplings ${\tilde{\lambda }}_i$ could be largely affected. In that case, vacuum stability and perturbativity of the model could give constraints on the assumed symmetry breaking scale $M_*$, which should be smaller than a violation scale of the vacuum stability and the perturbativity. We focus our study on this point in the next part.

3.4 Symmetry breaking pattern and a cut-off scale

We assume $\epsilon =0.07$ and $M_*=10^{12}$ GeV in the previous part, which means $\langle S\rangle = 7\times 10^{10}$ GeV. It is crucial for the consistency of the scenario whether $M_*$ is smaller than a scale where either the vacuum stability or the perturbativity is violated.⁸ We examine this problem by using the values of ${\tilde{\lambda }}_3$ and $\lambda _4$ for which the required DM abundance is realized. Since the violation of the perturbativity is considered to suggest a scale for the applicability of the model defined by Eq. (11), it should be larger than $M_*$. This allows us to judge whether the $\epsilon$ value assumed in the above phenomenological study is consistent with the assumed symmetry breaking pattern.

One-loop $\beta$-functions for the scalar quartic coupling constants in the effective model at energy regions below $M_S(\equiv \langle S\rangle )$ are given as follows [98, 99],

$$\begin{aligned} \beta _{{\tilde{\lambda }}_1}= & {} 24{\tilde{\lambda }}_1^2 +{\tilde{\lambda }}_3^2+({\tilde{\lambda }}_3+\lambda _4)^2 +{\tilde{\lambda }}_5^2 \nonumber \\&+\frac{3}{8}\left( 3g^4+g^{\prime 4}+2g^2g^{\prime 2}\right) \nonumber \\&-3{\tilde{\lambda }}_1\left( 3g^2+g^{\prime 2}-4h_t^2\right) -6h_t^4, \nonumber \\ \beta _{{\tilde{\lambda }}_2}= & {} 24{\tilde{\lambda }}_2^2+{\tilde{\lambda }}_3^2 +({\tilde{\lambda }}_3+\lambda _4)^2+{\tilde{\lambda }}_5^2 \nonumber \\&+\frac{3}{8}\left( 3g^4+g^{\prime 4}+2g^2g^{\prime 2}\right) -3{\tilde{\lambda }}_2\left( 3g^2+g^{\prime 2}\right) , \nonumber \\ \beta _{{\tilde{\lambda }}_3}= & {} 2({\tilde{\lambda }}_1+{\tilde{\lambda }}_2) (6{\tilde{\lambda }}_3+2\lambda _4) +4{\tilde{\lambda }}_3^2+2\lambda _4^2+2{\tilde{\lambda }}_5^2 \nonumber \\&+\frac{3}{4}\left( 3g^4+g^{\prime 4}-2g^2g^{\prime 2}\right) -3{\tilde{\lambda }}_3\left( 3g^2+g^{\prime 2}-2h_t^2\right) , \nonumber \\ \beta _{\lambda _4}= & {} 4({\tilde{\lambda }}_1+{\tilde{\lambda }}_2)\lambda _4 +8{\tilde{\lambda }}_3\lambda _4+4\lambda _4^2 +8{\tilde{\lambda }}_5^2\nonumber \\&+3g^2g^{\prime 2} -3\lambda _4\left( 3g^2+g^{\prime 2}-2h_t^2\right) , \nonumber \\ \beta _{{\tilde{\lambda }}_5}= & {} 4({\tilde{\lambda }}_1+{\tilde{\lambda }}_2){\tilde{\lambda }}_5 +8{\tilde{\lambda }}_3{\tilde{\lambda }}_5+12\lambda _4{\tilde{\lambda }}_5\nonumber \\&-3{\tilde{\lambda }}_5\left( 3g^2+g^{\prime 2}-2h_t^2\right) , \end{aligned}$$

(31)

where $\beta _\lambda$ is defined as $\beta _\lambda =16\pi ^2\mu \frac{d\lambda }{d\mu }$ and the top Yukawa coupling is only taken into account among the Yukawa interactions. In these equations, the positive contributions of ${\tilde{\lambda }}_3$ and $\lambda _4$ to the $\beta$-functions of ${\tilde{\lambda }}_{1,2}$ are found to tend to save the model from violating the first condition in Eq. (15). On the other hand, the same contributions of ${\tilde{\lambda }}_3$ and $\lambda _4$ could induce the violation of the perturbativity of the model at a rather low energy scale since they give large positive contributions to $\beta _{{\tilde{\lambda }}_1}$, $\beta _{{\tilde{\lambda }}_2}$ and $\beta _{{\tilde{\lambda }}_3}$. If we identify an applicable scale of the model defined by Eq. (11) with a scale $\Lambda$ where any of the perturbativity conditions $\lambda _i<4\pi$ and $\kappa _i<4\pi$ is violated, $M_*<\Lambda$ should be satisfied. If $M_*$ is larger than $\Lambda$, the consistency of the scenario is lost.

We analyze this issue by solving the above one-loop RGEs at $\mu <M_S$ and also the ones which are given in [54] at $\mu >M_S$. The quartic couplings ${\tilde{\lambda }}_i$ in the tree-level potential at the energy scale $\mu <M_S$ are connected with the ones $\lambda _i$ at $\mu >M_S$ through Eq. (14). Since the masses of the right-handed neutrinos $N_{R_i}$ are considered to be of $O(10^{8-9})$ GeV, they decouple at the scale $\mu<M_i~{^<_\sim }~O(M_S)$ to be irrelevant to the RGEs there. On the other hand, the mass of the colored fields $Q_{L,R}^{(i)}$ are required to be much heavier than $N_{R_i}$ as discussed before, they can contribute mainly to the $\beta$-functions of the $SU(3)_c$ gauge coupling at the scales larger than their masses.

The free parameters in the scalar potential of the low energy effective model (12) are ${\tilde{\lambda }}_1,~{\tilde{\lambda }}_2,~{\tilde{\lambda }}_3,~\lambda _4$ and ${\tilde{\lambda }}_5$ at $M_Z$.⁹ ${\tilde{\lambda }}_1$ is fixed at ${\tilde{\lambda }}_1\simeq 0.13$ from the Higgs mass. Both ${\tilde{\lambda }}_3$ and $\lambda _4$ are fixed at the values determined through the DM relic abundance which are shown in the left panel of Fig. 2. ${\tilde{\lambda }}_5$ is fixed at ${\tilde{\lambda }}_5=5.4\times 10^{-3}$ which is used in the discussion of the neutrino mass and the leptogenesis. Thus, an only free parameter is ${\tilde{\lambda }}_2$. If we solve the RGEs varying the value of ${\tilde{\lambda }}_2$, we can search $\Lambda$ checking the vacuum stability and the perturbativity for each ${\tilde{\lambda }}_2$.

In the right panel of Fig. 2, we plot $\Lambda$ as a function of ${\tilde{\lambda }}_2$ for four sets of $({\tilde{\lambda }}_3,~\lambda _4)$ which are shown by the crosses in the left panel of Fig. 2. An end point found in a line for $(0.5,-0.875)$ represents a value of ${\tilde{\lambda }}_2$ for which the vacuum stability is violated before reaching a scale of the perturbativity violation. This figure shows that $\Lambda$ could be high enough to be consistent with an assumed value of $\epsilon$ as long as ${\tilde{\lambda }}_2$ takes a suitable value. The present scenario for the symmetry braking could be consistent with the explanation presented here for various phenomenological subjects. The simultaneous explanation of the neutrino masses and the DM abundance could be preserved in this extended model in the same way as in the original scotogenic model with the heavy right-handed neutrinos.

4 Summary

We have proposed a model which could solve the strong CP problem based on the PQ mechanism. The model is constructed to escape the domain wall problem and to keep the goodness of the PQ symmetry against the breaking due to the gravity effect. For this purpose, we introduce a local $U(1)_g$ symmetry and also a flavor dependent global $U(1)_{FN}$ symmetry. The PQ symmetry is induced from these as their linear combination through their spontaneous breaking. The resulting PQ symmetry becomes flavor dependent to realize $N_{DW}=1$. Its flavor dependence causes the hierarchical masses and the flavor mixing for quarks and leptons after the PQ symmetry breaking. The observed masses and flavor mixing seem to be obtained in this framework without serious fine tuning for the coupling constants of the nonrenormalizable operators. Moreover, after the $U(1)_{PQ}$ symmetry breaking, its subgroup $Z_2$ remains as a remnant exact symmetry at least in the leptonic sector. So, the leptonic part of the model is reduced to the well-known scotogenic model for the neutrino masses and the DM, in which the neutrino masses are generated through one-loop radiative effects and the DM abundance can be explained as the thermal relics of a neutral component of the extra doublet scalar.

The model can explain the cosmological baryon number asymmetry through the out-of-equilibrium decay of a right-handed neutrino in the same way as the ordinary thermal leptogenesis in the tree-level seesaw model. However, since the lower bound for the right-handed neutrino mass is relaxed in this model, the required reheating temperature could be low enough not to restore the PQ symmetry and also not to yield the heavy colored particles in a dangerous amount in the thermal plasma. We also show that these features could be consistently realized for suitable parameter sets. Although we do not address inflation of the Universe in this study, it might be introduced into the model in a similar way to the one discussed in [100,101,102,103,104]. Since the simple extension discussed here can relate the strong CP problem to the flavor structure of quarks and leptons, and the origin of neutrino masses and DM, it may be promising to consider an extended SM in this direction further.