Dark matter stability and one-loop neutrino mass generation based on Peccei–Quinn symmetry

Abstract

We propose a model which is a simple extension of the KSVZ invisible axion model with an inert doublet scalar. Peccei–Quinn symmetry forbids tree-level neutrino mass generation and its remnant $Z_2$ symmetry guarantees dark matter stability. The neutrino masses are generated by one-loop effects as a result of the breaking of Peccei–Quinn symmetry through a nonrenormalizable interaction. Although the low energy effective model coincides with an original scotogenic model which contains right-handed neutrinos with large masses, it is free from the strong CP problem.

1 Introduction

The standard model (SM) has been confirmed by the discovery of the Higgs scalar [1, 2]. However, it is now considered to be extended to explain several experimental and observational data such as neutrino masses and mixings [3,4,5,6,7,8,9,10], and dark matter (DM) [11, 12]. Strong CP problem is also one of such problems suggested by an experimental bound of the electric dipole moment of a neutron [13, 14]. Invisible axion models are known to give a simple and interesting solution to it [15,16,17,18]. The KSVZ model, which is one of such realizations, is an extension of the SM by a complex singlet scalar and a pair of colored fermions. It has a global U(1) symmetry, which is violated only by the QCD anomaly and plays a role of Peccei–Quinn (PQ) symmetry [19, 20]. If the spontaneous breaking of this $U(1)_{PQ}$ symmetry occurs, a pseudo Nambu–Goldstone boson associated to this breaking called axion appears to solve the strong CP problem [21, 22]. If the axion decay constant $f_a$ is large enough such as $10^9~\mathrm{GeV}<f_a<10^{12}~\mathrm{GeV}$ due to a vacuum expectation value (VEV) of the singlet scalar, the axion mass is very small and its coupling is extremely weak so as not to cause any contradiction with experiments and astrophysical observations [23,24,25].

On the other hand, the $U(1)_{PQ}$ breaking is known to cause N degenerate minima for the axion potential due to the QCD anomaly depending on both the field contents and the PQ charge assignment for them. As a result, the model is generally annoyed by the dangerous production of topologically stable domain walls [26]. It can be escapable only for $N=1$ unless one consider the domain wall free universe brought about by inflation. If a certain subgroup of $U(1)_{\mathrm{PQ}}$ remains as a discrete symmetry broken only by the QCD anomaly in a model with $N=1$, it could present an interesting scenario in relation to the DM physics at the low energy regions.¹

In this paper, we consider such a possibility in an extension of the KSVZ model, in which an inert doublet scalar and three right-handed neutrinos are added. The low energy effective model obtained from it after the breakdown of the $U(1)_{PQ}$ symmetry is reduced to the original scotogenic neutrino mass model with an effective $Z_2$ symmetry [30]. This $Z_2$ symmetry could guarantee the stability of a lightest neutral component of the inert doublet scalar to give a DM candidate. The neutrino masses are generated through a one-loop effect as a result of the $U(1)_{PQ}$ breaking. The relevant diagram is caused by both right-handed neutrinos and a nonrenormalizable interaction between the inert doublet scalar and the ordinary Higgs doublet. The model might be recognized as a well motivated simple framework at high energy regions for the original scotogenic model.

The remaining parts are organized as follows. In the next section, we introduce a model by fixing charge assignment of $U(1)_{PQ}$ to the field contents. We discuss basic features of the model such as remnant effective symmetry, scalar mass spectrum, vacuum stability and so on. In Sect. 3, phenomenological features such as neutrino mass generation, leptogenesis and DM abundance in this model are discussed. The consistency of the scenario is also studied from a viewpoint of the vacuum stability and a cut-off scale of the model. We summarize the paper in Sect. 4.

2 An extension of the KSVZ model

The KSVZ model is constructed by introducing a singlet complex scalar S and a vector-like colored fermions $(D_L, D_R)$ to the SM [15, 16]. We assume $D_{L,R}$ as triplets of the color SU(3). Although they are $SU(2)_L$ singlets, they could have a suitable weak hypercharge Y, in general. This point is crucial for phenomenological consistency of the model as discussed below. The model has a global $U(1)_{PQ}$ symmetry and its charge is assigned to S and $D_{L,R}$, but it is not assigned to the SM contents. We assume the existence of a gauge invariant Yukawa coupling $y_DS\bar{D}_LD_R$ so that the PQ mechanism could work to solve the strong CP problem. This requires that the PQ charge X of these new ingredients should satisfy $X_S=X_{D_L}-X_{D_R}$. On the other hand, this symmetry should be chiral to have the QCD anomaly and $X_{D_L}\not =X_{D_R}$ is satisfied. Thus, this $U(1)_{PQ}$ is spontaneously broken through the VEV of S.

The $U(1)_{PQ}$ transformation $D_{L,R}\rightarrow e^{iX_{D_{L,R}}\alpha }D_{L,R}$ for the colored fermions $D_{L,R}$ shifts the QCD $\theta$ parameter through the anomaly as [13, 14, 26]

$$\begin{aligned} \theta _{\mathrm{QCD}}\rightarrow \theta _\mathrm{QCD}-\frac{1}{2}(X_{D_R}-X_{D_L})\alpha . \end{aligned}$$

(1)

Since $\theta _{\mathrm{QCD}}$ has a period $2\pi$, the model is invariant for $\alpha =\frac{2\pi k}{N}$ where $N\equiv \frac{1}{2}|X_{D_R}-X_{D_L}|$ is an integer and $k=0,1,\ldots ,N-1$. This means that the model could have a discrete symmetry $Z_N$ after taking account of the QCD anomaly.² If we assign the $U(1)_{PQ}$ charge S as $X_S=2$, the model has $N=1$ and no degenerate minima in the axion potential. Thus, the model has no domain wall problem as is well known.³ Here, we note that an effective $Z_2$ symmetry could remain after the symmetry breaking due to $\langle S\rangle \not =0$ although it is violated by the QCD anomaly. Since the SM contents are supposed to have no PQ charge, it could play an important role in the leptonic sector of the model to guarantee the stability of the lightest $Z_2$ odd field in that sector, which could be DM.

If both $D_L$ and $D_R$ cannot couple with quarks, which occurs in case $Y(D_{L,R})=0$ for example, they are stable and then its relic abundance has to be smaller than the DM abundance [32]. Even if its relic abundance satisfies such a condition, the existence of the fractionally charged D hadrons is generally forbidden by the present bound obtained from the search of fractionally charged states. On the other hand, if we assign $Y=-\frac{1}{3}$ or $\frac{2}{3}$ to $D_{L,R}$, all the D hadrons can have integer charge. In that case, the D relic abundance will restrict the D mass into a narrow range such as $m_D~{^>_\sim }~1$ TeV [32]. Moreover, they are allowed to couple with quarks through a renormalizable Yukawa interaction as long as their PQ charge is zero. For example, using the left handed quark doublet $q_L$ and the Higgs doublet $\phi$ or ${{\tilde{\phi }}}(\equiv i\tau _2\phi ^*)$, the coupling ${{\tilde{\phi }}}{{\bar{q}}}_LD_R$ is allowed for $D_R$ with $X=0$ and $Y=-\frac{1}{3}$ and also $\phi {{\bar{q}}}_L D_R$ for $D_R$ with $X=0$ and $Y=\frac{2}{3}$. In these cases, $D_R$ decays to the SM fields through these couplings. $D_L$ can also decay via the mass mixing with $D_R$ induced by the coupling $y_DS{{\bar{D}}}_LD_R$ through $\langle S\rangle \not =0$. As a result, the mass $m_D$ has no constraint other than the bound obtained through the accelerator experiments. Anyway, in the model where the PQ charge is assigned as discussed above, the strong CP problem could be solved without inducing any cosmological and astrophysical difficulty, as long as the symmetry breaking scale satisfies $10^9~\mathrm{GeV}<\langle S\rangle <10^{12}~\mathrm{GeV}$.

Now, we consider a modification of this model by introducing an inert doublet scalar $\eta$ and three right-handed neutrinos $N_i$. The PQ charge assignment of the fields contained in the model is shown in Table 1. Invariant terms under the assumed symmetry for the Yukawa couplings and the scalar potential of the relevant fields are summarized as

$$\begin{aligned}&-{{{\mathcal {L}}}}_y=y_DS{{\bar{D}}}_LD_R + h_D{{\bar{q}}}_L{{\tilde{\phi }}} D_R + y_iS\bar{N}^c_iN_i\nonumber \\&\quad +\,h_{\alpha i}{{\bar{\ell }}}_\alpha \eta N_i +\mathrm{h.c.}, \nonumber \\&V=m_S^2S^\dagger S+\kappa _1(S^\dagger S)^2+\kappa _2(S^\dagger S)(\phi ^\dagger \phi ) +\kappa _3(S^\dagger S)(\eta ^\dagger \eta ) \nonumber \\&\quad +\,m_\eta ^2\eta ^\dagger \eta +m_\phi ^2\phi ^\dagger \phi +\lambda _1(\phi ^\dagger \phi )^2 +\lambda _2(\eta ^\dagger \eta )^2\nonumber \\&\quad +\,\lambda _3(\phi ^\dagger \phi )(\eta ^\dagger \eta ) +\lambda _4(\phi ^\dagger \eta )(\eta ^\dagger \phi ) \nonumber \\&\quad +\,\frac{\lambda _5}{2}\left[ \frac{S}{M_*}(\eta ^\dagger \phi )^2 +\mathrm{h.c.}\right] , \end{aligned}$$

(2)

where $\lambda _5$ is taken to be real and $M_*$ is a cut-off scale of the model. The quark generation index is abbreviated in the Yukawa coupling $h_D$. We find that V given in Eq. (2) is the most general scalar potential up to the dimension 5.

Table 1 The hypercharge Y and the $U(1)_{\mathrm{PQ}}$ charge X of new fields in the model. The SM contents are assumed to have no PQ charge

After the symmetry breaking due to $\langle S\rangle \not =0$, $D_{L,R}$, $N_i$ and S are found to get masses such as $m_D=y_D\langle S\rangle$, $M_i=y_i\langle S\rangle$ and $M_S^2=4\kappa _1\langle S\rangle ^2$, respectively. Since $D_{L,R}$ can decay to the SM fields through the second term in ${{{\mathcal {L}}}}_y$ as discussed above, there is no thermal relic of $D_{L,R}$ in the present Universe. The effective model at the scale below $M_S$ could be obtained by integrating out S [33]. This can be done by using the equation of motion for S. As its result, we obtain the corresponding effective model whose scalar potential of the light scalars can be written as

$$\begin{aligned} V_{\mathrm{eff}}= & {} {{\tilde{m}}}_\phi ^2(\phi ^\dagger \phi )+\tilde{m}_\eta ^2(\eta ^\dagger \eta ) +{{\tilde{\lambda }}}_1(\phi ^\dagger \phi )^2 +{{\tilde{\lambda }}}_2(\eta ^\dagger \eta )^2\nonumber \\&+\,{{\tilde{\lambda }}}_3(\phi ^\dagger \phi )(\eta ^\dagger \eta ) +\lambda _4(\phi ^\dagger \eta )(\eta ^\dagger \phi ) \nonumber \\&+\,\frac{{{\tilde{\lambda }}}_5}{2}\left[ (\phi ^\dagger \eta )^2 +\mathrm{h.c.}\right] , \end{aligned}$$

(3)

where we use the shifted parameters which are defined as

$$\begin{aligned} {{\tilde{\lambda }}}_1= & {} \lambda _1-\frac{\kappa _2^2}{4\kappa _1}, \qquad {{\tilde{\lambda }}}_2=\lambda _2-\frac{\kappa _3^2}{4\kappa _1}, \nonumber \\ {{\tilde{\lambda }}}_3= & {} \lambda _3-\frac{\kappa _2\kappa _3}{2\kappa _1}, \qquad {{\tilde{\lambda }}}_5=\lambda _5\frac{\langle S\rangle }{M_*}, \nonumber \\ {{\tilde{m}}}_\phi ^2= & {} m_\phi ^2+\kappa _2\langle S\rangle ^2, \qquad {{\tilde{m}}}_\eta ^2=m_\eta ^2+\kappa _3\langle S\rangle ^2. \end{aligned}$$

(4)

We note that the model contains the neutrino Yukawa couplings between heavy right-handed neutrinos and the inert doublet scalar as shown in the above ${{{\mathcal {L}}}}_y$.

Vacuum stability condition for the scalar potential $V_{\mathrm{eff}}$ in Eq. (3) is known to be given as [34,35,36]

$$\begin{aligned}&{{\tilde{\lambda }}}_1>0, \qquad {{\tilde{\lambda }}}_2>0, \qquad {{\tilde{\lambda }}}_3>-2\sqrt{{{\tilde{\lambda }}}_1{{\tilde{\lambda }}}_2}, \nonumber \\&{{\tilde{\lambda }}}_3+\lambda _4-|{{\tilde{\lambda }}}_5|> -2\sqrt{{{\tilde{\lambda }}}_1{{\tilde{\lambda }}}_2}, \end{aligned}$$

(5)

and these should be satisfied at the energy region $\mu <M_S$. On the other hand, at $M_S<\mu <M_*$, both the same conditions for $\lambda _{1,2,3}$ as Eq. (5) except for the last one and new conditions

$$\begin{aligned} \kappa _1>0, \qquad \kappa _2>-2\sqrt{\lambda _1\kappa _1}, \qquad \kappa _3>-2\sqrt{\lambda _2\kappa _1}, \end{aligned}$$

(6)

should be satisfied. The couplings in both regions should be connected through Eq. (4). We can examine whether these conditions could be satisfied or not by using one-loop renormalization group equations (RGEs). This is the subject studied later.

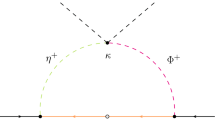
This effective model obtained after the spontaneous breaking of $U(1)_{PQ}$ is just the original scotogenic model [30].⁴ This model connects the neutrino mass generation with the DM existence. It has been extensively studied from various phenomenological view points [37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52]. In the present case, the right-handed neutrinos do not have their masses in a TeV region but they are considered to be much heavier. The coupling ${{\tilde{\lambda }}}_5$ which is crucial for the one-loop neutrino mass generation is derived from a nonrenormalizable term as a result of the PQ symmetry breaking. The model contains the inert doublet scalar $\eta$ which has odd parity of the remnant effective $Z_2$. It has charged components $\eta ^\pm$ and two neutral components $\eta _{R,I}$. Their mass eigenvalues can be expressed as

$$\begin{aligned} M_{\eta ^\pm }^2={{\tilde{m}}}_\eta ^2 +{{\tilde{\lambda }}}_3\langle \phi \rangle ^2, \quad M_{\eta _{R,I}}^2=\tilde{m}_\eta ^2+\left( {{\tilde{\lambda }}}_3+\lambda _4 \pm {{\tilde{\lambda }}}_5\right) \langle \phi \rangle ^2. \end{aligned}$$

(7)

We suppose ${{\tilde{m}}}_\eta =O(1)$ TeV although it requires fine tuning because of $|\langle S\rangle |\gg |\langle \phi \rangle |$. As a result of the effective $Z_2$ symmetry, the lightest one among the components of $\eta$ is stable to be a DM candidate if it is neutral. If it is supposed to be $\eta _R$, we find that this requires $\lambda _4<0$ and ${{\tilde{\lambda }}}_5<0$ as long as $|{{\tilde{\lambda }}}_5|\ll |\lambda _4|$ is satisfied. On the other hand, since ${{\tilde{m}}}_\eta ^2\gg \langle \phi \rangle ^2$ is satisfied in Eq. (7), the mass eigenvalues of the components $\eta$ are found to be degenerate enough so that the coannihilation processes among them are expected to be effective. This observation suggests that the abundance of $\eta _R$ could be suitably suppressed and then it could be a good DM candidate as the ordinary inert doublet model [53,54,55,56]. The charged states with the mass of O(1) TeV are also expected to be detected in the accelerator experiments.

3 Phenomenological features

3.1 Neutrino mass, leptogenesis and DM relic abundance

In this model, neutrino masses are forbidden at tree-level. However, since both the right-handed neutrino masses and the mass difference between $\eta _R$ and $\eta _I$ are induced after the $U(1)_{PQ}$ breaking, the small neutrino masses can be generated radiatively through one-loop diagrams in the same way as the original scotogenic model. Since $M_{\eta _{R,I}}^2\gg |M_{\eta _R}^2-M_{\eta _I}^2|$ is satisfied, the neutrino mass formula can be approximately written as

$$\begin{aligned} {{{\mathcal {M}}}}_{\alpha \beta }=\sum _i h_{\alpha i}h_{\beta i}\Lambda _i, \qquad \Lambda _i\simeq \frac{{{\tilde{\lambda }}}_5\langle \phi \rangle ^2}{8\pi ^2M_i} \ln \frac{M_i^2}{{{\bar{M}}}_\eta ^2}, \end{aligned}$$

(8)

where ${{\bar{M}}}_\eta ^2= {{\tilde{m}}}_\eta ^2 +\left( {{\tilde{\lambda }}}_3+\lambda _4\right) \langle \phi \rangle ^2$. In order to take account of the constraints from the neutrino oscillation data in the analysis, we may fix the flavor structure of neutrino Yukawa couplings $h_{\alpha i}$ at the one which induces the tri-bimaximal mixing [42, 43]⁵

$$\begin{aligned} h_{ej}= & {} 0, \quad h_{\mu j}=h_{\tau j}\equiv h_j \quad (j=1,2); \nonumber \\ h_{e3}= & {} h_{\mu 3}=-h_{\tau 3}\equiv h_3, \end{aligned}$$

(9)

where the charged lepton mass matrix is assumed to be diagonal. In that case, the mass eigenvalues are estimated as

$$\begin{aligned} m_1&=0, \qquad m_2= 3|h_3|^2\Lambda _3, \nonumber \\ m_3&=2\Big [|h_1|^4\Lambda _1^2+|h_2|^4\Lambda _2^2\nonumber \\&\quad + 2|h_1|^2|h_2|^2\Lambda _1\Lambda _2\cos 2(\theta _1-\theta _2) \Big ]^{1/2}, \end{aligned}$$

(10)

where $\theta _j=\mathrm{arg}(h_j)$.

As is known generally and found also from this mass formula, neutrino masses could be determined only by two right-handed neutrinos. It means that the mass and neutrino Yukawa couplings of a remaining right-handed neutrino could be free from the neutrino oscillation data as long as its contribution to the neutrino mass is negligible. In Eq. (10), such a situation can be realized for $|h_1|^2\Lambda _1 \ll |h_2|^2\Lambda _2$. This is good for the thermal leptogenesis [57] since a sufficiently small neutrino Yukawa coupling $h_1$ makes the out-of-equilibrium decay of the right-handed neutrino $N_1$ possible.⁶ We find that the squared mass differences required by the neutrino oscillation data could be explained if we fix the parameters relevant to the neutrino masses, for example, as

$$\begin{aligned} M_1= & {} 10^8~\mathrm{GeV}, \qquad M_2=4\times 10^8~\mathrm{GeV},\nonumber \\ M_3= & {} 10^9\mathrm{GeV}, \nonumber \\ |h_1|= & {} 10^{-4.5}, \qquad |h_2|\simeq 7.2\times 10^{-4}{{\tilde{\lambda }}}_5^{-0.5}, \nonumber \\ |h_3|\simeq & {} 3.1\times 10^{-4}{{\tilde{\lambda }}}_5^{-0.5}, \end{aligned}$$

(11)

for ${{\tilde{m}}}_\eta =1$ TeV. Using these values, we can estimate the expected baryon number asymmetry through the out-of-equilibrium decay of the thermal $N_1$ by solving the Boltzmann equation as done in [45, 46]. The numerical analysis shows that the required baryon number asymmetry could be generated for $M_1~{^>_\sim }~10^8$ GeV, which is somewhat smaller than the Davidson–Ibarra bound [61] in the ordinary thermal leptogenesis. In case of the parameter set given in (11), we find $Y_B\left( \equiv \frac{n_B}{s}\right) =4.0\times 10^{-10}$ if we assume ${{\tilde{\lambda }}}_5=2.5\times 10^{-3}$ and a maximal CP phase in the CP violation parameter $\varepsilon$. In Fig. 1, we plot $Y_B$ as a function of ${{\tilde{\lambda }}}_5$. Its feature can be easily understood by taking account of Eq. (11). If ${{\tilde{\lambda }}}_5$ takes larger values, the neutrino Yukawa couplings become smaller to make the CP violation $\varepsilon$ in the $N_1$ decay smaller but also the washout of the generated lepton number asymmetry smaller. On the other hand, if ${{\tilde{\lambda }}}_5$ takes smaller values, the neutrino Yukawa couplings become larger to induce the reverse effects. This makes the required baryon number asymmetry be generated only for the ${{\tilde{\lambda }}}_5$ in the limited regions as found in this figure.

Fig. 1

Baryon number asymmetry $Y_B$ generated through the out-of-equilibrium decay of $N_1$. $Y_B$ is plotted as a function of ${{\tilde{\lambda }}}_5$ for the parameter set shown in Eq. (11), which can explain the neutrino mass differences required by the neutrino oscillation data. Horizontal dotted lines show the required value for $Y_B$

The relic abundance of $\eta _R$ is tuned to the observed value if the couplings ${{\tilde{\lambda }}}_3$ and $\lambda _4$ take suitable values. In fact, since ${{\tilde{m}}}_\eta$ is assumed to be of O(1) TeV in this scenario, the mass of each component of $\eta$ could be degenerate enough for wide range values of ${{\tilde{\lambda }}}_3$ and $\lambda _4$ as remarked at Eq. (7). This makes the coannihilation among them effective enough to reduce the $\eta _R$ abundance [45, 46]. We search the region of ${{\tilde{\lambda }}}_3$ and $\lambda _4$, which realizes the required DM abundance as the $\eta _R$ relic abundance by taking the values of ${{\tilde{m}}}_\eta$ and ${{\tilde{\lambda }}}_5$ as the ones given below Eq. (11). They are suitable for the explanation of the neutrino oscillation data and the cosmological baryon number asymmetry. In the estimation of the DM relic abundance, we follow the procedure given in [62, 63] where the coannihilation effects are taken into account.

We present a brief review of the procedure adopted here. The $\eta _R$ relic abundance is estimated as

$$\begin{aligned} \Omega h^2\simeq \frac{1.07\times 10^9~\mathrm{GeV}^{-1}}{J(x_F)g_*^{1/2}m_{\mathrm{pl}}}, \end{aligned}$$

(12)

where $g_*$ is the relativistic degrees of freedom. The freeze-out temperature $T_F(\equiv \frac{M_{\eta _R}}{x_F})$ of $\eta _R$ and $J(x_F)$ are defined as

$$\begin{aligned}&x_F=\ln \frac{0.038m_{\mathrm{pl}}g_{\mathrm{eff}}M_{\eta _R}\langle \sigma _{\mathrm{eff}}v\rangle }{(g_*x_F)^{1/2}}, \nonumber \\&J(x_F)=\int ^\infty _{x_F}\frac{\langle \sigma _{\mathrm{eff}}v\rangle }{x^2}dx. \end{aligned}$$

(13)

In these formulas, the effective annihilation cross section $\langle \sigma _{\mathrm{eff}}v\rangle$ and the effective degrees of freedom $g_{\mathrm{eff}}$ are expressed as⁷

$$\begin{aligned} \langle \sigma _{\mathrm{eff}}v\rangle =\frac{1}{g_{\mathrm{eff}}^2}\sum ^4_{i,j=1} \langle \sigma _{ij}v\rangle \frac{n^{\mathrm{eq}}_i}{n^{\mathrm{eq}}_1} \frac{n^{\mathrm{eq}}_j}{n^{\mathrm{eq}}_1}, \qquad g_{\mathrm{eff}}=\sum _{i=1}^4\frac{n^{\mathrm{eq}}_i}{n^{\mathrm{eq}}_1}, \end{aligned}$$

(14)

where $\langle \sigma _{ij}v\rangle$ is the thermally averaged (co)annihilation cross section and $n^{\mathrm{eq}}_i$ is the thermal equilibrium number density of $\eta _i$. If the former is expanded by the thermally averaged relative velocity $\langle v^2\rangle$ as $\langle \sigma _{ij}v\rangle = a_{ij}+b_{ij}\langle v^2\rangle$, it could be approximated only by $a_{ij}$ since $\langle v^2\rangle \ll 1$ is satisfied for the cold DM. Final states of the relevant (co)annihilation are composed only of the SM contents. The corresponding $a_{\mathrm{eff}}$ can be approximately calculated as [45, 46, 56]

$$\begin{aligned} a_{\mathrm{eff}}= & {} \frac{(1+2c_w^4)g^4}{128\pi c_w^4M_{\eta _1}^2}\left( N_{11}+N_{22}+ 2N_{34}\right) \nonumber \\&+\frac{s_w^2g^4}{32\pi c_w^2M_{\eta _1}^2} \left( N_{13}+N_{14}+N_{23}+N_{24}\right) \nonumber \\&+\frac{1}{64\pi M_{\eta _1}^2}\left[ \left( {{\tilde{\lambda }}}_+^2+{{\tilde{\lambda }}}_-^2 +2{{\tilde{\lambda }}}_3^2\right) (N_{11}+N_{22})\right. \nonumber \\&+({{\tilde{\lambda }}}_+-{{\tilde{\lambda }}}_-)^2(N_{33}+N_{44}+ N_{12})\nonumber \\&+\left\{ ({{\tilde{\lambda }}}_+-{{\tilde{\lambda }}}_3)^2 +({{\tilde{\lambda }}}_--{{\tilde{\lambda }}}_3)^2\right\} \nonumber \\&\times (N_{13}+N_{14}+N_{23}+N_{24}) \nonumber \\&+\left. \left\{ ({{\tilde{\lambda }}}_+ +{{\tilde{\lambda }}}_-)^2 +4{{\tilde{\lambda }}}_3^2\right\} N_{34}\right] , \end{aligned}$$

(15)

where ${{\tilde{\lambda }}}_\pm ={{\tilde{\lambda }}}_3+\lambda _4\pm {{\tilde{\lambda }}}_5$ and $N_{ij}$ is defined by using $M_{\eta _i}$ given in Eq. (7) as

$$\begin{aligned} N_{ij}&\equiv \frac{1}{g_{\mathrm{eff}}^2} \frac{n_i^{\mathrm{eq}}}{n_1^{\mathrm{eq}}}\frac{n_j^{\mathrm{eq}}}{n_1^{\mathrm{eq}}}\nonumber \\&=\frac{1}{g_{\mathrm{eff}}^2} \left( \frac{M_{\eta _i}M_{\eta _j}}{M_{\eta _1}^2}\right) ^{3/2} \exp \left[ -\frac{M_{\eta _i}+M_{\eta _j}-2M_{\eta _1}}{T}\right] . \end{aligned}$$

(16)

Fig. 2

Points plotted by a red solid line in the $({{\tilde{\lambda }}}_3,~\lambda _4)$ plane can realize the required DM relic abundance $\Omega h^2=0.12$ as the relic $\eta _R$ abundance. The last condition in Eq. (5) is satisfied at a region above the straight line which represents ${{\tilde{\lambda }}}_3+\lambda _4=|{{\tilde{\lambda }}}_5|- 2\sqrt{{{\tilde{\lambda }}}_1{{\tilde{\lambda }}}_2}$ for a fixed ${{\tilde{\lambda }}}_2$

We use this procedure to find the points in the $({{\tilde{\lambda }}}_3,~\lambda _4)$ plane, where the required DM abundance $\Omega _{\mathrm{DM}}h^2=0.12$ is realized by $\eta _R$. In Fig. 2, we plot such points by a red solid line for ${{\tilde{m}}}_\eta =1$ TeV and ${{\tilde{\lambda }}}_5=2.5\times 10^{-3}$ which are used in the previous part. In this figure, we take account of the condition $\lambda _4<0$ which has been already discussed in relation to Eq. (7). Moreover, if we use the Higgs mass formula $m_{h^0}^2=4{{\tilde{\lambda }}}_1\langle \phi \rangle ^2$, we find ${{\tilde{\lambda }}}_1\simeq 0.13$ for $m_{h^0}=125$ GeV and then the last condition in Eq. (5) can be also plotted for a fixed ${{\tilde{\lambda }}}_2$ in the same plane.⁸ An allowed points are contained in the region above a straight line which is fixed by an assumed value of ${{\tilde{\lambda }}}_2$. We give two examples here. Although the DM abundance can be satisfied for the negative value of ${{\tilde{\lambda }}}_3$, we find that such cases contradict with the vacuum stability condition for ${{\tilde{\lambda }}}_3$ given in Eq. (5). The figure shows that ${{\tilde{\lambda }}}_3$ and/or $|\lambda _4|$ are required to take rather large values for realization of the DM abundance. This suggests that the RG evolution of the scalar quartic couplings ${{\tilde{\lambda }}}_i$ could be largely affected if they are used as initial values at the weak scale. In that case, vacuum stability and perturbativity of the model could give constraints on the model. In the next part, we focus our study on this point.

Before proceeding to this subject, we comment on the contribution of the axion to the DM abundance and also a possible violation of $U(1)_{PQ}$ by the quantum gravity effect. In this model, the axion could also contribute to the DM abundance through the misalignment mechanism. If the initial misalignment of the axion is written as $\langle \theta _i\rangle$, the axion contribution to the present energy density is estimated as [13, 14]

$$\begin{aligned} \Omega _ah^2=2\times 10^4\left( \frac{\langle S\rangle }{10^{16}~\mathrm{GeV}}\right) ^{7/6}\langle \theta _i^2\rangle . \end{aligned}$$

(17)

The axion contribution to the DM abundance crucially depends on the scale of $\langle S\rangle$ and $\langle \theta _i\rangle$. This estimation shows that it could be too small to give the required value $\Omega _{\mathrm{DM}} h^2=0.12$ for $\langle S\rangle < 10^{11}$ GeV even if we assume $\langle \theta _i\rangle =O(1)$.⁹ Thus, the axion contribution to the DM abundance is sub-dominant or negligible for $\langle S\rangle < 10^{11}$ GeV. In this region of $\langle S\rangle$, the result obtained for $({{\tilde{\lambda }}}_3,\lambda _4)$ through the above study can be still applicable even if the axion contribution to the DM abundance is taken into account.

Although we assume that $U(1)_{PQ}$ is exact in this study, continuous global symmetry is suggested to be violated by the quantum gravity. This possible effect on the PQ mechanism has been studied [68,69,70]. If the $U(1)_{\mathrm{PQ}}$ symmetry is violated by the gravity induced effective interaction which is suppressed by the Planck scale such as

$$\begin{aligned} \frac{|S|^{n+3}}{M_{\mathrm{pl}}^n}\left( gS+g^*S\right) , \end{aligned}$$

(18)

it has been shown that $n\ge 6$ should be satisfied for the PQ mechanism to give a solution to the strong CP problem in case that |g| is of O(1). If accidental appearance of global U(1) happens due to some discrete or continuous gauge symmetry [71,72,73,74,75,76,77,78], it might protect the PQ symmetry up to sufficiently higher order operators. The same breaking effect could also affect the axion CDM abundance [68,69,70]. If the contribution to the axion mass due to the quantum gravity is small compared to the one due to the QCD anomaly, $\langle S\rangle \simeq 10^{11}$ GeV is required for saturating $\Omega h^2=0.12$ by the axion contribution. Even if its contribution to the axion mass is larger than the one from the QCD anomaly within the bound which is required so as not to disturb the PQ mechanism, $\langle S\rangle \simeq 10^{11}$ GeV is required again for saturating $\Omega h^2=0.12$. Thus, $\eta _R$ could play a dominant role in the DM abundance as long as $\langle S\rangle$ is smaller than $10^{11}$ GeV.

The stability for $\eta _R$ could be also violated through the same effect. The most effective processes for the $\eta _R$ decay are induced by nonrenormalizable Yukawa couplings such as

$$\begin{aligned} \frac{S^{n}}{M_{\mathrm{pl}}^{n}}\left( h_u{{\bar{q}}}_Lu_R\eta +h_d{{\bar{q}}}_Ld_R{{\tilde{\eta }}} +h_e{{\bar{\ell }}}_Le_R{{\tilde{\eta }}}\right) . \end{aligned}$$

(19)

If the allowed dimension for these kind of operators is the same as the one which guarantees the PQ mechanism to work, the lifetime of $\eta _R$ could be longer than the age of our universe in case $m_\eta =O(1)$ TeV and $h_{u,d,e}=O(1)$ as long as we take $\langle S\rangle \simeq 10^{10}$ GeV. If the lower dimension operators such as $n< 6$ are allowed, its lifetime cannot be long enough to be the DM at the present universe.

3.2 Consistency of the scenario with a cut-off scale of the model

It is crucial to check what kind of values of the right-handed neutrino mass $M_i$ and ${{\tilde{\lambda }}}_5$ could be consistent with a value of $\langle S\rangle$ which is restricted by the axion physics. In this model, DM is identified with $\eta _R$ whose mass is of O(1) TeV. In such a mass region, we find that its abundance is determined by the values of the scalar quartic couplings ${{\tilde{\lambda }}}_3$ and $\lambda _4$. On the other hand, these couplings could affect the vacuum stability and also the perturbativity of the model through the radiative effects on the scalar quartic couplings ${{\tilde{\lambda }}}_i$. Here, we examine the consistency of the values of ${{\tilde{\lambda }}}_3$ and $\lambda _4$ required to realize of the DM abundance with these issues.¹⁰ Since the breaking of the perturbativity is considered to be relevant to a scale for the applicability of the model, we could obtain an information for the cut-off scale $M_*$. It allows us to judge whether the required value for ${{\tilde{\lambda }}}_5$ by the neutrino masses and the leptogenesis could be induced through the VEV of S.

The one-loop $\beta$-functions for the scalar quartic couplings in the effective model at energy regions below $M_S$ are given as follows [80, 81],

$$\begin{aligned} \beta _{{{\tilde{\lambda }}}_1}= & {} 24{{\tilde{\lambda }}}_1^2 +{{\tilde{\lambda }}}_3^2+({{\tilde{\lambda }}}_3+\lambda _4)^2 +{{\tilde{\lambda }}}_5^2 \nonumber \\&+\frac{3}{8}\left( 3g^4+g^{\prime 4}+2g^2g^{\prime 2}\right) \nonumber \\&-3{{\tilde{\lambda }}}_1\left( 3g^2+g^{\prime 2}-4h_t^2\right) -6h_t^4, \nonumber \\ \beta _{{{\tilde{\lambda }}}_2}= & {} 24{{\tilde{\lambda }}}_2^2 +{{\tilde{\lambda }}}_3^2 +({{\tilde{\lambda }}}_3+\lambda _4)^2+{{\tilde{\lambda }}}_5^2 \nonumber \\&+\frac{3}{8}\left( 3g^4+g^{\prime 4}+2g^2g^{\prime 2}\right) -3{{\tilde{\lambda }}}_2\left( 3g^2+g^{\prime 2}\right) , \nonumber \\ \beta _{{{\tilde{\lambda }}}_3}= & {} 2({{\tilde{\lambda }}}_1 +{{\tilde{\lambda }}}_2) (6{{\tilde{\lambda }}}_3+2\lambda _4) +4{{\tilde{\lambda }}}_3^2+2\lambda _4^2 +2{{\tilde{\lambda }}}_5^2 \nonumber \\&+\frac{3}{4}\left( 3g^4+g^{\prime 4}-2g^2g^{\prime 2}\right) -3{{\tilde{\lambda }}}_3\left( 3g^2+g^{\prime 2}-2h_t^2\right) , \nonumber \\ \beta _{\lambda _4}= & {} 4({{\tilde{\lambda }}}_1+{{\tilde{\lambda }}}_2)\lambda _4 +8{{\tilde{\lambda }}}_3\lambda _4+4\lambda _4^2 +8{{\tilde{\lambda }}}_5^2+3g^2g^{\prime 2}\nonumber \\&-3\lambda _4\left( 3g^2+g^{\prime 2}-2h_t^2\right) , \nonumber \\ \beta _{{{\tilde{\lambda }}}_5}= & {} 4({{\tilde{\lambda }}}_1 +{{\tilde{\lambda }}}_2){{\tilde{\lambda }}}_5 +8{{\tilde{\lambda }}}_3{{\tilde{\lambda }}}_5 +12\lambda _4{{\tilde{\lambda }}}_5\nonumber \\&-3{{\tilde{\lambda }}}_5\left( 3g^2+g^{\prime 2}-2h_t^2\right) , \end{aligned}$$

(20)

where $\beta _\lambda$ is defined as $\beta _\lambda =16\pi ^2\mu \frac{d\lambda }{d\mu }$. In these equations, we can expect that the positive contributions of ${{\tilde{\lambda }}}_3$ and $\lambda _4$ to the $\beta$-functions of ${{\tilde{\lambda }}}_{1,2}$ tend to save the model from violating the first two vacuum stability conditions in Eq. (5). On the other hand, the same contributions of ${{\tilde{\lambda }}}_3$ and $\lambda _4$ could induce the breaking of the perturbativity of the model at a rather low energy scale since they could give large positive contributions to $\beta _{{{\tilde{\lambda }}}_1}$, $\beta _{{{\tilde{\lambda }}}_2}$ and $\beta _{{{\tilde{\lambda }}}_3}$. Here, we identify a cut-off scale $M_*$ of the model with a scale where any of the perturbativity conditions $\lambda _i(M_*)<4\pi$ and $\kappa _i(M_*)<4\pi$ is violated.¹¹ In this case, $M_*>|\langle S\rangle |$ should be satisfied. If $M_*$ is smaller than $\langle S\rangle$, the consistency of the scenario is lost.

Fig. 3

Left panel: running of the scalar quartic couplings for $t=\ln \frac{\mu }{M_Z}$. ${{\tilde{\lambda }}}_2=0.23$, ${{\tilde{\lambda }}}_3=0.65$ and $\lambda _4=-\,0.806$ are used as the initial values at $\mu =M_Z$. A vertical line corresponds to $t=\ln \left( \frac{M_S}{M_Z}\right)$. The running of the SM Higgs quartic coupling $\lambda$ is also plotted as a reference. Right panel: the cut-off scale $M_*$ as a function of ${{\tilde{\lambda }}}_2$ which is fixed as a value at $M_Z$ for four points marked by the black bulbs in Fig. 2 where $\Omega h^2=0.12$ is satisfied

We analyze this issue by solving the above one-loop RGEs at $\mu <M_S$ and also the ones at $\mu >M_S$, which are given in Appendix. The quartic couplings ${{\tilde{\lambda }}}_i$ in the tree-level potential at the energy scale $\mu <M_S$ are connected with the ones $\lambda _i$ at $\mu >M_S$ through Eq. (4). Since the masses of the right-handed neutrinos $N_i$ are considered to be heavy in the present model, they decouple at the scale $\mu<M_i~^<_\sim ~O(M_S)$ to be irrelevant to the RGEs there. On the other hand, the mass of the colored fields $D_{L,R}$ can take any values larger than 1 TeV as discussed before, they can contribute to the RGEs at larger scales than their mass. In the present study, we assume that $D_{L,R}$ is light of O(1) TeV but its Yukawa coupling $h_D$ with the ordinary quarks is small enough.¹² Thus, they are considered to contribute substantially only to the $\beta$-functions of the gauge couplings. In this study, we take its hypercharge as $Y=-\frac{1}{3}$ as shown in Table 1.

The free parameters in the scalar potential of the effective model (3) are ${{\tilde{\lambda }}}_1,~{{\tilde{\lambda }}}_2,~{{\tilde{\lambda }}}_3,~\lambda _4$ and ${{\tilde{\lambda }}}_5$ at $M_Z$ as long as we assume ${{\tilde{m}}}_\eta =1$ TeV.¹³ Among them, we should fix ${{\tilde{\lambda }}}_5$ at a value used in the discussion of the neutrino mass and the leptogenesis. Both ${{\tilde{\lambda }}}_3$ and $\lambda _4$ are fixed at values determined through the DM relic abundance as shown in Fig. 2. We also have ${{\tilde{\lambda }}}_1\simeq 0.13$ from the Higgs mass. From this point of view, ${{\tilde{\lambda }}}_2$ is an only remaining parameter. Thus, if we solve the RGEs varying the value of ${{\tilde{\lambda }}}_2$ for other fixed parameters, we can find $M_*$ checking the vacuum stability for each ${{\tilde{\lambda }}}_2$.

In the left panel of Fig. 3, as an example, we present the running of the scalar quartic couplings ${{\tilde{\lambda }}}_{1,2,3}$ for the initial values ${{\tilde{\lambda }}}_2=0.23$, ${{\tilde{\lambda }}}_3=0.65$ and $\lambda _4=-\,0.806$ at $M_Z$ by assuming the $U(1)_{PQ}$ breaking scale as $\langle S\rangle =M_S=10^{10}$ GeV. In the same panel, we also plot the value of ${{\tilde{\lambda }}}_3+\lambda _4-|{{\tilde{\lambda }}}_5| +2\sqrt{{{\tilde{\lambda }}}_1{{\tilde{\lambda }}}_2}$ as $C[\lambda _{34}]$, which corresponds to the last one in Eq. (5). In this example, we can see that the vacuum stability is kept until the cut-off scale $M_*\simeq 1.54\,\times \, 10^{13}$ GeV. These values of $\langle S\rangle$ and $M_*$ can naturally realize the assumed value for ${{\tilde{\lambda }}}_5$ through the relation given in Eq. (4) just by taking $\lambda _5$ as a value of O(1). This feature can be verified for other allowed values of ${{\tilde{\lambda }}}_3$ and $\lambda _4$. Here, we note that the axion contribution to the DM abundance can be neglected for a value such as $\langle S\rangle <10^{11}$ GeV. In the right panel of Fig. 3, we plot $M_*$ as a function of ${{\tilde{\lambda }}}_2$ for four sets of $({{\tilde{\lambda }}}_3,~\lambda _4)$ which are shown by black bulbs in Fig. 2. End points found in the two lines represent the value of ${{\tilde{\lambda }}}_2$ for which the vacuum stability is violated before reaching $M_*$. This figure shows that ${{\tilde{\lambda }}}_2$ which is restricted to a rather narrow region can make $M_*$ appropriate values in order to realize a required value of ${{\tilde{\lambda }}}_5$ for $\langle S\rangle <10^{11}$ GeV. This study suggests that the scenario could work well without strict tuning of the relevant parameters.

As found from the above study, the simultaneous explanation of the neutrino masses and the DM abundance could be preserved in this extended model in the same way as in the original scotogenic model. We should stress that no other additional constraint from the DM physics and the neutrino physics is brought about by taking the present scenario. The cosmological baryon number asymmetry is expected to be explained through the out-of-equilibrium decay of the lightest right-handed neutrino. The required right-handed neutrino mass could be smaller compared with the Davidson–Ibarra bound in the ordinary thermal leptogenesis [61]. This is consistent with the result in [45, 46] where the mass bound of the right-handed neutrino for the successful leptogenesis is shown to be relaxed in the radiative neutrino mass model in comparison with the ordinary seesaw model .

Finally, we give brief comments on possible experimental signatures of the model. The present model might be examined through (i) the search of the $\eta _R$ DM and the charged scalars $\eta ^\pm$ through the DM direct detection experiments and the accelerator experiments, (ii) the search of the mixing of D with the ordinary quarks although it could be observed only in the light D case, and (iii) the search of the axion whose coupling with photon is characterized by $g_{a\gamma \gamma }=\frac{m_a}{\mathrm{eV}} \frac{2.0}{10^{10}{\mathrm{GeV}}}(6 Y^2-1.92)$, where Y is the hypercharge of D [32].

4 Summary

We have proposed an extension of the KSVZ invisible axion model so as to include a DM candidate and explain the small neutrino masses. An extra inert doublet scalar $\eta$ and three right-handed neutrinos $N_i$ are introduced as new ingredients. After the $U(1)_{PQ}$ symmetry breaking, its subgroup $Z_2$ could remain as a remnant effective symmetry, which is violated through the QCD anomaly but it can play the same role as the $Z_2$ in the scotogenic neutrino mass model. Since only the new ones $\eta$ and $N_i$ have its odd parity, the model reduces to the scotogenic model which has $Z_2$ in the leptonic sector. The neutrino masses are generated at one-loop level and the DM abundance can be explained by the thermal relics of the neutral component of $\eta$. The cosmological baryon number asymmetry could be generated through the out-of-equilibrium decay of a right-handed neutrino in the same way as the ordinary thermal leptogenesis in the tree-level seesaw model. However, the bound for the right-handed neutrino mass can be relaxed in this model. Since this simple extension can relate the strong CP problem to the origin of neutrino masses and DM, it may be a promising extension of both the KSVZ model and the scotogenic model.

Appendix

The $\beta$-function for the scalar quartic couplings at $\mu >M_S$ are given as

$$\begin{aligned} \beta _{\lambda _1}= & {} 24\lambda _1^2 +\lambda _3^2+(\lambda _3+\lambda _4)^2 + \kappa _2^2\nonumber \\&+\,\frac{3}{8}\left( 3g^4+g^{\prime 4}+2g^2g^{\prime 2}\right) \nonumber \\&-\,3\lambda _1\left( 3g^2+g^{\prime 2}-4h_t^2\right) -6h_t^4, \nonumber \\ \beta _{\lambda _2}= & {} 24\lambda _2^2+\lambda _3^2 +(\lambda _3+\lambda _4)^2 +\kappa _3^2\nonumber \\&+\,\frac{3}{8}\left( 3g^4+g^{\prime 4}+2g^2g^{\prime 2}\right) -3\lambda _2\left( 3g^2+g^{\prime 2}\right) \nonumber \\&+\,4\lambda _2\left[ 2(h_1^2+h_2^2)+3h_3^2\right] -8(h_1^2+h_2^2)^2-18h_3^4, \nonumber \\ \beta _{\lambda _3}= & {} 2(\lambda _1+\lambda _2) (6\lambda _3+2\lambda _4) +4\lambda _3^2+2\lambda _4^2 +2\kappa _2\kappa _3\nonumber \\&+\,\frac{3}{4}\left( 3g^4+g^{\prime 4}-2g^2g^{\prime 2}\right) \nonumber \\&-\,3\lambda _3\left( 3g^2+g^{\prime 2}-2h_t^2\right) +2\lambda _3\left[ 2(h_1^2+h_2^2)+3h_3^2\right] , \nonumber \\ \beta _{\lambda _4}= & {} 4(\lambda _1+\lambda _2)\lambda _4 +8\lambda _3\lambda _4+4\lambda _4^2 +3g^2g^{\prime 2}\nonumber \\&-\,3\lambda _4\left( 3g^2+g^{\prime 2}-2h_t^2\right) \nonumber \\&+\,2\lambda _4\left[ 2(h_1^2+h_2^2)+3h_3^2\right] , \nonumber \\ \beta _{\kappa _1}= & {} 20\kappa _1^2+2\kappa _2^2+2\kappa _3^2 +4\kappa _1\left( 3y_D^2+\sum _iy_i^2\right) \nonumber \\&-\,2\left( 3y_D^4+\sum _iy_i^4\right) , \nonumber \\ \beta _{\kappa _2}= & {} 4\kappa _2^2+2\kappa _2(6\lambda _1+4\kappa _1) +2\kappa _3(2\lambda _3+\lambda _4)\nonumber \\&+\,2\kappa _2\left( 3y_D^2+\sum _iy_i^2\right) \nonumber \\&-\,\frac{3}{2}\kappa _2(3g^2+g^{\prime 2}-4h_t^2), \nonumber \\ \beta _{\kappa _3}= & {} 4\kappa _3^2+2\kappa _3(6\lambda _2+4\kappa _1) +2\kappa _2(2\lambda _3+\lambda _4)\nonumber \\&+\,2\kappa _3\left( 3y_D^2+\sum _iy_i^2\right) \nonumber \\&-\,\frac{3}{2}\kappa _3\left[ 3g^2+g^{\prime 2}- \frac{4}{3}\left( 2(h_1^2+h_2^2)+3h_3^2\right) \right] , \end{aligned}$$

(21)

where Eq. (9) is assumed for the flavor structure of neutrino Yukawa couplings. The $\beta$-functions for the gauge couplings and the Yukawa couplings for top, D and neutrinos are given as

$$\begin{aligned} \beta _{g_s}= & {} -11+\frac{2}{3}(6+\delta )g_s^3, \quad \beta _g= -3g^3,\nonumber \\ \beta _{g^\prime }= & {} (7+4Y^2\delta )g^{\prime 3}, \nonumber \\ \beta _{h_t}= & {} h_t\left( \frac{9}{2}h_t^2-8g_s^2-\frac{9}{4}g^2 -\frac{17}{12}g^{\prime 2}\right) , \nonumber \\ \beta _{y_k}= & {} y_k\left( y_k^2+3y_D^2+\sum _iy_i^2\right) ,\nonumber \\ \beta _{y_D}= & {} y_D\left( -8g_3^3-6Y^2\delta g^{\prime 2}+4y_D^2+\sum _iy_i^2 \right) , \nonumber \\ \beta _{h_{1,2}}= & {} h_{1,2}\left[ -\frac{9}{4}g^2- \frac{3}{4}g^{\prime 2}+5(h_1^2+h_2^2)+3h_3^2+\frac{1}{2}\sum _iy_i^2\right] , \nonumber \\ \beta _{h_3}= & {} h_3\left[ -\frac{9}{4}g^2- \frac{3}{4}g^{\prime 2}+2(h_1^2+h_2^2)+6h_3^2 +\frac{1}{2}\sum _iy_i^2\right] ,\nonumber \\ \end{aligned}$$

(22)

where $\delta$ stands for the number of extra color triplets $D_{L,R}$. Since $D_{L,R}$ is assumed to be light in this study, $\delta$ is treated as 1. The Yukawa coupling $h_D$ with the ordinary quarks is assumed to be small enough and then its contribution is neglected in these equations.