1 Introduction

In particle physics, flavor symmetries [1,2,3,4] have played an important role in the understanding of the quark and lepton flavor mixings through the CKM [5, 6] and PMNS [7,8,9] mixing matrices, respectively. According to the experimental data, the values for the magnitudes of all CKM entries obtained from a global fit are [10]

$$\begin{aligned} \mathbf{V}_{\mathrm {CKM}}= \begin{pmatrix} 0.97434^{+0.00011}_{-0.00012} &{} 0.22506 \pm 0.00050 &{} 0.00357 \pm 0.00015 \\ 0.22492 \pm 0.00050 &{} 0.97351 \pm 0.00013 &{} 0.0411 \pm 0.0013 \\ 0.00875^{+0.00032}_{-0.00033} &{} 0.0403 \pm 0.0013 &{} 0.99915 \pm 0.00005 \end{pmatrix}. \end{aligned}$$
(1)

The Jarlskog invariant is \(J = \left( 3.04_{-0.20}^{+0.21} \right) \times 10^{-5}\). In the lepton sector, on the other hand, we know that active neutrinos have a small, but not negligible mass, which can be understood by the type I see-saw mechanism [11,12,13,14,15,16]. The mixings turn out to be non-trivial, so in the theoretical framework of three active neutrinos, the numerical values for the squared neutrino masses and flavor mixing angles obtained from a global fit to the current experimental data on neutrino oscillations [17,18,19], at Best-Fit Point (BFP) \(\pm 1 \sigma \) and \(3 \sigma \) ranges, are [17, 20]

$$\begin{aligned} \begin{array}{ll} &{}\Delta m^{2}_{21} \left( 10^{-5} \, \text {eV}^{2} \right) = 7.60_{-0.18}^{+0.19}, \, 7.11 - 8.18, \\ &{}\left| \Delta m^{2}_{31} \right| \left( 10^{-3} \, \text {eV}^{2} \right) = \left\{ \begin{array}{l} 2.48_{-0.07}^{+0.05}, 2.30 - 2.65 \\ 2.38_{-0.06}^{+0.05}, 2.20 - 2.54\\ \end{array} \right. , \\ &{}\sin ^{2} \theta _{12} / 10^{-1} = 3.23 \pm 0.16, \, 2.78 - 3.75 ,\\ &{} \sin ^{2} \theta _{23} / 10^{-1} = \left\{ \begin{array}{l} 5.67_{-1.24}^{+0.32} , \, 3.93 - 6.43 \\ 5.73_{-0.39}^{+0.25} , \, 4.03 - 6.40\\ \end{array} \right. , \\ &{} \sin ^{2} \theta _{13} / 10^{-2} = \left\{ \begin{array}{l} 2.26 \pm 0.12 , \, 1.90 - 2.62 \\ 2.29 \pm 0.12 , \, 1.93 - 2.65 \end{array} \right. . \end{array} \end{aligned}$$
(2)

The upper and lower rows are for a normal and inverted hierarchy of the neutrino mass spectrum, respectively. At the same time, there is not yet solid evidence on the Dirac CP-violating phase. So, from these data it is found (for inverted ordering) that the magnitude of the leptonic mixing matrix elements have the following values at \(3\sigma \) [18]:

$$\begin{aligned} \left( \begin{array}{ccc} 0.799 - 0.844 &{} 0.516 - 0.582 &{} 0.141 - 0.156 \\ 0.242 - 0.494 &{} 0.467 - 0.678 &{} 0.639 - 0.774 \\ 0.284 - 0.521 &{} 0.490 - 0.695 &{} 0.615 - 0.754 \end{array} \right) . \end{aligned}$$
(3)

Understanding the contrasted values between the CKM and PMNS mixing matrices is still a challenge in particle physics. In this line of thought, many flavor models such as \(S_{3}\) [21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64], \(A_{4}\) [65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94], \(S_{4}\) [95,96,97,98,99,100,101,102,103,104,105,106], \(D_{4}\) [107,108,109,110,111,112,113,114], \(Q_{6}\) [115,116,117,118,119,120,121,122,123,124,125], \(T_{7}\) [126,127,128,129,130,131,132,133,134], \(T_{13}\) [135,136,137,138], \(T^{\prime }\) [139,140,141,142,143,144], \(\Delta (27)\) [145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162], and \(A_{5}\) [163,164,165,166,167,168,169,170,171,172,173] have been proposed to face this open question.

From a phenomenological point of view, the CKM mixing matrix may be accommodated by the Fritzsch [174,175,176] and the Nearest Neighbor Interaction textures (NNI) [177,178,179,180], however, only the latter can fit with good accuracy the CKM matrix. On the other hand, as can be seen from the PMNS values, the lepton sector seems to obey approximately the \(\mu \leftrightarrow \tau \) symmetry [108, 181,182,183,184] since \(\left| V_{\mu i}\right| \approx \left| V_{\tau i}\right| \) (\(i=1, 2, 3.\)). At present, the long-baseline energy experiment NO\(\nu \)A has disfavored the exact \(\mu \leftrightarrow \tau \) symmetry; some work has explored the breaking and other ideas on this appealing symmetry [123, 185,186,187,188,189,190,191,192,193,194,195,196,197,198,199,200,201,202,203,204].

Along with this, \(\mu \leftrightarrow \tau \) reflection symmetry has gained relevance since it predicts the CP-violating Dirac phase (\(\delta _{CP}=-90^{\circ }\)), the atmospheric and the reactor angles are \(45^{\circ }\) and nonzero, respectively [205,206,207,208,209,210,211,212].

Even though the quark and lepton sectors seem to obey different physics, we proposed a framework [58] to simultaneously accommodate both sectors under the \(\mathbf{S_{3}\otimes Z_{2} \otimes Z^{e}_{2}}\) discrete symmetry within the left–right theory. Thus, we will recover the fermion mass matrices that were obtained previously [58], to make a complete study on fermion masses and mixings. In the present work, the quark sector will be studied in detail since this was only mentioned in [58]. As we will see, the up and down mass matrices possess the generalized Fritzsch textures [213] (which are not hierarchical [214]), so that the CKM mixing matrix is parametrized by the quark masses and some free parameters that will be tuned by a \(\chi ^{2}\) analysis in order to fit the mixings. In the lepton sector, on the other hand, the mixing angles can be understood by a soft breaking of the \(\mu \leftrightarrow \tau \) symmetry in the effective neutrino mass matrix that comes from the type I see-saw mechanism. In the current analysis, we found a set of free parameters that fit the PMNS mixing matrix for the inverted and degenerate hierarchy.

The paper is organized as follows: the fermion mass matrices will be introduced in Sect. 2. The CKM and PMNS mixing matrices will be obtained in Sects. 3 and 4, respectively, besides of a \(\chi ^{2}\) analysis is presented to fit the free parameters in the relevant mixing matrices for the quark and lepton sectors separately. Finally, in Sect. 5, we present our conclusions.

2 Fermion masses

The following mass matrices were obtained in a particular model [58] where the left–right theory [13, 215,216,217,218] and a \(\mathbf{S}_{3}\otimes \mathbf{Z}_{2}\otimes \mathbf{Z}^{e}_{2}\) symmetry are the main ingredients.

  • Pseudomanifest left–right theory (PLRT).

    $$\begin{aligned} \mathbf{M}_{q}&=\begin{pmatrix} a_{q}+b_{q} &{} b_{q} &{} c_{q} \\ b_{q} &{} a_{q}-b_{q} &{} c_{q} \\ c_{q} &{} c_{q} &{} g_{q} \end{pmatrix},\nonumber \\ \mathbf{M}_{\ell }&=\begin{pmatrix} a_{\ell } &{} 0 &{} 0 \\ 0 &{} b_{\ell }+c_{\ell } &{} 0 \\ 0 &{} 0 &{} b_{\ell }-c_{\ell } \end{pmatrix},\\ \mathbf{M}_{(L, R)}&=\begin{pmatrix} a_{(L, R)} &{} b_{(L, R)} &{} b_{(L, R)} \\ b_{(L, R)} &{} c_{(L, R)} &{} 0 \\ b_{(L, R)} &{} 0 &{} c_{(L, R)}\nonumber \\ \end{pmatrix}. \end{aligned}$$
    (4)

  • Manifest left–right theory (MLRT).

    $$\begin{aligned} \mathbf{M}_{q}&=\begin{pmatrix} a_{q}+b_{q} &{} b_{q} &{} c_{q} \\ b_{q} &{} a_{q}-b_{q} &{} c_{q} \\ c^{*}_{q} &{} c^{*}_{q} &{} g_{q} \end{pmatrix},\nonumber \\ \mathbf{M}_{\ell }&=\begin{pmatrix} a_{\ell } &{} 0 &{} 0 \\ 0 &{} b_{\ell }+c_{\ell } &{} 0 \\ 0 &{} 0 &{} b_{\ell }-c_{\ell } \end{pmatrix},\\ \mathbf{M}_{(L, R)}&=\begin{pmatrix} a_{(L, R)} &{} b_{(L, R)} &{} b_{(L, R)} \\ b_{(L, R)} &{} c_{(L, R)} &{} 0 \\ b_{(L, R)} &{} 0 &{} c_{(L, R)}\nonumber \\ \end{pmatrix}. \end{aligned}$$
    (5)

Here \(q=u,~d\) stands for the label of up and down quark sector, and \(\ell =e,~D\) for the charged leptons and Dirac neutrinos. On the other hand, as was stated in [58], the fermion mass matrices are complex in the PLRT. In MLRT, the charged lepton and the Dirac neutrino mass matrices are reals and the Majorana neutrino is complex.

Let us point out that an analytical study on the lepton mixing, in the PLRT, was already made in detail in the particular case where the Majorana phases are CP parities, and this means that these can be 0 or \(\pi \) [58]. In what follows, the theoretical PMNS mass mixing matrix is recovered but the Majorana phases can take any values, in general. At the same time, for the MLRT the neutrino mass matrix is easily included in the above framework as we will see below.

3 Quark sector

In this model, the quark mass matrices can be rotated to a basis in which these mass matrices acquire a form with some texture zeros. Also, in the PLRT and MLRT framework the quark mass matrices can be expressed in the following polar form:

$$\begin{aligned} \mathbf{M}_{q \texttt {j}} = \mathbf{U}_{\pi /4}^{\top } \mathbf{Q}_{q \texttt {j} } \left( \mu _{q \texttt {j}} \, {\mathbb {I}}_{3 \times 3} + \mathcal{M}_{q \texttt {j}} \right) \mathbf{P}_{q \texttt {j}} \mathbf{U}_{\pi /4} , \end{aligned}$$
(6)

where

$$\begin{aligned} \mathbf{U}_{\pi /4}= & {} \frac{1}{ \sqrt{2} } \left( \begin{array}{ccc} 1 &{} -1 &{} 0 \\ 1 &{} 1 &{} 0 \\ 0 &{} 0 &{} \sqrt{2} \end{array} \right) \quad \text {and}\nonumber \\ \mathcal{M}_{q\texttt {j}}= & {} \left( \begin{array}{ccc} D_{q \texttt {j}} &{} B_{q \texttt {j}} &{} 0 \\ B_{q \texttt {j}} &{} A_{q \texttt {j}} &{} C_{q \texttt {j}} \\ 0 &{} C_{q \texttt {j}} &{} 0 \end{array} \right) . \end{aligned}$$
(7)

The \(\mathbf{P}_{q \texttt {j}}\) and \(\mathbf{Q}_{q \texttt {j}}\) are diagonal matrices, whose explicit form depends on the theoretical framework in which we are working. In the above expressions, the \(\texttt {j}\) subscript denote the PLRT and MLRT frameworks. Concretely, \(\texttt {j} = 1\) refers to the PLRT framework, where we have \(\mu _{q 1} = |g_{q}|\),

$$\begin{aligned} \mathbf{Q}_{q 1} = \mathbf{P}_{q 1}^{\top } , \quad \text {and} \quad \mathbf{P}_{q 1} = \text {diag} \left( e^{ i \alpha _{q 1} }, e^{ i \beta _{q 1} }, e^{ i \gamma _{q 1} } \right) . \end{aligned}$$
(8)

The phase factors in the \(\mathbf{P}_{q 1}\) matrix must satisfy the relations

$$\begin{aligned} \begin{array}{l} 2 \alpha _{q1} = \arg \left( a_{q} + b_{q} \right) , \quad 2 \beta _{q1} = \arg \left( a_{q} - b_{q} \right) , \quad 2 \gamma _{q1} = \arg \left( g_{q} \right) , \\ \alpha _{q1} + \beta _{q1} = \arg \left( b_{q} \right) ,\quad \beta _{q1} + \gamma _{q1} = \arg \left( c_{q} \right) . \end{array} \end{aligned}$$
(9)

The entries of the \(\mathcal{M}_{q1}\) matrix have the form \(A_{q 1} = |a_{q} + b_{q}| - |g_{q}|\), \(B_{q 1} = |b_{q}|\), \(C_{1 q} = \sqrt{2} |c_{q}|\), and \(D_{q 1} = |a_{q} - b_{q}| - |g_{q}|\).

On the other hand, \(\texttt {j} = 2\) refers to the MLRT framework in which \(\mu _{q 2} = g_{q}\),

$$\begin{aligned} \mathbf{Q}_{q 2} = \mathbf{P}_{q 2}^{\dagger } , \quad \text {and} \quad \mathbf{P}_{q 2} = \text {diag} \left( 1, 1, e^{ i \gamma _{q 2} } \right) , \end{aligned}$$
(10)

where \(\gamma _{q2} = \arg \left( c_{q} \right) \). The entries of the \(\mathcal{M}_{q 2}\) matrix have the form \(A_{q 2} = a_{q} + b_{q} - g_{q}\), \(B_{q 2} = b_{q}\), \(C_{q 2} = \sqrt{2} |c_{q}|\), \(D_{2 q} = a_{q} - b_{q} - g_{q}\).

The real symmetric matrix \(\mathcal{M}_{q \texttt {j}}\) in Eq. (7), with \(\texttt {j} = 1, 2\), can be brought to diagonal shape by means of the following orthogonal transformation:

$$\begin{aligned} \mathcal{M}_{q \texttt {j}} = \mathbf{O}_{q \texttt {j}} \, \mathbf{\Delta }_{q \texttt {j}} \, \mathbf{O}_{q \texttt {j}}^{\top } , \end{aligned}$$
(11)

where \(\mathbf{O}_{q \texttt {j}}\) is a real orthogonal matrix, while

$$\begin{aligned} \mathbf{\Delta }_{q \texttt {j}} = \text {diag} \left( \sigma _{q1}^{^{(\texttt {j})}}, \sigma _{q2}^{^{(\texttt {j})}}, \sigma _{q3}^{^{(\texttt {j})}} \right) . \end{aligned}$$
(12)

In the last matrix the \(\sigma _{q\texttt {i}}^{^{(\texttt {j})}}\), with \(\texttt {i}=1,2,3\), are the shifted quark masses [42]. Now, it is easy to conclude that the quark mass matrices in both frameworks can be brought to diagonal shape by means of the following transformations:

$$\begin{aligned} \begin{array}{ll} \mathcal{U}_{q1} \, \mathbf{M}_{q1} \, \mathcal{U}_{q1}^{\top } = \text {diag} \left( m_{q1}, m_{q2}, m_{q3} \right) , &{} \quad \text {for }{PLRT}, \\ \mathcal{U}_{q2} \, \mathbf{M}_{q2} \, \mathcal{U}_{q2}^{\dagger } = \text {diag} \left( m_{q1}, m_{q2}, m_{q3} \right) , &{} \quad \text {for }{MLRT}. \end{array} \end{aligned}$$
(13)

In the above expressions the \(m_{q i}\) are the physical quark masses, while

$$\begin{aligned} \mathcal{U}_{q1} \equiv \mathbf{O}_{q}^{\top } \, \mathbf{P}_{q1}^{*} \, \mathbf{U}_{\pi /4} \quad \text {and} \quad \mathcal{U}_{q2} \equiv \mathbf{O}_{q}^{\top } \, \mathbf{P}_{q2} \, \mathbf{U}_{\pi /4}. \end{aligned}$$
(14)

The relation between the physical quark masses and the shifted masses is [39, 42]

$$\begin{aligned} \sigma _{q\texttt {i}}^{^{(\texttt {j})}} = m_{q\texttt {i}} - \mu _{q \texttt {j}} . \end{aligned}$$
(15)

From the invariants of the real symmetric matrix \(\mathcal{M}_{q \texttt {j}}\), \({\mathrm {tr}}\left\{ \mathcal{M}_{q \texttt {j}} \right\} \), \({\mathrm {tr}}\left\{ \mathcal{M}_{q \texttt {j}}^{2} \right\} \) and \({\mathrm {det}}\left\{ \mathcal{M}_{q \texttt {j}} \right\} \), the parameters \(A_{q \texttt {j}}\), \(B_{q \texttt {j}}\), \(C_{q \texttt {j}}\) and \(D_{q \texttt {j}}\) can be written in terms of the quark masses and two parameters. In this way, we see that the entries of the \(\mathcal{M}_{q \texttt {j}}\) matrix take the form

$$\begin{aligned} \begin{array}{ll} \widetilde{A}_{q \texttt {j}} = \frac{ A_{q \texttt {j} } }{ \sigma _{q 3}^{^{(\texttt {j})}} } = \widetilde{\sigma }_{q 1}^{^{(\texttt {j})}} - \widetilde{\sigma }_{q 2}^{^{(\texttt {j})}} + \delta _{q} , &{} \widetilde{B}_{q \texttt {j}} = \frac{ B_{q \texttt {j} } }{ \sigma _{q 3}^{^{(\texttt {j})}} } = \sqrt{ \frac{ \delta _{q} }{ 1 - \delta _{q} } \xi _{q 1}^{^{(\texttt {j})}} \xi _{q 2 }^{^{(\texttt {j})} } } , \\ \widetilde{C}_{q \texttt {j}} = \frac{ C_{q \texttt {j} } }{ \sigma _{q 3}^{^{(\texttt {j})}} } = \sqrt{ \frac{ \widetilde{\sigma }_{q 1}^{^{(\texttt {j})}} \widetilde{\sigma }_{q 2}^{^{(\texttt {j})}} }{ 1 - \delta _{q} } } , &{} \widetilde{D}_{q \texttt {j}} = \frac{ D_{q \texttt {j} } }{ \sigma _{q 3}^{^{(\texttt {j})}} } = 1 - \delta _{q} , \end{array} \end{aligned}$$
(16)

where

$$\begin{aligned} \begin{array}{ll} \xi _{q 1}^{^{(\texttt {j})}} = 1 - \widetilde{\sigma }_{q1}^{^{(\texttt {j})}} - \delta _{q} , &{} \xi _{q 2}^{^{(\texttt {j})}} = 1 + \widetilde{\sigma }_{q2}^{^{(\texttt {j})}} - \delta _{q} , \\ \widetilde{\sigma }_{q1}^{^{(\texttt {j})}} = \frac{ \sigma _{q1}^{^{(\texttt {j})}} }{ \sigma _{q3}^{^{(\texttt {j})}} } = \frac{ \widetilde{m}_{q1} - \widetilde{\mu }_{q \texttt {j} } }{ 1 - \widetilde{\mu }_{q \texttt {j} } }, &{} \widetilde{\sigma }_{q2}^{^{(\texttt {j})}} = \frac{ | \sigma _{q2}^{^{(\texttt {j})}} | }{ \sigma _{q3}^{^{(\texttt {j})}} } = \frac{ \left| \widetilde{m}_{q2} - \widetilde{\mu }_{q \texttt {j} } \right| }{ 1 - \widetilde{\mu }_{q \texttt {j} } },\\ \widetilde{\mu }_{q \texttt {j}} = \frac{ \mu _{q \texttt {j}} }{ m_{q3} } , \quad \widetilde{m}_{q1} = \frac{ m_{q1} }{ m_{q3} }, &{} \widetilde{m}_{q2} = \frac{ m_{q2} }{ m_{q3} }. \end{array} \end{aligned}$$
(17)

In order to obtain the above parametrization we considered \(\sigma _{q2}^{^{(\texttt {j})}} = -| \sigma _{q2}^{^{(\texttt {j})}} |\). With the aid of the expressions in Eqs. (16) and (17), we find that the parameters \(\delta _{q}\) and \(\widetilde{\mu }_{q \texttt {j}}\) must satisfy the following relations:

$$\begin{aligned} \widetilde{m}_{q1}> \widetilde{\mu }_{q \texttt {j}} \geqslant 0 \quad \text {and} \quad \frac{ 1 - \widetilde{m}_{q1} }{ 1 - \widetilde{\mu }_{q \texttt {j} } }> \delta _{q} > 0. \end{aligned}$$
(18)

From the conditions above, we conclude that the parameter \(\widetilde{\mu }_{q \texttt {j}}\) must be positive and smaller than one. As \(m_{q3} > 0\) and \(\widetilde{\mu }_{q \texttt {j} } \geqslant 0\) we have \(|g_{q}| = g_{q}\), which implies that \(\widetilde{\mu }_{q 1 } = \widetilde{\mu }_{q 2 }\).

Therefore, in this parameterization the difference between the quark flavor mixing matrix obtained in the PLRT framework and that obtained in the MLRT framework lies in the \(\mathbf{P}_{q \texttt {j}}\) matrix, which is a diagonal matrix of phase factors.

From now on we will suppress the \(\texttt {j}\) index in the expressions of Eqs. (16) and (17), whereby \(\sigma _{qi}^{\texttt {j}} \equiv \sigma _{qi}\), \(\widetilde{\sigma }_{q1,2}^{\texttt {j}} \equiv \widetilde{\sigma }_{q1,2}\), and \(\widetilde{\mu }_{q 1 } = \widetilde{\mu }_{q 2 } \equiv \widetilde{\mu }_{q}\), thus \(\xi _{q 1,2}^{^{(\texttt {j})}} \equiv \xi _{q 1,2}\). The real orthogonal matrix \(\mathbf{O}_{q\texttt {j}} \equiv \mathbf{O}_{q}\) in terms of the physical quark mass ratios has the form

$$\begin{aligned} \mathbf{O}_{q \texttt {j}} = \left( \begin{array}{ccc} \sqrt{ \frac{ \widetilde{\sigma }_{q1} \delta _{q} \xi _{q2} }{ \mathcal{D}_{q1} } } &{} - \sqrt{ \frac{ \widetilde{\sigma }_{q2} \delta _{q} \xi _{q1} }{ \mathcal{D}_{q2} } } &{} \sqrt{ \frac{ \xi _{q1} \xi _{q2} }{ \mathcal{D}_{q3} } } \\ - \sqrt{ \frac{ \widetilde{\sigma }_{q1} \left( 1 - \delta _{q} \right) \xi _{q1} }{ \mathcal{D}_{q1} } } &{} \sqrt{ \frac{ \widetilde{\sigma }_{q2} \left( 1 - \delta _{q}\right) \xi _{q2} }{ \mathcal{D}_{q2} } } &{} \sqrt{ \frac{ \delta _{q} \left( 1 - \delta _{q}\right) }{ \mathcal{D}_{q3} } } \\ - \sqrt{ \frac{ \widetilde{\sigma }_{q2} \xi _{q1} }{ \mathcal{D}_{q1} } } &{} - \sqrt{ \frac{ \widetilde{\sigma }_{q1} \xi _{q2} }{ \mathcal{D}_{q2} } } &{} \sqrt{ \frac{ \widetilde{\sigma }_{q1} \widetilde{\sigma }_{q2} \delta _{q} }{ \mathcal{D}_{q3} } } \end{array} \right) , \end{aligned}$$
(19)

where

$$\begin{aligned} \begin{array}{l} \mathcal{D}_{q1} = \left( 1 - \widetilde{\sigma }_{q1} \right) \left( \widetilde{\sigma }_{q1} + \widetilde{\sigma }_{q2} \right) \left( 1 - \delta _{q}\right) , \\ \mathcal{D}_{q2} = \left( 1 + \widetilde{\sigma }_{q2} \right) \left( \widetilde{\sigma }_{q1} + \widetilde{\sigma }_{q2} \right) \left( 1 - \delta _{q} \right) ,\\ \mathcal{D}_{q3} = \left( 1 - \widetilde{\sigma }_{q1} \right) \left( 1 + \widetilde{\sigma }_{q2} \right) \left( 1 - \delta _{q}\right) . \end{array} \end{aligned}$$
(20)

3.1 Quark flavor mixing matrix

The quark flavor mixing matrix CKM emerges from the mismatch between the diagonalization of u- and d-type quark mass matrices. Therefore, this mixing matrix is defined as \(\mathbf{V}_{\mathrm {CKM}} = \mathbf{U}_{u} \mathbf{U}_{d}^{\dagger }\), where \(\mathbf{U}_{u}\) and \(\mathbf{U}_{d}\) are the unitary matrices that diagonalize to the u- and d-type quark mass matrices, respectively.

From Eq. (14) we obtain

$$\begin{aligned} \mathbf{V}_{\mathrm {CKM}}= & {} \mathbf{O}_{u1}^{\top } \, \mathbf{P}_{u1}^{*} \, \mathbf{U}_{\pi /4} \left( \mathbf{O}_{d1}^{\top } \, \mathbf{P}_{d1}^{*} \, \mathbf{U}_{\pi /4} \right) ^{\dagger } \nonumber \\= & {} e^{ i \zeta _{1} } \, \mathbf{O}_{u1}^{\top } \mathbf{P}_{1}^{( u-d )} \mathbf{O}_{d1}, \quad \text {for }{PLRT}, \nonumber \\ \mathbf{V}_{\mathrm {CKM}}= & {} \mathbf{O}_{u2}^{\top } \, \mathbf{P}_{u2} \, \mathbf{U}_{\pi /4} \left( \mathbf{O}_{d2}^{\top } \, \mathbf{P}_{d2} \, \mathbf{U}_{\pi /4} \right) ^{\dagger }\nonumber \\= & {} \mathbf{O}_{u2}^{\top } \mathbf{P}_{2}^{( u-d )} \mathbf{O}_{d2}, \quad \text {for }{MLRT}, \end{aligned}$$
(21)

where

$$\begin{aligned} \mathbf{P}_{ \texttt {j} }^{ (u-d) } = \text {diag} \left( 1 , e^{i \Theta _{ \texttt {j} } }, e^{ i \Gamma _{ \texttt {j} } } \right) , \qquad \texttt {j} = 1,2, \end{aligned}$$
(22)

with

$$\begin{aligned} \begin{array}{ll} \Theta _{1} = \!- \!\left( \beta _{u1} \!-\! \beta _{d1} + \alpha _{d1} -\alpha _{u1} \right) , &{} \Gamma _{1} = - \left( \gamma _{u1} - \gamma _{d1} + \alpha _{d1} - \alpha _{u1} \right) \\ \Theta _{2} = 0, \quad \Gamma _{2} = \gamma _{u2} - \gamma _{d2}, &{} \zeta _{1} = - \left( \alpha _{u1} - \alpha _{d1} \right) . \end{array} \end{aligned}$$
(23)

From Eqs. (19) and (22) the explicit form of CKM mixing matrix in both frameworks has the form

$$\begin{aligned} \begin{array}{ll} V_{ud}^{^{(\texttt {j})}} = \sqrt{ \frac{ \widetilde{\sigma }_{c} \widetilde{\sigma }_{s} \xi _{d1} \xi _{u1} }{ \mathcal{D}_{u1} \mathcal{D}_{d1} } } e^{ i \Gamma _{\texttt {j}} } + \sqrt{ \frac{ \widetilde{\sigma }_{d} \widetilde{\sigma }_{u} }{ \mathcal{D}_{u1} \mathcal{D}_{d1} } } \varepsilon _{11}^{^{(\texttt {j})}} , &{} V_{us}^{^{(\texttt {j})}} = \sqrt{ \frac{ \widetilde{\sigma }_{c} \widetilde{\sigma }_{d} \xi _{d2} \xi _{u1} }{ \mathcal{D}_{u1} \mathcal{D}_{d2} } } e^{ i \Gamma _{\texttt {j}} } - \sqrt{ \frac{ \widetilde{\sigma }_{s} \widetilde{\sigma }_{u} }{ \mathcal{D}_{u1} \mathcal{D}_{d2} } } \varepsilon _{12}^{^{(\texttt {j})}} , \\ V_{ub}^{^{(\texttt {j})}} = - \sqrt{ \frac{ \widetilde{\sigma }_{c} \widetilde{\sigma }_{d} \widetilde{\sigma }_{s} \delta _{d} \xi _{u1} }{ \mathcal{D}_{u1} \mathcal{D}_{d3} } } e^{ i \Gamma _{\texttt {j}} } + \sqrt{ \frac{ \widetilde{\sigma }_{u} }{ \mathcal{D}_{u1} \mathcal{D}_{d3} } } \varepsilon _{13}^{^{(\texttt {j})}} , &{} V_{cd}^{^{(\texttt {j})}} = \sqrt{ \frac{ \widetilde{\sigma }_{u} \widetilde{\sigma }_{s} \xi _{d1} \xi _{u2} }{ \mathcal{D}_{u2} \mathcal{D}_{d1} } } e^{ i \Gamma _{\texttt {j}} } - \sqrt{ \frac{ \widetilde{\sigma }_{c} \widetilde{\sigma }_{d} }{ \mathcal{D}_{u2} \mathcal{D}_{d1} } } \varepsilon _{21}^{^{(\texttt {j})}} , \\ V_{cs}^{^{(\texttt {j})}} = \sqrt{ \frac{\widetilde{\sigma }_{d} \widetilde{\sigma }_{u} \xi _{d2} \xi _{u2} }{ \mathcal{D}_{u2} \mathcal{D}_{d2} } } e^{ i \Gamma _{\texttt {j}} } + \sqrt{ \frac{ \widetilde{\sigma }_{c} \widetilde{\sigma }_{s} }{ \mathcal{D}_{u2} \mathcal{D}_{d2} } } \varepsilon _{22}^{^{(\texttt {j})}} , &{} V_{cb}^{^{(\texttt {j})}} = - \sqrt{ \frac{ \widetilde{\sigma }_{d} \widetilde{\sigma }_{u} \widetilde{\sigma }_{s} \delta _{d} \xi _{u2} }{ \mathcal{D}_{u2} \mathcal{D}_{d3} } } e^{ i \Gamma _{\texttt {j}} } + \sqrt{ \frac{ \widetilde{\sigma }_{c} }{ \mathcal{D}_{u2} \mathcal{D}_{d3} } } \varepsilon _{23}^{^{(\texttt {j})}} , \\ V_{td}^{^{(\texttt {j})}} = - \sqrt{ \frac{ \widetilde{\sigma }_{s} \widetilde{\sigma }_{c} \widetilde{\sigma }_{u} \delta _{u} \xi _{d1} }{ \mathcal{D}_{u3} \mathcal{D}_{d1} } } e^{ i \Gamma _{\texttt {j}} } + \sqrt{ \frac{ \widetilde{\sigma }_{d} }{ \mathcal{D}_{u3} \mathcal{D}_{d1} } } \varepsilon _{31}^{^{(\texttt {j})}} , &{} V_{ts}^{^{(\texttt {j})}} = - \sqrt{ \frac{ \widetilde{\sigma }_{d} \widetilde{\sigma }_{c} \widetilde{\sigma }_{u} \delta _{u} \xi _{d2} }{ \mathcal{D}_{u3} \mathcal{D}_{d2} } } e^{ i \Gamma _{\texttt {j}} } - \sqrt{ \frac{ \widetilde{\sigma }_{s} }{ \mathcal{D}_{u3} \mathcal{D}_{d2} } } \varepsilon _{32}^{^{(\texttt {j})}} , \\ V_{tb}^{^{(\texttt {j})}} = \sqrt{ \frac{\widetilde{\sigma }_{d} \widetilde{\sigma }_{s} \widetilde{\sigma }_{c} \widetilde{\sigma }_{u} \delta _{d} \delta _{u} }{ \mathcal{D}_{u3} \mathcal{D}_{d3} } } e^{ i \Gamma _{\texttt {j}} } + \sqrt{ \frac{ 1 }{ \mathcal{D}_{u3} \mathcal{D}_{d3} } } \varepsilon _{33}^{^{(\texttt {j})}} , \\ \end{array} \end{aligned}$$
(24)

where

$$\begin{aligned} \begin{array}{ll} \varepsilon _{11}^{^{(\texttt {j})}} = \sqrt{ \delta _{d} \delta _{u} \xi _{d2} \xi _{u2} } + \sqrt{ \left( 1 - \delta _{d}\right) \left( 1 - \delta _{u}\right) \xi _{d1} \xi _{u1} } e^{i \Theta _{\texttt {j}} } , &{} \quad \varepsilon _{12}^{^{(\texttt {j})}} = \sqrt{ \delta _{d} \delta _{u} \xi _{d1} \xi _{u2} } + \sqrt{ \left( 1 - \delta _{d}\right) \left( 1 - \delta _{u}\right) \xi _{d2} \xi _{u1} } e^{i \Theta _{\texttt {j}} } , \\ \quad \varepsilon _{13}^{^{(\texttt {j})}} = \sqrt{ \delta _{u} \xi _{d1} \xi _{d2} \xi _{u2} } - \sqrt{ \left( 1 - \delta _{d}\right) \left( 1 - \delta _{u}\right) \delta _{d} \xi _{u1} } e^{i \Theta _{\texttt {j}} } , &{}\quad \varepsilon _{21}^{^{(\texttt {j})}} = \sqrt{ \delta _{d} \delta _{u} \xi _{d2} \xi _{u1} } + \sqrt{ \left( 1 - \delta _{d}\right) \left( 1 - \delta _{u}\right) \xi _{d1} \xi _{u2} } e^{i \Theta _{\texttt {j}} } , \\ \quad \varepsilon _{22}^{^{(\texttt {j})}} = \sqrt{ \delta _{d} \delta _{u} \xi _{d1} \xi _{u1} } + \sqrt{ \left( 1 - \delta _{d}\right) \left( 1 - \delta _{u}\right) \xi _{d2} \xi _{u2} } e^{i \Theta _{\texttt {j}} } ,&{}\quad \varepsilon _{23}^{^{(\texttt {j})}} = - \sqrt{ \delta _{u} \xi _{d1} \xi _{d2} \xi _{u1} } + \sqrt{ \left( 1 - \delta _{d}\right) \left( 1 - \delta _{u}\right) \delta _{d} \xi _{u2} } e^{i \Theta _{\texttt {j}} } , \\ \quad \varepsilon _{31}^{^{(\texttt {j})}} = \sqrt{ \delta _{d} \xi _{d2} \xi _{u1} \xi _{u2} } - \sqrt{ \left( 1 - \delta _{d}\right) \left( 1 - \delta _{u}\right) \delta _{u} \xi _{d1} } e^{i \Theta _{\texttt {j}} } ,&{}\quad \varepsilon _{32}^{^{(\texttt {j})}} = \sqrt{ \delta _{d} \xi _{d1} \xi _{u1} \xi _{u2} } - \sqrt{ \left( 1 - \delta _{d}\right) \left( 1 - \delta _{u}\right) \delta _{u} \xi _{d2} } e^{i \Theta _{\texttt {j}} } , \\ \quad \varepsilon _{33}^{^{(\texttt {j})}} = \sqrt{ \xi _{d1} \xi _{d2} \xi _{u1} \xi _{u2} } + \sqrt{ \left( 1 - \delta _{d}\right) \left( 1 - \delta _{u}\right) \delta _{u} \delta _{d} } e^{i \Theta _{\texttt {j}} }. \end{array} \end{aligned}$$
(25)
Table 1 Numerical values obtained for the six parameters as a \(\chi ^{2}\) function at BFP. These results were obtained by considering simultaneously to \(\Theta _{1}\), \(\Gamma _{1}\), \(\widetilde{\mu }_{d}\), \(\widetilde{\mu }_{u}\), \(\delta _{d}\), and \(\delta _{u}\) as free parameters in the scan of the parameter space
Full size table

The difference between the mixing matrices obtained in the frameworks of PLRT and MLRT lies in the number of phase factors which each one contains. From the model-independent point of view, the mixing matrix obtained in MLRT is a particular case of the matrix obtained in PLRT, since we only need make zero the \(\Theta _{\texttt {j}}\) phase factor in Eq. (25).

3.2 Likelihood test \(\chi ^{2}\)

In order to verify the viability of the model for describing the phenomenology associated with quarks. The first issue that we need check is that experimental values for the masses and flavor mixing in the quark sector are correctly reproduced by the model. To carry out the above, we perform a likelihood test \(\chi ^{2}\), in which we consider the values of the quark masses reported in Ref. [10] and using the RunDec program [219], we obtain the following values for the quark mass ratios at the top quark mass scale:

$$\begin{aligned} \begin{array}{ll} \widetilde{m}_{u} = \left( 1.33 \pm 0.73 \right) \times 10^{-5}, &{} \widetilde{m}_{c} = \left( 3.91 \pm 0.42 \right) \times 10^{-3}, \\ \widetilde{m}_{d} = \left( 1.49 \pm 0.39 \right) \times 10^{-3}, &{} \widetilde{m}_{s} = \left( 2.19 \pm 0.53 \right) \times 10^{-2}. \end{array} \end{aligned}$$
(26)

For performing the likelihood test we define the \(\chi ^{2}\) function as

$$\begin{aligned} \chi ^{2} = \sum _{i=d,s,b} \frac{ \left( \left| V_{ui}^{th} \right| - \left| V_{ui}^{ex} \right| \right) ^{2} }{ \sigma _{V_{ui}}^{2} } + \frac{ \left( \left| V_{cb}^{th} \right| - \left| V_{cb}^{ex} \right| \right) ^{2} }{ \sigma _{V_{cb}}^{2} }. \end{aligned}$$
(27)

In this expression the terms with superscript “ex” are the experimental data with uncertainty \(\sigma _{V_{kl}}\), whose values are [10]

$$\begin{aligned} \begin{array}{ll} \left| V_{ud}^{ex} \right| = 0.97417 \pm 0.00021, &{} \left| V_{us}^{ex} \right| = 0.2248 \pm 0.0006 , \\ \left| V_{ub}^{ex} \right| = \left( 4.09 \pm 0.39 \right) \times 10^{-3}, &{} \left| V_{cb}^{ex} \right| = \left( 40.5 \pm 1.5 \right) \times 10^{-3}. \end{array}\nonumber \\ \end{aligned}$$
(28)

The terms with superscript “th” in the same expression correspond to the theoretical expressions for the magnitude of the entries of the quark mixing matrix CKM. From Eqs. (15), (24) and (25) we see that the number of free parameters in \(\chi ^{2}\) function is six and five for the PLRT and MLRT, respectively. However, the \(\chi ^{2}\) function depends only on four experimental data values, which correspond to the magnitude of the entries of the quark mixing matrix. In this numerical analysis, we consider the quark mixing matrix in the lower row of Eq. (21) as a particular case of the mixing matrix in the upper row of the same equation. So, in the PLRT context, when we simultaneously consider to \(\widetilde{\mu }_{d}\), \(\widetilde{\mu }_{u}\), \(\Theta _{1}\), \(\Gamma _{1}\), \(\delta _{d}\), and \(\delta _{u}\) as free parameters in the likelihood test, we would only be able to determine the values of these parameters at the best-fit point (BFP). Here, we perform a scan of the parameter space where we sought the BFP through the minimizing the \(\chi ^{2}\) function. In Table 1 we show the numerical values for the six free parameters obtained at the BFP. All these results were obtained considering the values in Eq. (26) for the quark mass ratios. The values in the first row of Table 1 are valid for the MLRT and PLRT frameworks, since \(\Theta _{1} = \Theta _{2} = 0\).

Fig. 1
figure 1

Allowed regions in the parameter space at 70% CL (blue line) and 95% CL (red dashed line). Here, the black asterisk corresponds to the BFP, while the \(\Theta \), \(\widetilde{\mu }_{u}\), and \(\widetilde{\mu }_{d}\) parameters are fixed to the values given in the first row of Table 1

Full size image

Now, the \(\Theta _{2}\), \(\widetilde{\mu }_{u}\), and \(\widetilde{\mu }_{d}\) parameters are fixed to the values given in the first row of Table 1, thus the \(\chi ^{2}\) function has one degree of freedom. In Fig. 1, we show the allowed regions in the parameter space at 70% CL and 95% CL, as well as the BFP, which is denoted by a black asterisk. The resulting values for the free parameters \(\Gamma _{1}\), \(\delta _{d}\) and \(\delta _{u}\), at 70% (95%) CL, are

$$\begin{aligned} \Gamma _{1} \left( ^{\circ } \right)= & {} 71_{- 71 }^{+ 38 } \left( _{- 71 }^{+ 43 } \right) , \nonumber \\ \quad \delta _{u} \left( 10^{-1} \right)= & {} 1.210_{-0.966}^{+2.146} \left( _{-1.180}^{+2.270} \right) , \quad \nonumber \\ \delta _{d} \left( 10^{-1} \right)= & {} 1.514_{-1.126}^{+2.303} \left( _{-1.422}^{+2.446} \right) . \end{aligned}$$
(29)

In the BFP we find that \(\chi ^{2}_{\mathrm {min}} = 8.102 \times 10^{-1}\). From the likelihood test \(\chi ^{2}\) we find that the magnitudes of all quark mixing matrix elements, at 95% CL, are

$$\begin{aligned} \left( \begin{array}{ccc} 0.97433 \pm 0.00018 &{} 0.22508_{-0.00078}^{+0.00080} &{} \left( 4.09_{-0.62}^{+0.60} \right) \times 10^{-3} \\ 0.22481_{-0.00083}^{+0.00076} &{} 0.97356_{-0.00020}^{+0.00021} &{} \left( 4.053_{-0.241}^{+0.230} \right) \times 10^{-2} \\ \left( 1.1942_{-0.1156}^{+0.1914} \right) \times 10^{-2} &{} \left( 3.8948_{-0.2714}^{+0.2176} \right) \times 10^{-2} &{} 0.999170_{-0.000096}^{+0.000094} \end{array} \right) . \end{aligned}$$
(30)

The Jarlskog invariant is

$$\begin{aligned} J_{\mathrm {CP}} = \mathcal{I}m \left( V_{ud} V_{cs} V_{us}^{*} V_{cd}^{*} \right) = \left( 2.92_{-0.29}^{+0.38} \right) \times 10^{-5} . \end{aligned}$$
(31)

All these values are in good agreement with the experimental data. Also, the results of the above likelihood test can be considered as predictions of the PLRT and MLRT theoretical frameworks. This is so because when \(\Theta _{1} = \Theta _{2} = 0\) the two schemes are equivalent.

4 Lepton sector

As can be verified straightforwardly, the \(\mathbf{M}_{e}\) charged lepton mass matrix is diagonalized by \(\mathbf{U}_{e L}=\mathbf{S}_{23}\mathbf{P}_{e}\) and \(\mathbf{U}_{e R}=\mathbf{S}_{23}{} \mathbf{P}^{\dagger }_{e}\) in the case of PLRT and \(\mathbf{U}_{e L}=\mathbf{S}_{23}\) and \(\mathbf{U}_{e R}=\mathbf{S}_{23}\) in the MLRT

$$\begin{aligned} \mathbf{S}_{23}=\begin{pmatrix} 1 &{} 0 &{} 0 \\ 0 &{} 0 &{} 1 \\ 0 &{} 1 &{} 0 \end{pmatrix}, \quad \mathbf{P}_{e}= \text {diag} \left( e^{i\eta _{e}/2}, e^{i\eta _{\mu }/2}, e^{i\eta _{\tau }/2} \right) , \end{aligned}$$
(32)

with \(\vert m_{e}\vert =\vert a_{e}\vert \), \(\vert m_{\mu }\vert =\vert b_{e}-c_{e}\vert \) and \(\vert m_{\tau }\vert =\vert b_{e}+c_{e}\vert \) for the former framework and \( m_{e}=a_{e}\), \(m_{\mu }= b_{e}-c_{e}\) and \(m_{\tau }=b_{e}+c_{e}\) in the second one.

The \(\mathbf{M}_{\nu }\) neutrino mass matrix, which comes from the type I see-saw mechanism, is parametrized as

$$\begin{aligned} \mathbf{\mathcal {M}_{\nu }}\approx \begin{pmatrix} A_{\nu }&{} -B_{\nu }(1-\epsilon ) &{} -B_{\nu }(1+\epsilon ) \\ -B_{\nu }(1-\epsilon )&{} C_{\nu }(1-2\epsilon ) &{} D_{\nu } \\ -B_{\nu }(1+\epsilon )&{} D_{\nu } &{} C_{\nu }(1+2\epsilon ) \end{pmatrix} \end{aligned}$$
(33)

where \(A_{\nu }\), \(B_{\nu }\), \(C_{\nu }\) and \(D_{\nu }\) are complex parameters; \(\epsilon \) is a complex and real free parameter in the PLRT and MLRT frameworks, respectively. Along with this, the \(\epsilon \) parameter was considered as a perturbation to the effective mass matrix such that \(\vert \epsilon \vert \le 0.3\) in order to break softly the \(\mu \leftrightarrow \tau \) symmetry. Thus, the \(\left| \epsilon \right| ^{2}\) quadratic terms were neglected in the above matrix. Let us remark that the above neutrino mass matrix has already been rotated by the \(\mathbf{S}_{23}\) orthogonal matrix. As shown in [58], the \(\mathbf{{M}_{\nu }}\) effective neutrino mass matrix is diagonalized by \(\mathbf{U}_{\nu }\approx \mathbf{S}_{23}{} \mathbf{\mathcal {U}_{\nu }}\) such that \(\hat{\mathbf{M}}_{\nu }=\text {diag.}(m_{\nu _{1}}, m_{\nu _{2}}, m_{\nu _{3}})\approx \mathbf{U}^{\dagger }_{\nu }{} \mathbf{M}_{\nu }\mathbf{U}^{*}_{\nu }=\mathbf{\mathcal {U}^{\dagger }_{\nu }}{} \mathbf{\mathcal {M}_{\nu }}\mathbf{\mathcal {U}^{*}_{\nu }}\) where \(\mathbf{\mathcal U}_{\nu }\approx \mathbf{\mathcal {U}^{0}_{\nu }}{} \mathbf{\mathcal {U}^{\epsilon }}_{\nu }\). Here, \(\mathbf{\mathcal {U}^{0}_{\nu }}\) diagonalizes the \(\mathbf{\mathcal {M}^{0}_{\nu }}\) neutrino mass matrix with exact \(\mu \leftrightarrow \tau \) symmetry (\(\left| \epsilon \right| =0\)); this means that \(\mathbf{\mathcal {U}^{0 T}_{\nu }}{} \mathbf{\mathcal {{M}}^{0}_{\nu }}\) \(\mathbf{\mathcal {U}^{0}_{\nu }}=\hat{\mathbf{M}}^{0}_{\nu }=\text {diag}(m^{0}_{\nu _{1}}, m^{0}_{\nu _{2}}, m^{0}_{\nu _{3}})\). Along with this, the \(\epsilon \) parameter breaks the \(\mu \leftrightarrow \tau \) symmetry so that its contribution to the mixing matrix is contained in \(\mathbf{\mathcal {U}^{\epsilon }_{\nu }}\). We have

$$\begin{aligned} \mathbf{\mathcal {U}}^{0}_{\nu }&=\begin{pmatrix} \cos {\theta }_{\nu }~e^{i(\eta _{\nu }+\pi )} &{}\quad \sin {\theta }_{\nu }~e^{i(\eta _{\nu }+\pi )} &{}\quad 0 \\ -\frac{\sin {\theta }_{\nu }}{\sqrt{2}}&{}\quad \frac{\cos {\theta }_{\nu }}{\sqrt{2}} &{}\quad -\frac{1}{\sqrt{2}} \\ -\frac{\sin {\theta }_{\nu }}{\sqrt{2}}&{}\quad \frac{\cos {\theta }_{\nu }}{\sqrt{2}} &{}\quad \frac{1}{\sqrt{2}} \end{pmatrix},\nonumber \\ \mathbf{\mathcal {U}}^{\epsilon }_{\nu }&\quad \approx \begin{pmatrix} N_{1}&{}\quad 0 &{}\quad -N_{3}\sin {\theta }r_{1}\epsilon \\ 0 &{}\quad N_{2} &{}\quad N_{3}\cos {\theta _{\nu }}r_{2}\epsilon \\ N_{1}\sin {\theta _{\nu }}r_{1}\epsilon &{}\quad -N_{2}\cos {\theta _{\nu }}r_{2}\epsilon &{}\quad N_{3}, \end{pmatrix} \end{aligned}$$
(34)

where \(r_{(1, 2)}\equiv (m^{0}_{\nu _{3}}+m^{0}_{\nu _{(1, 2)}})/(m^{0}_{\nu _{3}}-m^{0}_{\nu _{(1, 2)}})\) and the \(N_{i}\), the normalization factors, are given by

$$\begin{aligned}&N_{1}=\left( 1+\sin ^{2}{\theta _{\nu }}\vert r_{1}\epsilon \vert ^{2}\right) ^{-1/2},\quad \nonumber \\&N_{2}=\left( 1+\cos ^{2}{\theta _{\nu }}\vert r_{2}\epsilon \vert ^{2}\right) ^{-1/2},\quad \nonumber \\&N_{3}=\left( 1+\sin ^{2}{\theta _{\nu }}\vert r_{1}\epsilon \vert ^{2}+\cos ^{2}{\theta _{\nu }}\vert r_{2}\epsilon \vert ^{2}\right) ^{-1/2}. \end{aligned}$$
(35)

Let us emphasize that two relative Majorana phases will be considered along this work in which the \(m^{0}_{\nu _{3}}\) neutrino mass is kept positive. Explicitly, we have \(\hat{\mathbf{M}}^{0}_{\nu }=\text {diag}(m^{0}_{\nu _{1}}, m^{0}_{\nu _{2}}, m^{0}_{\nu _{3}})= \text {diag}(\vert m^{0}_{\nu _{1}}\vert e^{i\alpha }, \vert m^{0}_{\nu _{2}}\vert e^{i\beta },\vert m^{0}_{\nu _{3}}\vert )\) where the associate Majorana phase of \(m^{0}_{\nu _{3}}\) has been absorbed in the neutrino field.

4.1 Lepton flavor mixing matrix

In the PLRT (MLRT) case, we found that \(V_\mathrm{PMNS}\approx \mathbf{P}^{\dagger }_{e}{} \mathbf{\mathcal {U}^{0}_{\nu }\mathbf{\mathcal {U}^{\epsilon }_{\nu }}}\) (\(\approx \mathbf{\mathcal {U}^{0}_{\nu }\mathbf{\mathcal {U}^{\epsilon }_{\nu }}}\)). Explicitly,

$$\begin{aligned}&\mathbf{V}_\mathrm{PMNS}\approx \mathbf{P}^{\dagger }_{e}\nonumber \\&\quad \times \begin{pmatrix} \cos {\theta _{\nu }}N_{1}&{} \sin {\theta _{\nu }}N_{2}&{} \sin {2\theta _{\nu }}\frac{N_{3}}{2}(r_{2}-r_{1})\epsilon \\ -\frac{\sin {\theta _{\nu }}}{\sqrt{2}}N_{1}(1+r_{1}\epsilon )&{} \frac{\cos {\theta _{\nu }}}{\sqrt{2}}N_{2}(1+r_{2}\epsilon ) &{} -\frac{N_{3}}{\sqrt{2}}\left[ 1-\epsilon ~r_{3}\right] \\ -\frac{\sin {\theta _{\nu }}}{\sqrt{2}}N_{1}(1-r_{1}\epsilon )&{} \frac{\cos {\theta _{\nu }}}{\sqrt{2}}N_{2}(1-r_{2}\epsilon ) &{} \frac{N_{3}}{\sqrt{2}}\left[ 1+\epsilon ~ r_{3}\right] \end{pmatrix} \end{aligned}$$
(36)

with \(r_{3}\equiv r_{2}\cos ^{2}{\theta _{\nu }}+r_{1}\sin ^{2}{\theta _{\nu }}\) and \(\mathbf{P}^{\prime }_{e}=\text {diag}.(e^{i(\eta _{e}/2-\eta _{\nu }-\pi )}, e^{i\eta _{\mu }/2}, e^{i\eta _{\tau }/2})\). On the other hand, comparing the magnitude of entries \(\mathbf{V}_\mathrm{PMNS}\) with the mixing matrix in the standard parametrization of the PMNS, we obtain the following expressions for the lepton mixing angles:

$$\begin{aligned} \sin ^{2}{\theta }_{13}&=\vert \mathbf{V}_{13}\vert ^{2} =\frac{\sin ^{2}{2\theta _{\nu }}}{4}N^{2}_{3}\vert \epsilon \vert ^{2}~\vert r_{2}-r_{1} \vert ^{2},\nonumber \\ \sin ^{2}{\theta }_{23}&=\dfrac{\vert \mathbf{V}_{23}\vert ^{2}}{1-\vert \mathbf{V}_{13}\vert ^{2}}=\dfrac{N^{2}_{3}}{2}\frac{\vert 1-\epsilon ~r_{3} \vert ^{2}}{1- \sin ^{2}{\theta _{13}}},\nonumber \\ \sin ^{2}{\theta _{12}}&=\dfrac{\vert \mathbf{V}_{12}\vert ^{2}}{1-\vert \mathbf{V}_{13}\vert ^{2}}= \dfrac{N^{2}_{2}\sin ^{2}{\theta _{\nu }}}{1-\sin ^{2}{\theta }_{13}}. \end{aligned}$$
(37)

In these mixing angles there are four free parameters namely, the absolute neutrino masses, two relative Majorana phase, the \(\epsilon \) parameter and the \(\theta _{\nu }\) angle. Some parameters could be reduced under certain considerations as follows: the \(\theta _{\nu }\) parameter, in good approximation, coincides with the solar angle \(\theta _{12}\) since we are in the limit of a soft breaking \(\mu \leftrightarrow \tau \) symmetry so the normalization factors, \(N_{i}\), are expected to be of the order 1, then \(\theta _{12}=\theta _{\nu }\). Along with this, the mixing angles may be written in terms of one relative Majorana phase and to do so we just have to observe that the reactor angle is nonnegligible when \(\left| r_{2}-r_{1}\right| ^{2}\) is large. We have

$$\begin{aligned} \left| r_{2}-r_{1}\right| ^{2}=\frac{4\left| m^{0}_{\nu _{3}}\right| ^{2}\left| m^{0}_{\nu _{2}}-m^{0}_{\nu _{1}}\right| ^{2}}{\left| m^{0}_{\nu _{3}}-m^{0}_{\nu _{1}}\right| ^{2}\left| m^{0}_{\nu _{3}}-m^{0}_{\nu _{2}}\right| ^{2}}. \end{aligned}$$
(38)

This happens if \(\beta -\alpha =\pi \); then we have

$$\begin{aligned} \left| m^{0}_{\nu _{2}}-m^{0}_{\nu _{1}}\right| ^{2}&=\left[ \left| m^{0}_{\nu _{2}}\right| +\left| m^{0}_{\nu _{1}}\right| \right] ^{2},\nonumber \\ \left| m^{0}_{\nu _{3}}-m^{0}_{\nu _{1}}\right| ^{2}&=\left| m^{0}_{\nu _{3}}\right| ^{2}+\left| m^{0}_{\nu _{1}}\right| ^{2}-2\left| m^{0}_{\nu _{1}}\right| \left| m^{0}_{\nu _{3}}\right| \cos {\alpha }\nonumber \\ \left| m^{0}_{\nu _{3}}-m^{0}_{\nu _{2}}\right| ^{2}&=\left| m^{0}_{\nu _{3}}\right| ^{2}+\left| m^{0}_{\nu _{2}}\right| ^{2}+2\left| m^{0}_{\nu _{2}}\right| \left| m^{0}_{\nu _{3}}\right| \cos {\alpha }, \end{aligned}$$
(39)

where the last two factors enhance the former one in order to get allowed values for the reactor angle. In addition, the factors \(r_{2}\) and \(r_{1}\) can be written in terms of the only relative Majorana phase, \(\alpha \). Then

$$\begin{aligned} r_{1}=\frac{\left| m^{0}_{\nu _{3}}\right| +\left| m^{0}_{\nu _{1}}\right| e^{i\alpha }}{\left| m^{0}_{\nu _{3}}\right| -\left| m^{0}_{\nu _{1}}\right| e^{i\alpha }},\quad r_{2}=\frac{\left| m^{0}_{\nu _{3}}\right| -\left| m^{0}_{\nu _{2}}\right| e^{i\alpha }}{\left| m^{0}_{\nu _{3}}\right| +\left| m^{0}_{\nu _{2}}\right| e^{i\alpha }}. \end{aligned}$$
(40)

In this way, the Majorana phases are related by the expression already mentioned, \(\beta -\alpha =\pi \). This analysis is valid for PLRT and MLRT; however, in the latter framework the \(\epsilon \) parameter is real.

4.2 Likelihood test \(\chi ^{2}\)

Once we fix the \(\theta _\nu \) parameter to the solar neutrino mixing angle \(\theta _{12}\), the \(\chi ^{2}\) analysis can be carried out to find the allowed values of the three remaining free parameters \(\epsilon \), the Majorana phase \(\alpha \) and the mass of the lightest (common) neutrino \(\left| m^{0}_{\nu _{3}}\right| \)(\(m_0\)). Two of the absolute neutrino masses can be written as a function of the lightest mass and \(\Delta m_{ij}^2\) as follows:

$$\begin{aligned} \vert m^{0}_{\nu _{2}}\vert= & {} \sqrt{\Delta m^{2}_{13}+\Delta m^{2}_{21}+\vert m^{0 }_{\nu _{3}}\vert ^{2}},\nonumber \\ \vert m^{0}_{\nu _{1}}\vert= & {} \sqrt{\Delta m^{2}_{13}+\vert m^{0}_{\nu _{3}}\vert ^{2}}\qquad \text {Inverted Hierarchy}\nonumber \\ \vert m^{0}_{\nu _{3}} \vert= & {} \sqrt{\Delta m^{2}_{31}+m^{2}_{0}},\nonumber \\ \vert m^{0}_{\nu _{2}} \vert= & {} \sqrt{\Delta m^{2}_{21}+m^{2}_{0}} \quad \text {Degenerate Hierarchy,} \end{aligned}$$
(41)

where \(\vert m^{0 }_{\nu _{3}}\vert \) and \(m_{0}\) (\(\gtrsim 0.1~eV\)) are the lightest and common neutrino masses for the inverted and degenerate ordering, respectively.

Fig. 2
figure 2

Allowed regions in the \(\sin (\alpha )\)–\(\epsilon \) plane, at 90%CL (blue) and 95% CL (red) for degenerate (left) and inverted (right) hierarchy. In this case the \(\theta _\nu \) parameter is fixed to the solar angle, and \(m_{0,3}\) is marginalized

Full size image
Fig. 3
figure 3

Allowed regions in the \(\sin (\alpha )\)–\(\epsilon \) plane, at 90%CL (blue) and 95% CL (red) for degenerate (left) and inverted (right) hierarchy. The \(\theta _\nu \) parameter is fixed to the solar angle and \(\epsilon \) is marginalized

Full size image

In this analysis, the normal hierarchy will be left out since this was discarded in the previous analytical study [58]. The inverted and the degenerate hierarchies will be discussed next.

The \(\chi ^{2}\) function is built as

$$\begin{aligned} \chi ^{2}\Bigg (\epsilon ,\alpha ,m_{0}\Bigg (\Bigg |m^{0}_{\nu _{3}}\Bigg |\Bigg )\Bigg )= & {} \frac{\Bigg (\sin ^{2 }{\theta ^{th}_{13}}-\sin ^{2 }{\theta ^{ex}_{13}}\Bigg )^{2}}{\sigma ^{2}_{13}}\nonumber \\&+\frac{\Bigg (\sin ^{2 }{\theta ^{th}_{23}}-\sin ^{2}{\theta ^{ex}_{23}}\Bigg )^{2}}{\sigma ^{2}_{23}}, \end{aligned}$$
(42)

where the experimental data and theoretical expressions for the mixing angles are given in Eqs. (2) and (37), respectively. We use the absolute neutrino masses in Eq. (41) as a function of \(m_{0} (|m^{0}_{\nu _{3}}|)\), fixing \(\Delta m^2_{ij}\) to the central values of the global fit [17] and letting \(m_{0} (|m^{0}_{\nu _{3}}|)\) as a free parameter. For \(\sigma _{13}\) and \(\sigma _{23}\) we take the one sigma upper and lower uncertainties using summation in quadrature.

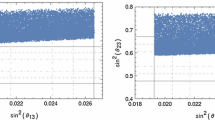
The results of the minimization of the \(\chi ^2\) function are shown in Figs. 2, 3 and 4; we show the allowed regions at 90% and 95% CL in the plane of pairs of the three parameters marginalizing the \(\chi ^2\) function for the parameter not shown. In the left (right) panel is shown the case of a degenerate (inverted) hierarchy for each figure. We notice that the \(\alpha \) parameter is more constrained in the case of an inverted hierarchy than in the degenerate hierarchy case, and that the fit prefers smaller values of the \(\epsilon \) parameter in the case of an inverted hierarchy. For illustration purposes only we show the BFP in each case as a black dot.

Fig. 4
figure 4

Allowed regions in the \(m_0\)–\(\epsilon \) plane, at 90%CL (blue) and 95% CL (red) for degenerate (left) and inverted (right) hierarchy. Again, the \(\theta _\nu \) parameter is fixed to the solar angle and the \(\alpha \) Majorana phase is marginalized

Full size image

From comparison of our \(\chi ^2\) analysis with the qualitative analysis in [58] we find that a wide region of the parameter space is still statistically compatible with the experimental data.

4.3 Prediction on the effective Majorana mass of the electron neutrino

From the neutrino oscillation experiments, we get information on the mass squared differences, but these experiments cannot say anything about the absolute neutrino mass scale. However, there are three processes that can address directly the determination of this important parameter: (i) analysis of CMB temperature fluctuations [220], (ii) single \(\beta \) decay [221] and (iii) neutrinoless double beta decay (\(0\nu \beta \beta \)) [222].

Fig. 5
figure 5

Effective mass \(\vert m_{ee} \vert \) as a function of the common mass \( m_{0}\) in the case of degenerate hierarchy or of the lightest neutrino mass \(\left| m^{0}_{\nu _{3}}\right| \) for inverted hierarchy. The horizontal regions defined by the blue dotted and purple dashed lines correspond to the limits by GERDA phase II [223] and KamLAND-Zen [224], respectively

Full size image

Here, we only focus on the last process which occurs if neutrinos are Majorana particles. With this decay process we can probe the absolute neutrino mass scale by measuring of the effective Majorana mass of the electron neutrino, which is defined by

$$\begin{aligned} \vert m_{ee} \vert = \left| \sum _{i=1}^{3} m_{\nu _{i}} V_{ei}^{2} \right| . \end{aligned}$$
(43)

The lowest upper bound on \(\vert m_{ee}\vert < 0.22\) eV was provided by GERDA phase-I data [225]. That value has been significantly reduced by GERDA phase-II data [226]; see Fig. 5. According to our model, the above quantity can be addressed directly using the fitted free parameters. Therefore, the plot in Fig. 5 shows the predicted regions for the effective Majorana mass of the electron neutrino.

5 Conclusions

We performed a complete study on the fermion masses and flavor mixing in the non-minimal left–right symmetric model where the scalar sector was extended by three Higgs bidoublets, three right-handed (left-handed) triplets. The lepton sector has been previously studied in [58], where the Majorana phases were considered as CP parities (0 or \(\pi \)). In the present analysis we obtained precise formulas for the mixing angles with arbitrary Majorana phases, and a chi squared statistical analysis was performed in order to fix the relevant free parameters using the updated neutrino oscillation data. Our results are in good agreement with [58], when fixed Majorana phases are considered.

On the other hand, we do this analysis for the first time in the quark sector where the quark mass matrices come out being symmetric and hermitian in the PLRT and MLRT frameworks, respectively. In the hadronic sector of the PLRT (MLRT) framework, we write the quarks flavor mixing matrix, CKM, in terms of quark mass ratios, two shifted mass parameters \(\widetilde{\mu }_{d}\) and \(\widetilde{\mu }_{u}\), two parameters \(\delta _{d}\) and \(\delta _{u}\), two (one) phase factors. So, the difference between the CKM matrices obtained in the PLRT and MLRT framework lies in the number of phase factors; namely, in PLRT we have two phase factors, \(\Gamma _{1}\) and \(\Theta _{1}\), while in MLRT we have only one, \(\Theta _{2}\). Therefore, the quark flavor mixing matrix in MRLT is a particular case of the CKM matrix obtained in PRLT, since we only need take \(\Theta _{2}=0\). We performed a likelihood test \(\chi ^{2}\), in which the \(\Theta _{2}\), \(\widetilde{\mu }_{u}\), and \(\widetilde{\mu }_{d}\) parameters are fixed to the values given in the first row of the Table 1. Thus the \(\chi ^{2}\) function has one degree of freedom. All values obtained in this \(\chi ^{2}\) analysis are in good agreement with the experimental data. Also, these values can be considered as predictions of the PLRT and MLRT theoretical frameworks, because when \(\Theta _{1} = \Theta _{2} = 0\) the two schemes are equivalent. The rich phenomenology of the model provides a region of the parameter space that is statistically compatible with the experimental data.