Abstract
A light singlino is a promising candidate for dark matter, and a light higgsino is natural in the parameter space of the NMSSM. We study the combined constraints on this scenario resulting from the dark matter relic density, the most recent results from direct detection experiments, LEP and the LHC. In particular limits from a recent search for electroweak production of charginos and neutralinos at \(\sqrt{s}=13\) TeV after 35.9 fb\(^{-1}\) by CMS and constraints on spin-independent dark matter–nucleon cross sections from XENON1T after 1 tonne \(\times \) year exposure are considered. We find that scenarios with higgsino masses below \(\sim 250\) GeV as well as singlino masses below \(\sim 100\) GeV are strongly constrained depending, however, on assumptions on the bino mass parameter \(M_1\). Benchmark points and branching fractions for future searches at the LHC are proposed.
Similar content being viewed by others
Explore related subjects
Find the latest articles, discoveries, and news in related topics.Avoid common mistakes on your manuscript.
1 Introduction
One of the promising aspects of supersymmetric extensions of the Standard Model is the natural presence of dark matter if R-parity is unbroken and the lightest supersymmetric particle (LSP) is neutral. Candidates for such LSPs are the neutral electroweak gauginos (bino and wino), the neutral fermionic partners of Higgs doublets (higgsinos) and, in the Next-to-Minimal Supersymmetric Standard Model (NMSSM), the fermionic partner of a scalar singlet (singlino).
Experiments searching for interactions of dark matter with standard matter have made considerable progress in the last years. The absence of signals has lead to upper bounds on dark matter-standard matter interaction cross sections, both in spin-independent (SI) and in spin-dependent (SD) channels. Such upper bounds have been obtained recently in SI channels by the PandaX-II [1], LUX [2] and XENON1T collaborations [3, 4], and in SD channels by the PICO-2L [5], LUX [6] and PandaX-II [7] collaborations.
Since the higgsino mass parameter \(\mu \) is supersymmetric, a large value \(|\mu | \gg M_Z\) would generate a “little fine-tuning problem”: The potential for the scalar Higgs doublets \(H_u\) and \(H_d\) contains positive mass terms \(|\mu |^2\), but it must be unstable at the origin to trigger \(SU(2)\times U(1)\) symmetry breaking. Hence at least one of the positive mass terms \(|\mu |^2\) must be cancelled by a negative soft supersymmetry breaking mass term. In order to generate Higgs vacuum expectation values (vevs) of \(\mathcal{O} (M_Z)\ll |\mu |\), this cancellation would have to be fine-tuned if \(|\mu | \gg M_Z\). Hence a higgsino mass parameter \(|\mu |\) not far above \(M_Z\) is natural.
However, assuming a standard thermal history of the universe and that the lightest supersymmetric particle (LSP) accounts for the complete relic density \(\Omega _{DM} h^2 \sim 0.1187\) in agreement with WMAP/Planck [8, 9], mostly higgsino-like dark matter is strongly constrained. In order to avoid a too large annihilation rate its mass is \(\gtrsim 1\) TeV according to [10,11,12,13,14,15,16] unless scalar top squarks (stops) are very heavy [17, 18] or \(\mu < 0\) [19].
In the NMSSM an effective \(\mu \) parameter is generated by the vev of a scalar singlet S, \({\mu _{\mathrm{{eff}}}} = \lambda \left\langle S \right\rangle \) [20, 21]. The fermionic partner of S, the singlino, is a promising dark matter candidate [22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56] which can account for the observed relic density and have sufficiently small dark matter-standard matter interaction cross sections, see Sect. 3. The singlino can be very light; then \(\mu _\text {eff}\) can be small as well (provided the higgsinos remain heavier than the singlino) solving this “little fine-tuning problem”. Only a lower bound \(|\mu _\text {eff}|\gtrsim 100\) GeV originates from the non-observation of a charged higgsino at LEP. Hence the “light higgsino–singlino scenario” in the NMSSM is quite attractive [57,58,59,60,61,62,63] (although an explanation of the galactic center gamma-ray excess seems to be difficult [64]).
Higgsinos (and winos) can be produced at colliders through electroweak processes. Denoting the lightest chargino by \(\chi ^\pm _1\) and the neutralinos by \(\chi ^0_i\) (ordered in mass) their typical decays are \(\chi ^\pm _1 \rightarrow W^{\pm (*)} + \chi ^0_1\), \(\chi ^0_i \rightarrow Z^{(*)} + \chi ^0_1\) or \(\chi ^0_i \rightarrow H^{(*)} + \chi ^0_1\) (\(i > 1\)) where H can correspond to the SM-like Higgs boson \(H_{SM}\) or, notably in the NMSSM, to a lighter mostly singlet-like CP-even or CP-odd scalar.
The most promising search channel is then \(pp \rightarrow W^{\pm *} \rightarrow \chi ^\pm _1 + \chi ^0_i\) with \(E_T^{miss}\) and three leptons from leptonic decays of \(W^{\pm (*)}\) and \(Z^{(*)}\) [65,66,67]. At the LHC with 13 TeV c.m. energy and \(\sim 36\) fb\(^{-1}\) of integrated luminosity these signatures – including hadronic decays of W and Z, and \(\chi ^0_i \rightarrow H_{SM} + \chi ^0_1\) – have been searched for by ATLAS [68,69,70,71] and CMS [72, 73]. No significant excesses have been observed which leads to upper bounds on \(\chi ^\pm _1 + \chi ^0_i\) production cross sections.
It is the aim of the present paper to study the combined constraints on the light higgsino–singlino scenario in the NMSSM from the dark matter relic density, spin-dependent and spin-independent direct detection experiments and from neutralino/chargino searches at the LHC at 36 fb\(^{-1}\).
We consider two \({\mathbb Z}_3\)-invariant versions of the NMSSM: the phenomenological model (pNMSSM) with arbitrary parameters at the weak scale, and the Non Universal Higgs model (NUH-NMSSM) with universal gaugino masses \(M_{1/2}\), universal sfermion masses masses \(m_0\) and universal sfermion trilinear soft terms \(A_0\) but arbitrary Higgs soft masses \(m_{H_u}\), \(m_{H_d}\) and \(m_S\) as well as Higgs trilinear soft terms \(A_\lambda \) and \(A_\kappa \).
We assume heavy squark, slepton and gluino masses well above 1 TeV; the squark and gluino masses have no impact on the light higgsino–singlino scenario. On the other hand bino and/or wino masses \(M_1\) and \(M_2\), respectively, can affect the production cross sections and branching fractions of the (mostly) higgsino-like chargino and neutralinos through mixing (see below). We consider two versions of the pNMSSM, both with \(M_2=600\) GeV but one with \(M_1=300\) GeV, another one with \(M_1\) arbitrary. In the NUH-NMSSM a (conservative) lower bound \(M_3 \gtrsim 1.6\) TeV on the gluino mass term at the weak scale implies \(M_{1/2}\gtrsim 440\) GeV and hence \(M_1\gtrsim 220\) GeV, \(M_2\gtrsim 370\) GeV at the weak scale. \(M_1\), \(M_2\) have some impact on \(A_\lambda \) and \(A_\kappa \) at the weak scale via the renormalization group equations, hence the NUH-NMSSM implies some correlations among the parameters of the pNMSSM. The scans over the parameter spaces are performed with help of the public code NMSSMTools [74,75,76]. The dark matter relic density and the spin-dependent and spin-independent direct detection cross sections are computed with help of micrOMEGAS_3 [77].
In the next section we review the relevant parts of the neutralino sector of the NMSSM, and in Sect. 3 the impact of a viable dark matter relic density and bounds from direct dark matter detection experiments. In Sect. 4 we discuss the implementation of bounds from searches for \(Z+W+E_T^{miss}\) at the LHC, in Sect. 5 the resulting constraints in the plane \(M_{\chi ^0_1}\) vs. \(M_{\chi ^\pm _1}\). In Sect. 6 we propose benchmark points and planes, and discuss realistic branching fractions to be used for future searches; Sect. 7 is devoted to a summary.
2 The neutralino sector of the NMSSM
We consider the \({\mathbb Z}_3\) invariant NMSSM with the superpotential
where the dots denote the Yukawa couplings of the superfields \(\hat{H}_u\) and \(\hat{H}_d\) to the quarks and leptons as in the MSSM. Once the scalar component of the superfield \(\hat{S}\) develops a vev \(\left\langle S \right\rangle \equiv s\), the first term in \(W_\text {NMSSM}\) generates an effective \(\mu \)-term with
Subsequently the index \(_\mathrm {eff}\) of \(\mu \) will be omitted for simplicity. \(\mu \) generates Dirac mass terms for the charged and neutral SU(2) doublet higgsinos \(\psi _u\) and \(\psi _d\).
In the “decoupling” limit \(\lambda , \kappa \rightarrow 0\) all components of the superfield \(\hat{S}\) decouple from all components of \(\hat{H}_u,\ \hat{H}_d\) and the matter superfields. However, since \(s\sim M_{Susy}/\kappa \) where \(M_{Susy}\) denotes the scale of soft Susy breaking masses and trilinear couplings, \(\mu _\mathrm {eff}\) remains of \(\mathcal{O}(M_{Susy})\) in the decoupling limit provided \(\lambda /\kappa \sim \mathcal{O}(1)\).
Including bino (\(\widetilde{B}\)) masses \(M_1\) and wino (\(\widetilde{W}^3\)) masses \(M_2\), the symmetric \(5 \times 5\) neutralino mass matrix \(\mathcal{M}_0\) in the basis \(\psi ^0 = (-i\widetilde{B} , -i\widetilde{W}^3, \psi _d^0, \psi _u^0, \psi _S)\) is given by [21]
where \(v_u^2 + v_d^2 =v^2 \simeq (174\ \text {GeV})^2\) and \(\frac{v_u}{v_d}=\tan \beta \). The eigenstates of \(\mathcal{M}_0\) are denoted by \(\chi _i^0\), \(i=1\ldots 5\) ordered in mass. Henceforth the LSP is identified with \(\chi _1^0\).
Another important rôle will be played by the singlet-like scalar and pseudoscalar Higgs masses. The CP-even sector comprises three physical states which are linear combinations of the real components \((H_{dR}, H_{uR}, S_R)\). The (3,3) element of the \(3 \times 3\) CP-even mass matrix \(\mathcal{M}_S^2\) reads in this basis
up to mixing it corresponds to the mass squared of the mostly singlet-like eigenstate. Another eigenstate must correspond to a Standard Model-like Higgs boson \(H_{SM}\) with its mass \(\sim 125\) GeV and nearly Standard Model-like couplings to quarks, leptons and gauge bosons. A third MSSM-like eigenstate has a mass of about \(\displaystyle {2\frac{\mu (A_\lambda +\kappa s)}{\sin 2\beta }}\). In the regions of the parameter space of interest here we always find that the mostly singlet-like eigenstate is the lightest CP-even scalar \(H_1\), the Standard-Model-like Higgs boson \(H_{SM}\) is the second lightest CP-even scalar \(H_2\), and the MSSM-like state is the third CP-even scalar \(H_3\).
The CP-odd sector consists in linear combinations of the imaginary components \((H_{dI}, H_{uI}, S_I)\). The (3,3) element of the \(3 \times 3\) CP-odd mass matrix \(\mathcal{M}_P^2\) reads in this basis
again it corresponds essentially to the mass squared of the mostly singlet-like eigenstate. Other eigenstates are the electroweak Goldstone boson, and an MSSM-like eigenstate again with a mass of about \(\displaystyle {2\frac{\mu (A_\lambda +\kappa s)}{\sin 2\beta }}\). The masses of the MSSM-like Higgs bosons are bounded from below by constraints from \(b\rightarrow s + \gamma \) on the charged Higgs boson whose mass is similar to the ones of the CP-even and CP-odd neutral scalars, and by direct searches [78, 79]. Subsequently the lightest mostly singlet-like CP-odd eigenstate will be denoted by \(A_1\).
From Eqs. (2.3)–(2.5) one can derive the sum rule [80]
which relates, up to modifications by mixing, the singlet-like neutralino, CP-even and CP-odd Higgs masses. In the decoupling limit, or for sizeable \(\tan \beta \) (i.e. small \(v_d\)) and not too large \(A_\lambda \) and Yukawa couplings \(\lambda \) and \(\kappa \), the last term in Eq. (2.6) is negligible.
3 Dark matter relic density and direct detection
As sketched in the Introduction, under the assumption of a standard thermal history of the universe and \(|\mu |\) well below 1 TeV the mostly singlet-like neutralino \(\psi _S\) remains practically the only viable candidate for dark matter. Its annihilation rate must be sufficiently large such that its relic density today complies with the WMAP/Planck value \(\Omega _{DM}h^2\simeq 0.1187\) [8, 9]. Various processes can give rise to a large enough annihilation cross section:
-
1.
Annihilation via a pseudoscalar in the s-channel. At least for singlino masses \(M_{\chi _1^0}\) below \(\mu \) as assumed here this pseudoscalar is the singlet-like \(A_1\) with its mass given in Eq. (2.5) (up to a small shift through mixing). \(M_{A_1}\) should be about \(2\times M_{\chi _1^0}\) such that the annihilation cross section is enhanced by the s-channel pole (depending on \(\kappa \) and the mixing of \(A_1\) with the MSSM-like SU(2)-doublet pseudoscalar which induces its couplings to quarks and leptons). For \(M_{\chi _1^0}\) above \(\approx 100\) GeV, \(M_{A_1}\) and hence the width of \(A_1\) increase and \(M_{A_1}\) can be smaller than \(2\times M_{\chi _1^0}\) allowing for LSP annihilation via \(A_1^* \rightarrow A_1+H_1\) provided \(M_{H_1}\) is small enough. For \(M_{\chi _1^0}\) above \( m_{top}\) the annihilation via \(A_1^* \rightarrow t\bar{t}\)x becomes possible.
-
2.
Annihilation via the Z boson or the Standard Model-like Higgs boson \(H_{SM}\) in the s-channel if the singlino mass is about half the Z or \(H_{SM}\) mass.
-
3.
Annihilation via a far off-shell Z boson into \(t\bar{t}\) if \(M_{\chi _1^0}> m_{top}\).
-
d)
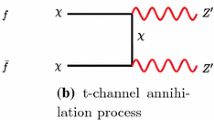
Annihilation into a pair of W / Z bosons via (higgsino-like) chargino/neutralino exchange in the t-channel. This t-channel process is strong enough to be dominant only for singlino masses above \(\sim 100\) GeV.
-
4.
Coannihilation with higgsinos becomes relevant for \(M_{\chi _1^0}\sim \mu \).
-
5.
Coannihilation with staus \(\tilde{\tau }\) becomes relevant for \(M_{\chi _1^0}\sim M_{\tilde{\tau }}\).
In the case of annihilation via \(A_1 \sim S_I\) in the s-channel with a pseudoscalar mass about twice the mass of the singlino Eq. (2.6) leads to
implying an intolerable negative CP-even scalar mass squared if off-diagonal terms in the mass matrices and the terms \(\sim v_u v_d\) are neglected, unavoidably in the decoupling limit \(\lambda , \kappa \rightarrow 0\). Hence most scenarios with singlino annihilation via a \(A_1\) in the s-channel are not compatible with the decoupling limit; in such scenarios we found \(\lambda \gtrsim 0.2\) (see Fig. 4 below). Only if the mostly singlino-like LSP is lighter than \(\sim 20\) GeV, smaller values of \(\lambda \) can suffice to generate the required mixing in the neutralino mass matrix (2.3) in order to avoid \(M_{H_1}^2 < 0\). Still \(M_{H_1}\) tends to be small, and \(A_\lambda \) to be large in this scenario.
The most recent and most stringent constraints on dark matter detection direct cross sections are from Xenon1T [4] (spin-independent) and PandaX-II [7] (spin-dependent). These constraints are still very weak for LSP masses below a few GeV, but affect the present scenario for LSP masses above \(\sim 5\) GeV.
Contributions to spin-independent singlino-nucleon cross sections originate from exchanges of the SM-like Higgs boson and the mostly singlet-like \(H_1\) in the t-channel. The coupling of the latter to nucleons is even smaller than the one of the SM-like Higgs boson, but \(H_1\) is typically much lighter (see above) and has larger couplings to the mostly singlino-like LSP. The contributions from the SM-like Higgs boson and \(H_1\) interfere negatively leading to blind spots, and can thus reduce the spin-independent singlino-nucleon cross section below the neutrino floor [32, 35, 48, 56].
At first sight the upper bounds on spin-dependent singlino-nucleon cross sections are about five orders of magnitude weaker. However, contributions to spin-dependent LSP-nucleon cross sections originate from Z-exchange in the t-channel, and Z–nucleon couplings are much larger than Higgs–nucleon couplings. A \(\chi ^0_1-\chi ^0_1-Z\) coupling originates from higgsino components of the mostly singlino-like \(\chi ^0_1\) induced by mixing \(\sim \lambda \). For a light mostly singlino-like LSP and not too small \(\tan \beta \) this higgsino component is \(\approx \lambda \times (174\ \text {GeV}/\mu )\), which is thus bounded from above by upper limits on the spin-dependent singlino-nucleon cross section depending on \(M_{\chi ^0_1}\) from PandaX-II. (For LSP masses below a few GeV where constraints from direct detection are weak, the higgsino component of the LSP is still bounded from above by its contribution to the invisible Z width.)
4 Constraints from searches for charginos and neutralinos at the LHC
As stated in the Introduction, the most stringent LHC bounds originate from searches for \(pp \rightarrow \chi ^\pm _1 + \chi ^0_i \rightarrow W^\pm + Z + E_T^{miss}\), dominantly from trileptons. The absence of significant excesses can be interpreted as upper bounds on production cross sections times branching fractions of charginos and neutralinos within simplified models. In Figs. 7 and 8a in [73], upper bounds on production cross sections of charginos \(\chi ^\pm _1\) and neutralinos \(\chi ^0_2\) are given as function of their mass (assumed to be degenerate), and the mass of \(\chi ^0_1\). We used the data in root format underlying these figures. In the same figures, limits on \(M_{\chi ^\pm _1}\) as function of \(M_{\chi ^0_1}\) are given assuming 100% branching fractions for the decays \(\chi ^\pm _1 \rightarrow W^{\pm (*)} + \chi ^0_1\) and \(\chi ^0_2 \rightarrow Z^{(*)} + \chi ^0_1\), and assuming production cross sections for wino-like charginos \(\chi ^\pm _1\) and neutralinos \(\chi ^0_2\).
As a first step we re-interprete the data as upper bounds on the sum of production cross sections times branching fractions of pure higgsino-like charginos \(\chi ^\pm \) and higgsino-like neutralinos \(\chi ^0_2\) and \(\chi ^0_3\) assuming \(M_{\chi ^\pm } = M_{\chi ^0_2} = M_{\chi ^0_3}\), as function of \(M_{\chi ^\pm }\) and the mass of \(\chi ^0_1\). Note that the production cross section for higgsinos is only half the one for winos despite the sum over \(\chi ^0_2\) and \(\chi ^0_3\). (Higgsino pair production has also been considered by ATLAS and CMS in [68, 69, 72, 73]. The assumed higgsino decays there differ, however, significantly from the scenario considered here where the higgsino decays are similar to the ones assumed for winos in [68, 69, 72, 73].)
It is instructive to compare this upper bound for a light LSP of mass \(M_{\chi ^0_1}=5\) GeV to the production cross sections of pure higgsino-like charginos and neutralinos, assuming a common higgsino mass. The upper limits from CMS in [73] are shown as function of a common chargino/neutralino mass as a red line in Fig. 1; the zig-zag behaviour (present in the root files) seems to originate from the combination of different signal regions. The sum of production cross sections for pure higgsino-like charginos and both higgsino-like neutralinos from the LHC SUSY Cross Section Working Group twiki page [81, 82] is shown as a blue line.
Red line: upper limits on the production cross section times branching fraction for \(pp \rightarrow \chi ^\pm _1 + \chi ^0_i \rightarrow W^\pm + Z + E_T^{miss}\), assuming \(M_{\chi ^0_1}=5\) GeV and 100% branching fractions for the decays \(\chi ^\pm _1 \rightarrow W^{\pm (*)} + \chi ^0_1\) and \(\chi ^0_2 \rightarrow Z^{(*)} + \chi ^0_1\), from [73]. Blue line: production cross sections from the LHC SUSY Cross Section Working Group twiki page for degenerate pure higgsino-like charginos and a pair of higgsino-like neutralinos
One observes that the limits are compatible with the production of pure higgsino-like charginos and higgsino-neutralinos only if their branching fractions into the considered final states are below 100%; the upper limits on these branching fractions are stronger for smaller \(\mu \). Hence we have to shed some light on the branching fractions of the higgsino-like charginos and neutralinos in the present scenario.
First, unless the stau’s or the bino are light, the chargino decay \(\chi ^\pm _1 \rightarrow W^{\pm (*)} + \chi ^0_1\) is the only possible decay and has a branching ratio of 100%. The possible decays of the neutral higgsinos \(\chi ^0_{2,3}\) are more involved: The couplings allowing for \(\chi ^0_{2,3} \rightarrow Z^{(*)} + \chi ^0_1\) originate from the higgsino components \(\sim \lambda \) of \(\chi ^0_1\), hence these partial widths are of \(\mathcal{O}(\lambda ^2)\) in the decoupling limit. Yukawa couplings for the decays \(\chi ^0_{2,3} \rightarrow H_{SM} + \chi ^0_1\) do not require mixing, but are induced by the term \(\lambda \hat{S} \hat{H}_u\cdot \hat{H}_d\) in the superpotential. Consequently these partial widths are equally of \(\mathcal{O}(\lambda ^2)\).
We find that, if both decays into Z and \(H_{SM}\) are kinematically allowed and after averaging over \(\chi ^0_{2}\) and \(\chi ^0_{3}\), \(BR(\chi ^0_{2,3} \rightarrow Z^{(*)} + \chi ^0_1)\approx 50-70\%\), and \(BR(\chi ^0_{2,3} \rightarrow H_{SM} + \chi ^0_1)\approx 30-50\%\). Upper bounds on the latter process have also been provided by CMS in [73], but the corresponding limits are considerably weaker than the ones from \(\chi ^0_{2,3} \rightarrow Z^{(*)} + \chi ^0_1\) (to which we confine ourselves). Hence an enhanced \(BR(\chi ^0_{2,3} \rightarrow H_{SM} + \chi ^0_1)\) alleviates the constraints from [73], and this happens notably for a bino mass term \(M_1\) close to \(\mu \) which induces bino components of the \(\chi ^0_{2,3}\) through mixing. These bino components reduce the couplings of \(\chi ^0_{2,3}\) to Z (but not to \(H_{SM}\)) and reduce their production cross sections. For these reasons the constraints from [73] are weaker for \(M_1\sim \mu \), but stronger for \(M_1\gg \mu \).
Additional allowed decays are \(\chi ^0_{2,3} \rightarrow H_{1} + \chi ^0_1\) and \(\chi ^0_{2,3} \rightarrow A_1 + \chi ^0_1\) with mostly singlet-like and possibly very light \(H_1\) and \(A_1\). The corresponding Yukawa couplings can originate from the term \(\frac{\kappa }{3} \hat{S}^3\) in the superpotential and singlino components of \(\chi ^0_{2,3}\), or from the term \(\lambda \hat{S} \hat{H}_u\cdot \hat{H}_d\) in the superpotential and higgsino components of \(\chi ^0_1\). However, both Yukawa couplings relevant for decays into \(H_1,\ A_1\) are considerably smaller than the ones for decays into Z or \(H_{SM}\), and the branching fractions are negligible unless on-shell decays into Z (and hence into \(H_{SM}\)) are kinematically impossible. In these latter cases the \(BR(\chi ^0_{2} \rightarrow H_1 + \chi ^0_1)\) can become \(\sim 100\%\).
Another exception are light binos with masses below the ones of higgsinos (which are now \(\chi ^0_{3,4}\)). Then, if kinematically allowed, decays \(\chi ^0_{3,4} \rightarrow H_1 + \chi ^0_2\) can have sizeable branching fractions. These imply more involved decay cascades of \(\chi ^0_{3,4}\) which we consider (conservatively) not to contribute to the signals studied in [73].
On the other hand the decays into both Z and \(H_{SM}\) dominate in most of the parameter space consistent with constraints from dark matter, and generally both decays have similar branching fractions of \(\mathcal{O}\)(30–70%).
In the realistic light higgsino–singlino scenario of the NMSSM considered here, the mostly higgsino-like fermions \(\chi ^\pm _1\), \(\chi ^0_2\) and \(\chi ^0_3\) are not exactly degenerate due to mixing, but the masses satisfy typically \(M_{\chi ^0_3}\gtrsim M_{\chi ^\pm _1} \gtrsim M_{\chi ^0_2}\) with \(M_{\chi ^0_3}-M_{\chi ^\pm _1} \sim M_{\chi ^\pm _1}-M_{\chi ^0_2} \lesssim \mathcal{O}(20\) GeV). Mixing affects also their production cross sections and branching fractions, the latter are computed using the code NMSDECAY [76] (based on SDECAY [85]). In order to obtain limits on these realistic scenarios into the considered final states we proceed as follows:
First we consider separately the pairs \(P_1=\chi ^\pm _1\), \(\chi ^0_2\) (with typically \(M_{\chi ^0_2} < M_{\chi ^\pm _1}\)) and \(P_2=\chi ^\pm _1\), \(\chi ^0_3\) (with typically \(M_{\chi ^0_3} > M_{\chi ^\pm _1}\)). Using Prospino 2 at NLO [86] we compute the production cross section at 13 TeV assuming pure higgsinos. For both \(P_1\) and \(P_2\), the production cross sections are weighted by \(X_1/(X_1+X_2)\), \(X_2/(X_1+X_2)\), respectively, where \(X_i\) are the products of the corresponding couplings squared of \(\chi ^0_i,\ \chi ^\pm _1\) to \(W^{\pm }\) (relevant for the production cross section) and the branching fractions \(BR(\chi ^0_i \rightarrow Z^{(*)} + \chi ^0_1)\). (For a bino mass \(M_1 \lesssim \mu \), \(\chi ^0_2\) and \(\chi ^0_3\) should be replaced by the mostly higgsino-like neutralinos here and below.)
Regions in the pNMSSM with heavy squarks, sleptons and gauginos which are excluded by the combined constraints from the dark matter relic density, limits on spin-dependent and spin-independent dark matter direct detection cross sections, and searches by CMS [73]. Red: arbitrary bino mass \(M_1 \sim \mu \) or \(M_1 < \mu \). Blue: \(M_1=300\) GeV
Decays into \(H_{SM}\), \(H_1\) and \(A_1\), on which the limits are much weaker, are not taken into account for estimates of the signal strength. Hence our limits will be conservative.
Next we look for a triplet of degenerate higgsinos with common mass \(M_h\) which would have the same production cross section times branching fraction. The contributions of \(P_1\) and \(P_2\) to the effective production cross section times branching fraction of the “fictitious” degenerate triplet are considered according to their relative weights \(X_i/(X_1+X_2)\). \(M_h\) is found from a table as function of \(M_{\chi ^0_3}-M_{\chi ^\pm _1}\) and \(M_{\chi ^\pm _1}-M_{\chi ^0_2}\) constructed again with help of Prospino. Typically one finds \(M_h \sim M_{\chi ^\pm _1}\).
Finally, the effective production cross section times branching fraction of the “fictitious” degenerate triplet is rescaled (mildly) by the ratio of higgsino production cross section from [81, 82] with respect to Prospino 2, and compared to the upper bounds in the data files corresponding to Figs. 7 and 8a in [73], whichever is stronger.
5 Results
We parametrize the higgsino–singlino scenario by \(M_{\chi ^0_1}\) and \(M_{\chi ^\pm _1}\approx \mu \). In Fig. 2 we show which regions are excluded by the combined constraints from the dark matter relic density, limits on spin-dependent and spin-independent dark matter direct detection cross sections, and CMS [73], for arbitrary bino mass \(M_1\) in red. Assuming \(M_1\gtrsim 300\) GeV, the blue regions are excluded in addition. (The structures for \(M_{\chi ^0_1}\sim \,\)5–60 GeV and \(M_{\chi ^\pm _1}\sim \,\)190–270 GeV originate from corresponding structures in the data files corresponding to Figs. 7 and 8a in [73].)
The following remarks are in order: First, in the diagonal red band for \(M_{\chi ^0_1}\lesssim M_{\chi ^\pm _1}\) the LSP has a large higgsino component through mixing, and the relic density is reduced below the WMAP/Planck value via coannihilation. In the blue/red “bulk” for \(M_{\chi ^0_1}\gtrsim 65\) GeV the combined constraints from the relic density and direct detection cannot be satisfied simultaneously. The constraints from CMS are not important there.
For \(M_{\chi ^0_1}\lesssim 65\) GeV the constraints from CMS start to play the dominant rôle and exclude regions notably for singlinos below the Z and \(H_{SM}\) funnels for dark matter annihilation. As discussed above these constraints from CMS depend on the assumptions on \(M_1\), and are stronger for \(M_1 \gtrsim 300\) GeV.
Around the Z-funnel (\(M_{\chi ^0_1}\sim 45\) GeV) and the \(H_{SM}\) funnel (\(M_{\chi ^0_1}\sim 62\) GeV) the singlet-like (pseudo-)scalars \(H_1/A_1\) are not needed for dark matter annihilation. The resulting freedom in the NMSSM parameter space allows them to be light and to have sizeable couplings to the neutral higgsinos \(\chi ^0_{2,3}\). This allows for large branching fractions for \(\chi ^0_{2,3}\rightarrow \chi ^0_1 +H_1/A_1\) which circumvent the constraints from searches for \(\chi ^0_{2,3} \rightarrow Z/H_{SM} + \chi ^0_1\).
Hence, both due to the reduced production cross sections for higgsino-like charginos/neutralinos and reduced branching fractions into the W / Z final states, the excluded regions are considerably smaller than for simplified models in [68, 69, 72, 73] assuming wino-like charginos/neutralinos.
Next we consider the NUH-NMSSM. In Fig. 3 we show possible points in the \(M_{\chi ^0_1}-M_{\chi ^\pm _1}\) plane satisfying the combined constraints from the dark matter relic density, dark matter direct detection and CMS as before. In addition we show the necessary fine tuning among the parameters at the GUT scale. The measure for fine tuning is the one of Barbieri and Giudice [83] implemented in NMSSMTools following [84]. We are aware of the fact that the measure for fine tuning in [83] has to be taken with care and might sometimes be misleading (too strong), but it serves nevertheless as a rough handwaving guide. For a given couple \(M_{\chi ^0_1}-M_{\chi ^\pm _1}\) the fine tuning is not unique but depends also on other parameters; the points selected for Fig. 3 (and others below) correspond to the minimal possible fine tuning within bins of size \(1~\text {GeV}\times 1~\text {GeV}\).
One finds that the complete unexcluded white (and parts of the blue) region in Fig. 2 is also allowed in the NUH-NMSSM. Regions where the fine tuning is relatively weak (not far above \(10^2\), i.e. light blue) correspond to different LSP annihilation processes:
-
(i)
Along \(M_{\chi ^0_1} \lesssim M_{\chi ^\pm _1}\): co-annihilation with higgsinos, and/or annihilation among higgsinos before these decay into the nearly degenerate \(\chi ^0_1\);
-
(ii)
via Z- or \(H_{SM}\) funnels for \(M_{\chi ^0_1} \approx 45\) GeV or \(M_{\chi ^0_1} \approx 62\) GeV;
-
(iii)
via a pseudoscalar in the s channel if \(M_{\chi ^0_1} \lesssim 30\) GeV and \(M_{\chi ^\pm _1}\gtrsim 200\) GeV;
-
(iv)
via both a pseudoscalar and a far off-shell \(Z\rightarrow t\bar{t}\) for \(M_{\chi ^0_1} \gtrsim 175\) GeV.
Annihilation via a pseudoscalar in the s channel is also typical in the other regions. Large fine tuning is required notably in regions where the constraints from trilepton searches at the LHC are strong (recall that these are not continuous in \(M_{\chi ^\pm _1}\)); then large radiative corrections to the Higgs sector (i.e. large stop masses) are necessary in order to satisfy simultaneously the constraints from direct detection and the relic density.
The different dark matter annihilation processes imply different dark matter detection cross sections. On the left hand side of Fig. 4 we show the spin-independent dark matter–proton cross section \(\sigma _{pSI}\) for points with minimal fine tuning. In the region i) where co-annihilation with higgsinos and/or annihilation among higgsinos reduces the \(\chi ^0_1\) relic density to the observed value, \(\chi ^0_1\) can be very singlino-like implying a small \(\sigma _{pSI}\). A very singlino-like \(\chi ^0_1\) corresponds to small higgsino–singlino mixing or a small coupling \(\lambda \), see the right hand side of Fig. 4. Also annihilation of a light \(\chi ^0_1\) (\(M_{\chi ^0_1} \lesssim 20\) GeV) via a light pseudoscalar in the s channel (or of a heavier \(\chi ^0_1\) via the \(H_{SM}\) or Z funnels) can correspond to a mostly singlino-like \(\chi ^0_1\) in order to avoid a too small relic density, implying \(\lambda \lesssim 0.2\). In most of the other regions where annihilation proceeds via a pseudoscalar in the s channel one finds \(\lambda \gtrsim 0.2\), i.e. not too small according to the arguments given below Eq. (3.1).
\(\sigma _{pSI}\) can even fall below the expected background from neutrinos [87], see Fig. 5 (a phenomenon observed before in [32, 35, 48, 53, 56]). This can happen for \(M_{\chi ^0_1} \lesssim 20\) GeV, and for larger \(M_{\chi ^0_1}\) in the region i). Such small cross sections can also occur for larger \(\lambda \) (see the dark blue regions/spots corresponding to \(\sigma _{pSI}\lesssim 10^{-13}\) pb on the left hand side of Fig. 4), due to negative interferences among the t-channel exchanges of the SM-like Higgs boson and \(H_1\).
\(\sigma _{pSI}\) (in pb) as function of \(M_{\chi ^0_1}\) for points with minimal fine tuning together with the expected background from neutrinos [87] as a black line
6 Benchmark points and planes
6.1 \(W + Z/H_{SM}\) final states
As we have seen the searches for \(pp\rightarrow \chi ^\pm + \chi ^0_i\) with \(\chi ^\pm \rightarrow W^{\pm } + \chi ^0_1\), \(\chi ^0_i \rightarrow Z + \chi ^0_1\) or \(\chi ^0_i \rightarrow H_{SM} + \chi ^0_1\) cover also regions of the parameter space of the light higgsino–singlino sector.
We recall that the realistic scenarios within the NMSSM differ from the simplified models used for current interpretations of limits on cross sections times branching fractions as follows:
-
Two neutral higgsino-like neutralinos can be produced together with a higgsino-like chargino. These three states are not exactly degenerate due to mixing. Mixing with the singlino (and/or the bino) also reduces their production cross sections relative to pure higgsino-like states. It would be desirable if the experimental collaborations could check the uncertainty introduced by the replacement of a degenerate chargino-higgsino system by a non-degenerate one using a weighting according to production cross sections and branching fractions as above. If these uncertainties are not too large, benchmark planes employing degenerate chargino-neutralino systems can simulate realistic scenarios within the NMSSM with reasonable accuracy. (Non-degenerate higgsinos have been considered by ATLAS in [68]. However, there the lighter higgsino was assumed to be the LSP.)
-
Branching fractions are different. Whereas the \(BR(\chi ^\pm _1\rightarrow \chi ^0_1 + W^{\pm (*)})\) is (nearly) always 100%, the ones of the two neutral higgsino-like neutralinos can vary over wide ranges; examples are given for benchmark points in Table 1. All points satisfy constraints from the dark matter relic density and direct dark matter detection. (Branching fractions into \(A_1\) are always below 4% and omitted for simplicity.)
For all points P1– P6 the sums of the branching fractions \(BR(\chi ^0_{2,3} \rightarrow Z + \chi ^0_1)\) and \(BR(\chi ^0_{2,3} \rightarrow H_{SM} + \chi ^0_1)\) are close to or above 90%. The individual branching fractions of \(\chi ^0_{2,3}\) vary considerably; the average branching fractions are, however, quite stable: 50%–70% into \(Z + \chi ^0_1\), 50%–30% into \(H_{SM} + \chi ^0_1\). Even for P6, where only off-shell decays of \(\chi ^0_{2,3}\rightarrow X + \chi ^0_1\) are possible, one finds \(BR(\chi ^0_{2} \rightarrow Z^* + \chi ^0_1)\sim 100\%\). P1– P3 correspond to a relatively light \(\chi ^0_{1}\). Using the averaging described above we find that they are not far from being excluded, hence they may serve to test the averaging described above.
Benchmark planes: In terms of a single \(\chi ^0_{2}\) representing the average branching fractions of \(\chi ^0_{2}\) and \(\chi ^0_{3}\) and assuming \(M_{\chi ^\pm _1} = M_{\chi ^0_2} = M_{\chi ^0_3}\), it remains useful to study upper limits on production cross sections in the plane \(M_{\chi ^\pm _1} - M_{\chi ^0_1}\). For the branching fractions of \(\chi ^0_{2}\) it is reasonable to assume \(BR(\chi ^0_{2} \rightarrow Z + \chi ^0_1)=50\%\), \(BR(\chi ^0_{2} \rightarrow H_{SM} + \chi ^0_1)=50\%\) (as already done in Fig. 8c in [73]) or \(BR(\chi ^0_{2} \rightarrow Z + \chi ^0_1)=70\%\), \(BR(\chi ^0_{2} \rightarrow H_{SM} + \chi ^0_1)=30\%\).
6.2 \(W + H_1/A_1\) final states
If the mostly singlet-like scalars \(H_1\) and/or pseudoscalars \(A_1\) are light and \(M_{\chi ^0_{2,3}} - M_{\chi ^0_{1}} < M_Z\), the branching fractions \(BR(\chi ^0_{2,3}\rightarrow \chi ^0_1 + H_1/A_1)\) can become dominant. The points P7–P9 in Table 2 correspond to such cases.
For P7 and P8, only the lighter higgsino \(\chi ^0_{2}\) decays via \(H_1\), whereas the heavier higgsino \(\chi ^0_{2}\) still prefers decays via an off-shell \(Z^*\). For P9 decays via \(H_1\) or \(A_1\) are dominant for both higgsinos. Although \(H_1\) and \(A_1\) have \(\sim 90\%\) branching fractions into \(b\bar{b}\) the fact that their (generally different) masses are not known a priori will make it hard to detect such scenarios despite possibly large production cross section like for P7 and P9. Note that \(\chi ^\pm _{1}\) will decay via an off-shell \(W^*\).
Benchmark planes: Still we propose studies in the plane \(M_{\chi ^\pm _1} - M_{\chi ^0_1} < M_Z\) for such scenarios. Instead of \(W + Z/H_{SM}\) final states the aims are now \(W^{(*)} + Z/H_1\) or pure \(W^{(*)} + H_1\) final states. Dedicated studies could start with different assumptions on \(M_{H_1}\), and optimize cuts correspondingly. Such studies seem necessary in order to cover all scenarios of light higgsino decays in the NMSSM.
6.3 Light binos and staus
For the previous points P1–P9 the bino mass parameter \(M_1\) satisfies \(M_1 > \mu \), and the production of the bino-like \(\chi ^0_4\) plays little role, see the cross sections in the last line of Table 2. The sitation changes if \(M_1 \lesssim \mu \) and \(\chi ^0_2\) is mostly bino-like, but \(\chi ^0_{3,4}\) are mostly higgsino-like. Now, due to mixing, all \(\chi ^0_{2,3,4}\) can have sizeable production cross sections (still together with \(\chi ^\pm _1\)), see P10–P12 in Table 2.
Moreover new decay cascades become possible. An example is P10 where \(\chi ^0_{4}\) decays dominantly into \(\chi ^0_{2}+ H_1\), and subsequently \(\chi ^0_{2}\) decays dominantly into \(\chi ^0_{1}+ A_1\). This point is thus both interesting and challenging.
Finally staus \(\tilde{\tau }\) (scalar partners of a right- or left handed tau or tau-neutrino) can be lighter than the higgsinos. Then both charged and neutral higgsinos can have large branching fractions into these states.
Decays of (degenerate) charginos/neutralinos into staus have been considered by CMS in [88]. Limits on production cross sections as function of \(M_{\chi ^\pm }\) and \(M_{\chi _1^0}\) depend on the assumed stau mass. The derived limits in the \(M_{\chi ^\pm }-M_{\chi _1^0}\) plane can be quite strong for \(M_{\tilde{\tau }}\) near \(M_{\chi ^\pm }\), but production cross sections for wino-like charginos/neutralinos are assumed. For higgsino-like charginos/neutralinos as considered here these limits will be weaker.
An example is given by P12 in Table 2 for which the stau masses are \(M_{\tilde{\tau }_1} \sim 178\) GeV, \(M_{\tilde{\nu }_\tau } \sim 162\) GeV. Here \(\chi ^0_{2}\) is also dominantly bino-like. One finds quite different decays for the three neutralinos \(\chi ^0_{2,3,4}\), but the branching fractions into \(\tilde{\tau }^\pm \) and/or \(\tilde{\nu }_\tau \) are sizeable. Not shown in Table 2 are the branching fractions of \(\chi ^\pm _1\) which are now \(BR(\chi ^\pm _1\rightarrow \tilde{\nu }_\tau + \tau ^\pm )\sim 34\%\), \(BR(\chi ^\pm _1\rightarrow \tilde{\tau }_1^\pm + \nu _\tau )\sim 3\%\) with 63% remaining for \(\chi ^\pm _1\rightarrow \chi ^0_1 + W^\pm \).
7 Summary
Light singlinos in the NMSSM are still promising candidates for dark matter, and light higgsinos (a \(\mu \) parameter not too far above the electroweak scale) are natural. Since the direct detection cross sections for singlino-like dark matter may fall below the neutrino floor, searches for this scenario at colliders are particularly relevant. The first purpose of the present paper is to interpret recent searches for electroweak production of supersymmetric particles at the LHC in this scenario, combined with constraints from dark matter.
Given the extended parameter space and the extended neutralino sector of the NMSSM implying wide ranges of masses, mixing angles and branching fractions, this is not a simple task. Here we assume not only that the singlino has all required properties of a good dark matter candidate, but also that winos have masses \(\gtrsim 600\) GeV which is motivated by wino-gluino mass unification at the GUT scale and lower bounds on the gluino mass. (Since wino decay cascades would be lengthy and very different from simplified models, constraints on wino pair production cannot be applied here. Allowing for lighter winos would require separate analyses.)
Within these assumptions our derived limits can be considered as quite conservative since we did not combine the W / Z final state with other search channels or other higgsino pair production modes. Still we find that the limits from CMS in [73] exclude regions of \(M_{\chi ^\pm _1}\sim \mu \) which would be allowed by constraints on dark matter alone. Assuming a bino mass above \(\sim 300\) GeV, motivated again by gaugino mass unification at the GUT scale and lower bounds on the gluino mass, few regions with \(M_{\chi ^\pm _1}\lesssim 250\) GeV remain viable for a singlino mass below \(\sim 60\) GeV.
However, we have also identified scenarios which are not visible in the search for \(W + Z/H_{SM}\) final states: Neutralino decays into NMSSM specific light scalars or pseudoscalars instead of \(Z/H_{SM}\), mixed bino-higgsino scenarios leading to possibly more involved decay chains, and notably staus lighter than higgsinos. All these scenarios are favoured by the good properties of the singlino LSP as dark matter. Since these different scenarios would have different impacts on all supersymmetric particle decay cascades their studies merit considerable efforts.
To this end we propose benchmark points and planes. These differ from simplified models by non degenerate higgsinos, and by different branching fractions. At least once different signal regions are combined using ranges of branching fractions discussed in Sect. 5 we are convinced that future searches at the LHC can test considerably more promising regions in the singlino–higgsino mass plane. In general the consequences of these unconventional scenarios are essentially that the sums of the branching fractions into \(W + Z/H_{SM}\) final states do not add up to 100%, i.e. upper limits on these branching fractions as function of the involved masses will be insufficient sources of information.
References
A. Tan et al. [PandaX-II Collaboration], Phys. Rev. Lett. 117(12), 121303 (2016). arXiv:1607.07400 [hep-ex]
D.S. Akerib et al. [LUX Collaboration], Phys. Rev. Lett. 118(2), 021303 (2017). arXiv:1608.07648 [astro-ph.CO]
E. Aprile et al. [XENON Collaboration], Phys. Rev. Lett. 119(18), 181301 (2017). arXiv:1705.06655 [astro-ph.CO]
E. Aprile et al. [XENON Collaboration]. arXiv:1805.12562 [astro-ph.CO]
C. Amole et al. [PICO Collaboration], Phys. Rev. D 93(6), 061101 (2016). arXiv:1601.03729 [astro-ph.CO]
D.S. Akerib et al. [LUX Collaboration], Phys. Rev. Lett. 116(16), 161302 (2016). arXiv:1602.03489 [hep-ex]
C. Fu et al. [PandaX-II Collaboration], Phys. Rev. Lett. 118(7), 071301, (2017). Erratum: [Phys. Rev. Lett. 120(4), 049902, (2018)].arXiv:1611.06553 [hep-ex]
G. Hinshaw et al. [WMAP Collaboration], Astrophys. J. Suppl. 208, 19 (2013). arXiv:1212.5226 [astro-ph.CO]
P.A.R. Ade et al. [Planck Collaboration], Astron. Astrophys. 571, A16 (2014). arXiv:1303.5076 [astro-ph.CO]
H. Baer, V. Barger, H. Serce, Phys. Rev. D 94(11), 115019 (2016). arXiv:1609.06735 [hep-ph]
P. Athron et al. [GAMBIT Collaboration], Eur. Phys. J. C 77(12), 824 (2017). arXiv:1705.07935 [hep-ph]
S. Profumo, T. Stefaniak, L. Stephenson Haskins, Phys. Rev. D 96(5), 055018 (2017). arXiv:1706.08537 [hep-ph]
L. Roszkowski, E.M. Sessolo, S. Trojanowski, Rep. Prog. Phys. 81(6), 066201 (2018). arXiv:1707.06277 [hep-ph]
E. Bagnaschi, Eur. Phys. J. C 78(3), 256 (2018). arXiv:1710.11091 [hep-ph]
K. Kowalska, E.M. Sessolo, Adv. High Energy Phys. 2018, 6828560 (2018). arXiv:1802.04097 [hep-ph]
H. Baer, V. Barger, D. Sengupta, X. Tata, Is natural higgsino-only dark matter excluded? arXiv:1803.11210 [hep-ph]
P. Huang, R.A. Roglans, D.D. Spiegel, Y. Sun, C.E.M. Wagner, Phys. Rev. D 95(9), 095021 (2017). arXiv:1701.02737 [hep-ph]
M. Badziak, M. Olechowski, P. Szczerbiak, Phys. Lett. B 770, 226 (2017). arXiv:1701.05869 [hep-ph]
M. Abdughani, L. Wu, J.M. Yang, Eur. Phys. J. C 78(1), 4 (2018). arXiv:1705.09164 [hep-ph]
M. Maniatis, Int. J. Mod. Phys. A 25, 3505 (2010). arXiv:0906.0777 [hep-ph]
U. Ellwanger, C. Hugonie, A.M. Teixeira, Phys. Rep. 496, 1 (2010). arXiv:0910.1785 [hep-ph]
D.G. Cerdeno, C. Hugonie, D.E. Lopez-Fogliani, C. Munoz, A.M. Teixeira, JHEP 0412, 048 (2004). arXiv:hep-ph/0408102
G. Belanger, F. Boudjema, C. Hugonie, A. Pukhov, A. Semenov, JCAP 0509, 001 (2005). arXiv:hep-ph/0505142
D.G. Cerdeno, E. Gabrielli, D.E. Lopez-Fogliani, C. Munoz, A.M. Teixeira, JCAP 0706, 008 (2007). arXiv:hep-ph/0701271
V. Barger, P. Langacker, I. Lewis, M. McCaskey, G. Shaughnessy, B. Yencho, Phys. Rev. D 75, 115002 (2007). arXiv:hep-ph/0702036
G. Belanger, C. Hugonie, A. Pukhov, JCAP 0901, 023 (2009). arXiv:0811.3224 [hep-ph]
D. Albornoz Vasquez, G. Belanger, C. Boehm, A. Pukhov, J. Silk, Phys. Rev. D 82, 115027 (2010). arXiv:1009.4380 [hep-ph]
M. Perelstein, B. Shakya, Phys. Rev. D 88(7), 075003 (2013). arXiv:1208.0833 [hep-ph]
J. Kozaczuk, S. Profumo, Phys. Rev. D 89(9), 095012 (2014). arXiv:1308.5705 [hep-ph]
J. Cao, C. Han, L. Wu, P. Wu, J.M. Yang, JHEP 1405, 056 (2014). arXiv:1311.0678 [hep-ph]
J.S. Kim, T.S. Ray, Eur. Phys. J. C 75, 40 (2015). arXiv:1405.3700 [hep-ph]
U. Ellwanger, C. Hugonie, JHEP 1408, 046 (2014). arXiv:1405.6647 [hep-ph]
K. Ishikawa, T. Kitahara, M. Takimoto, Phys. Rev. Lett. 113(13), 131801 (2014). arXiv:1405.7371 [hep-ph]
T. Han, Z. Liu, S. Su, JHEP 1408, 093 (2014). arXiv:1406.1181 [hep-ph]
C. Cheung, M. Papucci, D. Sanford, N.R. Shah, K.M. Zurek, Phys. Rev. D 90(7), 075011 (2014). arXiv:1406.6372 [hep-ph]
J. Huang, T. Liu, L.T. Wang, F. Yu, Phys. Rev. D 90(11), 115006 (2014). arXiv:1407.0038 [hep-ph]
M. Cahill-Rowley, J. Gainer, J. Hewett, T. Rizzo, JHEP 1502, 057 (2015). arXiv:1409.1573 [hep-ph]
J. Guo, J. Li, T. Li, A.G. Williams, Phys. Rev. D 91(9), 095003 (2015). arXiv:1409.7864 [hep-ph]
J. Cao, L. Shang, P. Wu, J.M. Yang, Y. Zhang, Phys. Rev. D 91(5), 055005 (2015). arXiv:1410.3239 [hep-ph]
T. Gherghetta, B. von Harling, A.D. Medina, M.A. Schmidt, T. Trott, Phys. Rev. D 91, 105004 (2015). arXiv:1502.07173 [hep-ph]
X.J. Bi, L. Bian, W. Huang, J. Shu, P.F. Yin, Phys. Rev. D 92, 023507 (2015). arXiv:1503.03749 [hep-ph]
C. Han, D. Kim, S. Munir, M. Park, JHEP 1507, 002 (2015). arXiv:1504.05085 [hep-ph]
C.T. Potter, Eur. Phys. J. C 76(1), 44 (2016). arXiv:1505.05554 [hep-ph]
R. Enberg, S. Munir, C. Pérez de los Heros, D. Werder, arXiv:1506.05714 [hep-ph]
J. Cao, L. Shang, P. Wu, J.M. Yang, Y. Zhang, JHEP 1510, 030 (2015). arXiv:1506.06471 [hep-ph]
A. Butter, T. Plehn, M. Rauch, D. Zerwas, S. Henrot-Versillé, R. Lafaye, Phys. Rev. D 93, 015011 (2016). arXiv:1507.02288 [hep-ph]
D. Barducci, G. Bélanger, C. Hugonie, A. Pukhov, JHEP 1601, 050 (2016). arXiv:1510.00246 [hep-ph]
M. Badziak, M. Olechowski, P. Szczerbiak, JHEP 1603, 179 (2016). arXiv:1512.02472 [hep-ph]
Q.F. Xiang, X.J. Bi, P.F. Yin, Z.H. Yu, Phys. Rev. D 94(5), 055031 (2016). arXiv:1606.02149 [hep-ph]
J. Cao, Y. He, L. Shang, W. Su, Y. Zhang, JHEP 1608, 037 (2016). arXiv:1606.04416 [hep-ph]
J. Cao, Y. He, L. Shang, W. Su, P. Wu, Y. Zhang, JHEP 1610, 136 (2016). arXiv:1609.00204 [hep-ph]
U. Ellwanger, JHEP 1702, 051 (2017). arXiv:1612.06574 [hep-ph]
C. Beskidt, W. de Boer, D.I. Kazakov, S. Wayand, Phys. Lett. B 771, 611 (2017). arXiv:1703.01255 [hep-ph]
Q. Mou, S. Zheng, Light neutralino dark matter in the NMSSM. arXiv:1703.00343 [hep-ph]
M. Badziak, M. Olechowski, P. Szczerbiak, JHEP 1707, 050 (2017). arXiv:1705.00227 [hep-ph]
S. Baum, M. Carena, N.R. Shah, C.E.M. Wagner, JHEP 1804, 069 (2018). arXiv:1712.09873 [hep-ph]
U. Ellwanger, JHEP 1311, 108 (2013). arXiv:1309.1665 [hep-ph]
U. Ellwanger, A.M. Teixeira, JHEP 1410, 113 (2014). arXiv:1406.7221 [hep-ph]
K.S. Jeong, Y. Shoji, M. Yamaguchi, JHEP 1411, 148 (2014). arXiv:1407.0955 [hep-ph]
B. Dutta, Y. Gao, B. Shakya, Phys. Rev. D 91(3), 035016 (2015). arXiv:1412.2774 [hep-ph]
B. Allanach, M. Badziak, C. Hugonie, R. Ziegler, Phys. Rev. D 92(1), 015006 (2015). arXiv:1502.05836 [hep-ph]
J.S. Kim, D. Schmeifer, J. Tattersall, Phys. Rev. D 93(5), 055018 (2016). arXiv:1510.04871 [hep-ph]
S. Akula, C. Balázs, L. Dunn, G. White, JHEP 1711, 051 (2017). arXiv:1706.09898 [hep-ph]
L. Shang, Y. He, J. Lian, Y. Pan, Eur. Phys. J. C 78(5), 390 (2018). arXiv:1804.08797 [hep-ph]
H. Baer, X. Tata, Phys. Lett. B 155, 278 (1985)
H. Baer, K. Hagiwara, X. Tata, Phys. Rev. D 35, 1598 (1987)
H. Baer, K. Hagiwara, X. Tata, Phys. Rev. Lett. 57, 294 (1986)
M. Aaboud et al. [ATLAS Collaboration], Phys. Rev. D 97(5), 052010 (2018) arXiv:1712.08119 [hep-ex]
M. Aaboud et al. [ATLAS Collaboration], Search for electroweak production of supersymmetric particles in final states with two or three leptons at \(\sqrt{s}=13\,\)TeV with the ATLAS detector. arXiv:1803.02762 [hep-ex]
M. Aaboud et al. [ATLAS Collaboration], Search for chargino–neutralino production using recursive jigsaw reconstruction in final states with two or three charged leptons in proton–proton collisions at \(\sqrt{s}\)=13 TeV with the ATLAS detector. arXiv:1806.02293 [hep-ex]
M. Aaboud et al. [ATLAS Collaboration], Search for pair production of higgsinos in final states with at least three \(b\)-tagged jets in \(\sqrt{s} = 13\) TeV \(pp\) collisions using the ATLAS detector. arXiv:1806.04030 [hep-ex]
A.M. Sirunyan et al. [CMS Collaboration], JHEP 1803, 166 (2018). arXiv:1709.05406 [hep-ex]
A.M. Sirunyan et al. [CMS Collaboration], JHEP 1803, 160 (2018). arXiv:1801.03957 [hep-ex]
U. Ellwanger, J.F. Gunion, C. Hugonie, JHEP 0502, 066 (2005). arXiv:hep-ph/0406215
U. Ellwanger, C. Hugonie, Comput. Phys. Commun. 175, 290 (2006). arXiv:hep-ph/0508022
D. Das, U. Ellwanger, A.M. Teixeira, Comput. Phys. Commun. 183, 774 (2012). arXiv:1106.5633 [hep-ph]
G. Belanger, F. Boudjema, A. Pukhov, A. Semenov, Comput. Phys. Commun. 185, 960 (2014). arXiv:1305.0237 [hep-ph]
M. Aaboud et al. [ATLAS Collaboration], JHEP 1801, 055 (2018). arXiv:1709.07242 [hep-ex]
A.M. Sirunyan et al. [CMS Collaboration], Search for additional neutral MSSM Higgs bosons in the \(\tau \tau \) final state in proton–proton collisions at \(\sqrt{s}=\) 13 TeV. arXiv:1803.06553 [hep-ex]
D. Das, U. Ellwanger, A.M. Teixeira, JHEP 1204, 067 (2012). arXiv:1202.5244 [hep-ph]
https://twiki.cern.ch/twiki/bin/view/LHCPhysics/SUSYCrossSections13TeVn2x1hino, using B. Fuks, M. Klasen, D.R. Lamprea, M. Rothering, JHEP 1210, 081 (2012). arXiv:1207.2159 [hep-ph]
B. Fuks, M. Klasen, D.R. Lamprea, M. Rothering, Eur. Phys. J. C 73, 2480 (2013). arXiv:1304.0790 [hep-ph]
R. Barbieri, G.F. Giudice, Nucl. Phys. B 306, 63 (1988)
U. Ellwanger, G. Espitalier-Noel, C. Hugonie, JHEP 1109, 105 (2011). arXiv:1107.2472 [hep-ph]
M. Muhlleitner, A. Djouadi, Y. Mambrini, Comput. Phys. Commun. 168, 46 (2005). hep-ph/0311167
W. Beenakker, M. Klasen, M. Kramer, T. Plehn, M. Spira, P.M. Zerwas, Phys. Rev. Lett. 83, 3780 (1999). Erratum: [Phys. Rev. Lett. 100, 029901 (2008) ]. arXiv:hep-ph/9906298
J. Billard, L. Strigari, E. Figueroa-Feliciano, Phys. Rev. D 89(2), 023524 (2014). arXiv:1307.5458 [hep-ph]
CMS Collaboration, Search for supersymmetry in events with tau leptons and missing transverse momentum in proton–proton collisions at sqrt(s)=13 TeV. CMS-PAS-SUS-17-002
Acknowledgements
We thank Lei Wu for helpful comments. The authors acknowledge the support of France-Grilles and the OCEVU Labex (ANR-11-LABX-0060) for providing computing resources on the French National Grid Infrastructure, and support from the French research project Défi InFIniti—AAP 2017. U. E. acknowledges support from the European Union’s Horizon 2020 research and innovation programmes H2020-MSCA-RISE No. 645722 (NonMinimalHiggs) and under the Marie Sklodowska-Curie Grant agreement no. 690575 (InvisiblesPlus).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
Funded by SCOAP3
About this article
Cite this article
Ellwanger, U., Hugonie, C. The higgsino–singlino sector of the NMSSM: combined constraints from dark matter and the LHC. Eur. Phys. J. C 78, 735 (2018). https://doi.org/10.1140/epjc/s10052-018-6204-3
Received:
Accepted:
Published:
DOI: https://doi.org/10.1140/epjc/s10052-018-6204-3