1 Introduction

For decades particle physicists and cosmologists have focused on beyond standard model physics and modified gravity theories to achieve a clear understanding of the character of two mysteries and challenges of standard cosmology in our age i.e “dark matter” (DM henceforth) and “dark energy” (DE henceforth). Despite the fact that none of them has any explicit evidence in laboratory physics, these two theories can separately provide a consistent explanation of surprising results indicated by the current astronomical observations [1,2,3,4,5,6,7,8]. Specifically, DM initially was suggested to explain the rotation curves of galaxies and cluster dynamics which it was not justifiable by standard baryonic matter. Later, the proposal of DM extended to cosmology concerning on the issue of structure formation at large scales. Also, to illustrate the accelerated expansion of our universe, the dominated existence of an unknown component called DE is essential. In continuing this path, unlike the original assumption that these two theories are different from each other, an interesting idea proposed that DM and DE can be two manifestations of a single physical entity. From the perspective of unification, it would be interesting to verify the possibility of a single unknown component (or field) rather than two ones which can explain the role of both. Such a unified framework of DM–DE (with a density ratio of approximately 0.3–0.7), in literatures was coined to name “quartessence”, see [9,10,11,12,13,14,15,16] for instance. The most interesting quartessence models studied so far are based on the Chaplygin gas model as well as its upgraded versions as an exotic background fluid with equation-of-state different from standard perfect fluid [17,18,19]. There are also other relevant equation-of-states which some authors [20, 21] have offered them as ansatzes which in asymptotic limit cases show the same behaviors for the background fluid. Chaplygin gas models are constrained by cosmic microwave background (CMB) and other astrophysical experiments [22,23,24,25]. However, there are some valid regions of parameter space which motivates us to consider them as consistent models with the current experimental data. These regions for an equation of state like \(p\propto -\,1/\rho ^n\) with some spacial values of n are not excluded, so that it can still behave like a matter component at early eras and a cosmological constant at late times [24,25,26]. Additionally, these models as candidates for dark energy are free of fine-tuning problem that appears in the standard cosmology and quintessence models [22]. Also, they can elevate the cosmic coincidence problem that appears in the relatively constant ratio of relic density of cosmological constant and matter content of the universe [27]. These models can explain the formation of large structures in the universe and the halo of DM in galaxies [28, 29]. Even if the origin of DM and DE are different, such models can be used as a simplified model to study all matter content of the universe as a single fluid illustrating the cosmic evolution [30].

However, in theoretical physics community this paradigm is ruling to get a complete and coherent view from the early moments until late universe, a quantum description of early moments of cosmology in the absence of micro-level singularity, is required. This is despite the fact that quartessence models as \(\Lambda \)CDM (cosmological constant and cold dark matter) are based on standard cosmology which suffers from initial conditions issue in particular past singularity. Clearly, an initial singular state with infinite values of physical quantities, such as temperature or energy density, should be excluded from any cosmological model. The prevailing belief is that quantum gravity (QG) settings as a framework which explores the universe at the micro-level spacetime (Planck scale), are natural solutions for solving this issue. So far, many intellectual efforts done by QG community has led to the view that at micro-level, spacetime continuum breaks down into a discrete one. So that even disjointed foam is very hard to peace with the GR principles due to the fact that it should endure a later transition to a spacetime continuum [31]. Despite the fact that most known proposals related to QG such as loop quantum gravity [32, 33], string theory [34, 35], deformed special relativity [36, 37], are currently at a development stage, they predict qualitatively a different spacetime beyond some characteristic scales such as Planck length (energy) and momentum. Therefore, in these models, Planck scale through separation of full quantum spacetime from classical one, acts as a natural border line or cutoffs which leads to the appearance of some corrections in the high energy physics. Indeed, the above mentioned invariant scales induce some extensions of the standard uncertainty relation (Heisenberg uncertainty principle) so called “generalized uncertainty principle” (GUP) [38, 39] which governs the motion of particles in micro-level spacetime. Also, need for existence of GUP proposals at some concrete scales of distances and energies is highly confirmed via gedanken experiments [40]. However, as a more advanced alternative to GUP(s), there is a non-commutative (NC) spacetime [41, 42] idea arising from the results of string theory in which moreover discarding the point like concept of the structure of spacetime can also be viewed as NC by changing the nature of the spacetime coordinates. Given that for each of the existing QG proposals, there is a relevant version of GUP. So it is important to mention that some GUPs, particularly generalized algebras designed by Kempf et al. [43, 44] via offering the possibility of space quantization, are compatible with NC spaces. One of the outstanding achievements of NC spacetime idea which is required to get a consistent framework of QG is that it leads to the removal of the paradox appeared due to the creation of a black hole for an event that is sufficiently localized in spactime, [45] see also discussions displayed in [46,47,48,49,50]. Also, by attaching the NC space idea to standard quantum field theory some positive feedbacks have been extracted. For instance, the singular behavior of the Einstein equations in very micro-level distances has cured within the NC space based on quantum field theory.

With this preface, in the present paper, through employing the methods of qualitative theory of dynamical systems [51, 52] we want to study the stability of a cosmology with GUP relevant to Snyder NC deformed Heisenberg algebra [53]. Moreover, we assume the background fluid is supported by quartessence Chaplygin models (QCMs). We have selected the Snyder NC space approach since it can be connected to some “deformed special relativity” models released in [54, 55] as well as it has some incentives from loop quantum gravity [56]. Another advantage of the underlying QG proposal for extending it into cosmology setup is that it respects rotational symmetry, unlike some of its other counterparts. Also within extended framework at hand the Big-Bang singularity can be absent due to bouncing mechanism induced by quantum correction terms in Friedmann dynamic equations [57]. The aforementioned positive feature concerning the resolving of initial condition problem from one side and valuable phenomenology functionality of the QCMs at large scales along with this fact that they are stable into standard cosmology [58, 59], from other side, motivates us to explore the response of this question: “Whether the quartessence Chaplygin cosmologies (QCCs) are still stable in a free initial singularity cosmological framework suggested by Snyder NC space approach to QG?”. The result would be desirable in case of “yes”. Since it means that the QCCs are also able to justify the current observations of a universe which has not been raised from a Big-Bang singularity. Of course in light of study done in [60, 61] we know that a fundamental cutoff as minimal length can play the role of dark energy (especially cosmological constant) at late time cosmology. Also recently, people shown that in the context of loop quantum cosmology, by taking an infrared natural cutoff within standard FRW cosmology, there is a possibility to explain the current acceleration of our universe tooFootnote 1 [62]. However, in what follows by admitting the existence of dark components in universe as the most common and challenging paradigm in modern cosmology which has been able to provide successful justifications of the the stability of galaxies and also observational data, then it turns out that the background fluid quartessence models can be consistent within a QG extended cosmological framework which is free of micro-level singularity. This consistency can have a dual function. First, it can be interpreted as a step towards providing a coherent theoretical picture from the beginning to the present day. Second, it will be seen that the conditions of \(H>0\) and \(c_s^2>0\) which refer to expanding and accelerating universe lead us to admission and subsequently rejection of some theoretically possibilities for the Snyder dimensionless characteristic parameter \(\mu _0\) via its connection with phenomenological parameters involved in underlying QCMs. More exactly, the present paper qualitatively suggests the possibility of control of the behavior of Planck scale characteristic parameter via the current astronomical signatures which indicates a down to up phenomenological view.

2 Deformed FRW cosmologies from Snyder-deformed Heisenberg algebras

Until the end of this section, we will derive Snyder deformed dynamics equations of the FRW cosmologies. More exactly, we will regard the corrections appeared from the NC Snyder background within the standard HUP, on the classical trajectory of the universe. Therefore, let us first start with a quick overview of the Snyder-deformed Heisenberg algebras by taking into account some details required.

2.1 Snyder-deformed Heisenberg algebras

By concerning on an n-dimensional NC deformed Euclidean space, the structure of the commutator between the coordinates can no longer be trivial rather it is deformed as follows

$$\begin{aligned}{}[\tilde{q}_i,{\tilde{q}}_j]=\mu M_{ij} \quad \{i,j,\ldots \}\in \{1,\ldots ,n\}, \end{aligned}$$
(1)

so that \({\tilde{q}}_i\)’s denote the NC coordinates. Here, \(\mu \) points to the NC Snyder deformation (or characteristic) parameter which its dimension and value is a squared length and a real number, respectively. By demanding two conjectures, we will deal with the (Euclidean) Snyder space [53]. First, the rotation generators \(M_{ij}=-\,M_{ji}=i(q_ip_j-q_jp_i)\) fulfill the usual SO(n) algebra as well as the translation group remains undeformed (i.e. \([p_i,p_j]=0\)). Secondly, under SO(n) rotations the NC coordinates transform as vectors which results in keeping the rotational symmetry. In the language of algebra the second assumption translates as follows

$$\begin{aligned}&[M_{ij},{\tilde{q}}_k]={\tilde{q}}_i\delta _{jk}-{\tilde{q}}_{j}\delta _{ik},\nonumber \\&[M_{ij},p_{k}]=p_{i}\delta _{jk}-p_{j}\delta _{ik}. \end{aligned}$$
(2)

However, it is very important to stress that there are countless number of commutator relations between \({\tilde{q}}_i\) and \(p_j\) which all of them are unanimously adapted to the relations (2). By rescaling of the NC coordinates \({\tilde{q}}_i\) in terms of variables used in common phase space i.e. (\(q_i,p_j\)), one gets a deeper understanding of the subject. By referring to works released in [64,65,66], we offer the most general SO(n) covariant realization for \({\tilde{q}}_i\) as follows

$$\begin{aligned} {\tilde{q}}_i=q_i\varphi _1(\mu p^2)+\mu (q_jp_j)p_i\varphi _2(\mu p^2), \end{aligned}$$
(3)

so that \(\varphi _1\) and \(\varphi _2\) represent two finite functions and also the convention \(a_ib_i=\sum _i a_ib_i\) is compatible. It is trivial that to restore the standard Heisenberg algebra (i.e. \(\mu =0\)) the boundary condition \(\varphi _1(0)=1\), should be administered. Note here the two functions \(\varphi _1\) and \(\varphi _2\) are not unique, at all. Indeed, for any given function \(\varphi _1\) which satisfies the boundary condition \(\varphi _1(0)=1\), there is a relevant function as \(\varphi _2\) which is characterized via the relation \(\varphi _2=(1+2{\dot{\varphi }}_1 \varphi _1)/(\varphi _1-2\mu p^2{\dot{\varphi }}_1)\) so that \({\dot{\varphi }}_1=d\varphi _1/d (\alpha p^2)\), see Ref. [67]. So the aforementioned realization of \({\tilde{q}}_i\) (i.e (3)) addresses the following commutator relation between \({\tilde{q}}_i\) and \(p_j\)

$$\begin{aligned}{}[{\tilde{q}}_i,p_j]=i\left( \delta _{ij}\varphi _1+\mu p_ip_j\varphi _2\right) , \end{aligned}$$
(4)

where results in such a GUP model for the Snyder NC space at hand

$$\begin{aligned} \Delta {\tilde{q}}_i\Delta p_j\ge \frac{1}{2}|\delta _{ij}\langle \varphi _1\rangle +\mu \langle p_ip_j\varphi _2\rangle |. \end{aligned}$$
(5)

The above commutator relation along with inequality, obviously imposes that the standard framework can be recoverable by setting \(\mu \rightarrow 0\). Interestingly, unlike three dimensional systems which we deal with countless realizations of the algebra and subsequently different GUPs (5), for one-dimensional systems, there is no such an issue. By concerning on the one-dimensional systems the symmetry group is trivial i.e \(SO(1)=\text {Id}\) and the most general realization can be written as \({\tilde{q}}=q\varphi (\mu p^2)=q\sqrt{1-\mu p^2}\) which makes the commutation relation (4) and inequality (5) to be re-expressed as

$$\begin{aligned}{}[{\tilde{q}},p]=i\sqrt{1-\mu p^2}, \end{aligned}$$
(6)

and

$$\begin{aligned} \Delta {\tilde{q}}\Delta p\ge \frac{1}{2}\left| \left\langle \sqrt{1-\mu p^2}\right\rangle \right| , \end{aligned}$$
(7)

respectively. It should be noted that to fix the sign of the Snyder deformation parameter \(\mu \), there is a freedom. Precisely, in case of \(\mu >0\) a natural cut-off as \(|p|<\sqrt{1/\mu }\) appears on the momentum while \(\mu <0\) derives an observable minimal length for \({\tilde{q}}\) from the uncertainty relation (7). As a noticable result, in case of negative sign for \(\mu \) at the first order, one gets the inequality \(\Delta q\gtrsim (1/\Delta p+l_s^2\Delta p)\) which is the same thing predicted by string theory (here \(l_s\) refers to string length which can be detected with \(\sqrt{-\mu /2}\)) [68, 69]. In conclusion, the Snyder-deformed commutator relation (6) addresses the existence of a fundamental cut-off as maximum momentum or minimal length if \(\mu >0\) or \(\mu <0\), respectively.

2.2 Snyder-deformed dynamical equations

By turning to above review of the Snyder NC algebra, we are going to extract the relevant deformed dynamics of the FRW cosmological models. Indeed, we want to derive classical dynamical equations ruling the universe which is affected by one of the possible initial corrections such as Snyder NC geometry (the corrections come from the algebra (6)). The classical Poisson bracket representation of the quantum-mechanical commutator (6) is

$$\begin{aligned} \{{\tilde{q}},p\}=\sqrt{1-\mu p^2}. \end{aligned}$$
(8)

According to the above classical representation for any two-dimensional phase space function the Snyder deformed Poisson bracket can be re-expressed asFootnote 2

$$\begin{aligned} \{F,G\}=\left( \frac{\partial F}{\partial {\tilde{q}}}\frac{\partial G}{\partial p}-\frac{\partial F}{\partial p}\frac{\partial G}{\partial {\tilde{q}}}\right) \sqrt{1-\mu p^2}. \end{aligned}$$
(9)

It is thus expected that the time evolution of the coordinate and momentum with respect to Hamiltonian \({\mathcal {H}}({\tilde{q}},p)\) can be deformed as

$$\begin{aligned} \dot{{\tilde{q}}}= & {} \{{\tilde{q}},{\mathcal {H}}\}=\frac{\partial {\mathcal {H}}}{\partial p}\sqrt{1-\mu p^2}, \qquad \dot{p}=\{p,{\mathcal {H}}\}\nonumber \\= & {} -\frac{\partial \mathcal H}{\partial {\tilde{q}}}\sqrt{1-\mu p^2}. \end{aligned}$$
(10)

Now, we expand the underlying framework to the cosmological context in particular FRW cosmological models with the following spatially isotropic metric

$$\begin{aligned} ds^2=-\,N^2dt^2{+}a^2\left( \frac{dr^2}{1-kr^2}+r^2d\theta ^2{+}r^2\sin ^2\theta d\phi ^2\right) ,\nonumber \\ \end{aligned}$$
(11)

where the lapse function \(N=N(t)\) and scale factor \(a=a(t)\). Also, its matter section obeys fluid energy conservation equation

$$\begin{aligned} \dot{\rho }+3H(\rho +p)=0, \end{aligned}$$
(12)

with a generic matter energy density \(\rho \) and pressure p. In line element (11), depending on the symmetry group, the curvature constant k can be fixed to 0, \(+\,1\) and \(-\,1\) by pointing to the spatially flat, closed and open universe, respectively. In order to compute the dynamic of the underlying FRW models the following scalar constraint should be satisfied

$$\begin{aligned} {\mathcal {H}}=-\,\frac{p_a^2}{12a}-3ak+a^3\rho =0, \quad 8\pi G\equiv 1, \end{aligned}$$
(13)

where its extended representation takes the following form

$$\begin{aligned} {\mathcal {H}}_E=\frac{N}{12}\frac{p_a^2}{a}+3Nak-Na^3\rho +\lambda \pi . \end{aligned}$$
(14)

Here, \(\lambda \) and \(\pi \) denote a Lagrange multiplier and the momenta conjugate attributable to N. By turning to the Poisson bracket (8), we can assume that the commutator relation between the isotropic scale factor a and relevant conjugate momentum \(p_a\) in the underlying Snyder-deformed minisuperspace obeys the following from

$$\begin{aligned} \{a,p_a\}=\sqrt{1-\mu p_a^2}, \end{aligned}$$
(15)

where if shutdowns the Snyder NC space deformation (i.e \(\mu =0\)), it comes back to standard form \(\{a,p_a\}=1\), as expected from GR based mini superspace. Now by having the extended Hamiltonian \(\mathcal H_E\) and Poisson bracket (15), one can obtain relevant deformed dynamics equations in two-dimensional phase space \((a,p_a)\), as follows

$$\begin{aligned} {\dot{a}}= & {} \{a,{\mathcal {H}}_E\}=\frac{Np_a}{6a}\sqrt{1-\mu p_a^2}, \nonumber \\ {\dot{p}}_a= & {} \{p_a,\mathcal H_E\}=N\left( \frac{p_a^2}{12a^2}-3k+3a^2\rho \nonumber \right. \\&\left. +a^3\frac{d\rho }{da}\right) \sqrt{1-\mu p_a^2}. \end{aligned}$$
(16)

Eventually, by solving the constraint (13) with respect to \(p_a\) as well as considering the first case in Eq. (16) and also fixing \(N=1\), the first Friedmann equation modified by leading order Snyder NC space correction, reveals as

$$\begin{aligned} H^2=\frac{\rho }{3}-\frac{k}{a^2}-4\mu \rho ^2 a^4+24\mu ka^2\rho -36\mu k^2. \end{aligned}$$
(17)

Subsequently by taking time derivation of the expansion rate equation (17), we arrive at

$$\begin{aligned} {\dot{H}}= & {} -\,\frac{\rho +p}{2}+\frac{k}{a^2}-8\mu a^4\rho ^2\nonumber \\&+12\mu a^4\rho (\rho +p) +\,24\mu ka^2\rho -36\mu k a^2(\rho +p),\nonumber \\ \end{aligned}$$
(18)

as second order deformed Friedmann equation. In above equations, the correction terms arisen from the Snyder NC geometry, are addressed with \(\mu \) parameter which is connected with Planck length \(\ell _{pl}\) via \(\mu \equiv \mu _0\frac{\ell _{pl}^{2}}{\hbar ^{2}}\). To the end of this paper, to facilitate our calculations the natural unit is adopted i.e. \( \ell _{pl}\) ,\(\hbar \) and c are fixed to unity (as before \(8\pi G\equiv 1\)). Therefore, in the following we will work with dimensionless parameter \(\mu _0\). In the QG literatures it is thought that the value of this parameter as well as other counterparts suggested by other GUP models, must be constant of order unity. Notably, by attaching the QG effects arisen from some common semi-classical approaches within different branches of physics (both theoretically and experimentally) so far for relevant dimensionless QG parameters released some explicit upper bounds (e.g. can be mentioned to works as [70,71,72,73,74,75]). As mentioned before, the above deformed dynamical equations explicitly show us that vanishing the \(\mu \)-terms leads to the restoration of Friedmann equations in their standard form. At the end, by plugging the Eqs. (17) and (18), we obtain

$$\begin{aligned} {\dot{H}}= & {} -H^2-\frac{\rho +3p}{6}+12\mu _0\rho p a^4\nonumber \\&+\,12\mu _0 k a^2(\rho -3p)-36\mu _0 k^2, \end{aligned}$$
(19)

where along with the continuity equation (12) are two out of three equations which forms a closed system for doing the Jacobian stability analysis of three different versions of Chaplygin quartessence models, within the quantum cosmological framework.

3 Stability of quartessence models in dynamical systems with natural UV cutoff

3.1 Analysis procedure

We begin the discussion of this section with a succinct and useful preview of our analysis method. Overall, there are two paths to provide a dynamical analysis of a differential equation as \({\dot{y}}=f(y)\): first, finding the relevant straight solutions. Second, reducing the analysis into a phase plane for all defined initial conditions. The latter is the basis of “qualitative dynamic analysis” in which all possible solutions are considered rather than analyzing an individual solution. More precisely, in this way one reduces dynamics into a two-dimensional (2D) phase space in which singular solutions \({\dot{y}}= 0 \) and also nonsingular ones are displayed via critical points (CP) and phase curves, respectively. Using the phase diagrams in a phase plane (2D space) we can clearly investigate some important issues such as “dynamical stability”. Generally, we are able to reduce every conventional cosmological dynamics to the 2D phase plane with an autonomous system of equations similar to \({\dot{x}} = Q_1(x, y), {\dot{y}} = Q_2(x, y)\), in which dot represents the differentiation with respect to cosmic time. Through linearization of the Jacobian matrix at a given CP and extracting relevant eigenvaluesFootnote 3 \(\lambda _{1,2}\), will be provided the possibility of categorizing the non-degenerated (or hyperbolic) CPs \((x_c,y_c)\). As a reminder, in case of the real part of both eigenvalues \(\lambda _{1,2}\) be nonvanishing at \((x_c,y_c)\), the relevant CP is non-degenerated. With a good approximation the dynamical behaviour of the above mentioned autonomous system in the vicinity of the CP \((x_c, y_c)\) is qualitatively traceable via the behaviour of its linear part

$$\begin{aligned} \left( \begin{array}{cc} {\dot{x}} \\ {\dot{y}} \\ \end{array} \right) ={{\varvec{M}}}_{2\times 2}|_{(x_c, y_c)}\cdot ~\left( \begin{array}{cc} x-x_c \\ y-y_c \\ \end{array} \right) ,\quad {{\varvec{M}}}{=}\left( \begin{array}{cc} \acute{Q_{1,x}} &{} \acute{Q_{1,y}}\\ \acute{Q_{2,x}} &{} \acute{Q_{2,y}}\\ \end{array} \right) ,\nonumber \\ \end{aligned}$$
(20)

where after integration, the above system gives the following solution

$$\begin{aligned} x-x_c= & {} Re\Big (A_1 \exp (\lambda _1t)+A_2\exp (\lambda _2t)\Big ), \nonumber \\ y-y_c= & {} Re\Big (A_1 k_1 \exp (\lambda _1t)+A_2 k_2\exp (\lambda _2t)\Big ), \end{aligned}$$
(21)

with \(k_1=\frac{\lambda _1}{\acute{Q_{1,y}}(x_c, y_c)} -\frac{\acute{Q_{1,x}}(x_c, y_c)}{\acute{Q_{1,y}}(x_c, y_c)}\) and \(k_2=\frac{\lambda _2}{\acute{Q_{1,y}}(x_c, y_c)} -\frac{\acute{Q_{1,x}}(x_c, y_c)}{\acute{Q_{1,y}}(x_c, y_c)}\). Here, the prime sign refers to the derivative in terms of variables x and y.

By specifying the sign of the trace and the discriminant within the 2D flows dynamical systems then the possibility of a solution for stability analysis, will be available [76].

  • In case of \(Det\, \mathbf M > 0\) and the discriminant: \(\mathbf D = (Tr\, \mathbf M )^2 -4\,Det\,\mathbf M >0\), the eigenvalues are real with the same sign which addresses the critical point as a node. If \(Tr\, \mathbf M > 0\), the critical point is an unstable node i.e. a repeller or source, while if \(Tr\, \mathbf M < 0\) it is a stable node i.e. an attractor or sink.

  • In case of \(Det\, \mathbf M > 0\) and the discriminant: \(\mathbf D = (Tr\, \mathbf M )^2 -4\,Det\,\mathbf M <0\), the eigenvalues are complex conjugates which address the critical point as a focus. If \(Tr\, \mathbf M > 0\) it is an unstable focus while if \(Tr \,\mathbf M <0\) it is a stable focus. Also, note that if eigenvalues are purely imaginary then the critical point is a stable neutral center.

  • In case of \(Det\,\mathbf M < 0\), the eigenvalues are real with opposite signs which address the critical point as a saddle point.

  • In case of \(Tr\,\mathbf M =0\) and \(Det\, \mathbf M > 0\), the eigenvalues of the critical points have complex values which address the stable neutrally center type. Otherwise, if \(Det\, \mathbf M < 0\) then the critical point represents a saddle point.

3.2 Model I: Generalized Chaplygin gas quartessence (GCGQ)

Historically, the so called Chaplygin gas fluid model originally studied by Chaplygin [77] in the early twentieth century within the framework of aerodynamics via offering an exotic equation-of-state as \(p=-\frac{A}{\rho }\). However, in recent years, this model with its upgraded versions, have been at the cosmology center of attention from phenomenological sense so that now we see them as one of the most popular candidates to DE-DM unified framework, [19, 78,79,80,81]. In the first updated model of Chaplygin gas, the relevant negative pressure of underlying background fluid is connected to energy density via the following more general equation-of-stateFootnote 4

$$\begin{aligned} p=-A\rho ^{-n},~~~~~A>0~~~~~\text{ and }~~~~0<n\le 1, \end{aligned}$$
(22)

In most literatures the above equation-of-state, describes a “generalized Chaplygin gas quartessence” (GCGQ) model and is intended as a starting point for investigations on the cosmological implication of Chaplygin gas models. Putting above equation-of-state into the energy conservation fluid equation (12), one arrives at

$$\begin{aligned} \rho =\bigg (A+B a^{-3(n+1)}\bigg )^{\frac{1}{n+1}}, \end{aligned}$$
(23)

for the evolution of GCGQ energy density. Here a(t) represents the cosmic scale factor which for case of today universe can be fixed to unity. By offering the new variables

$$\begin{aligned} \Omega _m^*\equiv \frac{B}{A+B}~~~\text{ and }~~~\rho _*\equiv (A+B)^{\frac{1}{n+1}}, \end{aligned}$$
(24)

then the Eq. (23) can be written as

$$\begin{aligned} \rho (a)=\rho _*\bigg ((1-\Omega _m^*)+\Omega _m^* a^{-3(n+1)}\bigg )^{\frac{1}{n+1}}. \end{aligned}$$
(25)

Here \(\rho _*\) can be interpreted as “today critical density” of universe since by fixing \(a=1\) then \(\rho (1)=\rho _*\). To provide a physical interpretation of variable \(\Omega _m^*\) it is necessary to compare the above equation with the following \(\Lambda CDM\) density energy

$$\begin{aligned} \rho (a)=\rho _*\bigg ((1-\Omega _m)a^{-3(\omega ^*+1)}+\Omega _m a^{-3}\bigg )^{\frac{1}{n+1}}, \end{aligned}$$
(26)

where \(\Omega _m\) and \((1-\Omega _m)\) denote the current CDM density parameter and dark energy density, respectively. It is clear that for spacial cases \(n=0\) and \(\omega ^*=-1\), these two models will meet each other which means that \(\Omega _m^*\) can be interpreted as “effective matter density parameter” in relevant Chaplygin gas model. Now let us follow our main aim i.e. the stability analysis of GCGQ model within the context of Snyder NC deformed quantum cosmology. By re-expressing the Eqs. (19) and (12) as follows

$$\begin{aligned} {\dot{H}}\equiv \frac{dH}{dt}= & {} -H^2-\frac{\rho +3p}{6}+12\mu _0\rho p a^4\nonumber \\&+\,12\mu _0 k a^2(\rho -3p)-36\mu _0 k^2=Q_1(H,\rho ),\nonumber \\ \end{aligned}$$
(27)

and

$$\begin{aligned} \dot{\rho }\equiv \frac{d\rho }{dt}=-3H(\rho +p)=Q_2(H,\rho ), \end{aligned}$$
(28)

we define our 2D dynamical system in which the quantities \((H,\rho )\) play the role of the phase space variables. More precisely, the evolution of the underlying system is traceable via trajectories into \((H,\rho )\)-space uniquely specified by the initial conditions \((H_{cp},\rho _{cp})\). Therefore, in this phase space the linearization matrix \({{\varvec{M}}}\) of the system at the around of CP \((H_{cp},\rho _{cp})\), reads off as

$$\begin{aligned} \mathbf M\mathbf =\left( \begin{array}{cc} \acute{Q_{1,H}} &{} \acute{Q_{1,\rho }}\\ \acute{Q_{2,H}} &{} \acute{Q_{2,\rho }}\\ \end{array} \right) _{(H_{cp},\rho _{cp})}, \end{aligned}$$
(29)

where for non-static CPs \((H_{cp},\rho _{cp})\), the trace and the determinant are obtained as

$$\begin{aligned} Tr\, \mathbf M= & {} \big (\acute{Q_{1,H}}+ \acute{Q_{2,\rho }}\big )_{(H_{cp},\rho _{cp})},\nonumber \\ Det\,\mathbf M= & {} \big (\acute{Q_{1,H}}. \acute{Q_{2,\rho }}-\acute{Q_{1,\rho }}.~\acute{Q_{2,H}}\big ) _{(H_{cp},\rho _{cp})}. \end{aligned}$$
(30)
Fig. 1
figure 1

Regions of existence \(H_{cp}>0\) (Eq. (31)) within \((\mu _0, \rho _*,c_s^2)\) parameter space, for flat, open (left panel) and closed (right panel) Snyder deformed quantum cosmology with equation-of-state parameter close to \(-1\) (here \(\omega =-0.98\)) and any arbitrary value \(\Omega _m^*\in (0.2,0.5)\)

Full size image

Now by setting Eqs. (27) and (28) to zero, non-static CPs are derived as

$$\begin{aligned} H_{cp}= & {} \bigg [\frac{\rho _*}{3}(1-\Omega _m^*)^{\frac{\omega }{\omega -c_{s}^2}}-12\mu _0\rho _*^2(1-\Omega _m^*)^{\frac{2}{n+1}}\nonumber \\&\times \,\bigg (\left( \frac{\omega +1}{\omega }\right) \left( \frac{\Omega _m^*-1}{\Omega _m^*}\right) \bigg )^{-\frac{4\omega }{3(\omega -c_{s}^2)}}\nonumber \\&+\,48\mu _0 k\rho _*(1-\Omega _m^*)^{\frac{\omega }{\omega -c_{s}^2}}\nonumber \\&\times \, \bigg (\left( \frac{\omega +1}{\omega }\right) \left( \frac{\Omega _m^*-1}{\Omega _m^*}\right) \bigg )^{-\frac{2\omega }{3(\omega -c_{s}^2)}}-36\mu _0k^2\bigg ]^\frac{1}{2},\nonumber \\ \rho _{cp}= & {} \rho _*(1-\Omega _m^*)^{\frac{\omega }{\omega -c_{s}^2}} \,~~~\text{ with }~~~n=-\frac{c_s^2}{\omega }, \end{aligned}$$
(31)

respectively. Note that, expressions relevant to scale factor terms in (27) obtained from mixing the equation-of-state index \(\omega \equiv \frac{p}{\rho }\) and the squared sound speed \(c_{s}^{2}\equiv \frac{dp}{d\rho }\) with (25). Finally for the above non static CP, we have

$$\begin{aligned}&Tr\mathbf M =-H_{cp}(3n+5),~~~Det\,\mathbf M =6H_{cp}^2(n+1),\nonumber \\&D=H_{cp}^2(9n^2+6n+1), \end{aligned}$$
(32)

At first look, one may think this is exactly what has already been achieved within standard cosmology. Therefore, Planck scale corrections induced by Snyder NC space into FRW cosmologies does not affect standard results. However, with a closer look one will find that the effect of UV natural cutoffs embeds into \(H_{cp}\) term. Expressions listed in (32) explicitly reflect this fact that determinant and discriminant are always positive so that to have a stable node CP there should be \(Tr\, \mathbf M >0\) i.e \(H_{cp}>0\). In another words, in an expanding universe, the CP (31) behaves as an asymptotically stable node. Despite that in the absence of underlying corrections, \(H_{cp}\) is trivially positive, here it should be checked carefully. Our consideration shows that concerning late time phase of the universe i.e. fixing values close to \(-1\) for equation-of-state parameter \(\omega \) and respect to standard constraints \(\Omega _m^*\in (0.2,0.4)\) into flat as well as open spatial geometry model universe at hand, the condition of \(H_{cp}>0\) holds only if \(\mu _0<0\) (i.e. adoption of a minimum invariant length in fundamental level of nature), as displayed in Fig. 1 (left panel). However, for case of closed universe (\(k=+1\)), we find that depending on the fixed values for present critical density of universe \(\rho _*\), also there is the possibility of admitting the positive value (moreover negative values) for the dimensionless Snyder characteristic parameter \(\mu _0>0\), as revealed in Fig. 1 (right panel).

Fig. 2
figure 2

The vector field portrait in phase space \((H,\rho )\) corresponding to Fig. 1. Left panel corresponds to any three curvature modes of Snyder deformed-FRW model with numerical values: \(\mu _0=-1\), \(\rho _*=5\), \(\omega =-0.98,~\Omega _m^*\in (0.2,0.5)\),  \(c_{s}^2\in (0,0.5]\). Right panel only corresponds to closed curvature mode with the same numerical values except \(\mu _0=1\), \(0<\rho _*<2\)

Full size image

Note that although in language of perfect fluid, the equation-of-state (22) covers \(-1\le \omega \le 0\), here for all three possible modes of spatial curvatures (i.e. \(k=0,~\pm 1\)), the condition of \(H_{cp}>0\) does not support exactly \(\omega =-1\). It is not hard to prove that the Snyder NC space correction terms include scale factor a into (19) are the main reason of the issue so that by rejecting them this issue could be disappeared. It is also worthy to refer that the above parameter volume addresses interestingly the possibility of connection between two seemingly unrelated phases of the universe. To say more exactly, the Snyder characteristic parameter \(\mu _0\) deals with the earliest phase of the universe linked to the two valuable quantities in current cosmology i.e. today critical density of universe \(\rho _*\) and the squared sound speedFootnote 5 \(c_s^2\). As a consequence, based on the conventional approaches to cosmology which highly support this belief that the spatial geometry of the universe is exactly flat, the stability of the GCGQ model within the underlying QG extended cosmological framework will be possible only in case of admitting a lower bound for length in nature, \(\mu _0<0\). However, observational data (primarily the CMB) tells us that the curvature constant must be close to flat but not exactly flat. Concerning the non-flat geometries, we see from Fig. 1 that the behavior of \(\mu _0\) for open universe is quite similar to flat one while the sign of \(\mu _0\) in closed universe is dependent on fixed values of \(\rho _*\). Also in Fig. 2, it is displayed that the phase portraits in physical domain (\(\rho >0\)) are equivalent to terms dictated by Fig. 1. As it is seen in the left panel, for each three curvature modes of the Snyder deformed-FRW model including a minimum length, there are two de Sitter nodes. de Sitter node in the region \(H>0\) is attractor and stable, while its counterpart in the region \(H<0\) is repeller and represents an unstable CP. Concerning closed curvature mode which includes the maximum momentum, the right panel shows circular trajectories around the static CP \((0,\rho )\) which is affiliated to a center equilibrium CP and represents a static universe. Note that in the left panel also one can see some static CPs associated to unstable saddle points which are located on the trajectories moving from the unstable de Sitter node (\(H<0\)) towards the stable de Sitter node (\(H>0\)).

3.3 Model II: Modified Chaplygin gas quartessence (MCGQ)

Over the years, for GCGQ models several modifications have been proposed. If one regards the modified Chaplygin gas quartessence (MCGQ) in which pressure p and energy density \(\rho \) are connected together via the following ansatzFootnote 6 [82,83,84]

$$\begin{aligned} p=C\rho -D\rho ^{-n}, \qquad C,~D>0, \qquad 0<n\le 1, \end{aligned}$$
(33)

then it results in

$$\begin{aligned} \rho =\bigg (\frac{D}{C+1}+Ea^{-3(n+1)(C+1)}\bigg )^{\frac{1}{n+1}}. \end{aligned}$$
(34)

By assuming the following new variables

$$\begin{aligned} \Omega _m^*\equiv \frac{E(C+1)}{D+E(C+1)}, \qquad \rho _*\equiv \bigg (\frac{D+E(C+1)}{C+1}\bigg )^\frac{1}{n+1},\nonumber \\ \end{aligned}$$
(35)

then Eq. (34) can be expressed as follows

$$\begin{aligned} \rho =\rho _*\bigg ((1-\Omega _m^*)+\Omega _m^*a^{-3(n+1)(C+1)}\bigg )^{\frac{1}{n+1}}, \end{aligned}$$
(36)

where by merging it with Eq. (33) in addition to equation-of-state index \(\omega \equiv \frac{p}{\rho }\) and the squared sound speed \(c_s^2\equiv \frac{dp}{d\rho }\), we get the following expression

$$\begin{aligned} a= & {} \bigg (\frac{\Omega _m^*-1}{\Omega _m^*}-\frac{D\rho _*^{-n-1}}{\Omega _m^*(\omega +1+ \frac{D\rho _*^{-n-1}}{\Omega _m^*-1})}\bigg )^{\frac{(\Omega _m^*-1)\rho _*^{n+1}}{3D(n+1)}},\nonumber \\&\quad n=\frac{c_s^2-C}{C-\omega }, \end{aligned}$$
(37)

for the scale factor a appeared in (19). With a simple calculation one can show that in the limit \(C\rightarrow 0\), the above expression reduces to its counterpart in GCGQ model. Note that, with the same argument mentioned in details previously, here also we can interpret variables \(\Omega ^*\) and \(\rho _*\) as effective matter density of MCGQ model and today energy density of the universe, respectively. Finally, in the context of quartessence model at hand, the relevant expressions for non-static CPs, take the following form

$$\begin{aligned} H_{cp}= & {} \left[ \frac{\rho _*}{3}(1-\Omega _m^*)^{\frac{1}{n+1}}-12\mu _0\rho _*^2(1-\Omega _m^*)^{\frac{2}{n+1}}\right. \nonumber \\&\times \,\left( \frac{\Omega _m^*-1}{\Omega _m^*}-\frac{D\rho _*^{-n-1}}{\Omega _m^*(\omega +1+ \frac{D\rho _*^{-n-1}}{\Omega _m^*-1})}\right) ^{\frac{4(\Omega _m^*-1)\rho _*^{n+1}}{3D(n+1)}}\nonumber \\&+4\,8\mu _0 k\rho _*(1-\Omega _m^*)^{\frac{1}{n+1}}\nonumber \\&\left. \times \, \left( \frac{\Omega _m^*-1}{\Omega _m^*}- \frac{D \rho _*^{-n-1}}{\Omega _m^*(\omega +1+\frac{D\rho _*^{-n-1}}{\Omega _m^*-1})}\right) ^{\frac{2(\Omega _m^*-1) \rho _*^{n+1}}{3D(n+1)}} -36\mu _0k^2\right] ^\frac{1}{2},\nonumber \\ \rho _{cp}= & {} \rho _*(1-\Omega _m^*)^{\frac{1}{n+1}}. \end{aligned}$$
(38)

Now, it is clear to show that, the result of (32) once again repeats. Namely, in the presence of UV invariant cutoff raised within Snyder NC space road to QG, the underlying MCGQ cosmological model in case of \(H_{cp}>0\) (expanding universe) is stable. However, due to existence of some correction terms, the condition \(H_{cp}>0\) is not trivial rather should be checked. As before, concerning the flat as well as open universe in late time phase, for equation-of-state indices close to \(\omega \approx -1\) (except -1) with \(\Omega _m^*\in (0.2,0.4)\), we find that independent of any arbitrary values \(C,~D>0\), the condition \(H_{cp}>0\) holds only in case of \(\mu _0<0\), as Fig. 1 (left panel). However, by taking \(k=+1\) into quantum cosmological model at hand then \((\mu _0,\rho _*,\Omega ^*)\) parameter space addresses both possibilities i.e. positive and negative signs for \(\mu _0\), dependent on relevant values for \(\rho _*\), as can be seen clearly in Fig. 3. In similar to the former quartessence cosmology model which \(H_{cp}\) has been divergent at \(\omega =-1\), here also this issue can be seen. Once again we mention that the root of this restriction is thanks to the Snyder NC correction terms include scale factor a into (19). In Fig. 4 we show the phase portraits equivalent to terms dictated by Fig. (3) in the physical domain, \(\rho >0\). As before, we see that in the presence of maximum momentum there are circular trajectories around static universe (\(0,\rho \)) which is affiliated to a stable center equilibrium CP. However, in the presence of minimum length there are two de Sitter nodes which in the case of an expanding universe, it is stable attractor while for its contracting counterpart, it is unstable repeller. Here there is also the possibility of static universe which behaves as an unstable saddle CP.

Fig. 3
figure 3

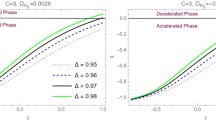
Regions of existence \(H_{cp}>0\) (Eq. (38)) within \((\mu _0, \rho _*,c_s^2)\) parameter volume, for closed Snyder NC quantum cosmology with equation-of-state indexes close to \(-1\) (here \(\omega =-0.95\)) and any arbitrary values \(n\in (0,1]\), \(\Omega _m^*\in (0.2,0.5)\) and \(C,~D>0\)

Full size image
Fig. 4
figure 4

The vector field portrait in phase space \((H,\rho )\) corresponding to Fig. 3. Left panel corresponds to closed curvature mode of Snyder deformed-FRW model in the presence of maximum momentum with numerical values: \(\mu _0=1\), \(\rho _*=3,~\omega =-0.95,~\Omega _m^*\in (0.2,0.5)\),  \(c_{s}^2\in (0,0.5]\) and \(C,~D>0\). Right panel is in the presence of minimum length with the same numerical values except \(\mu _0=-1,~\rho _*=6\)

Full size image

3.4 Model III: Modified generalized Chaplygin gas quartessence (MGCGQ)

The third proposed model for quartessence cosmology that we are interested in here to introduce is known as modified generalized Chaplygin gas (MGCG) with the following form of equation-of-state [85, 86]

$$\begin{aligned} p=\beta \rho -(\beta +1)A\rho ^{-n}, \end{aligned}$$
(39)

where \(\beta \) is an optional real constant so that in the absence of it (i.e \(\beta =0\)) the GCGQ model will be recovered. It is obvious that in the hot early universe the above equation-of-state reduces to \(p=\beta \rho \) which by fixing \(\beta =1/3\) it addresses the radiation dominated epoch. While in case of \(\beta =-1\) then \(p=-\rho \), corresponding to the equation-of-state of a cosmological constant. Here, the MGCG density evolves as

$$\begin{aligned} \rho =\bigg ((\beta +1)A+Fa^{-3(\beta +1)(n+1)}\bigg )^{\frac{1}{n+1}}\, ,\end{aligned}$$
(40)

where using the following new variables

$$\begin{aligned} \Omega _m^{*}\equiv \frac{F}{A+F},~~~~~\rho _*\equiv \bigg (A+F\bigg )^{\frac{1}{n+1}}, \end{aligned}$$
(41)

then the above MGCG density takes the following form

$$\begin{aligned} \rho =\rho _*\bigg ((1-\Omega _m^*)+\Omega _m^*a^{-3(\beta +1)(n+1)}\bigg )^{\frac{1}{n+1}}, \end{aligned}$$
(42)

In line with previous routes, here we arrive at the following expressions

$$\begin{aligned} H_{cp}= & {} \bigg [\frac{\rho _*}{3}(1-\Omega _m^*)^{\frac{\beta -\omega }{c_s^2-\omega }}-\,12\mu _0\rho _{*}^{2}(1-\Omega _m^*) ^{\frac{2(\beta -\omega )}{c_s^2-\omega }}\nonumber \\&\times \,\bigg (\left( \frac{\omega +1}{\beta -\omega }\right) \left( \frac{1-\Omega _m^*}{\Omega _m^*}\right) \bigg )^{-\,\frac{4(\beta -\omega )}{3(\beta +1)(c_s^2-\omega )}}\nonumber \\&+\,48\mu _0 \rho _* k(1-\Omega _m^*)^{\frac{\beta -\omega }{c_s^2-\omega }}\nonumber \\&\times \,\bigg (\left( \frac{\omega +1}{\beta -\omega }\right) \left( \frac{1-\Omega _m^*}{\Omega _m^*}\right) \bigg )^{-\frac{2(\beta -\omega )}{3(\beta +1)(c_s^2-\omega )}} -\,36\mu _0k^2\bigg ]^\frac{1}{2}, \nonumber \\&\rho _{cp}=\rho _*(1-\Omega _m^*)^{\frac{\beta -\omega }{c_s^2-\omega }}.\end{aligned}$$
(43)

for the relevant non-static CPs, so that in the limit \(\beta \rightarrow 0\) its counterpart in (31) can also be recovered, as expected.

Fig. 5
figure 5

The vector field portrait in phase space \((H,\rho )\) corresponding to MGCGQ model. Left panel corresponds to any three curvature modes of Snyder deformed-FRW model with numerical values: \(\mu _0=-1\), \(\rho _*=5\),  \(\omega =-0.98,~\Omega _m^*\in (0.2,0.5)\), \(c_{s}^2\in (0,0.5]\) and \(\beta >-1\). Right panel only corresponds to closed curvature mode with the same numerical values except \(\mu _0=1\), \(0<\rho _*<2\)

Full size image

Like the two previous models, we should follow the validity of the condition \(H_{cp}>0\) which guarantees an expanding universe. Our analysis interestingly shows that if the free parameter \(\beta \) is in range of \(\beta >-1\), and \(\Omega _m^*\in (0.2,0.4)\) then by fixing values close to \(-1\) for \(\omega \), we deal with \((\mu _0, \rho _*,\Omega ^*)\) parameter volumes similar to Fig. 1. Namely, for cases of flat and open spatial geometry modes the condition of \(H_{cp} > 0\) holds only in case of adoption of a minimum invariant length in fundamental level of nature, i.e. \(\mu _0<0\). While for case of closed mode, depending on fixed values for present critical density of universe \(\rho _*\) there is the possibility of admitting the maximum momentum and minimal length. The remarkable thing in above results is that for all three modes \(k=0,\pm 1\), the condition \(H_{cp}>0\), will not be satisfied for values of \(\beta \le -1\). In Fig. 5 we draw the vector field portraits of dynamical system relevant to MGCGQ model. Here also interpretation of the behavior of the trajectories in the neighborhood of the CPs is similar to the two previous models.

4 Concluding discussions

Quartessence as one of prevalent alternatives to \(\Lambda \)CDM, with a phenomenologically unified dark matter-energy framework, is based on past singular Friedmann–Robertson–Walker (FRW) cosmology. However, in order to provide a complete picture from the beginning of the universe to today, some ingredients should be attached to the standard theory. In this paper, we have focused on the stability of three quartessence models with generalized Chaplygin gas (GCG), modified Chaplygin gas (MCG) and generalized modified Chaplygin gas (GMCG) equation-of-state into a cosmology with generalized uncertainty principle arisen from non-commutative (NC) Snyder space leading to the absence of past singularity issue. The relevant dynamical equations have been derived within a FRW minisuperspace in the presence of some invariant UV cutoffs given by Snyder NC geometry which address a road to quantum gravity. The UV deformed Friedman equation governing our model includes an interesting feature. Due to freedom in the sign of the Snyder characteristic parameter \(\mu \) (by setting the natural unites (\(\ell _{pl}=\hbar =c=1\)) it becomes equal to its dimensionless counterpart, i.e, \(\mu _0\)), then the mentioned deformed Friedman equation can be linked to the cosmological dynamics of loop quantum gravity (LQG) by applying a cutoff on the momentum i.e \(\mu _0>0\) from one side and Randall–Sundrum braneworld in case of a cutoff on the length i.e. \(\mu _0<0\), from the other side. Using the method of qualitative theory of dynamical systems, our stability analysis is performed within \((H,\rho )\) phase plane at a finite domain by concerning the hyperbolic critical points. Generally speaking, for all three GCG, MCG and GMCG cases, within expanding (\(H>0\)) and accelerating universe (\(c_s^2>0)\), the quartessence models are stable in the neighborhood of the critical points \((H_{cp},\rho _{cp})\), in the case of admitting one of theoretically possible signs for \(\mu _0\). The outstanding feature of our stability analysis is that it restricts freedom to accept the expected invariant UV cutoffs via the connection between QG free parameter \(\mu _0\) and the phenomenological parameters involved in quartessence models \((\Omega _m^*, c_s^2, \rho _*)\). In particular, our analysis explicitly shows that the requirement of stability for above mentioned quartessence models unanimously within a flat accelerating universe free of Big-Bang singularity, will be possible only in case of acceptance of a minimum invariant length in fundamental level (i.e. \(\mu _0<0\)). Also, we have noticed that for all three of the above-mentioned background fluids within the underlying Snyder deformed cosmology with open spatial geometry, the possibility of stability in present time only exists in case of admitting a minimum length at the fundamental level. While for closed one, depending on the fixed values for today critical density of universe \(\rho _*\), one can accept one of possible cases for \(\mu _0\). For any three Chaplygin gas quartessence models, we have constructed the phase portraits in a 2D phase space (\(H,\rho \)) separately and discussed on the behavior of trajectories in the neighborhood of the CPs. As a result, it is common in all three quartessence models that in the presence of minimum length (\(\mu _0<0\)), there is the possibility of a stable expanding and accelerating universe with all three possible curvature modes. While, regarding the maximum momentum (\(\mu _0>0\)) within the FRW background, only shows a stable static universe with closed spatially geometry. As a consequence, our results are essentially independent of the free parameters of equation-of-states of Chaplygin gas models, which are constrained by experiments [22,23,24,25,26].

Briefly, this work contains the following important consequences. First, the requirement of stability for three quartessence models can yield an expanding and accelerating universe compatible with current observational evidences in which Big-Bang singularity is absent. To be more detailed, in case of setting the flat and open geometries for curvature constant modes within NC Snyder spacetime approach, it will be realized the braneword-like framework along with the relevant uncertainty relation of string theory. While for the case of closed universe depending on \(\rho _*\), also there is a chance to emerge of the LQG-like framework.Footnote 7 Secondly, by admitting a down to up phenomenological view, our analysis gives qualitatively a hint on the possibility of searching the micro-level spacetime via the control of the Planck scale characteristic parameter using the current astronomical observational signatures.

At the end, to emphasize on the importance of the latter as an incentive for proposing an upcoming project, we would like to refer to [87] in which via probing the effects of NC geometry using the latest CMB observations, authors have presented some positive feedbacks.