1 Introduction

The accepted definition of conserved quantity the energy–momentum with physical meaningful expression has been under investigation for a long time in the theory of general relativity. Einstein proposed the first energy–momentum complex in an attempt to define the local distribution of energy and momentum [1, 2]. After that, many definitions of energy–momentum complexes were proposed, for instance, Tolman [3], Papapetrou [4], Landau–Lifshitz [5], Bergman-Thomson [6], Møller [7, 8], Weinberg [9], Qadir-Sharif [10] and others. The energy–momentum prescriptions give meaningful results when the line element is transformed to Cartesian coordinates. Elias [11] evaluated the energy and momentum distributions associated with a three-dimensional rotating BTZ black hole solution, and a non-static and circularly symmetric space–time [12]. Yang et al. [13] investigated three-dimensional non-rotating black hole solutions with non-zero cosmological constant under various parameter conditions. In four-dimensions space–time, numerous works on evaluating the energy and momentum distributions using different complexes have been completed. For examples, Virbhadra [14,15,16,17,18,19,20], Virbhadra and his collaborators [21,22,23,24], Sharif [25,26,27,28], Ragab [29,30,31], and others [32,33,34,35,36,37,38,39] and found some encouraging results. Aguirregabiria et al. [40] showed that for any Kerr–Schild class metric, several energy–momentum complexes give the same results.

There is still doubts on the localization of energy and momentum in curved space–times. According to Misner et al. [41] the energy is localizable only for spherical systems, whereas for Cooperstock et al. [42] it is for all systems. Cooperstock [43] later proposed a hypothesis that the energy and momentum are confined to the region of non-vanishing stress-energy tensor (\(T^{\mu }_{\nu }\)) of matter and all non-gravitational fields in curved space–time. This hypothesis has neither been proved nor disproved. But there are many results which support this hypothesis (e.g. [44,45,46,47]). In the present work, we evaluate the energy and momentum distribution associated with a topological trivial Gödel-type metric using five energy–momentum complexes and found that the results may support the above hypothesis.

The first solution to the field equations containing closed timelike curves is the cylindrical symmetry Gödel universe [48]. This rotating cosmological solution has a great interest since it was the most well-known solution that describes a universe where the causality is violated. Investigation of relativistic quantum effects on scalar and spin-half particles in Gödel universe as well as Gödel-type space–times has been addressed by several authors. Soares et al. [49] studied the Klein–Gordon and Dirac equations in Gödel-type space–times with positive and negative curvatures, and also in flat Gödel-type space–time. Drukker et al. [50] (see also [51]) investigated the close relation between the energy levels of a scalar particle in a class of Gödel solutions and the Landau levels in curved backgrounds. In Ref. [52] the same relation between the flat Gödel solution (Som and Raychaudhuri space–time) and Landau problem in flat space was discussed. Carvalho et al. [53] investigated the Klein–Gordon equation in a class of Gödel solutions with a cosmic string. They solved the Klein–Gordon equation and analyzed the similarity of the energy levels with the Landau levels in flat, spherical and hyperbolic Gödel spaces. They demonstrated there that the presence of cosmic string modifies the energy levels and breaks the degeneracy of eigenvalues. In Ref. [54], quantum influence of topological defects in Gödel-type space–times (Som-Raychaudhuri space–time as well as in flat, spherical and hyperbolic spaces), was discussed. The relativistic quantum dynamics of Dirac particle with topological defect in a class of Gödel space–times with torsion have been investigated in [55]. Bakee et al. [56] studied the linear confinement of a relativistic scalar particle in Som-Raychaudhuri space–time in the presence of a topological defect. The Klein–Gordon equation with vector and scalar potentials of Coulomb types under the influence of non-inertial effects in a cosmic string space–time, was studied in [57].

The Klein–Gordon oscillator [58, 59] was inspired by the spin-\(\frac{1}{2}\) Dirac oscillator [60]. The relativistic quantum effects of confining potentials on the Klein–Gordon oscillator was investigated in [61]. Boumali et al. [62] have investigated the Klein–Gordon oscillator in the background of cosmic strings in the presence of a uniform magnetic field. Later, the Klein–Gordon oscillator was investigated in the presence of a Coulomb potential by two ways: (i) via a modification of mass term [63], and (ii) via the minimal coupling [64], in the latter case the linear scalar potential was also included. The Klein–Gordon oscillator on the curved background within the Kaluza–Klein theory was discussed in [54]. In the presence of uniform magnetic fields the Klein–Gordon oscillator in Som-Raychaudhuri space–time was discussed in [65]. Very recently, Santos et al. [57] investigated the Klein–Gordon oscillator in the background space–time generated by a cosmic string. In the present work, the relativistic quantum effects on scalar and spin-half particles without any potential in a topologically trivial Gödel-type space–time, is studied.

2 A topological trivial Gödel-type space–time

Consider the following stationary space–time [66] in the coordinates \((x^0=t, x^1=x, x^2=y, x^3=z)\) given by

$$\begin{aligned} ds^2= & {} -dt^2+dx^2+\left( 1-\alpha ^2\,x^2\right) dy^2-2\,\alpha \,x\,dt\,dy+dz^2\nonumber \\= & {} -[dt+H(x)\,dy]^2+dx^2+D^2(x)\,dy^2+dz^2, \end{aligned}$$
(1)

where \(\alpha >0\) is a real number, and the function \(H(x)=\alpha \,x\) and \(D(x)=1\). The ranges of the coordinates are \(-\infty< t,\,x,\, y,\, z < \infty \). The determinant of the metric tensor \(g_{\mu \nu }\) for the space–time (1) is

$$\begin{aligned} det\;g=-1, \end{aligned}$$
(2)

which indicates that the metric is regular everywhere even at \(x=0\). The covariant and contravariant components of the metric tensor for the space–time (1) are

$$\begin{aligned} g_{00}= & {} -1,\quad g_{11}=g_{33}=1,\quad g_{02}=-\alpha \,x=g^{02},\nonumber \\ g_{22}= & {} (1-\alpha ^2\,x^2),\quad g^{00}=-(1-\alpha ^2\,x^2),\nonumber \\ g^{11}= & {} g^{22}=g^{33}=1. \end{aligned}$$
(3)

And that the Christoffel symbols are

$$\begin{aligned} \varGamma ^{0}_{01}= & {} \frac{1}{2}\,\alpha ^2\,x=-\varGamma ^{2}_{12}=\frac{1}{2}\,\varGamma ^{1}_{22},\nonumber \\ \varGamma ^{0}_{12}= & {} \frac{1}{2}\,\alpha \,(1+\alpha ^2\,x^2),\quad \varGamma ^{1}_{02}=\frac{1}{2}\,\alpha =-\varGamma ^{2}_{01}. \end{aligned}$$
(4)

For the presented metric, the non-zero components of the Einstein tensor \(G^{\mu \nu }\) are

$$\begin{aligned} G^{0}_{0}=-\frac{3\,\alpha ^2}{4},\quad G^{0}_{2}=-\alpha ^3\,x,\quad G^{1}_{1}=G^{2}_{2}=-G^{3}_{3}=\frac{\alpha ^2}{4}. \end{aligned}$$
(5)

The scalar curvature invariants constructed from the Riemann tensor given by

$$\begin{aligned} R=\frac{\alpha ^2}{2},\quad R^{\mu \nu }\,R_{\mu \nu }=\frac{3}{4}\,\alpha ^4,\quad R^{\mu \nu \rho \sigma }\,R_{\mu \nu \rho \sigma }=\frac{11}{4}\,\alpha ^4, \end{aligned}$$
(6)

are non-vanishing constants which guaranteed that the studied metric is free-from curvature divergence.

The space–time (1) possess five Killing vector fields given by

$$\begin{aligned} \xi _{1}= & {} \partial _{t},\quad \xi _{2}=\partial _{y},\quad \xi _{3}=\partial _{z},\quad \xi _{4}=y\,\partial _{t}-\frac{1}{\alpha }\,\partial _{x}\nonumber \\ \xi _{5}= & {} (x^2-y^2)\,\partial _{t}+\frac{2}{\alpha }\,(y\,\partial _{x}-x\,\partial _{y}). \end{aligned}$$
(7)

The four-velocity of matter field is \(U^{\mu }=\delta ^{\mu }_{0}\) and the rotation vector is \(\omega ^{\mu }=-\frac{\alpha }{2}\,\delta ^{\mu }_{3}\), while the vorticity scalar is given by \(\varOmega =(\omega _{\mu }\,\omega ^{\mu })^{\frac{1}{2}}=\frac{\alpha }{2}\). In addition, the other kinematical parameters the expansion, the four-acceleration, and the shear of the fluid vanishes. Here \(\varOmega \) can be interpretated as the angular velocity of rotation of the space–time. In fact, all the matter content is rotating with respect to every point in space, because of the homogeneity of the space–time.

The necessary and sufficient conditions for a Gödel-type space–time to be space-time homogeneous (hereafter called ST homogeneous) [67,68,69,70] given by

$$\begin{aligned} \frac{H'}{D}=\alpha =2\,\varOmega ,\quad \frac{D''}{D}=0, \end{aligned}$$
(8)

where prime denotes ordinary differentiation w. r. t. x. Using anisotropic fluid as the stress-energy tensor, we have

$$\begin{aligned} \rho =\frac{3\,\alpha ^{2}}{4\,\kappa }=\frac{3\,\varOmega ^2}{8\,\pi },\quad p_{x}=p_{y}=-p_{z}=\frac{\alpha ^{2}}{4\,\kappa }=\frac{\varOmega ^2}{8\,\pi }, \end{aligned}$$
(9)

where the field equations are \(G^{\mu \nu }=\kappa \,T^{\mu \nu }\), \(\kappa =8\,\pi \) and the units are \(c=1=G=\hbar \). Here \(\rho \) is the energy-density of ansiotropic fluid and \(p_{i}, i=x,y,z\) are pressures.

Note that if one takes \(\varOmega =0\) which implies \(\alpha =0\), the studied space–time reduces to four-dimensional Minkowski metric.

2.1 The energy–momentum distributions

Here we evaluate the energy and momentum distributions of space–time (1) using the Møller, Einstein, Landau–Lifshitz, Papapetrou, and Bergmann–Thomson complexes.

2.1.1 Møller energy–momentum complex

The Møller energy–momentum complex [7] is given by

$$\begin{aligned} M_{\mu }^{\,\,\,\,\nu }=\frac{1}{8\,\pi }\,\chi _{\mu \,\,,\rho }^{\,\,\,\,\nu \rho }, \end{aligned}$$
(10)

where the superpotential \(\chi ^{\mu \rho }_{\nu }\) is

$$\begin{aligned} \chi _{\mu }^{\,\,\,\,\nu \rho }=-\chi _{\mu }^{\,\,\,\,\rho \nu }=\sqrt{-g}\,(g_{\mu \tau ,\beta }-g_{\mu \beta ,\tau })\,g^{\nu \beta }\,g^{\rho \tau }. \end{aligned}$$
(11)

The complex \(M_{\mu }^{\,\,\,\,\nu }\) satisfies the local conservation laws

$$\begin{aligned} \frac{\partial M_{\mu }^{\,\,\,\,\nu }}{\partial x^{\nu }}=0. \end{aligned}$$
(12)

Here \(M_{0}^{\,\,\,\,0}\) and \(M_{i}^{\,\,\,\,0}\) represents the energy and momentum density components, respectively [8].

The non-vanishing components of \(\chi _{\mu }^{\,\,\,\,\nu \sigma }\) using the space–time (1) are

$$\begin{aligned} \chi _{0}^{\,\,\,\,01}= & {} -\alpha ^2\,x,\quad \chi _{2}^{\,\,\,\,01}=-\alpha \,(1+\alpha ^2\,x^2),\nonumber \\ \chi _{0}^{\,\,\,\,12}= & {} -\alpha ,\quad \chi _{2}^{\,\,\,\,12}=-\alpha ^2\,x. \end{aligned}$$
(13)

Using the above components in (10) we obtain the energy and momentum densities

$$\begin{aligned} M_{0}^{\,\,\,\,0}= & {} \frac{1}{8\,\pi }\,\chi _{0\,,\rho }^{\,\,\,\,0\rho }=\frac{1}{8\,\pi }\,\chi _{0\,,1}^{\,\,\,01}=-\frac{\alpha ^2}{8\,\pi }=-\frac{\varOmega ^2}{2\,\pi },\nonumber \\ M_{1}^{\,\,\,\,0}= & {} \frac{1}{8\,\pi }\,\chi _{1\,,\rho }^{\,\,\,\,0\rho }=0,\nonumber \\ M_{2}^{\,\,\,\,0}= & {} \frac{1}{8\,\pi }\,\chi _{2\,,\rho }^{\,\,\,\,0\rho }=\frac{1}{8\,\pi }\,\chi _{2\,,1}^{\,\,\,\,01}=-\frac{\alpha ^3\,x}{4\,\pi }=-\frac{2\,\varOmega ^3}{\pi }\,x,\nonumber \\ M_{3}^{\,\,\,\,0}= & {} \frac{1}{8\,\pi }\,\chi _{3\,,\rho }^{\,\,\,\,0\rho }=0. \end{aligned}$$
(14)

At \(x=0\), the momentum density component vanishes \(M_{i}^{\,\,\,\,0}=0\). Therefore the energy component is

$$\begin{aligned} E_{M}=\int \int \int M_{0}^{\,\,\,0}\,dx\,dy\,dz=-\frac{\varOmega ^2}{2\,\pi } \int \int \int dx\,dy\,dz. \end{aligned}$$
(15)

2.1.2 Einstein energy–momentum complex

The energy–momentum complex as defined by Einstein [2] is given by

$$\begin{aligned} \varTheta _{\mu }^{\,\,\,\,\nu }=\frac{1}{16\,\pi }\,H_{\mu \,\,\,,\rho }^{\,\,\,\,\nu \rho }, \end{aligned}$$
(16)

where the superpotential \(H_{\mu \,\,\,,\rho }^{\,\,\,\,\nu \rho }\) is

$$\begin{aligned} H_{\mu }^{\,\,\,\,\nu \rho }=-H_{\mu }^{\,\,\,\,\rho \nu }=\frac{g_{\mu \tau }}{\sqrt{-g}}\,[-g\,(g^{\nu \tau }\,g^{\rho \sigma }-g^{\rho \tau }\,g^{\nu \sigma })]_{,\sigma }. \end{aligned}$$
(17)

The complex \(\varTheta _{\mu }^{\,\,\,\,\nu }\) satisfies the local conservation laws

$$\begin{aligned} \frac{\partial \varTheta _{\mu }^{\,\,\,\,\nu }}{\partial x^{\nu }}=0. \end{aligned}$$
(18)

Here \(\varTheta _{0}^{\,\,\,0}\) is the energy density, and \(\varTheta _{i}^{\,\,\,0}\) are the momentum density components.

The following components of \(H_{\mu }^{\,\,\,\,\nu \rho }\) are needed

$$\begin{aligned} H_{\mu }^{\,\,\,01}=(g_{0\mu }\,g^{00}_{\,\,,1}+g_{2\mu }\,g^{02}_{\,\,,1}). \end{aligned}$$
(19)

Using the above components in (16), we obtain the energy and momentum densities

$$\begin{aligned} \varTheta _{\mu }^{\,\,\,\,0}= & {} \frac{1}{16\,\pi }\,H_{\mu \,\,\,,\rho }^{\,\,\,\,0\rho },\nonumber \\ \varTheta _{0}^{\,\,\,0}= & {} \frac{1}{16\,\pi }\,H_{0\,\,,\rho }^{\,\,\,\,0\rho }=-\frac{\alpha ^2}{16\,\pi }=-\frac{\varOmega ^2}{4\,\pi },\nonumber \\ \varTheta _{1}^{\,\,\,0}= & {} \frac{1}{16\,\pi }\,H_{1\,\,,\rho }^{\,\,\,\,0\rho }=0,\nonumber \\ \varTheta _{2}^{\,\,\,0}= & {} \frac{1}{16\,\pi }\,H_{2\,\,,\rho }^{\,\,\,\,0\rho }=-\frac{\alpha ^3\,x}{8\,\pi }=-\frac{\varOmega ^3\,x}{\pi },\nonumber \\ \varTheta _{3}^{\,\,\,0}= & {} \frac{1}{16\,\pi }\,H_{3\,\,,\rho }^{\,\,\,\,0\rho }=0. \end{aligned}$$
(20)

At \(x=0\), the momentum density component vanishes \(\varTheta _{i}^{\,\,\,0}=0\). Therefore the energy component is

$$\begin{aligned} E_{Ein}=\int \int \int \varTheta _{0}^{\,\,\,\,0} dx\,dy\,dz=-\frac{\varOmega ^2}{4\,\pi } \int \int \int dx\,dy\,dz. \end{aligned}$$
(21)

Notice that the energy distribution in the prescriptions of Møller (M), and Einstein (Ein) are given by

$$\begin{aligned} E_{M}=2\,E_{Ein}=-\frac{\varOmega ^2}{2\,\pi }\,\int \int \int dx\,dy\,dz. \end{aligned}$$
(22)

2.1.3 Landau–Lifshitz’s energy–momentum complex

The energy–momentum complex in the sense of Landau–Lifshitz [5] is given by

$$\begin{aligned} L^{\mu \rho }=\frac{1}{16\,\pi }\,S^{\mu \nu \rho \sigma }_{\,\,\,\,,\nu \sigma }, \end{aligned}$$
(23)

where the superpotential \(S^{\mu \nu \rho \sigma }_{\,\,\,\,,\nu \sigma }\) is

$$\begin{aligned} S^{\mu \nu \rho \sigma }=-g\,(g^{\mu \rho }\,g^{\nu \sigma }-g^{\mu \sigma }\,g^{\nu \rho }), \end{aligned}$$
(24)

and has symmetries of the Riemann tensor \(R_{\mu \nu \rho \sigma }\). Here \(L^{00}\) represents the energy density and \(L^{i0}\) represent the components of momentum density, respectively. The energy–momentum complex \(L^{\mu \rho }\) satisfies the local conservation laws

$$\begin{aligned} \frac{\partial L^{\mu \nu }}{\partial x^{\nu }}=0. \end{aligned}$$
(25)

The non-zero components of \(S^{\mu \nu \rho \sigma }\) are

$$\begin{aligned} S^{0101}= & {} S^{1010}=-(1-\alpha ^2\,x^2),\quad S^{0121}=-\alpha \,x=S^{2101},\nonumber \\ S^{0202}= & {} -1. \end{aligned}$$
(26)

Substituting (26) in (23), we get the energy and momentum densities

$$\begin{aligned} L^{00}= & {} \frac{1}{16\,\pi }\,S^{0\nu 0\sigma }_{\,\,\,\,,\nu \sigma }=\frac{1}{16\,\pi }\,S^{0101}_{\,\,,11}=\frac{\alpha ^2}{8\,\pi }=\frac{\varOmega ^2}{2\,\pi },\nonumber \\ L^{i0}= & {} \frac{1}{16\,\pi }\,S^{i\nu 0\sigma }_{\,\,\,,\nu \sigma }=0. \end{aligned}$$
(27)

Therefore the energy component is

$$\begin{aligned} E_{L}=\int \int \int L^{00}\,dx\,dy\,dz=\frac{\varOmega ^2}{2\,\pi }\,\int \int \int dx\,dy\,dz. \end{aligned}$$
(28)

2.1.4 Papapetrou energy–momentum complex

The symmetric energy–momentum complex of Papapetrou [4] is defined as

$$\begin{aligned} \varOmega ^{\mu \nu }=\frac{1}{16\,\pi }\,N^{\mu \nu \rho \sigma }_{\,\,\,,\rho \sigma }, \end{aligned}$$
(29)

where the superpotential \(N^{\mu \nu \rho \sigma }_{\,\,\,,\rho \sigma }\) is

$$\begin{aligned} N^{\mu \nu \rho \sigma }=\sqrt{-g}\,(g^{\mu \nu }\,\eta ^{\rho \sigma }-g^{\mu \rho }\,\eta ^{\nu \sigma }+g^{\rho \sigma }\,\eta ^{\mu \nu }-g^{\nu \sigma }\,\eta ^{\mu \rho }), \end{aligned}$$
(30)

and \(\eta ^{\mu \nu }\) is the Minkowski spacetime. The quantities \(N^{\mu \nu \rho \sigma }\) are symmetric in its first two indices \(\mu \) and \(\nu \). The energy–momentum complex \(\varOmega ^{\mu \nu }\) satisfies the local conservation laws:

$$\begin{aligned} \frac{\partial \varOmega ^{\mu \nu }}{\partial x^{\nu }}=0. \end{aligned}$$
(31)

\(\varOmega ^{00}\) and \(\varOmega ^{i0}\) are the energy and momentum density components, respectively.

The following non-vanishing components of \(N^{\mu \nu \rho \sigma }\) are needed

$$\begin{aligned} N^{0011}=-(2-\alpha ^2\,x^2),\quad N^{0211}=-\alpha \,x=N^{2011}. \end{aligned}$$
(32)

Using the above components in (29), we get the energy and momentum densities

$$\begin{aligned} \varOmega ^{00}= & {} \frac{1}{16\,\pi }\,N^{00\rho \sigma }_{\,\,\,,\rho \sigma }=\frac{1}{16\,\pi }\,N^{0011}_{\,\,\,,11}=\frac{\varOmega ^2}{2\,\pi },\nonumber \\ \varOmega ^{i0}= & {} \frac{1}{16\,\pi }\,N^{i0\rho \sigma }_{\,\,\,,\rho \sigma }=\frac{1}{16\,\pi }\,N^{i011}_{\,\,\,,11}=0. \end{aligned}$$
(33)

Therefore the energy component is

$$\begin{aligned} E_{P}=\int \int \int \varOmega ^{00}\,dx\,dy\,dz=\frac{\varOmega ^2}{2\,\pi }\,\int \int \int dx\,dy\,dz. \end{aligned}$$
(34)

2.1.5 Bergmann–Thomson energy–momentum complex

The Bergmann–Thomson energy–momentum complex [6] is given by

$$\begin{aligned} B^{\mu \nu }=\frac{1}{16\,\pi }\,{\prod }^{\mu \nu \rho }_{\,\,\,,\rho }, \end{aligned}$$
(35)

where the superpotential \({\prod }^{\mu \nu \rho }_{\,\,\,,\rho }\) is

$$\begin{aligned} {\prod }^{\mu \nu \rho }=g^{\mu \alpha }\,V^{\,\,\nu \rho }_{\alpha } \end{aligned}$$
(36)

with

$$\begin{aligned} V^{\,\,\nu \rho }_{\alpha }=-V^{\,\,\rho \nu }_{\alpha }=\frac{g_{\alpha \beta }}{\sqrt{-g}}\,[-g\,(g^{\nu \beta }\,g^{\rho \sigma }-g^{\rho \beta }\,g^{\nu \sigma })]_{,\sigma }. \end{aligned}$$
(37)

Here \(B^{00}\) and \(B^{i0}\) are the energy and momentum densities, respectively. The energy–momentum \(B^{\mu \nu }\) satisfies the local conservation laws

$$\begin{aligned} \frac{\partial B^{\mu \nu }}{\partial x^{\nu }}=0. \end{aligned}$$
(38)

The following non-vanishing components of \(V^{\nu \rho }_{\,\,\alpha }\) and \({\prod }^{\mu \nu \rho }\) are needed

$$\begin{aligned}&V^{\,\,01}_{\alpha }=g_{\alpha \beta }\,(g^{0\beta }\,g^{11})_{,1}=g_{\alpha \beta }\,g^{0\beta }_{\,\,,1},\nonumber \\&{\prod }^{\mu 01}=g^{\mu \alpha }\,V^{\,\,01}_{\alpha }. \end{aligned}$$
(39)

Using the above components in (35), we get

$$\begin{aligned} B^{\mu 0}=\frac{1}{16\,\pi }\,{\prod }^{\mu 0\rho }_{\,\,\,\,,\rho }=\frac{1}{16\,\pi }\,{\prod }^{\mu 01}_{\,\,\,,1}=\frac{1}{16\,\pi }\,(g^{\mu }_{\beta }\,g^{0\beta }_{\,,1})_{,1}. \end{aligned}$$
(40)

So the energy and momentum densities are

$$\begin{aligned} B^{00}=\frac{1}{16\,\pi }\,(g^{0}_{\beta }\,g^{0\beta }_{\,,1})_{,1}=\frac{\varOmega ^2}{2\,\pi },\quad B^{i0}=\frac{1}{16\,\pi }\,g^{i0}_{,11}=0. \end{aligned}$$
(41)

Therefore the energy component is

$$\begin{aligned} E_{B}=\int \int \int B^{00}\,dx\,dy\,dz=\frac{\varOmega ^2}{2\,\pi }\,\int \int \int dx\,dy\,dz. \end{aligned}$$
(42)

Note that the energy distributions in Landau–Lifshitz, Papapetrou, and Bergmann–Thomson complexes are equal given by

$$\begin{aligned} E_{L}=E_{P}=E_{B}=\frac{\varOmega ^2}{2\,\pi }\,\int \int \int dx\,dy\,dz. \end{aligned}$$
(43)

From (22) and (43), we get the energy distributions for the metric (1) are

$$\begin{aligned} E_{L}= & {} E_{P}=E_{B}=-E_{M}=-2E_{Ein}\nonumber \\= & {} \frac{\varOmega ^2}{2\,\pi }\int \int \int dx\,dy\,dz. \end{aligned}$$
(44)

At \(x=0\), the stress-energy tensor components (9) are non-vanishing constant and the energy distributions using different energy–momentum complexes remains unaltered. Therefore the studied space–time may support the Cooperstock’s energy localization hypothesis.

2.2 The relativistic quantum effects on scalar and spin-half particles

Here we study the relativistic quantum dynamics of a scalar particle and the relativistic quantum effects on the Klein–Gordon oscillator without any scalar potential of the space–time .

2.2.1 The Klein–Gordon equation

The relativistic quantum dynamics of a free particle of mass m is described by the following KG-equation

$$\begin{aligned} \frac{1}{\sqrt{-g}}\,\partial _{\mu } (\sqrt{-g}\,g^{\mu \nu }\,\partial _{\nu }\,\varPsi )=m^2\,\varPsi , \end{aligned}$$
(45)

with g is the determinant of metric tensor with \(g^{\mu \nu }\) its inverse, and \(\partial _{\mu }\) is the ordinary derivative.

By considering the line element (1), we obtain the following differential equation:

$$\begin{aligned} \left[ -\frac{\partial ^2}{\partial t^2}+\left( \alpha \,x\,\frac{\partial }{\partial t}-\frac{\partial }{\partial y}\right) ^2 +\left( \frac{\partial ^2}{\partial x^2}+\frac{\partial ^2}{\partial z^2}\right) \right] \,\varPsi =m^2\,\varPsi , \end{aligned}$$
(46)

which is independent of t, y, z. One can choose the following ansatz for the function \(\varPsi \)

$$\begin{aligned} \varPsi (t,x,y,z)=e^{i\,(-E\,t+p_{y}\,y+p_{z}\,z)}\,\psi (x), \end{aligned}$$
(47)

where E, \(p_{y}\) and \(p_{z}\) are constants. Substituting this ansatz into Eq. (46), we obtain the following differential equation for \(\psi (x)\):

$$\begin{aligned} \psi ''(x)-[\alpha ^2\,E^2\,x^2+2\,\alpha \,E\,p_{y}\,x]\,\psi (x)=\beta \,\psi (x). \end{aligned}$$
(48)

Let us define \(r=\sqrt{\alpha \,E}\,x\), then Eq. (48) becomes

$$\begin{aligned} \psi ''(r)-[r^2+\delta \,r]\,\psi (r)=\lambda \,\psi (r), \end{aligned}$$
(49)

where

$$\begin{aligned} \delta =\frac{2\,p_{y}}{\sqrt{\alpha \,E}},\quad \lambda =\frac{\beta }{\alpha \,E},\quad \beta =(p^{2}_{y}+p^{2}_{z}+m^2-E^2). \end{aligned}$$
(50)

The asymptotic behaviour of the possible solution to Eq. (49) are to be determined for \(r\rightarrow 0\) and \(r\rightarrow \infty \). These conditions are necessary since the wave function must be well-behaved in this limits, and thus, bound states of energy can be obtained. Let us impose that \(\psi (r)\rightarrow 0\) when \(r\rightarrow 0\) and \(r\rightarrow \infty \), hence, the solution to Eq. (49) is given by

$$\begin{aligned} \psi (r)=e^{-\frac{r^2}{2}}\,e^{-\frac{\delta \,r}{2}}\,H(r). \end{aligned}$$
(51)

Substituting Eq. (51) into Eq. (49), we obtain

$$\begin{aligned} \frac{d^2 H}{dr^2}-(\delta +2\,r)\frac{d H}{dr}+\eta \,H=0, \end{aligned}$$
(52)

where \(\eta \) is given by

$$\begin{aligned} \eta =\frac{1}{4}\,\delta ^2-\lambda -1. \end{aligned}$$
(53)

Writing the solution as a power series expansion around the origin:

$$\begin{aligned} H(r)=\sum ^{\infty }_{i=0} c_{i}\,r^{i}. \end{aligned}$$
(54)

Substituting the series into Eq. (52), we obtain the following recurrence relation:

$$\begin{aligned} c_{n+2}=\frac{(2\,n-\eta )}{(n+1)(n+2)}\,c_{n}+\frac{\delta }{n+1}\,c_{n+1}. \end{aligned}$$
(55)

By starting with \(c_0=1\) using Eq. (55), one can calculate other co-efficients of the power series expansion. As examples, the coefficients \(c_2\) and \(c_3\) are given by

$$\begin{aligned} c_{2}=\frac{1}{2}\,(\delta \,c_1-\eta ),\quad c_{3}=\left( \frac{\delta ^2-\eta +2}{6}\right) \,c_1-\frac{\delta \,\eta }{6}. \end{aligned}$$
(56)

The power series expansion becomes a polynomial of \(r^n\) by imposing two conditions:

$$\begin{aligned} c_{n+1}=0,\quad \eta =2\,n, \end{aligned}$$
(57)

which implies \(c_1=\frac{\eta }{2\,\delta }\) by Eq. (56), where \(n=1,2,3\ldots \) is the quantum number. By analysing the condition \(\eta =2\,n\), one can obtain the relativistic energy levels of the system as follows:

$$\begin{aligned} E_{n}=\left( n+\frac{1}{2}\right) \,\alpha +\sqrt{\left( n+\frac{1}{2}\right) ^2\,\alpha ^2+(p^{2}_{z}+m^2)}. \end{aligned}$$
(58)

If one takes \(p_{z}=0=m\), then the energy eigenvalues Eq. (58) reduce to

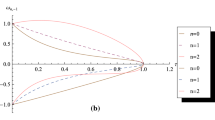
$$\begin{aligned} E_{n}=2\,\left( n+\frac{1}{2}\right) \,\alpha =4\,\left( n+\frac{1}{2}\right) \,\varOmega . \end{aligned}$$
(59)

One may compare Eq. (59) the energy-eigenvalues of the system are same the eigenvalues of the \(1-d\) harmonic oscillator (except ground state \(n=0\)) where the frequency is given by \(4\,\varOmega \).

2.2.2 The Klein–Gordon oscillator

To couple the Klein–Gordon oscillator [58, 59], the generalization of Mirza et al. prescription [71], in which the following change in the momentum operator is taken:

$$\begin{aligned} p_{\mu }\rightarrow p_{\mu }+i\,m\,\varOmega _0\,X_{\mu }, \end{aligned}$$
(60)

where m is the particle mass at rest, \(\varOmega _0\) is the frequency of the oscillator and \(X_{\mu }=(0,x,0,0)\), with x being the distance of the particle. In this way, the Klein–Gordon equation becomes

$$\begin{aligned}&\frac{1}{\sqrt{-g}}\,(\partial _{\mu }+m\,\varOmega _0\,X{\mu })\sqrt{-g}\,g^{\mu \nu }\,(\partial _{\nu }-m\,\varOmega _0\,X_{\nu })\,\varPsi \nonumber \\&\qquad =m^2\,\varPsi . \end{aligned}$$
(61)

Using the space–time (1), we obtain the following equation

$$\begin{aligned}&\left[ -\frac{\partial ^2}{\partial t^2}+\left( \alpha \,x\,\frac{\partial }{\partial t}-\frac{\partial }{\partial y}\right) ^2 +\frac{\partial ^2}{\partial z^2}\right] \,\varPsi \nonumber \\&\quad +\left( \frac{\partial }{\partial x}+m\,\varOmega _0\,x\right) \,\left( \frac{\partial \varPsi }{\partial x}-m\,\varOmega _0\,x\,\varPsi \right) =m^2\,\varPsi . \end{aligned}$$
(62)

The equation (62) is independent of t, y, z, so it is appropriate to choose the ansatz given in (47), and we obtain

$$\begin{aligned} \psi ''(x)-[\omega ^2\,x^2+2\,\alpha \,E\,p_{y}\,x]\,\psi (x)=\beta _0\,\psi (x), \end{aligned}$$
(63)

where

$$\begin{aligned} \omega =\sqrt{\alpha ^2\,E^2+m^2\,\varOmega _{0}^2},\quad \beta _0=\beta +m\,\varOmega _0. \end{aligned}$$
(64)

Let us define \(r=\sqrt{\omega }\,x\), then Eq. (64) becomes

$$\begin{aligned} \psi ''(r)-[r^2+\varTheta \,r]\,\psi (r)=\gamma \,\psi (r), \end{aligned}$$
(65)

where

$$\begin{aligned} \varTheta =\frac{2\,\alpha \,E\,p_{y}}{\omega ^{3/2}},\quad \gamma =\frac{\beta _0}{\omega }. \end{aligned}$$
(66)

The solution to Eq. (65) is

$$\begin{aligned} \psi (r)=e^{-\frac{r^2}{2}}\,e^{-\frac{\varTheta \,r}{2}}\,H(r). \end{aligned}$$
(67)

Substituting Eq. (67) into Eq. (65), we obtain

$$\begin{aligned} \frac{d^2 H}{dr^2}-(\varTheta +2\,r)\,\frac{d H}{dr}+\eta _0\,H=0, \end{aligned}$$
(68)

where \(\eta _0\) is given by

$$\begin{aligned} \eta _0=\frac{1}{4}\,\varTheta ^2-\gamma -1. \end{aligned}$$
(69)

Considering the solution of H(r) as a power series expansion done earlier, the following recurrence relation is obtained:

$$\begin{aligned} c_{n+2}=\frac{(2\,n-\eta _0)}{(n+1)(n+2)}\,c_{n}+\frac{\varTheta }{n+1}\,c_{n+1}, \end{aligned}$$
(70)

with few coefficients, for examples, \(c_2\) and \(c_3\) are given by

$$\begin{aligned} c_{2}=\frac{1}{2}\,(\varTheta \,c_1-\eta _0),\quad c_{3}=\left( \frac{\varTheta ^2-\eta _0+2}{6}\right) \,c_1-\frac{\varTheta \,\eta _0}{6}. \end{aligned}$$
(71)

The power series expansion becomes a polynomial of \(r^n\) by imposing two conditions:

$$\begin{aligned} c_{n+1}=0,\quad \eta _0=2\,n, \end{aligned}$$
(72)

which implies \(c_1=\frac{\eta _0}{\varTheta }\) by Eq. (71), where \(n=1,2,3\ldots \) is the quantum number. By analysing the condition \(\eta _0=2\,n\), one may evaluate the relativistic energy levels of the system using the following relation:

$$\begin{aligned}&\frac{\alpha ^2\,E^2\,p^{2}_{y}}{\omega ^2}-(\beta +m\,\varOmega _0)=(2\,n+1)\,\omega \nonumber \\&\quad \text{ or }\quad E^2-(p^{2}_{y}+p^{2}_{z}+m^2+m\,\varOmega _0)+\frac{\alpha ^2\,E^2\,p^{2}_{y}}{\omega ^2}\nonumber \\&\quad =(2\,n+1)\,\omega , \end{aligned}$$
(73)

where \(\omega \) is given by Eq. (64).

3 Conclusions

In this article, two interesting subjects, the energy momentum localization and the relativistic quantum effects on scalar and spin-half particles in a Gödel-type space–time, was studied. Computing the conserved quantities, such as energy and momentum in curved space–times is still an unsolved problem. Following Einstein’s original pseudo-tensor for energy–momentum, several expressions have been introduced in the literature. Rosen [72] and Cooperstock [73] calculated the energy and momentum distributions of a closed homogeneous isotropic universe described by Friedmann–Robertson–Walker (FRW) space–time using the Einstein complex and found that the total energy vanishes. Johri et al. [74] used the Landau–Lifshitz complex and found that the total energy of FRW spatially closed Universe vanishes. Many researchers considered different energy–momentum complexes to evaluate the energy and momentum distributions in different space–times and obtained some encouraging results.

The relativistic energy levels of scalar and spin-half particles with linear scalar potential, scalar and vector potentials of Coulomb types in Gödel universe, Gödel-type solutions in flat, spherical and hyperbolic spaces with(-out) cosmic string, and cosmic string background space–times were obtained by various authors. They demonstrated that the energy levels of the systems are modified and depend on the parameters characterizing the space–times. In Ref. [53], the energy eigenvalues of Gödel-type space–time (Som-Raychaudhuri metric) are reduced to the energy levels obtained in [50, 51] and to the Landau levels in the presence of cosmic string [75].

We have evaluated the energy and momentum distributions of a Gödel-type space–time using the Møller, Einstein, Landau–Lifshitz, Papapetrou, and Bergmann–Thomson complexes. We found that the energy distributions for the aforementioned prescriptions remain same throughout the space–time, while the momentum density component vanishes at \(x=0\). In addition, the physical parameters (the energy density and pressures) of the stress-energy tensor are non-vanishing constants which sustained the Cooperstock’s energy localization hypothesis. Finally, we investigated the influence of vorticity (or rotation) on relativistic scalar particle in this Gödel-type space–time. We found that the relativistic energy levels without any scalar potential in the Klein–Gordon equation given by Eq. (59) are same the energy levels of the \(1-d\) harmonic oscillator of frequency \(4\,\varOmega \). Furthermore, we obtained Eq. (73) the energy levels of the system without any potentials in the Klein–Gordon oscillator and found that the energy eigenvalues depend on the vorticity parameter characterizing the space–time. In future work, one may obtain the energy levels of the system by introducing a linear scalar potential, scalar and vector potentials of Coulomb types.