Spectroscopy and decays of the fully-heavy tetraquarks

Abstract

We discuss the possible existence of the fully-heavy tetraquarks. We calculate the ground-state energy of the $bb {\bar{b}} {\bar{b}}$ bound state, where b stands for the bottom quark, in a nonrelativistic effective field theory framework with one-gluon-exchange (OGE) color Coulomb interaction, and in a relativized diquark model characterized by OGE plus a confining potential. Our analysis advocates the existence of uni-flavor heavy four-quark bound states. The ground state $bb{\bar{b}}{\bar{b}}$ tetraquark mass is predicted to be $(18.72\pm 0.02)$ GeV. Mass inequality relations among the lowest $QQ\bar{Q}\bar{Q}$ states, where $Q\in \{c, b\}$, and the corresponding heavy quarkonia are presented, which give the upper limit on the mass of ground state $QQ\bar{Q}\bar{Q}$. The possible decays of the lowest $bb\bar{b}\bar{b}$ are highlighted, which might provide useful references in the search for them in ongoing LHC experiments, and its width is estimated to be a few tens of MeV.

1 Introduction

Heavy quarkonium spectroscopy is the arena of quark potential models, in which the full interaction incorporates the short-range one-gluon-exchange (OGE) and long-range confining potential [1,2,3,4,5,6]. To put heavy quarkonium spectroscopy in a model-independent framework, efforts have been made to develop a nonrelativistic effective field theory formalism [7,8,9]. For details, see recent review [10].

Higher-order perturbative calculations show that the lowest-lying heavy quarkonia can be regarded as weakly coupled states [11,12,13]. They are characterized by a momentum scale $m_Qv \gg \Lambda _\mathrm{QCD}$, where $m_Q$ and v are the heavy quark mass and velocity, respectively, and $\Lambda _\mathrm{QCD}$ is the nonperturbative scale of quantum chromodynamics (QCD) [14], and their dynamics is mainly dominated by the short-distance interaction. In particular, there is some evidence that the first few bottomonia and $B_c$ mesons can be identified as weakly coupled systems [15,16,17], while the $J/\psi$ lies on the borderline of this classification [9]. The lowest-lying doubly- and triply-heavy baryons have also been studied as weakly coupled bound states [18, 19] but, due to the lack of experimental incentive,¹ this area is not as well explored as that of heavy quarkonia.

It is also worth mentioning some recent indications of the existence of mesons whose properties and quantum numbers do not fit into a traditional quarkonium interpretation (for recent reviews, see [21,22,23,24,25,26,27]). These states, including $Z_b(10610)$ and $Z_b(10650)$ [28], $Z_c(3900)$ [29, 30], and $Z_c(4025)$ [31, 32], have similar features and must be made up of four valence quarks, as they are isovector states in the heavy quarkonium mass region. Another interesting example is X(3872) [33] which, because of its unusual properties, does not fit well into a pure charmonium picture [1,2,3,4]. Several alternative interpretations have been proposed [34,35,36,37,38,39,40,41,42,43,44].

Fully-heavy tetraquarks, such as $bb\bar{b}\bar{b}$ and the charm analog $cc\bar{c}\bar{c}$, are of considerable interest, since they are free of light degrees of freedom and might be used as an elegant probe to investigate the interplay between both aspects of QCD: perturbative and nonperturbative. Owing to the lack of experimental incentive, only a few theoretical studies have been conducted in this field, and whether Nature allows the bound states of fully-heavy tetraquarks or not is still an open question. If it does, what are their masses and decay properties? Recently, this debate has given rise to several studies within different approaches, including the constituent quark and diquark models [45,46,47,48], chiral quark model [49], chromo-electric potential model [50], and QCD sum rules [51, 52]. All of these predict the existence of fully-heavy (bottom) tetraquarks, except for Ref. [50], in which the authors argue that the stability of a fully-heavy system of quarks should rely on more subtle effects that are not included in the simple picture of constituent quarks. The fully-heavy tetraquark case is similar to that of polyelectrons $\text {Ps}_{2}$, the bound state of two electrons and two positrons ($e^- e^- e^+ e^+$), discussed long ago by Wheeler [53]. Just after the prediction of $\text {Ps}_{2}$, a debate on their stability started [54, 55], but it took half a century to get experimental evidence of them [56].

In this paper, we compute the $b b {\bar{b}} {\bar{b}}$ ground-state energy. The calculations are performed within the formalism of a nonrelativistic effective field theory (NREFT) at the leading order (LO), which neglects all spin-dependent and confining interactions, and in a relativized diquark–antidiquark model, both of which are characterized by the OGE potential. We also make a rough estimate of the $b b {\bar{b}} {\bar{b}}$ total width, in order to guide experimental searches.

The paper is organized as follows. In Sect. 2, we describe the NREFT approach to solve the system considered. At the end of this section, we include our diquark model results. Section 3 is devoted to discuss the results, and we compare our predictions of the mass of the $X_{bb\bar{b}\bar{b}}$ ground-state with those of previous studies. In Sect. 4, we derive a set of mass inequalities, and provide the upper limits of the ground state masses of several fully-heavy tetraquarks. In Sect. 5, we highlight some possible decay modes of the $X_{bb\bar{b}\bar{b}}$ and give the ballpark estimate of its total decay width. Finally, we provide a short summary.

2 Formalism

In this section, we describe an NREFT approach to the fully-heavy tetraquark spectroscopy, characterized by the OGE interaction. This is used to estimate the mass of the $b b {\bar{b}} {\bar{b}}$ ground state. As all of the four quarks are very heavy, the tetraquark system is weakly coupled with a small size of the order $1/(m_Q\alpha _s)\sim 1/(m_Q v)$, where $\alpha _s$ is the strong coupling strength and $v\ll 1$. In this case, the dynamics of the system is dominated by the OGE which provides a color Coulomb potential at the LO, and the long-distance confining potential and spin-dependent interactions become perturbations.

In addition, we also give a tetraquark (diquark–antidiquark) model prediction for the $b b {\bar{b}} {\bar{b}}$ ground-state mass.

2.1 Nonrelativistic Hamiltonian

The nonrelativistic Hamiltonian describing the $2Q-2\bar{Q}$ system takes the following form at the LO

$$\begin{aligned} \mathcal H^\mathrm{NR}=\sum _{i=1}^{4} T_i + \sum _{i<j} V_{\text {SI}}(\mathbf r _{ij}) , \end{aligned}$$

(1)

where $T_i = m_i +\mathbf{p _{i}^{2}}/{(2m_i)}$, $\mathbf r _{ij}\equiv |\mathbf r _{i}-\mathbf r _{j}|$, and the second term is the spin-independent OGE color Coulomb potential,

$$\begin{aligned} V_{\text {SI}}(\mathbf r _{ij})=\sum _{i<j} \frac{\varvec{\lambda }_i}{2} \cdot \frac{\varvec{\lambda }_j}{2} \frac{\alpha _s}{|\mathbf r _{i}-\mathbf r _{j}|} , \end{aligned}$$

(2)

where $\varvec{\lambda }_i$ and $\varvec{\lambda }_j$ are color matrices. The quark mass $m_b$ is to be determined from the ground state bottomonium masses, and $\alpha _s$ is taken at the scale of the typical momentum transfer. At order $\alpha _{s}^{2}$, we can write $m_b$ as [19]

$$\begin{aligned} m_b = \frac{M_{b{\bar{b}}(1S)}}{2}\left( 1+ \frac{2}{9} \alpha _s^2(\mu ) \right) . \end{aligned}$$

(3)

Here, we take the spin-averaged mass $M_{b\bar{b}(1S)}=\left( M_{\eta _{b}}+3 M_{\Upsilon } \right) /4$.

2.2 Solving the four-body problem

The four-body problem is notoriously delicate. One should be careful about the choice of the wave functions, because a crude adoption may give rise to misleading conclusions, as first illustrated by Ore in Ref. [54] in the case of polyelectrons ($e^- e^- e^+ e^+$ bound states). One year later the author, in collaboration with Hylleraas [55], came up with an elegant prescription to handle four-body systems. This is what we are willing to use to calculate the $bb {\bar{b}} {\bar{b}}$ ground-state energy, provided that we make the substitution $e^- \rightarrow b$, $e^+ \rightarrow {\bar{b}}$.

Since the ground state is non-degenerate and its symmetries are governed by those of the Hamiltonian $\mathcal H^\mathrm{NR}$, the spatial wave function should be symmetric under the exchange of $Q_1Q_2\leftrightarrow \bar{Q}_3 \bar{Q}_4$. This leads to $\psi _{\text {spatial}}(Q_1Q_2)=\psi _{\text {spatial}}(\bar{Q}_3 \bar{Q}_4)$. This symmetry [55] helps to reduce the number of integration variables and simplify the four-body problem. To describe the quark relative motion, we define the following Jacobi coordinates,

$$\begin{aligned} {\varvec{\sigma }} = \mathbf{r}_1 - \mathbf{r}_2 , \quad {\varvec{\rho }} = \mathbf{r}_3 - \mathbf{r}_4 , \quad {\varvec{\lambda }} = \frac{1}{2} (\mathbf{r}_1 + \mathbf{r}_2 - \mathbf{r}_3 - \mathbf{r}_4) ,\nonumber \\ \end{aligned}$$

(4)

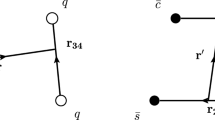
which are shown in Fig. 1.

Fig. 1

Tetraquark Jacobi coordinates of Eq. (4). Filled and open circles represent quarks and antiquarks, respectively

The “physical” tetraquark color wave function can be written as a superposition of different color configurations,²

$$\begin{aligned} |\psi _\mathrm{c} \rangle = \alpha | \bar{\mathbf{3 }}_{12}{} \mathbf 3 _{34}; \mathbf 1 _{1234} \rangle + \beta | \mathbf 6 _{12}\bar{\mathbf{6 }}_{34}; \mathbf 1 _{1234} \rangle , \end{aligned}$$

(5)

where the coefficients $\alpha$ and $\beta$ can be obtained by diagonalizing the model Hamiltonian on the tetraquark wave function. When the two identical heavy quarks are in the $\bar{\mathbf{3 }}$ color representation and in an S-wave, the spin must be equal to 1 so as to satisfy the Pauli principle. For the two heavy quarks being in the $\mathbf{6 }$ color representation and in an S-wave, the spin needs to be 0. Therefore, the mixing between $\bar{\mathbf{3 }}$ and $\mathbf{6 }$ color representations requires a flip of heavy quark spin, and thus is of higher order in NREFT (suppressed by $v^2\sim 0.1$). Since the OGE gives an attractive interaction for $\bar{\mathbf{3 }}$ and a repulsive interaction for $\mathbf{6 }$, at LO the ground-state color configuration should be $| \bar{\mathbf{3 }}_{12}{} \mathbf 3 _{34}; \mathbf 1 _{1234} \rangle$. Such a ground-state configuration has been suggested [57,58,59,60], and more recently in Refs. [46, 49, 61]. It is also supported by recent lattice QCD studies on fully-heavy four quark systems [62, 63].

On the basis of the $| \bar{\mathbf{3 }}_{12}{} \mathbf 3 _{34}; \mathbf 1 _{1234} \rangle$ color configuration, the kinetic energy matrix elements can be written as

$$\begin{aligned} T=\frac{\mathbf{p }_{\varvec{\sigma }}^{2}}{2m_{1}}+\frac{\mathbf{p }_{\varvec{\rho }}^{2}}{2m_{2}}+\frac{\mathbf{p }_{\varvec{\lambda }}^{2}}{2m_{3}}= \frac{1}{m_b} (\mathbf{p }_{\varvec{\sigma }}^{2}+\mathbf{p }_{\varvec{\rho }}^{2}+2\mathbf{p }_{\varvec{\lambda }}^{2} ), \end{aligned}$$

(6)

where $m_1$, $m_2$ and $m_3$ are the reduced masses of $Q_1 Q_2$, $\bar{Q}_3\bar{Q}_4$ and $Q_1 Q_2-\bar{Q}_3\bar{Q}_4$, respectively. The spatial trial wave function is written in terms of the Jacobi coordinates of Eq. (4) and Fig. 1,

$$\begin{aligned} \psi (\varvec{\sigma }, \varvec{\rho }, \varvec{\lambda })_{\text {spatial}} = \mathcal N \prod _{i=1}^3 \exp \left[ -\frac{1}{2} \beta ^{2}_i \varvec{\xi }_{i}^{2}\right] , \end{aligned}$$

(7)

where $(\varvec{\xi }_{1},\varvec{\xi }_{2},\varvec{\xi }_{3})\equiv (\varvec{\sigma }, \varvec{\rho }, \varvec{\lambda })$, $\beta _i$ are the oscillatory (variational) parameters, and

$$\begin{aligned} \mathcal N= \bigg (\frac{1}{\sqrt{\pi }} \bigg )^{9/2}~\prod _{i} \beta _{i}^{3/2}, \end{aligned}$$

(8)

is the overall normalization constant. It has been recently shown that the above Gaussian variational basis is a powerful tool to obtain the ground state energy of heavy tetraquarks [61].

It is worth noting that the color configurations $\left| \mathbf 1 _{13} \mathbf 1 _{24}; \mathbf 1 _{1234} \right\rangle$ and $\left| \mathbf 8 _{13} \mathbf 8 _{24}; \mathbf 1 _{1234} \right\rangle$ are linear superpositions of the two color representations of Eq. (5). In other words, one can alternatively use the bases $\{ | \bar{\mathbf{3 }}_{12}{} \mathbf 3 _{34}; \mathbf 1 _{1234} \rangle ; | \mathbf 6 _{12}\bar{\mathbf{6 }}_{34}; \mathbf 1 _{1234} \rangle \}$ or $\{ | \mathbf 1 _{13} \mathbf 1 _{24}; \mathbf 1 _{1234} \rangle ; | \mathbf 8 _{13} \mathbf 8 _{24}; \mathbf 1 _{1234} \rangle \}$. For the detailed arguments, we refer to Refs. [64, 65]. A physical transition between the $| \bar{\mathbf{3 }}_{12}{} \mathbf 3 _{34}; \mathbf 1 _{1234} \rangle$ tetraquark state and the $\left| \mathbf 1 _{13} \mathbf 1 _{24};\right.$ $\left. \mathbf 1 _{1234} \right\rangle$ two-meson state³ can occur, which is the well-known “flip-flop” transition [66]. This is an important ingredient while studying the decays into two mesons if the mass of the initial tetraquark is higher than the two-meson threshold.

2.3 $b b {\bar{b}} {\bar{b}}$ ground-state

The eigenvalue problem is solved by means of a numerical variational approach with Gaussian trial wave functions [67, 68]. The quark mass $m_b$ is extracted via Eq. (3), where one also has to include the spin-averaged mass of the 1S (ground-state) bottomonia,

$$\begin{aligned} M_{b\bar{b}}(1S)=\frac{1}{4} [3M_{\Upsilon (1S)}+M_{\eta _{b}(1S)} ] = 9.45~\text {GeV} . \end{aligned}$$

(9)

The other parameter, i.e., the running coupling constant $\alpha _s(\mu )$, is taken at the scale of the typical momentum transfer in the ground-state bottomonium ($\mu =1.5$ GeV). The extracted values are

$$\begin{aligned} m_b=4.82~\text {GeV} , \quad \alpha _\mathrm{s}(1.5~\mathrm{GeV})=0.31 . \end{aligned}$$

(10)

The spin-averaged binding energy of the 1S bottomonium is

$$\begin{aligned} E_{b\bar{b}}(1S) \equiv 2 m_b - M_{b{\bar{b}} (1S)} =(0.20\pm 0.01)~\text {GeV}. \end{aligned}$$

(11)

We can estimate the energy of the $X_{bb\bar{b}\bar{b}}$ ground-state by means of the variational method with Gaussian trial wave functions previously used in the bottomonium case and the model parameter values of Eq. (10). We get

$$\begin{aligned} M_{b b {\bar{b}} {\bar{b}}}^\mathrm{gs, NR} = (18.72\pm 0.02) \text{ GeV }, \end{aligned}$$

(12)

where the uncertainty is given by the product of the binding energy and $\alpha _\mathrm{s}(1.5~\mathrm{GeV})$. The binding energy of the lowest four b-quark bound state is obtained as

$$\begin{aligned} E_{bb\bar{b}\bar{b}}(1S) \equiv 4 m_b - M_{b b {\bar{b}} {\bar{b}}}^\mathrm{gs, NR} = (0.56\pm 0.02)~\text {GeV}. \end{aligned}$$

(13)

The extracted optimal values of the variational parameters $\beta _i$ are $\beta _1=\beta _2= 0.77$ GeV and $\beta _3= 0.60$ GeV, where $\beta _1=\beta _2$ is due to the symmetry of the spatial wave function [55], as discussed in the last subsection.

2.4 $b b {\bar{b}} {\bar{b}}$ ground state in a relativized diquark model

In this subsection, we provide an estimate of the fully-bottom tetraquark ground-state energy by treating the $X_{b b {\bar{b}} \bar{b}}$ configuration as a diquark, bb, and antidiquark, ${\bar{b}} \bar{b}$, bound state in a relativized diquark model. In this model, the diquark is an effective degree of freedom which describes two strongly correlated quarks with no internal spatial excitations. The lowest-energy diquark configurations, scalar and axial-vector, are both color anti-triplets but have different spin and flavor quantum numbers. The former, i.e., the scalar diquark, has spin-0 and its flavor wave function is antisymmetric. The latter has spin-1 and is flavor-symmetric. As mentioned in the last section, because of the Pauli principle, a (point-like) diquark made up of quarks of the same flavor can only be of the axial-vector type [57,58,59, 69].

To calculate the energy of the $b b{\bar{b}} {\bar{b}}$ ground state in diquark anti-diquark configuration, we need an evaluation of the bb axial-vector diquark mass, $M_{\mathrm{av}, bb}$. The diquark (antidiquark) mass is estimated by binding a bb (${\bar{b}} {\bar{b}}$) pair via the OGE plus a confining potential [3], and we have⁴

$$\begin{aligned} M_{\mathrm{av}, bb} = 9.85~\mathrm{GeV}. \end{aligned}$$

(14)

After doing that, we can compute the 1S, $0^{++}$ tetraquark ground-state energy in the relativized diquark model. The model Hamiltonian is characterized by the OGE plus confining potential. For more details on the model and the values of the model parameters, we refer to Ref. [70]. With the use of the previous value of $M_{\mathrm{av}, bb}$, we get

$$\begin{aligned} M_{b b {\bar{b}} {\bar{b}}}^\mathrm{gs, REL} = 18.75 \text{ GeV } , \end{aligned}$$

(15)

which is consistent with the result obtained in the previous subsection. See also Table 1, where our relativized diquark model prediction is compared to those of previous studies. The theoretical uncertainty in the above prediction can be estimated by using the typical error of the quark model calculations. The intrinsic error in the quark model predictions is of the order of 30–50 MeV [42,43,44]; therefore, this diquark model prediction has the cumulative uncertainty of $\mathcal O (50~\text {MeV})$.

3 Results and discussion

In Table 1, our NREFT and relativized diquark model results for the mass of the $b b {\bar{b}} {\bar{b}}$ ground-state are compared with those of previous studies. The results are strongly model-dependent and vary in the range of $(18.7\pm 0.2)$ GeV, approximately. The differences among the results mainly stem from different choices of effective Hamiltonians, the model-parameter fitting procedures, and the use of distinct approximations in the tetraquark wave function. This last is related to the possible ways of combining the quark color representations to obtain a color singlet wave function for the tetraquark. In the last column of the Table 1, we also report the differences between the predicted masses and the $\eta _b\eta _b$ threshold, $(18798 \pm 4)$ MeV [21] whose central value is used.

Table 1 Different theoretical predictions of masses for the ground state ($J^{PC}=0^{++}$) $X_{bb\bar{b}\bar{b}}$. The acronyms NR and REL refer to nonrelativistic and relativized results, respectively. In the last column, $\Delta \equiv m(X_{bb\bar{b}\bar{b}})-2m(\eta _b)$

It is worthwhile to remind some previous studies. For example, Karliner et al. [47] made a phenomenological estimation of the $Q Q {\bar{Q}} {\bar{Q}}$ ground-state energies, with $Q = b$ and c. The authors utilized a relation between meson and baryon masses to extrapolate the binding energy of $Q Q {\bar{Q}} {\bar{Q}}$ systems in the diquark model. They made the ballpark estimates of $B_{b\bar{b}}(1S)$ and the binding energy of the tetraquark with respect to the two-bb-diquark threshold, and obtained a value of about 1 / 2 for the ratio ${B_{b\bar{b}}(1S)}/{B_{bb\bar{b}\bar{b}}(1S)}$.

Bai et al. calculated the $b b {\bar{b}} {\bar{b}}$ ground-state energy by means of a phenomenological potential, whose parameters were fitted to the $b {\bar{b}}$ spectrum and verified by lattice simulation [45]. The $b b {\bar{b}} {\bar{b}}$ ground-state energy was obtained by solving the Schrödinger equation numerically; spin-dependent corrections and a linear confining potential were included. Their result agrees with our LO NREFT result very well, indicating that neglecting the spin-dependent and confining parts provides a very good approximation to the system under study.

A diquark model prediction of the $b b {\bar{b}} {\bar{b}}$ and $c c \bar{c} {\bar{c}}$ ground-state energies was given in Ref. [48]. There, the authors assumed tetraquarks to be made up of two almost point-like diquarks in the color-triplet configuration. The model parameters were fitted by solving a non-relativistic Schrödinger equation for the charmonium and bottomonium spectrum. The $bb{\bar{b}}{\bar{b}}$ ground-state mass agrees with our diquark model well.

In Ref. [71], the authors computed the $c c {\bar{c}} {\bar{c}}$ ground-state energy within a nonrelativistic potential model. The authors concluded that the possibility of obtaining bound states depends on the assumptions made on the quark dynamics and the flavor configurations. There are also early predictions for the mass [72] and width [73] of the fully-charm tetraquark, and the ground-state energies of $Q^2 \bar{Q}^2$ systems, with $Q\in \{s,c,b,t\}$ [74]. For the full mass spectrum of all-charm tetraquarks, we refer to Ref. [69]. All-charm four-quark bound state has also been studied in the Bethe–Salpeter approach and the ground state was reported to be deeply bound (650 MeV) below the $2\eta _c$ threshold [75].

A study of the importance of mixing effects between tetraquark and molecular-type components is also worthwhile to be carried out, especially for those states which are close to meson-meson thresholds. The probability of a fully-heavy tetraquark to be a $(Q\bar{Q})-(Q\bar{Q})$ hadronic molecule might be calculable without any ambiguity. It is worthwhile to mention that the possibility of an $\eta _\mathrm{b}-\eta _\mathrm{b}$ bound state has been studied by computing the QCD van der Vaals force in the framework of potential nonrelativistic QCD in Ref. [76]. Given that the recent lattice nonrelativistic QCD calculation did not find any state below the noninteracting $\eta _b\eta _b$ threshold [77], such a study seems necessary to understand what happens.

It would also be very interesting to test the possibility of a $bb{\bar{c}}{\bar{c}}$ tetraquark that remains stable against strong decays,⁵ but unfortunately there is no experimental evidence yet. The stability of heavy-light tetraquark systems is still an open question. The $QQ \bar{q} \bar{q}$ was shown to be stable against strong decays by Lipkin long ago⁶ [78]. Very recently, $bb \bar{q} \bar{q}$ was shown to be stable against strong decays but not its charm counterpart $cc \bar{q} \bar{q}$, nor the mixed (beauty+charm) $bc \bar{q} \bar{q}$ state [79, 80]. For a detailed discussion on the stability of such systems, we refer to the recent study in Ref. [81].

4 Tetraquark–meson mass inequalities

One can estimate the lower bounds of the ground state energy levels of the fully-heavy four-quark systems by using the variational approach, as suggested long ago by Nussinov [82,83,84] and by Bertlmann and Martin [85]. This approach was tested by the lattice QCD calculations of Weingarten [86] and also by the rigorous calculations in the vectorlike gauge theories (QCD) by Witten [87]. We attempt to extend Nussinov’s approach to the fully-heavy four-quark bound states and obtain inequalities between the tetraquark states and the corresponding heavy quarkonia in the following.

Let us consider the general Hamiltonian of four heavy quarks with pair-wise interactions:

$$\begin{aligned} H_{4}(Q_1 Q_2 \bar{Q}_3\bar{Q}_4)= & {} \sum _{i=1}^{4} T_i (Q_i)+ V_{Q_1 Q_2} + V_{\bar{Q}_3 \bar{Q}_4} \nonumber \\&+ V_{Q_1 \bar{Q}_3}+ V_{Q_1 \bar{Q}_4}+ V_{Q_2 \bar{Q}_3}+ V_{Q_2 \bar{Q}_4} .\nonumber \\ \end{aligned}$$

(16)

The color-antitriplet potential $V_{QQ}^{(\bar{\mathbf{3 }})}$ between any quark (or antiquark) pair can be related to the color-singlet quark–antiquark potential, $V_{Q\bar{Q}}^{(\mathbf 1 )}$ [88], via

$$\begin{aligned} V_{QQ}^{(\bar{\mathbf{3 }})}=\frac{1}{[N_c-1]} V_{Q\bar{Q}}^{(\mathbf 1 )}, \end{aligned}$$

(17)

where $1/[N_c -1]$ is the overall ratio of the color coefficient in the leading SU($N_c$) group. The above relation can also be verified by using the eigenvalues of the Casimir invariants from the Table 2, and it holds when the QQ and $Q\bar{Q}$ pairs are in the same spin and orbital quantum states. With the use of $V_{QQ}^{(\bar{\mathbf{3 }})}=\dfrac{1}{2}V_{Q\bar{Q}}^{(\mathbf 1 )}$ for SU(3), Eq. (16) can be rearranged as follows

$$\begin{aligned} H_{4}(Q_1 Q_2 \bar{Q}_3\bar{Q}_4)= & {} \sum _{i=1}^{4} T_i (Q_i) + \dfrac{1}{2} \left( V_{12}^{(\mathbf 1 )} + V_{34}^{(\mathbf 1 )} \right) \nonumber \\&+\sum _{i=1,2;j=3,4} V_{Q_i \bar{Q}_j} , \end{aligned}$$

(18)

where as before we consider only the color-antitriplet for $Q_iQ_j$ and triplet for ${\bar{Q}}_i{\bar{Q}}_j$, and we have written the color-singlet quark–antiquark ($Q_i{\bar{Q}}_j$) potential from applying Eq. (17) to $Q_iQ_j$ as $V_{ij}^{(\mathbf 1 )}$.

Table 2 Eigenvalues of the Casimir invariants $\hat{C}_i \cdot \hat{C}_j$ and $\hat{C}^2$

To work out the last term in the above equation, one has to calculate the eigenvalues of the color matrices, viz. the Casimir invariants

$$\begin{aligned} \sum _{i=1,2;j=3,4} V_{Q_i \bar{Q}_j} \propto \big \langle \bar{\mathbf{3 }}_{12} \mathbf 3 _{34} \big | \sum _{i,j} \hat{C}_i \cdot \hat{C}_j \big | \bar{\mathbf{3 }}_{12} \mathbf 3 _{34} \big \rangle , \end{aligned}$$

(19)

where $\hat{C}_{i,j}= \mathbf {\lambda }_{i,j}/2$. The eigenvalues of these Casimir invariants are explicitly given in Table 2. We need to know in which color representation the $Q_i {\bar{Q}}_j$ pair is. For instance, by writing down explicitly the color wave function (see, e.g., Ref. [89]), we can get

$$\begin{aligned} \big | \bar{\mathbf{3 }}_{12} \mathbf 3 _{34} \big \rangle _\mathbf 1= & {} \frac{1}{\sqrt{3}} \big | \mathbf 1 _{13} \mathbf 1 _{24} \big \rangle - \sqrt{\frac{2}{3}} \big | \mathbf 8 _{13} \mathbf 8 _{24} \big \rangle \nonumber \\= & {} -\frac{1}{\sqrt{3}} \big | \mathbf 1 _{14} \mathbf 1 _{23} \big \rangle + \sqrt{\frac{2}{3}} \big | \mathbf 8 _{14} \mathbf 8 _{23} \big \rangle . \end{aligned}$$

(20)

Using $\hat{C}_i \cdot \hat{C}_j = \big ({\hat{C}}_{ij}^2 - {\hat{C}}_i^2 - {\hat{C}}_j^2 \big )/2$, where ${\hat{C}}_{ij} = {\hat{C}}_i + {\hat{C}}_j$, we have

$$\begin{aligned} \big \langle \bar{\mathbf{3 }}_{12} \mathbf 3 _{34} \big | \hat{C}_{i} \cdot \hat{C}_{j} \big | \bar{\mathbf{3 }}_{12} \mathbf 3 _{34} \big \rangle= & {} \frac{1}{4} \big \langle \bar{\mathbf{3 }}_{12} \mathbf 3 _{34} \big | \hat{C}_{12} \cdot \hat{C}_{34} \big | \bar{\mathbf{3 }}_{12} \mathbf 3 _{34} \big \rangle \nonumber \\= & {} - \frac{1}{3} \end{aligned}$$

(21)

for $i=1,2; j=3,4$. This result enables us to write the pair-wise potential of four-quark state in terms of the quark–antiquark color-singlet potential, viz., the quarkonium potential,

$$\begin{aligned} \sum _{i<j} V_{ij}= & {} \frac{1}{2} \big (V_{12}^{(\mathbf 1 )} + V_{34}^{(\mathbf 1 )} \big )\nonumber \\&+ \frac{1}{4} \big ( V_{13}^{(\mathbf 1 )} + V_{14}^{(\mathbf 1 )} + V_{23}^{(\mathbf 1 )} + V_{24}^{(\mathbf 1 )} \big ) . \end{aligned}$$

(22)

This means that under the approximation of one-gluon exchange and that the two quarks are in color anti-triplet, the four-quark Hamiltonian [Eq. (18)] can be expressed in the following form,

$$\begin{aligned} H_{4}(Q_1 Q_2 \bar{Q}_3\bar{Q}_4)= & {} \frac{1}{2} \big ( H_{12} + H_{34} \big ) \nonumber \\&+ \frac{1}{4} \big ( H_{13} + H_{14} + H_{23} + H_{24} \big ), \end{aligned}$$

(23)

where $H_{ij}= T_i + T_j + V_{ij}^{(\mathbf 1 )} (\mathbf r _{ij})$ is the quarkonium Hamiltonian. Taking quarkonium wave functions as the trial wave function, and applying the variational principle [82,83,84], we obtain an upper bound on the ground state energy of four-heavy-quark system by computing the expectation value of the Hamiltonian of the subsystems, namely

$$\begin{aligned} E_{4Q}\equiv & {} \big \langle H_{4}(Q_1 Q_2 \bar{Q}_3\bar{Q}_4) \big \rangle \nonumber \\\lesssim & {} \frac{1}{2} \big ( \big \langle \psi _{12} \big | H_{12} |\psi _{12} \big \rangle + \big \langle \psi _{34} \big | H_{34} \big | \psi _{34} \big \rangle \big ) \nonumber \\&+ \frac{1}{4} \sum _{i=1,2;j=3,4} \big \langle \psi _{ij} \big | H_{ij} \big | \psi _{ij} \big \rangle , \end{aligned}$$

(24)

where $\psi _{ij}$ are the corresponding ground state wave functions of the ij subsystems. Here, we use $\lesssim$ instead of $\le$ because we have made the approximation that the two quarks are in color anti-triplet and the two anti-quarks are in color triplet, though it is expected to work rather well since the mixing with the sextet-antisextet configuration is expected to be suppressed by $v^2\sim 0.1$ for fully-bottom and $\sim 0.3$ for fully-charm four-quark systems. In this sense, the inequalities derived for baryons by Nussinov [82,83,84] are more rigorous because the two quarks in a baryon must be in an anti-triplet without any approximation.

Table 3 Mass inequality relations and upper bounds of the mass of ground-state fully-heavy tetraquarks formed of bottom and charm quarks

The inequalities for all possible fully-heavy tetraquarks are listed in Table 3. The corresponding numerical values are obtained using the spin-averaged quarkonium masses $M_{b\bar{b}}(1S)=9.445~\text {GeV}$, $M_{c\bar{c}}(1S)= 3.069~\text {GeV}$ and $M_{c\bar{b}}(1S)= 6.324~\text {GeV}$. Since the $B_{c}^* (1 ^3S_1)$ meson has not been observed, for $M_{c\bar{b}}(1S)$ we used the average value of the theoretical predictions of Godfrey–Isgur model [90] and the Cornell potential model from Ref. [91].

If we compare the so-obtained approximate upper bound in the fully-bottom sector with the earlier theoretical predictions listed in Table 1, we find this value is indeed larger than all the model predictions except for that of Ref. [52], which is calculated by means of QCD sum rules and has a large uncertainty.

5 Possible decays of $X_{bb\bar{b}\bar{b}}$

The main difficulties in the experimental observation of fully-bottom tetraquark mesons are related to the production mechanisms and observation of the main decay modes. A very recent study discussed the production of the $bb{\bar{b}}{\bar{b}}$ ground-state at the LHC, concluding that the $bb{\bar{b}}{\bar{b}}$ is supposed to be very narrow and likely to be discovered [46]. Another recent study [92] also discussed the possible production of a narrow scalar resonance around 18–19 GeV at the LHC.⁷ In the following, we will discuss the decays of such a state and provide a rough estimate of its width. We will argue that the width is at least a few tens of MeV.

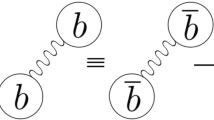
As shown in Table 1, most of the models predict the ground-state fully-bottom tetraquark to be below the $\eta _b\eta _b$ threshold. Because of this, one expects its width to be almost saturated by the following decay modes: (1) decays into final states containing a pair of bottom and anti-bottom quarks; (2) decays into hadrons of lighter flavors. The former is dominated by one-gluon exchange, while the latter should be dominated by two gluons. Figure 2 shows an example of the decay into a pair of open-bottom mesons. Because the gluons are at the scale of $m_b$, one expects the first type of decays to dominate over the second. As it is not an easy task to calculate partial decay widths into given exclusive decay modes, in the following we provide a rough estimate of the inclusive decay width of the $X_{bb{\bar{b}}{\bar{b}}}$ ground-state based on the first decay mode.

Fig. 2

Quark level description of hadronic decays $X_{bb\bar{b}\bar{b}} \rightarrow M_1 \bar{M}_2$, where $M_1$ and $\bar{M}_2$ are spin-parity and phase-space allowed bottom and anti-bottom meson, respectively

The inclusive width of the $X_{bb\bar{b}\bar{b}}$ into final states with a pair of b and ${\bar{b}}$ quarks can be described as a two-step process triggered by a transition operator $\mathcal T$ as

$$\begin{aligned} \langle h_1 h_2\ldots | \mathcal T| X_{bb\bar{b}\bar{b}}\rangle= & {} \langle h_1 h_2... | \mathcal T_2| b_1\bar{b}_4 g\rangle \nonumber \\&\cdot \langle b_1\bar{b}_4 g | \mathcal T_1| b_1 b_2 \bar{b}_3\bar{b}_4 \rangle , \end{aligned}$$

(25)

where $h_1$ and $h_2$ indicate possible bottom hadrons allowed by the spin-parity quantum numbers and the available phase space. Here $\mathcal T_1$ is operator for the coupling of a heavy quark–antiquark pair to a gluon, given by $\sqrt{4\pi \alpha _s}~\bar{Q} \frac{1}{2} \lambda _a \gamma ^{\mu } Q \epsilon ^{a}_{\mu }$, and $\mathcal T_2$ is responsible for the transition from $b{\bar{b}} g$ to the final hadronic states. We need to sum up all the possible final states generated at the second vertex of Fig. 2, which includes not only two-body but also many-body final states. As a result, only the second factor ($\mathcal T_1$) in the above equation matters.

The $\bar{Q}Q$ annihilation at short distances requires a direct dependence on the zero-point wave function of the color-octet $\bar{Q} Q$ inside the four-body bound state, $R_{Q\bar{Q}_{(8)}}(0)$. Hence,

$$\begin{aligned} \Gamma (X_{bb\bar{b}\bar{b}}\rightarrow h_1h_2\ldots ) \propto \alpha _s(m_b)~|R_{b\bar{b}_{(8)}}(0)|^2 . \end{aligned}$$

(26)

It is well-known that the $\eta _b$ decay width is saturated by two-gluon exchange, and the $\eta _b$ inclusive decay width is $\Gamma (\eta _{b} \rightarrow \text{ hadrons }) \propto \alpha _{s}^2(m_b)~ |R_{b\bar{b}_{(1)}}(0)|^2$ [93,94,95]. The wave function at origin of a color-octet $b\bar{b}_{(8)}$ pair might be larger than that of the asymptotic color-singlet $b\bar{b}_{(1)}$, namely a bottomonium [96]. However, at the present stage there is no need for a precise calculation of the width. For an order-of-magnitude estimate, one may simply assume $|R_{b\bar{b}_{(8)}}(0)|^2 \sim |R_{b\bar{b}_{(1)}}(0)|^2$. Therefore, we can estimate the inclusive width of the $X_{bb\bar{b}\bar{b}}$ decays into hadrons containing b and $\bar{b}$ as

$$\begin{aligned} \Gamma (X_{bb\bar{b}\bar{b}}\rightarrow h_1h_2\ldots ) \simeq \frac{1}{\alpha _s(m_b)} \Gamma (\eta _{b} \rightarrow \text{ hadrons }) .\end{aligned}$$

(27)

The $\eta _\mathrm{b}$ dominantly decays into hadrons, hence, $\Gamma (\eta _{b} \rightarrow \text{ hadrons })\approx \Gamma (\eta _{b})=10^{+5}_{-4}$ MeV [21]. Taking $\alpha _s(m_b)=0.22$ [21], and neglecting all other possible decay modes which should be subdominant, we get

$$\begin{aligned} \Gamma (X_{bb\bar{b}\bar{b}}) =\mathcal {O}(50~\text {MeV}) . \end{aligned}$$

(28)

The previous width (of the order of a few tens of MeV) is large enough to make the resonance observable. Our estimate of Eq. (28) is of the same order of magnitude as an earlier prediction for similar systems [73], while it is much larger than the estimate of Ref. [47], 1.2 MeV. Similarly, we expect the width of the fully-charm tetraquark, if below the $\eta _c\eta _c$ threshold, to be larger,

$$\begin{aligned} \Gamma (X_{cc{\bar{c}}{\bar{c}}}) \simeq \frac{\Gamma (\eta _c)}{\alpha _s(m_c)} = \mathcal {O}(100~\text {MeV}) . \end{aligned}$$

(29)

The fully-bottom tetraquark states could be searched in the final states including a pair of bottom hadrons, such as $B{\bar{B}}$, $\Lambda _b\bar{\Lambda }_b$, $\Xi _b\bar{\Xi }_b$, $\Sigma _b\bar{\Sigma }_b$ and $\Omega _b\bar{\Omega }_b$. They can also decay into a fully leptonic final state via an intermediate $\Upsilon (1S)X$ state as

$$\begin{aligned} X_{bb\bar{b}\bar{b}} \rightarrow \Upsilon (1S)X \rightarrow l^+l^- l^+l^-, \end{aligned}$$

(30)

where l can be $\tau$, $\mu$ or e, and X could be the off-shell lowest vector bottomonium, $X\equiv \Upsilon (1S)^*$. This decay involves the annihilation of two $b\bar{b}$ pairs into virtual photons, so the branching fraction is expected to be small, $\mathcal O (10^{-4}\sim 10^{-8})$, as estimated in [47].⁸ Despite of this, the multi-lepton final states are expected to provide a clean signal with a low background. The ideal place to look for the decays of Eq. (30) is the Large Hadron Collider experiments, where the Higgs boson cross section was measured by reconstructing a four-lepton final state [97]. Because of this, a scan at relatively lower energies, of the order of $2M_{\eta _{b}(1S)}$, should be almost straightforward at LHC.

6 Summary

We calculated the $b b {\bar{b}} {\bar{b}}$ ground-state energy in terms of two different approximations for the tetraquark wave function. They were used to simplify the solution of the four-body problem.

In the first case, we provided an evaluation of the $b b {\bar{b}} \bar{b}$ ground-state energy in an NREFT at the LO, where the potential is an OGE-induced color Coulomb potential. A nice feature of our approach is that the color wave function is completely given by $| \bar{\mathbf{3 }}_{12}{} \mathbf 3 _{34}; \mathbf 1 _{1234} \rangle$ at the LO, and its mixing with $| \mathbf 6 _{12}\bar{\mathbf{6 }}_{34}; \mathbf 1 _{1234} \rangle$ only occurs at higher orders. The solution of the four-body problem was simplified by making use of the symmetries introduced by Hylleraas and Ore in their study of polyelectrons, namely the bound states of two electrons and positrons. In our specific case, one of the above mentioned symmetries could be expressed as $\psi _{\text {spatial}}(bb)=\psi _{\text {spatial}}({\bar{b}} \bar{b})$, where $\psi _{\text {spatial}}(bb)$ and $\psi _{\text {spatial}}({\bar{b}} {\bar{b}})$ are the spatial wave functions of the bb and ${\bar{b}} {\bar{b}}$ systems, respectively. Thanks to this, the four-body problem was simplified by reducing the number of integration variables. In the second case, we calculated the $b b {\bar{b}} {\bar{b}}$ ground-state energy in a relativized diquark model. This model is characterized by OGE plus a confining potential. In the diquark model, the effective degree of freedom of the diquark, describing two strongly correlated quarks with no internal spatial excitations, is introduced. Tetraquark mesons are then obtained as two-body diquark–antidiquark bound states. Our results in both approaches – NREFT at LO ($18.72\pm 0.02$ GeV) and relativized diquark model (18.75 GeV) – only differ by a few tens of MeV, and suggest the existence of a $b b {\bar{b}} {\bar{b}}$ bound-state below the $\eta _b\eta _b$ threshold.

We also derived a set of approximate inequalities for the energies of the fully-heavy tetraquarks in terms of those of various heavy quarkonia. Instead of giving the values of the ground-state energies of the states of interest, the inequalities provide upper bounds on them. As expected, our LO NREFT and relativized diquark model results on the $X_{bb\bar{b}\bar{b}}$ ground-state mass satisfy the corresponding inequality.

Finally, we discussed the possible decay modes of the lowest fully-heavy tetraquarks and estimated the decay width of the ground state $bb{\bar{b}}{\bar{b}}$ to be of $\mathcal {O}(50~\text {MeV})$. We hope our results might provide useful references in the search for fully-heavy tetraquarks in ongoing LHC experiments. In particular, we suggest searching for the lowest $X_{bb\bar{b}\bar{b}}$ in the relevant center-of-mass energy region around 18.7 GeV in the final states of four leptons or a pair of bottom hadrons such as $B\bar{B}$, $\Lambda _b\bar{\Lambda }_b$, $\Xi _b\bar{\Xi }_b$, $\Sigma _b\bar{\Sigma }_b$ and $\Omega _b\bar{\Omega }_b$,