Anisotropic power-law inflation of the five dimensional scalar–vector and scalar-Kalb–Ramond model

Abstract

We will study the cosmological implications of the five dimensional scalar–vector and scalar-Kalb–Ramond model. In particular, a new set of Bianchi type I power-law analytic solution will be obtained for this model. The cosmic no-hair conjecture can be shown to break down in the presence of the scalar–vector and scalar-Kalb–Ramond couplings. The effect of the Kalb–Ramond field in the presence of the power-law solution will be shown explicitly. We will also show that the presence of a phantom field does, however, destabilize the corresponding Bianchi type I power-law inflationary solutions.

1 Introduction

An inflationary universe was proposed in 1981 by Guth as a resolution to some important cosmological puzzles such as the monopole, horizon, and flatness problems  [1,2,3]. The cosmic inflation has then become one of leading paradigms in modern cosmology. The theoretical predictions are highly consistent with the results obtained from the cosmic microwave background radiation (CMB) detectors including the observations from the Wilkinson Microwave Anisotropy Probe (WMAP) [4, 5] and Planck [6, 7]. The standard inflationary model is based on an assumption that the spacetime of the early universe can be described by the homogeneous and isotropic Friedmann–Lemaitre–Robertson–Walker (FLRW) metric [8]. Anomalies of the CMB such as the hemispherical asymmetry and the cold spot are, however, detected by WMAP and then Planck [4,5,6,7,8]. Hence we should consider the anisotropic Bianchi type space as an alternative resolution. Bianchi type spaces are classified as the nine types [9, 10]. Note also that some predictions of anisotropic inflationary model(s) for the CMB have been worked out in some earlier papers in Refs. [11, 12].

It is interesting to find out the evolution of late-time universe if the metric of the early universe is one of the Bianchi type spaces. Indeed, the well-known cosmic no-hair conjecture, proposed by Hawking and his colleagues [13, 14], states that the late-time universe has to be isotropic regardless of initial states of the early universe. A partial proof to this conjecture was carried out by Wald [15] for the evolution of the Bianchi spacetimes. There have also been many attempts to prove/disprove this conjecture in various cosmological theories/models [16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66].

There is an interesting counter-example to the conjecture with a stable and attractor anisotropic solution. The model is a supergravity motivated model proposed by Kanno, Soda, and Watanabe (KSW) [43, 44]. The KSW model has an interesting scalar–vector coupling term for the scalar and electromagnetic fields $f^2(\phi )F_{\mu \nu }F^{\mu \nu }$. The scalar–vector coupling term has been shown to be a source of stable anisotropy. Consequently, many cosmological aspects of this model have been investigated extensively [67,68,69,70,71,72,73,74,75,76]. Along this line of research, the validity of the cosmic no-hair conjecture has been investigated systematically in some non-canonical extensions of the KSW model with the canonical scalar field model is replaced by non-canonical models. For example, the Dirac–Born–Infeld (DBI), supersymmetry Dirac–Born–Infeld (SDBI), and covariant Galileon theories [49,50,51] have been proposed as alternative models. As a result, the cosmic no-hair conjecture has also been shown to be violated for these non-canonical extensions of the KSW model.

On the other hands, we have also shown that the no-hair conjecture remains valid with the inclusion of the phantom field with negative kinetic term [47, 48]. The phantom field is also known to be a resolution to the dark energy problem [77, 78]. As a result, the inclusion of the phantom field turns the corresponding anisotropic power-law solutions unstable. It is also true when the KSW model is extended to inflationary non-canonical models  [49,50,51] as the cosmic no-hair conjecture predicts.

Note that all investigations related to the KSW model focused mainly on the effect on the four dimensional (4D) spacetimes [43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76]. It is natural to ask if the cosmic no-hair conjecture holds in higher dimensional extensional KSW model. In this paper, therefore, we will consider the five dimensional Kalb–Ramond (KR) theory [79,80,81,82]. It is known that an effective action with a scalar-Kalb–Ramond interaction is equivalent to an effective action with a scalar–vector interaction in five dimensional (5D) spacetime [83,84,85,86]. Therefore the 5D KR model is a 5D extension of the KSW model. Note also that the KR theory has been studied extensively [83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100]. For example, its black hole solutions can be found in Refs. [83,84,85,86,87,88,89,90,91]. The related FLRW cosmological solutions can be seen in Refs. [92,93,94,95].

It is known that an effective action with a Kalb–Ramond interaction is equivalent to an effective action with a vector interaction in five dimensional (5D) spacetime [83,84,85,86]. Duality holds also between the scalar-KR coupling and the scalar–vector coupling. Although the duality has been known for a long time, the interchange of the kinetic term and spatial term due to the duality transformation has been, however, a trouble in the interpretation of the effective dual Lagrangian. In particular, duality transformation maps time-derivative kinetic terms to spatial-derivative terms. The effective kinetic terms also change sign derived from the dual transformation. To be more specific, the dual transformation will map the $\dot{B}_{ij}$ term to $\partial _k A_l$ resulting from the interchange of kinetic energy and spatial variation terms. The overlooked minus sign hence leads to quite a different result.

For heuristic reasons, we have made it clear, in the Appendix, that the Routh method can secure the negative sign in the effective dual Lagrangian due to the dual mapping. As the resulting dual Lagrangian indicates, there is quite a difference between the KR term and the effective dual Lagrangian. In particular, the dual $U_1$ vector field of the Kalb–Ramond field and EM field are different physical fields. Following Ref. [83], it is hence interesting to find out the precise effect of the KR 2-form in 5D space motivated by string theory. For simplicity, we will also focus on the lowest order terms with KR interaction.

In addition, the power-law solutions of the model with scalar–vector coupling provide a strong counterexample to the cosmic no-hair conjecture. One of the purpose of this paper is to show that the scalar-KR coupling also presents an counterexample to the cosmic no-hair conjecture in the presence of the scalar-vector coupling. The model with scalar–vector and scalar-KR couplings will be referred to as the SVKR model in this paper.

The theory turns out to be a higher dimensional extension of the KSW model. Note also that the Kalb–Ramond theory has been studied extensively. For example, its black hole solutions can be found in Refs. [83,84,85,86,87,88,89,90,91], while its FLRW cosmological solutions are obtained in Refs. [88, 89, 92,93,94,95].

In addition, the four and higher dimensional Bianchi type I solutions of the KR theory have also been found in Refs. [94,95,96,97]. More interestingly, the cosmological birefringence and large-scale magnetic fields effects have been discussed in the context of a CPT-even dimension-six Chern–Simons-like coupled with Kalb–Ramond and scalar fields [98, 99]. The KR field has also been used to reexamine the hierarchy problem in a Randall–Sundrum scenario [100]. All these papers indicate that the KR theory is an interesting theory with rich implications. Hence, examining the validity of the cosmic no-hair conjecture in the context of the five dimensional KR theory may provide useful information for the cosmological evolution.

This paper will be organized as follows: (i) A brief review and the motivation of this paper have been written in Sect. 1. (ii) The five dimensional SVKR model will be introduced in Sect. 2. (iii) A set of anisotropic power-law solutions of the SVKR model will be shown in Sect. 3. (iv) The stability and attractor features of this set of new solutions will be investigated in Sect. 4. (v) In Sect. 5, the effect of the phantom field to the stability of anisotropic power-law solution of quintom-vector-Kalb–Ramond (QKR) model will be discussed. (vi) Finally, concluding remarks will be given in Sect. 6.

2 The five dimensional scalar–vector-Kalb–Ramond theory

A 5D SVKR model with a scalar–vector and a scalar-Kalb–Ramond coupling term will be presented in this section. We will focus on the effect of the SVKR model in a 5D anisotropic metric space. A set of power-law ansatz will also be introduced here. Consequently, a set of algebraic equations will be derived representing the power-law nature of the field equations.

The bulk part of a low-energy string effective action describing a 3-brane embedded in a 5D bulk comes with a 2-form scalar-Kalb–Ramond coupling of the form $-h^2\left( \phi \right) H_{abc} H^{abc}$. Here $\phi$ is the scalar (dilaton) field, $H_{abc}\equiv \partial _{[a} B_{bc]}$ is the Kalb–Ramond field strength  [79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100], and $h(\phi )$ is a function of the scalar field $\phi$. Motivated by the string effective action, we will focus on the effect of the 5D scalar–vector-Kalb–Ramond model given by

$$\begin{aligned} S_\mathrm{bulk}= & {} \int {d^5 } x\sqrt{ g} \left[ -\frac{{R}}{2} - \frac{1}{2}\partial _a \phi \partial ^a \phi -V\left( \phi \right) \right. \nonumber \\&\left. -f^2(\phi )\mathcal{F}_{ab}\mathcal{F}^{ab} -\frac{1}{12}h^2\left( \phi \right) H_{abc}H^{abc} \right] , \end{aligned}$$

(2.1)

with $\mathcal{F}_{ab}=(\partial _a \mathcal{A}_b-\partial _b\mathcal{A}_a)/2$ the field strength of the 5D vector field $\mathcal{A}_a$. As a result, the following field equations can be derived from the action (2.1) [83]:

$$\begin{aligned}&D_c [{ f^2 \mathcal{F}^{ca} }]=0, \end{aligned}$$

(2.2)

$$\begin{aligned}&D_c [{ h^2 H^{cab} }]=0, \end{aligned}$$

(2.3)

$$\begin{aligned}&D^2 \phi -\partial _\phi V-2f\partial _\phi f \mathcal{F}_{ab}\mathcal{F}^{ab} \nonumber \\&\quad -\frac{1}{6}h\partial _\phi h H_{abc}H^{abc} =0, \end{aligned}$$

(2.4)

$$\begin{aligned}&\left( {R_{ab}-\frac{1}{2}g_{ab}R}\right) =-\partial _a \phi \partial _b \phi \nonumber \\&\quad +\frac{1}{2}g_{ab}\left[ {\partial _c \phi \partial ^c \phi +2V+ 2f^2 \mathcal{F}_{cd}\mathcal{F}^{cd} + \frac{1}{6}h^2 H_{cde}H^{cde}}\right] \nonumber \\&\quad -4 f^{2} \mathcal{F}_{ac}\mathcal{F}_{b}{}^{c} -\frac{1}{2}h^2 H_{acd}H_{b}{}^{cd} . \end{aligned}$$

(2.5)

Note that the 5D Kalb–Ramond field strength is related to the dual gauge field by the dual transformation

$$\begin{aligned} H^{cab}=\epsilon ^{cabde}\partial _d A_e h^{-2}\left( \phi \right) . \end{aligned}$$

(2.6)

Hence the 5D KR field should be equivalent to the 5D gauge field following the dual transformation. There is, however, a minus sign derived from the cyclic field nature of the dual transform. A resolution to this problem can be done by performing a Routh transformation [90,91,92, 98, 99, 101]. A heuristic derivation is shown in the “Appendix A” with the introduction of the Routh transformation. As a result, the action (2.1) is effectively equivalent to the following action with two scalar–vector couplings

$$\begin{aligned} S_\mathrm{eff}= & {} \int {d^5 } x\sqrt{ g} \biggl [ -\frac{{R}}{2} - \frac{1}{2}\partial _a \phi \partial ^a \phi -V\left( \phi \right) \nonumber \\&-f^2(\phi )\mathcal{F}_{ab}\mathcal{F}^{ab} - h^{-2}\left( \phi \right) F_{ab}F^{ab} \biggr ]. \end{aligned}$$

(2.7)

Here $F_{ab}=(\partial _a A_b -\partial _b A_a)/2$ is the field strength of the vector field $A_a$. Note also the minor difference, the 1/2 factor, in the definition of the gauge field strength. Therefore, we will be working on the following field equations:

$$\begin{aligned}&D_c [{ f^2 \mathcal{F}^{ca} }]=0, \end{aligned}$$

(2.8)

$$\begin{aligned}&D_b [{ h^{-2} F^{ab} }]=0, \end{aligned}$$

(2.9)

$$\begin{aligned}&D^2\phi -\partial _\phi V - 2 f\partial _\phi f \mathcal{F}_{ab}\mathcal{F}^{ab}\nonumber \\&\quad +2 h^{-3}\partial _\phi h F_{ab}F^{ab}=0, \end{aligned}$$

(2.10)

$$\begin{aligned}&\left( {R_{ab}-\frac{1}{2}g_{ab}R}\right) =-\partial _a \phi \partial _b \phi +g_{ab}\left[ \frac{1}{2} \partial _c \phi \partial ^c \phi +V\right. \nonumber \\&\quad \left. +f^{2} \mathcal{F}_{cd} \mathcal{F}^{cd}+ h^{-2} F_{cd}F^{cd}\right] \nonumber \\&\quad -4 f^{2} \mathcal{F}_{ac}\mathcal{F}_{b}{}^{c}-4 h^{-2} F_{ac}F_{b}{}^{c}. \end{aligned}$$

(2.11)

In addition, we will work on the 5D Kaluza–Klein like anisotropic metric $g_{ab}$ with a 4D Bianchi type I (BI) metric embedded as follows

$$\begin{aligned} ds^2= & {} -dt^2 + \exp \left[ {2\alpha (t)-4\sigma (t)}\right] dx_1^2+\exp \left[ 2\alpha (t)\right. \nonumber \\&\left. +2\sigma (t)\right] ( {dx_2^2+dx_3^2} ) + \exp [{2\gamma (t)}]dx_4^2, \end{aligned}$$

(2.12)

with $\gamma (t)$ an additional scale factor associated with the fifth dimension $x_4$. Note that the 5D metric is also a direct extension of a 5D anisotropic spacetime  [35, 38, 102, 103].

In addition, we will set the vector field $A_{a}$ as $A_a=\left( {0, A_{1}(t), 0,0,0}\right)$ as a compatible solution to the BI metric space. Note that the choice of non-vanishing component $A_1$ can be adjusted by a coordinate rotation to any preferred direction. We can also set the non-vanishing vector component as $A_2$ or $A_3$. A different choice will also affect the compatible form of the BI metric (2.12). Indeed, BI metric starts with $g_{22} \ne g_{33}$ for the choice of metric (2.12). Due to the fact that $A_2=A_3=0$, we can absorb the difference between $g_{22}$ and $g_{33}$ by a general coordinate transformation such that $g'_{33}=(\partial x_3 / \partial x'_3)^2 g_{33}=g_{22}$. As a result, $A_2=A_3=0$ will remain valid when the coordinate transformation is performed. This is the reason that we can choose the vector field $A_1 \ne 0$ compatible with the metric (2.12). Indeed, by solving the field equations with a more general BI metric will also end up with the same set of solutions with $g_{22} = g_{33}$.

In addition, the scalar field $\phi$ will also be assumed to be a homogeneous field with $\phi =\phi (t)$. Note that $\sigma$ stands for a deviation from the isotropy of spacetime characterized by $\alpha$. It means that $\sigma$ should be much smaller $\alpha$ in order to be consistent with the observations of WMAP and Planck. As a result, the corresponding solution to Eq. (2.9) is given by

$$\begin{aligned} \dot{A}_1 \left( t \right) = h^{2}\left( \phi \right) \exp [{-\alpha -4\sigma -\gamma }]p_A, \end{aligned}$$

(2.13)

with $p_A$ a constant of integration  [43, 44, 47,48,49,50,51]. Similarly, we will have

$$\begin{aligned} \dot{\mathcal{A}}_1 \left( t \right) = f^{-2}\left( \phi \right) \exp [{-\alpha -4\sigma -\gamma }]p_\mathcal{A}, \end{aligned}$$

(2.14)

for the $U_1$ gauge field. Therefore, Eq. (2.10) reduces to

$$\begin{aligned} \ddot{\phi }= & {} -\left( {3\dot{\alpha } + \dot{\gamma }}\right) \dot{\phi } -\partial _\phi V + (f^{-3} \partial _\phi f p_\mathcal{A}^2- h \partial _\phi h p_A^2~ )\nonumber \\&\quad \times \exp [{-4\alpha -4\sigma -2\gamma }]. \end{aligned}$$

(2.15)

The Einstein equation (2.11) can be split into four component equations:

$$\begin{aligned} \dot{\alpha }^2= & {} \dot{\sigma }^2 - \dot{\alpha } \dot{\gamma } +\frac{1}{3}\biggl [\frac{\dot{\phi }^2}{2}+V + \frac{1}{2}({f^{-2}}p_\mathcal{A}^2\nonumber \\&+ {h^2} p_A^2 )\exp \left[ {-4\alpha -4\sigma -2\gamma }\right] \biggr ], \end{aligned}$$

(2.16)

$$\begin{aligned} \ddot{\alpha }= & {} -2\dot{\alpha }^2-\dot{\sigma }^2+\frac{1}{3}\biggl [-\frac{\dot{\phi }^2}{2}+V\nonumber \\&- \frac{1}{2}({f^{-2}}p_\mathcal{A}^2 + {h^2}p_A^2 )\exp [{-4\alpha -4\sigma -2\gamma }] \biggr ], \end{aligned}$$

(2.17)

$$\begin{aligned} \ddot{\sigma }= & {} -3\dot{\alpha } \dot{\sigma } - \dot{\sigma } \dot{\gamma } +\frac{1}{3} ({f^{-2}}p_\mathcal{A}^2\nonumber \\&+ {h^2}p_A^2 )\exp [{-4\alpha -4\sigma -2\gamma }], \end{aligned}$$

(2.18)

$$\begin{aligned} \ddot{\alpha }+\frac{\ddot{\gamma }}{2}= & {} -3\dot{\alpha }^2-\frac{5}{2}\dot{\alpha } \dot{\gamma }-\frac{\dot{\gamma }^2}{2} + V\nonumber \\&+ \frac{1}{6}({f^{-2}}p_\mathcal{A}^2 + {h^2}p_A^2 )\exp [{-4\alpha -4\sigma -2\gamma }]. \end{aligned}$$

(2.19)

Note also that this set of four equations is related to the Bianchi identity. The only non-redundant equation is the Friedmann equation (2.16).

In addition, if $h=0$ and $\gamma$ is set to be a constant, i.e., $\dot{\gamma }=\ddot{\gamma }=0$, these equations will reduce to

$$\begin{aligned} \dot{\alpha }^2= & {} \dot{\sigma }^2 +\frac{\dot{\phi }^2}{6}+\frac{V}{3} + \frac{f^{-2}}{6}\exp \left[ {-4\alpha -4\sigma }\right] \hat{p}_\mathcal{A}^2 , \end{aligned}$$

(2.20)

$$\begin{aligned} \ddot{\alpha }= & {} -3\dot{\alpha }^2+V + \frac{f^{-2}}{6}\exp \left[ {-4\alpha -4\sigma }\right] \hat{p}_\mathcal{A}^2 , \end{aligned}$$

(2.21)

$$\begin{aligned} \ddot{\sigma }= & {} -3\dot{\alpha } \dot{\sigma } + \frac{f^{-2}}{3}\exp \left[ {-4\alpha -4\sigma }\right] \hat{p}_\mathcal{A}^2, \end{aligned}$$

(2.22)

with $\hat{p}_\mathcal{A}^2 \equiv \exp \left[ {-2\gamma }\right] p_\mathcal{A}^2$. It is straightforward to see that these reduced equations are similar to that obtained in the 4D KSW model  [43,44,45,46,47,48,49,50,51].

3 Anisotropic power-law solutions

A new set of power-law solutions will be obtained for the SVKR model with a set of exponential potentials in this section. Important properties of this set of solutions will also be discussed here. Note that we will focus on the model with an exponential potential and gauge kinetic functions of the form [43,44,45,46,47,48,49,50,51]:

$$\begin{aligned} V\left( \phi \right)= & {} V_0 \exp \left[ {\lambda \phi }\right] , \end{aligned}$$

(3.1)

$$\begin{aligned} f\left( \phi \right)= & {} f_0 \exp \left[ {-\rho _\mathcal{A}\phi }\right] , \end{aligned}$$

(3.2)

$$\begin{aligned} h\left( \phi \right)= & {} h_0 \exp \left[ {-\rho _A \phi }\right] . \end{aligned}$$

(3.3)

Following Refs.  [43, 44], we will try to find a new set of power-law solutions of the following forms  [43,44,45,46,47,48,49,50,51]:

$$\begin{aligned} \alpha = \zeta \log t; ~\sigma = \eta \log t;~ \gamma = \chi \log t; ~\phi = \xi \log t+\phi _0. \end{aligned}$$

(3.4)

Here $V_0$, $f_0$, $h_0$, $\phi _0$, $\lambda$, $\rho _\mathcal{A}$, and $\rho _A$ are positive constants. For convenience, we will introduce the following new variables:

$$\begin{aligned} u= & {} V_0 \exp \left[ {\lambda \phi _0}\right] , \end{aligned}$$

(3.5)

$$\begin{aligned} v_\mathcal{A}= & {} p_\mathcal{A}^2 f_0^{-2} \exp \left[ {2\rho _\mathcal{A} \phi _0}\right] , \end{aligned}$$

(3.6)

$$\begin{aligned} v_A= & {} p_A^2 h_0^2 \exp \left[ {-2\rho _A \phi _0}\right] . \end{aligned}$$

(3.7)

Note that u, $v_\mathcal{A}$, and $v_A$ must be positive. In addition, $\rho _A = -\rho _\mathcal{A}$ is required for the existence of the power-law solution. Hence we can write $\rho = \rho _A = -\rho _\mathcal{A}$ for convenience. In addition, we can define a new parameter v as

$$\begin{aligned} v = (f_0^{-2}p_\mathcal{A}^2+h_0^2p_{A}^2) \exp \left[ {-2\rho \phi _0}\right] \end{aligned}$$

(3.8)

such that the field equations (2.15), (2.16), (2.17), (2.18), and (2.19) can be brought to the following compact form:

$$\begin{aligned} -\xi + \left( {3\zeta +\chi }\right) \xi +\lambda u -\rho v= & {} 0, \end{aligned}$$

(3.9)

$$\begin{aligned} \zeta ^2-\eta ^2+\zeta \chi -\frac{\xi ^2}{6}-\frac{u}{3} -\frac{v}{6}= & {} 0, \end{aligned}$$

(3.10)

$$\begin{aligned} -\zeta +2\zeta ^2 +\eta ^2 +\frac{\xi ^2}{6}-\frac{u}{3} +\frac{v}{6}= & {} 0, \end{aligned}$$

(3.11)

$$\begin{aligned} -\eta +3\zeta \eta +\eta \chi -\frac{v}{3}= & {} 0, \end{aligned}$$

(3.12)

$$\begin{aligned} -\zeta -\frac{\chi }{2}+3\zeta ^2+\frac{5}{2}\zeta \chi +\frac{\chi ^2}{2} - u-\frac{v}{6}= & {} 0. \end{aligned}$$

(3.13)

The following constraint equations

$$\begin{aligned} \lambda \xi= & {} -2, \end{aligned}$$

(3.14)

$$\begin{aligned} 2\zeta +2\eta +\chi + \rho \xi= & {} 1 \end{aligned}$$

(3.15)

are necessary to make sure that all terms in the field equations have the same power in time. It turns out that Eqs. (3.9), (3.12), and (3.15) can be solved to give the following relations:

$$\begin{aligned} \chi= & {} -2\zeta -2\eta +2\frac{\rho }{\lambda }+1, \end{aligned}$$

(3.16)

$$\begin{aligned} u= & {} \frac{\left( {3\lambda \rho \eta +2}\right) \left( {\lambda \zeta -2\lambda \eta +2\rho }\right) }{\lambda ^3}, \end{aligned}$$

(3.17)

$$\begin{aligned} v= & {} \frac{3\eta \left( {\lambda \zeta -2\lambda \eta +2\rho }\right) }{\lambda }, \end{aligned}$$

(3.18)

with the help of Eq. (3.14). As a result, Eq. (3.13) leads to an equation:

$$\begin{aligned} \left( {\lambda \zeta -2\lambda \eta +2\rho }\right) \left[ \lambda \left( \lambda +2\rho \right) \left( 3\eta -1\right) +4\right] =0 \end{aligned}$$

(3.19)

with the help of Eqs. (3.16), (3.17) and (3.18). As a result, a trivial solution of u and v is given by one of the $\eta$-solution as

$$\begin{aligned} \eta =\eta _1=\frac{\lambda \zeta +2\rho }{2\lambda }. \end{aligned}$$

(3.20)

Indeed Eqs. (3.17) and (3.18) imply that $u=0$ and $v=0$ if $\eta =\eta _1$. In addition, Eq. (3.19) also admits a non-trivial solution of u and v led by the $\eta$ solution given by

$$\begin{aligned} \eta =\frac{1}{3}-\frac{4}{3\lambda \left( {\lambda +2\rho }\right) }. \end{aligned}$$

(3.21)

Note that this solution of $\eta$ is identical to the solution found in the 4D KSW model [43, 44]. With the non-trivial solution of $\eta$ given by Eq. (3.21), the variables, $\chi$, u, and v can be shown to be:

$$\begin{aligned} \chi= & {} -2\zeta +\frac{\lambda ^2+8\lambda \rho +12\rho ^2+8}{3\lambda \left( {\lambda +2\rho }\right) }, \end{aligned}$$

(3.22)

$$\begin{aligned} u= & {} \frac{\left( {\lambda \rho +2\rho ^2+2}\right) \left[ {3\lambda \left( {\lambda +2\rho }\right) \zeta -2\lambda ^2+2\lambda \rho +12\rho ^2+8}\right] }{3\lambda ^2\left( {\lambda +2\rho }\right) ^2}, \end{aligned}$$

(3.23)

$$\begin{aligned} v= & {} \frac{\left( {\lambda ^2+2\lambda \rho -4}\right) \left[ {3\lambda \left( {\lambda +2\rho }\right) \zeta -2\lambda ^2+2\lambda \rho +12\rho ^2+8}\right] }{3\lambda ^2\left( {\lambda +2\rho }\right) ^2}.\nonumber \\ \end{aligned}$$

(3.24)

It is clear that $\chi =0$ if $\gamma$ is set to be a constant. As a result, $\zeta$ is identical to the solution obtained in the 4D KSW model  [43, 44]:

$$\begin{aligned} \zeta =\frac{\lambda ^2+8\lambda \rho +12\rho ^2+8}{6\lambda \left( {\lambda +2\rho }\right) }. \end{aligned}$$

(3.25)

Hence the variables u and w (v in our notation here) are the same as the solutions found in  [43, 44]. With the Eqs. (3.22)–(3.24), we can simplify Eq. (3.10) as

$$\begin{aligned} \zeta ^2-M_1 \zeta - N_1 = 0, \end{aligned}$$

(3.26)

with

$$\begin{aligned} M_1= & {} \frac{\lambda ^2+12\lambda \rho +20\rho ^2+16}{6\lambda \left( {\lambda +2\rho }\right) }, \end{aligned}$$

(3.27)

$$\begin{aligned} N_1= & {} -\frac{\left( \lambda \rho +2 \rho ^2+2\right) \left( \lambda ^2+8 \lambda \rho +12 \rho ^2+8\right) }{9\lambda ^2\left( {\lambda +2\rho }\right) ^2}. \end{aligned}$$

(3.28)

On the other hand, Eq. (3.11) reduces to

$$\begin{aligned} 2\zeta ^2-M_2 \zeta - N_2 = 0, \end{aligned}$$

(3.29)

with

$$\begin{aligned} M_2= & {} \frac{5\lambda ^2+12\lambda \rho +4\rho ^2+8}{6\lambda \left( {\lambda +2\rho }\right) }, \end{aligned}$$

(3.30)

$$\begin{aligned} N_2= & {} - \frac{\left( \lambda \rho +2 \rho ^2+2\right) \left( 5 \lambda ^2+4 \lambda \rho -12 \rho ^2-8\right) }{9\lambda ^2\left( {\lambda +2\rho }\right) ^2}. \end{aligned}$$

(3.31)

As a result, both Eqs. (3.26) and (3.29) share the same non-trivial solution:

$$\begin{aligned} \zeta = \frac{2\left( {\lambda \rho +2\rho ^2+2}\right) }{3\lambda \left( {\lambda +2\rho }\right) }. \end{aligned}$$

(3.32)

Thanks to this solution, the variables $\chi$, u, and v can be shown to be

$$\begin{aligned} \chi= & {} \frac{2\rho }{3\lambda }+\frac{1}{3}, \end{aligned}$$

(3.33)

$$\begin{aligned} u= & {} \frac{2\left( {\lambda \rho +2\rho ^2+2}\right) \left( {-\lambda ^2+2\lambda \rho +8\rho ^2+6}\right) }{3\lambda ^2\left( {\lambda +2\rho }\right) ^2}, \end{aligned}$$

(3.34)

$$\begin{aligned} v= & {} \frac{2\left( {\lambda ^2+2\lambda \rho -4}\right) \left( {-\lambda ^2+2\lambda \rho +8\rho ^2+6}\right) }{3\lambda ^2\left( {\lambda +2\rho }\right) ^2}. \end{aligned}$$

(3.35)

It is easy to show that

$$\begin{aligned} \chi =\zeta +\eta . \end{aligned}$$

Hence the fifth dimension will also expand in time as expected by the power-law nature of the solution we are looking for. For the metric space we are working on, all directional scale factors tend to evolve in the same way. As a result, the expansion in 5D is also expected to slow down due to the equi-partition effect. In addition, the positivity of u implies that

$$\begin{aligned} -\lambda ^2+2\lambda \rho +8\rho ^2+6 >0. \end{aligned}$$

(3.36)

Note that v is also positive if the inequalities (3.36) and

$$\begin{aligned} \lambda ^2+2\lambda \rho >4 \end{aligned}$$

(3.37)

are both satisfied. Note that $\zeta +\eta >0$ and $\zeta -2\eta >0$ are required for expanding solutions. As a result, the first constraint $\zeta +\eta >0$ holds if $\lambda >0$ and $\rho >0$. Meanwhile, the constraint $\zeta -2\eta >0$ leads to another constraint

$$\begin{aligned} -\lambda ^2-\lambda \rho +2\rho ^2+6>0. \end{aligned}$$

(3.38)

It is also straightforward to see that the constraint (3.36) holds if the constraint (3.38) holds. If the expanding solutions represent inflationary solutions, the constraints should be changed to $\zeta +\eta \gg 1$ and $\zeta -2\eta \gg 1$ instead. As a result, the constraint $\zeta +\eta \gg 1$ implies that

$$\begin{aligned} \rho \gg \lambda \sim \mathcal{O}(1). \end{aligned}$$

(3.39)

Note that we have set the scale with the choice that $\lambda \sim \mathcal{O}(1)$. In addition, the inequalities (3.37) and (3.38) also remain valid during the inflationary phase for all $\rho \gg \lambda \sim \mathcal{O}(1)$. Note also that the average slow-roll parameter $\varepsilon$ can be shown to be [43, 44]

$$\begin{aligned} \varepsilon \equiv - \frac{{\dot{H}}}{{H^2 }} = \frac{4}{3\zeta +\chi }= \frac{12 \lambda (\lambda +2 \rho )}{(\lambda +2 \rho ) (\lambda +8 \rho )+12} . \end{aligned}$$

(3.40)

In addition, the anisotropy can be shown to be [43, 44]

$$\begin{aligned} \frac{\Sigma }{H} \equiv \frac{{\dot{\sigma } }}{{\dot{\alpha } }}=\frac{\eta }{\zeta } =\frac{\lambda ^2+2\lambda \rho -4}{2\left( {\lambda \rho +2\rho ^2+2}\right) }. \end{aligned}$$

(3.41)

Consequently, the average slow-roll parameter and the anisotropy is related by the equation

$$\begin{aligned} \frac{\Sigma }{H} = \frac{1}{3}I\varepsilon \end{aligned}$$

(3.42)

according to Eqs. (3.40) and (3.41). Here the parameter I is defined as

$$\begin{aligned} I = 3\eta +\frac{3\eta ^2}{4\zeta }. \end{aligned}$$

(3.43)

It is clear that $I \simeq 1$ during the inflationary phase with $\rho \gg \lambda \sim \mathcal{O}(1)$. Additionally, the field variables $\zeta ,~ \chi ,~ \eta ,~ u$ and v can be approximated as

$$\begin{aligned}&\zeta \simeq \chi \simeq \frac{2\rho }{3\lambda } \gg 1;~\eta \simeq \frac{1}{3};~u\simeq 6\zeta ^2>0;\nonumber \\&v\simeq 4\zeta -\frac{16}{3\lambda ^2} >0 \end{aligned}$$

(3.44)

during the inflationary phase. It is apparent that the scale factor $\zeta \simeq 2\rho /(3\lambda )$ in the 5D SVKR model is smaller than the scale factor $\zeta _\mathrm{KSW} (\simeq \rho /\lambda )$ in the 4D KSW model as expected. The anisotropic scale factor $\eta$ is, however, the same as the 4D counterpart in 4D KSW model [43, 44]. This is also within our expectation that the 5D universe is expanding more slowly than the 4D universe.

4 Stability analysis of the anisotropic inflationary solutions

The stability problem of the solutions obtained in Sect. 3 will be presented here. It will be shown that this new set of power-law solutions is indeed stable in the inflationary era. The proof will be presented with two different approaches. The first approach will be done by a straightforward perturbation to the field equations. The second proof will be presenting the attractor nature of the corresponding autonomous equations.

4.1 Power-law perturbations

The 4D Bianchi type I power law inflationary solutions of the KSW model are known to be stable and attractive [43, 44]. It is also true for the noncanonical scalar field $\phi$ models including the Dirac–Born–Infeld, supersymmetric Dirac–Born–Infeld, and covariant Galileon forms [49,50,51]. To answer the stability question for the 5D SVKR model, we will perform the power-law perturbation of fields defined as $\delta \alpha = A_\alpha t^n$, $\delta \sigma = A_\sigma t^n$, $\delta \gamma = A_\gamma t^n$, and $\delta \phi = A_\phi t^n$ [47,48,49,50,51]. As a result, perturbing the field equations (2.15), (2.17), (2.18), and (2.19) around the anisotropic solutions obtained earlier leads to a set of algebraic equations that can be written as a matrix equation:

$$\begin{aligned} \mathcal{D} \left( {\begin{array}{*{20}c} A_\alpha \\ A_\sigma \\ A_\gamma \\ A_\phi \\ \end{array} } \right) \equiv \left[ {\begin{array}{*{20}c} {A_{11} } &{} {A_{12} } &{} {A_{13} } &{} {A_{14}} \\ {A_{21} } &{} {A_{22} } &{} {A_{23} } &{} {A_{24}} \\ {A_{31} } &{} {A_{32} } &{} {A_{33} } &{} {A_{34}} \\ {A_{41} } &{} {A_{42} } &{} {A_{43} } &{} {A_{44}} \\ \end{array} } \right] \left( {\begin{array}{*{20}c} A_\alpha \\ A_\sigma \\ A_\gamma \\ A_\phi \\ \end{array} } \right) = 0, \end{aligned}$$

(4.1)

with

$$\begin{aligned} A_{11}= & {} \frac{6}{\lambda }n-4\rho v;~A_{12}=-4\rho v;~A_{13}=\frac{2}{\lambda }n-2\rho v;\nonumber \\ ~A_{14}= & {} -n^2 - \left( {3\zeta +\chi -1}\right) n - \lambda ^2 u -2\rho ^2v, \end{aligned}$$

(4.2)

$$\begin{aligned} A_{21}= & {} n^2+\left( {4\zeta -1}\right) n -\frac{2}{3}v;~A_{22}=2\eta n -\frac{2}{3}v;\nonumber \\ ~A_{23}= & {} -\frac{v}{3};~A_{24}=-\frac{2n}{3\lambda }-\frac{\lambda }{3}u-\frac{\rho }{3}v, \end{aligned}$$

(4.3)

$$\begin{aligned} A_{31}= & {} 3\eta n +\frac{4}{3}v;~A_{32}=n^2+\left( {3\zeta +\chi -1}\right) n\nonumber \\&+\frac{4}{3}v;~A_{33}=\eta n +\frac{2}{3}v;~A_{34}=\frac{2}{3}\rho v, \end{aligned}$$

(4.4)

$$\begin{aligned} A_{41}= & {} n^2+\left( {6\zeta +\frac{5}{2}\chi -1}\right) n+\frac{2}{3}v;~A_{42}=\frac{2}{3}v;~A_{43}\nonumber \\= & {} \frac{n^2}{2}+\left( {\frac{5}{2}\zeta +\chi -\frac{1}{2}}\right) n+\frac{v}{3};~A_{44}= -\lambda u +\frac{\rho }{3}v.\nonumber \\ \end{aligned}$$

(4.5)

In order to reduce the complexity of complicate calculations, we will extract the leading approximations for inflationary solutions according to:

$$\begin{aligned}&A_{14}\simeq -n^2 - \left( {3\zeta +\chi }\right) n - \lambda ^2 u -2\rho ^2v;~ A_{21}\simeq n^2\nonumber \\&\quad +4\zeta n -\frac{2}{3}v;~A_{32}\simeq n^2+\left( {3\zeta +\chi }\right) n+\frac{4}{3}v, \nonumber \\&A_{41}\simeq n^2+\left( {6\zeta +\frac{5}{2}\chi }\right) n+\frac{2}{3}v;~A_{43} \nonumber \\&\quad \simeq \frac{n^2}{2}+\left( {\frac{5}{2}\zeta +\chi }\right) n+\frac{v}{3}. \end{aligned}$$

(4.6)

Note that nontrivial solutions of Eq. (4.1) exist only when

$$\begin{aligned} \det \mathcal{D} =0. \end{aligned}$$

(4.7)

In addition, we can write the determinant equation explicitly as

$$\begin{aligned} n^2f\left( {n}\right)\equiv & {} n^2(a_8 n^6+a_7n^5+a_6n^4+a_5n^3+a_4n^2 \nonumber \\&+a_3n+a_2)=0, \end{aligned}$$

(4.8)

with

$$\begin{aligned}&a_8=\frac{1}{2}>0;~a_7\simeq \frac{19\rho }{3\lambda }>0;~ a_6 \simeq \frac{8\rho ^3}{3\lambda }>0;~a_5 \simeq \frac{80\rho ^4}{3\lambda ^2}>0, \nonumber \\&a_4 \simeq \frac{256\rho ^5}{3\lambda ^3}>0;~a_3 \simeq \frac{7168\rho ^6}{81\lambda ^4}>0;~a_2\simeq \frac{7168\rho ^6}{81\lambda ^4}>0. \end{aligned}$$

(4.9)

Here we have used the leading approximations for $\zeta$, $\eta$, $\chi$, u, and v in Eq. (3.44) in order to define the parameters $a_i$’s. Indeed, we have only kept leading terms in the definition of $a_i$’s ($i=2-8$) for simplicity. As a result, Eq. (4.8) only admits negative roots due to the fact that the coefficients $a_i$’s of f(n) are all positive definite. This implies that the 5D anisotropic power-law inflationary solution of SVKR model is indeed stable against the power-law field perturbations. It also implies that the anisotropic solution really violates the prediction of the cosmic no-hair conjecture. This result is also consistent with the results shown in the papers with noncanonical extensions of the KSW model  [49,50,51].

4.2 Attractor behavior of the solutions

In this subsection, we will show the attractor behavior of the anisotropic power-law inflationary solutions for the SVKR theory. We will introduce the dynamical variables as [43, 44, 49,50,51]

$$\begin{aligned} {X}_1= & {} \frac{\dot{\sigma }}{\dot{\alpha }};~{X}_2= \frac{\dot{\gamma }}{\dot{\alpha }};~{Y}=\frac{\dot{\phi }}{\dot{\alpha }}; ~ \nonumber \\ {Z}= & {} \frac{h_0 p_A}{ \dot{\alpha }} \exp [{-\rho }\phi -2\alpha -2\sigma -\gamma ]. \end{aligned}$$

(4.10)

As a result, a set of the autonomous equations of these dynamical variables can be defined from the field equations as

$$\begin{aligned} \frac{dX_1}{d\alpha }= & {} 2X_1 \left( X_1^2 +\frac{Y^2}{6} +\frac{Z^2}{6}-X_2-1\right) +\frac{Z^2}{3}, \end{aligned}$$

(4.11)

$$\begin{aligned} \frac{dX_2}{d\alpha }= & {} 2\left( X_2-1\right) \left( X_1^2 +\frac{Y^2}{6}+\frac{Z^2}{6}-X_2-1\right) +\frac{Z^2}{3}, \end{aligned}$$

(4.12)

$$\begin{aligned} \frac{dY}{d\alpha }= & {} \left( 2Y+3 \lambda \right) \left( X_1^2+\frac{Y^2}{6}+\frac{Z^2}{6}-X_2-1\right) +\rho Z^2, \end{aligned}$$

(4.13)

$$\begin{aligned} \frac{dZ}{d\alpha }= & {} Z\left[ 2X_1^2 +\frac{Y^2}{3}+\frac{Z^2}{3}-2X_1-2X_2-\rho Y -1\right] .\nonumber \\ \end{aligned}$$

(4.14)

Here, we have used the Hamiltonian equation (2.16),

$$\begin{aligned} \frac{V}{\dot{\alpha }^2} = - 3(X_1^2 -X_2 -1 )-\frac{Y^2}{2}-\frac{Z^2}{2}, \end{aligned}$$

(4.15)

in order to define the dynamical system. Note that the anisotropic power-law solutions of KSW model and their noncanonical extensions have been shown to be equivalent to anisotropic fixed points of the corresponding dynamical system for the models studied in Refs. [43, 44, 49,50,51]. The attractor behavior of fixed points provides a proof that the anisotropic power-law solutions are indeed stable solutions. Therefore, we need to find the anisotropic fixed point of the dynamical system for the 5D SVKR model. In fact, the fixed point is a non-trivial solution to the following set of equations, $dX_1/d\alpha =d X_2 /d\alpha =dY/d\alpha =dZ/d\alpha =0$. As a result, it is straightforward to find the relation

$$\begin{aligned} X_1 =X_2-1 \end{aligned}$$

(4.16)

from the equations $dX_1/d\alpha =0$ and $dX_2/d\alpha =0$. Note that this equation is equivalent to the result $\gamma = \zeta +\eta$ for the power-law solution.

Furthermore, a useful relation can also be obtained from the equations $dX_1/d\alpha =0$ and $dY/d\alpha =0$ as follows

$$\begin{aligned} Y=-\frac{3}{2}\left( \lambda -2\rho X_1\right) . \end{aligned}$$

(4.17)

In addition, the relation

$$\begin{aligned} Z^2 =-3X_1 \left( 2X_1 + \rho Y -1\right) \end{aligned}$$

(4.18)

follows from the equations $dX_1/d\alpha =0$ and $dZ/d\alpha =0$. $dX_1/d\alpha =0$ leads to the equation

$$\begin{aligned} X_1[2({\lambda \rho +2\rho ^2+2}) X_1 - (\lambda ^2+2\lambda \rho -4)]=0, \end{aligned}$$

(4.19)

with the help of Eqs. (4.17) and (4.18). This equation can be solved to give a non-trivial solution ($X_1 \ne 0$):

$$\begin{aligned} X_1= \frac{\lambda ^2+2\lambda \rho -4}{2\left( {\lambda \rho +2\rho ^2+2}\right) }. \end{aligned}$$

(4.20)

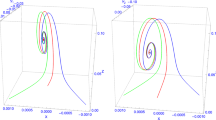
Note that similar expressions for the dynamical variables $X_2$, Y, and Z can also be derived from the Eqs. (4.16), (4.17), and (4.18). As a result, we will show that this anisotropic fixed point of 5D SVKR model is indeed an attractor solution to the dynamical system with the help of numerical plots (Fig. 1).

Fig. 1

Trajectories in the phase space of $X_1$, Y, and Z (left figure) and $X_2$, Y, and Z (right figure) with different initial conditions all converge to the anisotropic fixed point. The field parameters have been chosen as $\lambda =0.1$ and $\rho =50$. In addition, the initial conditions $(X_1(t=0),~X_2(t=0),~Y(t=0),~Z(t=0))$ are set as $(0.1,~0.2,~ -0.05,~ 0.02)$ for the thin solid red curve, (0.1,  0.25,  0.1,  0.025) for the thick solid green curve, and $(0.15,~0.2,~-0.1,~0.01$) for the blue dotted curve, respectively

5 Scalar–vector-Kalb–Ramond model with a phantom field

A phantom field will be introduced to the SVKR model in this section. Since the effect of the KR field acts similarly to the vector field in the presence of the power-law solution, we will ignore the scalar–vector coupling for convenience. The effect can be restored simply by setting $v = (f_0^{-2}p_\mathcal{A}^2+h_0^2p_{A}^2) \exp [{-2\rho \phi _0}]$. For completeness, we will briefly go through the details by showing explicitly that a set of power-law solutions does exist in the presence of the phantom field without bring too much complication. As a result, we will show that the presence of the phantom field does destabilize the corresponding power-law solutions.

5.1 The model and its anisotropic power-law solutions

A phantom (scalar) field $\psi$ with negative kinetic energy [77, 78] will be introduced to the action (2.1) of the SKR model in this section. We wish to find out if the presence of the phantom field acts in favour of the cosmic no-hair conjecture. The motivation is based on the results shown in Refs.  [47,48,49,50,51] that the phantom field does make the anisotropic power-law inflationary solution unstable. Note that the phantom field has been regarded as one of alternative solutions to the dark energy problem  [77, 78]. Note that the action of QKR model is given by

$$\begin{aligned} S_\mathrm{bulk}= & {} \int {d^5 } x\sqrt{ g} \biggl [- \frac{{R}}{2} - \frac{1}{2}\partial _a \phi \partial ^a \phi + \frac{1}{2}\partial _a \psi \partial ^a \psi -V_1\left( \phi \right) \nonumber \\&-V_2 \left( \psi \right) -\frac{1}{12}h^2\left( \phi ,\psi \right) H_{abc}H^{abc} \biggr ]. \end{aligned}$$

(5.1)

Here we used the same notations $h(\phi ) \rightarrow h(\phi ,\psi )$ and $V(\phi ) \rightarrow V_1(\phi )$ for convenience. In addition, the Planck mass $M_p$ has been set as 1 for convenience. Note also that the two-scalar-field model with both canonical (quintessence) and phantom fields has been referred to as a quintom model [77, 78]. Accordingly, the model (5.1) with two scalar fields will be referred to as the quintom-Kalb–Ramond (QKR) model.

Similar to the scalar-KR (SKR) model, the QKR action (5.1) can be shown to be equivalent with the following effective action

$$\begin{aligned} S_\mathrm{eff}= & {} \int {d^5 } x\sqrt{ g} \biggl [- \frac{{R}}{2} - \frac{1}{2}\partial _a \phi \partial ^a \phi + \frac{1}{2}\partial _a \psi \partial ^a \psi \nonumber \\&-V_1\left( \phi \right) -V_2 \left( \psi \right) -h^2\left( \phi ,\psi \right) F_{ab}F^{ab} \biggr ]. \end{aligned}$$

(5.2)

Here we have replaced the KR term according to the the dual transformation given by

$$\begin{aligned} H^{cab}=\epsilon ^{cabde}\partial _d A_e h^{-2}\left( \phi ,\psi \right) . \end{aligned}$$

(5.3)

As a result, the effective field equations can be shown to be

$$\begin{aligned}&D_b [{ h^{-2} F^{ab} }]=0, \end{aligned}$$

(5.4)

$$\begin{aligned}&D^2 \phi -\partial _\phi V_1 +2h^{-3}\partial _\phi h F_{mn}F^{mn}=0, \end{aligned}$$

(5.5)

$$\begin{aligned}&-D^2 \psi -\partial _\psi V_2 +2 h^{-3}\partial _\psi h F_{mn}F^{mn}=0, \end{aligned}$$

(5.6)

$$\begin{aligned}&\left( {R_{ab}-\frac{1}{2}g_{ab}R}\right) =-\partial _a \phi \partial _b \phi +\partial _a \psi \partial _b \psi \nonumber \\&+g_{ab}\left[ {\frac{1}{2} \partial _c \phi \partial ^c \phi -\frac{1}{2} \partial _c \psi \partial ^c \psi +V_1+V_2+ h^{-2} F_{cd}F^{cd}}\right] \nonumber \\&\quad -4 h^{-2} F_{ac}F_{b}{}^{c}. \end{aligned}$$

(5.7)

Following Sect. 2, we will study the QKR model on the metric space specified by the 5D metric (2.12). It can be shown that the solution to Eq. (5.4) is given by (2.13) with the replacement of $h(\phi ) \rightarrow h(\phi ,\psi )$. As a result, we can show that Eqs. (5.5), (5.6) and (5.7) reduce to the following set of algebraic equations:

$$\begin{aligned} \ddot{\phi }= & {} -\left( {3\dot{\alpha } + \dot{\gamma }}\right) \dot{\phi } -\partial _\phi V_1 \nonumber \\&- h \partial _\phi h \exp \left[ {-4\alpha -4\sigma -2\gamma }\right] p_A^2, \end{aligned}$$

(5.8)

$$\begin{aligned} \ddot{\psi }= & {} -\left( {3\dot{\alpha } + \dot{\gamma }}\right) \dot{\psi } +\partial _\psi V_2 \nonumber \\&+ h \partial _\psi h \exp \left[ {-4\alpha -4\sigma -2\gamma }\right] p_A^2, \end{aligned}$$

(5.9)

$$\begin{aligned} \dot{\alpha }^2= & {} \dot{\sigma }^2 - \dot{\alpha } \dot{\gamma } +\frac{1}{3}\left[ \frac{\dot{\phi }^2}{2}-\frac{\dot{\psi }^2}{2}+V_1\right. \nonumber \\&\left. +V_2 + \frac{h^2}{2}\exp \left[ {-4\alpha -4\sigma -2\gamma }\right] p_A^2 \right] , \end{aligned}$$

(5.10)

$$\begin{aligned} \ddot{\alpha }= & {} -2\dot{\alpha }^2-\dot{\sigma }^2+\frac{1}{3}\left[ -\frac{\dot{\phi }^2}{2}+\frac{\dot{\psi }^2}{2}+V_1\right. \nonumber \\&\left. +V_2 - \frac{h^2}{2}\exp \left[ {-4\alpha -4\sigma -2\gamma }\right] p_A^2 \right] , \end{aligned}$$

(5.11)

$$\begin{aligned} \ddot{\sigma }= & {} -3\dot{\alpha } \dot{\sigma } - \dot{\sigma } \dot{\gamma } + \frac{h^2}{3}\exp \left[ {-4\alpha -4\sigma -2\gamma }\right] p_A^2, \end{aligned}$$

(5.12)

$$\begin{aligned} \ddot{\alpha }+\frac{\ddot{\gamma }}{2}= & {} -3\dot{\alpha }^2-\frac{5}{2}\dot{\alpha } \dot{\gamma }-\frac{\dot{\gamma }^2}{2} + V_1 + V_2\nonumber \\&+\frac{h^2}{6}\exp \left[ {-4\alpha -4\sigma -2\gamma }\right] p_A^2. \end{aligned}$$

(5.13)

In addition, we will work on the model with exponential potentials and gauge kinetic function [47, 48], given by

$$\begin{aligned} V_1\left( \phi \right)= & {} V_{01} \exp \left[ {\lambda _1 \phi }\right] , \end{aligned}$$

(5.14)

$$\begin{aligned} V_2\left( \psi \right)= & {} V_{02} \exp \left[ {\lambda _2 \psi }\right] , \end{aligned}$$

(5.15)

$$\begin{aligned} h\left( \phi ,\psi \right)= & {} h_0 \exp \left[ {-\rho _1 \phi -\rho _2\psi }\right] , \end{aligned}$$

(5.16)

with the new variables

$$\begin{aligned} u_1= & {} V_{01} \exp \left[ {\lambda _1\phi _0}\right] , \end{aligned}$$

(5.17)

$$\begin{aligned} u_2= & {} V_{02} \exp \left[ {\lambda _2\psi _0}\right] , \end{aligned}$$

(5.18)

$$\begin{aligned} \hat{v}= & {} p_A^2 h_0^2 \exp \left[ {-2\rho _1\phi _0-2\rho _2\psi _0}\right] . \end{aligned}$$

(5.19)

We will hence try to find a compatible set of power-law solutions according to the ansatz:

$$\begin{aligned} \alpha= & {} \zeta \log t;~ \sigma = \eta \log t;~ \gamma = \chi \log t;\nonumber \\ \phi= & {} \xi _1 \log t+\phi _0; ~ \psi =\xi _2 \log t+\psi _0. \end{aligned}$$

(5.20)

As a result, we can derive the following set of algebraic equations

$$\begin{aligned} -\xi _1 + \left( {3\zeta +\chi }\right) \xi _1+\lambda _1 u_1 -\rho _1 \hat{v}= & {} 0, \end{aligned}$$

(5.21)

$$\begin{aligned} -\xi _2 + \left( {3\zeta +\chi }\right) \xi _2-\lambda _2 u_2 +\rho _2 \hat{v}= & {} 0, \end{aligned}$$

(5.22)

$$\begin{aligned} \zeta ^2-\eta ^2+\zeta \chi -\frac{\xi _1^2}{6} +\frac{\xi _2^2}{6}-\frac{u_1}{3}- \frac{u_2}{3}-\frac{\hat{v}}{6}= & {} 0, \end{aligned}$$

(5.23)

$$\begin{aligned} -\zeta + 2\zeta ^2 +\eta ^2 +\frac{\xi _1^2}{6}-\frac{\xi _2^2}{6}-\frac{u_1}{3} - \frac{u_2}{3}+\frac{\hat{v}}{6}= & {} 0, \end{aligned}$$

(5.24)

$$\begin{aligned} -\eta + 3\zeta \eta +\eta \chi -\frac{\hat{v}}{3}= & {} 0, \end{aligned}$$

(5.25)

$$\begin{aligned} -\zeta -\frac{\chi }{2}+3\zeta ^2+\frac{5}{2}\zeta \chi +\frac{\chi ^2}{2} - u_1 - u_2-\frac{\hat{v}}{6}= & {} 0, \end{aligned}$$

(5.26)

along with the constraint equations:

$$\begin{aligned} \lambda _1 \xi _1 =\lambda _2\xi _2= & {} -2, \end{aligned}$$

(5.27)

$$\begin{aligned} 2\zeta +2\eta +\chi + \rho _1\xi _1+\rho _2\xi _2= & {} 1 \end{aligned}$$

(5.28)

from the field equations (5.8), (5.9), (5.10), (5.11), (5.12), and (5.13), respectively. In addition, we can obtain the following solutions and constraints

$$\begin{aligned} \chi= & {} -2\zeta -2\eta +2\left( {\frac{\rho _1}{\lambda _1}+\frac{\rho _2}{\lambda _2}}\right) +1, \end{aligned}$$

(5.29)

$$\begin{aligned} u_1= & {} \frac{3\lambda _1\rho _1\eta +2}{\lambda _1^2}\left[ {\zeta -2\eta +2\left( {\frac{\rho _1}{\lambda _1}+\frac{\rho _2}{\lambda _2}}\right) }\right] , \end{aligned}$$

(5.30)

$$\begin{aligned} u_2= & {} \frac{3\lambda _2\rho _2\eta -2}{\lambda _2^2}\left[ {\zeta -2\eta +2\left( {\frac{\rho _1}{\lambda _1}+\frac{\rho _2}{\lambda _2}}\right) }\right] , \end{aligned}$$

(5.31)

$$\begin{aligned} \hat{v}= & {} 3\eta \left[ {\zeta -2\eta +2\left( {\frac{\rho _1}{\lambda _1}+\frac{\rho _2}{\lambda _2}}\right) }\right] , \end{aligned}$$

(5.32)

from Eqs. (5.21), (5.22), (5.25), and (5.28) with the help of Eq. (5.27). With these results, Eq. (5.26) leads to the following equation for $\eta$:

$$\begin{aligned}&\left[ {\zeta -2\eta +2\left( {\frac{\rho _1}{\lambda _1}+\frac{\rho _2}{\lambda _2}}\right) }\right] \nonumber \\&\quad \left[ 3 \Pi \eta - (\Pi +4\lambda _1^2 -4\lambda _2^2) \right] =0, \end{aligned}$$

(5.33)

with

$$\begin{aligned} \Pi \equiv \lambda _1 \lambda _2 \left( \lambda _1 \lambda _2 +2\lambda _1 \rho _2 +2\lambda _2\rho _1\right) . \end{aligned}$$

(5.34)

It is clear that Eq. (5.33) leads to the non-trivial solution:

$$\begin{aligned} \eta = \frac{1}{3}+\frac{4\left( {\lambda _1^2-\lambda _2^2}\right) }{3\Pi }, \end{aligned}$$

(5.35)

with the assumption that $u_1>0$, $u_2>0$, and $\hat{v}>0$. Note that this $\eta$ solution is identical to the $\eta$ solution for the 4D two-scalar-field KSW model [47, 48].

As a result, Eq. (5.23) becomes

$$\begin{aligned} \zeta ^2 - \bar{M}_1 \zeta -\bar{N}_1 =0, \end{aligned}$$

(5.36)

with

$$\begin{aligned} \bar{M}_1= & {} \frac{4 \left( \lambda _1 \rho _2 +\lambda _2 \rho _1\right) \left[ 3\lambda _1 \lambda _2 +5\left( \lambda _1 \rho _2 +\lambda _2 \rho _1\right) \right] +\lambda _1^2\lambda _2^2 -16\lambda _1^2 +16\lambda _2^2}{6\Pi }, \end{aligned}$$

(5.37)

$$\begin{aligned} \bar{N}_1= & {} -\frac{\left[ \left( \lambda _1 \rho _2 +\lambda _2\rho _1\right) \left( \lambda _1 \lambda _2 +2\lambda _1 \rho _2 +2\lambda _2\rho _1\right) -2\lambda _1^2 +2\lambda _2^2\right] }{9\Pi ^2} \nonumber \\&\times [4\left( \lambda _1 \rho _2 +\lambda _2\rho _1\right) \left( 2\lambda _1 \lambda _2 +3\lambda _1 \rho _2 +3\lambda _2\rho _1\right) +\lambda _1^2\lambda _2^2-8\lambda _1^2 +8\lambda _2^2].\nonumber \\ \end{aligned}$$

(5.38)

On the other hand, Eq. (5.24) reduces to

$$\begin{aligned} 2\zeta ^2 - \bar{M}_2 \zeta -\bar{N}_2 =0, \end{aligned}$$

(5.39)

with

$$\begin{aligned} \bar{M}_2= & {} \frac{4 \left( \lambda _1 \rho _2 +\lambda _2 \rho _1\right) \left( 3\lambda _1 \lambda _2 +\lambda _1 \rho _2 +\lambda _2 \rho _1\right) +5\lambda _1^2\lambda _2^2 -8\lambda _1^2 +8\lambda _2^2}{6\Pi }, \end{aligned}$$

(5.40)

$$\begin{aligned} \bar{N}_2= & {} -\frac{\left[ \left( \lambda _1 \rho _2 +\lambda _2\rho _1\right) \left( \lambda _1 \lambda _2 +2\lambda _1 \rho _2 +2\lambda _2\rho _1\right) -2\lambda _1^2 +2\lambda _2^2\right] }{9\Pi ^2} \nonumber \\&\times \, \left[ 4\left( \lambda _1 \rho _2 +\lambda _2\rho _1\right) \left( \lambda _1 \lambda _2 -3\lambda _1 \rho _2 -3\lambda _2\rho _1\right) \right. \nonumber \\&\left. \,+\,5\lambda _1^2\lambda _2^2+8\lambda _1^2 -8\lambda _2^2\right] . \end{aligned}$$

(5.41)

Hence the Eqs. (5.36) and (5.39) admit a common solution:

$$\begin{aligned} \zeta =\frac{2}{3}\left( {\frac{\rho _1}{\lambda _1}+\frac{\rho _2}{\lambda _2}}\right) + \frac{4\left( {\lambda _2^2-\lambda _1^2}\right) }{3\Pi }. \end{aligned}$$

(5.42)

Consequently, we can write the variables $\chi$, $u_1$, $u_2$, and $\hat{v}$ as

$$\begin{aligned} \chi= & {} \frac{2}{3}\left( {\frac{\rho _1}{\lambda _1}+\frac{\rho _2}{\lambda _2}}\right) +\frac{1}{3} =\zeta +\eta , \end{aligned}$$

(5.43)

$$\begin{aligned} u_1= & {} \frac{2\Omega \times \left[ {\lambda _2^2\left( {\lambda _1\rho _1+2\rho _1^2+2}\right) +2\lambda _1\lambda _2\rho _1\rho _2+4\left( {\lambda _1\rho _1+\lambda _2\rho _2}\right) }\right] }{3\Pi ^2}, \end{aligned}$$

(5.44)

$$\begin{aligned} u_2= & {} \frac{2\Omega \times \left[ {\lambda _1^2\left( {\lambda _2\rho _2+2\rho _2^2-2}\right) +2\lambda _1\lambda _2\rho _1\rho _2-4\left( {\lambda _1\rho _1+\lambda _2\rho _2}\right) }\right] }{3\Pi ^2}, \end{aligned}$$

(5.45)

$$\begin{aligned} \hat{v}= & {} \frac{2\Omega \times \left[ {\Pi -4\left( {\lambda _2^2-\lambda _1^2}\right) }\right] }{3\Pi ^2}, \end{aligned}$$

(5.46)

with

$$\begin{aligned} \Omega\equiv & {} 2\left( {\lambda _1\rho _2+\lambda _2\rho _1}\right) \left( {\lambda _1\lambda _2+4\lambda _1\rho _2+4\lambda _2\rho _1}\right) \nonumber \\&-\lambda _1^2\lambda _2^2+6({\lambda _2^2-\lambda _1^2}). \end{aligned}$$

(5.47)

It is straightforward to show that these solutions are identical to the same set of solutions of the SKR model shown in Sect. 4 in the limit $\rho _2 \rightarrow 0$ and $\lambda _2 \rightarrow \infty$.

Similarly, the positivity of $u_1$ and $u_2$ implies the following constraints:

$$\begin{aligned}&\Omega >0, \end{aligned}$$

(5.48)

$$\begin{aligned}&\lambda _1^2({\lambda _2\rho _2+2\rho _2^2-2})+2\lambda _1\lambda _2\rho _1\rho _2 -4\left( {\lambda _1\rho _1+\lambda _2\rho _2}\right) >0,\nonumber \\ \end{aligned}$$

(5.49)

while $\hat{v}$ will be positive if the inequality (5.48) holds along with the constraint:

$$\begin{aligned} \Pi -4({\lambda _2^2-\lambda _1^2}) >0. \end{aligned}$$

(5.50)

Note that the constraints $\zeta +\eta >0$ and $\zeta -2\eta >0$ are required for expanding solutions. Hence we have

$$\begin{aligned}&\left( {\lambda _1\rho _2+\lambda _2\rho _1}\right) \left( -\lambda _1 \lambda _2 + 2\lambda _1\rho _2+2\lambda _2\rho _1 \right) \nonumber \\&\quad -\lambda _1^2\lambda _2^2+6({\lambda _2^2-\lambda _1^2}) >0 . \end{aligned}$$

(5.51)

It is also straightforward to show that $\Omega$ will be positive if the inequality (5.51) holds. In addition, for inflationary solutions with $\zeta +\eta \gg 1$ and $\zeta -2\eta \gg 1$, the constraint $\zeta +\eta \gg 1$ implies that

$$\begin{aligned} \frac{\rho _1}{\lambda _1} +\frac{\rho _2}{\lambda _2} \gg 1. \end{aligned}$$

(5.52)

In addition, the constraint $\zeta -2\eta \gg 1$ holds if the inequality (5.52) remains valid. Note also that the constraint (5.52) will be $=$ satisfied if we also choose the parameters with the property

$$\begin{aligned} \rho _i \gg \lambda _i \sim \mathcal{O}(1). \end{aligned}$$

(5.53)

It turns out that the inequalities (5.49) and (5.50) also follow this choice of parameters. Similar to the result in Sect. 4, we can show that the average slow-roll parameter becomes [43, 44]

$$\begin{aligned}&\varepsilon \equiv - \frac{{\dot{H}}}{{H^2 }} = \frac{4}{3\zeta +\chi }\nonumber \\&\quad =\frac{12\Pi }{2\left( {\lambda _1\rho _2+\lambda _2\rho _1}\right) \left( {5\lambda _1\lambda _2+8\lambda _1\rho _2+8\lambda _2\rho _1}\right) +\lambda _1^2\lambda _2^2+12\left( {\lambda _2^2-\lambda _1^2}\right) }\nonumber \\ \end{aligned}$$

(5.54)

along with the anisotropy given by [43, 44]

$$\begin{aligned}&\frac{\Sigma }{H} \equiv \frac{{\dot{\sigma }}}{{\dot{\alpha } }}\nonumber \\&\quad =\frac{{\Pi -4\left( {\lambda _2^2-\lambda _1^2}\right) }}{{2\left[ { \left( {\lambda _1\rho _2+\lambda _2\rho _1}\right) \left( {\lambda _1\lambda _2+2\lambda _1\rho _2+2\lambda _2\rho _1}\right) +2\left( {\lambda _2^2-\lambda _1^2}\right) }\right] }}.\nonumber \\ \end{aligned}$$

(5.55)

Finally, we would like to remark that the variables can be approximated as

$$\begin{aligned} \zeta\simeq & {} \chi \simeq \frac{2}{3}\left( \frac{\rho _1}{\lambda _1}+\frac{\rho _2}{\lambda _2}\right) ;~\eta \simeq \frac{1}{3};~u_1 \simeq 4 \frac{\rho _1}{\lambda _1}\zeta ;\nonumber \\ ~u_2\simeq & {} 4 \frac{\rho _2}{\lambda _2}\zeta ;~\hat{v} \simeq 4\zeta -\frac{16}{3} \left( \frac{1}{\lambda _1^2}-\frac{1}{\lambda _2^2}\right) \end{aligned}$$

(5.56)

during the inflationary phase with $\rho _i \gg \lambda _i \sim \mathcal{O}(1)$. Moreover, the isotropic scale factor $\zeta$ in the 5D QKR is also smaller than the scale factor $\eta$ in the 4D two-scalar-field extension of KSW model for the same reason. On the other hand, the anisotropic scale factor $\eta$ is still identical to the $\eta$ solution of the 4D two-scalar-field extension of KSW model [47,48,49,50,51].

5.2 Stability analysis of the anisotropic inflationary solutions

In this subsection, we will see how the phantom field affects the stability of the anisotropic power-law inflationary solution shown above by performing the power-law perturbations: $\delta \alpha = B_\alpha t^n$, $\delta \sigma = B_\sigma t^n$, $\delta \gamma = B_\gamma t^n$, $\delta \phi = B_\phi t^n$, and $\delta \psi = B_\psi t^n$  [47,48,49,50,51]. As a result, we can derive a set of algebraic equations by perturbing the field equations (5.8), (5.9), (5.11), (5.12), and (5.13):

$$\begin{aligned} \mathcal{\hat{D}} \left( {\begin{array}{*{20}c} B_\alpha \\ B_\sigma \\ B_\gamma \\ B_\phi \\ B_\psi \\ \end{array} } \right) \equiv \left[ {\begin{array}{*{20}c} {B_{11} } &{} {B_{12} } &{} {B_{13} } &{} {B_{14}} &{} {B_{15}} \\ {B_{21} } &{} {B_{22} } &{} {B_{23} } &{} {B_{24}} &{} {B_{25}}\\ {B_{31} } &{} {B_{32} } &{} {B_{33} } &{} {B_{34}} &{} {B_{35}} \\ {B_{41} } &{} {B_{42} } &{} {B_{43} } &{} {B_{44}} &{} {B_{45}}\\ {B_{51} } &{} {B_{52} } &{} {B_{53} } &{} {B_{54}} &{} {B_{55}}\\ \end{array} } \right] \left( {\begin{array}{*{20}c} B_\alpha \\ B_\sigma \\ B_\gamma \\ B_\phi \\ B_\psi \\ \end{array} } \right) = 0, \end{aligned}$$

(5.57)

where

$$\begin{aligned} B_{11}= & {} A_{11};~ B_{12}=A_{12};~B_{13}= A_{13};~B_{14}\nonumber \\= & {} A_{14};~ B_{15}=- 2\rho _1\rho _2 \hat{v}, \end{aligned}$$

(5.58)

$$\begin{aligned} B_{21}= & {} \frac{6}{\lambda _2}n+4\rho _2 \hat{v};~B_{22}=4\rho _2 \hat{v};~B_{23}=\frac{2}{\lambda _2}n+2\rho _2 \hat{v}; \nonumber \\ B_{24}= & {} 2\rho _1\rho _2\hat{v};~ B_{25}=-n^2\nonumber \\&-\left( {3\zeta +\chi -1}\right) n + \lambda _2^2 u_2 +2\rho _2^2 \hat{v}, \end{aligned}$$

(5.59)

$$\begin{aligned} B_{31}= & {} A_{21}; B_{32}=A_{22}; B_{33}= A_{23}; B_{34} =A_{24}; B_{35}\nonumber \\= & {} \frac{2n}{3\lambda _2}-\frac{\lambda _2}{3}u_2-\frac{\rho _2}{3}\hat{v}, \end{aligned}$$

(5.60)

$$\begin{aligned} B_{41}= & {} A_{31}; B_{42}=A_{32}; B_{43}=A_{33}; B_{44}\nonumber \\= & {} A_{34}; B_{45}=\frac{2}{3}\rho _2 \hat{v}, \end{aligned}$$

(5.61)

$$\begin{aligned} B_{51}= & {} A_{41}; B_{52}=A_{42}; B_{53}=A_{43}; B_{54}\nonumber \\= & {} A_{44}; B_{55}= -\lambda _2 u_2 +\frac{\rho _2}{3} \hat{v}, \end{aligned}$$

(5.62)

where $A_{ij}$ $(i,j=1-4)$ are defined in Eqs. (4.2), (4.3), (4.4), and (4.5) with the replacements: $\lambda \rightarrow \lambda _1$, $\rho \rightarrow \rho _1$, $u \rightarrow u_1$, and $v \rightarrow \hat{v}$. It is known that nontrivial solutions of Eq. (5.57) exist only when

$$\begin{aligned} \det \mathcal{\hat{D}} =0. \end{aligned}$$

(5.63)

As a result, this determinant equation leads to a degree 10 polynomial equation of n:

$$\begin{aligned} n^2\hat{f}\left( n\right) \equiv n^2 \left( {b_{10}n^8+ \cdots +b_2}\right) =0, \end{aligned}$$

(5.64)

with

$$\begin{aligned}&b_{10} = a_8 =\frac{1}{2} >0, \end{aligned}$$

(5.65)

$$\begin{aligned}&b_2 \simeq -\frac{57344}{243} \lambda _1 \lambda _2 \rho _1 \rho _2 \left( \frac{\rho _1}{\lambda _1}+\frac{\rho _2}{\lambda _2}\right) ^6 <0. \end{aligned}$$

(5.66)

Note that we have only kept the leading terms in deriving $b_2$. As a result, $b_2 <0$ and $b_{10}>0$ imply that the equation $\hat{f}(n)=0$ admits at least one positive root n.

This conclusion is based on an observation [47,48,49,50,51] that $\hat{f}(n=0)=b_2 <0$ and $\hat{f}(n\gg 1) \sim n^8/2 >0$. Hence, the curve $y=\hat{f}(n)$ on the $n-y$ plane will cross the positive n-axis at least once with the crossing point(s) representing the positive root(s) to the equation $\hat{f}(n)=0$. Hence we can conclude that the inclusion of the phantom field in the QKR model does destabilize the corresponding anisotropic power-law inflationary solution as expected.

6 Conclusions

Note that the cosmic inflation has served as a central paradigm in modern cosmology. The nature of the CMB anomalies such as the hemispherical asymmetry and the cold spot observed by WMAP and Planck should be related to the initial anisotropy of the metric space. One is naturally led to a question whether these anomalies disappear in the late-time future universe. These anomalies will disappear at the late-time universe if the cosmic no-hair conjecture [13, 14] holds. Unfortunately, a complete proof to this conjecture has yet been a great challenge to all physicists and cosmologists for several decades. Before a final proof is handy, its validity should be examined not only in four dimension cosmological theories/models but also in higher dimensional spaces. In particular, counter-examples have been found in the KSW model [43,44,45,46] and its noncanonical extensions [49,50,51]. Hence we are led to the investigation whether the cosmic no-hair conjecture is truly violated in higher dimensional extensions of KSW model. In particular, we have chosen to study the 5D scalar-Kalb–Ramond model [79,80,81,82,83,84,85,86] in this paper. The effective action with a scalar-Kalb–Ramond interaction can be shown to be equivalent to an effective action with a scalar–vector interaction in 5D spacetime [83,84,85,86], a higher dimensional extension of KSW model.

Note that the power-law solutions for a model with scalar–vector coupling term [43,44,45,46] are known counterexamples to the cosmic no-hair conjecture. The existence of power-law solutions also puts, however, strong constraints on the possible form of the compatible coupling terms. This is also the reason that the special form exponential potential are considered in this paper. Indeed, any deviation from the exponential type gauge couplings and scalar potential could jeopardize the existence of the power-law solutions.

In summary, a 5D SVKR model with a scalar-Kalb–Ramond coupling term and a scalar–vector coupling was introduced in Sect. 2. We focus on the effect of the SVKR model in a 5D anisotropic metric space. A set of power-law ansatz was hence introduced. Consequently, a set of algebraic equations were derived representing the power-law nature of the field equations. The extra dimension scale factor $\exp [\gamma ]$ does share part of the expanding energy and slow down the expansion of the 4D scale factor $\exp [ \alpha ]$.

In addition, a new set of power-law solutions was obtained for the SVKR model with a set of exponential potentials in Sect. 3. Important properties of this set of solutions had also been discussed. We had focussed on the model with an exponential potential and gauge kinetic functions of the form [43,44,45,46,47,48,49,50,51], $V\left( \phi \right) = V_0 \exp \left[ {\lambda \phi }\right]$, $f(\phi )= f_0 \exp \left[ {\rho \phi }\right]$, and $h\left( \phi \right) = h_0 \exp \left[ {-\rho \phi }\right]$.

Consequently, it was shown that this new set of power-law solutions is indeed stable in the inflationary era. The result is identical to the result of a scalar–vector model with the identification given by $v = (f_0^{-2}p_\mathcal{A}^2+h_0^2p_{A}^2) \exp \left[ {-2\rho \phi _0}\right]$. This constraint and simplification are derived from the requirement for the existence of the power-law solutions. As a result, the presence of the SKR term contributes to the model with a non-trivial effect on the stability nature of the power-law solutions. The proof was presented with two different approaches. The first approach is done by a straightforward perturbation to the field equations. The second proof is presenting the attractor nature of the corresponding autonomous equations. A phantom field was thus introduced to the SVKR model in Sect. 5. It was hence shown that the presence of the phantom field does destabilize the corresponding power-law solutions as expected. The results indicates that the physics of the 5D Kalb–Ramond model deserves more attention.

Phantom field is known to suffer from the unitary and future divergence problems  [109,110,111,112]. The loop quantum cosmology proposal could be a resolution to these problems [113, 114]. In addition, the presence of the phantom field in the early universe tends to turn the power-law solution unstable unlike its non-trivial effects on the stability of black holes. Indeed, it has been known that the presence of the phantom field leads to complicate constraints on the black hole solutions  [115]. This is also the reason we need to explore explicitly the possible effects of the phantom field on the power-law solutions found in this paper. To be more specific, we will only focus on the effect of the phantom field to the evolution of the early universe when the phantom field tends to provide critical input.

Appendices

Appendix A: 5D Kalb–Ramond field and its dual gauge field

We will focus on the quintom-Kalb–Ramond model (QKR) in 5D spacetime with the following coupling

$$\begin{aligned} S_\mathrm{5H}= \int {d^5 } x \sqrt{ g} \left[ -\frac{\kappa }{12}h^2\left( \phi ,\psi \right) H_{abc}H^{abc} \right] , \end{aligned}$$

(A1)

with $H_{abc} \equiv \partial _{[a} B_{bc]}$ the KR field strength  [79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100]. Note that the QKR interaction is a new form of interaction with both canonical scalar and phantom fields coupling that we have studied in this paper. To be more specific, $H_{abc}\equiv (\partial _{a} B_{bc} + \partial _{b} B_{ca}+ \partial _{c} B_{ab} )/3$. Here $g \equiv -\det \mathbf g$ with $(\mathbf{g})_{ab} \equiv g_{ab}$ denoting the matrix $\mathbf{g}$ mapped from the metric $g_{ab}$. Note that the minus sign of the determinant is derived from the Lorentzian signature $(-1,1,1,1,1)$. In addition, $\kappa$ is a constant that can be either positive or negative corresponding to the KR or anti-KR field.

Ignoring the irrelevant coupling term $\kappa h^2$ for the moment, the field equations of the KR field can be derived from the action (A1) as [83,84,85, 90,91,92, 98, 99]

$$\begin{aligned} D_c H^{cab} =0. \end{aligned}$$

(A2)

Note that the 5D KR field $H_{abc}$ is related to a rank-2 antisymmetric tensor field $F_{ab}$ via the relation

$$\begin{aligned} H_{abc}= \epsilon _{abcde} F^{de} \end{aligned}$$

(A3)

with $\epsilon _{abcde}$ the totally skew-symmetric Levi-Civita tensor. Note that the Levi-Civita tensor $\epsilon ^{abcde}$ and the flat-Levi-Civita tensor $e^{abcde}$ is related by the definition $\epsilon ^{abcde} = e^{abcde}/\sqrt{g}$. Here the flat-Levi-Civita tensor $e^{abcde}$ is defined as the totally skew-symmetric tensor with $e^{01234}=1$ on a 5D flat Euclidean space $\mathbf{R}^5$ with Euclidean signature (1, 1, 1, 1, 1).

There are two important facts that could be easily overlooked concerning the dual transformation of the KR field $B_{ab}$ and the gauge field $A_a$ in 5D spacetime. First of all, the Lorentzian signature comes with a minus sign in defining the determinant of the metric $g_{ab}$. Indeed, it can be shown that, for example,

$$\begin{aligned} \epsilon _{abcde} \epsilon ^{abcde}= - 5!. \end{aligned}$$

(A4)

The minus sign on the RHS, derived from the Lorentzian signature, appears when we derive the type T(0,5) tensor $\epsilon _{abcde}$ from lowering all the tensor indexes of the type T(5,0) Levi-Civita tensor $\epsilon ^{abcde}$. This sign can easily be overlooked when the tensor $\epsilon _{abcde}$ is involved.

Secondly, the effective action of the gauge field derived from the KR field also carries a wrong sign when the dual transformation is performed. Indeed, it can be shown that

$$\begin{aligned} -\frac{1}{12}H_{abc}H^{abc} \rightarrow F^2 \end{aligned}$$

(A5)

once the dual transform is performed. As a result, a direct transformation of the KR action generates an effective gauge action with a wrong sign.

Note that the second minus sign has nothing to do with the signature of the metric space. It has to do only with the dual transformation of the Hodge operator. This happens quite often when some of the cyclic field equations are integrated directly. The wrong sign in the kinetic term of the effective field can be resolved by the Routh transform dealing with the effective action derived from a cyclic field. For heuristic reasons, we will present a brief review on both problems in this section.

1.1 Lorentzian signature and the tensor $\epsilon _{abcde}$

First of all, we will deal with the first problem derived from a metric space with Lorentzian signature. Note that the definition of $\epsilon _{abcde} \equiv g_{aa'}g_{bb'}g_{cc'}g_{dd'}g_{ee'} \epsilon ^{a'b'c'd'e'}$ can be shown to be

$$\begin{aligned} \epsilon _{abcde} = -\sqrt{g}\; e_{abcde} \end{aligned}$$

(A6)

due to the definition of $g=- \det \mathbf{g}$ derived from the Lorentzian signature $(-1,1,1,1,1)$ of the metric space. Note also that $e_{abcde}$ is understood to be lowered from $e^{a'b'c'd'e'}$ by the flat metric $\delta _{aa'} \cdots \delta _{ee'}$. A brief review of the proof will be presented in appendix B.

1.2 Dual transform

We will show here that the structure of the rank-2 antisymmetric tensor field $F_{ab}$ is identical to an $U_1$-symmetry gauge field. Indeed, it can be shown that $F_{ab}=(\partial _aA_b -\partial _bA_a)/2$ with a rank-1 field $A_a$ for a space M with $H^2 (M)=0$, i.e., the second cohomology group [105,106,107,108] is trivial. In particular, it is known that $H^2(\mathbf{R}^n)=0$ for all $n > 2$ [108]. In addition, an n-dimensional manifold is defined as an atlas of locally diffeomorphism of $\mathbf{R}^n$ spaces. Note that the field tensor $F_{ab}$ defined here endorses a factor of 1/2 difference from the conventional definition. In addition, the nth de Rham cohomology group $H^n(M)$ of a space M is defined as the set of closed n-forms modulo the exact n-forms. Indeed, $H^2(M)=0$ means that all closed forms are exact forms. To be more specific, an $H^2 (M)=0$ space is a space with the property “$dF=0$ implies $F=dA$” for a 2-form F and a 1-form A. Note that the Hodge operator $*$ maps a 3-form into its dual 2-form via the dual transformation

$$\begin{aligned} * \; dx^c \wedge dx^d \wedge dx^e = e^{abcde} dx^a \wedge dx^b. \end{aligned}$$

(A7)

The field equation (A2) implies that

$$\begin{aligned}&\partial _c \left( \sqrt{g} \epsilon ^{cabde} F_{de} \right) = e^{cabde} \partial _c F_{de} =0 . \end{aligned}$$

(A8)

Dressing above equation with $dx^a \wedge dx^b$, we can write Eq. (A8) as

$$\begin{aligned}&* ( \partial _c F_{de} dx^c \wedge dx^d \wedge dx^e \; ) =*dF = 0 . \end{aligned}$$

(A9)

Hence Eq. (A2) is equivalent to $dF=0$.

1.3 The effective gauge action with a wrong sign

Consequently, if $H^2 (M)=0$, there exists a one-form $A=A_adx^a$ such that

$$\begin{aligned} F=dA . \end{aligned}$$

(A10)

Note that the Levi-Civita tensor obeys the relations

$$\begin{aligned} \epsilon _{abcde} \epsilon ^{abcde}= & {} - 5! , \end{aligned}$$

(A11)

$$\begin{aligned} \epsilon _{abcde} \epsilon ^{abcde'}= & {} - 4! \; g^e_{\;\;e'}, \end{aligned}$$

(A12)

$$\begin{aligned} \epsilon _{abcde} \epsilon ^{abcd'e'}= & {} - 3! \; ( g^d_{\;\;d'} g^e_{\;\;e'} -g^d_{\;\;e'} g^e_{\;\;d'} ), \end{aligned}$$

(A13)

$$\begin{aligned} \epsilon _{abcde} \epsilon ^{abc'd'e'}= & {} - 2! \; \left[ (c,d,e)+(d,e,c)+(e,c,d)\right. \nonumber \\&\left. -(d,c,e)-(e,d,c)-(c,e,d) \right] , \end{aligned}$$

(A14)

with $(c,d,e) \equiv g^c_{\;\;c'} g^d_{\;\;d'} g^e_{\;\;e'}$. The minus signs on the RHS of above equations are derived from the Lorentzian signature. Indeed, the proof will be presented in “Appendix C”.

As a result, we can show that

$$\begin{aligned} H_{abc} H^{abc}= & {} \epsilon _{abcde} \epsilon ^{abcd'e'} F^{de} F^{d'e'} = -12 F^2, \end{aligned}$$

(A15)

$$\begin{aligned} H_{abc} H^{a'bc}= & {} \epsilon _{abcde} \epsilon ^{a'bcd'e'} F^{de} F^{d'e'} \nonumber \\= & {} -4 ( g_{aa'} F^2- 2 F_{ac}F_{a'}^{\;\;c} ). \end{aligned}$$

(A16)

Hence, the Lagrangian $-H^2/12$ can be shown to be

$$\begin{aligned} - { 1 \over 12 } H^2 = F^2 . \end{aligned}$$

(A17)

Note that 5D space is an odd-dimensional space such that the dual form respects the same parity symmetry in contrast to the case in even-dimensional space. Therefore, the parity of the dual field $A_a$ is exactly the same as the original field $B_{ab}$. There is, however, a wrong sign shows up in the effective kinetic term of the effective gauge field on the RHS of Eq. (A17).

1.4 The model and the correct QKR field equations for the dual gauge field

Recall the 5D action with the QKR interaction term studied in the previous sections

$$\begin{aligned} S_\mathrm{bulk}= & {} \int {d^5 } x\sqrt{ g} \biggl [ -\frac{{R}}{2} - \frac{1}{2}\partial _a \phi \partial ^a \phi +\frac{1}{2} \partial _a \psi \partial ^a \psi \nonumber \\&-\frac{\kappa }{12}h^2\left( \phi ,\psi \right) H_{abc}H^{abc} \biggr ]. \end{aligned}$$

(A18)

Here $h(\phi ,\psi )$ is a gauge kinetic function of $\phi$ and $\psi$. Note that the two scalar fields model is a generalization of the one scalar field model [79, 83,84,85,86,87, 90,91,92, 94, 95, 98,99,100]. As a result, the field equations can be derived from the action (A18):

$$\begin{aligned}&D_c [{ h^2\left( \phi ,\psi \right) H^{cab} }]=0, \end{aligned}$$

(A19)

$$\begin{aligned}&D^2 \phi -\frac{\kappa }{6}h\partial _\phi h H_{abc}H^{abc}=0, \end{aligned}$$

(A20)

$$\begin{aligned}&-D^2 \psi -\frac{\kappa }{6}h\partial _\psi h H_{abc}H^{abc}=0, \end{aligned}$$

(A21)

$$\begin{aligned}&{R_{ab}-\frac{1}{2}g_{ab}R}= -\partial _a \phi \partial _b \phi +\partial _a \psi \partial _b \psi \nonumber \\&\quad +\frac{1}{2}g_{ab}\left[ {\partial _c \phi \partial ^c \phi -\partial _c \psi \partial ^c \psi +\frac{\kappa }{6}h^2 H_{cde}H^{cde}}\right] \nonumber \\&\quad -\frac{\kappa }{2}h^2 H_{acd}H_{b}{}^{cd}. \end{aligned}$$

(A22)

Once the KR field is solved with the help of Eq. (A19) and the dual symmetry, the field equations can be shown to be  [83]

$$\begin{aligned}&\partial _b [{\sqrt{ g} h^{-2} F^{ab} }]=0, \end{aligned}$$

(A23)

$$\begin{aligned}&D^2 \phi +2\kappa h^{-3}\partial _\phi h F_{mn}F^{mn}=0, \end{aligned}$$

(A24)

$$\begin{aligned}&-D^2 \psi +2\kappa h^{-3}\partial _\psi h F_{mn}F^{mn}=0, \end{aligned}$$

(A25)

$$\begin{aligned}&{R_{ab}-\frac{1}{2}g_{ab}R}=-\partial _a \phi \partial _b \phi +\partial _a \psi \partial _b \psi \nonumber \\&\quad +g_{ab}\left[ {\frac{1}{2} \partial _c \phi \partial ^c \phi -\frac{1}{2}\partial _c \psi \partial ^c \psi +\kappa h^{-2} F_{cd}F^{cd}}\right] \nonumber \\&\quad -4\kappa h^{-2} F_{ac}F_{b}{}^{c}, \end{aligned}$$

(A26)

in terms of the gauge field $A_a$. Note that Eq. (A23) is the direct result of the conservation law associated with the effective energy momentum tensor $T^{ab}({A_c})$ appears on the RHS of Eq. (A26). In particular, the energy momentum tensor of KR field transforms as

$$\begin{aligned} T_{ab}^H= & {} {-2 \over \sqrt{g}} \frac{ \delta ( -\frac{1}{12}\sqrt{g} h^2 H^2 )}{\delta g_{ab}} \nonumber \\= & {} \frac{1}{12} h^2 H^2 \; g_{ab} -\frac{1}{2}h^2 H_{acd}H_{b}{}^{cd}\nonumber \\= & {} h^{-2} F_{cd}F^{cd}g_{ab} -4 h^{-2} F_{ac}F_{b}{}^{c} \; \end{aligned}$$

(A27)

under the dual transform with the dual field replaced properly. In addition, we can also show that the energy momentum tensor of effective gauge field, derived from the variational equation of $-F^2$-term, also leads to the same expression:

$$\begin{aligned} T_{ab}^A= & {} {-2 \over \sqrt{g}} \frac{\delta ( - \sqrt{g} h^{-2} F^2 ) }{\delta g_{ab} } \nonumber \\= & {} h^{-2} F_{cd}F^{cd}g_{ab} -4 h^{-2} F_{ac}F_{b}{}^{c} . \end{aligned}$$

(A28)

This proves the the correct effective Lagrangian of $-h^2 H^2/12$ should be $-h^{-2} F^2$ instead of $h^{-2}F^2$. To be more specific, the correct effective gauge field equations (A23)–(A26) are identical to the variational equations derived from the effective action

$$\begin{aligned} \int {d^5 } x \sqrt{ g} \left[ - \kappa h^{-2} \left( \phi ,\psi \right) F^2 \right] \end{aligned}$$

(A29)

instead of the effective action derived directly from the dual-transformation:

$$\begin{aligned} \int {d^5 } x \sqrt{ g} [ \kappa h^{-2} \left( \phi ,\psi \right) F^2 ] . \end{aligned}$$

(A30)

Indeed, the effective action derived from setting $H_{abc}= \epsilon _{abcde} h^{-2} F^{de}$ ends up with a negative kinetic term due to the Hodge * operation. As a result, it can be shown that

$$\begin{aligned} S_\mathrm{KR}= & {} \int {d^5 } x \sqrt{ g} \left[ -\frac{\kappa }{12}h^2\left( \phi ,\psi \right) H^2 \right] \nonumber \\= & {} \int {d^5 } x \sqrt{ g} [\kappa h^{-2} \left( \phi ,\psi \right) F^2 ] \end{aligned}$$

(A31)

endorse a gauge field action with a negative kinetic energy term. Consequently, the $h^{-2}F^2$ term on the RHS of Eq. (A31) fails to derive the correct field equation as an effective action.

1.5 The Routh transform

In summary, we have shown that the effective action always carries a wrong sign when the KR field is solved for the effective gauge field. The resolution has been known as the Routh transform when we are dealing with the cyclic variables (e.g. $B_{bc}$ in this paper) [90,91,92, 98, 99, 101]. Indeed, Routh suggests that a Legendre transformations of cyclic variables can resolve the problem and leave all other field variables unaffected in the associated Hamiltonian-Lagrangian (or Routhian) system. To be more specific, we can define the Routhian $H_L$ via the Legendre transform

$$\begin{aligned}&H_L(\phi _1,\ldots , \phi _k; \dot{\phi }_1,\ldots , \dot{\phi }_k; \pi _{k+1},\ldots , \pi _n) \nonumber \\&\quad = \sum _{i=k+1}^n \pi _i \dot{\phi }_i - L ( \phi _1,\ldots , \phi _k; \dot{\phi }_1,\ldots , \dot{\phi }_n ) \end{aligned}$$

(A32)

as the effective Lagrangian of the system with cyclic variables $\phi _i$ with $i = k + 1, \ldots ,n$. Here $\pi _i$ with $i = k + 1, \ldots ,n$ are the conjugate momentum of the cyclic variables, and hence constants in time. The variational equation of L with respect to the cyclic variable is the same as the variational equation of L under constraint derived from the cyclic variables. For the KR model we are interested, the correct effective Lagrangian should be

$$\begin{aligned}&L_\mathrm{eff} ( \phi _1,\ldots , \phi _k; \dot{\phi }_1,\ldots , \dot{\phi }_n )\nonumber \\&\quad =-H_L(\phi _1,\ldots , \phi _k; \dot{\phi }_1,\ldots , \dot{\phi }_k; \pi _{k+1},\ldots , \pi _n) \end{aligned}$$

(A33)

with all the cyclic variables solved and replaced. For the model (A18), the effective Routhian goes like

$$\begin{aligned} \mathcal{L}_\mathrm{eff} ( A_a )=\mathcal{L}_H -\partial _aA_b {\delta \mathcal{L}_H \over \delta \partial _aA_b} = -F^2 \; \end{aligned}$$

(A34)

for the KR action. As a result, we can show that the effective action (or Routhian) of (A18) should be

$$\begin{aligned} S_\mathrm{eff}= & {} \int {d^5 } x\sqrt{ g} \biggl [ -\frac{ {R}}{2} - \frac{1}{2}\partial _a \phi \partial ^a \phi +\frac{1}{2} \partial _a \psi \partial ^a \psi \nonumber \\&-h^{-2} \left( \phi ,\psi \right) F^2 \biggr ], \end{aligned}$$

(A35)

when the Routh transform is applied. Accordingly, it is straightforward to show that the correct field equations (A23)–(A26) can be derived from the variational equations of (A35) with respect to $A_a$.

Appendix B: The minus sign derived form the Lorentzian signature

A short proof of (A6) will be presented here for heuristic reasons. First of all, the determinant of a matrix $\mathbf{g}$ is formally defined as

$$\begin{aligned} \det \mathbf{g} = e^{abcde} g_{0a}g_{1b}g_{2c}g_{3d}g_{4e} \; \end{aligned}$$

(B1)

with $e^{01234}=1$ defining the totally skew-symmetric flat Levi-Civita tensor. It can be shown from the property of skew-symmetry that   [104]

$$\begin{aligned} e^{abcde} \det \mathbf{g} = e^{a'b'c'd'e'} g_{aa'}g_{bb'}g_{cc'}g_{dd'}g_{ee'} \; \end{aligned}$$

(B2)

with the help of the definition (B1). Indeed, the proof goes with three steps. First of all, it can be shown that the left hand side (LHS) of Eq. (B2) is totally skew-symmetric with respect to a, b, c, d, e similar to the symmetry of the right hand side (RHS) of Eq. (B2). Secondly, it can be shown that the LHS of Eq. (B2) is a type T(0,5) tensor rank similar to its counter part on the RHS. Finally, we only need to show that Eq. (B2) is correct when $(a,b,c,d,e)=(0,1,2,3,4)$. As a result, the totally-skew symmetries will take care of the rest of the components. This concludes the proof that $e^{abcde} \det \mathbf{g} = e^{a'b'c'd'e'} g_{aa'}g_{bb'}g_{cc'}g_{dd'}g_{ee'}$.

As a result, we can contract Eq. (B2) with $1/\sqrt{g}$ and show that

$$\begin{aligned} - \sqrt{g} e^{abcde} ={1 \over \sqrt{g}} e^{a'b'c'd'e'} g_{aa'}g_{bb'}g_{cc'}g_{dd'}g_{ee'} . \end{aligned}$$

(B3)

From the definition of the Levi-Civita tensor $\epsilon ^{a'b'c'd'e'} \equiv e^{a'b'c'd'e'}/ \sqrt{g}$, the RHS of the above equation is exactly the type (0,5) Levi-Civita tensor $\epsilon _{abcde} \equiv \epsilon ^{a'b'c'd'e'} g_{aa'}g_{bb'}g_{cc'} g_{dd'}g_{ee'}$. Hence we have concluded the proof that

$$\begin{aligned} \epsilon _{abcde} = -\sqrt{g} e^{abcde} . \end{aligned}$$

(B4)

It is noted that the wrong sign leads to many misleading conclusions and interpretations. It appears that this is a common mistake and deserves more attentions. Indeed, this error can be found in Ref. [83], while the correct sign can be seen in Refs. [84, 85].

Appendix C: Identities concerning the contractions of the Levi-Civita tensors

Note that the Levi-Civita tensor obeys the relations

$$\begin{aligned}&\epsilon _{abcde} \epsilon ^{abcde}= - 5! , \end{aligned}$$

(C1)

$$\begin{aligned}&\epsilon _{abcde} \epsilon ^{abcde'}= - 4! \; g^e_{\;\;e'}, \end{aligned}$$

(C2)

$$\begin{aligned}&\epsilon _{abcde} \epsilon ^{abcd'e'}= - 3! \; ( g^d_{\;\;d'} g^e_{\;\;e'} -g^d_{\;\;e'} g^e_{\;\;d'} ), \end{aligned}$$

(C3)

$$\begin{aligned}&\epsilon _{abcde} \epsilon ^{abc'd'e'}= - 2! \; \left[ (c,d,e)+(d,e,c)+(e,c,d)\right. \nonumber \\&\left. \quad -(d,c,e)-(e,d,c)-(c,e,d) \right] , \end{aligned}$$

(C4)

with $(c,d,e) \equiv g^c_{\;\;c'} g^d_{\;\;d'} g^e_{\;\;e'}$. We would like to remark that the minus sign is derived from the Lorentzian signature. Indeed, the proof starts with an observation that

$$\begin{aligned}&e^{abcde} e^{abcde}= 5! , \end{aligned}$$

(C5)

$$\begin{aligned}&e^{abcde} e^{abcde'}= 4! \; \delta ^{ee'} , \end{aligned}$$

(C6)

$$\begin{aligned}&e_{abcde} e^{abcd'e'}= 3! \; (\delta ^{dd'} \delta ^{ee'} -\delta ^{de'} \delta ^{ed'} ) , \end{aligned}$$

(C7)

$$\begin{aligned}&e^{abcde} e^{abc'd'e'}= 2! \; \left[ (c,d,e)+(d,e,c)+(e,c,d)\right. \nonumber \\&\left. \quad -(d,c,e)-(e,d,c)-(c,e,d) \right] . \end{aligned}$$

(C8)

The proof can be done easily by comparing the symmetry of the open index in above equations.