Precise prediction for the Higgs-boson masses in the $\mu \nu$SSM

Abstract

The $\mu \nu \mathrm {SSM}$ is a simple supersymmetric extension of the Standard Model (SM) capable of predicting neutrino physics in agreement with experiment. In this paper we perform the complete one-loop renormalization of the neutral scalar sector of the $\mu \nu \mathrm {SSM}$ with one generation of right-handed neutrinos in a mixed on-shell/${\overline{\mathrm {DR}}}$ scheme. The renormalization procedure is discussed in detail, emphasizing conceptual differences to the minimal (MSSM) and next-to-minimal (NMSSM) supersymmetric standard model regarding the field renormalization and the treatment of non-flavor-diagonal soft mass parameters, which have their origin in the breaking of R-parity in the $\mu \nu \mathrm {SSM}$. We calculate the full one-loop corrections to the neutral scalar masses of the $\mu \nu \mathrm {SSM}$. The one-loop contributions are supplemented by available MSSM higher-order corrections. We obtain numerical results for a SM-like Higgs boson mass consistent with experimental bounds. We compare our results to predictions in the NMSSM to obtain a measure for the significance of genuine $\mu \nu \mathrm {SSM}$-like contributions. We only find minor corrections due to the smallness of the neutrino Yukawa couplings, indicating that the Higgs boson mass calculations in the $\mu \nu \mathrm {SSM}$ are at the same level of accuracy as in the NMSSM. Finally we show that the $\mu \nu \mathrm {SSM}$ can accomodate a Higgs boson that could explain an excess of $\gamma \gamma$ events at $\sim 96 \,\mathrm {GeV}$ as reported by CMS, as well as the $2\,\sigma$ excess of $b \bar{b}$ events observed at LEP at a similar mass scale.

1 Introduction

The spectacular discovery of a boson with a mass around $\sim 125 \,\mathrm {GeV}$ by the ATLAS and CMS experiments [1, 2] at CERN constitutes a milestone in the quest for understanding the physics of electroweak symmetry breaking (EWSB). While within the present experimental uncertainties the properties of the observed Higgs boson are compatible with the predictions of the Standard Model (SM) [3], many other interpretations are possible as well, in particular as a Higgs boson of an extended Higgs sector. Consequently, any model describing electroweak physics needs to provide a state that can be identified with the observed signal.

One of the prime candidates for physics beyond the SM is supersymmetry (SUSY), which doubles the particle degrees of freedom by predicting two scalar partners for all SM fermions, as well as fermionic partners to all bosons. The simplest SUSY extension is the Minimal Supersymmetric Standard Model (MSSM) [4, 5]. In contrast to the single Higgs doublet of the SM, the Higgs sector of the MSSM contains two Higgs doublets, which in the ${{\mathcal {C}\mathcal {P}}}$ conserving case leads to a physical spectrum consisting of two ${{\mathcal {C}\mathcal {P}}}$-even, one ${{\mathcal {C}\mathcal {P}}}$-odd and two charged Higgs bosons. The light (or the heavy) ${{\mathcal {C}\mathcal {P}}}$-even MSSM Higgs boson can be interpreted as the signal discovered at $\sim 125 \,\mathrm {GeV}$ [6].

Going beyond the MSSM, a well-motivated extension is given by the Next-to-Minimal Supersymmetric Standard Model (NMSSM), see e.g. [7, 8] for reviews. In particular the NMSSM provides a solution for the so-called “$\mu$ problem” by naturally associating an adequate scale to the $\mu$ parameter appearing in the MSSM superpotential [9, 10]. In the NMSSM a new singlet superfield is introduced, which only couples to the Higgs- and sfermion-sectors, giving rise to an effective $\mu$-term, proportional to the vacuum expectation value (vev) of the scalar singlet. Assuming ${{\mathcal {C}\mathcal {P}}}$ conservation, as we do throughout the paper, the states in the NMSSM Higgs sector can be classified as three ${{\mathcal {C}\mathcal {P}}}$-even Higgs bosons, $h_i$ ($i = 1,2,3$), two ${{\mathcal {C}\mathcal {P}}}$-odd Higgs bosons, $a_j$ ($j = 1,2$), and the charged Higgs boson pair $H^\pm$. In addition, the SUSY partner of the singlet Higgs (called the singlino) extends the neutralino sector to a total of five neutralinos. In the NMSSM the lightest but also the second lightest ${{\mathcal {C}\mathcal {P}}}$-even neutral Higgs boson can be interpreted as the signal observed at about $125\,\mathrm {GeV}$, see, e.g., [11, 12].

A natural extension of the NMSSM is the $\mu \nu \mathrm {SSM}$, in which the singlet superfield is interpreted as a right-handed neutrino superfield [13, 14] (see Refs. [15,16,17] for reviews). The $\mu \nu \mathrm {SSM}$ is the simplest extension of the MSSM that can provide massive neutrinos through a see-saw mechanism at the electroweak scale. In this paper we will focus on the $\mu \nu \mathrm {SSM}$ with one family of right-handed neutrino superfields, and the case of three families will be studied in a future publication.¹ The $\mu$ problem is solved analogously to the NMSSM by the coupling of the right-handed neutrino superfield to the Higgs sector, and a trilinear coupling of the right-handed neutrino generates an effective Majorana mass at the electroweak scale. The unique feature of the $\mu \nu \mathrm {SSM}$ is the introduction of a Yukawa coupling for the right-handed neutrino of the order of the electron Yukawa coupling that induces the explicit breaking of R-parity. One of the consequences is that there is no lightest stable SUSY particle anymore. Nevertheless, the model can still provide a dark matter candidate with a gravitino that has a life time longer than the age of the observable universe [22,23,24,25]. Since the lightest particle beyond the SM is not stable, it can carry electrical charge or even be coloured. The explicit violation of lepton number and lepton flavor can modify the spectrum of the neutral and charged fermions in comparison to the NMSSM. The three families of charged leptons will mix with the chargino and the Higgsino and form five massive charged fermions. However, the mixing will naturally be tiny since the breaking of R-parity is governed by the small neutrino Yukawa couplings. In the neutral fermion sector the three left-handed neutrinos mix with the right-handed neutrino and the four MSSM-like neutralinos. When just one family of right-handed neutrino is considered (as we do in this paper), the mass matrix of the neutral fermions is of rank six, so just one light neutrino mass is generated at tree-level, while the other two light-neutrino masses will be generated by quantum corrections. For the Higgs sector the breaking of R-parity has dramatic consequences. The three left-handed and the right-handed sneutrinos will mix with the doublet Higgses and form six massive ${{\mathcal {C}\mathcal {P}}}$-even and five massive ${{\mathcal {C}\mathcal {P}}}$-odd states, assuming that there is no ${{\mathcal {C}\mathcal {P}}}$-violation. Additionally, since the vacuum of the model is not protected anymore by lepton number, the sneutrinos will acquire a vev after spontaneous EWSB. While the vev of the right-handed sneutrino can easily take values up to the TeV-scale, the stability of the vacuum together with the smallness of the neutrino Yukawa couplings force the vevs of the left-handed sneutrinos to be several orders of magnitude smaller [13, 14]. As in the NMSSM, the couplings of the doublet-like Higgses to the gauge-singlet right-handed sneutrino provide additional contributions to the tree-level mass of the SM-like Higgs boson, relaxing the prediction of the MSSM, that it is bounded from above by the Z boson mass. Still it was shown in the NMSSM [26] that a consistent treatment of the quantum corrections is necessary for accurate Higgs mass predictions (see also Refs. [27,28,29]). In this paper we will investigate if this is also the case in the $\mu \nu \mathrm {SSM}$ and if its unique couplings generate significant corrections to the SM-like Higgs mass, that go beyond the corrections arising in the NMSSM.

The experimental accuracy of the measured mass of the observed Higgs boson has already reached the level of a precision observable, with an uncertainty of less than $300\,\mathrm {MeV}$ [3]. In the MSSM the masses of the ${{\mathcal {C}\mathcal {P}}}$-even Higgs bosons can be predicted at lowest order in terms of two SUSY parameters characterising the MSSM Higgs sector, e.g. $\tan \beta$, the ratio of the vevs of the two doublets, and the mass of the ${{\mathcal {C}\mathcal {P}}}$-odd Higgs boson, $M_A$, or the charged Higgs boson, $M_{H^\pm }$. This results in particular in an upper bound on the mass of the light ${{\mathcal {C}\mathcal {P}}}$-even Higgs boson given by the Z-boson mass. However, these relations receive large higher-order corrections. Beyond the one-loop level, the dominant two-loop corrections of ${\mathcal {O}}(\alpha _t\alpha _s)$ [30,31,32,33,34,35] and ${\mathcal {O}}(\alpha _t^2)$ [36, 37] as well as the corresponding corrections of ${\mathcal {O}}(\alpha _b\alpha _s)$ [38, 39] and ${\mathcal {O}}(\alpha _t\alpha _b)$ [38] are known since more than a decade. (Here we use $\alpha _f = (Y^f)^2/(4\pi )$, with $Y^f$ denoting the fermion Yukawa coupling.) These corrections, together with a resummation of leading and subleading logarithms from the top/scalar top sector [40] (see also [41, 42] for more details on this type of approach), a resummation of leading contributions from the bottom/scalar bottom sector [38, 39, 43,44,45,46] (see also [47, 48]) and momentum-dependent two-loop contributions [49, 50] (see also [51]) are included in the public code FeynHiggs [32, 40, 52,53,54,55,56,57,58]. A (nearly) full two-loop EP calculation, including even the leading three-loop corrections, has also been published [59, 60], which is, however, not publicly available as a computer code. Furthermore, another leading three-loop calculation of ${\mathcal {O}}(\alpha _t\alpha _s^2)$, depending on the various SUSY mass hierarchies, has been performed [61, 62], resulting in the code H3m and is now available as a stand-alone code [63]. The theoretical uncertainty on the lightest ${{\mathcal {C}\mathcal {P}}}$-even Higgs-boson mass within the MSSM from unknown higher-order contributions is still at the level of about $2{-}3\,\mathrm {GeV}$ for scalar top masses at the TeV-scale, where the actual uncertainty depends on the considered parameter region [40, 54, 64, 65].

In the NMSSM the status of the higher-order corrections to the Higgs-boson masses (and mixings) is the following. Full one-loop calculations including the momentum dependence have been performed in the ${\overline{\mathrm {DR}}}$ renormalization scheme in Refs. [66, 67], or in a mixed on-shell (OS)-${\overline{\mathrm {DR}}}$ scheme in Refs. [68,69,70]. Two-loop corrections of ${\mathcal {O}}(\alpha _t\alpha _s,\alpha _t^2)$ have been included in the NMSSM in the leading logarithmic approximation (LLA) in Refs. [71, 72]. In the EP approach at the two-loop level, the dominant ${\mathcal {O}}(\alpha _t\alpha _s, \alpha _b\alpha _s)$ in the ${\overline{\mathrm {DR}}}$ scheme became available in Ref. [66]. The two-loop corrections involving only superpotential couplings such as Yukawa and singlet interactions were given in [28]. A two-loop calculation of the ${\mathcal {O}}(\alpha _t\alpha _s)$ corrections with the top/stop sector renormalized in the OS scheme or in the ${\overline{\mathrm {DR}}}$ scheme were provided in Ref. [73]. A consistent combination of a full one-loop calculation with all corrections beyond one-loop in the MSSM approximation was given in Ref. [70], which is included in the (private) version of FeynHiggs for the NMSSM. A detailed comparison of the various higher-order corrections up to the two-loop level involving a ${\overline{\mathrm {DR}}}$ renormalization was performed in Ref. [29], and involving an OS renormalization of the top/stop sector for the ${\mathcal {O}}(\alpha _t\alpha _s)$ corrections in Ref. [74]. Accordingly, at present the theoretical uncertainties from unknown higher-order corrections in the NMSSM are expected to be still larger than for the MSSM.

In this paper we go one step beyond and investigate the scalar sector of the $\mu \nu \mathrm {SSM}$, containing (mixtures of) Higgs bosons and scalar neutrinos. As a first step we present the renormalization at the one-loop level of the neutral scalar sector in detail. Here a crucial point is that the NMSSM part of the $\mu \nu \mathrm {SSM}$ is treated exactly in the same way as in Ref. [70]. Consequently, differences (at the one-loop level) appearing for, e.g., mass relations or couplings can be directly attributed to the richer structure of the $\mu \nu \mathrm {SSM}$. As for the NMSSM in Ref. [70], the full one-loop calculation is supplemented with higher-order corrections in the MSSM limit (as provided by FeynHiggs [32, 40, 52,53,54,55,56,57,58]).² In our numerical analysis we evaluate several “representative” scenarios using the full one-loop results together with the MSSM-type higher-order contributions. Differences found w.r.t. the NMSSM can be interpreted in a twofold way. On the one hand, if non-negligible differences are found, they might serve as a probe to distinguish the two models experimentally. On the other hand, they indicate the level of theoretical uncertainties of the Higgs-boson/scalar neutrino mass calculation in the $\mu \nu \mathrm {SSM}$, which should be brought to the same level of accuracy as in the (N)MSSM.

The paper is organized as follows. In Sect. 2 we describe the $\mu \nu \mathrm {SSM}$, including the details for all sectors relevant in this paper. The full one-loop renormalization of the neutral scalar potential is presented in Sect. 3. We will establish a convenient set of free parameters and fix their counterterms in a mixed OS-${\overline{\mathrm {DR}}}$ scheme. The counterterms are calculated and applied in the renormalized ${{\mathcal {C}\mathcal {P}}}$-even and ${{\mathcal {C}\mathcal {P}}}$-odd one-loop scalar self-energies in Sect. 4. In this work we focus on the application to the renormalized ${{\mathcal {C}\mathcal {P}}}$-even self-energies, but the calculation of the renormalized ${{\mathcal {C}\mathcal {P}}}$-odd ones constitutes a good additional test for the counterterms. We also describe the incorporation of higher-order contributions taken over from the MSSM. Our numerical analysis, including an analysis of differences w.r.t. NMSSM, is presented in Sect. 5. We conclude in Sect. 6.

2 The model: $\mu \nu \mathrm {SSM}$ with one generation of right handed neutrinos

In the three-family notation of the $\mu \nu \mathrm {SSM}$ with one generation of right-handed neutrinos the superpotential is written as

$$\begin{aligned} W= & {} \epsilon _{ab} \left( Y^e_{ij} \, \hat{H}_d^a\, \hat{L}^b_i \, \hat{e}_j^c + Y^d_{ij} \, \hat{H}_d^a\, \hat{Q}^{b}_{i} \, \hat{d}_{j}^{c} + Y^u_{ij} \, \hat{H}_u^b\, \hat{Q}^{a}_{i} \, \hat{u}_{j}^{c} \right) \nonumber \\&+\,\epsilon _{ab} \left( Y^{\nu }_{i} \, \hat{H}_u^b\, \hat{L}^a_i \, \hat{\nu }^c - \lambda \, \hat{\nu }^c\, \hat{H}_u^b \hat{H}_d^a \right) + \frac{1}{3} \kappa \hat{\nu }^c\hat{\nu }^c\hat{\nu }^c. \end{aligned}$$

(1)

where $\hat{H}_d^T=(\hat{H}_d^0, \hat{H}_d^-)$ and $\hat{H}_u^T=(\hat{H}_u^+, \hat{H}_u^0)$ are the MSSM-like doublet Higgs superfields, $\hat{Q}_i^T=(\hat{u}_i, \hat{d}_i)$ and $\hat{L}_i^T=(\hat{\nu }_i, \hat{e}_i)$ are the left-chiral quark and lepton superfield doublets, and $\hat{u}_{j}^{c}$, $\hat{d}_{j}^{c}$, $\hat{e}_j^c$ and $\hat{\nu }^c$ are the right-chiral quark and lepton superfields. i and j are family indices running from one to three and $a,b=1,2$ are indices of the fundamental representation of SU(2) with $\epsilon _{ab}$ the totally antisymmetric tensor and $\varepsilon _{12}=1$. The colour indices are undisplayed. $Y^u$, $Y^d$ and $Y^e$ are the usual Yukawa couplings also present in the MSSM. The right-handed neutrino is a gauge singlet, which permits us to write the gauge-invariant trilinear self coupling $\kappa$ and the trilinear coupling with the Higgs doublets $\lambda$ in the second row, which are analogues to the couplings of the singlet in the superpotential of the trilinear NMSSM. The $\mu$-term is generated dynamically after the spontaneous EWSB, when the right-handed sneutrino obtains a vev. The $\kappa$-term forbids a global U(1) symmetry and we avoid the existence of a Goldstone boson in the ${{\mathcal {C}\mathcal {P}}}$-even sector. The remarkable difference to the NMSSM is the additional Yukawa coupling $Y^\nu _i$, which induces explicit breaking of R-parity through the $\lambda$- and $\kappa$-term, and which justifies the interpretation of the singlet superfield as a right-handed neutrino superfield. It should be pointed out that in this case lepton number is not conserved anymore, and also the flavor symmetry in the leptonic sector is broken. A more complete motivation of this superpotential can be found in Refs. [13, 14, 17].

Working in the framework of low-energy SUSY the corresponding soft SUSY-breaking Lagrangian can be written as

$$\begin{aligned}&-\mathcal {L}_{\text {soft}} = \epsilon _{ab} \left( T^e_{ij} \, H_d^a \, \widetilde{L}^b_{iL} \, \widetilde{e}_{jR}^* + T^d_{ij} \, H_d^a\, \widetilde{Q}^b_{iL} \, \widetilde{d}_{jR}^{*} \right. \nonumber \\&\left. \quad +\, T^u_{ij} \, H_u^b \widetilde{Q}^a_{iL} \widetilde{u}_{jR}^* + \text {h.c.} \right) \nonumber \\&\quad +\, \epsilon _{ab} \left( T^{\nu }_{i} \, H_u^b \, \widetilde{L}^a_{iL} \widetilde{\nu }_{R}^* - T^{\lambda } \, \widetilde{\nu }_{R}^* \, H_d^a H_u^b \right. \nonumber \\&\quad \left. +\, \frac{1}{3} T^{\kappa } \, \widetilde{\nu }_{R}^* \widetilde{\nu }_{R}^* \widetilde{\nu }_{R}^* \ + \text {h.c.}\right) \nonumber \\&\quad + \left( m_{\widetilde{Q}_L}^2\right) _{ij} \widetilde{Q}_{iL}^{a*} \widetilde{Q}^a_{jL} +\left( m_{\widetilde{u}_R}^{2}\right) _{ij} \widetilde{u}_{iR}^* \widetilde{u}_{jR} \nonumber \\&\quad +\left( m_{\widetilde{d}_R}^2\right) _{ij} \widetilde{d}_{iR}^* \widetilde{d}_{jR} + \left( m_{\widetilde{L}_L}^2\right) _{ij} \widetilde{L}_{iL}^{a*} \widetilde{L}^a_{jL}\nonumber \\&\quad + \left( m_{H_d\widetilde{L}_L}^2 \right) _{i}H_d^{a*} \widetilde{L}_{iL}^a + m_{\widetilde{\nu }_R}^2 \widetilde{\nu }_{R}^* \widetilde{\nu }_{R} + \left( m_{\widetilde{e}_R}^2\right) _{ij} \widetilde{e}_{iR}^* \widetilde{e}_{jR} \nonumber \\&\quad +\, m_{H_d}^2 {H^a_d}^* H^a_d + m_{H_u}^2 {H^a_u}^* H^a_u\nonumber \\&\quad +\, \frac{1}{2}\, \left( M_3\, {\widetilde{g}}\, {\widetilde{g}} + M_2\, {\widetilde{W}}\, {\widetilde{W}} +M_1\, {\widetilde{B}}^0 \, {\widetilde{B}}^0 + \text {h.c.} \right) . \end{aligned}$$

(2)

In the first four lines the fields denote the scalar component of the corresponding superfields. In the last line the fields denote the fermionic superpartners of the gauge bosons. The scalar trilinear parameters $T^{e,\nu ,d,u,\lambda ,\kappa }$ correspond to the trilinear couplings in the superpotential. The soft mass parameters $m_{\widetilde{Q}_L,\widetilde{u}_R,\widetilde{d}_R, \widetilde{L}_L,\widetilde{e}_R}^2$ are hermitian $3\times 3$ matrices in family space. $m_{H_d,H_u,\widetilde{\nu }_R}^2$ are the soft masses of the doublet Higgs fields and the right-handed sneutrino, and $m_{H_d\widetilde{L}_L}^2$ is a 3-dimensional vector in family space allowed by gauge symmetries since the left-handed lepton fields and the down-type Higgs field share the same quantum numbers. In the last row the parameters $M_{3,2,1}$ define Majorana masses for the gluino, wino and bino, where the summation over the gauge-group indices in the adjoint representation is undisplayed. While all the soft parameters except $m_{H_d}^2$, $m_{H_u}^2$ and $m_{\widetilde{\nu }_R}^2$ can in general be complex, they are assumed to be real in the following to avoid ${{\mathcal {C}\mathcal {P}}}$-violation. Additionally, we will neglect flavor mixing at tree-level in the squark and the quark sector, so the soft masses will be diagonal and we write $m_{\widetilde{Q}_{iL} }^2$, $m_{\widetilde{u}_{iR}}^2$ and $m_{\widetilde{d}_{iR}}^2$, as well as for the soft trilinears $T^u_i=A^u_i Y^u_i$, $T^d_i=A^d_i Y^d_i$, where the summation convention on repeated indices is not implied, and the quark Yukawas $Y^u_{ii}=Y^u_i$ and $Y^d_{ii}=Y^d_i$ are diagonal. For the sleptons we define $T^e_{ij}=A^e_{ij}Y^e_{ij}$ and $T^\nu _{i}=A^\nu _i Y^\nu _i$, again without summation over repeated indices.

Some care has to be taken with the parameters $(m_{\widetilde{L}_L}^2)_{ij}$ contributing to the tree-level neutral scalar potential, because these parameters cannot be set flavor-diagonal a priori. The reason is that during the renormalization procedure (see Sect. 3.2) the non-diagonal elements receive a counterterm. Of course, the tree-level value of the non-diagonal elements can and should be set to zero to avoid too large flavor mixing. This assures that the contributions generated by virtual corrections will always be small.

Similarly to the off-diagonal elements of the squared sfermion mass matrices, the parameters $( m_{H_d\widetilde{L}_L}^2 )_{i}$ are usually not included in the tree-level Lagrangian of the $\mu \nu \mathrm {SSM}$. In the latter case because they contribute to the minimization equations of the left-handed sneutrinos and spoil the electroweak seesaw mechanism that generates neutrino masses of the correct order of magnitude. Theoretically, the absence of these parameters mixing different fields at tree level, $( m_{H_d\widetilde{L}_L}^2 )_{i}$, $(m_{\widetilde{L}_L}^2)_{ij}$, $(m_{\widetilde{Q}_L}^2)_{ij}$, etc., can be justified by the diagonal structure of the Kähler metric in certain supergravity models, or when the dilaton field is the source of SUSY breaking in string constructions [17]. Notice also that when the down-type Higgs doublet superfield is interpreted as a fourth family of leptons, the parameters $m_{H_d\widetilde{L}_L}^2$ can be seen as non-diagonal elements of $m_{\widetilde{L}_L}^2$ [75]. Nevertheless, we include them in the soft SUSY-breaking Lagrangian in this paper, because these terms are generated at (one-)loop level, and in our renormalization approach we need the functional dependence of the scalar potential on $m_{H_d\widetilde{L}_L}^2$.

After the electroweak symmetry breaking the neutral scalar fields will acquire a vev. This includes the left- and right-handed sneutrinos, because they are not protected by lepton number conservation as in the MSSM and the NMSSM. We define the decomposition

$$\begin{aligned} H_d^0= & {} \frac{1}{\sqrt{2}} \left( H_{d}^{\mathcal {R}} + v_d + \text {i}\ H_{d}^{\mathcal {I}}\right) , \end{aligned}$$

(3)

$$\begin{aligned} H^0_u= & {} \frac{1}{\sqrt{2}} \left( H_{u}^{\mathcal {R}} + v_u +\text {i}\ H_{u}^{\mathcal {I}}\right) , \end{aligned}$$

(4)

$$\begin{aligned} \widetilde{\nu }_{R}= & {} \frac{1}{\sqrt{2}} \left( \widetilde{\nu }^{\mathcal {R}}_{R}+ v_{R} + \text {i}\ \widetilde{\nu }^{\mathcal {I}}_{R}\right) , \end{aligned}$$

(5)

$$\begin{aligned} \widetilde{\nu }_{iL}= & {} \frac{1}{\sqrt{2}} \left( \widetilde{\nu }_{iL}^{\mathcal {R}}+ v_{iL} +\text {i}\ \widetilde{\nu }_{iL}^{\mathcal {I}}\right) , \end{aligned}$$

(6)

which is valid assuming ${{\mathcal {C}\mathcal {P}}}$-conservation, as we will do throughout this paper.

2.1 The $\mu \nu \mathrm {SSM}$ Higgs potential

The neutral scalar potential $V_H$ of the $\mu \nu \mathrm {SSM}$ with one generation of right-handed neutrinos is given at tree-level with all parameters chosen to be real by the soft terms and the F- and D-term contributions of the superpotential. We find

$$\begin{aligned} V^{(0)} = V_{\text {soft}} + V_F + V_D, \end{aligned}$$

(7)

with

$$\begin{aligned} V_{\text {soft}}= & {} \left( T^{\nu }_{i} \, H_u^0\, \widetilde{\nu }_{iL} \, \widetilde{\nu }_{R}^* - T^{\lambda } \, \widetilde{\nu }_{R}^*\, H_d^0 H_u^0\phantom {\frac{1}{2}}\right. \nonumber \\&\left. +\, \frac{1}{3} T^{\kappa } \, \widetilde{\nu }_{R}^* \widetilde{\nu }_{R}^* \widetilde{\nu }_{R}^*\ + \text {h.c.}\right) \nonumber \\&+ \left( m_{\widetilde{L}_L}^2\right) _{ij} \widetilde{\nu }_{iL}^* \widetilde{\nu }_{jL} + \left( m_{H_d\widetilde{L}_L}^2 \right) _{i}H_d^{0*}\widetilde{\nu }_{iL} + m_{\widetilde{\nu }_R}^2 \widetilde{\nu }_{R}^* \widetilde{\nu }_{R} \nonumber \\&+\, m_{H_d}^2 {H^0_d}^* H^0_d+ m_{H_u}^2 {H^0_u}^* H^0_u, \end{aligned}$$

(8)

$$\begin{aligned} V_{F}= & {} \lambda ^2 H^0_{d}H_d^0{^{^*}}H^0_{u}H_u^0{^{^*}} + \lambda ^2\tilde{\nu }^{*}_{R}\tilde{\nu }_{R}H^0_{d}H_d^0{^*}\nonumber \\&+\,\lambda ^2 \tilde{\nu }^{*}_{R}\tilde{\nu }_{R} H^0_{u}H_u^0{^*} +\kappa ^2\left( \tilde{\nu }^*_{R}\right) ^2 \left( \tilde{\nu }_{R}\right) ^2\nonumber \\&-\left( \kappa \lambda \left( \tilde{\nu }^{*}_{R}\right) ^2 H_d^{0*}H_u^{0*} -Y^{\nu }_{i}\kappa \tilde{\nu }_{iL}\left( \tilde{\nu }_{R}\right) ^2H^0_{u} \right. \nonumber \\&+\, \left. Y^{\nu }_{i}\lambda \tilde{\nu }_{iL} H_d^{0*}H_{u}^{0*}H^0_{u} +{Y^{\nu }_{i}}\lambda \tilde{\nu }_{iL}^{*}\tilde{\nu }_{R}\tilde{\nu }_{R}^* H^0_{d} + \text {h.c.}\right) \nonumber \\&+\, Y^{\nu }_{i}{Y^{\nu }_{i}} \tilde{\nu }^{*}_{R} \tilde{\nu }_{R}H^0_{u}H_u^0{^*} + Y^{\nu }_{i}{Y^{\nu }_{j}}\tilde{\nu }_{iL}\tilde{\nu }_{jL}^{*}\tilde{\nu }_{R}^{*} \tilde{\nu }_{R}\nonumber \\&+\,Y^{\nu }_{i}{Y^{\nu }_{j}}\tilde{\nu }_{i}\tilde{\nu }_{j}^* H^0_{u}H_u^{0*},\end{aligned}$$

(9)

$$\begin{aligned} V_D= & {} \frac{1}{8}\left( g_1^{2}+g_2^{2}\right) \left( \widetilde{\nu }_{iL}\widetilde{\nu }_{iL}^* +H^0_d {H^0_d}^* - H^0_u {H^0_u}^* \right) ^{2}. \end{aligned}$$

(10)

Using the decomposition from Eqs. (345)–(6) the linear and bilinear terms in the fields define the tadpoles $T_{\varphi }$ and the scalar ${{\mathcal {C}\mathcal {P}}}$-even and ${{\mathcal {C}\mathcal {P}}}$-odd neutral mass matrices $m_{\varphi }^2$ and $m_{\sigma }^2$ after electroweak symmetry breaking,

$$\begin{aligned} V_H=\cdots - T_{\varphi _i}\varphi _i + \frac{1}{2} \varphi ^T m_{\varphi }^2 \varphi + \frac{1}{2} \sigma ^T m_{\sigma }^2 \sigma + \cdots , \end{aligned}$$

(11)

where we collectively denote with $\varphi ^T=(H_d^{\mathcal {R}},H_u^{\mathcal {R}}, \widetilde{\nu }_{R}^{\mathcal {R}},\widetilde{\nu }_{iL}^{\mathcal {R}})$ and $\sigma ^T=(H_d^{\mathcal {I}},H_u^{\mathcal {I}}, \widetilde{\nu }_{R}^{\mathcal {I}},\widetilde{\nu }_{iL}^{\mathcal {I}})$ the ${{\mathcal {C}\mathcal {P}}}$-even and ${{\mathcal {C}\mathcal {P}}}$-odd scalar fields. The linear terms are only allowed for ${{\mathcal {C}\mathcal {P}}}$-even fields and given by:

$$\begin{aligned} T_{H_d^{\mathcal {R}}}= & {} -m_{H_d}^2v_d - \left( m_{H_d\widetilde{L}_L}^2 \right) _{i} v_{iL} \nonumber \\&-\,\frac{1}{8}\left( g_1^2+g_2^2\right) v_d \left( v_d^2 + v_{iL}v_{iL} -v_u^2\right) \nonumber \\&-\,\frac{1}{2}\lambda \left( v_R^2+v_u^2\right) \left( \lambda v_d-v_{iL}Y^\nu _i\right) \nonumber \\&+\, \frac{1}{\sqrt{2}}T^\lambda v_R v_u+\frac{1}{2}\kappa \lambda v_R^2 v_u, \end{aligned}$$

(12)

$$\begin{aligned} T_{H_u^{\mathcal {R}}}= & {} -m_{H_u}^2v_u+ \frac{1}{8}\left( g_1^2+g_2^2\right) v_u\left( v_d^2+v_{iL}v_{iL}-v_u^2\right) \nonumber \\&-\,\frac{1}{2}\lambda ^2\left( v_d^2+v_R^2\right) +\frac{1}{\sqrt{2}}T^\lambda v_d v_R \nonumber \\&+\,\lambda v_d v_u v_{iL}Y^\nu _i+\frac{1}{2}\kappa \lambda v_d v_R^2- \frac{1}{2}\kappa v_R^2v_{iL}Y^\nu _i\nonumber \\&-\,\frac{1}{2}v_u\left( v_{iL}Y^\nu _i\right) ^2- \frac{1}{\sqrt{2}}v_Rv_{iL}T^\nu _i\nonumber \\&-\,\frac{1}{2}v_R^2v_u Y^\nu _i Y^\nu _i, \end{aligned}$$

(13)

$$\begin{aligned} T_{\widetilde{\nu }_R^{\mathcal {R}}}= & {} -m_{\widetilde{\nu }_R}^2 v_R-\frac{1}{\sqrt{2}}T^\kappa v_R^2-\kappa ^2 v_R^3 \nonumber \\&+\,\frac{1}{\sqrt{2}}T^\lambda v_d v_u-\frac{1}{2}\lambda ^2 v_R\left( v_d^2+v_u^2\right) \nonumber \\&+\,\lambda v_d v_R v_{iL}Y^\nu _i +\kappa \lambda v_d v_R v_u \nonumber \\&-\,\kappa v_R v_u v_{iL} Y^\nu _i-\frac{1}{2}v_R\left( v_{iL}Y^\nu _i\right) ^2\nonumber \\&-\,\frac{1}{\sqrt{2}}v_u v_{iL}T^\nu _i-\frac{1}{2}v_Rv_u^2 Y^\nu _i Y^\nu _i, \end{aligned}$$

(14)

$$\begin{aligned} T_{\widetilde{\nu }_{iL}^{\mathcal {R}}}= & {} -\left( m_{\widetilde{L}_L}^2\right) _{ij}v_{jL}-\left( m_{H_d\widetilde{L}_L}^2 \right) _{i}v_d \nonumber \\&-\,\frac{1}{8}\left( g_1^2+g_2^2\right) v_{iL}\left( v_d^2+v_{jL}v_{jL}-v_u^2\right) \nonumber \\&+\,\frac{1}{2}\lambda v_d v_R^2 Y^\nu _i-\frac{1}{\sqrt{2}}v_R v_u T^\nu _i-\frac{1}{2}\kappa v_R^2v_uY^\nu _i\nonumber \\&+\,\frac{1}{2}\lambda v_d v_u^2 Y^\nu _i-\frac{1}{2}v_R^2Y^\nu _i v_{jL}Y^\nu _j-\frac{1}{2}v_u^2Y^\nu _i v_{jL}Y^\nu _j.\nonumber \\ \end{aligned}$$

(15)

The tadpoles vanish in the true vacuum of the model. During the renormalization procedure they will be treated as OS parameters, i.e., finite corrections will be canceled by their corresponding counterterms. This guarantees that the vacuum is stable w.r.t. quantum corrections.

The bilinear terms

$$\begin{aligned} m_{\varphi }^2= \left( \begin{array}{c@{\quad }c@{\quad }c@{\quad }c} m_{H_{d}^{\mathcal {R}}H_{d}^{\mathcal {R}}}^{2}&{} m_{H_{d}^{\mathcal {R}}H_{u}^{\mathcal {R}}}^{2} &{} m_{H_{d}^{\mathcal {R}}\widetilde{\nu }_{R}^{\mathcal {R}}}^{2} &{} m_{H_{d}^{\mathcal {R}}\widetilde{\nu }_{jL}^{\mathcal {R}}}^{2}\\ m_{H_{u}^{\mathcal {R}}H_{d}^{\mathcal {R}}}^{2} &{} m_{H_{u}^{\mathcal {R}}H_{u}^{\mathcal {R}}}^{2}&{} m_{H_{u}^{\mathcal {R}}\widetilde{\nu }_{R}^{\mathcal {R}}}^{2} &{} m_{H_{u}^{\mathcal {R}}\widetilde{\nu }_{jL}^{\mathcal {R}}}^{2}\\ m_{\widetilde{{\nu }}^{\mathcal {R}}_{R} H_{d}^{\mathcal {R}}}&{} m_{\widetilde{{\nu }}^{\mathcal {R}}_{R} H_{u}^{\mathcal {R}}}&{} m_{\widetilde{{\nu }}^{\mathcal {R}}_{R} \widetilde{{\nu }}^{\mathcal {R}}_{R}}^{2} &{} m_{\widetilde{{\nu }}^{\mathcal {R}}_{R} \widetilde{{\nu }}^{\mathcal {R}}_{jL}}^{2}\\ m_{\widetilde{\nu }_{iL}^{\mathcal {R}} H_{d}^{\mathcal {R}}}^{2} &{} m_{\widetilde{\nu }_{iL}^{\mathcal {R}} H_{u}^{\mathcal {R}}}^{2} &{} m_{\widetilde{\nu }_{iL}^{\mathcal {R}} \widetilde{\nu }^{\mathcal {R}}_{R}}^{2} &{} m_{\widetilde{\nu }_{iL}^{\mathcal {R}} \widetilde{\nu }_{jL}^{\mathcal {R}}}^{2} \end{array} \right) , \end{aligned}$$

(16)

and

$$\begin{aligned} m^2_{\sigma }= \left( \begin{array}{c@{\quad }c@{\quad }c@{\quad }c} m_{H_{d}^{\mathcal {I}}H_{d}^{\mathcal {I}}}^{2} &{} m_{H_{d}^{\mathcal {I}}H_{u}^{\mathcal {I}}}^{2} &{} m_{H_{d}^{\mathcal {I}}\widetilde{\nu }_{R}^{\mathcal {I}}}^{2} &{} m_{H_{d}^{\mathcal {I}}\widetilde{\nu }_{jL}^{\mathcal {I}}}^{2}\\ m_{H_{u}^{\mathcal {I}}H_{d}^{\mathcal {I}}}^{2} &{} m_{H_{u}^{\mathcal {I}}H_{u}^{\mathcal {I}}}^{2}&{} m_{H_{u}^{\mathcal {I}}\widetilde{\nu }_{R}^{\mathcal {I}}}^{2} &{} m_{H_{u}^{\mathcal {I}}\widetilde{\nu }_{jL}^{\mathcal {I}}}^{2}\\ m_{\widetilde{{\nu }}^{\mathcal {I}}_{R} H_{d}^{\mathcal {I}}}^2&{} m_{\widetilde{{\nu }}^{\mathcal {I}}_{R} H_{u}^{\mathcal {I}}}^2&{} m_{\widetilde{{\nu }}^{\mathcal {I}}_{R} \widetilde{{\nu }}^{\mathcal {I}}_{R}}^{2} &{} m_{\widetilde{{\nu }}^{\mathcal {I}}_{R} \widetilde{{\nu }}^{\mathcal {I}}_{jL}}^{2}\\ m_{\widetilde{\nu }_{iL}^{\mathcal {I}} H_{d}^{\mathcal {I}}}^{2} &{} m_{\widetilde{\nu }_{iL}^{\mathcal {I}} H_{u}^{\mathcal {I}}}^{2} &{} m_{\widetilde{\nu }_{iL}^{\mathcal {I}} \widetilde{\nu }^{\mathcal {I}}_{R}}^{2} &{} m_{\widetilde{\nu }_{iL}^{\mathcal {I}} \widetilde{\nu }_{jL}^{\mathcal {I}}}^{2} \end{array} \right) , \end{aligned}$$

(17)

are $6\times 6$ matrices in family space whose rather lengthy entries are given in the Appendices A.1 and A.2. We transform to the mass eigenstate basis of the ${{\mathcal {C}\mathcal {P}}}$-even scalars through a unitary transformation defined by the matrix $U^H$, that diagonalizes the mass matrix $m_{\varphi }^2$,

$$\begin{aligned} U^H m^2_{\varphi }\ {U^H}^{^T}= m^2_{h}, \end{aligned}$$

(18)

with

$$\begin{aligned} \varphi = {U^H}^{^T} h, \end{aligned}$$

(19)

where the $h_i$ are the ${{\mathcal {C}\mathcal {P}}}$-even scalar fields in the mass eigenstate basis. Without ${{\mathcal {C}\mathcal {P}}}$-violation in the scalar sector the matrix $U^H$ is real. Similarly, for the ${{\mathcal {C}\mathcal {P}}}$-odd scalar we define the rotation matrix $U^A$, that diagonalizes the mass matrix $m_{\sigma }^2$,

$$\begin{aligned} U^A m^2_{\sigma }\ {U^A}^{^T}= m^2_{A}, \quad \text {with } \sigma ={U^A}^T A. \end{aligned}$$

(20)

Because of the smallness of the neutrino Yukawa couplings $Y^\nu _i$, which also implies that the left-handed sneutrino vevs $v_{iL}$ have to be small, so that the tadpole coefficients vanish at tree-level [14], the mixing of the left-handed sneutrinos with the doublet fields and the singlet will be small.

It is a well known fact that the quantum corrections to the Higgs potential are highly significant in supersymmetric models, see e.g. Refs. [64, 76, 77] for reviews. As in the NMSSM [7], the upper bound on the lowest Higgs mass squared at tree-level is relaxed through additional contributions from the singlet [14];

$$\begin{aligned} M_Z^2 \left( \cos ^2 2\beta + \frac{2\lambda ^2}{g_1^2+g_2^2}\sin ^2 2\beta \right) . \end{aligned}$$

(21)

Nevertheless, quantum corrections were still shown to contribute significantly especially in the prediction of the SM-like Higgs boson mass [26, 68, 70, 74, 78,79,80,81]. In this paper we will investigate how important the unique loop corrections of the $\mu \nu \mathrm {SSM}$ beyond the NMSSM are in realistic scenarios. Before that we briefly describe the other relevant sectors of the $\mu \nu \mathrm {SSM}$.

2.2 Squark sector

The numerically most important one-loop corrections to the scalar potential are expected from the stop/top-sector, analogous to the (N)MSSM [79,80,81,82,83,84] due to the huge Yukawa coupling of the (scalar) top. The tree-level mass matrices of the squarks differ slightly from the ones in the MSSM. Neglecting flavor mixing in the squark sector, one finds for the up-type squark mass matrix $M^{\widetilde{u}_i}$ of flavor i,

$$\begin{aligned} M^{\widetilde{u}_i}_{11}= & {} m_{\widetilde{Q}_{iL}}^2 + \frac{1}{24}(3g_2^{2}-g_1^2)(v_d^2+v_{jL}v_{jL}-v_u^2)+\frac{1}{2}v_u^2{Y^{u}_i}^2\nonumber \\ \end{aligned}$$

(22)

$$\begin{aligned} M^{\widetilde{u}_i}_{12}= & {} \frac{1}{2}(\sqrt{2}A^u_i v_u + v_RY^u v_{jL}Y^\nu _j -\lambda v_d v_R) \end{aligned}$$

(23)

$$\begin{aligned} M^{\widetilde{u}_i}_{22}= & {} m_{\widetilde{u}_{iR}}^2+\frac{1}{6}g_1^2(v_d^2+v_{jL}v_{jL}-v_u^2)+\frac{1}{2}v_u^2{Y^u_i}^2. \end{aligned}$$

(24)

It should be noted that in the non-diagonal element explicitly appear the neutrino Yukawa couplings. This term arises in the F-term contributions of the squark potential through the quartic coupling of up-type quarks and one left-handed and the right-handed sneutrino after EWSB. The mass eigenstates $\widetilde{u}_{i1}$ and $\widetilde{u}_{i2}$ are obtained by the unitary transformation

$$\begin{aligned} \begin{pmatrix} \widetilde{u}_{i1} \\ \widetilde{u}_{i2} \end{pmatrix} =U^{\widetilde{u}}_i \begin{pmatrix} \widetilde{u}_{iL} \\ \widetilde{u}_{iR} \end{pmatrix}, \quad U^{\widetilde{u}}_i{U^{\widetilde{u}}_i}^\dagger =\mathbb {1}. \end{aligned}$$

(25)

Similarly, for the down-type squarks it is

$$\begin{aligned} M^{\widetilde{d}_i}_{11}= & {} m_{\widetilde{Q}_{iL}}^2 -\frac{1}{24}(3g_2^{2}+g_1^2)(v_d^2+v_{jL}v_{jL}-v_u^2)\nonumber \\&-\,\frac{1}{2}v_d^2{Y^{d}_i}^2 \end{aligned}$$

(26)

$$\begin{aligned} M^{\widetilde{d}_i}_{12}= & {} \frac{1}{2}(\sqrt{2}A^d_i v_d -\lambda v_d v_R) \end{aligned}$$

(27)

$$\begin{aligned} M^{\widetilde{d}_i}_{22}= & {} m_{\widetilde{d}_{iR}}^2- \frac{1}{12}g_1^2(v_d^2+v_{jL}v_{jL}-v_u^2)+\frac{1}{2}v_d^2{Y^d_i}^2. \end{aligned}$$

(28)

The mass eigenstates $\widetilde{d}_{i1}$ and $\widetilde{d}_{i2}$ are obtained by the unitary transformation

$$\begin{aligned} \begin{pmatrix} \widetilde{d}_{i1} \\ \widetilde{d}_{i2} \end{pmatrix} =U^{\widetilde{d}}_i \begin{pmatrix} \widetilde{d}_{iL} \\ \widetilde{d}_{iR} \end{pmatrix}, \quad U^{\widetilde{d}}_i{U^{\widetilde{d}}_i}^\dagger =\mathbb {1}. \end{aligned}$$

(29)

2.3 Charged scalar sector

Since R-parity, lepton number and lepton-flavor are broken, the six charged left- and right-handed sleptons mix with each other and with the two charged scalars from the Higgs doublets. In the basis $C^T= ({H^-_d}^*,{H^+_u},\widetilde{e}_{iL}^*,\widetilde{e}_{jR}^*)$ we find the following mass terms in the Lagrangian:

$$\begin{aligned} {\mathcal {L}}_{C} \; = \; -{C^*}^T {m}^2_{H^+} C, \end{aligned}$$

(30)

where ${m}^2_{H^+}$ assuming ${{\mathcal {C}\mathcal {P}}}$ conservation is a symmetric matrix of dimension 8,

$$\begin{aligned} m_{H^+}^2= \left( \begin{array}{c@{\quad }c@{\quad }c@{\quad }c} m_{H_{d}^-{H^{-}_d}^{*}}^{2} &{} m_{H_{d}^- H_{u}^+}^{2} &{} m_{{H_d^-} \widetilde{e}^*_{jL}}^2 &{} m_{{H_d^-} \widetilde{e}^*_{jR}}^2 \\ m_{{H_{u}^+}^* {H_d^-}^*}^{2} &{} m_{{H^{+}_u}^{*} H_{u}^{+}}^{2} &{} m_{{H_u^+}^*\widetilde{e}^*_{jL}}^{2} &{} m_{{H_u^+}^*\widetilde{e}^*_{jR}}^{2} \\ m_{\widetilde{e}_{iL} {{H^{-}_d}}^{*}}^2 &{} m_{\widetilde{e}_{iL} H_u^+}^2 &{} m_{\widetilde{e}_{iL} \widetilde{e}_{jL}^{*}}^{2} &{} m_{\widetilde{e}_{iL} \widetilde{e}_{jR}^{*}}^{2}\\ m_{\widetilde{e}_{iR} {{H^{-}_d}}^{*}}^2 &{} m_{\widetilde{e}_{iR} H_u^+}^2 &{} m_{\widetilde{e}_{iR} \widetilde{e}_{jL}^{*}}^{2} &{} m_{\widetilde{e}_{iR} \widetilde{e}_{jR}^{*}}^{2} \end{array} \right) . \nonumber \\ \end{aligned}$$

(31)

The entries are given in Appendix A.3. The mass matrix is diagonalized by an orthogonal matrix $U^+$:

$$\begin{aligned} U^+ m^2_{H^+}\ {U^+}^{^T} = \left( m^2_{H^+}\right) ^{\text {diag}}, \end{aligned}$$

(32)

where the diagonal elements of $(m^2_{H^+})^{\text {diag}}$ are the squared masses of the mass eigenstates

$$\begin{aligned} H^+=U^+\; C, \end{aligned}$$

(33)

which include the charged Goldstone boson $H^+_1=G^\pm _0$.

2.4 Charged fermion sector

The charged leptons mix with the charged gauginos and the charged higgsinos. Following the notation of Ref. [17] we write the relevant part of the Lagrangian in terms of two-component spinors $(\chi ^-)^T = ({({e_{iL})}^{c}}^{^*}, \widetilde{W}^-, \widetilde{H}^-_d)$ and $(\chi ^+)^T = (({e_{jR}})^c, \widetilde{W}^+, \widetilde{H}^+_u)$:

$$\begin{aligned} {\mathcal {L}}_{\chi ^\pm } = -({\chi ^{-}})^T {m}_{e} \chi ^+ + {\mathrm {h.c.}}. \end{aligned}$$

(34)

The $5\times 5$ mixing matrix $m_e$ is defined by

$$\begin{aligned} m_e= \left( \begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} \frac{v_d Y^e_{11}}{\sqrt{2}} &{} \frac{v_d Y^e_{12}}{\sqrt{2}} &{} \frac{v_d Y^e_{13}}{\sqrt{2}} &{} \frac{g_2 v_{1L}}{\sqrt{2}} &{} -\frac{v_R Y^\nu _1}{\sqrt{2}} \\ \frac{v_d Y^e_{21}}{\sqrt{2}} &{} \frac{v_d Y^e_{22}}{\sqrt{2}} &{} \frac{v_d Y^e_{23}}{\sqrt{2}} &{} \frac{g_2 v_{2L}}{\sqrt{2}} &{} -\frac{v_R Y^\nu _2}{\sqrt{2}} \\ \frac{v_d Y^e_{31}}{\sqrt{2}} &{} \frac{v_d Y^e_{32}}{\sqrt{2}} &{} \frac{v_d Y^e_{33}}{\sqrt{2}} &{} \frac{g_2 v_{3L}}{\sqrt{2}} &{} -\frac{v_R Y^\nu _3}{\sqrt{2}} \\ 0 &{} 0 &{} 0 &{} M_2 &{} \frac{g_2 v_{u}}{\sqrt{2}} \\ -\frac{v_{iL}Y^e_{1i}}{\sqrt{2}} &{} -\frac{v_{iL}Y^e_{2i}}{\sqrt{2}} &{} -\frac{v_{iL}Y^e_{3i}}{\sqrt{2}} &{} \frac{g_2 v_{d}}{\sqrt{2}} &{} \frac{\lambda v_R}{\sqrt{2}} \end{array}\right) . \end{aligned}$$

(35)

It is diagonalized by two unitary matrices $U^e_L$ and $U^e_R$:

$$\begin{aligned} {U_R^e}^{^*} m_{e} {U_L^e}^{^\dagger } = m_{e}^{\text {diag}}, \end{aligned}$$

(36)

where $m_{e}^{\text {diag}}$ contains the masses of the charged fermions in the mass eigenstate base

$$\begin{aligned} \chi ^{+}= & {} {U_L^e}^{^\dagger } \lambda ^+, \end{aligned}$$

(37)

$$\begin{aligned} \chi ^{-}= & {} {U_R^e}^{^\dagger } \lambda ^-. \end{aligned}$$

(38)

The smallness of the left-handed sneutrino vevs in comparison to the doublet ones assures the decoupling of the three leptons from the Higgsino and the wino.

2.5 Neutral fermion sector

The three left-handed neutrinos and the right-handed neutrino mix with the neutral Higgsinos and gauginos. Again, following Ref. [17] we write the relevant part of the Lagrangian in terms of two-component spinors $({\chi ^{0}})^T=({(\nu _{iL})^{c}}^{^*},\widetilde{B}^0, \widetilde{W}^{0},\widetilde{H}_{d}^0,\widetilde{H}_{u}^0,\nu _{R}^*)$ as

$$\begin{aligned} {\mathcal {L}}_{\chi ^0} =-\frac{1}{2} ({\chi ^{0}})^T {m}_{\nu } \chi ^0 + {\mathrm {h.c.}}, \end{aligned}$$

(39)

where ${m}_{\nu }$ is the $8\times 8$ symmetric mass matrix. The neutral fermion mass matrix is determined by

$$\begin{aligned} {m}_{\nu }= \left( \begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} 0 &{} 0 &{} 0 &{} -\frac{g_1 v_{1L}}{2} &{} \frac{g_2 v_{1L}}{2} &{} 0 &{} \frac{v_{R} Y^\nu _1}{\sqrt{2}} &{} \frac{v_{u}Y^\nu _1}{\sqrt{2}} \\ 0 &{} 0 &{} 0 &{} -\frac{g_1 v_{2L}}{2} &{} \frac{g_2 v_{2L}}{2} &{} 0 &{} \frac{v_{R} Y^\nu _2}{\sqrt{2}} &{} \frac{v_{u}Y^\nu _2}{\sqrt{2}} \\ 0 &{} 0 &{} 0 &{} -\frac{g_1 v_{3L}}{2} &{} \frac{g_2 v_{3L}}{2} &{} 0 &{} \frac{v_{R} Y^\nu _3}{\sqrt{2}} &{} \frac{v_{u}Y^\nu _3}{\sqrt{2}} \\ -\frac{g_1 v_{1L}}{2} &{} -\frac{g_1 v_{2L}}{2} &{} -\frac{g_1 v_{3L}}{2} &{} M_1 &{} 0 &{} -\frac{g_1 v_{d}}{2} &{} \frac{g_1 v_{u}}{2} &{} 0 \\ \frac{g_2 v_{1L}}{2} &{} \frac{g_2 v_{2L}}{2} &{} \frac{g_2 v_{3L}}{2} &{} 0 &{} M_2 &{} \frac{g_2 v_{d}}{2} &{} -\frac{g_2 v_{u}}{2} &{} 0 \\ 0 &{} 0 &{} 0 &{} -\frac{g_1 v_{d}}{2} &{} \frac{g_2 v_{d}}{2} &{} 0 &{} -\frac{\lambda v_{R}}{\sqrt{2}} &{} -\frac{\lambda v_{u}}{\sqrt{2}} \\ \frac{v_R Y^\nu _1}{\sqrt{2}} &{} \frac{v_R Y^\nu _2}{\sqrt{2}} &{} \frac{v_R Y^\nu _3}{\sqrt{2}} &{} \frac{g_1 v_u}{2} &{} -\frac{g_2 v_u}{2} &{} -\frac{\lambda v_R}{\sqrt{2}} &{} 0 &{} \frac{-\lambda v_d + v_{kL}Y^\nu _k}{\sqrt{2}} \\ \frac{v_u Y^\nu _1}{\sqrt{2}} &{} \frac{v_u Y^\nu _2}{\sqrt{2}} &{} \frac{v_u Y^\nu _3}{\sqrt{2}} &{} 0 &{} 0 &{} -\frac{\lambda v_u}{\sqrt{2}} &{} \frac{-\lambda v_d +v_{iL}Y^\nu _i}{\sqrt{2}} &{} \sqrt{2}\kappa v_R \end{array}\right) . \end{aligned}$$

(40)

Because of the Majorana nature of the neutral fermions we can diagonalize ${m}_{\nu }$ with the help of just a single – but complex – unitary matrix $U^V$,

$$\begin{aligned} {U^V}^{^*} m_{\nu }\ {U^V}^{^\dagger } = m_{\nu }^{\text {diag}}, \end{aligned}$$

(41)

with

$$\begin{aligned} \chi ^{0} = {U^V}^{^\dagger } \lambda ^0, \end{aligned}$$

(42)

where $\lambda ^0$ are the two-component spinors in the mass basis. The eigenvalues of the diagonalized mass matrix $m_{\nu }^{\text {diag}}$ are the masses of the neutral fermions in the mass eigenstate basis. It turns out that the matrix $m_\nu$ is of rank six, so it can only generate a single neutrino mass at tree-level.³ The remaining two light neutrino masses can be generated by loop-effects.

Table 1 Set of independent parameters initially entering the tree-level Higgs potential of the $\mu \nu \mathrm {SSM}$ in the first row, and final choice of free parameters after the substitutions mentioned in the text

3 Renormalization of the Higgs potential at one-loop

The first step in renormalizing the neutral scalar potential is to choose the set of free parameters. These free parameters will receive a counter term fixed by consistent renormalization conditions to cancel all ultraviolet divergences that are produced by higher-order corrections.

At tree-level the relevant part of the Higgs potential $V_H$ is given by the tadpole coefficients Eqs. (12)–(15) and the ${{\mathcal {C}\mathcal {P}}}$-even and ${{\mathcal {C}\mathcal {P}}}$-odd mass matrix elements in Eqs. (16) and (17). The following parameters appear in the Higgs potential:

• Scalar soft masses: $m_{H_d}^2$, $m_{H_u}^2$, $m_{\widetilde{\nu }_R}^2$, $\left( m_{\widetilde{L}_L}^2 \right) _{ij}$, $\left( m_{H_d\widetilde{L}_L}^2 \right) _{i}$    (12 parameters)

• Vacuum expectation values: $v_d$, $v_u$, $v_R$, $v_{iL}$    (6 parameters)

• Gauge couplings: $g_1$, $g_2$    (2 parameters)

• Superpotential parameters: $\lambda$, $\kappa$, $Y^\nu _i$    (5 parameters)

• Soft trilinear couplings: $T^\lambda$, $T^\kappa$, $T^\nu _i$    (5 parameters)

The complexity of the $\mu \nu \mathrm {SSM}$ Higgs scalar sector becomes evident when we compare the numbers of free parameters (30) with the one in the real MSSM (7) [55] and the NMSSM (12) [26]. While the number of free parameters is fixed, we are free to replace some of the parameters by physical parameters. We chose to make the following replacements:

The soft masses $m_{H_d}^2$, $m_{H_u}^2$, $m_{\widetilde{\nu }_R}^2$, and the diagonal elements of the matrix $m_{\widetilde{L}_L}^2$ will be replaced by the tadpole coefficients. The substitution is defined by the tadpole Eqs. (12)–(15) solved for the soft mass parameters just mentioned. This will give us the possibility to define the renormalization scheme in a way that the true vacuum is not spoiled by the higher-order corrections. The Higgs doublet vevs $v_d$ and $v_u$ will be replaced by the MSSM-like parameters $\tan \beta$ and v according to

$$\begin{aligned} \tan \beta =\frac{v_u}{v_d} \quad \text {and} \quad v^2=v_d^2+v_u^2+v_{iL}v_{iL}. \end{aligned}$$

(43)

Note that the definition of $v^2$ differs from the one in the MSSM by the term $v_{iL}v_{iL}$. This allows to maintain the relations between $v^2$ and the gauge boson masses as they are in the MSSM. Numerically, the difference in the definition of $v^2$ is negligible, since the $v_{iL}$ are of the order of $10^{-4}\,\mathrm {GeV}$ in realistic scenarios. Analytically, however, maintaining the functional form of $\tan \beta$ as it is in the (N)MSSM is convenient to facilitate the comparison of the quantum corrections in the $\mu \nu \mathrm {SSM}$ and the NMSSM. In particular, we can still express the one-loop counterterm of $\tan \beta$ without having to include the counterterms for the left-handed sneutrino vevs. For the vev of the right-handed sneutrino we chose to make the same substitution as was done in previous calculations in the NMSSM [26]

$$\begin{aligned} \mu =\frac{v_R \lambda }{\sqrt{2}}, \end{aligned}$$

(44)

where we make use of the fact that when the sneutrino obtains the vev, the $\mu$-term of the MSSM is dynamically generated. The gauge couplings $g_1$ and $g_2$ will be replaced by the gauge boson masses $M_{W}$ and $M_Z$ via the definitions

$$\begin{aligned} M_{W}^2=\frac{1}{4}g_2^2v^2 \quad \text {and} \quad M_Z^2=\frac{1}{4}\left( g_1^2+g_2^2\right) v^2. \end{aligned}$$

(45)

This is reasonable because the gauge boson masses are well measured physical observables, so we can define them as OS parameters. Interestingly, the mass counterterm for $M_{W}^2$ drops out at one-loop, but it will contribute in the definition of the counterterm for $v^2$, so it is not a redundant parameter. For the soft trilinear couplings we chose to adopt the redefinitions

$$\begin{aligned} T^\lambda = A^\lambda \lambda , \quad T^\kappa = A^\kappa \kappa , \quad T^\nu _i=A^\nu _i Y^\nu _i. \end{aligned}$$

(46)

The reparametrization from the initial to the physical set of independent parameters is summarized in Table 1.

In the following we will regard the entries of the neutral scalar mass matrix as functions of the final set of parameters,

$$\begin{aligned} m_{\varphi }^2= & {} m_{\varphi }^2\left( M_Z^2, v^2, \tan \beta , \lambda , \dots \right) , \end{aligned}$$

(47)

$$\begin{aligned} m_{\sigma }^2= & {} m_{\sigma }^2\left( M_Z^2, v^2, \tan \beta , \lambda , \dots \right) , \end{aligned}$$

(48)

and we define their renormalization as

$$\begin{aligned} m_{\varphi }^2\rightarrow & {} m_{\varphi }^2+\delta m_{\varphi }^2, \end{aligned}$$

(49)

$$\begin{aligned} m_{\sigma }^2\rightarrow & {} m_{\sigma }^2+\delta m_{\sigma }^2. \end{aligned}$$

(50)

The mass counterterms $\delta m_{\varphi }^2$ and $\delta m_{\sigma }^2$ enter the renormalized one-loop scalar self-energies. They have to be expressed as a linear combination of the counterterms of the independent parameters. We define their one-loop renormalization as

$$\begin{aligned} \begin{aligned} T_{H_d^{\mathcal {R}}}&\rightarrow T_{H_d^{\mathcal {R}}}+\delta T_{H_d^{\mathcal {R}}}, \\ T_{H_u^{\mathcal {R}}}&\rightarrow T_{H_u^{\mathcal {R}}}+\delta T_{H_u^{\mathcal {R}}}, \\ T_{\widetilde{\nu }_{R}^{\mathcal {R}}}&\rightarrow T_{\widetilde{\nu }_{R}^{\mathcal {R}}}+\delta T_{\widetilde{\nu }_{R}^{\mathcal {R}}}, \\ T_{\widetilde{\nu }_{iL}^{\mathcal {R}}}&\rightarrow T_{\widetilde{\nu }_{iL}^{\mathcal {R}}}+ \delta T_{\widetilde{\nu }_{iL}^{\mathcal {R}}}, \\ {m_{\widetilde{L}_L}^2}_{i\ne j}&\rightarrow {m_{\widetilde{L}_L}^2}_{i\ne j}+ \delta {m_{\widetilde{L}_L}^2}_{i\ne j}, \\ {m_{H_d\widetilde{L}_L}^2}_i&\rightarrow {m_{H_d\widetilde{L}_L}^2}_i+\delta {m_{H_d\widetilde{L}_L}^2}_i, \end{aligned} \quad \begin{aligned} \tan \beta&\rightarrow \tan \beta +\delta \tan \beta , \\ v^2&\rightarrow v^2+\delta v^2, \\ \mu&\rightarrow \mu +\delta \mu , \\ v_{iL}^2&\rightarrow v_{iL}^2+\delta v_{iL}^2, \\ M_{W}^2&\rightarrow M_{W}^2 +\delta M_{W}^2, \\ M_Z^2&\rightarrow M_Z^2 +\delta M_Z^2, \\ \end{aligned} \quad \begin{aligned} \lambda&\rightarrow \lambda + \delta \lambda , \\ \kappa&\rightarrow \kappa + \delta \kappa , \\ Y^\nu _i&\rightarrow Y^\nu _i + \delta Y^\nu _i, \\ A^\lambda&\rightarrow A^\lambda +\delta A^\lambda , \\ A^\kappa&\rightarrow A^\kappa + \delta A^\kappa , \\ A^\nu _i&\rightarrow A^\nu _i + \delta A^\nu _i. \end{aligned} \end{aligned}$$

(51)

Since the $\mu \nu \mathrm {SSM}$ is a renormalizable theory, the divergent parts of the counterterms are fixed to cancel the UV divergences. The finite pieces, and thus the meaning of the parameters have to be fixed by renormalization conditions. We will adopt a mixed renormalization scheme, where tadpoles and gauge boson masses are fixed OS, and the other parameters are fixed in the $\overline{\text {DR}}$ scheme. The exact renormalization conditions will be given in Sect. 3.2. The dependence of the mass counterterms $\delta m_{\varphi }^2$ and $\delta m_{\sigma }^2$ on the counterterms of the free parameters is given at one-loop by

$$\begin{aligned} \delta m_{\varphi }^2= & {} \sum _{X\in \text {Free param.}} \left( \frac{\partial }{\partial X} m_{\varphi }^2 \right) \delta X, \nonumber \\ \delta m_{\sigma }^2= & {} \sum _{X\in \text {Free param.}} \left( \frac{\partial }{\partial X} m_{\sigma }^2 \right) \delta X. \end{aligned}$$

(52)

In our calculation the mixing matrices are defined in a way to diagonalize the renormalized mass matrices, so they do not have to be renormalized, because they are defined exclusively by renormalized quantities. The expressions for the counterterms of the scalar mass matrices in the mass eigenstate basis are then simply

$$\begin{aligned} \delta m_{h}^2=U^H \delta m_{\varphi }^2 {U^H}^T, \quad \delta m_{A}^2=U^A \delta m_{\sigma }^2{U^A}^T. \end{aligned}$$

(53)

It should be noted at this point that the counterterm matrices in the mass eigenstate basis $\delta m_{h}^2$ and $\delta m_{A}^2$ are not diagonal, as they would be in a purely OS renormalization procedure, which is often used in theories with flavor mixing [85].

In the following chapter we will discuss the field renormalization, which is necessary to obtain finite scalar self-energies at arbitrary momentum.

3.1 Field renormalization

We write the renormalization of the neutral scalar-component fields as

$$\begin{aligned} \begin{pmatrix} H_d \\ H_u \\ \widetilde{\nu }_R \\ \widetilde{\nu }_{iL} \end{pmatrix} \rightarrow \sqrt{Z} \begin{pmatrix} H_d \\ H_u \\ \widetilde{\nu }_R \\ \widetilde{\nu }_{iL} \end{pmatrix}= \left( \mathbb {1} + \frac{1}{2} \delta Z \right) \begin{pmatrix} H_d \\ H_u \\ \widetilde{\nu }_R \\ \widetilde{\nu }_{iL} \end{pmatrix}, \end{aligned}$$

(54)

where $\sqrt{Z}$ and $\delta Z$ are $6\times 6$ dimensional matrices and the equal sign is valid at one-loop. It should be emphasized that in contrast to the MSSM and the NMSSM these matrices cannot be made diagonal even in the interaction basis. The reason is that the $\mu \nu \mathrm {SSM}$ explicitly breaks lepton number and lepton flavor, so the fields $H_d$ and $\widetilde{\nu }_{iL}$ share exactly the same quantum numbers and kinetic mixing terms are already generated at one-loop order.

Fig. 1

Generic Feynman diagrams for the tadpoles $T_{h_i}$

For the ${{\mathcal {C}\mathcal {P}}}$-even and ${{\mathcal {C}\mathcal {P}}}$-odd neutral scalar fields the definition in Eq. (54) implies the following field renormalization in the mass eigenstate basis:

$$\begin{aligned} h \rightarrow \left( \mathbb {1} + \frac{1}{2} \delta Z^H \right) h, \quad A \rightarrow \left( \mathbb {1} + \frac{1}{2} \delta Z^A \right) A, \end{aligned}$$

(55)

with

$$\begin{aligned} \delta Z^H = U^H \left( \delta Z \right) {U^H}^T \quad \text {and} \quad \delta Z^A = U^A \left( \delta Z \right) {U^A}^T. \end{aligned}$$

(56)

As renormalization conditions for the field renormalization counterterms we chose to adopt the $\overline{\text {DR}}$ scheme. We calculate the UV-divergent part of the derivative of the scalar ${{\mathcal {C}\mathcal {P}}}$-even self-energies in the interaction basis and define

$$\begin{aligned} \delta Z_{ij}=-\left. \frac{d}{dp^2}\Sigma _{\varphi _i \varphi _j} \right| ^{\mathrm{div}}. \end{aligned}$$

(57)

Here $^{{\mathrm{div}}}$ denotes taking the divergent part only, proportional to $\Delta$,

$$\begin{aligned} \Delta = \frac{1}{\varepsilon }-\gamma _E+\ln {4\pi }, \end{aligned}$$

(58)

where loop integral are solved in $4-2\varepsilon$ dimensions and $\gamma _E=0.5772\dots$ is the Euler–Mascheroni constant. Since the field renormalization constants contribute only via divergent parts, they do not contribute to the finite result after canceling divergences in the self-energies. As regularization scheme we chose dimensional reduction [86, 87], which was shown to be SUSY conserving at one-loop [88]. In contrast to the OS renormalization scheme our field renormalization matrices are hermitian. This holds also true for the field renormalization in the mass eigenstate basis, because as already mentioned the rotations in Eqs. (18) and (20) diagonalize the renormalized tree-level scalar mass matrices, so Eq. (56) do not introduce non-hermitian parts into the field renormalization, that would have to be canceled by a renormalization of the mixing matrices $U^H$ and $U^A$ themselves.

In Appendix B.1 we list our field renormalization counterterms $\delta Z_{ij}$ in terms of the divergent quantity $\Delta$. Note that the field counterterms mixing the down-type Higgs and the left-handed sleptons are proportional to the neutrino Yukawa couplings $Y^\nu _i$, while the counterterms mixing different flavors of left-handed sneutrinos contain terms proportional to non-diagonal lepton Yukawa couplings $Y^e$ and terms proportional to $Y^\nu _i Y^\nu _j$. This is why their numerical impact is negligible, but they are needed for a consistent renormalization of the scalar self-energies.

3.2 Renormalization conditions for free parameters

In this section we describe our choice for the renormalization conditions, where we stick to the one-loop level everywhere. We start with the OS conditions for the gauge boson mass parameters and the tadpole coefficients followed by our definitions for the ${\overline{\mathrm {DR}}}$ renormalized parameters.

The SM gauge boson masses are renormalized OS requiring

$$\begin{aligned} \text {Re}\left[ {\hat{\Sigma }_{ZZ}}^T\left( M_Z^2 \right) \right] =0 \quad \text {and} \quad \text {Re}\left[ {\hat{\Sigma }_{WW}}^T\left( M_{W}^2 \right) \right] =0, \end{aligned}$$

(59)

where $\hat{\Sigma }^T$ stands for the transverse part of the renormalized gauge boson self-energy. For their mass counterterms these conditions yield

$$\begin{aligned} \delta M_Z^2= & {} \text {Re}\left[ {\Sigma }_{ZZ}^T\left( M_Z^2 \right) \right] \quad \text {and} \nonumber \\ \delta M_{W}^2= & {} \text {Re}\left[ {\Sigma }_{WW}^T\left( M_{W}^2 \right) \right] . \end{aligned}$$

(60)

Here the ${\Sigma }^T$ (without the hat) denote the transverse part of the unrenormalized gauge boson self-energies.

For the tadpole coefficients $T_{\varphi _i}$ the OS conditions read

$$\begin{aligned} T_{\varphi _i}^{(1)}+\delta T_{\varphi _i}=0, \end{aligned}$$

(61)

where $T_{\varphi _i}^{(1)}$ are the one-loop contributions to the linear terms of the scalar potential, stemming from tadpole diagrams shown in Fig. 1. The tadpole diagrams are calculated in the mass eigenstate basis h. The one-loop tadpole contributions in the interaction basis $\varphi$ are then obtained by the rotation

$$\begin{aligned} T_\varphi ^{(1)} = {U^H}^T T_h^{(1)}. \end{aligned}$$

(62)

Accordingly we find for the one-loop tadpole counterterms

$$\begin{aligned} \delta T_{\varphi _i}=-T_{\varphi _i}^{(1)}. \end{aligned}$$

(63)

For practical purposes we decided to renormalize all remaining parameters in the ${\overline{\mathrm {DR}}}$ scheme (reflecting the fact that there are no physical observables that could be directly related to them). The counterterms of each parameter were obtained by calculating the divergent parts of one-loop corrections to different scalar and fermionic two- and three-point functions. We state the determination of the counterterms in the (possible) order in which they can be successively derived. We start with the counterterms that were obtained by renormalizing certain neutral fermion self-energies.

Fig. 2

Diagrams contributing to the neutral fermion self-energies in the interaction basis

Renormalization of $\varvec{\mu }$: The $\mu$ parameter appears isolated in the Majorana-type mass matrix of the neutral fermions

$$\begin{aligned} \left( m_\nu \right) _{67}=-\frac{\lambda v_R}{\sqrt{2}}=-\mu , \end{aligned}$$

(64)

which is the element mixing the down-type and the up-type Higgsinos $\widetilde{H}_d$ and $\widetilde{H}_u$. The entries $\left( m_\nu \right) _{ij}$ get one-loop corrections via the neutral fermion self-energies ${\sum }_{\tilde{\chi }_{i}^0 \tilde{\chi }_{j}^0}$, that for Majorana fermions can be decomposed as⁴

(65)

The part $\Sigma _{\tilde{\chi }_{i}^0 \tilde{\chi }_{j}^0}^F$ is renormalized through field renormalization and the part $\Sigma _{\tilde{\chi }_{i}^0 \tilde{\chi }_{j}^0}^S$ is renormalized by both the field renormalization and a mass counter term. Since we are interested in the mass renormalization we focus on $\Sigma _{\tilde{\chi }_{i}^0 \tilde{\chi }_{j}^0}^S$ and write for the renormalized self-energy at zero momentum

$$\begin{aligned} \hat{\Sigma }_{\tilde{\chi }_{i}^0 \tilde{\chi }_{j}^0}^S\left( 0\right)= & {} \Sigma _{\tilde{\chi }_{i}^0\tilde{\chi }_{j}^0}^S\left( 0\right) -\frac{1}{2} \left( \delta Z_{ki}^\chi \left( m_\nu \right) _{kj} \phantom {Z_{kj}^\chi }\right. \nonumber \\&\left. + \left( m_\nu \right) _{ik} \delta Z_{kj}^\chi \right) -\delta \left( m_\nu \right) _{ij}. \end{aligned}$$

(66)

The field renormalization constants can be obtained by calculating the divergent part of $\Sigma _{\tilde{\chi }_{i}^0 \tilde{\chi }_{j}^0}^F$:

$$\begin{aligned} \delta Z_{ij}^\chi =-\left. \Sigma _{\tilde{\chi }_{i}^0\tilde{\chi }_{j}^0}^F\right| ^{\mathrm{div}}, \end{aligned}$$

(67)

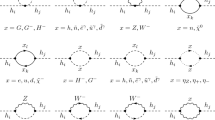
where we make use of the fact that there are no divergences proportional to $p^2$ in our case. The divergent parts of the self-energies of the neutral fermions are calculated diagrammatically in the interaction basis, where diagrams with mass insertions have to be included. In Fig. 2 we show the generic diagrams potentially contributing to the divergent part of the self-energies. Diagrams with a scalar mass insertion or more than one fermionic mass insertion are power-counting finite, so we do not depict them. The diagram shown in Fig. 2 with a mass insertion on the chargino propagator can be divergent depending on the expressions for the couplings of the charginos.

Fig. 3

Potentially divergent one-particle irreducible diagrams contributing to the three-point vertex between two right-handed neutrinos and one right-handed sneutrino

We checked that our results for the field renormalization counterterms for the neutral fermions are consistent with the one-loop anomalous dimensions $\gamma _{ij}^{(1)}$ of the corresponding superfields, i.e.,

$$\begin{aligned} \delta Z_{ij}^\chi =\frac{\gamma _{ij}^{(1)}\Delta }{16 \pi ^2}. \end{aligned}$$

(68)

To extract $\delta \mu$ we now just have to identify

$$\begin{aligned} \delta \left( m_\nu \right) _{67}=-\delta \mu , \end{aligned}$$

(69)

and calculate the divergent part of $\Sigma _{\widetilde{H}_d \widetilde{H}_u}^S$, which again is not momentum dependent. $\delta \mu$ is then given by

$$\begin{aligned} \delta \mu= & {} \frac{1}{2}\mu \left( -\left( \delta Z_{66}^\chi + \delta Z_{77}^\chi \right) + \frac{1}{\lambda }\left( \delta Z_{16}^\chi Y^\nu _1 \right. \right. \nonumber \\&\quad \left. \left. + \delta Z_{26}^\chi Y^\nu _2+ \delta Z_{36}^\chi Y^\nu _3 \right) \phantom {\frac{1}{\lambda }}\right) - \left. \Sigma _{\widetilde{H}_d \widetilde{H}_u}^S\right| ^{\mathrm{div}}, \end{aligned}$$

(70)

where we made us of the fact that the matrix $\delta Z_{ij}^\chi$ is real and symmetric and that components mixing left-handed neutrinos and the down-type Higgsino are the only non-diagonal elements contributing here.

Explicit formulas for the counterterms of the parameters renormalized in the ${\overline{\mathrm {DR}}}$ scheme are listed in the Appendix B.2. For the ${\overline{\mathrm {DR}}}$ counterterms we checked that in the limit $Y^\nu _i\rightarrow 0$ our results coincide with the one in the NMSSM [7].

Renormalization of $\varvec{\kappa }$: The parameters $\kappa$ appears isolated at tree-level in the three-point vertex that couples the right-handed neutrino to the right-handed sneutrino,

$$\begin{aligned} \Gamma _{\nu _R \nu _R \widetilde{\nu }_R}^{(0)}=-\sqrt{2}\kappa . \end{aligned}$$

(71)

The divergences induced to this coupling at one-loop have to be absorbed by the field renormalization of the right-handed neutrino and sneutrino and the counterterm for $\kappa$, which is the only parameter in the tree-level expression. We find

$$\begin{aligned} \delta \kappa = \frac{1}{\sqrt{2}} \left. \Gamma {\nu _R \nu _R \widetilde{\nu }_R}^{(1)}\right| ^{\mathrm{div}} - \frac{1}{2}\kappa \left( \delta Z_{33}+2 \delta Z^\chi _{88}\right) , \end{aligned}$$

(72)

where $\Gamma {\nu _R \nu _R \widetilde{\nu }_R}^{(1)}|^{\mathrm{div}}$ is the divergent part of the corresponding one-loop three-point function, and the terms containing the field renormalization is trivial, because there is only one singlet-like superfield so that no non-diagonal field renormalization constants appear. The divergent one-loop contributions to the vertex are calculated diagrammatically in the interaction basis. The only contributing generic diagrams are shown in Fig. 3.

All other topologies, including diagrams with one or more mass insertion, are finite, and there are no diagrams with gauge bosons instead of scalars in the loop, because there are three gauge-singlet fields on the outer legs. It turns out that the sum over the diagrams shown in Fig. 3 is also finite, so that $\Gamma _{\nu _R \nu _R\widetilde{\nu }_R}^{(1)}|^{\mathrm{div}}$ vanishes.

Fig. 4

Potentially divergent one-particle irreducible topologies contributing to a scalar three-point vertex at one-loop in the interaction basis. Diagrams with scalar mass insertions or more than one fermionic mass insertions are finite

Renormalization of $\varvec{\lambda }$: Having calculated $\delta \mu$ and $\delta \kappa$ we can extract the counterterm for $\lambda$ in the neutral fermion sector. $\lambda$ appears in the mass matrix element

$$\begin{aligned} \left( m_\nu \right) _{88}=\frac{2\kappa \mu }{\lambda }. \end{aligned}$$

(73)

Making use of Eq. (66) we find

$$\begin{aligned} \delta \lambda = \lambda \left( \delta Z^\chi _{88}+\frac{\delta \kappa }{\kappa } +\frac{\delta \mu }{\mu } \right) -\frac{\lambda ^2}{2\mu \kappa } \left. \Sigma _{\nu _R \nu _R}^S\right| ^{\mathrm{div}}, \end{aligned}$$

(74)

where we calculated the divergent part of the right-handed neutrino self-energy $\Sigma _{\nu _R \nu _R}^S|^{\mathrm{div}}$ diagrammatically in the interaction basis using the diagrams already shown in Fig. 2.

Renormalization of $\varvec{A_\kappa }$: The counterterm for the parameter $A_\kappa$ can be extracted from the one-loop corrections to the scalar three-point vertex of right-handed sneutrinos when $\delta \kappa$ is known and using the one-loop relation

$$\begin{aligned} \left[ \frac{\delta \mu }{\mu } - \frac{\delta \lambda }{\lambda } \right] ^{\mathrm{div}} =\left. \frac{1}{2}\delta Z_{33}\right| ^{\mathrm{div}}, \end{aligned}$$

(75)

which was found in the NMSSM [89] and confirmed for this work also in the $\mu \nu \mathrm {SSM}$. For the trilinear singlet vertex we have at tree-level

$$\begin{aligned} \Gamma _{\widetilde{\nu }_R\widetilde{\nu }_R\widetilde{\nu }_R}^{(0)}= -\sqrt{2}\kappa \left( A_\kappa +\frac{6\kappa \mu }{\lambda }\right) . \end{aligned}$$

(76)

The tree-level vertex does not depend on the momentum, so the one-loop counterterm for $A_\kappa$ can be calculated through

$$\begin{aligned} \delta A_\kappa= & {} \frac{1}{\sqrt{2}\kappa }\left( \left. \Gamma _{\widetilde{\nu }_R\widetilde{\nu }_R\widetilde{\nu }_R}^{(1)}\right| ^{\mathrm{div}} +\frac{3}{2} \delta Z_{33} \Gamma _{\widetilde{\nu }_R\widetilde{\nu }_R\widetilde{\nu }_R}^{(0)} \right) \nonumber \\&-\,A_\kappa \frac{\delta \kappa }{\kappa }- \frac{6\kappa \mu }{\lambda } \left( 2\frac{\delta \kappa }{\kappa }+ \frac{1}{2}\delta Z_{33} \right) . \end{aligned}$$

(77)

Here $\Gamma _{\widetilde{\nu }_R\widetilde{\nu }_R\widetilde{\nu }_R}^{(1)}|^{\mathrm{div}}$ is the divergent part of the one-loop corrections to the three-point vertex, which was calculated diagrammatically in the interaction basis. The number of contributing diagrams is rather high, so for simplicity we just show the topologies of the diagrams contributing, that potentially lead to divergences, in Fig. 4. In the case of the vertex $\Gamma _{\widetilde{\nu }_R\widetilde{\nu }_R\widetilde{\nu }_R}$ we can neglect the diagrams with gauge bosons, because the right-handed sneutrinos are gauge singlets.

Renormalization of $\mathbf{A}_{\varvec{\lambda }}$: The counterterm for the parameter $A_\lambda$ is like in the previous case extracted from the one-loop corrections to a scalar three-point function. Here we consider $\Gamma _{H_d H_u \widetilde{\nu }_R}$, the coupling between the two doublet-type Higgses and the right-handed sneutrino. At tree-level it is

$$\begin{aligned} \Gamma _{H_d H_u \widetilde{\nu }_R}^{(0)}= \frac{A_\lambda \lambda }{\sqrt{2}}+ \sqrt{2}\kappa \mu , \end{aligned}$$

(78)

so we will make use of the fact that we already know the counterterms for $\lambda$, $\kappa$ and $\mu$.

The final expression defining $\delta A_\lambda$ will also contain the tree-level expressions for the couplings where the down-type Higgs is replaced by one of the left-handed sneutrinos. They are induced by the non-diagonal field renormalization of $H_d$ and $\widetilde{\nu }_{iL}$ and enter the renormalization of $\Gamma _{H_d H_u \widetilde{\nu }_R}$ at one-loop. We find

$$\begin{aligned} \delta A_\lambda= & {} \left. -\frac{\sqrt{2}}{\lambda }\Gamma _{H_d H_u \widetilde{\nu }_R}^{(1)}\right| ^{\mathrm{div}}-\frac{1}{\sqrt{2}\lambda }\left( \delta Z_{11}\Gamma _{H_d H_u \widetilde{\nu }_R}^{(0)} \right. \nonumber \\&+\,\delta Z_{14}\Gamma _{\widetilde{\nu }_{1L}H_u\widetilde{\nu }_R}^{(0)}+\delta Z_{15}\Gamma _{\widetilde{\nu }_{2L}H_u\widetilde{\nu }_R}^{(0)}\nonumber \\&+\,\left. \delta Z_{16}\Gamma _{\widetilde{\nu }_{3L}H_u\widetilde{\nu }_R}^{(0)}+\delta Z_{22}\Gamma _{H_d H_u \widetilde{\nu }_R}^{(0)}+\delta Z_{33}\Gamma _{H_d H_u \widetilde{\nu }_R}^{(0)} \right) \nonumber \\&-\,\frac{A_\lambda }{\lambda }\delta \lambda -\frac{2\kappa }{\lambda } \delta \mu -\frac{2\mu }{\lambda }\delta \kappa , \end{aligned}$$

(79)

with

$$\begin{aligned} \Gamma _{\widetilde{\nu }_{iL}H_u\widetilde{\nu }_R}^{(0)}= \frac{-Y^\nu _i\left( A^\nu _i+\frac{2\kappa \mu }{\lambda } \right) }{\sqrt{2}}. \end{aligned}$$

(80)

Renormalization of ${{{\varvec{v}}}}^{{{\varvec{2}}}}$: The SM-like vev is renormalized via the renormalization of the electromagnetic coupling in the Thompson limit, which can be done when the counterterms for the gauge boson masses are fixed. We follow here the approach of Ref. [26] used in the NMSSM to be able to compare the results in both models as best as possible.

The renormalization of the electromagnetic coupling is defined by

$$\begin{aligned} e \rightarrow e ( 1+ \delta Z_e ), \end{aligned}$$

(81)

and the counterterm $\delta Z_e$ can be calculated via

$$\begin{aligned} \left. \delta Z_e\right| ^{\mathrm{div}}= \left[ \frac{1}{2} \left( \frac{\partial \Sigma _{\gamma \gamma }^T}{\partial p^2} \left( 0 \right) \right) + \frac{s_\mathrm {w}}{c_\mathrm {w}M_Z^2} \Sigma _{\gamma Z}^T \left( 0 \right) \right] ^{\mathrm{div}}, \end{aligned}$$

(82)

where $\Sigma _{\gamma \gamma }^T(0)$ is the transverse part of the photon self-energy and $\Sigma _{\gamma Z}^T$ is the transverse part of the mixed photon-Z boson self-energy. $s_\mathrm {w}$ and $c_\mathrm {w}$ are defined as $s_\mathrm {w}= \sqrt{1 - c_\mathrm {w}^2}$ with $c_\mathrm {w}= M_{W}/M_Z$. $v^2$ and e are related by

$$\begin{aligned} v^2=\frac{2s_\mathrm {w}^2 M_{W}^2}{e^2}, \end{aligned}$$

(83)

so the counterterm $\delta v^2$ can be obtained through

$$\begin{aligned} \delta v^2 = \frac{4 s_\mathrm {w}^2 M_{W}^2}{e^2}\left. \left( \frac{\delta s_\mathrm {w}^2}{s_\mathrm {w}^2}+\frac{\delta M_{W}^2}{M_{W}^2}- 2\delta Z_e \right) \right| ^{\mathrm{div}}, \end{aligned}$$

(84)

where

$$\begin{aligned} s_\mathrm {w}^2 \rightarrow s_\mathrm {w}^2 + \delta s_\mathrm {w}^2, \quad \text {with } \delta s_\mathrm {w}^2=-c_\mathrm {w}^2 \left( \frac{\delta M_{W}^2}{M_{W}^2} -\frac{\delta M_Z^2}{M_Z^2} \right) . \end{aligned}$$

(85)

Here we take only the divergent parts of the counterterms $\delta M_Z^2$, $\delta M_{W}^2$ and $\delta Z_e$, so that $\delta v^2$ is renormalized in the ${\overline{\mathrm {DR}}}$ scheme. This implies that the counterterm $\delta Z_e$ is not a free parameter, even if we calculated it as if it would be to determine $\delta v^2$. Instead $\delta Z_e$ is a dependent parameter defined by $\delta v^2$ in the ${\overline{\mathrm {DR}}}$ scheme and $\delta M_Z^2$ and $\delta M_W^2$ in the OS scheme through Eqs. (84) and (85),

$$\begin{aligned} \delta Z_e = \frac{1}{2 s_\mathrm {w}^2} \left( c_\mathrm {w}^2 \frac{\delta M_Z^2}{M_Z^2} +\left( s_\mathrm {w}^2-c_\mathrm {w}^2 \right) \frac{\delta M_{W}^2}{M_{W}^2} -\frac{e^2}{4M_{W}^2}\delta v^2 \right) . \end{aligned}$$

(86)

Renormalization of ${{{\varvec{v}}}}_{{{\varvec{iL}}}}^{{{\varvec{2}}}}$: The counterterms for the three vevs of the left-handed sneutrinos $v_{iL}$ can be extracted from the divergent part of the one-loop self-energies $\Sigma _{\widetilde{B}\nu _{iL}}$ between the bino and the corresponding left-handed neutrino. The tree-level mass matrix entries we renormalize are defined by

$$\begin{aligned} \left( m_\nu \right) _{4i}=-\frac{g_1 v_{iL}}{2}, \end{aligned}$$

(87)

so it is necessary to have the counterterm of the gauge coupling $g_1$, whose renormalization we define as $g_1\rightarrow g_1+\delta g_1$. We then can obtain $\delta g_1$ from $\delta M_{W}^{2}$, $\delta M_{Z}^{2}$ and $\delta v^2$ through the definitions of the gauge boson masses in Eq. (45),

$$\begin{aligned} \delta g_1 = \frac{2}{g_1 v^2}( \delta M_Z^2-\delta M_W^2 ) -\frac{g_1}{2}\frac{\delta v^2}{v^2}. \end{aligned}$$

(88)

Renormalizing the self-energies $\Sigma _{\widetilde{B}\nu _{iL}}$ using Eq. (66) we find the following expression for the $\delta v_{iL}^2$:

$$\begin{aligned} \delta v_{iL}^2= & {} \frac{4 v_{iL}}{g_1}\left. \Sigma _{\widetilde{B}\nu _{iL}}^S\right| ^{\mathrm{div}}-v_{iL}\left( \delta Z_{44}^\chi v_{iL} \phantom {Z_{ij}^\chi }\right. \nonumber \\&\left. +\,\delta Z_{ij}^\chi v_{jL} + \delta Z_{i6}^\chi v_d \right) - 2v_{iL}^2\left. \frac{\delta g_1}{g_1}\right| ^{\mathrm{div}}, \end{aligned}$$

(89)

where again the divergent contributions of $\Sigma _{\widetilde{B}\nu _{iL}}^S$ are calculated diagrammatically in the interaction basis.

Renormalization of ${{{\varvec{Y}}}}^{\varvec{\nu }}_{{{\varvec{i}}}}$: The counterterm for the neutrino Yukawas $Y^\nu _i$ can be extracted in the neutral fermion sector as well. We decide to use the renormalization of the tree-level masses

$$\begin{aligned} \left( m_\nu \right) _{i7}=\frac{\mu Y^\nu _i}{\lambda }, \end{aligned}$$

(90)

that mix the left-handed neutrinos and the up-type Higgsino. Since we already found $\delta \lambda$ and $\delta \mu$ we can get $\delta Y^\nu _i$ from the divergent part of the one-loop self-energies $\Sigma _{\nu _{iL}\widetilde{H}_u}^S$,

$$\begin{aligned} \delta Y^\nu _i= & {} \frac{1}{2}\left( \delta Z_{16}^\chi \lambda -\delta Z_{77}^\chi Y^\nu _i - \delta Z_{ij}^\chi Y^\nu _j \right) \nonumber \\&-\left( \frac{\delta \mu }{\mu }-\frac{\delta \lambda }{\lambda } \right) +\frac{\lambda }{\mu }\left. \Sigma _{\nu _{iL}\widetilde{H}_u}^S\right| ^{\mathrm{div}}. \end{aligned}$$

(91)

Renormalization of ${\varvec{\tan \beta }}$: We adopted the usual definition for $\tan \beta$ as in the MSSM (see Eq. (43)). If we define the renormalization for the vevs of the doublet fields as

$$\begin{aligned} v_d^2 \rightarrow v_d^2 + \delta v_d^2, \quad v_u^2 \rightarrow v_u^2 + \delta v_u^2, \end{aligned}$$

(92)

the counterterm for $\tan \beta$ can be written at one-loop as a linear combination of the counterterms for the vevs of the doublet Higgses,

$$\begin{aligned} \delta \tan \beta = \frac{1}{2}\tan \beta \left( \frac{\delta v_u^2}{v_u^2} - \frac{\delta v_d^2}{v_d^2} \right) . \end{aligned}$$

(93)

Note that our renormalization of $v_u^2$ and $v_d^2$ in Eq. (92) includes the contributions from the field renormalization constants inside the counterterms $\delta v_u^2$ and $\delta v_d^2$. This approach is equivalent as defining

$$\begin{aligned} v_d \rightarrow \sqrt{Z_{11}} \left( v_d + \delta \hat{v}_d\right) , \quad v_u \rightarrow \sqrt{Z_{22}} \left( v_u + \delta \hat{v}_u\right) , \end{aligned}$$

(94)

and writing the counterterm of $\tan \beta$ as

$$\begin{aligned} \delta \tan \beta = \frac{1}{2}\tan \beta \left( \delta Z_{22} - \delta Z_{11} \right) + \tan \beta \left( \frac{\delta \hat{v}_u}{v_u} - \frac{\delta \hat{v}_d}{v_d} \right) . \end{aligned}$$

(95)

This notation was convenient in the MSSM and the NMSSM, because the second bracket in Eq. (95) is finite at one-loop [26, 68, 90, 91] and can be set to zero in the ${\overline{\mathrm {DR}}}$ scheme, so that $\delta \tan \beta$ can be expressed exclusively by the field renormalization constants. In contrast, in the $\mu \nu \mathrm {SSM}$ we find

$$\begin{aligned} \left. \left( \frac{\delta \hat{v}_u}{v_u} - \frac{\delta \hat{v}_d}{v_d} \right) \right| ^{\mathrm{div}} =-\frac{\Delta \lambda v_{iL} Y^\nu _i }{32 \pi ^2 v_d}. \end{aligned}$$

(96)

There are several possibilities to extract the counterterms $\delta v_d^2$ and $\delta v_u^2$. A convenient choice is to extract $\delta v_d^2$ from the renormalization of the entry of the neutral fermion mass matrix mixing the up-type Higgsino and the right-handed neutrino,

$$\begin{aligned} \left( m_\nu \right) _{78}=\frac{-\lambda v_d + v_{iL}Y^\nu _i}{\sqrt{2}}, \end{aligned}$$

(97)

because in this case no non-diagonal field renormalization counterterms are needed. Calculating the divergent part of $\Sigma _{\widetilde{H}_u v_R}^S$ and using the counterterms previously calculated we can extract $\delta v_d^2$ via the expression

$$\begin{aligned} \delta v_d^2= & {} -\frac{2\sqrt{2}v_d}{\lambda }\left. \Sigma _{\widetilde{H}_u v_R}^S\right| ^{\mathrm{div}}+\frac{v_d}{\lambda }\left( \delta Z_{77}^\chi + \delta Z_{88}^\chi \right) \nonumber \\&\times \left( -v_d\lambda + v_{iL}Y^\nu _i \right) -2v_d^2\frac{\delta \lambda }{\lambda } \nonumber \\&+\,\frac{v_d}{\lambda } Y^\nu _i \left( \frac{\delta v_L^2}{v_L} \right) _i+\frac{2v_d}{\lambda }v_{iL}\delta Y^\nu _i. \end{aligned}$$

(98)

Since all counterterms appearing in Eq. (98) are renormalized in the ${\overline{\mathrm {DR}}}$ scheme also $\delta v_d^2$ has no finite part. There are now two ways to determine $\delta v_u^2$. Firstly, we could similarly to $\delta v_d^2$ extract the counterterm $\delta v_u^2$ by renormalizing the up-type Higgsino self-energy $\Sigma _{\widetilde{H}_u \widetilde{H}_u}^S$. Alternatively, we can deduce $\delta v_u^2$ from the definition of $v^2$ in Eq. (43) and simply write

$$\begin{aligned} \delta v_u^2 = \delta v^2 -\delta v_d^2 - \delta v_{1L}^2 - \delta v_{2L}^2 - \delta v_{3L}^2. \end{aligned}$$

(99)

We verified that both options yield the same result, which constitutes a consistency test for the counterterms $\delta v_{iL}^2$, which are unique for the $\mu \nu \mathrm {SSM}$. Inserting $\delta v_d^2$ from Eq. (98) and $\delta v_u^2$ from Eq. (99) into Eq. (93) finally gives the counterterm for $\tan \beta$. We checked that the final expression for $\tan \beta$ in Eq. (172) agrees with the NMSSM result in the limit $Y^\nu _i\rightarrow 0$.

The renormalization of $\tan \beta$ in the ${\overline{\mathrm {DR}}}$ scheme is manifestly process-independent and has shown to give stable numerical results in the MSSM [92, 93] and the NMSSM [26, 68].

Renormalization of ${{\varvec{A}}}^\nu _{{\varvec{i}}}$: The soft trilinears $A^\nu _i$ can be renormalized through the calculation of the radiative corrections to the corresponding scalar vertex in the interaction basis. The tree-level expression for the interaction between the up-type Higgs, one left-handed sneutrinos and the right-handed sneutrino is given by

$$\begin{aligned} \Gamma _{H_u \widetilde{\nu }_R \widetilde{\nu }_{iL}}^{(0)}= -\left( \frac{A^\nu _i}{\sqrt{2}}+\frac{\sqrt{2}\kappa \mu }{\lambda } \right) Y^\nu _i. \end{aligned}$$

(100)

The renormalized one-loop corrected vertex will define the counterterm for $A^\nu _i$ since the counterterms for $\kappa$, $\mu$ and $\lambda$ were already determined. We showed in Fig. 4 the topologies of the diagrams that have to be calculated in the interaction basis to get the divergent part of one-loop corrections $\Gamma _{H_u \widetilde{\nu }_R \widetilde{\nu }_{iL}}^{(1)}$. As in the case of the renormalization of $A^\lambda$ the renormalization of the scalar vertex will contain the tree-level expressions of all the vertices with the same quantum numbers of the external fields, because of the non-diagonal field renormalization. Solved for $\delta A^\nu _i$ the renormalization of the vertex leads to

$$\begin{aligned} \delta A^\nu _i= & {} \frac{\sqrt{2}}{Y^\nu _i}\left. \Gamma _{H_u \widetilde{\nu }_R \widetilde{\nu }_{iL}}^{(1)}\right| ^{\mathrm{div}}+ \frac{1}{\sqrt{2}Y^\nu _i}\left( \left( \delta Z_{22}+ \delta Z_{33} \right) \Gamma _{H_u \widetilde{\nu }_R \widetilde{\nu }_{iL}}^{(0)}\right. \nonumber \\&\left. +\,\delta Z_{1,3+i} \Gamma _{H_u \widetilde{\nu }_R H_d}^{(0)} +\delta Z_{3+j,3+i}\Gamma _{H_u \widetilde{\nu }_R \widetilde{\nu }_{jL}}^{(0)}\right) \nonumber \\&-\,\frac{A^\nu _i}{Y^\nu _i}\delta Y^\nu _i - \frac{2\mu }{\lambda }\delta \kappa - \frac{2\kappa }{\lambda }\delta \mu -\frac{2\kappa \mu }{\lambda Y^\nu _i}\delta Y^\nu _i + \frac{2\kappa \mu }{\lambda ^2}\delta \lambda ,\nonumber \\ \end{aligned}$$

(101)

with

$$\begin{aligned} \Gamma _{H_u \widetilde{\nu }_R H_d}^{(0)} = \frac{\lambda A^\lambda }{\sqrt{2}}+\sqrt{2}\kappa \mu . \end{aligned}$$

(102)

Renormalization of ${{{\varvec{m}}}_{{{\varvec{H}}}_{{\varvec{d}}}\widetilde{{{\varvec{L}}}}_{{\varvec{L}}}}^{{\varvec{2}}}}_{{\varvec{i}}}$: The soft scalar masses appear in the bilinear terms of the Higgs potential. They can be renormalized by calculating radiative corrections to scalar self-energies. It proved to be convenient to calculate the ${{\mathcal {C}\mathcal {P}}}$-odd scalar self-energies in the mass basis, and then to rotate the self-energies back to the interaction basis.

We find ${m_{H_d\widetilde{L}_L}^2}_i$ at tree-level in

$$\begin{aligned} m_{\widetilde{\nu }_{iL}^{\mathcal {I}} H_{d}^{\mathcal {I}}}^{2}= & {} \left( m_{H_d\widetilde{L}_L}^2\right) _i- \frac{1}{2}v_R^2\lambda Y^\nu _i- \frac{1}{2}v_u^2\lambda Y^\nu _i. \end{aligned}$$

(103)

The general form of the renormalized scalar self-energies at one-loop is

$$\begin{aligned} \hat{\Sigma }_{X_i X_j}(p^2)= & {} \Sigma _{X_i X_j}(p^2)+ \frac{1}{2} p^2 \left( \delta Z_{ji} + \delta Z_{ij} \right) \nonumber \\&-\,\frac{1}{2} \left( \delta Z_{ki} \left( m_{X}^2 \right) _{kj} +\left( m_{X}^2 \right) _{ik} \delta Z_{kj} \right) \nonumber \\&-\,\delta \left( m_{X}^2 \right) _{ij}, \end{aligned}$$

(104)

where $X=(\varphi ,\sigma )$ represents either the ${{\mathcal {C}\mathcal {P}}}$-even or the ${{\mathcal {C}\mathcal {P}}}$-odd scalar fields and we made use of the fact that the field renormalization constants $\delta Z$ and the mass matrix $m_{X}^2$ are real. Demanding that the renormalized self-energies $\hat{\Sigma }_{A_i A_j}$ are finite in the mass eigenstate basis we can define the divergent parts of the mass counterterms via

$$\begin{aligned} \left. \delta \left( m_{A}^2 \right) _{ij}\right| ^{\mathrm{div}}= & {} \left. \Sigma _{A_i A_j}\left( 0 \right) \right| ^{\mathrm{div}} - \frac{1}{2}\left( \left( \delta Z^A\right) _{ji} m_{A_j}^2 \right. \nonumber \\&\left. +\, m_{A_i}^2 \left( \delta Z^A\right) _{ij} \right) , \end{aligned}$$

(105)

where the field counterterms in the mass eigenstate basis were defined in Eq. (56) and the masses $m_{A_i}^2$ are the eigenvalues of the diagonal ${{\mathcal {C}\mathcal {P}}}$-odd scalar mass matrix $m_{A}^2$. In Fig. 5 we show the diagrams that have to be calculated to get the quantum corrections to scalar self-energies at one-loop in the mass eigenstate basis.

Fig. 5

Generic diagrams for the ${{\mathcal {C}\mathcal {P}}}$-even (h) and ${{\mathcal {C}\mathcal {P}}}$-odd (A) scalar self-energies in the mass eigenstate basis

We calculated all diagrams in the ’t Hooft-Feynman gauge, in which the Goldstone bosons $A_1$ and $H^\pm _1$ and the ghost fields $u^\pm$ and $u^Z$ have the same masses as the corresponding gauge bosons. Calculating the ${{\mathcal {C}\mathcal {P}}}$-odd self-energies $\Sigma _{A_i A_i}$ diagrammatically, we get the mass counterterms in mass eigenstate basis through the Eq. (105). Now inverting the rotation in Eq. (53) we can get the mass counterterms for the ${{\mathcal {C}\mathcal {P}}}$-odd self-energies in the interaction basis via

$$\begin{aligned} \left. \delta m_{\sigma }^2\right| ^{\mathrm{div}}= {U^A}^T \left. \delta m_{A}^2\right| ^{\mathrm{div}} U^A. \end{aligned}$$

(106)

Recognizing that

$$\begin{aligned} \left( \delta m_{\sigma }^2\right) _{3+i,1}= \delta m_{\widetilde{\nu }_{iL}^{\mathcal {I}} H_{d}^{\mathcal {I}}}^{2}, \end{aligned}$$

(107)

and that $m_{\widetilde{\nu }_{iL}^{\mathcal {I}} H_{d}^{\mathcal {I}}}^{2}$ depends on $(m_{H_d\widetilde{L}_L}^2)_i$, we can extract $\delta (m_{H_d\widetilde{L}_L}^2)_i$ through

$$\begin{aligned} \delta \left( m_{H_d\widetilde{L}_L}^2\right) _i= & {} \left. \left( \delta m_{\sigma }^2\right) _{3+i,1}\right| ^{\mathrm{div}}+ \frac{2\mu Y^\nu _i}{\lambda }\delta \mu \nonumber \\&+\,\lambda \left( v_d^2+v_u^2\right) Y^\nu _i \cos ^3\beta \sin \beta \; \delta \tan \beta \nonumber \\&+\,\frac{1}{2}\lambda Y^\nu _i \sin ^2\beta \; \delta v^2 \nonumber \\&-\,\frac{1}{2}\lambda \sin ^2\beta Y^\nu _i\left( \delta v_{1L}^2 + \delta v_{2L}^2 + \delta v_{3L}^2 \right) \nonumber \\&+ \left( \frac{\mu ^2}{\lambda }+\frac{1}{2}\lambda \left( v_d^2+v_u^2 \right) \sin ^2\beta \right) \delta Y^\nu _i \nonumber \\&-\left( \frac{\mu ^2 Y^\nu _i}{\lambda ^2}-\frac{1}{2}\left( v_d^2+v_u^2 \right) Y^\nu _i\sin ^2\beta \right) \delta \lambda .\nonumber \\ \end{aligned}$$

(108)

Renormalization of ${{{\varvec{m}}}_{\widetilde{{{\varvec{L}}}}_{{\varvec{L}}}}^{{\varvec{2}}}}_{ij}$: Since we neglect ${{\mathcal {C}\mathcal {P}}}$-violation the counterterms for the non-diagonal elements of the hermitian matrix ${m_{\widetilde{L}_L}^2}_{ij}$ are symmetric under the exchange of the indices i and j. Then we can extract the counterterms for the non-diagonal elements in the same way as the ones for ${m_{H_d\widetilde{L}_L}^2}_i$ in the ${{\mathcal {C}\mathcal {P}}}$-odd scalar sector. They appear in the tree-level mass matrix in

$$\begin{aligned} m_{\widetilde{\nu }_{iL}^{\mathcal {I}} \widetilde{\nu }_{jL}^{\mathcal {I}}}^{2}= \left( m_{\widetilde{L}}^2\right) _{ij}+ \frac{1}{2}\left( v_R^2+v_u^2\right) Y^\nu _iY^\nu _j \quad \text {for } i\ne j. \end{aligned}$$

(109)

Hence, the counterterms $\delta \left( {m_{\widetilde{L}_L}^2}\right) _{ij}$ for $i\ne j$ are given by

$$\begin{aligned} \delta \left( {m_{\widetilde{L}_L}^2}\right) _{ij}= & {} \left. \left( \delta m_{\sigma }^2\right) _{3+i,3+j}\right| ^{\mathrm{div}} \nonumber \\&-\,\frac{1}{2}\left( v_R^2+v_u^2 \right) \left( Y^\nu _i\delta Y^\nu _j - Y^\nu _j\delta Y^\nu _i \right) \nonumber \\&-\,\frac{2\mu Y^\nu _i Y^\nu _j}{\lambda ^2}\left( \frac{\delta \mu }{\mu }- \frac{\delta \lambda }{\lambda } \right) - \frac{1}{2}Y^\nu _i Y^\nu _j \sin ^2\beta \; \delta v^2 \nonumber \\&-\left( v_d^2+v_u^2 \right) Y^\nu _i Y^\nu _j \cos ^3\beta \sin \beta \;\delta \tan \beta \nonumber \\&+\,\frac{1}{2}Y^\nu _i Y^\nu _j\sin ^2\beta \left( \delta v_{1L}^2 + \delta v_{3L}^2 + \delta v_{3L}^2 \right) .\nonumber \\ \end{aligned}$$

(110)

FeynArts    modelfile: The diagrams and their amplitudes that had to be calculated to obtain the counterterms, as described in this section, were generated using the Mathematica package FeynArts [94] and further evaluated with the package FormCalc [95]. The FeynArts model file for the $\mu \nu \mathrm {SSM}$ was created with the Mathematica program SARAH [96]. We modified the model file to neglect ${{\mathcal {C}\mathcal {P}}}$-violation by choosing all relevant parameters to be real. We also neglected flavor-mixing in the squark- and the quark-sector in this work. The FeynArts model file can be provided by the authors upon request. The calculation of renormalized two- and three-point functions of the neutral scalars of the $\mu \nu \mathrm {SSM}$ at one-loop accuracy is thereby fully automated. (as it is in the MSSM [97]).

In Sect. 5 we will present our predictions for the Higgs masses in the $\mu \nu \mathrm {SSM}$ compared to the ones of the NMSSM. To be able to make this comparison, we had to calculate the NMSSM-predictions in the same renormalization scheme and using the same conventions as were used in the $\mu \nu \mathrm {SSM}$. This is why we calculated the one-loop self-energies in the NMSSM with our own NMSSM-modelfile for FeynArts/FormCalc created with SARAH using the same procedure as for the $\mu \nu \mathrm {SSM}$. We verified that the results calculated in the NMSSM with our modelfile are equal to the results calculated with the modelfile presented in Ref. [98], which was a good check that the generation of the modelfiles for the NMSSM and the $\mu \nu \mathrm {SSM}$ was correct.

4 Loop corrected Higgs boson masses

In the previous section we have derived an OS/${\overline{\mathrm {DR}}}$ renormalization scheme for the $\mu \nu \mathrm {SSM}$ Higgs sector. This can be applied (via the future FeynArts model file, once the counterterms are implemented) to any higher-order correction in the $\mu \nu \mathrm {SSM}$. As a first application, we evaluate the full one-loop corrections to the ${{\mathcal {C}\mathcal {P}}}$-even scalar sector in the $\mu \nu \mathrm {SSM}$. Due to the still missing implementation of counterterms in the FeynArts model file, the calculation of the renormalized scalar self-energies is done in two steps. Firstly, the unrenormalized self-energies are calculated using FeynArts and FormCalc, and subsequently the self-energies are renormalized subtracting (by hand) the field renormalization and mass counterterms, as will be described in the next section.

4.1 Evaluation at one-loop

Here we describe the final form of the renormalized ${{\mathcal {C}\mathcal {P}}}$-even scalar self-energies $\hat{\Sigma }_{hh}$ and how the loop corrected physical masses of the Higgs boson masses are evaluated.

The one-loop renormalized self-energies in the mass eigenstate basis are given by

$$\begin{aligned} \hat{\Sigma }_{h_i h_j}^{(1)}(p^2)= & {} \Sigma _{h_i h_j}^{(1)}(p^2) + \delta Z^H_{ij} \left( p^2 - \frac{1}{2}\left( m_{h_i}^2 + m_{h_j}^2 \right) \right) \nonumber \\&-\left( \delta m_{h}^2\right) _{ij}, \end{aligned}$$

(111)

with the field renormalization constants $\delta Z^H$ and the mass counter terms $\delta m_{h}^2$ in the mass eigenstate basis defined by the rotations in Eqs. (56) and (53). $\Sigma _{h_i h_j}$ is the unrenormalized self-energy obtained by calculating the diagrams shown in Fig. 5 with the ${{\mathcal {C}\mathcal {P}}}$-even states h on the external legs. The self-energies were calculated in the Feynman gauge, so that gauge-fixing terms do not yield counterterm contributions in the Higgs sector at one-loop. The loop integrals were regularized using dimensional reduction [86, 87] and numerically evaluated for arbitrary real momentum using LoopTools [95]. The contributions from complex values of $p^2$ were approximated using a Taylor expansion with respect to the imaginary part of $p^2$ up to first order.

In Eq. (111) we already made use of the fact that $\delta Z^H$ is real and symmetric in our renormalization scheme. The mass counterterms are defined as functions of the counterterms of the free parameters following Eqs. (52) and (53). They contain finite contributions from the tadpole counterterms and from the counterterm for the gauge boson mass $M_Z^2$. The matrix $\delta m_{h}^2$ is real and symmetric.

The renormalized self-energies enter the inverse propagator matrix

$$\begin{aligned} \hat{\Gamma }_{h}=\text {i}\left[ p^2\; \mathbb {1} - \left( m_{h}^2 - \hat{\Sigma }_{h}\left( p^2\right) \right) \right] ,\,\, \text {with } \left( \hat{\Sigma }_{h}\right) _{ij} = \hat{\Sigma }_{h_i h_j}. \end{aligned}$$

(112)

The loop-corrected scalar masses squared are the zeroes of the determinant of the inverse propagator matrix. The determination of corrected masses has to be done numerically when we want to account for the momentum-dependence of the renormalized self-energies. This is done by an iterative method that has to be carried out for each of the six squared loop-corrected masses [99].

4.2 Inclusion of higher orders

In Eq. (112) we did not include the superscript $^{(1)}$ in the self-energies. Restricting the numerical evaluation to a pure one-loop calculation would lead to very large theoretical uncertainties. These can be avoided by the inclusion of corrections beyond the one-loop level. Here we follow the approach of Ref. [70] and supplement the $\mu \nu \mathrm {SSM}$ one-loop results by higher-order corrections in the MSSM limit as provided by FeynHiggs (version 2.13.0) [32, 40, 52,53,54,55,56, 58]. In this way the leading and subleading two-loop corrections are included, as well as a resummation of large logarithmic terms, see the discussion in Sect. 1,

$$\begin{aligned} \hat{\Sigma }_{h}(p^2) = \hat{\Sigma }_{h}^{(1)}(p^2) + \hat{\Sigma }_{h}^{(2')} + \hat{\Sigma }_{h}^\mathrm{resum}. \end{aligned}$$

(113)

In the partial two-loop contributions $\hat{\Sigma }_{h}^{(2')}$ we take over the corrections of ${\mathcal {O}}(\alpha _s\alpha _t,\alpha _s\alpha _b,\alpha _t^2,\alpha _t\alpha _b)$, assuming that the MSSM-like corrections are also valid in the $\mu \nu \mathrm {SSM}$. This assumption is reasonable since the only difference between the squark sector of the $\mu \nu \mathrm {SSM}$ in comparison to the MSSM are the terms proportional to $Y^\nu _i v_{iL}$ in the non-diagonal element of the up-type squark mass matrices (see Eq. (23)) and the terms proportional to $v_{iL}v_{iL}$ in the diagonal elements of the up- and down-type squark mass matrices (see Eqs. (22), (24), (2627) and (28)), which numerically will always be negligible in realistic scenarios since $v_{iL}\ll v_d,v_u,v_R$. Furthermore,. in Ref. [26] the quality of the MSSM approximation was tested in the NMSSM, showing that the genuine NMSSM contributions are in most cases sub-leading. The same is expected for the contributions stemming from the resummation of large logarithmic terms given by $\hat{\Sigma }_{h}^\mathrm{resum}$.

5 Numerical analysis

In the following we present for the first time the full one-loop corrections to the scalar masses in the $\mu \nu \mathrm {SSM}$, with one generation of right-handed neutrinos obtained in the Feynman-diagrammatic approach, taking into account all parameters of the model and the complete dependence on the external momentum, which includes a consistent treatment of the imaginary parts of the scalar self-energies. Our results extend the known ones in the literature of the MSSM and the NMSSM to a model, which has a rich and unique phenomenology through explicit R-parity breaking. The one-loop results are supplemented by known higher-loop results from the MSSM (see the previous section) to reproduce the Higgs mass value of $\sim 125 \,\mathrm {GeV}$ [3]. Here the theory uncertainty must be kept in mind. In the MSSM it is estimated to be at the level of $2{-}3 \,\mathrm {GeV}$ [54, 57], and in extended models it is naturally slightly larger.

Table 2 Input parameters for the NMSSM-like crossing point scenario; all masses and values for trilinear parameters are in GeV

We will present results in several different scenarios, in all of which one scalar with the correct SM-like Higgs mass is reproduced. To get an estimation of the significance of quantum corrections to the Higgs masses that are unique for the $\mu \nu \mathrm {SSM}$, we compare the results to the corresponding ones in the NMSSM. The results in the NMSSM are obtained by a calculation based on Ref. [26], but with slightly changed renormalization conditions to be as close as possible to the calculation in the $\mu \nu \mathrm {SSM}$. While Ref. [26] uses the mass squared of the charged Higgs mass as input parameter and renormalizes it as OS parameter we instead use ${\overline{\mathrm {DR}}}$ conditions for $A^\lambda$.

The benchmark points used in the following were not tested in detail against experimental bounds including the R-parity violating effects of the $\mu \nu \mathrm {SSM}$. They have been chosen to exemplify the potential magnitude of unique $\mu \nu \mathrm {SSM}$-like corrections. Nevertheless, the values we picked for the free parameters should be close to realistic and experimentally allowed scenarios: the parameters in the scalar sector are taken over from calculations in the NMSSM [26], and unique $\mu \nu \mathrm {SSM}$ parameters are chosen in a range to reproduce neutrino masses of the correct order of magnitude. That means that the neutrino Yukawas $Y^\nu _i$ should be of the order $10^{-6}$ to generate neutrino masses of the order less than $1\,\, \mathrm {eV}$. For the left-handed sneutrino vevs this directly implies $v_{iL}\ll v_d, v_u$ so that the tadpole coefficients vanish at tree-level [14]. We will leave a more detailed discussion of numerical results for a future publication, in which we will also include three generations of right-handed neutrinos.

5.1 NMSSM-like crossing point scenario

The first scenario we want to analyze is one studied in the NMSSM with a singlet becoming the LSP in the region of $\lambda > \kappa$ taken from Ref. [26]. This scenario was tested therein against the experimental limits implemented in HiggsBounds 4.1.3 [100,101,102,103,104]. It has the nice feature that there is a crossing point when $\lambda \approx \kappa$ in the neutral scalar sector, in which the masses of the singlet and the SM-like Higgs become degenerate and NMSSM-like loop corrections become significant [70].

In Table 2 we list the values chosen for the parameters. The SM-like parameters from the electroweak sector and the lepton and quark masses are given in Appendix C in Table 5. The parameters present in the $\mu \nu \mathrm {SSM}$ and the NMSSM are of course chosen equally in both models. The region $\lambda < 0.026$ is excluded because the left-handed sneutrinos become tachyonic at tree-level. The flavor-changing non-diagonal elements in the slepton sector are zero. The value for $A^\lambda$ is chosen to correspond to a mass of $m_{H^\pm }= 1000 \,\mathrm {GeV}$ for the charged Higgs mass in the NMSSM with $m_{H^\pm }$ renormalized OS and $A^\lambda$ not being a free parameter. $A^\kappa$ should be chosen to be negative in our convention (when $\kappa$ is positive) to avoid false vacua [14] or tachyons in the pseudo-scalar sector [105]. It should be kept in mind that the diagonal soft scalar masses in the neutral sector are extracted from the values for $v_{iL}$, $\tan \beta$ and $\mu$ via the tadpole equations, and their non-diagonal, flavor-violating elements are always set to zero at tree-level. This is of crucial importance for the comparison of the scalar masses in the $\mu \nu \mathrm {SSM}$ and the NMSSM, since in the NMSSM the soft slepton masses $m_{\widetilde{L}}^2$ are independent parameters, while in the $\mu \nu \mathrm {SSM}$ the diagonal elements are dependent parameters fixed by the tadpole Eq. (15), when the vevs are used as input. The latter strategy is particularly convenient since the order of magnitude of the vevs is roughly fixed through the electroweak seesaw mechanism by demanding neutrino masses below the eV scale, while the soft scalar masses are not directly related to any physical observable. Consequentially, for each parameter point calculated in the $\mu \nu \mathrm {SSM}$, the corresponding values that have to be chosen for $m_{\widetilde{L}}^2$ in the NMSSM have to be adjusted accordingly, defined as a function of all the free parameters appearing in the Higgs potential.

In Fig. 6 we show the resulting spectrum of the ${{\mathcal {C}\mathcal {P}}}$-even scalars at tree-level and including the full one-loop and two-loop contributions.⁵ The standard model Higgs mass value is reproduced accurately when the quantum corrections are included. The heavy MSSM-like Higgs H and the left-handed sneutrinos are at the TeV-scale and rather decoupled from the SM-like Higgs boson. The three left-handed sneutrinos are degenerate because the $\mu \nu \mathrm {SSM}$-like parameters are set equal for all flavors.

The singlet-like scalar mass heavily depends on $\lambda$, because when $\mu$ is fixed, increasing $\lambda$ leads to a smaller value for $v_R$ (see Eq. (44)). As was observed in Ref. [26], the loop-corrected mass of the singlet becomes smaller than the SM-like Higgs boson mass at about $\lambda \approx \kappa$. We observe non-negligible loop-corrections to the singlet in the region of $\lambda$ where the singlet is the lightest neutral scalar.

Due to the similarity of the Higgs sectors of the NMSSM and the $\mu \nu \mathrm {SSM}$, the masses of the doublet-like Higgs bosons and the right-handed sneutrino will be of comparable size as the masses predicted for the doublet-like Higgses and the singlet in the NMSSM. In Fig. 7 we show the tree-level and the one- and two-loop corrected mass of the SM-like Higgs boson in the crossing-point scenario. One can see that, as expected, the two-loop corrections are crucial to predict a SM-like Higgs mass of $125\,\mathrm {GeV}$. Indeed, our analysis confirmed that differences in the prediction of the SM-like Higgs boson mass are negligible compared to the current experimental uncertainty [3] and the anticipated experimental accuracy of the ILC of about  [109], even when there is a substantial mixing between left-handed sneutrinos and the SM-like Higgs at tree-level or one-loop. Apart from that, they are clearly exceeded by the (future) parametric uncertainties in the Higgs-boson mass calculations. Consequently, the Higgs sector alone will not be sufficient to distinguish the $\mu \nu \mathrm {SSM}$ from the NMSSM. On the other hand, we can regard the theoretical uncertainties in the NMSSM and the $\mu \nu \mathrm {SSM}$ to be at the same level of accuracy.

Fig. 6

Spectrum of ${{\mathcal {C}\mathcal {P}}}$-even scalar masses in NMSSM-like crossing point scenario. The three left-handed sneutrinos $\widetilde{\nu }_{iL}$ are degenerate (All plots have been produced using ggplot2 [106] and tikzDevice [107] in R [108])

Fig. 7

Tree-level, one-loop and two-loop corrected masses of the SM-like Higgs boson in the $\mu \nu \mathrm {SSM}$ in the NMSSM-like crossing point scenario

5.2 Light $\tau$-sneutrino scenario

In the previous scenario we observed that, in a scenario where the left-handed sneutrinos where practically decoupled from the SM-like Higgs boson, the unique $\mu \nu \mathrm {SSM}$-like corrections do not account for a substantial deviation of the SM-like Higgs mass prediction compared to the NMSSM. In this section we will investigate a scenario in which one of the left-handed sneutrinos has a small mass close to SM Higgs boson mass. The phenomenology of such a spectrum was recently studied in detail, including a comparison of its predictions with the LHC searches [17, 110]. It was found that a light left-handed sneutrino as the LSP can give rise to distinct signals for the $\mu \nu \mathrm {SSM}$ (for instance, final states with diphoton plus missing energy, diphoton plus leptons and multileptons).

Table 3 Input parameters for the light $\tau$-sneutrino scenario; all masses and values for trilinear parameters are in GeV

In Table 3 we list the relevant parameters that were chosen to obtain a light left-handed $\tau$-sneutrino. The parameters not shown here are chosen to be the same as in the previous case, shown in Table 2. One can see that the vev $v_{3L}$ (corresponding to $\widetilde{\nu }_{3L}$) was increased w.r.t. the NMSSM-like scenario. The reason for this becomes clear when one extracts the leading terms of the diagonal tree-level mass matrix element of the left-handed sneutrinos,

$$\begin{aligned} m_{\widetilde{\nu }_{iL}^{\mathcal {R}} \widetilde{\nu }_{iL}^{\mathcal {R}}}^{2} \approx \frac{Y^\nu _i v_R v_u}{2v_{iL}} \left( - \sqrt{2}A^\nu _i-\kappa v_R +\frac{\sqrt{2}\mu }{\tan \beta } \right) . \end{aligned}$$

(114)

The tree-level masses of the left-handed sneutrinos are roughly proportional to the inverse of their vev. We also decreased $A^\nu _3$ in comparison to the previous scenario, keeping it negative, so that it is of order $\kappa v_R$ and the sum in the brackets of Eq. (114) becomes small.

Fig. 8

${{\mathcal {C}\mathcal {P}}}$-even scalar mass spectrum of the $\mu \nu \mathrm {SSM}$ in the light $\tau$-sneutrino scenario, see Table 3. On the right side we state the dominant composition of the mass eigenstates

In Fig. 8 we show the tree-level and loop-corrected spectrum of the scalars in the region of $\lambda$ where there are no tachyons at tree-level. For too small $\lambda$ the tree-level mass of $\widetilde{\nu }_{3L}$ becomes tachyonic, because when $\mu =(v_R \lambda )/ \sqrt{2}$ is fixed $v_R$ has to grow and the second term in the bracket of Eq. (114) will grow larger than the sum of the first and the third term. For too large $\lambda$, the tree-level mass of the SM-like Higgs boson becomes tachyonic. In particular, it starts to mix with the tree-level singlet mass, which becomes tachyonic because $v_R$ decreases when $\lambda$ increases. The central value of the SM Higgs boson mass is reproduced in this scenario up to values of $\lambda \le 0.22$. However, considering the theoretical uncertainty even higher values of $\lambda$ can be viable. For $\lambda =0.236$ the prediction for the SM-like Higgs mass decreases below $m_{h_1}\approx 122\,\mathrm {GeV}$. As discussed in the introduction we assume a theory uncertainty of $\sim 3 \,\mathrm {GeV}$ on the mass evaluation, so we consider in this scenario the region $\lambda \le 0.236$ to be valid regarding the SM Higgs boson mass. An interesting observation is that the masses of light left-handed sneutrinos are mainly induced via quantum corrections, while the tree-level mass approaches 0 for small values of $\lambda$. This indicates that a consistent treatment of quantum corrections to light sneutrino masses is of crucial importance.

The large upward shift of the left-handed sneutrino masses through the one-loop corrections is due to the fact that in the $\mu \nu \mathrm {SSM}$ the sneutrino fields are part of the Higgs potential, each with an associated tadpole coefficient $T_{\widetilde{\nu }_{iL}}$. To ensure the stability of the vacuum w.r.t. quantum corrections, the tadpoles are renormalized OS, absorbing all finite corrections into the counterterms $\delta T_{\widetilde{\nu }_{iL}}$ (see Sect. 3.2). In the mass counterterms for the left-handed sneutrinos the finite parts $\delta T_{\widetilde{\nu }_{iL}}^\mathrm{fin}$ introduce the main finite contribution in the form

$$\begin{aligned} \delta m_{\widetilde{\nu }_{iL}^{\mathcal {R}} \widetilde{\nu }_{iL}^{\mathcal {R}}}^{2\;\mathrm{fin}} = -\frac{\delta T_{\widetilde{\nu }_{iL}}^\mathrm{fin}}{v_{iL}} + \cdots , \end{aligned}$$

(115)

which is enhanced by the inverse of the vev of $\widetilde{\nu }_{iL}$. It is these terms inside the counterterms of the renormalized self-energies $\hat{\sum }_{\widetilde{\nu }_{iL}^{\mathcal {R}} \widetilde{\nu }_{iL}^{\mathcal {R}}}^{(1)}$ that shift the poles of the propagator matrix and increase the masses of the left-handed sneutrinos, especially in cases where the tree-level masses are small.

Fig. 9

Light $\tau$-sneutrino scenario, see Table 3. In the shaded region the prediction for the SM-like Higgs mass is below $122\,\mathrm {GeV}$. Left: Masses of the SM-like Higgs, the left-handed $\tau$-sneutrino and the right-handed sneutrino in the $\mu \nu \mathrm {SSM}$ at tree-level and one-loop. Right: Masses of the SM-like Higgs and the singlet in the NMSSM at tree-level and one-loop

Fig. 10

Light $\tau$-sneutrino scenario, see Table 3. We show the absolute values of the mixing matrix elements at tree-level $|U_{1i}^{H(0)}|$ (left) and $|U_{2i}^{H(0)}|$ (right), whose squared value define the admixture of the two-lightest ${{\mathcal {C}\mathcal {P}}}$-even scalar mass eigenstate $h_{1,2}$ with the fields $\varphi _i=(H_d,H_u,\widetilde{\nu }_R,\widetilde{\nu }_{1L}, \widetilde{\nu }_{2L},\widetilde{\nu }_{3L})$ in the interaction basis. A substantial mixing of the $\tau$-sneutrino $\widetilde{\nu }_{3L}$ with the SM-like Higgs boson $h^{125}$ and with the singlet $\widetilde{\nu }_R$ is present in the narrow region where the corresponding tree-level masses are degenerate (for example in the right plot at $\lambda \sim 0.20237$ and $\lambda \sim 0.29692$)

This behavior is a peculiarity of the $\mu \nu \mathrm {SSM}$, meaning that the leptonic sector and the Higgs sector are mixed through the breaking of R-parity. The relations between the vevs $v_{iL}$ and the soft masses $m_{\widetilde{L}}^2$ via the tadpole equations automatically lead to dependences between the sneutrino masses and, for instance, the neutrino or the Higgs sector. In the NMSSM, on the other hand, the sneutrinos are not part of the Higgs potential, since the fields are protected by lepton-number conservation. There, the soft masses $m_{\widetilde{L}}^2$ are, without further assumptions, free parameters that can be chosen without taking into account any leptonic observable (such as neutrino masses and mixings). In principle, the additional dependences of the $\mu \nu \mathrm {SSM}$ scalar (neutrino) masses on the neutrino sector could be used (e.g. when all neutrino masses and mixing angles will be known with sufficient experimental accuracy) to restrict the possible range of $m_{\widetilde{L}}^2$, and thus the possible values for the left-handed sneutrino masses. However, with our current experimental knowledge on the neutrino masses, the possible values for the vevs $v_{iL}$, and hence the possible range of left-handed sneutrino masses, are effectively not yet constrained.

It should be noted as well, that the soft masses $m_{\widetilde{L}}^2$ also appear in the mass matrix of the charged scalars (see Eq. (155156157)) and the pseudoscalars (see Eq. (147)). In many cases they are the dominant term in the tree-level masses of the left-handed sleptons and sneutrinos, so the values of the masses of charged sleptons and sneutrino of the same family will be close. A precise treatment of quantum corrections of the size observed in Fig. 8 is extremely important in those cases, since they might easily change the relative sign of their mass differences. This can result in a complete change of the phenomenology of the corresponding benchmark point, for instance when either the neutral (pseudo)scalar or the charged scalar is the LSP [17, 110].

We compare the relevant spectrum of the $\mu \nu \mathrm {SSM}$ to the corresponding one in the NMSSM in Fig. 9. We show the tree-level and one-loop corrected masses of the light scalars in the $\mu \nu \mathrm {SSM}$, and the masses of the SM-like Higgs boson and the singlet in the NMSSM on the right, with parameters set accordingly. We shade in grey the region of $\lambda$ where the prediction for the SM-like Higgs boson mass is below $122\,\mathrm {GeV}$ if two-loop corrections are included. As expected, the SM-like Higgs-boson mass and the mass of the singlet turn out to be equal in both models. Even in regions where there is a substantial mixing of the SM-like Higgs boson with the left-handed sneutrinos, something that cannot occur in the NMSSM, the differences in the SM-like Higgs mass prediction are not larger than a few keV.

It is rather surprising that the SM-like Higgs masses coincide this precisely in both models, considering the fact that a substantial mixing with the sneutrino is possible at tree-level, as we show in Fig. 10. We individually plot the mixing matrix elements of the two lightest ${{\mathcal {C}\mathcal {P}}}$-even scalars, whose squared values define the composition of each mass eigenstate at tree-level. In the cross-over point of the $\tau$-sneutrino and the SM-like Higgs boson the lightest scalar results to be a mixture of $\widetilde{\nu }_\tau$ and the doublet-components $H_u$ and $H_d$, as one can see in the upper left plot of Fig. 10. For example, if we fine-tune $\lambda = 0.20237$ we find that the lightest Higgs boson is composed of approximately

$$\begin{aligned} H_d\rightarrow & {} |U_{11}^{H(0)}|^2\sim 1\%, \end{aligned}$$

(116)

$$\begin{aligned} H_u\rightarrow & {} |U_{12}^{H(0)}|^2\sim 80\%, \end{aligned}$$

(117)

$$\begin{aligned} \widetilde{\nu }_{3L}\rightarrow & {} |U_{16}^{H(0)}|^2\sim 19\%. \end{aligned}$$

(118)

Nevertheless, due to the upward shift, as explained before, the one-loop corrections break the degeneracy and no trace on the SM-like Higgs mass remains, which would deviate it from the NMSSM prediction.

Table 4 Input parameters for the scenario featuring the right-handed sneutrino in the mass range of the LEP and CMS excesses and a SM-like Higgs boson as next-to-lightest ${{\mathcal {C}\mathcal {P}}}$-even scalar; all masses and values for trilinear parameters are in GeV

5.3 The $\mu \nu \mathrm {SSM}$ and the CMS $\gamma \gamma$ excess at $96 \,\mathrm {GeV}$

In this section we will investigate a scenario in which the SM-like Higgs boson is not the lightest ${{\mathcal {C}\mathcal {P}}}$-even scalar. This is inspired by the reported excesses of LEP [111] and CMS [112, 113] in the mass range around $\sim 96\,\mathrm {GeV}$, that (as we will show) can be explained simultaneously by the presence of a light scalar in this mass window. While in the NMSSM the light scalar can be interpreted as the ${{\mathcal {C}\mathcal {P}}}$-even scalar singlet and can accommodate both excesses at $1\sigma$ level without violating any known experimental constraints [114, 115],⁶ we will interpret the light scalar as the ${{\mathcal {C}\mathcal {P}}}$-even right-handed sneutrino of the $\mu \nu \mathrm {SSM}$. Since the singlet of the NMSSM and the right-handed sneutrino of the $\mu \nu \mathrm {SSM}$ are both gauge-singlets, they share very similar properties. However, the explanation of the excesses in the $\mu \nu \mathrm {SSM}$ avoids bounds from direct detection experiments, because R-parity is broken in the $\mu \nu \mathrm {SSM}$ and the dark matter candidate is not a neutralino as in the NMSSM but a gravitino with a lifetime longer than the age of the universe [16]. This is important because the direct detection measurements were shown to be very constraining in the NMSSM while trying to explain the dark matter abundance on top of the excesses from LEP and CMS [114].

In Table 4 we list the values of the parameters we used to account for the lightest ${{\mathcal {C}\mathcal {P}}}$-even scalar as the right-handed sneutrino and the second lightest one the SM-like Higgs boson. $\lambda$ is chosen to be large to account for a sizable mixing of the right-handed sneutrino and the doublet Higgses. In the regime where the SM-like Higgs boson is not the lightest scalar, one does not need large quantum corrections to the Higgs boson mass, because the tree-level mass is already well above $100\,\mathrm {GeV}$. This is why $\tan \beta$ can be low and the soft trilinears $A^{u,d,e}$ are set to zero. The values of $A^{\lambda }$ and $\left| A^\nu \right|$ are chosen to be around $1\,\mathrm {TeV}$ to get masses for the heavy MSSM-like Higgs and the left-handed sneutrinos of this order, so they do not play an important role in the following discussion. On the other hand, $\kappa$ is small to bring the mass of the right-handed sneutrino below the SM-like Higgs boson mass. Finally, the two parameters that are varied are $\mu$ and $A^\kappa$. By increasing $\mu$ the mixing of the right-handed sneutrino with the SM-like Higgs boson is increased, which is needed to couple the gauge-singlet to quarks and gauge-bosons. At the same time we used the value of $A^\kappa$ to keep the mass of the right-handed sneutrino in the correct range. Accordingly, the results in this chapter will all be displayed in the scanned $A^\kappa$–$\mu$ plane.

The process measured at LEP was the production of a Higgs boson via Higgstrahlung associated with the Higgs decaying to bottom-quarks:

$$\begin{aligned} \mu _\mathrm{LEP}=\frac{\sigma \left( e^+e^- \rightarrow Z h_1 \rightarrow Zb\bar{b} \right) }{\sigma ^{SM}\left( e^+e^- \rightarrow Z h \rightarrow Zb\bar{b} \right) } = 0.117 \pm 0.057, \end{aligned}$$

(119)

where $\mu _\mathrm{LEP}$ is called the signal strength, which is the measured cross section normalized to the standard model expectation, with the SM Higgs boson mass at $\sim 96\,\mathrm {GeV}$. The value for $\mu _\mathrm{LEP}$ was extracted in Ref. [114] using methods described in Ref. [120]. We can find an approximate expression for $\mu _\mathrm{LEP}$ factorizing the production and the decay of the scalar and expressing it in terms of couplings to the massive gauge bosons $C_{h_1VV}$ and the up- and down-type quarks $C_{h_1u\bar{u}}$ and $C_{h_1d\bar{d}}$, respectively, normalized to the SM predictions for the corresponding couplings (where with $^{\mu \nu }$ we denote the $\mu \nu \mathrm {SSM}$ prediction, and $\Gamma$ is the Higgs-boson decay width):

$$\begin{aligned} \mu _\mathrm{LEP}^{\mu \nu }= & {} \frac{\sigma ^{\mu \nu }\left( Z^*\rightarrow Zh_1 \right) }{\sigma ^\mathrm{SM}\left( Z^*\rightarrow Zh \right) }\times \frac{\text {BR}^{\mu \nu }\left( h_1\rightarrow b \bar{b}\right) }{\text {BR}^\mathrm{SM}\left( h\rightarrow b \bar{b}\right) } \nonumber \\\approx & {} \left| C_{h_1VV} \right| ^2\times \frac{\Gamma ^{\mu \nu }_{b\bar{b}}}{\Gamma ^\mathrm{SM}_{b\bar{b}}} \times \frac{\Gamma ^\mathrm{SM}_\mathrm{tot}}{\Gamma ^{\mu \nu }_\mathrm{tot}} \nonumber \\\approx & {} \frac{ \left| C_{h_1VV} \right| ^2\times \left| C_{h_1d\bar{d}} \right| ^2 }{ \left| C_{h_1d\bar{d}} \right| ^2 (\text {BR}^\mathrm{SM}_{b\bar{b}}+ \text {BR}^\mathrm{SM}_{\tau \bar{\tau }}) + \left| C_{h_1u\bar{u}} \right| ^2 (\text {BR}^\mathrm{SM}_{gg}+ \text {BR}^\mathrm{SM}_{c\bar{c}})}.\nonumber \\ \end{aligned}$$

(120)

The SM branching ratios dependent on the Higgs boson mass can be obtained from Ref. [121]. The denominator is the ratio of the total decay width of $h_1$ in the $\mu \nu \mathrm {SSM}$ and h in the SM when all SM branching ratios larger than $1\%$ are considered. The off-shell decay to W and Z bosons is in principle also possible, but the BRs are very small for a SM Higgs boson with a mass around $95\,\mathrm {GeV}$ ($\text {BR}^\mathrm{SM}_{WW}\sim 0.5\%$ and $\text {BR}^\mathrm{SM}_{ZZ}\sim 0.06\%$) [121, 122]. It is worth noticing that although the right-handed neutrino mass is small, $m_{\nu _R}\sim 62-63\,\mathrm {GeV}$, in the investigated parameter region, it is nevertheless larger than half of the SM-like Higgs boson mass in all benchmark points, so the decay of the Higgs to the right-handed neutrino is kinematically forbidden and cannot spoil the properties of the SM-like Higgs. Neglecting the vevs $v_{iL}$ the normalized couplings of the scalars are given at leading order by the admixture of the mass eigenstate $h_i$ with the doublet like Higgs $H_d$ and $H_u$ via

$$\begin{aligned} C_{h_i d \bar{d}}= & {} \frac{U^{H,(2')}_{i1}}{\cos \beta }, \quad C_{h_i u \bar{u}}=\frac{U^{H,(2')}_{i2}}{\sin \beta }, \nonumber \\ C_{h_i V V}= & {} U^{H,(2')}_{i1}\cos \beta +U^{H,(2')}_{i2}\sin \beta , \end{aligned}$$

(121)

where the partial two-loop plus resummation corrected mixing matrix elements $U^{H,(2')}_{ij}$ were calculated in the approximation of vanishing momentum, see the discussion in Sect. 4.2. We show in Fig. 11 the masses (top row) and the normalized couplings ($|C_{h_1 d \bar{d}}|$ second row, $|C_{h_1 u \bar{b}}$| third row, $|C_{h_1 VV}|$ lowest row) of the lightest and the next-to-lightest ${{\mathcal {C}\mathcal {P}}}$-even scalar. The lower right corner (marked in gray) results in the right-handed sneutrino becoming tachyonic (at tree-level). The largest mixing of the right-handed sneutrino and the SM-like Higgs boson is achieved where $\mu$ is largest and $|A^\kappa |$ is smallest. The mass of $h_2$ is in the allowed region for a SM-like Higgs boson at $\sim 125\,\mathrm {GeV}$ if we assume a theory uncertainty of up to $3\,\mathrm {GeV}$ (see the previous subsections). The LHC measurements of the SM-like Higgs boson couplings to fermions and massive gauge bosons are still not very precise [123], with uncertainties between 10 and $20\%$ at the $1\sigma$ confidence level (obtained with the assumption that no beyond-the-SM decays modify the total width of the SM-like Higgs boson). Therefore, it would be challenging to exclude parts of the parameter space by considering the deviations of the normalized couplings of $h_2$. However, possible future lepton colliders like the ILC could measure these couplings to a $\%$-level [109, 124], which could exclude (or confirm) most of the parameter space presented here. Seen from a more optimistic perspective, the precise measurement of the SM-like Higgs boson couplings at future colliders could be used to make predictions for the properties of the lighter right-handed sneutrino in this scenario.

Fig. 11

Properties of the lightest (left) and next-to-lightest (right) ${{\mathcal {C}\mathcal {P}}}$-even scalar in the $\mu$–$A^\kappa$ plane. The couplings are normalized to the SM-prediction of a Higgs particle of the same mass. The gray area is excluded because the right-handed sneutrino becomes tachyonic at tree-level. First row: two-loop masses, second row: coupling to down-type quarks, third row: coupling to up-type quarks, fourth row: coupling to massive gauge bosons

Fig. 12

Signal strengths for the lightest $\widetilde{\nu }_R$-like neutral scalar at CMS ($pp\rightarrow h_1 \rightarrow \gamma \gamma$) (left) and LEP (${e^+e^-\rightarrow h_1 Z \rightarrow b\bar{b} Z}$) (right) in the $\mu$-$A^\kappa$ plane. The gray area is excluded because the right-handed sneutrino becomes tachyonic at tree-level

The CMS excess was observed in the diphoton channel with a signal strength of [125]

$$\begin{aligned} \mu _\mathrm{CMS}=\frac{\sigma \left( gg\rightarrow h_1 \rightarrow \gamma \gamma \right) }{\sigma ^\mathrm{SM}\left( gg\rightarrow h \rightarrow \gamma \gamma \right) } = 0.6 \pm 0.2. \end{aligned}$$

(122)

We calculate the signal strength using the approximation that the Higgs production via gluonfusion is described at leading order exclusively by the loop-diagram with a top quark running in the loop, and that the diphoton decay is described by the diagrams with W bosons or a top quark in the loop, which is sufficient in the investigated mass range of $h_1$. One can then write

$$\begin{aligned} \mu _\mathrm{CMS}^{\mu \nu }= & {} \frac{\sigma ^{\mu \nu }\left( gg\rightarrow h_1 \right) }{\sigma ^\mathrm{SM}\left( gg\rightarrow h \right) } \times \frac{\text {BR}^{\mu \nu }_{\gamma \gamma }}{\text {BR}^\mathrm{SM}_{\gamma \gamma }} \nonumber \\\approx & {} \left| C_{h_1 u \bar{u}}\right| ^2 \times \frac{\Gamma ^{\mu \nu }_{\gamma \gamma }}{\Gamma ^\mathrm{SM}_{\gamma \gamma }} \times \frac{\Gamma ^\mathrm{SM}_\mathrm{tot}}{\Gamma ^{\mu \nu }_\mathrm{tot}} \nonumber \\\approx & {} \frac{\left| C_{h_1 u \bar{u}}\right| ^2 \times \left| C^\mathrm{eff}_{h_1 \gamma \gamma }\right| ^2}{\left| C_{h_1d\bar{d}} \right| ^2 (\text {BR}^\mathrm{SM}_{b\bar{b}}+ \text {BR}^\mathrm{SM}_{\tau \bar{\tau }}) + \left| C_{h_1u\bar{u}} \right| ^2 (\text {BR}^\mathrm{SM}_{gg}+ \text {BR}^\mathrm{SM}_{c\bar{c}})}. \nonumber \\ \end{aligned}$$

(123)

The effective coupling of the neutral scalars to photons $C^\mathrm{eff}_{h_i\gamma \gamma }$ has to be calculated in terms of the couplings to the W boson and the up-type quarks. In the SM the dominant contributions to the decay to photons can be written as [126]

$$\begin{aligned} \Gamma ^\mathrm{SM}_{\gamma \gamma } = \frac{G_\mu \,\alpha ^2 \, m_h^3}{128\, \sqrt{2}\, \pi ^3} \left| \frac{4}{3} A_{1/2}\left( \tau _t \right) + A_{1}\left( \tau _W \right) \right| ^2, \end{aligned}$$

(124)

where $G_\mu$ is the Fermi-constant and the form factors $A_{1/2}$ and $A_{1}$ are defined as

$$\begin{aligned} A_{1/2}\left( \tau \right)= & {} 2\left( \tau +\left( \tau -1\right) \arcsin ^2\sqrt{\tau } \right) \tau ^{-2},\end{aligned}$$

(125)

$$\begin{aligned} A_{1}\left( \tau \right)= & {} -\left( 2\tau ^2+3\tau +3\left( 2\tau -1 \right) \arcsin ^2\sqrt{\tau } \right) \tau ^{-2},\nonumber \\ \end{aligned}$$

(126)

for $\tau \le 1$, and the arguments of these functions are $\tau _t = m_h^2/(4 m_t^2)$ and $\tau _W = m_h^2/(4 M_W^2)$. In our approximation the only difference between the $\mu \nu \mathrm {SSM}$ and the SM will be that the couplings of $h_i$ to the top quark and the W boson is modified by the factors $C_{h_i t\bar{t}}$ and $C_{h_i VV}$, so the effective coupling of the Higgses to photons in the $\mu \nu \mathrm {SSM}$ normalized to the SM predictions can be written as

$$\begin{aligned} \left| C^\mathrm{eff}_{h_i \gamma \gamma }\right| ^2= \frac{\left| \frac{4}{3} C_{h_i t\bar{t}} A_{1/2}\left( \tau _t \right) + C_{h_i VV} A_{1}\left( \tau _W \right) \right| ^2}{\left| \frac{4}{3} A_{1/2}\left( \tau _t \right) + A_{1}\left( \tau _W \right) \right| ^2}. \end{aligned}$$

(127)

Using Eqs. (120) and (123) we can calculate the two signal strengths. The result are shown in Fig. 12, the LEP (left) and the CMS excesses (right) in the $\mu$–$A^{\kappa }$ plane. While the LEP excess is easily reproduced in the observed parameter space, we cannot achieve the central value for $\mu _\mathrm{CMS}$, but only slightly smaller values. As already observed in Ref. [114], the reason for this is that for explaining the LEP excess a sizable coupling to the bottom quark is needed. On the contrary, the CMS excess demands a small value for $C_{h_1 d\bar{d}}$ so that the denominator in Eq. (123) becomes small and $\mu _\mathrm{CMS}$ is enhanced. Nevertheless, considering the large experimental uncertainties in $\mu _\mathrm{CMS}$ and $\mu _\mathrm{LEP}$, the scenario presented in this section accommodates both excesses comfortably well (at approximately $1\sigma$), and it is a good motivation to keep on searching for light Higgses in the allowed mass window below the SM-like Higgs mass. Apart from that, this scenario illustrates the importance of an accurate calculation of the loop-corrected scalar masses and mixings, since already small changes in the parameters can have a big impact on the production and the decay modes of the ${{\mathcal {C}\mathcal {P}}}$-even Higgs bosons.

6 Conclusion and outlook

The $\mu \nu \mathrm {SSM}$ is a simple SUSY extension of the SM that is capable of predicting neutrino physics in agreement with experimental data. As in other SUSY models, higher-order corrections are crucial to reach a theoretical uncertainty at the same level of (anticipated) experimental accuracy. So far, higher-order corrections in the $\mu \nu \mathrm {SSM}$ had been restricted to ${\overline{\mathrm {DR}}}$ calculations, which suffer from the disadvantage that they cannot be directly connected to (possibly future observed) new BSM particles.

In this paper we have performed the complete one-loop renormalization of the neutral scalar sector of the $\mu \nu \mathrm {SSM}$ with one generation of right-handed neutrinos in a mixed on-shell/${\overline{\mathrm {DR}}}$ scheme. The renormalization procedure was discussed in detail for each of the free parameters appearing in the $\mu \nu \mathrm {SSM}$ Higgs sector. We have emphasized the conceptual differences to the MSSM and the NMSSM regarding the field renormalization and the treatment of non-flavor-diagonal soft mass parameters, which have their origin in the breaking of R-parity in the $\mu \nu \mathrm {SSM}$. However, we have ensured that the renormalization of the relevant (N)MSSM parts in the $\mu \nu \mathrm {SSM}$ are in agreement with previous calculations in those models. Consequently, numerical differences found can directly be attributed to the extended structure of the $\mu \nu \mathrm {SSM}$. The derived renormalization can be applied to any higher-order correction in the $\mu \nu \mathrm {SSM}$. The one-loop counterterms derived in this paper are implemented into the FeynArts model file, so the computation of these corrections can be done fully automatically.

We have applied the newly derived renormalization to the calculation of the full one-loop corrections to the neutral scalar masses of the $\mu \nu \mathrm {SSM}$, where we found that all UV-divergences cancel. In our numerical analysis the newly derived full one-loop contributions are supplemented by available MSSM higher-order corrections as provided by the code FeynHiggs (leading and subleading fixed-order corrections as well as resummed large logarithmic contributions obtained in an EFT approach.) We investigated various representative scenarios, in which we obtained numerical results for a SM-like Higgs boson mass consistent with experimental bounds. We compared our results to predictions of the various neutral scalars in the NMSSM to investigate the relevance of genuine $\mu \nu \mathrm {SSM}$-like contributions. We find negligible corrections w.r.t. the NMSSM, indicating that the Higgs boson mass calculations in the $\mu \nu \mathrm {SSM}$ are at the same level of accuracy as in the NMSSM.

Finally we showed that the $\mu \nu \mathrm {SSM}$ can accommodate a right-handed (${{\mathcal {C}\mathcal {P}}}$-even) scalar neutrino in a mass regime of $\sim 96 \,\mathrm {GeV}$, where the full Higgs sector is in agreement with the Higgs-boson measurements obtained at the LHC, as well as with the Higgs exclusion bounds obtained at LEP, the Tevatron and the LHC. This includes in particular a SM-like Higgs boson at $\sim 125 \,\mathrm {GeV}$. We have demonstrated that the light right-handed sneutrino can explain an excess of $\gamma \gamma$ events at $\sim 96 \,\mathrm {GeV}$ as reported recently by CMS in their Run I and Run II date. It can simultaneously describe the $2\,\sigma$ excess of $b \bar{b}$ events observed at LEP at a similar mass scale. We are eagerly awaiting the corresponding ATLAS Higgs-boson search results.

Appendices

Appendix A: Mass matrices

Here we state the entries of the following scalar mass matrices.

1.1 A.1 ${{\mathcal {C}\mathcal {P}}}$-even scalars

In the interaction basis $\varphi ^T=(H_d^{\mathcal {R}},H_u^{\mathcal {R}}, \widetilde{\nu }_{R}^{\mathcal {R}},\widetilde{\nu }_{iL}^{\mathcal {R}})$ the mass matrix for the ${{\mathcal {C}\mathcal {P}}}$-even scalars $m_{\varphi }^2$ is defined by:

$$\begin{aligned} m_{H_{d}^{\mathcal {R}}H_{d}^{\mathcal {R}}}^{2}= & {} m_{H_d}^2+\frac{1}{8}\left( g_1^2+g_2^2\right) \left( 3v_d^2+v_{iL}v_{iL}-v_u^2\right) \nonumber \\&+\,\frac{1}{2}\lambda ^2\left( v_R^2+v_u^2\right) , \end{aligned}$$

(128)

$$\begin{aligned} m_{H_{u}^{\mathcal {R}}H_{u}^{\mathcal {R}}}^{2}= & {} m_{H_u}^2+\frac{1}{8}\left( g_1^2+g_2^2\right) \left( 3v_u^2-v_d^2-v_{iL}v_{iL}\right) \nonumber \\&+\,\frac{1}{2}\lambda ^2\left( v_R^2+v_d^2\right) \nonumber \\&+\,\frac{1}{2}v_R^2Y^\nu _iY^\nu _i-v_d\lambda v_{iL}Y^\nu _i, \end{aligned}$$

(129)

$$\begin{aligned} m_{H_{u}^{\mathcal {R}}H_{d}^{\mathcal {R}}}^{2}= & {} -\frac{1}{4}\left( g_1^2+g_2^2\right) v_dv_u-\frac{1}{2}v_R^2\kappa \lambda +v_dv_u\lambda ^2 \nonumber \\&-\,v_u\lambda v_{iL}Y^\nu _i-\frac{1}{\sqrt{2}}T^\lambda , \end{aligned}$$

(130)

$$\begin{aligned} m_{\widetilde{\nu }^{\mathcal {R}}H_{d}^{\mathcal {R}}}^{2}= & {} -v_Rv_u\kappa \lambda +v_dv_R\lambda ^2-v_R\lambda v_{iL}Y^\nu _i-\frac{1}{\sqrt{2}}v_uT^\lambda ,\nonumber \\ \end{aligned}$$

(131)

$$\begin{aligned} m_{\widetilde{\nu }^{\mathcal {R}}H_{u}^{\mathcal {R}}}^{2}= & {} -v_dv_R\kappa \lambda +v_Rv_u\lambda ^2 +v_R\kappa v_{iL}Y^\nu _i\nonumber \\&+\,v_Rv_u Y^\nu _iY^\nu _i+\frac{1}{\sqrt{2}}v_{iL}T^\nu _i-\frac{1}{\sqrt{2}}v_dT^\lambda , \end{aligned}$$

(132)

$$\begin{aligned} m_{\widetilde{\nu }^{\mathcal {R}}\widetilde{\nu }^{\mathcal {R}}}^{2}= & {} m_{\widetilde{v}_R}^2+3v_R^2\kappa ^2-v_dv_u\kappa \lambda +\frac{1}{2}\lambda ^2\left( v_d^2+v_u^2\right) \nonumber \\&+\,v_u\kappa v_{iL}Y^\nu _i-v_d\lambda v_{iL}Y^\nu _i \nonumber \\&+\,\frac{1}{2}v_u^2Y^\nu _iY^\nu _i+\frac{1}{2}\left( v_{iL}Y^\nu _i\right) ^2+\sqrt{2}v_RT^\kappa , \end{aligned}$$

(133)

$$\begin{aligned} m_{\widetilde{\nu }_{iL}^{\mathcal {R}} H_{d}^{\mathcal {R}}}^{2}= & {} \left( m_{H_d\widetilde{L}}^2\right) _i+\frac{1}{4}\left( g_1^2+g_2^2\right) v_dv_{iL} \nonumber \\&-\,\frac{1}{2}v_R^2\lambda Y^\nu _i-\frac{1}{2}v_u^2\lambda Y^\nu _i, \end{aligned}$$

(134)

$$\begin{aligned} m_{\widetilde{\nu }_{iL}^{\mathcal {R}} H_{u}^{\mathcal {R}}}^{2}= & {} -\frac{1}{4}\left( g_1^2+g_2^2\right) v_uv_{iL}+\frac{1}{2}v_R^2\kappa Y^\nu _i-v_dv_u\lambda Y^\nu _i \nonumber \\&+\,v_uv_{jL}Y^\nu _j Y^\nu _i+\frac{1}{\sqrt{2}}v_RT^\nu _i, \end{aligned}$$

(135)

$$\begin{aligned} m_{\widetilde{\nu }_{iL}^{\mathcal {R}} \widetilde{\nu }^{\mathcal {R}}_{R}}^{2}= & {} -\lambda v_d v_R Y^\nu _i +\frac{1}{\sqrt{2}}v_u T^\nu _i\nonumber \\&+v_R v_u \kappa Y^\nu _i+v_R Y^\nu _i v_{jL}Y^\nu _j, \end{aligned}$$

(136)

$$\begin{aligned} m_{\widetilde{\nu }_{iL}^{\mathcal {R}} \widetilde{\nu }_{jL}^{\mathcal {R}}}^{2}= & {} \left( m_{\widetilde{L}}^2\right) _{ij}+\frac{1}{8}\delta _{ij}\left( g_1^2+g_2^2\right) \left( v_d^2+v_{kL}v_{kL}\right) \nonumber \\&+\,\frac{1}{4}\left( g_1^2+g_2^2\right) v_{iL}v_{jL}+\frac{1}{2}\left( v_R^2+v_u^2\right) Y^\nu _iY^\nu _j\nonumber \\ \end{aligned}$$

(137)

1.2 A.2 ${{\mathcal {C}\mathcal {P}}}$-odd scalars

In the interaction basis $\sigma ^T=(H_d^{\mathcal {I}},H_u^{\mathcal {I}},\widetilde{\nu }_{R}^{\mathcal {I}},\widetilde{\nu }_{iL}^{\mathcal {I}})$ the mass matrix for the ${{\mathcal {C}\mathcal {P}}}$-odd scalars $m_{\sigma }^2$ is defined by:

$$\begin{aligned} m_{H_{d}^{\mathcal {I}}H_{d}^{\mathcal {I}}}^{2}= & {} m_{H_d}^2+\frac{1}{8}\left( g_1^2+g_2^2\right) \left( v_d^2+v_{iL}v_{iL}-v_u^2\right) \nonumber \\&+\,\frac{1}{2}\lambda ^2\left( v_R^2+v_u^2\right) , \end{aligned}$$

(138)

$$\begin{aligned} m_{H_{d}^{\mathcal {I}}H_{d}^{\mathcal {I}}}^{2}= & {} m_{H_u}^2+\frac{1}{8}\left( g_1^2+g_2^2\right) \left( v_u^2-v_d^2-v_{iL}v_{iL}\right) \nonumber \\&+\,\frac{1}{2}\lambda ^2\left( v_R^2+v_d^2\right) +v_d\lambda v_{iL}Y^\nu _i \nonumber \\&+\,\frac{1}{2}v_R^2Y^\nu _iY^\nu _i+\frac{1}{2}\left( v_{iL}Y^\nu _i\right) ^2, \end{aligned}$$

(139)

$$\begin{aligned} m_{H_{u}^{\mathcal {I}}H_{d}^{\mathcal {I}}}^{2}= & {} \frac{1}{2}v_R^2\kappa \lambda +\frac{1}{\sqrt{2}}v_R T^\lambda , \end{aligned}$$

(140)

$$\begin{aligned} m_{\widetilde{{\nu }}^{\mathcal {I}}_{R} H_{d}^{\mathcal {I}}}^{2}= & {} v_Rv_u\kappa \lambda -\frac{1}{\sqrt{2}}v_uT^\lambda , \end{aligned}$$

(141)

$$\begin{aligned} m_{\widetilde{{\nu }}^{\mathcal {I}}_{R} H_{u}^{\mathcal {I}}}^{2}= & {} v_dv_R\kappa \lambda -v_R\kappa v_{iL}Y^\nu _i+\frac{1}{\sqrt{2}}v_{iL}T^\nu _i-\frac{1}{\sqrt{2}}v_d T^\lambda ,\nonumber \\ \end{aligned}$$

(142)

$$\begin{aligned} m_{\widetilde{{\nu }}^{\mathcal {I}}_{R}\widetilde{{\nu }}^{\mathcal {I}}_{R}}^{2}= & {} m_{\widetilde{\nu }}^2+v_R^2\kappa ^2+v_dv_u\kappa \lambda +\frac{1}{2}\lambda ^2\left( v_d^2+v_u^2\right) \nonumber \\&-\,v_u\kappa v_{iL}Y^\nu _i-v_d\lambda v_{iL}Y^\nu _i \nonumber \\&+\,\frac{1}{2}v_u^2 Y^\nu _iY^\nu _i+\frac{1}{2}\left( v_{iL}Y^\nu _i\right) ^2-\sqrt{2}v_R T^\kappa , \end{aligned}$$

(143)

$$\begin{aligned} m_{\widetilde{\nu }_{iL}^{\mathcal {I}} H_{d}^{\mathcal {I}}}^{2}= & {} \left( m_{H_d\widetilde{L}}^2\right) _i-\frac{1}{2}v_R^2\lambda Y^\nu _i-\frac{1}{2}v_u^2\lambda Y^\nu _i, \end{aligned}$$

(144)

$$\begin{aligned} m_{\widetilde{\nu }_{iL}^{\mathcal {I}} H_{u}^{\mathcal {I}}}^{2}= & {} -\frac{1}{2}v_R^2\kappa Y^\nu _i-\frac{1}{\sqrt{2}}v_R T^\nu _i, \end{aligned}$$

(145)

$$\begin{aligned} m_{\widetilde{\nu }_{iL}^{\mathcal {I}} \widetilde{\nu }^{\mathcal {I}}_{R}}^{2}= & {} -v_Rv_u\kappa Y^\nu _i+\frac{1}{\sqrt{2}}v_u T^\nu _i, \end{aligned}$$

(146)

$$\begin{aligned} m_{\widetilde{\nu }_{iL}^{\mathcal {I}} \widetilde{\nu }_{jL}^{\mathcal {I}}}^{2}= & {} \left( m_{\widetilde{L}}^2\right) _{ij}+\frac{1}{8}\delta _{ij}\left( g_1^2+g_2^2\right) \left( v_d^2+v_{kL}v_{kL}-v_u^2\right) \nonumber \\&+\,\frac{1}{2}\left( v_R^2+v_u^2\right) Y^\nu _iY^\nu _j. \end{aligned}$$

(147)

1.3 A.3 Charged scalars

In the eigenstate basis $C^T= ({H^-_d}^*,{H^+_u},\widetilde{e}_{iL}^*,\widetilde{e}_{jR}^*)$ the entries of $m_{H^+}^2$ are given by:

$$\begin{aligned} m_{H_{d}^-{H^{-}_d}^{*}}^{2}= & {} m_{H_d}^2+\frac{1}{8}g_1^2\left( v_d^2+v_{iL}v_{iL}-v_u^2\right) \nonumber \\&+\,\frac{1}{8}g_2^2\left( v_d^2-v_{iL}v_{iL}+v_u^2\right) \nonumber \\&+\,\frac{1}{2}v_R^2\lambda ^2 Y^e_{ij}Y^e_{ik}v_{jL}v_{kL}, \end{aligned}$$

(148)

$$\begin{aligned} m_{{H_{u}^+}^* {H_d^-}^*}^{2}= & {} m_{H_u}^2+\frac{1}{8}g_1^2\left( v_u^2-v_d^2-v_{iL}v_{iL}\right) \nonumber \\&+\,\frac{1}{8}g_2^2\left( v_u^2+v_d^2+v_{iL}v_{iL}\right) +\frac{1}{2}v_R^2\lambda ^2 \nonumber \\&+\,\frac{1}{2}v_R^2 Y^\nu _iY^\nu _i, \end{aligned}$$

(149)

$$\begin{aligned} m_{H_{d}^-{H^{+}_u}}^{2}= & {} \frac{1}{4}g_2^2v_dv_u+\frac{1}{2} v_R^2\lambda \kappa -\frac{1}{2} v_d v_u\lambda ^2 \nonumber \\&+\,\frac{1}{2}v_u\lambda v_{iL}Y^\nu _i+\frac{1}{\sqrt{2}}v_R T^\lambda , \end{aligned}$$

(150)

$$\begin{aligned} m_{\widetilde{e}_{iL} {{H^{-}_d}}^{*}}^2= & {} \left( m_{H_d\widetilde{L}}^2\right) _i+\frac{1}{4}g_2^2v_dv_{iL}-\frac{1}{2}v_d Y^e_{ji}Y^e_{jk}v_{kL} \nonumber \\&-\,\frac{1}{2}v_R^2\lambda Y^\nu _i, \end{aligned}$$

(151)

$$\begin{aligned} m_{\widetilde{e}_{iL} H_u^+}^2= & {} \frac{1}{4}g_2^2v_u v_{iL}-\frac{1}{2}v_R^2\kappa Y^\nu _i+\frac{1}{2}v_d v_u \lambda Y^\nu _i \nonumber \\&-\,\frac{1}{2}v_u v_{jL}Y^\nu _j Y^\nu _i-\frac{1}{\sqrt{2}}v_R T^\nu _i, \end{aligned}$$

(152)

$$\begin{aligned} m_{\widetilde{e}_{iR} {{H^{-}_d}}^{*}}^2= & {} -\frac{1}{\sqrt{2}}v_{jL}T^e_{ij}-\frac{1}{2}v_R v_u Y^e_{ij}Y^\nu _j, \end{aligned}$$

(153)

$$\begin{aligned} m_{\widetilde{e}_{iR} H_u^+}^2= & {} -\frac{1}{2}v_R\lambda v_{jL}Y^e_{ij}-\frac{1}{2}v_d v_R Y^e_{ij}Y^\nu _j, \end{aligned}$$

(154)

$$\begin{aligned} m_{\widetilde{e}_{iL} \widetilde{e}_{jL}^{*}}^{2}= & {} \left( m_{\widetilde{L}}^2\right) _{ij}+\frac{1}{8}\delta _{ij}\left( g_1^2-g_2^2\right) \left( v_d^2-v_u^2+v_{kL}v_{kL}\right) \nonumber \\&+\,\frac{1}{4}g_2^2v_{iL}v_{jL}+\frac{1}{2}v_d^2 Y^e_{ki}Y^e_{kj}+\frac{1}{2}v_R^2 Y^\nu _i Y^\nu _j, \end{aligned}$$

(155)

$$\begin{aligned} m_{\widetilde{e}_{iR} \widetilde{e}_{jR}^{*}}^{2}= & {} \left( m_{\widetilde{e}}^2\right) _{ij}+\frac{1}{4}\delta _{ij}g_1^2\left( v_u^2-v_d^2-v_{kL}v_{kL}\right) \nonumber \\&+\,\frac{1}{2}v_d^2Y^e_{ik}Y^e_{jk}+\frac{1}{2}v_{kL}v_{lL}Y^e_{ik}Y^e_{jl}, \end{aligned}$$

(156)

$$\begin{aligned} m_{\widetilde{e}_{iR} \widetilde{e}_{jL}^{*}}^{2}= & {} \frac{1}{\sqrt{2}}v_d T^e_{ij}-\frac{1}{2}v_R v_u \lambda Y^e_{ij}. \end{aligned}$$

(157)

Appendix B: Explicit expressions for counterterms

In this section we will state the one-loop counterterms that were calculated diagrammatically in the ${\overline{\mathrm {DR}}}$ scheme and checked against master formulas for the one-loop beta functions and anomalous dimensions of soft SUSY breaking parameters [127,128,129], superpotential parameters [129, 130], vacuum expectation values [89] and wave-functions with kinetic mixing [131, 132]. The master formulas were evaluated using the mathematica package SARAH [133].

1.1 B.1 Field renormalization counterterms

We list the field renormalization counterterms defined in Eq. (57) in the ${\overline{\mathrm {DR}}}$ scheme in the interaction basis $(H_d,H_u,\widetilde{\nu }_{R},\widetilde{\nu }_{1L}, \widetilde{\nu }_{2L},\widetilde{\nu }_{3L})$:

$$\begin{aligned} \delta Z_{11}= & {} -\frac{\Delta }{16 \pi ^2}\left( \lambda ^2 + Y^e_{ij}Y^e_{ij}+3\left( Y^d_iY^d_i\right) \right) \;, \end{aligned}$$

(158)

$$\begin{aligned} \delta Z_{1,3+i}= & {} \frac{\Delta }{16 \pi ^2}\lambda Y^\nu _i, \end{aligned}$$

(159)

$$\begin{aligned} \delta Z_{22}= & {} -\frac{\Delta }{16 \pi ^2}\left( \lambda ^2+ Y^\nu _iY^\nu _i+3\left( Y^u_iY^u_i\right) \right) , \end{aligned}$$

(160)

$$\begin{aligned} \delta Z_{33}= & {} -\frac{\Delta }{16 \pi ^2}\left( \lambda ^2+\kappa ^2+Y^\nu _iY^\nu _i \right) , \end{aligned}$$

(161)

$$\begin{aligned} \delta Z_{3+i,3+j}= & {} -\frac{\Delta }{16 \pi ^2}\left( Y^e_{ki}Y^e_{kj} + Y^\nu _i Y^\nu _j \right) . \end{aligned}$$

(162)

We checked that the coefficients of the divergent part of the field renormalization counterterms are equal to the one-loop anomalous dimensions of the corresponding superfields $\gamma _{ij}^{(1)}$, neglecting the terms proportional to the gauge couplings $g_1$ and $g_2$, and divided by the loop factor $16 \pi ^2$, i.e.,

$$\begin{aligned} \delta Z_{ij}=\left. \frac{\gamma _{ij}^{(1)}\Delta }{16 \pi ^2}\right| ^{g1,g2\rightarrow 0}, \end{aligned}$$

(163)

which is the same relation that holds in the (N)MSSM.

Table 5 Values for parameters of the standard model in GeV

1.2 B.2 Parameter counterterms

We list the explicit form of the counterterms of the free parameters renormalized in the ${\overline{\mathrm {DR}}}$ scheme:

$$\begin{aligned} \delta \mu= & {} \frac{\mu \Delta }{32\pi ^2}\left( -\frac{4\pi \alpha \left( s_\mathrm {w}^2+3c_\mathrm {w}^2\right) }{s_\mathrm {w}^2c_\mathrm {w}^2}+2\lambda ^2 \right. \nonumber \\&\left. +\,3\left( Y^u_iY^u_i+Y^d_iY^d_i\right) +Y^e_{ij}Y^e_{ij}+2Y^\nu _iY^\nu _i \right) , \end{aligned}$$

(164)

$$\begin{aligned} \delta \kappa= & {} \frac{3\kappa \Delta }{16\pi ^2}\left( \kappa ^2+\lambda ^2+Y^\nu _iY^\nu _i \right) , \end{aligned}$$

(165)

$$\begin{aligned} \delta \lambda= & {} \frac{\lambda \Delta }{32\pi ^2}\left( -\frac{4\pi \alpha \left( s_\mathrm {w}^2+3c_\mathrm {w}^2\right) }{s_\mathrm {w}^2c_\mathrm {w}^2}+4\lambda ^2+2\kappa ^2 \right. \nonumber \\&\left. +\,3\left( Y^u_iY^u_i+Y^d_iY^d_i\right) +Y^e_{ij}Y^e_{ij}+4Y^\nu _iY^\nu _i \right) , \end{aligned}$$

(166)

$$\begin{aligned} \delta A^\kappa= & {} \frac{3\Delta }{8\pi ^2}\left( A^\kappa \kappa ^2 + A^\lambda \lambda ^2 +A^\nu _i {Y^\nu _i}^2 \right) , \end{aligned}$$

(167)

$$\begin{aligned} \delta A^\lambda= & {} \frac{\Delta }{32\pi ^2}\left( \frac{8\pi \alpha \left( 3c_\mathrm {w}^2 M_2 + s_\mathrm {w}^2 M_1 \right) }{c_\mathrm {w}^2s_\mathrm {w}^2}+4 A^\kappa \kappa ^2 \right. \nonumber \\&+\, A^\lambda \left( 8\lambda ^2 + Y^\nu _iY^\nu _i \right) \nonumber \\&+\,\left. 6 \left( A^u_i{Y^u_i}^2+A^d_i{Y^d_i}^2 \right) + 7 A^\nu _i{Y^\nu _i}^2 + 2 A^e_{ij} {Y^e_{ij}}^2\right) ,\nonumber \\ \end{aligned}$$

(168)

$$\begin{aligned} \delta v^2= & {} \frac{\Delta }{32\pi ^2}\left( \frac{4\pi \alpha v^2 \left( s_\mathrm {w}^2+3c_\mathrm {w}^2\right) }{s_\mathrm {w}^2c_\mathrm {w}^2} -2 \left( v_d^2 \left( 3 Y^d_iY^d_i \right. \right. \right. \nonumber \\&\left. \left. \left. +\,Y^e_{ij}Y^e_{ij} \right) +v_u^2 \left( 3Y^u_iY^u_i + Y^\nu _iY^\nu _i \right) \right. \right. \nonumber \\&\left. \left. +\, Y^e_{ij}Y^e_{ik} v_{jL}v_{kL} \right) +2 v_{iL} Y^\nu _i \left( 2\lambda v_d - v_{jL}Y^\nu _j \right) \right) ,\nonumber \\ \end{aligned}$$

(169)

$$\begin{aligned} \delta v_{iL}^2= & {} \frac{v_{iL} \Delta }{32\pi ^2} \left( \frac{4\pi \alpha v_{iL}\left( s_\mathrm {w}^2+3c_\mathrm {w}^2\right) }{s_\mathrm {w}^2c_\mathrm {w}^2}+2\left( v_d \lambda Y^\nu _i \right. \right. \nonumber \\&\left. \left. -\, v_{kL}Y^e_{ji}Y^e_{jk} -v_{jL}Y^\nu _iY^\nu _j \right) \right) , \end{aligned}$$

(170)

$$\begin{aligned} \delta Y^\nu _i= & {} \frac{\Delta }{32\pi ^2}\left( -\frac{4\pi \alpha Y^\nu _i\left( s_\mathrm {w}^2+3c_\mathrm {w}^2 \right) }{s_\mathrm {w}^2c_\mathrm {w}^2}+Y^\nu _i\left( 3Y^u_iY^u_i \right. \right. \nonumber \\&\left. \left. +\, 2\kappa ^2 + 4\lambda ^2 + 4 Y^\nu _jY^\nu _j\right) +Y^e_{ji}Y^e_{jk}Y^\nu _k\right) , \end{aligned}$$

(171)

$$\begin{aligned} \delta \tan \beta= & {} \frac{\tan \beta \Delta }{32\pi ^2}\left( 3\left( Y^d_iY^d_i-Y^u_iY^u_i \right) + Y^e_{ij}Y^e_{ij} \right. \nonumber \\&\left. -\,Y^\nu _iY^\nu _i - \frac{\lambda }{v_d} v_{iL}Y^\nu _i\right) , \end{aligned}$$

(172)

$$\begin{aligned} \delta A^\nu _i= & {} \frac{\Delta }{32\pi ^2 Y^\nu _i} \left( \frac{8\pi \alpha Y^\nu _i\left( M_1 s_\mathrm {w}^2+3 M_2 c_\mathrm {w}^2\right) }{s_\mathrm {w}^2c_\mathrm {w}^2}\right. \nonumber \\&+\,Y^e_{ji}Y^e_{jk}T^\nu _k + 2T^e_{ji}Y^e_{jk}Y^\nu _k+Y^\nu _i\left( 7Y^\nu _jT^\nu _j \right. \nonumber \\&\left. +\,6Y^u_{ij}T^u_{ij}+4\kappa ^2 A^\kappa +7\lambda ^2 A^\lambda \right) \nonumber \\&\left. +\,A^\nu _i \left( \left( \lambda ^2+Y^\nu _jY^\nu _j\right) Y^\nu _i -Y^e_{ji}Y^e_{jk}Y^\nu _k\right) \right) , \end{aligned}$$

(173)

$$\begin{aligned} \delta \left( m_{H_d\widetilde{L}}^2\right) _i= & {} -\frac{\lambda \Delta }{32\pi ^2} \left( Y^\nu _i \left( 2m_{\widetilde{\nu }}^2 + 2A^\lambda A^\nu _i +m_{H_d}^2 \right. \right. \nonumber \\&\left. \left. +\, 2m_{H_u}^2 \right) + Y^\nu _j \left( m_{\widetilde{L}}^2\right) _{ji}\right) , \end{aligned}$$

(174)

$$\begin{aligned} \delta \left( m_{\widetilde{L}}^2\right) _{ij}= & {} \frac{\Delta }{32\pi ^2} \left( 2 m_{H_d} Y^e_{ki}Y^e_{kj} + 2 T^e_{ki}T^e_{kj} \right. \nonumber \\&+\,Y^e_{li}Y^e_{lk}\left( m_{\widetilde{L}}^2\right) _{jk} +2 Y^e_{ki}Y^e_{lj}\left( m_{\widetilde{e}}^2\right) _{kl}\nonumber \\&+\left( m_{\widetilde{L}}^2\right) _{ki}Y^e_{lk}Y^e_{lj} -\lambda \left( m_{H_d\widetilde{L}}^2\right) _j Y^\nu _i \nonumber \\&+\,Y^\nu _i \left( m_{\widetilde{L}}^2\right) _{jk} Y^\nu _k +\left( m_{\widetilde{L}}^2\right) _{ki} Y^\nu _k Y^\nu _j\nonumber \\&\left. +\, Y^\nu _i Y^\nu _j \left( 2 m_{H_u}^2 + 2 m_{\widetilde{\nu }}^2 \right) + 2 T^\nu _i T^\nu _j\right) \nonumber \\&\quad \text {for}\ i\ne j. \end{aligned}$$

(175)

The counterterms in Eqs. (164)–(173) were all calculated diagrammatically in this form and afterwards checked to fulfill the one-loop relation

$$\begin{aligned} \delta X = \frac{\beta _X^{(1)}\Delta }{32\pi ^2}, \end{aligned}$$

(176)

where $\delta X$ stands for one of the counterterms just mentioned, and $\beta _X^{(1)}$ is the one-loop coefficient of the beta function of the parameter X, which could be obtained by the help of the mathematica package SARAH [133].

On the contrary, the counterterms of the soft masses stated in Eqs. (174) and (175) are the ones derived from the one-loop beta function we obtained with SARAH, which were then numerically checked to be equal to the counterterms for $(m_{H_d\widetilde{L}}^2)_i$ and $(m_{\widetilde{L}}^2)_{ij}$ we calculated diagrammatically in the scalar ${{\mathcal {C}\mathcal {P}}}$-odd sector.

Appendix C: Standard model values

Table 5 summarizes the values for the SM-like parameters we chose in our calculation. The value for v corresponds to a value for the Fermi constant of $G_F=1.16638\times 10^{-5}{GeV^{-2}}$. The values for the gauge boson masses define the cosine of the weak mixing angle to be $c_\mathrm {w}=0.881\,535$. Note that since the SM leptons mix with the Higgsinos and gauginos in the $\mu \nu \mathrm {SSM}$, the lepton masses are not the real physical input parameters. However, the mixing is tiny, so there will always be three mass eigenstates in the charged fermion sector corresponding to the three standard model leptons, having approximately the masses $m_e$, $m_\mu$ and $m_\tau$. This is why we use the values for these masses from Table 5 and then calculate the real input parameters, which are the Yukawa couplings

$$\begin{aligned} Y^e_1=\frac{\sqrt{2}m_e}{v_d}, \quad Y^e_2=\frac{\sqrt{2}m_\mu }{v_d}, \quad Y^e_3=\frac{\sqrt{2}m_\tau }{v_d}. \end{aligned}$$

(177)