Loop-corrected Higgs masses in the NMSSM with inverse seesaw mechanism

Abstract

In this study, we work in the framework of the Next-to-Minimal extension of the Standard Model (NMSSM) extended by six singlet leptonic superfields. Through the mixing with the three doublet leptonic superfields, the non-zero tiny neutrino masses can be generated through the inverse seesaw mechanism. While R-parity is conserved in this model lepton number is explicitly violated. We quantify the impact of the extended neutrino sector on the NMSSM Higgs sector by computing the complete one-loop corrections with full momentum dependence to the Higgs boson masses in a mixed on-shell-$\overline{\text{ DR }}$ renormalization scheme, with and without the inclusion of CP violation. The results are consistently combined with the dominant two-loop corrections at $\mathcal{O}(\alpha _t(\alpha _s+\alpha _t))$ to improve the predictions for the Higgs mixing and the loop-corrected masses. In our numerical study we include the constraints from the Higgs data, the neutrino oscillation data, the charged lepton flavor-violating decays $l_i \rightarrow l_j + \gamma$, and the new physics constraints from the oblique parameters S, T, U. We present in this context the one-loop decay width for $l_i \rightarrow l_j + \gamma$. The loop-corrected Higgs boson masses are included in the Fortran code NMSSMCALC-nuSS.

1 Introduction

Both cosmological and neutrino oscillation data have indicated the existence of three neutrino flavors, non-zero neutrino masses, and neutrino mixing. The three observed neutrinos are called active neutrinos. Cosmological data constrain the sum of the three active neutrino masses to be below $0.12\,~\text {eV}$ [1]. Their absolute values must hence be less than $0.12\,~\text {eV}$. As a result, the effect from the three active neutrinos on the Higgs sector is negligible. However, models with an extended neutrino sector contain three active neutrinos and at least one sterile neutrino. The sterile neutrino can mix with the active neutrinos and help to explain the tininess of the active neutrino masses through the seesaw mechanism. The number of sterile neutrinos and their masses are model dependent. Current experiments have not observed sterile neutrinos yet but still allow for a small mixing between sterile and active neutrinos. For precise investigations and meaningful interpretations of both the Higgs and the neutrino sector, it is therefore worthwhile and mandatory to consider the effects of these sterile neutrinos on the Higgs sector. With the increasing amount of the experimental LHC data on the Higgs mass, couplings, production, and decay processes, one can expect stronger constraints on new physics affecting directly and/or indirectly the Higgs sector.

In this study, we consider the impact on the Higgs boson masses in a supersymmetric theory. More specifically, we work in the framework of the Next-to-Minimal Supersymmetric extension of the Standard Model (NMSSM) [2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17] with a Higgs sector consisting of two complex Higgs doublets and a complex Higgs singlet. After electroweak symmetry breaking (EWSB), the NMSSM Higgs sector features seven Higgs bosons, five neutral and two charged Higgs bosons. One of the neutral Higgs states is identified with the Standard Model (SM) Higgs boson. In the minimal supersymmetric extension of the SM (MSSM) its mass is bounded to be below the Z boson mass so that substantial radiative Higgs mass corrections are required to shift the tree-level mass value to the 125 GeV observed by the LHC experiments ATLAS [18] and CMS [19]. In the NMSSM, there is an additional contribution to the tree-level mass arising from the Higgs doublets mixing with the additional complex singlet, so that less substantial radiative corrections are required in order to comply with experiment. The neutrino sector in this model is extended to include six singlet leptonic superfields. R-parity is conserved while the lepton number is explicitly violated by an interaction term between two singlet neutrino superfields and a singlet Higgs superfield. This type of model was first discussed in [20]. The six singlet neutrinos mix with the three doublet ones to generate nine neutrino mass eigenstates. Three of them have very light masses, that can be explained through the inverse seesaw mechanism [21,22,23]. The six remaining neutrinos can have masses of order TeV which may be observable in collider experiments. The presence of heavy neutrinos allows the neutrino Yukawa couplings to be large. Hence heavy neutrinos and their superpartners loops can give significant contributions to loop-corrected Higgs boson masses even though their mixings with active neutrinos are small. This is the focus of our study.

In the literature, there exist many studies on the effects of the (s)neutrinos on the loop-corrected Higgs boson masses in the context of a supersymmetric theory with the type I or inverse seesaw mechanism. We briefly review here those studies that are close to our subject. The impact of the extended neutrino and sneutrino sector on the lightest CP-even Higgs mass in the NMSSM with the inverse seesaw mechanism (ISS), was presented in [24] using an approximate one-loop correction neglecting the effects from external momentum dependence and mixings between Higgs bosons. The authors of [25] have computed the one-loop corrections stemming solely from the neutrino/sneutrino sector to the lightest CP-even Higgs boson in the NMSSM extended by a right-handed neutrino superfield with R-parity conservation. The full one-loop corrections to neutral Higgs boson masses were presented in a mixed on-shell (OS)-$\overline{\text {DR}}$ scheme for the $\mu \nu \text {SSM}$ model with only one generation in [26] and for three generations of right-handed neutrinos in [27]. In the $\mu \nu \text {SSM}$, the Higgs sector contains two Higgs doublets while the neutrino sector is extended to include singlet right-handed neutrino superfields. Lepton number and R-parity are not protected in the $\mu \nu \text {SSM}$ so that the superpartners of the singlet right-handed neutrinos can develop vacuum expectation values (VEVs). In the Minimal Supersymmetric Standard Model (MSSM) extended by the type I seesaw mechanism, the full one-loop corrections with full momentum dependence combined with the dominant two-loop corrections to the Higgs boson masses were presented in [28], which showed a non-decoupling effect for a large right-handed neutrino scale. The authors of [29] have shown that the decoupling property is preserved with a suitable renormalization scheme of the parameter $\tan \beta$, which denotes the ratio of the two vacuum expectation values of the two Higgs doublets in the MSSM. With the inverse seesaw mechanism incorporated in the MSSM, the one-loop corrections of (s)neutrinos have been studied in [30, 31] by using the one-loop effective potential approach.

Our goal is to present here the complete one-loop corrections with full momentum dependence to the Higgs boson masses in a mixed OS-$\overline{\text {DR}}$ renormalization scheme using the Feynman diagrammatic approach. The calculation has been done both in the real and the complex NMSSM. We consistently combine our result with the dominant two-loop corrections of $\mathcal{O}(\alpha _s\alpha _t)$ [32] and $\mathcal{O}(\alpha _t^2)$ [33] computed by our group. In order to investigate the impact of our newly computed corrections, we perform a numerical study where we apply constraints from the Higgs data, the neutrino oscillation data, the charged lepton flavor-violating decays $l_i\rightarrow l_j+\gamma$, and the constraints on new physics from the oblique parameters S, T, U. The explicit computation of the one-loop decay width for $l_i\rightarrow l_j+\gamma$ is also presented in this study. We furthermore provide the Fortran code, dubbed NMSSMCALC-nuSS, for the computation of the loop-corrected Higgs boson masses and Higgs boson decay branching ratios incorporating higher-order corrections. This code is adapted from the code NMSSMCALC [34] published by our group.¹

The paper is organized as follows. In Sect.  2, we describe the model and the masses and mixings of each sector at tree level. In Sect.  3, we present details of our calculation of the loop-corrected Higgs boson masses and mixing. We also discuss our renormalization scheme for parameters and fields needed to obtain finite renormalized Higgs self-energies. In Sect.  4 we present all constraints related to the Higgs data, the neutrino oscillation data, the oblique parameters S, T, U, and the charged lepton flavor-violating decays $l_i\rightarrow l_j+\gamma$ that we apply in our phenomenological study. Section  5 is dedicated to the numerical analysis. We present the size of the loop corrections and their dependencies on the parameters of the neutrino and sneutrino sectors. We furthermore discuss the effects of different constraints on the neutrino sector parameters. Finally, we present our conclusions in Sect. 6.

2 The NMSSM with inverse seesaw mechanism

The NMSSM realization of the seesaw mechanism through the $\mathbb {Z}_3$ discrete symmetry with a unit charge of $\omega = e^{i2\pi /3}$ has been introduced in [20, 24]. Depending on the $\mathbb {Z}_3$ charge assignment for the lepton doublet superfields and the two Higgs doublet superfields, the neutrino masses may arise from effective dimension five, six or seven operators. We consider in this paper the case of the dimension six operator. Tiny neutrino masses are obtained through the well-known inverse seesaw mechanism. This is an interesting case because the dimension six operators generating neutrino masses are not present in the non-supersymmetric seesaw models.² Another reason that makes this case more interesting is that the new appearing particles need not to be too heavy in order to obtain tiny masses for the observed neutrinos. They can be at the TeV scale and hence in the reach of present and future colliders. We consider the simple case where we introduce six gauge singlet chiral superfields, $\hat{N}_i, \hat{X}_i$ ($i=1,2,3$). These superfields carry lepton number. The $\mathbb {Z}_3$ charge assignment³ used in this paper for the relevant NMSSM superfields is given in Table  1.

Table 1 Quantum numbers associated with the gauge symmetry group $SU(2)_L, U(1)_Y$, the $\mathbb {Z}_3$ charge ($\omega =e^{i2\pi /3}$) and the lepton number L for the NMSSM superfields. The generation index i runs from one to three

The NMSSM superpotential including the new superfields is given by

$$\begin{aligned} W_{\text {NMSSM}}&= W_{\text {MSSM}} - \epsilon _{ab} \lambda \hat{S} \hat{H}_d^a \hat{H}_u^b + \frac{1}{3} \kappa \hat{S}^3\nonumber \\&\quad - y_\nu \epsilon _{ab} \hat{H}_u^a \hat{L}^b \hat{N}^{c} + \lambda _X \hat{S} \hat{X} \hat{X} + \mu _X \hat{X} \hat{N}^{c} , \end{aligned}$$

(2.1)

where $\epsilon _{ab}$ is the totally antisymmetric tensor with $\epsilon _{12}=\epsilon ^{12}=1$, $\hat{H}_u,\hat{H}_d$ denote the two complex Higgs doublet superfields and $\hat{S}$ the complex singlet superfield. The MSSM superpotential reads

$$\begin{aligned} W_{\text {MSSM}}&= - \epsilon _{ab} \bigl ( y_u \hat{H}_u^a \hat{Q}^b \hat{U}^c\nonumber \\&\quad - y_d \hat{H}_d^a \hat{Q}^b \hat{D}^c - y_e \hat{H}_d^a \hat{L}^b \hat{E}^c\bigr ) , \end{aligned}$$

(2.2)

in terms of the left-handed quark and lepton superfield doublets $\hat{Q}$ and $\hat{L}$ and the right-handed up-type, down-type and electron-type superfield singlets $\hat{U}$, $\hat{D}$ and $\hat{E}$, respectively. Charge conjugation is denoted by the superscript c, and color and generation indices have been omitted. The NMSSM superpotential contains the coupling $\kappa$ of the self-interaction of the singlet superfield $\hat{S}$, the coupling $\lambda$ for the $\hat{S}$ interaction with the two Higgs doublet superfields, and the coupling $\lambda _X$ for the interaction of the Higgs singlet with the two singlets $\hat{X}$. In general, the coupling $\lambda _X$ is a $3\times 3$ matrix. This is the only term in the superpotential that violates the lepton number. Note that in the model we consider here, we allow for explicit lepton number violation, however, we consider only the violation of two units ($\Delta L=2$). This will forbid the nine scalar fields that carry lepton number to develop VEVs. As consequence, lepton number violation appears only in the (s)neutrino sector and we stay in the simplest possible parameter space. The $3\times 3$ matrix $\mu _X$ is the only parameter with the dimension of mass in the superpotential so that it can be of the order of the SUSY conserving mass scale and is naturally large. This is essential for the seesaw mechanism. The quark and lepton Yukawa couplings $y_d,$ $y_u, y_e,y_\nu$ and the couplings $\lambda ,\kappa ,\lambda _X, \mu _X$ are in general complex. In the numerical analysis, we chose $y_d,y_u, y_e, \lambda _X, \mu _X$ to be diagonal. However in the code $\lambda _X, \mu _X$ can be chosen to be non-diagonal. The soft SUSY breaking NMSSM Lagrangian respecting the gauge symmetry and the $\mathbb {Z}_3$ symmetry reads

$$\begin{aligned} \mathcal L_{\text {NMSSM}}^{\text {soft}} =&\quad \mathcal L_{\text {MSSM}}^{\text {soft}} - \tilde{m}_S^2 |S|^2 + \left( \epsilon _{ab} A_{\lambda } \lambda S H_d^a H_u^b \right. \nonumber \\&\left. - \frac{1}{3} A_{\kappa }\kappa S^3 + \epsilon _{ab} y_\nu A_{\nu } H_u^a \tilde{L}^b\tilde{N}^* + \lambda _X A_X S\tilde{X} \tilde{X} \right. \nonumber \\&\quad \left. +\mu _X B_{\mu _X} \tilde{X} \tilde{N}^* + h.c.\right) - \tilde{m}^2_X |\tilde{X}|^2 - \tilde{m}^2_N |\tilde{N}|^2 , \end{aligned}$$

(2.3)

and contains the soft SUSY breaking trilinear couplings $A_\lambda , A_\kappa , A_\nu$ and $A_X$, the soft SUSY breaking masses $\tilde{m}_S^2,\tilde{m}_X^2,\tilde{m}_N^2$ and the soft SUSY breaking bilinear mass $B_{\mu _X}$. In general, $A_\lambda , A_\kappa , A_\nu ,A_X$ and $B_{\mu _X}$ are complex parameters. For simplicity, in our numerical analysis we chose $\tilde{m}_X, \tilde{m}_N, A_X,$ and $B_{\mu _X}$ to be diagonal. The SM-type and SUSY fields corresponding to a superfield (denoted with a hat) are represented by a letter without and with a tilde, respectively. The soft SUSY breaking MSSM contribution can be cast into the form

$$\begin{aligned} \mathcal L_{\text {MSSM}}^{\text {soft}} =&- \tilde{m}_{H_d}^2 |H_d|^2 - \tilde{m}_{H_u}^2 |H_u|^2 - \tilde{m}_{Q}^2 |\tilde{Q}|^2 - \tilde{m}_{U}^2 |\tilde{u}_R|^2 \nonumber \\&\quad - \tilde{m}_{D}^2 |\tilde{d}_R|^2 - \tilde{m}_{L}^2 |\tilde{L}|^2 -\tilde{m}_{E}^2 |\tilde{e}_R|^2 \nonumber \\&\quad + \epsilon _{ab} \left( y_u A_u H_u^a \tilde{Q}^b \tilde{u}^*_R \right. \nonumber \\&\quad \left. - y_d A_d H_d^a \tilde{Q}^b \tilde{d}^*_R - y_e A_e H_d^a \tilde{Q}^b \tilde{e}^*_R + h.c.\right) \nonumber \\&\quad - \frac{1}{2} (M_1 \tilde{B} \tilde{B} + M_2 \tilde{W}_i \tilde{W}_i + M_3 \tilde{G} \tilde{G} + h.c) . \end{aligned}$$

(2.4)

The indices of the soft SUSY breaking masses, Q (L), stand for the left-handed doublet of the three quark (lepton) generations, and U, D, E are the indices for the right-handed up-type and down-type quarks and charged leptons, respectively. In the trilinear coupling parameters, the indices u, d, e represent the up-type and down-type quarks and charged leptons. While the trilinear couplings $A_u$, $A_d$ and $A_e$ are complex, the soft SUSY breaking mass terms $\tilde{m}_x^2$ ($x=S,H_u,H_d,Q,U,D,L,E$) are real. The soft SUSY breaking mass parameters of the gauginos, $M_1$, $M_2$, $M_3$, for the bino, the winos and the gluinos, $\tilde{B}$, $\tilde{W}_i$ ($i=1,2,3$) and $\tilde{G}$, corresponding to the weak hypercharge $U(1)_Y$, the weak isospin $SU(2)_L$ and the colour $SU(3)_C$ symmetry, are in general complex. In this paper we are working in complex NMSSM where the parameters are kept complex. Furthermore, we apply flavor conservation in the charged (s)lepton and (s)quark sectors so that all matrices including soft mass matrices $\tilde{m}_L^2, \tilde{m}_E^2, \tilde{m}_Q^2, \tilde{m}_U^2, \tilde{m}_D^2$, the trilinear couplings $A_{e,d,u}$ and the Yukawa matrices $Y_{e,d,u}$ are diagonal in any basis. Flavor mixing occurring in our model arises solely from the neutrino and sneutrino sectors. The Lagrangian contains two lepton number violating terms, namely $\lambda _X \hat{S} \hat{X} \hat{X}$ and $\lambda _X A_X S \tilde{X} \tilde{X}$.

The Higgs, neutralino, chargino, (s)quark and charged (s)lepton sectors are the same as in the usual NMSSM without seesaw. For completeness, we recall briefly these sectors here to introduce our notation. The sectors that receive significant changes are the neutrino and sneutrino ones. We will present them in detail later on. Expanding the scalar Higgs fields about their vacuum expectation values (VEVs) $v_u$, $v_d$, and $v_s$, we have

$$\begin{aligned} H_d&= \begin{pmatrix}\frac{1}{\sqrt{2}}(v_d + h_d + i a_d) \\ h_d^- \end{pmatrix},\nonumber \\ H_u&= e^{i\varphi _u}\begin{pmatrix} h_u^+ \\ \frac{1}{\sqrt{2}}(v_u + h_u + i a_u) \end{pmatrix} ,\nonumber \\ S&= e^{i\varphi _s}\frac{1}{\sqrt{2}} (v_s + h_s + i a_s) , \end{aligned}$$

(2.5)

where two additional complex phases, $\varphi _u,\varphi _s$, have been introduced. The fields $h_i$ and $a_i$ with $i = d, u, s$ correspond to the CP-even and CP-odd part, respectively, of the neutral entries of $H_u$, $H_d$ and S. The charged components are denoted by $h_{d,u}^\pm$.

After EWSB, there are mixings between the three CP-even and the three CP-odd Higgs interaction states. In the basis $\phi =(h_d, h_u, h_s,a_d,a_u,a_s)$, the mass term is given by

$$\begin{aligned} {\mathcal{L}}= \frac{1}{2} \phi ^T M_{\phi \phi }\phi . \end{aligned}$$

(2.6)

The explicit expression of the mass matrix $M_{\phi \phi }$ can be found in [33]. The transformation into mass eigenstates at tree-level can be performed in two steps. First, $\mathcal R^G$ is used to single out the Goldstone boson whose mass is equal to the Z boson mass in the ’t Hooft-Feynman gauge,

$$\begin{aligned}&M_{hh}^{(6)}=\mathcal R^G M_{\phi \phi }\left( \mathcal R^G \right) ^T, \end{aligned}$$

(2.7)

$$\begin{aligned}&(h_d,h_u,h_s,a,a_s,G)^T = {\mathcal R}^{G} (h_d, h_u, h_s,a_d,a_u,a_s)^T. \end{aligned}$$

(2.8)

Here one can remove the Goldstone state from the rest by crossing out the sixth row and column of $M_{hh}^{(6)}$, so that it becomes a $5\times 5$ mass matrix in the basis $(h_d,h_u,h_s,a,a_s)$. In the second step, we diagonalize the thus obtained $5\times 5$ matrix $M_{hh}$ with an orthogonal matrix $\mathcal R$

$$\begin{aligned}&{\text {diag}}(m_{h_1}^2, m_{h_2}^2,m_{h_3}^2,m_{h_4}^2,m_{h_5}^2)=\mathcal R M_{hh} \mathcal R^T, \end{aligned}$$

(2.9)

$$\begin{aligned}&(h_1,h_2,h_3,h_4,h_5)^T = \mathcal R (h_d, h_u, h_s,a,a_s)^T . \end{aligned}$$

(2.10)

The tree-level Higgs mass eigenstates are denoted by the small letter h. The masses are ordered as $m_{h_1} \le m_{h_2} \le m_{h_3} \le m_{h_4} \le m_{h_5}$.

The mass matrix in the ’t Hooft-Feynman gauge for the charged components of the Higgs doublets,

$$\begin{aligned} \begin{pmatrix} h_d^+, h_u^+ \end{pmatrix} M_{h^+h^+} \begin{pmatrix} h_d^-\\ h_u^- \end{pmatrix}, \end{aligned}$$

(2.11)

is given by

$$\begin{aligned} M_{h^+h^+}&= \frac{1}{2} \begin{pmatrix} {t_{\beta }}&{} 1 \\ 1 &{} 1/{t_{\beta }}\end{pmatrix}\nonumber \\&\quad \times \bigg [ M_W^2 s_{2\beta } + \frac{|\lambda |v_s}{\cos \left( \varphi _\lambda +\varphi _u+ \varphi _s\right) } \left( \sqrt{2} \,\text { Re} A_\lambda \right. \nonumber \\&\quad \left. +|\kappa |v_s \cos \left( \varphi _\kappa +3\varphi _s\right) \right) \nonumber \\&\quad -\frac{2 |\lambda |^2 M_W^2 s_{\theta _W}^2}{e^2}s_{2\beta } \bigg ] + M_W^2 \begin{pmatrix} {c_{\beta }}^2 &{} -{c_{\beta }}{s_{\beta }}\\ -{c_{\beta }}{s_{\beta }}&{} {s_{\beta }}^2 \end{pmatrix}, \end{aligned}$$

(2.12)

where $M_W$ is the mass of the W boson, $\theta _W$ the electroweak mixing angle, e the electric charge and $\varphi _\lambda ,$ $\varphi _\kappa$ the complex phases of $\lambda$ and $\kappa$, respectively. The angle $\beta$ is defined as

$$\begin{aligned} \tan \beta =\frac{ v_u}{v_d} . \end{aligned}$$

(2.13)

Here and in the following we use the short hand notation $c_x = \cos x$, $s_x = \sin x$ and $t_x = \tan x$. The mass matrix, $M_{h^+h^+}$, can be diagonalized by a rotation matrix with the angle $\beta _c=\beta$ leading to the charged Higgs mass given by

$$\begin{aligned}&M_{H^\pm }^2 = M_W^2 +\frac{|\lambda |v_s}{s_{2\beta }\cos ( \varphi _\lambda +\varphi _u+ \varphi _s) }\nonumber \\&\quad \times \left( \sqrt{2} \text { Re} A_\lambda +|\kappa |v_s \cos ( \varphi _\kappa + 3\varphi _s) \right) -\frac{2 |\lambda |^2 M_W^2 s_{\theta _W}^2}{e^2}.\nonumber \\ \end{aligned}$$

(2.14)

The mass of the charged Goldstone boson $G^\pm$ is equal to $M_W$.

The fermionic superpartners of the neutral Higgs bosons, $\tilde{H}_d^0$, $\tilde{H}_u^0$, $\tilde{S}$, and of the neutral gauge bosons, $\tilde{B}$, $\tilde{W}_3$, mix, and in the Weyl spinor basis $\psi ^0 = (\tilde{B},\tilde{W}_3, \tilde{H}^0_d,\tilde{H}^0_u, \tilde{S})^T$ the neutralino mass matrix $M_N$ is given by

$$\begin{aligned}&M_N = \begin{pmatrix} M_1 &{} 0 &{} - c_\beta M_Z s_{\theta _W} &{} M_Z s_\beta s_{\theta _W} e^{-i \varphi _u} &{} 0\\ 0 &{} M_2 &{} c_\beta M_W &{} - M_W s_\beta e^{-i \varphi _u} &{} 0\\ - c_\beta M_Z s_{\theta _W} &{} c_\beta M_W &{} 0 &{} - \lambda \frac{v_s}{\sqrt{2}} e^{i \varphi _s} &{} - \frac{\sqrt{2} M_W s_\beta s_{\theta _W} \lambda e^{i\varphi _u}}{e} \\ M_Z s_\beta s_{\theta _W} e^{-i \varphi _u} &{} - M_W s_\beta e^{-i \varphi _u} &{} - \lambda \frac{v_s}{\sqrt{2}}e^{i \varphi _s} &{} 0 &{} - \frac{\sqrt{2} M_W c_\beta s_{\theta _W} \lambda }{e} \\ 0 &{} 0 &{} - \frac{\sqrt{2}M_W s_\beta s_{\theta _W}\lambda e^{i \varphi _u}}{e} &{} - \frac{\sqrt{2} M_W c_\beta s_{\theta _W}\lambda }{e} &{} \sqrt{2} \kappa v_s e^{i \varphi _s} \end{pmatrix} \end{aligned}$$

(2.15)

after EWSB, where $M_Z$ is the Z boson mass. The neutralino mass matrix is symmetric and can be diagonalized by a $5 \times 5$ matrix N, yielding $\text {diag}(m_{\tilde{\chi }^0_1}, m_{\tilde{\chi }^0_2},m_{\tilde{\chi }^0_3},m_{\tilde{\chi }^0_4}, m_{\tilde{\chi }^0_5}) = N^* M_N N^\dagger$, where the mass values are ordered as $m_{\tilde{\chi }^0_1}\le \cdots \le m_{\tilde{\chi }^0_5}$. The neutralino mass eigenstates $\tilde{\chi }^0_i$, expressed as a Majorana spinor, are then obtained by

$$\begin{aligned} \tilde{\chi }_i^0 = \left( \begin{array}{c} \chi _i^0 \\ \overline{\chi _i^0} \end{array} \right) \quad \ \text {with}\quad \ \chi ^0_i = N_{ij} \psi ^0_j,\quad \ i,\,j = 1,\dots ,5, \end{aligned}$$

(2.16)

where

$$\begin{aligned} \overline{\chi _i^0} = i \sigma _2 \chi _i^{0*} \end{aligned}$$

(2.17)

in terms of the Pauli matrix $\sigma _2$.

The fermionic superpartners of the charged Higgs and gauge bosons are given in terms of the Weyl spinors $\tilde{H}_d^\pm$, $\tilde{H}_u^\pm$, $\tilde{W}^-$, and $\tilde{W}^+$. With

$$\begin{aligned} \psi ^-_R = \begin{pmatrix} \tilde{W}^- \\ \tilde{H}_d^- \end{pmatrix} \quad \text{ and } \quad \psi ^+_L = \begin{pmatrix} \tilde{W}^+ \\ \tilde{H}_u^+ \end{pmatrix}, \end{aligned}$$

(2.18)

the mass term for these spinors reads

$$\begin{aligned} \mathcal{L}= (\psi ^-_R)^T M_C \psi ^+_L + h.c. , \end{aligned}$$

(2.19)

where

$$\begin{aligned} M_C = \begin{pmatrix} M_2 &{} \sqrt{2} s_\beta M_W e^{-i \varphi _u}\\ \sqrt{2} c_\beta M_W &{} \lambda \frac{v_s}{\sqrt{2}} e^{i \varphi _s} \end{pmatrix}. \end{aligned}$$

(2.20)

The chargino mass matrix $M_C$ can be diagonalized with the help of two unitary $2 \times 2$ matrices, U and V, resulting in

$$\begin{aligned} \text {diag}(m_{\tilde{\chi }^\pm _1}, m_{\tilde{\chi }^\pm _2}) = U^* M_C V^\dagger , \end{aligned}$$

(2.21)

with $m_{\tilde{\chi }^\pm _1} \le m_{\tilde{\chi }^\pm _2}$. The left-handed and the right-handed part of the mass eigenstates are

$$\begin{aligned} \tilde{\chi }^+_L = V \psi ^+_L \quad \text{ and } \quad \tilde{\chi }^-_R = U \psi ^-_R, \end{aligned}$$

(2.22)

respectively, with the mass eigenstates ($i=1,2$)

$$\begin{aligned} \tilde{\chi }^+_i = \left( \begin{array}{c} \tilde{\chi }^+_{L_i} \\ \overline{\tilde{\chi }^-_{R_i}}^T \end{array} \right) \end{aligned}$$

(2.23)

written as Dirac spinors.

The scalar partners of the left- and right-handed quarks are denoted as $\tilde{q}_L$ and $\tilde{q}_R$, respectively. Assuming no generation mixing in the squark sector the mass matrix for the top squark in the interaction basis $(\tilde{t}_L,\tilde{t}_R)$ reads

$$\begin{aligned} M_{\tilde{t}} = \begin{pmatrix} m_{\tilde{Q}_3}^2 + m_t^2 + M_Z^2c_{ 2\beta }(\frac{1}{2} - \frac{2}{3} s^2_{\theta _W}) &{} m_t\left( A_t^* e^{-i\varphi _u }- {\mu _{\text {eff}}}/{t_{\beta }}\right) \\ m_t\left( A_t e^{i\varphi _u }- {\mu _{\text {eff}}}^*/{t_{\beta }}\right) &{} m_t^2 + m_{\tilde{t}_R}^2 +\frac{2}{3} M_Z^2 c_{ 2\beta } s^2_{\theta _W} \end{pmatrix}, \end{aligned}$$

(2.24)

while the bottom squark mass matrix is given by

$$\begin{aligned} M_{\tilde{b}} = \begin{pmatrix} m_{\tilde{Q}_3}^2 + m_b^2 + M_Z^2c_{ 2\beta }(-\frac{1}{2} + \frac{1}{3} s^2_{\theta _W}) &{} m_b\left( A_b^* - e^{i\varphi _u }{\mu _{\text {eff}}}{t_{\beta }}\right) \\ m_b\left( A_b -e^{-i\varphi _u }{\mu _{\text {eff}}}^* {t_{\beta }}\right) &{} m_b^2 + m_{\tilde{b}_R}^2 -\frac{1}{3} M_Z^2 c_{ 2\beta }s^2_{\theta _W} \end{pmatrix}, \end{aligned}$$

(2.25)

where

$$\begin{aligned} {\mu _{\text {eff}}}= \frac{\lambda v_s e^{i\varphi _s }}{\sqrt{2}}. \end{aligned}$$

(2.26)

The mass eigenstates are obtained by diagonalizing these squark matrices with the unitary transformations

$$\begin{aligned}&\text {diag}(m_{\tilde{q}_1}^2,m_{\tilde{q}_2}^2 ) = U_{\tilde{q}} M_{\tilde{q}} U_{\tilde{q}}^\dagger , \quad \begin{pmatrix} \tilde{q}_1\\ \tilde{q}_2\end{pmatrix} = U_{\tilde{q}} \begin{pmatrix} \tilde{q}_L\\ \tilde{q}_R\end{pmatrix}, q=t,b, \nonumber \\ \end{aligned}$$

(2.27)

with the usual convention $m_{\tilde{q}_1}\le m_{\tilde{q}_2}$.

For the charged leptonic sector, we use the same assumption of no generation mixing as in the squark sector. In each generation, the left- and right-handed sleptons mix. For example, the mixing matrix for the third generation, i.e. for the left- and right-handed stau, is given by

$$\begin{aligned} M_{\tilde{\tau }} = \begin{pmatrix} m_{\tilde{L}_3}^2 + m_\tau ^2 + M_Z^2c_{ 2\beta }\left( -\frac{1}{2} + s^2_{\theta _W}\right) &{} m_\tau \left( A_\tau ^* - e^{i\varphi _u }{\mu _{\text {eff}}}{t_{\beta }}\right) \\ m_\tau \left( A_\tau -e^{-i\varphi _u }{\mu _{\text {eff}}}^* {t_{\beta }}\right) &{} m_\tau ^2 + m_{\tilde{\tau }_R}^2 - M_Z^2 c_{ 2\beta }s^2_{\theta _W} \end{pmatrix}, \end{aligned}$$

(2.28)

Upon diagonalization we obtain the mass eigenstates $\tilde{\tau }_1$ and $\tilde{\tau }_2$ whose masses are ordered as $m_{\tilde{\tau }_1}\le m_{\tilde{\tau }_2}$.

In the neutral leptonic sector, the three left-handed neutrinos, $\nu _{L_i}$, mix with the six leptonic component fields of the six singlet superfields $\hat{N}_i^c, \hat{X}_i$, $i=1,2,3$, and the mass term in the Lagrangian reads

$$\begin{aligned} \mathcal{L}_{\text {mass}}^\nu =-\frac{1}{2} \begin{pmatrix} \nu _L&N^c&X \end{pmatrix} M_\text {ISS}^\nu \begin{pmatrix} \nu _L\\ N^c\\ X \end{pmatrix} \end{aligned}$$

(2.29)

where the mixing mass matrix is given by

$$\begin{aligned} M_{\text {ISS}}^\nu = \begin{pmatrix} 0 &{} M_D &{} 0 \\ M_D^T &{} 0 &{} \mu _X \\ 0 &{} \mu _X^T &{} M_X \end{pmatrix}. \end{aligned}$$

(2.30)

Note that $\nu _{L_i}, N_i^c, X_i$ are left-handed Weyl spinors and the products of them are defined in such a way that they are Lorentz invariant. For example, $\nu _{L_i} N^c_j= \epsilon ^{ab}\nu _{L_i,a}N^c_{j,b}$, where the spinor indices are denoted by $a,b=1,2$, and the generation indices by $i,j=1,2,3$. The blocks $M_D, \mu _X$ and $M_X$ are $3\times 3$ matrices with $\mu _X$ defined in Eq. (2.1) and

$$\begin{aligned} M_D =\frac{v_u e^{i\varphi _u}}{\sqrt{2}} y_\nu , \quad M_X = \frac{v_se^{i\varphi _s}}{\sqrt{2}} (\lambda _X + \lambda _X^T). \end{aligned}$$

(2.31)

The mass matrix $M^{\nu }_{\text {ISS}}$ can be diagonalized by a $9\times 9$ unitary matrix as

$$\begin{aligned} U_\nu ^* M_{\text {ISS}}^\nu U^\dagger _\nu = \text {diag}(m_{n_1},\ldots ,m_{n_9}). \end{aligned}$$

(2.32)

The diagonalization process is done numerically in our code. It can be performed, however, by using an expansion approximation [37, 38] to separate the $3\times 3$ light neutrino mass matrix from the $6\times 6$ heavy states exploiting the fact that all matrix elements of $M_D,M_X$ are much smaller than the eigenvalues of $\mu _X$. In particular, at the lowest order, the $3\times 3$ light neutrino mass matrix can be expressed as

$$\begin{aligned} M_{\text {light}} = M_D M_N^{-1} M_D^T, \; \text{ with } \; M_N= \mu _X M_X^{-1} \mu _X^T. \end{aligned}$$

(2.33)

One then defines Majorana neutrino fields as

$$\begin{aligned}&n_i = \left( \begin{array}{c} \nu _i \\ \overline{\nu _i} \end{array} \right) \nonumber \\&\quad \text {with}\quad \ \nu _i = (U_\nu )_{ik} \nu _{L,k}+ (U_\nu )_{i(k+3)} N^c_{k} + (U_\nu )_{i(k+6)} X_{k}, \end{aligned}$$

(2.34)

where $i=1,\ldots ,9,\quad k=1,2,3,$ and

$$\begin{aligned} \overline{\nu _i} = i \sigma _2 \nu _i^{*}. \end{aligned}$$

(2.35)

The neutrino spectrum should contain three light active neutrinos $n_i$ ($i=1,2,3$) with masses of order eV and six heavy neutrinos $n_{I}$, $I=4,\ldots ,9$. Their masses can be of order TeV. The diagonalization process can lead to negative mass eigenvalues, $m_{n_x}$, which in the version of the code for the CP-violating NMSSM we make positive by multiplying the corresponding $x_{\text {th}}$ rotation matrix row with the imaginary unit i. So in our convention, the neutrino masses are all positive. In principle, one gives arbitrary inputs for $M_D, \mu _X, M_X$ and then obtains the corresponding neutrino masses and their rotation matrix. However, the obtained masses and mixing angles must satisfy the experimental data of the three active neutrinos. The chance to get parameter points passing these constraints starting from arbitrary input values is very low. A way out of this technical difficulty is to use a parameterization of $M_D$ in terms of $\mu _X, M_X$ and the light neutrino masses and mixing angles. We follow the Casas–Ibarra parameterization [39], that makes use of the leading order relation for the light neutrino mass matrix

$$\begin{aligned} U_{\text {PMNS}}^* M_{\text {light}} U_{\text {PMNS}}^\dagger = m_\nu , \end{aligned}$$

(2.36)

with

$$\begin{aligned} m_\nu = \text {diag}({m_{\nu _1}},{m_{\nu _2}},{m_{\nu _3}}) . \end{aligned}$$

(2.37)

Using the expression of $M_{\text {light}}$ given in (2.33) one then gets

$$\begin{aligned} M_D = U_{\text {PMNS}}^T \sqrt{m_\nu } R \sqrt{{\mathcal{M}}_N} V, \end{aligned}$$

(2.38)

where

$$\begin{aligned} {\mathcal{M}}_N=\text {diag}({M_{N_1}},{M_{N_2}},{M_{N_3}}) . \end{aligned}$$

(2.39)

The Pontecorvo–Maki–Nakagawa–Sakata (PMNS) matrix $U_{\text {PMNS}}$ and the active neutrino masses $m_{\nu _i}$ (i = 1, 2, 3) are input values based on the available experimental data, while $M_{N_1},M_{N_2},M_{N_3}$ are the positive roots of $M_N$ and V is a unitary matrix diagonalizing $M_N$ as

$$\begin{aligned} \text {diag}(M_{N_1},M_{N_2},M_{N_3}) = V^* M_N V^\dagger , \end{aligned}$$

(2.40)

and R is a complex orthogonal matrix that can be written in terms of three complex angles $\theta _i$ ($\mathrm {i}=1,2,3$)

$$\begin{aligned} R=\begin{pmatrix} c_2s_3&{} -c_1s_3-s_1s_2c_3&{} s_1s_3-c_1s_2c_3\\ c_2s_3 &{} c_1c_3-s_1s_2s_3 &{} -s_1c_3 -c_1s_2s_3 \\ s_2 &{} s_1c_2&{} c_1c_2 \end{pmatrix}, \end{aligned}$$

(2.41)

with $c_i=\cos \theta _i,\, s_i=\sin \theta _i$. In this study we set the three angles $\theta _{1,2,3}$ to be real. Using this Casas–Ibarra parameterization, the light neutrino masses denoted $m_{n_i}$ ($i=1,2,3$) in (2.32) are approximately the input neutrino masses $m_{\nu _i}$ in (2.36). If the relative difference, defined as the maximum of $|(m_{n_i}-m_{\nu _i})/m_{\nu _i}|$ ($i=1,2,3$), is more than one percent, the code will print out a warning about the breakdown of the Casas–Ibarra parameterization.

With the introduction of the new superfields, the sneutrino sector is also changed. To incorporate CP violation, each sneutrino field is separated into its CP-even and CP-odd components as

$$\begin{aligned}&{\tilde{\nu }}= \frac{1}{\sqrt{2}} \left( {\tilde{\nu }}_+ + i {\tilde{\nu }}_-\right) \end{aligned}$$

(2.42)

$$\begin{aligned}&{\tilde{N}}^{*} = \frac{1}{\sqrt{2}} \left( {\tilde{N}}_+ + i {\tilde{N}}_-\right) \end{aligned}$$

(2.43)

$$\begin{aligned}&{\tilde{X}}= \frac{1}{\sqrt{2}} \left( {\tilde{X}}_+ + i {\tilde{X}}_-\right) . \end{aligned}$$

(2.44)

The mass term in the basis $\psi = ({\tilde{\nu }}_+,{\tilde{N}}_+,{\tilde{X}}_+,{\tilde{\nu }}_-,{\tilde{N}}_-,{\tilde{X}}_-)^T$ (generation indices are suppressed) is given by

$$\begin{aligned} \mathcal{L}= \frac{1}{2} \psi ^T M_{{\tilde{\nu }}}\psi , \end{aligned}$$

(2.45)

where the mass matrix $M_{\tilde{\nu }}$ is an $18\times 18$ symmetric matrix that can be found in Appendix B. An orthogonal matrix ${U_{\tilde{\nu }}}$ can be used to find the masses of the sneutrinos as follows,

$$\begin{aligned} \text {diag}\left( m^2_{\tilde{n}_1},\ldots ,m^2_{\tilde{n}_{18}}\right) = {U_{\tilde{\nu }}}M_{\tilde{\nu }}{U_{\tilde{\nu }}}^T, \end{aligned}$$

(2.46)

where their mass values are ordered as $m^2_{\tilde{n}_1} \le \cdots \le m^2_{\tilde{n}_{18}}$.

3 Calculation of the neutral Higgs boson masses and mixings

In this section, we describe in detail our computation of the complete one-loop contribution to the loop-corrected neutral Higgs boson masses including the full momentum dependence and give a detailed description of the renormalization procedure. We apply dimensional reduction (DRED) [40, 41] to regularize the UV-divergences, which has been proven to conserve SUSY at one-loop order. We have used several programs to compute the one-loop self-energies. To generate the Feynman diagrams and self-energies we use FeynArts [42, 43] together with a model file created by SARAH [44,45,46,47]. The output self-energies were further processed using FeynCalc [48, 49] for the simplification of the Dirac matrices and for the tensor reduction. The one-loop one- and two-point integrals were evaluated with a modified loop library of NMSSMCALC [50], in particular we used quadruple precision and complex external momentum squared for the two-point integrals to increase the convergence and stability of the code.⁴ The new model and the calculation of the loop-corrected Higgs boson masses and mixings have been implemented in the code, called NMSSMCALC-nuSS. The code can be downloaded from the url:

https://www.itp.kit.edu/~maggie/NMSSMCALC-nuSS/

3.1 Loop-corrected Higgs boson masses and mixings

The loop-corrected Higgs boson masses can be obtained from the real parts of the complex mass eigenvalues of the $5\times 5$ Higgs mass matrix with its elements

$$\begin{aligned} \mathcal {M}_{h_i h_j}= m_{h_i}^2 \delta _{h_i h_j} - \hat{\Sigma }_{h_i h_j} (p^2), \quad i,j=1,\ldots ,5, \end{aligned}$$

(3.47)

where $\hat{\Sigma }_{h_i h_j} (p^2)$ is the renormalized self-energy of the transition $h_i\rightarrow h_j$ at external momentum squared $p^2$. We do not include the contributions due to the transitions $h_i\rightarrow G/Z$, since their contributions are negligible for light Higgs bosons. For extremely heavy Higgs bosons, they can have some effect as shown in [51].

The renormalized Higgs self-energies at one-loop level can be written in terms of the unrenormalized self-energies $\Sigma _{h_i h_j} (p^2)$ and the counterterms as

$$\begin{aligned} \hat{\Sigma }_{h_i h_j} (p^2)&= \Sigma _{h_i h_j} (p^2) + \frac{1}{2}p^2 \left[ \mathcal {R}\left( \delta {Z}_{hh}^\dagger + \delta {Z}_{hh}\right) \mathcal {R}^T\right] _{ij} \nonumber \\&\quad - \frac{1}{2}\left[ \mathcal {R}\left( \delta {Z}_{hh}^\dagger M_{hh} + M_{hh} \delta {Z}_{hh}\right) \mathcal {R}^T\right] _{ij} \nonumber \\&\quad - \left[ \mathcal {R}\delta M_{hh} (\mathcal {R})^T\right] _{ij}. \end{aligned}$$

(3.48)

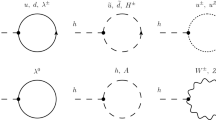
where the Higgs mass counterterm matrix is denoted by $\delta M_{hh}$ and the wave-function renormalization constant matrix by $\delta {Z}_{hh}$ in the basis $(h_d,h_u,h_s,a,a_s)$. In Fig. 1, the one-loop Feynman diagrams contributing to the unrenormalized self-energies $\Sigma _{h_i h_j} (p^2)$ are shown. In the following sections, we will discuss the counterterms and renormalization conditions in detail. We furthermore include the dominant two-loop corrections of order $\mathcal{O}(\alpha _s\alpha _t)$ [52] and $\mathcal{O}(\alpha _t^2)$ [33], which are available both for the real and for the complex NMSSM, to increase the precision for the phenomenological analysis presented in Sect. 5.

For the diagonalization of the loop-corrected mass matrix we apply the iterative method presented in [33, 52,53,54].⁵ For the loop-corrected n-th Higgs boson mass in the first iteration, the external momentum squared is set equal to the tree-level Higgs boson mass, $p^2 = m_{h_n}^2$. The obtained matrix is then diagonalized, yielding the n-th diagonal element. This value is then used as input momentum squared for the new iteration. The process is repeated until the change in $p^2$ between two consecutive iterations is less than $10^{-9}$. The n-th loop-corrected mass squared $M_{h_n}^2$ is then defined as the real part of the last iterative n-th diagonal element.⁶ The algorithm is repeated for all neutral Higgs boson masses. The loop-corrected masses are then sorted in ascending order, $M_{h_1} \le M_{h_2} \le M_{h_3} \le M_{h_4} \le M_{h_5}$. These loop-corrected masses obtained by the iterative method will be the outputs used in the decay width calculations and in the phenomenological study, if not stated otherwise.

Fig. 1

Generic Feynman diagrams contributing to the one-loop neutral Higgs self-energies. The indices k, l take several sets of values depending on the fields that they go with: $k,l=1,\ldots ,5$ for $x=h,\tilde{\chi }^0$, $k,l=1,\ldots ,3$ for $x=e,u,d,\tilde{e},\tilde{u},\tilde{d}$,  $k,l=1,\ldots ,18$ for $x=\tilde{n}$ and $k,l=1,\ldots ,9$ for $x=n$. The index $\gamma$ denotes the left- and right-handed scalars. Color indices for the quarks and squarks are suppressed

We now define the loop-corrected mixing matrix that will be used to compute the effective couplings of the Higgs bosons with gauge bosons, fermions and among themselves. We define the loop-corrected mixing matrix $R^0$ to be the rotation of the loop-corrected mass matrix in the approximation of vanishing external momentum,

$$\begin{aligned}&\text {diag}(M_{0,H_1}^2,M_{0,H_2}^2,M_{0,H_3}^2,M_{0,H_4}^2,M_{0,H_5}^2)\nonumber \\&\quad =R^0 \mathcal {M}_{hh}(0) (R^0)^T . \end{aligned}$$

(3.49)

The corresponding loop-corrected mass eigenvalues are denoted by an index 0 and sorted in ascending order, $M_{0,H_1} \le M_{0,H_2}\le M_{0,H_3} \le M_{0,H_4}\le M_{0,H_5}$. In this approximation, the mixing matrix $R^0$ is unitary but does not capture the proper OS properties of the external loop-corrected states as momentum-dependent effects are neglected. Using these thus defined mixing matrix elements, we obtain the Higgs effective couplings. Following the strategy presented in the NMSSMCALC [50], these Higgs effective couplings will be used to compute the Higgs decay widths, taking into account also higher-order QCD corrections when available.

3.2 Counterterms of the Higgs sector

Closely following the renormalization procedure at one-loop level described in [53, 54], we choose the following set of quantities as our independent input,

$$\begin{aligned}&\left( t_{h_d}, t_{h_u}, t_{h_s}, t_{a_d}, t_{a_s},e,M_W,M_Z,M_{H^\pm },\right. \nonumber \\&\quad \left. \tan \beta , v_s, \left| \lambda \right| , \left| \kappa \right| , \text { Re} A_\kappa , \varphi _\lambda , \varphi _\kappa , \varphi _u, \varphi _s\right) , \end{aligned}$$

(3.50)

where the five soft SUSY breaking parameters $\tilde{m}_{ H_d}^2,\tilde{m}_{H_u}^2,\tilde{m}_{S}^2, \text { Re} A_\lambda , \text { Re} A_\kappa$ have been replaced by the five independent tadpoles $t_{h_d}, t_{h_u}, t_{h_s}, t_{a_d}, t_{a_s}$ which vanish at tree level. The complex phases $\varphi _\lambda , \varphi _\kappa , \varphi _u, \varphi _s$ do not need to be renormalized at one-loop level. The remaining input parameters are replaced by the sum of the corresponding renormalized parameters and their counterterm as

$$\begin{aligned} t_{\phi }&\rightarrow t_{\phi } + \delta t_{\phi } \text { with } \phi = \left( h_d, h_u, h_s, a_d, a_s\right) \end{aligned}$$

(3.51)

$$\begin{aligned} M^2_{H^\pm }&\rightarrow M^2_{H^\pm } + \delta M^2_{H^\pm }\end{aligned}$$

(3.52)

$$\begin{aligned} M^2_{W }&\rightarrow M^2_{W} + \delta M^2_{W}\end{aligned}$$

(3.53)

$$\begin{aligned} M^2_{Z}&\rightarrow M^2_{Z} + \delta M^2_{Z}\end{aligned}$$

(3.54)

$$\begin{aligned} e&\rightarrow e(1 + \delta Z_e) \end{aligned}$$

(3.55)

$$\begin{aligned} \tan \beta&\rightarrow \tan \beta + \delta \tan \beta \end{aligned}$$

(3.56)

$$\begin{aligned} v_{s}&\rightarrow v_s + \delta v_s \end{aligned}$$

(3.57)

$$\begin{aligned} \left| \lambda \right|&\rightarrow \left| \lambda \right| + \delta \left| \lambda \right| \end{aligned}$$

(3.58)

$$\begin{aligned} \left| \kappa \right|&\rightarrow \left| \kappa \right| + \delta \left| \kappa \right| \end{aligned}$$

(3.59)

$$\begin{aligned} \text { Re} A_\kappa&\rightarrow \text { Re} A_\kappa + \delta \text { Re} A_\kappa \end{aligned}$$

(3.60)

The neutral Higgs boson counterterm matrix $\delta M_{hh}$ in (3.48) can be written in terms of the counterterms of the input parameters. The analytical expression of $\delta M_{hh}$ in terms of these counterterms can be found in Appendix C. In order to determine the counterterms, we need renormalization conditions. In this study, we use a mixture of the $\overline{\text {DR}}$and the OS scheme specified as

$$\begin{aligned}&\underbrace{t_{h_d}, t_{h_u}, t_{h_s}, t_{a_d}, t_{a_s}, e,M_W,M_Z,M_{H^\pm }}_{\text {OS scheme}},\nonumber \\&\underbrace{\tan \beta , v_s, \left| \lambda \right| , \left| \kappa \right| , \text { Re} A_\kappa }_{{\overline{\text {DR}}\text {scheme}}}. \end{aligned}$$

(3.61)

In our code, there is also the possibility to chose$\text { Re} A_\lambda$ to be the input parameter instead of the charged Higgs mass. In this case ${\Re A_\lambda }$ is renormalized in the $\overline{\text {DR}}$scheme, while $M_{H^\pm }$ is computed at the same order as the one of the neutral Higgs boson masses.

The neutral Higgs wave function renormalization constants are introduced for the neutral components of both doublets and the singlet as

$$\begin{aligned}&H_{d} \rightarrow \left( 1 + \frac{1}{2}\delta Z_{H_d}\right) H_d \ ,\quad H_{u}\rightarrow \left( 1 + \frac{1}{2}\delta Z_{H_u}\right) H_u ,\nonumber \\&S\rightarrow \left( 1 + \frac{1}{2}\delta Z_S\right) S . \end{aligned}$$

(3.62)

Hence the wave-function renormalization constant matrix introduced in (3.48) in the basis $\phi = (h_d, h_u, h_s, a, a_s)^T$ is given by

$$\begin{aligned}&\phi \rightarrow \left( 1 + \frac{1}{2}\delta {Z}_{hh}\right) \phi , \end{aligned}$$

(3.63)

$$\begin{aligned}&\delta {Z}_{hh} = \text {diag}\left( \delta Z_{H_d},\delta Z_{H_u}, \delta Z_S,s_\beta ^2 \delta Z_{H_d}+ c_\beta ^2 \delta Z_{H_u}, \delta Z_S\right) . \end{aligned}$$

(3.64)

3.2.1 The neutral wave function renormalization constants

We use the $\overline{\text {DR}}$scheme to define the Higgs wave function renormalization constants.⁷ The $\overline{\text {DR}}$scheme requires that the divergent part of the first derivative of the renormalized self-energies with respect to the momentum squared vanishes,

$$\begin{aligned} \widetilde{\text {Re}} \frac{\partial \hat{\Sigma }_{h_i h_j}(p^2)}{\partial p^2}\bigg |_{\text {div}} = 0, \quad \forall i,j=1,\ldots ,5 , \end{aligned}$$

(3.65)

where the notation $\widetilde{\text {Re}}$ means that only the real part of the loop integral is taken, and the superscript ‘div’ denotes the divergent part. This equation should hold for any external momentum. In practice we chose $p^2=0$. This renormalization condition leads to the equation

$$\begin{aligned} \delta {Z}_{h_ih_i} = - \left[ \mathcal {R}^T \widetilde{\text {Re}} \frac{\partial \Sigma _{hh}}{\partial p^2}\bigg |_{\text {div}} \mathcal {R}\right] _{ii}, \end{aligned}$$

(3.66)

which is real by definition and the off-diagonal elements vanish. Since $\delta {Z}_{hh}$ contains only three unknown variables $\delta Z_{H_u}, \delta Z_{H_d}$ and $\delta Z_S$, one needs a set of three independent equations. Any chosen set must give the same solution due to the $SU(2)_L$ symmetry.

3.2.2 Tadpole renormalization

The tadpole counterterms are defined such that the minima of the Higgs potential do not change at higher order. The tadpole counterterms hence have to cancel any contribution from the diagrams at one-loop level leading to the renormalization conditions

$$\begin{aligned} \delta t_\phi = t_\phi , \phi = h_d, h_u, h_s, a_d, a_s , \end{aligned}$$

(3.67)

with the one-loop tadpole diagrams contributing to $t_\phi$ depicted in Fig. 2.

3.2.3 Renormalization of $M_W,M_Z,M_{H^\pm }$

For the masses $M_W,M_Z$ of the massive gauge bosons as well as $M_{H^\pm }$ of the charged Higgs boson we apply OS renormalization by requiring that the pole of the corresponding two-point correlation function at one-loop level occurs at the value of the input mass. In particular, the mass counterterms are given by the unrenormalized self-energies as

$$\begin{aligned}&\delta M_{H^\pm }^2 = \widetilde{\text {Re}} \Sigma _{H^+ H^-} (M_{H^\pm }^2), \end{aligned}$$

(3.68)

$$\begin{aligned}&\delta M_W^2 = \widetilde{\text {Re}} \Sigma ^{T}_{WW} (M_W^2) , \end{aligned}$$

(3.69)

$$\begin{aligned}&\delta M_Z^2 = \widetilde{\text {Re}} \Sigma ^{T}_{ZZ} (M_Z^2), \end{aligned}$$

(3.70)

where the superscript T denotes the transverse parts of the respective self-energies. The wave function renormalization constants $\delta Z_{H^+H^-}$ for the charged Higgs boson, $\delta Z_{H^+G^-}$, $\delta Z_{H^+W^-}$ for the $H^+-G^+/W^+$ mixings, $\delta Z_{W^+W^-}$ for the W boson, $\delta Z_{Z^+Z^-}$ for the Z boson and $\delta Z_{ZG}, \delta Z_{Z\gamma }$ for the $Z-G/\gamma$ mixings are all renormalized in the OS scheme, so that there is no additional contribution to Eqs. (3.68)–(3.70).

Fig. 2

Generic Feynman diagrams contributing to the one-loop tadpole counterterms. The index k is given by $k=1,\dots ,18$ for $x=\tilde{n}$, $k=1,\dots ,5$ for $x=h,\chi ^0$, $k=1,\dots ,9$ for $x=n$ and $k=1,\dots ,3$ for $x=e,u,d,\tilde{e},\tilde{u},\tilde{d}$. The index $\gamma$ denotes the left- and right-handed scalars. Color indices for the quarks and squarks are suppressed

3.2.4 Renormalization of the electric charge

The electric charge is renormalized in the OS scheme [56, 57]. We take, however, the fine structure constant at the Z boson mass, $\alpha (M_Z^2)$, as input so that the counterterm is given by

$$\begin{aligned} \delta Z_e= & {} \frac{1}{2}\left. \frac{\partial \Sigma ^T_{\gamma \gamma }(k^2)}{\partial k^2} \right| _{k^2=0}\nonumber \\&+ \frac{s_W}{c_W} \frac{\Sigma ^T_{\gamma Z} (0)}{M_Z^2}- \frac{1}{2} \Delta \alpha (M_Z), \end{aligned}$$

(3.71)

$$\begin{aligned} \Delta \alpha (M_Z)= & {} \left. \frac{\partial \Sigma ^{\text {light},T}_{\gamma \gamma }(k^2) }{\partial k^2} \right| _{k^2=0} - \frac{\widetilde{\text {Re}} \Sigma ^{\text {light},T}_{\gamma \gamma }(M_Z^2) }{M_Z^2}, \end{aligned}$$

(3.72)

where the photon self-energy $\Sigma ^{\text {light},T}_{\gamma \gamma }$ includes only the light SM fermion (f with $m_f <m_t$) contributions.

3.2.5 Renormalization of $\tan \beta$

The ratio of the two vacuum expectation values, $\tan \beta$, is renormalized in the $\overline{\text {DR}}$scheme with the counterterm given by [58,59,60],

$$\begin{aligned} \delta \tan \beta = \left. \frac{1}{2}\tan \beta \left( \delta Z_{H_u} - \delta Z_{H_d}\right) \right| _{\text {div}}. \end{aligned}$$

(3.73)

3.2.6 Renormalization of the remaining $\overline{\text {DR}}$ quantities

The renormalization of the remaining $\overline{\text {DR}}$quantities, $\delta v_S, \delta \left| \lambda \right| , \delta \left| \kappa \right| , \delta \text {Re}A_k$ is defined such that

$$\begin{aligned} \hat{\Sigma }_{h_i h_j}\bigg |_{\text {div}} = 0. \end{aligned}$$

(3.74)

This system has more equations than the number of unknown counterterms. We need only four independent equations to solve for the four counterterms. Any set of four chosen equations resulted in the same values for the counterterms, confirming that the renormalization procedure works. The resulting counterterms are checked numerically against the ones extracted from the one-loop beta-functions and anomalous dimensions obtained from the package SARAH [44,45,46,47]. The differences between our computed counterterms and SARAH’s are less than one per-mille.

4 Constraints

In this section, we discuss all constraints that have been taken into account in our present study. Since we concentrate on the effects of the loop corrections of the extended (s)neutrino sector on the loop-corrected Higgs masses and their mixing, we consider here only the most relevant constraints from the Higgs data, the active light neutrino oscillations, the electroweak precision observables, and the lepton flavor-violating radiative decays $l_1 \rightarrow l_2 +\gamma$.

4.1 Higgs data

Our model, which contains five neutral and two charged Higgs bosons, must satisfy the experimental results on the $125\,~\text {GeV}$ Higgs boson and the experimental constraints on new scalars. For a parameter point, we will calculate the Higgs boson masses including the available two-loop corrections at $\mathcal{O}\left( \alpha _t\alpha _s+\alpha _t^2\right)$ described in Sect.  3 and the Higgs decay widths and branching ratios including the state-of-the-art higher-order QCD corrections which we take from the code NMSSMCALC [50]. To check if a parameter point passes all the exclusion limits from searches at LEP, Tevatron and LHC we make use of the code HiggsBounds-5 [61]. We provide the Higgs spectrum, decay widths, and the effective couplings as required by HiggsBounds in an SLHA file [62]. If the parameter point is allowed by HiggsBounds, it then will be checked against the $125\,~\text {GeV}$ Higgs boson data by using the code HiggsSignals [63]. We allow the uncertainty of the SM-like Higgs boson mass to be $3\,~\text {GeV}$ which means that at least one Higgs boson must have a mass in the range $[122, 128]\, ~\text {GeV}$. For the experimental data set, we use the “latestresults” option. Using our input parameters, HiggsSignals computes the $\chi ^2$ from 107 observables including the signal strength peak, simplified template cross sections, the LHC Run-1 signal rates, and Higgs masses. We allow the total $\chi ^2$ to vary within $2\sigma$ from the total $\chi ^2$ obtained from the SM Higgs boson. In HiggsSignals-2.5.1, the SM $\chi ^2$ is 84.44 and the $2\sigma$ for two degrees of freedom corresponds to a 6.18 $\chi ^2$ difference. Therefore the NMSSM $\chi ^2$ is allowed in the range [78.26, 90.62].

4.2 The active light neutrino data

In our neutrino sector, there are three light neutrinos which correspond to the three types of neutrinos observed in experiments. As discussed in Sect.  2, for the neutrino sector, we use the Casas–Ibarra parameterization. This means that we need three light mass values $m_{\nu _i}$, $i=1,2,3$, three angles and one complex phase of the PMNS matrix, three complex angles of the orthogonal matrix R, defined in Eq. (2.41), together with the matrices $\mu _X$ and $M_X$ to compute the mass matrix $M_D$ specified in (2.38). The obtained $M_D$ will be used to compute the neutrino Yukawa couplings $y_\nu$ and the neutrino mass matrix in (2.30). We then diagonalize this mass matrix using quadruple precision. The obtained mass eigenvalues $m_{n_j}$ ($j=1,\ldots ,9$) are the neutrino mass eigenvalues. From the $9\times 9$ neutrino mixing matrix we take the $3\times 3$ block which describes the mixing between the three light neutrinos and define

$$\begin{aligned} N_{ij} = U^{\nu }_{ij}, \quad i,j=1,2,3. \end{aligned}$$

(4.75)

The N matrix is not unitary and can be written as

$$\begin{aligned} N= (I-\eta )U_{\text {PMNS}}. \end{aligned}$$

(4.76)

We require that our input parameters, $m_{\nu _i}$, $i=1,2,3$, and $U_{\text {PMNS}}$, satisfy the active light neutrino data. We take the best fit points and the $3\sigma$ ranges from the global fit, NuFIT 5.0 [64]. For convenience, we list here the $3\sigma$ ranges for the mass differences and the mixing angles that are obtained from the combined analysis including the latest neutrino oscillation data presented at the “Neutrino2020” conference with the Super-Kamiokande atmospheric neutrino data. As usual, we define

$$\begin{aligned}&\Delta m_{ij}^2 =m_{\nu _i}^2 -m_{\nu _j}^2,\nonumber \\&U_{\text {PMNS}} =\begin{pmatrix} c_{12} c_{13} &{} s_{12}c_{13} &{} s_{13}e^{-i\delta _{CP}}\\ -s_{12}c_{23}- c_{12}s_{23}s_{13} e^{i\delta _{CP}}&{} c_{12}c_{23} - s_{12}s_{23}s_{13} e^{i\delta _{CP}} &{} s_{23}c_{13}\\ s_{12}s_{23}-c_{12}c_{23}s_{13} e^{i\delta _{CP}}&{} -c_{12}s_{23}- s_{12}c_{23}s_{13} e^{i\delta _{CP}} &{} c_{23}c_{13}\end{pmatrix}, \end{aligned}$$

(4.77)

where the short-hand notation $c_{ij}=\cos \theta _{ij}$ and $s_{ij}=\sin \theta _{ij}$ has been used. We request that

$$\begin{aligned} \Delta m_{21}^2\in [6.82,8.04] \times 10^{-5} \;~\text {eV}^2 , \quad s_{12}^2\in [0.269,0.343], \end{aligned}$$

(4.78)

and for the normal ordering

$$\begin{aligned} \Delta m_{31}^2&\in [2.435,2.598]\times 10^{-3}\,~\text {eV}^2,\nonumber \\ \quad s_{23}^2&\in [0.415,0.616],\nonumber \\ s_{13}^2&\in [0.02032,0.02410], \quad \delta _{CP} \in [120,369], \end{aligned}$$

(4.79)

and for the inverted ordering

$$\begin{aligned} \Delta m_{23}^2&\in [2.414,2.581]\times 10^{-3}\,~\text {eV}^2,\nonumber \\ \quad s_{23}^2&\in [0.419,0.617],\nonumber \\ s_{13}^2&\in [0.02052,0.02428], \quad \delta _{CP} \in [193,352]. \end{aligned}$$

(4.80)

In our analysis we use the constraint on the non-unitary N matrix that arises from a combined analysis of short and long-baseline neutrino oscillation data [65]. We use the three most stringent bounds at the 3$\sigma$ CL expressed in a parameterization-independent way, in particular

$$\begin{aligned} 1 - \sum _{k=1}^3 N_{e k}N_{e k}^*< & {} 0.07, \nonumber \\ 1 - \sum _{k=1}^3 N_{\mu k}N_{\mu k}^*< & {} 0.07, \nonumber \\ \sum _{k=1}^3 N_{e k}N_{\mu k}^*< & {} 0.03. \end{aligned}$$

(4.81)

This constraint will be denoted as non-unitary constraint in the numerical Sect. 5.2.

Furthermore, we use the Planck 2018 results for the upper limit of the sum of the three light neutrino masses,

$$\begin{aligned} \sum _{i=1}^3 m_{\nu _i} < 0.12 \, \text {eV}. \end{aligned}$$

(4.82)

Fig. 3

Generic Feynman diagrams contributing to the charged lepton flavor-violating decays $l_1 \rightarrow l_2 +\gamma$. The ranges of the indices are $i=1,\ldots ,18, k=1,2$ and $l=1,\ldots ,9$

4.3 The oblique parameters

The presence of the supersymmetric particles, multiple Higgs boson states and sterile neutrinos affects the masses and decay properties of the electroweak bosons and the low-energy data. We use the three well-known gauge self-energy parameters S, T and U [66] at the one-loop level to describe the effects arising from new particles. Following [67], we also define the parameters S, T, U from the transverse part of the gauge boson self-energies as

$$\begin{aligned} T&= \frac{1 }{\alpha }\left( \frac{\Pi ^{\text {new}}_{WW}(0)}{M_W^2}-\frac{\Pi ^{\text {new}}_{ZZ}(0)}{M_Z^2} \right) , \end{aligned}$$

(4.83)

$$\begin{aligned} S&= \frac{4 s^2_W c^2_W }{\alpha } \Bigg (\frac{\Pi ^{\text {new}}_{ZZ}(M_Z^2)-\Pi ^{\text {new}}_{ZZ}(0)}{M_Z^2} \nonumber \\&\quad -\frac{c_W^2-s_W^2}{s_Wc_W}\frac{\Pi ^{\text {new}}_{Z\gamma }(M_Z^2)}{M_Z^2} - \frac{\Pi ^{\text {new}}_{\gamma \gamma }(M_Z^2)}{M_Z^2}\Bigg ), \end{aligned}$$

(4.84)

$$\begin{aligned} S+U&=\frac{4 s^2_W}{\alpha } \Bigg (\frac{\Pi ^{\text {new}}_{WW}(M_W^2)-\Pi ^{\text {new}}_{WW}(0)}{M_W^2}\nonumber \\&\quad -\frac{c_W}{s_W}\frac{\Pi ^{\text {new}}_{Z\gamma }(M_Z^2)}{M_Z^2}- \frac{\Pi ^{\text {new}}_{\gamma \gamma }(M_Z^2)}{M_Z^2}\Bigg ), \end{aligned}$$

(4.85)

where the fine structure constant $\alpha$ is given at the scale $M_Z$. The superscript “new” means that we have subtracted the SM contribution computed with a Higgs boson mass of $125\,~\text {GeV}$ so that only new physics contributions remain. Using data from physics at the Z pole, [67] has found the following best fit point and $1\sigma$ uncertainties for these parameters,

$$\begin{aligned} T&= 0.03\pm 0.12, \end{aligned}$$

(4.86)

$$\begin{aligned} S&= -0.01\pm 0.10, \end{aligned}$$

(4.87)

$$\begin{aligned} U&= 0.02 \pm 0.11. \end{aligned}$$

(4.88)

In our analysis, a valid parameter point satisfies constraints on new physics if the S, T, U values vary within the $1\sigma$ uncertainty ranges around the best fit point.

4.4 The radiative $l_1 \rightarrow l_2 +\gamma$ decays

We work in the NMSSM in which the soft SUSY breaking mass matrices $\tilde{m}_L^2, \tilde{m}_E^2$ and trilinear couplings $A_{e}$ as well as the Yukawa couplings $y_e$ are diagonal in any basis. In general, if off-diagonal elements of these matrices exist, they have large effects on charged lepton flavor-violating (LFV) processes which have been severely constrained [68]. Although in our setting these matrices are flavor conserving, the presence of the low-scale sterile neutrinos and mixings with active neutrinos can still induce large charged LFV processes. The most constraining LFV processes are the radiative decays $\tau \rightarrow \mu \gamma$, $\tau \rightarrow e \gamma$ and $\mu \rightarrow e \gamma$, which are calculated in this section. The corresponding experimental bounds at 90% confidence level [67] are

$$\begin{aligned} \text {BR}(\mu ^- \rightarrow e^-\gamma ) \;&< \; 4.2 \times 10^{-13}, \end{aligned}$$

(4.89)

$$\begin{aligned} \text {BR}(\tau ^- \rightarrow e^-\gamma ) \;&< \; 3.3 \times 10^{-8}, \end{aligned}$$

(4.90)

$$\begin{aligned} \text {BR}(\tau ^- \rightarrow \mu ^-\gamma ) \;&< \; 4.4 \times 10^{-8}. \end{aligned}$$

(4.91)

These processes have been widely studied in the literature for non-supersymmetric models and the MSSM using the exact diagonalization of the mass matrices or using the mass insertion approximation, for a review see [69] and references therein. In our calculation we use the exact diagonalization of the relevant (s)neutrino mass matrices. We have used the model file obtained from SARAH to generate one-loop Feynman diagrams and amplitudes using FeynArts, and further simplified the amplitudes with the help of the package FeynCalc. The one-loop Feynman diagrams contributing to the decay processes

$$\begin{aligned} l_1 (p) \rightarrow l_2 (p-q) + \gamma (q) \end{aligned}$$

(4.92)

are depicted in Fig. 3. The amplitude of this process is given by

$$\begin{aligned} \mathcal{A}= i \epsilon ^*_\mu (q) \mathcal{M}^\mu , \end{aligned}$$

(4.93)

where $\epsilon _\mu$ denotes the polarization vector of the external photon. Using gauge invariance, $q_\mu \mathcal{M}^\mu = 0$, we can prove that $\mathcal{M}^\mu$ must take the form

$$\begin{aligned} \mathcal{M}^\mu = \bar{u}_2 \sigma ^{\mu \nu } q_\nu \left( F_L P_L + F_R P_R\right) u_1, \end{aligned}$$

(4.94)

where $\sigma ^{\mu \nu } = i/2 \left[ \gamma ^{\mu },\gamma ^\nu \right]$, $P_{L/R} = (1 \mp \gamma _5)/2$ and $F_{L/R}$ are left- and right-handed form factors. The partial width is then given by

$$\begin{aligned} \Gamma (l_1\rightarrow l_2 \gamma ) = \frac{m_1^3}{16\pi } \left( |F_L|^2 + |F_R|^2\right) , \end{aligned}$$

(4.95)

where $m_1$ is the mass of $l_{1}$ and we have neglected the mass of $l_2$ since $m_2 \ll m_1$ for the processes considered here. Following the common procedure presented in [70], the branching ratios of the decays $l_1\rightarrow l_2 \gamma$ can be written in terms of the branching ratios of $l_1\rightarrow l_2\bar{\nu }_2 \nu _1$ which are experimentally measured. In the NMSSM, the tree-level decay width for the decays $l_1\rightarrow l_2\bar{\nu }_2 \nu _1$ is the same as that of the SM, i.e.

$$\begin{aligned} \Gamma (l_1\rightarrow l_2\bar{\nu }_2 \nu _1) = \frac{G_F^2 m_1^5}{192 \pi ^3}; \end{aligned}$$

(4.96)

therefore,

$$\begin{aligned}&\text {BR}(l_1\rightarrow l_2 \gamma ) \nonumber \\&=\frac{12\pi ^2}{G_F^2 m_1^2} \left( |F_L|^2 + |F_R|^2\right) \text {BR}(l_1\rightarrow l_2\bar{\nu }_2 \nu _1). \end{aligned}$$

(4.97)

We use the following numerical values taken from [68] for the branching ratios,

$$\begin{aligned}&\text {BR}(\mu \rightarrow e\bar{\nu }_e \nu _\mu ) = 1, \quad \text {BR}(\tau \rightarrow e\bar{\nu }_e \nu _\tau ) = 17.82 \%, \nonumber \\&\text {BR}(\tau \rightarrow \mu \bar{\nu }_\mu \nu _\tau ) = 17.39 \%. \end{aligned}$$

(4.98)

The contributions to the form factors in our model can be decomposed into three parts as

$$\begin{aligned} F_{L,R} = F^{W^\pm }_{L,R} + F_{L,R}^{H^\pm } + F_{L,R}^{\tilde{\chi }^\pm } , \end{aligned}$$

(4.99)

where $F^{W^\pm }_{L,R}, F_{L,R}^{H^\pm }$ and $F_{L,R}^{\tilde{\chi }^\pm }$ denote the contributions from the one-loop diagrams with $W^\pm$ and charged Goldstone bosons, charged Higgs bosons and charginos, respectively, on the internal lines. Their explicit expressions are given in Appendix A. Since in the numerical analysis, all the $\overline{\text {DR}}$input parameters are given at the SUSY scale, we do not consider contributions from the off-diagonal elements of $\tilde{m}_L^2, \tilde{m}_E^2,A_{e}$ due to the renormalization group equations as discussed in [39].

It is also possible to keep the lepton masses of the external lines in the three-point loop integrals. However, we explicitly checked that the differences between the branching ratios obtained with the full lepton masses using Mathematica and the ones with zero lepton masses are below the per-mille level. The same result has been found in the Standard Model case [71]. We, therefore, use the zero lepton mass approximation implemented in the code NMSSMCALC-nuSS in the numerical analysis.

5 Numerical analysis

In this section we will discuss the numerical impact of the neutrino and sneutrino sectors on the loop-corrected neutral Higgs boson masses and on the charged lepton flavor-violating decays. We have performed a scan over the parameter space of our model to obtain parameter points that satisfy all our constrains mentioned in Sect.  4. We chose SM input parameters as [67, 72]

The light neutrino inputs are in the normal ordering and according to the constraints in Sect. 4.2 are chosen randomly in the following ranges

$$\begin{aligned}&m_{\nu _1} \in [0, 2.98152\times 10^{-11}] \,~\text {GeV}, \nonumber \\&m_{\nu _2} \in \bigg [\sqrt{ m_{\nu _1}^2 + 6.82\times 10^{-23}},\nonumber \\&\sqrt{ m_{\nu _1}^2 + 8.04\times 10^{-23}} \bigg ]\, ~\text {GeV},\nonumber \\&m_{\nu _3} \in \bigg [\sqrt{ m_{\nu _1}^2 + 2.435\times 10^{-21}},\nonumber \\&\sqrt{ m_{\nu _1}^2 + 2.598\times 10^{-21}} \bigg ]\, ~\text {GeV},\nonumber \\&\theta _{12} \in [\arcsin (\sqrt{0.269}),\arcsin (\sqrt{0.343})],\nonumber \\&\theta _{23} \in [\arcsin (\sqrt{0.415}),\arcsin (\sqrt{0.617})],\nonumber \\&\theta _{13} \in [\arcsin (\sqrt{0.02052}),\arcsin (\sqrt{0.02428})],\nonumber \\&\delta _{CP} \in [120,369]. \end{aligned}$$

(5.101)

Following the convention of the SUSY Les Houches Accord (SLHA) format [62], the soft SUSY breaking masses and trilinear couplings are understood as $\overline{\text {DR}}$ parameters at the scale

$$\begin{aligned} \mu _R = M_{\text {SUSY}}= \sqrt{m_{\tilde{Q}_3} m_{\tilde{t}_R}} . \end{aligned}$$

(5.102)

This is also the renormalization scale that we use in all of our computations of the higher-order corrections. In the Higgs sector we use per default the mixed $\overline{\text {DR}}$-OS scheme specified in Sect.  3.2 and the OS charged Higgs boson mass as input parameters. Furthermore, we choose OS renormalization for the top/stop sector and include the two-loop corrections of order $\mathcal{O}(\alpha _s\alpha _t +\alpha _t^2)$ which are computed in [32, 33] and are implemented in NMSSMCALC. We perform the scan in the framework of the CP-violating NMSSM where we chose the phase $\delta _{CP}$ in the neutrino sector as the only non-vanishing complex phase. All other SUSY parameters are assumed to be real and are varied in the ranges specified in Table  2.

Table 2 Scan ranges for the random scan over the NMSSM parameter space

The remaining parameters are fixed as follows

$$\begin{aligned}&M_3= 1850\,~\text {GeV}, \quad m_{\tilde{Q}_{1/2}}=m_{\tilde{L}_{1/2}}=m_{\tilde{x}_R}= 3\,~\text {TeV},\nonumber \\&A_{b,\tau }= 2\,~\text {TeV}\end{aligned}$$

(5.103)

where $x=u,d,c,s,b,e,\mu$. To ensure perturbativity below the GUT scale [73] we omit points with

$$\begin{aligned} \kappa ^2 +\lambda ^2 >(0.7)^2, \end{aligned}$$

(5.104)

and/or any element of the neutrino Yukawa matrix $y_\nu$ being larger than $\sqrt{4\pi }$. Note that in our numerical analysis we take the various input parameters of the (s)neutrino sector to be the same for all three generations.

5.1 Impact of the (s)neutrinos on the loop-corrected Higgs boson masses

For the investigation of the impact of the (s)neutrino contributions on the loop-corrected Higgs boson masses we choose a parameter point from our generated scan sample satisfying all the described constraints. We subsequently vary individual parameters of the neutrino and/or sneutrino sectors to analyze their impact on the loop-corrected Higgs boson masses. Our chosen parameter point is called P1. The light neutrino input parameters are set equal to their best-fit values together with a fixed value for the lightest neutrino mass, in particular,

$$\begin{aligned}&m_{\nu _1} = 10 ^{-11} \quad&\theta _{12} = \arcsin (\sqrt{0.297}),\\&m_{\nu _2} = \sqrt{ m_{\nu _1}^2 + 7.37\times 10^{-23}}\, ~\text {GeV},\quad&\theta _{23} = \arcsin (\sqrt{0.425}),\\&m_{\nu _3} = \sqrt{ m_{\nu _1}^2 + 2.525\times 10^{-21}}\, ~\text {GeV}\quad&\theta _{13}= \arcsin (\sqrt{0.0215}),\\&\delta _{CP} = 248.4^\circ . \end{aligned}$$

All other complex phases are set to zero and the remaining input parameters are given by

$$\begin{aligned} M_{H^\pm }&= 850 \, ~\text {GeV},\qquad m_{\tilde{X}} =1\, ~\text {TeV}, \nonumber \\ M_1&=660 \, ~\text {GeV},\qquad m_{\tilde{N}} =1 \, ~\text {TeV}, \nonumber \\ M_2&=580 \, ~\text {GeV},\qquad A_{\nu } =1.2 \, ~\text {TeV}, \nonumber \\ {\mu _{\text {eff}}}&=208 \, ~\text {GeV},\qquad A_{X} =1 \, ~\text {TeV}, \nonumber \\ m_{\tilde{Q}_3}&= 1300 \, ~\text {GeV},\qquad \mu _X =40 \, ~\text {TeV}, \nonumber \\ m_{\tilde{t}_R}&=1100 \, ~\text {GeV},\qquad B_{\mu _X} =1 \, ~\text {TeV}, \nonumber \\ m_{\tilde{\tau }_R}&=1900 \, ~\text {GeV},\qquad \lambda _X =6.5 \times 10^{-10}, \nonumber \\ A_t&=-1500 \, ~\text {GeV},\qquad \theta _{1} =2 , \nonumber \\ \text{ Re } A_k&=-791 \, ~\text {GeV},\qquad \theta _{2} =3 , \nonumber \\ \tan \beta&=4.4 ,\qquad \theta _{3} =4 , \nonumber \\ \lambda&= 0.30 ,\qquad \kappa =0.30 . \end{aligned}$$

(5.105)

In Table  3, we present the Higgs mass spectrum with and without inverse seesaw mechanism at tree-level, one-loop, two-loop $\mathcal{O}\left( \alpha _t\alpha _s\right)$ and two-loop $\mathcal{O}\left( \alpha _t \alpha _s + \alpha _t^2\right)$. The main components of the Higgs mass eigenstates are also shown in the last row. We have chosen the OS condition for the top/stop sector. In order to quantify the impact of the (s)neutrino contributions on the Higgs boson masses we define the relative correction $\Delta _i$ as

$$\begin{aligned} \Delta _i= \left| \frac{M_{i} -M_{i}^{\text {no}} }{M_{i}^{\text {no}}} \right| \, \end{aligned}$$

(5.106)

where $M_i$ is the loop-corrected mass of the Higgs boson i computed in the NMSSM with ISS and $M_{i}^{\text {no}}$ the one in the NMSSM without ISS. Note that the NMSSM without ISS mechanism contains three massless neutrinos and three complex sneutrinos which do not mix with each other. The massless neutrinos do not interact with the Higgs bosons while the sneutrinos couple to the Higgs bosons through the D-terms with couplings proportional to $g_1$ and $g_2$. For this parameter point the second lightest Higgs boson is the $h_u$-like one and hence behaves SM-like. The $h_s$-like Higgs boson is the lightest one with a mass of $90\,~\text {GeV}$. The $h_d$- and a-like states have masses of about $850\,~\text {GeV}$ while the $a_s$-like Higgs boson mass is about $700\,~\text {GeV}$. Although we have a non-zero complex phase in the $U_{\text {PMNS}}$ matrix, the mixing between CP-even and CP-odd states is negligible. The $h_u$-like Higgs boson mass is affected the most by the inclusion of the ISS mechanism which raises $M_{h_u}$ by about $7 \,~\text {GeV}$, $5\,~\text {GeV}$ and $5.6\,~\text {GeV}$ at one-loop level, $\mathcal{O}\left( \alpha _t \alpha _s \right)$ and $\mathcal{O}\left( \alpha _t^2\right)$, respectively. If we quantify this change by using the relative correction defined in (5.106) we see that $\Delta _{h_u}$ is about $5.3\%$ at one-loop level, then decreases to $4.2\%$ at $\mathcal{O}\left( \alpha _t\alpha _s\right)$ and reaches $4.7\%$ at $\mathcal{O}\left( \alpha _t \alpha _s + \alpha _t^2\right)$. We remind the reader that we have used the iterative method to evaluate the loop-corrected Higgs boson masses. This means that we have mixed orders of perturbation theory. As common in supersymmetric theories, loop contributions from particles and their superpartners are opposite in sign. This is the case for the neutrinos and sneutrinos here as well. While the sneutrinos give positive contributions to the mass $M_{h_u}$, those of the neutrinos are negative. Soft-SUSY breaking terms together with electroweak symmetry breaking prohibit the cancellation between the two contributions. We will elaborate this further in the following by varying parameters related to the change of these two contributions. We finish our comments on Table  3 by remarking that the other Higgs boson masses are only slightly changed by the ISS for this particular point.

Table 3 Parameter point P1: mass values in GeV and main components of the neutral Higgs bosons at tree-level, one-loop, two-loop $\mathcal{O}\left( \alpha _t\alpha _s\right)$ and two-loop $\mathcal{O}\left( \alpha _t \alpha _s + \alpha _t^2\right)$ obtained for the NMSSM without or with the inverse seesaw mechanism together with $\text {OS}$ conditions in the top/stop sector

Fig. 4

Parameter point P1: The loop-corrected Higgs boson masses in GeV at order $\mathcal{O}\left( \alpha _t \alpha _s + \alpha _t^2\right)$ as function of the parameter $\lambda _X$ (upper left) and of $\mu _X$ (upper right) The relative corrections $\Delta$ defined in (5.106) are shown in the lower panels. The five Higgs boson masses are denoted by their main components ($h_u,h_d,h_s,a,a_s$) corresponding to the five colors (red, black, blue, yellow, green). The gray area on the plots denotes the points satisfying our constraints. $Y_{\nu }^{\text {max}}$ denotes the maximum element of the neutrino Yukawa matrix

We continue by investigating the effects of the various neutrino parameters on the loop-corrected Higgs boson masses. From now on we present only the masses at two-loop $\mathcal{O}\left( \alpha _t \alpha _s + \alpha _t^2\right)$ which is the highest precision of our numerical code that includes the ISS.⁸ In Fig. 4 we show the dependence of the loop-corrected Higgs boson masses on the coupling $\lambda _X$ in the left panel and on the mass $\mu _X$ in the right panel and the dependence of the correction $\Delta$ defined in (5.106) in the lower panels. We remind the reader that both $\lambda _X$ and $\mu _X$ appear in the neutrino mixing matrix as shown in (2.30) and (2.31). In the Casas–Ibarra parameterization which is used in our computation, both $\lambda _X$ and $\mu _X$ enter the evaluation of the neutrino Dirac mass matrix $M_D$, see (2.38), therefore directly affect the neutrino Yukawa matrix $Y_\nu =\sqrt{2} M_D/(v_u e^{i\varphi _u})$ that can be written as

$$\begin{aligned} Y_\nu \propto \frac{m_\nu \sqrt{\mu _X}}{v_u\sqrt{\lambda _X v_s}}. \end{aligned}$$

(5.107)

We denote the maximum element of the neutrino Yukawa matrix by $Y_{\nu }^{\text {max}}$. We chose the range of variation for $\lambda _X$ and $\mu _X$ such that $Y_{\nu }^{\text {max}}$ is smaller than the perturbativity limit $\sqrt{4\pi }$ applied in our analysis. On the x-axis on top of each plot in Fig. 4, we see the variation of $Y_{\nu }^{\text {max}}$ corresponding to the range of variation for $\lambda _X$ and $\mu _X$. For our chosen parameter point P1, the value of $Y_{\nu }^{\text {max}}$ is equal to 1.15. As can be inferred from the plots, the impact from the (s)neutrino sector is less than 2.3% on $M_{h_u}$ if $Y_{\nu }^{\text {max}}$ is smaller than 0.85 (0.89) corresponding to $\lambda _X> 1.2\times 10^{-9}$ ($\mu _X<31\, ~\text {TeV}$) in the left (right) plot. With increasing value of $Y_{\nu }^{\text {max}}$ ($\lambda _X$ becomes smaller or $\mu _X$ gets larger) the effect increases significantly. The relative correction $\Delta _{h_u}$ can even go up to 100% for $\lambda _X=1.24\times 10^{-10}$ ($Y_{\nu }^{\text {max}}=2.63$) or $\mu _X=83\,~\text {TeV}$ ($Y_{\nu }^{\text {max}}=2.39$). This makes us question the perturbativity limit of $\sqrt{4\pi }$ applied on $Y_{\nu }^{\text {max}}$ at the SUSY scale. A more stringent constraint that demands $Y_{\nu }^{\text {max}}<\sqrt{4\pi }$ up to the Planck scale may imply a much smaller value for $Y_{\nu }^{\text {max}}$ at the SUSY scale. A recent study in [75] found that $Y_{\nu }^{\text {max}}<0.8$ at the TeV scale for the SM with inverse seesaw mechanism. We expect a similar value for the model in our study. The large value of $\mu _X$ results in large mass values for the sterile neutrinos and additional sneutrinos. One then has to worry about the validity of the fixed-order calculation used in the computation of the Higgs mass corrections. In order to understand the role of $y_\nu$ and $\mu _X$, we present in Appendix D the approximate expressions for the additional contributions from the NMSSM with inverse seesaw mechanism after subtracting the usual NMSSM contributions to the renormalized $h_u$-like Higgs self-energy. Caution should be taken here when using these approximate formulae to reproduce the results. We have applied many conditions specified in the appendix to derive these approximate formulae. We have checked that the expression given in Eq. (D.166) can deviate by about 10% from the full one-loop (s)neutrino corrections with full momentum dependence and mixing between different neutral Higgs bosons. If the specified conditions are not satisfied, however, the deviation can be much larger and these approximations are not reliable. In (D.172), there is a term proportional to $\log \left( \frac{\mu _X}{\mu _R}\right)$ which causes large corrections if $\mu _X\gg \mu _R$. The question of what should be done to improve the precision and to reduce the theoretical uncertainty of the loop-corrected Higgs masses will be left for future study. In this study we retain parameter points where $\log \left( \frac{\mu _X}{\mu _R}\right)$ is less than four. The question whether this logarithm is the main source of the large correction can be answered by choosing a much smaller value for $\mu _X$, for example of $\mathcal{O}(\mu _R)$. We can still get a large value for $\Delta _{h_u}$, as long as $Y_{\nu }^{\text {max}}$ is large. In particular, for $\mu _X =1500\,\text {GeV}$ and $\lambda _X = 1.8\times 10^{-12}$, $\Delta _{h_u}$ is of order $5\%$. With a low mass spectrum of sterile neutrinos and sneutrinos one can get large branching ratios for the charged lepton flavor-violating processes $l_1 \rightarrow l_2 +\gamma$ that will be discussed in Sect. 5.2. The parameter point with $\mu _X =1500\,\text {GeV}$ and $\lambda _X = 1.8\times 10^{-12}$ does not pass the charged lepton flavor-violating constraint. The question arises whether $\Delta _{h_u}\sim 5\%$ with low $\mu _X$ can be realized for parameter points satisfying all our considered constraints. We can find such parameter points where $M_D$ in (2.38) is almost a diagonal matrix. As a result, the decay widths of $l_1 \rightarrow l_2 +\gamma$ are close to zero, since they are proportional to off-diagonal components of $y_\nu$. In such a case, it may be better to use, for example, the $\mu _X$-parameterization [76] instead of the Casas–Ibarra parameterization. In the $\mu _X$-parameterization, $\lambda _X$ is not an input parameter but computed from the relations

$$\begin{aligned} M_X= & {} \mu _X^T M_D^{-1} U_{\text {PMNS}}^* m_\nu U_{\text {PMNS}}^\dagger M_D^{T,-1} \mu _X, \nonumber \\ M_X= & {} \frac{v_se^{i\varphi _s}}{\sqrt{2}} (\lambda _X + \lambda _X^T), \end{aligned}$$

(5.108)

where $y_\nu$ is now an input parameter. One can easily choose $y_\nu$ to be the unit matrix, then with $\mu _X =1500\,\text {GeV}$, one can get $\Delta _{h_u}\sim 5\%$.

From Fig. 4, we see that not only the $h_u$-like Higgs boson is strongly affected by large $Y_{\nu }^{\text {max}}$ but also the $h_d$- and $h_s$-like states. While both the $h_{u}$- and $h_d$-like Higgs boson mass get positive corrections, the $h_{s}$-like Higgs boson mass receives negative corrections. On the left plot $\Delta _{h_{d}}$ can go up to $21\%$ at $Y_{\nu }^{\text {max}}=2.93$ while $\Delta _{h_{s}}$ goes to 12%. Note that neutrinos interact with $h_u$ interaction states through the interaction term $h_u \bar{\nu }_i(Y_\nu P_L+Y_\nu ^\dagger P_R )\nu _j$ and with $h_s$ through the interaction term $h_s\bar{\nu }_i(\lambda _X P_L + \lambda _X^\dagger P_R)\nu _j$ where $\lambda _X$ is a very small number. Neutrinos do not interact with $h_d$, but sneutrino do interact through D-terms. For this particular parameter point, the dominantly $h_d$- and $h_s$-like Higgs mass eigenstates have a significant admixture of the $h_u$ component. The impact of the neutrinos on the other Higgs bosons depends on their mixtures with $h_u$. The states a and $a_s$ are less affected.

Fig. 5

The same as Fig. 4 but now we show the dependence on: a the neutrino trilinear coupling parameter $A_\nu$ and b the complex phase of $A_\nu$. The gray triangles denote the points satisfying our constraints

We now move on to the discussion of the dependence of the loop-corrected Higgs boson masses on the neutrino trilinear coupling parameter $A_\nu$ that affects only the sneutrino sector and leaves the neutrino sector unchanged. In Fig. 5 we vary the value of $A_\nu$ in the left plots and the complex phase of $A_\nu$ in the right plots. The color code and notation of the left plots are the same as in Fig. 4. In the right plot, we show only the loop-corrected mass of the $h_u$-like Higgs boson, since the impact of the complex phase on the other Higgs boson masses is negligible. As can be inferred from the plots, the loop-corrected $h_u$-like Higgs boson mass is strongly affected by $A_\nu$. This dependence looks like the dependence on the top trilinear coupling $A_t$ and its complex phase, see for example [32, 33], but the relative size of the corrections can cover a larger range if $Y_{\nu }^{\text {max}}$ is large. The correction $\Delta _{h_u}$ is about 4.7% at $A_\nu = 0$ and maximal (14.5%) at $A_\nu \approx \pm 26\,~\text {TeV}$. The $h_s$-like Higgs boson mass depends slightly on $A_\nu$ while the other Higgs boson masses are barely affected by the variation of $A_\nu$. We remind the reader that the maximum value of $Y_\nu$ that is obtained during the variation of $A_\nu$ is given by $Y_{\nu }^{\text {max}}= 1.15$. In our analysis we also reduced $Y_{\nu }^{\text {max}}$ to 0.8 by setting $\lambda _X=1.33\times 10^{-9}$ and varying $A_\nu$. We then obtained the variation of $\Delta _{h_u}$ in the range [2, 3.6]%. In the right panel of Fig. 5, we observe a change of $0.08\%$ for $\Delta _{h_u}$ when the complex phase $\varphi _{A_\nu }$ is varied in the range $[-\pi ,\pi ]$. Other complex phases of the neutrino sector like $\delta _{CP}$, of the phases of $\lambda _X,$ and $\mu _X$ have an insignificant impact on the loop-corrected Higgs masses.

Note that in Figs. 4 and 5 we present parameter points that satisfy all constraints by the gray area, respectively, the gray triangles. The other points violate charged flavor-violating lepton decays, the S,  T,  U parameters and/or the Higgs data.

In the remainder of this section, we present scatter plots in Fig. 6 which we obtained from our scan keeping only parameter points that satisfy all our mentioned constraints. The points are depicted in two-dimensional planes with $M_X$ on the x-axis and $\mu _X$ on the y-axis. Note that $M_X$ is related to $\lambda _X$ and $v_s$ as given in (2.31). Since $\lambda _X$ and $v_s$ are both varied in the scan, $M_X$ may be a more appropriate parameter than $\lambda _X$ for the scatter plots. The color code in the plot quantifies the size of the relative corrections $\Delta$ for the respective Higgs boson in the individual plots. The light gray points denote $\Delta \le 0.2\%$, gray $0.2\%<\Delta \le 0.5\%$, violet $0.5\%<\Delta \le 1\%$, purple $1\%<\Delta \le 2\%$, yellow $2\%<\Delta \le 5\%$, orange $5\%<\Delta \le 10\%$ and green $10\%<\Delta \le 20\%$. The left plot of the Fig. 6 presents the relative corrections for the $h_u$-like Higgs boson, while the right plot for the $h_d$-like state. The $\Delta$ for the other Higgs bosons are less significant and therefore we do not present them here.

Most of the points obtained in our scan have small relative corrections $\Delta \le 0.2\%$. Larger relative corrections are realized for $\mu _X$-$M_X$ towards the top-left corner of each plot, corresponding to increasing values of $Y_{\nu }^{\text {max}}$. In the top-left corner, there are no points because they either violate the perturbativity constraint of $Y_{\nu }^{\text {max}}<\sqrt{4\pi }$ or they lead to unstable numerical results due to large corrections. The color pattern is rather clear for the $h_u$-like Higgs boson, which confirms our conclusion on the strong dependence of $\Delta _{h_u}$ on $Y_{\nu }^{\text {max}}$. There are some outliers which do not lie in their color bands, since $\Delta _{h_u}$ depends not only on $Y_{\nu }^{\text {max}}$ but also on the sneutrino soft SUSY breaking parameters.

Fig. 6

Scatter plots in the plain of two variables of the neutrino sector, $(M_X,\mu _X)$ for the $h_u$-like (left) and the $h_d$-like (right) Higgs boson. The color code indicates the relative correction $\Delta$ (defined in (5.106)) for each Higgs state in percent

5.2 Impact of the (s)neutrinos on the LFV decays

In this section, we investigate the impact of the neutrinos and sneutrinos in the NMSSM with ISS on the radiative $l_1\rightarrow l_2\gamma$ decays. As explained in Sect. 4.4, we consider three decay processes, namely $\mu \rightarrow e\gamma$, $\tau \rightarrow e\gamma$, and $\tau \rightarrow \mu \gamma$ among which the most stringent constraint exists for the decay $\mu \rightarrow e\gamma$. For all processes, the dominant contributions arise from the right-handed form factors $F_R$. The ratio between the contributions from the right- and left-handed form factors is approximately proportional to the ratio $m_{l_1}^2/m_{l_2}^2$ as can be inferred from the analytic expressions in Appendix A. One can therefore safely neglect the contribution from the left-handed form factors. We have divided the contributions to the form factors into three parts given by $F_{L,R}^{W^\pm }$, $F_{L,R}^{H^\pm }$, and $F_{L,R}^{\tilde{\chi }^\pm }$.

In our scan, the constraint on $\mu \rightarrow e\gamma$ is very important and rules out many points. The branching ratios are very sensitive to the spectrum of the neutrino and sneutrino sectors. In particular, they increase when the mixings between sterile neutrinos and active neutrinos increase. Both $\mu _X$ and $\lambda _X$ have strong impacts on these mixings. We investigate this dependence by taking the parameter point P1 of the previous section and varying again the parameters $\mu _X$ and $\lambda _X$.

In the left plot of Fig. 7, we show the dependence of the branching ratio (red line) for the decay $\mu \rightarrow e\gamma$ on $\lambda _X$. We also depict the individual contributions from the squared form factors $(F_{L,R}^{x})^2$ with $x=W^\pm$ (black), $H^\pm$ (blue), and $\tilde{\chi }^\pm$ (orange) lines, as well as the interference terms $2(F_{L,R}^{x})(F_{L,R}^{y})$ with $(x,y)=(W^\pm ,H^\pm )$ (green) $(W^\pm ,\tilde{\chi }^\pm )$ (purple), and $(H^\pm ,\tilde{\chi }^\pm )$ (yellow). For this parameter point scenarios, we find that the contributions from the W boson and from the charged Higgs boson are dominant, and the interference term between the W boson and charged Higgs form factors adds a significant contribution to the sum. We observed that the form factors $F_{L,R}^{W^\pm }$ and $F_{L,R}^{H^\pm }$ have the same sign while they are opposite in sign compared to $F_{L,R}^{\tilde{\chi }^\pm }$. The chargino contributions hence suppress the total decay widths. In the right plot of Fig. 7, we present the branching ratios for the three considered decay processes, $\mu \rightarrow e\gamma$, $\tau \rightarrow e\gamma$, and $\tau \rightarrow \mu \gamma$. We observe that the branching ratio for the process $\mu \rightarrow e\gamma$ is larger than for the other two processes. While the contributions from the W boson and charged Higgs form factors depend only on the spectrum and mixing of the neutrinos, the chargino contributions depend on those of the sneutrinos. One can vary the parameters of the sneutrino sector such as $m_{\tilde{N}}$ and $m_{\tilde{X}}$ to change the sign and the magnitude of the chargino contributions. We show the dependence of the branching ratio (red line) for the decay $\mu \rightarrow e\gamma$ on $m_{\tilde{N}}$ and $m_{\tilde{X}}$ in the left and right plot of Fig. 8, respectively.

Fig. 7

Left: Branching ratio and its individual contributions for the decay $\mu \rightarrow e\gamma$ as a function of $\lambda _X$. The interference contributions $W^\pm \times \tilde{\chi }^\pm$ between the chargino and the $W^\pm$ form factors (violet), and $H^\pm \times \tilde{\chi }^\pm$ between the chargino and charged Higgs form factors (yellow) are negative. In order to present them in one plot we have changed the sign. The black line for $W^\pm$ is hidden under the blue line and the purple line is under the yellow one. The horizontal black line shows the experimental upper limit on the branching ratio. Right: Branching ratios for the three decays $\mu \rightarrow e\gamma$ (red), $\tau \rightarrow e\gamma$ (black), and $\tau \rightarrow \mu \gamma$ (blue) as function of $\lambda _X$

Fig. 8

Same as the left plot of Fig. 8, but $m_{\tilde{N}}$ (left) and $m_{\tilde{X}}$ (right) are varied instead

Fig. 9

Scatter plot in the $\mu _X$ and $\lambda _X$ plane starting from the parameter point P1. The color code is used to distinguish between points that pass all three constraints LFV, STU, NoU (light gray), that do not pass any of the three constraints (dark gray) and that violate individual constraints or combinations of two constraints: LFV (green), STU (orange), LFV and STU (pink), LFV and NoU (yellow). See text for details

We now investigate the impact of the parameters in the neutrino sector on the S, T, U parameters (STU), on the LFV decays and on the non-unitary $3\times 3$ neutrino mixing matrix (NoU) discussed in Sect. 4.2. We started from the parameter point P1 and we changed only the following parameters in the corresponding ranges,

$$\begin{aligned} \mu _X \in [10,10^5] ~\text {GeV},\quad \lambda _X\in [10^{-14}, 10^{-4}]. \end{aligned}$$

(5.109)

All remaining parameters are kept fixed. We show in Fig. 9 a scatter plot in the plane of $\mu _X$ and $\lambda _X$. We have considered also the HiggsBounds and the HiggsSignals constraints, but simply not shown in this particular plot since we want to focus on the three mentioned constraints. The gray color denotes points which pass all three constraints while dark gray reflects points that violate all three constraints. The orange and green colors are for points violating STU and LFV constraints, respectively. The pink and yellow points, respectively, violate combinations of two constraints, namely LFV-STU and LFV-NoU. The white area on the plot is not accessible since we encounter either negative values for one of the Higgs boson masses or $Y_{\nu }^{\text {max}}>\sqrt{4\pi }$. As can be inferred from the plot, small values of $\lambda _X$ () are not preferred, independent of $\mu _X$, since this parameter region is very sensitive to the constraints from LFV and NoU. For $\lambda _X>10^{-12}$, the STU constraint is important in the region $\mu _X\in [10^3,10^4]~\text {GeV}$ and for $\mu _X=320$ GeV, independent of $\lambda _X$. There are also regions such as $\mu _X<300\,~\text {GeV}$ or $\mu _X>20\,~\text {TeV}$ with $\lambda _X>8\times 10^{-10}$ where the three mentioned constraints do not play a role. This plot demonstrates the importance of taking into account the STU and LFV constraints when performing numerical analysis. Although the magnitude of $\lambda _X$ signifies the magnitude of charged lepton flavor violation, i.e. the larger $\lambda _X$ is the more violation we would expect, the reverse happens here. The reason is as follows. When we fix light neutrino masses $m_\nu$, $\lambda _X$ becomes inversely proportional to $y_\nu$. Smaller $\lambda _X$, or larger $y_\nu$, yields a larger mixing between sterile and active neutrinos, or a weaker GIM mechanism, and thus a larger LFV decay rate. This is also why small values of $\lambda _X$ violate unitarity. Note that in our scan, we have assumed $\lambda _X$ and $\mu _X$ to be diagonal. The results will change if these assumptions are not applied. Especially in the case where the off-diagonal components of $y_\nu$ are close to zero, and the LFV constraint is not as severe as in our case.

6 Conclusions

In this paper, we studied the impact of an extended neutrino sector on the NMSSM Higgs sector. We considered the framework of both the CP-conserving and CP-violating NMSSM extended by six singlet leptonic superfields. Their mixing with the three doublet leptonic superfields allows for the explanation of the tiny non-zero neutrino masses through the inverse seesaw mechanism. While R-parity is conserved in this model lepton number is explicitly violated through the interaction between two singlet neutrino superfields and a singlet Higgs superfield.

We quantified the indirect neutrino effects on the NMSSM Higgs sector by computing the complete one-loop corrections to the Higgs boson masses at non-vanishing external momentum. For the renormalization, we applied a mixed OS-$\overline{\text{ DR }}$ scheme and consistently combined our one-loop result with the two-loop $\mathcal{O}(\alpha _t (\alpha _s + \alpha _t))$ results computed previously by our group. In the numerical analysis, we performed a parameter scan of the model and kept only those points for our study that respect the constraints from the Higgs data, the neutrino oscillation data, the charged lepton flavor-violating decays $l_i \rightarrow l_j + \gamma$, and the new physics constraints from the oblique parameters S, T, U. We presented the explicit calculation of the one-loop decay width for $l_i \rightarrow l_j + \gamma$. Our one-loop results have been implemented in the Fortran code NMSSMCALC-nuSS, that has been made publicly available and is based on the code NMSSMCALC that also computes the Higgs decays widths and branching ratios.

We found for our investigated benchmark point that the one-loop corrections from the neutrinos to the $h_u$-like, and hence SM-like, Higgs boson mass can shift its value by about 5%, decreasing slightly when the two-loop corrections are included, see Table  3. While the neutrino and sneutrino contributions come with opposite signs, their complete cancellation is prohibited by the soft-SUSY breaking terms in combination with electroweak symmetry breaking. We furthermore showed that a large neutrino Yukawa coupling has a significant impact on the loop corrections. The same is true for the soft-SUSY breaking trilinear coupling $A_\nu$ and its complex phase that affects the sneutrino sector while leaving the neutrino sector unchanged. Our findings on the dependence on the neutrino Yukawa coupling are confirmed by the presented scatter plots taking into account all of the parameter points passing the constraints. Large sterile neutrino masses, characterized by a large value of $\mu _X$, can lead to large loop corrections due to the presence of the logarithmic term $\log \frac{\mu _X}{\mu _R}$. In case of a large ratio $\frac{\mu _X}{\mu _R}$ the reduction of the theoretical uncertainty is mandatory. This subject will be left for future study.

Our investigation of the one-loop corrected LFV decay $l_1 \rightarrow l_2 \gamma$ shows that the constraints from this decay are relevant and need to be taken into account. This result is underlined by an analysis of the impact of all considered constraints that shows the importance of the S, T, U and LFV constraints on the validity of the parameter scenarios.

In summary, the one-loop analysis of the impact of an extended (s)neutrino sector on the NMSSM demonstrates the importance of taking into account these indirect effects through loop contributions. Together with the usual constraints from Higgs data and new physics as well as from LFV decays, they constrain the valid parameter space of the model.

Appendices

Appendix A: Form factors

In this appendix we give the left- and right-handed form factors for the LFV radiative decays $l_1 \rightarrow l_2 + \gamma$ discussed in Sect.  4.4. For simplicity, we introduce the following abbreviations for the one-loop three-point integrals

$$\begin{aligned} C_{i...}^{W}&= C_{i...} \left( m_1^2,0,m_2^2, m_{\nu _i}^2,M_W^2,M_W^2\right) \end{aligned}$$

(A.110)

$$\begin{aligned} C_{i...}^{H}&= C_{i...} \left( m_1^2,0,m_2^2, m_{\nu _i}^2,M_{H^\pm }^2,M_{H^\pm }^2\right) \end{aligned}$$

(A.111)

$$\begin{aligned} C_{i...}^{\chi }&= C_{i...} \left( m_1^2,0,m_2^2,m_{\tilde{n}_i}^2,m_{\tilde{\chi }_j^\pm }^2,m_{\tilde{\chi }_j^\pm }^2\right) . \end{aligned}$$

(A.112)

We use the following conventions,

$$\begin{aligned}&C_0^W = \frac{(\mu _R^2 \pi )^{(4-D)/2}}{i\pi ^2}\int dq^D\frac{1}{D_x}, \end{aligned}$$

(A.113)

$$\begin{aligned}&C_1^W k_1^\mu + C_2^W k_2^\mu = \frac{(\mu _R^2 \pi )^{(4-D)/2}}{i\pi ^2}\int dq^D\frac{q^\mu }{D_x}, \end{aligned}$$

(A.114)

$$\begin{aligned}&C_{00}^W g^{\mu \nu } + C_{11}^W k_1^\mu k_1^\nu + C_{12}^W (k_1^\mu k_2^\nu + k_1^\nu k_2^\mu )+ C_{22}^W k_2^\mu k_2^\nu \nonumber \\&\quad = \frac{(\mu _R^2 \pi )^{(4-D)/2}}{i\pi ^2}\int dq^D\frac{q^\mu q^\nu }{D_x}, \end{aligned}$$

(A.115)

where the denominator $D_x$ is given by

$$\begin{aligned} D_x=(q^2- m_{n_i}^2)((q-k_1)^2- M_W^2)((q-k_2)^2- M_W^2), \end{aligned}$$

(A.116)

with $k_1^2= m_1^2, k_2^2=m_2^2$ and $(k_1-k_2)^2=0$ and $m_1$ ($m_2$) denoting the $l_1$ ($l_2$) mass, $m_{n_i}$ the mass of all the neutrinos, the active and the sterile ones.

In the ’t Hooft–Feynman gauge, the left- and right-handed form factors, $F^{W^\pm , H^\pm , \chi ^\pm }_{L,R}$, defined in (4.99) are given by

$$\begin{aligned} F^{W^\pm }_{L}&= \frac{e^3m_{2}}{16 \pi ^2M_W^2s_W^2}\sum _{i=1}^{9} U_{\nu \;il_1}U_{\nu \;il_2}^*\nonumber \\&\quad \times \bigg [m_{n_i}^2\left( C_0^{W} + C_1^W + 2 C_2^W + C_{12}^W + C_{22}^W \right) \nonumber \\&\quad +M_W^2 \left( -2 C_1^W + 2 C_{12}^W \right. \nonumber \\&\quad \left. + 2 C_{22}^W\right) + m_{1}^2 \left( C_1^W + C_{11}^W+C_{12}^W \right) \bigg ] \end{aligned}$$

(A.117)

$$\begin{aligned} F^{W^\pm }_{R}&= \frac{e^3m_{1}}{16 \pi ^2M_W^2s_W^2}\sum _{i=1}^{9} U_{\nu \;il_1}U_{\nu \;il_2}^*\nonumber \\&\quad \times \bigg [m_{n_i}^2\left( C_0^{W} + 2C_1^W + C_2^W + C_{11}^W + C_{12}^W \right) \nonumber \\&\quad +M_W^2 \left( -2 C_2^W + 2 C_{11}^W + 2 C_{12}^W\right) \nonumber \\&\quad + m_{2}^2 \left( C_2^W + C_{12}^W+C_{22}^W \right) \bigg ], \end{aligned}$$

(A.118)

for the $W^\pm$ and charged Goldstone boson triangle diagrams,

$$\begin{aligned} F^{H^\pm }_{L}&= \frac{e^3m_{2}}{16 \pi ^2M_W^2s_W^2}\sum _{i=1}^{9} U_{\nu \;il_1}U_{\nu \;il_2}^*\nonumber \\&\quad \times \bigg [m_{n_i}^2\left( -(C_0^{H^\pm } + C_1^{H^\pm } +C_2^{H^\pm })\right. \nonumber \\&\quad \left. + \frac{1}{t_\beta ^2}( C_2^{H^\pm } + C_{12}^{H^\pm } + C_{22}^{H^\pm }) \right) \nonumber \\&\quad + m_{1}^2 t_\beta ^2 \left( C_1^{H^\pm } + C_{11}^{H^\pm }+C_{12}^{H^\pm } \right) \bigg ] \end{aligned}$$

(A.119)

$$\begin{aligned} F^{H^\pm }_{R}&=\frac{e^3m_{1}}{16 \pi ^2M_W^2s_W^2}\sum _{i=1}^{9} U_{\nu \;il_1}U_{\nu \;il_2}^*\nonumber \\&\quad \times \bigg [m_{n_i}^2\left( -(C_0^{H^\pm } + C_1^{H^\pm } + C_2^{H^\pm } )\right. \nonumber \\&\quad \left. + \frac{1}{t_\beta ^2}\left( C_1^{H^\pm }+ C_{11}^{H^\pm } + C_{12}^{H^\pm }\right) \right) \nonumber \\&\quad + m_{2}^2 t_\beta ^2 \left( C_2^{H^\pm } + C_{12}^{H^\pm }+C_{22}^{H^\pm } \right) \bigg ], \end{aligned}$$

(A.120)

for the charged Higgs triangle diagram, and

$$\begin{aligned} F_{L}^{\tilde{\chi }^\pm }&=-\frac{e}{8 \pi ^2} \sum _{i=1}^{18}\sum _{j=1}^{2} \nonumber \\&\quad \times \bigg [ m_1 g^{L*}_{e^+_{l_1}\tilde{\chi }_j \tilde{\nu }_i} g^L_{e^+_{l_2}\tilde{\chi }_j \tilde{\nu }_i} \left( C_1^{\tilde{\chi }^\pm _j}+C_{12}^{\tilde{\chi }^\pm _j}+C_{11}^{\tilde{\chi }^\pm _j}\right) \nonumber \\&\quad +m_{\tilde{\chi }^\pm _j} g^{R*}_{e^+_{l_1}\tilde{\chi }_j \tilde{\nu }_i} g^L_{e^+_{l_2}\tilde{\chi }_j \tilde{\nu }_i} \left( C_1^{\tilde{\chi }^\pm _j}+C_2^{\tilde{\chi }^\pm _j}\right) \nonumber \\&\quad + m_2 g^{R*}_{e^+_{l_1}\tilde{\chi }_j \tilde{\nu }_i} g^R_{e^+_{l_2}\tilde{\chi }_j \tilde{\nu }_i} \left( C_2^{\tilde{\chi }^\pm _j}+C_{22}^{\tilde{\chi }^\pm _j} +C_{12}^{\tilde{\chi }^\pm _j}\right) \bigg ] \end{aligned}$$

(A.121)

$$\begin{aligned} F_{R}^{\tilde{\chi }^\pm }&=-\frac{e}{8 \pi ^2}\sum _{i=1}^{18}\sum _{j=1}^{2} \nonumber \\&\quad \times \bigg [ m_2g^{L*}_{e^+_{l_1}\tilde{\chi }_j \tilde{\nu }_i} g^L_{e^+_{l_2}\tilde{\chi }_j \tilde{\nu }_i}\left( C_2^{\tilde{\chi }^\pm _j}+C_{12}^{\tilde{\chi }^\pm _j}+C_{22}^{\tilde{\chi }^\pm _j}\right) \nonumber \\&\quad + m_{\tilde{\chi }^\pm _j} g^{L*}_{e^+_{l_1}\tilde{\chi }_j \tilde{\nu }_i} g^R_{e^+_{l_2}\tilde{\chi }_j \tilde{\nu }_i} \left( C_1^{\tilde{\chi }^\pm _j}+C_2^{\tilde{\chi }^\pm _j}\right) \nonumber \\&\quad + m_1 g^{R*}_{e^+_{l_1}\tilde{\chi }_j \tilde{\nu }_i} g^R_{e^+_{l_2}\tilde{\chi }_j \tilde{\nu }_i}\left( C_1^{\tilde{\chi }^\pm _j}+C_{11}^{\tilde{\chi }^\pm _j}+C_{12}^{\tilde{\chi }^\pm _j}\right) \bigg ], \end{aligned}$$

(A.122)

for the triangle diagrams with sneutrinos and charginos in the internal lines. The left- and right-handed couplings between the leptons, charginos and sneutrinos are defined in the interaction Lagrangian,

$$\begin{aligned} \bar{e}_k ( i g^L_{e^+_{k}\tilde{\chi }_j \tilde{\nu }_i} P_L + i g^R_{e^+_{k}\tilde{\chi }_j \tilde{\nu }_i} P_R ) \chi _j^- \tilde{\nu }_i , \end{aligned}$$

(A.123)

where

$$\begin{aligned}&g^L_{e^+_{k}\tilde{\chi }_j \tilde{\nu }_i} = \frac{m_k}{v c_\beta }\left( U^{\tilde{\nu }}_{ik} + i U^{\tilde{\nu }}_{i(k+9)}\right) U^*_{j2} \end{aligned}$$

(A.124)

$$\begin{aligned}&g^R_{e^+_{k}\tilde{\chi }_j \tilde{\nu }_i} \nonumber \\&\quad = -\frac{g_2V_{j1}}{\sqrt{2}}\left( U^{\tilde{\nu }}_{ik} + i U^{\tilde{\nu }}_{i(k+9)} \right) \nonumber \\&\qquad +\frac{1}{\sqrt{2}}V_{j2} \sum _{n=1}^3 \left( U^{\tilde{\nu }}_{i(n+3)} + iU^{\tilde{\nu }}_{i(n+12)}\right) Y^*_{\nu ,kn} . \end{aligned}$$

(A.125)

In the numerical analysis we used the massless limit for the external lines. In this limit, one has the following simple expressions for the one-loop three-point integrals [70]

$$\begin{aligned} C_0(0,0,0,x,y,y)&= \frac{1}{x}\left( -\frac{1}{t-1} + \frac{\ln (t)}{(t-1)^2}\right) \end{aligned}$$

(A.126)

$$\begin{aligned} C_1(0,0,0,x,y,y)&= \frac{1}{x} \left( \frac{(t - 3)}{4(t - 1)^2} + \frac{\ln (t)}{2(t - 1)^3} \right) \end{aligned}$$

(A.127)

$$\begin{aligned} C_{11}(0,0,0,x,y,y)&=\frac{1}{x} \left( \frac{(-2 t^2 + 7 t - 11)}{18(t - 1)^3} + \frac{\ln (t)}{3(t - 1)^4} \right) \end{aligned}$$

(A.128)

$$\begin{aligned} C_2(0,0,0,x,y,y)&= C_1(0,0,0,x,y,y)\end{aligned}$$

(A.129)

$$\begin{aligned} C_{22}(0,0,0,x,y,y)&=2 C_{12}(0,0,0,x,y,y)\nonumber \\&=C_{11}(0,0,0,x,y,y), \end{aligned}$$

(A.130)

where $t= y/x$.

Appendix B: Sneutrino mass matrix

The mass matrix of the sneutrinos written in each $3\times 3$ block is given by

$$\begin{aligned} (M_{\tilde{\nu }})_{{\tilde{\nu }}_+ {\tilde{\nu }}_+}&= \frac{1}{2}I_3 M_z^2 \cos 2\beta + \frac{1}{2}\left( \tilde{m}_L^2 + \tilde{m}_L^{2T}\right) \nonumber \\&\quad + \frac{1}{2} v_u^2 \text {Re} \left( y_\nu y_\nu ^\dagger \right) \end{aligned}$$

(B.131)

$$\begin{aligned} (M_{\tilde{\nu }})_{{\tilde{\nu }}_+ {\tilde{N}}_+}&= \frac{1}{\sqrt{2}} v_u \text {Re}\left( e^{i\varphi _u} y_\nu A_\nu \right) - \frac{1}{2} v_d v_s \text {Re}\left( (e^{i\varphi _s} \lambda y_\nu ^* \right) \end{aligned}$$

(B.132)

$$\begin{aligned} (M_{\tilde{\nu }})_{{\tilde{\nu }}_+ {\tilde{X}}_+}&= \frac{1}{\sqrt{2}} v_u \text {Re}\left( e^{i\varphi _u} y_\nu \mu _X^* \right) \end{aligned}$$

(B.133)

$$\begin{aligned} (M_{\tilde{\nu }})_{{\tilde{\nu }}_+ {\tilde{\nu }}_-}&= \frac{i}{2} \left( \tilde{m}_L^2 - \tilde{m}_L^{2T}\right) + \frac{1}{2} v_u^2 \Im \left( y_\nu y_\nu ^\dagger \right) \end{aligned}$$

(B.134)

$$\begin{aligned} (M_{\tilde{\nu }})_{{\tilde{\nu }}_+ {\tilde{N}}_-}&= \frac{1}{\sqrt{2}} v_u \Im \left( e^{i\varphi _u} y_\nu A_\nu \right) - \frac{1}{2} v_d v_s \Im \left( e^{i\varphi _s} \lambda y_\nu ^* \right) \end{aligned}$$

(B.135)

$$\begin{aligned} (M_{\tilde{\nu }})_{{\tilde{\nu }}_+ {\tilde{X}}_-}&= \frac{1}{\sqrt{2}} v_u \Im \left( e^{i\varphi _u} y_\nu \mu _X^* \right) \end{aligned}$$

(B.136)

$$\begin{aligned} (M_{\tilde{\nu }})_{{\tilde{N}}_+ {\tilde{N}}_+}&= \frac{1}{2}\left( \tilde{m}^2_N + \tilde{m}^{2T}_N\right) + \text {Re}\left( \mu _X \mu _X^\dagger \right) + \frac{1}{2} v_u^2 \text {Re} \left( y_\nu ^T y_\nu ^*\right) \end{aligned}$$

(B.137)

$$\begin{aligned} (M_{\tilde{\nu }})_{{\tilde{N}}_+ {\tilde{X}}_+}&= \text {Re}\left( \mu _X B_{\mu _X}\right) + \frac{1}{\sqrt{2}} v_s \text {Re}\left[ e^{-i\varphi _s}\mu _X\left( \lambda _X^\dagger + \lambda _X^*\right) \right] \end{aligned}$$

(B.138)

$$\begin{aligned} (M_{\tilde{\nu }})_{{\tilde{N}}_+ {\tilde{\nu }}_-}&= -\frac{1}{\sqrt{2}} v_u \Im \left( e^{i\varphi _u}A_\nu ^T y_\nu ^T\right) - \frac{1}{2} v_d v_s \Im \left( e^{i\varphi _s} \lambda y_\nu ^\dagger \right) \end{aligned}$$

(B.139)

$$\begin{aligned} (M_{\tilde{\nu }})_{{\tilde{N}}_+ {\tilde{N}}_-}&= \frac{i}{2}\left( \tilde{m}^2_N - \tilde{m}^{2T}_N\right) - \Im \left( \mu _X \mu _X^\dagger \right) - \frac{1}{2} v_u^2 \Im \left( y_\nu ^T y_\nu ^*\right) \end{aligned}$$

(B.140)

$$\begin{aligned} (M_{\tilde{\nu }})_{{\tilde{N}}_+ {\tilde{X}}_-}&= -\Im \left( \mu _X B_{\mu _X}\right) + \frac{1}{\sqrt{2}} v_s \Im \left[ e^{-i\varphi _s}\mu _X\left( \lambda _X^\dagger + \lambda _X^*\right) \right] \end{aligned}$$

(B.141)

$$\begin{aligned} (M_{\tilde{\nu }})_{{\tilde{X}}_+ {\tilde{X}}_+}&= \frac{1}{2}\left( \tilde{m}_X^2 + \tilde{m}_X^{2T}\right) + \text {Re}\left( \mu _X^T \mu _X^*\right) \nonumber \\&\quad + \frac{1}{2}\text {Re}\left[ \left( e^{2i\varphi _s}v_s^2 \kappa - e^{i\varphi _u}v_d v_u \lambda \right) \left( \lambda _X^* + \lambda _X^\dagger \right) \right] \nonumber \\&\quad + \frac{1}{2}v_s^2 \text {Re}\left[ \left( \lambda _X + \lambda _X^T \right) \left( \lambda _X^\dagger + \lambda _X^*\right) \right] \nonumber \\&\quad + \frac{1}{\sqrt{2}} v_s \text {Re} \left[ e^{i\varphi _s}\left( \lambda _X A_X + A_X^T\lambda _X^T\right) \right] \end{aligned}$$

(B.142)

$$\begin{aligned} (M_{\tilde{\nu }})_{{\tilde{X}}_+ {\tilde{\nu }}_-}&= -\frac{1}{\sqrt{2}} v_u \Im \left( e^{i\varphi _u} \mu _X^\dagger y_\nu ^T \right) \end{aligned}$$

(B.143)

$$\begin{aligned} (M_{\tilde{\nu }})_{{\tilde{X}}_+ {\tilde{N}}_-}&= \Im \left( B_{\mu _X}^T \mu _X^T\right) \nonumber \\&\quad + \frac{1}{\sqrt{2}} v_s \Im \left[ e^{-i\varphi _s} \left( \lambda _X^\dagger + \lambda _X^*\right) \mu ^T_X \right] \end{aligned}$$

(B.144)

$$\begin{aligned} (M_{\tilde{\nu }})_{{\tilde{X}}_+ {\tilde{X}}_-}&= \frac{i}{2} \left( \tilde{m}_X^2 - \tilde{m}_X^{2T}\right) \nonumber \\&\quad + \Im \left( \mu _X^T \mu _X^*\right) \nonumber \\&\quad + \frac{1}{2}\Im \left[ \left( e^{2i\varphi _s}v_s^2 \kappa - e^{i\varphi _u}v_d v_u \lambda \right) \left( \lambda _X^* + \lambda _X^\dagger \right) \right] \nonumber \\&\quad + \frac{1}{2}v_s^2 \Im \left[ \left( \lambda _X + \lambda _X^T \right) \left( \lambda _X^\dagger + \lambda _X^*\right) \right] \nonumber \\&\quad - \frac{1}{\sqrt{2}} v_s \Im \left[ e^{i\varphi _s}\left( \lambda _X A_X + A_X^T\lambda _X^T\right) \right] \end{aligned}$$

(B.145)

$$\begin{aligned} (M_{\tilde{\nu }})_{{\tilde{\nu }}_- {\tilde{\nu }}_-}&= \frac{1}{2}I_3 M_z^2 \cos 2\beta + \frac{1}{2}\left( \tilde{m}_L^2 + \tilde{m}_L^{2T}\right) + \frac{1}{2} v_u^2 \text {Re} \left( y_\nu y_\nu ^\dagger \right) \end{aligned}$$

(B.146)

$$\begin{aligned} (M_{\tilde{\nu }})_{{\tilde{\nu }}_- {\tilde{N}}_-}&= \frac{1}{\sqrt{2}} v_u \text {Re}\left( e^{i\varphi _u} y_\nu A_\nu \right) - \frac{1}{2} v_d v_s \text {Re}\left( e^{i\varphi _s} \lambda y_\nu ^* \right) \end{aligned}$$

(B.147)

$$\begin{aligned} (M_{\tilde{\nu }})_{{\tilde{\nu }}_- {\tilde{X}}_-}&= \frac{1}{\sqrt{2}} v_u \text {Re}\left( e^{i\varphi _u} y_\nu \mu _X^* \right) \end{aligned}$$

(B.148)

$$\begin{aligned} (M_{\tilde{\nu }})_{{\tilde{N}}_- {\tilde{N}}_-}&= \frac{1}{2}\left( \tilde{m}^2_N + \tilde{m}^{2T}_N \right) + \text {Re}\left( \mu _X \mu _X^\dagger \right) + \frac{1}{2} v_u^2 \text {Re} \left( y_\nu ^T y_\nu ^*\right) \end{aligned}$$

(B.149)

$$\begin{aligned} (M_{\tilde{\nu }})_{{\tilde{N}}_- {\tilde{X}}_-}&= \text {Re}\left( \mu _X B_{\mu _X}\right) - \frac{1}{\sqrt{2}} v_s \text {Re}\left[ e^{-i\varphi _s}\mu _X\left( \lambda _X^\dagger + \lambda _X^*\right) \right] \end{aligned}$$

(B.150)

$$\begin{aligned} (M_{\tilde{\nu }})_{{\tilde{X}}_- {\tilde{X}}_-}&= \frac{1}{2}\left( \tilde{m}_X^2 + \tilde{m}_X^{2T}\right) + \text {Re}\left( \mu _X^T \mu _X^* \right) \nonumber \\&\quad - \frac{1}{2}\text {Re}\left[ \left( e^{2i\varphi _s}v_s^2 \kappa - e^{i\varphi _u}v_d v_u \lambda \right) \left( \lambda _X^* + \lambda _X^\dagger \right) \right] \nonumber \\&\quad + \frac{1}{2}v_s^2 \text {Re}\left[ \left( \lambda _X + \lambda _X^T \right) \left( \lambda _X^\dagger + \lambda _X^*\right) \right] \nonumber \\&\quad - \frac{1}{\sqrt{2}} v_s \text {Re} \left[ e^{i\varphi _s}\left( \lambda _X A_X + A_X^T\lambda _X^T\right) \right] . \end{aligned}$$

(B.151)

Appendix C: Neutral Higgs mass matrix counterterm

In this section we present the counterterm mass matrix for the neutral Higgs bosons in the basis $\left( h_d,h_u,h_s,a,a_s\right) ^T$. We use the convention $\varphi _y = \varphi _\kappa -\varphi _\lambda +2\varphi _s - \varphi _u$, $\varphi _\omega = \varphi _\kappa + 3 \varphi _s$ and the short-hand notation $s_x \equiv \sin x, c_x \equiv \cos x$.

$$\begin{aligned}&\left( \delta ^{(1)}M_{hh}\right) _{h_d h_d} \nonumber \\&= c_{\beta }^3 s_{\beta } \delta ^{(1)}{t_{\beta }} \left( v^2 \left| \lambda \right| ^2-2 M_W^2-2 M_Z^2+2 M^2_{H^\pm }\right) \nonumber \\&\quad +v^2 \left| \lambda \right| s_{\beta }^2 \delta ^{(1)}{\left| \lambda \right| } +v \left| \lambda \right| ^2 s_{\beta }^2 \delta ^{(1)} v-\frac{\left( c_{2 \beta }-3\right) c_{\beta } \delta ^{(1)}{t_{h_d}}}{2 v}\nonumber \\&\qquad -\frac{c_{\beta }^2 s_{\beta } \delta ^{(1)}{t_{h_u}}}{v}+c_{\beta }^2 \delta ^{(1)}{M_Z^2} -s_{\beta }^2 \delta ^{(1)}{M_W^2}+\delta ^{(1)}{M^2_{H^\pm }} s_{\beta }^2 \end{aligned}$$

(C.152)

$$\begin{aligned}&\left( \delta ^{(1)}M_{hh}\right) _{h_d h_u} \nonumber \\&\quad = \frac{1}{2} c_{2 \beta } c_{\beta }^2 \delta ^{(1)}{t_{\beta }} \left( v^2 \left| \lambda \right| ^2+2 M_W^2-2 M_Z^2-2 M^2_{H^\pm }\right) \nonumber \\&\qquad +v^2 \left| \lambda \right| c_{\beta } s_{\beta } \delta ^{(1)}{\left| \lambda \right| }+v \left| \lambda \right| ^2 c_{\beta } s_{\beta } \delta ^{(1)} v+\frac{c_{\beta }^3 \delta ^{(1)}{t_{h_u}}}{v}\nonumber \\&\qquad +c_{\beta } s_{\beta } \delta ^{(1)}{M_W^2}-c_{\beta } s_{\beta } \delta ^{(1)}{M_Z^2}\nonumber \\&\qquad -c_{\beta } \delta ^{(1)}{M^2_{H^\pm }} s_{\beta }+\frac{s_{\beta }^3 \delta ^{(1)}{t_{h_d}}}{v} \end{aligned}$$

(C.153)

$$\begin{aligned}&\left( \delta ^{(1)}M_{hh}\right) _{h_d h_s} = -\frac{v c_{\beta }^2 \delta ^{(1)}{t_{\beta }}}{2 v_s}\left( 2 c_{\beta }^2 s_{\beta } \left( v^2 \left| \lambda \right| ^2-2 M_W^2+2 M^2_{H^\pm }\right) +\left| \kappa \right| \right. \nonumber \\&\qquad \times \left. \left| \lambda \right| c_{\beta } v_s^2 c_{\varphi _y}+s_{\beta }^3 \left( -\left( v^2 \left| \lambda \right| ^2-2 M_W^2+2 M^2_{H^\pm }\right) \right) +2 \left| \lambda \right| ^2 s_{\beta } v_s^2\right) \nonumber \\&\qquad +\frac{v \delta ^{(1)}{v_s} \left( c_{\beta } \left( s_{\beta }^2 \left( v^2 \left| \lambda \right| ^2-2 M_W^2\right) +2 \left| \lambda \right| ^2 v_s^2\right) +s_{\beta } \left( M^2_{H^\pm } s_{2 \beta }-\left| \kappa \right| \left| \lambda \right| v_s^2 c_{\varphi _y}\right) \right) }{2 v_s^2}\nonumber \\&\qquad +\frac{\delta ^{(1)} v \left( s_{\beta } \left( M_W^2 s_{2 \beta }-\left| \kappa \right| \left| \lambda \right| v_s^2 c_{\varphi _y}\right) +c_{\beta } \left( 2 \left| \lambda \right| ^2 v_s^2-s_{\beta }^2 \left( 3 v^2 \left| \lambda \right| ^2+2 M^2_{H^\pm }\right) \right) \right) }{2 v_s}\nonumber \\&\qquad +\delta ^{(1)}{\left| \lambda \right| } \left( c_{\beta } \left( 2 v \left| \lambda \right| v_s-\frac{v^3 \left| \lambda \right| s_{\beta }^2}{v_s}\right) -\frac{1}{2} v \left| \kappa \right| s_{\beta } v_s c_{\varphi _y}\right) -\frac{1}{2} v \left| \lambda \right| s_{\beta } v_s \delta ^{(1)}{\left| \kappa \right| } c_{\varphi _y} +\frac{1}{2} v \left| \kappa \right| \left| \lambda \right| s_{\beta } v_s s_{\varphi _y} \delta ^{(1)}{\varphi _y}\nonumber \\&\qquad +\frac{c_{\beta }^3 s_{\beta } \delta ^{(1)}{t_{h_u}}}{v_s}+\frac{v c_{\beta } s_{\beta }^2 \delta ^{(1)}{M_W^2}}{v_s}-\frac{v c_{\beta } \delta ^{(1)}{M^2_{H^\pm }} s_{\beta }^2}{v_s} +\frac{s_{\beta }^4 \delta ^{(1)}{t_{h_d}}}{v_s} \end{aligned}$$

(C.154)

$$\begin{aligned}&\left( \delta ^{(1)}M_{hh}\right) _{h_d a}=\frac{\delta ^{(1)}{t_{a_d}}\cot \beta }{v}\end{aligned}$$

(C.155)

$$\begin{aligned}&\left( \delta ^{(1)}M_{hh}\right) _{h_d a_s} = \frac{\delta ^{(1)}{t_{a_d}}}{v_s} +\frac{3}{2} v \left| \kappa \right| \left| \lambda \right| c_{\beta }^3 v_s s_{\varphi _y} \delta ^{(1)}{t_{\beta }}+\frac{3}{2} v \left| \kappa \right| \left| \lambda \right| s_{\beta } v_s c_{\varphi _y} \delta ^{(1)}{\varphi _y}+\frac{3}{2} v \left| \lambda \right| s_{\beta } v_s \delta ^{(1)}{\left| \kappa \right| } s_{\varphi _y}\nonumber \\&\qquad +\frac{3}{2} v \left| \kappa \right| s_{\beta } v_s \delta ^{(1)}{\left| \lambda \right| } s_{\varphi _y}+\frac{3}{2} v \left| \kappa \right| \left| \lambda \right| s_{\beta } \delta ^{(1)}{v_s} s_{\varphi _y}+\frac{3}{2} \left| \kappa \right| \left| \lambda \right| s_{\beta } v_s \delta ^{(1)} v s_{\varphi _y} \end{aligned}$$

(C.156)

$$\begin{aligned}&\left( \delta ^{(1)}M_{hh}\right) _{h_u h_u} = c_{\beta }^3 s_{\beta } \delta ^{(1)}{t_{\beta }} \left( -v^2 \left| \lambda \right| ^2 +2 M_W^2+2 M_Z^2-2 M^2_{H^\pm }\right) +v^2 \left| \lambda \right| c_{\beta }^2 \delta ^{(1)}{\left| \lambda \right| }+v \left| \lambda \right| ^2 c_{\beta }^2 \delta ^{(1)} v-\frac{c_{\beta } s_{\beta }^2 \delta ^{(1)}{t_{h_d}}}{v}\nonumber \\&\qquad +\frac{\left( c_{2 \beta }+3\right) s_{\beta } \delta ^{(1)}{t_{h_u}}}{2 v}-c_{\beta }^2 \delta ^{(1)}{M_W^2}+c_{\beta }^2 \delta ^{(1)}{M^2_{H^\pm }}+s_{\beta }^2 \delta ^{(1)}{M_Z^2}\end{aligned}$$

(C.157)

$$\begin{aligned}&\left( \delta ^{(1)}M_{hh}\right) _{h_u h_s} = \frac{v c_{\beta }^2 \delta ^{(1)}{t_{\beta }}}{2 v_s} \left( 2 c_{\beta } \left( \left| \lambda \right| ^2 v_s^2+2 s_{\beta }^2 \left( M^2_{H^\pm }-M_W^2\right) \right) +c_{\beta }^3 \left( -\left( v^2 \left| \lambda \right| ^2-2 M_W^2+2 M^2_{H^\pm }\right) \right) \right. \nonumber \\&\qquad \left. +\left| \lambda \right| s_{\beta } \left( \left| \kappa \right| v_s^2 c_{\varphi _y}+v^2 \left| \lambda \right| s_{2 \beta }\right) \right) +\frac{1}{2} v \delta ^{(1)}{v_s} \left( \frac{c_{\beta }^2 s_{\beta } \left( v^2 \left| \lambda \right| ^2-2 M_W^2+2 M^2_{H^\pm }\right) }{v_s^2}-\left| \kappa \right| \left| \lambda \right| c_{\beta } c_{\varphi _y}+2 \left| \lambda \right| ^2 s_{\beta }\right) \nonumber \\&\qquad +\delta ^{(1)} v \left( -\frac{c_{\beta }^2 s_{\beta } \left( 3 v^2 \left| \lambda \right| ^2-2 M_W^2+2 M^2_{H^\pm }\right) }{2 v_s}-\frac{1}{2} \left| \kappa \right| \left| \lambda \right| c_{\beta } v_s c_{\varphi _y}+\left| \lambda \right| ^2 s_{\beta } v_s\right) +\delta ^{(1)}{\left| \lambda \right| } \left( -\frac{v^3 \left| \lambda \right| c_{\beta }^2 s_{\beta }}{v_s}\right. \nonumber \\&\qquad \left. -\frac{1}{2} v \left| \kappa \right| c_{\beta } v_s c_{\varphi _y}+2 v \left| \lambda \right| s_{\beta } v_s\right) -\frac{1}{2} v \left| \lambda \right| c_{\beta } v_s \delta ^{(1)}{\left| \kappa \right| } c_{\varphi _y}+\frac{1}{2} v \left| \kappa \right| \left| \lambda \right| c_{\beta } v_s s_{\varphi _y} \delta ^{(1)}{\varphi _y}+\frac{c_{\beta } s_{\beta }^3 \delta ^{(1)}{t_{h_d}}}{v_s}\nonumber \\&\qquad +\frac{c_{\beta }^4 \delta ^{(1)}{t_{h_u}}}{v_s}+\frac{v c_{\beta }^2 s_{\beta } \delta ^{(1)}{M_W^2}}{v_s}-\frac{v c_{\beta }^2 \delta ^{(1)}{M^2_{H^\pm }} s_{\beta }}{v_s}\end{aligned}$$

(C.158)

$$\begin{aligned}&\left( \delta ^{(1)}M_{hh}\right) _{h_u a} = \frac{\delta ^{(1)}{t_{a_d}}}{v}\end{aligned}$$

(C.159)

$$\begin{aligned}&\left( \delta ^{(1)}M_{hh}\right) _{h_u a_s} = \frac{\cot \beta \delta ^{(1)}{t_{a_d}}}{v_s}-\frac{3}{2} v \left| \kappa \right| \left| \lambda \right| c_{\beta }^2 s_{\beta } v_s s_{\varphi _y} \delta ^{(1)}{t_{\beta }}+\frac{3}{2} v \left| \lambda \right| c_{\beta } v_s \delta ^{(1)}{\left| \kappa \right| } s_{\varphi _y}+\frac{3}{2} v \left| \kappa \right| c_{\beta } v_s \delta ^{(1)}{\left| \lambda \right| } s_{\varphi _y}\nonumber \\&\qquad +\frac{3}{2} v \left| \kappa \right| \left| \lambda \right| c_{\beta } \delta ^{(1)}{v_s} s_{\varphi _y}+\frac{3}{2} v \left| \kappa \right| \left| \lambda \right| c_{\beta } v_s c_{\varphi _y} \delta ^{(1)}{\varphi _y}+\frac{3}{2} \left| \kappa \right| \left| \lambda \right| c_{\beta } v_s \delta ^{(1)} v s_{\varphi _y} \end{aligned}$$

(C.160)

$$\begin{aligned}&\left( \delta ^{(1)}M_{hh}\right) _{h_s h_s}= -\frac{v s_{\beta } \delta ^{(1)}{t_{h_u}} c_{\beta }^4}{v_s^2} +\frac{v^2 s_{\beta }^2 \delta ^{(1)}{M^2_{H^\pm }} c_{\beta }^2}{v_s^2}-\frac{v^2 s_{\beta }^2 \delta ^{(1)}{M_W^2} c_{\beta }^2}{v_s^2}+\frac{1}{2} v^2 c_{2 \beta } \nonumber \\&\qquad \times \left( -\left| \kappa \right| \left| \lambda \right| c_{\varphi _y}+\frac{3 i \left( -1+e^{2 i \varphi _{\omega }}\right) \left| \kappa \right| \left| \lambda \right| s_{\varphi _y}}{1+e^{2 i \varphi _{\omega }}}+\frac{\left( v^2 \left| \lambda \right| ^2-2 M_W^2+2 M^2_{H^\pm }\right) s_{2 \beta }}{v_s^2}\right) \delta ^{(1)}{t_{\beta }} c_{\beta }^2 +\frac{i \left( -1+e^{2 i \varphi _{\omega }}\right) v \delta ^{(1)}{t_{a_d}} c_{\beta }}{\left( 1+e^{2 i \varphi _{\omega }}\right) v_s^2}\nonumber \\&\qquad -\frac{v s_{\beta }^4 \delta ^{(1)}{t_{h_d}} c_{\beta }}{v_s^2}+\frac{v^2 \left| \kappa \right| \left| \lambda \right| s_{\beta } \left( 3 i \left( -1+e^{2 i \varphi _{\omega }}\right) c_{\varphi _y}+\left( 1+e^{2 i \varphi _{\omega }}\right) s_{\varphi _y}\right) \delta ^{(1)}{\varphi _y} c_{\beta }}{2 \left( 1+e^{2 i \varphi _{\omega }}\right) }\nonumber \\&\qquad +\frac{1}{2} v \delta ^{(1)} v s_{2 \beta } \left( -\left| \kappa \right| \left| \lambda \right| c_{\varphi _y}+\frac{3 i \left( -1+e^{2 i \varphi _{\omega }}\right) \left| \kappa \right| \left| \lambda \right| s_{\varphi _y}}{1+e^{2 i \varphi _{\omega }}}+\frac{\left( v^2 \left| \lambda \right| ^2-M_W^2+M^2_{H^\pm }\right) s_{2 \beta }}{v_s^2}\right) \nonumber \\&\qquad +\left( \frac{1}{2} \left| \lambda \right| c_{\beta } s_{\beta } \left( \frac{3 i \left( -1+e^{2 i \varphi _{\omega }}\right) s_{\varphi _y}}{1+e^{2 i \varphi _{\omega }}}-c_{\varphi _y}\right) v^2+v_s \left( \frac{\sqrt{2} e^{i \varphi _{\omega }} \text {Re}A_{\kappa }}{1+e^{2 i \varphi _{\omega }}}+4 \left| \kappa \right| v_s\right) \right) \delta ^{(1)}{\left| \kappa \right| }+\frac{1}{4} v^2 s_{2 \beta } \left( \frac{\left| \lambda \right| s_{2 \beta } v^2}{v_s^2}-\left| \kappa \right| c_{\varphi _y}\right. \nonumber \\&\qquad \left. +\frac{3 i \left( -1+e^{2 i \varphi _{\omega }}\right) \left| \kappa \right| s_{\varphi _y}}{1+e^{2 i \varphi _{\omega }}}\right) \delta ^{(1)}{\left| \lambda \right| }+\frac{\sqrt{2} e^{i \varphi _{\omega }} \left| \kappa \right| v_s \delta ^{(1)}{ \text {Re}A_{\kappa }}}{1+e^{2 i \varphi _{\omega }}}+\frac{\left( i-i e^{2 i \varphi _{\omega }}\right) \delta ^{(1)}{t_{a_s}}}{e^{2 i \varphi _{\omega }} v_s+v_s}\nonumber \\&\qquad +\frac{\delta ^{(1)}{t_{h_s}}}{v_s}+\left( -\frac{\left| \lambda \right| ^2 c_{\beta }^2 s_{\beta }^2 v^4}{v_s^3}-\frac{\left( M^2_{H^\pm }-M_W^2\right) s_{2 \beta }^2 v^2}{2 v_s^3}+\left| \kappa \right| \left( \frac{\sqrt{2} e^{i \varphi _{\omega }} \text {Re}A_{\kappa }}{1+e^{2 i \varphi _{\omega }}}+4 \left| \kappa \right| v_s\right) \right) \delta ^{(1)}{v_s}\nonumber \\&\qquad +\frac{\left( -6 e^{2 i \varphi _{\omega }} \left| \kappa \right| \left| \lambda \right| c_{\beta } s_{\beta } s_{\varphi _y} v^2-i \sqrt{2} e^{i \varphi _{\omega }} \left( -1+e^{2 i \varphi _{\omega }}\right) \left| \kappa \right| \text {Re}A_{\kappa } v_s\right) \delta ^{(1)}{\varphi _{\omega }}}{\left( 1+e^{2 i \varphi _{\omega }}\right) {}^2}\end{aligned}$$

(C.161)

$$\begin{aligned}&\left( \delta ^{(1)}M_{hh}\right) _{h_s a} = \frac{\delta ^{(1)}{t_{a_d}}}{s_{\beta } v_s}-\frac{1}{2} v \left| \kappa \right| \left| \lambda \right| v_s c_{\varphi _y} \delta ^{(1)}{\varphi _y}-\frac{1}{2} v \left| \lambda \right| v_s \delta ^{(1)}{\left| \kappa \right| } s_{\varphi _y}-\frac{1}{2} v \left| \kappa \right| v_s \delta ^{(1)}{\left| \lambda \right| } s_{\varphi _y}-\frac{1}{2} v \left| \kappa \right| \left| \lambda \right| \delta ^{(1)}{v_s} s_{\varphi _y}\nonumber \\&\qquad -\frac{1}{2} \left| \kappa \right| \left| \lambda \right| v_s \delta ^{(1)} v s_{\varphi _y}\end{aligned}$$

(C.162)

$$\begin{aligned}&\left( \delta ^{(1)}M_{hh}\right) _{h_s a_s} = -\frac{2 v c_{\beta }\delta ^{(1)}{t_{a_d}}}{v_s^2}+\frac{2 \delta ^{(1)}{t_{a_s}}}{v_s}-2 v^2 \left| \kappa \right| \left| \lambda \right| c_{\beta }^2 c_{2 \beta } s_{\varphi _y} \delta ^{(1)}{t_{\beta }} -2 v^2 \left| \lambda \right| c_{\beta } s_{\beta } \delta ^{(1)}{\left| \kappa \right| } s_{\varphi _y}\nonumber \\&\qquad -2 v^2 \left| \kappa \right| c_{\beta } s_{\beta }\delta ^{(1)}{\left| \lambda \right| } s_{\varphi _y}-2 v^2 \left| \kappa \right| \left| \lambda \right| c_{\beta } s_{\beta } c_{\varphi _y} \delta ^{(1)}{\varphi _y}-4 v \left| \kappa \right| \left| \lambda \right| c_{\beta } s_{\beta } \delta ^{(1)} v s_{\varphi _y}\end{aligned}$$

(C.163)

$$\begin{aligned}&\left( \delta ^{(1)}M_{hh}\right) _{a a} = v^2 \left| \lambda \right| \delta ^{(1)}{\left| \lambda \right| }+v \left| \lambda \right| ^2\delta ^{(1)} v-\delta ^{(1)}{M_W^2}+\delta ^{(1)}{M^2_{H^\pm }} \end{aligned}$$

(C.164)

$$\begin{aligned}&\left( \delta ^{(1)}M_{hh}\right) _{a a_s} = \frac{v c_{2 \beta }c_{\beta }^2 \delta ^{(1)}{t_{\beta }} \left( v^2 \left| \lambda \right| ^2-2 M_W^2+2 M^2_{H^\pm }\right) }{2 v_s} -\frac{v \delta ^{(1)}{v_s} \left( 6 \left| \kappa \right| \left| \lambda \right| v_s^2 c_{\varphi _y}+s_{2 \beta } \left( v^2\left| \lambda \right| ^2-2 M_W^2+2 M^2_{H^\pm }\right) \right) }{4 v_s^2} \nonumber \\&\qquad +\delta ^{(1)} v \left( \frac{s_{2 \beta } \left( 3 v^2 \left| \lambda \right| ^2-2 M_W^2+2 M^2_{H^\pm }\right) }{4 v_s}-\frac{3}{2} \left| \kappa \right| \left| \lambda \right| v_s c_{\varphi _y}\right) +\delta ^{(1)}{\left| \lambda \right| } \left( \frac{v^3 \left| \lambda \right| c_{\beta } s_{\beta }}{v_s}-\frac{3}{2} v \left| \kappa \right| v_s c_{\varphi _y}\right) \nonumber \\&\qquad -\frac{3}{2} v \left| \lambda \right| v_s \delta ^{(1)}{\left| \kappa \right| } c_{\varphi _y} +\frac{3}{2} v \left| \kappa \right| \left| \lambda \right| v_s s_{\varphi _y} \delta ^{(1)}{\varphi _y}-\frac{c_{\beta }^3 \delta ^{(1)}{t_{h_u}}}{v_s}-\frac{v c_{\beta } s_{\beta } \delta ^{(1)}{M_W^2}}{v_s}+\frac{v c_{\beta }\delta ^{(1)}{M^2_{H^\pm }} s_{\beta }}{v_s}-\frac{s_{\beta }^3 \delta ^{(1)}{t_{h_d}}}{v_s}\end{aligned}$$

(C.165)

$$\begin{aligned}&\left( \delta ^{(1)}M_{hh}\right) _{a_s a_s} = -\frac{v s_{\beta }\delta ^{(1)}{t_{h_u}} c_{\beta }^4}{v_s^2} +\frac{v^2 s_{\beta }^2\delta ^{(1)}{M^2_{H^\pm }} c_{\beta }^2}{v_s^2} -\frac{v^2 s_{\beta }^2 \delta ^{(1)}{M_W^2} c_{\beta }^2}{v_s^2}+\frac{1}{2} v^2 c_{2 \beta } \left( 3 \left| \kappa \right| \left| \lambda \right| c_{\varphi _y}\right. \nonumber \\&\qquad \left. -\frac{9 i \left( -1+e^{2 i \varphi _{\omega }}\right) \left| \kappa \right| \left| \lambda \right| s_{\varphi _y}}{1+e^{2 i \varphi _{\omega }}}+\frac{\left( v^2 \left| \lambda \right| ^2-2 M_W^2+2 M^2_{H^\pm }\right) s_{2 \beta }}{v_s^2}\right) \delta ^{(1)}{t_{\beta }} c_{\beta }^2-\frac{3 i \left( -1+e^{2 i \varphi _{\omega }}\right) v \delta ^{(1)}{t_{a_d}} c_{\beta }}{\left( 1+e^{2 i \varphi _{\omega }}\right) v_s^2}\nonumber \\&\qquad -\frac{v s_{\beta }^4 \delta ^{(1)}{t_{h_d}} c_{\beta }}{v_s^2}+\frac{3}{2} v^2 \left| \kappa \right| \left| \lambda \right| s_{\beta } \left( -\frac{3 i \left( -1+e^{2 i \varphi _{\omega }}\right) c_{\varphi _y}}{1+e^{2 i \varphi _{\omega }}}-s_{\varphi _y}\right) \delta ^{(1)}{\varphi _y} c_{\beta }+\delta ^{(1)} v \left( \frac{2 \left| \lambda \right| ^2 c_{\beta }^2 s_{\beta }^2 v^3}{v_s^2}+3 \left| \kappa \right| \left| \lambda \right| c_{\beta } s_{\beta } \left( c_{\varphi _y}\right. \right. \nonumber \\&\qquad \left. \left. -\frac{3 i \left( -1+e^{2 i \varphi _{\omega }}\right) s_{\varphi _y}}{1+e^{2 i \varphi _{\omega }}}\right) v+\frac{\left( M^2_{H^\pm }-M_W^2\right) s_{2 \beta }^2 v}{2 v_s^2}\right) +\left( \frac{3}{2} v^2 \left| \lambda \right| c_{\beta } s_{\beta } \left( c_{\varphi _y}-\frac{3 i \left( -1+e^{2 i\varphi _{\omega }}\right) s_{\varphi _y}}{1+e^{2 i \varphi _{\omega }}}\right) \right. \nonumber \\&\qquad \left. -\frac{3 \sqrt{2} e^{i \varphi _{\omega }}\text {Re}A_{\kappa } v_s}{1+e^{2 i \varphi _{\omega }}}\right) \delta ^{(1)}{\left| \kappa \right| }+\frac{1}{4} v^2 s_{2 \beta }\left( \frac{\left| \lambda \right| s_{2 \beta } v^2}{v_s^2}+3\left| \kappa \right| c_{\varphi _y}-\frac{9 i \left( -1+e^{2 i \varphi _{\omega }}\right) \left| \kappa \right| s_{\varphi _y}}{1+e^{2 i \varphi _{\omega }}}\right) \delta ^{(1)}{\left| \lambda \right| }\nonumber \\&\qquad -\frac{3 \sqrt{2} e^{i \varphi _{\omega }} \left| \kappa \right| v_s \delta ^{(1)}{\text {Re}A_{\kappa }}}{1+e^{2 i \varphi _{\omega }}}+\frac{3 i \left( -1+e^{2 i \varphi _{\omega }}\right) \delta ^{(1)}{t_{a_s}}}{\left( 1+e^{2 i \varphi _{\omega }}\right) v_s}+\frac{\delta ^{(1)}{t_{h_s}}}{v_s}\nonumber \\&\qquad +\left( -\frac{v^2 \left( v^2 \left| \lambda \right| ^2-2 M_W^2+2 M^2_{H^\pm }\right) s_{2 \beta }^2}{4 v_s^3}-\frac{3 \sqrt{2} e^{i \varphi _{\omega }} \left| \kappa \right| \text {Re}A_{\kappa }}{1+e^{2 i \varphi _{\omega }}}\right) \delta ^{(1)}{v_s}\nonumber \\&\qquad +\frac{3 e^{i \varphi _{\omega }} \left| \kappa \right| \left( 6 e^{i \varphi _{\omega }} \left| \lambda \right| c_{\beta } s_{\beta } s_{\varphi _y} v^2+i \sqrt{2} \left( -1+e^{2 i \varphi _{\omega }}\right) \text {Re}A_{\kappa } v_s\right) \delta ^{(1)}{\varphi _{\omega }}}{\left( 1+e^{2 i \varphi _{\omega }}\right) {}^2}. \end{aligned}$$

(C.166)

Appendix D: Neutrino-sneutrino contributions to the $h_u$-like Higgs self-energy

In this section we present approximate expressions for the $h_u$-like self-energy. We have used several assumptions which are mentioned in the following. For simplicity, we take $(y_\nu )_{ij} = y_\nu \delta _{ij}, (\mu _X)_{ij} = \mu _X \delta _{ij}, (\lambda _X)_{ij} = \lambda _X \delta _{ij}, (A_\nu )_{ij} = A_\nu \delta _{ij}, (A_X)_{ij} = A_X \delta _{ij}, (A_e)_{ij} = A_e \delta _{ij}, (B_{\mu _X})_{ij} = B_{\mu _X} \delta _{ij}, (\tilde{m}_L)_{ij} = \tilde{m}_L \delta _{ij}, (\tilde{m}_N)_{ij} = \tilde{m}_N \delta _{ij}, (\tilde{m}_X)_{ij} = \tilde{m}_X \delta _{ij}, (\tilde{m}_E)_{ij} = \tilde{m}_E \delta _{ij}$, and assume that $\tilde{m}_X = \tilde{m}_N$. Moreover, we restrict ourselves to the CP-conserving case where additionally $\mu _X, B_{\mu _X}, \tilde{m}_X, \tilde{m}_N$, $\tilde{m}_L, A_\nu \gg v$, the couplings $y_\nu$ and $\lambda$ are small, and $\lambda _X \ll y_\nu , \lambda$. We use the $\overline{\text {DR}}$ renormalization scheme for $M_W, M_Z$ and $M_{H^\pm }$. Excluding the contribution from the NMSSM without seesaw mechanism, we obtain the new contributions from the inverse seesaw mechanism to the renormalized self-energy of the $h_u$-like Higgs in the vanishing external momentum limit

$$\begin{aligned}&\hat{\Sigma }_{h_u h_u}(0) \supset \frac{3 c_{\beta }^4 y_{\nu }^2}{8 \pi ^2} \mu _X^2 \log \left( \frac{\mu _X^2}{\mu _R^2}\right) \nonumber \\&\quad -\frac{3 \alpha _+ y_{\nu }^2}{512 \pi ^2 } m_{\tilde{n}_+}^2 \log \left( \frac{m_{\tilde{n}_+}^2}{\mu _R^2}\right) \nonumber \\&\quad -\frac{3 \alpha _- y_{\nu }^2}{512 \pi ^2 } m_{\tilde{n}_-}^2 \log \left( \frac{m_{\tilde{n}_-}^2}{\mu _R^2}\right) \nonumber \\&\quad +\frac{3 y_{\nu }^2}{256 \pi ^2} \left[ 16 c_{\beta }^4 \left( \tilde{A}_{\nu }^2+\tilde{m}_L^2+\tilde{m}_N^2\right) -\rho \right] \nonumber \\&\quad -\frac{3 y_{\nu }^2}{256 \pi ^2} \log \left( \frac{\tilde{m}_L^2}{\mu _R^2}\right) \left( \frac{16 \tilde{\rho } c_{\beta }^4}{C_\beta M_Z^2} \tilde{m}_L^2 + \rho _1 + \rho _2\right) , \end{aligned}$$

(D.167)

with $m^2_{\tilde{n}_\pm } = \tilde{m}_N^2 \pm \mu _X B_{\mu _X}+\mu ^2 _X,\ \tilde{A}_{\nu } = A_{\nu }+ \lambda v_S t_{\beta }/\sqrt{2},\ C_\beta = 19 c_{2 \beta }+2 c_{4 \beta }+c_{6 \beta }-14 ,\ \mu ^2 = \tilde{m}_N^2 + \mu _X^2 - \tilde{m}_L^2$, and

(D.168)

(D.169)

(D.170)

(D.171)

In the limit $\mu _X \gg B_{\mu _X}, \tilde{m}_X, \tilde{m}_N, \tilde{m}_L, A_\nu$, the renormalized $h_u$-like Higgs self-energy is further simplified as follows

$$\begin{aligned}&\hat{\Sigma }_{h_u h_u}(0) \supset -\frac{3 y_{\nu }^2}{256 \pi ^2} \log \left( \frac{\mu _X^2}{\mu _R^2}\right) \nonumber \\&\quad \times \left( 16 c_{\beta }^4 \tilde{A}_{\nu }^2+2 C'_{\beta } \left( \tilde{m}_L^2+\tilde{m}_N^2\right) +C_{\beta } M_Z^2\right) \nonumber \\&\quad + \frac{3 y_{\nu }^2}{256 \pi ^2} \left[ 16 c_{\beta }^4 \tilde{A}_{\nu } \left( \tilde{A}_{\nu }-2 B_{\mu _X}\right) +2 C'_{\beta } \left( \tilde{m}_L^2-\tilde{m}_N^2\right) \right. \nonumber \\&\quad \left. +C_{\beta } M_Z^2\right] , \end{aligned}$$

(D.172)

with $C'_{\beta } = 4 c_{2 \beta }+c_{4 \beta }+3$.