1 Introduction

Recent observations indicate that General Relativity might indeed be modified at large distances. Scalar-tensor theories are a prototype alternative and also they are most probably the simplest, consistent and nontrivial modification of the General Relativity [4]. Gregory Horndeski [15] proposed the most general action of the scalar-tensor gravity. The same results were formulated in terms of Galileons interactions [9, 10, 24]. Therefore, Horndeski/Galileons is the most general class of scalar-tensor field models with second-order field equations and it may be considered as a proper generalization of General Relativity in high energy regime [27]. We consider the following action which is a subclass of general Horndeski/Galileons class

$$\begin{aligned} S=\int d^{4}x\sqrt{-g}\left[ \zeta R-\eta (\partial \phi )^{2}+\beta G^{\mu \nu }\partial _{\mu }\phi \partial _{\nu }\phi -2\Lambda \right] . \end{aligned}$$
(1)

Here R is the Einstein–Hilbert term, \(G^{\mu \nu }\) is the Einstein tensor, \(\phi \) is the scalar field, \(\Lambda \) is a cosmological constant term, \(\zeta >0\), \(\eta \) and \(\beta \) are model parameters. On astrophysical scales, which covers also static and spherically symmetric solutions, this scalar-tensor theory may play a crucial role. On the other hand, any modification of General Relativity must be consistent with astrophysical observations. So, it is important to see how astrophysical processes such as accretion onto black holes work in this scalar-tensor framework and can be used also as a probe to see viability of these theories from experimental viewpoint. The issue of black hole accretion disk is studied in some subclasses of scalar-tensor theories. However, there is a gap in literature since black hole accretion disk has not been studied in the mentioned scalar-tensor theory as a subclass of the general Horndeski/Galileon scenario. This is the motivation of the present study and we are going to fill this gap in this paper.

Accretion disks are constructed by rotating gaseous materials that move in bounded orbits because of the gravitational force of central mass, such as Young Stellar Objects (YSO), main-sequence stars (MSs), neutron stars (NSs), and supermassive black holes in Active Galactic Nuclei (AGN). In such systems, particles orbits are stable, but when the orbits of these materials become unstable, following it, accretion will be happened. Accretion is the process by which a massive central object such as a black hole captures particles from a fluid in its vicinity. The particles which accelerate from rest must be passed through a critical point, the point where the velocity of the gas matches its local sound speed. Then the gas falls onto the central mass at supersonic velocities. This process leads to increase in mass of the black hole [28]. In addition, extra energy would be released in this process where this energy can be source of some astrophysical phenomena, such as the production of powerful jets, high-energy radiation, and quasars [21]. Therefore, the study of the geodesic structure of particles in the vicinity of black holes and specially investigation about some characteristic radii such as marginally bound orbits \((r_{mb})\) and innermost stable circular orbits \((r_{isco})\) are interesting issues for a careful study of the subject matter. These radii are very important in the study of black hole accretion disks. For example, in thin accretion disks, the inner edge of the disk coincides with the innermost stable circular orbit (ISCO) and the efficiency of the energy released, which describes the significance of converting rest-mass energy into radiative energy [44], can be determined from this radii.

The location of unstable or stable circular orbits is consistent with the maximum or minimum of the effective potential respectively. In Newtonian theory, for any value of the angular momentum, the effective potential has a minimum and then stable circular orbit is free to have arbitrary radius, that is, there is no minimum radius of stable circular orbit, (ISCO) [20]. But this situation is different when the effective potential has a complicated form depending on the particle angular momentum and other parameters or when one incorporates general relativistic effects. For example, in General Relativity and for particles moving around the Schwarzschild black hole, for any value of the angular momentum, the effective potential has two extrema (minimum or maximum). But, only for a specific value of the angular momentum the two points coincide. This point introduces ISCO where is located at \(r=3r_{g}\) [20, 26] where \(r_{g}\) is the Schwarzschild radius. In different metrics, the properties of spacetime affects the locations of these radii and some parameters such as: specific energy, angular momentum and angular velocity are important in the position of these points. A lot of research programs are devoted to study these radii and their physical significance. Ruffini et al. [36] and Bardeen et al. [7] studied the properties of innermost stable circular orbits around the Kerr black hole. Even Hobson et al. [14] described these features in details in their textbook on General Relativity. The radiation efficiency of accretion disks, \(\eta \), for Schwarzschild and Kerr black holes was obtained by Novikov and Thorne [32] which its value lies in the range of 0.057–0.43 depending on the black hole spin. The Kerr-like metric was constructed by Johannsen and Psaltis [19] and then Johannsen [18] has studied the accretion disks around such black holes. The study of the geodesic motion and the circular orbits of charged particles around weakly magnetized rotating black holes are carried out by Tursunov et al. [40].

In an accretion disk particles move in stable orbits but when a perturbations, as a result of restoring forces, act on the particles, oscillations around the circular orbit can take place in vertical and radial directions with epicyclic frequencies. Happening the oscillations (in response to perturbations) in the inner region of an accretion disk is another important characteristic of these regions. Oscillations can be source of strong and chaotic time variations in spectrum of such systems. Therefore, study about orbital and epicyclic frequencies (radial and vertical) play an important role in the physics of relativistic accretion disks around the black holes. Isper [16, 17], Wagoner [43], Kato [22] and Ortega-Rodriges et al. [34] have studied in this field. Resonance between such a frequency modes which proposed by Kluzniak and Abromowicz [23] can be a physical mechanism for existing Quasi-periodic oscillations (QPOs). QPOs in the X-ray fluxes of some astrophysical objects such as a neutron star and black hole sources have been reviewed by many researches including van der Klis [42] and McClintock et al. [30]. Johannsen [18] has examined the radial and vertical epicyclic frequencies in the Kerr-like metric.

With these preliminaries, in this paper we study nonrotating black hole solutions with accretion disk in a subclass of Horndeski/Galileons spacetime general class. For simplicity we restrict our study to equatorial plane in a polar coordinates system. Firstly, the singularity and event horizon in this spacetime geometry are presented. Then, in order to investigate the circular orbits, effective potential is obtained in this setup. We study the locations of several characteristic radii, such as: marginally stable circular orbits \(r_{isco}\), marginally bounded circular orbits \(r_{mb}\) and photon orbits \(r_{ph}\) in equatorial plane. Also, the ISCO binding energy, the maximum radiation efficiency, the emission and temperature in equatorial epicyclic frequencies are computed. Finally, some dynamical parameters and critical accretion of isothermal fluid are investigated in details.

This paper is organized as follows: in Sect. 2 we introduce Horndeski/Galileon spacetime. The general formalism of a test particle’s motion is discussed in Sect. 3 where circular motion, stable circular orbits and oscillations are examined in Sects. 3.1, 3.2 and 3.3. In Sect. 4 and it’s subsections, the general form of some dynamical parameters such as critical speed of the flow, accretion rate and the time of accretion for an isothermal fluid are obtained. In Sect. 5 we have explained physically all of these results for a subclass of general solution of the Horndeski/Galileon black hole. Finally, Sect. 6 is devoted to summary and discussion.

2 Horndeski/Galileon spacetime

We study static and spherically symmetric limit of black hole solutions in a subclass of general Horndeski/Galileon theories (see Maselli [29] for the case of slowly rotating black holes in Horndeski theory and also Babichev et al. [4] for black hole and star solutions for Horndeski theory). The general form of the line-element for such systems with the metric signature \((+, -, -, -)\) is described by

$$\begin{aligned} ds^{2}=h(r)dt^{2}-\frac{1}{f(r)}dr^{2}-r^{2}(d\theta ^{2}+\sin ^{2}\theta d\varphi ^{2}). \end{aligned}$$
(2)

The metric functions, f(r) and h(r), depend only on the radial coordinate r and are given as follows [38]

$$\begin{aligned} f(r)= & {} \frac{(\beta +\eta r^2)h(r)}{\beta (r h(r))'},\end{aligned}$$
(3)
$$\begin{aligned} h(r)= & {} -\frac{\mu }{r}+\frac{1}{r}\int \frac{k(r)}{(\beta +\eta r^2)}dr,\end{aligned}$$
(4)
$$\begin{aligned} \phi (r)= & {} qt+\psi (r). \end{aligned}$$
(5)

In these relations, \(\mu \) plays the role of the mass term and k is obtained from the following constraint equation

$$\begin{aligned} q^{2}\beta (\beta +\eta r^2)^{2}-[2\zeta \beta +(2\zeta \eta -\lambda )r^{2}]k+C_{0}k^{\frac{3}{2}}=0,\nonumber \\ \end{aligned}$$
(6)

where \(C_{0}\) is a constant of integration. It is important to note that the static metric (2) has the time rescaling symmetry. So, if h(r) is a solution then ch(r) should be also a solution where c is a constant. This means that c should be set for t to describe the proper time in the relevant region, namely \(h \rightarrow 1\). We note also that Eq. (5) is not a solution, but rather an ansatz on the scalar field. This type of scalar configuration was firstly considered by Babichev and Charmousis [3] in which the solution for \(\psi (r)\) is also presented. About the stability of solutions, Ogawa et al. [33] and Takahashi and Suyama [37] showed that solutions with nonzero q are generically plagued by ghost or gradient instability. However, for solutions with \(q=0\), there exist some stable solutions (see Kobayashi et al. [25], Takahashi and Suyama [37], and Tretyakova and Takahashi [39]). We note that recently it has been pointed out by Babichev et al. [5, 6] that the conclusion of Ogawa et al. [33] and Takahashi and Suyama [37] is incorrect. Now from the recent relations, various solutions for different values of \(C_{0}\) and q can be obtained. We are going to discuss a common expression in this paper.

Now we study the properties of a subclass of black hole solutions in Horndeski/Galileon gravity as has been introduced above. The mentioned Horndeski spacetime contains a singularity at the location where the following condition holds

$$\begin{aligned} f(r)=0. \end{aligned}$$
(7)

The event horizon is a null surface. A surface that is defined as \(f(x^{\mu })=0\) will be null if

$$\begin{aligned} g^{\mu \nu }n_{\mu } n_{\nu }=0, \end{aligned}$$
(8)

where \(n_{\mu }\) is the normal 4-vector to the surface and it is defined as \(n_{\mu }=\nabla _{\mu }f\). Since we are interested in to study the problem in the equatorial plane, then the relation (8) can be written as \(g^{rr}(\partial _{r}f)^{2}=0\). Therefore, in the radial distance that \(g^{rr}=0\) or equivalently \(f(r)=0\), we would have an event horizon. The location of the event horizon in the geometry is a radial distance from the center of the core where the metric is singular, except the intrinsic singularity which cannot be removed via coordinate transformation.

3 Test particle’s motion: general formalism

The motion of a test particle is governed by the geodesic structure of the underlying spacetime manifold. In this section, we study general form of timelike geodesics around a subclass of Horndeski/Galileon black hole. Spacetime around this black hole is static and symmetric with two Killing vectors \(\xi _{t} =\partial _{t} \) and \(\xi _{\varphi }=\partial _{\varphi } \) which imply two constants of motion E and L (conserved energy and angular momentum per unit mass) along the trajectory as follows

$$\begin{aligned}&E=-g_{\mu \nu }\xi ^{\mu }_{t} u^{\nu }\equiv -u_{t},\nonumber \\&L=g_{\mu \nu }\xi ^{\mu }_{\varphi } u^{\nu }\equiv u_{\varphi }, \end{aligned}$$
(9)

where \(u^{\mu }=(u^{t}, u^{r}, u^{\theta }, u^{\varphi })\) is the four-velocity of the test particle. Using the normalization condition for four-velocity, that is \(u^{\mu }u_{\mu }=1\), we have

$$\begin{aligned}{}[g_{rr}(u^{r})^{2}+g_{\theta \theta }(u^{\theta })^{2}]=[1-g^{tt}(u_{t})^{2}-g^{\varphi \varphi }(u_{\varphi })^{2}]. \end{aligned}$$
(10)

From Eqs. (9) and (10) and in equatorial plane with \(\theta =\frac{\pi }{2}\), four-velocity will be given by the following components

$$\begin{aligned}&u^{t}=-\frac{E}{h(r)}\nonumber \\&u^{\theta }=0\nonumber \\&u^{\varphi }=-\frac{L}{r^{2}}\nonumber \\&u^{r}=\left[ -f(r)\left( 1-\frac{E^{2}}{h(r)}+\frac{L^{2}}{r^{2}}\right) \right] ^{\frac{1}{2}}. \end{aligned}$$
(11)

Also the following equation can be derived easily

$$\begin{aligned} \frac{h(r)}{f(r)}(u^{r})^{2}+V_{eff}=E^{2}. \end{aligned}$$
(12)

In this equation \(V_{eff}\) is the effective potential for the test particle motion that is given by

$$\begin{aligned} V_{eff}=h(r)\left[ 1+\frac{L^{2}}{r^{2}}\right] . \end{aligned}$$
(13)

It is clear that effective potential depends on the particle’s specific angular momentum radial distribution and the spacetime parameter via h(r). The study of effective potential is very useful in geodesic motion. For example, the local exterma of the effective potential determine the location of the circular orbits.

3.1 Circular motion

For circular motion in the equatorial plane, radial component r must be constant and so \(u^{r}=\dot{u}^{r}=0\) must be satisfied. Therefore, from Eq. (12) we would have \(V_{eff}=E^{2}\) and \(\frac{d}{dr}V_{eff}=0\). From these relations the specific energy E, the specific angular momentum L, the angular velocity \(\Omega _{\varphi }\) and angular momentum l can be obtained by the following relations respectively

$$\begin{aligned} E^{2}= & {} \frac{2h^{2}(r)}{2h(r)-r h'(r)},\end{aligned}$$
(14)
$$\begin{aligned} L^{2}= & {} \frac{r^{3}h'(r)}{2h(r)-r h'(r)},\end{aligned}$$
(15)
$$\begin{aligned} \Omega _{\varphi }= & {} \frac{d\varphi }{dt}\equiv \frac{u^{\varphi }}{u^{t}}\Rightarrow \Omega _{\varphi }^{2}=\frac{1}{2r}h'(r),\end{aligned}$$
(16)
$$\begin{aligned} l^{2}= & {} \frac{L^{2}}{E^{2}}=\frac{r^{3}}{2h^{2}(r)}h'(r). \end{aligned}$$
(17)

In order the energy and angular momentum to be real, the following condition must be satisfied

$$\begin{aligned} 2h(r)-r h'(r)>0. \end{aligned}$$
(18)

By solving this inequality, the limited area of circular orbit can be obtained. Therefore, this is the condition for existence of the circular orbits. For bound orbit the relation \(E^{2}<1\) must be hold and in marginally bound orbits we have \(E^{2}=1\). Then from Eq. (14) we fined

$$\begin{aligned} rh'(r)+2h(r)[h(r)-1]=0 \end{aligned}$$
(19)

By solving this equation, marginally bound orbits can be obtained easily. From Eqs. (14) and (15) it is seen that the energy and angular momentum diverge at the radius where the following relation holds

$$\begin{aligned} 2h(r)-r h'(r)=0. \end{aligned}$$
(20)

Photon sphere can be obtained by solving this relation. In a photon sphere, photon moves on circular orbits. This region plays a crucial role in the study of gravitational lensing, since lensing effect cannot be observed below this region.

3.2 Stable circular orbits and radiant energy flux

The local minima of the effective potential correspond to the stable circular orbits. Thus a stable circular orbit exists if \(\frac{d^{2}}{dr^{2}}V_{eff}>0\) and in addition to this condition, in marginally stable circular orbits, \(r_{isco}\), the condition \(\frac{d^{2}}{dr^{2}}V_{eff}=0\) must be satisfied. From Eq. (13) we have

$$\begin{aligned} \frac{d^{2}}{dr^{2}}V_{eff}=h''(r)\left( 1+\frac{L^{2}}{r^{2}}\right) -4h'(r)\frac{L^{2}}{r^{3}}+6h(r)\frac{L^{2}}{r^{4}}.\nonumber \\ \end{aligned}$$
(21)

Accretion process is possible in \(r<r_{isco}\). When falling particles from rest at infinity accrete onto the central mass, the released gravitational energy of falling particles can convert into radiation where this energy is the source of the most energetic phenomena in astrophysics. The flux of the radiant energy over the disk can be expressed in terms of the specific angular momentum L, the specific energy E and the angular velocity \(\Omega _{\varphi }\) by the following relation (see for instance Kato et al. [21])

$$\begin{aligned} K=-\frac{\dot{M}\Omega _{\varphi ,r}}{4\pi \sqrt{-g}(E-L \Omega _{\varphi })^{2}}\int _{r_{ms}}^{r}(E-L \Omega _{\varphi })L_{,r}dr, \end{aligned}$$
(22)

where \(\dot{M}\) is the accretion rate, \(\Omega _{\varphi ,r}\equiv \frac{d\Omega _{\varphi }}{dr}\) and the parameter g is determinant of \(g_{\mu \nu }\) given by

$$\begin{aligned} g=det(g_{\mu \nu })=-\frac{h(r)}{f(r)}r^{4}\sin ^{2}\theta . \end{aligned}$$
(23)

We set \(\sin \theta =1\), since we restrict our studies in equatorial plan. From relations (14)–(16) we would have

$$\begin{aligned} K(r)= & {} -\frac{\dot{M}}{4\pi r^{4}}\sqrt{\frac{r f(r)}{2 h(r)h'(r)}}\nonumber \\&\times \left( \frac{[2 h(r)-r h'(r)][r h''(r)-h'(r)]}{[2 h(r)+r h'(r)]^{2}}\right) \int _{r_{ms}}^{r}\mathcal {F}(r)dr,\nonumber \\ \end{aligned}$$
(24)

where by definition

$$\begin{aligned} \mathcal {F}(r)\equiv \sqrt{\frac{r}{2h'(r)}}\frac{[2 h(r)+r h'(r)][- h''(r)r h(r)+2r h'^{2}(r)-3h'(r) h(r)]}{[2 h(r)-r h'(r)]^{2}}.\nonumber \\ \end{aligned}$$
(25)

The steady-state accretion disk model is supposed to be in thermodynamical equilibrium. Then the radiation emitted from the surface of the disk can be as a black body radiation. So, the relation \(K(r)=\sigma T^{4}(r)\) can be hold between energy flux emitted at the surface of the disk and effective temperature of the disk (\(\sigma \) is the Stefan-Boltzman constant). Using this relation, temperature distribution on the disk by assuming thermal black body radiation can be obtained easily and then we can compute the luminosity \(L(\nu )\) of the disk. The observed luminosity at the distance d to the source with the disk inclination angle \(\gamma \) has the following form [41]

$$\begin{aligned} L(\nu )=4 \pi d^{2} I(\nu )=\frac{8}{\pi }(\cos \gamma )\int _{r_{i}}^{r_{f}}\int _{0}^{2\pi } \frac{\nu _{e}^{3}\,r\, d\varphi \,\, dr}{\exp (\frac{\nu _{e}}{T})-1},\nonumber \\ \end{aligned}$$
(26)

where \(I(\nu )\) is the thermal energy flux. In this relation \(r_{i}\) indicates the position of the inner edge and we take \(r_{i}=r_{ms}\). Also \(r_{f}\) indicates the outer edge of the disk. Since for any kind of general relativistic compact object the flux over the disk surface could be vanishing at \(r\rightarrow \infty \), we take \(r_{f}\rightarrow \infty \). The emitted frequency is given by \(\nu _{e}=\nu (1+z)\) where the redshift factor z, by neglecting the light bending, can be written as follows

$$\begin{aligned} z=\frac{1+\Omega _{\varphi } r \sin \varphi \, \sin \gamma }{\sqrt{-g_{tt}-\Omega _{\varphi }^{2}g_{\varphi \varphi }}}-1. \end{aligned}$$
(27)

The efficiency of the accreting flow is another important characteristic of the mass accretion process. The maximum efficiency of transforming gravitational energy into radiative flux of such particles between innermost circular orbit and infinity, \(\eta ^{*}\), is defined as the ratio of the specific binding energy of the innermost circular orbit to the specific rest mass energy which is given by the following relation

$$\begin{aligned} \eta ^{*}=1-E_{isco}, \end{aligned}$$
(28)

where \(E_{isco}\) is the specific energy of a particle rotating in an innermost stable circular orbit. This relation is valid for the case where all the emitted photons can escape to infinity.

Now we focus on perturbations. If a perturbation acts on the fluid element, the motion of a test particle will be nearly circular orbit in the equatorial plane and the particle will oscillate around the circular orbit with three components of motion, the issue which is discussed in the next section.

3.3 Oscillations

In an accretion disk, various types of oscillatory motions as a result of restoring forces are expected. Restoring forces act on perturbations in the accretion disks resulting Horizontal and Vertical oscillations. Some of these restoring forces in accretion disks are resulting from rotation of the disk and from a vertical gravitational filed. When a fluid element is displaced in the radial direction, it will return to its equilibrium position due to a restoring force resulting from rotation of the fluid. In accretion disks, because of existence of central object, centrifugal force is balanced by the gravitational force. When the former dominates over the latter or the reverse happens, the element of flow will be pushed inward or outward to return to the original radius with epicyclic frequency \(\Omega _{r}\). On the other hand, when a fluid element is perturbed in the vertical direction, the vertical component of the gravitational field returns the perturbed element toward equilibrium position, that is, the equatorial plane. As a result of this restoring force, the element of the fluid makes harmonic oscillation around the equatorial plane with vertical epicyclic oscillations \(\Omega _{\theta }\) [21].

In a general relativistic discussion about the motion of the fluid in an accretion disk, three frequencies around the central object are important. Circular motion at the orbital frequency \(\Omega _{\varphi }\), harmonic radial motion at the radial frequency \(\Omega _{r}\) and the harmonic vertical motion at the vertical frequency \(\Omega _{\theta }\). As we have stated, resonance between such frequencies can be source of quasi-periodic oscillations which leads to chaotic and quasi-periodic variability in X-ray fluxes from many galactic black holes. Study in this field is important in some sense. For this purpose, radial and vertical motions around a circular equatorial plane are discussed in this section.

Radial and vertical motions can be explained by \(\frac{1}{2}(\frac{dr}{dt})^{2}=V^{(r)}_{eff}\) and \(\frac{1}{2}(\frac{d\theta }{dt})^{2}=V^{(\theta )}_{eff}\) where from Eq. (10), to describe radial motion \(u^{\theta }=0\), and also for describing the vertical motion we have \(u^{r}=0\). By setting \(u^{r}=\frac{dr}{d\tau }=\frac{dr}{dt}u^{t}\) and \(u^{\theta }=\frac{d\theta }{d\tau }=\frac{d\theta }{dt}u^{t}\), we find

$$\begin{aligned}&\frac{1}{2}\left( \frac{dr}{dt}\right) ^{2}=-\frac{1}{2}\frac{f(r)h^{2}(r)}{E^{2}}\left[ 1-\frac{E^{2}}{h(r)}+\frac{L^{2}}{r^{2}sin^{2}\theta }\right] =V^{(r)}_{eff},\nonumber \\&\frac{1}{2}\left( \frac{d\theta }{dt}\right) ^{2}=-\frac{1}{2}\frac{h^{2}(r)}{r^{2}E^{2}}\left[ 1-\frac{E^{2}}{h(r)}+\frac{L^{2}}{r^{2}sin^{2}\theta }\right] =V^{(\theta )}_{eff}.\nonumber \\ \end{aligned}$$
(29)

In order to investigate the radial and vertical epicyclic frequencies, small perturbations \(\delta r\) and \(\delta \theta \) around the circular orbit in equatorial plane are considered. By taking the time-derivative of the first equation in (29), equation describing the radial oscillations can be obtained as follows

$$\begin{aligned} \frac{d^{2}r}{dt^{2}}=\frac{dV_{eff}^{(r)}}{dr}. \end{aligned}$$
(30)

For a particle which is perturbed from its original radius at \(r=r_{0}\) by a deviation \(\delta r=r-r_{0}\), the perturbed equation of motion is given by

$$\begin{aligned} \frac{d^{2}(\delta r)}{dt^{2}}=\frac{d^{2}V_{eff}^{(r)}}{dr^{2}}(\delta r)\Rightarrow (\delta {\ddot{r}})+\Omega ^{2}_{r}(\delta r)=0, \end{aligned}$$
(31)

where a dote denotes differential with respect to time coordinate t and \(\Omega _{r}^{2}\equiv -\frac{d^{2}V_{eff}^{(r)}}{dr^{2}}\). By the same procedure, for a perturbation in the vertical direction by a deviation given as \(\delta \theta =\theta -\theta _{0}\) we find

$$\begin{aligned} \frac{d^{2}(\delta \theta )}{dt^{2}}=\frac{d^{2}V_{eff}^{(\theta )}}{dr^{2}}\delta \theta \Rightarrow (\delta \ddot{\theta })+\Omega ^{2}_{\theta }(\delta \theta )=0, \end{aligned}$$
(32)

where \(\Omega ^{2}_{\theta }=-\frac{d^{2}}{d\theta ^{2}}V^{(\theta )}_{eff}\). Then from Eq. (29) in equatorial plane we would have respectively

$$\begin{aligned} \Omega ^{2}_{r}= & {} \frac{1}{2r^{4}E^{2}}\left\{ \left[ (r^{2}+L^{2})r^{2}h^{2}(r)-h(r)r^{4}E^{2}\right] f''(r)\right. \nonumber \\&\left. +\left[ (r^{2}+L^{2})2h(r)-r^{2}E^{2}\right] r^{2}f(r)h''(r)\right. \nonumber \\&+2r^{2}f(r)h'^{2}(r)(r^{2}+L^{2})-2r\left[ [-(r^{2}+L^{2})2h(r)\right. \nonumber \\&\left. +\,r^{2}E^{2}]r f'(r)+4f(r)h(r)L^{2}\right] h'(r)\nonumber \\&\left. -4h^{2}(r)L^{2}(-\frac{3}{2}f(r)+r f'(r)) \right\} , \end{aligned}$$
(33)

and

$$\begin{aligned} \Omega ^{2}_{\theta }=\frac{h^{2}(r)L^{2}}{r^{4}E^{2}}. \end{aligned}$$
(34)

In these equations, a prime denotes differential with respect to the radial coordinate, r. To proceed further, now we present basic dynamical equations in this subclass of general Horndeski/Galileons black hole spacetime.

4 Basic dynamical equations

In this section we provide the basic dynamical equations for our forthcoming arguments (we refer to Babichev et al. [1, 2] for more details). Here we consider a perfect fluid which is specified by the following energy-momentum tensor

$$\begin{aligned} T^{\mu \nu }=(p+\rho )u^{\mu }u^{\nu }-p g^{\mu \nu }, \end{aligned}$$
(35)

where p and \(\rho \) are pressure and energy density of the fluid respectively. In this relation, \(u^{\mu }\) is the fluid elements four-velocity. Because of background symmetries, in relation (35) all of the components are functions of only the radial coordinate, r. Since we are assuming the fluid is flowing radially in the equatorial plane (\(\theta =\frac{\pi }{2}\)), the general form of the four-velocity will be as follows

$$\begin{aligned} u^{\mu }=\frac{dx^{\mu }}{d\tau }=(u^{t},u^{r},0,0), \end{aligned}$$
(36)

where \(\tau \) is the proper time along the geodesic. From this relation and under the normalization condition \(u^{\mu }u_{\mu }=1\), we obtain

$$\begin{aligned} u^{t}=\sqrt{\frac{f(r)+(u^{r})^{2}}{h(r)f(r)}}, \end{aligned}$$
(37)

where for forward flow in time, \(u^{t}\) must be positive and for accretion (inward flow), \(u^{r}<0\). By deriving the energy-momentum and also particle-number conservation equations, all of the required equations for studying the accretion are obtained. Conservation of the energy- momentum tensor is given by

$$\begin{aligned} T^{\mu \nu }_{;\mu }=0\Rightarrow T^{\mu \nu }_{;\mu }=\frac{1}{\sqrt{-g}}(\sqrt{-g}T^{\mu \nu })_{,\mu }+\Gamma ^{\nu }_{\alpha \mu }T^{\alpha \mu }=0,\nonumber \\ \end{aligned}$$
(38)

where in this relation (; ) shows the covariant differentiation, \(\sqrt{-g}=r^{2}\sin \theta \sqrt{\frac{h(r)}{f(r)}}\) and \(\Gamma \) is the second kind Christoffel symbol (affine connection) where its non-zero components are as follows

$$\begin{aligned}&\Gamma ^{0}_{01}=\Gamma ^{0}_{10}=\frac{1}{2}\frac{h'(r)}{h(r)}\nonumber \\&\Gamma ^{1}_{00}=\frac{1}{2}h'(r)f(r), \Gamma ^{1}_{11}=-\frac{1}{2}\frac{f'(r)}{f(r)},\nonumber \\&\Gamma ^{1}_{22}=-r f(r), \Gamma ^{1}_{33}=-r f(r)\sin \theta \nonumber \\ {}&\Gamma ^{2}_{12}=\Gamma ^{2}_{21}=\frac{1}{r}\nonumber \\&\Gamma ^{3}_{13}=\Gamma ^{3}_{31}=\frac{1}{r}. \end{aligned}$$
(39)

From these relations, equation (38) yields

$$\begin{aligned} T^{10}_{,r}+\frac{1}{\sqrt{-g}}T^{10}(\sqrt{-g})_{,r}+2\Gamma ^{0}_{01}T^{10}=0, \end{aligned}$$
(40)

where after some manipulations we obtain

$$\begin{aligned} (p+\rho )u^{r}r^{2}\sqrt{(u^{r})^{2}+f(r)}\frac{h(r)}{f(r)}=A_{0}, \end{aligned}$$
(41)

with \(A_{0}\) as an integration constant. Projecting the energy-momentum conservation law onto the four-velocity via \(u_{\mu }T^{\mu \nu }_{;\nu }=0\), yields

$$\begin{aligned}&(p+\rho )_{,\nu } u_{\mu }u^{\mu }u^{\nu }+(p+\rho )u^{\mu }_{;\nu }u_{\mu }u^{\nu }+(p+\rho )u_{\mu }u^{\mu }u^{\nu }_{;\nu }\nonumber \\&\quad +p_{,\nu }g^{\mu \nu }u_{\mu }+pu_{\mu } g^{\mu \nu }_{;\nu }=0. \end{aligned}$$
(42)

By considering the normalization conditions as \(u_{\mu }u^{\mu }=1\) and since \(g^{\mu \nu }_{;\nu }=0\), this relation reduces to

$$\begin{aligned} (p+\rho )u^{\nu }_{;\nu }+u^{\nu }\rho _{,\nu }=0. \end{aligned}$$
(43)

Since \(A^{b}_{;a}=\partial _{a}A^{b}+\Gamma ^{b}_{ac}A^{c}\), we find

$$\begin{aligned} u^{r}\rho _{,r}+(p+\rho )\left[ \Gamma ^{0}_{0c}u^{c}+\left( u^{r}_{,r}+\Gamma ^{1}_{1c}u^{c}\right) +\Gamma ^{2}_{2c}u^{c}+\Gamma ^{3}_{3c}u^{c}\right] =0.\nonumber \\ \end{aligned}$$
(44)

By using the non-zero components of the connection, this relation after some simplification yields

$$\begin{aligned} \frac{\rho '}{(p+\rho )}+\frac{1}{2}\frac{h'(r)}{h(r)}-\frac{1}{2}\frac{f'(r)}{f(r)}+\frac{u'}{u}+\frac{2}{r}=0, \end{aligned}$$
(45)

which after integration, we would have

$$\begin{aligned} r^{2}u^{r}\sqrt{\frac{h(r)}{f(r)}} \exp \left( \int \frac{d\rho }{p+\rho }\right) =-A_{1}, \end{aligned}$$
(46)

where \(A_{1}\) is an integration constant. Since in the left hand side \(u^{r}<0\), the right hand side takes a minus sign too. So we find finally

$$\begin{aligned} (p+\rho )\sqrt{h(r)\left[ \frac{(u^{r})^{2}}{f(r)}+1\right] }\exp \left( -\int \frac{d\rho }{p+\rho }\right) =A_{2},\nonumber \\ \end{aligned}$$
(47)

where \(A_{2}\) is an integration constant. The equation of mass flux in this setup which is given by

$$\begin{aligned} (\rho u^{\mu })_{;}\equiv \frac{1}{\sqrt{-g}}(\sqrt{-g} \rho u^{\mu })_{,\mu }=0 \end{aligned}$$
(48)

can be rewritten as

$$\begin{aligned} \frac{1}{\sqrt{-g}}(\sqrt{-g} \rho u^{\mu })_{,r}+\frac{1}{\sqrt{-g}}(\sqrt{-g} \rho u^{\theta })_{,\theta }=0. \end{aligned}$$
(49)

Since we are interested in to study just in equatorial plane, the second term in Eq. (49) vanishes. Therefore, \(\sqrt{-g} \rho u^{\mu }\) would be as a constant, that is

$$\begin{aligned} \rho u^{r}r^{2}\sqrt{\frac{h(r)}{f(r)}}=A_{3}, \end{aligned}$$
(50)

where \(A_{3}\) is an integration constant. We note that while we have restricted our study to equatorial plane by symmetry considerations, the general case is not so complicated in essence. Because of symmetry all important characteristics of the model can be obtained in \(\theta =\frac{\pi }{2}\) plane as well. Now we are going to determine dynamical parameter, critical accretion and accretion rate in this setup.

4.1 Dynamical parameters

To proceed further, we assume isothermal fluids. These fluids flow at a constant temperature. Therefore, \(p\propto \rho \) and then the speed of sound throughout the accretion process remains constant. For such fluids, the equation of state is of the form \(p=k \rho \) where k is the equation of state parameter. Then Eqs. (46), (47) and (50) yield

$$\begin{aligned} \frac{p+\rho }{\rho }\sqrt{h(r)\Big [\frac{(u^{r})^{2}}{f(r)}+1\Big ]}=A_{4}, \end{aligned}$$
(51)

where \(A_{4}\) is an integration constant. By substituting \(p=k \rho \), we can obtain u as follows

$$\begin{aligned} u=\left( \frac{1}{k+1}\right) \sqrt{f(r)\left[ \frac{A_{4}^{2}}{h(r)}-(k+1)^{2}\right] }. \end{aligned}$$
(52)

Then from Eq. (50) the density of the fluid can be obtained as

$$\begin{aligned} \rho =\frac{A_{3}}{r^{2}}\frac{(k+1)}{\sqrt{A_{4}^{2}-(k+1)^{2}h(r)}}. \end{aligned}$$
(53)

Finally, from the relation \(p=k \rho \), the pressure can be obtained easily.

4.2 Mass evolution

In realistic astrophysical cases, the mass of the black hole is not fixed in essence. By some processes such as accreting of mass from accretion disk onto black hole and also Hawking radiation, its mass will be changed gradually. The rate of change of mass can be obtained by integrating the flux of the fluid over the surface of the black hole, that is \(\dot{M}\equiv \frac{dM}{dt}=-\int T^{r}_{t} ds\) where a dot denotes the time derivative, \(ds=\sqrt{-g}\, d\theta \, d\varphi \) and \(T^{r}_{t}=(p+\rho )u_{t}u^{r}\). By substituting these relations, \(\dot{M}\) can be obtained as follows

$$\begin{aligned} \dot{M}=-4\pi r^{2}u(p+\rho )\frac{h(r)}{f(r)}\sqrt{u^{2}+f(r)}\equiv -4\pi A_{0}, \end{aligned}$$
(54)

where \(A_{0}=-A_{1}A_{2}\), and \(A_{2}=(p_{\infty }+\rho _{\infty })\sqrt{h(r_{\infty })}\). Therefore, we obtain

$$\begin{aligned} \dot{M}=4\pi A_{1}(p_{\infty }+\rho _{\infty })\sqrt{h(r_{\infty })}M^{2}. \end{aligned}$$
(55)

Now, time evolution of mass of the black hole with initial mass \(M_{i}\) can be obtained by integration of Eq. (55) that can be rewritten as

$$\begin{aligned} \frac{d M}{M^{2}}=\mathcal {F}t \end{aligned}$$
(56)

where \(\mathcal {F}\equiv 4\pi A_{1}(p+\rho )\sqrt{h(r_{\infty })}\). By integrating from Eq. (56) we obtain

$$\begin{aligned} M_{t}=\frac{M_{i}}{1-\mathcal {F}M_{i}t}\equiv \frac{M_{i}}{1-\frac{t}{t_{cr}}} \end{aligned}$$
(57)

where \(t_{cr}= \Big [4\pi A_{1}(p+\rho )\sqrt{h(r_{\infty })}M_{i} \Big ]^{-1}\) is the critical accretion time. In the case \(t=t_{cr}\) the denominator of Eq. (57) vanishes and the black hole mass grows up to infinity in a finite time. After determining the time evolution of the disk and black hole mass, now we study critical accretion in this setup.

4.3 Critical accretion

Very far from the black hole, the flow is at rest but gravitational field of black hole tends to accelerate it inwards. When flow moves inwards, it must pass through critical point (sonic point) where in this point \(r=r_{c}\), the four-velocity of the fluid matches the local speed of sound, \(u=c_{s}\). In order to obtain sonic point, an expression for the radial velocity gradient with no other derivatives is required. From Eqs. (50) and (51), the following two equations are obtained

$$\begin{aligned} \frac{\rho '}{\rho }+\frac{u'}{u}+\frac{1}{2}\left[ \frac{h'(r)}{h(r)}-\frac{f'(r)}{f(r)}\right] +\frac{2}{r}=0, \end{aligned}$$
(58)

and

$$\begin{aligned}&\frac{\rho '}{\rho }\left[ \frac{d\ln (p+\rho )}{d\ln \rho }-1\right] +\frac{1}{2}\left[ \frac{h'(r)}{h(r)}-\frac{f'(r)}{f(r)}\right] +\frac{u u'}{u^{2}+f(r)}\nonumber \\&\quad +\frac{1}{2}\frac{f'(r)}{u^{2}+f(r)}=0. \end{aligned}$$
(59)

From these equations we obtain

$$\begin{aligned} \frac{d\ln u}{d\ln r}=\frac{\mathcal {D}_{1}}{\mathcal {D}_{2}}, \end{aligned}$$
(60)

where by definition

$$\begin{aligned} \mathcal {D}_{1}=-\left[ \frac{r}{2}(V^{2}-1)\left( \frac{h'(r)}{h(r)}-\frac{f'(r)}{f(r)}\right) +2V^{2}-\frac{r f'(r)}{2(u^{2}+f(r))}\right] ,\nonumber \\ \end{aligned}$$
(61)

and

$$\begin{aligned} \mathcal {D}_{2}=\left[ V^{2}-\frac{u^{2}}{u^{2}+f(r)}\right] . \end{aligned}$$
(62)

With these two equations, the following relation can be obtained

$$\begin{aligned} V^{2}=\frac{d\ln (p+\rho ) }{d\ln \rho }-1. \end{aligned}$$
(63)

The condition for critical points is \(\mathcal {D}_{1}=\mathcal {D}_{2}=0\). This condition yields

$$\begin{aligned} V_{c}^{2}=\frac{r h'(r)}{4h(r)+rh'(r)}, \end{aligned}$$
(64)

and

$$\begin{aligned} u_{c}^{2}=\frac{1}{4}\frac{r f(r)h'(r)}{h(r)}, \end{aligned}$$
(65)

where index c refers to the critical point. Since the right hand side of the relation (64) must be positive, then if dependence of h(r) is known, by solving the following inequality the range of critical radius can be obtained

$$\begin{aligned} 4h(r)+rh'(r)>0. \end{aligned}$$
(66)

Finally the sound speed \(c_{s}^{2}=\frac{dp}{d\rho }\) can be obtained from (52) as

$$\begin{aligned} c_{s}^{2}=A_{4}\sqrt{\frac{f(r)}{h(r)}\left[ u^{2}+f(r)\right] }-1. \end{aligned}$$
(67)

5 A subclass of Horndeski/Galileon black hole solutions

As we have stated in Sect. 2, a huge variety of solutions can be obtained from Eqs. (4)–(6). Here we present a solution of this subclass of the Horndeski/Galileon setup that are characterized by the parameters A, B, C and \(\gamma \) (see for instance Tretyakova [38]). The solutions are as follows

$$\begin{aligned} h(r)=C-\frac{\mu }{r}+Ar^{2}+\Delta , \end{aligned}$$
(68)

and

$$\begin{aligned} f(r)=\left( 1+\frac{\eta }{\beta }r^{2}\right) \left[ \frac{\Delta +A r^{2}+C-\frac{\mu }{r}}{3A r^{2}+C+\frac{B}{1+r^{2}\gamma ^{2}}}\right] , \end{aligned}$$
(69)

where we have set \(\Delta \equiv B\frac{\tan ^{-1}( r\gamma )}{r\gamma }\). The coefficients C, A, B and \(\gamma \) are defined as follows

$$\begin{aligned}&A=-\frac{\eta }{3\beta },\,\,\, B=\frac{2(1+\gamma ^{2})\epsilon }{\zeta +y},\,\,\, \epsilon \ll \mid y-1 \mid \nonumber \\&\gamma =\sqrt{\frac{\eta }{\mid \beta \mid }}\frac{\zeta +y}{\zeta -3y},\,\,\, C=1-\frac{2\epsilon }{\zeta +y},\,\,\,\, y=\frac{\Lambda \beta }{\eta }. \end{aligned}$$
(70)

Here \(\epsilon \) is a small parameter which marks the deviation from the inherent de Sitter solution. Also the scalar field in this case is given by

$$\begin{aligned} \psi ^{2}(r)=-\frac{2(2\eta )^{2}r^{2}(2\eta +2\Lambda \beta )[(2\eta -2\Lambda \beta )r^{2}+4\beta ]^{2}}{2\beta (2\eta -2\Lambda \beta )^{2}(2\eta r^{2}+2\beta )^{3}f(r)}, \end{aligned}$$
(71)

where \(\psi =\frac{d\phi }{dr}\). As we have said, singular points can be obtained by solving the relation \(f(r) = 0\). From this relation singular point is located at \(r_{sing}=\frac{\mu }{B+C}\).

An important issue should be stressed here: about the behavior of the scalar field at the black hole horizon (say, \(r_{h}\)), the scalar field seems to be divergent at the horizon from Eq. (71). But since \(f(r_h )=0\) and \(\frac{df}{dr}(r_h)\ne 0\), one can expand f(r) in Taylor series to find \(f(r)=f_0+f_{1}(r-r_{h} )+f_{2}(r-r_{h})^{2}+\cdots \) . For \(\psi (r)\) this approximates to \(\frac{1}{\sqrt{f(r)}}\) in near horizon which gives for the scalar field \(\phi (r)=\phi _{0}+\phi _{1}(r-r_h )^{1/2}+\phi _{2}(r-r_h )^{3/2}+\cdots \) . Therefore, the scalar field remains finite in the near horizon region (a similar analysis can be found in the paper by [31]). We note that although the scalar field itself does not diverge at the horizon, its derivative does. However, there is no physical divergence since all invariants, such as \(g^{\mu \nu }\partial _{\mu }\phi \partial _{\nu }\phi \) remain finite. For more discussion on this issue we refer to Feng et al. [11] (see also Hadar and Reall [13] and Caceres et al. [8]).

We note that for nonzero \(\eta \) the model given by Eqs. (68)–(70) admits solutions in which the \(\Lambda \)-term in action (1) is totally screened. The metric then is not asymptotically flat but rather de Sitter with the effective cosmological constant proportional to \(\eta \)/\(\beta \) since the scalar kinetic term becomes constant around the present time (Gubitosi and Linder [12]). It is important to note that as has been shown by Tretyakova [38], for \(1-(B+C) < 3 \times 10^{-4}\) this metric must be equivalent to the Schwarzschild metric in the sense that it matches with the observations of the gravitational light deflection and perihelion precession. This feature guarantees the existence of bounds orbits for \((B+C)>0\) (for more discussion on this issue see Tretyakova [38]).

Fig. 1
figure 1

Effective potential for massive particles versus the radial coordinate (in the unit of \(\frac{1}{r_{g}}\)). The left panel represents \(V_{eff}\) for \(B=-0.1\) and for several values of the angular momentum. The solid circle in the left panel denotes the effective potential in ISCO. In the right panel, effect of the Horndeski/Galileon correction parameter B on effective potential for \(L=5\) is shown

Full size image

It is necessary to mention that for calculations, the assumption \(A\simeq 0\) is considered. Then the components of metric (2) will be as \(h(r)=C-\frac{\mu }{r}+\Delta \) and \(f(r)=\frac{h(r)}{B+C}\). On the other hand, since \(\gamma \simeq \sqrt{A}\), due to smallness of \(\gamma \), it is more suitable to substitute \(\tan ^{-1}(r\gamma )\simeq r\gamma \) and therefore \(\Delta \simeq B\). All calculations are done with these approximations and also with assumption \(C=1\) and \(0<B+C<1.125\) [38]. By these assumptions, we focus mainly on the role of parameter B as Horndeski/Galileon correction factor in our forthcoming treatment.

5.1 Circular equatorial geodesics

In order to investigate circular geodesics in equatorial plane, we need the explicit form of the effective potential which is governed by Eq. (12) as

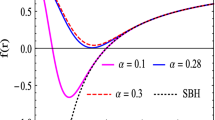
$$\begin{aligned} V_{eff}=\left( C-\frac{\mu }{r}+Ar^{2}+\Delta \right) \left( 1+\frac{L^{2}}{r^{2}}\right) , \end{aligned}$$
(72)

where \(\Delta \equiv B\frac{\tan ^{-1} (r\gamma )}{r\gamma }\). From the condition \(\frac{d^{2}}{dr^{2}}V_{eff}>0\) for existence of the stable circular orbits, we see that for \(r<\frac{3}{2}\frac{\mu }{B+C}\) and \(r>3\frac{\mu }{B+C}\) this condition holds, which with regard to Eq. (20), the location of the stable circular orbits would be at \(r\ge 3\frac{\mu }{B+C}\). Then

$$\begin{aligned} r_{isco}= 3\frac{\mu }{B+C}, \end{aligned}$$
(73)

is introduced as the radius of the innermost stable circular orbit. The left panel of Fig. 1 represents the effective potential versus r for several values of the angular momentum L in the case with \(B=-0.1\). We see that for \(L<2.2 \sqrt{3}\) no extremum can be observed and the first extremum is observed at \(L=2.2 \sqrt{3}\) (solid circle in the figure). This point represents the location of the innermost stable circular orbit located at \(r=6.6\). For larger values of the angular momentum, \(V_{eff}\) has two extremum where the maximum one denotes the location of the unstable circular orbit and the minimum one denotes the stable circular orbit. By increasing the angular momentum, \(V_{eff}\) will be larger and the maximum point turns to the smaller radii whereas the minimum point goes to larger radii. From the right panel of Fig. 1 the effect of Horndeski/Galileon correction factor B on the effective potential can be seen. The effective potential achieves larger values for larger values of B and by increasing this parameter, the loci of unstable circular orbit becomes closer to the central mass and stable orbits will be located farther from the central mass. Also the enhancement of the distance between these points by increasing B is obvious.

In addition to innermost stable circular orbit which is very important in studying the accretion around the black hole, there are other special radii where considering them is necessary. As we have stated previously, the circular orbits exist only for radii larger than the photon radius \(r_{ph}\). For \(r_{ph}<r<r_{ms}\), the motion of the particle will be unstable against the small perturbations. This means that particle falls into the black hole or flee away to infinity. In the region \(r>r_{ms}\) the particle moves on stable circular orbits.

From Eqs. (18)–(20), other characteristic radii including the photon sphere \(r_{ph}\), circular orbit \(r_{circ}\) and marginally bound orbit \(r_{mb}\) can be obtained respectively as

$$\begin{aligned} r_{ph}= & {} \frac{3}{2}\frac{\mu }{B+C},\end{aligned}$$
(74)
$$\begin{aligned} r_{circ}> & {} \frac{3}{2}\frac{\mu }{B+C}, \end{aligned}$$
(75)

and

$$\begin{aligned} r_{mb}=\frac{1}{4}\mu \frac{4(B+C)-3\pm \sqrt{9-8(B+C)}}{(B+C)(B+C-1)}. \end{aligned}$$
(76)

We have plotted the characteristic radii versus the Horndeski/Galileon correction factor B in Fig. 2. The value of this parameter affects the location of the characteristic radii in the vicinity of the black hole. For larger values of B, the location of \(r_{ph}\), \(r_{isco}\) and \(r_{sing}\) will be closer to the black hole, whereas the behavior of \(r_{mb}\) for negative and positive values of \(B=0\) is different. For \(B<0\), marginally bound radius decreases by increasing B, but for \(B>0\) this behavior becomes reverse as it finally matches the innermost stable circular orbit. Since \(r_{isco}\) represents the inner edge of the accretion disk, we see that in larger values of B, the disk will be extended close to the central mass.

Fig. 2
figure 2

The effect of the Horndeski/Galileon correction factor B on characteristic radius and comparison between these radii. The vertically dotted line represents the location of these radii in Schwarzschild spacetime

Full size image

For a particle which moves in a circular orbit, the specific energy, specific angular momentum, angular velocity and angular momentum in equatorial plane can be derived as

$$\begin{aligned} E^{2}= & {} \frac{2\Big (C-\frac{\mu }{r}+Ar^{2}+\Delta \Big )^{2}}{\Big (2C-3\frac{\mu }{r}+3\Delta -\frac{B}{1+r^{2}\gamma ^{2}}\Big )},\end{aligned}$$
(77)
$$\begin{aligned} L^{2}= & {} r^{2}\frac{\Big (\frac{\mu }{r}+2Ar^{2}-\Delta +\frac{B}{1+r^{2}\gamma ^{2}}\Big )}{\Big (2C-3\frac{\mu }{r}+3\Delta -\frac{B}{1+r^{2}\gamma ^{2}}\Big )},\end{aligned}$$
(78)
$$\begin{aligned} \Omega _{\varphi }^{2}= & {} \frac{1}{2r^{2}}\Big (\frac{\mu }{r}+2Ar^{2}-\Delta +\frac{B}{1+r^{2}\gamma ^{2}}\Big ),\end{aligned}$$
(79)
$$\begin{aligned} l^{2}= & {} \frac{r^{2}}{2}\frac{\Big (\frac{\mu }{r}+2Ar^{2}-\Delta +\frac{B}{1+r^{2}\gamma ^{2}}\Big )}{\Big (-\frac{\mu }{r}+Ar^{2}+\Delta +C\Big )^{2}}, \end{aligned}$$
(80)

respectively. For the innermost stable circular orbit, these relations reduce to

$$\begin{aligned}&E^{2}_{isco}= \frac{8}{9}(B+C),\end{aligned}$$
(81)
$$\begin{aligned}&L^{2}_{isco}= \frac{3\mu ^{2}}{(B+C)^{2}},\end{aligned}$$
(82)
$$\begin{aligned}&\Omega ^{2}_{isco}=\frac{1}{54}\frac{(B+C)^{3}}{\mu ^{2}},\end{aligned}$$
(83)
$$\begin{aligned}&l^{2}=\frac{27}{8}\frac{\mu ^{2}}{(B+C)}, \end{aligned}$$
(84)

respectively.

Fig. 3
figure 3

The behavior of energy (upper panel) and angular momentum (lower panel) versus the radial distance from the central mass for several values of the Horndeski/Galileon parameter B. The innermost stable circular orbits are represented by the solid circles in the upper right panel. The empty circles at the energy diagram denote the limit of the bound orbit. The lower panel shows that the angular momentum gets smaller values by increasing B. The loci of these parameters in innermost stable circular orbits are represented by circles on the lower right panel of the figure

Full size image
Fig. 4
figure 4

Energy efficiency of a massive particle falling from infinity into the black hole is shown versus the radial distance for several values of the Horndeski/Galileon parameter B. The maximum efficiency at the innermost stable circular orbit is represented by a circle in each case in the right panel

Full size image
Fig. 5
figure 5

Dependence of the emission rate and temperature T on radius r and Horndeski/Galileon parameter B (\(B=-0.1, 0, 0.1\) from top to down respectively). Dotted curve represents the case of the Schwarzschild black hole (\(B=0\))

Full size image
Fig. 6
figure 6

A comparison between the epicyclic frequencies. The dashed curve in the left panel represents the vertical frequency. The radial epicyclic frequencies for several values of the Horndeski/Galileon parameter B are shown by the solid curves where the dotted curve is for the Schwarzschild black hole with \(B=0\). The effect of Horndeski/Galileon parameter on the ratio of the vertical frequency to the radial frequency as a function of r is shown in the right panel

Full size image

In Fig. 3, the behavior of specific energy and angular momentum versus the radius are shown and the effect of the Horndeski/Galileon correction factor B is studied. The upper left panel represents variation of the specific energy versus r. In the upper right panel the location of this radius in innermost stable circular orbits is shown by the solid circle. The empty circle denotes the limit of the bound orbit. Increasing the Horndeski/Galileon correction factor enhances the energy and decreases the range of bound orbit radius. The lower left panel represents the angular momentum where it gets smaller values by increasing B. The loci of these parameters in innermost stable circular orbits are represented by circles on the lower right panel of the figure.

Now by knowing E in ISCO, we are able to determine the radiation energy efficiency of accretion. As we have said previously, the efficiency of accretion is \(1-E\), where the maximum efficiency of accretion given by \(1-E_{isco}\) in innermost stable orbit in this setup is \(1-\sqrt{\frac{8}{9}(B+C)}\). In Fig. 4, the efficiency of accretion is plotted versus r for different values of the Horndeski/Galileon correction factor B where we have denoted the maximum with a circle in this figure. In the case \(B=0\) where coincides with the Schwarzschild black hole (dashed line), the efficiency equals to 0.057 at \(r=6 r_{g}\) as usual. For negative values of the Horndeski/Galileon parameter, efficiency goes up and becomes greater than the Schwarzschild black holes ones. For example, in the case with \(B=-0.1\), the efficiency equals to 0.105 at \(r=6.66 r_{g}\) where is tangible. On the other hand, positive values of B is accompanied with decreasing of the efficiency.

Now we can study radiation flux from the surface of the accretion disk by knowing E, L and \(\Omega _{\varphi }\) in equatorial plane and \(r_{ms}\). The Flux of the radiation energy of the accretion disk is obtained from Eqs. (24) and (25) as

$$\begin{aligned}&K(r)=-\frac{1}{8}\dot{M}\sqrt{\frac{2r^{2}(1+\frac{\eta }{\beta }r^{2})}{(3Ar^{2}+C+\frac{B}{1+r^{2}\gamma ^{2}})(2Ar^{2}+\frac{\mu }{r}+ \frac{B}{1+r^{2}\gamma ^{2}}-\Delta )}} \nonumber \\&\quad \times \frac{1}{r}\left\{ 3\Delta +2C-3\frac{\mu }{r}-\frac{B}{1+r^{2}\gamma ^{2}}\right\} \nonumber \\&\quad \times \left\{ 3\Delta -3\frac{\mu }{r}-3\frac{B}{1+r^{2}\gamma ^{2}}-2\frac{Br^{2}\gamma ^{2}}{(1+r^{2}\gamma ^{2})^{2}}\right\} \nonumber \\&\quad \times \left\{ \pi r^{4}(\Delta +4Ar^{2}+2C-\frac{\mu }{r}+\frac{B}{1+r^{2}\gamma ^{2}})^{2}\right\} ^{-1}\int _{r_{_{m_{s}}}}^{r}\mathcal {F}(r) dr,\nonumber \\ \end{aligned}$$
(85)

where by definition

$$\begin{aligned} \mathcal {F}(r)= & {} \frac{1}{2}\left\{ \sqrt{\frac{2r^{2}}{2Ar^{2}+\frac{\mu }{r}-\Delta +\frac{B}{1+r^{2}\gamma ^{2}}}}(4Ar^{2}-\frac{\mu }{r}+ \Delta +\frac{B}{1+r^{2}\gamma ^{2}}+2C)\right. \nonumber \\&\times \Bigg (\frac{1}{r}\Big (\Delta +Ar^{2}+C-\frac{\mu }{r}\Big )\Bigg (\Delta -8Ar^{2}-\frac{\mu }{r}-\frac{B}{1+r^{2}\gamma ^{2}}+\frac{2Br^{2}\gamma ^{2}}{(1+r^{2}\gamma ^{2})^{2}}\Bigg )\nonumber \\&+2\left( \frac{B}{1+r^{2}\gamma ^{2}}-\Delta +2Ar^{2}+\frac{\mu }{r}\right) \Bigg )\Bigg \}\Bigg \{-3\frac{\mu }{r}+3\Delta +2C-\frac{B}{1+r^{2}\gamma ^{2}}\Bigg \}^{-2}. \end{aligned}$$
(86)

Then the temperature can be obtained by using the equation \(K=\sigma T^{4}\). In Fig. 5, the relation between the radiation flux and temperature is shown. The radiation flux has a maximum in the vicinity of the black hole and decreases at the smaller radii. By increasing the Horndeski/Galileon correction factor B, the energy flux raises and the maximum of emission flux tends to the smaller radii but the reverse happens after this point. The dependence on this parameter is very considerable in the vicinity of the black hole, but it is relatively weak far from the black hole. These behaviors are the same for the temperature. As we have said in Sect. 3.2, the luminosity can be compute from Eq. (26), but because of complexity of the required equations, solving this equation is not possible analytically.

5.2 Epicyclic frequencies

If a perturbation acts on a particle moving on a circular orbit in the equatorial plane, the particle experiences small oscillations in the vertical and radial directions. Using the epicyclic frequencies given by Eqs. (33) and (34), we derive the radial and vertical epicyclic frequencies as follows

$$\begin{aligned} \Omega _{\theta }^{2}=\frac{2Ar^{2}+\frac{\mu }{r}-\Delta +\frac{B}{1+r^{2}\gamma ^{2}}}{2r^{2}}, \end{aligned}$$
(87)

and

$$\begin{aligned} \Omega _{r}^{2}= & {} -\frac{3}{2}\left( 1+\frac{\eta }{\beta }r^{2}\right) \Bigg \{\Bigg [ -\frac{8}{9}A\gamma ^{4}r^{8}\left( \frac{15}{8}\Delta +C\right) +\frac{5}{3}A\gamma ^{4}r^{7}\mu +\gamma ^{2} r^{6}\Bigg (\frac{1}{9}\Delta \gamma ^{2}(3\Delta +C)\nonumber \\&+A\left( -\frac{16}{9}C-\frac{10}{3}\Delta +B\right) \Bigg )+\frac{10}{3}\mu \gamma ^{2}r^{5}\Bigg (\left( -\frac{1}{30}C-\frac{1}{5}\Delta \right) \gamma ^{2}\nonumber \\&+A\Bigg )\Bigg (\frac{1}{3}\mu ^{2}\gamma ^{2}+\Bigg [\frac{1}{9}(2\Delta +B)C-\frac{1}{3}\Delta (-2\Delta +B)\Bigg ] \gamma ^{2}+\frac{7}{9}A\left( B-\frac{15}{7}\Delta -\frac{8}{7}C\right) \Bigg )r^{4}\nonumber \\&+\Bigg (\left( \frac{1}{3}B-\frac{2}{9}C-\frac{4}{3}\Delta \right) \gamma ^{2}+\frac{5}{3}A\Bigg )\mu r^{3}\Bigg (\frac{2}{3}\mu ^{2}\gamma ^{2}+\frac{2}{9}(-\Delta +B)\left( B-\frac{3}{2}\Delta -\frac{1}{2}C\right) \Bigg )r^{2}\nonumber \\&+\frac{5}{9}\left( -\frac{6}{5}\Delta -\frac{1}{5}C+B\right) \mu r+\frac{1}{3}\mu ^{2}\Bigg ]\Bigg \}\nonumber \\&\times \Bigg \{(1+r^{2}\gamma ^{2})\Bigg [Ar^{4}\gamma ^{2}+\left( \frac{1}{3}\gamma ^{2}C+A\right) r^{2}+\frac{1}{3}B+\frac{1}{3}C\Bigg ]r^{4}\Bigg \}^{-1}. \end{aligned}$$
(88)

respectively. From Eqs. (79), (87) and (88) it is clear that

$$\begin{aligned} \Omega _{\theta }^{2}=\Omega _{\varphi }^{2} \end{aligned}$$

and

$$\begin{aligned} \Omega _{r}^{2}=\Omega _{\theta }^{2}\left[ \frac{C+3\Delta -2B-3\frac{\mu }{r}}{(B+C)}\right] . \end{aligned}$$
Fig. 7
figure 7

The left panel represents the location of three resonances: parametric resonance(3:2) and forced resonance (3:1, 2:1). The dependence of these locations to the Horndeski/Galileon parameter B is shown in the right panel

Full size image

In the left hand side of Fig. 6 we have plotted epicyclic frequencies versus the radius for several values of the Horndeski/Galileon correction factor B in order to have a comparison. The angular and vertical epicyclic frequencies are shown in the left panel of this figure by the dashed lines which are coincide and will decrease by increasing r. We see explicitly that they are not dependent on parameter B. The radial epicyclic frequency is shown by the solid and dotted curves (Schwarzschild black hole) with a maximum where increasing the parameter B shifts this maximum to the smaller radii. The radial oscillation frequency increases by increasing the values of the parameter B. Dependence on this parameter is significant close to the black hole, but far from the central mass this effect is weak. We see that \(\Omega _{r}<\Omega _{\theta }\). The ratio of \(\frac{\Omega _{\theta }}{\Omega _{r}}\) is plotted in the right hand side panel of Fig. 6 which is a decreasing function of r. It is clear that in the vicinity of the black hole, this ratio is very greater than unity but far from the black hole it turns to unity and decreases by increasing B. In the left panel of Fig. 7, the locations of three particular resonances such as the parametric resonance with condition \(\frac{\Omega _{\theta }}{\Omega _{r}}=\frac{3}{2}\) and the forced resonance with ratio 3:1 and 2:1 are shown. The dependence of these characteristic radii to the metric parameter B is shown in the right panel of Fig. 7 where such radii are monotonically decreasing functions of this parameter. On the other hand, resonance will be happened in smaller distance from the central mass for larger values of the metric parameter, B.

Fig. 8
figure 8

The radial velocity profile as a function of the dimensionless parameter r for the equation of state parameter \(k=\frac{1}{2}\) and constant of integration \(A_{4}=1.4\). The dotted, dashed and solid lines are corresponding to the cases with \(B=0\) (Schwarzschild geometry), \(B=-0.05\) and \(B=-0.1\) respectively. For each curve, the critical radii are marked by a solid circle which their coordinates are stated in the right panel

Full size image

5.3 Mass evolution and critical points

In this Horndeski/Galileon accretion disk, the energy density and radial velocity for an isothermal fluid are given by

$$\begin{aligned} \rho =\frac{A_{3}(k+1)}{r^{2}\sqrt{A_{4}^{2}-(k+1)^{2}\Big (\Delta +A r^{2}+C-\frac{\mu }{r}\Big )}}, \end{aligned}$$
(89)

and

$$\begin{aligned} u=\frac{1}{(k+1)}\sqrt{\left( 1+\frac{\eta }{\beta }r^{2}\right) \left( \frac{A_{4}^{2}-\left( \Delta +A r^{2}+C-\frac{\mu }{r}\right) \left( 1+k)^{2}\right) }{\left( 3 A r^{2}+C+\frac{B}{1+r^{2}\gamma ^{2}}\right) }\right) },\nonumber \\ \end{aligned}$$
(90)

respectively. For critical points we find

$$\begin{aligned} r_{c}= & {} -\frac{3}{4}\frac{\mu (k+1)^{2}}{A_{4}^{2}-(B+C)(k+1)^{2}},\end{aligned}$$
(91)
$$\begin{aligned} V_{c}^{2}= & {} \frac{\mu }{4r(B+C)-3\mu }, \end{aligned}$$
(92)

and

$$\begin{aligned} u_{c}=\frac{1}{4}\left( 1+\frac{\eta }{\beta }r^{2}\right) \frac{\left( \frac{\mu }{r}+2Ar^{2}-\Delta +\frac{B}{1+r^{2}\gamma ^{2}}\right) }{\left( 3Ar^{2}+C+\frac{B}{1+r^{2}\gamma ^{2}}\right) }. \end{aligned}$$
(93)

It is clear that \(r_{c}\) depends on the equation of state parameter k. This is means that the location of a critical point is not the same for all fluids. The profiles of radial velocity, density and accretion rate are presented in Figs. 8, 9 and 10 versus the dimensionless parameter r for equation of state parameter \(k=\frac{1}{2}\) and constants integration \(A_{4} = 1.4\) and \(A_{3} = 1\) respectively. The dotted, dashed and solid curves are corresponding to cases with \(B=0\), \(B=-0.05\) and \(B=-0.1\) respectively.

The left panel of Fig. 8 represents the radial velocity versus the radius. The locations of the critical points are marked by solid circles and their coordinates are stated in the right panel. The fluid has zero radial velocity far from the black hole and flows at the sub-sonic speed before the critical points. In a critical point, the speed of flow matches the speed of sound. After passing this point, in the vicinity of the black hole the speed of flow increases and turns to the super-sonic domain because of strong gravity. It can be observed that velocity decreases by increasing the Horndeski/Galileon correction factor B and the loci of the critical points get shifted to the black hole. Therefore, the speed of infalling particle reaches the speed of sound closer to the central mass.

The density profile of the fluid around the black hole for different values of B is shown in Fig. 9. Increasing the value of the parameter B increases the density. In addition, for such isothermal fluids, the mass of the black hole changes with time by the following relation

$$\begin{aligned} \dot{M}=4\pi A_{1}(p+\rho )\sqrt{B+C}M^{2}. \end{aligned}$$
(94)
Fig. 9
figure 9

Density profile as a function of the dimensionless parameter r for the equation of state parameter \(k=\frac{1}{2}\) and constants of integration as \(A_{4}=1.4\) and \(A_{3}=1\). The dotted, dashed and solid curves are corresponding to the cases with \(B=0\), \(B=-0.05\) and \(B=-0.1\) respectively

Full size image
Fig. 10
figure 10

Accretion rate of isothermal fluid with equation of state parameter \(k=\frac{1}{2}\) versus the dimensionless radial parameter r for different values of the parameter B. The constant parameters of integration are set \(A_{4}=1.4\) and \(A_{3}=1\). The dotted, dashed and solid curves are corresponding to the cases with \(B=0\), \(B=-0.05\) and \(B=-0.1\) respectively

Full size image

We see that accretion rate for a general spherically symmetric static black hole in Horndeski/Galileon gravity is different from the case of a Schwarzschild black hole. In Horndeski/Galileon case, the accretion rate completely depends on the nature of the accreting fluid and also the metric parameter (here, parameter B). So \(\dot{M}>0\) for a normal fluid which satisfies \((p+\rho )>0\). The change of accretion rate for different values of the parameter B with the same equation of state parameter are shown in Fig. 10. It is seen that accretion rate is higher in the vicinity of the black hole because of strong gravitational effect. Also, increment of the parameter B enhances the accretion rate. By using Eq. (57), the critical accretion time and the mass of the black hole are given by

$$\begin{aligned} t_{cr}=[4\pi A_{1}(p+\rho )\sqrt{B+C}M_{i}]^{-1} \end{aligned}$$
(95)

and

$$\begin{aligned} M_{t}=M_{i}\left[ 1-4\pi A_{1}(p+\rho )\sqrt{B+C}M_{i}t \right] ^{-1}, \end{aligned}$$
(96)

respectively. We see that for normal fluid, the black hole mass increases by accretion matter subject to Horndeski/Galileon gravity and increasing correction factor B will increase the black hole mass further. This behavior is studied by Rodrigues et al. [35] for a Schwarzschild black hole in the presence of a non-minimally coupled scalar filed. They found that for black hole with initial masses smaller than a certain critical value, the accretion of the scalar filed can led to mass decreasing even in the absence of Hawking radiation and phantom energy. Also the black holes with initial masses greater than critical value grow by accreting the scalar filed similar to the minimally coupled scalar case.

6 Summary and conclusion

In this paper, the geodesic motion and accretion process of a test particle in a subclass of the general Horndeski/Galileon gravity theories in the equatorial plane of a non-rotating black hole are investigated. In this framework, the circular geodesics, the stability of such orbits, oscillations under the action of small perturbations, unstable orbits and finally accretion process of the fluid flowing around the black hole have been investigated in a general form. Expressions for the effective potential, energy, momentum, characteristic radii, emission rate, epicyclic frequencies and dynamical parameters of the system and also the mass evolution of the black hole are derived in details. Then isothermal fluid with equation of state \(p=k \rho \) is considered and some discussions are done for this subclass of solutions of the Horndeski/Galileon black holes. In this manner, the metric parameters with some approximations are obtained as \(h(r)\approx C-\frac{\mu }{r}+B\) and \(f(r)\approx \frac{h(r)}{B+C}\), where by assumption we have set \(C=1\). The effect of the Horndeski/Galileon correction factor B is considered for each case and our solutions are compared with the Schwarzschild black hole solutions. Our analysis has revealed that these Horndeski/Galileon solutions have deviations from the Schwarzschild solutions (which is recovered where \(B=0\)) substantially. Our results show that Horndeski/Galileon correction factor affects the effective potential and as a result changes the loci of the stable and unstable circular orbits. For larger values of this parameter, \(V_{eff}\) achieves larger value and unstable circular orbits will be located at smaller radii, whereas stable orbits will be located at farther distances from the central mass. When the metric parameter B decreases, two points joint together at ISCO.

In this spacetime the location of the characteristic radii such as \(r_{isco}\), \(r_{ph}\), \(r_{sing}\) and \(r_{mb}\) have considerable deviation from the Schwarzschild solutions. These radii, except \(r_{mb}\), are decreasing functions with respect to the Horndeski/Galileon correction factor B, that is, they will be closer to the central mass for larger values of B. As \(r_{isco}\) represents the inner edge of the accretion disk, our results show that for larger deviations, the disk will be extended close to the central mass. The behavior of \(r_{mb}\) is different and has a minima at the Schwarzschild case. This radii is a decreasing function for \(B\in (-1, 0)\) and it is a growing function for \(B\in (0, 1.125)\), and finally it coincides with the innermost stable circular orbit.

As Horndeski/Galileon correction factor B grows, the energy raises whereas angular momentum decreases and one can see from the energy diagram that the range of bound orbit will be smaller for larger deviations. Increasing the parameter B enhances the \(E_{isco}\) and then the efficiency of accretion will be decreased accordingly. In the case of Schwarzschild black hole the efficiency equals to 0.057 at \(r = 6r_{g}\). For negative values of the correction factor B, efficiency grows up and becomes greater in the Schwarzschild black hole limit (\(B=0\)), where this behavior is reverse for positive values of the correction factor. The flux of the radiation energy has a maximum in the vicinity of the black hole and decreases at smaller radii. By increasing the parameter B, the flux raises and the maximum of the flux turns to the smaller radii but the reverse happens after this point. The dependence on this parameter is very considerable in the vicinity of the black hole, but it is weak far from the black hole. These behaviors are the same for temperature.

In this paper, in addition to investigation of the circular orbits and their properties, epicyclic frequencies are studied. Vertical epicyclic frequency is monotonically decreasing function of r and has no extrema. Deviation from the Schwarzschild case in this Horndeski/Galileon setup has no effect on the vertical epicyclic frequency, while the radial epicyclic frequency always has a maximum and the effect of Horndeski/Galileon correction factor on it is considerable. Dependence on this parameter is significant close to the black hole, but far from the central mass this effect is weak. Increasing the parameter B shifts the maximum to the smaller radii. We found that \(\Omega _{r}<\Omega _{\theta }\) and the ratio of \(\frac{\Omega _{\theta }}{\Omega _{r}}\) is decreasing function with respect to r. In the vicinity of the black hole, this ratio is very larger than unity but far from the black hole, it turns to the unity and it decreases by increasing B. The dependence of some important resonances such as parametric and forced resonances with respect to Horndeski/Galileon parameter B is obtained, which this dependence is a monotonically decreasing function, that is, larger values of the Horndeski/Galileon correction factor lead to happening the resonance at the smaller radii.

Finally, the accretion process of the isothermal fluid is discussed for equation of state parameter \(k=\frac{1}{2}\) and the behavior of the radial velocity and density are studied. Radial velocity is a decreasing function of r as fluids have zero radial velocity in far from the black hole. When accretion happens, fluid passes at a critical point where in this point, the speed of flow matches the speed of sound. The fluid flows at sub-sonic speed before the critical point. After passing this point and in the vicinity of the black hole, because of strong gravitational field, the speed of flow increases and will be super-sonic then after. Our results show that velocity decreases by increasing B and the loci of the critical point shifts towards the black hole. Therefore, the speed of infalling particles reaches the speed of sound closer to the central mass. Finally, the rate of accretion is discussed where we found that this rate depends on the nature of the fluid and also the metric parameter. For normal fluid, \(\dot{M}>0\) and its value is larger in the vicinity of the black hole because of strong gravitational effect and positive deviation from the Schwarzschild case increases the accretion rate.

We note that in this paper a non-spinning particle is considered. When a particle has spin, this spin has considerable influence on the particle’s orbit. Also, a perfect fluid is considered and viscosity as well as magnetic field of the accretion disk are ignored for simplicity. However, these effects can affect the motion of the test particle and therefore they can affect the structure and the emission rate of the accretion disk. So, we are going to study the behavior of spinning particles and accretion of viscose fluids subject to the Horndeski/Galileon gravity in presence of a magnetic field in our future work.