1 Introduction

General relativity is one of the cornerstones that provides basic understanding of astrophysical phenomena as well as the cosmos. The structure of self-gravitating systems is attained by solving the famous Einstein field equations. Schwarzschild was the first who determined vacuum solution of these equations describing the geometry of region exterior to a prefect fluid sphere in hydrostatic equilibrium. Tolman [1] found several solutions by solving the field equations for static sphere of perfect fluid with cosmological constant and discussed the matching of resulting interior solutions with exterior one. After that, many exact solutions for isotropic and anisotropic static as well as non-static configurations have been obtained [2].

The formulation of interior solutions for self-gravitating systems is a difficult task due to the existence of non-linearity in the field equations. In this regard, the minimal gravitational decoupling (MGD) approach has been very useful in finding exact and physically feasible solutions for spherically symmetric stellar distributions. This strategy was genuinely proposed by Ovalle [3] to find an exact solution for compact stars in the context of the braneworld. In this framework, Ovalle and Linares [4] developed an exact interior solution to the field equations for isotropic spherically symmetric compact distribution. They concluded that this solution represents braneworld version of the Tolman IV solution [1]. Casadio et al. [5] used MGD concept by modifying the temporal as well as radial metric function and found a new exterior solution for spherical self-gravitating system which presents a naked singularity at the Schwarzschild radius. Ovalle [6] decoupled gravitational sources to construct anisotropic solutions from perfect fluid solutions with spherical symmetry. Ovalle et al. [7] extended isotropic interior solution [1] by means of MGD for static stellar models to include the effects of anisotropy.

In astrophysical context, pressure anisotropy (generated by various physical phenomena) plays a key role in the evolution of stellar bodies. Mak and his collaborators [8, 9] obtained exact solutions by taking a particular form of anisotropy (difference of radial and tangential pressures) and found that spherical star supports positive and finite density as well as pressures. They also discussed that the obtained radius and mass can describe realistic astrophysical objects. Gleiser and Dev [10] explored the existence of anisotropic self-gravitating sphere and found that anisotropy can support stars with compactness \(2M/R=8/9\) (M and R represent mass and radius, respectively). They also concluded that stable configurations exist for smaller values of the adiabatic index as compared to isotropic fluid. Sharma and Maharaj [11] obtained some exact solutions for spherically symmetric anisotropic matter distribution satisfying linear equation of state (EoS) to describe compact stars. We investigated the equilibrium structure of static spherical as well as cylindrical polytropic configurations with anisotropic source [12]. Azam et al. [13] generalized these structures for generalized polytropic EoS.

The inclusion of electromagnetic field in stellar models is very fascinating in describing their evolution. Xingxiang [14] discussed the characteristics of an exact solution for static spherical symmetry with charged perfect fluid distribution. Di Prisco et al. [15] investigated the impact of electromagnetic field on the dynamics of imperfect collapsing sphere and discussed a relationship between the Weyl tensor and inhomogeneity of energy density. Sharif and Bhatti [16] analyzed the behavior of physical parameters and energy conditions for charged anisotropic spherically symmetric solutions. Takisa and Maharaj [17] formulated exact solutions of the Einstein-Maxwell field equations with polytropic EoS which can be used to model charged anisotropic compact objects. Singh and Pant [18] presented charged anisotropic spherical solution and found that the developed model is stable and well-behaved for a wide range of anisotropy as well as charge parameter. They also obtained that charged anisotropic neutron and quark stars with large masses can be modeled from the resulting solution. Khan et al. [19] studied the effects of charge on anisotropic spherical collapse with cosmological constant and concluded that electromagnetic field enhances the rate of destruction.

The significance of relativistic models is based on their stable structure. Herrera [20] proposed the notion of cracking as well as overturning (when the total radial forces in a system reverse their signs from positive to negative, cracking occurs while the opposite situation experiences overturning) to investigate the behavior of isotropic and anisotropic configurations just after the equilibrium state is perturbed. He concluded that perfect fluid distribution remains stable while cracking appears in anisotropic case. Abreu et al. [21] broadened the idea of cracking by means of sound speed for anisotropic spherical configuration and concluded that the system is unstable for \(v_{st}^2>v_{sr}^2\) (\(v_{sr}^2\) and \(v_{st}^2\) indicate radial and tangential sound speeds, respectively). We explored the stability of charged anisotropic polytropes and found that compact object remains stable for a reasonable choice of perturbed polytropic index [22]. Mardan and Azam [23] examined the stability of charge anisotropic cylindrical system admitting generalized polytropic EoS and concluded that the constructed model is unstable for several choices of polytropic parameters.

In this paper, we explore exact charged anisotropic spherical solutions using a known charged isotropic solution with MGD approach. The plan of the paper is as follows. In Sect. 2, we deal with the basic formalism of MGD and formulate the corresponding field equations. The matching of interior spacetime with the exterior one is also investigated. In Sect. 3, we obtain two types of exact solutions for anisotropic spherical source in the presence of electromagnetic field and investigate physical characteristics of all solutions. Finally, we conclude our results in the last section.

2 Fluid configuration and MGD approach

We consider static spherically symmetric spacetime describing the interior geometry as

$$\begin{aligned} ds^2_{-}=-e^{\eta _{-}(r)}dt^{2}+e^{\chi _{-}(r)} dr^{2}+r^{2}\left( d\theta ^{2}+\sin ^{2}\theta d\phi ^2\right) . \end{aligned}$$
(1)

The energy-momentum tensor for internal constitution is given as

$$\begin{aligned} T_{\alpha \beta }^{(tot)}=T_{\alpha \beta }^{(m)}+\alpha \Theta _{\alpha \beta }, \end{aligned}$$
(2)

where

$$\begin{aligned} T_{\alpha \beta }^{(m)}= & {} (\rho +P)V_\alpha V_\beta +Pg_{\alpha \beta }\nonumber \\&+\frac{1}{4\pi }\left( F_{\alpha }~^{\mu }F_{\beta \mu }- \frac{1}{4}F^{\mu \nu }F_{\mu \nu }g_{\alpha \beta }\right) , \end{aligned}$$
(3)

which represents charged perfect fluid distribution with \(\rho ,~P\) and \(V_{\alpha }\) indicating the density, pressure and four velocity, respectively. The term \(\Theta _{\alpha \beta }\) is an additional source coupled to gravity through constant \(\alpha \) which may contain some new fields (scalar, vector or tensor) and generate anisotropies in self-gravitating bodies. In Eq. (3), \(F_{\alpha \beta }=\phi _{\beta ,\alpha }-\phi _{\alpha ,\beta }\) is the Maxwell field tensor and \(\phi _\alpha \) is four potential. The Maxwell field tensor satisfies the following field equations

$$\begin{aligned} F^{\alpha \beta }_{~~;\beta }={\mu }_{0}J^{\alpha },\quad F_{[\alpha \beta ;\gamma ]}=0, \end{aligned}$$

here, \(\mu _0\) is the magnetic permeability and \(J^{\alpha }\) is the four current. In comoving coordinates, we have

$$\begin{aligned} \phi _{\alpha }={\phi } {\delta ^{0}_{\alpha }},\quad J_{\alpha }=\zeta V_{\alpha },\quad V^{\alpha }=e^{-\eta /2}\delta _{0}^{\alpha }, \end{aligned}$$

where \(\zeta =\zeta (r)\) and \(\phi =\phi (r)\) represent scalar potential and charge density, respectively. The Maxwell field equation for our spacetime yields

$$\begin{aligned} \phi ^{\prime \prime }+\left( \frac{2}{r}-\frac{\eta '}{2}-\frac{\chi '}{2}\right) \phi '= 4\pi \zeta e^{\frac{\eta }{2}+\chi }, \end{aligned}$$

where prime denotes differentiation with respect to r. Integration of the above equation yields

$$\begin{aligned} {\phi }'=\frac{e^{\frac{\eta +\chi }{2}}q(r)}{r^{2}}. \end{aligned}$$

Here \(q(r)=4\pi \int ^r_{0}{\zeta }e^{\frac{\chi }{2}}{r^2}dr\) indicates total charge inside the sphere.

The Einstein-Maxwell field equations corresponding to Eqs. (1) and (2) turn out to be

$$\begin{aligned}&8\pi \left( \rho +\frac{q^2}{8\pi r^4}-\alpha \Theta _{0}^{0}\right) \nonumber \\&\quad =\frac{1}{r^2}+e^{-\chi }\left( \frac{\chi '}{r}-\frac{1}{r^{2}}\right) ,\end{aligned}$$
(4)
$$\begin{aligned}&8\pi \left( P-\frac{q^2}{8\pi r^4}+\alpha \Theta _{1}^{1}\right) \nonumber \\&\quad =-\frac{1}{r^2}+e^{-\chi }\left( \frac{\eta '}{r}+\frac{1}{r^{2}}\right) ,\end{aligned}$$
(5)
$$\begin{aligned}&8\pi \left( P+\frac{q^2}{8\pi r^4}+\alpha \Theta _{2}^{2}\right) \nonumber \\&\quad =e^{-\chi }\left( \frac{\eta ''}{2}+\frac{\eta '^{2}}{4}-\frac{\eta '\chi '}{4} +\frac{\eta '}{2r}-\frac{\chi '}{2r}\right) . \end{aligned}$$
(6)

The equilibrium structure of stellar object is described by hydrostatic equilibrium equation obtained through the conservation of energy-momentum tensor (\(T^{(tot)\alpha }_{~~~~\beta ;\alpha }=0\)) as

$$\begin{aligned} \frac{dP}{dr}+ & {} \alpha \frac{d\Theta _{1}^{1}}{dr}+\frac{\eta '}{2}(\rho +P)+\frac{\alpha \eta '}{2} \left( \Theta _{1}^{1}-\Theta _{0}^{0}\right) \nonumber \\+ & {} \frac{2\alpha }{r}\left( \Theta _{1}^{1}-\Theta _{2}^{2}\right) -\frac{qq'}{4\pi r^4}=0. \end{aligned}$$
(7)

We see that Eqs. (4–7) form a system of four non-linear differential equations consisting of eight unknowns (\(\eta ,~\chi ,~\rho ,~P,q,~\Theta _{0}^{0},~\Theta _{1}^{1},~\Theta _{2}^{2}\)). In order to find these unknowns, we follow a systematic scheme developed by Ovalle [7]. From Eqs. (4–6), we identify the matter components as

$$\begin{aligned} \bar{\rho }=\rho -\alpha \Theta _{0}^{0},\quad \bar{P}_{r}=P+\alpha \Theta _{1}^{1},\nonumber \\ \quad \bar{P}_{t}=P+\alpha \Theta _{2}^{2}, \end{aligned}$$
(8)

where \(\bar{\rho },~\bar{P}_{r},~\bar{P}_{t}\) represent effective energy density, radial/tangential pressure, respectively. This shows that the source \(\Theta _{\alpha \beta }\) can produce anisotropy \(\bar{\Delta }=\bar{P}_{t}-\bar{P}_{r}=\alpha (\Theta _{2}^{2}-\Theta _{1}^{1})\) in the interior of stellar distribution.

Now, we consider the MGD approach to solve the system of Eqs. (4–6). The basic ingredient of MGD is to consider a perfect fluid solution (\(\xi ,~\lambda ,~\rho ,~P,~q\)) for the line-element given as

$$\begin{aligned} ds^2=-e^{\xi (r)}dt^{2}+\frac{dr^{2}}{\lambda (r)}+r^{2}\left( d\theta ^{2}+\sin ^{2}\theta d\phi ^2\right) , \end{aligned}$$

where \(\lambda =1-\frac{2m}{r}+\frac{q^2}{r^2}\) with m representing the Misner-Sharp mass of fluid configuration. In order to incorporate the effects of source \(\Theta _{\alpha \beta }\) in charged isotropic model, we consider the geometric deformation as [7]

$$\begin{aligned} \xi \rightarrow \eta = \xi ,\quad \lambda \rightarrow e^{-\chi }=\lambda +\alpha g^{*}, \end{aligned}$$
(9)

where \(g^{*}\) is the deformation endured by radial metric function. Making use of the above radial coefficient, the field equations can be divided into two sets. The first set is given as

$$\begin{aligned}&8\pi \rho +\frac{q^2}{r^4} =\frac{1}{r^2}+e^{-\chi }\left( \frac{\chi '}{r}-\frac{1}{r^{2}}\right) ,\end{aligned}$$
(10)
$$\begin{aligned}&8\pi P-\frac{q^2}{r^4} =-\frac{1}{r^2}+e^{-\chi }\left( \frac{\eta '}{r}+\frac{1}{r^{2}}\right) ,\end{aligned}$$
(11)
$$\begin{aligned}&8\pi P+\frac{q^2}{r^4}=e^{-\chi }\left( \frac{\eta ''}{2}+\frac{\eta '^{2}}{4}-\frac{\eta '\chi '}{4} +\frac{\eta '}{2r}-\frac{\chi '}{2r}\right) , \end{aligned}$$
(12)

while the second one is

$$\begin{aligned}&\alpha \Theta _{0}^{0}=\frac{g^{*'}}{r}+\frac{g^{*}}{r^{2}},\end{aligned}$$
(13)
$$\begin{aligned}&\alpha \Theta _{1}^{1}=g^{*}\left( \frac{\eta '}{r}+\frac{1}{r^{2}}\right) ,\end{aligned}$$
(14)
$$\begin{aligned}&\alpha \Theta _{2}^{2}=g^{*}\left( \frac{\eta ''}{2}+\frac{\eta '^{2}}{4}-\frac{\eta '\chi '}{4} +\frac{\eta '}{2r}-\frac{\chi '}{2r}\right) . \end{aligned}$$
(15)

The above set of equations looks like the field equations for anisotropic spherical source (\(\bar{\rho }=\Theta _{0}^{*0}=\Theta _{0}^{0}-\frac{1}{8\pi r^2},~\bar{P}_{r}=\Theta _{1}^{*1}=\Theta _{1}^{1}-\frac{1}{8\pi r^2},~\bar{P}_{t}=\Theta _{2}^{*2}=\Theta _{2}^{2}\)) with the metric

$$\begin{aligned} ds^2=-e^{\eta }dt^{2}+\frac{dr^{2}}{g^{*}}+r^{2}\left( d\theta ^{2}+\sin ^{2}\theta d\phi ^2\right) . \end{aligned}$$

The matching of interior and exterior regions is obtained by junction conditions which yield a smooth matching of two regions and play a vital role in the study of evolution of relativistic objects. If we consider the general outer metric as

$$\begin{aligned} ds^2_{+}=-e^{\eta _{+}}dt^{2}+e^{-\chi _{+}}dr^{2}+r^{2}\left( d\theta ^{2}+\sin ^{2}\theta d\phi ^2\right) , \end{aligned}$$

then the first fundamental form (\([ds^{2}]_{\Sigma }=0,~\Sigma \) represents the hypersurface) of junction conditions yield

$$\begin{aligned} \eta _{-}(R)= & {} \eta _{+}(R),\quad 1-\frac{2M_{0}}{R}+\frac{Q_{0}^{2}}{R^2}\nonumber \\&+\,\,\alpha g^{*}(R)=e^{-\chi _{+}(R)}, \end{aligned}$$
(16)

where \(\lambda =e^{-\chi }-\alpha g^{*}\) has been used. Here, \(M_{0}\) and \(Q_{0}\) indicate total mass and charge within the sphere, respectively. The second fundamental form (\([T_{\alpha \beta }S^{\beta }]_{\Sigma }=0\), \(S^{\beta }\) is the unit four-vector in radial direction) [7] gives

$$\begin{aligned} P(R)-\frac{Q_{0}^{2}}{8\pi R^4}+\alpha (\Theta _{1}^{1}(R))_{-}=\alpha (\Theta _{1}^{1}(R))_{+}, \end{aligned}$$

which leads to

$$\begin{aligned}&P(R)-\frac{Q_{0}^{2}}{8\pi R^4}+\frac{\alpha g^{*}(R)}{8\pi }\left( \frac{1}{R^2}+\frac{\eta '(R)}{R}\right) \nonumber \\&\quad =\frac{\alpha h^{*}(R)}{8\pi R^2} \left( 1+\frac{2\mathcal {M}R-2\mathcal {Q}^2}{\left( R^2 -2\mathcal {M}R+\mathcal {Q}^2\right) }\right) , \end{aligned}$$
(17)

where \(h^{*}\) describes deformation in the radial metric function of Riessner-Nordström (RN) spacetime while \(\mathcal {M}\) and \(\mathcal {Q}\) indicate mass and charge in the exterior region. The necessary and sufficient conditions for the smooth matching of interior MGD metric with spherically symmetric exterior described by deformed RN line-element (which can be filled with fields contained in source \(\Theta _{\alpha \beta }\)) are given by Eqs. (16) and (17). If the exterior geometry is considered as the standard RN metric, Eq. (17) yields

$$\begin{aligned}&\bar{P}(R)-\frac{Q_{0}^{2}}{8\pi R^4}\equiv P(R)-\frac{Q_{0}^{2}}{8\pi R^4}\nonumber \\&\quad +\frac{\alpha g^{*}(R)}{8\pi }\left( \frac{1}{R^2}+\frac{\eta '(R)}{R}\right) =0. \end{aligned}$$
(18)

In the following, we consider a known solution of isotropic spherical system in the presence of charge to continue our systematic analysis.

3 Anisotropic solutions

A crucial ingredient in obtaining the anisotropic solutions using MGD approach is to consider solution of the field equations for spherically symmetric charged perfect fluid configuration. For this purpose, we consider Krori and Barua’s solution [24] given as

$$\begin{aligned}&e^{\eta }=e^{Br^2+C},\end{aligned}$$
(19)
$$\begin{aligned}&e^{\chi }=\lambda ^{-1}=e^{Ar^2},\end{aligned}$$
(20)
$$\begin{aligned}&\rho =\frac{e^{-Ar^2}}{16\pi }\left( 5A-B(B-A)r^2-\frac{1}{r^2}\right) +\frac{1}{16\pi r^2},\end{aligned}$$
(21)
$$\begin{aligned}&P=\frac{e^{-Ar^2}}{16\pi }\left( 4B-A+B(B-A)r^2+\frac{1}{r^2}\right) -\frac{1}{16\pi r^2},\end{aligned}$$
(22)
$$\begin{aligned}&q^{2}=\frac{e^{-Ar^2}}{2r^4}\left( B(B-A)r^2-A-\frac{1}{r^2}\right) +\frac{1}{2r^6}, \end{aligned}$$
(23)

where A,  B and C are constants that can be determined from matching conditions. The rationale behind the choice of the above solution lies in a fact that it is singularity-free and satisfies physical conditions inside the sphere. For RN spacetime as an exterior geometry, the matching conditions yield

$$\begin{aligned}&A=\frac{-\ln (1-\frac{2M_{0}}{R}+\frac{Q_{0}^{2}}{R^2})}{R^2},\end{aligned}$$
(24a)
$$\begin{aligned}&B=\frac{2M_{0}R-Q_{0}^{2}}{2R^2(R^2+Q_{0}^{2}-2M_{0}R)}, \end{aligned}$$
(24b)
$$\begin{aligned}&C=\frac{1}{2}\left\{ 1+2\ln \left( 1-\frac{2M_{0}}{R}+\frac{Q_{0}^{2}}{R^2}\right) \right. \nonumber \\&\qquad \left. -\frac{R^2}{R^2-2M_{0}R+Q_{0}^2}\right\} , \end{aligned}$$
(25)

with the compactness parameter \(\frac{M_{0}}{R}<\frac{4}{9}\). The above equations ensure continuity of the interior solution (19–23) with the exterior region at the boundary and will definitely be changed after adding the source \(\Theta _{\alpha \beta }\) in the interior of sphere.

Now we move towards anisotropic solutions and turn \(\alpha \) on in the interior. The temporal and radial metric coefficients are given by Eqs. (19) and (9), respectively, while the deformation \(g^{*}\) is related to \(\Theta _{\alpha \beta }\) through Eqs. (13–15) whose solution will be determined by specifying an additional constraint. In order to achieve this goal, we impose some conditions and find two exact solutions.

3.1 Solution I

Here, we apply a constraint on \(\Theta _{1}^{1}\) and find solution of the field equations for \(g^{*}\) and \(\Theta _{\alpha \beta }\). From Eq. (18), we see that RN exterior solution is compatible with isotropic interior matter as long as \(P(R)-\frac{Q_{0}^2}{8\pi R^4}\sim \alpha (\Theta _{1}^{1}(R))_{-}\). Thus the simplest choice is to take

$$\begin{aligned} \Theta _{1}^{1}=P-\frac{q^2}{8\pi r^4}~\Rightarrow ~g^{*}=\lambda -\frac{1}{1+r\eta '}, \end{aligned}$$
(26)

where Eqs. (11) and (14) have been used. The above equation leads to the radial metric function as

$$\begin{aligned} e^{-\chi }=(1+\alpha )\lambda -\frac{\alpha }{1+2r^2B}. \end{aligned}$$
(27)

The metric functions of interior spacetime in Eqs. (19) and (27) represent the Krori and Barua solution minimally deformed by the generic anisotropic source \(\Theta _{\alpha \beta }\). It is worthwhile to mention here that \(\alpha \rightarrow 0\) leads to the standard isotropic charged spherical solution (19–23).

The continuity of first fundamental form of matching conditions yields

$$\begin{aligned} \ln \left( 1-\frac{2\mathcal {M}}{R}+\frac{\mathcal {Q}^2}{R^2}\right)= & {} Br^2+C,\end{aligned}$$
(28)
$$\begin{aligned} 1-\frac{2\mathcal {M}}{R}+\frac{\mathcal {Q}^2}{R^2}= & {} (1+\alpha )\lambda -\frac{\alpha }{1+2R^2B}, \end{aligned}$$
(29)

while the continuity of second fundamental form (\(P(R)-\frac{Q_{0}^2}{8\pi R^4}+\alpha (\Theta _{1}^{1}(R))_{-}=0\)) leads to

$$\begin{aligned} P(R)-\frac{Q_{0}^{2}}{8\pi R^4}=0\quad \Rightarrow \quad A= \frac{\ln (2BR^2+1)}{R^2}, \end{aligned}$$
(30)

where the constraint in Eq. (25) has been used. Eliminating \(\frac{2\mathcal {M}}{R}\) from Eq. (29), we find

$$\begin{aligned}&\frac{2\mathcal {M}}{R}=\frac{2M_{0}}{R}+\frac{\mathcal {Q}^{2} -Q_{0}^{2}}{R^2}\nonumber \\&\quad -\alpha \left( 1-\frac{2M_{0}}{R}+\frac{Q_{0}^2}{R^2}\right) +\frac{\alpha }{1+2R^2B}. \end{aligned}$$
(31)

Inserting the above equation in (28), we obtain

$$\begin{aligned}&BR^2+C=\ln \left( 1-\frac{2M_{0}}{R}+\frac{Q_{0}^{2}}{R^2}\right. \nonumber \\&\quad \left. +\,\,\alpha \left( 1-\frac{2M_{0}}{R}+\frac{Q_{0}^2}{R^2}\right) -\frac{\alpha }{1+2R^2B}\right) , \end{aligned}$$
(32)

which yields the constant C in terms of B. Here, the necessary and sufficient conditions for the smooth matching of interior and exterior metrics are given by Eqs. (30–32). In this case, the anisotropic solution, i.e., the expressions of \(\bar{\rho },~\bar{P}_{r},~\bar{P}_{t},~\bar{\Delta }\) and q are obtained as

$$\begin{aligned}&\bar{\rho }=\frac{1+4B^2r^4+4Br^2(1-\alpha )+2\alpha }{16\pi \left( r+2Br^3\right) ^2}\\&\qquad + \frac{e^{-Ar^2}}{16\pi r^2}\left( Ar^2\left( 5+Br^2+4\alpha \right) \right. \\&\qquad -\left. 1-B^2r^4-2\alpha \right) ,\\&\bar{P}_{r}=\frac{e^{-Ar^2}\left\{ 1+4Br^2(1+\alpha )+B^2r^4-A\left( r^2+B r^4\right) +2\alpha \right\} -1-2\alpha }{16\pi r^2},\\&\bar{P}_{t}=\frac{e^{-Ar^2}\left\{ \left( 1+Ar^2-Br^2\right) \left( 1+2Br^2\right) ^2\right\} -1-3Br^2+2B^2r^4}{8\pi r^2\left( 1+2Br^2\right) }\\&\qquad +\frac{e^{-Ar^2}\left\{ 1+4Br^2(1+\alpha )+B^2r^4-A\left( r^2+B r^4\right) +2\alpha \right\} -1-2\alpha }{16\pi r^2},\\&\bar{\Delta }=\frac{e^{-Ar^2}\left( \left( 1+Ar^2-Br^2\right) \left( 1+2Br^2\right) ^2\right) +\left( -1-3Br^2+2B^2r^4\right) }{8\pi r^2\left( 1+2Br^2\right) },\\&q=\frac{1}{\sqrt{2}}\left[ e^{-A r^2}r^2\left\{ \left( 1+B r^2\right) \left( 1+Br^2+2\alpha \right) \right. \right. \\&\qquad -Ar^2 \left( 3+Br^2+2\alpha \right) \\&\qquad +\left. \left. e^{Ar^2}\left( 1-2Ar^2\left( 2+B r^2\right) (1+\alpha )\right) \right\} \right] ^{1/2}. \end{aligned}$$
Fig. 1
figure 1

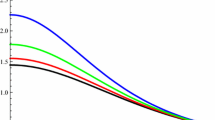
Plots of \(\bar{\rho }\) (left plot, first row), \(\bar{P}_{r}\) (right plot, first row), \(\bar{P}_{t}\) (left plot, second row) and \(\bar{\Delta }\) (right plot, second row) versus r and \(\alpha \) with \(Q_{0}=1\) (rust), \(Q_{0}=3\) (multicolors), \(M_{0}=1M_{\odot }\) and \(R=0.3M_{\odot }\) for solution I

Full size image

In order to examine physical characteristics of the above solution, we plot this model. For graphical analysis, we fix the constant A as given in Eq. (30) while B is a free parameter and will be taken as mentioned in the isotropic case (Eq. 24b). The compact stars demand that the behavior of energy density and radial pressure should be positive, finite and maximum in the interior of compact stars. The plot of \(\bar{\rho }\) for two values of \(Q_{0}\) is shown in the left plot (first row of Fig. 1). We observe that density is maximum in the interior and monotonically decreases with increasing r. It is found that density attains larger values for \(Q_{0}=1\) while \(Q_{0}=3\) yields smaller \(\bar{\rho }\) leading to the fact that increase in charge makes the sphere less dense. Moreover, we find that \(\bar{\rho }\) remains constant with increasing \(\alpha \).

The behavior of \(\bar{P}_{r}\) is similar to that of density for increasing \(Q_{0}\), r and \(\alpha \) (right plot, first row of Fig. 1). The plot of \(\bar{P}_{t}\) (left plot, second row of Fig. 1) shows that tangential pressure decreases with increasing r while corresponding to \(\alpha \), it increases. It is also found that the generic anisotropy remains same with increasing coupling constant \(\alpha \) while it acquires smaller values for larger \(Q_{0}\) (right plot, second row of Fig. 1).

Fig. 2
figure 2

Plots of energy conditions versus r and \(\alpha \) with \(Q_{0}=1\) (rust), \(Q_{0}=3\) (multicolors), \(M_{0}=1M_{\odot }\) and \(R=0.3M_{\odot }\) for solution I

Full size image

In order to check physical viability of the resulting solutions, we investigate the behavior of energy conditions which are the constraints imposed on the energy-momentum tensor and describe physically realistic matter distribution. For charged anisotropic fluid configuration, these conditions turn out to be

$$\begin{aligned}&\bar{\rho }+\frac{q^2}{8\pi r^4}\ge 0,\quad \bar{\rho }+\bar{P}_{r}\ge 0,\quad \\&\quad \bar{\rho }+\bar{P}_{t}\ge 0,\quad \bar{\rho }-\bar{P}_{r}+\frac{q^2}{4\pi r^4}\ge 0,\\&\bar{\rho }-\bar{P}_{t}\ge 0,\quad \bar{\rho }+\bar{P}_{r}+2\bar{P}_{t}+\frac{q^2}{4\pi r^4}\ge 0. \end{aligned}$$

These are shown in Fig. 2 which indicate that all the conditions are satisfied confirming the physically viability of the developed anisotropic solution. The stability is analyzed through sound speed condition, i.e., \(0<|v_{st}^2-v_{sr}^2|\le 1\). The plots of stability condition for \(Q_{0}=1,3\) are shown in Fig. 3. It is found that \(|v_{st}^2-v_{sr}^2|\le 1\) when \(Q_{0}=1\) for very small values of \(\alpha \) while it is violated with increasing \(\alpha \). As the value of charge parameter is increased, i.e., \(Q_{0}=3\), stability criterion is fulfilled for all values of \(\alpha \) leading to the result that stability of charged anisotropic sphere is enhanced with increasing charge parameter.

3.2 Solution II

In this case, we consider specific form of \(\Theta _{0}^{0}\) to obtain second type of anisotropic solution. The constraint is taken as

$$\begin{aligned} \Theta _{0}^{0}=\rho . \end{aligned}$$

Making use of Eqs. (13) and (21) in the above equation, it follows that

$$\begin{aligned} g^{*'}-\frac{g^{*}}{r}-8\pi r\left\{ \frac{e^{-Ar^2}}{16\pi }\left( 5A-B(B-A)r^2-\frac{1}{r^2}\right) +\frac{1}{16\pi r^2}\right\} =0, \end{aligned}$$

whose solution is

$$\begin{aligned} g^{*}= & {} rD+\frac{1}{8A^{3/2}}\left\{ 2e^{-Ar^2}\sqrt{A}\left( B^2r^2 +A(2-2e^{Ar^2}+Br^2)\right) \right. \nonumber \\&+\left. \left( 14A^2+AB-B^2\right) \sqrt{\pi }r\text {Erf}(\sqrt{A}r)\right\} , \end{aligned}$$
(33)

where \(``\text {Erf}\)” indicates the error function and D is an integration constant. By following the same procedure as for solution I, we find the matching conditions as

$$\begin{aligned}&1-e^{-Ar^2}(1+2BR^2)-\alpha (1+2BR^2)\left( RD+\frac{G}{8A^{3/2}}\right) =0,\end{aligned}$$
(34)
$$\begin{aligned}&\frac{2M_{0}}{R}+\frac{\mathcal {Q}^{2}-Q_{0}^{2}}{R^2}-\alpha RD-\frac{\alpha e^{-AR^2}G}{8A^{3/2}}=\frac{2\mathcal {M}}{R},\end{aligned}$$
(35)
$$\begin{aligned}&1-\frac{2M_{0}}{R}+\frac{Q_{0}^{2}}{R^2}-e^{BR^2+C}+\alpha RD+\frac{\alpha e^{-AR^2}G}{8A^{3/2}}=0,\nonumber \\ \end{aligned}$$
(36)

where

$$\begin{aligned} G= & {} 2e^{-AR^2}\sqrt{A}\left( B^2R^2+A(2-2e^{AR^2}+BR^2)\right) \\&+\left( 14A^2+AB-B^2\right) \times \sqrt{\pi }R\text {Erf}(\sqrt{A}R). \end{aligned}$$

In this case, the anisotropic solution is obtained as

$$\begin{aligned} \bar{\rho }= & {} \frac{e^{-Ar^2}\left( e^{Ar^2}-1-B^2r^4+Ar^2\left( 5+B r^2\right) \right) (1-\alpha )}{16\pi r^2},\\ \bar{P}_{r}= & {} \frac{1}{16\pi }\left\{ \frac{1}{r^2}+\frac{e^{-Ar^2}}{r^2} \left( A-4B-1+B(A-B)r^2\right) \right. \\&-\frac{2\alpha \left( 2 Br^2+1\right) }{r^2}\\&\times \left. \left( \frac{e^{-Ar^2}}{4A}\left( B^2r^2+A \left( 2-Br^2-e^{Ar^2}(2-4rD)\right) \right) \right. \right. \\&+\frac{\left( 14 A^2+AB-B^2\right) }{8 A^{3/2}} \left. \sqrt{\pi }r\text {Erf}\left( \sqrt{A}r\right) \!\right) \!\Bigg \},\\ \bar{P}_{t}= & {} \frac{e^{-A r^2}}{128A^{3/2}\pi r^2}\left[ 2\sqrt{A} \left\{ B^2r^2\left( 3+3Br^2-2B^2r^4\right) \alpha \right. \right. \\&-2A^2r^2\left( 1+Br^2\right) \\&\times \left. \left. \left( 2+\left( 5+Br^2\right) \alpha \right) -A\left( B^2r^4(5\alpha -4)\right. \right. \right. \\&-(8+4B^3r^6) \alpha -Br^2(16+5\alpha )\\&-4+4e^{Ar^2}\left( 1+\alpha \left( 2-3rD+Br^2(2-3rD)\right. \right. \\&\left. \left. \left. \left. -B^2r^4(1-2rD)\right) \right) \right) \right\} \\&+\left. \left( 14A^2+AB-B^2\right) e^{Ar^2}\sqrt{\pi }r\left( 3+3Br^2-2 B^2r^4\right) \right. \\&\left. \alpha \text {Erf}\left( \sqrt{A}r\right) \right] , \end{aligned}$$
Fig. 3
figure 3

Plot of \(|v_{st}^2-v_{sr}^2|\) versus r and \(\alpha \) with \(Q_{0}=1\) (rust), \(Q_{0}=3\) (multicolors), \(M_{0}=1M_{\odot }\) and \(R=0.3M_{\odot }\) for solution I

Full size image
$$\begin{aligned} \bar{\Delta }= & {} \frac{-e^{-Ar^2}\left( 1+Br^2\right) \alpha }{128A^{3/2}\pi r^2}\left[ 2\sqrt{A}\Big \{2A^2r^2\left( 5+B r^2\right) \right. \\&-B^2r^2\left( 1-2Br^2\right) \\&-A\left( 4-5Br^2+4B^2r^4\right. \\&\left. \left. -e^{Ar^2}\left( 4-4rD-4Br^2 (1-2rD)\right) \right) \right\} \\&+\left. \left( 14A^2+AB-B^2\right) e^{Ar^2} \sqrt{\pi }r\left( -1+2Br^2\right) \right. \\&\left. \text {Erf}\left( \sqrt{A}r\right) \right] ,\\ q= & {} \frac{1}{2\sqrt{2}}\left[ \frac{-e^{-Ar^2} r^2}{A^{3/2}}\left( 2\sqrt{A}\left( 2A^2r^2\left( 3+Br^2\right. \right. \right. \right. \\&\left. +\,\,2e^{Ar^2}\left( 2+B r^2\right) \right) +B^2r^2\alpha \\&+\left. \left. \left. A\left( e^{Ar^2}(-2+\alpha (4rD-2))-2B^2r^4-2(1-\alpha )\right) \right) \right. \right. \\&-Br^2 (4+\alpha )\\&+\left. \left. \left( 14A^2+A B-B^2\right) e^{Ar^2}\sqrt{\pi }r\alpha \text {Erf}\left( \sqrt{A} r\right) \right) \right] ^{1/2}. \end{aligned}$$
Fig. 4
figure 4

Plots of \(\bar{\rho }\) (left plot, first row), \(\bar{P}_{r}\) (right plot, first row), \(\bar{P}_{t}\) (left plot, second row) and \(\bar{\Delta }\) (right plot, second row) versus r and \(\alpha \) with \(Q_{0}=1\) (rust), \(Q_{0}=6\) (multicolors), \(M_{0}=1M_{\odot }\) and \(R=0.01M_{\odot }\) for solution II

Full size image

In order to plot the developed solution, we fix the constant B by solving Eqs. (34 and 36) (which is not mentioned here due to lengthy expression) while A is a free parameter which will be taken as given in Eq. (24a) and \(D=1\). The behavior of density and radial/tangential pressure (Fig. 4) corresponding to the variation in r is similar to that obtained in solution I. However, the behavior of \(\bar{\rho }\) and \(\bar{P}_{r}\) is different with respect to \(\alpha \), i.e., it is an increasing function as the parameter \(\alpha \) is increased while the behavior of \(\bar{P}_{t}\) is consistent with solution I. This shows that \(\Theta _{\alpha \beta }\) increases the compactness of spherical matter configuration. Moreover, we find that the change in charge parameter does not yield much difference between the values of all physical parameters. We find that the generated anisotropy is greater for the larger values of \(\alpha \) (last plot, Fig. 4) and decreases towards surface which is opposite to the anisotropic behavior in the absence of electromagnetic field.

Fig. 5
figure 5

Plots of energy conditions versus r and \(\alpha \) with \(Q_{0}=1\) (rust), \(Q_{0}=6\) (multicolors), \(M_{0}=1M_{\odot }\) and \(R=0.01M_{\odot }\) for solution II

Full size image

The plots of all energy conditions are shown in Fig. 5. It is found that the resulting solution meets all the energy bounds except \(\bar{\rho }-\bar{P}_{t}\). This shows that the solution II is not physically viable for both values of \(Q_{0}\). Furthermore, we plot the stability condition \(0<|v_{st}^2-v_{sr}^2|\le 1\) (Fig. 6) and obtain that it is violated throughout the system.

4 Final remarks

The search for interior solutions describing self-gravitating systems has captivated the attention of many researchers. Recently, the minimal gravitational decoupling technique has widely been used to find exact solutions for interior constitution of stellar objects. In this paper, we have explored exact solutions of the charged anisotropic field equations from known isotropic model using MGD approach. For this purpose, a new source is added to the charged isotropic energy-momentum tensor which leads to the effective field equations with anisotropic matter distribution. Then, we have introduced a geometric deformation for the radial metric function of the line-element (used in the known solution). This deformation leads to two sets of the field equations: the first set is similar to the standard Einstein equations for charged isotropic source while the second one corresponds to the additional source and the deformed metric coefficient. We have also formulated junction conditions for the smooth matching of the interior region with the exterior one described by the deformed Riessner-Nordström spacetime.

Fig. 6
figure 6

Plot of \(|v_{st}^2-v_{sr}^2|\) versus r and \(\alpha \) with \(Q_{0}=1\) (rust), \(Q_{0}=6\) (multicolors), \(M_{0}=1M_{\odot }\) and \(R=0.01M_{\odot }\) for solution II

Full size image

In order to seek anisotropic solutions, we have firstly considered the known isotropic solution with electromagnetic field and then incorporated the effects of source added to charged perfect fluid. For this purpose, we have imposed two constraints depending upon pressure and density leading to solutions I and II, respectively. We have analyzed physical characteristics of constructed models and found that density and radial/tangential pressure exhibit viable behavior. The physical acceptability has also been investigated through energy conditions. It is found that the first solution fulfils these conditions while one of them is violated for the solution II. We have examined the stability through sound speed criterion and concluded that the first model is stable whereas the second does not meet the stability condition. Moreover, we have found that the increase in charge parameter increases the stability of the first model. It is interesting to mention here that the solution I is physically acceptable as it satisfies all the conditions required for stellar objects. We would like to point out here that such conditions are not checked for the uncharged solutions [7].