Abstract
We study the propagation of a neutrino in a medium that consists of two or more thermal backgrounds of electrons and nucleons moving with some relative velocity, in the presence of a static and homogeneous electromagnetic field. We calculate the neutrino self-energy and dispersion relation using the linear thermal Schwinger propagator, we give the formulas for the dispersion relation and discuss general features of the results obtained, in particular the effects of the stream contributions. As a specific example we discuss in some detail the case of a magnetized two-stream electron, i.e., two electron backgrounds with a relative velocity \({\mathbf {v}}\) in the presence of a magnetic field. For a neutrino propagating with momentum \({\mathbf {k}}\), in the presence of the stream the neutrino dispersion relation acquires an anisotropic contribution of the form \({\hat{k}}\cdot {\mathbf {v}}\) in addition to the well known term \({\hat{k}}\cdot {\mathbf {B}}\), as well as an additional contribution proportional to \({\mathbf {B}}\cdot {\mathbf {v}}\). We consider the contribution from a nucleon stream background as an example of other possible stream backgrounds, and comment on possible generalizations to take into account the effects of inhomogeneous fields. We explain why a term of the form \({\hat{k}}\cdot ({\mathbf {v}}\times {\mathbf {B}})\) does not appear in the dispersion relation in the constant field case, while a term of similar form can appear in the presence of an inhomogeneous field involving its gradient.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction and Summary
Since the discovery of the MSW effect [1,2,3,4], for many years a lot of attention has been given to the calculation of the properties of neutrinos in a matter background under various conditions. The matter background modifies the neutrino dispersion relations [5,6,7,8], and also induces electromagnetic couplings that can lead to effects in several astrophysical and/or cosmological settings [9]. In supernova environments the presence of the neutrino background leads to neutrino collective oscillations [10,11,12,13,14,15] that have been the subject of significant work in the context of instabilities in supernovas [14,15,16].
It is now well known that the presence of a magnetic field produces an angular asymmetry in the neutrino dispersion relation when it propagates in an otherwise isotropic background medium [17]. Since many of the physical environments of interest in the contexts mentioned include the presence of a magnetic field, a significant amount of work has been dedicated to study the calculation of the neutrino self-energy in the presence of a magnetic field, or a magnetized background medium [18], and the study of the properties and propagation of neutrinos in such media [19].
In the previous calculations of the neutrino dispersion relation or index of refraction in matter in the presence of a magnetic field [20,21,22,23,24], the electron and nucleon backgrounds are taken to be at rest since there is no other reference frame defined in the problem at hand. In the present work we extend those calculations by considering a medium that contains various stream matter backgrounds, which have a non-zero velocity relative to each other, and including the presence of a magnetic field. The effects of moving and polarized matter on neutrino spin/magnetic moment oscillations and \(\nu _L \rightarrow \nu _R\) conversions have been studied by several authors [20,21,22,23,24]. We emphasize that our focus is different. We are concerned with the calculation of the index of refraction or dispersion relation in the magnetized stream media for a chiral Standard Model neutrino state.
In the context of plasma physics the propagation of photons in magnetized or unmagnetized two stream plasma systems is a well studied subject [25,26,27,28,29,30]. Here we consider the analogous problem for neutrinos. It is expected on general grounds that the presence of the streams will produce corrections to both the the anisotropic and isotropic terms in the neutrino dispersion relations, which depend on the stream relative velocities and the magnetic field. Our goal is to determine the corrections to the neutrino dispersion relation for a neutrino that propagates in such magnetized stream systems. Beyond the intrinsic interest, the results are of practical application in astrophysical contexts in which the asymmetric neutrino propagation is believed to produce important effects such as the dynamics of pulsars [31, 32] and supernovas [33,34,35].
In the previous calculations related to the propagation of neutrinos in a matter, including the presence of a magnetic field, the electron and nucleon backgrounds are taken to be at rest since there is no other reference frame defined in the problem at hand. In the present work, we consider the case in which the medium contains various stream matter backgrounds, which have a non-zero velocity relative to each other, and including the presence of a magnetic field.
Before embarking on the details, we state our assumptions more precisely. We assume that the medium contains a matter background and a magnetic field. In the common notation, the velocity four-vector of this background is denoted by \(u^\mu \), and its reference frame is defined by setting
We will refer to it as the normal background. We assume that in that frame there is a constant magnetic field \({\mathbf {B}} = B{\hat{b}}\), and in that frame we define
We can then write the corresponding EM tensor in the form
and its dual, defined as usual by \({\tilde{F}}_{\mu \nu } = \frac{1}{2}\epsilon _{\mu \nu \alpha \beta }F^{\alpha \beta }\), is given by
\(F_{\mu \nu }\) and \({\tilde{F}}_{\mu \nu }\) are such that
In the present work we assume that there are additional backgrounds, to which we refer to as the stream backgrounds, which are superimposed on the normal matter background having non-zero velocity relative to the normal matter background. For definiteness, we consider only the contributions from the electrons and nucleons (\(N = n,p\)) in both the backgrounds, and to refere them we use the symbols \(s = e,N\) and \(s^\prime = e^\prime ,N^\prime \) respectively. We also use \(f_e = e,e^\prime \) to refer the electrons in either background, and similarly for the nucleons \(f_N = N,N^\prime \). The symbol f stands for any fermion in either background. In particular, \(u^{\mu }_f\) denotes the velocity four-vector of any of the backgrounds.
As already stated the normal background can be taken to be at rest, so that for all the species in the normal background we set
But for the stream backgrounds
in that same frame.
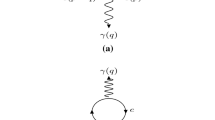
The main objective of the present work is the calculation of the neutrino dispersion relations with the simultaneous presence of the stream background and the magnetic field. Our work is based on the calculation of the thermal self-energy diagrams shown in Fig. 1, using the thermal Schwinger propagator, linearized in B, including only the electrons in both backgrounds, and to the leading order \(O(1/m^2_W)\) terms. The results of the calculation are summarized in Eqs. (60)–(63) for the self-energy, and in Eqs. (68)–(72) for the corresponding dispersion relations. The main result is that for a neutrino propagating with momentum \({\mathbf {k}}\) in the presence of a stream, the neutrino dispersion relation acquires an anisotropic contribution of the form \({\hat{k}}\cdot {\mathbf {u}}_{s^\prime }\) in addition to the well known term \({\hat{k}}\cdot {\mathbf {B}}\), and the standard isotropic term receives an additional contribution proportional to \({\mathbf {B}}\cdot {\mathbf {u}}_{s^\prime }\). The term involving \({\hat{k}}\cdot ({\mathbf {u}}_{s^\prime }\times {\mathbf {B}})\) does not appear in the dispersion relation, due to time-reversal invariance.
In Sect. 2 we summarize the general parametrization of the self-energy, review the relevant formulas for the electron thermal propagator and the main ingredients involved in the calculation are given in Sect. 3. The formulas for the parameter coefficients that appear in the neutrino thermal self-energy are obtained and summarized in Sect. 4. The calculation of the contribution of a nucleon stream is also given there as an illustration of possible generalizations. In Sect. 5 we discuss and summarize the main features of the results obtained for the neutrino dispersion relation, and comment on related work, in particular the calculation in the case of an inhomogeneous external field.
2 General considerations
We denote by \(\varSigma _{eff}\) the background-dependent contribution to the neutrino self-energy, determined from the calculation of the diagrams in Fig. 1.
The diagrams that contribute to the neutrino self-energy in a background of electrons and nucleons to the lowest order for a given neutrino flavor \(\nu _\ell \; (\ell = e,\mu ,\tau )\). Diagram a contributes only to the \(\nu _e\) self-energy, while Diagram b contributes for the three neutrino flavors. In our calculation we consider two sets of these two diagrams, one set with the normal background (\(s = e,n,p\)) and another set with the stream backgrounds (\(s^\prime = e^\prime ,n^\prime ,p^\prime \))
Chirality of the neutrino interactions then imply that
and the dispersion relation for a given neutrino flavor \(\nu _{\ell }\) is then obtained by solving the equation

In the lowest (1-loop) order each background gives a separate contribution \(\varSigma _f\) to the total self-energy. In the presence of a constant electromagnetic field each term \(\varSigma _f\) is a function of \(k^\mu \), \(u^\mu _f\) as well as \(F^{\mu \nu }\), and its general form is

In the present calculation we restrict ourselves to the contact \(O(1/m^2_W)\) term of the W propagator, and we do not consider the momentum dependent terms nor its dependence on the magnetic field. To this order in \(1/m^2_W\) the \(a_f, g_f, {\tilde{g}}_f\) terms in Eq. (10) vanish and we do not consider them any further. Regarding the other terms, for our particular case in which the field is a pure B field in the rest frame of the normal background, Eq. (5) implies that \(\varSigma _s\), \((s=e,n,p)\), is reduced to

which is the form used in Ref. [17]. However, for the stream backgrounds, using Eq. (4),

where
In the rest frame of the normal background \(E^\mu _{s^\prime }\) has components
which can be interpreted as the electric field that the stream background particles “see”. Thus the \(d_{s^\prime }\) term represents an electric dipole type of coupling of the stream background particles. As we will see, the \(d_{s^\prime }\) is actually not present in our final result for \(\varSigma _{s^\prime }\), which we understand as a consequence of the fact that such couplings require time-reversal violating effects for which there is no source in the context of our calculation. We will discuss this in further detail in Sect. 5.
In summary, the contribution from each background to the self-energy can be parametrized in the form

Therefore for the total self-energy we can write
with
which using Eq. (4) can be expressed in the equivalent form
3 Thermal propagators
3.1 Electron propagator
The internal fermion lines in the diagrams in Fig. 1 stand for the thermal fermion propagator in an external electromagnetic field, for which we will adopt the linearized Schwinger propagator used in Refs. [36, 37]. We consider first the propagator for the electron, for either the normal or stream background, and use the notation \(f_e = e,e^\prime \) to refer to any of them. Following that reference, we write the Schwinger propagator (in the vacuum) in the form
where \(S^{(e)}_0\) is the free propagator

and \(S^{(e)}_B\) is the linearized B-dependent part of the Schwinger propagator for the electron [38,39,40,41,42,43,44,45]
with

Ordinarily the thermal propagator is then constructed by the rule [46],
with \(\eta \) defined, as usual (see below), in terms of the distribution function of the background electrons, and
For the calculation in this work the propagator for each electron background (\(f_e = e,e^\prime \)) is taken to be similar to Eq. (23), but with \(\eta (p\cdot u) \rightarrow \eta _{f_e}(p\cdot u_{f_e})\), i.e.,
with \(S^{(e)}_F\) as defined in Eq. (19). For any background fermion f the function \(\eta _f(p\cdot u_f)\) is given by
with
\(\beta _f\) and \(\mu _f\) being the inverse temperature and the chemical potential of the background. \(S^{(f_e)}_{11}\) can be written in the form
where \(S^{(e)}_0\) and \(S^{(e)}_B\) are the background-independent terms, given above, while \(S^{(f_e)}_{T}\) is the thermal, but B-independent, part

and
which is the part that is of most interest to us. Notice that the factor \(G_e(p)\) that appears here is the same for both the normal and stream backgrounds, defined in Eq. (22), since it refers to the B-dependent part of the vacuum Schwinger propagator. It is useful to note that
where \({\tilde{F}}_{\mu \nu }\) is given in Eq. (4) and \(\sigma _{\mu \nu } = \frac{i}{2}[\gamma _\mu ,\gamma _\nu ]\).
3.2 Nucleon propagator
A nucleon (\(N = n,p\)) has an anomalous magnetic moment coupling that also contributes to the B-dependent part of the neutrino thermal self-energy. The formula analogous to Eq. (28) for the thermal Schwinger propagator for a nucleon including the anomalous magnetic moment coupling, was obtained in Ref. [37]. Adapting that result to our case, the thermal Schwinger propagator for a nucleon in either the normal or stream background (\(f_N = N,N^\prime )\) is
where \(S^{(N)}_{0}\) is the free nucleon propagator, and

Here we denote by \(u^\mu _{f_N}\) the velocity four-vector of the nucleon background, while \(e_N\) and \(\kappa _N\) stand for the nucleon electric charge and anomalous magnetic moment, respectively. As in the electron case above, our working rule is that Eq. (33) holds for either a normal or stream nucleon background, with the corresponding choice of \(u^\mu _{f_N}\). \(G_N(p)\) is the same function given by Eqs. (22) and (31), with the substitution \(m_e\rightarrow m_N\), while

In analogy with Eq. (31), here we note that \(H_N(p)\) can be rewritten in the form

4 Calculation
4.1 W-diagram
For a given background \(f_e = e,e^\prime \), the W diagram in Fig. 1 gives a contribution to the neutrino thermal self-energy
Using Eq. (25) and retaining only the background-dependent part,
where
which correspond to the B-independent and B-dependent contribution to the neutrino thermal self-energy, respectively. By simple Dirac algebra they can be expressed in the form

where we have used Eq. (31), and
The integrals \(I_{f\mu }, J_{f\mu }\) must be of the form
with the coefficients given by
which can then be evaluated in any reference frame since they are scalar integrals. A convenient one to use is the rest frame of each background f. Denoting the energy and momentum of the background particles in that reference frame by \(\mathcal{E}_f\) and \(\mathbf {P}\), a straightforward evaluation yields
where
and
Therefore

where
4.2 Z-diagram
For the Z diagram we need the following neutral current couplings,
where
and
The parameters \(X_N,Y_N\) are the vector and axial vector form factors of the nucleon neutral-current at zero momentum transfer. In Eq. (50), \(g_A\) stands for the normalization constant of the axial charged vector of the nucleon, \(g_A = 1.26\).
The Z diagram contribution is
and retaining only the background-dependent part,
where
We consider the contributions from the electron and the nucleon backgrounds separately.
4.2.1 Electron background contribution
In terms of the integrals \(I_{f\mu }, J_{f\mu }\) defined in Eq. (40),

Comparing with Eq. (39), we then obtain
with he final expressions for \(\left( \varSigma ^{(W)}_{f_e}\right) _{T}\) and \(\left( \varSigma ^{(W)}_{f_e}\right) _{TB}\) given in Eq. (46).
4.2.2 Nucleon background contribution
We consider here the nucleon backgrounds. As with the electron case, what interests us is the contribution to the neutrino self-energy arising from \(S^{(f_N)}_{T}\) and \(S^{(f_N)}_{TB}\), corresponding to the B-independent and B-dependent contributions of each background (\(f_N = N,N^\prime \)). Denoting them by \(\left( \varSigma ^{(Z)}_{f_N}\right) _{T}\) and \(\left( \varSigma ^{(Z)}_{f_N}\right) _{TB}\), respectively. From Eq. (53),
where X stands for either subscript, T or TB. The calculation involving \(S^{(f_N)}_{T}(p)\) and the \(G_N(p)\) term of \(S^{(f_N)}_{TB}(p)\) follows the steps that lead to Eq. (54). On the other hand, using Eq. (35) it follows that
Thus we obtain

where \(I_{f_N\mu }\) and \(J_{f_N\mu }\) are the integrals given by Eq. (40), with \(f = f_N\). Thus, the contribution of a nucleon background to the neutrino self-energy is given by

with
4.3 Summary
Using the results given in Eqs. (46), (55) and (59), the thermal self-energy for each neutrino flavor
is given by

where, for \(f_e = e,e^\prime \),
The formulas for \(b_{f_N}\) and \(c_{f_N}\) (\(f_N = N,N^\prime \)) are given in Eq. (60) and they hold for any neutrino flavor. Thus, \(\varSigma \) is of the expected form discussed in Sect. 2 [e.g., Eq. (15)], in particular with \(d_{e^\prime } = 0\) as anticipated there, with the coefficients \(b_f,c_f\) given above in Eqs. (63) and (60).
5 Discussion and conclusions
5.1 Dispersion relations
For the purpose of determining the dispersion relations we use the expression for \(\varSigma \) in terms of \(V^\mu \), Eq. (16). The equation for the propagating neutrino modes, Eq. (9), then becomes

and the dispersion relations are obtained by solving
Remembering that \(V^\mu \) does not depend on k (to the order \(1/m^2_W\) that we are considering in this work), the solutions are \(k^0 = \omega _{\pm }({\mathbf {k}})\), where
with \({\hat{k}}\) being the unit vector along the direction of propagation. The dispersion relation for the neutrino and the antineutrino are identified as usual,
which to the lowest order yield
where the upper(lower) sign holds for the neutrino(antineutrino) and
Explicitly, using Eq. (18),
with
The fact that the dispersion relation in the presence of a magnetic field has an anisotropic term proportional to \({\hat{k}}\cdot {\mathbf {B}}\) is well known. As we have already mentioned many of its possible effects have been studied and more complete calculations involving higher order contributions have been performed in the references cited. The above results show that in the presence of a stream (with a velocity four-vector \(u^\mu _f\) relative to the normal background), the dispersion relation acquires another anisotropic term of the form \({\hat{k}}\cdot {\mathbf {u}}_f\). Furthermore, the standard isotropic (Wolfenstein) term receives an additional contribution proportional to \({\mathbf {B}}\cdot {\mathbf {u}}_f\) that involves the stream velocity and the magnetic field.
It has been suggested repeatedly in the literature that the anisotropic terms in the neutrino dispersion relations can have effects in several astrophysical environments including pulsars [31] and the dynamics of supernovas [33,34,35]. The resonance condition for neutrino oscillations in a magnetic field depends on \({\hat{k}}\cdot {\mathbf {B}}\), and therefore is satisfied at different depths, corresponding to different densities and temperatures. This difference results in an asymmetry in the momentum distributions of the neutrinos. In the presence of a stream background, the neutrino asymmetry will depend on the relative orientation of the three vectors \({\mathbf {k}},{\mathbf {B}},{\mathbf {u}}_f\).
As an example, let us consider specifically the two-stream electron background. Denoting the velocity four-vector of the stream by \(v^\mu \), then
We wish to compare the size of the term proportional to \({{\hat{k}}}\cdot {{\mathbf {v}}}\) relative to \({{\hat{k}}}\cdot {{\mathbf {B}}}\), thus we consider the quantity
For simplicity we will take \(v^0 \sim 0\), and for definiteness we will assume that the two backgrounds are described by the classical thermal distribution functions. In that case,
and similarly for \(f_{\bar{f}}\), and therefore,
where we have defined \(\Delta N_f = n_f - n_{\bar{f}}\) and \(B_c = m^2_e/e\). On the other hand,
in any case. We can consider two possibilities, according to whether \(c_e \gg c_{e^\prime }\) or the way around. For definiteness let us consider the case \(c_e \gg c_{e^\prime }\). This situation can occur, for example, if the temperature of the normal background is greater than the temperature of the stream. In this case
The indication is that it is possible that \(r \sim 1\) for acceptable values of the parameters involved. In other words, it is conceivable that there are environments where the conditions are such that the asymmetries due to the \({\hat{k}}\cdot v\) and \({\hat{k}}\cdot {\mathbf {B}}\) terms can be comparable. The above formulas are based on the linear approximation in the magnetic field and therefore are valid only for \(B \ll B_c\).
We mention that in the discussion above, in particular in writing Eq. (72), we have considered a two-stream system without explaining its physical origin, therefore in this sense the stream velocity \({\mathbf {v}}\) is not specified. However, the results can be used in specific applications or situations in which the stream velocity is determined and/or restricted by the particular physical conditions of the problem, for example if the stream velocity is due to the drift of electrons in the B field. In such a case, since the Lorentz forces makes charged particles drift only along the B axis but not in the perpendicular plane, the results can be applied to that case as well by taking \({\mathbf {v}}\) to be on the \({\mathbf {B}}\) axis.
Similar results are obtained in other cases as well. To include other backgrounds we just have to add to \(\delta \) the corresponding \(\delta _f\). For example, for a stream nucleon background,
The quantitative estimates of the effects in realistic situations of the additional asymmetric terms that we have reported above involve stellar astrophysics studies that are beyond the scope of the present work. But as we have suggested they are subjects worth of further study.
5.2 Comment on the \(F^{\mu \nu }u_{f\nu }\gamma _\mu \) term
The calculations of Sect. 4 confirm explicitly that the \(d_f\) term in the general expression for the thermal self-energy [Eq. (10)] is zero, as it was anticipated in Sect. 2. This result can be understood by making reference to previous work [47], where the conditions under which such dipole-type couplings may appear in the neutrino effective Lagrangian were studied. To establish contact with that reference, notice that the terms involving \(c_f, d_f\) in Eq. (10) are represented by the operators
in the neutrino effective Lagrangian. The coefficients \(c_f, d_f\) here correspond to the coefficients that were denoted by \(d^{\,\prime }_{M,E}\) there, respectively (evaluated at \(k = 0\)). Borrowing the results of that reference [e.g., Eqs. (14) and (16b)] the presence of \(O^\prime _E\) requires time-reversal violation at some level. Since there is no source of T violation in the context of our calculation, the \(O^\prime _E\) term is not generated. On the other hand \(O^\prime _M\) is even under time-reversal but odd under CP, and therefore it can be generated if the background is CP asymmetric.
Here we would like to point out the following. In the presence of non-constant fields (non-static and/or nonhomogeneous) there can be additional terms involving the derivatives of \(F_{\mu \nu }\) and/or \({\tilde{F}}_{\mu \nu }\). For example, limiting ourselves to terms with first derivatives, consider the following
This term is even under CP and even under time-reversal. Therefore, it can be present in the effective Lagrangian without implying time-reversal violation and even if the background and the interactions are CP-symmetric. This contrasts with \(O^\prime _{M}\) which is CP-odd and therefore does not exist if the background is CP-symmetric (neglecting the CP violating effects of the weak interactions). \(O^{\prime \prime }_E\) can give additional anisotropic contributions to the neutrino dispersion relation [e.g., Eq. (72)] that are not present otherwise, with different kinematic properties from the constant field case. For example, in the presence of a static but inhomogeneous field, it gives a term involving the gradient of \({\hat{k}}\cdot ({\mathbf {v}}\times {\mathbf {B}})\).
Of course this type of term (with derivatives of the electromagnetic field) do not appear in the approach we are using in the present work based on the electron thermal propagator in a constant B field. Instead we have to resort to the type of approach employed in Ref. [17], which is based on calculating the electromagnetic vertex first, and then taking the static limit in a suitable way to obtain the self-energy in the (inhomogeneous) external field. We have performed this calculation and the results are presented separately [48].
5.3 Conclusions
To summarize, in this work we have studied the propagation of a neutrino in a magnetized two stream plasma system. Specifically, we considered a medium that consists of a normal electron background plus another electron stream background that is moving as a whole relative to the normal background. In addition, we assume that in the rest frame of the normal background there is a constant magnetic field.
Using the thermal Schwinger propagator for the electrons in the medium we have calculated the neutrino self-energy in such environment, linearized in B and to the leading order \(O(1/m^2_W)\) terms. The results of the calculation are summarized in Eqs. (60)–(63). From the self-energy the dispersion relations were obtained in the standard way, and the corresponding formulas are summarized in Eqs. (68)–(72).
In the presence of the stream (with velocity \({\mathbf {v}}\) relative to the normal background), the dispersion relation acquires an anisotropic term of the form \({\hat{k}}\cdot {\mathbf {v}}\) in addition to the well known term of the form \({\hat{k}}\cdot {\mathbf {B}}\), and the standard isotropic term receives an additional contribution proportional to \({\mathbf {B}}\cdot {\mathbf {v}}\) that involves the stream velocity and the magnetic field. We explained why a term of the form \({\hat{k}}\cdot ({\mathbf {v}}\times {\mathbf {B}})\) does not appear in the dispersion relation, due to time-reversal invariance, and why a term of similar kinematic form can appear in the presence of an inhomogeneous magnetic field, involving the derivative of the field. We have given the explicit formulas for the dispersion relations and outlined possible generalizations, for example to include the nucleon contribution or the case of non-homogeneous fields. We have made simple estimates of the magnitude of the asymmetric terms proportional to \({\hat{k}}\cdot {\mathbf {v}}\) and \({\hat{k}}\cdot {\mathbf {B}}\), and found that they can be comparable for acceptable values of the parameters involved.
In the context of plasma physics the propagation of photons in two stream plasma systems is a well studied subject. Here we have started to carry out an analogous study for the case of neutrinos. The present work is limited in several ways, for example by restricting ourselves to an electron background and stream, the linear approximation in the B field, and the calculation of only the leading \(O(1/m^2_W)\) terms. However, the results reveal interesting effects that are potentially important in several physical contexts, such as supernova dynamics and gamma-ray bursts physics where the effects of such systems are a major focus of current research, and in this sense our work motivates and paves the way for further calculations without these simplifications.
S.S is thankful to Japan Society for the promotion of science (JSPS) for the invitational fellowship. The work of S.S. is partially supported by DGAPA-UNAM (México) Project No. IN110815 and PASPA-DGAPA, UNAM.
References
L. Wolfenstein, Phys. Rev. D 17, 2369 (1978). https://doi.org/10.1103/PhysRevD.17.2369
P. Langacker, J.P. Leveille, J. Sheiman, Phys. Rev. D 27, 1228 (1983). https://doi.org/10.1103/PhysRevD.27.1228
S.P. Mikheev, A.Y. Smirnov, Sov. J. Nucl. Phys. 42, 913 (1985)
S.P. Mikheev, A.Y. Smirnov, Yad. Fiz. 42, 1441 (1985)
D. Notzold, G. Raffelt, Nucl. Phys. B 307, 924 (1988). https://doi.org/10.1016/0550-3213(88)90113-7
P.B. Pal, T.N. Pham, Phys. Rev. D 40, 259 (1989). https://doi.org/10.1103/PhysRevD.40.259
J.F. Nieves, Phys. Rev. D 40, 866 (1989). https://doi.org/10.1103/PhysRevD.40.866
J.C. D’Olivo, J.F. Nieves, M. Torres, Phys. Rev. D 46, 1172 (1992). https://doi.org/10.1103/PhysRevD.46.1172
See, G. G. Raffelt, Chicago, USA: Univ. Pr. 664 p and references therein (1996)
J.T. Pantaleone, Phys. Lett. B 287, 128 (1992). https://doi.org/10.1016/0370-2693(92)91887-F
S. Samuel, Phys. Rev. D 48, 1462 (1993). https://doi.org/10.1103/PhysRevD.48.1462
V.A. Kostelecky, J.T. Pantaleone, S. Samuel, Phys. Lett. B 315, 46 (1993). https://doi.org/10.1016/0370-2693(93)90156-C
H. Duan, G .M. Fuller, Y .Z. Qian, Ann. Rev. Nucl. Part. Sci. 60, 569 (2010). https://doi.org/10.1146/annurev.nucl.012809.104524. arXiv:1001.2799 [hep-ph]
A. Mirizzi, S. Pozzorini, G.G. Raffelt, P.D. Serpico, JHEP 0910, 020 (2009). https://doi.org/10.1088/1126-6708/2009/10/020. arXiv:0907.3674 [hep-ph]
S. Chakraborty, R. Hansen, I. Izaguirre, G. Raffelt, Nucl. Phys. B 908, 366 (2016). https://doi.org/10.1016/j.nuclphysb.2016.02.012. arXiv:1602.02766 [hep-ph]
E. Akhmedov, Nucl. Phys. B 908, 382 (2016). https://doi.org/10.1016/j.nuclphysb.2016.02.011. arXiv:1601.07842 [hep-ph] and references therein
J.C. D’Olivo, J.F. Nieves, P.B. Pal, Phys. Rev. D 40, 3679 (1989). https://doi.org/10.1103/PhysRevD.40.3679
A. Erdas, Phys. Rev. D 80, 113004 (2009). https://doi.org/10.1103/PhysRevD.80.113004. arXiv:0908.4297 [hep-ph]
A. Ioannisian, N. Kazarian. arXiv:1702.00943 [hep-ph]
A.E. Lobanov, A.I. Studenikin, Phys. Lett. B 515, 94 (2001). https://doi.org/10.1016/S0370-2693(01)00858-9. arXiv:hep-ph/0106101
A. Grigoriev, A. Lobanov, A. Studenikin, Phys. Lett. B 535, 187 (2002). https://doi.org/10.1016/S0370-2693(02)01776-8. arXiv:hep-ph/0202276
A.I. Studenikin, Phys. Atom. Nucl. 67, 993 (2004)
A.I. Studenikin, Yad. Fiz. 67, 1014 (2004). https://doi.org/10.1134/1.1755390
E .V. Arbuzova, A .E. Lobanov, E .M. Murchikova, Phys. Rev. D 81, 045001 (2010). https://doi.org/10.1103/PhysRevD.81.045001. arXiv:0903.3358 [hep-ph]
R. Shaisultanov, Y. Lyubarsky, D. Eichler, Astrophys. J. 744, 182 (2012). https://doi.org/10.1088/0004-637X/744/2/182. arXiv:1104.0521 [astro-ph.HE]
A. Yalinewich, M. Gedalin, Phys. Plasmas 17, 062101 (2010)
A.R. Soto-Chavez, S.M. Mahajan, Phys. Rev. E 81, 026403 (2010)
H. Che, J .F. Drake, M. Swisdak, P .H. Yoon, Phys. Rev. Lett. 102, 145004 (2009). https://doi.org/10.1103/PhysRevLett.102.145004. arXiv:0903.1311 [physics.space-ph]
V.N. Oraevsky, V.B. Semikoz, Phys. Atom. Nucl. 66, 466 (2003)
V.N. Oraevsky, V.B. Semikoz, Yad. Fiz. 66, 494 (2003). https://doi.org/10.1134/1.1563706
A. Kusenko, G. Segre, Phys. Rev. Lett. 77, 4872 (1996). https://doi.org/10.1103/PhysRevLett.77.4872. arXiv:hep-ph/9606428
T. Maruyama et al., Phys. Rev. C 89(3), 035801 (2014). https://doi.org/10.1103/PhysRevC.89.035801. arXiv:1301.7495 [astro-ph.SR]
S. Sahu, V .M. Bannur, Phys. Rev. D 61, 023003 (2000). https://doi.org/10.1103/PhysRevD.61.023003. arXiv:hep-ph/9806427
H. Duan, Phys. Rev. D 69, 123004 (2004). https://doi.org/10.1103/PhysRevD.69.123004. arXiv:astro-ph/0401634
A.A. Gvozdev, I.S. Ognev, Astron. Lett. 31, 442 (2005)
T .K. Chyi, C .W. Hwang, W .F. Kao, G .L. Lin, K .W. Ng, J .J. Tseng, Phys. Rev. D 62, 105014 (2000). https://doi.org/10.1103/PhysRevD.62.105014. arXiv:hep-th/9912134
J.F. Nieves, Phys. Rev. D 70, 073001 (2004). https://doi.org/10.1103/PhysRevD.70.073001. arXiv:hep-ph/0403121
We follow the convention that \(e\) stands for the electric charge of the electron (\(e < 0\))
V.C. Zhukovsky, T.L. Shoniya, P.A. Eminov, J. Exp. Theor. Phys. 77, 539 (1993)
V.C. Zhukovsky, T.L. Shoniya, P.A. Eminov, Zh Eksp, Teor. Fiz. 104, 3269 (1993)
A.V. Borisov, A.S. Vshivtsev, V.C. Zhukovsky, P.A. Eminov, Phys. Usp. 40, 229 (1997)
A.V. Borisov, A.S. Vshivtsev, V.C. Zhukovsky, P.A. Eminov, Usp. Fiz. Nauk 167, 241 (1997). https://doi.org/10.1070/PU1997v040n03ABEH000209
P.A. Eminov, Adv. High Energy Phys. 2523062, 2016 (2016). https://doi.org/10.1155/2016/2523062. arXiv:1510.03280 [hep-ph]
P.A. Eminov, J. Exp. Theor. Phys. 122(1), 63 (2016)
P.A. Eminov, Zh Eksp, Teor. Fiz. 149(1), 76 (2016). https://doi.org/10.1134/S1063776115120067
See for example, P. Elmfors, D. Grasso and G. Raffelt, Nucl. Phys. B 479, 3 (1996) https://doi.org/10.1016/0550-3213(96)00431-2. arXiv:hep-ph/9605250 and refences therein. Since we will restrict ourselves to calculate the real part of the self-energy and dispersion relation, we need only the 11 element of the thermal propagator
J.F. Nieves, P.B. Pal, Phys. Rev. D 40, 1693 (1989). https://doi.org/10.1103/PhysRevD.40.1693
J. F. Nieves and S. Sahu, arXiv:1706.09484 [hep-ph]
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
Funded by SCOAP3
About this article
Cite this article
Nieves, J.F., Olivas, Y.D. & Sahu, S. Neutrino dispersion relation in a magnetized multi-stream matter background. Eur. Phys. J. C 78, 400 (2018). https://doi.org/10.1140/epjc/s10052-018-5884-z
Received:
Accepted:
Published:
DOI: https://doi.org/10.1140/epjc/s10052-018-5884-z