1 Introduction and summary

The subject matter of this paper is the propagation of neutrinos in a medium in the presence of an external electromagnetic field. There are various problems of interest associated with this subject that have been well studied in previous works. In most previous studies the interest has been on a medium consisting of a thermal background of various particle species, which can be taken to be at rest, in the presence of an external magnetic field in the same frame, which is assumed to be homogeneous. In those studies typically the focus is on the dispersion relation of a neutrino that propagates in such environments. The assumptions underlying the previous works do not allow us to consider situations in which the thermal backgrounds of the different particle species move with some relative velocity relative to each other, and/or situations in which the external field is not homogeneous.

There are several reasons why considering the more general situations just mentioned above are of interest. For example, the propagation of photons in two-stream plasma systems is a well studied subject in the context of plasma physics, particularly with regard to the so-called two-stream instabilities [1,2,3], many aspects of which have been studied both analytically and numerically [4,5,6,7,8]. In recent works, similar studies have been carried out for magnetized two-stream plasma systems [9,10,11]. In these works the focus is typically the dispersion relation of the photon when it propagates in the environment that is being considered. The case of propagation through inhomogeneous plasmas has also been studied [12]. Several authors have studied the propagation of neutrinos in moving media in the presence of an external electromagnetic field [13,14,15]. Also the effects of moving and polarized matter on neutrino spin/magnetic moment oscillations and \(\nu _L \rightarrow \nu _R\) conversions are considered [16,17,18,19]. In Ref. [1], the growth rates for different instabilities of the relativistic ion beams propagating through a hot electron background are studied analytically and checked with numerical simulations. This configuration can be of relevance to study the relativistic, collisionless shock structures in astrophysical scenarios where oppositely directed particle beams (protons) pass through an isotropic electron gas [2, 20].

From a fundamental and conceptual point of view the problem we want to consider is the counterpart for neutrinos. The problem of the propagation of neutrinos in magnetized media is relevant in several physical contexts, such as pulsars [21], supernovas [22,23,24] and gamma-ray bursts [25, 26], where the magnetic fields are believed to have important implications. Also the effects of stream neutrino background have been suggested as a mechanism of large scale magnetic field generation in the hot plasma of the Early Universe [27]. In those contexts, the effects of stream backgrounds and/or inhomogeneous fields can be of practical interest.

In a recent work [28] we initiated the study of the propagation of neutrinos in medium along these lines, calculating the self-energy and dispersion relation of a neutrino that propagates in a magnetized two-stream background medium. Specifically, we considered a medium composed of an electron background, which can be taken to be at rest, and a second electron background that moves with a velocity four-vector \(v^\mu \) relative to the first. We refer to them as the normal and stream backgrounds, respectively. In addition we assumed that, in the rest frame of the normal background, there is a magnetic field (\(\mathbf {B}\)) that is homogeneous. The calculation was based on the local limit of the weak interactions, and therefore restricted to the leading \(O(1/m^2_W)\) terms, and on the application of the Schwinger propagator method, adapted to the two-stream background, but keeping only up to the linear terms in \(\mathbf {B}\).

The main results obtained in Ref. [28] are summarized as follows. For a neutrino that propagates in a two-electron background and a constant magnetic field, as described above, the dispersion relation acquires an anisotropic contribution of the form \({\hat{k}}\cdot \mathbf {v}\) (where \({\hat{k}}\) is the unit vector along the incoming neutrino momentum \(\mathbf {k}\)), in addition to the well known term \({\hat{k}}\cdot \mathbf {B}\) [29,30,31,32]. As discussed and explained in Ref. [28], a term of the form \({\hat{k}}\cdot (\mathbf {v}\times \mathbf {B})\) does not appear in the constant \(\mathbf {B}\) case. The physical reason behind this result is that such a term is odd under time-reversal and there is no source of time-reversal breaking effects in the context of our calculations. However it was noted that terms of similar form, but involving the derivative of the electromagnetic field, are even under time-reversal and therefore could be present in the case that the electromagnetic field is not homogeneous.

As a continuation of the above work, here we calculate the electromagnetic vertex function of a neutrino that propagates in a two-stream electron background. This complements and extends our previous work in at least two ways. On one hand, the knowledge of the vertex function allows us to determine the neutrino electromagnetic properties and to calculate the rate for various processes involving neutrinos in such media, in analogy with the study of electromagnetic neutrino processes in ordinary media (See for example, [33] and references therein).

On the other hand, which we pursue here, by considering the effective neutrino interaction with an external electromagnetic field, the result for the vertex function is used to determine the self-energy and dispersion relation of a neutrino that propagates in the two-stream electron medium with an inhomogeneous magnetic field. The self-energy and dispersion relation for the case in which there is only one electron background can be obtained as a special case, whether it is moving or at rest relative to the external magnetic field. This work complements our previous calculation of the dispersion relation based on the Schwinger propagator method, which is restricted to a uniform magnetic field. The dispersion relation obtained can be used as the basis for studying the effects of inhomogeneous fields on the neutrino oscillations in several environments such as pulsars, supernovas, and gamma-ray bursts that have been considered in the literature cited, as well as several related application contexts where the inhomogeneity of the magnetic fields may have a prominent role such as transition radiation induced by a magnetic field [34], neutrino-induced plasma instabilities in supernova [35], neutrino driven magnetic field instability in a compact star [36] and the effects of asymmetric neutrino propagation in proto-neutrons stars [37].

It is appropriate to mention here that the calculation of the neutrino electromagnetic vertex function in the two-stream electron background is based on the local limit of the weak interactions, i.e., it is limited to the \(O(1/m^2_W)\) contributions. Moreover, in the application to the calculation of neutrino self-energy and dispersion relation mentioned above we retain only the terms that are at most linear in the derivatives of the field.

The results of the calculations confirm that in the case of an inhomogeneous field the dispersion relation acquires additional anisotropic terms that involve the derivatives of the magnetic field. In particular, a term of the form \({\hat{k}}\cdot (\nabla \times \mathbf {B})\), which is independent of the stream background velocity, can be present even in the absence of the stream background. Other terms, such as the gradient of \({\hat{k}}\cdot (\mathbf {v}\times \mathbf {B})\) already mentioned above, depend on the stream background velocity, but they can be present even in the case in which \(\nabla \times \mathbf {B} = 0\). Moreover, all these additional terms are even under the CP transformation and as a result they are proportional to the sum of the particle and antiparticle densities. This is in contrast with the \({\hat{k}}\cdot \mathbf {v}\) and \({\hat{k}}\cdot \mathbf {B}\) terms, which are even under CP and depend on the difference of the particle and antiparticle densities. In situations where the medium is CP-symmetric and the particle and antiparticle densities are equal, the \(O(1/m^2_W)\) the contributions from the \({\hat{k}}\cdot \mathbf {v}\) and \({\hat{k}}\cdot \mathbf {B}\) terms vanish, and the contributions from the terms involving the derivatives of the magnetic field could gain more importance, depending on the degree of inhomogeneity of the magnetic field.

It is worth mentioning that, in order to calculate properly the stream contribution to the vertex function, and more specifically the vertex function’s zero photon momentum limit (which is related to the neutrino index of refraction), the screening effects of the electron background must be taken into account. The technical reason is that the electric form factors [those that couple to the electric components of the electromagnetic field \(\sim {\hat{k}}\cdot (\mathbf {v}\times \mathbf {B})\)] diverge in the zero photon-momentum limit, unless the screening effects are taken into account. In the case in which there is only one background (\(\mathbf {v} = 0\)), or the magnetic field is uniform, only the magnetic form factor couplings enter in the effective interaction with the electromagnetic field, for which the screening corrections are not relevant. An important ingredient of the present work is the proper inclusion of the background screening effects that are present in the kind of medium that we are envisaging, in the calculation of the neutrino index of refraction.

In Sect. 2.1 we summarize some of the notations and conventions that are used throughout. The 1-loop formulas for the vertex function are given in Sect. 2.2, generalizing the formulas given in Ref. [29], adapted to the present notation and context. As already mentioned, they are based on the local limit of the weak interactions, i.e., they are restricted to the \(O(1/m^2_W)\) contributions. The vertex function is expressed in terms of a set of form factors that are given as integrals over the distribution functions of the background electrons. Since the calculation of the self-energy and dispersion relation in a non-homogeneous external field involves evaluating the vertex function in the static limit appropriately, specially in the context of the two-stream system, in Sect. 2.3 we define precisely this limiting operation. There we also summarize the static limit value of the integrals involved in such formulas, which are relevant in the calculation of the self-energy and dispersion relation. Some of the calculation details regarding those formulas are provided in Appendices A, B and C. The actual calculation of the self-energy in the presence of an external inhomogeneous field is carried out in Sect. 3, retaining the terms that are at most linear in the derivatives of the field, and paying attention to the treatment and incorporation of the screening effects of the electron background. There we first enumerate the possible terms that may appear in the B-dependent part of the self-energy under the specified conditions, and write down its generic form in terms of a set of structure tensors with corresponding coefficients to be determined. The coefficients are then identified by considering the transition amplitude in the presence of an external field, using the results of the one-loop expression for the neutrino electromagnetic vertex function. The need to include the screening effects for properly determining the self-energy in the two-stream background case is explained there in more detail. The corresponding dispersion relations are obtained and discussed in Sect. 4, focusing on some of the features that illustrate the salient implications of the results for the self-energy. In Sect. 5 we review our work and summarize the main results.

2 The vertex function

2.1 Notation and conventions

We borrow some of the notation from Ref. [28], which we briefly summarize here for convenience as follows. We use the symbols e and \(e^\prime \) to refer to the electrons in the normal and stream backgrounds, respectively, while the symbol f stands for either e or \(e^\prime \). Denoting by \(u^\mu _f\) the velocity four-vector of each background, the convention stated above means that the velocity four vector of the normal background is set to

$$\begin{aligned} u^\mu _e = u^\mu , \end{aligned}$$
(1)

where, as usual,

$$\begin{aligned} u^\mu \equiv (1,\mathbf {0}), \end{aligned}$$
(2)

while for the stream

$$\begin{aligned} u^\mu _{e^\prime } = v^\mu , \end{aligned}$$
(3)

with

$$\begin{aligned} v^\mu = (v^0,\mathbf {v}). \end{aligned}$$
(4)

The relevant diagrams for the calculation of the electron background contributions to the neutrino electromagnetic vertex are shown in Fig. 1. For the calculation we will need the following neutral current couplings

$$\begin{aligned} L_Z = - g_Z Z^\mu \left[ {\bar{e}}\gamma _\mu (X_e + Y_e\gamma _5)e + \sum _\ell {\bar{\nu }}_{L\ell }\gamma _\mu \nu _{L\ell }\right] , \end{aligned}$$
(5)

where

$$\begin{aligned} g_Z= & {} g/(2\cos \theta _W) ,\nonumber \\ X_e= & {} -\frac{1}{2} + 2\sin ^2\theta _W,\nonumber \\ Y_e= & {} \frac{1}{2}. \end{aligned}$$
(6)

We denote the momentum vectors of the incoming and outgoing neutrino by \(k,k^\prime \), respectively, and

$$\begin{aligned} q = k^\prime - k, \end{aligned}$$
(7)

denotes the momentum vector of the incoming photon [This convention is opposite to the convention adopted in Ref. [29] in which q denotes the momentum of the outgoing photon. This difference is reflected in the sign of the P term in Eq. (12)]

The form factors of each background contribution are functions of the scalar variables

$$\begin{aligned} {\varOmega }_f= & {} q\cdot u_f,\nonumber \\ Q_f= & {} \sqrt{{\varOmega }^2_f - q^2} . \end{aligned}$$
(8)

Physically, \({\varOmega }_f\) represents the energy of the photon in the rest frame of the normal background, while \(Q_f\) is the magnitude of the 3-momentum vector in the same frame, which we denote by \(\mathbf {Q}_f\).

2.2 1-loop formulas

As already mentioned, the relevant diagrams for the calculation of the electron background contributions to the neutrino electromagnetic vertex function are shown in Fig. 1. We denote by \({\varGamma }^{(W,Z)}_{f\mu }\) the contribution from diagrams (a) and (b), respectively, and write the total vertex function as

$$\begin{aligned} {\varGamma }_\mu = {\varGamma }_{e\mu } + {\varGamma }_{e^\prime \mu }. \end{aligned}$$
(9)

where

$$\begin{aligned} {\varGamma }_{f\mu } = \left\{ \begin{array}{ll} {\varGamma }^{(W)}_{f\mu } + {\varGamma }^{(Z)}_{f\mu } &{}\quad (\hbox { for}\ \nu _e) \\ {\varGamma }^{(Z)}_{f\mu } &{}\quad (\hbox { for}\ \nu _{\mu ,\tau }) \end{array}\right. \end{aligned}$$
(10)
Fig. 1
figure 1

The diagrams that contribute to the neutrino electromagnetic vertex in an electron background to the lowest order for a given neutrino flavor \(\nu _\ell \; (\ell = e,\mu ,\tau )\). Diagram a contributes only to the \(\nu _e\) vertex function, while Diagram b contributes for the three neutrino flavors

Full size image

We now rely on the results obtained in Ref. [29], adapted for our present purposes. The results of the one-loop calculation of \({\varGamma }^{(W,Z)}_{f\mu }\) is that \({\varGamma }_{f\mu }\) can be written in the form

$$\begin{aligned} {\varGamma }_{f\mu } = T_{f\mu \nu }\gamma ^\nu L, \end{aligned}$$
(11)

where the tensors \(T_{f\mu \nu }\) do not contain any gamma matrices and have the decomposition

$$\begin{aligned} T_{f\mu \nu } = T_{fT} R_{f\mu \nu } + T_{fL} Q_{f\mu \nu } - T_{fP} P_{f\mu \nu } , \end{aligned}$$
(12)

with \(T_{eT,L,P}\) and \(T_{e^\prime T,L,P}\) being scalar functions of \({\varOmega }_e,Q_e\) and \({\varOmega }_{e^\prime },Q_{e^\prime }\), respectively. In writing the last term in Eq. (12) we have taken into account the fact that the definition of q here [Eq. (7)] is the opposite to that in Ref. [29], as already mentioned in Sect. 2.1. The basis tensors \(R_{f\mu \nu },Q_{f\mu \nu },P_{f\mu \nu }\) that appear in Eq. (12) are defined by

$$\begin{aligned} R_{f\mu \nu }= & {} {\tilde{g}}_{\mu \nu } - Q_{f\mu \nu }\nonumber \\ Q_{f\mu \nu }= & {} \frac{{\tilde{u}}_{f\mu }{\tilde{u}}_{f\nu }}{{\tilde{u}}^2_f}\nonumber \\ P_{f\mu \nu }= & {} \frac{i}{Q_f}\varepsilon _{\mu \nu \alpha \beta } q^\alpha u^\beta _f, \end{aligned}$$
(13)

where

$$\begin{aligned} {\tilde{g}}_{\mu \nu } = g_{\mu \nu } - \frac{q_\mu q_\nu }{q^2} , \end{aligned}$$
(14)

and

$$\begin{aligned} {\tilde{u}}_{f\mu } = {\tilde{g}}_{\mu \nu }u^\nu _f. \end{aligned}$$
(15)

The tensors \(R_{f\mu \nu },Q_{f\mu \nu },P_{f\mu \nu }\) satisfy the relations

$$\begin{aligned} R_{f\mu \nu }R^{\mu \nu }_f= & {} -P_{f\mu \nu }P^{\mu \nu }_f = 2,\nonumber \\ Q_{f\mu \nu }Q^{\mu \nu }_f= & {} 1, \end{aligned}$$
(16)

while the contractions of anyone of them with the others vanish.

The functions \(T_{fT,L,P}\) that appear in Eq. (12) are given by

$$\begin{aligned} T_{fT,L,P} = \left\{ \begin{array}{ll} T^{(W)}_{fT,L,P} + T^{(Z)}_{fT,L,P} &{}\quad (\hbox { }\ \nu _e)\\ T^{(Z)}_{fT,L,P} &{}\quad (\hbox { }\ \nu _{\mu ,\tau }) \end{array}\right. \end{aligned}$$
(17)

where

$$\begin{aligned} T^{(Z)}_{fT}= & {} \frac{2eg^2_Z}{m^2_Z} X_e A^\prime _f,\nonumber \\ T^{(Z)}_{fL}= & {} \frac{4eg^2_Z}{m^2_Z} X_e \frac{B_f}{{\tilde{u}}^2_f},\nonumber \\= & {} -\frac{4eg^2_Z}{m^2_Z} X_e \frac{q^2}{Q^2_f}B_f,\nonumber \\ T^{(Z)}_{fP}= & {} -\frac{4eg^2_Z}{m^2_Z} Y_e Q_f C_f, \end{aligned}$$
(18)

with

$$\begin{aligned} A^\prime _f({\varOmega }_f, Q_f)\equiv & {} A_f({\varOmega }_f, Q_f) - \frac{B_f({\varOmega }_f, Q_f)}{{\tilde{u}}^2_f},\nonumber \\ A_f({\varOmega }_f, Q_f)= & {} \int \frac{d^3p}{(2\pi )^3 2E}(f_{f} + f_{{\bar{f}}})\nonumber \\&\times \left[ \frac{2m^2 - 2p\cdot q}{q^2 + 2p\cdot q} + (q\rightarrow -q)\right] ,\nonumber \\ B_f({\varOmega }_f, Q_f)= & {} \int \frac{d^3p}{(2\pi )^3 2E}(f_{f} + f_{{\bar{f}}})\nonumber \\&\times \left[ \frac{2(p\cdot u_f)^2 + 2(p\cdot u_f)(q\cdot u) - p\cdot q}{q^2 + 2p\cdot q} \right. \nonumber \\&\left. + (q\rightarrow -q)\right] ,\nonumber \\ C_f({\varOmega }_f, Q_f)= & {} \int \frac{d^3p}{(2\pi )^3 2E}(f_{f} - f_{{\bar{f}}}) \nonumber \\&\times \frac{p\cdot {\tilde{u}}_f}{{\tilde{u}}^2_f} \left[ \frac{1}{q^2 + 2p\cdot q} + (q\rightarrow -q)\right] .\nonumber \\ \end{aligned}$$
(19)

In these formulas, m is the electron mass,

$$\begin{aligned} p^\mu = (E,\mathbf {p}), \quad E = \sqrt{\mathbf {p}^{\,2} + m^2}, \end{aligned}$$
(20)

and \(f_{f,{\bar{f}}}\) are the electron and positron thermal distribution functions

$$\begin{aligned} f_{f,{\bar{f}}} = \frac{1}{e^{\beta _f(p\cdot u_f \mp \mu _f)} + 1}, \end{aligned}$$
(21)

where \(1/\beta _{e,e^\prime }\) and \(\mu _{e,e^\prime }\) are the temperature and chemical potential of the normal and stream background electrons, respectively. The corresponding formulas for the functions \(T^{(W)}_{fT,L,P}\) corresponding to diagram (a) in Fig. 1 are obtained from Eq. (18) by making the replacements

$$\begin{aligned} \frac{g^2_Z}{m^2_Z} \rightarrow \frac{g^2}{2m^2_W},\quad X_e \rightarrow \frac{1}{2},\quad Y_e \rightarrow -\frac{1}{2}. \end{aligned}$$
(22)

From Eq. (17),

$$\begin{aligned} T_{fT}= & {} \frac{eg^2}{2m^2_W}A^\prime _f \times \left\{ \begin{array}{ll} 1 + X_e &{} (\nu _e)\\ X_e &{} (\nu _{\mu ,\tau }) \end{array}\right. \nonumber \\ T_{fL}= & {} \frac{eg^2}{m^2_W}B_f \times \left\{ \begin{array}{ll} 1 + X_e &{} (\nu _e)\\ X_e &{} (\nu _{\mu ,\tau }) \end{array}\right. \nonumber \\ T_{fP}= & {} \frac{eg^2}{m^2_W}C_f \times \left\{ \begin{array}{ll} 1 - Y_e &{} (\nu _e) \\ -Y_e &{} (\nu _{\mu ,\tau }) \end{array}\right. \end{aligned}$$
(23)

2.3 Static limit

As we have mentioned, the results for the electromagnetic vertex function will be used as the starting point to determine the self-energy and dispersion relation in an external field, which involves evaluating the vertex function in static limit. It is appropriate to state precisely what we mean by this limit, specially in the context of our calculation that includes the effects of the stream background and possibly a non-homogeneous external field.

Let us look first at the case considered in Ref. [29], namely the normal electron background contribution to the neutrino index of refraction in the presence of an external constant B field, that is a field that is constant in time and homogeneous in space. This requires the evaluation of the normal background contribution to the vertex function in the zero momentum limit, which operationally is implemented by first setting

$$\begin{aligned} {\varOmega }_e = 0, \end{aligned}$$
(24)

maintaining \(Q_e\) fixed, and then taking the limit

$$\begin{aligned} Q_e \rightarrow 0. \end{aligned}$$
(25)

We indicate this two-step process by the notation

$$\begin{aligned} ({\varOmega }_e = 0, Q_e \rightarrow 0). \end{aligned}$$
(26)

The idealization involved here is that the \(\nu \nu \) transition amplitude is being calculated over a region that is microscopically large, but macroscopically sufficiently small such that the external field is constant over the region. In this situation, the terms in the \(\nu \nu \) transition amplitude that contain factors of q multiplying the external field do not contribute.

In the present work we consider the possibility that the external field is not necessarily homogeneous. This is taken into account by interpreting each factor of \(q_\mu \) multiplying the external field in the \(\nu \nu \) amplitude as a derivative

$$\begin{aligned} q_\mu \rightarrow i\partial _\mu , \end{aligned}$$
(27)

acting on the external field.

In addition, in the presence of the stream, the limit \(Q_e\rightarrow 0\) is complicated by the fact that the stream contributions to the neutrino electromagnetic vertex function depend on the variables

$$\begin{aligned} {\varOmega }_{e^\prime }\equiv & {} q\cdot u_{e^\prime } = {\varOmega }_e u^0_{e^\prime } - \mathbf {Q}_e\cdot \mathbf {u}_{e^\prime },\nonumber \\ Q_{e^\prime }\equiv & {} \sqrt{{\varOmega }^2_{e^\prime } - q^2} , \end{aligned}$$
(28)

where \({\varOmega }_{e^{\prime }}\) represents the energy of the photon in the rest frame of the stream background while \(Q_{e^\prime }\) is the magnitude of the 3-momentum vector in that frame. For \({\varOmega }_e = 0\), they are given by

$$\begin{aligned} {\varOmega }^0_{e^\prime }= & {} - \mathbf {Q}_e\cdot \mathbf {u}_{e^\prime }, \nonumber \\ Q^0_{e^\prime }= & {} \sqrt{\left( \mathbf {u}_{e^\prime }\cdot \mathbf {Q}_e\right) ^2 + Q^2_e}. \end{aligned}$$
(29)

Therefore, there is a separate dependence on \(\mathbf {u}_{e^\prime }\cdot \mathbf {Q}_e\), and not just on the magnitude \(Q_e\), and as a consequence the process of taking the zero momentum limit \(Q_e \rightarrow 0\) is not unique.

For our purposes (calculating the self-energy in the presence of an external field), we take the zero momentum limit in this case in the following manner. First, after setting \({\varOmega }_e = 0\), make an expansion of the stream contribution to the vertex function in powers of \(\mathbf {u}_{e^\prime }\cdot \mathbf {Q}_e\), and then in harmony with the treatment of the terms with \(q_\mu \) specified above in Eq. (27), interpret each such factor as a derivative

$$\begin{aligned} \mathbf {u}_{e^\prime }\cdot \mathbf {Q}_e \rightarrow \frac{1}{i}\mathbf {u}_{e^\prime }\cdot \mathbf {\nabla }, \end{aligned}$$
(30)

acting on the external field. Since the remaining factors then depend only on \(Q_e\) after making this replacement, the \(Q_e \rightarrow 0\) limit can be taken subsequently in an unambiguous way. In particular, the stream contribution form factors, which are functions of \({\varOmega }_{e^\prime }\) and \(Q_{e^\prime }\), are evaluated in this limit according to a rule analogous to Eq. (26), that is

$$\begin{aligned} ({\varOmega }_{e^\prime } = 0, Q_{e^\prime } \rightarrow 0). \end{aligned}$$
(31)

In this work we retain the terms that are at most linear in the derivatives acting on the external magnetic field after making the identifications made in Eqs. (27) and (30). In the idealized situation that the external field is strictly homogeneous all such terms vanish.

For easy reference we quote here the following formulas that are given in Eqs. (2.27–2.29) and (3.2) of Ref. [29],

$$\begin{aligned} A_f(0,Q_{f} \rightarrow 0)= & {} A^0_f + O\left( Q^2_{f}\right) ,\nonumber \\ B_f(0,Q_{f} \rightarrow 0)= & {} A^0_f + O\left( Q^2_f\right) ,\nonumber \\ C_f(0,Q_{f} \rightarrow 0)= & {} C^0_f + O\left( Q^2_f\right) , \end{aligned}$$
(32)

where

$$\begin{aligned} A^0_f= & {} \frac{1}{2}\int \frac{d^3P}{(2\pi )^3} \frac{\partial }{\partial {\mathscr {E}}}\left[ f_f({\mathscr {E}}) + f_{{\bar{f}}}({\mathscr {E}})\right] , \nonumber \\ C^0_f= & {} \frac{1}{4}\int \frac{d^3P}{(2\pi )^3}\frac{1}{{\mathscr {E}}} \frac{\partial }{\partial {\mathscr {E}}}\left[ f_f({\mathscr {E}}) - f_{{\bar{f}}}({\mathscr {E}})\right] . \end{aligned}$$
(33)

In particular, \(A_f(0,Q_f)\) and \(B_f(0,Q_f)\) are equal at \(Q_f = 0\), which implies that \(A^\prime _f(0,Q_f)\) and \(T_{fT}(0,Q_f)\) are zero at \(Q_f = 0\). The derivation of the above formulas is sketched in Appendix A, and in Appendix B we derive the formula for the static limit value of \(A^\prime _f\), including the \(O(Q^2_f)\) term,

$$\begin{aligned} A^{\prime }_f(0, Q_f\rightarrow 0) = Q^2_f A^{\prime \,0}_f + O\left( Q^4_f\right) , \end{aligned}$$
(34)

where

$$\begin{aligned} A^{\prime \,0}_f = -\frac{1}{6} \int \frac{d^3P}{(2\pi )^3}\frac{1}{{\mathscr {E}}} \frac{\partial }{\partial {\mathscr {E}}} \left[ \frac{f_f({\mathscr {E}}) + f_{{\bar{f}}}({\mathscr {E}})}{{\mathscr {E}}}\right] , \end{aligned}$$
(35)

which will be relevant in the discussion in Sect. 3.

The integrals defined in Eqs. (33) and (35) can be performed straightforwardly once the distribution functions are specified. For guidance and reference purposes we give below the results of their evaluation in the particular case that the distribution functions can be taken to be those of the classical ideal gas. Using the fact that in that the classical distribution function satisfies

$$\begin{aligned} \frac{\partial f}{\partial {\mathscr {E}}} = -\beta f, \end{aligned}$$
(36)

(independently of whether the gas is relativistic or not), it follows simply that

$$\begin{aligned} A^0_f = -\frac{\beta _f}{4}(n_f + n_{{\bar{f}}}). \end{aligned}$$
(37)

In the case of \(C^0\) and \(A^{\prime \,0}\) the results in the relativistic and non-relativistic cases are different. In the non-relativistic limit (\(\beta _f m \gg 1\))

$$\begin{aligned} C^0_f= & {} -\frac{\beta _f}{8m}\left( n_f - n_{{\bar{f}}}\right) ,\nonumber \\ A^{\prime \,0}= & {} \frac{\beta _f}{12m^2}\left( n_f + n_{{\bar{f}}}\right) , \end{aligned}$$
(38)

while in the extremely relativistic limit (\(\beta _f m \ll 1\))

$$\begin{aligned} C^0_f= & {} -\left( \frac{\beta _f}{4}\right) ^2 \left( n_f - n_{{\bar{f}}}\right) , \nonumber \\ A^{\prime \,0}_f= & {} \frac{\beta ^3_f}{48}\sqrt{\frac{2\pi }{\beta _f m}} (n_f + n_{{\bar{f}}}). \end{aligned}$$
(39)

The derivation of Eqs. (38) and (39) is sketched in Appendix C.

3 Neutrino self-energy in a static magnetic field

3.1 General form

The chirality of the neutrino interactions implies that the background contribution to the neutrino self-energy, \({\varSigma }_{\mathrm{eff}}\), is of the form

$$\begin{aligned} {\varSigma }_{\mathrm{eff}} = R{\varSigma }L, \end{aligned}$$
(40)

and we will decompose \({\varSigma }\) in the form

$$\begin{aligned} {\varSigma }= {\varSigma }^{(m)} + {\varSigma }^{(B)}, \end{aligned}$$
(41)

where \({\varSigma }^{(B)}\) stands for part that depends on B and \({\varSigma }^{(m)}\) for the B-independent part. The neutrino dispersion relation is obtained by solving the equation

(42)

As is well known, in the two-stream electron background \({\varSigma }^{(m)}\) is of the form

(43)

where, to order \(1/m^2_W\),

$$\begin{aligned} b_f = \frac{g^2}{4m^2_W}(n_f - n_{{\bar{f}}})\times \left\{ \begin{array}{ll} 1 + X_e &{}\quad (\nu _e)\\ X_e &{}\quad (\nu _{\mu ,\tau }) \end{array}\right. \end{aligned}$$
(44)

The coefficients \(a_f\) are \(O(1/m^4_W)\) and therefore we will discard them.

The issue that we address now is the enumeration of the possible terms that can appear in \({\varSigma }^{(B)}\) for the two-stream background with the external electromagnetic field. The situation we consider is that in the rest frame of the normal background there is a magnetic field \(\mathbf {B} = B{\hat{b}}\), and in that frame we define

$$\begin{aligned} B^\mu = B b^\mu , \quad b^\mu = (0, {\hat{b}}). \end{aligned}$$
(45)

We can then write the corresponding EM tensor in the form

$$\begin{aligned} F_{\mu \nu } = \varepsilon _{\mu \nu \alpha \beta } u^\alpha B^\beta , \end{aligned}$$
(46)

and its dual, as usual, is given by

$$\begin{aligned} {\tilde{F}}_{\mu \nu }= & {} \frac{1}{2}\varepsilon _{\mu \nu \alpha \beta }F^{\alpha \beta } \nonumber \\= & {} B_\mu u_\nu - u_\mu B_\nu . \end{aligned}$$
(47)

In the enumeration of the possible terms that may appear in the result of the 1-loop calculation of \({\varSigma }^{(B)}\), we must remember the following working conditions:

  1. 1.

    restrict ourselves to the terms that are most linear in the derivatives of the field;

  2. 2.

    omit the terms that depend on the neutrino momentum k since they would be of \(O(1/m^4_W)\) that we are not considering;

  3. 3.

    in the 1-loop calculation each background contributes independently, so that terms involving the products of vectors \(u^\mu _f\) corresponding to different backgrounds do not appear.

The following is then the list of the terms that can appear:

  1. (a)

    Terms with no derivatives of the electromagnetic field: \(F^{\mu \nu } u_{f\nu }\gamma _\mu \)

  2. (b)

    Terms with one derivative of the electromagnetic field:

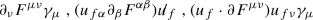
  3. (c)

    Terms similar to those in (a) and (b), with \(F_{\mu \nu }\rightarrow {\tilde{F}}_{\mu \nu }\)

Thus, under these conditions the most general form of \({\varSigma }^{(B)}\) is

$$\begin{aligned} {\varSigma }^{(B)}= & {} \sum _f\left[ c_f {\tilde{F}}^{\mu \nu } u_{f\nu } + d_f F^{\mu \nu } u_{f\nu } + h_{f1} \partial _\nu F^{\mu \nu } \right. \nonumber \\&\left. +\, {\tilde{h}}_{f1} \partial _\nu {\tilde{F}}^{\mu \nu } + h_{f2} \left( u_{f\alpha }\partial _\beta F^{\alpha \beta }\right) u^\mu _f \right. \nonumber \\&\left. +\, {\tilde{h}}_{f2} \left( u_{f\alpha } \partial _\beta {\tilde{F}}^{\alpha \beta }\right) u^\mu _f + h_{f3}\left( u_f\cdot \partial F^{\mu \nu }\right) u_{f\nu } \right. \nonumber \\&\left. +\, {\tilde{h}}_{f3}\left( u_f\cdot \partial {\tilde{F}}^{\mu \nu }\right) u_{f\nu }\right] \gamma _\mu . \end{aligned}$$
(48)

The coefficients defined here will be determined by calculating the \(\nu \nu \) transition amplitude in the presence of an external electromagnetic field, using the 1-loop formulas for the vertex function given in Sect. 2.

3.2 \(\nu \nu \) transition amplitude in an external electromagnetic field

We are now set to consider the \(\nu \nu \) transition amplitude in the presence of an external electromagnetic field. The external electromagnetic potential is represented by

$$\begin{aligned} A_\mu (x) = \int \frac{d^4q^\prime }{(2\pi )^4}a_\mu (q^\prime ) e^{-iq^\prime \cdot x} , \end{aligned}$$
(49)

and the corresponding field by

$$\begin{aligned} F_{\mu \nu }(x) = \int \frac{d^4q^\prime }{(2\pi )^4}f_{\mu \nu }(q^\prime ) e^{-iq^\prime \cdot x} , \end{aligned}$$
(50)

where

$$\begin{aligned} f_{\mu \nu }(q^\prime ) = -i\left( q^\prime _\mu a_\nu (q^\prime ) - q^\prime _\nu a_\mu (q^\prime )\right) . \end{aligned}$$
(51)

The diagram for the process is shown in Fig. 2. As shown schematically in that figure, it includes the photon polarization tensor in order to take into account the screening effects of the background electrons.

Fig. 2
figure 2

Schematic diagrams for the effective neutrino electromagnetic vertex taking into account the polarization effects of the background electrons as expressed in Eq. (52)

Full size image

The off-shell \(\nu -\nu \) scattering amplitude in the presence the external electromagnetic potential is then given by

$$\begin{aligned} S_{\nu \nu } = -i{\varGamma }_{\lambda }(k,k^\prime ) D^{\lambda \mu }(k^\prime - k) a_\mu (k^\prime - k), \end{aligned}$$
(52)

where \({\varGamma }_{\mu }\) is the total neutrino electromagnetic vertex function given in Eq. (9) and omitting the indices, the diagrams in Fig. 2 indicate that \(D = (1 + {{\varDelta }}_0\pi + \cdots ) = {{\varDelta }}_{eff}{{\varDelta }}^{-1}_0\), where \({{\varDelta }}^{\mu \nu }_0 = \frac{-g^{\mu \nu }}{q^2}\) is the free photon propagator and \({{\varDelta }}^{\mu \nu }_{eff}\) is the effective photon propagator in the medium determined from Eq. (54)

$$\begin{aligned} D^{\mu \nu }(q) = -q^2 {\varDelta }^{\mu \nu }_{eff}(q), \end{aligned}$$
(53)

with \({\varDelta }^{\mu \nu }_{eff}(q)\) being the photon propagator in the medium. The latter quantity is determined by solving

$$\begin{aligned} \left( q^2 {\tilde{g}}^{\mu \lambda } - \pi ^{\mu \lambda }\right) {\varDelta }_{eff\,\lambda \nu } = -{\tilde{g}}^\mu _\nu , \end{aligned}$$
(54)

where \(\pi _{\mu \nu }\) is the two-background contribution to the photon polarization tensor. Denoting by \(\pi _{e\mu \nu }\) and \(\pi _{e^\prime \mu \nu }\) the contributions due to the normal and stream backgrounds, respectively, then

$$\begin{aligned} \pi _{\mu \nu } = \pi _{e\mu \nu } + \pi _{e^\prime \mu \nu }. \end{aligned}$$
(55)

Each term in the previous relation can be decomposed according to

$$\begin{aligned} \pi _{f\mu \nu } = \pi _{fT} R_{f\mu \nu } + \pi _{fL} Q_{f\mu \nu }, \end{aligned}$$
(56)

where the photon self-energy functions \(\pi _{fT,L}\) are given by

$$\begin{aligned} \pi _{fT}= & {} -2e^2\left[ A_f - \frac{B_f}{{\tilde{u}}^2_f}\right] \nonumber \\= & {} -2e^2\left[ A_f + \frac{q^2}{Q^2_f} B_f\right] ,\nonumber \\ \pi _{fL}= & {} -4e^2\frac{B_f}{{\tilde{u}}^2_f},\nonumber \\= & {} 4e^2\frac{q^2}{Q^2_f} B_f, \end{aligned}$$
(57)

with \(A_{f}, B_{f}\) being the integrals defined in Eq. (19) (Omitting the subscript \(f = e,e^\prime \), the longitudinal and transverse components of the dielectric constants in each background medium is are given by \(\varepsilon _{\ell } = 1 - \frac{\pi _{L}}{q^2}\) and \(\varepsilon _{t} = 1 - \frac{\pi _{T}}{{\varOmega } ^2}\) respectively)

Let us look at the case considered in Ref. [29], an external magnetic field and only the normal background. In this case

$$\begin{aligned} {\varDelta }^{\mu \nu }_{eff} = \frac{-R^{\mu \nu }_e}{q^2 - \pi _{eT}} + \frac{-Q^{\mu \nu }_e}{q^2 - \pi _{eL}}, \end{aligned}$$
(58)

and

$$\begin{aligned} Q_{e\mu \nu } a^\mu (q) = 0. \end{aligned}$$
(59)

Equation (59) follows from the fact that for a pure magnetic field \({\tilde{u}}\cdot a = 0\), which can be seen in various ways. For example, with the usual convention in which \(A^\mu = (0,\mathbf {A})\) with \(\nabla \cdot \mathbf {A} = 0\), it follows that \(u\cdot a = 0\) and \(q\cdot a = 0\), and therefore \({\tilde{u}}\cdot a = 0\). More generally, \({\tilde{u}}\cdot a = \frac{i}{q^2} q_\mu u_\nu f^{\mu \nu }\), while \(u_\nu f^{\mu \nu } = 0\) when \(f_{\mu \nu }\) corresponds to a magnetic field. Thus, remembering that \(\pi _{eT}\rightarrow 0\) (and \(T_{eT}\rightarrow 0\)) in the static limit, Eqs. (58) and (59) imply that \(D^{\lambda \mu }a_\mu \rightarrow a^\lambda \) in the static limit, and therefore the screening corrections are not relevant in that case.

With the stream contributions the situation is different. The stream electrons, in their own rest frame, “see” an electric field in addition to the magnetic field, and the screening corrections are relevant in that case. The present situation is complicated by the fact that in the presence of the two backgrounds the inversion required in Eq. (54) is not as simple in the general case as the one leading to the one-background result given in Eq. (58).

We overcome this difficulty here as follows. In the limit \(\mathbf {u}_{e^\prime } \rightarrow 0\), each of the tensors \(R_{e^\prime },Q_{e^\prime },P_{e^\prime }\) coincides with its corresponding counterpart \(R_{e},Q_{e},P_{e}\). It is straightforward to show that, in general, the corresponding primed and unprimed tensors differ by terms \(\sim (\mathbf {u}_{e^\prime }\cdot \mathbf {Q}_e)^2\), e.g.,

$$\begin{aligned} R_{e^\prime \mu \nu } = R_{e\mu \nu } + O\left( (\mathbf {u}_{e^\prime }\cdot \mathbf {Q}_e)^2\right) , \end{aligned}$$
(60)

with analogous relations for \(Q_{e^\prime \mu \nu }\) and \(P_{e^\prime \mu \nu }\). Since, as stated in Sect. 1, in this work we will retain only up to the linear terms \(\mathbf {u}_{e^\prime }\cdot \mathbf {Q}_e\) in the calculation of the self-energy, we then can then write

$$\begin{aligned} {\varGamma }_{\lambda }(k,k^\prime ){\varDelta }^{\lambda }_{eff\mu }(q)= & {} T_{e\lambda \nu }\gamma ^\nu L\left[ \frac{-R^\lambda _{e\mu }}{q^2 - \pi _T} + \frac{-Q^\lambda _{e\mu }}{q^2 - \pi _L}\right] \nonumber \\&+ T_{e^\prime \lambda \nu }\gamma ^\nu L\left[ \frac{-R^\lambda _{e^\prime \mu }}{q^2 - \pi _T} + \frac{-Q^\lambda _{e^\prime \mu }}{q^2 - \pi _L}\right] ,\nonumber \\ \end{aligned}$$
(61)

where

$$\begin{aligned} \pi _T= & {} \pi _{eT} + \pi _{e^\prime T},\nonumber \\ \pi _L= & {} \pi _{eL} + \pi _{e^\prime L}. \end{aligned}$$
(62)

We reiterate that Eq. (61) is valid assuming that we are dropping the terms proportional to \((\mathbf {u}_{e^\prime }\cdot \mathbf {Q}_e)^2\) and higher powers, which translate to terms containing second and higher derivatives of the external field, by making the identification shown in Eq. (30). Using Eq. (12) and the multiplication rules of the tensors R, Q, P, then

$$\begin{aligned} {\varGamma }_{\lambda }(k,k^\prime ) {D^{\lambda }}_{\mu }(q) = {\varGamma }^{(eff)}_{e\mu }(k,k^\prime ) + {\varGamma }^{(eff)}_{e^\prime \mu }(k,k^\prime ), \end{aligned}$$
(63)

where

$$\begin{aligned} {\varGamma }^{(eff)}_{f\mu }(k,k^\prime ) {=} \left[ {\tilde{T}}_{fT}R_{f\mu \nu } {+} {\tilde{T}}_{fL}Q_{f\mu \nu } {-} {\tilde{T}}_{fP}P_{f\mu \nu } \right] \gamma ^\nu L ,\nonumber \\ \end{aligned}$$
(64)

with

$$\begin{aligned} {\tilde{T}}_{fT,P}= & {} \frac{q^2 T_{fT,P}}{q^2 - \pi _{T}},\nonumber \\ {\tilde{T}}_{fL}= & {} \frac{q^2 T_{fL}}{q^2 - \pi _{L}}. \end{aligned}$$
(65)

Using Eqs. (52) and (63), the \(\nu \nu \) amplitude is then given by

$$\begin{aligned} S_{\nu \nu } = -i\left( {\varGamma }^{(eff)}_{e\mu }(k,k^\prime ) + {\varGamma }^{(eff)}_{e^\prime \mu }(k,k^\prime )\right) a^\mu (k^\prime - k). \end{aligned}$$
(66)

An equivalent expression for the functions \({\varGamma }^{(eff)}_{f\mu }\), which is more convenient for the purpose of the interpretation of the form factors and for taking the static limit, is [29]

(67)

where, using the formulas given in Eq. (13) for the tensors \(R_{f\mu \nu }, Q_{f\mu \nu }, P_{f\mu \nu }\),

$$\begin{aligned} F_{f1}= & {} {\tilde{T}}_{fT} + \frac{{\varOmega }^2_f}{Q^2_f}\left( {\tilde{T}}_{fL} - {\tilde{T}}_{fT}\right) ,\nonumber \\ F_{f2}= & {} \frac{1}{{\tilde{u}}^2_f} \left( {\tilde{T}}_{fL} - {\tilde{T}}_{fT}\right) ,\nonumber \\ iF_{f3}= & {} -\frac{{\varOmega }_f}{Q^2_f} \left( {\tilde{T}}_{fL} - {\tilde{T}}_{fT}\right) ,\nonumber \\ F_{f4}= & {} \frac{{\tilde{T}}_{fP}}{Q_f} . \end{aligned}$$
(68)

It follows from Eq. (67) that

$$\begin{aligned} {\varGamma }^{(eff)}_{f\mu }(k,k^\prime ) a^\mu (k^\prime - k) = M_{f\mu \nu }f^{\mu \nu }(k^\prime - k), \end{aligned}$$
(69)

where \(f^{\mu \nu }\) is defined in Eq. (51) and the \(M_{f\mu \nu }\) are given by

(70)

and from Eq. (66)

$$\begin{aligned} S_{\nu \nu } = -i \left( M_{e\mu \nu } + M_{e^\prime \mu \nu }\right) f^{\mu \nu }(k^\prime - k). \end{aligned}$$
(71)

Equation (71) is a useful starting point to determine the contribution to the neutrino self-energy in a static field, including the case of an inhomogeneous field, which we consider next.

3.3 Self-energy

We now consider the \(\nu \nu \) transition amplitude for the case of a static magnetic field \(F_{\mu \nu }\). As stated in Sect. 2.3, we make the idealization that we are calculating it over a region that is microscopically large but macroscopically sufficiently small such that the external field and its space derivatives are constant over that region. In addition we retain only the terms that are most linear in the derivatives. Operationally this means that in Eq. (71) we can take

$$\begin{aligned} f_{\mu \nu }(k^\prime - k)= & {} (2\pi )^4 \delta ^{(4)}(k^\prime - k) F_{\mu \nu } ,\nonumber \\ q_\lambda f_{\mu \nu }(k^\prime - k)= & {} (2\pi )^4 \delta ^{(4)}(k^\prime - k) i\partial _\lambda F_{\mu \nu }, \end{aligned}$$
(72)

while neglecting the terms with higher powers of q, which would translate to terms with higher order derivatives of the external field.

To state our working assumptions more precisely let us denote by \({\varDelta }x\) the distance over which the magnetic field B changes appreciably. Since the variation of B over a given distance \(\delta x\) is \( \delta B = \left( \frac{\partial B}{\partial x}\right) \delta x, \) and \({\varDelta }x\) is determined by the condition that \( \delta B \sim B, \) we have

$$\begin{aligned} {\varDelta }x \sim \frac{B}{\left( \frac{\partial B}{\partial x}\right) }. \end{aligned}$$

In the calculations, as in every QFT calculation, we idealize a region (of linear size L) that is microscopically large (\(L \gg \lambda \)) compared to the neutrino Compton wavelength \(\lambda = \frac{1}{k}\), such that it is valid to take the usual \(L \rightarrow \infty \) limit (or \(\lambda /L \rightarrow 0\)). If \(\lambda \) is sufficiently small such that \( \lambda \ll L \ll {\varDelta }x \) can be satisfied, then the field B can be taken as constant over the region and in such cases the first formula given in Eq. (72) is strictly valid, which is the usual homogeneous field case. In the present paper we assume that L is not necessarily much smaller than \({\varDelta }x\), in which case we cannot take the field as being constant over the region L. What we assume by adopting the formulas in Eq. (72) is that the field variations can be treated perturbatively, so that we can keep only the leading term in a Taylor series expansion in each formula. In cases in which the inhomogeneities of the background medium are important on a level comparable to the homogeneous background, this assumption would not hold and Eq. (72) is not valid. Our calculations and treatment hold under the assumption that the inhomogeneities are small and whence can be taken into account by a perturbative treatment, in the sense just indicated.

Under the conditions we have stated, Eq. (71) then becomes

$$\begin{aligned} S_{\nu \nu } = -i (2\pi )^4 \delta ^{(4)}(k - k^\prime ) \left( M^{(static)}_{e\mu \nu } + M^{(static)}_{e^\prime \mu \nu }\right) F^{\mu \nu },\nonumber \\ \end{aligned}$$
(73)

where \(M^{(static)}_{f\mu \nu }\) is obtained from Eq. (70) by keeping the terms that are at most linear in \((\mathbf {u}_{e^\prime }\cdot \mathbf {Q}_e)\) and/or q and following the procedure outlined in Sect. 2.3: make the identification stated in Eqs. (27) and (30), and then take the \(q\rightarrow 0\) limit in the remaining terms as indicated in Eqs. (26) and (31). The B-dependent part of the self-energy, \({\varSigma }^{(B)}\), which is identified by writing

$$\begin{aligned} S_{\nu \nu } = -i (2\pi )^4 \delta ^{(4)}(k - k^\prime ){\varSigma }^{(B)}L, \end{aligned}$$
(74)

is then given by

$$\begin{aligned} {\varSigma }^{(B)} = {\varSigma }^{(B)}_e + {\varSigma }^{(B)}_{e^\prime }, \end{aligned}$$
(75)

where

$$\begin{aligned} {\varSigma }^{(B)}_{f} = M^{(static)}_{f\mu \nu }F^{\mu \nu }. \end{aligned}$$
(76)

Calculating \(M^{(static)}_{f\mu \nu }\) as we have indicated,

$$\begin{aligned} {\varSigma }^{(B)}_{f}= & {} \left[ t_{fT}\partial _\nu F^{\mu \nu } + t_{fL} (u_{f\alpha } \partial _\beta F^{\alpha \beta })u^\mu _{f} \right. \nonumber \\&\left. - t_{fL}(u_f\cdot \partial \, F^{\mu \nu }) u_{f\nu } + t_{fP} {\tilde{F}}^{\mu \nu }u_{f\nu }\right] \gamma _\mu L , \end{aligned}$$
(77)

where the coefficients \(t_{fT,L,P}\) are defined by

$$\begin{aligned} t_{fT}= & {} \left. \frac{T_{fT}(0,Q)}{Q^2}\right| _{Q\rightarrow 0} ,\nonumber \\ t_{fL}= & {} \left. \frac{T_{fL}(0,Q)}{\pi _{eL}(0,Q) + \pi _{e^\prime L}(0,Q)}\right| _{Q\rightarrow 0} ,\nonumber \\ t_{fP}= & {} \left. \frac{T_{fP}(0,Q)}{Q}\right| _{Q\rightarrow 0}. \end{aligned}$$
(78)

Using Eqs. (18), (32), (34) and (57) we obtain the following explicit formulas,

$$\begin{aligned} t_{fT}= & {} \frac{eg^2}{2m^2_W}A^{\prime \,0}_f \times \left\{ \begin{array}{ll} 1 + X_e &{} (\nu _e) \\ X_e &{} (\nu _{\mu ,\tau }) \end{array}\right. \nonumber \\ t_{fL}= & {} \frac{-g^2}{4e m^2_W}\left( \frac{A^0_f}{A^0_e + A^0_{e^\prime }} \right) \times \left\{ \begin{array}{ll} 1 + X_e &{} (\nu _e)\\ X_e &{} (\nu _{\mu ,\tau }) \end{array}\right. \nonumber \\ t_{fP}= & {} \frac{eg^2}{m^2_W}C^0_f \times \left\{ \begin{array}{ll} 1 - Y_e &{} (\nu _e)\\ -Y_e &{} (\nu _{\mu ,\tau }) \end{array}\right. \end{aligned}$$
(79)

where \(A^0_f, C^0_f, A^{\prime \,0}_f\) are the integrals defined in Eqs. (33) and (35).

Equations (77) and (79) summarize the result of our calculation of the contribution to the neutrino self-energy due to its interaction with an external electromagnetic field that is not necessarily homogeneous. The result given in Eq. (77) corresponds to the general form given in Eq. (48), with the coefficients given specifically by

$$\begin{aligned} c_f= & {} t_{fP},\nonumber \\ h_{f1}= & {} t_{fT},\nonumber \\ h_{f2}= & {} t_{fL},\nonumber \\ h_{f3}= & {} -t_{fL},\nonumber \\ d_f= & {} {\tilde{h}}_{f1} = {\tilde{h}}_{f2} = {\tilde{h}}_{f3} = 0. \end{aligned}$$
(80)

4 Dispersion relations

For the purpose of determining the dispersion relation, it is convenient to express the total self-energy, Eq. (41), in the form

(81)

with

$$\begin{aligned} V^\mu = \sum _f V^\mu _f. \end{aligned}$$
(82)

The formula for the \(V^\mu _f\) follows from Eqs. (43) and (48), which we summarize in the form

$$\begin{aligned} V^\mu _f = V^{(h)\mu }_f + V^{(i)\mu }_f, \end{aligned}$$
(83)

where

$$\begin{aligned} V^{(h)\mu }_f= & {} b_f u^\mu _f + c_f {\tilde{F}}^{\mu \nu } u_{f\nu },\nonumber \\ V^{(i)\mu }_f= & {} h_{f1} \partial _\nu F^{\mu \nu } + h_{f2} \left( u_{f\alpha }\partial _\beta F^{\alpha \beta }\right) u^\mu _f \nonumber \\&+\,h_{f3}\left( u_f\cdot \partial F^{\mu \nu }\right) u_{f\nu }. \end{aligned}$$
(84)

\(V^{(i)\mu }_f\) is non-zero only if the field is inhomogeneous. In writing Eq. (84) we have dropped the terms that vanish according to the results we have obtained in Eq. (80). We can express \(V^{(i,h)\mu }_f\) more explicitly as,

$$\begin{aligned} V^{(h)}_{f\mu }= & {} b_f u_{f\mu } + c_f\left[ (u_f\cdot u)B_\mu - (u_{f}\cdot B) u_\mu \right] ,\nonumber \\ V^{(i)\mu }_f= & {} -h_{f1}m^\mu - h_{f2}(u_f\cdot m)u^\mu _f \nonumber \\&- h_{f3}\varepsilon ^{\mu \nu \alpha \beta } u_{f\nu } u_\alpha n_{f\beta }. \end{aligned}$$
(85)

In the expression for \(V^{(h)}_{f\mu }\) we have used Eq. (47), and for \(V^{(i)}_{f\mu }\) we have introduced the vectors

$$\begin{aligned} m^\mu= & {} \partial _\lambda F^{\lambda \mu },\nonumber \\ n^\mu _{f}= & {} -(u_f\cdot \partial )B^\mu , \end{aligned}$$
(86)

which in the rest frame of the matter background have components

$$\begin{aligned} m^\mu= & {} (0, \mathbf {m}) ,\nonumber \\ n^{\mu }_f= & {} (0, \mathbf {n}_f) , \end{aligned}$$
(87)

where

$$\begin{aligned} \mathbf {m}= & {} \nabla \times \mathbf {B},\nonumber \\ \mathbf {n}_f= & {} (\mathbf {u}_f\cdot \nabla )\mathbf {B}. \end{aligned}$$
(88)

The equation for the propagating modes, Eq. (42), implies that the dispersion relations are given by

$$\begin{aligned} k^0 - V^0 = \pm \left| \mathbf {k} - \mathbf {V}\right| . \end{aligned}$$
(89)

Thus to the lowest order in \(1/m^2_W\) considered in this work, which among other things implies that \(V^\mu \) does not depend on k, and the solutions are \(k^0 = \omega _{\pm }(\mathbf {k})\), where

$$\begin{aligned} \omega _{\pm }(\mathbf {k}) = \pm \left[ |\mathbf {k}| - {\hat{k}}\cdot \mathbf {V}\right] + V^0. \end{aligned}$$
(90)

In Eq. (90) \({\hat{k}}\) denotes the unit vector along the direction of propagation. The neutrino and antineutrino dispersion relations, which are identified in the usual way as,

$$\begin{aligned} \omega _\nu= & {} \omega _{+}(\mathbf {k}),\nonumber \\ \omega _{{\bar{\nu }}}= & {} -\omega _{-}(-\mathbf {k}), \end{aligned}$$
(91)

are then given by

$$\begin{aligned} \omega _{\nu ,{\bar{\nu }}} = |\mathbf {k}| \pm \delta , \end{aligned}$$
(92)

where

$$\begin{aligned} \delta = \sum _f\left( V^0_f - {\hat{k}}\cdot \mathbf {V}_f\right) . \end{aligned}$$
(93)

According to the decomposition in Eq. (83), we can write

$$\begin{aligned} \delta = \sum _f\left( \delta ^{(h)}_f + \delta ^{(i)}_f\right) , \end{aligned}$$
(94)

with

$$\begin{aligned} \delta ^{(h,i)}_f = V^{(h,i)0}_f - {\hat{k}}\cdot \mathbf {V}^{(h,i)}_f , \end{aligned}$$
(95)

and from Eq. (85),

$$\begin{aligned} \delta ^{(h)}_f= & {} b_f u^0_f + c_f\mathbf {B}\cdot \mathbf {u}_f - b_f {\hat{k}}\cdot \mathbf {u}_f - c_f u^0_f {\hat{k}}\cdot B,\nonumber \\ \delta ^{(i)}_f= & {} h_{f1}({\hat{k}}\cdot \mathbf {m}) + h_{f2} u^0_f (\mathbf {u}_f\cdot \mathbf {m}) - h_{f2}(\mathbf {u}_f\cdot \mathbf {m})({\hat{k}}\cdot \mathbf {u}_f) \nonumber \\&+\,h_{f3}{\hat{k}}\cdot (\mathbf {u}_f\times \mathbf {n}_f). \end{aligned}$$
(96)

For the two-stream electron background specifically, using Eqs. (2)–(4) and (80),

$$\begin{aligned} \delta ^{(h)}_e= & {} b_e - c_e{\hat{k}}\cdot \mathbf {B},\nonumber \\ \delta ^{(h)}_{e^\prime }= & {} b_{e^\prime } v^0 + c_{e^\prime }\mathbf {v}\cdot \mathbf {B} - b_{e^\prime } {\hat{k}}\cdot \mathbf {v} - c_{e^\prime } v^0{\hat{k}}\cdot \mathbf {B}, \end{aligned}$$
(97)

and

$$\begin{aligned} \delta ^{(i)}_e= & {} t_{eT}({\hat{k}}\cdot \mathbf {m}),\nonumber \\ \delta ^{(i)}_{e^\prime }= & {} t_{e^\prime L} v^0 (\mathbf {v}\cdot \mathbf {m}) + t_{e^\prime T}({\hat{k}}\cdot \mathbf {m}) - t_{e^\prime L}(\mathbf {v}\cdot \mathbf {m})({\hat{k}}\cdot \mathbf {v})\nonumber \\&- t_{e^\prime L}{\hat{k}}\cdot (\mathbf {v}\times \mathbf {n}_{e^\prime }), \end{aligned}$$
(98)

where

$$\begin{aligned} \mathbf {n}_{e^\prime } = (\mathbf {v}\cdot \nabla )\mathbf {B}. \end{aligned}$$
(99)

In this case,

$$\begin{aligned} \delta = \delta ^{(h)}_e + \delta ^{(h)}_{e^\prime } + \delta ^{(i)}_e+ \delta ^{(i)}_{e^\prime }. \end{aligned}$$
(100)

Together with Eqs. (92), (94) and (96) provide a general and concise expression for the neutrino and antineutrino dispersion relations in the kind of situation that we are envisaging, and Eqs. (97), (98) and (100) in particular for the two-stream electron background we are specifically considering. In these formulas the stream velocity \(\mathbf {v}\) is left unspecified since we do not consider the possible physical origin of the stream background. However, the results can be used in specific applications in which the stream velocity is determined and/or restricted by the particular physical conditions of the problem. For example, if the stream velocity is due to the drift of electrons in the B field, since the Lorentz force makes charged particles drift only along the \(\mathbf {B}\) axis but not in the perpendicular plane, the results can be applied to that case as well by taking \(\mathbf {v}\) to be on the \(\mathbf {B}\) axis. But as we have just stated, we do not assume anything in particular about the origin of the streams or what determines their velocities, and the results hole for more general cases as well in which the stream velocity need not be along the magnetic field.

It is useful to consider some special situations that illustrate particular features of the general results.

4.1 Homogeneous external field

It is simple to verify that the results obtained in [28] are reproduced as a special case. Thus, if the external field is homogeneous,

$$\begin{aligned} \delta = \delta ^{(h)}_e + \delta ^{(h)}_{e^\prime }, \end{aligned}$$
(101)

which is the result obtained in [28]. In particular, in the absence of the stream background,

$$\begin{aligned} \delta = b_e - c_e {\hat{k}}\cdot \mathbf {B}, \end{aligned}$$
(102)

which leads by Eq. (92) to the result obtained in Ref. [29] for the dispersion relation in a magnetized electron background. The angular asymmetry of the dispersion relation in this case has been subject of much interest in the literature in connection to the problem of pulsar kick and related issues. The terms in Eq. (97) due to the stream background (in the same case of a homogeneous field) give an additional asymmetric contribution that depends on the direction of propagation relative to the stream background velocity.

4.2 Inhomogeneous magnetic field

4.2.1 \(\nabla \times \mathbf {B} = 0\)

In the case of a non-homogeneous field, the additional terms given by \(\delta ^{(i)}_{e^\prime }\) can be present. As an example, let us consider the case in which \(\nabla \times \mathbf {B} = 0\). In this case, only the term involving \(h_{e^\prime 3}\) in Eq. (98) survives and therefore, from Eq. (100),

$$\begin{aligned} \delta= & {} b_e + c_{e^\prime }\mathbf {B}\cdot \mathbf {v} + b_{e^\prime } v^0 - b_{e^\prime } {\hat{k}}\cdot \mathbf {v} \nonumber \\&- \left( c_e + c_{e^\prime } v^0\right) {\hat{k}}\cdot \mathbf {B} - t_{e^\prime L}{\hat{k}}\cdot \left( \mathbf {v}\times \mathbf {n}_{e^\prime }\right) , \end{aligned}$$
(103)

where \(\mathbf {n}_{e^\prime }\) has been defined in Eq. (99). In particular, in addition to the angular dependence involving the direction of propagation relative to \(\mathbf {B}\) and \(\mathbf {v}\), there is a dependence involving a third vector \(\mathbf {v}\times \mathbf {n}_{e^\prime }\).

4.2.2 \(\nabla \times \mathbf {B} \not = 0\)

On the other hand, if the conditions are such that \(t_{e^\prime L}\) terms in Eq. (100) are negligible, then

$$\begin{aligned} \delta= & {} b_e + c_{e^\prime }\mathbf {B}\cdot \mathbf {v} + b_{e^\prime } v^0 - b_{e^\prime } {\hat{k}}\cdot \mathbf {v} \nonumber \\&- \left( c_e + c_{e^\prime } v^0\right) {\hat{k}}\cdot \mathbf {B} + \left( t_{eT}+t_{e^\prime T}\right) ({\hat{k}}\cdot \mathbf {m}). \end{aligned}$$
(104)

Notice in particular that even in the absence of the stream, in which case

$$\begin{aligned} \delta = b_e - c_e {\hat{k}}\cdot \mathbf {B} + t_{eT}({\hat{k}}\cdot \mathbf {m}), \end{aligned}$$
(105)

there is an additional anisotropic term of the form \({\hat{k}}\cdot (\nabla \times \mathbf {B})\), besides the usual one proportional to \({\hat{k}}\cdot \mathbf {B}\).

4.3 Discussion

One point that stands out in these results is the following. To the order \(1/m^2_W\), the coefficients \(b_{e,e^\prime }, c_{e,e^\prime }\) are proportional to the electron-positron asymmetry in the corresponding backgrounds. Therefore in a CP-symmetric medium \(b_{e,e^\prime }\) and \(c_{e,e^\prime }\) vanish to the order \(1/m^2_W\), and in such cases the order \(1/m^4_W\) contributions to these parameters must be included. In contrast, to the order \(1/m^2_W\), the \(t_{eT}\) term in \(\delta ^{(i)}_e\), and similarly the \(t_{e^\prime L,T}\) terms in \(\delta ^{(i)}_{e^\prime }\), are proportional to the sum of the electron-positron number densities (in the normal and stream backgrounds respectively), and whence need not be zero even in a CP-symmetric medium. Thus, in a CP-symmetric medium (e.g., the Early Universe) the dominant contribution to the neutrino index of refraction could be due to the terms contained in \(\delta ^{(i)}_{e,e^\prime }\), which are of order \(1/m^2_W\).

To quantify somewhat these statements, recall that the \(O(1/m^4_W)\) contribution to \(b_e\) is [38]

$$\begin{aligned} b^{(4)}_e \sim \frac{g^2 |\mathbf {k}|T_e}{m^4_W} N_e, \end{aligned}$$
(106)

where

$$\begin{aligned} N_e = n_e + n_{{\bar{e}}}, \end{aligned}$$
(107)

and similarly for \(b^{(4)}_{e^\prime }\). Equation (106) holds for the case the electron gas can be adequately described by a classical distribution in the relativistic limit (\(T_e \gg m\)). For illustrative purposes the question we ask is under what conditions the term \(t_{e^\prime L}{\hat{k}}\cdot (\mathbf {v}\times \mathbf{n_{e^\prime }})\) could be as important, or more important, than the \(b^{(4)}_e\) term in the dispersion relation. Under the example idealized conditions that we have assumed for the purpose of this discussion (classical relativistic electron backgrounds), using Eqs. (37) and (79) the question translates to see for what parameters it is possible that

$$\begin{aligned} \frac{g^2}{em^2_W} \left( \frac{\beta _{e^\prime } N_{e^\prime }}{\beta _{e} N_{e} + \beta _{e^\prime } N_{e^\prime }}\right) |\nabla \mathbf {B}| \sim \frac{g^2 E_\nu T_e}{m^4_W}N_e , \end{aligned}$$
(108)

where we have put \(E_\nu \sim |\mathbf {k}|\). Taking the quantity in parenthesis to be O(1) and \(N_e \sim T^3_e\), the condition would be that

$$\begin{aligned} \frac{1}{e}|\nabla \mathbf {B}| \sim \frac{T^4_e E_\nu }{m^2_W} , \end{aligned}$$
(109)

which yields

$$\begin{aligned} \frac{1}{e}|\nabla \mathbf {B}| \sim 10^3 \left( \frac{T_e}{MeV}\right) ^4 \left( \frac{E_\nu }{MeV}\right) \frac{MeV^2}{meter}, \end{aligned}$$
(110)

or

$$\begin{aligned} |\nabla \mathbf {B}| \sim \left( \frac{T_e}{MeV}\right) ^4 \left( \frac{E_\nu }{MeV}\right) \frac{10^{15}G}{cm}. \end{aligned}$$
(111)

We can ask the same question for the term \(t_{e^\prime T}({\hat{k}}\cdot \mathbf {m})\). Using Eqs. (39) and (79), the condition that this term be of the same order as \(b^{(4)}_e\) would be

$$\begin{aligned} \frac{eg^2}{4m^2_W}\frac{\beta ^3_{e^\prime }}{48} \sqrt{\frac{2\pi }{\beta _{e^\prime } m}}N_{e^\prime }|\nabla \mathbf {B}| \sim \frac{g^2 E_\nu T_e}{m^4_W}N_e , \end{aligned}$$
(112)

or, taking again \(N_f \sim T^3_f\),

$$\begin{aligned} |\nabla \mathbf {B}| \sim \left( \frac{T_e}{MeV}\right) ^4 \left( \frac{T_{e^\prime }}{MeV}\right) ^{-1/2} \left( \frac{E_\nu }{MeV}\right) \frac{10^{17} G}{cm}. \end{aligned}$$
(113)

Similarly, the condition for the term \(t_{eT}({\hat{k}}\cdot \mathbf {m})\) to be comparable to \(b^{(4)}_e\) is given by this same relation, with the replacement \(T_{e^\prime }\rightarrow T_e\).

On the other hand, if the medium is electron-positron asymmetric, the effects of the inhomogeneous terms seem to be unimportant compared to the standard terms. As an specific example, let us compare the \(t_{e^\prime T}({\hat{k}}\cdot \mathbf {m})\) against the term \(c_e B\), which is also a source of an asymmetry in the dispersion relation. The condition that it be of the same order as \(c_e B\) is

$$\begin{aligned} \frac{eg^2}{4m^2_W}\frac{\beta ^3_{e^\prime }}{48} \sqrt{\frac{2\pi }{\beta _{e^\prime } m}}N_{e^\prime }|\nabla \mathbf {B}| \sim \frac{eg^2}{2m^2_W}\left( \frac{\beta _e}{4}\right) ^2{\varDelta }N_e B, \end{aligned}$$
(114)

or

$$\begin{aligned} \frac{|\nabla \mathbf {B}|}{B}\sim & {} \left( \frac{T_{e^\prime }}{T_e}\right) ^2 \sqrt{m T_{e^\prime }}\left( \frac{{\varDelta }N_{e}}{N_{e^\prime }}\right) \nonumber \\\sim & {} \left( \frac{T_{e^\prime }}{T_e}\right) ^2 \sqrt{\frac{T_{e^\prime }}{MeV}}\left( \frac{{\varDelta }N_{e}}{N_{e^\prime }}\right) 10^{11} cm^{-1}, \end{aligned}$$
(115)

where we have used Eqs. (79) and (80), and defined \({\varDelta }N_e = n_e - n_{{\bar{e}}}\). Similarly, comparing \(t_{eT}({\hat{k}}\cdot \mathbf {m})\) against \(c_e B\) would require

$$\begin{aligned} \frac{|\nabla \mathbf {B}|}{B} \sim \sqrt{\frac{T_{e}}{MeV}}\left( \frac{{\varDelta }N_{e}}{N_{e}}\right) 10^{11} cm^{-1}. \end{aligned}$$
(116)

Thus if we assume, for example, that \({\varDelta }N_{e} \sim N_{e} \sim N_{e^\prime }\) and \(T_e \sim T_{e^\prime }\), the conditions become

$$\begin{aligned} \frac{|\nabla \mathbf {B}|}{B} \sim \sqrt{\frac{T_{e}}{MeV}}\; 10^{11} cm^{-1}. \end{aligned}$$
(117)

As these particular cases illustrate, the contributions to the dispersion relation due to the inhomogeneity of the magnetic field do not seem to be significant if the background is electron-positron asymmetric.

However, more generally, it is not inconceivable that those contributions may be relevant under the appropriate environmental conditions including an electron-positron symmetric background. While we have not considered a specific application, the example estimates above show that the gradient-dependent contributions could be comparable to the standard terms in such environments. Since they give rise to distinctive kinematic features in the dispersion relation (e.g., angular asymmetries) the possible need to include their effects in some specific application contexts should be kept in mind.

5 Conclusions and outlook

In this work we have calculated the electromagnetic vertex function of a neutrino that propagates in a medium consisting of a normal electron background plus another electron stream background which is moving with a velocity relative to the normal background. The results obtained were used to determine the neutrino self-energy and dispersion relation in such a medium in the presence of an external magnetic field (\(\mathbf {B}\)), paying special attention to the case in which B is inhomogeneous, keeping the terms that are linear in B and its spatial derivatives.

The 1-loop formulas for the vertex function were given in Sect. 2. The calculation is based on the local limit of the weak interactions, that is, it is restricted to the order \(1/m^2_W\) terms only. The formulas generalize those given in [29], adapted to the present context. The vertex function is expressed in terms of a set of form factors that are given as integrals over the distribution functions of the background electrons. We also summarized the static limit value of the integrals involved in such formulas, which are subsequently used in the calculation of the neutrino self-energy and dispersion relation in the two-stream medium in the presence of a non-homogeneous external field.

In Sect. 3 we used the results for the vertex function in the two-stream medium to determine neutrino self-energy in the presence of a static external magnetic field. In contrast to the previous calculations of the neutrino index of refraction in magnetized media, we took into account and emphasized the case in which the field is not homogeneous. There we explained in some detail the need to include the screening effects of the background electrons in the calculation of the self-energy in the two-stream medium case. The results for the B-dependent part of the self-energy are summarized in Eqs. (77) and (79).

The corresponding dispersion relations were obtained and discussed in Sect. 4, focusing on some of the features that depend on the inhomogeneity of the B field and/or the presence of the stream electron background. In the presence of an inhomogeneous field the dispersion relation acquires additional anisotropic terms, in particular one of the form \({\hat{k}}\cdot (\nabla \times \mathbf {B})\), which is independent of the stream background velocity and can be present even in the absence of the stream background, and other terms, such as the gradient of \({\hat{k}}\cdot (\mathbf {v}\times \mathbf {B})\), that depend on the stream background velocity and can be present even in the case in which \(\nabla \times \mathbf {B} = 0\). As we showed, the terms that depend on the field derivatives, in contrast to those that depend on B itself, are proportional to the sum of the electron and positron densities, and therefore are non-zero to order \(1/m^2_W\) in a CP-symmetric medium in which the particle and antiparticle densities are equal. Thus, in a CP-symmetric medium the dominant contribution to the neutrino index of refraction could be due to the terms that depend on the derivatives of \(\mathbf {B}\), which are of order \(1/m^2_W\), in contrast with the constant B terms which to that order vanish and are of order \(1/m^4_W\) in that case.

From a more general point of view, the present work is a step in our effort to study problems related to the propagation of neutrinos in a medium that consists of various particle backgrounds that may be streaming with different velocities. The results of our first step in this direction were presented in [28], in which we considered the propagation of a neutrino in a magnetized two-stream electron background medium. There we considered the self-energy and dispersion relation of neutrino that propagates in a two-stream electron medium, that is a medium composed of an electron background taken to be at rest (to which we refer as the normal background), and a second electron background that moves with some velocity relative to the first. In addition we assumed that, in the rest frame of the normal background, there is a magnetic field that is homogeneous. Here we have extended that work by considering the neutrino electromagnetic vertex function in the two-stream electron medium. As already mentioned in the Introduction, the knowledge of the vertex function allows us to determine the neutrino electromagnetic properties and to calculate the rate for various processes involving neutrinos in such media, but we do not consider these applications here. Alternatively, by considering the effective neutrino interaction with an external electromagnetic field, we have used the results for the vertex function to determine the self-energy and dispersion relation of a neutrino that propagates in a two-stream medium with an inhomogeneous magnetic field. In particular this extends the previous works on neutrino propagation in magnetized media which are restricted to the case of a homogeneous magnetic field. There is an extensive literature related to the effects of an external magnetic field in the propagation of neutrinos in dense media in a variety of astrophysical and cosmological contexts. The results of this work provide a firm setting for exploring the effects of the combined presence of stream backgrounds and inhomogeneities of external fields along the same lines, which can be applicable in real astrophysical and cosmological situations, such as: pulsars, supernova, gamma-ray bursts and Early Universe as already mentioned in the introduction.