Cosmological aspects of the Eisenhart–Duval lift

Abstract

A cosmological extension of the Eisenhart–Duval metric is constructed by incorporating a cosmic scale factor and the energy-momentum tensor into the scheme. The dynamics of the spacetime is governed by the Ermakov–Milne–Pinney equation. Killing isometries include spatial translations and rotations, Newton–Hooke boosts and translation in the null direction. Geodesic motion in Ermakov–Milne–Pinney cosmoi is analyzed. The derivation of the Ermakov–Lewis invariant, the Friedmann equations and the Dmitriev–Zel’dovich equations within the Eisenhart–Duval framework is presented.

1 Introduction

The Eisenhart–Duval (ED) lift [1,2,3] provides a convenient framework for treating time-dependent dynamical systems and their symmetries [4]. Such systems include time-dependent harmonic oscillators (TDHO’s). TDHO’s and their symmetries have a large literature. In particular, they are conveniently studied using the Ermakov–Milne–Pinney (EMP) equation [5,6,7].

An important tool for solving the EMP equation is a constant of the motion known as the Ermakov–Lewis invariant – which is in fact an exact invariant for any TDHO. It is then natural to inquire about the relationship between the ED lift and the EMP equation. Can one obtain the Ermakov–Lewis invariant using the ED lift?

There is also a considerable body of work in which methods based on the EMP equation have been applied to cosmology [8,9,10,11,12,13,14,15], in particular to finding solutions and the symmetries of the Friedmann equations. This leads to the further question of what insights can be gained into cosmology using the ED lift?

A first attempt to incorporate a cosmic scale factor into the ED scheme has been reported recently [16]. Yet, because these considerations relied upon the EMP equation with a constant frequency, the resulting spacetime turned out to be stationary. It is then natural to wonder whether a dynamical spacetime with cosmological features can also be constructed along the same lines.

The purpose of this paper is to address the questions raised above, focusing on the cosmological aspects of the ED lift.

The paper is organized as follows. In Sect. 2 we provide a thorough review of the EMP equation for readers who may not be familiar with the rather extensive literature on this subject.

In Sect. 3.1 a brief account of the ED lift is given. It is shown that any Newtonian mechanical system can be represented by a metric which solves the Einstein equations provided the energy momentum tensor is chosen in a suitable way. In Sect.  3.2 the Ermakov–Lewis constant is obtained by using a conformal transformation of the associated ED metric. An explicit formula which depends upon a solution of the EMP equation is presented.

Then in Sect. 3.3 the ED lift involving a scale factor analogous to that in the Friedmann metrics is given. It is shown that the dynamics of the spacetime is governed by the EMP equation. Section 3.4 contains a detailed derivation of the conformal symmetries of this modified metric. Geodesic motion in EMP cosmoi is analyzed in Sect.  3.5.

Sect. 4.1 contains some introductory material on Friedmann–Lemaître–Robertson–Walker (FLRW) metrics, establishing the terminology and the conventions. The Einstein equations reduce to the Friedmann and Raychaudhuri equations; in the case of radiation and dark energy, they reduce to the EMP equation.

Sect. 4.2 deals with conformal symmetries and what we refer to as temporal diffeomorphisms, which may be used to provide explicit solutions to the Friedmann equations. These cases include the reduction to a time-independent harmonic oscillator.

Sect. 4.3 contains a derivation of the ED lift of geodesic motion in FLRW spacetimes. This allows describing the system’s dynamical symmetries, and relating them to the null geodesics of the EMP spacetime of Sect. 3.5. The result is generalized to obtain the lift of the Dmitriev–Zel’dovich equations.

Finally in Sect. 4.4 we regard the Friedmann equations as a dynamical system with a constraint and provide a generalised ED lift of it.

In Sect. 5 we summarize our results.

Throughout the paper summation over repeated indices is understood.

2 The Ermakov–Milne–Pinney Equation

In this section we shall give a brief account of the EMP equation [5,6,7] and of its uses. The most important of these are:

• In dynamics: using its solutions to map problems involving TDHO’s to problems involving time-independent harmonic oscillators (TIHO’s).

• In quantum mechanics: using its solutions to map problems involving the one-dimensional time-independent Schrödinger equation into Schrödinger equations which have explicit solutions.

For historical remarks about the origins of the subject the reader may consult [17]. More ambitious in scope is the Master Thesis [18]. The reader should be aware that in many papers either Milne, or Pinney is omitted from the name of the equation. The order of authors used here merely reflects the order of publication.

2.1 Comparison of two time dependent harmonic oscillators

This is perhaps the most direct approach to the EPM equation. Apparently due originally to Dingle [19], this proceeds as follows [20]. We have two TDHO equations

$$\begin{aligned} \frac{d^2q}{dt^2 } + \omega ^2(t) q= & {} 0 \end{aligned}$$

(II.1a)

$$\begin{aligned} \frac{d^2Q}{d\tau ^2} + \Omega ^2(\tau ) Q= & {} 0, \end{aligned}$$

(II.1b)

which may be obtained by varying respectively the two integrals

$$\begin{aligned}&\int \frac{1}{2}\left( \left( \frac{dq}{dt} \right) ^2 - \omega ^2(t) q^2\right) dt,\end{aligned}$$

(II.2a)

$$\begin{aligned}&\int \frac{1}{2}\left( \left( \frac{dQ}{d\tau } \right) ^2 - \Omega ^2(\tau ) Q^2 \right) d \tau . \end{aligned}$$

(II.2b)

We seek a temporal diffeomorphism $\tau = \tau (t)$ taking one integral into the other up to a boundary term. If

$$\begin{aligned} f(t)= \left( \frac{d \tau }{dt }\right) ^{-\frac{1}{2}}, \end{aligned}$$

(II.3)

and

$$\begin{aligned} q(t) = \left( \frac{d\tau }{dt}\right) ^{-\frac{1}{2}} Q(\tau ) = f(t) Q(\tau ) \end{aligned}$$

(II.4)

we find that

$$\begin{aligned}&\int \left( \left( \frac{dQ}{d\tau }\right) ^2 -\Omega ^2(\tau ) Q^2\right) d \tau \nonumber \\&\quad = \int \frac{1}{2}\left( \left( \frac{dq}{dt} \right) ^2 - \omega ^2(t) q^2 \right) d t -\int \frac{d}{dt} \left( q^2 \frac{1}{f^2} \frac{df}{dt} \right) dt, \end{aligned}$$

(II.5)

where

$$\begin{aligned} \omega ^2(t) = \frac{\Omega ^2(\tau )}{f^4 } - \frac{1}{f}\frac{d^2f}{dt^2} \end{aligned}$$

(II.6)

or

$$\begin{aligned} \frac{d^2f}{dt^2} + \omega ^2 f = \frac{\Omega ^2(\tau )}{f^3} . \end{aligned}$$

(II.7)

This equation may be read in different ways.

• If the solutions $Q(\tau )$ of equation (II.1b) are known and we want the solutions q(t) of Eq. (II.1a), we need to solve for f(t) and hence obtain $\tau (t)$ by integration

  $$\begin{aligned} \tau = \int \frac{dt}{f^2}. \end{aligned}$$

  (II.8)

• Conversely, if the solutions q(t) of (II.1a) are known and we want the solutions of Eq. (II.1b), we need to solve Eq. (II.7) for f(t).

In both cases the procedure is complicated by the need to express $\Omega ^2 (\tau )$ as a function of t. Because this involves the integral (II.8) giving $\tau (t)$, this leads in general to very complicated equations, for which the only feasible strategy appears to involve extensive iterations of the type described in [20].

2.2 The Ermakov–Milne–Pinney equation and the Ermakov–Lewis invariant

Considerable simplification results if we assume

$$\begin{aligned} \Omega ^2(\tau )= \lambda , \end{aligned}$$

(II.9)

where $\lambda$ is a constant which need not necessarily be positive. This leads to the original form of the Ermakov–Milne–Pinney equation:

$$\begin{aligned} \frac{d^2f}{dt^2} + \omega ^2(t)f = \frac{\lambda }{f^3}, \end{aligned}$$

(II.10)

which may be thought of as a TDHO with a non-linear term. We remark here that the inverse-square potential is known to have the Schrödinger-type 2:1 scaling symmetry [21].

The EMP equation has the remarkable property [5, 7] that its general solution may be expressed in terms of two linearly independent solutions, $q_1(t)$ and $q_2(t)$, of (II.1a).

$$\begin{aligned} f(t)= \Bigl ( A q_1^2(t) + B q^2_2(t) + 2C q_1(t)q_2(t) \Bigr )^\frac{1}{2}\end{aligned}$$

(II.11)

where A, B, C are constants satisfying

$$\begin{aligned} AB-C^2 = \frac{\lambda }{W^2}, \qquad W= q_1 \frac{dq_2}{dt} - q_2 \frac{dq_1}{dt}. \end{aligned}$$

(II.12)

W is the constant Wronskian of the pair of linearly independent solutions $q_1,\,q_2$.

Given a solution of the EMP Eq. (II.7) one has the identity

$$\begin{aligned} H= & {} \frac{1}{2}\Bigl ( (\frac{dQ}{d\tau })^2 - \lambda Q^2 \Bigr ) \end{aligned}$$

(II.13a)

$$\begin{aligned}= & {} \frac{1}{2}\Bigl ( \frac{q^2}{f^2}+(\frac{dq}{dt}f -\frac{df}{dt} q)^2 \Bigr ) =I , \end{aligned}$$

(II.13b)

which equates the conserved Hamiltonian (II.13a) of the TIHO (II.1b) with the conserved Ermakov–Lewis invariant (II.13b) of the TDHO (II.1a) [22, 23]. This derivation is essentially the same as the one given in [24].

One may regard the Lewis invariant as an exact form of the adiabatic invariant for a TDHO, and as such, has obvious applications to the quantum theory as will be seen shortly.

Subsequent to the paper by Lewis, the idea was extended to charged particles moving in a spatially uniform magnetic field and a time dependent harmonic potential [25, 26]. This is in effect covered by the theorems of Larmor and Kohn which allow one to eliminate the magnetic field by passing to a rotating frame [27,28,29]. Despite its great experimental, astronomical and technological importance, we shall not pursue this issue further.

We mention for completeness that generalizations of the Ermakov–Lewis invariant (II.13b) were obtained by considering modifications of the pair of EMP Eqs. (II.1a) and (II.10) [30, 31].

Further insight is provided by the observation by Eliezer and Gray [32] that two TDHO’s of the form (II.1a), $q_1(t)$ and $q_2(t)$, may be considered as a particle in the Euclidean plane $\mathbb {E}^2$, moving under the influence of an axisymmetric harmonic potential. Moreover, if one introduces polar coordinates $r,\theta$ such that $q_1+ i q_2=r\,e^{i\theta }$, the equations of motion of the Lagrangian

$$\begin{aligned} L= \frac{1}{2}\bigl (\dot{r} ^2 + r^2 \dot{\theta }^2 - \omega ^2 (t) r^2 \bigr ), \end{aligned}$$

(II.14)

imply the conservation of the angular momentum (per unit mass)

$$\begin{aligned} r^2 \dot{\theta }=h . \end{aligned}$$

(II.15)

Then substitution back to the radial equation of motion gives

$$\begin{aligned} \ddot{r} + \omega ^2(t) r = \frac{h^2}{r^3} \end{aligned}$$

(II.16)

which, in the case $\lambda = h^2 >0$, coincides with the EMP Eq. (II.10) if $r=f$.

If one substitutes $q=r \cos \theta ,\, f= r , \, \lambda = h^2$ into (II.13b), one finds that the Ermakov–Lewis quantity is in fact the square of the angular momentum¹

$$\begin{aligned} I= h^2 . \end{aligned}$$

(II.17)

A list of cases for which there are explicit solutions of the radial Eq. (II.16) are given in [32, 34]. Because of its application to cosmology which we will describe later, we reproduce it here.

• $$\begin{aligned} \omega= & {} \mathrm{constant} =\omega _0 ,\nonumber \\ r^2= & {} (A \cos \omega _0t + B \sin \omega _0 t)^2+ \frac{h^2}{A^2 \omega _0^2} \sin ^2 \omega _0 t .\nonumber \\ \end{aligned}$$

  (II.18)

  The orbit in the plane is an ellipse.

• $$\begin{aligned} \omega = \frac{b}{t^2}, \qquad \theta - \theta _0= -\frac{b}{t}, \qquad r= \sqrt{\frac{h}{b}}\, t =\frac{ \sqrt{ hb}}{\theta _0 -\theta } . \end{aligned}$$

  (II.19)
• $$\begin{aligned}&\omega = \frac{b}{t},\quad r^2 = bt ,\quad b=\frac{h}{\sqrt{b^2-\frac{1}{4} }},\nonumber \\&b \ne \frac{1}{2}, \quad \theta =\theta _0 + \frac{h}{b}\ln t , \quad r= b \exp {\frac{b}{h} (\theta -\theta _0)},\nonumber \\ \end{aligned}$$

  (II.20)

  which yields a logarithmic spiral.

• $$\begin{aligned} \omega= & {} bt^k , \, r^2 =\pi h A t \Bigl ( J^2_n( 2 A b^2 t^{k+1} ) + Y^2_n( 2 A b^2 t^{k+1}) \Bigr ) ,\nonumber \\&n= \frac{1}{2}(k+1) , \quad \end{aligned}$$

  (II.21)

  where $J_n , Y_n$ are Bessel functions. If $k>0$ , then $r \rightarrow 0$ as $t \rightarrow \infty$, and if $k<0$ then $r \rightarrow \infty$ as $t \rightarrow \infty$.

2.3 The one-dimensional Schrödinger equation and the Liouville–Green–Jeffreys–Wentzel–Kramers–Brillouin approximation

If we now think of the temporal coordinates $t,\tau$ as spatial coordinates x, X, the complexified positions $q(t),Q(\tau )$ as wave functions $\psi (x),\Psi (X)$ and the frequencies $\omega (x)$ and $\Omega (\tau )$ as wave vectors k(x) and K(x), we may transcribe all of the fore-going theory into quantum mechanical language. The TDHO Eqs. (II.1a)–(II.1b) become

$$\begin{aligned}&\frac{d^2 \psi (x)}{dx^2} + k^2(x) \psi =0 , \end{aligned}$$

(II.22a)

$$\begin{aligned}&\frac{d^2 \Psi (x)}{dX^2} + K^2(X) \Psi =0 , \end{aligned}$$

(II.22b)

where $k^2 = 2 (E-V(x))$ and we have used units in which $\hbar ^2 = m$, E is the energy, and V(x) is the potential energy.

The relation to the Liouville–Green–Jeffreys–Wentzel–Kramers–Brillouin method may be seen by noting that (II.3) and (II.4), (II.8), and (II.7), are identical to (2), (6), (3) in Sect. 17.122 of [35], which contains a systematic procedure for obtaining asymptotic expansions, provides a list of references and justifies the addition of the names of Liouville, Green and Jeffreys to the better known Wentzel, Brillouin, and Kramers.

If we choose $K^2 =X^2$ we find formal bound state solutions of (II.22a) which take the form

$$\begin{aligned} \psi (x) \propto r(x) \sin \Bigl (\int ^x_{x_o}\frac{d \tilde{x}}{r^2(\tilde{x})} \Bigr ) , \end{aligned}$$

(II.23)

where the dependence of r(x) on E has been suppressed. Eqn. (II.23) implies the Milne quantization condition² for the allowed values of the energy E [6],

$$\begin{aligned} \frac{1}{\pi } \int _{-\infty }^{\infty } \frac{dx}{r^2(x,E)} = n+1,\,\qquad n=0,1,2,3,\dots , \end{aligned}$$

(II.24)

where we have re-instated the dependence of r on E as well as x.³

The quantum mechanical treatment presented above was based on the formal equivalence of the TDHO Eq. (II.1a) and the time-independent Schrödinger Eq. (II.22a) effected by exchanging the time coordinate for the spatial coordinate of the latter. A deeper connection may be obtained by considering a wave packet solution of the time-dependent Schrödinger equation in one spatial dimension [37,38,39,40],

$$\begin{aligned} i \hbar \frac{{\partial }\Psi (x,t)}{{\partial }t}= \Big [-\frac{\hbar ^2}{2m} \frac{{\partial }^2}{{\partial }x ^2} + \frac{1}{2}m \omega ^2(t) x^2 \Big ]\,\Psi (x,t) \, \end{aligned}$$

(II.25)

for

$$\begin{aligned} \Psi (x,t)= N(t) \exp \big [i \bigl (y(t) \tilde{x}^2 + K(t) \bigl )\big ] , \end{aligned}$$

(II.26)

where $\tilde{x}= x-q(t)$, and

$$\begin{aligned} q(t) \langle x \rangle = \int ^\infty _{-\infty } \bar{\Psi }x \Psi dx \end{aligned}$$

(II.27)

is the real valued expectation value of the position of the “classical” trajectory and $\langle p \rangle = m \dot{q}$ is the classical momentum; the functions N(t) and K(t) not relevant for the following discussion. In [37] it is claimed that substitution of (II.26) into (II.25) leads to the TDHO Eq. (II.1a) and the complex Riccati-type equation

$$\begin{aligned} \frac{2 \hbar }{m} \dot{y} + (\frac{2 \hbar }{m}y ) ^2 + \omega ^2 t=0 . \end{aligned}$$

(II.28)

Moreover, if

$$\begin{aligned} \mathfrak {R}\,y= \frac{m}{2 \hbar } = \frac{1}{f^2}, \end{aligned}$$

(II.29)

then f satisfies the EMP Eq. (II.10); the Ermakov–Lewis quantity I given by (II.13b) is a dynamical invariant.

We remark en passant that the EMP equation may be incorporated into the formalism of supersymmetric quantum mechanics [36, 37].

2.4 The Ermakov–Milne–Pinney equation and Madelung’s hydrodynamic transcription

The time-dependent Schrödinger equation with a general potential $V({\varvec{x}})$,

$$\begin{aligned} i \hbar \frac{{\partial }\Psi }{{\partial }t} = -\frac{\hbar ^2}{2m} \varvec{\nabla }^2 \Psi + V \Psi , \end{aligned}$$

(II.30)

can be brought into the hydrodynamical form : Setting $\Psi = \sqrt{\rho }\, e^{i\frac{S}{\hbar }} ,$ defining the velocity $\mathbf{v}= \frac{d{\varvec{x}}}{dt} = \frac{1}{m} \varvec{\nabla }S$ and taking real and imaginary parts, one gets equations which resemble Euler’s equations for a compressible irrotational fluid, called a Madelung fluid [41]

$$\begin{aligned} \frac{{\partial }\rho }{{\partial }t}+ \varvec{\nabla }\cdot (\rho \mathbf{v}) =0\end{aligned}$$

(II.31a)

$$\begin{aligned} \frac{{\partial }\mathbf{v}}{{\partial }t}+ \mathbf{v}\cdot \varvec{\nabla }\mathbf{v}&= - \frac{1}{m} \varvec{\nabla }\tilde{V}. \end{aligned}$$

(II.31b)

For a stationary state one has $\frac{{\partial }S}{{\partial }t}=-E , \; \frac{{\partial }\rho }{{\partial }t}=0.$

One may also require that the probability density be independent of time [37]. In general one typically assumes that $\varvec{\nabla }S =0$ and hence $\sqrt{\rho }$ satisfies the linear equation

$$\begin{aligned} - \frac{\hbar ^2}{2m} \varvec{\nabla }^2 \sqrt{\rho } + V \sqrt{\rho } =E \sqrt{\rho }. \end{aligned}$$

(II.32)

On the other hand in one spatial dimension, taking note of (III.17), one may alternatively assume

$$\begin{aligned} \frac{dS}{dx}= \frac{C}{\rho } \end{aligned}$$

(II.33)

for some constant C. This leads to the non-linear EMP Eq. (II.10) for $f= \sqrt{\rho (x)}$ [37],

$$\begin{aligned}&\frac{ d^2 \sqrt{\rho } }{dx^2 } + \omega ^2(x) \sqrt{\rho } =\frac{C^2}{\hbar ^2} \frac{1}{ (\sqrt{\rho })^3} \qquad \text { with}\nonumber \\&\omega ^2(x)= \frac{2m}{\hbar } (E-V(x)) . \end{aligned}$$

(II.34)

Similar applications of the EMP equation in this context, including those with magnetic fields, may be found in [42, 43].

2.5 Bose–Einstein condensates

Among the many applications of the EMP equation is one to Bose–Einstein condensates (BEC’s) [44, 45].

The authors start with the spherically symmetric but time-dependent Gross-Pitaevski equation in d spatial dimensions with radial coordinate r,

$$\begin{aligned} i\,\frac{{\partial }\Psi (r,t)}{{\partial }t}= -\frac{1}{2}\nabla ^2 \Psi (r,t) + \Bigl (\lambda (t)r^2 + \nu (t) |\Psi (r,t)|^2 \Bigr ) \Psi (r,t) , \end{aligned}$$

(II.35)

which may be derived from the Hamiltonian

$$\begin{aligned} H = \frac{1}{2}\int \Bigl ( \big | \nabla \Psi \big |^2 + \nu (t) \big | \Psi (r,t) \big | ^4 + 2 \lambda (t) r^2 \big | \Psi (r,t) \big | ^2 \Bigr ) r^{d-1} dr . \end{aligned}$$

(II.36)

Then, using standard “moment methods” in the literature, an equation is obtained for a quantity y(t) [44, 45]

$$\begin{aligned} \frac{d}{dt} \Bigl ( y \ddot{y} -\frac{1}{2}\dot{y}^2 -2K \nu (t) + 4 \lambda (t) y^2 \Bigr ) = 2 (d-2)K y \frac{d}{dt}\Bigl (\frac{\nu (t)}{y}\Bigr ) \end{aligned}$$

(II.37)

with K a constant. The case $d=2$ is evidently special and in that case, setting $f=\sqrt{y(t)}$ and $\omega ^2(t)=2\lambda (t)$, one obtains (II.7), with

$$\begin{aligned} \Omega ^2 (\tau )= \frac{1}{2}C + K \nu (t). \end{aligned}$$

(II.38)

3 The Eisenhart–Duval Lift and the Ermakov–Milne–Pinney Equation

3.1 Eisenhart–Duval lift of Newtonian mechanics

As originally formulated in [1,2,3], the ED lift provides a geometric description of a mechanical system with d degrees of freedom $x_i$, $i=1,\dots ,d$, and the potential energy U(t, x) in terms of geodesics of the Lorentzian metric on a $(d+2)$–dimensional spacetime

$$\begin{aligned} g_{\mu \nu }(y) dy^\mu dy^\nu =-2 U({t},x) d t^2-dt dv+dx_i dx_i, \end{aligned}$$

(III.1)

where $y^\mu =(t,v,x_i)$. Computing the Christoffel symbols and analyzing the geodesic equations one finds that t is affinely related to the proper time $\tau$

$$\begin{aligned} \frac{d^2t}{d \tau ^2}=0 \quad \Rightarrow \quad \frac{d t}{d \tau }=\kappa , \end{aligned}$$

(III.2)

where $\kappa$ is a constant, $x_i$ obeys Newton’s Eq. (passing from $\tau$ to t)

$$\begin{aligned} \frac{d^2 x_i}{d t^2}+\partial _i U({t},x)=0, \end{aligned}$$

(III.3)

while the dynamics of v is fixed from the condition that the geodesic is null or time–like

$$\begin{aligned} \frac{d v}{d t}=\frac{d x_i}{dt} \frac{d x_i}{dt}-2 U-\frac{\epsilon }{\kappa ^2}, \end{aligned}$$

(III.4)

where $\epsilon =0$ is for null geodesics and $\epsilon =-1$ for time–like geodesics. Newtonian mechanics is thus recovered by implementing the null reduction along v [1]. Note that the original construction [1,2,3] dealt with null geodesics only.

The spacetime (III.1) belongs to the Kundt class as it admits the covariantly constant null Killing vector field

$$\begin{aligned} \xi ^\mu \partial _\mu =\partial _v, \qquad \nabla _\mu \xi _\nu =0, \qquad \xi ^2=0. \end{aligned}$$

(III.5)

The latter can be used to construct the trace–free energy–momentum tensor in a geometrically rather appealing way⁴

$$\begin{aligned}&T_{\mu \nu }=\frac{d}{2\pi } \Omega (y)^2 \xi _\mu \xi _\nu , \qquad {T^\mu }_\mu =0, \nonumber \\&\nabla _\rho T_{\mu \nu }=\frac{d}{\pi } \Omega \, \partial _\rho \Omega \,\xi _\mu \xi _\nu , \end{aligned}$$

(III.6)

where $\Omega (y)^2$ is an arbitrary function (the energy density). The only non–vanishing component of $\xi _\mu$ is $\xi _t=-\frac{1}{2}$, which gives $T_{tt}=\frac{d }{8\pi } \Omega ^2$ while the rest vanishes. Because $\xi ^\mu \partial _\mu \Omega =0$ holds true if $\Omega$ does not depend on v, the energy–momentum tensor is conserved,

$$\begin{aligned} \nabla ^\mu T_{\mu \nu }=0, \end{aligned}$$

(III.7)

provided $\Omega =\Omega (t,x)$.

The Ricci tensor which derives from (III.1) has only one nonzero component while the scalar curvature vanishes,

$$\begin{aligned} R_{tt}=\partial _i \partial _i U, \qquad R=0. \end{aligned}$$

(III.8)

Given the ED metric (III.1) and the energy–momentum tensor (III.6), the Einstein equations

$$\begin{aligned} R_{\mu \nu }-\frac{1}{2} g_{\mu \nu }(R+2\Lambda )=8\pi T_{\mu \nu } \end{aligned}$$

(III.9)

imply that the contribution of the cosmological term necessarily vanishes, $\Lambda =0$, thus reducing (III.9) to

$$\begin{aligned} R_{\mu \nu }=8\pi T_{\mu \nu }. \end{aligned}$$

(III.10)

Only the (tt)–component is non–trivial; it links $\Omega$ to U, as

$$\begin{aligned} \Omega ^2=\frac{1}{d} \partial _i \partial _i U. \end{aligned}$$

(III.11)

A particularly interesting example of the ED geometry occurs if U and $\Omega$ are t-independent. Setting

$$\begin{aligned} \Omega ^2(x)=\frac{4\pi G}{d} \rho (x) \end{aligned}$$

(III.12)

and interpreting G as Newton’s constant and $\rho (x)$ as the mass density, one recovers the Newton equation for the gravitational potential.

In conclusion, Newtonian mechanics can be represented in terms of a metric which solves the Einstein Eqs. (III.10) provided the energy–momentum tensor is chosen in the form (III.6).

3.2 Lifting the Ermakov–Lewis invariant

The aim of this subsection is to show how applying the ED lift to a TDHO allows one to obtain the Ermakov–Lewis invariant by performing a conformal transformation of the metric [1,2,3].

The equations of motion of a TDHO follow from the Hamiltonian

$$\begin{aligned} H= \frac{1}{2}\Bigl ( m^{-1} (t) p_q^2 + m(t) \omega ^2(t) q^2 \Bigr ) . \end{aligned}$$

(III.13)

Let $H=-p_t$ and let

$$\begin{aligned} \mathcal{H}(x^\mu ,p_\mu ) = 2 p_t p_v + m^{-1} p_q^2 + m \omega ^2 q^2 p_v^2 = g^{\mu \nu }p_\mu p_\nu \end{aligned}$$

(III.14)

with $x^\mu = (t,v,q)$, $p_\mu =(p_t,p_v,p_q)$ . The ED metric on the extended (“Bargmann” [2, 3]) spacetime $M=\{\mathbb {R}^3, g \}$ is given by,

$$\begin{aligned} g_{\mu \nu }dx^\mu dx^\nu = 2 dt dv + m dq^2 - m \omega ^2 q^2 d t^2 . \end{aligned}$$

(III.15)

The null geodesics, considered as unparametrised curves, of a Lorentzian metric $g_{\mu \nu }$ are the same as for any conformally related Lorentzian metric. They are given by the Hamiltonian flow on $T^\star M$ with Hamiltonian

$$\begin{aligned} \mathcal{H} = g^{\mu \nu } p_\mu p_\nu \end{aligned}$$

(III.16)

subject to the constraint

$$\begin{aligned} \mathcal{H}=0. \end{aligned}$$

(III.17)

Hamilton’s equations following from the Hamiltonian (III.16) with constraint (III.17) for two conformally related metrics $g_{\mu \nu }$ and $\Omega ^2(x) g_{\mu \nu }$ are identical.

The vector field $V= \frac{{\partial }}{{\partial }v}$ is a null Killing vector field and thus

$$\begin{aligned} p_v= \mathrm{constant}. \end{aligned}$$

(III.18)

To obtain the motion in 2 spacetime dimensions we perform a Marsden–Weinstein reduction (referred to as “ignoration of cyclic coordinates” in old fashioned books) bearing in mind the constraint (III.17) and setting $p_v=1$ to recover the Hamiltonian system (III.13). We now set

$$\begin{aligned} Q=\frac{q}{f} \end{aligned}$$

(III.19)

for some function f(t) to be determined. In (Q, t, v) coordinates the metric may be cast in the form

$$\begin{aligned} ds^2 = 2 dt(dv + A) + mf^2 dQ^2 - Q^2 g(t) dt^2, \end{aligned}$$

(III.20)

where A is the one-form

$$\begin{aligned} A = mf\dot{f} Q dQ + \frac{1}{2}mQ^2 (\dot{f}^2 -f^2 \omega ^2) dt + \frac{1}{2}Q^2 g(t) dt \end{aligned}$$

(III.21)

and g(t) is an arbitrary function of time. If A is closed, $dA=0$, then we may define a new coordinate $\tilde{v}$ by

$$\begin{aligned} d \tilde{v} = dv + A, \end{aligned}$$

(III.22)

in terms of which the metric becomes

$$\begin{aligned} ds ^2 = 2 dt d \tilde{v} + mf^2 dQ^2 - Q^2 g^2 dt ^2. \end{aligned}$$

(III.23)

Now introducing a new time coordinate $\tau$ by

$$\begin{aligned} dt = mf^2 d\tau , \end{aligned}$$

(III.24)

we have

$$\begin{aligned} ds ^2 = mf^2 \Bigl \{ 2 d \tau d \tilde{v} + dQ^2 - mf^2 Q^2 g d \tau ^2 \Bigr \} . \end{aligned}$$

(III.25)

The condition for A to be closed is

$$\begin{aligned} \frac{d}{dt}(m \dot{f}) + m\omega ^2 f = \frac{g}{f}. \end{aligned}$$

(III.26)

If

$$\begin{aligned} g = \frac{\Omega ^2 }{mf^2}, \end{aligned}$$

(III.27)

where $\Omega$ an arbitrary constant, then the metric becomes

$$\begin{aligned} ds^2 = mf^2 \Bigl \{ 2 d \tau d \tilde{v} + dQ^2 - Q^2 d \tau ^2 \Bigr \} . \end{aligned}$$

(III.28)

As noted above, two conformally related metrics have the same null geodesics, although their affine parameters differ. From this we deduce that the null geodesics of the static metric inside the braces in (III.28) are the same as those for our time dependent metric (III.15).

If we now perform a null reduction on the Killing vector $\frac{{\partial }}{{\partial }\tilde{v}}$, we obtain the Hamiltonian of a TIHO

$$\begin{aligned} \tilde{H} = \frac{1}{2}(p_Q^2 + \Omega ^2 Q^2). \end{aligned}$$

(III.29)

3.3 Ermakov–Milne–Pinney cosmology

Now we show that the EMP equation naturally arises if one incorporates a cosmic scale factor into a suitably chosen Bargmann metric, when the energy-momentum tensor is chosen in a proper way.

Consider a $(d+2)$–dimensional spacetime parametrized by the coordinates $y^\mu =(t,v,x_i)$, $i=1,\dots ,d$, and endowed with the Lorentzian metric [16]

$$\begin{aligned} ds^2=-\frac{\gamma ^2 x_i x_i }{a(t)^2} dt^2-dt dv+a(t)^2 dx_i dx_i, \end{aligned}$$

(III.30)

where a(t) is an arbitrary function and $\gamma$ is a constant. For a fixed value of t the line element in the d–dimensional slice parametrized by $x_i$ is given by ${a(t)}^2 dx_i dx_i$. Therefore ${a(t)}^2$ may be interpreted as a cosmic scale factor. The metric (III.30) possesses, as does its conventional counterpart (III.1), a covariantly constant null Killing vector field, namely (III.5). The choice of (III.30) will be justified a posteriori in Sect. 4.

Constructing the energy-momentum tensor following the prescription (III.6) and specifying to the class of energy densities which depend on t only, $\Omega =\Omega (t)$, from Eq. (III.10) one finds

$$\begin{aligned} \ddot{a}+\Omega ^2(t) a=\frac{\gamma ^2}{a^3}. \end{aligned}$$

(III.31)

Thus the dynamics of (III.30) is governed by the EMP equation. The instance of  $\Omega =\text{ const }$ has been discussed recently in [16], in which case the EMP equation reduces to conformal mechanics in one dimension [21].

One can learn more about the geometry of (III.30) by analyzing the geodesic equations. Computing the Christoffel symbols, one concludes that t is affinely related to the proper time,

$$\begin{aligned} \frac{d^2 t}{d \tau ^2}=0\, . \end{aligned}$$

(III.32)

The coordinate $x_i$ obeys in turn the oscillator–like equation

$$\begin{aligned} a^2 \frac{d}{dt} \left( a^2 \frac{d}{dt} x_i \right) +\gamma ^2 x_i=0, \end{aligned}$$

(III.33)

in which we passed from $\tau$ to t, while the evolution of v is fixed from the condition that the geodesic be null or time–like. Equation  (III.33) prompts one to introduce the conformal time

$$\begin{aligned} a^2(t) \frac{d}{dt}=\frac{d}{d\eta } , \qquad \eta (t)=\int _{t_0}^t \frac{d\tilde{t}}{a^2(\tilde{t})} , \end{aligned}$$

(III.34)

which brings the metric (III.30) to the form

$$\begin{aligned} ds^2=a^2(\eta )\left( -\gamma ^2 x_i x_i d\eta ^2-d\eta dv+dx_i dx_i\right) , \end{aligned}$$

(III.35)

where $a(\eta )=a(t(\eta ))$, and $t(\eta )$ is the inverse of $\eta (t)$ in (III.34). Equation (III.35) is an analog of the flat (k=0) FLRW cosmological model in which the Minkowski metric has been changed into the simplest PP–wave; the Friedmann equation which determines the evolution of the cosmic scale factor is replaced, in this case, by the EMP equation.

To conclude this section we note that the coordinate transformation

$$\begin{aligned} t'=t, \qquad x'_i=a(t) x_i, \qquad v'=v+a(t) \dot{a}(t) x_i x_i \end{aligned}$$

(III.36)

brings (III.30) to the form

$$\begin{aligned} ds^2= \left( \frac{\ddot{a}}{a}-\frac{\gamma ^2}{a^4} \right) x_i x_i dt^2-dt dv+dx_i dx_i, \end{aligned}$$

(III.37)

where we omitted the primes, or, in view of (III.31),

$$\begin{aligned} ds^2= -\Omega (t)^2 x_i x_i dt^2-dt dv+dx_i dx_i \end{aligned}$$

(III.38)

which is the $d+2$ dimensional Bargmann metric associated with an isotropic oscillator in (d, 1) dimensions with time–dependent frequency $\Omega (t)$, the motions of which are the projections of the null geodesics of (III.38).

3.4 Symmetries as conformal Killing isometries

Finding the symmetries of time dependent harmonic oscillators generated an extensive literature in the early 1980’s, including [46,47,48,49]. A discussion in terms of canonical transformations is in [51]. An alternative approach is presented below in terms of the ED lift. For simplicity, we stick to Eq. (III.38).

Following [2, 3], the symmetries of a non-relativistic system in (d, 1) dimensions can be obtained as a subgroup of the conformal symmetries of the $d+2$ dimensional Bargmann manifold: one selects those conformal transformations that leave invariant the covariantly constant null vector ${\partial }_v$.

In our case, the symmetries given in Ref. [49] are seen to be consistent with the Schrödinger group in d dimensions – which is a subgroup of the conformal group of the extended (Bargmann) spacetime. Now we re-derive the above-mentioned symmetries in the specific case of our EMP spacetime of Sect.3.3.

Consider indeed a generic infinitesimal transformation

$$\begin{aligned} t'=t+\delta t, \qquad v'=v+\delta v, \qquad x'_i=x_i+\delta x_i , \end{aligned}$$

(III.39)

where $\delta t$, $\delta v$, $\delta x_i$ are arbitrary functions of t, v, x. Demanding (III.38) to be invariant under (III.39) up to a conformal factor,

$$\begin{aligned} ds'^2=(1+\Lambda ) ds^2, \end{aligned}$$

(III.40)

one gets a coupled set of partial differential equations to fix $\delta t$, $\delta v$, $\delta x_i$ and $\Lambda$. Omitting details, we present the (conformal) isometries of (III.38),

$$\begin{aligned}&t'=t+\lambda (t)+\frac{1}{2} \epsilon x^2-x_i \rho _i(t),\end{aligned}$$

(III.41a)

$$\begin{aligned}&x'_i=x_i+\mu _i (t)+\omega _{ij} x_j+\frac{1}{2} \kappa x_i +\frac{1}{2} \dot{\lambda }(t) x_i+\frac{1}{2} v \epsilon x_i\end{aligned}$$

(III.41b)

$$\begin{aligned}&\qquad +\,\frac{1}{2} x^2 \dot{\rho }_i (t)-x_i x_j \dot{\rho }_j (t)-\frac{1}{2} v \rho _i(t),\end{aligned}$$

(III.41c)

$$\begin{aligned}&v'=v+\nu +2{\dot{\mu }}_i(t) x_i+\frac{1}{2} \ddot{\lambda }(t) x^2-\frac{1}{2} \epsilon \, \Omega ^2x^2 x^2+\kappa v+\frac{1}{2} \epsilon v^2 \end{aligned}$$

(III.41d)

$$\begin{aligned}&\qquad +\,\Omega ^2 x^2 x_i \rho _i(t)-v x_i \dot{\rho }_i (t), \end{aligned}$$

(III.41e)

where $\epsilon$, $\nu$, $\kappa$, $\omega _{ij}=-\omega _{ji}$ are constant infinitesimal parameters, $x^2=x_i x_i$, the functions $\mu _i(t)$, $\rho _i(t)$, and $\lambda (t)$ obey the ordinary differential equations

$$\begin{aligned}&\ddot{\mu }_i+\Omega ^2 \mu _i=0, \qquad \ddot{\rho }_i+\Omega ^2 \rho _i=0,\nonumber \\&\lambda ^{(3)}+4 \Omega ^2\, \dot{\lambda }+4 \Omega \dot{\Omega }\, \lambda =0, \end{aligned}$$

(III.42)

while the conformal factor is

$$\begin{aligned} \Lambda =\kappa +\dot{\lambda }(t)+v \epsilon -2 x_i \dot{\rho }_i (t). \end{aligned}$$

(III.43)

Taking into account the order of the differential Eq. (III.42), one finds that the transformations (III.41) involve $6+4d+\frac{d(d-1)}{2}=\frac{(4+d)(3+d)}{2}$ independent infinitesimal parameters – the same as that of the flat-space conformal group in $d+2$ dimensions.

From Eq. (III.43) one concludes that the $\kappa$, $\dot{\lambda }(t)$, $\epsilon$, and $\rho _i(t)$-transformations give rise to conformal Killing vectors,⁵ while the $\nu$, $\mu _i(t)$, $\omega _{ij}$ and constant $\lambda$-transformations generate Killing vectors. In view of (III.42), the isometry with constant parameter $\lambda$ is only possible for constant frequency $\Omega$ which corresponds to a stationary spacetime. Time translations are broken in general.

We notice that, while distinct conformal isometries act on the coordinates as in (III.41), the functions $\lambda (t)$, $\rho _i(t)$ and $\mu _i(t)$ are not independent. Obviously, $\rho _i(t)$ differs from $\mu _i(t)$ by an inessential constant. If $\mu$ satisfies the first equation in (III.42), then $\lambda (t) = \mu ^2(t)$ will satisfy the second. Moreover, if $\mu _1$ and $\mu _2$ are independent solutions of the first equation, then the three independent solutions of the second are given by $\mu _1^2$, $\mu _2^2$, $\mu _1 \mu _2$. The deeper reason why this happens is that the conformal Killing vectors form a Lie algebra, which we identify below with $so(2,2+d)$.

The interpretation of the (conformal) Killing vectors above and their algebra becomes more transparent if one switches to conformal time, (III.35). It is evident that all (conformal) isometries of the PP-wave metric

$$\begin{aligned} ds^2=-\gamma ^2 x_i x_i d\eta ^2-d\eta dv+dx_i dx_i, \end{aligned}$$

(III.44)

will be automatically transmitted to become (conformal) isometries of (III.35), because the two expressions only differ by the cosmic scale factor $a(\eta )$. In particular, all the symmetry transformations of (III.44), which do not involve $\eta$ explicitly, will be transformed into the Killing vectors of (III.35), while those affecting $\eta$ will be transmitted into conformal Killing vectors.

Our clue is that the metric above is conformally flat. This follows from the vanishing of the Weyl tensor. Skipping details we merely mention that it can also be seen, explicitly, by applying the Arnold transformation, see [4, 38, 39].

The group of conformal transformations of any $(1,1+d)$-dimensional conformally flat spacetime is isomorphic to that of Minkowski space, explaining the “coincidence” we noted earlier.

The explicit form of the (conformal) isometries of (III.44) follows from Eqs. (III.41) and (III.42) at $\Omega =1$ after the substitution $t \rightarrow \eta$. In particular, conformal time translations, $\eta \rightarrow \eta +\theta$, are now symmetries, because $\gamma =\mathrm{const.}$ in (III.44).

From the first equation in (III.42) one finds,

$$\begin{aligned} \mu _i(\eta )=\alpha _i \cos {(\eta )}+\beta _i \sin {(\eta )}, \end{aligned}$$

(III.45)

where the infinitesimal parameters $\alpha _i$ and $\beta _i$ are associated with spatial translations and Newton–Hooke boosts [52]. The second equations generate

$$\begin{aligned} \rho _i(\eta )=\tilde{\alpha }_i \cos {(\eta )}+\tilde{\beta }_i \sin {(\eta )}, \end{aligned}$$

(III.46)

which involve the infinitesimal parameters $\tilde{\alpha }_i$, $\tilde{\beta }_i$ and provide contributions to Eq. (III.41) which are nonlinear in $x_i$. The third equation yields

$$\begin{aligned} \lambda (\eta )=\theta +\sigma \cos {(2\eta )}+\rho \sin {(2\eta )}, \end{aligned}$$

(III.47)

where the infinitesimal parameters $\theta$, $\sigma$, $\rho$, linked to time translations, special conformal transformations, and dilatations form an so(2, 1) subalgebra. Along with spatial rotations described by $\omega _{ij}$, the $\mu _i(\eta )$ and $\lambda (\eta )$–transformations form the conformal Newton–Hooke algebra. For a detailed discussion of the Schrödinger and conformal Newton–Hooke algebras and their realizations in spacetime see e.g. [53,54,55].

As it follows from (III.41), the isometries of (III.44) also involve the translation in the v-direction, while the set of conformal isometries contains the $\kappa$, and $\epsilon$–transformations.

Note that the $\kappa$-transformation in (III.41) and (III.43) is realized in a way analogous to conventional dilatation in the Schrödinger algebra. It derives from the latter by replacing the temporal variable t by the “null” coordinate v; it has appeared before in the context of gravitational waves [56]. The $\epsilon$-transformation is in turn an analog of special conformal transformation, again t replaced by v. It is straightforward to verify that, along with the translations in the v–direction, $v'=v+\nu$, they form an so(2, 1) subalgebra. Interestingly enough and extending the Galilei-Carroll “duality” [57], the latter acts upon the null coordinate v in very much the same way as so(2, 1) entering the conformal Newton–Hooke algebra affects the temporal coordinate t.

To summarize, the algebra of vector fields which involve both Killing and conformal Killing vectors can be identified with $so(2,2+d)$, the conformal Newton–Hooke algebra being its subalgebra.

Having identified the conformal isometries of the metric (III.38), the symmetries of the underlying classical system in one fewer dimension (i.e., the time-dependent oscillator) could now be derived. Skipping details, we just mention that implementing the null reduction along v, the SO(2, 1) conformal subgroup with parameters $\nu$, $\kappa$ and $\epsilon$ in (III.41) will be broken, allowing us to recover the Schrödinger symmetry found in [49]. The generators are conveniently identified using the formulae in Sect. 3 of [50].

3.5 Geodesic motion in Ermakov–Milne–Pinney cosmoi

Having established a link between the EMP equation and the ED lift, let us study the geodesic motion in EMP cosmoi. The analysis is facilitated by switching to the conformal time (III.35) which allows one to solve the geodesic equations by quadrature,

$$\begin{aligned}&\tau =\kappa \int _{\eta _0}^\eta a^2(\tilde{\eta }) d\tilde{\eta }+\tau _0,\end{aligned}$$

(III.48a)

$$\begin{aligned}&x_i(\eta )=\alpha _i \cos {(\gamma \eta )}+\beta _i \sin {(\gamma \eta )}, \end{aligned}$$

(III.48b)

$$\begin{aligned}&v(\eta )=v_0-\frac{1}{2}(\alpha ^2-\beta ^2) \gamma \sin {(2\gamma \eta )}+\alpha \beta \gamma \cos {(2\gamma \eta )}\nonumber \\&\qquad \quad \ \,-\,\epsilon \kappa ^2 \int _{\eta _0}^\eta a^2(\tilde{\eta }) d\tilde{\eta }, \end{aligned}$$

(III.48c)

where $\tau _0$, $\kappa$, $\alpha _i$, $\beta _i$, $v_0$ are constants of integration and $\alpha ^2=\alpha _i \alpha _i$, $\alpha \beta =\alpha _i \beta _i$. It is assumed that $\epsilon =0$ for null geodesics and $\epsilon =-1$ for time-like geodesics.

Before proceeding, it is worth mentioning that, because for null geodesics Eq. (III.48a) admit a particular solution

$$\begin{aligned} x_i(\eta )=0, \qquad v(\eta )=v_0, \end{aligned}$$

(III.49)

the metric (III.35) is formulated in a reference frame comoving with a light signal which travels along the v-axis. This correlates with the fact that (III.35) differs from a PP-wave by a scale factor only.

The first line in (III.48a) defines $\eta$ as an implicit function of the proper time $\tau$. Although in most cases of interest the integral $\int _{\eta _0}^\eta a^2(\tilde{\eta }) d\tilde{\eta }$ cannot be evaluated exactly, Eq. (III.48a) prove to be sufficient to comprehend a qualitative behaviour of geodesics. Indeed, Eq. (III.48b) defines an ellipse. By making use of rotational invariance, one can set the ellipse to lie, say, in the $x_1 x_2$-plane. As v evolves with time, geodesics in the EMP cosmology wrap around the elliptic cylinder, v being its axis.

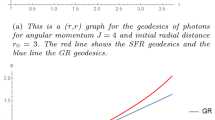
For null geodesics ($\epsilon =0$), the trajectory is a closed loop and the motion is periodic (see Fig. 1). For time-like geodesics ($\epsilon =-1$), the orbit wraps around the cylinder remaining in a compact region of space for some time, then the $\epsilon$-term in Eq. (III.48c) starts dominating and the particle escapes (see Fig. 2). Given the coordinate system in which the metric (III.35) is formulated, this happens because massive particles travel slower than a reference frame comoving with a light signal which propagates along the v-axis.

Fig. 1

Null geodesics in EMP cosmoi are closed loops which wrap around elliptic cylinders. The graph lies in three–dimensional space with $(x_1,x_2,v)$ parametrizing the two horizontal and the vertical axes, respectively

Fig. 2

Time-like geodesics in EMP cosmoi wrap around elliptic cylinders. They remain in a compact region of space for some time before escaping. The graph is given in three-dimensional space, $(x_1,x_2,v)$ parametrizing the two horizontal and one vertical axes, respectively

Little is known about analytic solutions to the EMP equation. Assuming that the energy density $\Omega ^2(t)$ decreases with time (which happens in an expanding universe), one has (see, e.g., [23] and Sect. 2.4.2 in [34])⁶

$$\begin{aligned}&\Omega ^2(t)=\frac{h^{n-2}}{4 \nu ^2 t^n}, \qquad \nu =\frac{1}{2-n}, \qquad n\ne 2,\end{aligned}$$

(III.50a)

$$\begin{aligned}&a(t)=\sqrt{\pi \gamma \nu t(J_\nu ^2 (\lambda )+Y_\nu ^2 (\lambda ))}, \qquad \lambda ={\left( \frac{t}{h}\right) }^{\frac{1}{2\nu }}, \end{aligned}$$

(III.50b)

where n is a rational number such that $\nu$ is positive, h is a positive constant, and $J_\nu$, $Y_\nu$ are Bessel functions. Note that in these cases a(t) is a monotonically increasing convex function which tends to a fixed nonzero value as $t\rightarrow 0$.

Other interesting examples are provided by negative integer $\nu$; then $\nu$ should be replaced by $|\nu |$ in the expression for a(t) in Eq. (III.50b). These models are represented by monotonically increasing convex functions starting at $a(0)=0$. The instance $t=0$ can be interpreted as the Big Bang. A typical example is shown in Fig. 3.

A notable simplification takes place for $\ddot{a}=0$, when the solution is expressed in terms of elementary functions

$$\begin{aligned} \Omega (t)=\frac{h}{t^2}, \qquad a(t)=\sqrt{\frac{\gamma }{h}}\, t \qquad \Rightarrow \qquad \Omega (t)=\frac{\gamma }{{a(t)}^2}. \end{aligned}$$

(III.51)

This case corresponds to a linearly expanding universe in which the energy density of matter decreases consistently with the inverse square law. The general solution to the geodesic equations is,

Fig. 3

A graph of the cosmic scale factor in the EMP cosmological model at $n=3$

$$\begin{aligned}&t=t_0+\tau /\kappa , \end{aligned}$$

(III.52a)

$$\begin{aligned}&x_i(\tau )=\alpha _i \cos {\left( h/t\right) }+\beta _i \sin {\left( h/t\right) }, \end{aligned}$$

(III.52b)

$$\begin{aligned}&v(\tau )=v_0-\epsilon \kappa ^2 t- \alpha \beta \gamma \cos {\left( 2h/t\right) }\nonumber \\&\qquad \qquad +\,\frac{1}{2}(\alpha ^2-\beta ^2) \gamma \sin {\left( 2h/t\right) }, \end{aligned}$$

(III.52c)

where $t_0$, $\kappa$, $\alpha _i$, $\beta _i$, $v_0$ are constants of integration.

Although the graphs representing the cosmic scale factors in the EMP cosmology look quite reasonable, the geodesic motion is apparently unrealistic. This happens because Eq. (III.48b) defines an ellipse. An obvious cure is to generalize the construction to the case of time-dependent $\gamma$ which will alter the qualitative behaviour of geodesics. It proves sufficient to replace $\gamma$ in (III.30) by an arbitrary function $\gamma (t)$ which will then show up on the right hand side of Eq. (III.31), viewed as an algebraic equation to fix $\gamma (t)$ in terms of a(t) and $\Omega (t)$. In this way one can model a reasonable geodesic behavior in the generalized EMP cosmoi by properly choosing the cosmic scale factor and the energy density. Note, however, that, as the associated geodesic equations involve a time-dependent oscillator, with frequency $\gamma (t)^2$, finding an analytic solution may be complicated.

4 Friedmann–Lemaître–Robertson–Walker spacetimes

There has been considerable interest in the past few years in applying the ideas circling around the EMP equation to problems in cosmology, both classical and quantum, [8,9,10,11,12,13,14,15]. In this section we shall establish some connections. Before doing so we shall begin by establishing our notations and conventions.

A Friedmann–Lemaître–Robertson–Walker (FLRW) spacetime is one carrying the metric

$$\begin{aligned} g_{\mu \nu }dx^\mu dx^\nu = - dt ^2 + a^2(t)\, d {\Sigma ^2}_K , \end{aligned}$$

(IV.1)

where $d{\Sigma ^2}_K$ is a 3-dimensional metric of constant curvature K. The scale factor a(t) is governed by three equations of which, if $\dot{a} \ne 0$, only two are independent. These are the Raychaudhuri equation

$$\begin{aligned} \frac{\ddot{a}}{a} = -\frac{4 \pi G}{3} (\rho +3P) + \frac{\Lambda }{3} , \end{aligned}$$

(IV.2)

the Friedmann equation

$$\begin{aligned} {\left( \frac{\dot{a}}{a} \right) }^2 + \frac{K}{a^2} = \frac{8\pi G}{3}\rho + \frac{\Lambda }{3} , \end{aligned}$$

(IV.3)

and the conservation equation

$$\begin{aligned} \dot{\rho }+ 3\frac{ \dot{a}}{a} ( \rho + P) =0 , \end{aligned}$$

(IV.4)

where $\rho$ is the energy density, P is the pressure and $\Lambda$ is the cosmological constant.

4.1 Matter models

The simplest models for the matter content are those in which it consists of a perfect fluid with constant barotropic index. This means that

$$\begin{aligned} P=(\gamma -1) \rho = w \rho , \end{aligned}$$

(IV.5)

where $\gamma$, or equivalently w, is constant. It follows from (IV.4) that

$$\begin{aligned} \rho = \frac{\rho _0}{a^{3 \gamma }} . \end{aligned}$$

(IV.6)

One has the following special cases

• $\gamma =1$ corresponds to pressure–free matter.

• $\gamma =\frac{4}{3}$ to radiation.

• $\gamma =0$ to a cosmological constant which is equivalent to a constant energy density $\rho = \frac{\Lambda }{8\pi G}$.

• $\gamma =2$ is the largest value of $\gamma$ consistent with the dominant energy condition. If the energy density is positive it is sometimes known as “stiff matter”. If $\gamma >2$ there exist solutions for which the scale factor blows up in finite time.

• $\gamma = \frac{2}{3}$ corresponds to a gas of cosmic strings.

• $\gamma = \frac{1}{3}$ corresponds to a gas of membranes.

• If $\gamma < \frac{2}{3}$, there exist solutions exhibiting a “big rip”, that is for which the scale factor blows up in finite time [58] .

Another simple model is to suppose that the matter consists of a scalar field $\phi$ with potential $V(\phi )$

$$\begin{aligned} \rho = \frac{1}{2}\dot{\phi }^2 + V(\phi ) , \quad P= \frac{1}{2}\dot{\phi }^2 -V(\phi ). \end{aligned}$$

(IV.7)

It follows from (IV.4) that

$$\begin{aligned} \ddot{\phi }+ 3 \frac{\dot{a}}{a} \dot{\phi }+ V^\prime (\phi ) =0. \end{aligned}$$

(IV.8)

If $|V(\phi )|<< \frac{1}{2}\dot{\phi }^2$ this behaves like stiff matter, $\gamma =2$. If $|V(\phi )|>> \frac{1}{2}\dot{\phi }^2$ this behaves like a cosmological constant.

4.2 Cosmic clocks and temporal diffeomorphisms

The coordinate t is called cosmic time and may be measured by atomic clocks. To good approximation it also coincides with local astronomical time. For some purposes it is convenient to introduce another coordinate $\eta$ called conformal time, defined by

$$\begin{aligned} \eta = \int \frac{dt}{a(t)} , \end{aligned}$$

(IV.9)

in terms of which the FLRW metric is manifestly conformally static

$$\begin{aligned} ds ^2 = a^2(t) \Bigl \{-d \eta ^2 + d {\Sigma ^2_K} \Bigr \}\, . \end{aligned}$$

(IV.10)

If $\chi$ is radial distance, conformal time may be measured by light clocks. In other words, the ticks of a light clock correspond to light rays being bounced between two co-moving mirrors. This procedure is often attributed to Marzke and Wheeler [59], but in fact it goes back to Einstein, Robb, Milne, Whitrow and Walker. A survey of explicit solutions of the Friedmann equations for matter with a constant barotropic index both as a function of cosmic time and of conformal time may be found in [60].

Concerns about the notion of a Big Bang and the beginning of the universe have led to consideration of other cosmic clocks or choices of what have variously been called time scales or time graduations [61,62,63]. One obvious choice is the temperature or equivalently the redshift

$$\begin{aligned} T=\frac{a(t_0)}{a(t)} T_0 = T_0(1+z) , \end{aligned}$$

(IV.11)

where $T_0\approx 3K$ and the subscript 0 denotes the present epoch. Now if a(t) runs from 0 at the Big Bang to $\infty$ in the infinite future then T runs from $\infty$ to 0. In fact given three successive instants of time $t_1 \prec t_2 \prec t_3$ the temperature changes, $T_{12} = \frac{T (t_1)}{T(t_2)}$ etc behave multiplicatively

$$\begin{aligned} T_{13} = T_{12} T_{23} , \end{aligned}$$

(IV.12)

but taking logarithms $T= e^{-\Omega }$ gives an additive scale [62, 63]:

$$\begin{aligned} \Omega _{13}= \Omega _{12}+ \Omega _{23} , \end{aligned}$$

(IV.13)

which runs from $-\infty$ to $+ \infty$. Because from (IV.3) we have

$$\begin{aligned} d\Omega = \frac{da}{a} = \frac{\dot{a}}{a} dt \end{aligned}$$

(IV.14)

the FLRW metric takes the Eternal Peripatetic Form

$$\begin{aligned} g_{\mu \nu }dx^\mu dx^\nu = - \frac{ d \Omega ^2}{ \frac{8 \pi G \rho }{3} + \frac{\Lambda }{3} - K^2 e^{-2 \Omega } } + e^{2 \Omega } d {\Sigma ^2_K} . \end{aligned}$$

(IV.15)

Of course merely introducing a new time coordinate will not turn a geodesically incomplete spacetime into a geodesically complete one, but it does underscore the point that rejecting a geodesically incomplete spacetime as being singular requires a physical justification, not merely a convenient mathematical definition in order to prove theorems.

For a perfect fluid with constant barotropic index and vanishing cosmological constant, another temporal diffeomorphism defined by

$$\begin{aligned} d\tau = \frac{2}{3 \gamma -2}{2a} dt \end{aligned}$$

(IV.16)

combined with the definition

$$\begin{aligned} x=\sqrt{\frac{3}{8 \pi G \rho _0} } a^{\frac{3 \gamma -2}{2}} \, \quad \Longleftrightarrow \quad a= \Bigl (\frac{8 \pi G \rho _0}{3} x^2 \Bigr ) ^{\frac{1}{3 \gamma -2}} \end{aligned}$$

(IV.17)

reduces the Friedmann equation (IV.3) to that of a TIHO

$$\begin{aligned} \bigl (\frac{dx}{d\tau }\bigr )^2 + Kx^2 = 1 . \end{aligned}$$

(IV.18)

If $K>0$ this is a simple harmonic oscillator. If $K<0$ this is an “inverted” simple harmonic oscillator. Both may be construed as a free particle moving in a 2-dimensional Newton–Hooke spacetime with coordinates $(\tau ,x)$ [52]. The systems are invariant under the conformal extensions of Newton–Hooke-groups $NH_\pm$ [52, 55].

A related construction works if $K=0$ but we include a cosmological constant term or dark energy term.

If $\Lambda >0$ multiplication of (IV.3) by $a^{3\gamma }$ leads to an upside down simple harmonic oscillator equation for $a^{\frac{3 \gamma }{2}}$ with solutions of the form

$$\begin{aligned} a= \Bigg [ \sqrt{ \frac{8 \pi G \rho _0}{\Lambda }} \sinh \Bigg ( \frac{3 \gamma }{2} \sqrt{\frac{\Lambda }{3}} t \Bigg ) \Bigg ] ^{\frac{2}{3 \gamma }}. \end{aligned}$$

(IV.19)

One may calculate the jerk [64]

$$\begin{aligned} j= \frac{a^2 \frac{d^3 a}{dt ^3}}{ \bigl ( \frac{da}{dt} \bigr )^3} = 1 + \frac{9 \gamma (\gamma -1)}{ 2 \cosh ^2 ( \frac{3 \gamma }{2} \sqrt{\frac{\Lambda }{3}} t ) } . \end{aligned}$$

(IV.20)

If $\gamma =1$, $j=1$ for all times. Otherwise it merely starts from a value greater than one and monotonically decreases to 1 at late times. For example for radiation, $\gamma =\frac{4}{3}$, the jerk starts from 3.

If $\Lambda <0$ the motion is converted to a standard harmonic oscillator. For radiation $\gamma =\frac{4}{3}$ and (IV.2) becomes

$$\begin{aligned} \ddot{a} + \frac{|\Lambda |}{3} a= - \frac{8 \pi G \rho _0}{a^3 } , \end{aligned}$$

(IV.21)

which is a variant of the EMP equation [12]. Eq. (IV.19) gives the particular solution:

$$\begin{aligned} a= & {} \Bigg [\sqrt{ \frac{8 \pi G \rho _0}{|\Lambda |}} \sin \Bigg (2 \sqrt{\frac{|\Lambda |}{3}} t \Bigg ) \Bigg ] ^{\frac{1}{2}}\nonumber \\= & {} \Bigg [\sqrt{ \frac{8 \pi G \rho _0}{-\Lambda }} 2 \sin \Bigg ( \sqrt{\frac{|\Lambda |}{3}} t \Bigg ) \cos \Bigg ( \sqrt{\frac{|\Lambda |}{3}} t \Bigg ) \Bigg ] ^{\frac{1}{2}}. \end{aligned}$$

(IV.22)

One may check that the solution (IV.22) is a special case of the general solution given by (II.11) and (II.12).

The instance $\gamma = \frac{2}{3}$ or $w=\gamma -1 = -\frac{1}{3}$ and $\Lambda <0$ gives the special $k=0$ case of the so-called simple harmonic universe [15]. It takes the form

$$\begin{aligned} a = \frac{4 \pi G \rho _0}{|\Lambda |} \Bigg ( 1- \cos \Bigg ( \sqrt{\frac{| \Lambda |}{3}} t \Bigg ) \Bigg ). \end{aligned}$$

(IV.23)

The general solution of (IV.2) subject to the constraint (IV.3) and an origin of time is

$$\begin{aligned} a = \frac{4 \pi G \rho _0}{|\Lambda |} - \sqrt{ \Bigg (\frac{4 \pi G \rho _0}{|\Lambda |} \Bigg ) ^2 - \frac{3K}{|\Lambda |} } \cos \Bigg (\sqrt{\frac{|\Lambda |}{3}} t \Bigg ). \end{aligned}$$

(IV.24)

If $K=0$ this coincides with our previous solution; if $K>0$ it is the non-singular cyclic universe of [15] .

For more examples of solutions of the Friedmann and Raychaudhuri equations the reader is referred to [65,66,67].

4.3 Lifting the Friedmann-Lemaître-Robertson-Walker geodesics

Having presented the main features of FLRW cosmologies, now we show how the ED lift can be applied to geodesic motion in FLRW spacetimes and how to derive its dynamical symmetries. We then extend the result to the Dmitriev–Zel’dovich equations.

Our starting point is the geodesic Hamiltonian

$$\begin{aligned} H_{FLRW} = \frac{1}{2a^2} \left( - p_\eta ^2 + h^{ij} p_i p_j \right) , \end{aligned}$$

(IV.25)

where $\eta$ is the conformal time introduced in the previous section, and $h_{ij}$, $i, j, = 1, \dots 3$ is the metric on the 3–dimensional space. Setting $H_{FLRW} = - {m^2}/{2}$ and solving for $p_\eta$, we get :

$$\begin{aligned} p_\eta = \sqrt{m^2 a^2(\eta )+ h^{ij} p_i p_j} \,\, . \end{aligned}$$

(IV.26)

We identify the low-energy regime as $\frac{p_i p_i}{m^2 a^2(\eta )}<< 1$. In an expanding universe $p_i$ is constant. Therefore the dynamics will, unlike in the usual non-relativistic case, always enter this regime for large enough $\eta$. In this limit

$$\begin{aligned} p_\eta = m a(\eta ) + \frac{h^{ij} p_i p_j}{2ma(\eta )} \, , \end{aligned}$$

(IV.27)

which is a relationship between dynamical variables of order 2 in the momenta. Then an important step is to transform this relation into a homogeneous one by introducing a conserved momentum, $p_v$ — which is the physical equivalent of constructing a projective conic from a standard one, as described in [68].

In our case the process transforms (IV.27) into

$$\begin{aligned} p_\eta p_v = m a(\eta ) p_v^2 + \frac{h^{ij} p_i p_j}{2ma(\eta )} \, . \end{aligned}$$

(IV.28)

This dynamical relation can be recovered by studying the null geodesics of the Hamiltonian

$$\begin{aligned} \mathcal {H} = \frac{h^{ij} p_i p_j}{2ma(\eta )} - p_\eta p_v + m a(\eta ) p_v^2 \, , \end{aligned}$$

(IV.29)

which is associated with the metric

$$\begin{aligned} ds^2 = m a(\eta ) h^{ij} dx_i dx_j - 2ma(\eta ) d\eta ^2 - 2 d\eta dv \, . \end{aligned}$$

(IV.30)

After a translation, $v = \tilde{v} - m \int ^\eta a(\eta ^\prime ) d\eta ^\prime$, we obtain

$$\begin{aligned} ds^2 = m a(\eta ) h^{ij} dx_i dx_j - d\eta d\tilde{v} \, . \end{aligned}$$

(IV.31)

In particular, if the spatial slices are flat then the metric is conformally flat. Its conformal symmetries contain the Schrödinger group as a subgroup, providing us with symmetries also of the original FLRW Hamiltonian $H_{FLRW}$ in (IV.25).

Another consequence is that the null geodesics of the ED lift just constructed are the same as the null geodesics of the EMP spacetime, described in Sect.3.3.

We conclude this subsection by generalizing our findings to N particles in a FLRW spacetime, subject to their mutual gravitational interaction. The Hamiltonian we use is

$$\begin{aligned} \frac{1}{2a^2} \left[ - p_{\eta }^2 + \sum _{A=1}^N h^{ij} p^A_i p^A_j \right] - \sum _{1\le A < B \le N} \frac{G m_i m_j}{a|\mathbf {r}^A - \mathbf {r}^B |} \, , \end{aligned}$$

(IV.32)

where the $p_i^A$ are the spatial momenta of the individual particles and $\mathbf {r}^A$ their coordinates.

Our Hamiltonian relies on the assumption that the proper times of all particles can be synchronized and described by the same parameter. This is possible because the spacetime is spatially homogeneous. As before, we set the Hamiltonian equal to a constant value $-{M^2}/{2}$, calculate the low-energy limit and make the relationship homogeneous in the momenta. We obtain the null Hamiltonian

$$\begin{aligned} \mathcal {H} = - p_\eta p_{\tilde{v}} + \frac{1}{2Ma} \sum _{A=1}^N h^{ij} p^A_i p^A_j - \frac{1}{M} \sum _{1\le A < B \le N} \frac{G m_i m_j}{|\mathbf {r}^A - \mathbf {r}^B |} p_{\tilde{v}}^2 \, , \end{aligned}$$

(IV.33)

where again we have redefined the v variable in order to remove the term $Ma(\eta ) p_v^2$. Going back to cosmic time, with $p_\eta = a p_t$, we obtain

$$\begin{aligned} \mathcal {H}= & {} a(t) \left[ - p_t p_{\tilde{v}} + \frac{1}{2Ma^2} \sum _{A=1}^N h^{ij} p^A_i p^A_j \right. \nonumber \\&\left. - \frac{1}{Ma} \sum _{1\le A < B \le N} \frac{G m_i m_j}{|\mathbf {r}^A - \mathbf {r}^B |} p_{\tilde{v}}^2 \right] \, , \end{aligned}$$

(IV.34)

which belongs to the same conformal class as the ED lift of the Hamiltonian presented in [70].

This gives rise to the Dmitriev–Zel’dovich equations [52, 69, 70]. If we consider, as is done in almost all numerical studies of large scale structure, the motion of N non-uniformities about a FLRW background metric, they are governed by the Dmitriev-Zeldovich equations [69, 70]

$$\begin{aligned} \frac{d}{dt} \Bigl ( a^2(t) \dot{\mathbf{x}}_a \Bigr ) = \frac{1}{a(t)} \sum _{b\ne a} \frac{Gm_b( \mathbf{x}_b-\mathbf{x}_a) }{ | \mathbf{x}_b -\mathbf{x}_a |} \end{aligned}$$

(IV.35)

where $a,b=1,2,\dots ,N$ label the non-uniformities and $m_a$ are their masses. It is simple to verify that if one replaces every $\mathbf{x}_a$ in (IV.35) by

$$\begin{aligned} \mathbf{x}_a + \mathbf{a} + \mathbf{b} \int _0^t \frac{dt ^\prime }{a(t^\prime ) } \end{aligned}$$

(IV.36)

then the Dmitriev-Zeldovich equations are left invariant.

Equation (IV.35) may be derived from a Lagrangian [70, 71]

$$\begin{aligned} L= \frac{1}{2} \sum _ {1\le a \le N} a^2(t) m_a {\dot{\mathbf{x}}_a}^2 + \frac{1}{a(t)} \sum _ {1\le a < b \le N} \frac{Gm_am_b}{|\mathbf{x}_a-\mathbf{x}_b|}. \end{aligned}$$

(IV.37)

This system Eisenhart-Duval lifts to

$$\begin{aligned} ds ^2= & {} \sum _ {1\le a \le N} a^2(t) m_a d \mathbf{x}_a^2 + 2 dt dv\nonumber \\&+ 2 \frac{1}{a(t)} \sum _ {1\le a < b \le N} \frac{Gm_am_b}{|\mathbf{x}_a-\mathbf{x}_b|} dt^2 . \end{aligned}$$

(IV.38)

Up to signs and factors this coincides with the metric (III.30) as long as $\gamma =0$ and $G=0$. In other words a free non-relativistic particle in a background Friedmann universe lifts to a null geodesic of (III.30) provided $\gamma =0$. In fact the time-dependent harmonic oscillator in (III.30) looks very much like a cosmological constant term.

4.4 The Eisenhart–Duval lift of the Friedmann equations

The action density of Einstein gravity coupled to a scalar field is

$$\begin{aligned} \mathcal{L}= \Bigl \{ \frac{1}{16 \pi G} R -\frac{1}{2}g^{\mu \nu } {\partial }_\nu \phi {\partial }_\nu \phi - V(\phi ) \Bigr \} . \end{aligned}$$

(IV.39)

Substituting in the FLWR metric and assuming $\phi$ depends on t we find that up to a total time derivative

$$\begin{aligned} \mathcal{L}= \frac{6}{1 6 \pi G} (-a \dot{a} ^2 + K a ) + a^3 (\frac{1}{2}\dot{\phi }^2 + V(\phi )). \end{aligned}$$

(IV.40)

Variation with respect to $\phi$ and a yields the field equation for $\phi$ and the following second order ODE for a

$$\begin{aligned} \frac{\ddot{a}}{a} + \frac{\dot{a} ^2}{a^2} = -\frac{4 \pi G}{3} (\dot{\phi }^2 - 4 V(\phi ) ) . \end{aligned}$$

(IV.41)

One may check that (IV.41) is a linear combination of the second order Raychaudhuri equation and the first order Friedmann equation. If one calculates the Hamiltonian density $\mathcal H$ of $\mathcal L$ one finds that the two canonical momenta are

$$\begin{aligned} p_\phi = a^3 \dot{\phi }, \qquad p_a =- \frac{3}{4 \pi G} a \dot{a} , \end{aligned}$$

(IV.42)

and considered as a function of the velocities $(\dot{a}, \dot{\phi })$, we find that

$$\begin{aligned} \mathcal{H}= \frac{6}{1 6 \pi G} (-a \dot{a} ^2 - K a) + a^3 ( \frac{1}{2}\phi ^2 + V(\phi ) ). \end{aligned}$$

(IV.43)

One may check that the Friedmann ODE is the same as the constraint

$$\begin{aligned} \mathcal{H}=0. \end{aligned}$$

(IV.44)

To understand better what is happening we note that in setting $g_{tt}=-1$ in the Friedmann metric we have used up some gauge freedom and as a consequence the $\mathcal L$ does not depend upon sufficiently many independent variables in order to obtain the full set of equations of motion. To rectify this problem, on considers the more general metric

$$\begin{aligned} ds^2 =-N^2(t) dt ^2 + a^2(t) d \Sigma _K ^2 \end{aligned}$$

(IV.45)

which however differs from our previous form by no more than a temporal diffeomorphism or clock regraduation.The function N(t) is called the lapse function. It measures the lapse of time relative to cosmic time. Now

$$\begin{aligned} \tilde{\mathcal{L}}= \frac{6}{1 6 \pi G} (- N^{-1}a \dot{a} ^2 +N K a ) + a^3 ( N^{-1} \frac{1}{2}\dot{\phi }^2 + N V(\phi )) . \end{aligned}$$

(IV.46)

We see that the lapse function N enters (IV.46) as a Lagrange multiplier and varying the Lagrangian $\tilde{\mathcal{L}}$ with respect to N and then setting $N=1$ one gets the Friedmann equation, i.e. the Hamiltonian constraint (IV.44). In fact in terms of the canonical momenta we have⁷

$$\begin{aligned} \mathcal{H}= N \Bigl \{ - \frac{2 \pi G}{3} \frac{p_a^2}{a} - \frac{3 K}{8 \pi G} + \frac{1}{2}\frac{p_\phi ^2 }{a^3} + a^3 V(\phi ) \bigr \} . \end{aligned}$$

(IV.47)

We are now in the situation to perform an ED lift or Marsden-Weinstein oxidation, we set

$$\begin{aligned} p_t= -\mathcal{H} \end{aligned}$$

(IV.48)

and introduce an ignorable momentum $p_v$ and rewrite (IV.47) as

$$\begin{aligned}&2 H_\mathrm{{Eisenhart-Duval}}= 2p_t p_v \nonumber \\&\quad + 2 N \Bigl \{ - \frac{2 \pi G}{3} \frac{p_a^2}{a} - \frac{3 K}{8 \pi G} p_v^2 + \frac{1}{2}\frac{p_\phi ^2 }{a^3} + a^3 V(\phi ) p_v^2 \Bigr \}=0.\nonumber \\ \end{aligned}$$

(IV.49)

Note that if we set $N=1$ and compute the 4- metric then the coefficients of $da ^2$ and $d \phi ^2$ have the opposite sign. If we regard N as a further coordinate, then we have a Galilean or Newton-Cartan metric.

5 Conclusion

Let us recapitulate the results obtained in this work:

• Any Newtonian mechanical system can be described in terms of the Eisenhart-Duval metric which solves the Einstein equations (III.10). The key ingredient involved in the construction is the energy–momentum tensor (III.6) built out of the covariantly constant null Killing vector field (III.5) and a proper energy density function.

• The celebrated Ermakov–Lewis invariant of a time-dependent harmonic oscillator can be obtained in purely geometric way by applying the Eisenhart-Duval lift.

• A cosmological extension of the Eisenhart-Duval metric is constructed by properly incorporating into the scheme a cosmic scale factor and the energy-momentum tensor. The evolution of spacetime is governed by the Ermakov–Milne–Pinney equation.

• Killing isometries include spatial translations and rotations, Newton–Hooke boosts and translation in the null direction.

• The algebra of vector fields which involve both Killing and conformal Killing vectors is identified with $so(2,2+d)$, the conformal Newton–Hooke algebra being its subalgebra.

• Geodesic motion in Ermakov–Milne–Pinney cosmoi is described.

• The Eisenhart-Duval lift of geodesics in the Friedmann–Lemaître–Robertson–Walker spacetimes is found and then generalized to the Dmitriev–Zel’dovich equations.

• The derivation of the Friedmann equations within the framework of the Eisenhart–Duval lift is presented.