1 Introduction

Inflation is a generic intermediate attractor in the direction of expansion of the universe, and in the case of pure \(R^2\) gravity it is an exact attractor [1]. However, it is not an attractor in the opposite direction in time. Thus, if we are interested in the most generic behavior before inflation, more general anisotropic and inhomogeneous solutions should be considered. We know from general relativity (GR) that already anisotropic homogeneous solutions help us much in understanding the structure of a generic space-like curvature singularity. Thus, a natural question is to investigate anisotropic solutions in the \(R+R^2\) gravity, too.

In the light of the latest Cosmic Microwave Background constraints by PLANCK [2], the pioneer inflationary model based on the modified \(R+R^2\) gravity (with small one-loop corrections from quantum fields)  [3] represents one of the most favorable models. It lies among the simplest ones from all viable inflationary models since it contains only one free adjustable parameter taken from observations. Also it provides a graceful exit from inflation and a natural mechanism for creation of known matter after its end, which is actually the same as that used to generate scalar and tensor perturbations during inflation. This theory can be read as a particular form of f(R)-theories of gravity which, in turn, is a limiting case of scalar-tensor gravity when the Brans–Dicke parameter \(\omega _{BH}\rightarrow 0\), and it contains an additional scalar degree of freedom (scalar particles, or quasi-particles, in quantum language) compared to GR which is purely geometrical. The existence of a scalar degree of freedom (an effective scalar field) is needed if we want to generate scalar (matter) inhomogeneities in the universe from “vacuum” fluctuations of some quantum field [4, 5]. Such generalizations of the familiar Einstein–Hilbert action have been also studied as an explanation for dark energy and late-time acceleration of the universe’s expansion [6,7,8,9] and to include quantum behavior in the gravitational theory [10].

As is already very well known, through the Gauss–Bonnet term which in four dimensions is a surface term, the most general theory up to quadratic in curvature terms is of the type \(R+R^2+C_{abcd}C^{abcd}\), where \(C_{abcd}\) is the Weyl tensor. The investigations of this type of models began with [11,12,13,14]. After them, many authors have analyzed the cosmological evolutions of such a model [15,16,17,18,19,20,21,22,23,24,25,26,27,28,29]. Particular attention is given to the asymptotic behavior in [30,31,32,33,34]. The addition of a Weyl square term creates a richer set of solutions, and in particular, in [1, 35, 36], it has been shown that the cosmic no-hair theorems no longer hold.

Quadratic theory, like \(R+R^2\) gravity, is a particular case of the more general quadratic type, and it has higher order time derivatives in the equations of motion and this leads to the appearance of solutions which have no analogs in GR. One of such solutions corresponds to the scale factor \(a \sim \sqrt{t}\) behavior, which coincides with a radiation dominated solution in GR. In quadratic gravity, this solution represents a vacuum solution which is also a stable past attractor for Bianchi I model and probably for all Bianchi models [36]. The other solution, being an analog of a GR solution with matter with equation of state, \(p=(\gamma -1)\rho \), is \(a \sim t^{4/3 \gamma }\) (instead of usual \(a \sim t^{2/3 \gamma }\) in GR), and it can be naively considered as a solution which would describe the last stages of a collapsing universe when quadratic terms dominate. However, this solution appears to be a saddle, so a collapsing universe for a general initial condition ends up with a vacuum “false radiation” regime, in principle not possible in GR.

The \(a(t)\propto \sqrt{t}\) behavior near singularity in the \(R+R^2\) model does not mean that the \(R^2\) term behaves as radiation generically. This behavior is specific only for the purely isotropic case, as it will be shown in the present paper (and even in the isotropic case the late-time behavior is different: \(a(t)\propto t^{2/3}\) modulated by small high-frequency oscillations). Neither does it behave as an ideal fluid in the anisotropic case.

When shear is taken into account the situation becomes more complicated. Vacuum solutions exist in GR also, and in the simplest case of a flat anisotropic metrics (which is the case analyzed in the present paper) this is the famous Kasner solution [37]. On the other hand, studies of cosmological evolution in a general quadratic gravity (which includes apart from \(R^2\) the Weyl tensor square term in the quadratic part of the action) indicate that the isotropic vacuum “false radiation” still exists and, moreover, it is an attractor [36]. Kasner solution is also a solution in quadratic gravity. Due to complicated nature of dynamics near the Kasner solution a generic trajectory could end up in Kasner or isotropic solution depending on initial conditions [38].

For these reasons, the stability and the full behavior of quadratic theories of gravity is still subject of investigation and one powerful tool to address these problems is the dynamical system approach [39] which allows one to find exact solutions of the theory through the determination of fixed points and gives a description of the evolution of the system, at least at qualitative level.

Despite the obvious fact that the general quadratic gravity at the level of the action includes \(R+R^2\) gravity (which can be obtained setting the coefficient before Weyl square term to zero) it is not so at the level of corresponding equations of motion for the universe model in question. The reason is that the number of degrees of freedom in a general quadratic gravity is bigger than in \(R+R^2\) theory (which, in its turn, is bigger than in GR). That is why we cannot simply put the corresponding constant to zero in cosmological equations of motion. This means that cosmological evolution of a flat anisotropic universe in \(R+R^2\) gravity needs a special investigation which is the matter of the present paper.

The paper is organized as follows: in Sect. 2, we present the basic equations of the model. In Sect. 3 we describe schematically the strategy adopted to obtain the correct degrees of freedom and then we analyze the dynamics of \(R^2\)-gravity both in the vacuum case and in the case with matter; we find exact solutions and determine their stability. In Sect. 4, we derive the analytic behavior of the shear using a general line element. Finally, Sect. 5 contains a summary of the results and conclusions.

2 System under consideration

The gravitational action considered in our analysis is the following:

$$\begin{aligned} S=\frac{1}{16\pi G}\int d^{4}x \sqrt{-g}\left[ \left( R-2\Lambda \right) +\beta R^{2}\right] , \end{aligned}$$
(1)

where g is the determinant of the metric, G is the Newton constant, and \(\beta \) is a parameter.

This theory can be interpreted as a particular form of f(R) gravity. Observations tell us that the dimensionless coefficient \(\frac{\beta }{16\pi G}\) is very large, \(\approx 5 \times 10^8\). This follows from the fact that its expression in terms of observable quantities, in the leading order of the slow-roll approximation, is \(\frac{\beta }{16\pi G}= \frac{N^2}{288\,\pi ^2 P_{\zeta }(k)}\) where \(P_{\zeta }(k)\) is the power spectrum of primordial scalar (adiabatic) perturbations, N is both \( \ln {k_f/k}\) and the number of e-folds from the end of inflation, \(k_f\) being the wave vector corresponding to the comoving scale equal to the Hubble radius at the end of inflation (\(k_f/a(t_0)\) is slightly less than the CMB temperature now); see e.g. [40]. For the \(R+R^2\) inflationary model, \(P_{\zeta }\propto N^2\), so \(\beta \) is a constant indeed. Note also that \(\beta =\frac{1}{6M^2}\) where M is the scalaron mass after the end of inflaton (and in flat space-time too). On the other hand, the coefficient of the Weyl square term (which is present in a general quadratic model of gravity) in the Lagrangian density generated by one-loop quantum gravitational effects is not expected to be so large. Typically it is of the order of unity (or even significantly less due to small numerical factors) multiplied by the number of elementary quantum fields. Thus, there exists a large range of the Riemann and Ricci curvature where the \(R^2\) term dominates, while the contribution from the Weyl square term is still small. For this reason, anisotropic solutions preceding the inflationary stage may be studied using the same \(R+R^2\) model up to curvatures of the order of the Planck one.

Metric variation of the theory in (1) gives the following fields equations:

$$\begin{aligned} E_{ab}\equiv \left( G_{ab}+g_{ab}\Lambda \right) +\beta H_{\, ab}^{(1)}=0, \end{aligned}$$
(2)

where

$$\begin{aligned} G_{ab}= & {} R_{ab}-\frac{1}{2}g_{ab}R\,,\nonumber \\ H_{ab}^{(1)}= & {} -\frac{1}{2}g_{ab}R^{2}+2RR_{ab}+2g_{ab}\nabla ^2 R-2R_{;ab}. \end{aligned}$$
(3)

\(H_{ab}^{(1)}\) is the contribution coming from the variation of \(R^2\) term. Let us emphasize that every Einstein metric satisfying \(R_{ab}=g_{ab}\Lambda \) is an exact solution of (2). This implies that all vacuum solutions of GR are also exact solutions of the quadratic theory (1). Any source that satisfies \(\nabla ^{c}T_{ca}=0\), can consistently be added to the right hand side of (2).

As anticipated, a powerful tool for finding exact solutions of a quadratic theory of gravity is the dynamical system approach, which allows for the determination of fixed point and for a qualitative description of the global dynamics of the system. It is particularly suited for the study of the dynamics of anisotropic space-times [39], like spatially homogeneous Bianchi metrics. In this case we can write the line element as

$$\begin{aligned}&ds^{2}=-\frac{dt^{2}}{H(t)^{2}}+\delta _{ij}\mathbf{{\omega }}^{i}\otimes \omega ^{j}, \end{aligned}$$
(4)

where the \(i,\, j\) indices refer to the spatial part and \(\omega ^{j}\) is a triad of one-forms,

$$\begin{aligned} d \omega ^{i}=-\frac{1}{2}C^{a}_{\,bc} \omega ^{b}\otimes \omega ^{c}, \end{aligned}$$
(5)

where \(C^{a}_{\,bc}\) are the spatial structure constants of the Bianchi group, and depend only on time. They are usually defined as

$$\begin{aligned} C^{a}_{\,bc}=\varepsilon _{bcd} n^{da}-\delta ^{a}_{\,b} a_{c} + \delta ^{a}_{\,c}a_{b}, \end{aligned}$$
(6)

where the values of the symmetric matrix \(n^{ab}\) and the vector \(a_{b}\) define the various Bianchi models. In our case, where we focus on Bianchi I metric, we have \(n_{ab}=0\) and \(a_{b}=0\).

Defining the time-like vector \(u^{a}=(H,0,0,0)\), which satisfies the normalization condition \(u^{a}u_{a}=-1\), and the projection tensor \(h_{ab}=g_{ab}+u_{a}u_{b}\), we can define the relevant kinematical quantities

$$\begin{aligned}&\nabla _{a}u_{b}=\sigma _{ab}+\omega _{ab}+\frac{1}{3}\theta \delta _{ab}-\dot{u}_{a}u_{b},\nonumber \\&\sigma _{ab}=u_{(a;b)}-\frac{1}{3}\theta \delta _{ab}+\dot{u}_{(a}u_{b)},\nonumber \\&\omega _{ab}=u_{[a;b]}+\dot{u}_{[a}u_{b]},\nonumber \\&\dot{u}_{a}=u^{b}\nabla _{b}u_{a},\nonumber \\&\theta =\nabla _{c}u^{c}, \end{aligned}$$
(7)

where \(\sigma _{ab}\) is the symmetric shear tensor \((\sigma _{ab}=\sigma _{(ab)}, \sigma _{ab}u^{b}=0, \sigma ^{a}_{\;a}=0)\), \(\omega _{ab}\) is the vorticity tensor \((\omega _{ab}=\omega _{(ab)}, \omega _{ab}u^{b}=0)\) and \(\dot{u}_{a}\) is the acceleration vector. \(\theta \) is the volume expansion, and it is related to the Hubble parameter by

$$\begin{aligned} \theta =\frac{1}{3}H. \end{aligned}$$
(8)

In our analysis we consider a cosmological model where the shear is diagonal and is defined as

$$\begin{aligned}&\sigma _{ij}=\text{ diag }\left[ -\frac{2\sigma _{+}}{H},\frac{\sigma _{+}+\sqrt{3}\sigma _{-}}{H},\frac{\sigma _{+}-\sqrt{3}\sigma _{-}}{H}\right] , \end{aligned}$$
(9)

and since we will consider spatially homogeneous space-times, the time-like vector is geodesic \(\dot{u}^{a}=0\) with zero vorticity \(\omega _{ab}=0\), being normal to the time slices.

We consider a perfect fluid source with no anisotropic pressures so the energy-momentum tensor is

$$\begin{aligned} T_{ab}=(\rho +p)u_au_b +pg_{ab}\,, \end{aligned}$$
(10)

and it can be decomposed schematically as

$$\begin{aligned} 8\pi GT_{ab}=\text{ diag } [3\Omega _m, 3wH^2\Omega _m,3wH^2\Omega _m,3wH^2\Omega _m]\,, \end{aligned}$$
(11)

where w is the equation of state (EoS) parameter.

In order to have a system of autonomous first order differential equations we divide the shear \(\sigma _{\pm }\), given in (9), and density parameters by appropriate powers of H, defining in this way the new dimensionless expansion-normalized variables (ENVs)

$$\begin{aligned} \Sigma _{\pm }= & {} \frac{\sigma _{\pm }}{H}\,,\nonumber \\ \Omega _{m}= & {} \frac{8 \pi G \rho }{3H^{2}}\,,\nonumber \\ \Omega _{\Lambda }= & {} \frac{\Lambda }{3H^{2}}, \end{aligned}$$
(12)

where \(\rho /H^2= T_{00}\) is the energy density.

The rest of the ENV are zero since we are restricting ourselves to the Bianchi I case. The time evolution of the sources follows directly from the conservation of the energy-momentum tensor (\(\nabla ^{b} T_{ab}=0\)) and from the definition itself of (12),

$$\begin{aligned} \dot{\Omega }_{m}= & {} -3(w+1)\Omega _{m}-2Q_1\Omega _{m}\,,\nonumber \\ \dot{\Omega }_{\Lambda }= & {} -2Q_1\Omega _{\Lambda }\,. \end{aligned}$$
(13)

The fact that we have higher order theory of gravity requires the introduction of additional ENVs, which reflect the higher order time derivatives in the equations of motion, as first done in [36],

$$\begin{aligned} Q_{1}= & {} \frac{\dot{H}}{H}\,,\nonumber \\ Q_{2}= & {} \frac{\ddot{H}}{H^2}\,,\nonumber \\ B= & {} \frac{1}{3\beta H^{2}}\,. \end{aligned}$$
(14)

According to their own definitions, these ENV must satisfy the following differential equations:

$$\begin{aligned}&\dot{\Sigma }_{\pm }=\Sigma _{\pm 1}-\Sigma _{\pm }Q_{1}\,,\nonumber \\&\dot{B}=-2Q_{1}B\,,\nonumber \\&\dot{Q}_{1}=Q_{2}-Q_{1}^{2}\,. \end{aligned}$$
(15)

So now we have all the ingredients the compute the evolution of our theory. The complete dynamical system is given by Eqs. (13), (15) and by the differential equations shown in Appendix A.

3 Generalized anisotropic solutions

Now we start from this particular line element for the space-times:

$$\begin{aligned} ds^{2}=-d\tau ^{2}+\tau ^{2p_{1}}dx^{2}+\tau ^{2p_{2}}dy^{2}+\tau ^{2p_{3}}dz^{2}. \end{aligned}$$
(16)

For vanishing cosmological constant, and near the singularity when \(\tau \rightarrow 0\), the Einstein tensor for the above line element goes like \(G_{ab}\sim 1/\tau ^2\), so it becomes negligible in comparison to the \(H^{(1)}_{ab}\sim 1/\tau ^4\) given in (3). By direct substituting the line element (16) into the field equations (2) for the vacuum source, a purely algebraic equation is obtained when \(B=\frac{1}{3\beta H^2}\rightarrow 0\):

$$\begin{aligned} p_{2}^{2}+ & {} p_{2}(-1+p_{1}+p_{3})-(p_{1}+p_{3}-p_{1}^{2}\nonumber \\- & {} p_{3}^{2}-p_{1}p_{3})=0. \end{aligned}$$
(17)

The set of solutions (17) can be parametrized using the two angles \(\psi \) and \(\phi \),

$$\begin{aligned} p_{1}= & {} \sqrt{\frac{3}{8}}\sin \phi \left( \frac{\cos \psi +\sqrt{2}\sin \psi }{\sqrt{2}}\right) +\frac{1}{4},\nonumber \\ p_{3}= & {} \sqrt{\frac{3}{8}}\sin \phi \left( \frac{\cos \psi -\sqrt{2}\sin \psi }{\sqrt{2}}\right) +\frac{1}{4},\nonumber \\ p_{2}= & {} \frac{1}{4}-\sqrt{\frac{3}{8}}\sin \phi \frac{\cos \psi }{\sqrt{2}}+\sqrt{\frac{3}{8}}\cos \phi , \end{aligned}$$
(18)

where \(\psi =[0,2\pi ]\) and \(0<\phi <\pi , \) and this set lies in the surface of an ellipsoid as shown in Fig. 1. In this surface are contained both the generalized Kasner solution and the isotropic solution.

Fig. 1
figure 1

Ellipsoid in the parameter space \(p_1\), \(p_2\) and \(p_3\) given by Eq. (18)

Full size image

The expansion-normalized variables for the line element (16) read

$$\begin{aligned} Q_{1}= & {} -\frac{3}{p_{1}+p_{2}+p_{3}},\nonumber \\ Q_{2}= & {} \frac{9}{(p_{1}+p_{2}+p_{3})^{2}},\nonumber \\ \Sigma _{+}= & {} \frac{-3p_{1}+(p_{1}+p_{2}+p_{3})}{2(p_{1}+p_{2}+p_{3})},\nonumber \\ \Sigma _{-}= & {} \frac{\sqrt{3}(p_{2}-p_{3})}{2(p_{1}+p_{2}+p_{3})}. \end{aligned}$$
(19)

The solution space given by Eq. (17) can be written in a more compact form using the variables \(u=p_1^2+p_2^2+p_3^2\) and \(s=p_1+p_2+p_3\), with \(\tau \rightarrow 0\),

$$\begin{aligned} \frac{u}{2} +\frac{s^2}{2}-s=0, \end{aligned}$$
(20)

or with respect to ENV with \(B\rightarrow 0\), as

$$\begin{aligned} 2+Q_1+\Sigma _-^2+\Sigma _+^2=0. \end{aligned}$$
(21)

The solution of (20) is easily obtained as

$$\begin{aligned} u=2s-s^2. \end{aligned}$$
(22)

This compact way of writing the equation, is particular suitable to check the solutions: in fact it can easily be seen that the Kasner (\(s=1\) and \(u=1\)) and the isotropic vacuum (\(s=3/2\) and \(u=3/4\)) are both particular solutions of this equation.Footnote 1 We also remember that, in terms of the ENV, the generalized Kasner solution is given by \(Q_1=-3\), \(\Sigma _+^2+\Sigma _-^2=1\), and the isotropic vacuum solution by \(Q_1=-2\) and \(\Sigma _+=\Sigma _-=0\). Both of these solutions belong to the solution set given by (20).

The Ricci scalar can be written in terms of the ENV, and in terms of variables s and u, like

$$\begin{aligned} R= & {} \frac{2}{\beta B}\left( 2+Q_{1}+\Sigma _{+}^{2}+\Sigma _{-}^{2}\right) ,\nonumber \\ R= & {} \frac{6}{\beta B}\left( \frac{s^2/2 +u/2-s}{s^2}\right) , \end{aligned}$$
(23)

such that the solution given in (22) and (21) as long as \(B\ne 0\), results in

$$\begin{aligned} R=0. \end{aligned}$$

By looking at (3), it is not difficult to convince ourselves that a zero Ricci scalar (\(R=0\)) is in fact the asymptotic solution of Eq. (2). If near the singularity when \(\tau \rightarrow 0\), the most important contribution to (2) comes from \(H^{(1)}_{ab}\) given in (3), the field equation can be approximated by

$$\begin{aligned} H^{(1)}_{ab}\approx 0, \end{aligned}$$
(24)

then \(R=const.=0\) implies \(H^{(1)}_{ab} = 0\). Let us stress that this solution is only valid if the other terms in the field equation (2) are negligible in comparison to \(H^{(1)}_{ab}\).

On the other hand for vanishing cosmological constant and in the absence of classical sources, in a non-perturbative picture in the sense that the Einstein tensor \(G_{ab}\) is not disregarded, it behaves as an effective source for field equations. Even though it diverges at the singularity (20), the ratios of the effective pressures to energy densities obtained directly from (16),

$$\begin{aligned} \epsilon _1= & {} \frac{G_1^1}{G_{00}}=-\frac{p_3^2-p_3+p_3p_2+p_2^2-p_2}{p_2p_1+p_3p_1+p_3p_2},\\ \epsilon _2= & {} \frac{G_2^2}{G_{00}}=-\frac{p_1^2-p_1+p_3^2-p_3+p_1p_3}{p_2p_1+p_3p_1+p_3p_2},\\ \epsilon _3= & {} \frac{G_3^3}{G_{00}}=-\frac{p_1^2-p_1+p_2^2-p_2+p_2p_1}{p_2p_1+p_3p_1+p_3p_2}, \end{aligned}$$

do have a well-defined limit. The trace indicates that at the singularity, given by (20), the effective EOS parameter behaves as in radiation,

$$\begin{aligned} \epsilon _1+\epsilon _2+\epsilon _3=1. \end{aligned}$$
(25)

3.1 Stability analysis

In the dynamical system approach, the field equations are rewritten with respect to the ENV, such that the solutions are fixed points. In particular, the solution space described in the previous section constitutes an invariant set of fixed points. The linearization around the fixed points reveals the local stability of the theory. In fact, since all eigenvalues \(\lambda _i \ge 0\), this solution set is an attractor to the past, as all trajectories to the future deviate exponentially from this solution set. Stability with and without a matter source is going to be addressed, and the presence of matter is irrelevant for sufficiently big shear.

3.1.1 Obtaining the dynamical system

In order to describe the evolution of the correct degrees of freedom, in this section we will describe the strategy that we have adopted in order to simplify the system of equations of motion. From the \(E_{11}, E_{22}\) and \(E_{33}\) equations in (2) we can isolate the variable related to the higher order time derivative \(Q_{2}\); then we find a system of three differential equations,

$$\begin{aligned} \dot{Q}_{2}= & {} f_{1}(Q_{1},Q_{2},\Sigma _{\pm 2},\Sigma _{\pm 1},\Sigma _{\pm },\Omega ,B),\nonumber \\ \dot{Q}_{2}= & {} f_{2}(Q_{1},Q_{2},\Sigma _{\pm 2},\Sigma _{\pm 1},\Sigma _{\pm },B),\nonumber \\ \dot{Q}_{2}= & {} f_{3}(Q_{1},Q_{2},\Sigma _{\pm 2},\Sigma _{\pm 1},\Sigma _{\pm },B), \end{aligned}$$
(26)

where f is a generic function of all the remaining ENV. From the \(E_{00}\) component of (2), we obtain a constraint equation,

$$\begin{aligned} 0=C_{1}(\Sigma _{\pm 1},\Sigma _{\pm },Q_{1},Q_{2},\Omega ,B), \end{aligned}$$
(27)

which, as we will see, will be important to check the stability of the numerical evolution of the dynamical system.

By making a linear combination of the field equations (26), we can obtain two additional constraints, which read

$$\begin{aligned} 0= & {} C_{2}(\Sigma _{\pm 1},\Sigma _{\pm },Q_{1},Q_{2},\Omega ,B),\nonumber \\ 0= & {} C_{3}(\Sigma _{\pm 1},\Sigma _{\pm }Q_{1},Q_{2},\Omega ,B). \end{aligned}$$
(28)

So now, from the constraints (27) and (28), it is possible to write three algebraic equation for \(Q_{2}\), \(\Sigma _{+1}\) and \(\Sigma _{-1}\), which will be a function of the remaining variables and we write it schematically as

$$\begin{aligned}&Q_{2}(\Sigma _{\pm },Q_{1},\Omega ,B),\nonumber \\&\Sigma _{+1}(\Sigma _{\pm },Q_{1},\Omega ,B),\nonumber \\&\Sigma _{-1}(\Sigma _{\pm },Q_{1},\Omega ,B). \end{aligned}$$
(29)

If now we consider the ENV related to \(\ddot{\sigma }_{\pm }\), defined as \(\Sigma _{\pm 2}=\frac{\ddot{\sigma }_{\pm }}{H}\), we can use its definition to derive the equation \(\dot{\Sigma }_{\pm 1}=\Sigma _{\pm 2}-Q_{1}\Sigma _{\pm 1}\). Using (29), it is now possible to derive the equation for \(\Sigma _{\pm 2}\)

$$\begin{aligned} \Sigma _{\pm 2}(\Sigma _{\pm },Q_{1},\Omega ,B). \end{aligned}$$
(30)

Substituting the last equation and Eq. (29) into the original dynamical system equations we finally obtain also the equation for \(\dot{Q}_{2}=f_{1}(\Sigma _{\pm },Q_{1},\Omega ,B)\).

Then the complete dynamical system is described by the following equations:

$$\begin{aligned}&\dot{Q}_{1}=Q_{2}(\Sigma _{\pm },Q_{1},\Omega ,B)-Q_{1}^{2},\nonumber \\&\dot{\Sigma }_{\pm }=\Sigma _{\pm 1}(\Sigma _{\pm },Q_{1},\Omega ,B)-Q_{1}\Sigma _{\pm },\nonumber \\&\dot{B}=-2Q_{1}B,\nonumber \\&\dot{\Omega }_{m}=\left( -2Q_{1}-3(w+1)\right) \Omega _{m},\nonumber \\&\dot{Q}_{2}=f_{1}(\Sigma _{\pm },Q_{1},\Omega ,B), \end{aligned}$$
(31)

where in our analysis the last equation will be integrated numerically to be compared with the algebraic relation \(Q_{2}(\Sigma _{\pm },Q_{1},\Omega ,B)\) contained in (29). Moreover, we will use one of the constraints to obtain a conserved quantity to numerically check the stability of our results. The last equation is not a dynamical degree of freedom, but just an artifact to check numerically the solutions.

Looking at the above set of equations, it can be noted that there is only one additional dynamical degree of freedom compared to General Relativity, which is the first equation for \(\dot{Q}_{1}\). This can be easily understood by remembering that, through a conformal transformation, this gravitational theory is equivalent to GR plus a scalar field [42].

As we have described above, the linearization of the dynamical system (31) around the solution (21) gives rise to the following eigenvalues, which will be discussed in the next subsections.

3.1.2 Pure geometric modes

As a first case we consider the vacuum case (without the matter modes). In this case the stability of the system is characterized by the following eigenvalues:

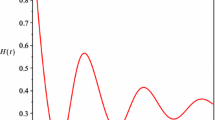
$$\begin{aligned} \lambda _{1}= & {} 2(2+\Sigma _{-}^2+\Sigma _{+}^2),\nonumber \\ \lambda _{2}= & {} 3(\Sigma _{+})^{2}+3(\Sigma _{-})^{2}+3,\nonumber \\ \lambda _{3}= & {} 0_{2}. \end{aligned}$$
(32)

Except for the two zero eigenvalues this solution is an attractor to the past. These two zero eigenvalues appear naturally because in fact we have a two-dimensional set of fixed points So, according to this theory, the universe began as a generalized non-isotropic solution as shown in Fig. 2. It can be seen in panel (b) that an arbitrary initial condition approaches Eq. (19), which defines this solution set. Even if not reported the constraint was numerically verified.

Fig. 2
figure 2

Backwards time evolution, showing the approach to the singularity. The expansion-normalized shear variables \(\Sigma _+\) and \(\Sigma _-\) and \(Q_1\) approach constant asymptotic values. We explicitly checked that asymptotically \(Q_1<-4.37\). In a) it can be seen that the Ricci scalar decreases, which is consistent with Eq. (61) when \(Q_1<-3\). In b) it is explicitly shown that the numerical solution approaches Eq. (19), as it should for all points of the past attractor. Even if not reported in the plot, the constraint has been checked to be satisfied numerically

Full size image

3.1.3 Matter modes

Allowing perturbations in the matter sector \((\Omega _{\Lambda },\,\Omega _{m})\) we have the following eigenvalues:

$$\begin{aligned} \lambda _{1}= & {} 3(\Sigma _{+})^{2}+3(\Sigma _{-})^{2}+3,\nonumber \\ \lambda _{2}= & {} 1-3w+2(\Sigma _{+})^{2}+2(\Sigma _{-})^{2},\nonumber \\ \lambda _{3}= & {} 0_{2},\nonumber \\ \lambda _{4}= & {} (4+2(\Sigma _{+})^{2}+2(\Sigma _{-})^{2})_2. \end{aligned}$$
(33)

Excluding the zero eigenvalues, it is interesting that this solution is an attractor to the past in the presence of a cosmic substance for any initial values for \(\Sigma _{+}\) and \(\Sigma _{-}\) as long as the EoS parameter \(-1<w<1/3\). For \(1/3<w<1\), the solution will still be an attractor to the past for sufficiently big initial values of \(\Sigma _{+}\) and \(\Sigma _{-}\) such that \(\lambda _{2}\) is positive.

We focused on solutions which are attractors to the past; however, there can be other solutions [36].

4 Analytic behavior

Now, starting from a remarkable property of any f(R) gravity, obtained in [14], it is possible to determine the dynamical evolution of the shear as an exact, analytical result. Considering a Lagrangian like

$$\begin{aligned} \mathcal {L}=\sqrt{-g}f(R)\,, \end{aligned}$$
(34)

the variation with respect to the metric gives the following field equation:

$$\begin{aligned} f^\prime R_{ab} -\frac{1}{2} f g_{ab} -\nabla _a\nabla _b f^\prime + \nabla ^2 f^\prime g_{ab}=\kappa T_{ab}\,, \end{aligned}$$
(35)

where \(f'\) is used to denote derivative w.r.t. to R, and \('\) represents derivative w.r.t. to the proper time. \(T_{ab}\) is the energy-momentum tensor of some matter source. Since we are considering a spatially homogeneous space-time, with corresponding sources, the following combinations are zero: \(a)\,T_{22}-T_{33}=0\), \(b)\,T_{11}-T_{22}/2-T_{33}/2=0\). In the same way, taking the same combinations of the left hand side of the field equations (35), we have

$$\begin{aligned}&a)\;2H\sqrt{3}\left( \frac{d}{dt}\sigma _- +3\sigma _-\right) f^\prime +2H\sqrt{3}\sigma _-\frac{d}{dt}f^\prime =0\,,\end{aligned}$$
(36)
$$\begin{aligned}&b)\; 3H\left( \frac{d}{dt}\sigma _+ +3\sigma _+\right) f^\prime +3 H\sigma _+\frac{d}{dt}f^\prime =0\,. \end{aligned}$$
(37)

We can see that these equations admit as solutions

$$\begin{aligned} a)\;\sigma _-= & {} \frac{C_- e^{-3t}}{f^\prime }\,,\end{aligned}$$
(38)
$$\begin{aligned} b)\;\sigma _+= & {} \frac{C_+ e^{-3t}}{f^\prime }\,. \end{aligned}$$
(39)

Now we can connect the constants (\(C_{\pm }\)) with the parameters \(p_1, p_2\) and \(p_3\). As in [14] we can write the scale factors given in (16) as

$$\begin{aligned} a=rg_1,\;\; b=rg_2,\;\;c=rg_3,\;\;\;\;\; \text{ with } \;\;\;\;\; abc=r^3, \end{aligned}$$
(40)

such that assuming \(\prod _ig_i=1\), we have

$$\begin{aligned} \frac{\dot{g}_1}{g_1}+\frac{\dot{g}_2}{g_2}+\frac{\dot{g}_3}{g_3}=0. \end{aligned}$$
(41)

Taking into account (7), (8) and (9) we find that

$$\begin{aligned} \frac{\dot{r}}{r}= & {} H\,,\end{aligned}$$
(42)
$$\begin{aligned} \frac{\dot{g}_1}{g_1}= & {} -2\sigma _+,\;\;\;\frac{\dot{g}_2}{g_2}=\sigma _+ +\sqrt{3}\sigma _-,\;\;\; \frac{\dot{g}_3}{g_3}=\sigma _+- \sqrt{3}\sigma _-.\nonumber \\ \end{aligned}$$
(43)

Remembering that derivatives with respect to proper time are related to derivatives with respect to dynamical time by \(\frac{d}{d\tau }=\frac{dt}{d\tau } \frac{d}{dt}=H\frac{d}{dt}\), we can solve the first of (43),

$$\begin{aligned} r=e^{t}\,, \end{aligned}$$
(44)

which, when substituted into (39) and (43), gives

$$\begin{aligned} \frac{\dot{g}_i}{g_i}=\frac{C_i}{r^3f^\prime }\,. \end{aligned}$$
(45)

The relation found here is the same as Eq. (10) in [14] with the constant \(C_{\pm }\) related to \(C_1\), \(C_2\) and \(C_3\) by

$$\begin{aligned} C_1=-2C_+,\;\; C_2=C_+ +\sqrt{3}C_-,\; \;C_3=C_+-\sqrt{3}C_-\,. \end{aligned}$$
(46)

When we consider the asymptotic solution discussed above we finally find that the relation with the coefficient \(p_1\), \(p_2\) and \(p_3\) is the following:

$$\begin{aligned} C_1=p_1-\frac{s}{3}, \;\;C_2=p_2-\frac{s}{3}, \;\; \text{ and } C_3=p_3-\frac{s}{3}\,, \end{aligned}$$
(47)

where again \(s=p_1+p_2+p_3\) and (22) must be satisfied. \(C_\pm \) can also be expressed as

$$\begin{aligned} C_+= & {} \frac{-2p_1+p_2+p_3}{6}\,,\nonumber \\ C_-= & {} \frac{3p_2-p_3}{6\sqrt{3}}\,. \end{aligned}$$
(48)

It is now possible to understand the space of solutions close to the singularity, when \(B\rightarrow 0\), as long as the solution stays near the asymptotic solution given in (20), which must be fulfilled since as explained in Sect. 3.1 the solution is an attractor to the past.

First of all, taking the trace of (2) bearing in mind (3), gives the following equation for R in the absence of sources:

$$\begin{aligned}&-R+6\beta \Box R=0,\nonumber \\&-R-\frac{1}{3\beta B}(\ddot{R}+(Q_1+3)\dot{R})=0 . \end{aligned}$$
(49)

Near the singularity, when \(t \rightarrow -\infty \), \(Q_1=-3/s=const.\) and \(B=\frac{e^{6t/s}}{3 \beta H_0^2 }\) and Eq. (49)

$$\begin{aligned} \ddot{R}+(-3/s+3)\dot{R}+R\frac{e^{6t/s}}{H_0^2 }=0 \end{aligned}$$
(50)

has an analytical solution given by the Bessel function of the first type \(J_a\) and the Bessel function of the second type \(Y_a\), which when written with respect to proper time \(\tau \), \(\exp (3t/s)\propto \tau \), is given by

$$\begin{aligned} R= & {} \{\hat{C}_1J_{(s-1)/2}(s\tau /(3H_0))\nonumber \\&+\hat{C}_2Y_{(s-1)/2}(s\tau /(3H_0))\}\tau ^{(1-s)/2}. \end{aligned}$$
(51)

Asymptotically, as \(\tau \rightarrow 0\) and \(B\rightarrow 0\), (50) simplifies to

$$\begin{aligned} \ddot{R}+(-3/s+3)\dot{R}=0, \end{aligned}$$
(52)

and when \(s\ne 1\) the solution is

$$\begin{aligned} R=C +C_0\exp [-(Q_1+3)t]=\frac{C}{3(1-s)}+\tilde{C} \tau ^{(1-s)},\nonumber \\ \end{aligned}$$
(53)

while for \(s=1\), which means \(Q_1=-3\), it is

$$\begin{aligned} R=C_1+\tilde{C_1}t=C_2+\tilde{C_2}\frac{s}{3}\ln (\tau ), \end{aligned}$$
(54)

where all the C are constants.

This asymptotic behavior of R can be substituted into (39) for the particular theory analyzed hitherto, for which we have \(f^\prime =1\,+\,2\beta R\),

$$\begin{aligned} \Sigma _+= & {} \frac{\sigma _+}{H}\nonumber \\= & {} \left( \frac{1}{\exp (Q_1 t)}\right) \frac{C_+ e^{-3t}}{1+2\beta (C+C_0\exp [-(Q_1+3)t] )},\nonumber \\ \Sigma _-= & {} \frac{\sigma _-}{H}\nonumber \\= & {} \left( \frac{1}{\exp (Q_1 t)}\right) \frac{C_- e^{-3t}}{1+2\beta (C+C_0\exp [-(Q_1+3)t] )}.\nonumber \\ \end{aligned}$$
(55)

When \(Q_1>-3\), which corresponds to \(s>1\), this expression gives at the singularity (\(t\rightarrow -\infty \))

$$\begin{aligned} \Sigma _+= & {} \frac{C_+}{2\beta C_0}, \end{aligned}$$
(56)
$$\begin{aligned} \Sigma _-= & {} \frac{C_-}{2\beta C_0}, \end{aligned}$$
(57)

and since \(2+Q_1+\Sigma _-^2+\Sigma _+^2=0\) with \(Q_1=-3/s=const.\), it results in the following asymptotic form for the Ricci scalar:

$$\begin{aligned} R=C+\frac{\sqrt{C_-^2+C_+^2}}{2\beta \sqrt{-Q_1-2}}\exp [-(Q_1+3)t], \end{aligned}$$
(58)

and since the Ricci scalar must be real, \(Q_1<-2\), which gives \(s<3/2\).

We can also obtain the constant C since we know that, interchangeably when \(s<1\) or \(Q_1<-3\), the asymptotic solution set (22) must continue to be a past attractor; see Sect. 3.1. This attractor has constant well-defined values for \(Q_1\), \(\Sigma _\pm \) satisfying (19) and when \(Q_1<-3\) this will only occur if there is a particular cancellation in the denominator of (55) \(f^\prime \rightarrow 0\) giving a well-defined limit for \(\Sigma _\pm \) at the singularity

$$\begin{aligned} 1+2\beta C =0 \rightarrow C=-\frac{1}{2\beta }\,. \end{aligned}$$
(59)

We have the final asymptotic form for the Ricci scalar

$$\begin{aligned} R=-\frac{1}{2\beta }+\frac{\sqrt{C_-^2+C_+^2}}{2\beta \sqrt{-Q_1-2}}\exp [-(Q_1+3)t]\,, \end{aligned}$$
(60)

which is valid through \(0<s<3/2\). Through (48), this last expression can be written as

$$\begin{aligned} R= & {} -\frac{1}{2\beta }\nonumber \\&+\frac{\sqrt{9p_1^2-9p_1p_2-9p_1p_3+9p_2^2+3p_3^2}}{18\beta \sqrt{3/s-2}}\exp [-(-3/s+3)t].\nonumber \\ \end{aligned}$$
(61)

The numerical behavior of the Ricci scalar is shown in Fig. 2 in panel (a). It can be seen that the asymptotic constant value \(R \simeq -1/(2\beta )\) is not reproduced exactly in the plot. The reason is the fact that, in the dynamical system described in the appendix, the denominator, \(4\Sigma _{+}^{2}+4\Sigma _{-}^{2}+4Q_{1}+B+8\), occurs in all equations and it vanishes on the attractor set. Although it is not possible to check numerically the asymptotic time evolution of the Ricci scalar it is possible to see in Fig. 2 panel (a) that the Ricci scalar decreases asymptotically as expected for \(Q_1<-3\).

5 Conclusions

In the present paper we have considered the past attractor solution for the evolution of the flat anisotropic universe in \(R+R^2\) gravity. Our results, in combination with already known results, indicate that the properties of the evolution of the universe near a cosmological singularity change significantly taking into account anisotropy and/or modifications of gravity. Indeed, the evolution of an isotropic universe is determined solely by the matter equation of state. When anisotropy is taken into account, this isotropic solution becomes a future asymptotic solution, while the generalized vacuum Kasner solution becomes a past attractor (except for a stiff fluid with a Jacobs solution).

In general quadratic gravity without anisotropy new vacuum isotropic solution (“false radiation” solution) is stable to the past. The anisotropic case instead has two sub-cases, because general quadratic corrections to the gravitational action have two independent terms, which can be chosen as proportional to the squares of scalar curvature and the Weyl tensor. In a general situation, when these two terms are of the same order, the dynamical system describing the universe past evolution has both “false radiation” and a generalized Kasner solution as attractors (the latter is, more precisely, a saddle-node fixed point). So the nature of a cosmological singularity (isotropic or anisotropic) depends on the initial conditions imposed.

However, since the \(R+R^2\) inflationary model is observationally well motivated, and we have argued in Sect. II above that there exists a large range of the Riemann and Ricci curvatures where the anomalously large \(R^2\) term dominates the Einstein term R, while a “normal-size” Weyl squared term is still small, one can expect that a new solution appears. It has two parameters (so it is a two-dimensional set of solutions) and includes both isotropic “false radiation” and a generalized anisotropic Kasner solution (which is a one-dimensional set) as subsets. Moreover, in some sense, it interpolates between them, because it is possible to construct a line of solutions with one end being an isotropic solution and the other end being a point in the generalized Kasner set.

All these intermediate points disappear when the correction proportional to the Weyl square term is added to the action, leaving only isotropic and generalized Kasner solutions and this represents one of the main results of our paper. However, since an \(R^2\) inflation model is observationally well motivated we can neglect the coefficient in front of the Weyl term, and we can expect that the two-dimensional set of solutions discussed in this paper could be a good approximation for realistic models in quadratic gravity.

In the present paper we have restricted the analysis to flat metrics. However, a positive spatial curvature could, in principle, destroy this regime and generate a more complicated behavior similar to the Belinsky–Khalatnikov–Lifshitz (BKL) [43] singularity in General Relativity. We leave this problem for future analysis.