On possibility of time reversal symmetry violation in neutrino elastic scattering on polarized electron target

Abstract

In this paper we indicate a possibility of utilizing the elastic scattering of Dirac low-energy ($\sim 1$ MeV) electron neutrinos ($\nu _e$s) on a polarized electron target (PET) in testing the time reversal symmetry violation (TRSV). We consider a scenario in which the incoming $\nu _e$ beam is a superposition of left chiral (LC) and right chiral (RC) states. LC $\nu _e$ interact mainly by the standard $V-A$ and small admixture of non-standard scalar $S_L$, pseudoscalar $P_L$, tensor $T_L$ interactions, while RC ones are only detected by the exotic $V + A$ and $S_R, P_R, T_R$ interactions. As a result of the superposition of the two chiralities the transverse components of $\nu _{e}$ spin polarization (T-even and T-odd) may appear. We compute the differential cross section as a function of the recoil electron azimuthal angle and scattered electron energy, and show how the interference terms between standard $V-A$ and exotic $S_R, P_R, T_R$ couplings depend on the various angular correlations among the transversal $\nu _e$ spin polarization, the polarization of the electron target, the incoming neutrino momentum and the outgoing electron momentum in the limit of relativistic $\nu _e$. We illustrate how the maximal value of recoil electrons azimuthal asymmetry and the asymmetry axis location of outgoing electrons depend on the azimuthal angle of the transversal component of the $\nu _e$ spin polarization, both for the time reversal symmetry conservation (TRSC) and TRSV. Next, we display that the electron energy spectrum and polar angle distribution of the recoil electrons are also sensitive to the interference terms between $V-A$ and $S_R, P_R, T_R$ couplings, proportional to the T-even and T-odd angular correlations among the transversal $\nu _e$ polarization, the electron polarization of the target, and the incoming $\nu _e$ momentum, respectively. We also discuss the possibility of testing the TRSV by observing the azimuthal asymmetry of outgoing electrons, using the PET without the impact of the transversal $\nu$ polarization related to the production process. In this scenario the predicted effects depend only on the interferences between $S_R$ and $T_R$ couplings. Our model-independent analysis is carried out for the flavor $\nu _e$. To make such tests feasible, the intense (polarized) artificial $\nu _e$ source, PET and the appropriate detector measuring the directionality of the outgoing electrons and/or the recoil electrons energy with a high resolution have to be identified.

1 Introduction

One of the fundamental problems in neutrino physics is whether the TRSV takes place in purely leptonic processes at low energies [e.g. the neutrino–electron elastic scattering (NEES)]. According to the standard electro-weak model (SM) [1,2,3,4,5], the V and A couplings of LC $\nu _e$ may only participate in the NEES and the hermiticity conditions of the interaction lagrangian require the real coupling constants. This means that there is no possibility of appearing the TRSV correlations in the differential cross section for the NEES, even when the electron target is polarized. The qualitative change emerges when the exotic scalar (S), tensor (T), pseudoscalar (P) and (V + A) couplings of the interacting RC $\nu$s beyond the SM in addition to the standard $V-A$ ones are introduced. The presence of the exotic complex couplings together with the PET may generate the non-vanishing T-even and T-odd angular correlations in the differential cross section. It is worth pointing out that the TRSV (equivalent CP violation in the case of CPT-invariant theory) is observed in the decays of neutral kaons and B-mesons [6,7,8], and described by a single phase of the Cabibbo–Kobayashi–Maskawa quark-mixing matrix (CKM) [9]. However, this CP-violating phase does not allow for explanation of the existing matter-antimatter asymmetry of universe and new T-violating phases are needed [10]. It is important to note that the available experimental results still do not rule out the scenarios with the exotic S, T, P and $V+A$ weak interactions and leave a little space for the interacting RC $\nu$s. The various non-standard gauge models including exotic TRSV interactions, RC $\nu$s, mechanisms explaining the origin of parity violation and of fermion generations, masses, mixing and smallness of $\nu$ mass have been proposed. We mean, e.g., the left–right symmetric models (LRSM) [11,12,13,14,15,16,17], composite models [18,19,20], models with extra dimensions (MED) [21] and the unparticle models (UP) [22,23,24,25,26,27,28,29,30,31,32,33,34]. Concerning the UP theory, it is noteworthy that in this scheme $\nu$s with different chiralities can interact with the spin-0 scalar, spin-1 vector, spin-2 tensor unparticle sectors and consequently one gets the amplitudes for the low-energy leptonic processes in the form of unparticle four-fermion contact interaction with the non-standard S, T, P, $V+A$ lorentz interactions.

In spite of experimental limitations and lack of unambiguous indication of the non-standard model, the precision of present tests at low energies is constantly increased, and on the other hand, it seems sensible to search for new tools sensitive to the linear effects from the exotic complex couplings of RC $\nu$s, because the measurements of these observables may shed some new light on the TRSV in the leptonic interactions. As is well known the future superbeam and neutrino factory projects aim at the tests of the CP violation in the lepton sector, where simultaneously $\nu$ and $\overline{\nu }$ oscillations would be measured [35, 36]. Also other proposals of observables for the tests on the TRSV in the leptonic and semileptonic processes: the precise measurements of T-odd triple-correlations for the massive charged leptons [37,38,39,40,41], of electric dipole moments of the neutron and atoms are worth noticing [42,43,44,45,46]. Till now, all the evidence is consistent with the TRSC scenario.

Our considerations show that the NEES on the PET offers new scientific opportunities for the studies on the TRSV in the leptonic reactions. From the perspective of the main goals of this paper, it is essential to mention the recent tests confirming the possibility of realizing the polarized target crystal of $\mathrm{{Gd}}_{2}\mathrm{{SiO}}_{5}$ doped with cesium [47], as suggested in [48]. The concepts of using the PET to probe the neutrino magnetic moments, the flavor composition of (anti)neutrino beam, axions, spin–spin interaction in gravitation [49,50,51,52,53,54,55,56] are also worth noting.

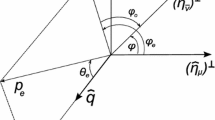
In this study we focus on the elastic scattering of low-energy Dirac $\nu _e$s on the PET. We show in a model-independent way how the admixture of the exotic S, T, P, $V+A$ complex couplings of RC $\nu _e$s in addition to the standard V, A real couplings of LC ones affects the azimuthal distribution and asymmetry of the recoil electrons, polar distribution of scattered electrons and their energy spectrum, and consequently the possibility of TRSV in the relativistic $\nu _e$ limit. We also consider the scenario which allows one to test the TRSV by the measurement of the azimuthal asymmetry of recoil electrons without the impact of the transversal $\nu$ polarization connected with the production process, i.e. when $\theta _\nu =\pi$; see Fig. 1. Our studies are made for the flavor-eigenstate (current) Dirac $\nu _e$s and when the monochromatic $\nu _e$ source is deployed at a short distance from the detector. We analyze the various scenarios assuming that the hypothetical detector is able to measure both the azimuthal angle $\phi _{e}$ and polar angle $\theta _e$ of the recoil electrons, and/or also the energy of the outgoing electrons with a high resolution. In order to compute the expected effects, we use the experimental values of standard couplings: $c_{V}^{L}= 1 + (-0.04 \,\pm \, 0.015), c_{A}^{L}= 1+ (-0.507\, \pm \, 0.014)$ [57].

Fig. 1

The production plane of the $\nu _{e}$ beam is spanned by the polarization unit vector $\hat{S}$ of source and the $\nu _{e}$ LAB momentum unit vector $\hat{\mathbf{q}}$. The reaction plane is spanned by $\hat{\mathbf{q}}$ and the transverse electron polarization vector of target $(\hat{\eta }_{e})^\perp$ (due to $\hat{\eta }_{e} \perp \hat{\mathbf{q}}$) for $\nu _{e} + e^{-}\rightarrow \nu _{e} +e^{-}$. $\theta _{e}$ is the polar angle between $\hat{\mathbf{q}}$ and the unit vector $\hat{\mathbf{p}}_{e}$ of recoil electron momentum. $\phi _{e}$ is the angle between $(\hat{\eta }_{e})^\perp$ and the transversal component of outgoing electron momentum $(\hat{\mathbf{p}}_{e})^{\perp }$. $\hat{\eta }_{\nu }=(\sin \theta _\nu \,\cos \phi _{\nu }, \sin \theta _\nu \,\sin \phi _{\nu }, \cos \theta _\nu )$

2 Elastic scattering of Dirac electron neutrinos on polarized electrons-basic assumptions

We assume (see Fig. 1) that the incoming Dirac $\nu _{e}$ beam is generated by the monochromatic low-energy ($\sim 1 \mathrm{MeV}$) and polarized source ( $\nu _{e}$ emitter with a high intensity). Let us recall that the $^{51}\mathrm{{Cr}}$ unpolarized emitter with a high activity $\sim 370 \; PBq$ in the SOX experiment [58] (Short distance Oscillation with boreXino) at the Borexino detector is planed to search for among other the sterile $\nu _e$s [59,60,61,62,63,64,65]. Moreover, one supposes that the initial $\nu _{e}$ flux is the superposition of LC states with RC ones. LC $\nu _e$s are detected mainly by the standard $V-A$ and small admixture of non-standard scalar $S_L$, pseudoscalar $P_L$, tensor $T_L$ interactions, while RC ones are detected only by the exotic $V + A$ and $S_R, P_R, T_R$ interactions. As a result of the superposition of the two chiralities the transverse components of $\nu _{e}$ spin polarization (T-even and T-odd) may appear. In order to illustrate the possibility of producing the $\nu$ beam with the non-zero transversal spin polarization, we refer to Ref. [66], where the muon capture by a proton as the production process of L-R chiral superposition has been considered. The obtained formulas on the transversal $\nu$ polarizations (both T-even and T-odd) consist only of the interferences between the $(V,A)_{L}$ and $(S, T, P)_{R}$ couplings and do not vanish in the relativistic $\nu$ limit. We have a completely different situation for the longitudinal $\nu$ polarization, where all the interferences between the $V-A$ and $(S, T, P)_{R}$ interactions are strongly suppressed by $\nu$ mass. It means that only the squares of exotic RC couplings (at most the interferences within exotic couplings) and of standard LC ones may generate the possible effect. In the next studies, the other sources are going to be analyzed. The amplitude for $\nu _{e} e^{-}$ scattering takes the form

$$\begin{aligned} M^{D}_{\nu _{e} e^{-}}= & {} \frac{G_{F}}{\sqrt{2}}\Bigg \{\left( \overline{u}_{e'}\gamma ^{\alpha }(c_{V}^{L} - c_{A}^{L}\gamma _{5})u_{e}\right) \left( \overline{u}_{\nu _{e'}} \gamma _{\alpha }(1 - \gamma _{5})u_{\nu _{e}}\right) \nonumber \\&+ \left( \overline{u}_{e'}\gamma ^{\alpha }(c_{V}^{R} + c_{A}^{R}\gamma _{5})u_{e}\right) \left( \overline{u}_{\nu _{e'}} \gamma _{\alpha }(1 + \gamma _{5})u_{\nu _{e}}\right) \nonumber \\&+ c_{S}^{R}(\overline{u}_{e'}u_{e})\left( \overline{u}_{\nu _{e'}} (1 + \gamma _{5})u_{\nu _{e}}\right) \nonumber \\&+ c_{P}^{R}(\overline{u}_{e'}\gamma _{5}u_{e})\left( \overline{u}_{\nu _{e'}} \gamma _{5}(1 + \gamma _{5})u_{\nu _{e}}\right) \nonumber \\&+ \frac{1}{2}c_{T}^{R}\left( \overline{u}_{e'}\sigma ^{\alpha \beta }u_{e})(\overline{u}_{\nu _{e'}} \sigma _{\alpha \beta }(1 + \gamma _{5})u_{\nu _{e}}\right) \nonumber \\&+ c_{S}^{L}(\overline{u}_{e'}u_{e})\left( \overline{u}_{\nu _{e'}} (1 - \gamma _{5})u_{\nu _{e}}\right) \nonumber \\&+ c_{P}^{L}\left( \overline{u}_{e'}\gamma _{5}u_{e})(\overline{u}_{\nu _{e'}} \gamma _{5}(1 - \gamma _{5})u_{\nu _{e}}\right) \nonumber \\&+ \frac{1}{2}c_{T}^{L}\left( \overline{u}_{e'}\sigma ^{\alpha \beta }u_{e})(\overline{u}_{\nu _{e'}} \sigma _{\alpha \beta }(1 - \gamma _{5})u_{\nu _{e}}\right) \Bigg \}, \end{aligned}$$

(1)

where $G_{F} = 1.1663788(7)\times 10^{-5}\,\hbox {GeV}^{-2} (0.6 \; ppm)$ [67] is the Fermi constant. The coupling constants are denoted with the superscripts L and R as $c_{V}^{L, R}$, $c_{A}^{L, R}$, $c_{S}^{R, L}$, $c_{P}^{R, L}$, $c_{T}^{R, L}$, respectively, to the incoming $\nu _{e}$ of left- and right-handed chirality. Because we admit the TRSV, the non-standard coupling constants $c_{S}^{R, L}$, $c_{P}^{R, L}$, $c_{T}^{R, L}$ are the complex numbers denoted as $c_S^R = |c_S^R|e^{i\,\theta _{S,R}}$, $c_S^L = |c_S^L|e^{i\,\theta _{S,L}}$, etc. Moreover, the relations between the exotic couplings, $c_{S, T, P}^{ L}=c_{S, T, P}^{*R}$, appearing at the level of interaction lagrangian should be taken into account. It manifests the lack of dependence of the square terms coming from the S, T, P interactions in the cross section on the longitudinal $\nu _{e}$ polarization $\hat{\eta }_{\nu }\cdot \hat{\mathbf{q}}$. Calculations are carried out with the use of the covariant projectors for the incoming $\nu _{e}$s (including both the longitudinal and transversal components of the spin polarization) in the relativistic limit and for the polarized target-electrons, respectively [68].

Fig. 2

Dependence of $\mathrm{{d}}^2 \sigma /\mathrm{{d}}\phi _e \mathrm{{d}}\,\theta _e$ on $\phi _e$ for the standard $V-A$ interaction, $E_\nu =1\,\mathrm{{MeV}}$: $\theta _e=\pi /12$ (dotted line), $\theta _e=\pi /6$ (solid line), $\theta _e=\pi /3$ (dashed line)

3 Azimuthal distribution and asymmetry of recoil electrons

In this section, we analyze the possibility of using the azimuthal distribution of recoil electrons for the investigation of TRSV in the $\nu$ elastic scattering on the PET. According to the SM, the mentioned azimuthal distribution has a local maximum at $\varPhi =\pi /2$, as is illustrated in Figs. 2 and 3, respectively. Figure 2 is the polar plot of $\mathrm{{d}}^2 \sigma /\mathrm{{d}}\phi _e \mathrm{{d}}\theta _e=\left( \mathrm{{d}}^2 \sigma /\mathrm{{d}}\phi _e \mathrm{{d}} \,y\right) \cdot \left( \mathrm{{d}} \,y/\mathrm{{d}}\theta _e\right)$ as a function of $\phi _e$ for the assigned values of $\theta _e$. Figure 3 is the polar plot of $\mathrm{{d}}^2 \sigma /\mathrm{{d}}\phi _e \mathrm{{d}} \,y$ as a function of $\phi _e$ for the assigned values of y. These two plots reveal the up-down azimuthal symmetry measured with respect to $\varPhi =0$ and the left–right azimuthal asymmetry with the asymmetry axis directed along $\varPhi =\pi /2$, clearly visible for $\mathrm{{d}}^2 \sigma /\mathrm{{d}}\phi _e \mathrm{{d}}\theta _e$. Moreover, it is important to stress that in the case of the standard $V-A$ interaction, the asymmetry axis is fixed at $\varPhi =\pi /2$ and independent of the variations of y, $\theta _e$, $E_{\nu }$, and the standard $c_V^L$, $c_A^L$ couplings values but the degree of the asymmetry can change. Usually to quantify the azimuthal asymmetry one makes use of the asymmetry functions (see Appendix 2 for the definitions). Figure 4 displays the maximal values of the azimuthal asymmetries $A_y(\varPhi =\pi /2)$ and $A_{\theta _e}(\varPhi =\pi /2)$ as functions of y and $\theta _e$ for the standard $V-A$ interaction. In both cases the maximal values of the $A_y$ and $A_{\theta _e}$ are equal to 0.0794, and these are obtained at $y^{max} \approx 0.5$ and $\theta _{e}^\mathrm{max} \approx \pi /6$, respectively. In order to illustrate how the phase of a given exotic coupling and the azimuthal angle of $(\hat{\eta }_{\nu })^{ \perp }$ affect the azimuthal asymmetry of recoil electrons, and consequently to hint at the possibility of TRSV, we present the explicit form of the $A(\varPhi )$ asymmetry function for the scenario with $V-A$ and $S_R$ interactions:

Fig. 3

Dependence of $\mathrm{{d}}^2 \sigma /\mathrm{{d}}\phi _e \mathrm{{d}}\,y$ on $\phi _e$ for the standard V–A interaction, $E_\nu =1\,MeV$: $y=0.1$ (dotted line), $y=0.2$ (solid line), $y=0.5$ (dashed line)

Fig. 4

Standard $V-A$ interaction, $E_\nu =1\,MeV$. Plot of the azimuthal asymmetry functions: $A_y(\varPhi =\pi /2)$ as a function y (dotted line) and $A_{\theta _e}(\varPhi =\pi /2)$ as a function of $\theta _e$ (solid line)

$$\begin{aligned} A_{V-A}^{S,R}(\varPhi )= & {} 3 \sqrt{m_e (2 E_{\nu } + m_e)} \bigg [-(c_{A}^{L} - c_V^L) (3 c_A^L E_{\nu } + c_V^L E_{\nu } \nonumber \\&+ 2 c_A^L m_e) \sin ^2{\frac{\theta _{\nu }}{2}} \sin {\varPhi } \nonumber \\&- |c_S^R| c_V^L (2 E_{\nu } + m_e)\sin {\theta _\nu } \sin {(\theta _{S,R} + \varPhi - \phi _{\nu })}\bigg ]/ \nonumber \\&\bigg [4 \left( |c_S^R|^2 + 4 (c_A^L{}^2 + c_A^L c_V^L + c_V^L{}^2)\right) E_{\nu }^2 \nonumber \\&+ 12 \left( 2 c_A^L{}^2 + |c_S^R|^2 + c_A^L c_V^L + c_V^L{}^2\right) E_{\nu } m_e \nonumber \\&+ 3 (3 c_A^L{}^2 + 2 |c_S^R|^2 + c_V^L{}^2) m_e^2 \nonumber \\&- (4 c_A^L c_V^L E_{\nu } (4 E_{\nu } + 3 m_e) + c_A^L{}^2 (4 E_{\nu } + 3 m_e)^2 \nonumber \\&+ c_V^L{}^2 (16 E_{\nu }^2 + 12 E_{\nu } m_e + 3 m_e^2)) \cos {\theta _{\nu }} \nonumber \\&- |c_S^R| (6 (c_A^L + c_V^L) E_{\nu }^2 + (13 c_A^L + 5 c_V^L) E_{\nu } m_e \nonumber \\&+ 6 c_A^L m_e^2) \sin {\theta _\nu } \cos {(\theta _{S,R} - \phi _{\nu })}\bigg ]. \end{aligned}$$

(2)

It can be noticed that the formula on $A_{V-A}^{S,R}(\varPhi )$ contains a factor $\sin {\theta _\nu }$ at the interference terms which is related to the transverse $\nu$ polarization of the production process. The remaining interferences between the standard and exotic couplings are also proportional to $\sin {\theta _\nu }$. We see that if $|c_S^R|\,\sin {(\theta _{S,R} - \phi _{\nu })} = 0$ then the local extremum of $A_{V-A}^{S,R}(\varPhi )$ is at $\varPhi =\pi /2$. Assuming there to be no $T_R$ and $P_R$ interactions, it follows that any departure from the $\varPhi _\mathrm{max}=\pi /2$ orientation of the asymmetry axis signalizes the presence of the exotic $c_S^R$ interaction. Moreover, if the location of the asymmetry axis is sensitive to the relative orientation of PET and $(\hat{\eta }_{\nu })^{ \perp }$, one can conclude that $\theta _{S,R}-\phi _{\nu }\ne 0$; ideally, experimental control of $\phi _{\nu }$ would give an opportunity to measure $\theta _{S,R}$. For example, $\theta _{S,R}$ can be determined as $\phi _{\nu }$ for the value of $\phi _{\nu }$ which fixes the asymmetry axis at the standard $\pi /2$ location. A similar regularity holds for the case of $V-A$ and $T_R$ interactions, i.e. when $|c_T^R|\,\sin {(\theta _{T,R} - \phi _{\nu })} = 0$; then the local extremum of $A_{V-A}^{T,R}(\varPhi )$ must be at $\varPhi =\pi /2$. For the variant with $V-A$ and $P_R$ couplings the situation is different: in this case $\varPhi _\mathrm{max}=\pi /2$ independently of the coupling $c_P^R$ and the azimuthal angle $\phi _{\nu }$.

Fig. 5

Dependence of $A(\varPhi _\mathrm{max})$ on $\phi _\nu$ (solid line) and $\varPhi _\mathrm{max}$ on $\phi _\nu$ (dashed line), for $\hat{\eta }_{\nu }\cdot \hat{\mathbf{q}}=-0.95, E_\nu =1\,MeV$. TRSC: upper left plot for the case of $V-A$ and $S_R$ when $|c_S^R|=0.2, \theta _{S,R}=0$; middle left plot for the combination of $V-A$ with $T_R$ when $|c_T^R|=0.2, \theta _{T,R}=0$; lower left plot for the case of $V-A$ with $P_R$ when $|c_P^R|=0.2, \theta _{P,R}=0$. TRSV: upper right plot for the scenario with $V-A$ and $S_R$ when $|c_S^R|=0.2, \theta _{S,R}=\pi /2$; middle right plot for the case of $V-A$ and $T_R$ when $|c_T^R|=0.2, \theta _{T,R}=\pi /2$; lower right plot for the combination of $V-A$ with $P_R$ when $|c_P^R|=0.2, \theta _{P,R}=\pi /2$.

Fig. 6

Dependence of $A(\varPhi _\mathrm{max})$ on $\phi _\nu$ (solid line) and $\varPhi _\mathrm{max}$ on $\phi _\nu$ (dashed line), for $\theta _\nu =\pi /2$, $E_\nu =1\,MeV$. TRSC: upper left plot for the case of $V-A$ and $S_R$ when $|c_S^R|=0.2, \theta _{S,R}=0$; middle left plot for the combination of $V-A$ with $T_R$ when $|c_T^R|=0.2, \theta _{T,R}=0$; lower left plot for the case of $V-A$ with $P_R$ when $|c_P^R|=0.2, \theta _{P,R}=0$. TRSV: upper right plot for the scenario with $V-A$ and $S_R$ when $|c_S^R|=0.2, \theta _{S,R}=\pi /2$; middle right plot for the case of $V-A$ and $T_R$ when $|c_T^R|=0.2, \theta _{T,R}=\pi /2$; lower right plot for the combination $V-A$ with $P_R$ when $|c_P^R|=0.2, \theta _{P,R}=\pi /2$

Fig. 7

Upper plot: dependence of $\varPhi _{max}$ on $\varDelta \theta _{ST,R}$ for $\theta _\nu =\pi , E_\nu =1\,MeV$ in the case of $V-A$ with $S_R$ and $T_R$ when $|c_S^R|=|c_T^R|=0.2$ (dashed line); plot of $\varPhi _\mathrm{max}$ on $\varDelta \theta _{PT,R}$ for $\theta _\nu =\pi , E_\nu =1\,MeV$ in the presence of $V-A$, $P_R$ and $T_R$ when $|c_P^R|=|c_T^R|=0.2$ (dotted line). Lower plot: dependence of $A(\varPhi _\mathrm{max})$ on $\varDelta \theta _{ST,R}$ (dashed line) and on $\varDelta \theta _{PT,R}$ (dotted line), respectively, with the same assumptions as for $\varPhi _\mathrm{max}$

The diagrams on Figs. 5 (for $\hat{\eta }_{\nu }\cdot \hat{\mathbf{q}}=-0.95$) and 6 (for $\theta _\nu =\pi /2$) show the dependence of $A(\varPhi _\mathrm{max})$ (solid lines) and $\varPhi _\mathrm{max}$ (dashed lines) on $\phi _\nu$ for the various scenarios with TRSC (left plots) and TRSV (right plots).

From an experimental point of view, the control of $(\hat{\eta }_{\nu })^{\perp }$ makes the TRSV tests extremely difficult, so the measurement of T-odd observable independent of $(\hat{\eta }_{\nu })^{\perp }$ would be preferable. The suitable quantity built from $\hat{\mathbf{q}}, \hat{\mathbf{p}}_{e}, (\hat{\eta }_{e})^{\perp }$ vectors indeed appears in the differential cross section [see last term of Eq. (9)]. To illustrate the possibility of testing the TRSV for $\theta _\nu =\pi$, we give the explicit formula for the azimuthal asymmetry for the scenario with $V-A$, $S_R$ and $T_R$ interactions, assuming the experimental values of the standard couplings, $E_\nu =1\,\mathrm{{MeV}}, |c_S^R|=|c_T^R|=0.2$:

$$\begin{aligned} A_{S,R}^{T,R}(\varPhi )= & {} \bigg [1.699 (0.402 \sin (\varDelta \theta _{ST,R}) \cos \varPhi \nonumber \\&+ (-0.322 \cos (\varDelta \theta _{ST,R}) - 3.07) \sin \varPhi \bigg ]/ \nonumber \\&\bigg [0.885 \cos (\varDelta \theta _{ST,R}) - 82.191\bigg ], \end{aligned}$$

(3)

where $\varDelta \theta _{ST,R}=\theta _{S,R}-\theta _{T,R}$ and $\varDelta \theta _{PT,R}=\theta _{P,R}-\theta _{T,R}$. Figure 7 displays how $\varPhi _\mathrm{max}$ and $A(\varPhi _\mathrm{max})$ depend on $\varDelta \theta _{ST,R}$ and $\varDelta \theta _{PT,R}$. The dashed lines correspond to the combination of $V-A$ with $S_R$ and $T_R$ when $\theta _\nu =\pi$. The dotted lines involve the case of $V-A$ with $P_R$ and $T_R$ when $\theta _\nu =\pi$. Any generic departure of the asymmetry axis from $\varPhi =\pi /2$ signals the TRSV.

Fig. 8

Plot of $\mathrm{{d}}\sigma /\mathrm{{d}}\theta _e$ as a function of $\theta _e$ for $\hat{\eta }_{\nu }\cdot \hat{\mathbf{q}}= - 0.95$, $E_\nu =1\,\mathrm{{MeV}}$, $\phi _\nu =0$. Upper plot for TRSC: standard $V-A$ interaction (solid line); the combination of $V-A$ and $T_R$ when $|c_T^R|=0.2, \theta _{T,R}=0$ (dashed line); the case of $V-A$ and $S_R$ when $|c_S^R|=0.2, \theta _{S,R}=0$ (dotted line); $V-A$ with $P_R$ when $|c_P^R|=0.2, \theta _{P,R}=0$ (dashed-dotted line). Lower plot for TRSV: standard $V-A$ interaction (solid line); the combination of $V-A$ and $T_R$ when $|c_T^R|=0.2, \theta _{T,R}=\pi /2$ (dashed line); the case of $V-A$ and $S_R$ when $|c_S^R|=0.2, \theta _{S,R}=\pi /2$ (dotted line); $V-A$ with $P_R$ when $|c_P^R|=0.2, \theta _{P,R}=\pi /2$ (dashed-dotted line)

Fig. 9

Plot of $\mathrm{{d}}\sigma /\mathrm{{d}}\theta _e$ as a function of $\theta _e$ for $\theta _\nu =\pi /2$, $E_\nu =1\,MeV$, $\phi _\nu =0$. Upper plot for TRSC: standard $V-A$ interaction (solid line); the combination of $V-A$ and $T_R$ when $|c_T^R|=0.2, \theta _{T,R}=0$ (dashed line); the case of $V-A$ and $S_R$ when $|c_S^R|=0.2, \theta _{S,R}=0$ (dotted line); $V-A$ with $P_R$ when $|c_P^R|=0.2, \theta _{P,R}=0$ (dashed-dotted line). Lower plot for TRSV: standard $V-A$ interaction (solid line); the combination of $V-A$ and $T_R$ when $|c_T^R|=0.2, \theta _{T,R}=\pi /2$ (dashed line); the case of $V-A$ and $S_R$ when $|c_S^R|=0.2, \theta _{S,R}=\pi /2$ (dotted line); $V-A$ with $P_R$ when $|c_P^R|=0.2, \theta _{P,R}=\pi /2$ (dashed-dotted line)

4 Spectrum of recoil electrons and polar angle distribution of scattered electrons

In this section, we indicate the usefulness of both the polar angle distribution and the spectrum of recoil electrons in testing the TRSV phenomenon. Let us stress that the probed scenarios correspond to the laboratory differential cross section integrated over $\phi _{e}$. We see that this independence of $\phi _{e}$ does not eliminate all the interference terms between the standard and exotic $(S,T,P)_R$ couplings, and in this way there is still the possibility of detecting the TRSV by a precise measurement of these observables. Figure 8 shows the dependence of $\mathrm{{d}}\sigma /\mathrm{{d}}\theta _e=\left( \mathrm{{d}}\sigma /\mathrm{{d}} \,y\right) \, \left( \mathrm{{d}} \,y/\mathrm{{d}}\theta _e \right)$ on $\theta _e$ for the various scenarios. The upper plot concerns the TRSC ($\theta _{T,R}=\theta _{S,R}=\theta _{P,R}=0$) case, while the lower one corresponds to TRSV ($\theta _{T,R}=\theta _{S,R}=\theta _{P,R}=\pi /2$). Figure 9 displays the same dependence as Fig. 8, but for the pure contribution from $(\hat{\eta }_{\nu })^{ \perp }$, i.e. when $\theta _\nu =\pi /2$. The significant departure from the standard prediction in the polar angle distribution of recoil electrons for the scenario with $V-A$ and $T_R$ interactions can be noticed. For the two remaining cases the differences are much smaller. The dashed lines in Fig. 8 correspond to the case of TRSC (upper plot) with $\theta _{e}^\mathrm{max}(T_R)=33.7^{\circ }$ and TRSV (lower plot) with $\theta _{e}^\mathrm{max}(T_R)= 33.3^{\circ }$, respectively. A similar regularity for the extreme situation with $\theta _\nu =\pi /2$ is seen in Fig. 9.

Fig. 10

Dependence of $d\sigma /d \,y$ on y for $\hat{\eta }_{\nu }\cdot \hat{\mathbf{q}}=-0.95, E_\nu =1\,MeV$, $\phi _\nu =0$. Upper plot for TRSC: standard $V-A$ interaction (solid line); the combination of $V-A$ and $T_R$ when $|c_T^R|=0.2, \theta _{T,R}=0$ (dashed line); the case of $V-A$ and $S_R$ when $|c_S^R|=0.2, \theta _{S,R}=0$ (dotted line); $V-A$ with $P_R$ when $|c_P^R|=0.2, \theta _{P,R}=0$ (dashed-dotted line). Lower plot for TRSV: standard $V-A$ interaction (solid line); the combination of $V-A$ and $T_R$ when $|c_T^R|=0.2, \theta _{T,R}=\pi /2$ (dashed line); the case of $V-A$ and $S_R$ when $|c_S^R|=0.2, \theta _{S,R}=\pi /2$ (dotted line); $V-A$ with $P_R$ when $|c_P^R|=0.2, \theta _{P,R}=\pi /2$ (dashed-dotted line)

Fig. 11

Dependence of $\mathrm{{d}}\sigma /\mathrm{{d}}\,y$ on y for $\theta _\nu =\pi /2$, $E_\nu =1\,\mathrm{{MeV}}$, $\phi _\nu =0$. Upper plot for TRSC: standard $V-A$ interaction (solid line); the combination of $V-A$ and $T_R$ when $|c_T^R|=0.2, \theta _{T,R}=0$ (dashed line); the case of $V-A$ and $S_R$ when $|c_S^R|=0.2, \theta _{S,R}=0$ (dotted line); $V-A$ with $P_R$ when $|c_P^R|=0.2, \theta _{P,R}=0$ (dashed-dotted line). Lower plot for TRSV: standard $V-A$ interaction (solid line); the combination of $V-A$ and $T_R$ when $|c_T^R|=0.2, \theta _{T,R}=\pi /2$ (dashed line); the case of $V-A$ and $S_R$ when $|c_S^R|=0.2, \theta _{S,R}=\pi /2$ (dotted line); $V-A$ with $P_R$ when $|c_P^R|=0.2, \theta _{P,R}=\pi /2$ (dashed-dotted line)

Figures 10, 11 are the plots of $\mathrm{{d}}\sigma /\mathrm{{d}} \,y$ as a function of y depicted with similar assumptions to Figs. 8 and 9.

We present the recoil electrons energy spectrum $\mathrm{{d}}\sigma /\mathrm{{d}} \,y$ for the scenario with $V-A$ and $S_R$ interactions to illustrate the impact of the phase of exotic coupling and azimuthal angle of $(\hat{\eta }_{\nu })^{ \perp }$ on the possibility of TRSV:

$$\begin{aligned} \bigg (\frac{\mathrm{{d}}\sigma }{\mathrm{{d}} y}\bigg )_{V-A}^{S_{R}}= & {} \bigg (\frac{\mathrm{{d}}\sigma }{\mathrm{{d}} y}\bigg )_{V-A} +\; B\,\bigg [ |c_S^R|^2\, f_{S}(y) \nonumber \\&+ |c_S^R|\sin {\theta _\nu }\cos {(\theta _{S,R}-\phi _{\nu })} g_{S}(y)\bigg ], \end{aligned}$$

(4)

with the y-dependent coefficients

$$\begin{aligned} f_{S}(y)= & {} 2\,y\,\left( \frac{2 m_e}{E_{\nu }}+y\right) \nonumber \\ g_{S}(y)= & {} y \left[ \left( -2(c_A^L + c_V^L\right) + y (c_A^L-c_V^L)\frac{m_e}{E_{\nu }} - 4 c_A^L \frac{m_e}{E_{\nu }}\right] .\nonumber \\ \end{aligned}$$

(5)

A similar decomposition but with different coefficients f, g holds for the $V-A$ and $T_R$, and also for the $V-A$ and $P_R$ interactions. Let us remark that the low-energy region of the recoil electrons spectrum largely deviates from the standard expectation for the $V-A$ and $T_R$ couplings (dashed line in Figs. 10, 11). The cases of $V-A$ with $S_R$ and $V-A$ with $P_R$ indicate the relatively small deviation for the higher outgoing electrons energy.

5 Conclusions

We have shown that the PET may be the useful tool for the detection of the non-standard couplings of RC interacting $\nu _e$s and the effects of TRSV caused by the triple correlations present in the differential cross section for the NEES. First, according to the SM prediction the left–right azimuthal asymmetry of the recoil electrons has the maximal value at $\varPhi =\pi /2$ and the location of asymmetry axis is fixed, Figs. 2, 3 and 4. If exotic $(S, T, P)_{R}$ complex couplings are admitted in the NEES on the PET, both the magnitude $A(\varPhi _\mathrm{max})$ and axis $\varPhi _{max}$ of the azimuthal asymmetry may change due to the non-vanishing interferences between the $V-A$ and $(S, T, P)_{R}$ proportional to the TRSC and TRSV correlations; see Figs. 5 and 6. This departure from the standard prediction is mainly caused by the dependence of the azimuthal asymmetry on the azimuthal angle $\phi _\nu$ connected with $(\hat{\eta }_{\nu })^{ \perp }$ as shown in Eq. (2) for the scenario involving $V-A$ and $S_R$ couplings. Second, even if the differential cross section is integrated over $\phi _{e}$, but there is PET, the energy spectrum of the recoil electrons and the distribution of outgoing electrons’ polar angles are still sensitive to the interferences, proportional to the angular correlations among $\hat{\mathbf{q}}, (\hat{\eta }_{\nu })^{ \perp }, (\hat{\eta }_{e})^{\perp }$ vectors; see Figs. 8, 9, 10, and 11. In the above detection methods the transversal part of the $\nu _e$ polarization was essential. Further investigations of the choice of a suitable production process, in which the non-standard couplings of the right chiral $\nu$s in addition to the left chiral ones take part, are needed to clarify the key role of $\nu$ source in generating the transverse $\nu$ polarization.

In order to avoid the difficulties connected with the $\nu$ source, the measurement of the T-odd observable independent of $(\hat{\eta }_{\nu })^{\perp }$ would be expected. However, all relevant interferences between the standard and exotic couplings proportional to $(\hat{\eta }_{e})^{\perp }\cdot (\hat{\mathbf{q}} \times (\hat{\mathbf{p}}_{\mathbf{e}})^{\perp })$ depend on $(\hat{\eta }_{\nu })^{\perp }$. This is a direct consequence of the general structure of the hermitian interaction lagrangian. The only $(\hat{\eta }_{\nu })^{\perp }$-independent TRSV observable comes from the interference between the exotic $c_{S}^{R }$ and $c_{T}^{R}$ interactions and results in the azimuthal asymmetry of scattered electrons shown in Fig. 7. On the other hand the spectrum and polar distribution of the scattered electrons are not sensitive to $(\hat{\eta }_{e})^{\perp }\cdot (\hat{\mathbf{q}} \times (\hat{\mathbf{p}}_{\mathbf{e}})^{\perp })$ for $\hat{\eta }_{\nu }\cdot \hat{\mathbf{q}}=-1$.

It is worth pointing out that the measurements of the azimuthal asymmetry and of the polar angle distribution require intense low-energy $\nu _{e}$ sources, polarized target-electrons (the feasibility of an electron polarized scintillating GSO target has been confirmed [47]), and detectors observing both the azimuthal angle and polar angle of the scattered electrons with the good angular resolution. The detectors with the very low threshold for the precise measurements of the outgoing electrons’ spectrum would be needed. Let us recall that the ideas of proper detectors such as Hellaz [69,70,71] and Heron [72, 73] have been considered in the literature. Silicon cryogenic detectors (Neganov et al. hep-ex/0105083), high purity germanium detectors, semiconductor detectors and bolometers [74, 75] also seem to be interesting proposals. Our investigation is made in the hope of encouraging the neutrino laboratories working with artificial (un)polarized $\nu$ sources, and to revive the discussion on the feasibility of PET and on the development of ultra-low threshold high-precision detection techniques in the context of TRSV in low-energy leptonic and semileptonic weak interaction processes.

Appendices

Appendix 1: General formula on laboratory differential cross section for NEES in PET case

The general formula for the laboratory differential cross section with the dependence on the azimuthal angle of outgoing electron momentum, when $\hat{\eta }_{e}\perp \hat{\mathbf{q}}$, is of the form

$$\begin{aligned}&\frac{\mathrm{{d}}^{2} \sigma }{\mathrm{{d}} y \mathrm{{d}} \phi _{e}}\nonumber \\&\quad = \bigg (\frac{\mathrm{{d}}^{2} \sigma }{\mathrm{{d}} y \mathrm{{d}} \phi _{e}}\bigg )_{V- A} + \bigg (\frac{\mathrm{{d}}^{2} \sigma }{\mathrm{{d}} y \mathrm{{d}} \phi _{e}}\bigg )_{V+A} \nonumber \\&\qquad + \bigg (\frac{\mathrm{{d}}^{2} \sigma }{\mathrm{{d}} y \mathrm{{d}} \phi _{e}}\bigg )_{(S,T,P)_R} + \bigg ( \frac{\mathrm{{d}}^{2} \sigma }{\mathrm{{d}} y \mathrm{{d}} \phi _{e}} \bigg )_{V-A}^{S_{R}} \nonumber \\&\qquad + \bigg ( \frac{\mathrm{{d}}^{2} \sigma }{\mathrm{{d}} y \mathrm{{d}} \phi _{e}} \bigg )_{V-A}^{P_{R}} + \bigg ( \frac{\mathrm{{d}}^{2} \sigma }{\mathrm{{d}} y \mathrm{{d}} \phi _{e}} \bigg )_{V-A}^{T_{R}} + \bigg ( \frac{\mathrm{{d}}^{2} \sigma }{\mathrm{{d}} y \mathrm{{d}} \phi _{e}} \bigg )_{V+A}^{S_{R}} \nonumber \\&\qquad + \bigg (\frac{\mathrm{{d}}^{2} \sigma }{\mathrm{{d}} y \mathrm{{d}} \phi _{e}} \bigg )_{V+A}^{P_{R}} + \bigg (\frac{\mathrm{{d}}^{2} \sigma }{\mathrm{{d}} y \mathrm{{d}} \phi _{e}} \bigg )_{V+A}^{T_{R}},\end{aligned}$$

(6)

$$\begin{aligned}&\bigg ( \frac{\mathrm{{d}}^{2} \sigma }{\mathrm{{d}} y \mathrm{{d}} \phi _{e}} \bigg )_{V- A} = B (1-\hat{\eta }_{\nu }\cdot \hat{\mathbf{q}}) \bigg \{ (c_{A}^{L})^2 \bigg [ (y-2)y + 2\nonumber \\&\qquad + \frac{m_e}{E_\nu } y -(\hat{\eta }_{e})^{\perp }\cdot (\hat{\mathbf{p}}_{\mathbf{e}})^{\perp }\sqrt{ \frac{2 m_{e}}{E_{\nu }}+y} \left( \sqrt{y^{3}}-2\sqrt{y}\right) \bigg ]\nonumber \\&\qquad - (c_{V}^{L})^2 \bigg [ (\hat{\eta }_{e})^{\perp }\cdot (\hat{\mathbf{p}}_{\mathbf{e}})^{\perp }\sqrt{y^{3}}\sqrt{\frac{2m_e}{E_\nu }+y} - y^{2} \nonumber \\&\qquad + y\left( \frac{m_e}{E_\nu } + 2\right) -2 \bigg ] + 2(c_{V}^L c_A^{L}) \bigg [ (2-y)y \nonumber \\&\qquad + (\hat{\eta }_{e})^{\perp }\cdot (\hat{\mathbf{p}}_{\mathbf{e}})^{\perp }(y-1)\sqrt{y \left( \frac{2m_e}{E_\nu }+y\right) } \bigg ] \bigg \}, \end{aligned}$$

(7)

$$\begin{aligned}&\bigg (\frac{\mathrm{{d}}^{2} \sigma }{\mathrm{{d}} y \mathrm{{d}} \phi _{e}}\bigg )_{V+A} = B (1+\hat{\eta }_{\nu }\cdot \hat{\mathbf{q}}) \bigg \{ (c_{A}^{R})^2 \bigg [ (y-2)y + 2\nonumber \\&\qquad + \frac{m_e}{E_\nu } y +(\hat{\eta }_{e})^{\perp }\cdot (\hat{\mathbf{p}}_{\mathbf{e}})^{\perp }\sqrt{ \frac{2 m_{e}}{E_{\nu }}+y} \left( \sqrt{y^{3}}-2\sqrt{y}\right) \bigg ]\nonumber \\&\qquad + (c_{V}^{R})^2 \bigg [ (\hat{\eta }_{e})^{\perp }\cdot (\hat{\mathbf{p}}_{\mathbf{e}})^{\perp }\sqrt{y^{3}}\sqrt{\frac{2m_e}{E_\nu }+y} + y^{2} \nonumber \\&\qquad - y\left( \frac{m_e}{E_\nu } + 2\right) +2 \bigg ] + 2(c_{V}^R c_A^{R}) \bigg [ (2-y)y \nonumber \\&\qquad + (\hat{\eta }_{e})^{\perp }\cdot (\hat{\mathbf{p}}_{\mathbf{e}})^{\perp }(1-y)\sqrt{y \left( \frac{2m_e}{E_\nu }+y\right) } \bigg ] \bigg \}, \end{aligned}$$

(8)

$$\begin{aligned}&\bigg (\frac{\mathrm{{d}}^{2} \sigma }{\mathrm{{d}} y \mathrm{{d}} \phi _{e}}\bigg )_{(S,T,P)_{R}} = B\bigg \{ y\left( y+2\frac{m_{e}}{E_{\nu }}\right) |c_{S}^{R}|^{2} + y^{2}|c_{P}^{R}|^{2} \nonumber \\&\qquad + 2 \bigg [ \bigg ( (2-y)^2 -\frac{m_{e}}{E_{\nu }}y - (\hat{\eta }_{e})^{\perp }\cdot (\hat{\mathbf{p}}_{\mathbf{e}})^{\perp }\hat{\eta }_{\nu }\cdot \hat{\mathbf{q}} \sqrt{ \frac{2 m_{e}}{E_{\nu }}+y} \nonumber \\&\qquad \cdot \left( \sqrt{y^{3}}-2\sqrt{y}\right) \bigg )|{c_{T}^{R}}|^{2} + y\bigg ( (y-2) \nonumber \\&\qquad -(\hat{\eta }_{e})^{\perp }\cdot (\hat{\mathbf{p}}_{\mathbf{e}})^{\perp }\hat{\eta }_{\nu }\cdot \hat{\mathbf{q}} \sqrt{\left( \frac{2 m_{e}}{E_{\nu }}+y\right) y} \bigg ) Re(c_{P}^{R} c_{T}^{*R}) \nonumber \\&\qquad - (\hat{\eta }_{e})^{\perp }\cdot (\hat{\mathbf{p}}_{\mathbf{e}})^{\perp }\hat{\eta }_{\nu } \cdot \hat{\mathbf{q}} \sqrt{\frac{2 m_{e}}{E_{\nu }}+y}\,\sqrt{y^{3}}\, Re(c_{S}^{R} c_{P}^{*R})\nonumber \\&\qquad + (y-2)\bigg ( y - (\hat{\eta }_{e})^{\perp }\cdot (\hat{\mathbf{p}}_{\mathbf{e}})^{\perp }\hat{\eta }_{\nu }\cdot \hat{\mathbf{q}} \sqrt{y\left( \frac{2 m_{e}}{E_{\nu }} +y\right) } \bigg ) \nonumber \\&\qquad \cdot Re(c_{S}^{R}c_{T}^{*R}) - 2 \sqrt{ y\left( y+2\frac{m_{e}}{E_{\nu }}\right) } (\hat{\eta }_{e})^{\perp }\cdot (\hat{\mathbf{q}} \times (\hat{\mathbf{p}}_{\mathbf{e}})^{\perp })\nonumber \\&\qquad \cdot Im(c_{S}^{R}c_{T}^{*R})\bigg ] \bigg \}, \end{aligned}$$

(9)

$$\begin{aligned}&\bigg ( \frac{\mathrm{{d}}^{2} \sigma }{\mathrm{{d}} y \mathrm{{d}} \phi _{e}} \bigg )_{V-A}^{S_R} = B \Bigg \{ c_{A}^{L} \frac{E_{\nu }}{m_e}\Bigg [ \sqrt{y\left( \frac{2 m_{e}}{E_{\nu }} +y\right) ^{3}} \nonumber \\&\qquad \cdot \left( -(\hat{\mathbf{p}}_{\mathbf{e}})^{\perp }\cdot ( (\hat{\eta }_{e})^{\perp }\times (\hat{\eta }_{\nu })^{ \perp })Im (c_{S}^{R})\right) -\bigg (y^{2} + \frac{2 m_{e}y}{E_{\nu }}\bigg ) \nonumber \\&\qquad \cdot \Bigg ((\hat{\eta }_{e})^{\perp }\cdot (\hat{\mathbf{p}}_{\mathbf{e}})^{\perp }\bigg ( (\hat{\eta }_{\nu })^{ \perp }\cdot (\hat{\mathbf{p}}_{\mathbf{e}})^{\perp }Re(c_{S}^{R})\nonumber \\&\qquad +(\hat{\eta }_{\nu })^{ \perp }\cdot (\hat{\mathbf{q}} \times (\hat{\mathbf{p}}_{\mathbf{e}})^\perp )Im (c_{S}^{R})\bigg ) - \hat{\mathbf{q}}\cdot ((\hat{\eta }_{e})^{\perp }\times (\hat{\eta }_{\nu })^{ \perp })\nonumber \\&\qquad \cdot Im (c_{S}^{R})+ \frac{ m_{e}}{E_{\nu }}(\hat{\eta }_{e})^{\perp }\cdot (\hat{\eta }_{\nu })^{ \perp }Re(c_{S}^{R}))\Bigg )\Bigg ] \nonumber \\&\qquad + c_{V}^{L}\Bigg [ \sqrt{\frac{2 m_{e}}{E_{\nu }}+y)y} \Bigg ( 2\bigg ( (\hat{\eta }_{\nu })^{ \perp }\cdot (\hat{\mathbf{p}}_{\mathbf{e}})^{\perp }Re(c_{S}^{R})\nonumber \\&\qquad + (\hat{\eta }_{\nu })^{ \perp }\cdot (\hat{\mathbf{q}} \times (\hat{\mathbf{p}}_{\mathbf{e}})^\perp )Im (c_{S}^{R})\bigg ) \nonumber \\&\qquad - y (\hat{\mathbf{p}}_{\mathbf{e}})^{\perp }\cdot ( (\hat{\eta }_{e})^{\perp }\times (\hat{\eta }_{\nu })^{ \perp })Im (c_{S}^{R})\Bigg ) \nonumber \\&\qquad + y(y -2) (\hat{\eta }_{e})^{\perp }\cdot (\hat{\eta }_{\nu })^{ \perp }Re(c_{S}^{R})\nonumber \\&\qquad + \bigg (\frac{E_{\nu }}{m_{e}}y^{2} + 2 y \bigg ) (\hat{\eta }_{\nu })^{ \perp }\cdot (\hat{\mathbf{p}}_{\mathbf{e}})^{\perp }\bigg ((\hat{\eta }_{e})^{\perp }\cdot (\hat{\mathbf{p}}_{\mathbf{e}})^{\perp }Re(c_{S}^{R})\nonumber \\&\qquad + (\hat{\eta }_{e})^{\perp }\cdot (\hat{\mathbf{q}} \times (\hat{\mathbf{p}}_{\mathbf{e}})^{\perp })Im (c_{S}^{R})\bigg ) \Bigg ] \Bigg \}, \end{aligned}$$

(10)

$$\begin{aligned}&\bigg ( \frac{\mathrm{{d}}^{2} \sigma }{\mathrm{{d}} y \mathrm{{d}} \phi _{e}} \bigg )_{V-A}^{P_R} = B \Bigg \{ c_{V}^{L} \frac{E_{\nu }}{m_e}\Bigg [ y \sqrt{y\left( \frac{2 m_{e}}{E_{\nu }} +y\right) } \nonumber \\&\qquad \cdot \left( -(\hat{\mathbf{p}}_{\mathbf{e}})^{\perp }\cdot ( (\hat{\eta }_{e})^{\perp }\times (\hat{\eta }_{\nu })^{ \perp })Im (c_{P}^{R})\right) + \bigg (y^{2} + \frac{2 m_{e}y}{E_{\nu }}\bigg ) \nonumber \\&\qquad \cdot \Bigg ((\hat{\eta }_{e})^{\perp }\cdot (\hat{\mathbf{p}}_{\mathbf{e}})^{\perp }\bigg ( - (\hat{\eta }_{\nu })^{ \perp }\cdot (\hat{\mathbf{p}}_{\mathbf{e}})^{\perp }Re(c_{P}^{R})\nonumber \\&\qquad - (\hat{\eta }_{\nu })^{ \perp }\cdot (\hat{\mathbf{q}} \times (\hat{\mathbf{p}}_{\mathbf{e}})^\perp )Im (c_{P}^{R})\bigg )\Bigg ) - \bigg (-\hat{\mathbf{q}}\cdot ((\hat{\eta }_{e})^{\perp }\times (\hat{\eta }_{\nu })^{ \perp })\nonumber \\&\qquad \cdot Im (c_{P}^{R})+ \frac{ m_{e}}{E_{\nu }}(\hat{\eta }_{e})^{\perp }\cdot (\hat{\eta }_{\nu })^{ \perp }Re(c_{P}^{R})\bigg )y^2\Bigg ] \nonumber \\&\qquad + c_{A}^{L}\Bigg [- y \sqrt{\left( \frac{2 m_{e}}{E_{\nu }}+y\right) y} (\hat{\mathbf{p}}_{\mathbf{e}})^{\perp }\cdot ( (\hat{\eta }_{e})^{\perp }\times (\hat{\eta }_{\nu })^{ \perp })\nonumber \\&\qquad \cdot Im (c_{P}^{R})+ y(y -2) (\hat{\eta }_{e})^{\perp }\cdot (\hat{\eta }_{\nu })^{ \perp }Re(c_{P}^{R})\nonumber \\&\qquad + \bigg (\frac{E_{\nu }}{m_{e}}y^{2} + 2 y \bigg ) (\hat{\eta }_{\nu })^{ \perp }\cdot (\hat{\mathbf{p}}_{\mathbf{e}})^{\perp }\bigg ((\hat{\eta }_{e})^{\perp }\cdot (\hat{\mathbf{p}}_{\mathbf{e}})^{\perp }Re(c_{P}^{R})\nonumber \\&\qquad + (\hat{\eta }_{e})^{\perp }\cdot (\hat{\mathbf{q}} \times (\hat{\mathbf{p}}_{\mathbf{e}})^{\perp })Im (c_{P}^{R})\bigg ) \Bigg ] \Bigg \}, \end{aligned}$$

(11)

$$\begin{aligned}&\bigg ( \frac{\mathrm{{d}}^{2} \sigma }{\mathrm{{d}} y \mathrm{{d}} \phi _{e}} \bigg )_{V-A}^{T_R} = 2 B \Bigg \{ \frac{E_{\nu }}{m_e}\Bigg [c_{A}^{L}\Bigg ( - \sqrt{y\left( \frac{2 m_{e}}{E_{\nu }}+y\right) } \nonumber \\&\qquad \cdot \left( 1-2y + \frac{2 m_{e}y}{E_{\nu }}\right) (\hat{\mathbf{p}}_{\mathbf{e}})^{\perp }\cdot ( (\hat{\eta }_{e})^{\perp }\times (\hat{\eta }_{\nu })^{ \perp })Im (c_{T}^{R})\nonumber \\&\qquad - 2 \bigg (y^{2} + \frac{2 m_{e}y}{E_{\nu }}\bigg ) \bigg ((\hat{\eta }_{\nu })^{ \perp }\cdot (\hat{\mathbf{p}}_{\mathbf{e}})^{\perp }(\hat{\eta }_{e})^{\perp }\cdot (\hat{\mathbf{q}} \times (\hat{\mathbf{p}}_{\mathbf{e}})^{\perp })\nonumber \\&\qquad - (\hat{\eta }_{e})^{\perp }\cdot (\hat{\mathbf{p}}_{\mathbf{e}})^{\perp }(\hat{\eta }_{\nu })^{ \perp }\cdot (\hat{\mathbf{q}} \times (\hat{\mathbf{p}}_{\mathbf{e}})^\perp )\bigg ) Im(c_{T}^{R})\nonumber \\&\qquad - (2y-1)\left( y +\frac{2 m_{e}}{E_{\nu }}\right) \hat{\mathbf{q}}\cdot ((\hat{\eta }_{e})^{\perp }\times (\hat{\eta }_{\nu })^{ \perp })Im (c_{T}^{R}) \nonumber \\&\qquad - \left( \frac{ m_{e}}{E_{\nu }}\right) (y-2)(\hat{\eta }_{e})^{\perp }\cdot (\hat{\eta }_{\nu })^{ \perp }Re(c_{T}^{R})\nonumber \\&\qquad + \left( \frac{ m_{e}}{E_{\nu }}\right) \sqrt{y\left( \frac{2 m_{e}}{E_{\nu }}+y\right) } \bigg ((\hat{\eta }_{\nu })^{ \perp }\cdot (\hat{\mathbf{p}}_{\mathbf{e}})^{\perp }Re(c_{T}^{R})\nonumber \\&\qquad + (\hat{\eta }_{\nu })^{ \perp }\cdot (\hat{\mathbf{q}} \times (\hat{\mathbf{p}}_{\mathbf{e}})^\perp )Im(c_{T}^{R})\bigg ) \Bigg ) \nonumber \\&\qquad + c_{V}^{L} \Bigg (-\left( 2(1-y) + \left( \frac{ m_{e}}{E_{\nu }}\right) (1-2y)\right) \sqrt{\left( \frac{2 m_{e}}{E_{\nu }}+y\right) y} \nonumber \\&\qquad \cdot \left( (\hat{\mathbf{p}}_{\mathbf{e}})^{\perp }\cdot ( (\hat{\eta }_{e})^{\perp }\times (\hat{\eta }_{\nu })^{ \perp })Im (c_{T}^{R})\right) - 2\bigg ( y^{2} + \frac{2 m_{e}y}{E_{\nu }}\bigg ) \nonumber \\&\qquad \cdot \bigg ((\hat{\eta }_{\nu })^{ \perp }\cdot (\hat{\mathbf{p}}_{\mathbf{e}})^{\perp }(\hat{\eta }_{e})^{\perp }\cdot (\hat{\mathbf{q}} \times (\hat{\mathbf{p}}_{\mathbf{e}})^{\perp })\nonumber \\&\qquad - (\hat{\eta }_{e})^{\perp }\cdot (\hat{\mathbf{p}}_{\mathbf{e}})^{\perp }(\hat{\eta }_{\nu })^{ \perp }\cdot (\hat{\mathbf{q}} \times (\hat{\mathbf{p}}_{\mathbf{e}})^\perp )\bigg )Im (c_{T}^{R}) \nonumber \\&\qquad - 2\left( y-1\right) \left( y+\frac{ m_{e}}{E_{\nu }}\right) \hat{\mathbf{q}}\cdot ((\hat{\eta }_{e})^{\perp }\times (\hat{\eta }_{\nu })^{ \perp })Im (c_{T}^{R})\Bigg ] \nonumber \\&\qquad + \left( 2-y +\frac{ m_{e}y}{E_{\nu }}\right) (\hat{\eta }_{e})^{\perp }\cdot (\hat{\eta }_{\nu })^{ \perp }Re(c_{T}^{R})\Bigg )\Bigg \}, \end{aligned}$$

(12)

$$\begin{aligned}&\bigg ( \frac{\mathrm{{d}}^{2} \sigma }{\mathrm{{d}} y \mathrm{{d}} \phi _{e}} \bigg )_{V+A}^{S_R} = B \Bigg \{ c_{A}^{R} \frac{E_{\nu }}{m_e}\Bigg [- \sqrt{y\left( \frac{2 m_{e}}{E_{\nu }}+y\right) ^{3}} \nonumber \\&\qquad \cdot \left( (\hat{\mathbf{p}}_{\mathbf{e}})^{\perp }\cdot ( (\hat{\eta }_{e})^{\perp }\times (\hat{\eta }_{\nu })^{ \perp })Im (c_{S}^{R})\right) -\bigg (y^{2} + \frac{2 m_{e}y}{E_{\nu }}\bigg ) \nonumber \\&\qquad \cdot \Bigg ((\hat{\eta }_{e})^{\perp }\cdot (\hat{\mathbf{p}}_{\mathbf{e}})^{\perp }\bigg ( (\hat{\eta }_{\nu })^{ \perp }\cdot (\hat{\mathbf{p}}_{\mathbf{e}})^{\perp }Re(c_{S}^{R})\nonumber \\&\qquad +(\hat{\eta }_{\nu })^{ \perp }\cdot (\hat{\mathbf{q}} \times (\hat{\mathbf{p}}_{\mathbf{e}})^\perp )Im (c_{S}^{R})\bigg ) - \hat{\mathbf{q}}\cdot ((\hat{\eta }_{e})^{\perp }\times (\hat{\eta }_{\nu })^{ \perp })\nonumber \\&\qquad \cdot Im (c_{S}^{R})+ \frac{ m_{e}}{E_{\nu }}(\hat{\eta }_{e})^{\perp }\cdot (\hat{\eta }_{\nu })^{ \perp }Re(c_{S}^{R}))\Bigg )\Bigg ] \nonumber \\&\qquad + c_{V}^{R}\Bigg [ \sqrt{\left( \frac{2 m_{e}}{E_{\nu }}+y\right) y} \Bigg ( 2\bigg ( (\hat{\eta }_{\nu })^{ \perp }\cdot (\hat{\mathbf{p}}_{\mathbf{e}})^{\perp }Re(c_{S}^{R})\nonumber \\&\qquad + (\hat{\eta }_{\nu })^{ \perp }\cdot (\hat{\mathbf{q}} \times (\hat{\mathbf{p}}_{\mathbf{e}})^\perp )Im (c_{S}^{R})\bigg ) \nonumber \\&\qquad - y (\hat{\mathbf{p}}_{\mathbf{e}})^{\perp }\cdot ( (\hat{\eta }_{e})^{\perp }\times (\hat{\eta }_{\nu })^{ \perp })Im (c_{S}^{R})\Bigg ) \nonumber \\&\qquad + y(y -2) (\hat{\eta }_{e})^{\perp }\cdot (\hat{\eta }_{\nu })^{ \perp }Re(c_{S}^{R})\nonumber \\&\qquad + \bigg (\frac{E_{\nu }}{m_{e}}y^{2} + 2 y \bigg ) (\hat{\eta }_{\nu })^{ \perp }\cdot (\hat{\mathbf{p}}_{\mathbf{e}})^{\perp }\bigg ((\hat{\eta }_{e})^{\perp }\cdot (\hat{\mathbf{p}}_{\mathbf{e}})^{\perp }Re(c_{S}^{R})\nonumber \\&\qquad + (\hat{\eta }_{e})^{\perp }\cdot (\hat{\mathbf{q}} \times (\hat{\mathbf{p}}_{\mathbf{e}})^{\perp })Im (c_{S}^{R})\bigg ) \Bigg ] \Bigg \}, \end{aligned}$$

(13)

$$\begin{aligned}&\bigg ( \frac{\mathrm{{d}}^{2} \sigma }{\mathrm{{d}} y \mathrm{{d}} \phi _{e}} \bigg )_{V+A}^{P_R} = B \Bigg \{ c_{V}^{R} \frac{E_{\nu }}{m_e}\Bigg [- y \sqrt{y\left( \frac{2 m_{e}}{E_{\nu }}+y\right) } \nonumber \\&\qquad \cdot \left( (\hat{\mathbf{p}}_{\mathbf{e}})^{\perp }\cdot ( (\hat{\eta }_{e})^{\perp }\times (\hat{\eta }_{\nu })^{ \perp })Im (c_{P}^{R})\right) + \bigg (y^{2} + \frac{2 m_{e}y}{E_{\nu }}\bigg ) \nonumber \\&\qquad \cdot \Bigg ( (\hat{\eta }_{e})^{\perp }\cdot (\hat{\mathbf{p}}_{\mathbf{e}})^{\perp }\bigg ( - (\hat{\eta }_{\nu })^{ \perp }\cdot (\hat{\mathbf{p}}_{\mathbf{e}})^{\perp }Re(c_{P}^{R})\nonumber \\&\qquad - (\hat{\eta }_{\nu })^{ \perp }\cdot (\hat{\mathbf{q}} \times (\hat{\mathbf{p}}_{\mathbf{e}})^\perp )Im (c_{P}^{R})\bigg )\Bigg ) + \bigg (\hat{\mathbf{q}}\cdot ((\hat{\eta }_{e})^{\perp }\times (\hat{\eta }_{\nu })^{ \perp })\nonumber \\&\qquad \cdot Im (c_{P}^{R})-\frac{ m_{e}}{E_{\nu }}(\hat{\eta }_{e})^{\perp }\cdot (\hat{\eta }_{\nu })^{ \perp }Re(c_{P}^{R})\bigg )y^2\Bigg ] \nonumber \\&\qquad + c_{A}^{R}\Bigg [- y \sqrt{\left( \frac{2 m_{e}}{E_{\nu }}+y\right) y} (\hat{\mathbf{p}}_{\mathbf{e}})^{\perp }\cdot ( (\hat{\eta }_{e})^{\perp }\times (\hat{\eta }_{\nu })^{ \perp })\nonumber \\&\qquad \cdot Im (c_{P}^{R})+ y(y -2) (\hat{\eta }_{e})^{\perp }\cdot (\hat{\eta }_{\nu })^{ \perp }Re(c_{P}^{R})\nonumber \\&\qquad + \bigg (\frac{E_{\nu }}{m_{e}}y^{2} + 2 y \bigg ) (\hat{\eta }_{\nu })^{ \perp }\cdot (\hat{\mathbf{p}}_{\mathbf{e}})^{\perp }\bigg ((\hat{\eta }_{e})^{\perp }\cdot (\hat{\mathbf{p}}_{\mathbf{e}})^{\perp }Re(c_{P}^{R})\nonumber \\&\qquad + (\hat{\eta }_{e})^{\perp }\cdot (\hat{\mathbf{q}} \times (\hat{\mathbf{p}}_{\mathbf{e}})^{\perp })Im (c_{P}^{R})\bigg ) \Bigg ] \Bigg \}, \end{aligned}$$

(14)

$$\begin{aligned}&\bigg ( \frac{\mathrm{{d}}^{2} \sigma }{\mathrm{{d}} y \mathrm{{d}} \phi _{e}} \bigg )_{V+A}^{T_R} = 2 B \Bigg \{ \frac{E_{\nu }}{m_e}\Bigg [c_{A}^{R} \Bigg (- \sqrt{y\left( \frac{2 m_{e}}{E_{\nu }}+y\right) } \nonumber \\&\qquad \cdot \left( 1-2y + \frac{2 m_{e}y}{E_{\nu }}\right) (\hat{\mathbf{p}}_{\mathbf{e}})^{\perp }\cdot ( (\hat{\eta }_{e})^{\perp }\times (\hat{\eta }_{\nu })^{ \perp })Im (c_{T}^{R})\nonumber \\&\qquad - 2 \bigg (y^{2} + \frac{2 m_{e}y}{E_{\nu }}\bigg ) \bigg ((\hat{\eta }_{\nu })^{ \perp }\cdot (\hat{\mathbf{p}}_{\mathbf{e}})^{\perp }(\hat{\eta }_{e})^{\perp }\cdot (\hat{\mathbf{q}} \times (\hat{\mathbf{p}}_{\mathbf{e}})^{\perp })\nonumber \\&\qquad - (\hat{\eta }_{e})^{\perp }\cdot (\hat{\mathbf{p}}_{\mathbf{e}})^{\perp }(\hat{\eta }_{\nu })^{ \perp }\cdot (\hat{\mathbf{q}} \times (\hat{\mathbf{p}}_{\mathbf{e}})^\perp )\bigg ) Im(c_{T}^{R})\nonumber \\&\qquad - (2y-1)\left( y +\frac{2 m_{e}}{E_{\nu }}\right) \hat{\mathbf{q}}\cdot ((\hat{\eta }_{e})^{\perp }\times (\hat{\eta }_{\nu })^{ \perp })Im (c_{T}^{R}) \nonumber \\&\qquad - \left( \frac{ m_{e}}{E_{\nu }}\right) (y-2)(\hat{\eta }_{e})^{\perp }\cdot (\hat{\eta }_{\nu })^{ \perp }Re(c_{T}^{R})\nonumber \\&\qquad + \left( \frac{ m_{e}}{E_{\nu }}\right) \sqrt{y\left( \frac{2 m_{e}}{E_{\nu }}+y\right) } \bigg (-(\hat{\eta }_{\nu })^{ \perp }\cdot (\hat{\mathbf{p}}_{\mathbf{e}})^{\perp }Re(c_{T}^{R})\nonumber \\&\qquad - (\hat{\eta }_{\nu })^{ \perp }\cdot (\hat{\mathbf{q}} \times (\hat{\mathbf{p}}_{\mathbf{e}})^\perp )Im(c_{T}^{R})\bigg )\Bigg ) \nonumber \\&\qquad + c_{V}^{R} \Bigg (-\left( 2(1-y) + \left( \frac{ m_{e}}{E_{\nu }}\right) (1-2y)\right) \sqrt{\left( \frac{2 m_{e}}{E_{\nu }}+y\right) y} \nonumber \\&\qquad \cdot \left( (\hat{\mathbf{p}}_{\mathbf{e}})^{\perp }\cdot ( (\hat{\eta }_{e})^{\perp }\times (\hat{\eta }_{\nu })^{ \perp })Im (c_{T}^{R})\right) - 2\bigg ( y^{2} + \frac{2 m_{e}y}{E_{\nu }}\bigg ) \nonumber \\&\qquad \cdot \bigg ((\hat{\eta }_{\nu })^{ \perp }\cdot (\hat{\mathbf{p}}_{\mathbf{e}})^{\perp }(\hat{\eta }_{e})^{\perp }\cdot (\hat{\mathbf{q}} \times (\hat{\mathbf{p}}_{\mathbf{e}})^{\perp })\nonumber \\&\qquad - (\hat{\eta }_{e})^{\perp }\cdot (\hat{\mathbf{p}}_{\mathbf{e}})^{\perp }(\hat{\eta }_{\nu })^{ \perp }\cdot (\hat{\mathbf{q}} \times (\hat{\mathbf{p}}_{\mathbf{e}})^\perp )\bigg )Im (c_{T}^{R}) \nonumber \\&\qquad - 2\left( y-1\right) \left( y+\frac{ m_{e}}{E_{\nu }}\right) \hat{\mathbf{q}}\cdot ((\hat{\eta }_{e})^{\perp }\times (\hat{\eta }_{\nu })^{ \perp })Im (c_{T}^{R})\Bigg ] \nonumber \\&\qquad + \left( 2-y +\frac{ m_{e}y}{E_{\nu }}\right) (\hat{\eta }_{e})^{\perp }\cdot (\hat{\eta }_{\nu })^{ \perp }Re(c_{T}^{R})\Bigg )\Bigg \}; \end{aligned}$$

(15)

$$\begin{aligned} y\equiv & {} \frac{T_e}{E_\nu }=\frac{m_{e}}{E_{\nu }}\frac{2 cos^{2}\theta _{e}}{(1+\frac{m_{e}}{E_{\nu }})^{2}-cos^{2}\theta _{e}} \end{aligned}$$

(16)

is the ratio of the kinetic energy of the recoil electron $T_{e}$ to the incoming $\nu _e$ energy $E_{\nu }$. $m_{e}$ is the electron mass; $B\equiv \left( E_{\nu }m_{e}/4\pi ^2\right) \left( G_{F}^{2}/2\right)$. $\hat{\eta }_{\nu }$is the unit 3-vector of $\nu _{e}$ spin polarization in its rest frame; see Fig. 1. $(\hat{\eta }_{\nu }\cdot \hat{\mathbf{q}})\hat{\mathbf{q}}$ is the longitudinal component of $\nu _{e}$ spin polarization. $|\hat{\eta }_{\nu }\cdot \hat{\mathbf{q}}| = |1- 2 Q_{L}^{\nu }|$, where $Q_{L}^{\nu }$ is the probability of producing the LC $\nu _{e}$. We see that the interferences between standard $V-A$ and exotic $S_R, P_R, T_R$ couplings survive in the limit of relativistic $\nu _e$, and they depend on the various angular correlations among the transversal $\nu _e$ spin polarization, the polarization of the electron target, the incoming neutrino momentum and the outgoing electron momentum.

Appendix 2: Definitions of the asymmetry functions

The asymmetry function $A(\varPhi )$ is defined as

$$\begin{aligned} A(\varPhi ) := \frac{\int \limits _{\varPhi }^{\varPhi +\pi }\frac{\mathrm{d}\sigma }{\mathrm{d} \phi _{e}}\,\mathrm{d}\phi _e - \int \limits _{\varPhi +\pi }^{\varPhi +2\pi }\frac{\mathrm{d}\sigma }{\mathrm{d} \phi _{e}}\,d\phi _e}{\int \limits _{\varPhi }^{\varPhi +\pi }\frac{\mathrm{d}\sigma }{\mathrm{d} \phi _{e}}\,\mathrm{d}\phi _e + \int \limits _{\varPhi +\pi }^{\varPhi +2\pi }\frac{\mathrm{d}\sigma }{\mathrm{d} \phi _{e}}\,\mathrm{d}\phi _e}. \end{aligned}$$

(17)

Two other asymmetry functions are employed:

$$\begin{aligned} A_y(\varPhi ):= & {} \frac{\int \limits _{\varPhi }^{\varPhi +\pi }\frac{\mathrm{d}^2\sigma }{\mathrm{d} \phi _{e} \mathrm{d}y}\,\mathrm{d}\phi _e - \int \limits _{\varPhi +\pi }^{\varPhi +2\pi }\frac{\mathrm{d}^2\sigma }{\mathrm{d} \phi _{e} dy}\,\mathrm{d}\phi _e}{\int \limits _{\varPhi }^{\varPhi +\pi }\frac{\mathrm{d}^2\sigma }{\mathrm{d} \phi _{e} \mathrm{d}y}\,\mathrm{d}\phi _e + \int \limits _{\varPhi +\pi }^{\varPhi +2\pi }\frac{\mathrm{d}^2\sigma }{\mathrm{d} \phi _{e} \mathrm{d}y}\,\mathrm{d}\phi _e}, \end{aligned}$$

(18)

$$\begin{aligned} A_{\theta _e}(\varPhi ):= & {} \frac{\int \limits _{\varPhi }^{\varPhi +\pi }\frac{\mathrm{d}^2\sigma }{\mathrm{d} \phi _{e}\mathrm{d}\theta _e}\,\mathrm{d}\phi _e - \int \limits _{\varPhi +\pi }^{\varPhi +2\pi }\frac{\mathrm{d}^2\sigma }{\mathrm{d} \phi _{e} \mathrm{d}\theta _e}\,\mathrm{d}\phi _e}{\int \limits _{\varPhi }^{\varPhi +\pi }\frac{\mathrm{d}^2\sigma }{\mathrm{d} \phi _{e} \mathrm{d}\theta _e}\,\mathrm{d}\phi _e + \int \limits _{\varPhi +\pi }^{\varPhi +2\pi }\frac{\mathrm{d}^2\sigma }{\mathrm{d} \phi _{e} \mathrm{d}\theta _e}\,\mathrm{d}\phi _e}. \end{aligned}$$

(19)