Magnetar crust electron capture for $^{55}$Co and $^{56}$Ni

Abstract

Based on the relativistic mean-field effective interaction principle and random phase approximation theory in superstrong magnetic fields (SMFs), we present an analysis of the influence of SMFs on the electron Fermi energy, nuclear blinding energy, single-particle level structure and electron capture for $^{55}$Co, and $^{56}$Ni by the shell-model Monte Carlo method in the magnetar’s crust. The electron capture rates increase by two orders of magnitude due to an increase in the electron Fermi energy and a change in single-particle level structure by SMFs. Then the rates decrease by more than two orders of magnitude due to an increase in the nuclear binding energy and a reduction in the electron Fermi energy by SMFs.

1 Introduction

Electron capture (EC) has always been an interesting problem in the study of massive stars and supernova explosions. Fuller et al. [1,2,3] (hereafter FFN), Dean et al. [4], Aufderheide et al. [5, 6] (hereafter AUFD), Langanke et al. [7, 8], Nabi [9] (hereafter NKK), and Juodagalvis [10] discussed the EC problem ignoring the influence of SMFs. In our previous work [11,12,13,14,15,16,17,18] we investigated the weak interaction and neutrino energy loss and found that the matter properties of manetars powered by the magnetic field energy [15,16,17,18] could be modified significantly by SMFs. The properties of strongly magnetized ultradense matter and their imprints on magnetar were discussed in detail by Lai et al. [19,20,21].

Very recently, Mereghetti et al. [22] reviewed explicitly the magnetars’ properties, origin and evolution. Some interesting behaviors such as a wide array of X-ray activity including short bursts, large outbursts, giant flares, quasi-periodic oscillations, enhanced spin-down, glitches and anti-glitches are displayed in magnetars and discussed by Kaspi and Beloborodov [23]. The electron Fermi energy, and the electron fraction in SMFs and the dipole magnetic field and spin-down evolutions were explored in detail by Gao et al. [24,25,26,27,28] and Zhu et al. [29].

A new improved relativistic mean-field effective interaction theory (RMFEIT) with explicit density dependence of the meson-nucleon couplings is used to calculate the energy level for nuclear ground state and properties of excited states [30, 31]. RMFEIT has recently gained considerable success in describing various facets of nuclear structure properties. RMFEIT also can give a quantitative description of ground state properties of spherical and deformed nuclei and has been used to discuss the properties of nuclear matter by some authors (e.g., [30,31,32,33]).

Our work differs from previous work [1,2,3, 5, 6, 9]. FFN, and AUFD based their work on the theory of the Brink hypothesis. The Brink hypothesis is a very crude approximation, which assumes that the Gamow–Teller (GT) strength distribution on excited states is the same as that on the ground state. The GT strength distribution is only shifted by the excitation energy of the states. NKK [9] investigated the EC issue by using the quasi-particle random phase approximation and addressed the problem only in the case without SMFs. We analyze the EC in SMFs according to the shell-model Monte Carlo (SMMC) method and random phase approximation (RPA) theory [7, 8]. Although Refs. [7, 8] investigated in detail the EC process, they have lost sight on the influence of SMFs on the EC. Our discussions also differ from [34], which analyzed the EC process by using the method of the Brink hypothesis only in non-zero temperature crusts of neutron stars.

In this paper, based on the Lai dong model [19,20,21] and the RMFEIT [30,31,32,33], we improve our previous work (i.e., [12, 13]) and study the electron Fermi energy, nuclear blinding energy, single-particle level structure and the EC problem in SMFs. In Sect. 2, we describe the theoretical framework and analyze the effect of SMFs on the electron property and nuclear blinding energy in magnetars. The SMMC method, Gamow–Teller response functions, and the EC in SMFs are also discussed. In Sect. 3 we present numerical results and discussion and summarize our conclusions in Sect. 4.

2 Theoretical framework

2.1 The electron properties in magnetar’s crust

The properties of matter are significantly modified by strong magnetic fields, such as the equation of state, the electron energy, the outer crust structure and the composition in neutron stars. Some work presented the motions of charged particle in a SMF with the quantum mechanism in detail (e.g., [35,36,37]). At first, we consider the non-relativistic motion of a charged particle (charge $e_i$ and mass $m_i$) in a uniform magnetic field, which is assumed to be along the z-axis, the circular orbit radius and the cyclotron frequency in the process of particle gyrates are given by $r=m_icv_{\bot }/|e_i|B$, $\omega _c=|e_i|B/m_ic$, respectively, here $v_{\bot }$ is the velocity perpendicular to the magnetic field. The kinetic energy for the electron ($m_i\rightarrow m_e$, $e_i\rightarrow -e$) transverse motion is quantized and can be written

$$\begin{aligned} E_\mathrm{kin}=\frac{1}{2}m_iv^2_{\bot }\rightarrow \left( n_l+\frac{1}{2}\right) \hbar \omega _c \end{aligned}$$

(1)

where $n_l=0, 1, 2...,$ is the Landau level number. The cyclotron energy for an electron is given by

$$\begin{aligned} E_\mathrm{cyc}=\hbar \omega _c=\hbar \frac{eB}{ec}=11.577B_{12}~~~ \mathrm {keV}, \end{aligned}$$

(2)

where $B_{12}=B/10^{12}~\mathrm {G}$ is the magnetic field strength in units of $10^{12}$ G, The total electron energy, which includes the kinetic energy associated with the z-momentum ($p_z$) and the spin energy in non-relativistic quantum environment can be written as [35,36,37]

$$\begin{aligned} E_{n}=\nu \hbar \omega _{c}+\frac{p_z^2}{2m_e}, \end{aligned}$$

(3)

where $\nu =n_l+(1+\sigma _z)/2$. $\sigma _z=-1$, $\sigma _z=\pm 1$ are the spin degeneracy for the ground Landau level ($n_l=0$), and excited levels, respectively.

We define a critical magnetic field strength $B_\mathrm{cr}$ from the relation of $\hbar \omega _{c}=m_ec^2$ (i.e. $B_\mathrm{{cr}}=m_e^2c^3/e\hbar =4.414\times 10^{13}$ G). The transverse motion of the electron becomes relativistic when $\hbar \omega _c\ge m_ec^2$ (i.e. $B\ge B_\mathrm{{cr}}$) for extremely strong magnetic fields. The energy eigenstates of electrons must obey the relativistic Dirac equation and are given by [35,36,37]

$$\begin{aligned} E_n=\left[ c^2p_z^2+m_e^2c^4\left( 1+2\nu \frac{B}{B_\mathrm{{cr}}}\right) \right] ^{1/2}, \end{aligned}$$

(4)

where the shape of the Landau wavefunction in the relativistic theory is the same as that in the non-relativistic theory due to the fact that the cyclotron radius is independent of the particle mass.

In SMFs the number density of electrons $n_{e}$ is related to the chemical potential $U_\mathrm{{F}}$ by [19,20,21]

$$\begin{aligned} n_{e}^{{B}}=\frac{1}{(2\pi \widehat{\rho })^2\hbar }\sum _0^\infty g_{n0} \int _{-\infty } ^{+\infty } f \mathrm{d}p_\mathrm{{z}}, \end{aligned}$$

(5)

where $\widehat{\rho }=(\hbar c/eB)^{1/2}=2.5656\times 10^{-10}B_{12}^{1/2}\mathrm {cm}$ is the cyclotron radius (the characteristic size of the wave packet), and $g_{n0}$ is the spin degeneracy of the Landau level, $g_{00}=1$ and $g_{n0}=2$ for $n\ge 1$, and $f=[1+\exp ((E_n-U_\mathrm{{F}})/kT)]^{-1}$ is the Fermi–Dirac distribution.

According to the relation of the usual relativistic energy and momentum from Eq. (4), the interaction energy term, which is proportional to the quantum number $\nu$, cannot exceed the electron chemical potential due to the electron interaction with the magnetic field. Thus the maximum number of Landau levels $\nu _\mathrm{max}$, related to the highest value of the allowed interaction energy, should be satisfied with $E_n=U_\mathrm{{F}}$ when $\nu _\mathrm{{max}}$, and $p_z=0$. So we have $\nu _\mathrm{{max}}=B_\mathrm{{cr}}/2B(U_\mathrm{{F}}^2/(m_e^2c^4)-1).$ However, in the general case (i.e., $0\le \nu \le \nu _\mathrm{{max}}$), when the maximum electron momentum is equaled to the Fermi momentum $P_\mathrm{{F}}$ for different Landau level value $\nu$, the electron chemical potential from Eq. (4) can be computed as follows:

$$\begin{aligned} E_n(\nu )=\left[ c^2p_\mathrm{{F}}^2+m_e^2c^4\left( 1+2\nu \frac{B}{B_\mathrm{{cr}}}\right) \right] ^{1/2}=U_\mathrm{{F}}. \end{aligned}$$

(6)

If we define a non-dimensional Fermi momentum $x_e(\nu ) = p_\mathrm{{F}}/m_ec$, and a non-dimensional Fermi energy $\gamma _e = U_\mathrm{{F}}/m_ec^2$, the electron density, the electron energy, and the electron pressure can be written as [19,20,21]

$$\begin{aligned} n_{e}^B= & {} \frac{B}{2\pi ^2B_\mathrm{{cr}}\lambda _e^3}\sum _{\nu =0}^{\nu _\mathrm{{max}}}g_{n0}x_e(\nu ), \end{aligned}$$

(7)

$$\begin{aligned} \varepsilon _{e}= & {} \frac{Bm_ec^2}{2\pi ^2B_\mathrm{{cr}}\lambda _e^3}\sum _{\nu =0}^{\nu _\mathrm{{max}}}g_{n0}\left( 1+2\nu \frac{B}{B_\mathrm{{cr}}}\right) \vartheta _{+}\left[ \frac{x_e(\nu )}{(1+2\nu B/B_\mathrm{{cr}})^{1/2}}\right] , \nonumber \\ \end{aligned}$$

(8)

and

$$\begin{aligned} P_{e}=\frac{Bm_ec^2}{2\pi ^2B_\mathrm{{cr}}\lambda _e^3}\sum _{\nu =0}^{\nu _\mathrm{{max}}}g_{n0}\left( 1+2\nu \frac{B}{B_\mathrm{{cr}}}\right) \vartheta _{-} \left[ \frac{x_e(\nu )}{(1+2\nu B/B_\mathrm{{cr}})^{1/2}}\right] , \end{aligned}$$

(9)

respectively, where $\vartheta _{\pm }(x)=\frac{1}{2}x\sqrt{1+x^2}\pm \frac{1}{2}\ln (x+\sqrt{1+x^2})$, $\lambda _\mathrm{{e}}=\hbar /m_\mathrm{{e}}c$ is the electron Compton wavelength.

2.2 The nuclear energy in magnetar’s crust

The matter in the outer crust of a cold ($T=0$ K) magnetar consists of a Coulomb lattice of completely ionized atoms and a uniform Fermi gas of relativistic electrons. The Gibbs free energy per baryon g(A, z, P) at a constant pressure and zero temperature is given by [38]

$$\begin{aligned} g(A, Z, P)=\frac{E(A,z,p)+PV}{A}=\varepsilon +\frac{P}{n}, \end{aligned}$$

(10)

where $\varepsilon$ is the corresponding energy per nucleon, $n=A/V$ is the baryon density in a cell, and V is the volume occupied by a unit cell of the Coulomb lattice. The energy per nucleon $\varepsilon$, which consists of three different contributions from nucleus, electrons, and lattice is given by

$$\begin{aligned} \varepsilon =\varepsilon _n(A, z)+\varepsilon _e(A, z, P)+\varepsilon _l(A, z, n), \end{aligned}$$

(11)

where the nuclear contribution to the total energy per nucleus is simple and independent of the density and is written as

$$\begin{aligned} \varepsilon _n(A, z)=\frac{M(A, z)}{A}=\frac{1}{A}[zm_p+(A-z)m_n-\varepsilon _{{b}}(A, z)], \end{aligned}$$

(12)

where M(A, z) is the nucleus mass, $\varepsilon _{{b}}(A, z)$ is the corresponding binding energy, and $m_n$ and $m_p$ are neutron and proton masses, respectively.

Based on RMFEIT [32, 33], Pena Arteaga et al. [39] discussed the influence of SMFs on the nuclear binding energies. An effective Lagrangian with nucleons and mesons is given by the simple and independent density function [39,40,41]

$$\begin{aligned} L=L_\mathrm{N}+L_\mathrm{m}+L_\mathrm{int}+L_\mathrm{BO}+L_\mathrm{BM}, \end{aligned}$$

(13)

where $L_\mathrm{N}$, $L_\mathrm{m}$, and $L_\mathrm{int}$ are the Lagrangian of the free nucleus, the free meson fields and the electromagnetic field generated by protons, and the Lagrangian describing the interactions, respectively. These Lagrangians are represented as

$$\begin{aligned} L_\mathrm{N}= & {} \bar{\psi }(i\gamma ^\mu \partial _{\mu }-m_\mathrm{nu})\psi , \end{aligned}$$

(14)

$$\begin{aligned} L_\mathrm{m}= & {} \frac{1}{2}\partial _{\mu } \sigma \partial ^{\mu }\sigma -\frac{1}{2}m_{\sigma }\sigma ^2-\frac{1}{4}\Omega _{\mu \nu }\Omega ^{\mu \nu }+\frac{1}{2}m^2_{\omega }\omega _{\mu }\omega ^{\mu } \nonumber \\&-\frac{1}{4}\mathrm{R}_{\mu \nu }\mathrm{R}^{\mu \nu }+\frac{1}{2}m^2_{\rho }\mathbf {\rho }_{\mu }\mathbf {\rho }^{\mu }-\frac{1}{4}F_{\mu \nu }F^{\mu \nu }-U(\sigma ),\nonumber \\ \end{aligned}$$

(15)

and

$$\begin{aligned} L_\mathrm{int}= & {} -g_{\sigma }\bar{\psi } \sigma \psi -g_{\omega }\bar{\psi }\gamma ^{\mu }\omega _{\mu } \sigma \psi -g_{\rho }\bar{\psi } \gamma ^{\mu } \mathbf {\tau } \mathbf {\rho }^{\mu }\psi \nonumber \\&-e \bar{\psi }\gamma ^{\mu }A_{\mu } \psi , \end{aligned}$$

(16)

respectively, where $\psi$ is the Dirac spinor. $m_\mathrm{nu}$, and $m_{\sigma }, m_{\omega }, m_{\rho },$ are the nucleon and meson masses, respectively. $U(\sigma )=(g_2/3)\sigma ^3+g_3/4)\sigma ^4$ is the standard form for the nonlinear coupling of the $\sigma$ meson field. $g_{\sigma }, g_{\omega }, g_{\rho }$ are the coupling constants for the $\sigma , \omega , \rho ,$ respectively. e is photon fields which vanishes for neutrons.

The coupling of the proton orbital motion with the external magnetic field, and the coupling of proton and neutron intrinsic dipole magnetic moments with the external magnetic field can be expressed as [42]

$$\begin{aligned} L_\mathrm{BO}=e \bar{\psi }\gamma ^{\mu }A_{\mu }^\mathrm{(ext)} \psi , \end{aligned}$$

(17)

and

$$\begin{aligned} L_\mathrm{BM}=-\bar{\psi }\chi _{\tau _3}^\mathrm{(ext)} \psi , \end{aligned}$$

(18)

respectively, where $\chi _{\tau _3}^\mathrm{(ext)}=\kappa _{\tau _3}\mu N\frac{1}{2}\sigma _{\mu \nu }F^{\mathrm{(ext)}\mu \nu }$, $F^{\mathrm{(ext)}\mu \nu }$ is the external field strength tensor. $\sigma _{\mu \nu }=\frac{i}{2}[\gamma ^{\mu }, \gamma ^{\nu }]$, $\mu _N=e\hbar /2m$ is the nuclear magneton, $\kappa _n=g_n/2$, $\kappa _p=g_p/2-1$ (here $g_n=-3.8263, g_p=5.5856$) are the intrinsic magnetic moments of protons and neutrons, respectively.

The contribution of electrons, which are treated as a degenerate free Fermi gas, is given by

$$\begin{aligned} \varepsilon _{e}(A, z, P)= & {} \frac{1}{n\pi ^2}\int _0^{p_\mathrm{{F}}}p^2\sqrt{p^2+m_e^2c^4}\mathrm{d}p\nonumber \\= & {} \frac{m_e^4c^8}{8n\pi ^2}[x_e(\nu )\gamma _e(x_e^2(\nu )+\gamma ^2_e)\nonumber \\&-\ln (x_e(\nu )+\gamma _e)]. \end{aligned}$$

(19)

The lattice energy per baryon $\varepsilon _l(A, Z, n)$ can be written as [42]

$$\begin{aligned} \varepsilon _l(A, Z, n)=-1.81962\frac{(ze)^2}{a}=-C_{bcc}\frac{z^2}{A^{4/3}}p_\mathrm{{F}}, \end{aligned}$$

(20)

where $C_{bcc}=3.40665\times 10^{-3}$, and a is the lattice constant. Similar calculations such as faced-centered cubic or simple cubic ones can be carried out by evaluating different lattice configurations.

2.3 The SMMC method and Gamow–Teller response functions

Here we neglect the effect of SMFs on the GT properties here because the GT transition matrix elements for electron capture do not depend on the magnetic fields [35, 43]. A detailed discussion of the SMMC method can be found in [44]. Based on a statistical formulation of the nuclear many-body problem in the finite-temperature version of this approach, an observable is calculated as the canonical expectation value of a corresponding operator $\hat{A}$ by the SMMC method at a given temperature T, and is written by [45,46,47,48]

$$\begin{aligned} \hat{A}=({ \mathrm{Tr}_{A}[\hat{A}e^{-\beta \hat{{H}}}]})/({\mathrm{Tr}_{A}[e^{-\beta \hat{{H}}}]}). \end{aligned}$$

(21)

The problem of the shell-model Hamiltonian $\hat{{H}}$ has been investigated in detail by Ref. [48]. When a certain many-body Hamiltonian $\hat{{H}}$ is given, a tractable expression for an imaginary-time evolution operator is written by $\hat{U}=\exp ^{-\beta \hat{{H}}},$ where $\beta =1/T_\mathrm{{N}}$, $T_\mathrm{{N}}$ is the nuclear temperature in units of MeV. $\mathrm{Tr}_A{\hat{U}}$ is the canonical partition function for A nucleons. In terms of a spectral expansion, the total strength of a transition operator $\hat{A}$ is then given by the following expectation value:

$$\begin{aligned} B({A})\equiv \langle \hat{A}^{\dagger }\hat{A} \rangle =\frac{\sum _{i,f}e^{-\beta E_i}|\langle f|\hat{A}|i\rangle |^2}{\sum _{i}e^{-\beta E_i}}, \end{aligned}$$

(22)

here $|i\rangle$, $|f\rangle$ are the many-body states of the initial and final nucleus with energy $E_i, E_f$, respectively.

The SMMC method is used to calculate the response function $R_{{A}}(\tau )$ of an operator $\hat{{{A}}}$ at an imaginary time $\tau$. By using a spectral distribution of initial and final states $|i\rangle$ and $|f\rangle$ with energies $E_i$ and $E_f$. $R_{{A}}(\tau )$ is given by [4, 7, 8]

$$\begin{aligned} R_{{A}}(\tau )\equiv & {} \langle \hat{A}^{\dagger }(\tau )\hat{A}(0) \rangle = \frac{{\mathrm{Tr}_{A}[e^{-(\beta -\tau )\hat{{H}}}}\hat{A}^\dag e^{-\tau \hat{{H}}}\hat{A}]}{{\mathrm{Tr}_{A}[e^{-\beta \hat{{H}}}]}} \nonumber \\= & {} \frac{\sum _{if}(2J_i+1)e^{-\beta E_i}e^{-\tau (E_f-E_i)}|\langle f|\hat{A}|i\rangle |^2}{\sum _i (2J_i+1)e^{-\beta E_i}}. \end{aligned}$$

(23)

Note that the total strength for the operator is given by $R(\tau =0)$. $S_{\mathrm{{GT}}^+}$ is the total amount of the GT strength available for an initial state given by summing over a complete set a final states in GT transition matrix elements $|M_{\mathrm{{GT}}}|^{2}_{if}$. The strength distribution is given by [4]

$$\begin{aligned} S_{\mathrm{{GT}}^+}(E)= & {} \frac{\sum _{if}\delta (E-E_f+E_i)(2J_i+1)e^{-\beta E_i}|\langle f|\hat{A}|i\rangle |^2}{\sum _i (2J_i+1)e^{-\beta E_i}} \nonumber \\= & {} S_{{{A}}}(E), \end{aligned}$$

(24)

which is related to $R_{{A}}(\tau )$ by a Laplace transform, $R_{{A}}(\tau )=\int _{-\infty }^{\infty }S_{{A}}(E)e^{-\tau E}\mathrm{d}E$. Note that here E is the energy transfer within the parent nucleus, and the strength distribution $S_{\mathrm{{GT}}^+}(E)$ has units of $\mathrm {MeV^{-1}}$.

2.4 The study of EC

The weak interactions were investigated by some authors, e.g., Refs. [8, 10], by using the RPA theory and SMMC method with a global parameterizations of the single-particle numbers, The EC rate in the absence of a SMFs is related to the electron capture cross-section and can be given by Eq. (4) in Ref. [4]. We can compute the EC rates from one of the initial states to all possible final states in a SMFs and in a weak magnetic field approximation ($B<<B_\mathrm{cr}$). The EC rates in both cases are expressed by [12, 13]

$$\begin{aligned} \lambda ^{0}_\mathrm{ec}(\mathrm {LJ})= & {} \frac{\ln 2}{6163}\int ^{\infty }_{0}\mathrm{d}\xi S_\mathrm{GT}\frac{c^3}{(m_{e}c^2)^5}\nonumber \\&\times \int ^{\infty }_{p_0}\mathrm{d}p_{e}p^2_e(-\xi +\varepsilon _n)^2 F(Z,\varepsilon _n)f(\varepsilon _{n},U_\mathrm{{F}},T), \nonumber \\ \end{aligned}$$

(25)

and

$$\begin{aligned} \lambda _\mathrm{ec}^{{B}}(\mathrm {LJ})=\frac{\ln 2}{6163}\int ^{\infty }_{0}\mathrm{d}\xi S_\mathrm{GT}\frac{c^3}{(m_{e}c^2)^5} \frac{b}{2}\sum _{0}^{\infty }\theta _n, \end{aligned}$$

(26)

respectively, where $\theta _n=g_{no}\int ^{\infty }_{p_0^B}\mathrm{d}p_{e}p^2_e(-\xi +\varepsilon _n)^2 F(Z,\varepsilon _n)f(\varepsilon _{n},U_\mathrm{{F}},T)$, $b=B/B_\mathrm{\mathrm{cr}}$, the $\varepsilon _n$ is the total rest mass and kinetic energies, and $F(Z, \varepsilon _n)$ is the Coulomb wave correction.

In the case without and with SMFs, the $p_0$ and $p_0^B$ are defined as

$$\begin{aligned} p_0=\left\{ \begin{array}{ll}\sqrt{Q^2_{if}-m_e^2c^4} &{}\quad ( Q_{if}<-m_ec^2)\\ ~0 &{} \quad (\mathrm {otherwise}); \end{array} \right. \end{aligned}$$

(27)

and

$$\begin{aligned} p_0^B=\left\{ \begin{array}{ll} \sqrt{Q^2_{if}-\Theta },&{} \quad ( Q_{if}<\Theta ^{1/2})\\ 0 &{} \quad (\mathrm{{otherwise}}), \end{array} \right. \end{aligned}$$

(28)

respectively, where $\Theta =m_e^2c^4(1+2\nu B/B_\mathrm{{cr}})=m_e^2c^4(1+2\nu b)$.

3 Results and discussions

The magnetar surface thermal temperature is high as $(4-6)\times 10^6$ K, and the crust temperature may be higher, about several $10^8$ K. For example, the maximum of inner crust temperature for some light elements may be as high as $2\times 10^8$ K (e.g., [23, 49]), but the maximum of inner crust temperature for some iron elements may be as high as $10^9$ K (e.g., [50,51,52]). In this paper, we discuss the electron capture for iron group nuclei, so we select several typical inner crust temperature value at the order of $10^9$ K.

Fig. 1

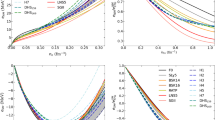
The EC rates for $^{55}$Co and $^{56}$Ni as a function of electron Fermi energy $U_\mathrm{F}$ when $10<B_{12}<10^6$ under the different conditions $\mathrm {CD}_i$, $i=1$–5, corresponding to $\rho _7=5.86, Y_e=0.47, T_9=3.40$; $\rho _7=6.63, Y_e=0.46, T_9=3.51$; $\rho _7=11.7, Y_e=0.45, T_9=3.73$; $\rho _7=14.5, Y_e=0.44, T_9=3.80$; and $\rho _7=106, Y_e=0.43, T_9=4.93$

In considering relativistic electrons in magnetar crust, the electron chemical potential should range from 10 $m_ec^2$ to 100 $m_ec^2$. Figure 1 shows the EC rates of $^{55}$Co, and $^{56}$Ni as a function of $U_\mathrm{{F}}$ (note $\rho _7$ and $T_9$ are in units of $10^7$ $\mathrm {g/cm^3}$ and $10^9$ K, respectively). The electron chemical potential effects greatly on EC process in SMFs due to the different Q-value and transition orbits. When density and temperature are given (e.g., $\rho _7=5.86, Y_e=0.47, T_9=3.40$), the rates decrease when 1 $m_ec^2<U_\mathrm{{F}}< 5$ $m_ec^2$, then increase by about more than one order of magnitude as electron chemical potential increases when 5 $m_ec^2<U_\mathrm{{F}}\le$ 100 $m_ec^2$. According to the discussions in Refs. [19,20,21], the electron chemical potential is strongly depended on the factor $B_{12}^{-2}(Y_e\rho )^2$. When magnetic field strength is given, the higher the density, the larger the electron chemical potential. When the density and temperature are given, the smaller the magnetic fields, the larger the electron chemical potential becomes. Thus, a large number of electrons involve an EC reaction because their chemical potential exceeds the Q-value.

A SMFs has a great influence on EC rates. From Fig. 2, one sees that the higher the density, the larger the rates become. Because the electron kinetic energy and electron chemical potential are so high that the influence of SMFs on rates is dramatic at relativity higher density. As the SMFs increases, the rates increase by about two orders of magnitude. Then the rates decrease by more than two orders magnitude when $10^{14}\mathrm {G}<B<10^{15}$ G. But then another increase of the EC rates appears when $B>10^{15}$ G.

Fig. 2

The EC rates for $^{55}$Co and $^{56}$Ni as a function of magnetic field strength B under the different conditions $\mathrm {CD}_i$, $i=1$–5, corresponding to $\rho _7=5.86, Y_e=0.47, T_9=3.40$; $\rho _7=6.63, Y_e=0.46, T_9=3.51$; $\rho _7=11.7, Y_e=0.45, T_9=3.73$; $\rho _7=14.5, Y_e=0.44, T_9=3.80$; and $\rho _7=106, Y_e=0.43, T_9=4.93$

Fig. 3

The GT$^+$ distributions $S_\mathrm{{GT}^+}$ for nuclei $^{55}$Co and $^{56}$Ni as a function of the energy transfer from the electron, $E=E_f-E_i$ at the temperature of $T=0.8$ MeV

Form Fig. 2, we find that the EC rates decrease when $B_{12}>100$. According to Eqs. (4)–(8), when $\nu _\mathrm{{max}}\gg 1$, for electron Fermi energy, the Landau energy level spacing becomes a very small fraction. When the electron gas is in a mildly relativistic state, we have $\nu _\mathrm{{max}}\rightarrow U_e/\hbar \omega _c$. But for relativistic electron gas, the $\nu _\mathrm{{max}}\ge 100/ B_{12}$ when the $U_e\ge 1$ MeV. Thus, the $\nu _\mathrm{{max}}$ tends to the order of unity, and the electron Landau levels will be termed strongly quantized as the magnetic field strength increases (i.e. when $B_{12}\ge 10\sim 100$).

Based on the RMFEFT models of [32, 33], we study the effect of SMFs on the binding energy per particle, which has a parabolic increase as the SMFs increases. According to Eqs. (12)–(18), we calculate the binding energy for $^{56}$Ni, and $^{55}$Co, and find that the binding energies increase by 0.601, and 0.402 MeV, respectively when the SMFs increases from $10^{16}$ to $10^{18}$ G. This is equivalent to significantly raise the threshold energy of EC due to an increase in nuclear binding energy. Thus, the EC is crippled greatly by a SMFs. Meanwhile, because of the interaction between the electrons and SMFs, the electron Fermi energy decreases as a SMFs increases. This actually discourages the EC reaction.

Based on Eqs. (17) and (18), and Refs. [32, 33], we find that an abrupt increase is shown for EC rates when $10^{14} \, \mathrm{{G}}\le B\le 10^{16}$ G shown as in Fig. 2. Such a jump shows that the underlying shell structure may be changed in a fundamental way. This jump in nuclear properties can be traced to the single-particle behavior. A particle will move from a level going upwards and go to a level downward with increasing spin by SMFs. Because of the two levels have opposite angular momentum along the symmetry axis, the nucleus becomes spin-polarized. The single-particle structure for protons and neutrons is strongly modified by a SMFs. Firstly, the strong interaction between the magnetic field and the neutron (proton) magnetic dipole moment will lead to the nucleon paramagnetism. Secondly, the coupling of the orbital motion of protons with SMFs also make the proton orbital magnetism. The interaction between the nucleus and SMFs maybe removes all degeneracies in the single-particle spectrum, and it breaks significantly the formerly degenerate levels with opposing signs of the angular momentum projection. A reduction of the neutron and proton pairing gaps will show because of splitting from single-particle energy as the SMFs increases. Finally, it will lead to their disappearance.

Table 1 Comparisons of the maximum value of our calculations $\lambda ^B_\mathrm{{max}}(\mathrm {LJ})$ with those of minimum value $\lambda ^B_\mathrm{{min}}(\mathrm {LJ})$ for $^{55}$Co, and $^{56}Ni$ when $10^{13}\mathrm{{G}}\le B \le 10^{18}$G under the conditions $\mathrm {CD}_i$, $i=1$–6, corresponding to $\rho _7=5.86, Y_e=0.47, T_9=3.40$; $\rho _7=6.63, Y_e=0.46, T_9=3.51$; $\rho _7=11.7, Y_e=0.45, T_9=3.73$; $\rho _7=14.5, Y_e=0.44, T_9=3.80$; $\rho _7=106, Y_e=0.43, T_9=4.93$, and $\rho _7=4010,Y_e=0.41, T_9=7.33$. The ratio is computed as $s=\lambda ^B_\mathrm{{max}}(\mathrm {LJ})/\lambda ^B_\mathrm{{min}}(\mathrm {LJ})$

Table 2 Comparisons of the no SMFs rates of FFN [2] ($\lambda ^0_\mathrm{{ec}}(\mathrm {FFN})$), AUFD [6] ($\lambda ^0_\mathrm{{ec}}(\mathrm {AUFD})$), and our rates ($\lambda ^0_\mathrm{ec}(\mathrm {LJ}))$, with those of ours $\lambda ^{{B}}_\mathrm{{ec}}(\mathrm {LJ})$ in SMFs for $\rho _{7}=4.32, Y_e=0.47, T_9=3.26$, respectively

Table 3 Comparisons of the rates of FFN [2] ($\lambda ^0_\mathrm{{ec}}(\mathrm {FFN})$), AUFD [6] ($\lambda ^0_\mathrm{{ec}}(\mathrm {AUFD})$), NKK [9] ($\lambda ^0_\mathrm{ec}(\mathrm {NKK}))$, and our rates ($\lambda ^0_\mathrm{ec}(\mathrm {LJ}))$, which are in the case without SMFs with those of ours $\lambda ^{{B}}_\mathrm{{ec}}(\mathrm {LJ})$ in the case with SMFs for $\rho _{7}=5.86, Y_e=0.47, T_9=3.40$, respectively

Here we neglect the effect of SMFs on the GT because the GT transition matrix elements for electron capture do not depend on the SMFs [35, 43]. Figure 3 shows the strength distributions $S_\mathrm{{GT}^+}$ for $^{55}$Co and $^{56}$Ni as a function of the daughter state excitation energy. According to Eqs. (21)–(23), we calculate the $S_\mathrm{{GT}^+}$ and find the peak of it reaches to 2.211, and 4.89 MeV$^{-1}$ at 3.5, 1.45 MeV of daughter nuclei $^{55}$ Fe, and $^{56}$Co, respectively. The total GT strength for $^{56}$Ni in a full pf-shell may be calculated by ${B}(\mathrm {GT})=10.1 g_A^2$ according to the data of experiment. For $^{55}$Co, we discuss the total GT strength and the distribution in a truncated calculation, in which five particles in the final nucleus are maximally allowed to be excited out of the state of $f_{7/2}$. We obtain a total GT strength of $8.7g^2_A$ from the ground states of $^{55}$Co, and $8.9g^2_A$ from both of the excited states of $J = 3/2$.

According to Eqs. (6)–(8) and (25), we calculate the maximum and the minimum value of the EC rates in SMFs for the two typical nuclei by considering the effect of all evaluating factors, and list them in Table 1. The maximum rates reach $5.875\times 10^5$ $\mathrm {s}^{-1}$, and $3.062\times 10^5$ $\mathrm {s}^{-1}$ when $B=3.432\times 10^{16}$ G for $^{55}$Co, $^{56}$Ni, at $\rho _7=4010, Y_e=0.41,T_9=7.33$, respectively. However, the minimum EC rates are 7.207 $\mathrm {s}^{-1}$, and 2.873 $\mathrm {s}^{-1}$ when $B=3.678\times 10^{14}$ G for $^{55}$Co, $^{56}$Ni, at $\rho _7=5.86, Y_e=0.47, T_9=3.40$, respectively. The rates increase by about three orders magnitude as the SMFs increases.

FFN [1,2,3], AUFD [5, 6], and NKK [9] studied EC rates in the case that there are no SMFs. In Tables 2 and 3, we present the comparisons of our results in SMFs with those of FFN, AUFD, and NKK. Our results in the case that there are no SMFs are about 14.7, and 26.07% lower than FFN, and AUFD, respectively, but they are about one order of magnitude larger than that of NKK (e.g. at $\rho _7=5.86, T_9=3.40, Y_e=0.47$). Our SMFs rates are by about six orders of magnitude higher than those of FFN (AUFD), and NKK when $10<B_{12}<10^6$ for $^{55}$Co, and $^{56}$Ni. FFN used the semi-empirical atomic mass formula from Ref. [53] to estimate the Q-value and the EC rates, thus the Q-value used in the effective rates are quite different. Based on the nuclear shell model and the Brink hypothesis method, AUFD expanded the FFN work and analyzed the nuclear excited level by a simple calculation on the nuclear excitation levels transitions. The Brink hypothesis is a very crude approximation. Thus the calculation method is a little rough. Using the quasi-particle random phase approximation theory, NKK expanded the nuclear excitation energy distribution by considering the particle emission processes, which constrained the parent excitation energies. However, only low angular momentum states are considered. The SMMC method actually draws an average of GT intensity distribution of the EC process, and the calculated results are in good agreement with experiments. Thus the method is relatively accurate.

4 Summary

In this work, we investigate the EC for $^{55}$Co, and $^{56}$Ni and the influences of SMFs on electron Fermi energy, binding energy per nuclei, and single-particle level structure in magnetar crust based on the RMFEIT, and Lai dong model; we compare our results with those of FFN, AUFD, and NKK. Our results increase by about two orders of magnitude as SMFs increase, and then decrease by more than two orders magnitude. There is an abrupt increase in EC rates around $B=3\times 10^{14}$ G for $\rho _7<100$ (but around $B=3\times 10^{15}$ G for $\rho _7>100$). Such a jump may be an indication that the underlying shell structure has changed in a fundamental way because of single-particle behavior by SMFs. We find that the EC rates in the case that there are no SMFs are about 14.70, and 26.07 % lower than those of FFN, and AUFD (e.g. for $^{55}$Co at $\rho _7=4.32, T_9=3.26, Y_e=0.47$), but they are about one order of magnitude larger than that of NKK (e.g., at $\rho _7=5.86, T_9=3.40, Y_e=0.47$). But our EC rates in SMFs are by about six orders of magnitude higher than those of FFN, AUFD, and NKK when $10<B_{12}<10^6$ for $^{55}$Co, and $^{56}$Ni.

The observations show that the persistent X-ray emission of a magnetar could originate from magnetic field decay or heating from magnetospheric current and/or from the EC reaction in the crust. The research on EC reaction in magnetar’s crust is still a long-term and arduous task. Our results may be helpful to the future study of the magnetar thermal evolution, and soft X-ray emission mechanism.