1 Introduction

The exact solution of the Einstein–Maxwell field equations has a great importance in the modeling of viable relativistic compact object (CO). The physical viability of these solutions is always remains a crucial test. In this context, Delgaty [1] presented the elementary criteria to test the physical acceptability of solutions and found that only limited number of solutions satisfy the physical test.

In general relativity (GR), the presence of charge has significant role in the modeling of astrophysical CO. It has been shown that presence of electromagnetic field influences the values of redshift, luminosities and maximum mass of CO [2, 3]. Gupta and Maurya [4, 5] found regular and well behaved charged models of super-dense star for particular choice of metric potential \(\textit{g}_{44}\) and electric field intensity. Pant et al. [6] shown that a charged solution possess positively finite pressure and density at the center which fulfill the casuality condition, i.e., \(\frac{d P_r}{d\rho }\le 1\). Maurya and Gupta [7, 8] derived charged solutions with metric potential \(\textit{g}_{44}=B(1+Cr^{2})^{n}\) for every integral value of n, by specifying electric field intensity in terms of parameter \({\mathcal {K}}\) and remarked that all solutions for \(n\ge 4\) are well behaved for some range of parameter \({\mathcal {K}}\).

In order to find the exact solutions of field equations, different limitations have been set by the authors on the symmetry of spacetime and matter distribution. With the assumption that the hypersurface are spheroidal \((t=constant)\), Komathiraj and Maharaj [9] found new class of exact solution for particular values of electromagnetic field and spheroidal parameter. The new exact solutions of Einstein–Maxwell field equations have been derived by Thirukkanesh and Maharaj [10] and Komathiraj and Maharaj [11], for a particular form of electric field intensity. The obtained models do not satisfy the barotropic equation of state (EoS). Varela et al. [12] highlighted the significance of EoS in the modeling of compact stars and provid the general techniques of proceeding with anisotropic matter. Sharma and Maharaj [13] found the solution to field equations with an anisotropic inner fluid distribution and also discussed the discriminating attributes of solution with linear EoS. The charged anisotropic sphere with linear EoS was modeled by Thirukkanesh and Maharaj [14] and Takisa and Maharaj [15]. The obtained solution with isotropic pressure by Hansraj and Maharaj [16] satisfies the barotropic EoS. The models with quadratic EoS were presented by Feroze and Siddique [17] and Maharaj and Takisa [18].

The theory of polytropes in GR has its own importance in the modeling of relativistic CO. Azam et al. [19,20,21,22] presented a brief study of Newtonian and relativistic polytropes with GPEoS. The GPEoS is a combination of linear and polytropic EoS i.e.,

$$\begin{aligned} P_{r}=\alpha \rho +\kappa \rho ^\Gamma , \end{aligned}$$
(1)

where \(\Gamma =1+\frac{1}{\eta }\) and \(\eta \) is polytropic index. Different values of specified polytropic index leads to various astrophysical objects like convective stellar cores of red giant, brown dwarfs, main sequence stars, neutron stars and relativistic degenerate core of white dwarfs. The polytrope has an infinite radius for \(\eta =5\), was discussed by Kippenhahn et al. [23]. An uncharged exact solutions with a polytropic EoS for \(\eta = 1\) and \(\eta = 2\) was provided by Thirukkanesh and Ragel [24, 25]. Takisa and Maharaj [26] found exact solutions with anisotropic pressure and electromagnetic field with polytropic EoS for \(\eta = 1/2, 2/3, 1, 2\).

In this work, our interest is to formulate new exact solutions to the Einstein–Maxwell field equations for anisotropic charged compact objects with GPEoS. In Sect. 2, we rewrite Einstein–Maxwell field equations as analogue system of differential equations using a coordinate transformation purposed by Durgapal [27]. In Sect. 3, we select particular form of the gravitational potential and the electric field to obtain main equation for modeling of physical models. Section 4 provides physical attributes of different values of polytropic index and present new exact solutions for specific values of polytropic indices. In Sect. 5, we examine the physical features of model graphically. Finally, the concluding remarks are presented in Sect. 6.

2 The fundamental anisotropic equations

Consider the line element for a static spherically symmetric spacetime in Schwarzschild coordinates

$$\begin{aligned} ds^2=-\,e^{2\mu (r)}dt^{2}+e^{2\psi (r)}dr^{2}+r^{2}(d\theta ^{2} +\sin ^2\theta {d\phi ^2}), \end{aligned}$$
(2)

where \(\mu (r)\) and \(\psi (r)\) are the arbitrary functions. For charged anisotropic inner fluid distribution, the energy momentum tensor is defined by

$$\begin{aligned} T_{\delta \lambda }=dia\text {g}~\left[ -\rho -\frac{1}{2}E^{2},P_{r} -\frac{1}{2}E^{2},P_{t}+\frac{1}{2}E^{2},P_{t}+\frac{1}{2}E^{2}\right] , \end{aligned}$$
(3)

where energy density, radial pressure, tangential pressure and electric field intensity are represented by \(\rho , P_{r}, P_{t}\) and E respectively. From Eqs. (2) and (3), we have a system of nonlinear equations

$$\begin{aligned}&\frac{1}{r^{2}}[r(1-e^{-2\psi })]'=\rho +\frac{1}{2}E^{2}, \end{aligned}$$
(4)
$$\begin{aligned}&-\frac{1}{r^{2}}(1-e^{-2\psi })+\frac{2\mu '}{r}e^{-2\psi } =P_{r}-\frac{1}{2}E^{2}, \end{aligned}$$
(5)
$$\begin{aligned}&e^{-2\psi }\left( \mu ''+\mu '^2+\frac{\mu '}{r}-\mu '\psi ' -\frac{\psi '}{r}\right) =P_{t}+\frac{1}{2}E^{2}, \end{aligned}$$
(6)
$$\begin{aligned}&\sigma =\frac{1}{r^{2}}e^{\psi }(r^{2}E^{2})', \end{aligned}$$
(7)

where \(\sigma \) represent proper charged density and differentiation with respect to radial component r is denoted by prime. The Einstein–Maxwell field Eqs. (4)–(7) is a system of three independent equations in six independent variables \((\mu , \psi , \rho , P_r, P_t, E~ \)or\(~ \sigma )\). Now using the transformation introduced by Durgapal [27] in terms of new metric functions y and Z

$$\begin{aligned} x=Cr^{2}, ~ Z(x)=e^{-2\psi (r)}, ~ A^{2}y^{2}(x)=e^{2\mu (r)}, \end{aligned}$$
(8)

here A and C are arbitrary constants. Consequently, the system of Eqs. (4)–(7) along with Eq. (1) can restrains the behavior of gravitational field for charged anisotropic fluid distribution

$$\begin{aligned} \frac{\rho }{C}= & {} \frac{1-Z}{x}-2{\dot{Z}}-\frac{E^{2}}{2C}, \end{aligned}$$
(9)
$$\begin{aligned} P_{t}= & {} P_{r}+\Delta , \end{aligned}$$
(10)
$$\begin{aligned} P_{r}= & {} \alpha \rho +\kappa \rho ^{1+\frac{1}{\eta }}, \end{aligned}$$
(11)
$$\begin{aligned} \frac{P_{r}}{C}= & {} 4Z\frac{{\dot{y}}}{y}-\frac{1-Z}{x} +\frac{E^{2}}{2C}, \end{aligned}$$
(12)
$$\begin{aligned} \frac{P_{t}}{C}= & {} 4xZ\frac{\ddot{y}}{y}+{\dot{Z}} +(4Z+2x{\dot{Z}})\frac{{\dot{y}}}{y}-\frac{E^{2}}{C}, \end{aligned}$$
(13)
$$\begin{aligned} \frac{\Delta }{C}= & {} 4xZ\frac{\ddot{y}}{y}+{\dot{Z}} \left( 1+2x\frac{{\dot{y}}}{y}\right) +\frac{1-Z}{x}-\frac{E^{2}}{C}, \end{aligned}$$
(14)
$$\begin{aligned} \frac{\sigma ^{2}}{C}= & {} \frac{4Z}{x}(E+{\dot{E}}x)^{2}, \end{aligned}$$
(15)
$$\begin{aligned} \frac{{\dot{y}}}{y}= & {} \frac{1-Z}{4xZ}-\frac{E^{2}}{8CZ} +\frac{\alpha }{4Z} \left( \frac{1-Z}{x}-2{\dot{Z}}-\frac{E^{2}}{2C}\right) \nonumber \\&+\frac{\kappa C^{\frac{1}{\eta }}}{4Z}\left( \frac{1-Z}{x} -2{\dot{Z}}-\frac{E^{2}}{2C}\right) ^{1+\frac{1}{\eta }}, \end{aligned}$$
(16)

where dot represents derivative w.r.t x and \(\Delta =P_{t}-P_{r}\) is the anisotropy parameter. The equivalent form of Eqs. (9)–(16), with linear EoS, was analyzed by Thirukanesh and Maharaj [10] and with quadratic EoS by Feroze and Siddiqui [17] as well as by Maharaj and Takisa [18]. Also, Takisa and Maharaj [26] dealt it with polytropic EoS. Here, we are investigating this system with GPEoS i.e., Eq. (1), which provides the relation between \(\rho \) and \(P_{r}\). To solve the system it is essential to specify two of the unknowns, in this situation we assume forms for Z and E. The obtained system will remain nonlinear due to polytropic index \(\eta \). The mass function for the sphere with radius r is defined as

$$\begin{aligned} {\mathcal {M}}(r)=\frac{1}{2}\int ^r_0\omega ^2 \rho (\omega )d\omega . \end{aligned}$$
(17)

Using Eq. (8) in above equation, we have

$$\begin{aligned} {\mathcal {M}}(x)=\frac{1}{4C^{\frac{3}{2}}}\int ^x_0\sqrt{\omega } \rho (\omega )d\omega . \end{aligned}$$
(18)

3 Ansatz for Z and E

For the sake of exact solution of Einstein–Maxwell field equations, we need to choose physically admissible ansatz. For this purpose, we solve the system (9)–(16) by selecting particular form of E and gravitational potential Z motivated by Takisa and Maharaj [26]. The same choice of Z was used in [10, 17] which is

$$\begin{aligned} Z=\frac{1+c_2x}{1+c_1x},~~~~ c_1\ne c_2,~ c_2\ne 0 , \end{aligned}$$
(19)

where \(c_1\) and \(c_2\) are arbitrary real constants. This form of Z is continuous and also regular at the origin due to the flexibility provided by the parameters \(c_1\) and \(c_2\). In GR, various stellar models have been obtained corresponding to different values of \(c_1\) and \(c_2\). For instance, Durgapal [27] obtained neutral stellar model for \(c_1=1\) and \(c_2=\frac{-1}{2}\), while Tikekar [28] obtained super dense stars corresponding to \(c_1=7\) and \(c_2=-1\). Thus this choice of Z is credible to develop physical acceptable models for charged anisotropic sphere with the GPEoS. Here, we take electric field

$$\begin{aligned} \frac{E^{2}}{2C}=\frac{\xi x}{(1+c_1x)^{2}}, \end{aligned}$$
(20)

where \(\xi \) is arbitrary real constant. It is worthwhile to mentioned here that for \(\xi =0\), one can easily recover the uncharged models. This choice of E has its own physical attributes, i.e., it is finite at the origin of the star, continuous and also bounded in the interior of the stellar body while for increasing values of x it gives constant value. Hansraj and Maharaj [16] formulated charged models for the same form of E, these models reduces to the Finch and Skea [29] uncharged models. Thus the choice for E is credible to formulate charged anisotropic models with GPEoS. Using values of Z and E, Eqs. (9), (15) and (16) implies

$$\begin{aligned} \frac{\rho }{C}= & {} \left( \frac{(c_1-c_2)(3+c_1x) -\xi x}{(1+c_1x)^2}\right) , \end{aligned}$$
(21)
$$\begin{aligned} \frac{\sigma ^{2}}{C^{2}}= & {} \left( \frac{2\xi (1+c_2x)(3+c_1x)^{2}}{(1+c_1x)^5}\right) , \end{aligned}$$
(22)
$$\begin{aligned} \frac{{\dot{y}}}{y}= & {} \frac{c_1-c_2}{4(1+c_2x)} -\frac{\xi x}{4(1+c_1x)(1+c_2x)}\nonumber \\&+\nonumber \frac{\alpha }{4(1+c_2x)}\times \left( \frac{(c_1-c_2)(3+c_1x)-\xi x}{1+c_1x}\right) \nonumber \\&+\frac{\kappa C^{\frac{1}{\eta }}}{4(1+c_2x)} \left( \frac{(c_1-c_2)(3+c_1x) -\xi x}{(1+c_2x)^{2}}\right) ^{1+\frac{1}{\eta }}.\nonumber \\ \end{aligned}$$
(23)

The above equation is first order non-linear differential equation whose solution yields different physical models corresponding to different values of polytropic index \(\eta \).

The mass function (18) takes the form

$$\begin{aligned} {\mathcal {M}}(x)=\frac{1}{4C^{\frac{1}{2}}} \left[ \frac{[2c_1(c_1-c_2)+\xi ] x^{\frac{3}{2}}}{c_1(1+c_1x)}-\frac{\xi x \arctan \sqrt{c_1x}}{c_1^{\frac{3}{2}}}\right] . \end{aligned}$$
(24)

4 Polytropic models

The polytropic EoS in Newtonian regime are very essential in describing a variety of situations like inner pressure, type of inner fluid distribution etc. Chanderashekhar [30] described the initial results of Newtonian polytropes revealed through law of thermodynamics for polytropic sphere. The model of early and late universe was developed by Chavanis [31, 32] for \(\eta >0\) and \(\eta <0\) with GPEoS. The formation of polytropic fluid sphere for \(\eta =1,\frac{3}{2},\frac{5}{2}\) and 3 was studied by Tooper [33] who also provide some numerical results in this regard. Comprehensive results of relativistic polytropes in the set \(\frac{1}{2}\le \eta \le 3\) was found by Pandey et al. [34]. The energy and structure of singular general relativistic polytropes for the index \(0 \le \eta \le 4.5\) was studied by de Felice et al. [35]. The fact that the models for general relativistic perfect fluid have finite radius for the polytropic index in the range \(0 \le \eta \le 3.339\) was revealed numerically by Nilsson and Uggla [36]. Boehmer and Harko [37] and Andreasson [38] provided the mass-radius ratio for anisotropic matter distribution for a CO, which is accordingly applicable for polytropes. In this paper, we derive the exact solution of Einstein–Maxwell field equations in the presence of anisotropy and the electromagnetic field corresponding to polytropic index \(\eta = 1/2, 2/3, 1, 2\).

4.1 Model 1, when \(\eta =1\)

For \(\eta =1\), the GPEoS (1) takes the form

$$\begin{aligned} P_{r}=\alpha \rho +\kappa \rho ^{2}, \end{aligned}$$
(25)

and consequently, integration of Eq. (23) leads to

$$\begin{aligned} y=F(1+c_1x)^{k}(1+c_2x)^{l}\exp [Q(x)], \end{aligned}$$
(26)

where F is a constant of integration. The expressions for variable Q(x) and constants k and l are given as

$$\begin{aligned} Q(x)= & {} \frac{C\kappa [2(c_1-2c_2)(1+c_1x)-(c_1-c_2)]}{2(1+c_1x)^{2}}\nonumber \\&- \frac{C\kappa \xi [4c_1(c_1-c_2)+\xi ]}{8c_1^{2}(c_1-c_2)(1+c_1x)^{2}}\nonumber \\&- \frac{C\kappa \xi [c_2(2c_1c_2+\xi ) -2c_1(c_1^{2}+\xi )]}{4c_1^{2}(c_1-c_2)^{2}(1+c_1x)},\nonumber \\ k= & {} -\,C\kappa (c_1-c_2)^{2}\nonumber \\&\times \left[ \frac{c_2^{2}}{(c_2-c_1)^{3}} +\frac{c_2}{(c_2-c_1)^{2}}+\frac{1}{4(c_2-c_1)}\right] \nonumber \\&-\frac{C\kappa \xi (c_1-3c_2)}{2(c_1-c_2^{2})} +\frac{\xi [(c_1-c_2)^{2}+C\kappa \xi c_1]}{4c_1(c_1-c_2)^{3}}\nonumber \\&+\frac{\alpha }{2}\left( 1+\frac{\xi }{2c_1(c_1-c_2)}\right) ,\nonumber \\ l= & {} \frac{(c_1-c_2)}{4c_2}+C\kappa (c_1-c_2)^{2}\nonumber \\&\times \left[ \frac{c_2^{2}}{(c_2-c_1)^{3}} +\frac{c_2}{(c_2-c_1)^{2}}+\frac{1}{4(c_2-c_1)}\right] \nonumber \\&+\frac{C\kappa \xi (c_1-3c_2)}{2(c_1-c_2)^{2}} -\frac{\xi [(c_1-c_2)^{2}+C\kappa \xi c_2]}{4c_1(c_1-c_2)^{3}}\nonumber \\&+\frac{\alpha (c_1-c_2)(c_1-3c_2)-\xi }{4c_2(c_1-c_2)}. \end{aligned}$$
(27)

If we take \(A^{2}F^{2}=H\) and \(\hbox {C}=1\), then line element become

$$\begin{aligned} ds^2= & {} -H(1+c_1r^{2})^{2k}(1+c_2r^{2})^{2l}\exp [2(Q(r^{2}))]dt^{2}\nonumber \\&+\frac{1+c_1r^{2}}{1+c_2r^{2}}dr^{2}\nonumber \\&+r^{2}\left( d\theta ^{2} +\sin ^2\theta {d\phi ^2}\right) . \end{aligned}$$
(28)

For uncharge case (\(\xi =0\), \(E=0\)), we have following model corresponding to \(\eta =1\)

$$\begin{aligned}&ds^{2}=-H(1+c_1r^{2})^{2\left[ -C^{2}\kappa (c_1-c_2)^{2} \left\{ \frac{c_2^{2}}{(c_2-c_1)^{3}} +\frac{c_2}{(c_2-c_1)^{2}}+\frac{1}{4(c_2-c_1)}\right\} +\frac{\alpha }{2}\right] }\nonumber \\&\quad \times (1+c_2r^{2})^{2\left[ \frac{(c_1-c_2)}{4c_2}+C^{2}\kappa (c_1-c_2)^{2} \left\{ \frac{c_2^{2}}{(c_2-c_1)^{3}}+\frac{c_2}{(c_2-c_1)^{2}} +\frac{1}{4(c_2-c_1)}\right\} +\frac{\alpha (c_1-3c_2)}{4c_2}\right] }\nonumber \\&\quad \times exp\left[ \phantom {\left. \frac{C\kappa \xi (4c_1(c_1-c_2)+\xi )}{8c_1^{2}(c_1-c_2) (1+c_1r^{2})^{2}}\right] }2\frac{C\kappa \{2(c_1-2c_2)(1+c_1r^{2}) -(c_1-c_2)\}}{2(1+c_1r^{2})^{2}}\right. \nonumber \\&\quad -\left. \frac{C\kappa \xi (4c_1(c_1-c_2)+\xi )}{8c_1^{2}(c_1-c_2) (1+c_1r^{2})^{2}}\right] dt^{2} +\frac{1+c_1r^{2}}{1+c_2r^{2}}dr^{2}\nonumber \\&\quad +r^{2}\left( d\theta ^{2} +\sin ^2\theta {d\phi ^2}\right) , \end{aligned}$$
(29)

Using Eq. (26) in (13) and (14), we get the expressions \(P_t\) and \(\Delta \) for \(\eta =1\), i.e, given in Appendix (45).

4.2 Model 2, when \(\eta =2\)

For \(\eta =2\), Eq. (1) become

$$\begin{aligned} P_{r}=\alpha \rho +\kappa \rho ^{\frac{3}{2}}, \end{aligned}$$
(30)

and integration of Eq. (23) leads to

$$\begin{aligned} y= & {} F\frac{(1+c_1x)^{\frac{(c_1-c_2)^{2}+\alpha (c_1-3c_2)(c_1-c_2) -\xi (1+\alpha )}{4c_2(c_1-c_2)}}}{(1+c_2x)^{\frac{2\alpha c_1(c_2-c_1) -\xi (1+\alpha )}{4c_1(c_1-c_2)}}} \exp [R(x)] \nonumber \\&\times \left( \frac{\sqrt{(c_1-c_2)(3c_2-c_1)+\xi } -\sqrt{c_2}\sqrt{(3+c_1x)(c_1-c_2)-x\xi }}{\sqrt{(c_1-c_2)(3c_2-c_1)+\xi }+ \sqrt{c_2}\sqrt{(3+c_1x)(c_1-c_2)-x\xi }}\right) ^{\frac{m}{2}}\nonumber \\&\times \left( \frac{\sqrt{2c_1(c_1-c_2)+\xi }-\sqrt{c_1} \sqrt{(3+c_1x)(c_1-c_2)-x\xi }}{\sqrt{2c_1(c_1-c_2)+\xi } +\sqrt{c_1}\sqrt{(3+c_1x)(c_1-c_2)-x\xi }}\right) ^{\frac{w}{2}}, \end{aligned}$$
(31)

where F is a constant of integration. The expression for variable R(x) and the constants m and w are defined as

$$\begin{aligned} R(x)= & {} \frac{-C^{\frac{1}{2}}\kappa \sqrt{(3+c_1x)(c_1-c_2)+x\xi }}{2(1+c_1x)}\nonumber \\&-\frac{C^{\frac{1}{2}}\kappa \xi \sqrt{(3+c_1x)(c_1-c_2)-x\xi }}{4c_1(c_1-c_2)(1+c_1x)} ,\nonumber \\ m= & {} \frac{C^{\frac{1}{2}}\kappa \left[ (3c_2-c_1)(c_1-c_2) +\xi \right] ^{\frac{3}{2}}}{2(c_1-c_2)^{2}\sqrt{c_2}},\nonumber \\ w= & {} \frac{C^{\frac{1}{2}}\kappa \left[ 2c_1^{2}(3c_1\!-\!7c_2)(c_1\!-\!c_2)^{2} \!-\!c_1\xi (3c_1\!+\!5c_2)(c_1\!-\!c_2)-\xi ^{2}(3c_1-c_2)\right] }{4c_1^{\frac{3}{2}}(c_1-c_2)^{2}\sqrt{2c_1(c_1-c_2)+\xi }}.\nonumber \\ \end{aligned}$$
(32)

If we take \(A^{2}F^{2}=H\) and \(\hbox {C}=1\) then the line element become

$$\begin{aligned} ds^{2}= & {} -H(1+c_2r^{2})^{2\left[ \frac{(c_1-c_2)^{2} +\alpha (c_1-3c_2)(c_1-c_2) -\xi (1+\alpha )}{4c_2(c_1-c_2)}\right] }\nonumber \\&\times (1+c_1r^{2})^{2\left[ \frac{2\alpha c_1(c_2-c_1) -\xi (1+\alpha )}{4c_1(c_1-c_2)}\right] }\nonumber \\&\times \left( \frac{\sqrt{(c_1\!-\!c_2)(3c_2\!-\!c_1)\!+\!\xi }\!-\!\sqrt{c_2} \sqrt{(3+c_1x)(c_1-c_2)-x\xi }}{\sqrt{(c_1-c_2)(3c_2-c_1)\!+\!\xi }\!+\! \sqrt{c_2}\sqrt{(3+c_1x)(c_1-c_2)-x\xi }}\right) ^{m}\nonumber \\&\times \left( \frac{\sqrt{2c_1(c_1-c_2)+\xi }-\sqrt{c_1} \sqrt{(3+c_1x)(c_1-c_2)-x\xi }}{\sqrt{2c_1(c_1-c_2)+\xi } +\sqrt{c_1}\sqrt{(3+c_1x)(c_1-c_2)-x\xi }}\right) ^{w}\nonumber \\&\times \exp [2R(r^{2})]dt^{2}+\frac{1+c_1r^{2}}{1+c_2r^{2}}dr^{2} +r^{2}\left( d\theta ^{2} +\sin ^2\theta {d\phi ^2}\right) . \end{aligned}$$
(33)

Similar to the above case, the polytropic model for uncharge case corresponding to \(\eta =2\) takes the form

$$\begin{aligned} ds^{2}= & {} -H(1+c_2r^{2})^{2\left[ \frac{(c_1-c_2) +\alpha (c_1-3c_2)-\xi (1+\alpha )}{2c_2}\right] } (1+c_1r^{2})^{\alpha }\nonumber \\&\times \left( \frac{\sqrt{(3c_2-c_1)} -\sqrt{c_2}\sqrt{(3+c_1r^{2})}}{\sqrt{(3c_2-c_1)} +\sqrt{c_2}\sqrt{(3+c_1r^{2})}}\right) ^ {\frac{\kappa [(3c_2-c_1)(c_1-c_2)]^{\frac{3}{2}}}{2(c_1-c_2)^{2}\sqrt{c_2}}}\nonumber \\&\times \left( \frac{\sqrt{2c_1}-\sqrt{c_1}\sqrt{(3+c_1r^{2})}}{\sqrt{2c_1}+\sqrt{c_1}\sqrt{(3+c_1r^{2})}}\right) ^ {\frac{\kappa \sqrt{c_1}(3c_1-7c_2)}{2\sqrt{2c_1(c_1-c_2)}}}\nonumber \\&\times \exp \left[ \frac{-\kappa \sqrt{(3+c_1r^{2}) (c_1-c_2)}}{(1+c_1r^{2})}\right] dt^{2}\nonumber \\&+\frac{1+c_1r^{2}}{1+c_2r^{2}}dr^{2}+r^{2}\left( d\theta ^{2} +\sin ^2\theta {d\phi ^2}\right) . \end{aligned}$$
(34)

The expressions \(P_t\) and \(\Delta \) for \(\eta =2\), are given in Appendix (46), which can be obtained by substituting Eq. (31) in (13) and (14).

4.3 Model 3, when \(\eta =\frac{2}{3}\)

The Eq. (1) become

$$\begin{aligned} P_{r}=\alpha \rho +\kappa \rho ^{\frac{5}{2}}. \end{aligned}$$
(35)

Integrating Eq. (23), we have

$$\begin{aligned} y= & {} F\frac{(1+c_2x)^{\frac{(c_1-c_2)^{2}+\alpha (c_1-3c_2)(c_1-c_2)-\xi (1+\alpha )}{4c_2(c_1-c_2)}}}{(1+c_1x)^{\frac{2\alpha c_1(c_2-c_1)-\xi (1+\alpha )}{4c_1(c_1-c_2)}}} \exp [S(x)] \nonumber \\&\times \left( \frac{\sqrt{(c_1-c_2)(3c_2-c_1)+\xi } -\sqrt{c_2}\sqrt{(3+c_1x)(c_1-c_2)-x\xi }}{\sqrt{(c_1-c_2)(3c_2-c_1) +\xi }+\sqrt{c_2}\sqrt{(3+c_1x)(c_1-c_2)-x\xi }}\right) ^{\frac{p}{2}}\nonumber \\&\times \left( \frac{\sqrt{2c_1(c_1-c_2)+\xi }-\sqrt{c_1} \sqrt{(3+c_1x)(c_1-c_2)-x\xi }}{\sqrt{2c_1(c_1-c_2)+\xi } +\sqrt{c_1}\sqrt{(3+c_1x)(c_1-c_2)-x\xi }}\right) ^{\frac{q}{2}}, \end{aligned}$$
(36)

where F is constant of integration. The expression for variable S(x) and the constants p and q are given as

$$\begin{aligned} S(x)= & {} \frac{-C^{\frac{3}{2}}\kappa (2c_1(c_1-c_2)+\xi )^{2}\Omega }{12c_1^{2}(c_1-c_2)(1+c_1x)^{3}}\nonumber \\&+\frac{C^{\frac{3}{2}}\kappa ((c_1-c_2)(4c_1\xi (c_1^{2}-\xi ) -8c_1^{3}(c_1^{2}-\xi )))\Omega }{32c_1^{2}(c_1-c_2)^{3}(1+c_1x)}\nonumber \\&-\frac{C^{\frac{3}{2}}\kappa (2c_1(c_1-c_2)+\xi )((c_1-c_2) (13c_1^{2}-25c_1c_2)-\xi (13c_1-7c_2)) \Omega }{48c_1^{2}(c_1-c_2)^{2}(1+c_1x)^{2}}\nonumber \\&+\frac{C^{\frac{3}{2}}\kappa (-9c_1^{2}c_2^{4} -206c_1^{3}c_2^{2}(c_1-c_2)-70c_1^{2}c_2^{2}(c_2^{2}-\xi ))\Omega }{32c_1^{2}(c_1-c_2)^{3}(1+c_1x)}\nonumber \\&+\frac{C^{\frac{3}{2}}\kappa ((-c_1^{3}(3c_1^{3} -c_2^{3})-c_1\xi (8c_2^{3}+7c_1\xi )))\Omega }{32c_1^{2}(c_1-c_2)^{3} (1+c_1x)}\nonumber \\&+\frac{C^{\frac{3}{2}}\kappa (72c_1^{3}c_2(c_1^{2}-\xi )+10c_1^{4}\xi +15c_1^{3}c_2^{3}-c_2^{2}\xi ^{2})\Omega }{32c_1^{2}(c_1-c_2)^{3} (1+c_1x)},\nonumber \\ p= & {} \frac{C^{\frac{3}{2}}\kappa \sqrt{c_2}((c_1-c_2)(3c_2-c_1) +\xi )^{\frac{5}{2}}}{2(c_1-c_2)^{4}}, \nonumber \\ q= & {} \frac{C^{\frac{3}{2}}\kappa (-51c_1^{2}c_2^{4} \xi (c_1+c_2)-30c_1^{3}c_2(c_1+c_2) -1468c_1^{5}c_2\xi ^{3}(c_1-c_2))}{32c_1^{\frac{5}{2}} (c_1-c_2)^{4}\sqrt{2c_1(c_1-c_2)+\xi }}\nonumber \\&+\frac{C^{\frac{3}{2}}\kappa [(c_2-c_1)(498c_1^{4}c_2^{2}\xi +15c_1^{6}\xi +5c_1c_2\xi ^{3}-5c_1^{8}-15c_1^{4}\xi ^{2})]}{32c_1^{\frac{5}{2}}(c_1-c_2)^{4}\sqrt{2c_1(c_1-c_2)+\xi }}\nonumber \\&+\frac{C^{\frac{3}{2}}\kappa \xi [c_2(42c_2^{2}-75c_1^{4})-\xi ^{2}(2c_1+5c_2) -6c_2^{2}(c_1^{3}+3c_2^{3})]}{16c_1^{\frac{1}{2}} (c_1-c_2)^{4}\sqrt{2c_1(c_1-c_2)+\xi }}\nonumber \\&+\frac{C^{\frac{3}{2}}\kappa [-\xi ^{3}(c_1^{3}+c_2^{3})-c_1c_2\xi ^{2} (9c_2^{3}+15c_1^{3})+535c_1^{5}c_2^{2}(c_1^{2}+c_2^{2})]}{32c_1^{\frac{5}{2}}(c_1-c_2)^{4}\sqrt{2c_1(c_1-c_2)+\xi }}\nonumber \\&+\frac{C^{\frac{3}{2}}\kappa [c_1^{3}c_2^{5} (353c_2-1354c_1)+c_1^{5}c_2(16c_2^{3}-85c_1^{3})]}{32c_1^{\frac{5}{2}}(c_1-c_2)^{4}\sqrt{2c_1(c_1-c_2)+\xi }}, \end{aligned}$$
(37)

where \(\Omega =\sqrt{(3+c_1x)(c_1-c_2)-\xi x}\). If we take \(A^{2}F^{2}=H\) and C=1 then line element become

$$\begin{aligned} ds^{2}= & {} -\,H(1+c_2r^{2})^{2\left[ \frac{(c_1-c_2)^{2} +\alpha (c_1-3c_2)(c_1-c_2) -\xi (1+\alpha )}{4c_2(c_1-c_2)}\right] }\nonumber \\&\times (1+c_1r^{2})^{2\left[ \frac{2\alpha c_1(c_2-c_1) -\xi (1+\alpha )}{4c_1(c_1-c_2)}\right] }\nonumber \\&\times \left( \frac{\sqrt{(c_1-c_2)(3c_2-c_1)+\xi } -\sqrt{c_2}\sqrt{(3+c_1x)(c_1-c_2)-x\xi }}{\sqrt{(c_1-c_2)(3c_2-c_1)+\xi }+ \sqrt{c_2}\sqrt{(3+c_1x)(c_1-c_2)-x\xi }}\right) ^{p}\nonumber \\&\times \left( \frac{\sqrt{2c_1(c_1-c_2)+\xi }-\sqrt{c_1} \sqrt{(3+c_1x)(c_1-c_2)-x\xi }}{\sqrt{2c_1(c_1-c_2)+\xi } +\sqrt{c_1}\sqrt{(3+c_1x)(c_1-c_2)-x\xi }}\right) ^{q}\nonumber \\&\times \exp [2S(r^{2})]dt^{2}+\frac{1+c_1r^{2}}{1+c_2r^{2}}dr^{2}\nonumber \\&+\,r^{2}\left( d\theta ^{2} +\sin ^2\theta {d\phi ^2}\right) , \end{aligned}$$
(38)

and for uncharge case with \(\eta =\frac{2}{3}\), we have

$$\begin{aligned} ds^{2}= & {} -H(1+c_2r^{2})^{2\left[ \frac{(c_1-c_2) +\alpha (c_1-3c_2)}{2c_2}\right] } (1+c_1r^{2})^{\alpha }\nonumber \\&\times \left( \frac{\sqrt{(3c_2-c_1)} -\sqrt{c_2}\sqrt{(3+c_1x)}}{\sqrt{(3c_2-c_1)}+ \sqrt{c_2}\sqrt{(3+c_1x)}}\right) ^{p}\nonumber \\&\times \left( \frac{\sqrt{2c_1}-\sqrt{c_1}\sqrt{(3+c_1x)}}{\sqrt{2c_1} +\sqrt{c_1}\sqrt{(3+c_1x)}}\right) ^{q}\nonumber \\&\times \exp [2S(r^{2})]dt^{2} +\frac{1+c_1r^{2}}{1+c_2r^{2}}dr^{2}\nonumber \\&+\,r^{2}\left( d\theta ^{2} +\sin ^2\theta {d\phi ^2}\right) . \end{aligned}$$
(39)

The expressions \(P_t\) and \(\Delta \) for \(\eta =\frac{2}{3}\) , i.e., Eq. (47) given in Appendix, which is calculated by substituting Eq. (36) in (13) and (14).

4.4 Model 4, when \(\eta =\frac{1}{2}\)

The Eq. (1) become

$$\begin{aligned} P_{r}=\alpha \rho +\kappa \rho ^{3}. \end{aligned}$$
(40)

Integration of Eq. (23) yields

$$\begin{aligned} y=F(1+c_1x)^{s}(1+c_2x)^{u}\exp [T(x)], \end{aligned}$$
(41)

here F is the constant of integration. The expression for the variable T(x) and the constants s and u are written as

$$\begin{aligned} T(x)= & {} \frac{-C^{2}\kappa [(c_1-c_2)(c_1-3c_2)-\xi ]^{3}}{4(c_1-c_2)^{4}(1+c_1x)}\nonumber \\&-\frac{C^{2}\kappa [2c_1(c_1-c_2)+\xi ]^{3}}{16c_1^{3} (c_1-c_2)^{4}(1+c_1x)^{4}}\nonumber \\&-\frac{C^{2}\kappa [2c_1(c_1-c_2)+\xi ]^{2}[(c_1-c_2)(c_1(3c_1-5c_2) -2\xi )-c_1\xi ]}{12c_1^{3}(c_1-c_2)^{2}(1+c_1x)^{3}}\nonumber \\&-\frac{C^{2}\kappa [6c_1^{4}(c_1^{3}+6c_2\xi )+4c_1^{4}c_2^{2} (29c_1+10c_2)+3c_1\xi ^{3}]}{8c_1^{3}(c_1-c_2)^{2}(1+c_1x)^{2}}\nonumber \\&-\frac{C^{2}\kappa c_2\xi [c_2\xi ^{2}+3c_1(\xi (c_2^{2}+3c_1^{2}) +c_1c_2(c_2^{2}-c_1^{2}))]}{8c_1^{3}(c_1-c_2)^{3}(1+c_1x)^{2}}\nonumber \\&-\frac{C^{2}\kappa [36c_1^{4}c_2(c_2^{3}-c_1^{3})+12c_1^{2}c_2^{2} ((c_1c_2-\xi )\xi +c_1^{2}c_2^{2})]}{8c_1^{3}(c_1-c_2)^{3}(1+c_1x)^{2}}\nonumber \\&-\frac{C^{2}\kappa [3c_1^{4}(-3c_1^{2}-c_2^{2})\xi +2c_1^{3}c_2^{3}(47c_1c_2-40c_1^{2}-13c_2^{2})]}{8c_1^{3}(c_1-c_2)^{3}(1+c_1x)^{2}},\nonumber \\ s= & {} -\frac{C^{2}c_2\kappa (c_1-3c_2)^{3}}{4(c_1-c_2)^{2}}\nonumber \\&+\frac{C^{2}c_2\kappa \xi (c_1-3c_2)^{2}}{4(c_1-c_2)^{3}}\nonumber \\&+\frac{C^{2}c_2\kappa \xi ^{2}[3(c_1-c_2)(c_1-3c_2)-\xi ]}{4(c_1-c_2)^{5}}\nonumber \\&+\frac{\alpha [2c_1(c_1-c_2)^{2}+\xi ]}{4c_1(c_1-c_2)} +\frac{\xi }{4c_1(c_1-c_2)} \nonumber \\ u= & {} \frac{C^{2}c_2\kappa (c_1-3c_2)^{3}}{4(c_1-c_2)^{2}}\nonumber \\&-\frac{C^{2}c_2\kappa \xi (c_1-3c_2)^{2}}{4(c_1-c_2)^{3}}\nonumber \\&-\frac{C^{2}c_2\kappa \xi ^{2}[3(c_1-c_2)(c_1-3c_2)-\xi ]}{4(c_1-c_2)^{5}}\nonumber \\&+\frac{\alpha [c_1^{2}-c_2^{2}-\xi ]}{4c_2(c_1-c_2)} +\frac{(c_1-c_2)^{2}-\xi }{4c_1(c_1-c_2)}. \end{aligned}$$
(42)

If we take \(A^{2}F^{2}=H\) and C=1 then line element become

$$\begin{aligned} ds^2= & {} -\,H(1+c_1r^{2})^{2s}(1+c_2r^{2})^{2u}\exp [2(T(r^{2}))]dt^{2}\nonumber \\&+\frac{1+c_1r^{2}}{1+c_2r^{2}}dr^{2}+r^{2}(d\theta ^{2} +\sin ^2\theta {d\phi ^2}). \end{aligned}$$
(43)

For uncharge case, the model for polytropic index \(\eta =\frac{1}{2}\) become

$$\begin{aligned} ds^2= & {} -\,H(1+c_1r^{2})^{2s}(1+c_2r^{2})^{2u}\exp [2(T(r^{2}))]dt^{2}\nonumber \\&+\frac{1+c_1r^{2}}{1+c_2r^{2}}dr^{2}+r^{2}(d\theta ^{2} +\sin ^2\theta {d\phi ^2}), \end{aligned}$$
(44)

The expressions \(P_t\) and \(\Delta \) for \(\eta =\frac{1}{2}\), i.e., Eq. (48) is given in Appendix. It is worthwhile to mentioned here that the exact solution obtained by Takisa and Maharaj [26] can easily be recovered for \(\alpha =0\).

5 Physical analysis

In this section, we show that the exact solutions with generalized polytropic equation of state found in Sect. 4 are physically acceptable. The choices for gravitational potential and electric field have been made on physical grounds which is discussed in Sect. 3. For the selective values of x, it is shown that quantities \(E,~\rho \) and \(\sigma \) described in Eqs. (20), (21) and (22) are decreasing functions.

Fig. 1
figure 1

Radial pressure for \(c_1=5.5,~c_2=4,~\xi =1,~\alpha =0.3,~\kappa =0.01\) with different values of \({\eta =1,2,\frac{1}{2},\frac{2}{3}}\)

Full size image
Fig. 2
figure 2

Tangential pressure for \(c_1=5.5,~c_2=4,~\xi =1,~\alpha =0.3,~\kappa =0.01\) with different values of \({\eta =1,2,\frac{1}{2},\frac{2}{3}}\)

Full size image
Fig. 3
figure 3

Anisotropy for \(c_1=5.5,~c_2=4,~\xi =1,~\alpha =0.3,~\kappa =0.01\) with different values of \({\eta =1,2,\frac{1}{2},\frac{2}{3}}\)

Full size image

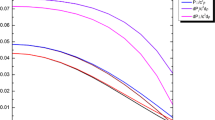
We plot the physical quantities like radial pressure, tangential pressure and anisotropy for particular values of polytropic index \(\eta =\frac{1}{2},\frac{2}{3},1,2\) using software Mathematica. For this, we fixed the parameters \(c_1=5.5, c_2=4, C=1\) and \(\xi =1\) as \(\xi \ne 0\) for charged anisotropic matter distribution. In order to maintain the casuality condition \(\frac{dP_r}{d\rho }\le 1\), we impose constraints on the values of \(\alpha \) and \(\kappa \).

The graph for \(\eta =\frac{1}{2},\frac{2}{3},1,2\) are represented by blue, green, red and black curves respectively. Figure 1 depicts the behavior of radial pressure, it shows that \(P_r\) is decreasing, positive and also finite as desired. Figure 2 represents the tangential pressure \(P_t\), which is positive at the center and monotonically decreasing towards boundary. This implies that tangential pressure \(P_t\) possess the desirable physical attributes. In Fig. 3, we have plotted the anisotropy parameter \(\Delta \) such that \(\Delta (0)=0\) as \(P_t\) and \(P_r\) are equal at center, which is desirable physical condition described by Bowers and Liang [39] and Ivanov [40]. For \(\eta =\frac{1}{2},\frac{2}{3},1\), the profile of \(\Delta \) is negative, initially decreasing then increasing while for \(\eta =2\) , \(\Delta \) possess the opposite behavior which is similar to Thirukkanesh and Maharaj [10]. Figure 4 depicts the behavior of speed of sound \(\frac{dP_r}{d\rho }\) which satisfies the casuality condition explained by Delgaty [1].

Fig. 4
figure 4

Speed of sound for \(c_1=5.5,~c_2=4,~\xi =1,~\alpha =0.3,~\kappa =0.01\) with different values of \({\eta =1,2,\frac{1}{2},\frac{2}{3}}\)

Full size image

6 Discussion

In this work, we have obtained new exact solution to the Einstein–Maxwell field equations with GPEoS. The obtained solutions are used to model charged anisotropic CO. We have written the solutions in terms of elementary functions which fulfill the physical acceptability criteria. The gravitational potential and the matter variable are regular at the origin and also well behaved in the stellar interior. It would be fascinating to compare these obtained solutions to certain astronomical CO such as SAX J1804.4-3658 in the absence of charge and in the presence of charge as done by Dey at al [41,42,43] and Takisa and Maharaj [15]. Such kind of investigation will brace the astrophysical importance of the models in this work. It is worthwhile to mentioned here that all our results are reduced to case of polytropic EoS for \(\alpha =0\) [26].

7 Appendix

Here, we list the expressions for \(P_t\) and \(\Delta \) for every value of \(\eta \) treated in this paper.

(a) For polytropic index \(\eta =1\)

$$\begin{aligned} P_t= & {} \frac{4Cx(1+c_2x)}{(1+c_1x)}\nonumber \\&\times \left[ \frac{k(k-1)c_1^{2}}{(1+c_1x)^{2}} +\frac{2klc_1c_2}{(1+c_1x)(1+c_2x)} +\frac{2kc_1{\dot{Q}}(x)}{(1+c_1x)}\right. \nonumber \\&+\, \left. \frac{l(l-1)c_2^{2}}{(1+c_2x)^{2}}+\frac{2lc_2{\dot{Q}}(x)}{(1+c_2x)} +{\ddot{Q}}(x)+{\dot{Q}}(x)^{2}\right] \nonumber \\&+\, \frac{2C(c_2-c_1)x}{(1+c_1x)^{2}} \left[ \frac{kc_1}{(1+c_1x)}+\frac{c_2l}{(1+c_2x)} +{\dot{Q}}(x)\right] \nonumber \\&+\, C\left[ \frac{(c_1-c_2)c_1x-2x\xi }{(1+c_1x)^{2}}\right] \nonumber \\&+\, C\alpha \left[ \frac{(c_1-c_2)(3+c_1x)-x\xi }{(1+c_1x)^{2}}\right] \nonumber \\&+\, C^{2}\kappa \left[ \frac{(c_1-c_2)(3+c_1x)-x\xi }{(1+c_1x)^{2}}\right] ^{2},\nonumber \\ \Delta= & {} \frac{4Cx(1+c_2x)}{(1+c_1x)}\nonumber \\&\times \left[ \frac{k(k-1)c_1^{2}}{(1+c_1x)^{2}} +\frac{2klc_1c_2}{(1+c_1x)(1+c_2x)}+\frac{2kc_1{\dot{Q}}(x)}{(1+c_1x)} \right. \nonumber \\&+\, \left. \frac{l(l-1)c_2^{2}}{(1+c_2x)^{2}} +\frac{2lc_2{\dot{Q}}(x)}{(1+c_2x)}+{\ddot{Q}}(x) +{\dot{Q}}(x)^{2}\right] \nonumber \\&+\, \frac{2C(c_2-c_1)x}{(1+c_1x)^{2}}\left[ \frac{kc_1}{(1+c_1x)} +\frac{c_2l}{(1+c_2x)}+{\dot{Q}}(x)\right] \nonumber \\&+\, C\left[ \frac{(c_1-c_2)c_1x-2x\xi }{(1+c_1x)^{2}}\right] . \end{aligned}$$
(45)

(b) For polytropic index \(\eta =2\)

$$\begin{aligned} P_t= & {} \frac{4Cx(1+c_2x)}{(1+c_1x)}\nonumber \\&\, \times \left[ \frac{d}{dx}\left( {\dot{R}}(x) +\frac{\alpha {(c_1-c_2)(3+c_1x)-x\xi }}{4(1+c_1x)(1+c_2x)} \right. \right. \nonumber \\&+\, \frac{(c_1-c_2)(1+c_1x)-x\xi }{4(1+c_1x)(1+c_2x)}\nonumber \\&\left. \left. +\, \frac{2\sqrt{c_2}m\sqrt{(c_1-c_2)(3c_2-c_1) +\xi }}{4(1+c_2x)\Omega }\right. \right. \nonumber \\&+\, \left. \left. \frac{2\sqrt{c_1}w\sqrt{2c_1(c_1-c_2)+\xi }}{4(1+c_1x)\Omega }\right) +\frac{{\dot{y}}^{2}}{y^{2}}\right] \nonumber \\&+\, \frac{2C(c_2-c_1)x}{(1+c_1x)^{2}}\left[ {\dot{R}}(x)\right. \nonumber \\&+\, \frac{\alpha {(c_1-c_2)(3+c_1x)-x\xi }}{4(1+c_1x)(1+c_2x)}\nonumber \\&+\, \left. \frac{(c_1-c_2)(1+c_1x)-x\xi }{4(1+c_1x)(1+c_2x)}\right. \nonumber \\&+\, \frac{2\sqrt{c_2}m\sqrt{(c_1-c_2)(3c_2-c_1)+\xi }}{4(1+c_2x)\Omega }\nonumber \\&\left. +\, \frac{2\sqrt{c_1} w\sqrt{2c_1(c_1-c_2)+\xi }}{4(1+c_1x)\Omega }\right] \nonumber \\&+\, C\left[ \frac{(c_1-c_2)c_1x-2x\xi }{(1+c_1x)^{2}}\right] \nonumber \\&+\, C\alpha \left[ \frac{(c_1-c_2)(3+c_1x)-x\xi }{(1+c_1x)^{2}}\right] \nonumber \\&+\, C^{\frac{3}{2}}\kappa \left[ \frac{(c_1-c_2)(3+c_1x)-x\xi }{(1+c_1x)^{2}}\right] ^{\frac{3}{2}}\nonumber \\ \end{aligned}$$
$$\begin{aligned} \Delta= & {} \frac{4Cx(1+c_2x)}{(1+c_1x)}\nonumber \\&\times \left[ \frac{d}{dx} \left( {\dot{R}}(x)+\frac{\alpha {(c_1-c_2)(3+c_1x)-x\xi }}{4(1+c_1x)(1+c_2x)} \right. \right. \nonumber \\&+\, \frac{(c_1-c_2)(1+c_1x)-x\xi }{4(1+c_1x)(1+c_2x)}\nonumber \\&\left. \left. +\, \frac{2\sqrt{c_2}m\sqrt{(c_1-c_2)(3c_2-c_1)+\xi }}{4(1+c_2x)\Omega }\right. \right. \nonumber \\&+\, \left. \left. \frac{2\sqrt{c_1}w\sqrt{2c_1(c_1-c_2)+\xi }}{4(1+c_1x)\Omega }\right) +\frac{{\dot{y}}^{2}}{y^{2}}\right] \nonumber \\&+\, \frac{2C(c_2-c_1)x}{(1+c_1x)^{2}}\left[ {\dot{R}}(x)\right. \nonumber \\&+\, \frac{\alpha {(c_1-c_2)(3+c_1x)-x\xi }}{4(1+c_1x)(1+c_2x)}\nonumber \\&\left. +\, \frac{(c_1-c_2)(1+c_1x)-x\xi }{4(1+c_1x)(1+c_2x)}\right. \nonumber \\&+\, \frac{2\sqrt{c_2}m\sqrt{(c_1-c_2)(3c_2-c_1)+\xi }}{4(1+c_2x)\Omega }\nonumber \\&\left. +\, \frac{2\sqrt{c_1}w\sqrt{2c_1(c_1-c_2)+\xi }}{4(1+c_1x)\Omega }\right] \nonumber \\&+\,\, C\left[ \frac{(c_1-c_2)c_1x-2x\xi }{(1+c_1x)^{2}}\right] . \end{aligned}$$
(46)

(c) For polytropic index \(\eta =\frac{2}{3}\)

$$\begin{aligned} P_t= & {} \frac{4Cx(1+c_2x)}{(1+c_1x)}\nonumber \\&\times \left[ \frac{d}{dx}\left( {\dot{S}}(x) +\frac{\alpha {(c_1-c_2)(3+c_1x)-x\xi }}{4(1+c_1x)(1+c_2x)}\right. \right. \nonumber \\&+\, \frac{(c_1-c_2)(1+c_1x)-x\xi }{4(1+c_1x)(1+c_2x)}\nonumber \\&\left. \left. +\, \frac{2\sqrt{c_2}p\sqrt{(c_1-c_2)(3c_2-c_1)+\xi }}{4(1+c_2x)\Omega }\right. \right. \nonumber \\&+\, \left. \left. \frac{2\sqrt{c_1}q\sqrt{2c_1(c_1-c_2)+\xi }}{4(1+c_1x)\Omega }\right) +\frac{{\dot{y}}^{2}}{y^{2}}\right] \nonumber \\&+\, \frac{2C(c_2-c_1)x}{(1+c_1x)^{2}}\nonumber \\&\times \left[ {\dot{S}}(x)+\frac{\alpha {(c_1-c_2)(3+c_1x)-x\xi }}{4(1+c_1x)(1+c_2x)}\right. \nonumber \\&+\, \frac{(c_1-c_2)(1+c_1x)-x\xi }{4(1+c_1x)(1+c_2x)}\nonumber \\&\left. +\, \frac{2\sqrt{c_2}p\sqrt{(c_1-c_2)(3c_2-c_1)+\xi }}{4(1+c_2x)\Omega }\right. \nonumber \\&+\, \left. \frac{2\sqrt{c_1}q\sqrt{2c_1(c_1-c_2)+\xi }}{4(1+c_1x)\Omega }\right] \nonumber \\&+\,\, C\left[ \frac{(c_1-c_2)c_1x-2x\xi }{(1+c_1x)^{2}}\right] \nonumber \\&+\,\, C\alpha \left[ \frac{(c_1-c_2)(3+c_1x)-x\xi }{(1+c_1x)^{2}}\right] \nonumber \\&+\,\, C^{\frac{5}{2}}\kappa \left[ \frac{(c_1-c_2)(3+c_1x)-x\xi }{(1+c_1x)^{2}}\right] ^{\frac{5}{2}}\nonumber \\ \end{aligned}$$
$$\begin{aligned} \Delta= & {} \frac{4Cx(1+c_2x)}{(1+c_1x)}\nonumber \\&\times \left[ \frac{d}{dx} \left( {\dot{S}}(x)+\frac{\alpha {(c_1-c_2)(3+c_1x)-x\xi }}{4(1+c_1x)(1+c_2x)}\right. \right. \nonumber \\&+\, \frac{(c_1-c_2)(1+c_1x)-x\xi }{4(1+c_1x)(1+c_2x)}\nonumber \\&\left. \left. +\, \frac{2\sqrt{c_2}p\sqrt{(c_1-c_2)(3c_2-c_1)+\xi }}{4(1+c_2x)\Omega }\right. \right. \nonumber \\&+\, \left. \left. \frac{2\sqrt{c_1}q\sqrt{2c_1(c_1-c_2)+\xi }}{4(1+c_1x)\Omega }\right) +\frac{{\dot{y}}^{2}}{y^{2}}\right] \nonumber \\&+\, \frac{2C(c_2-c_1)x}{(1+c_1x)^{2}}\nonumber \\&\times \left[ {\dot{S}}(x)+\frac{\alpha {(c_1-c_2)(3+c_1x)-x\xi }}{4(1+c_1x)(1+c_2x)}\right. \nonumber \\&+\, \frac{(c_1-c_2)(1+c_1x)-x\xi }{4(1+c_1x)(1+c_2x)}\nonumber \\&\left. +\, \frac{2\sqrt{c_2}p\sqrt{(c_1-c_2)(3c_2-c_1)+\xi }}{4(1+c_2x)\Omega }\right. \nonumber \\&+\, \left. \frac{2\sqrt{c_1}q\sqrt{2c_1(c_1-c_2)+\xi }}{4(1+c_1x)\Omega }\right] \nonumber \\&+\,\, C\left[ \frac{(c_1-c_2)c_1x-2x\xi }{(1+c_1x)^{2}}\right] . \end{aligned}$$
(47)

(d) For polytropic index \(\eta =\frac{1}{2}\)

$$\begin{aligned} P_t= & {} \frac{4Cx(1+c_2x)}{(1+c_1x)}\nonumber \\&\times \left[ \frac{s(s-1)c_1^{2}}{(1+c_1x)^{2}} +\frac{2suc_1c_2}{(1+c_1x)(1+c_2x)}+\frac{2sc_1{\dot{T}}(x)}{(1+c_1x)} \right. \nonumber \\&+\, \left. \frac{u(u-1)c_2^{2}}{(1+c_2x)^{2}} +\frac{2uc_2{\dot{T}}(x)}{(1+c_2x)}+{\ddot{T}}(x)+{\dot{T}}(x)^{2}\right] \nonumber \\&+\, \frac{2C(c_2-c_1)x}{(1+c_1x)^{2}}\left[ \frac{sc_1}{(1+c_1x)}+\frac{c_2u}{(1+c_2x)} +{\dot{T}}(x)\right] \nonumber \\&+\,\, C\left[ \frac{(c_1-c_2)c_1x-2x\xi }{(1+c_1x)^{2}}\right] \nonumber \\&+\,\, C\alpha \left[ \frac{(c_1-c_2)(3+c_1x)-x\xi }{(1+c_1x)^{2}}\right] \nonumber \\&+\,\, C^{3}\kappa \left[ \frac{(c_1-c_2)(3+c_1x)-x\xi }{(1+c_1x)^{2}}\right] ^3,\nonumber \\ \Delta= & {} \frac{4Cx(1+c_2x)}{(1+c_1x)}\nonumber \\&\times \left[ \frac{s(s-1)c_1^{2}}{(1+c_1x)^{2}} +\frac{2suc_1c_2}{(1+c_1x)(1+c_2x)}+\frac{2sc_1{\dot{T}}(x)}{(1+c_1x)} \right. \nonumber \\&+\,\, \left. \frac{u(u-1)c_2^{2}}{(1+c_2x)^{2}}+\frac{2uc_2{\dot{T}}(x)}{(1+c_2x)} +{\ddot{T}}(x)+{\dot{T}}(x)^{2}\right] \nonumber \\&+\,\, \frac{2C(c_2-c_1)x}{(1+c_1x)^{2}} \left[ \frac{sc_1}{(1+c_1x)}+\frac{c_2u}{(1+c_2x)} +{\dot{T}}(x)\right] \nonumber \\&+\,\, C\left[ \frac{(c_1-c_2)c_1x-2x\xi }{(1+c_1x)^{2}}\right] . \end{aligned}$$
(48)