1 Introduction

In the description of the early universe, spatially homogeneous and anisotropic cosmological models may be allowed. These models via some mechanism, such for example dissipation [1], could evolve to an homogeneous and isotropic one. The evidence comes from the existence of small anisotropy deviations from isotropy of the CMB radiation and the presence of large angle anomalies, which represent real features of the CMB map of the universe [2]. These anomalies seem to indicate a preferred orientation in the space, and it is unclear whether they originate from some unknown systematic error (present in both the COBE and the WMAP data) or if they have a physical origin [3].

Using a Bianchi type-I metric, in [4] it was obtained a model which becomes to be an almost FRW in time that is consistent with current data of the CMB. In this work it was assumed that the matter component forms the deviations from isotropy in the CMB density fluctuations when matter and radiation decouples. Some authors suggest that the ellipsoidal cosmological model is a viable alternative that could account for the detected large scale anomalies in the cosmic microwave anisotropies [5, 6], although the description of polarization modes, specifically B modes, are not properly described in the framework Bianchi type-I cosmologies [7].

On the other hand, the anisotropy of the universe can be associated with dark energy, since anisotropic stresses at the perturbative level are characteristics of various cosmological models of dark energy, which are compatible with the homogeneity and isotropy of the FRW geometry [8,9,10,11]. An explicit field theory for the anisotropically stressed dark energy in a universe described by the Bianchi type-I metric was formulated in [12], and the parameters were constrained using the luminosity-redshift relationship of the SNIa data. For an ellipsoidal universe, which is Bianchi Type I cosmological model with highest symmetry in the spacial sections of the spacetime geometry, the actual skewness and shear of the dark energy component were constrained using Union2 data for supernovae [13]. The EoS for dark energy described by an energy density \(\rho _{\mathrm{DE}}\) was assumed in this work of the form \(p_{\parallel }=\omega _{\parallel }\rho _{\mathrm{DE}}\), \(p_{\perp }=\omega _{\perp }\rho _{\mathrm{DE}}\), with \(\omega _{\parallel }\) and \(\omega _{\perp }\) constants.

In more formal studies, Bianchi type-I anisotropic cosmological models have been extensively investigated for a wide types of matter content. In terms of discussing properties of the dark energy it is of interest the inclusion of a nonzero cosmological constant in this type of models. A detailed analysis of the dynamical systems corresponding to a Bianchi type-I anisotropic universe filled with a cosmological constant and a fluid with bulk viscosity was realized in [14]. Anisotropic universes of this type filled with perfect fluid matter with or without dissipative process and a cosmological constant has been investigated in [15,16,17,18,19,20]. A variable cosmological constant has also been taken into consideration in related research. This is the case of a magnetized Bianchi I universe that was investigated in [21]. The inclusion of a bulk viscous fluid was considered in [22].

Anisotropic dark energy also has been investigated in the framework of the holographic principle [23, 24], which is believed to be a fundamental principle for the quantum theory of gravity. Based on this principle, holographic dark energy models have been recently advanced [25,26,27]. Therefore these models incorporate significant features of the underlying theory of dark energy. The holographic principle is a conjecture stating that all the information stored within some volume can be described by the physics at the boundary of the volume and, in the cosmological context, this principle will set an upper bound on the entropy of the universe. With the Bekenstein bound in mind, it seems to make sense to require that for an effective quantum field theory in a box of size L with a short distance cutoff (UV cutoff: \(\Lambda \)), the total entropy should satisfy the relation

$$\begin{aligned} L^{3}\Lambda ^{3}\le S_{\mathrm{BH}} = \pi L^{2}M_{p}^{2}, \end{aligned}$$
(1)

where \(M_{p}\) is the reduced Planck mass and \(S_{\mathrm{BH}}\) is the entropy of a black hole of radius L which acts as a long distance cutoff (IR cutoff: L). However, based on the validity of effective quantum field theory Cohen et al. [25] suggested a more stringent bound, requiring that the total energy in a region of size L should not exceed the mass of a black hole of the same size. Therefore, this UV-IR relationship gives an upper bound on the zero point energy density

$$\begin{aligned} \rho _{\Lambda }\le L^{-2}M_{p}^{2}, \end{aligned}$$
(2)

which means that the maximum entropy is \( S_{\mathrm{max}}\approx S^{3/4}_{ \mathrm{BH}}\). The largest L is chosen by saturating the bound in Eq. (2) so that we obtain the holographic dark energy density

$$\begin{aligned} \rho _{\Lambda }=3c^{2}M_{p}^{2}L^{-2}, \end{aligned}$$
(3)

where c is a free dimensionless \(\mathcal {O}\)(1) parameter and the coefficient 3 is chosen for convenience. Interestingly, this \(\rho _{\Lambda }\) is comparable to the observed dark energy density \(10^{-10}~\mathrm{eV}^{4}\) for \(H = H_{0}\sim 10^{-33}~\mathrm{eV}\), the Hubble parameter at the present epoch. This means that if we choose the IR cutoff as the current horizon size we obtain the current observed dark energy scale. The fact that quantum field theory over-counts the independent physical degrees of freedom inside the volume explains the success of this estimate over the value \(\rho _{\Lambda }= \mathcal {O}(M_{p}^{4})\). Therefore, holographic dark energy models have the advantage over other models of dark energy in that they do not need an ad hoc mechanism to cancel the \(\mathcal {O}(M_{p}^{4})\) zero point energy of the vacuum.

Nevertheless, as was pointed out by Hsu [26], the current Hubble horizon as IR cutoff in the Friedmann equation \(\rho = 3M_{P}^{2}H^{2}\) makes the dark energy behaves like matter rather than a negative pressure fluid, and prohibits accelerating expansion of the universe. In fact, in this case we have \(\rho _m \thicksim H^2\) and \(\rho _\mathrm{DE} \thicksim H^2\). This tracker behavior of dark components implies that the dark matter and holographic dark energy scale with the universe scale factor as \(a^{-3}\), leading to a pressureless dark energy.

Due to the above limitation of taking current Hubble horizon as IR cutoff, other cutoff has been investigated in the framework of an homogeneous and isotropic cosmology, such as the Ricci scalar [28] associated to the causal connection scale for perturbations, the event horizon [27], and the proposed in [29], which is of the form \(\rho \approx \alpha H^{2}+\beta \dot{H}^{2}\), where \(\alpha , \beta \) are constants. In the holographic framework, Bianchi Type I has been analyzed for a universe filled with matter and generalized holographic or generalized Ricci dark energy, using the statefinder parameters [30]. Exact solutions for a homogeneous axially symmetric Bianchi type-I universe filled with matter and holographic dark energy were found in [31]. In this work it was used the cutoff proposed in [29] and a constant deceleration parameter was assumed.

The main aim of this paper consists of studying Bianchi type-I cosmologies filled with a holographic dark energy by choosing the IR cutoff as the size of our universe. For doing this we derive the general ellipsoidal metric induced by a holographic energy density of the form (3), when \(L=H^{-1}\). It is remarkable that the generated metric allows one to consider accelerated expansion in all directions, which is in agreement with observations. This behavior is not typical for all Bianchi type-I cosmologies since often there are solutions where simultaneously some directional scale factors expand while others contract. Another aspect that deserves consideration is that the obtained holographic metric is not asymptotically FRW since it is always anisotropic due to the presence of a constant parameter, which can be constrained by observations.

This holographic ellipsoidal metric is coupled to compatible matter sources. We consider accelerating cosmological models filled with an isotropic dark matter component and an anisotropic holographic dark energy, satisfying the relations \(\rho _m \thicksim H^2\) and \(\rho _\mathrm{DE} \thicksim H^2\) during all cosmic evolution (or at late times), where now H is the mean Hubble parameter (see Eq. (10)).

Ellipsoidal metrics are homogeneous and anisotropic Bianchi type-I models with the highest (planar) symmetry in the spatial sections of the geometry. As we stated above, we consider the Hubble length as the IR cutoff. Despite the drawbacks with this cutoff in obtaining a well behaved EoS for the dark energy FRW cosmologies, we explore their properties and consequences in anisotropic metrics, and constraint them by using the values obtained for the present level of anisotropy of the large scale geometry of the universe.

The organization of the paper is as follows: in Sect. 2 we present the field equations for a spatially homogeneous and anisotropic Bianchi type-I universe with planar symmetry, and derive the general ellipsoidal metric induced by the considered holographic energy density. In Sect. 3, we discuss an ellipsoidal cosmological solution filled with an isotropic dark matter component and an anisotropic holographic dark energy. This model, as well as the model with the holographic dark energy dominating the expansion, are constrained using the data for the actual shear and skewness of the universe. Finally, in Sect. 4 we present the conclusion of our results.

2 Anisotropic holographic model and Einstein field equations

We shall consider a particular case of spatially homogeneous and anisotropic Bianchi type-I models described by the line element

$$\begin{aligned} \mathrm{d}s^2=\mathrm{d}t^2-a^2(t) (\mathrm{d}x^2+\mathrm{d}y^2)-b^2(t) \mathrm{d}z^2, \end{aligned}$$
(4)

where a(t) and b(t) are the directional scale factors and are functions of the cosmic time t. This spacetime possesses spatial sections with planar symmetry, with axis of symmetry directed along the z-axis. The metric (4) describes a space that has an ellipsoidal rate of expansion at any moment of the cosmological time.

In this case the Einstein field equations are given by

$$\begin{aligned}&\kappa \rho =\frac{\dot{a}^2}{a^2}+2 \frac{\dot{a} \, \dot{b}}{a \, b}, \end{aligned}$$
(5)
$$\begin{aligned}&\kappa p_1=-\left( \frac{\ddot{a}}{a} + \frac{\dot{a} \, \dot{b}}{a \, b} +\frac{\ddot{b}}{b} \right) , \end{aligned}$$
(6)
$$\begin{aligned}&\kappa p_3= - \left( 2 \frac{\ddot{a}}{a}+\frac{\dot{a}^2}{a^2} \right) , \end{aligned}$$
(7)

where \(\kappa = 8\pi G = M_{p}^{-2}\). Note that we have put for the longitudinal and transversal pressures \(p_x=p_y=p_1\) and \(p_z=p_3\).

Now on we shall consider that the energy density filling this universe has a holographic character. At this point we assume that the IR cutoff for anisotropic universes is the mean Hubble parameter H, i.e. \(L = H^{-1}\), therefore the holographic energy density given by Eq. (3) becomes

$$\begin{aligned} \kappa \rho _{H}= 3 c^2 H^2. \end{aligned}$$
(8)

For the metric (4) we can define the average scale factor \(\bar{a}(t)\) as

$$\begin{aligned} \bar{a}(t)=(a^2(t) \, b(t))^{1/3}, \end{aligned}$$
(9)

and the mean Hubble parameter takes the form

$$\begin{aligned} H=\frac{\dot{\bar{a}}}{\bar{a}}=\frac{1}{3} \left( 2 \frac{\dot{a}}{a}+\frac{\dot{b}}{b} \right) , \end{aligned}$$
(10)

obtaining for the holographic energy the relation

$$\begin{aligned} \kappa \rho _{H} =\frac{c^2}{3} \left( 2 \frac{\dot{a}}{a}+\frac{\dot{b}}{b} \right) ^2. \end{aligned}$$
(11)

Thus from Eqs. (5) and (11) we have the following differential equation:

$$\begin{aligned} \frac{\dot{a}^2}{a^2}+2 \frac{\dot{a} \, \dot{b}}{a \, b}=\frac{c^2}{3} \left( 2 \frac{\dot{a}}{a}+\frac{\dot{b}}{b} \right) ^2, \end{aligned}$$
(12)

which implies that the directional scale factors are related by

$$\begin{aligned} a(t)= b(t)^{\alpha }, \end{aligned}$$
(13)

where

$$\begin{aligned} \alpha =\frac{3-2c^2 \pm 3 \sqrt{1-c^2}}{4c^2-3}, \end{aligned}$$
(14)

and, without any loss of generality, the integration constant has been set equal to 1, since we can rescale the coordinates x and y.

Note that in order to have real values for the parameter \(\alpha \) the condition \(0 \le c^2 \le 1\) must be required. Thus from Eq. (14) we obtain \(0 \le \alpha \le 1\) for the minus sign, while for the plus sign we have \(\alpha \ge 1\) for \(\sqrt{3/4}< c \le 1\), and \(\alpha \le -2\) for \(0 \le c < \sqrt{3/4}\). Besides, for \(c^{2}=3/4\), \(\alpha \) becomes infinity for the plus sign, while \(\alpha \rightarrow 1/4\) for the minus sign.

The holographic metric takes the following form:

$$\begin{aligned} \mathrm{d}s^2=\mathrm{d}t^2-b(t)^{2\alpha } (\mathrm{d}x^2+\mathrm{d}y^2)-b(t)^2 \mathrm{d}z^2. \end{aligned}$$
(15)

Clearly this metric becomes isotropic for \(\alpha =1\), or equivalently for \(c^2=1\). For \(0 \le c^2 < 1\) we can have models which expands (or contracts) at different rates at different directions (for \(\alpha >0\)), or, as well as occur with vacuum Kasner cosmology, expands (contracts) only along two perpendicular axes, and contracts (expands) along the z-axis (for \(\alpha \le -2\)).

It is interesting to note that the metric (15) is characterized by the condition that expansion scalar \(\Theta =u^\alpha _{; \alpha }= (2+\alpha ) H_a\) is proportional to shear scalar \(\sigma ^2=\frac{1}{2} \sigma _{a b}\sigma ^{a b}\).

Let us now consider solutions to these spacetimes in terms of the pressures of the dark energy fluid.

2.1 Isotropic pressure

We begin studying the simplest case where the holographic dark energy has isotropic pressure. For doing this we put \(p_1=p_3=p\) into the field equations (5)–(7), and by taking into account Eq. (13), the metric function takes the form

$$\begin{aligned} b(t)= \left( c_1 t +c_2 \right) ^\frac{1}{(2\alpha +1)}, \end{aligned}$$
(16)

where \(c_1\) and \(c_2\) are integration constants. In this case the energy density and pressure are given by

$$\begin{aligned} \rho _{H}=p=\frac{\alpha (\alpha +2)c_1^2}{\kappa (2 \alpha +1)^2 (c_1 t+ c_2)^2}. \end{aligned}$$
(17)

This means that the isotropic requirement for the pressure implies that the holographic matter filling the universe is a stiff one, and the holographic dimensionless parameter may be written through the relevant model parameter \(\alpha \) as

$$\begin{aligned} c^2 = \frac{3 \alpha (\alpha +2)}{(2\alpha +1)^2}. \end{aligned}$$
(18)

The energy density is positive for \(\alpha < -2\) or \(\alpha >0\). The metric of Bianchi Type I in this case of isotropic pressure takes the form

$$\begin{aligned} \mathrm{d}s^2= & {} \mathrm{d}t^2-(c_1 t+c_2)^{\frac{2 \alpha }{2 \alpha +1}} (\mathrm{d}x^2+\mathrm{d}y^2) \nonumber \\&-\,(c_1 t+c_2)^\frac{2}{2 \alpha +1} \mathrm{d}z^2. \end{aligned}$$
(19)

This one-parametric family of anisotropic metrics is the Kasner metric for a stiff fluid. The scale factor of the symmetric plane increases as \(t^{\alpha /(2 \alpha +1)}\), which means that for \(\alpha > 0\) and \(\alpha < -1\) there is no accelerated expansion. For \(-1< \alpha < -1/2\) there is an accelerated expansion of the symmetric plane and a contraction along the z-axis. For \(\alpha >0\) there is no accelerated expansion in all directions.

In order to consider more general solutions than those provided by stiff holographic energy, we can require for the pressures the following isotropic barotropic equation of state (EoS):

$$\begin{aligned} p_1=p_3=\omega \rho _{H}, \end{aligned}$$
(20)

where \(\omega \) is a constant state parameter. From Eqs. (5), (6) and (20) we obtain

$$\begin{aligned} b(t)=(c_1 t +c_2)^{\frac{\alpha +1}{\alpha ^2 \omega +\alpha ^2+2 \omega \alpha + \alpha +1}}, \end{aligned}$$
(21)

while from Eqs. (5), (7) and (20) we have that

$$\begin{aligned} b(t)=(c_1 t +c_2)^{\frac{2}{3 \alpha +\omega \alpha +2\omega }}. \end{aligned}$$
(22)

Thus the power-law expressions (21) and (22) imply the following constraint:

$$\begin{aligned} \alpha ^2 \omega -\alpha ^2 +\omega \alpha -\alpha -2\omega +2=0. \end{aligned}$$
(23)

From this relation we obtain \(\omega =1\) for any \(\alpha \), or \(\alpha =1,-2\) for any \(\omega \). The case \(\omega =1\) for any \(\alpha \) was discussed before and describes a stiff holographic energy. The second case \(\alpha =1\) for any \(\omega \) describes the standard isotropic FRW models with scale factor given by \(a(t)=b(t)=a_0 t^{2/(3 \omega +3)}\). The third case \(\alpha =-2\) describes a vacuum Kasner anisotropic spacetime given by

$$\begin{aligned} \mathrm{d}s^2=\mathrm{d}t^2-t^{4/3} (\mathrm{d}x^2+\mathrm{d}y^2)- t^{-2/3} \mathrm{d}z^2. \end{aligned}$$
(24)

In conclusion, the only relevant non-vacuum solution with anisotropic pressure is described by the metric (19) and the stiff holographic energy (17). The condition \(a(t)=b(t)^{\alpha }\) is fundamental to obtaining this result. Therefore, it is not possible to describe accelerated expansion in ellipsoidal cosmologies filled with isotropic dark energy.

3 Ellipsoidal universes with anisotropic pressure

Now we shall consider anisotropic holographic models with anisotropic pressures \(p_1 \ne p_3\). In general the Einstein field equations for a Bianchi type-I metric may be written in the following form [32]:

$$\begin{aligned}&3H^2=\kappa \rho +\frac{\sigma ^2}{2},\end{aligned}$$
(25)
$$\begin{aligned}&-2 \dot{H}=\kappa (\rho + p) +\sigma ^2,\end{aligned}$$
(26)
$$\begin{aligned}&\dot{\rho }+ 3 H (\rho +p) = \vec \sigma \cdot \vec \Gamma ,\end{aligned}$$
(27)
$$\begin{aligned}&\dot{ \vec {\sigma }}+3H \vec \sigma =\vec \Gamma , \end{aligned}$$
(28)

where \(\kappa =8 \pi G\) (we will consider \(\kappa =1\) from now on), H and p are the average expansion rate and the average pressure. The new physical quantities \(\vec \sigma \) and \(\vec \Gamma \) are the shear vector and the transverse pressure vector respectively, and are defined as

$$\begin{aligned} \sigma _i= & {} H_i-H,\end{aligned}$$
(29)
$$\begin{aligned} \Gamma _i= & {} p_i-p, \end{aligned}$$
(30)

where \(i=1,2,3\). From Eqs. (29)–(30) we see that the quantities \(\vec \sigma \) and \(\vec \Gamma \) satisfy the constraints

$$\begin{aligned} \sigma _1+\sigma _2+\sigma _3=0,\end{aligned}$$
(31)
$$\begin{aligned} \Gamma _1+\Gamma _2+\Gamma _3=0, \end{aligned}$$
(32)

respectively.

From the ellipsoidal metric (4) we have

$$\begin{aligned} \sigma ^2= & {} \frac{2}{3} (H_1-H_3)^2,\end{aligned}$$
(33)
$$\begin{aligned} \vec {\sigma }\cdot \vec {\Gamma }= & {} \frac{2}{3} \, (p_3-p_1)(H_3-H_1). \end{aligned}$$
(34)

In the following subsections we shall consider different holographic models, filled with an isotropic and anisotropic dark components, and we will contrast them with observational data.

3.1 Tracker ellipsoidal holographic solution with dark matter and dark energy

First, we shall study the ellipsoidal version of the tracker FRW holographic cosmology for which the IR cutoff is the Hubble parameter [26, 27]. In order to do this, we shall use the holographic spacetime (15) filled with an isotropic dark matter component and a holographic dark energy with anisotropic pressures. It becomes clear that if the total energy includes the dark matter and dark energy density, we can develop a tracker cosmological model by writing for dark components the relations

$$\begin{aligned} \rho _{m}= & {} 3 c_1^2 H^2,\end{aligned}$$
(35)
$$\begin{aligned} \rho _\mathrm{DE}= & {} 3 c_2^2 H^2, \end{aligned}$$
(36)

then the total energy density is given by

$$\begin{aligned} \rho =\rho _m+\rho _\mathrm{DE}=3c^2 H^2, \end{aligned}$$
(37)

where \(c^2=c_1^2+c_2^2\).

We shall suppose that the dark matter and dark energy are not interacting and then the isotropic and anisotropic components are conserved separately. These conditions are imposed by requiring for the conservation equation (27) that

$$\begin{aligned}&\dot{\rho }_m + 3H \rho _m=0,\end{aligned}$$
(38)
$$\begin{aligned}&\dot{\rho }_\mathrm{DE} + 3H(\rho _\mathrm{DE}+p_\mathrm{DE}) + \frac{2}{3} (p_1-p_3)(H_1-H_3)=0. \nonumber \\ \end{aligned}$$
(39)

For the metric (15) the anisotropic pressures have the form

$$\begin{aligned} p_1= & {} -\frac{(\alpha +1)\ddot{b}}{b}-\alpha ^2 \frac{\dot{b}^2}{b^2},\end{aligned}$$
(40)
$$\begin{aligned} p_3= & {} -\alpha (3\alpha -2) \frac{\dot{b}^2}{b^2}-2 \frac{\ddot{b}}{b}. \end{aligned}$$
(41)

Notice that the dark matter is a pressureless perfect fluid, then \(p_1\) and \(p_3\) are the pressures of the anisotropic dark energy.

From Eq. (38) we have

$$\begin{aligned} \rho _m(t)=\rho _{m0} b^{-1-2\alpha }, \end{aligned}$$
(42)

where \(\rho _{m0}\) is a constant of integration. From Eqs. (39)–(41) we have \(\rho _\mathrm{DE}(t)=\tilde{C} b^{-1-2\alpha }+\alpha (2+\alpha ) \, \frac{\dot{b}^2}{b^2}\), where \(\tilde{C}\) is an integration constant. The Friedmann equation (25) imposes the requirement that \(\tilde{C}=-\rho _{m0}\), and then we see that the energy density of the dark component is given by

$$\begin{aligned} \rho _\mathrm{DE}(t)=\alpha (2+\alpha ) \, \frac{\dot{b}^2}{b^2}-\rho _{m0} b^{-1-2\alpha }. \end{aligned}$$
(43)

We can find the tracker ellipsoidal version for the considered holographic cosmology (15) by imposing on energy densities the conditions (35) and (36). In such a way, from Eqs. (35) and (42) we see that the scale factor is given by

$$\begin{aligned} b(t)=\left( \frac{3 \rho _{m0} \left( t+C\right) ^2}{4c_1^2} \right) ^{\frac{1}{2 \alpha +1}}, \end{aligned}$$
(44)

where C is a constant of integration. Then we have

$$\begin{aligned} \rho _{m}=\frac{4c_1^2}{3(t+C)^2}. \end{aligned}$$
(45)

From Eqs. (36) and (43) we also obtain \(b(t) \thicksim (t+C)^{2/(2 \alpha +1)}\), but the solution must be self consistent, then we shall put the scale factor (44) into Eq. (43), obtaining

$$\begin{aligned} \rho _\mathrm{DE}=\frac{4\alpha (\alpha +2)}{(2\alpha +1)^2 (t+C)^2}-\frac{4c_1^2}{3(t+C)^2}. \end{aligned}$$
(46)

For dark energy pressures we obtain

$$\begin{aligned} p_1=\frac{2(\alpha -1)}{(2 \alpha +1)^2(t+C)^2},\end{aligned}$$
(47)
$$\begin{aligned} p_2=\frac{4(3\alpha -1)(1-\alpha )}{(2 \alpha +1)^2(t+C)^2}. \end{aligned}$$
(48)

Let us now suppose that the longitudinal and transversal pressures of the dark energy are given by

$$\begin{aligned} p_1=\omega _{1_{\mathrm{DE}}} \rho _\mathrm{DE},\end{aligned}$$
(49)
$$\begin{aligned} p_3=\omega _{3_{\mathrm{DE}}} \rho _\mathrm{DE}, \end{aligned}$$
(50)

respectively, where \(\omega _{1_{\mathrm{DE}}}\) and \(\omega _{3_{\mathrm{DE}}}\) are state parameters, which in general are functions of the cosmological time. The pressures \(p_1\) and \(p_3\) represent the longitudinal and transversal pressures of the holographic dark energy, since the dark matter is a pressureless cosmic fluid. In this case the state parameters are constant and are given by

$$\begin{aligned} \omega _{1_{\mathrm{DE}}}= & {} \frac{3(1-\alpha )}{2(-3\alpha (\alpha +2)+c_1^2 (1+2\alpha )^2)},\end{aligned}$$
(51)
$$\begin{aligned} \omega _{3_{\mathrm{DE}}}= & {} \frac{3(1-\alpha )(1-3\alpha )}{-3\alpha (\alpha +2)+c_1^2 (1+2\alpha )^2}. \end{aligned}$$
(52)

Note that for \(\alpha =1\) we obtain the FRW model, with \(b(t) \thicksim t^{2/3}\) and \(p_1=p_2=0 \) (or equivalently \(\omega _{1_{\mathrm{DE}}}=\omega _{3_{\mathrm{DE}}}=0\)), so the holographic energy density behaves like pressureless fluid as we would expect. For \(\alpha \ne 1\) the pressures \(p_1 \ne 0\) and \(p_3 \ne 0\), and the holographic energy becomes anisotropic.

In order to have an accelerated expansion in all directions Eq. (44) and \(a(t)=b(t)^\alpha \) imply that

$$\begin{aligned} \frac{2}{2\alpha +1}> & {} 1,\end{aligned}$$
(53)
$$\begin{aligned} \frac{2\alpha }{2\alpha +1}> & {} 1. \end{aligned}$$
(54)

It is clear that the \(\alpha \)-parameter must be positive for having increasing scale factors. Then from Eq. (53) we have \(0<\alpha <1/2\), while condition (54) cannot be satisfied since \(0 \le \frac{2\alpha }{2\alpha +1} <1\) for \(0 \le \alpha <\infty \). This implies that we have for \(0< \alpha <1/2\) an accelerated expansion only in the x- and y-directions, while in the z-direction the expansion is decelerated.

In conclusion, the tracker ellipsoidal version is mathematically self-consistent with non-vanishing pressures for the holographic energy, however this solution is ruled out since we have an accelerated expansion only in two directions: in the third direction the expansion is decelerated.

3.2 Ellipsoidal scenarios with dominating holographic dark energy

Now we shall consider anisotropic scenarios where the holographic dark energy component dominates over the dark matter content. In such a way, this model will describes late time stages in the evolution of an ellipsoidal cosmology where the contribution of the dark matter density is neglected, and the anisotropic behavior will be kept due to the presence of anisotropic holographic dark energy with barotropic anisotropic pressure, satisfying (8).

Let us suppose that the longitudinal and transversal pressures of the holographic dark energy are given by

$$\begin{aligned} p_1=\omega _1 \rho ,\end{aligned}$$
(55)
$$\begin{aligned} p_3=\omega _3 \rho , \end{aligned}$$
(56)

respectively, where \(\omega _1\) and \(\omega _3\) are a constant state parameters (from now on in this section we use the notation \(\omega _{1_{\mathrm{DE}}}\equiv \omega _1\) and \(\omega _{3_{\mathrm{DE}}}\equiv \omega _3\)). Thus, by taking into account that \(a(t)=b(t)^\alpha \), from Eqs. (5) and (6) we obtain

$$\begin{aligned} b(t)=(c_1 t+c_2)^{\frac{\alpha +1}{\alpha ^2 \omega _1 +\alpha ^2+2\alpha \omega _1 +\alpha +1}}, \end{aligned}$$
(57)

and the metric (15) takes the following form:

$$\begin{aligned} \mathrm{d}s^2= & {} \mathrm{d}t^2-t^{\frac{\alpha (\alpha +1)}{\alpha ^2 \omega _1 +\alpha ^2+2\alpha \omega _1 +\alpha +1}} (\mathrm{d}x^2+\mathrm{d}y^2) \nonumber \\&-\,t^{\frac{\alpha +1}{\alpha ^2 \omega _1 +\alpha ^2+2\alpha \omega _1 +\alpha +1}} dz^2. \end{aligned}$$
(58)

The energy density and the pressure \(p_3\) are given by

$$\begin{aligned} \rho _\mathrm{DE}=\frac{\alpha (\alpha +2)(\alpha +1)^2}{(\alpha ^2 \omega _1 +\alpha ^2+2\alpha \omega _1 +\alpha +1)^2 \, t^2}, \end{aligned}$$
(59)
$$\begin{aligned} p_3=\frac{1+2\alpha \omega _1-\alpha }{1+\alpha } \, \rho _\mathrm{DE}, \end{aligned}$$
(60)

respectively. From Eq. (60) we conclude that the state parameter of the transversal pressure is given by

$$\begin{aligned} \omega _{3} =\frac{1+2\alpha \omega _1-\alpha }{1+\alpha }. \end{aligned}$$
(61)

Let us now study the deviation of this model from the assumed homogeneity and isotropy of the universe on large cosmological scales. From Eqs. (61) and (69) we conclude that the dark energy skewness parameter takes the form

$$\begin{aligned} \delta _\mathrm{DE}=\frac{(1-\omega _1)(1-\alpha )}{1+\alpha }. \end{aligned}$$
(62)

It is interesting to note that Eq. (33) may be rewritten with the help of Eqs. (62) and (68) in the following form:

$$\begin{aligned} \vec {\sigma }\cdot \vec {\Gamma }=2 \delta _\mathrm{DE} \Sigma H \rho _\mathrm{DE}. \end{aligned}$$
(63)

Then the conservation equation for the dark energy component (39) may be rewritten as

$$\begin{aligned} \dot{\rho }_\mathrm{DE}+ 3 H \left( 1+ \omega _{\mathrm{eff}} + \frac{2}{3} \, \delta _\mathrm{DE} \, \Sigma \right) \rho _\mathrm{DE}=0, \end{aligned}$$
(64)

where \(\omega _{\mathrm{eff}}=(2 \omega _1+\omega _{3})/3\). Since the state parameters, skewness and cosmic shear are constant, then for scaling scenarios where the dark energy is the dominating component the quantity \(\delta _\mathrm{DE} \, \Sigma \) is constant, and from Eq. (64) we have

$$\begin{aligned} \rho =\rho _0 \, \bar{a}^{-3(1+\omega _{\mathrm{eff}})-2 \delta _\mathrm{DE} \Sigma }. \end{aligned}$$
(65)

Thus, the quantity \(\delta _\mathrm{DE} \Sigma \) characterizes the deviation from the standard isotropic FRW model, remaining constant during all evolution of the anisotropic holographic cosmology. Note that if \(\omega _1=1\), then \(\omega _{\mathrm{eff}}=1\), \(\omega _{3}=1\) and \(\delta _\mathrm{DE}=0\), and we obtain the anisotropic stiff holographic solution discussed in the previous section. For \(\alpha =1\) we have \(\Sigma =\delta _\mathrm{DE}=0\), obtaining the standard isotropic FRW model.

Now we shall assume that the ranges of current shear and skewness values, obtained in Ref. [13], characterize the deviation from the isotropy of a universe dominated, at late times, by an anisotropic dark energy. Then we shall use these values to constraint the parameters of our holographic dark energy model. With these constraints upon our model we can find its degree of consistence in terms of the range allowed for the effective EoS of the holographic dark energy component. As we will show below the corresponding EoS lies in the range of quintessence or even phantom dark energy.

However, it is important to note that here we deal with an exact solution, and it can be shown that \(\Sigma \), \(\delta _\mathrm{DE}\) and \(\omega _{\mathrm{eff}}\) are not all independent quantities. In general, in ellipsoidal cosmologies each of these three cosmological parameters may be written as functions of the scale factors with their derivatives and constants of integration. In the specific case of the holographic ellipsoidal cosmology (58), we have that the relation

$$\begin{aligned} \omega _{\mathrm{eff}}=1+\frac{2 \delta _\mathrm{DE}}{3\Sigma } \end{aligned}$$
(66)

is fulfilled.

As we stated above, Bianchi type-I cosmologies are very useful to test possible anisotropies of the universe. So, it is interesting to contrast with observations, the deviation of considered by us anisotropic models from the assumed homogeneity and isotropy of the universe on large cosmological scales. In Ref. [13] an ellipsoidal universe is considered, assuming that the mater source is composed by a noninteracting isotropic pressureless dark matter and an anisotropic dark energy component. Solving numerically the Einstein field equations and analyzing the magnitude–redshift data of type-Ia supernovae, it was shown that supernova data are compatible with a large level of anisotropy, both in the geometry of the universe and in the EoS of dark energy: best-fit values are given, and the \(1\sigma \) and \(2\sigma \) confidence level intervals derived from the Union2 data analysis, for the cosmologically relevant parameters \(\Sigma \), \(\delta \), \(w_{\mathrm{eff}}\), and \(\Omega _m\).

In such a way, for constraining the model parameters, we shall consider the deviation from isotropy of the EoS, and the amount of anisotropy in the geometry (15) by calculating the cosmic shear \(\Sigma \), the skewness \(\delta \) and the effective state parameter \(\omega _{\mathrm{eff}}\).

Let us introduce the cosmic shear \(\Sigma \), defined by [13]

$$\begin{aligned} \Sigma =\frac{H_{1}-H}{H}, \end{aligned}$$
(67)

where \(H=\dot{\bar{a}}/\bar{a}\) is the mean Hubble parameter defined by Eq. (10), and \(H_{1}= \dot{a}/a\) is the Hubble parameter for the spatial section of metric (4). The parameter \(\Sigma \) characterizes the amount of anisotropy in the geometry since from Eq. (67) we obtain \(\Sigma \sim (\dot{a}/a-\dot{b}/b)/H\).

For the holographic metric (15), the cosmic shear (67) takes the form

$$\begin{aligned} \Sigma =\frac{\alpha -1}{2\alpha +1}. \end{aligned}$$
(68)

It must be noticed that in general the cosmic shear is time dependent, however in this case it is constant thanks to the relation \(a(t)=b(t)^\alpha \). With the help of Eqs. (14) and (68) we can constraint the holographic parameter c.

The deviation from isotropy of the EoS of the dark energy we shall characterize with the help of the skewness parameter \(\delta _\mathrm{DE}\) defined by

$$\begin{aligned} \delta _\mathrm{DE}=\omega _{3_{\mathrm{DE}}}-\omega _{1_{\mathrm{DE}}}. \end{aligned}$$
(69)

It becomes clear that the deviation from isotropy depends only on the anisotropic character of the dark energy, since the dark matter fluid is a pressureless one.

From the analysis made in Ref. [13] we see that the present level of anisotropy of the large scale geometry of the universe, the actual shear \(\Sigma _0\), and the amount of deviation from isotropy of the EoS of dark energy, the skewness \(\delta _\mathrm{DE}\), are constrained in the ranges

$$\begin{aligned}&- 0.012< \Sigma _0 < 0.012,\end{aligned}$$
(70)
$$\begin{aligned}&-0.016 \le \delta _\mathrm{DE} \le 0.12, \end{aligned}$$
(71)

respectively.

From Eqs. (68) and (70), and Eqs. (62) and (71), we obtain the constraints in the form

$$\begin{aligned} - 0.012< & {} \frac{\alpha -1}{2\alpha +1} < 0.012,\end{aligned}$$
(72)
$$\begin{aligned} - 0.016< & {} \frac{(1-\omega _1)(1-\alpha )}{1+\alpha } < 0.012, \end{aligned}$$
(73)

respectively.

On the other hand, we are interested in describing an accelerated stage of the universe, so we need to require that this model expands in all directions in an accelerated way, by requiring \(\alpha > 0\) and

$$\begin{aligned} \frac{\alpha (\alpha +1)}{\alpha ^2 \omega _1 +\alpha ^2+2\alpha \omega _1 +\alpha +1}> & {} 1, \\ \frac{\alpha +1}{\alpha ^2 \omega _1 +\alpha ^2+2\alpha \omega _1 +\alpha +1}> & {} 1. \end{aligned}$$

These inequalities imply that

$$\begin{aligned} \omega _1< & {} - \frac{1}{\alpha (\alpha +2)},\end{aligned}$$
(74)
$$\begin{aligned} \omega _1< & {} - \frac{\alpha }{\alpha +2}, \end{aligned}$$
(75)

respectively.

In order to constraint the model parameters we must use the inequalities (72),  (73), (74), (75) and (83).

From Eq. (72) we see that the parameter \(\alpha \) is constrained as follows:

$$\begin{aligned} 0.96484< \alpha < 1.03688. \end{aligned}$$
(76)

The constraint on the \(\omega _1\)-parameter follows from Eqs. (73), (74), (75) and (83). By taking into account the constraint (76) on the \(\alpha \)-parameter Eqs. (74) and (75) give

$$\begin{aligned} \omega _1< - 0.3496. \end{aligned}$$
(77)

Now, the constraint (73) allows \(\omega _1\)-parameter to take any value satisfying Eq. (77). Effectively, we can see that for a given value of \(\omega _1\) (even for too big values \(|\omega _1|\)) always there exist values for \(\alpha \)-parameter, very close to 1 such that Eq. (73) will be satisfied.

Therefore, we have shown that for the considered ellipsoidal holographic universe (58), filled with an holographic energy with density (8) and anisotropic pressures (55) and (56), the deviation from the assumed homogeneity and isotropy of the universe on large cosmological scales remains constant during all evolution of this type of anisotropic cosmology if the state parameter \(\omega _1\) satisfies the constraint (77). Note that Eqs. (76) and (77) imply that the transversal pressure satisfies the constraint \(\omega _3<-0.3256\), and then in general the holographic energy is characterized by a quintessence or phantom anisotropic dark energy EoS.

Now from Eqs. (62), (66) and (68) we find that

$$\begin{aligned} \omega _{\mathrm{eff}}=\frac{2\omega _1-\alpha +1+4\alpha \omega _1}{3(1+\alpha )}. \end{aligned}$$
(78)

Therefore, from Eqs. (76) and (77) we conclude that the effective state parameter has the upper bound \(\omega _{\mathrm{eff}}<-0.3415\), so the effective parameter of state may describe a dark energy component with a negative pressure. To find the lower bound we consider that in this case the average scale factor is given by \(\bar{a}(t)=t^m\), where \(m=\frac{(2\alpha +1)(\alpha +1)}{3(\alpha ^2\omega _1+\alpha ^2+2\alpha \omega _1+\alpha +1)}\). For \(\alpha \) in the range (76) the average scale factor describes an accelerated expansion if \(-\sqrt{3/4}<\omega _1<-0.3496\) (in this case \(m>1.0122\) and the expression \(\alpha ^2\omega _1+\alpha ^2+2\alpha \omega _1+\alpha +1\) does not vanish). For \(\alpha \) satisfying the constraint (76) and \(\omega _1<-\sqrt{3/4}\) the average scale factor also may describe accelerated expansion. In this case the expression \(\alpha ^2\omega _1+\alpha ^2+2\alpha \omega _1+\alpha +1\) vanishes at \(\alpha _{\pm }=-\frac{2 \omega _1+1\pm \sqrt{4 \omega _1^2-3}}{2(1+\omega _1)}\) and we need to study each case separately. However, despite this, it can be shown that there exist regimes with \(m>1\) for \(-1.0122<\omega _1<-\sqrt{\frac{3}{4}}\).

This result imposes the lower bound \(-1.0243\) on the effective state parameter, implying finally that this parameter satisfies the constraint \(-1.0243<\omega _{\mathrm{eff}}<-0.3415\), allowing one to have holographic ellipsoidal universes driven by a quintessence or phantom matter component.

It is interesting to note that CMB data provide tighter constraints on the anisotropy than the SNe-Ia data. Specifically, for Bianchi type-I models the present shear is constrained by \(\sigma /\theta \lesssim 10^{-9}\) [4], and since for metric (58) is valid \(\sigma /\theta =\sqrt{\frac{2}{3}} \, \frac{H_1-H_3}{2H_1+H_3}\), we see that \(1 \le \alpha \le 1.000000004\). Therefore we have for the cosmic shear \(0 \le \Sigma \le 1.33333 \times 10^{-9}\) and \(\omega _1 \le \omega _3 \le 1.000000002 \, \omega _1-2 \times 10^{-9}\). This implies that \(\omega _3 \gtrapprox \omega _1\). Note that from Eqs. (74) and (75) we see that \(\omega _1<-1/3\), thus \(\omega _3<-1/3\) (including \(\omega _{\mathrm{eff}}\)), and then the holographic ellipsoidal model may describe accelerated expansion driven by dark energy or even phantom matter. This is possible due to the metric (58) not belonging to an asymptotically FRW spacetime.

3.3 Ellipsoidal cosmology with asymptotic behavior determined by the holographic dark energy

Now, we are interested in constructing an ellipsoidal cosmological solution, filled with dark matter and dark energy, whose asymptotic metric for late times is of the form of Eq. (15). In order to do this we shall impose the following condition on energy densities and longitudinal pressure:

$$\begin{aligned} p_1=\omega _1 \left( \rho _m+\rho _\mathrm{DE} \right) , \end{aligned}$$
(79)

where \(\omega _1\) is a constant parameter.

By taking into account that \(a(t)=b(t)^\alpha \), from Eqs. (5), (6) and (79) we see that the directional scale factor b(t) and the ellipsoidal metric are given by Eqs. (57) and (58), respectively. The energy densities and transversal pressure in this case are given by

$$\begin{aligned} \rho _m(t)= & {} \rho _{m0} t^{-\frac{\left( \alpha +1 \right) \left( 2\,\alpha +1 \right) }{{\alpha }^{2}{} { \omega _1}+{\alpha }^{2}+2\,{ \omega _1}\,\alpha +\alpha +1}},\end{aligned}$$
(80)
$$\begin{aligned} \rho _\mathrm{DE}(t)= & {} \frac{\alpha \, \left( \alpha +1 \right) ^{2} \left( \alpha +2 \right) }{ \left( {\alpha }^{2}{} { \omega _1}+{\alpha }^{2}+2\, { \omega _1}\,\alpha +\alpha +1 \right) ^{2}{t}^{2}} \nonumber \\&-\rho _{m0} t^{-{\frac{ \left( \alpha +1 \right) \left( 2\,\alpha +1 \right) }{{\alpha }^{2}{} { \omega _1}+{\alpha }^{2}+2\,{ \omega _1}\,\alpha +\alpha +1}} },\end{aligned}$$
(81)
$$\begin{aligned} p_3(t)= & {} \frac{\alpha \, \left( \alpha +1 \right) \left( \alpha +2 \right) (1+2 \alpha \omega _1-\alpha )}{ \left( {\alpha }^{2}{ \omega _1}+{\alpha }^{2}+2\, { \omega _1}\,\alpha +\alpha +1 \right) ^{2}{t}^{2}}, \end{aligned}$$
(82)

respectively.

It is interesting to note that the dark matter component (80) satisfies the conservation equation (38), while the dark energy (82) satisfies Eq. (39), so they are conserved separately and there is not change of energy between these dark components.

Notice that in order to find the obtained holographic solution we have not used Eqs. (26) and (28). In this regard, we can see that by taking into account the metric (4), and imposing on Eq. (26) the holographic condition (8) we obtain Eqs. (13) and (14), which implies that the line element (4) becomes metric (15). Therefore, the use of Eq. (26) will finally give a result consistent with those obtained by using the metric (15) with Eqs. (25) and (27). On the other hand, it can be shown that Eq. (28) is satisfied identically by the metric (15), and Eqs. (40) and (41) (and therefore by the obtained holographic solution).

From Eq. (82), we can see that there exist scenarios with holographic energy dominating over the matter component by requiring \(\frac{\left( \alpha +1 \right) \left( 2\,\alpha +1 \right) }{{\alpha }^{2}{} { \omega _1}+{\alpha }^{2}+2\,{ \omega _1}\,\alpha +\alpha +1}>2\). This relation may be rewritten as \(2 \alpha ^2 \omega _1+4\omega _1 \alpha -\alpha +1<0\) or equivalently

$$\begin{aligned} \omega _1 < \frac{\alpha -1}{2 \alpha (\alpha +2)}, \end{aligned}$$
(83)

implying that in general the parameters \(\alpha \) and \(\omega _1\) vary in the ranges \(\alpha > 0\) and \(\omega _1 < \frac{1}{4(\sqrt{3}+2)}\), respectively.

It is clear that for the metric (58) the cosmic shear is given by (68). In this ellipsoidal cosmology the state parameters of dark energy \(\omega _{1_{{\mathrm{DE}}}}\) and \(\omega _{3_\mathrm{DE}}\) are not constants and its effective parameter of state is given by

$$\begin{aligned} \omega _{\mathrm{eff}_{\mathrm{DE}}}= \frac{\alpha (\alpha +1)(\alpha +2)(4\alpha \omega _1+2\omega _1-\alpha +1)}{\left( {\alpha }^{2}{ \omega _1}+{\alpha }^{2}+2\, { \omega _1}\,\alpha +\alpha +1 \right) ^{2}{t}^{2-\gamma } \rho _{m0}-\alpha (\alpha {+}1)^2(\alpha +2)},\nonumber \\ \end{aligned}$$
(84)

while the skewness parameter takes the form

$$\begin{aligned} \delta _\mathrm{DE} = \frac{\alpha (\alpha +1)(\alpha +2)(\alpha -1)( \omega _1-1)}{\left( {\alpha }^{2}{} { \omega _1}+{\alpha }^{2}+2\, { \omega _1}\,\alpha +\alpha +1 \right) ^{2}{t}^{2-\gamma } \rho _{m0}-\alpha (\alpha +1)^2(\alpha +2)},\nonumber \\ \end{aligned}$$
(85)

where \(\gamma =\frac{\left( \alpha +1 \right) \left( 2\,\alpha +1 \right) }{{\alpha }^{2}{} { \omega _1}+{\alpha }^{2}+2\,{ \omega _1}\,\alpha +\alpha +1}\).

Now, we shall use the best fit values given in Ref. [13], which can be considered reasonable ones in observationally testing the viability of this holographic tracking cosmology. From Eqs. (68), (84) and (85), we see that the model parameters must take the values \(\alpha =0.98809\), \(\omega _1=0.13501\), \(t_0 \rho _0=1.13869\), in order to satisfy the best fit values \(\Sigma _0=-0.004\), \(\delta _\mathrm{DE}=-0.05\), \(\omega _{\mathrm{eff}_{\mathrm{DE}}}=-1.32\) of Ref. [13]. Note that the value \(\alpha =0.98809\) implies that the free dimensionless parameter in Eq. (8) is constrained as \(1\le c^2< 0.99986\), implying that the bound (2) will be nearly saturated.

It must be remarked that the best fit values of Ref. [13] are obtained for ellipsoidal cosmological models with constant state parameters of the dark energy component. So strictly speaking, we must have constant \(\omega _{1_{\mathrm{DE}}}\) and \(\omega _{3_\mathrm{DE}}\). It can be seen that these state parameters become constant at stages when the holographic dark energy is dominating the cosmic evolution.

Lastly, as in the previous subsection, we shall use more tighter constraints provided by CMB data. We see that the present shear is constrained by \(\sigma /\theta \lesssim 10^{-9}\) [4], which implies for the metric (58) that \(1 \le \alpha \le 1.000000004\), and \(0 \le \Sigma \le 1.33333 \times 10^{-9}\). Note that Eq. (83) implies that \(\omega _1<6.7 \times 10^{-10}\), so values \(\omega _1 <-1/3\) (for which the expansion is accelerated in all directions) are allowed.

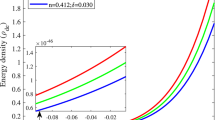
In Figs. 1 and 2 we show the qualitative behavior of dark energies and effective state parameter of dark energy for \(-1<\omega _1<-1/3\). For doing this we have imposed on dark energy the condition \(\rho _{\mathrm{DE}}(t_0)=\rho _{\mathrm{DE}0}\), where \(t_0\) is a constant. Notice that for \(\omega _1<-1\) the holographic dark energy becomes negative, so we have excluded this case of our study.

Fig. 1
figure 1

The figure shows the qualitative behavior of energy densities of dark matter (dotted and dash-dotted lines for \(-1<\omega<<-1/3\) and \(\omega \lesssim -1/3\) respectively) and holographic dark energy (solid and dashed lines for \(-1<\omega<<-1/3\) and \(\omega \lesssim -1/3\) respectively). We see that at \(t_0\) the expansion is dominated by dark matter, and at some \(t>t_0\) the holographic dark energy begins dominate

Full size image
Fig. 2
figure 2

The figure shows the qualitative behavior of effective state parameter of holographic dark energy for \(-1/3>\omega _1> 0\) (solid line), \(\omega _1=-1/3\) (dotted line), and \(\omega <-1/3\) (dashed line). It can be seen that for \(\omega <-1/3\) at \(t_0\) we have \(\omega _\mathrm{eff}<-1\), so the holographic dark energy initially behaves like phantom matter

Full size image

4 Conclusion

In this paper we have studied spatially homogeneous and anisotropic ellipsoidal models of a universe filled with an holographic dark energy with the Hubble length as the IR cutoff. Despite the drawbacks with this cutoff (for obtaining a well behaved EoS for the dark energy in FRW universes) we explored their properties and consequences in anisotropic universes, and we have shown that in the framework of ellipsoidal cosmologies it is possible to develop observationally testable cosmologies.

The main result consists of the derivation of the general ellipsoidal metric induced by a holographic energy density of the form (8). Essentially, the dark energy density (8) imposes a specific relation on the directional scale factors of the ellipsoidal metric (4), giving the spacetime (15). For saturated holographic dark energy \(c=1\) (or equivalently \(\alpha =1\)) the flat isotropic space is obtained. It is remarkable that for \(0 \le c^2 < 1\) the obtained metric (15) allows one to consider anisotropic accelerated expansion in all directions, which is in agreement with observations. This behavior is not typical for all Bianchi type-I cosmologies since often there are solutions where simultaneously some directional scale factors expand while others contract.

Based on the derived metric (15), we develop a tracker ellipsoidal holographic cosmology, filled with a dark matter and a dark energy components. This solution is the ellipsoidal version of the FRW tracker solution, for which the Friedmann equations impose the requirement that the holographic dark energy behaves like pressureless fluid. The ellipsoidal tracker version allows one to consider cases with \(\alpha \ne 1\), so in general the holographic dark energy does not behave like a pressureless fluid. We show that this ellipsoidal cosmology expands in an accelerated way only in two directions; in the third direction the expansion is decelerated.

We study also accelerated cosmic regimes where the dark matter is neglected and the holographic dark energy dominates the expansion. Finally, we construct an exact ellipsoidal solution, filled with dark matter and dark energy, which has the form of the derived metric (15) with variable state parameters of the holographic dark energy.

We apply to considered holographic models the constraint values on the shear and skewness parameters, obtained by Campanelli et al. by using Union2 data for supernovae [13]. These constraints characterize the deviation from the isotropy of ellipsoidal cosmological models, and allow our holographic models to be ruled by an equation of state, whose range belongs to quintessence or even phantom matter, when the dark energy is dominating the expansion. The range (76), imposed by observations on the relevant \(\alpha \)-parameter, implies that the free dimensionless parameter in Eq. (8) is constrained as follows: \(1\le c^2< 0.99986\), then the bound (2) will be nearly saturated.

By construction, for considered holographic ellipsoidal cosmologies, the deviation from the assumed homogeneity and isotropy of the universe on large cosmological scales remains constant during all evolution. This means that if the bound (2) is nearly saturated today, then it remains nearly saturated for all cosmic time.

It is interesting to note that CMB data provide tighter constraints on the anisotropy than the SNe-Ia data. Specifically, for Bianchi type-I models the present shear is constrained by \(\sigma /\theta \lesssim 10^{-9}\) [4]. We also used it for constraining models of Sects. 3.2 and 3.3.

Another aspect that deserves consideration is that the obtained holographic anisotropic metric (15) is not asymptotically FRW for \(\alpha \ne 1\). Observational constraints allow this parameter to be \(\alpha \ne 1\), although \(\alpha \approxeq 1\) (\(c \approxeq 1\)). This implies that observations do not exclude the possibility of having an anisotropic expansion, characterized by the relation \(a(t)=b(t)^\alpha \) for the scale factors. In such a way, the drawbacks with the used IR cutoff present in holographic FRW cosmologies are substantially alleviated in ellipsoidal scenarios.