1 Introduction

In recent times many efforts have been devoted to the investigation of the low-frequency, hydrodynamic limit of quantum field theories (QFTs) with holographic gravitational duals in the AdS/CFT framework. This hydrodynamic limit is a powerful tool to compute transport coefficients for strongly coupled QFTs, e.g. the quark–gluon plasma phase of QCD. In the hydrodynamic regime of thermal QFTs with gravitational duals, the shear viscosity to entropy density ratio \(\eta /s\) is of particular interest. In fact, this ratio takes the universal value \(1/4\pi \) for all QFTs with Einstein gravity duals [1,2,3,4,5,6,7,8]. This has led to the conjecture of the existence of a fundamental lower bound \(\eta /s\geqslant 1/4\pi \) – the Kovtun–Son–Starinets (KSS) bound [9] – which is supported both by energy-time uncertainty principle arguments and by quark–gluon plasma experimental data [9,10,11].

In the usual setting of the AdS/CFT correspondence, the holographic dualities are utilized to learn about transport coefficients in the hydrodynamic limit of strongly coupled QFTs by investigating bulk gravity configurations, typically black branes. However, this paradigm can be reversed and the properties of the dual QFT can be used to infer about the behavior of bulk gravity solutions.Footnote 1 In this perspective, transport coefficients computed in the hydrodynamic limit of the dual QFT can lead to a deeper understanding of black-hole (BH) physics. In particular, the aim of this paper is to better understand the rich thermodynamical phase structure of AdS BHs with spherical horizons (characterized by meta-stabilities and Van der Waals-like behavior [14,15,16]) by investigating the relationship between the shear viscosity of the dual QFT and the thermodynamics of these BHs.

It is well known that the KSS bound can be violated by two different kinds of effects: higher-curvature terms in the Einstein–Hilbert action [17,18,19,20,21,22,23,24,25,26,27,28] and breaking of the translational or rotational symmetry of the black brane background [28,29,30,31,32,33,34,35,36,37]. These two effects were the motivation to consider spherical AdS BHs for which the translational symmetry is intrinsically broken, both in general relativity (GR) and in a higher-curvature theory, namely the Gauss–Bonnet (GB) gravity.

The violation of the KSS bound in higher-curvature gravity theories, although not completely understood, can be traced back to finite-\(\mathscr {N}\), finite-\(\lambda _{tH}\) effects and to the inequality of the two central charges of the dual QFT [38, 39]. This lends support to the possibility of formulating modified bounds on \(\eta /s\), based for instance on causality and positivity of energy in the dual QFT [18, 40, 41].

On the other hand, the violation of the KSS bound due to the breaking of the translational symmetry has a more fundamental nature. In this case the shear viscosity does not have the usual hydrodynamic meaning but might be interpreted as the rate of entropy production due to a strain [31,32,33,34,35, 42]. In this framework, the behavior of \(\eta /s\) as a function of the temperature T is non-trivial [43, 44] and carries information about the infrared (IR) and ultraviolet (UV) behavior of the QFT, the existence of global diffusive modes of the system and the nature of the effect responsible for the breaking of translational invariance. For instance, when this breaking is generated by the presence of a non-homogeneous scalar field in the bulk, the behavior of \(\eta /s\) at small T is determined by the flow of the QFT in the IR. If the translational invariance is restored in the IR then \(\eta /s\) goes to a constant as \(T\rightarrow 0\), signalizing the presence of an IR collective diffusive mode. Conversely, if the translational invariance is not restored, \(\eta /s\) scales as \(T^{2\nu }\) for \(T\rightarrow 0\) and the IR geometry in \(D+2\) dimensions is typically \(\text {AdS}_2\times \mathbb {R}_D\) [34]. We will discuss the general validity of this behavior for spherical BH backgrounds. In this case the translational symmetry is intrinsically broken and cannot be restored in the IR but holds only in the UV where the spherical horizon can be approximated by a plane.

In a recent letter [45], a definition of the shear viscosity for QFTs living in manifolds whose spatial sections are spheres is proposed. This has allowed us to compute the spherical analog of the shear viscosity \(\tilde{\eta }\) for QFTs dual to five-dimensional AdS–Reissner–Nordström (AdS-RN) BHs in GR. Here a detailed derivation of these results is presented and the discussion to five-dimensional asymptotically AdS neutral and charged BHs in GB gravity is extended.

We start by defining the (analog) shear viscosity \(\tilde{\eta }\) for a QFT living on a D-sphere in the hydrodynamic limit. Although the shear viscosity does not have the usual interpretation pertaining to a QFT in a translation-invariant background, it is shown that it still satisfies a Kubo formula and can be interpreted in terms of entropy production due to a strain.

For a given tensorial perturbation of the spherical background it is possible to define three different correlators corresponding to shear, sound and transverse propagating modes [17]. If all the background symmetries are unbroken they lead to the same value of the shear viscosity. If this is not the case, in general the value of \(\tilde{\eta }\) becomes channel dependent [46]. Therefore, in the case under consideration there will be three different determinations of the viscosity for shear, sound and transverse modes. In this paper the focus will be only on the shear viscosity for transverse perturbations for which computations are easier.

Following the approach of Refs. [34, 47] \(\tilde{\eta }/s\) for QFTs dual to five-dimensional asymptotically AdS neutral and charged BHs in GR and GB gravity are computed. By considering linear perturbations of the field equations the computation of \(\tilde{\eta }\) is reduced to the determination of the non-normalizable mode of the perturbation evaluated at the horizon. The perturbation satisfies a linear second-order differential equation analog to a massive scalar equation in a curved background whose non-vanishing mass term encodes the breaking of the translational invariance. Whereas the large and small T behavior of \(\tilde{\eta }/s\) is determined analytically, its global behavior is determined numerically. It is shown that for certain regimes of the temperature \(\tilde{\eta }/s\) is a monotonic function. It saturates the KSS bound at large T (or the GB coupling constant dependent bound in the GB case) where the translational invariance is restored. When the BH has a regular, stable extremal limit \(\tilde{\eta }/s\) goes to zero with a \(T^{2\nu }\) scaling law at small temperatures.

An interesting and somehow unexpected behavior of \(\tilde{\eta }/s\) emerges in the parameter regions where the BH has a Van der Wall-like behavior, characterized by the presence of both a second- and a first-order phase transition. Once the control parameter (the GB coupling constant or the BH charge) falls below a critical value, the system undergoes a second-order phase transition. In this condition BHs may undergo a first-order phase transition from small to large BHs, controlled by the temperature. Small and large black holes are connected through a meta-stable intermediate region. As a result it is found that \(\tilde{\eta }/s\) exhibits a temperature-dependent hysteresis and, close to the phase transition, it becomes multi-valued as expected for a first-order phase transition [29]. We further explain this behavior in terms of the non-equilibrium thermodynamics underlying the Van der Waals-like phase portrait.

The structure of the paper is as follows. In Sect. 2 the problems related to the hydrodynamic limit for QFTs dual to spherical BHs, the definition and the computation of \(\tilde{\eta }\) is discussed and the Kubo formula for \(\tilde{\eta }\) is derived. In Sect. 3 known facts about solutions, thermodynamics, phase structure and perturbations for AdS spherical BHs in GR and GB gravity are reviewed. In Sect. 4 the general formula for \(\tilde{\eta }/s\) is given, its large and small T behavior is computed, the numerical results for its global behavior is given and its relationship with the thermodynamical phase portrait of the dual BH solutions is discussed. Finally, in Sect. 5 our conclusions are stated.

Throughout this paper indices \(a, b, \dots \) refer either to the whole \(D+2\)-dimensional bulk spacetime or to its \(D+1\)-dimensional conformal boundary, while \(i, j, \dots \) refer to the transverse D-dimensional spatial sections.

2 Hydrodynamic limit for QFTs dual to spherical black holes and the analog viscosity

Relativistic hydrodynamics is an effective long-distance description for a classical or quantum many-body system at non-zero temperature. In particular, it can be used to describe the non-equilibrium real-time macroscopic slow evolution of the system, both in space and time, with respect to a certain microscopic scale.

In the holographic framework of the AdS/CFT correspondence, the QFT lives in the boundary of a certain gravitational bulk region. In some cases, the QFT can be described by a kinetic theory and the microscopic scale is determined by the mean free path of particles \(l_\text {mfp}\) and the typical momentum scale of the process k. When the kinetic theory is absent or unknown it is still possible to give a thermal description and interpret the inverse temperature as the microscopic scale [48, 49]. Thus, the hydrodynamic limit of a QFT corresponds to large relaxation time, i.e. small frequencies, and large scales compared to the typical one of the system, i.e. \(\tilde{\lambda }\gg 1/T\sim l_\text {mfp}\), where \(\tilde{\lambda }\) is the wavelength of the excitations of the system.

In general, the existence of a hydrodynamic description is essentially due to the presence of conserved quantities, i.e. to the isometries of the system, whose densities can evolve (oscillate or relax to equilibrium) at arbitrarily long times provided the fluctuations are of large spatial size. Correspondingly, the expectation values of such densities are the hydrodynamic fields. However, it is still possible to give a hydrodynamic description of a system without conserved quantities in terms of expansion in derivatives of hydrodynamic fields (as the fluid velocity) [48]. This approach is followed to formulate the hydrodynamic description of a fluid in a spherical background holographically dual to AdS spherical BHs.

On the sphere, due to its intrinsic geometry, the translational invariance is broken. As a consequence, the momentum is not conserved and it is not possible to define an associated conserved current. At first sight this should prevent us from studying transport coefficients as the shear viscosity \(\eta \), which is, by definition, a measure of the momentum diffusivity due to a strain in a fluid. Hence, in principle, without translational symmetry it is not possible to define a conserved current from which the Fick law of diffusion [50] can be derived. Nevertheless, as seen below, these difficulties can be circumvented and a rigorous definition of \(\eta \) for the hydrodynamic limit of a QFT in a spatial background without translational isometries can be given.

Consider a QFT living on the boundary of \(\text {AdS}_{D+2}\) whose spatial sections have spherical topology. Although bulk BHs allow for dual QFTs living on a sphere [51,52,53,54], in the explicit form of the holographically dual QFT is not of interest here. However, its hydrodynamic limit can be studied in the sense described above. The boundary metric is conformal to \(\mathbb {R}\times S^D\)

$$\begin{aligned} \mathrm{d}s^2=\frac{r^2}{L^2}\left( -\mathrm{d}t^2 + L^2\,\mathrm{d}\bar{\varOmega }_D^2\right) , \end{aligned}$$
(1)

where \(d\bar{\varOmega }_D^2=\bar{g}_{ij}\,dx^i dx^j\) is the metric of a D-sphere. In this case, due to the spherical shape of the boundary, the metric perturbations used to describe the non-equilibrium real-time macroscopic slow evolution of the system are characterized by two parameters, the relaxation time or the frequency \(\omega \) and \(L/\ell \) which “measures” angular distances on the sphere. The integer number \(\ell \) parametrizes the eigenvalue of the Lichnerowicz operator on the sphere (see Eq. (7) below) and is analog to the momentum scale k for a flat topology. In the spacetime (1), the hydrodynamic limit of the holographic QFT is defined as the limit in which the metric perturbations have slow relaxation time and are much larger than the typical scale of the system, i.e. \(\omega \rightarrow 0\) and \(L/\ell \gg 1/T\). Since we are dealing with a D-sphere, the number \(\ell \) cannot be arbitrarily small, i.e. there is a minimum value \(\ell _0\) [55,56,57] which corresponds to a maximum spatial scale and to a maximum size for the global modes propagating on the sphere. On the contrary, in flat space is no constraint on the values of k. Thus, one can set \(k\rightarrow 0\) which corresponds to fluctuations of very large (in principle infinite) wavelength.

2.1 Hydrodynamics in curved spacetime

Relativistic hydrodynamics for a fluid in curved spacetimes can be formulated starting from the following definition for the stress-energy tensor [42, 48]

$$\begin{aligned} T^{ab}=\varepsilon u^a u^b + T_{\perp }^{ab}\,, \end{aligned}$$
(2)

where \(\varepsilon \) is the energy density and the fluid velocity \(u^a\) (commonly evaluated in the frame in which the fluid is at rest) is time-like. The tensor \(T_{\perp }^{ab}\) is the spatial part of the stress-energy tensor and it is made by time-independent functions of the hydrodynamic variables \(\varepsilon \), \(u^a\) and their derivatives. In a generic curved background it is not always possible to globally define conserved currents associated with symmetries of the system. However, the hydrodynamic equations can always be derived by requiring the stress-energy tensor to be covariantly conserved, i.e. \(\nabla _a T^{ab}=0\). In general, the hydrodynamic modes are infinitely slower than all other modes and the latter can be integrated out. Thus, all quantities appearing in the hydrodynamic equations are averaged over these fast modes and are functions of the slow-varying hydrodynamic variables.

Equation (2) can be expanded in powers of derivatives of the velocity. At first order the most general expansion is given by

$$\begin{aligned} T^{ab}= \left( \varepsilon + P\right) u^a u^b + P g^{ab} + \varPi ^{ab}\,, \end{aligned}$$
(3)

where \(P=P(\varepsilon )\) is a scalar function and it can be interpreted as the thermodynamical pressure. The tensor \(\varPi ^{ab}\) contains the derivatives of the fluid velocities, i.e. the dissipative contributions to \(T^{ab}\). Its explicit form is given by [42, 48]Footnote 2

$$\begin{aligned} \varPi ^{ab} =&-\eta \sigma ^{ab} - \eta \tau _{\varPi }\left[ {}^{\langle }\mathscr {D}\sigma ^{ab\rangle } + \frac{1}{D}\sigma ^{ab}(\nabla _cu^c)\right] \nonumber \\&+\kappa \left[ R^{\langle {}ab\rangle } - (D-1) u_c R^{c\langle {}ab\rangle {}d}u_d\right] + \cdots \end{aligned}$$
(4)

where the dots represent the non-linear terms in the fluid velocity and \(\eta ,\tau _{\varPi }\) and \(\kappa \) are transport coefficients. The symbol \(\mathscr {D}\) represents the derivative with respect to the velocity direction, i.e. \(\mathscr {D}=u_a\nabla ^a\). The tensor \(\sigma ^{ab}\) is a symmetric, transverse \(u_a\sigma ^{ab}=0\) and traceless \(g_{ab}\sigma ^{ab}=0\) tensor constructed with the first derivative in the fluid velocity given by \(\sigma ^{ab}=2\phantom {u}^{\langle }\nabla ^{a}u^{b\rangle }\). The parameter \(\eta =\eta (\varepsilon )\) is the shear viscosity and \(\tau _{\varPi }\) is the relaxation time.

2.2 Kubo formulas and the analog viscosity

The Kubo formula relates thermal correlators to kinetic coefficients such as dissipative ones. For a relativistic QFT in flat spacetime, the Kubo formula gives a general definition of the shear viscosity in terms of the retarded Green function for the stress-energy tensor [10, 34, 58]

$$\begin{aligned} \eta =\lim _{\omega \rightarrow 0}\frac{1}{\omega }{{\mathrm{Im}}}{} G_{T^{ij}T^{ij}}^R(\omega ,k\rightarrow 0)\,, \end{aligned}$$
(5)

where \(i=x,\ j=y\) and \(T^{ij}\) are the spatial components of the stress-energy tensor. \(\omega \) and k are the frequency and wave vector of the perturbation. When the translational invariance is preserved and a hydrodynamic limit exists Eq. (5) becomes the Kubo formula for the transverse momentum. In this case \(\eta \) defined by Eq. (5) coincides with the usual hydrodynamical definition in terms of conserved quantities obtained from the Einstein relation \(C=\eta /sT\), where C is the diffusion constant appearing in the Fick law [34]. In a holographic setup based on the AdS/CFT correspondence, \(G_{T^{ij}T^{ij}}\) can be calculated using the usual AdS/CFT rules by considering small perturbations of the bulk metric.

In order to extend the Kubo formula (5) to spherical backgrounds, small metric perturbations around the boundary background metric (1) are considered, i.e. \(g_{ab}\rightarrow g_{ab} + h_{ab}\). In general, three different types of perturbations can be considered: shear, sound and transverse (scalar) modes. The behavior of these modes will be encoded in three different correlators \(G_{1,2,3}(\omega ,k)\). In the translationally invariant case (and also when translation invariance is broken by external matter fields) at \(k=0\) these three functions are equal, due to rotational symmetry [17]. By contrast, in the spherical case under consideration k cannot be taken to zero by construction and the correlators will be different. Thus, in general, any definition of the shear viscosity in a spherical background based on linear response to small disturbances will be channel dependent. In this paper the focus will be on the transverse perturbations. The computations for the sound and shear channel is left for future investigations.

Choosing transverse and traceless perturbations with \(h_{ab}=0\) if \((a,b)\ne (i,j)\), \(h_{ij}=h_{ij}(t,\mathbf {x})\) (where \(\mathbf {x}\) denote the angular directions) in Eq. (3) and considering the fluid at rest, i.e. \(u^a= (1,\mathbf {0})\), we obtain

$$\begin{aligned} T^{ij}= & {} -Ph_{ij}-\eta \dot{h}_{ij}+\eta \tau _{\varPi }\ddot{h}_{ij}\nonumber \\&-\frac{\kappa }{2}\left[ (D-2)\ddot{h}_{ij}+L^2\bar{\bigtriangleup }_Lh_{ij}\right] , \end{aligned}$$
(6)

where \(\bar{\bigtriangleup }_L=\bar{\nabla }_k\bar{\nabla }^k\) is the Lichnerowicz operator and it corresponds to a generalization of the Laplacian for the D-sphere, with \(D\geqslant 3\). Equation (6) is analog to the one obtained in Ref. [48] for planar topology. As required by the linear response theory, the retarded Green function for the tensor channel is computed: by choosing a harmonic time dependence for the perturbation, \(h_{ij}(t,\mathbf {x})=e^{-i\omega t}\,h_{ij}(\mathbf {x})\) and by expanding in hyper-spherical harmonics [59,60,61], the retarded Green function from Eq. (6) can be extracted

$$\begin{aligned} G_{T^{ij}T^{ij}}^R(\omega ,\ell )=&-P-i\omega \eta -\omega ^2\eta \tau _{\varPi }\nonumber \\&-\frac{\kappa }{2}\left[ (D-2)\omega ^2+L^2\gamma \right] , \end{aligned}$$
(7)

where \(\gamma =\ell (\ell +D-1)-2\) are the eigenvalues of the Lichnerowicz operator and \(\ell =1,2,3,\ldots \) is an integer associated with the hyper-spherical harmonic expansion. The eigenvalues \(\gamma \) are positive and form a discrete set [55,56,57, 61]. Given the retarded Green function above the dissipative coefficients, \(\eta \) and \(\tau _{\varPi }\) can be extracted. In particular, the analog of shear viscosity in the hydrodynamic limit for a QFT in a spatial spherical background in the transverse channel can be defined

$$\begin{aligned} \tilde{\eta }\equiv -\lim _{\omega \rightarrow 0}\frac{1}{\omega }{{\mathrm{Im}}}G_{T^{ij}T^{ij}}^R(\omega ,\ell \rightarrow \ell _0)\,, \end{aligned}$$
(8)

where \(\ell _0\) is the minimum value of \(\ell \). Notice that the shear viscosity \(\tilde{\eta }\) in Eq. (8) is defined as the \(\ell \rightarrow \ell _0\) limit of the retarded Green function in analogy with Eq. (5). In planar hydrodynamics the \(k\rightarrow 0\) limit describes long-wavelength modes and probes large scales on the plane. In the spherical case, the \(\ell \rightarrow \ell _0\) modes probe large angles on the sphere.

It is also important to stress that, with respect to the planar case, the expression in square brackets in Eq. (6) has an additional contribution to the stress-energy tensor ruled by the transport coefficient \(\kappa \). However, this contribution drops out in the Kubo formula (8) when we take the imaginary part of the Green function.

We conclude with some remarks about the conservation of the stress-energy tensor. For translation-invariant backgrounds the conservation of the stress-energy tensor leads to the conservation of global currents and to the Fick law [50]. More generally, from the projection of \(\nabla _a T^{ab}\) along the fluid velocity \(u_b\), second-order hydrodynamics can be related with the second law of thermodynamics [48]. In particular, by using Eqs. (3) and (4) at linear order the following can be found:

$$\begin{aligned} \dot{s}=\frac{\eta }{2T}\,\sigma _{ij}\sigma ^{ij}\,, \end{aligned}$$
(9)

where s is the entropy density. Equation (9) represents the rate of entropy production in a fluid due to a slowly varying strain \(h_{ij}\). It can be used to define the shear viscosity [34].

In this case only local conservation can be considered with the background metric (1) since the translational invariance is broken and the Fick law is not satisfied but Eq. (9) still holds.

3 Black-hole solutions in five dimensions

The field equations of five-dimensional Einstein–Gauss–Bonnet gravity sourced by any form of matter fields described by the stress-energy tensor \(T_{(M)}{}_a^b\) are [62,63,64]

$$\begin{aligned} G_{(1)}{}_a^b + \alpha _2\,G_{(2)}{}_a^b = 8\pi G_5\,T_{(M)}{}_a^b\,, \end{aligned}$$
(10)

where \(G_{(1)}{}_a^b\equiv R_a^b-\frac{1}{2}R\delta _a^b\) is the Einstein tensor, \(\alpha _2\) is the GB coupling constant, \(G_5\) is the five-dimensional Newton constant, and \(G_{(2)}{}_a^b\) is the GB contribution,

$$\begin{aligned} G_{(2)}{}_a^b\equiv & {} R_{ca}{}^{de} R_{de}{}^{cb} - 2R_d^c R_{ca}{}^{db} - 2R_a^c R_c^b + R R_a^b\nonumber \\&-\frac{1}{4}\delta _a^b\left( R_{cd}{}^{ef}R_{ef}{}^{cd} - 4R_c^d R_d^c + R^2\right) . \end{aligned}$$
(11)

For later convenience \(\lambda \equiv \alpha _2/L^2\) is defined. L is the AdS length. Throughout this paper the source term contains only a negative cosmological constant and an electromagnetic field. In particular, static BH solutions are considered to (10) i.e. solutions with spherical horizons in the form

$$\begin{aligned} \mathrm{d}s^2=-f(r)\,\mathrm{d}t^2+\frac{\mathrm{d}r^2}{f(r)}+r^2\,\mathrm{d}\bar{\varOmega }_{3}^2\,. \end{aligned}$$
(12)

For the AdS-RN BHs of GR the metric function is

$$\begin{aligned} f_\text {RN}(r) = 1+\frac{r^2}{L^2}- \frac{8 G_5 M}{3\pi r^2}+\frac{4\pi G_5 Q^2}{3r^4}\,, \end{aligned}$$
(13)

while, in the branch that allows for BH solutions, the metric function for GB gravity is

$$\begin{aligned} f_\text {GB}(r)=&1+\frac{r^2}{2\lambda L^2}\nonumber \\&\Bigg [1-\sqrt{1-4\lambda L^2\left( \frac{1}{L^2}-\frac{8 G_5 M}{3\pi r^4}+\frac{4\pi G_5Q^2}{3 r^6}\right) }\Bigg ]. \end{aligned}$$
(14)

In Eqs. (13) and (14), M and Q are, respectively, the BH mass and charge.

3.1 Black holes in Gauss–Bonnet gravity

As in the black brane case asymptotically AdS BH solutions of GB gravity exist only for \(\lambda <1/4\). Moreover, it is well known that the unitarity bounds for the dual QFT constrain the value of \(\lambda \) [17, 20, 65], so that in this paper we will take \(\lambda \) in the following range: \(0<\lambda \leqslant 9/100\).

The BH horizons are determined by the positive zeros of the function

$$\begin{aligned} h(Y)=\frac{Y^3}{L^2}+ Y^2-\sigma Y+\rho \,, \end{aligned}$$
(15)

where \(Y=r^2,\, \sigma = 8 G_5 M/3\pi -\lambda L^2,\, \rho = 4\pi G_5 Q^2/3\). The BH becomes extremal when \(h'(Y)=0\).

Asymptotically AdS BH solutions with inner (\(r_-\)) and outer (\(r_+\)) horizons exist for

$$\begin{aligned} M\geqslant \frac{3\pi }{8 G_5} \left[ \lambda L^2+ \frac{L^2}{3}\left( z_0^2+2z_0\right) \right] , \end{aligned}$$
(16)

where \(z_0\) is the real, positive solution of the cubic equation \(2z^3 + 3z^2 -27\rho /L^4=0\). When the inequality is saturated the inner and outer horizons merge, i.e. the BH becomes extremal and in the near-horizon regime the solution factorizes as \(\text {AdS}_2\times S^3\)

$$\begin{aligned} \mathrm{d}s^2=- \frac{r^2}{l^2}\,\mathrm{d}t^2+\frac{l^2 \mathrm{d}r^2}{r^2}+r_0^2\,\mathrm{d}\bar{\varOmega }_3^2\,, \end{aligned}$$
(17)

where \(r_0\) is BH radius at extremality, determined by the solution \(Y_0=r_0^2\) of the cubic equation

$$\begin{aligned} h_\text {ext}(Y)=\frac{2Y^3}{L^2}+Y^2-\rho =0\,, \end{aligned}$$
(18)

and l is the \(\text {AdS}_2\) length

$$\begin{aligned} l^{-2}= \frac{2 h''(r_0)}{r_0^2+ 2\lambda L^2} = \frac{2(6r_0^2+2L^2)}{L^2(r_0^2+ 2\lambda L^2)}\,. \end{aligned}$$
(19)

The BH thermodynamical parameters temperature T, mass M and entropy S can be expressed in terms of the horizon radius \(r_+\) as [64]

$$\begin{aligned} T(r_+)&= \frac{\frac{4r_+^4}{L^2}+2r_+^2-\frac{8\pi G_5Q^2}{3r_+^2}}{4\pi r_+(r_+^2+2\lambda L^2)}, \end{aligned}$$
(20)
$$\begin{aligned} M(r_+)&= \frac{3\pi r_+^4}{8 G_5}\left( \frac{1}{L^2}+\frac{1}{r_+^2}+\frac{\lambda L^2}{r_+^4} +\frac{4\pi G_5Q^2}{3r_+^6}\right) , \end{aligned}$$
(21)
$$\begin{aligned} S(r_+)&= \frac{\pi ^2r_+^3}{2G_5}\left( 1+\frac{6\lambda L^2}{r_+^2}\right) . \end{aligned}$$
(22)

The spherical geometry of the horizon introduces another scale in the system, i.e. the radius of the sphere, which couples in a non-trivial way to the higher-curvature terms in the equations of motion (10). This scale introduces dependency on the GB coupling in the mass bound (16) and in the thermodynamical expression (20) to (22). As a result the thermodynamical- and near-horizon behavior of the GB BHs is completely different from their brane counterparts. Indeed, for charged GB black branes such behavior is universal, i.e. does not depend on \(\lambda \), and is essentially the same as the RN black branes of GR [28].

Notice that although the extremal radius \(r_0\) is determined only by the BH charge and the cosmological constant, the \(\text {AdS}_2\) length l and hence the extremal geometry (17) depend on the GB coupling constant. Notice also that the expression in the parenthesis in Eq. (20) is proportional to \(h_\text {ext}(Y_+)\) meaning that the extremal geometry is obtained at zero temperature.

The thermodynamical parameters (20) to (22) near extremality are

$$\begin{aligned} T(r_+)= & {} \frac{2}{\pi L^2} \frac{3r_0^2+L^2}{r_0^2+2\lambda L^2} (r_+-r_0) +\mathscr {O}\left( {(r_+-r_0)}^2\right) ,\nonumber \\ \end{aligned}$$
(23)
$$\begin{aligned} M(T)= & {} \frac{3\pi }{8 G_5}\left( \frac{3r_0^4}{L^2} + 2 r_0^2+\lambda L^2\right) \nonumber \\&\phantom {=}+ \frac{3\pi ^3}{8 G_5}\frac{L^2 (r_0^2+2\lambda L^2)^2}{L^2 + 3r_0^2}\,T^2 +\mathscr {O}\left( T^3\right) , \end{aligned}$$
(24)
$$\begin{aligned} S(T)= & {} \frac{\pi ^2 r_0^3}{2G_5}\left( 1+\frac{6\lambda L^2}{r_0^2}\right) \nonumber \\&\phantom {=}+ \frac{3\pi ^3}{4G_5} \frac{L^2(r_0^2+2\lambda L^2)^2}{L^2+3r_0^2}\,T +\mathscr {O}\left( T^2\right) . \end{aligned}$$
(25)

The first terms in Eqs. (24) and (25) represent, respectively, the BH mass and entropy at extremality.

3.2 Phase structure of AdS–Reissner–Nordström black holes

Although the metric function \(f_\text {GB}\) in Eq. (14) is singular for \(\lambda =0\), the thermodynamical behavior of the charged AdS-RN solution can be simply obtained by putting \(\lambda =0\) in Eqs. (16) and (20) to (22).

To characterize the phase structure of these BHs, a distinction can be made between two cases: fixed electric potential or fixed electric charge [14, 15]. In this paper we only discuss the canonical ensemble, i.e. we work at fixed charge. We will not consider the grand canonical ensemble, i.e. the case of fixed chemical potential. As the charge of BH decreases to a critical value \(Q_c\), the system undergoes a second-order phase transition. Below the critical charge there are three possible branches of solutions that depend on the radius and therefore on the temperature of the system. For small temperatures a small BH is the only locally stable solution; as the temperature increases a meta-stable configuration describing intermediate BHs can be found; for sufficiently high temperatures large BHs are globally preferred. The evolution from small to large BHs through the meta-stable region corresponds to a first-order phase transition. Above the critical charge the BH solution is always globally preferred. This behavior can be understood by analyzing the temperature as a function of the BH radius given by Eq. (20) with \(\lambda =0\). For \(Q>Q_c\) it is a monotonic function, whereas it develops local extrema for \(0<Q<Q_c\) and an inflection point for \(Q=Q_c\). Notice that the case \(Q=0\) is not included in the range of existence of the first-order phase transition. In fact, \(Q=0\) corresponds to the AdS-Schwarzschild BH. The phase portrait of the AdS-RN BHs is very similar to a liquid/gas Van der Waals phase transition where the BH temperature plays the role of the pressure, the BH radius that of the volume and the BH charge that of the temperature [14, 15]. This portrait has been extended by Kubizňák et al. in Refs. [66, 67] and to topological AdS BHs in massive gravity [68].

We make a brief comment on the zero-charge limit. For \(Q=0\) the metric (13) reduces to that of an AdS-Schwarzschild BH. However, from the thermodynamical point of view, this limit is singular. There is a discontinuity at \(Q=0\). The phase diagram of an AdS-Schwarzschild BH cannot be obtained as the \(Q\rightarrow 0\) limit of the AdS-RN one. In fact, the BH temperature serves as a function of the radius, Eq. (20), when \(Q=0\) becomes a monotonic function and shows no Van der Waals-like behavior as in the RN case [45].

3.3 Phase structure of neutral Gauss–Bonnet black holes

Neutral GB BH solutions and their thermodynamical parameters are obtained by putting \(Q=0\) in Eqs. (14) and (20) to (22). These BHs are characterized by the absence of a regular, zero temperature extremal limit which, in turn, means the absence of an IR fixed point for the dual QFT in the holographic description. For positive \(\lambda \) the \(T=0\) extremal limit is a state with \(r_+=0\), zero entropy and positive non-vanishing mass. Therefore, the small temperature thermodynamical behavior is always singular.

Neutral GB BHs exhibit an interesting phase structure. Different from Einstein gravity where small BHs are not stable and a thermal AdS state is energetically preferred [69, 70], in GB gravity exists a stable small BH.Footnote 3 It starts with a small positive free energy, becomes unstable and evolves to a thermal AdS phase. Additionally, we also have the usual stable BH phase for large radii [53]. By inspecting the behavior of the specific heat and the free energy, it is found that the phase structure of neutral GB BHs strictly depends on the values of the GB coupling constant and the BH radius [63]. For values of the GB coupling constant below the critical one, \(\lambda _c=1/36\), there are three different branches of solutions, corresponding to small, intermediate and large BHs. The specific heat is positive in the first and third branch, whereas it is negative in the second branch. This behavior is a consequence of the fact that \(T(r_+)\), given by Eq. (20) with \(Q=0\), is monotonically increasing for \(\lambda >\lambda _c\), whereas it develops local extrema for \(\lambda <\lambda _c\) [63]. For \(\lambda \geqslant \lambda _c\) the second branch disappears and BHs are always locally stable but not necessarily globally preferred. Computing the free energy one finds that the BH solution is globally stable and energetically preferred with respect to thermal AdS in the parameter region \(\lambda _1(r_+) \leqslant \lambda \leqslant \lambda _2(r_+)\), where \(\lambda _1(r_+)\) and \(\lambda _2(r_+)\) are some functions of the horizon radius [63]. Outside this region a Hawking–Page phase transition exists. BHs become globally unstable and thermal AdS is energetically preferred. Therefore, in the parameter region where BHs are energetically preferred with respect to thermal AdS, the phase diagram of uncharged GB BHs has the same Van der Waals form described in the previous section for AdS-RN BHs, with the GB parameter \(\lambda \) playing the role of the BH charge Q.

Analog to the \(Q\rightarrow 0\) limit, the limit \(\lambda \rightarrow 0\) is singular from the thermodynamical point of view. In fact for \(\lambda \rightarrow 0\) the phase diagram of an AdS-Schwarzschild BH can not be recovered. First, the metric (14) becomes singular. Second, similarly to what we have seen for charged BHs in GR, the temperature as a function of the horizon radius exhibits a discontinuous behavior in the \(\lambda \rightarrow 0\) limit. The limits \(Q\rightarrow 0\) and \(\lambda \rightarrow 0\) have a similar singular behavior also in the case of charged GB BHs.

3.4 Phase structure of charged Gauss–Bonnet black holes

The thermodynamical description of charged GB BHs is determined by the GB coupling constant \(\lambda \) and the charge Q. There are critical values of these parameters, such that these BHs can exhibit the typical Van der Waals gas behavior in the T–S plane [72, 73].Footnote 4 Thus, charged GB BHs possess the Hawking–Page phase transition [16, 69] and a second-order one [73]. The former represents the transition from a stable AdS thermal state to a stable BH spacetime. When \(T_c\) is the \(r_+\)-dependent critical value of the temperature and \(r_c^2=6\lambda L^2\), for \(T>T_c\) and \(r_+>r_c\) (or \(T<T_c\) and \(r_+<r_c\)) AdS is preferred with respect to the BH, whereas for \(T<T_c\) and \(r_+>r_c\) (or \(T>T_c\) and \(r_+<r_c\)), the BH is preferred with respect to AdS. It is remarkable that due to presence of \(\lambda \) and Q the standard critical point becomes a critical line in the T-\(r_+\) phase diagram [16].

Again, the phase portrait has the Van der Waals-like form described in Sects. 3.2 and 3.3 if one considers only the parameter region where the BH phase is globally preferred with respect to the thermal AdS phase and if one holds either Q or \(\lambda \) fixed. In the former (latter) case, at the critical value \(\lambda _c\) (\(Q_c\)) the system undergoes a second-order phase transition. For \(\lambda <\lambda _c\) (\(Q<Q_c\)), varying the temperature we have again a stable small BH phase and a stable large BH phase connected by a meta-stable phase. Moreover, the function \(T(r_+)\) always has the typical behavior described in Sects. 3.2 and 3.3.

3.5 Linear perturbations in Einstein–Gauss–Bonnet gravity

In this section, linear tensorial perturbations about the background (12) in Einstein–Gauss–Bonnet gravity, i.e. \(g_{ab}\rightarrow g_{ab} + h_{ab}\), are studied. After suitable manipulations the linearized equation of motion (10) is

$$\begin{aligned} \delta R_i^j + \lambda L^2\,\delta G_{(2)}{}_i^j + 8\pi \,G_5\left( T_{(M)}{}_i^k h_k^j - \frac{\delta T_{(M)}{}_{ij}}{h_{ij}}\,h_i^j\right) =0,\nonumber \\ \end{aligned}$$
(26)

where \(\delta T_{(M)}{}_{ij}=\left( \frac{\delta T_{(M)}{}_{ij}}{h_{ij}}\right) h_{ij}\) and the explicit form of the tensors \(\delta R_i^j\) and \(\delta G_{(2)}{}_i^j\) can be found in Refs. [75, 76]. In the transverse and traceless gauge (\(\nabla ^a h_{ab} = g^{ab}h_{ab}=0\)), with \(h_{ab}=0\) unless \((a,b)=(i,j)\) the following can be written:

$$\begin{aligned} h_{ij}(r,t,\mathbf {x})=r^2\,\phi (r,t)\,\bar{h}_{ij}(\mathbf {x})\,, \end{aligned}$$
(27)

where \(\mathbf {x}\) is the direction of the sphere along which the perturbation propagates and \(\bar{h}_{ij}\) is the eigentensor of the Lichnerowicz operator built on the background 3-sphere

$$\begin{aligned} \left( \bar{\bigtriangleup }_L+\gamma \right) \bar{h}_{ij}=0\,,\quad \gamma =\ell (\ell +2)-2\,. \end{aligned}$$
(28)

The perturbations \(h_{ij}\) are both gauge-invariant and decouple [55,56,57, 75, 76]. This decoupling is a consequence of the spherical symmetry of the background and occurs for every value of \(\ell \) and not only in the hydrodynamic limit \(\ell =\ell _0\). Furthermore, assuming a harmonic time dependence of the perturbation, \(h_i^j=\phi (r,t)\,\bar{h}_i^j(\mathbf {x})=\psi (r)\,e^{-i\omega t}\,\bar{h}_i^j(\mathbf {x})\), the perturbation \(h_i^j\) factorizes leading to a set of equations which depend only on t and r [75, 76]. Thus Eq. (26) reduces to a massive scalar equation

$$\begin{aligned} \frac{1}{r^3}\frac{\mathrm{d}}{\mathrm{d}r}\left[ r^3f(r)F(r)\frac{\mathrm{d}\psi }{\mathrm{d}r}\right] +\omega ^2\,\frac{F(r)}{f(r)}\,\psi - m^2(r)\,\psi =0\,, \end{aligned}$$
(29)

where \(F(r)\equiv 1-\lambda L^2 f'(r)/r\) and the mass term is

$$\begin{aligned} m^2(r) = \frac{2-\gamma }{r^2}\left[ 1-\lambda L^2 f''(r)\right] + T_{(M)}{}_i^i - \frac{\delta T_{(M)}{}_{ij}}{\delta g_{ij}}\,.\nonumber \\ \end{aligned}$$
(30)

Notice that the mass term depends on the angular part of the perturbation through the eigenvalue \(\gamma \) of the Lichnerowicz operator (28) and on higher-curvature corrections through the GB constant \(\lambda \). In the black brane case, if translational invariance is preserved, the mass term is identically zero [10]. We stress that, although Eq. (29) holds for any \(\ell \) since we are interested in computing the shear viscosity (8), in the following \(\ell \) will be taken equal to its minimum value \(\ell _0=1\) implying \(\gamma =1\).

There are no general exact analytical solutions of Eq. (29) but approximate analytical solutions can be found for \(r\rightarrow \infty \) and in the near-horizon limit. In the generic case the solutions can only be computed numerically.

The asymptotic solutions of Eq. (29) with \(\omega =0\) are given in terms of the modified Bessel functions of the first and second kind. For \(r\rightarrow \infty \), the non-normalizable mode \(\psi _0\) and the normalizable mode \(\psi _1\) behave as

$$\begin{aligned} \psi _0&= 1 - \frac{\lambda L^2}{2\left( 1-\sqrt{1-4\lambda }\right) r^2} + \mathscr {O}\left( \log r/r^4\right) , \end{aligned}$$
(31)
$$\begin{aligned} \psi _1&= \frac{1}{r^4} + \mathscr {O}\left( 1/r^6\right) . \end{aligned}$$
(32)

In Eq. (31) the integration constant is chosen such that the non-normalizable mode \(\psi _0\) goes to 1 as \(r\rightarrow \infty \).

The near-horizon behavior of \(\psi _0(r)\) is different for non-extremal and extremal BHs. In the case of non-extremal BHs at temperature T and extremal \(T=0\) BHs the metric function is written, respectively,

$$\begin{aligned} f(r)&= 4\pi T\,(r-r_+) + \frac{f''(r_+)}{2}\,(r-r_+)^2 + \mathscr {O}\left( {(r-r_+)}^3\right) , \end{aligned}$$
(33)
$$\begin{aligned} f(r)&= \frac{(r-r_0)^2}{l^2} + \mathscr {O}\left( {(r-r_+)}^3\right) , \end{aligned}$$
(34)

where the extremal BH radius \(r_0\) is defined in Eq. (18) and the \(\text {AdS}_2\) length l is given by Eq. (19). In the non-extremal case we write \(\psi _0(r)\) using a power-series expansion and Eq. (29) is solved order by order. At leading order the following is found:

$$\begin{aligned} \psi _0(r) =&~\psi _0(r_+)\left[ 1 + \frac{1-\lambda L^2 f''(r_+)}{4\pi T r_+^2 - \lambda L^2 r_+ (4\pi T)^2}\,(r-r_+)\right] \nonumber \\&+ \mathscr {O}\left( {(r-r_+)}^2\right) . \end{aligned}$$
(35)

For the extremal case, the leading quadratic behavior of f(r) implies \(\psi _0(r_+)=0\). The behavior of \(\psi _0(r)\) in the near-horizon region is

$$\begin{aligned} \psi _0(r) = (r-r_0)^\nu , \quad \nu = \frac{1}{2}\left( -1+\sqrt{1+ \frac{4 l^2-8\lambda L^2}{r_0^2}}\right) .\nonumber \\ \end{aligned}$$
(36)

4 The shear viscosity to entropy density ratio

In this section, following the method proposed in Refs. [34, 47], the shear viscosity to the entropy ratio for the QFTs dual to the BH solutions discussed in Sect. 3 is computed. For Einstein gravity coupled to matter \(\tilde{\eta }/s\) of the dual QFT is determined by means of the retarded Green function in Eq. (8). It is given by the non-normalizable mode \(\psi _0\) of the perturbation evaluated at the horizon,

$$\begin{aligned} \frac{\tilde{\eta }}{s}=\frac{1}{4\pi }\,\psi _0(r_+)^2\,. \end{aligned}$$
(37)

This method can be generalized to include higher-curvature contributions. The computation uses a Wronskian method to determine the relation between the normalizable mode \(\psi _1\) and the non-normalizable mode \(\psi _0\). Since this relation does not depend on the mass term \(m^2(r)\) in Eq. (29), the formula of Ref. [34] also holds for BHs in GB gravity:

$$\begin{aligned} \frac{\tilde{\eta }}{s} =&\frac{1}{4\pi }\,\psi _0(r_+)^2\,\nonumber \\&\times \left[ 1-4\lambda \left( 1-\frac{2\pi G_5 Q^2 L^2}{3 r_+^6}\right) \right] \left( 1+\frac{6\lambda L^2}{r_+^2}\right) ^{-1}\,, \end{aligned}$$
(38)

where \(\psi _0(r)\) is the non-normalizable solution of Eq. (29) with \(\omega =0\).

For background solutions which do not break translational invariance, e.g. branes, the mass term \(m^2(r)\) is identically zero and the zero-frequency solution is \(\psi _0(r)=1\) everywhere [28, 34]. On the contrary, in BH backgrounds, the translational invariance is broken, the mass term \(m^2(r)\) is non-vanishing, the \(\omega =0\) solution for \(\psi _0(r)\) is not constant and \(\psi _0(r_+)\) must be calculated by integrating Eq. (29) with \(\omega =0\).

Large radius BHs \(r_+\gg L\) correspond to the large temperature regime \(T\gg 1/L\). In this approximation \(T(r_+)\) can be inverted in Eq. (20) to get \(r_+(T)= \pi L^2 T+ \mathscr {O}\left( 1/T\right) \). Then, using Eq. (31) and (38),

Fig. 1
figure 1

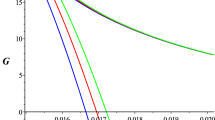
Global behavior of \(\tilde{\eta }/s\) as a function of the temperature for GR BHs. Left panel: neutral AdS BHs. The solid line is the region above the critical radius and the dotted line represents (part of) the region below the critical radius, where the BH is unstable and a thermal AdS solution is preferred; the dot marks the critical radius at \(T=\sqrt{2}/\pi \). Right panel: AdS-RN BHs. \(\tilde{\eta }/s\) are plotted for three selected values of the BH charge: above, at and below the critical value \(Q_c=1/6\sqrt{5\pi }\), at which the system undergoes the second-order phase transition. The dots (square) mark the maximum (minimum) of the temperature as a function of the BH radius

Full size image
$$\begin{aligned} \frac{\tilde{\eta }}{s}= \frac{1-4\lambda }{4\pi } \left[ 1 - \frac{\lambda L^2 \left( 7 -6\sqrt{1-4\lambda }\right) }{\pi ^2\left( 1-\sqrt{1-4\lambda }\right) L^4 T^2} + \mathscr {O}\left( 1/T^4\right) \right] .\nonumber \\ \end{aligned}$$
(39)

As expected, in the large T regime \(\tilde{\eta }/s\) does not depend on the charge. For GR BHs Eq. (39) is a decreasing function of the temperature. Thus the KSS bound is violated and the universal value \(1/4\pi \) is attained only for \(T\rightarrow \infty \). For GB BHs the behavior is qualitatively similar but as \(T\rightarrow \infty \) the value of \(\tilde{\eta }/s\) tends to \((1-4\lambda )/4\pi \).

In the extremal case the metric function and its first derivative vanish when evaluated on the horizon. Following Ref. [34] the shear viscosity to entropy ratio is given by

$$\begin{aligned} \frac{\tilde{\eta }}{s}= \frac{1}{4\pi }\,\psi _0(r_+)^2 \left( 1+\frac{6\lambda L^2}{r_0^2}\right) ^{-1}. \end{aligned}$$
(40)

Equation (36) tells that \(\psi _0(r_+)=0\) which substituted in Eq. (40) means that \(\tilde{\eta }/s\) goes to zero in the \(T=0\) extremal limit. The scaling at low temperatures of \(\tilde{\eta }/s\) follows from simple matching argument [34] between scaling of the Green function and the near-horizon scaling (36)

$$\begin{aligned} \frac{\tilde{\eta }}{s}\sim T^{2\nu }\,, \end{aligned}$$
(41)

where \(\nu \) is given by (36). The scaling exponent satisfies \(\nu \leqslant 1\) for

$$\begin{aligned} \lambda \geqslant \frac{l^4}{L^2r_0^2} +\frac{l^2}{2L^2}\,. \end{aligned}$$
(42)

The global behavior of \(\tilde{\eta }/s\) as a function of T is obtained by numerically integrating Eq. (29) supplied with a power-series boundary condition for \(\psi _0(r)\). In the following, we choose units \(G_5=L=1\). For each value of the charge and the GB parameter there exists a minimum mass (and hence a minimum radius) given by Eq. (16). Equation (29) is then integrated outwards from the horizon to infinity. Next, a shooting method is used to determine \(\psi _0(r_+)\) by requiring that \(\psi _0(\infty )=1\). Finally, the temperature and \(\tilde{\eta }/s\) for each solution are computed with Eqs. (20) and (38).

4.1 AdS–Reissner–Nordström black holes

The plots of \(\tilde{\eta }/s\) resulting from our numerical calculations for GR are shown in Fig. 1 for electrically neutral (left panel) and charged (right panel) BHs.

The KSS bound is always violated for small and intermediate values of temperature, whereas it is saturated from below for large temperatures. In this section we extend the discussion of Ref. [45]. For neutral AdS BHs \(\tilde{\eta }/s\) starts at the universal value \(1/4\pi \) at large temperatures and decreases monotonically as T decreases, reaching a minimum non-zero value for the non-vanishing minimum temperature \(T=\sqrt{2}/\pi \). Such a temperature corresponds to the minimum value of the BH radius, \(r_0=1/\sqrt{2}\). At \(r=r_0\) there is the Hawking–Page transition. For \(r_+\leqslant r_0\) there are no stable BH solutions [70] and thermal AdS is energetically preferred with respect to the BH. The dotted line in the left panel of Fig.1 gives \(\tilde{\eta }/s\) for BHs with radii less than \(r_0\) whose behavior is a consequence of the growing of T for \(r_+\leqslant r_0\).

For AdS-RN BHs \(\tilde{\eta }/s\) decreases from \(1/4\pi \) at large temperatures (independently from the charge) but the behavior for small and intermediate temperatures depends on the charge. As explained in Sect.3.2 there exists a critical value of the charge \(Q_c=1/6\sqrt{5\pi }\) under which the system undergoes a phase transition. On the right panel of Fig. 1, the numerical results are plotted for \(\tilde{\eta }/s\) for the critical charge and for representative values of the charge above, at and below the critical value. The dots (squares) in the curves with \(Q\leqslant Q_c\) mark the critical temperature \(T_{\max }\) (\(T_{\min }\)), corresponding to the two local extrema of the function \(T(r_+)\) of Eq. (20). At these critical temperatures the specific heat changes sign according to the discussion in Sect. 3.2. For \(Q=Q_c\) it is found that \(T_{\min }=T_{\max }\) and the function \(T(r_+)\) has an inflection point. For \(Q>Q_c\) the function \(T(r_+)\) is monotonically increasing and BHs are always stable. The numerical values \(T_{\min }\) and \(T_{\max }\) are listed in Table 1 for a representative value of the charge below and at \(Q_c\).

Interestingly, \(\tilde{\eta }/s\) develops hysteresis for \(0<Q<Q_c\). This is evident for the \(Q=1/100\) solid black curve in the right panel of Fig. 1. We have also checked that curves with \(Q<Q_c\) have a similar hysteretic behavior, whereas those with \(Q>Q_c\) (as the \(Q=1/10\) orange dashed line) do not show this feature. Notice that the limit \(Q\rightarrow 0\) in the plot of l.h.s. of Fig. 1 is singular. As explained in Sect. 3.2 we have a discontinuity for \(Q\rightarrow 0\), i.e. there is no phase transition at \(Q=0\). Because the existence of the phase transition is a necessary condition for having hysteresis in \(\tilde{\eta }/s\), this means that also \(\tilde{\eta }/s\) as a function of the temperature is discontinuous at \(Q=0\): there is a more pronounced hysteretical behavior for \(Q\rightarrow 0\) but hysteresis disappears completely at \(Q=0\). This hysteretic behavior is a direct consequence of the Van der Waals-like behavior of the AdS-RN BHs discussed in Sect. 3.2. It is related to the presence of two local extrema in the function \(T(r_+)\) in Eq. (20) or, equivalently, to the presence of two stable states (small and large BHs) connected by a meta-stable region (intermediate BHs). This phase portrait has been considered as a general explanation of hysteretic behavior for some variables of the system [77]. In particular, when the system evolves from high (low) to lower (higher) temperatures, a potential barrier prevents the evolution of the system from occurring as an equilibrium path between the two stable states [78]. Equilibrium will be reached passing through a meta-stable region. Then a path-dependence of \(\tilde{\eta }/s\) is generated. In particular, starting from high temperatures, the system will reach low temperatures going directly from the minimum and vice versa. The presence of these local extrema determines the patterns of signs of the BH specific heat and free energy, hence the local thermodynamical stability [14, 63]. Thus, hysteresis in \(\tilde{\eta }/s\) and thermodynamical phase transition have the same origin and pattern. In fact, as already noted in Sect. 3.2, the phase diagram of AdS-RN BHs is very similar to that of a Van der Waals liquid/gas transition.

This is a very interesting result: \(\tilde{\eta }/s\) for the dual QFT carries direct information about the thermodynamic phase transitions of the system. In the holographic context a hysteretic behavior in the shear viscosity has been already observed in Ref. [29, 30] for AdS BHs with broken rotational symmetry and with a p-wave holographic superfluid dual. Moreover, it is well known that nanofluids may exhibit hysteresis in the \(\eta \)–T plane [79].

Notice that, even though solutions with \(Q>Q_c\) describe stable BHs in the overall range of T, our numerical computation does not hold in the small T regime as it uses a power-series near-horizon expansion. However, \(\tilde{\eta }/s\rightarrow 0\) as \(T\rightarrow 0\) with analytical scaling law (41) and scaling exponent \(\nu \) given by Eq. (36) with \(\lambda =0\).

4.2 Neutral Gauss–Bonnet black holes

Our numerical results for \(\tilde{\eta }/s\) as a function of T for neutral GB BHs are shown in Fig. 2 for selected values of the GB parameter \(\lambda \) in the range \(0<\lambda \leqslant 5/100\).

Fig. 2
figure 2

Global behavior of \(\tilde{\eta }/s\) as a function of the temperature for GB BHs with \(Q=0\) for selected values of the GB coupling constant above, at and below the critical value. Dots (squares) mark the maximum (minimum) of the temperature as a function of the BH radius

Full size image

For large temperatures, the KSS bound is always violated due to the GB contribution and \(4\pi \tilde{\eta }/s\rightarrow 1-4\lambda \). At intermediate temperatures the behavior is qualitatively similar to that of RN BHs, with the GB parameter \(\lambda \) playing the role of the charge Q. As discussed in Sect. 3.3 there exists a critical value \(\lambda _c\) under which GB BHs can undergo a phase transition: by numerical investigation this value is \(\lambda _c=1/36\), in good agreement with Refs. [63, 73]. Curves with \(0<\lambda <\lambda _c\) (black solid and red dotted lines) show a hysteretic behavior of \(\tilde{\eta }/s\) as a function of the temperature, whereas those with \(\lambda >\lambda _c\) do not. For a given value \(\lambda <\lambda _c\) there are two critical temperatures \(T_{\max },T_{\min }\), which are marked, respectively, by dots and squares in the curves of Fig. 2. Their numerical values for selected values of \(\lambda \) are listed in Table 1. Notice that similarly to the \(Q\rightarrow 0\) case the limit \(\lambda =0\) in the plots of Fig. 2 is singular. As explained in Sect. 3.3, for \(\lambda =0\) there is a discontinuity. This implies that also that \(\tilde{\eta }/s\) as a function of the temperature is discontinuous at \(\lambda =0\). There is a more pronounced hysteretical behavior for smaller and smaller values of \(\lambda \) but hysteresis disappears completely at \(\lambda =0\).

The physical interpretation of the appearance of hysteresis in \(\tilde{\eta }/s\) for the QFT dual to the neutral GB BH is completely analog to that discussed for the AdS-RN BH. When \(\lambda \) reaches the critical value the system undergoes a second-order Van der Waals-like phase transition and exhibits the hysteretic behavior in \(\tilde{\eta }/s\).

Fig. 3
figure 3

Global behavior of \(\tilde{\eta }/s\) as a function of the temperature for charged GB BHs. Left panel: GB BHs with fixed charge \(Q=1/100\), and selected values of GB constant \(\lambda =1/1000,\ 5/1000,\ \sim 0.25,\ 5/100\). The value of \(\tilde{\eta }/s\) is rescaled by a factor \(1-4\lambda \); in this way the large T behavior of \(4\pi \tilde{\eta }/s\) which for GB gravity is \(\lambda \)-dependent has been normalized to 1. Right panel: GB BHs with fixed value of GB constant \(\lambda =1/100\) and selected values of charge \(Q=1/100,\ 2/100,\ \sim 3/100,\ 4/100\). Inset: zoom of the hysteresis region. Dots (squares) mark the local maximum \(T_{\max }\) (local minimum \(T_{\min }\)) of the temperature

Full size image
Table 1 Critical temperatures for selected values of \(\lambda \) and Q below and at the critical values
Full size table

4.3 Charged Gauss–Bonnet black holes

The presence of both a non-vanishing charge and a GB coupling constant makes the case of charged GB BHs more involved. However, as discussed in Sect. 3.4, the phase portrait becomes much simpler and has a Van der Waals-like form if we restrict our considerations to the region where BHs are globally stable and either holds Q or \(\lambda \) fixed. In this situation we expect the qualitative behavior of \(\tilde{\eta }/s\) as a function of T to be quite similar to that found for the AdS-RN and the neutral GB BHs. The numerical results for \(\tilde{\eta }/s\) as a function of T confirm our expectation. They are shown in Fig. 3 for Q fixed and selected values of the GB parameter \(\lambda \) (left panel) and for \(\lambda \) fixed and selected values of the charge Q (right panel). In both cases the numerical results corroborate the analytical ones. For large temperatures the KSS bound is always violated as \(4\pi \tilde{\eta }/s\rightarrow 1-4\lambda \). At intermediate temperatures the behavior of \(\tilde{\eta }/s\) depends crucially on the values of the parameters Q and \(\lambda \). For large values of Q (or for values of \(\lambda \) near to the unitarity bound \(\lambda \lesssim 9/100\)), large BHs are always stable, \(\tilde{\eta }/s\) decreases monotonically with T and there is no hysteresis.

Notice that the limits \(\lambda \rightarrow 0\), respectively \(Q\rightarrow 0\), are singular in the plot on the left, respectively on the right, of Fig. 3. Here we have a discontinuous behavior of \(\tilde{\eta }/s\) similar to that found in the \(Q\rightarrow 0\) limit for charged BHs in GR and to the \(\lambda \rightarrow 0\) for the uncharged BHs of GB gravity.

The situation changes drastically for Q (or \(\lambda \)) of order 3 / 100 and smaller: the system may undergo a Van der Waals-like phase transition. The function \(T(r_+)\) develops two local extrema \(T_{\min }\) and \(T_{\max }\), signalizing the presence of two different stable thermodynamical phase (small and large BHs), connected by a meta-stable one, correspondingly, the \(\tilde{\eta }/s\) curve as a function of T develops hysteresis. Two typical examples of this hysteretic behavior are shown in Fig. 3. On the left panel, for fixed \(Q=1/100\) the onset of hysteresis can be seen, corresponding to the thermodynamical phase transition when \(\lambda \lesssim 0.025\). On the right panel, for fixed \(\lambda =1/100\), the onset of hysteresis can be seen and the thermodynamical phase transition when \(Q\lesssim 3/100\). The corresponding values of the critical temperatures are marked by the dots (\(T_{\max }\)) and squares (\(T_{\min }\)) in Fig. 3. Their numerical values are listed in Table 1 for selected values of the parameters Q and \(\lambda \). Analog results can be found by choosing different Q and \(\lambda \). Notice that for stable BH solutions with values of \(\lambda \) and Q above the critical values our numerical computation cannot reach \(T\sim 0\) because it uses a power-series near-horizon expansion which does not hold in the extremal case. However, from Eqs. (36) and (41), which describe analytically the near-extremal behavior, we conclude that \(\tilde{\eta }/s\rightarrow 0\) smoothly as \(T\rightarrow 0\).

5 Summary and outlook

In this paper we have used the AdS/CFT correspondence to obtain information about the behavior of bulk BHs by studying the hydrodynamic properties of the dual QFTs. In particular, we have defined and computed the shear viscosity to entropy ratio in the transverse channel for QFTs holographically dual to five-dimensional AdS BH solutions of GR and GB gravity. In this way, we have extended the usual derivation of \(\tilde{\eta }/s\) for QFTs dual to gravitational bulk backgrounds with planar horizons to backgrounds with spherical horizons. We have shown that in holographic models the shear viscosity to entropy ratio of the QFT is closely related and keeps detailed information about the thermodynamical phase structure of the dual BH background. This is not completely unexpected because experience with another holographic condensed matter system, like holographic superconductors, has shown us that transport features of the dual QFT may be strongly related to phase transitions of the dual black brane.

In general, the definition of a transport coefficient such as the shear viscosity is associated with the translational invariance of the system, i.e. the conservation of the momentum. As a consequence the Fick law of diffusion can be derived from the associated conserved current. For systems that break translational invariance the hydrodynamic interpretation in terms of conserved quantities fails but hydrodynamics can be still defined as an expansion in the derivatives of the hydrodynamic fields. In this way it is possible to define the shear viscosity through a Kubo formula, also for QFTs on a spherical background, see Eq. (8), where the stress-energy tensor is only covariantly conserved. In addition, one can understand \(\tilde{\eta }\) as the rate of entropy production due to a strain which is the typical interpretation when the homogeneity is broken by external matter fields. From this point of view QFTs dual to spherical BHs are very similar to QFTs dual to black branes where the translational symmetry is broken by non-homogeneous external fields, e.g. scalars [34,35,36].

The definition of the hydrodynamic limit of a QFT on the sphere is plagued by an issue related to the compactness of the space. In fact, in a compact space the usual hydrodynamic limit as an effective theory describing the long-wavelength modes of the QFT has not a straightforward interpretation. Our proposal is that for QFTs dual to bulk spherical BHs the hydrodynamical, long wavelength modes can be described by the \(\ell \rightarrow \ell _0\) modes that probe large angles on the sphere. This is in analogy with the \(k\rightarrow 0\) modes for QFTs dual to bulk black branes which probe large scales on the plane.

There is still a crucial difference between the two cases. When the breaking of translational symmetry is generated by external fields, the symmetry may be restored or not when the system flows to the IR [34]. Instead, in the BH case because the breaking has a geometric and topological origin, translational symmetry cannot be restored in the IR.

As expected, the large T behavior of \(\tilde{\eta }/s\), corresponding to the flow to the UV fixed point reproduces the universal value \(1/4\pi \) or \((1-4\lambda )/4\pi \) in the GB case. When the bulk BH solution has a regular and stable extremal limit (like e.g. charged BHs) and remains stable at small T, \(\tilde{\eta }/s\rightarrow 0\) as \(T\rightarrow 0\) with a \(T^{2\nu }\) scaling law. In the latter case the system flows in the IR to the \(\text {AdS}_2\times S^3\) geometry.

Our most important result is the behavior of \(\tilde{\eta }/s\) at intermediate temperatures. A second-order Van der Waals-like phase transition occurs when the control parameters go below their critical values [14, 15]. In this situation BHs may also undergo a first-order phase transition controlled by the temperature. This corresponds to the transition from small to large BHs connected through a meta-stable intermediate region. As a consequence \(\tilde{\eta }/s\) as a function of T always develops hysteresis and it becomes multi-valued as expected of a first-order phase transition [29]. Notice that in this case the first- and second-order phase transitions are both necessary in order to have the hysteretic behavior in \(\eta /s\). Even though similarly to the case discussed in Ref. [29] the multi-valuedness of \(\eta /s\) is directly related only to the first-order one. The role of the second-order phase transition is to allow for the existence of the first-order one.

The mechanism that generates hysteresis in \(\tilde{\eta }/s\) is the same that is responsible for the phase transition and can be traced back to non-equilibrium thermodynamics. When a control parameter, i.e. the charge Q or the GB coupling constant \(\lambda \), is below its critical value, the function \(T(r_+)\) develops both a local maximum and minimum. The regions below the maximum and above the minimum correspond to two stable solutions, i.e. small and large BHs, respectively. The region between these two is represented by an unstable (meta-stable) region of intermediate BHs. When the system evolves from large (small) BHs to small (large) BHs a potential barrier prevents the evolution of the system from occurring as an equilibrium path between the two stable states [78]. Equilibrium will be reached passing through a meta-stable region [77] and a path-dependence of \(\tilde{\eta }/s\) is generated. The presence of these local extrema determines the patterns of signs of the BH specific heat and free energy, hence the local thermodynamical stability [14, 63]. This interesting result represents the first attempt to infer about BH thermodynamics through a detailed analysis of a transport coefficient as the shear viscosity.

Our definition of \(\tilde{\eta }\) for spherical backgrounds is channel dependent. In general we have three different determinations of \(\tilde{\eta }\) for shear, sound and transverse (scalar) perturbations. In this paper we have focused on transverse perturbations. It would be of interest to check whether the behavior of the viscosity found in this paper for the transverse channel also extends to the sound and shear channels. The computation of our analog \(\tilde{\eta }\) in these other two channels is rather involved and we have left it for future investigations.