1 Introduction

The discovery of the Vaidya solution [2] which describes uniquely the exterior atmosphere of a spherically symmetric radiating star has spawned various research areas within the realm of relativistic astrophysics. There were many notable attempts at seeking solutions of the Einstein field equations describing a radiating body which was simultaneously undergoing gravitational collapse. The boundary of a collapsing star divides the spacetime into two distinct regions, the interior spacetime, \({\mathscr {M}^{-}}\) and the exterior spacetime, \({\mathscr {M}^{+}}\). The interior spacetime has to match smoothly to the exterior spacetime in order to generate a complete model of a radiating star. Early attempts by Glass et al. utilised the Darmois and Lincherowitz matching conditions to establish these matching conditions [3]. It was Santos who correctly articulated the matching conditions for a spherically symmetric, shear-free time-dependent metric being joined smoothly to the exterior Vaidya metric [4]. The Santos matching condition showed that, for a star dissipating energy in the form of a radial heat flux, the pressure at the boundary is nonvanishing. This is a necessary condition that ensures continuity of the momentum flux across the boundary of the radiating star. The Santos junction conditions have been generalised to include shear [5, 6], the cosmological constant as well as the electromagnetic field [7, 8]. Since 1985 there has been a concerted effort in generating exact models of dissipative collapse with Herrera and co-workers establishing many of the fundamental results in terms of stability, energy conditions and thermodynamics of these models [9,10,11,12,13,14]. Maartens et al. investigated the temperature and luminosity profiles of these models by employing casual thermodynamics [15,16,17]. In order to find exact solutions of the field equations describing dissipative collapse, various assumptions on the gravitational potentials and matter content of the gravitating body were made. These included acceleration-free collapse, Weyl-free collapse, expansion-free collapse, anisotropic pressure profiles, inclusion of bulk viscosity and an equation of state [18,19,20,21]. The Santos junction conditions leads to a differential equation governing the temporal behaviour of the model. Solutions of this junction condition included ad hoc assumptions of the gravitational potentials, applying the method of Lie symmetries and ’spotting’ of particular solutions [22,23,24].

In the present paper we will employ a novel way of generating a model of a radiating star. Recently there has been widespread interest in finding static exact solutions of the Einstein field equations describing spherically symmetric compact objects. These models are generated via embedding of a spherically symmetric metric in four dimensions into a five-dimensional flat metric. In general, an n-dimensional Riemannian spacetime is said to be of class p if it can be embedded into a flat space of dimension \(n + p\). The Karmarkar condition relates to class 1 spacetimes. Pandey and Sharma [25] later showed that the Karmarkar condition is only a necessary condition for a spacetime to be of class 1. A further requirement has to be imposed for sufficiency of the Karmarkar condition. The derivation of the Karmarkar condition is purely geometric in nature which gives a relationship between the two gravitational potentials. This is useful: to obtain a complete description of the gravitational behaviour of the model one needs just specify one of the metric functions and the other is obtained via the Karmarkar condition. It is also interesting to note that the Karmarkar condition together with the assumption of pressure isotropy picks out the interior Schwarzschild solution as the only bounded matter configuration. Recent attempts at modeling compact objects such as 4U 1538-52,PSR J1614-2230, Vela X-1 and Cen X-3 using the Karmarkar condition have been highly successful in producing stellar characteristics such as radius, mass, compactness and redshift which are consistent with observations [26,27,28,29,30,31,32]. In our present work we employ the Karmarkar condition to generate a nonstatic model of a radiating star. We believe that this is a first attempt at producing a model of a radiating star with exterior spacetime being the Vaidya metric satisfying the embedding condition.

This paper is structured as follows: In Sect. 2 we present a shearing radiating metric and give Karmarkar’s condition. In Sect. 3 we introduce the interior spacetime and present the matter variables. Sect. 4 explores the exterior spacetime and junction conditions, as well as the resulting Karmarkar condition and a particular solution. The energy conditions are studied in Sect. 5. Sect. 6 focuses on the thermodynamics and Sect. 7 is a full discussion of the results obtained.

2 Time-dependent Karmarkar condition

We begin with the most general spherically symmetric line element

$$\begin{aligned} \mathrm{d}s^2 = -A(r,t)^2 \mathrm{d}t^2 + B(r,t)^2 \mathrm{d}r^2 + Y(r,t)^2 [\mathrm{d}\Omega ^2] , \end{aligned}$$
(1)

where \(\mathrm{d}\Omega ^2 = \mathrm{d}\theta ^2 + \sin ^2{\theta }\mathrm{d}\phi ^2\) and the functions (A, B, Y) describe a shearing, radiating solution of the Einstein field equations.

Karmarkar’s condition [1] can be written as

$$\begin{aligned} \mathscr {R}_{1010} \mathscr {R}_{2323} = \mathscr {R}_{1212} \mathscr {R}_{3030} - \mathscr {R}_{2102} \mathscr {R}_{3103} , \end{aligned}$$
(2)

where we have used the notation (0, 1, 2, 3) to represent coordinates \((t,r,\theta ,\phi )\).

We then consider the metric (1) and calculate Karmarkar’s condition for a shearing nonstatic spherically symmetric metric. The nonzero Riemann tensor components are

$$\begin{aligned} \mathscr {R}_{1010}= & {} \frac{1}{A B} \bigg (-A B^2 \ddot{B} + {A}^2 B {A}^{\prime \prime } - A^2 {A}^{\prime } {B}^{\prime } + B^2 \dot{A} \dot{B} \bigg ) , \nonumber \\ \mathscr {R}_{2323}= & {} \frac{Y^2 \sin ^2{\theta }}{A^2 B^2} \bigg (A^2 B^2 - A^2 {{Y}^{\prime }}^2 + B^2 \dot{Y}^2 \bigg ) , \nonumber \\ \mathscr {R}_{1212}= & {} \frac{Y}{A^2 B} \bigg (-A^2 B {Y}^{\prime \prime } + A^2 {B}^{\prime } {Y}^{\prime } + B^2 \dot{B} \dot{Y} \bigg ) , \nonumber \\ \mathscr {R}_{3030}= & {} \frac{Y\sin ^2{\theta }}{A B^2} \bigg (-A B^2 \ddot{Y} + A^2 {A}^{\prime }{Y}^{\prime } + B^2 \dot{A} \dot{Y} \bigg ) , \nonumber \\ \mathscr {R}_{2102}= & {} -\frac{Y}{A B} \bigg (- A B {\dot{Y}}^{\prime } + A \dot{B} {Y}^{\prime } + B {A}^{\prime } \dot{Y} \bigg ) , \nonumber \\ \mathscr {R}_{3103}= & {} \sin ^2{\theta } R_{2102} , \nonumber \\ \mathscr {R}_{1313}= & {} \frac{Y \sin ^2{\theta }}{A^2 B} \bigg (A^2 {B}^{\prime }{Y}^{\prime } - A^2 B {Y}^{\prime \prime } + B^2 \dot{B} \dot{Y} \bigg ) , \nonumber \\ \mathscr {R}_{2020}= & {} \frac{Y}{A B^2}\bigg (- A B^2 \ddot{Y} + A^2 {A}^{\prime } {Y}^{\prime } + B^2 \dot{A} \dot{Y} \bigg ) . \end{aligned}$$
(3)

In the above, dots and primes refer to differentiation with respect to t and r, respectively. Then the resulting Karmarkar condition is

$$\begin{aligned} 0= & {} \frac{Y^2 \sin ^2{\theta }}{A^3 B^3} \bigg [A B \bigg (A \dot{B} {Y}^{\prime } + B \bigg ({Y}^{\prime } \dot{A} - A {\dot{Y}}^{\prime } \bigg ) \bigg ) ^2 \nonumber \\&+ \bigg (B^2 \dot{Y}^2 + A^2 \bigg ( B^2 - {{Y}^{\prime }}^2\bigg ) \bigg ) \bigg ( B^2 \bigg (\dot{A} \dot{B} - A^2 \ddot{B} \bigg ) \nonumber \\&- A^2 {A}^{\prime } {B}^{\prime } + A^2 B {A}^{\prime \prime }\bigg ) - \bigg (B^2 \bigg (\dot{A} \dot{Y} - A \ddot{Y} \bigg ) + A^2 {A}^{\prime } {Y}^{\prime } \bigg ) \nonumber \\&+ \bigg (B^2 \dot{B}\dot{Y} + A^2 {B}^{\prime } {Y}^{\prime } - A^2 B {Y}^{\prime \prime } \bigg )\bigg ] . \end{aligned}$$
(4)

The full Karmarkar condition (4) is nonlinear, with three unknown functions (A, B, Y). In the next section we will use the Karmarkar condition to obtain a model of a radiating star undergoing gravitational collapse.

3 Interior spacetime

In order to generate a complete model of dissipative collapse we assume that the gravitational potentials are separable in spatial and temporal coordinates. This scenario has been studied by several authors yielding rich insights into the collapse process [12,13,14, 19,20,21]. The interior spacetime of our radiating stellar model is described by a spherically symmetric shear-free line element in simultaneously comoving and isotropic coordinates. The metric assumes the following form:

$$\begin{aligned} \mathrm{d}s^2 = -A_0(r)^2\mathrm{d}t^2 + B_0^2(r)f^2(t)\left[ \mathrm{d}r^2 + r^2\mathrm{d}\Omega ^2\right] , \end{aligned}$$
(5)

where f(t) encodes the dynamical nature of the model and the functions \((A_0, B_0)\) describe a static fluid solution of the Einstein field equations in isotropic coordinates. We utilise the following stress-energy-momentum tensor for our dynamical model:

$$\begin{aligned} T_{ab} = (\rho \,+\, p_\mathrm{T}) u_a u_b + p_\mathrm{T} g_{ab} + (p_\mathrm{R} - p_\mathrm{T})\chi _a\chi _b + q_a u_b + q_b u_a, \end{aligned}$$
(6)

where \(\rho \), \(p_\mathrm{R}\), \(p_\mathrm{T}\) and \(q = (q_aq^a)^{1/2}\) are the proper energy density, radial pressure, tangential pressure and magnitude of the heat flux, respectively. In comoving coordinates we have

$$\begin{aligned} u^a = A^{-1}\delta ^a_0, {\quad } \chi ^a = B^{-1}\delta ^a_1, {\quad } q^a = q\chi ^a, \end{aligned}$$
(7)

where we identify \(u^a\) as the unit time-like four-velocity vector and \(\chi ^a\) is a unit space-like vector along the radial direction.

Then the Einstein field equations for the metric (5) are

$$\begin{aligned} \rho= & {} \frac{1}{f^2} \bigg [\frac{3}{{A_0}^2}{\dot{f}}^2 -\frac{1}{{B_0}^2}\left( \frac{2 {B_0}^{\prime \prime }}{B_0}- \frac{{{B_0}^{\prime }}^2}{{B_0}^2} + \frac{4{B_0}^{\prime }}{r B_0}\right) \bigg ] , \end{aligned}$$
(8)
$$\begin{aligned} {p}_\mathrm{R}= & {} \frac{1}{f^2} \bigg [-\frac{1}{{A_0}^2}\left( 2f \ddot{f} + {\dot{f}}^2\right) \nonumber \\&+ \,\frac{1}{{B_0}^2}\left( \frac{{{B_0}^{\prime }}^2}{{B_0}^2} + \frac{2{A_0}^{\prime } {B_0}^{\prime }}{A_0 B_0}+ \frac{2}{r}\left( \frac{{A_0}^{\prime }}{A_0}+\frac{{B_0}^{\prime }}{B_0}\right) \right) \bigg ] , \end{aligned}$$
(9)
$$\begin{aligned} {p}_\mathrm{T}= & {} \displaystyle \frac{1}{f^2} \bigg ( \displaystyle \frac{1}{{B_0}^2}\bigg [\displaystyle \frac{1}{r}\displaystyle \frac{{A_0}^{\prime }}{A_0} + \displaystyle \frac{1}{r}\displaystyle \frac{{B_0}^{\prime }}{{B_0}^3} + \displaystyle \frac{{A_0}^{\prime \prime }}{A_0} \nonumber \\&- \left( \displaystyle \frac{{B_0}^{\prime }}{B_0}\right) ^2 + \displaystyle \frac{{B_0}^{\prime \prime }}{B_0}\bigg ] - \displaystyle \frac{1}{{A_0}^2}\left( 2f{\ddot{f}} + {\dot{f}}^2\right) \bigg ) , \end{aligned}$$
(10)
$$\begin{aligned} q= & {} -\frac{2 {A_0}^{\prime } \dot{f}}{f^3 {A_0}^2 {B_0}^2} . \end{aligned}$$
(11)

4 Exterior spacetime and junction conditions

In order to obtain a complete model of a collapsing star we need to invoke the junction conditions which allow for the smooth matching of the interior spacetime to the exterior spacetime. Since the star is radiating energy in the form of a radial heat flux, the exterior spacetime is no longer empty and is described by Vaidya’s outgoing solution [2]

$$\begin{aligned} \mathrm{d}s_{+}^2 = -\left( 1-\frac{2m(v)}{\mathsf {r}}\right) \mathrm{d}v^2 - 2\mathrm{d}v\mathrm{d}{{\mathsf {r}}} + {{\mathsf {r}}}^2 \mathrm{d} \Omega ^2 , \end{aligned}$$
(12)

where the mass function m(v) is a function of the retarded time v. The junction conditions for the matching of the line element (5) and the exterior Vaidya spacetime (12) across a time-like hypersurface are

$$\begin{aligned} (rB_{0}f)_{\varSigma }= & {} \mathsf{{r}}_{\varSigma }, \end{aligned}$$
(13)
$$\begin{aligned} (p_\mathrm{R})_{\varSigma }= & {} (qB_{0}f)_{\varSigma }, \end{aligned}$$
(14)
$$\begin{aligned} m(v)= & {} \left( \displaystyle \frac{r^3{B_0}^3f{\dot{f}}^2}{2{A_0}^2} - r^2{B_0^{\prime }}f - \displaystyle \frac{r^3}{2} \displaystyle \frac{{{B_0}^{\prime }}^2f}{B_0} \right) _{\varSigma }. \end{aligned}$$
(15)

As pointed out by Santos, condition (14) represents the conservation of momentum across the boundary of the collapsing sphere.

Using the junction condition (14) together with (9) and (11), we obtain

$$\begin{aligned} 2f{\ddot{f}} + {\dot{f}}^2 + a{\dot{f}} = n, \end{aligned}$$
(16)

valued on \(\varSigma \). Equation (16) governs the behaviour of f. The constants a and n are

$$\begin{aligned} a= & {} \frac{-2 r_0}{b \sqrt{{r_0}^2 + C_1}}, \end{aligned}$$
(17)
$$\begin{aligned} n= & {} \frac{2(C_2 + \sqrt{{r_0}^2 + C_1})}{b^2 \sqrt{{r_0}^2 + C_1}}, \end{aligned}$$
(18)

and they are evaluated at the boundary, \(r = r_0\). Equation (16) can easily be integrated to yield

$$\begin{aligned} t = \displaystyle \frac{1}{a} \left[ \displaystyle \frac{1}{2}f + b\sqrt{f} + b^2\ln {\left( 1 - \displaystyle \frac{\sqrt{f}}{b} \right) } \right] , \end{aligned}$$
(19)

where the time coordinate was rescaled to account for the constant of integration. The temporal evolution of the model is now completely known. Previous models of dissipative gravitational collapse in which the metric functions were separable utilised various assumptions for the static body ranging from: (1) a known static solution of the Einstein field equations, (2) ad hoc assumptions of the gravitational potentials, (3) departure from pressure isotropy and (4) imposition of an equation of state. The novelty of our approach is to use the Karmarkar condition together with the boundary condition (16) to generate a complete model of a radiating star.

The nonzero Riemann tensor components for the metric (5) are given by

$$\begin{aligned} \mathscr {R}_{1010}= & {} \frac{1}{A_0 B_0 f} \bigg (-A_0 {B_0}^3 f^2 \ddot{f} + {A_0}^2 B_0 f {A_0}^{\prime \prime } \nonumber \\&-\, {A_0}^2 {A_0}^{\prime } {B_0}^{\prime } f\bigg ) , \nonumber \\ \mathscr {R}_{2323}= & {} \frac{r^2 \sin ^2{\theta }}{{A_0}^2} \bigg ({A_0}^2 {B_0}^2 f^2 - {A_0}^2 {B_0 f + r {B_0}^{\prime } f}^2 \nonumber \\&+\, r^2 {B_0}^4 f^2 \dot{f}^2 \bigg ) , \nonumber \\ \mathscr {R}_{1212}= & {} \frac{r}{{A_0}^2} \bigg (-{A_0}^2 B_0 f^2 (2 {B_0}^{\prime } + r {B_0}^{\prime \prime }) + {A_0}^2 {B_0}^{\prime } f^2 \times \nonumber \\&\left( B_0 + r {B_0}^{\prime } + r {B_0}^{4} f^2 \dot{f}^{2}\right) \bigg ) , \nonumber \\ \mathscr {R}_{3030}= & {} \frac{r \sin ^2{\theta }}{A_0 B_0 f} \left( -\,r A_0 {B_0}^3 f^2 \ddot{f} + {A_0}^2 {A_0}^{\prime } f \left( B_0 + r {B_0}^{\prime }\right) \right) , \nonumber \\ \mathscr {R}_{2102}= & {} -\frac{r}{A_0} \left( r {A_0}^{\prime } {B_0}^2 f \dot{f}\right) , \nonumber \\ \mathscr {R}_{3103}= & {} \sin ^2{\theta } R_{2102} , \nonumber \\ \mathscr {R}_{1313}= & {} \frac{r \sin ^2{\theta }}{{A_0}^2} \bigg ({A_0}^2 f^2 \left( {B_0}^{\prime }(B_0 + r {B_0}^{\prime }) - B_0 (2 {B_0}^{\prime } \right. \nonumber \\&\left. +\, r {B_0}^{\prime \prime })\right) + r {B_0}^4 f^2 \dot{f}^2 \bigg ), \nonumber \\ \mathscr {R}_{2020}= & {} \frac{r}{A_0 B_0 f}\left( -\,r A_0 {B_0}^3 f^2 \ddot{f} + {A_0}^2 {A_0}^{\prime } f (B_0 + r {B_0}^{\prime }) \right) ,\nonumber \\ \end{aligned}$$
(20)

from (3). The condition (2) becomes

$$\begin{aligned} 0= & {} -\, r {A_0}^2 {B_0}^2 f \ddot{f} (- r {{B_0}^{\prime }}^2 + B_0 ({B_0}^{\prime } + r {B_0}^{\prime \prime })) \nonumber \\&+\, r^2 {B_0}^4 {\dot{f}}^2 ({{A_0}^{\prime }}^2 + {B_0}^2 f \ddot{f}) -\, r A_0 {B_0}^3 {\dot{f}}^2 \left( 2r {A_0}^{\prime } {B_0}^{\prime } \right. \nonumber \\&\left. +\, B_0 ({A_0}^{\prime } - r {A_0}^{\prime \prime }) + r {B_0}^3 f \ddot{f}\right) \nonumber \\&+\, {A_0}^3 (B_0 ({B_0}^{\prime }({A_0}^{\prime } - 2r{A_0}^{\prime \prime }) + r{A_0}^{\prime }{B_0}^{\prime \prime }) \nonumber \\&+\, r {B_0}^{\prime }({B_0}^{\prime }(2{A_0}^{\prime } - r{A_0}^{\prime \prime })+ r {A_0}^{\prime } {B_0}^{\prime \prime } ) \nonumber \\&+\,2r {B_0}^3 f {B_0}^{\prime } \ddot{f} +r^2 {B_0}^2 {{B_0}^{\prime }}^2 \ddot{f}) . \end{aligned}$$
(21)

The above equation is highly nonlinear with the radial and temporal behaviour of the model coupled in a nontrivial manner. In order to generate a complete model of radiative collapse we must ensure that Eqs. (16) and (21) are simultaneously satisfied. We observe that a particular solution of (16) is simply the linear solution

$$\begin{aligned} f(t) = -\,Ct , \end{aligned}$$
(22)

where \(C > 0\) is a constant of integration [34].

With (22), Karmarkar’s condition (21) becomes

$$\begin{aligned} 0= & {} C^2 r^2 {B_0}^4 {{A_0}^{\prime }}^2 + C^2 r A_0 {B_0}^3 \left( - {A_0}^{\prime } (B_0 + 2r {B_0}^{\prime })\right. \nonumber \\&\left. +\,r B_0 {A_0}^{\prime \prime } \right) \nonumber \\&+\, {A_0}^3 \bigg [{B_0}^{\prime }({A_0}^{\prime } (B_0 + 2 r {B_0}^{\prime }) -r {A_0}^{\prime \prime } \left( 2 B_0 + r {B_0}^{\prime }\right) \nonumber \\&+\, r {A_0}^{\prime } {B_0}^{\prime \prime } (B_0 + r {B_0}^{\prime }) \bigg ] , \end{aligned}$$
(23)

which is independent of time. We are left with an equation in \(A_0\) and \(B_0\). At this point we should highlight the fact that the embedding class condition (2) together with pressure isotropy (\(p_\mathrm{R} = p_\mathrm{T}\)) yields only two exact solutions for uncharged static fluids: (1) the interior Schwarzschild solution and (2) the Kohler–Chao solution [33]. The Kohler–Chao solution cannot be used to model a bounded configuration such as a star since there is no surface at which the radial pressure vanishes. Such a surface would define the boundary of the star. The Schwarzschild interior solution describes the interior gravitational field of a uniform density sphere and suffers various pathologies such as the prediction of superluminal propagation velocities within the fluid as well it being unstable against radial perturbations. Recently, the Karmarkar condition has been used extensively in modeling compact stars within the framework of classical general relativity. The departure from pressure isotropy and neutral fluids has generated physically viable models of static compact stars which stand up to observations of radius, mass and compactness of these bodies. In order to close the system of equations we choose \(B_0\) to be

$$\begin{aligned} B_0 = b , \end{aligned}$$
(24)

where b is a constant. This form of \(B_0\) was used by Banerjee et al. [34] to study horizon-free collapse models. Substituting (24) into (23) we obtain

$$\begin{aligned} A_0 = \sqrt{r^2 + C_1} + C_2 , \end{aligned}$$
(25)

where \(C_1\) and \(C_2\) are integration constants. Hence we have found an exact solution for a radiating star, matching to the Vaidya exterior, which satisfies the nonlinear Karmarkar condition.

With (24), (25) and (22), the matter variables in terms of r and t are

$$\begin{aligned} \rho= & {} \frac{3}{t^2 (r^2 + {C}_1){{C}_2}^2} , \end{aligned}$$
(26)
$$\begin{aligned} p_R= & {} \frac{-b^2 C^2 + 2 {C_2}^2}{b^2 C^2 t^2 (r^2 + {C}_1){C_2}^2} , \end{aligned}$$
(27)
$$\begin{aligned} p_T= & {} \frac{\frac{r^2 + 2{C}_1}{b^2 C^2}- \frac{r^2 + {C}_1}{C_2^2}}{t^2 (r^2 + {C}_1)^2} , \end{aligned}$$
(28)
$$\begin{aligned} q= & {} -\frac{2 r}{b^2 C^2 t^3 (r^2 + {C}_1)^{3/2} C_2} . \end{aligned}$$
(29)

The mass function becomes

$$\begin{aligned} m = - \frac{b^3 C^3 r^3 t}{2(r^2 + {C}_1){C_2}^2} . \end{aligned}$$
(30)

5 Energy conditions

We will now examine the physical viability of our stellar model. First, we require that the thermodynamical quantities be positive within the star

Fig. 1
figure 1

Density as a function of time at the center (dashed line) and surface (solid line) of the star

Full size image
Fig. 2
figure 2

Radial pressure as a function of time at the center (dashed line) and surface (solid line) of the star

Full size image
$$\begin{aligned} \rho \ge 0, \quad p_\mathrm{R} \ge 0, \quad p_\mathrm{T} \ge 0 . \end{aligned}$$
(31)

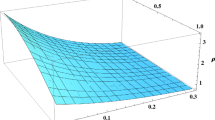
These conditions are confirmed in Figs. 1, 2 and 3 which display the evolution of the central and surface densities as functions of time. Next, the energy density and radial pressure must decrease outward from the center of the star to its surface

$$\begin{aligned} \rho ^{\prime }< 0, p_\mathrm{R} ^{\prime } < 0 . \end{aligned}$$
(32)

In order to fulfill the energy conditions we further require

$$\begin{aligned}&\left( \rho + p_\mathrm{R} \right) ^2 - 4 q^2 > 0 , {\qquad }(E1) \end{aligned}$$
(33)
$$\begin{aligned}&\rho - p_\mathrm{R} -2 p_\mathrm{T} + \left[ (\rho + p_\mathrm{R})^2 - 4 q^2 \right] ^{1/2} > 0, {\qquad } (E2) \end{aligned}$$
(34)

to hold within the stellar interior. With the particular solution \(f(t) = -\,Ct\) for (16), and (17) and (18) we have

$$\begin{aligned} C= & {} \frac{1}{2} \bigg (\frac{-2r_0}{b \sqrt{{r_0}^2 + C_1}} + \bigg [\frac{4 {r_0}^2}{b^2 ({r_0}^2 + C_1)} \end{aligned}$$
(35)
$$\begin{aligned}&+ \frac{8(C_2 + \sqrt{{r_0}^2 + C_1})}{b^2 \sqrt{{r_0}^2 + C_1}} \bigg ]^{1/2} \bigg ) . \end{aligned}$$
(36)

Here C is chosen to be positive to coincide with collapse as \(-\,\infty<t<0\). In order to avoid the formation of the horizon we must have

$$\begin{aligned} 1- \bigg (\frac{2m}{rB} \bigg )_{\varSigma } > 0 , \end{aligned}$$
(37)

where rB is the proper radius of the collapsing star. This condition places the following restriction on C:

$$\begin{aligned} C^2 < \frac{({r_0}^2 + C_1){C_2}^2}{b^2 {r_0}^2} . \end{aligned}$$
(38)

The energy conditions (33) and (34) together with \(\rho \, -\, p_\mathrm{R} > 0\) lead to

$$\begin{aligned} C^2 > \frac{(2{C_2})^2}{b^2} . \end{aligned}$$
(39)

Finally we may write

$$\begin{aligned} \frac{2{C_2}^2}{b^2}< C^2 < \frac{({r_0}^2 + C_1){C_2}^2}{b^2 {r_0}^2} . \end{aligned}$$
(40)

6 Thermodynamics

Causal heat flow in relativistic systems has generated fruitful results and new insights into the connection between pre-relaxation processes and temperature evolution, entropy generation and stability of astrophysical bodies. The evolution of the temperature profile of the stellar fluid gives a good measure of the departure from hydrostatic equilibrium. Apart from relaxational processes contributing to higher core temperatures it has been shown that the presence of anisotropy, shear and charge can lead to very different temperature profiles. In a recent study, Naidu et al. [35] have shown that the inhomogeneity of the atmosphere affects the temperature distribution of the stellar fluid, with the effect becoming more pronounced at later stages in the collapse of the radiating star. Heat flow in relativistic astrophysics has been widely studied within the context of extended irreversible thermodynamics. Various studies have demonstrated that relaxational effects lead to higher core temperatures during dissipative collapse. The causal transport equation for the line element (5) is given by

$$\begin{aligned} \tau {(qB_0f)}^{.} + A_0qB_0f = -\frac{\kappa (A_0T)'}{B_0f}\,, \end{aligned}$$
(41)

where

$$\begin{aligned} \kappa =\gamma T^3{\tau }_\mathrm{c}, \tau _\mathrm{c} =\left( {\psi \over \gamma }\right) T^{-\sigma }, \tau =\left( {\beta \gamma \over \psi }\right) \tau _\mathrm{c} \end{aligned}$$
(42)

are physically reasonable choices for the thermal conductivity \(\kappa \), the mean collision time between massive and massless particles \(\tau _c\), and the relaxation time \(\tau \). The quantities \(\psi \ge 0\), \(\beta \ge 0\) and \(\sigma \ge 0\) are constants. With these assumptions the causal heat transport equation (41) becomes

$$\begin{aligned} \beta (qB_0f)^{.} T^{-\sigma } + A_0(qB_0f) = - \,\psi \frac{T^{3 -\sigma }(A_0T)'}{B_0f}. \end{aligned}$$
(43)

The integration of (43) for constant and variable collision times has been provided by Govinder and Govender [36] and has been used by several authors. We are in a position to integrate (43) and obtain both the causal and the noncausal temperature profiles for our model. The explicit form of the temperature is complicated so we opted to display the behaviour of the temperature profiles in Fig. 7.

Fig. 3
figure 3

Tangential pressure as a function of time at the center (dashed line) and surface (solid line) of the star

Full size image
Fig. 4
figure 4

Mass of the star as a function of time

Full size image
Fig. 5
figure 5

Energy condition 1

Full size image
Fig. 6
figure 6

Energy condition 2

Full size image
Fig. 7
figure 7

Causal (dashed line) and noncausal (solid line) temperature profiles

Full size image

7 Discussion of results

We have presented a complete model of a radiating star within the framework of general relativity. The collapse starts off from an initial static configuration and proceeds to evolve with dissipation of energy in the form of a radial heat flux. We close the system of field equations by imposing, for the first time, a time-dependent Karmarkar condition. With a particular solution of the boundary condition which describes fully the temporal behaviour of our model, the Karmarkar condition reduces to a differential equation relating the two gravitational potentials which describe the initial static configuration. Motivated by the horizon-free collapse model of Banerjee et al. [34] we specify one of the gravitational potential and the Karmarkar condition admits the other potential in closed form. We have interrogated the physical plausibility of our approach by studying the energy conditions and thermodynamics of our model. From (26) and (27) we observe that our model obeys a linear equation of state of the form \(p_R = \omega \rho \) where \(\omega = \frac{3b^2C^2}{2C_2^2\, -\, b^2C^2}\) is a constant. The constant \(C_2\) is arbitrary which means that we can choose different forms for \(\omega \) which describe different fluids ranging from stiff fluids, radiation fluid models and even dark energy models [20]. We have shown that the collapse proceeds without the formation of the horizon. As pointed out by Banerjee et al. [34] such a collapse scenario is possible when the rate of collapse is balanced by the rate at which energy is radiated to the exterior spacetime. Figures 1, 2 and 3 show that the energy density, radial pressure and tangential pressure are positive throughout the interior of the collapsing body. As time progresses these quantities increase as the collapse proceeds leading to a hotter, denser core. The mass function is shown in Fig. 4. It is clear that the mass varies linearly with t, which further confirms that the ratio of the mass function and area radius of the star is independent of time. Figures 5 and 6, together with the behaviour of the density and pressure confirm that all the energy conditions are satisfied at each interior point of the star. In Fig. 7 we plot the causal and noncausal temperature profiles. We observe that the causal temperature is everywhere greater than its noncausal counterpart. This is in keeping with previous investigations of temperature profiles of radiating stars within the framework of causal thermodynamics.