$J/\psi$ production in polarized and unpolarized ep collision and Sivers and $\cos 2\phi$ asymmetries

Abstract

We calculate the Sivers and $\cos 2\phi$ azimuthal asymmetries in $J/\psi$ production in the polarized and unpolarized semi-inclusive ep collision, respectively, using the formalism based on the transverse momentum-dependent parton distributions (TMDs). The non-relativistic QCD-based color octet model is employed in calculating the $J/\psi$ production rate. The Sivers asymmetry in this process directly probes the gluon Sivers function. The estimated Sivers asymmetry at $z=1$ is negative, which is in good agreement with the COMPASS data. The effect of TMD evolution on the Sivers asymmetry is also investigated. The $\cos 2\phi$ asymmetry is sizable and probes the linearly polarized gluon distribution in an unpolarized proton.

1 Introduction

Single spin asymmetry (SSA) has been playing a vital role in spin physics since the observation of large SSA in high energy pp collision experimentally [1,2,3,4,5]. SSA arises in a scattering process in which the target or one of the colliding proton is transversely polarized with respect to the scattering plane. In order to explain the SSA theoretically nonperturbative quark or gluon correlators are required. There are two approaches to this. The first one is based on generalized factorization [6] where one includes intrinsic transverse momentum in the parton distribution functions and fragmentation functions (TMDs). This approach is applicable when the process involves two scales, namely a hard and a soft scale. An example of such a process is the semi-inclusive deep inelastic scattering ( SIDIS) where the hard scale is the virtuality of the gauge boson exchanged and the soft scale can be characterized by the transverse momentum of the observed hadron. Another such process is the Drell–Yan (DY) process where the hard scale is the same as the SIDIS and the soft scale is the transverse momentum of the lepton pair produced. This approach is phenomenologically well studied [7,8,9,10,11,12,13,14,15]. The second approach describes the SSAs in terms of collinear higher twist quark-gluon correlators. This formalism uses collinear factorization and was originally proposed in [16,17,18,19,20] and further developed by [21,22,23]. This is useful for processes having only one hard scale like SSA in pp collision.

Among the single spin asymmetries the Sivers asymmetry is one of the most important and well studied asymmetry, both theoretically and experimentally. This asymmetry involves the Sivers function [24]. The asymmetry arises because the distribution of quarks and gluons in a transversely polarized proton is not left–right symmetric with respect to the plane formed by its transverse momentum and spin direction. The Sivers effect leads to an asymmetry in the azimuthal angle of the hadron produced in SIDIS and has been observed in HERMES [25, 26] and COMPASS experiments [27, 28] for proton target and by JLab Hall-A collaboration for $^{3}{\mathrm {He}}$ target [29]. The Sivers function has been shown in a model dependent way to be related to the orbital angular momentum of the quarks and gluons [30, 31]. The first transverse moment of the Sivers function is related to the quark–gluon twist three Qiu–Sterman function [32]. A detailed discussion of such relations can be found in [33].

The Sivers function is a T-odd (time reversal odd) object. The operator definitions of the quark and gluon Sivers function need gauge links (one for the quark Sivers function and two for the gluon Sivers function) for the color gauge invariance. As these gauge links or Wilson lines depend on the specific process under consideration non-universality or process dependence in the Sivers function [32] is introduced. For the gluon Sivers function there are two gauge links and the process dependence is more involved. However, the gluon Sivers function for any process can be written in terms of two “universal” gluon Sivers functions [34], one involving a C-even operator (f-type), the other a C-odd operator (d-type).

The gluon Sivers function (GSF) plays an important role in understanding the SSAs observed in the pp collision as those in the SIDIS over a wide kinematical region. What is more interesting is that different experiments probe different gluon Sivers functions. Burkardt’s sum rule [35] gives a bound on the GSF. This sum rule is derived from the fact that the total transverse momentum of all partons in a transversely polarized proton should vanish. Fits to the SIDIS data at low scale have found that this sum rule is almost saturated by contribution from the u and d quark’s Sivers function [36]. However, there is still room for about $30\%$ contribution from the GSF. Moreover, one of the gluon Sivers functions (d-type) is not constrained by Burkardt’s sum rule. Apart from the SIDIS and the DY [36,37,38], the Sivers effect has been studied theoretically in several $ep^\uparrow$ collision processes; among them photoproduction of $J/\psi$ [39,40,41], heavy quark pair and dijet production in $ep^{\uparrow }$ scattering [42]. In the SSA in proton–proton collision the process- dependent initial and final state interactions play a major role and usually need to be carefully taken into account [43].

The $J/\psi$ production in $ep^{\uparrow }$ scattering provides direct access to the GSF (f-type) through the leading order (LO) subprocess. It has been shown that [44], due to the final state interaction in ep and pp scattering processes, the SSA in the heavy quarkonium production is zero in ep scattering when the heavy quark pair is produced in a color singlet state, whereas for the pp scattering the SSA is zero when the heavy quark pair is produced in color octet state. The quarkonium production has been studied in unpolarized pp scattering within the TMD evolution formalism in [45, 46]. In Refs. [39,40,41], SSA in $J/\psi$ production in $ep^{\uparrow }$ collision using a low virtuality electroproduction approximation (photoproduction) is studied in a color evaporation model (CEM) and sizable asymmetries are reported. In this work the Sivers asymmetry in the semi-inclusive process $e+p^{\uparrow }\rightarrow e+J/\psi +X$ and the $\cos 2\phi$ azimuthal asymmetry in the unpolarized process $e+p\rightarrow e+J/\psi +X$ using a non-relativistic Quantum Chromo Dynamics (NRQCD)- based color octet model (COM) [47] are investigated. In the COM, the $c\bar{c}$ pair is produced in the color octet state that forms $J/\psi$ by emitting soft gluons [48]. The COM is based on a factorization formula in NRQCD. The cross section is described in terms of a product of a perturbative part where the initial state partons form a $c\bar{c}$ pair having a definite color and total angular momentum quantum numbers and a nonperturbative matrix element through which the $c\bar{c}$ pair forms $J/\psi$. These matrix elements are obtained by fitting data. They are universal. We use a recent extraction [49] for the gluon Sivers function from the SSA data in pp collision at RHIC.

The TMDs (unpolarized as well as the Sivers function) depend on the scale. As a result the SSA also depends on the scale [50]. The scale dependence is given by the TMD evolution and is usually performed in the impact parameter or $b_\perp$-space [51, 52]. There are different schemes of performing the TMD evolution and an improved evolution scheme called CSS2 has been proposed. A detailed discussion of the evolution schemes is presented and the scheme transformation issues are discussed in the recent paper [53]. The evolution in the renormalization scale and rapidity scales are performed using a renormalization group and Collins–Soper (CS) equations. To incorporate the correct evolution at a large $b_\perp$ value a nonperturbative Sudakov factor is included in the evolution which is usually obtained by fitting the data. Also the effect of the TMD evolution on the Sivers asymmetry in the $J/\psi$ production in the COM has been studied.

The $\cos 2\phi$ azimuthal asymmetry long ago was observed experimentally both in unpolarized SIDIS [54, 55] and in DY [56, 57] processes. Recently the HERMES [58] and COMPASS [59] experiments reported sizable azimuthal asymmetries in a low transverse momentum region. In [12] it was suggested that the $\cos 2\phi$ asymmetry could be explained by the Boer–Mulders effect. The $\cos 2\phi$ asymmetry arises in the unpolarized cross section due to the correlation between the transverse spin and transverse momentum of the parton inside the nucleon. As a result the Boer–Mulders TMD function appears along with the $\cos 2\phi$ term in the unpolarized cross section. The quark (anti-quark) version of the Boer–Mulders function, $h_1^{\perp q}$ (T-odd), represents the transversely polarized quark (anti-quark) distribution inside an unpolarized hadron. $h_1^{\perp q}$ has been extracted in [60,61,62] from the $\cos 2\phi$ asymmetry SIDIS data assuming a relation with the Sivers function. However, the gluon Boer–Mulders function, $h_1^{\perp g}$ (T-even), has not been extracted yet. $h_1^{\perp g}$ represents the linearly polarized gluon distribution inside an unpolarized hadron. The $\cos 2\phi$ asymmetry in the production of $J/\psi$ in the unpolarized semi-inclusive ep collision process directly allows us to probe $h_1^{\perp g}$. The paper is organized as follows. The Sivers asymmetry and the TMD evolution are presented in Sects. 2 and 3, respectively. Sections 4 and 5 discuss the $\cos 2\phi$ azimuthal asymmetry and numerical results, respectively, along with the conclusion in Sect. 6.

2 Sivers asymmetry

The single spin asymmetry for the semi-inclusive process $A^{\uparrow }+ B\rightarrow C + X$ is defined

$$\begin{aligned} A_{N}=\frac{\mathrm{d} \sigma ^{\uparrow }-\mathrm{d} \sigma ^{\downarrow }}{\mathrm{d} \sigma ^{\uparrow }+\mathrm{d} \sigma ^{\downarrow }}, \end{aligned}$$

(1)

where $\mathrm{d}\sigma ^{\uparrow }$ and $\mathrm{d}\sigma ^{\downarrow }$ are, respectively, the differential cross-sections measured when one of the particles is transversely polarized up ($\uparrow$) and down ($\downarrow$) with respect to the scattering plane. We consider the process

$$\begin{aligned} e(l)+p^{\uparrow }(P)\rightarrow e(l^\prime )+J/\psi (P_h) +X, \end{aligned}$$

(2)

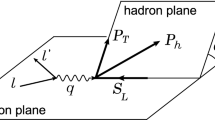
where the electron scatters by the transversely polarized proton target. The letters within the brackets represent the four momentum of the corresponding particle. We follow the generalized factorization theorem where the intrinsic partonic transverse momentum is taken into account, unlike the collinear factorization. The kinematics considered below is different from [39,40,41]. We consider the frame as shown in Fig. 1 in which the proton and virtual photon are moving along the $-z$ and $+z$ axes, respectively. The four momenta of target system P and virtual photon $q=l-l^\prime$ are given by

$$\begin{aligned} P= & {} n_{-}+\frac{M_\mathrm{p}^2}{2}n_+\approx n_{-}~~\mathrm {and}~~q=-x_\mathrm{B}n_{-}+\frac{Q^2}{2x_\mathrm{B}}n_{+} \nonumber \\\approx & {} -x_\mathrm{B}P+(P \cdot q)n_{+}, \end{aligned}$$

(3)

with $Q^2=-q^2$ and we have the Bjorken variable $x_\mathrm{B}=\frac{Q^2}{2P \cdot q}$ (up to proton mass correction). Here $M_\mathrm{p}$ is the mass of the proton. The leptonic four momenta are expanded in terms of $n_-=P$ and $n_+=n=(q+x{_\mathrm{B}}P)/P \cdot q$ [63] as follows:

$$\begin{aligned} l= & {} \frac{1-y}{y}x_\mathrm{B}P+\frac{1}{y}\frac{Q^2}{2x_\mathrm{B}}n+\frac{\sqrt{1-y}}{y}Q\hat{l}_\perp \nonumber \\= & {} \frac{1-y}{y} x_\mathrm{B}P+\frac{s}{2}n+\frac{\sqrt{1-y}}{y}Q\hat{l}_\perp , \end{aligned}$$

(4)

$$\begin{aligned} l^\prime= & {} \frac{1}{y}x_\mathrm{B}P+\frac{1-y}{y}\frac{Q^2}{2x_\mathrm{B}}n+\frac{\sqrt{1-y}}{y}Q\hat{l}_\perp \nonumber \\= & {} \frac{1}{y} x_\mathrm{B}P+(1-y)\frac{s}{2}n+\frac{\sqrt{1-y}}{y}Q\hat{l}_\perp ; \end{aligned}$$

(5)

Fig. 1

Definition of azimuthal angles ($\phi _s,~\phi _h$), lepton and hadron scattering planes in semi-inclusive deep inelastic scattering

here $y=\frac{P \cdot q}{P \cdot l}$. The invariant mass of the electron–target system is $s=(P+l)^2=2P \cdot l=\frac{2P \cdot q}{y}$ and then we have $Q^2=x_\mathrm{B}ys$. The virtual photon–target invariant mass is defined as $W^2=(q+P)^2=\frac{Q^2(1-x_\mathrm{B})}{x_\mathrm{B}}$. Using the Sudakov decomposition, the four momenta of the initial gluon k and the final hadron $P_h$ are

$$\begin{aligned} k= & {} xP+k_\perp +\frac{{\varvec{k}}^2_\perp }{2x}n\approx xP+k_\perp , \end{aligned}$$

(6)

$$\begin{aligned} P_h= & {} z(P \cdot q)n+\frac{M^2+{{\varvec{P}}}_{hT}^2}{2zP \cdot q}P+P_{hT}, \end{aligned}$$

(7)

where $x=k \cdot n$ is the longitudinal momentum fraction, $z=P \cdot P_h/P \cdot q$ and $P^2_{hT}=-{\varvec{P}}^2_{hT}$. The mass of the $J/\psi$ is denoted with M. In line with Ref. [63] we assume that the generalized factorization theorem allows one to factorize the unpolarized differential cross section,

$$\begin{aligned} \mathrm{d}\sigma= & {} \frac{1}{2s}\frac{\mathrm{d}^3l^\prime }{(2\pi )^32E^\prime _l}\frac{\mathrm{d}^3P_h}{(2\pi )^32E_h}\int \mathrm{d}x \mathrm{d}^2{{\varvec{k}}}_\perp (2\pi )^4\delta ^4(q+k-P_h)\nonumber \\&\times \frac{1}{Q^4}L^{\nu \nu ^\prime }(l,q)\Phi ^{\mu \mu ^\prime }_{g}(x,{{\varvec{k}}}_\perp ) \mathcal {M}_{\mu \nu }^{\gamma ^*g\rightarrow J/\psi }\mathcal {M}_{\mu ^\prime \nu ^\prime }^{*~\gamma ^*g\rightarrow J/\psi }. \end{aligned}$$

(8)

The leptonic tensor is given by

$$\begin{aligned} L^{\nu \nu ^\prime }(l,q)=e^2\left( -g^{\nu \nu ^\prime }Q^2+2(l^\nu l^{\prime \nu ^\prime }+l^{\nu ^\prime } l^{\prime \nu })\right) . \end{aligned}$$

(9)

The gluon–gluon correlator, $\Phi _{g}^{\mu \mu ^\prime }(x,{{\varvec{k}}}_\perp )$, describes the transition of the hadron to the parton, which is parametrized in terms of eight TMDs at leading twist. The gluon correlator is defined for an unpolarized and transversely polarized hadron, respectively, [64]

$$\begin{aligned} \Phi _{g}^{\mu \mu ^\prime }(x,{\varvec{k}}_\perp )= & {} \frac{1}{2x}\Bigg \{-g_{T}^{\mu \mu ^\prime } f_1^g(x,{{\varvec{k}}}^2_\perp )+\left( \frac{k_{\perp }^{\mu } k_{\perp }^{\mu ^\prime }}{M_p^2}\right. \nonumber \\&\left. +g_{T}^{\mu \mu ^\prime }\frac{{{\varvec{k}}}^2_\perp }{2M_p^2} \right) h^{\perp g}_1(x,{{\varvec{k}}}^2_\perp )\Bigg \}, \end{aligned}$$

(10)

$$\begin{aligned} \Phi _{g}^{T\mu \mu ^\prime }(x,{{\varvec{k}}}_\perp )= & {} -\frac{1}{2x}g_{T}^{\mu \mu ^\prime }\frac{\epsilon _T^{\rho \sigma }k_{\perp \rho }S_{T\sigma }}{M_p} f_{1T}^{\perp g}(x,{{\varvec{k}}}^2_\perp ), \end{aligned}$$

(11)

where $g_{T}^{\mu \mu ^\prime }=g^{\mu \mu ^\prime }-P^{\mu }n^{\mu ^\prime }/P \cdot n-P^{\mu ^\prime }n^{\mu }/P \cdot n$ is the transverse metric tensor. Here we have kept only the part of the hadronic tensor for the transverse polarization that contributes to the Sivers asymmetry. $f_1^g$ and $h_1^{\perp g}$ represent the unpolarized and linearly polarized gluon distribution functions inside the unpolarized hadron, respectively. $f_{1T}^{\perp g}$, the gluon Sivers function, describes the density of the unpolarized gluons inside the transversely polarized hadron. The only LO subprocess for $J/\psi$ production is $\gamma ^*g\rightarrow c\bar{c}$. In Eq. (8), $\mathcal {M}^{\gamma ^*g\rightarrow J/\psi }$ is the amplitude of $J/\psi$ production. The $J/\psi$ production mechanism for instance contains both perturbative and nonperturbative regimes which have to be separated out systematically. We employ the COM to calculate the amplitude of the $J/\psi$ bound state. The detailed calculation is discussed in the appendix. In the COM framework initially a heavy quark pair is produced in a definite quantum state which can be calculated using the perturbation theory up to a fixed order in $\alpha _s$. The long distance matrix element (LDME), $\langle 0\vert \mathcal {O}^{J/\psi }_n\vert 0\rangle$, contains the transition probability of $J/\psi$ production from heavy quark pair. The momentum conservation delta function can be decomposed

$$\begin{aligned} \delta ^4(q+k-P_h)= & {} \frac{2}{ys}\delta \left( x-x_\mathrm{B}-\frac{M^2+{{\varvec{P}}}_{hT}^2}{zys} \right) \nonumber \\&\times \delta (1-z)\delta ^2({{\varvec{k}}}_\perp -{{\varvec{P}}}_{hT}). \end{aligned}$$

(12)

The phase space factors in Eq. (8) can be written as follows:

$$\begin{aligned} \frac{\mathrm{d}^3l^\prime }{(2\pi )^32E^\prime _l}=\frac{1}{16\pi ^2}sy\mathrm{d}x_\mathrm{B}\mathrm{d}y,~~~ \frac{\mathrm{d}^3P_h}{(2\pi )^32E_h}=\frac{\mathrm{d}z\mathrm{d}^2{{\varvec{P}}}_{hT}}{(2\pi )^32z}.\nonumber \\ \end{aligned}$$

(13)

The differential cross section can be expressed in terms of TMDs by substituting the parameterization of gluon correlator, the leptonic tensor and Eqs. (A.65)–(A.69) in Eq. (8). Using Eqs. (9)–(13) and after integrating with respect to x and z

$$\begin{aligned} \frac{\mathrm{d}\sigma }{\mathrm{d}y\mathrm{d}x_\mathrm{B}d^2{{\varvec{P}}}_{hT}}= & {} \frac{\alpha }{8sxQ^4}\int \mathrm{d}^2{{\varvec{k}}}_\perp \left[ \mathcal {A}_0 \right. \nonumber \\&\left. +\,\mathcal {A}_1\cos \phi \right] f_{g/p}(x,{{\varvec{k}}}_{\perp }^2)\delta ^2({{\varvec{k}}}_\perp -{{\varvec{P}}}_{hT}),\nonumber \\ \end{aligned}$$

(14)

is obtained, with correction $\mathcal {O}\left( \frac{k_\perp ^2}{(M^2+Q^2)^2}\right)$. The azimuthal angle of the initial gluon transverse momentum is denoted with $\phi$. For obtaining Eq. (14), $\phi =\phi _h$ is understood where $\phi _h$ is the azimuthal angle of the $J/\psi$. In Eq. (14) only the unpolarized gluon contribution is taken into consideration. The effect of the linearly polarized gluon contribution will be discussed in Sect. 4. We define $\mathcal {A}_0$ and $\mathcal {A}_1$ by

$$\begin{aligned} \mathcal {A}_0= & {} \left[ 1+(1-y)^2\right] \frac{\mathcal {N}Q^2}{y^2M}\Bigg \{\langle 0\vert \mathcal {O}_8^{J/\psi }(^1{S}{_0})\vert 0\rangle \nonumber \\&+\frac{4}{3M^2}\frac{ (3 M^2+Q^2)^2}{(M^2+Q^2)^2} \langle 0\vert \mathcal {O}_8^{J/\psi }(^3{P}{_0})\vert 0\rangle \nonumber \\&+\frac{8 Q^2}{3M^2(M^2+Q^2)^2}\left( \frac{4M^2 (1-y)}{1+(1-y)^2}\right. \nonumber \\&\left. +Q^2\right) \langle 0\vert \mathcal {O}_8^{J/\psi }(^3{P}{_1})\vert 0\rangle \nonumber \\&+\frac{8 }{15M^2 \left( M^2+Q^2\right) ^2}\left( 6 M^4+Q^4 \right. \nonumber \\&\left. +12 M^2 Q^2 \frac{1-y}{1+(1-y)^2}\right) \langle 0\vert \mathcal {O}_8^{J/\psi }(^3{P}{_2})\vert 0\rangle \Bigg \}, \end{aligned}$$

(15)

$$\begin{aligned} \mathcal {A}_1= & {} (2-y)\sqrt{1-y}\frac{4\mathcal {N}Q^3}{y^2M}\Bigg \{- \langle 0\vert \mathcal {O}_8^{J/\psi }(^1{S}{_0})\vert 0\rangle \nonumber \\&-\frac{2}{3M^2Q^2}\frac{(3 M^2+Q^2)^2}{M^2+Q^2} \langle 0\vert \mathcal {O}_8^{J/\psi }(^3{P}{_0})\vert 0\rangle \nonumber \\&-\frac{8 Q^2}{3M^2(M^2+Q^2)}\langle 0\vert \mathcal {O}_8^{J/\psi }(^3{P}{_1})\vert 0\rangle \nonumber \\&-\frac{4 }{15 M^2}\frac{7M^2+Q^2}{M^2+Q^2} \langle 0\vert \mathcal {O}_8^{J/\psi }(^3{P}{_2})\vert 0\rangle \Bigg \}\frac{k_\perp }{M^2+Q^2},\nonumber \\ \end{aligned}$$

(16)

with $\mathcal {N}=2(4\pi )^2\alpha _s\alpha e_c^2$. $\mathcal {A}_1$ does not contribute to the Sivers asymmetry. The numerical values of the different states LDME are taken from Ref. [46], Set-I in Table I. Following Ref. [65], the numerator term of the Sivers asymmetry is given now when the target proton is transversely polarized,

$$\begin{aligned}&\frac{\mathrm{d}\sigma ^{\uparrow }}{\mathrm{d}y\mathrm{d}x_\mathrm{B}\mathrm{d}^2{{\varvec{P}}}_{hT}}-\frac{\mathrm{d}\sigma ^{\downarrow }}{\mathrm{d}y\mathrm{d}x_\mathrm{B}\mathrm{d}^2{{\varvec{P}}}_{hT}}\nonumber \\&\quad =\frac{\alpha }{8sxQ^4}\left[ \mathcal {A}_0+\mathcal {A}_1\cos \phi _h\right] \Delta ^Nf_{g/p^{\uparrow }}(x,{{\varvec{P}}}_{hT}). \end{aligned}$$

(17)

The gluon Sivers function as per Trento convention is given by [66]

$$\begin{aligned} \Delta ^Nf_{g/p^{\uparrow }}(x,{{\varvec{P}}}_{hT},Q_f)= & {} -2f_{1T}^{\perp g}(x,{{\varvec{P}}}_{hT},Q_f) \frac{(\hat{{\varvec{P}}}\times {{\varvec{P}}}_{hT}) \cdot {{\varvec{S}}}}{M_p}.\nonumber \\ \end{aligned}$$

(18)

The scale dependency in the definition of the TMD is suppressed in this section. The denominator term is given by

$$\begin{aligned}&\frac{\mathrm{d}\sigma ^{\uparrow }}{\mathrm{d}y\mathrm{d}x_\mathrm{B}\mathrm{d}^2{{\varvec{P}}}_{hT}}+\frac{\mathrm{d}\sigma ^{\downarrow }}{\mathrm{d}y\mathrm{d}x_\mathrm{B}\mathrm{d}^2{{\varvec{P}}}_{hT}} \nonumber \\&\quad =\frac{2\alpha }{8sxQ^4}\left[ \mathcal {A}_0+\mathcal {A}_1\cos \phi _h\right] f_{g/p}(x,{{\varvec{P}}}_{hT}^2), \end{aligned}$$

(19)

where the GSF $\Delta ^Nf$ describes the probability of finding an unpolarized gluon inside a transversely polarized proton, which is defined by

$$\begin{aligned} \Delta ^Nf_{g/p^{\uparrow }}(x,{{\varvec{P}}}_{hT})= & {} f_{g/p^{\uparrow }}(x,{{\varvec{P}}}_{hT})- f_{g/p^{\downarrow }}(x,{{\varvec{P}}}_{hT})\nonumber \\= & {} \Delta ^Nf_{g/p^{\uparrow }}(x,P_{hT})~{{\varvec{S}}}.(\hat{{\varvec{P}}}\times \hat{{\varvec{P}}}_{hT}). \end{aligned}$$

(20)

3 Evolution of TMDs

In this section the evolution of TMDs is studied. It is generally assumed that the unpolarized gluon TMDs obey the Gaussian distribution. The Gaussian parameterization of an unpolarized TMD is given by

$$\begin{aligned} f_{g/p}(x,{{\varvec{k}}}^2_{\perp })=f_{g/p}(x,\mu )\frac{1}{\pi \langle k^2_{\perp }\rangle } e^{-{{\varvec{k}}}^2_{\perp }/\langle k^2_{\perp }\rangle }. \end{aligned}$$

(21)

Here, the x and $k_\perp$ dependencies of the TMD are factorized. $f_{g/p}(x,\mu )$ is the collinear PDF, which is measured at the scale $\mu =M$ (mass of $J/\psi$). The collinear PDF obeys the Dokshitzer–Gribov–Lipatov–Altarelli–Parisi (DGLAP) scale evolution. A frame is chosen where the polarized proton is moving along the $-z$ axis with momentum ${\varvec{P}}$ and is transversely polarized with $S=S_T(\cos \phi _s,\sin \phi _s,0)$. The transverse momentum of the $J/\psi$ is ${\varvec{P}}_{hT}=P_{hT}(\cos \phi _h,\sin \phi _h,0)$

$$\begin{aligned} {\varvec{S}} \cdot (\hat{{\varvec{P}}}\times \hat{{\varvec{P}}}_{hT})=\sin (\phi _h-\phi _s), \end{aligned}$$

(22)

where $\phi _s$ and $\phi _h$ are the azimuthal angles, which are defined in Fig. 1. The parameterization of GSF is given by [49, 67]

$$\begin{aligned} \Delta ^{N}f_{g/p^{\uparrow }}(x, k_{\perp })=2\mathcal {N}_g(x)f_{g/p}(x,\mu )h(k_\perp ) \frac{e^{-k^2_\perp /\langle k^2_\perp \rangle }}{\pi \langle k^2_\perp \rangle };\nonumber \\ \end{aligned}$$

(23)

here

$$\begin{aligned} \mathcal {N}_g(x)=N_gx^\alpha (1-x)^\beta \frac{(\alpha +\beta )^{(\alpha +\beta )}}{ \alpha ^\alpha \beta ^\beta }. \end{aligned}$$

(24)

$h(k_\perp )$ is defined as follows:

$$\begin{aligned} h(k_\perp )=\sqrt{2e}\frac{k_\perp }{M_1}e^{-k^2_\perp /M^2_1}. \end{aligned}$$

(25)

Therefore, the $k_\perp$ dependent part of the Sivers function can now be written

$$\begin{aligned} h(k_\perp )\frac{e^{-k^2_\perp /\langle k^2_\perp \rangle }}{\pi \langle k^2_\perp \rangle } =\frac{\sqrt{2e}}{\pi }\sqrt{\frac{1-\rho }{\rho }}k_\perp \frac{e^{-k^2_{\perp }/\rho \langle k^2_\perp \rangle }}{\langle k^2_\perp \rangle ^{3/2}}, \end{aligned}$$

(26)

where we defined

$$\begin{aligned} \rho =\frac{M^2_1}{\langle k^2_\perp \rangle + M^2_1}. \end{aligned}$$

(27)

The GSF has been extracted for the first time in the pion production at RHIC [68] by D’Alesio et al. [49]. In this analysis [49] the best fit parameter sets are denoted SIDIS1 and SIDIS2. Recently, Anselmino et al. [67] have extracted the quark and the anti-quark Sivers function from the latest SIDIS data. However, GSF has not been extracted yet from the SIDIS data. Therefore, in order to estimate the asymmetry, the best fit parameters of the Sivers function corresponding to u and d quark will be used in the following parameterizations [69]:

$$\begin{aligned} \mathrm{{(a)}}~~\mathcal {N}_g(x)= & {} ({N}_u(x)+{N}_d(x))/2 , \nonumber \\ \mathrm{{(b)}}~~\mathcal {N}_g(x)= & {} {N}_d(x) . \end{aligned}$$

(28)

We call the parameterization (a) and (b) BV-a and BV-b, respectively. The best fit parameters are tabulated in Table 1.

Table 1 The best fit parameters of the Sivers function

We use the nonuniversality property of the Sivers function only for the SIDIS1 and SIDIS2 parameters, since these parameters are extracted in the DY process [70],

$$\begin{aligned} \Delta ^{N}_{\mathrm {DY}}f_{g/p^{\uparrow }}(x, k_{\perp })=- \Delta ^{N}_{\mathrm {SIDIS}}f_{g/p^{\uparrow }}(x, k_{\perp }). \end{aligned}$$

(29)

Finally the final expressions of Eq. (1) can be written within DGLAP evolution formalism. Using Eqs. (21)–(28), the $\sin (\phi _h-\phi _s)$ weighted numerator part of Eq. (1) is given by

$$\begin{aligned}&\frac{\mathrm{d}\sigma ^{\uparrow }}{\mathrm{d}y\mathrm{d}x_\mathrm{B}\mathrm{d}^2{\varvec{P}}_{hT}}-\frac{\mathrm{d}\sigma ^{\downarrow }}{\mathrm{d}y\mathrm{d}x_\mathrm{B}\mathrm{d}^2{\varvec{P}}_{hT}}\nonumber \\&\quad =\frac{\alpha }{8sxQ^4}\left[ \mathcal {A}_0+\mathcal {A}_1\cos \phi _h\right] 2\mathcal {N}_g(x)\frac{\sqrt{2e}}{\pi } \sqrt{\frac{1-\rho }{\rho }}P_{hT}\nonumber \\&\quad \times \frac{e^{-P_{hT}^2/\rho \langle P^2_{hT}\rangle }}{\langle P^2_{hT}\rangle ^{3/2}} f_{g/p}(x)\sin ^2(\phi _h-\phi _s), \end{aligned}$$

(30)

and the denominator term as follows:

$$\begin{aligned}&\frac{\mathrm{d}\sigma ^{\uparrow }}{\mathrm{d}y\mathrm{d}x_\mathrm{B}\mathrm{d}^2{\varvec{P}}_{hT}}+\frac{\mathrm{d}\sigma ^{\downarrow }}{\mathrm{d}y\mathrm{d}x_\mathrm{B}\mathrm{d}^2{\varvec{P}}_{hT}} \nonumber \\&\quad =\frac{2\alpha }{8sxQ^4}\left[ \mathcal {A}_0+\mathcal {A}_1\cos \phi _h\right] \frac{e^{-P_{hT}^2/\langle P^2_{hT}\rangle }}{\pi \langle P^2_{hT}\rangle } f_{g/p}(x). \end{aligned}$$

(31)

Now, the framework implemented in Ref. [70] to study the TMD evolution can be adopted. In general, TMDs are defined in an impact parameter ($b_\perp$)-space

$$\begin{aligned} f(x,b_\perp ,\mu )=\int \mathrm{d}^2{\varvec{k}}_\perp e^{-i{\varvec{b}}_\perp \cdot {\varvec{k}}_\perp }f(x,k_\perp ,\mu ) \end{aligned}$$

(32)

and the inverse Fourier transformation is

$$\begin{aligned} f(x,k_\perp ,\mu )=\frac{1}{(2\pi )^2}\int \mathrm{d}^2{\varvec{b}}_\perp e^{i{\varvec{b}}_\perp .{\varvec{k}}_\perp }f(x,b_\perp ,\mu ). \end{aligned}$$

(33)

Generally TMDs depend on both a renormalization scale ($\mu$) and an auxiliary scale ($\zeta$) which are introduced to regularize the light-cone divergences in the TMD factorization formalism [6, 51]. Taking the scale evolution in account with respect to the $\mu$ and $\zeta$, the renormalization group (RG) and Collins–Soper (CS) equations are obtained. By solving these equations one obtains the TMD–PDF expression which is evolved from the initial scale $Q_i=c/b_{*}(b_{\perp })$ to the final scale $Q_f=\sqrt{\zeta }=M$ [6, 51, 70, 71],

$$\begin{aligned} {} f(x,b_{\perp },Q_f,\zeta )= & {} f(x,b_\perp ,Q_i)R_{\text {pert}}\left( Q_f,Q_i,b_{*}\right) \nonumber \\&R_{NP}\left( Q_f,Q_i,b_{\perp }\right) . \end{aligned}$$

(34)

Here, $R_{\text {pert}}$ is the perturbative part. The nonperturbative part of the TMDs is denoted with $R_{NP}$. The initial scale of the TMDs is $Q_i=c/b_{*}(b_{\perp })$, where $c=2e^{-\gamma _\epsilon }$ with $\gamma _\epsilon \approx 0.577$. The widely used $b_{*}$ prescription is adopted to avoid hitting the Landau pole by freezing the scale $b_{\perp }$. Here, $b_{*}(b_{\perp })=\frac{b_{\perp }}{\sqrt{1+\left( \frac{b_{\perp }}{b_{\mathrm {max}}}\right) ^2}} \approx b_{\mathrm {max}}$ when $b_{\perp }\rightarrow \infty$ and $b_{*}(b_{\perp })\approx b_{\perp }$ when $b_{\perp }\rightarrow 0$. The perturbative evolution kernel is given by

$$\begin{aligned} R_{\text {pert}}\left( Q_f,Q_i,b_{*}\right) =\mathrm {exp}\left\{ {-\int _{c/b_{*}}^{Q_f}\frac{\mathrm{d}\mu }{\mu }\left( A\log \left( \frac{Q_f^2}{\mu ^2}\right) +B\right) }\right\} , \end{aligned}$$

(35)

where the anomalous dimensions are denoted with A an B, respectively. These have a perturbative expansion

$$\begin{aligned} A=\sum _{n=1}^{\infty }\left( \frac{\alpha _s(\mu )}{\pi }\right) ^nA_n \end{aligned}$$

and

$$\begin{aligned} B=\sum _{n=1}^{\infty }\left( \frac{\alpha _s(\mu )}{\pi }\right) ^nB_n. \end{aligned}$$

Here the anomalous dimension coefficients $A_1=C_A$, $A_2=\frac{1}{2}C_F\left( C_A\left( \frac{67}{18}-\frac{\pi ^2}{6}\right) -\frac{5}{9}C_AN_f\right)$ and $B_1=-\frac{1}{2}(\frac{11}{3}C_A-\frac{2}{3}N_f)$. These coefficients are derived up to 3-loop level in Ref. [72]. The nonperturbative part is given by

$$\begin{aligned} R_{NP}=\mathrm {exp}\Bigg \{-\Big [g_1^{\mathrm {TMD}}+\frac{g_2}{2} \log \frac{Q_f}{Q_0} \Big ]b_{\perp }^2\Bigg \}. \end{aligned}$$

(36)

It is well known [51] that the derivative of the Sivers function, $f^{\prime \perp } (x,b_{\perp },Q_f)$, follows the same evolution as that of the unpolarized TMD. The TMD evolution equation of the unpolarized gluon TMD–PDF is

$$\begin{aligned} f_{g/p}(x,b_\perp ,Q_f)= & {} f_1^g(x,b_\perp ,Q_i) \nonumber \\&\times \, \mathrm {exp}\Bigg \{-\int _{c/b_{*}}^{Q_f} \frac{\mathrm{d}\mu }{\mu }\left( A\log \left( \frac{Q_f^2}{\mu ^2}\right) +B\right) \Bigg \}\nonumber \\&\times \, \mathrm {exp}\Bigg \{-\Big [g_1^{\mathrm {pdf}}+\frac{g_2}{2} \log \frac{Q_f}{Q_0} \Big ]b_{\perp }^2\Bigg \} \end{aligned}$$

(37)

and the derivative of the gluon Sivers function is

$$\begin{aligned} f_{1T}^{\prime \perp g }(x,b_\perp ,Q_f)= & {} f_{1T}^{\prime \perp g }(x,b_\perp ,Q_i) \nonumber \\&\times \, \mathrm {exp}\Bigg \{ -\int _{c/b_{*}}^{Q_f} \frac{\mathrm{d}\mu }{\mu }\left( A\log \left( \frac{Q_f^2}{\mu ^2}\right) +B\right) \Bigg \}\nonumber \\&\times \, \mathrm {exp}\Bigg \{-\Big [g_1^{\mathrm {Sivers}}+\frac{g_2}{2} \log \frac{Q_f}{Q_0} \Big ]b_{\perp }^2\Bigg \}. \end{aligned}$$

(38)

The TMD density function at the initial scale, $f_1^{g}(x,b_\perp ,Q_i)$, can be written as the convolution of the coefficient function times the regular collinear PDF [51]

$$\begin{aligned} f_1^{g}(x,b_\perp ,Q_i)= & {} \sum _{i=g,q}\int _x^1\frac{\mathrm{d}\hat{x}}{\hat{x}} C_{i/g}(x/\hat{x},b_{\perp },\alpha _s,Q_i) f_{i/p}(\hat{x},c/b_{*}) \nonumber \\&+\,\mathcal {O}(b_{\perp }\varLambda _{QCD}), \end{aligned}$$

(39)

where $C_{i/g}$ is the perturbatively calculated coefficient function which is process independent. $C_{i/g}$ is different for each type of TMD–PDF. The collinear PDF is probed at the scale $c/b_{*}$ rather than at the scale $\mu$ in contrast to the DGLAP evolution. The unpolarized and Sivers function TMDs in terms of collinear PDF at leading order in $\alpha _{s}$ are given by [51, 70]

$$\begin{aligned} f_1^g(x,b_\perp ,Q_i)= & {} f_{g/p}(x,c/b_{*})+\mathcal {O}(\alpha _s), \end{aligned}$$

(40)

$$\begin{aligned} f_{1T}^{\prime \perp g }(x,b_\perp ,Q_i)\simeq & {} \frac{M_pb_\perp }{2}T_{g,F}(x,x,Q_i), \end{aligned}$$

(41)

where $T_{g,F}(x,x,Q_i)$ is the Qiu–Sterman function proportional to the collinear PDF [21]

$$\begin{aligned} T_{g,F}(x,x,Q_i)=\mathcal {N}_g(x)f_{g/p}(x,Q_i), \end{aligned}$$

(42)

where the $\mathcal {N}_g(x)$ definition is given in Eq. (24). The numerical values of the free parameters are estimated [70] by a global fit of SSA in the SIDIS process from the pion, kaons and charged hadrons production at Jlab, HERMES and COMPASS, which are tabulated in Table  1. However, only the u and d quark’s free parameters are extracted and gluon parameters are not known yet. To estimate the SSA we use two parameterizations, given in Eq. (28). We call the parameterizations (a) and (b) TMD-a and TMD-b, respectively. The numerical values of the best fit parameters are estimated [70] $Q_0=\sqrt{2.4}~\mathrm {GeV}$, $b_{\mathrm {max}}=1.5\mathrm {~GeV^{-1}}$, $g_2=0.16\mathrm {~GeV^2}$ and $\langle k^2_{s\perp }\rangle =0.282\mathrm {~GeV^2}$ with $g_1^{\mathrm {pdf}}=\langle k^2_{\perp }\rangle /4$ and $g_1^{\mathrm {sivers}}=\langle k^2_{s \perp } \rangle /4$. The gluon Sivers function $f_{1T}^{\perp g}(x,{\varvec{P}}_{hT},Q_f)$ and its derivative are related by the Fourier transformation [51]

$$\begin{aligned} f_{1T}^{\perp g}(x,{\varvec{P}}_{hT},Q_f)= & {} -\frac{1}{2\pi P_{hT}}\int _0^\infty \mathrm{d}b_\perp b_\perp \nonumber \\&J_1(P_{hT}b_\perp )f_{1T}^{\prime \perp g}(x,b_\perp ,Q_f), \end{aligned}$$

(43)

and the unpolarized gluon TMD is given by

$$\begin{aligned} f_{g/p}(x, P_{hT},Q_f)= & {} \frac{1}{2\pi }\int _0^\infty \mathrm{d}b_\perp b_\perp \nonumber \\&J_0({P}_{hT}b_\perp )f_{g/p}(x,b_\perp ,Q_f). \end{aligned}$$

(44)

Using the above expressions, Eq. (17), including the weight factors $\sin (\phi _h-\phi _s)$ and (19) in the TMD evolution framework can be written as follows:

$$\begin{aligned}&\frac{\mathrm{d}\sigma ^{\uparrow }}{\mathrm{d}y\mathrm{d}x_\mathrm{B}\mathrm{d}^2{\varvec{P}}_{hT}}-\frac{\mathrm{d}\sigma ^{\downarrow }}{\mathrm{d}y\mathrm{d}x_\mathrm{B}d^2{\varvec{P}}_{hT}}\nonumber \\&\quad =\frac{\alpha }{8\pi sxQ^4M_p} \int _0^\infty \mathrm{d}b_\perp b_\perp J_1(P_{hT}b_\perp ) f_{1T}^{\prime \perp g}(x,b_\perp ,Q_f)\nonumber \\&\quad \quad \times \sin ^2(\phi _h-\phi _s)\left[ \mathcal {A}_0+\mathcal {A}_1\cos \phi _h\right] , \end{aligned}$$

(45)

$$\begin{aligned}&\frac{\mathrm{d}\sigma ^{\uparrow }}{\mathrm{d}y\mathrm{d}x_\mathrm{B}\mathrm{d}^2{\varvec{P}}_{hT}}+\frac{\mathrm{d}\sigma ^{\downarrow }}{\mathrm{d}y\mathrm{d}x_\mathrm{B}\mathrm{d}^2{\varvec{P}}_{hT}} \nonumber \\&\quad =\frac{\alpha }{8\pi sxQ^4} \int _0^\infty \mathrm{d}b_\perp b_\perp J_0(P_{hT}b_\perp ) f_{g/p}(x,b_\perp ,Q_f)\nonumber \\&\quad \quad \times \left[ \mathcal {A}_0+\mathcal {A}_1\cos \phi _h\right] . \end{aligned}$$

(46)

4 $\cos 2\phi$ azimuthal asymmetry

Now, the unpolarized process, i.e. $e(l)+p(P)\rightarrow e(l^\prime )+J/\psi (P_h) +X$, is considered. Taking into account the linearly polarized gluons along with the unpolarized gluons in the gluon correlator, Eq. (14) can be written

$$\begin{aligned} \frac{\mathrm{d}\sigma }{\mathrm{d}y\mathrm{d}x_\mathrm{B}\mathrm{d}^2{\varvec{P}}_{hT}}= & {} \frac{\alpha }{8sxQ^4}\int \mathrm{d}^2{\varvec{k}}_\perp \Big \{ \left[ \mathcal {A}_0+\mathcal {A}_1\cos \phi \right] f_{g/p}(x,{\varvec{k}}_{\perp }^2)\nonumber \\&+\,\,{\varvec{k}}_\perp ^2\left[ \mathcal {B}_0\cos 2\phi +\mathcal {B}_1\cos \phi \right] h_1^{\perp g}(x,{\varvec{k}}^2_\perp )\Big \}\delta ^2({\varvec{k}}_\perp -{\varvec{P}}_{hT}),\nonumber \\ \end{aligned}$$

(47)

with correction $\mathcal {O}\left( \frac{k_\perp ^2}{(M^2+Q^2)^2}\right)$. The definitions of $\mathcal {A}_0$ and $\mathcal {A}_1$ are given in Eqs. (15) and (16), respectively. $\mathcal {B}_0$ and $\mathcal {B}_1$ are defined by

$$\begin{aligned} \mathcal {B}_0= & {} (1-y)\frac{\mathcal {N}Q^2}{y^2M}\Bigg \{-\langle 0\vert \mathcal {O}_8^{J/\psi }(^1{S}{_0})\vert 0\rangle \nonumber \\&+\frac{4}{3M^2}\frac{ \left( 3 M^2+Q^2\right) ^2 }{ \left( M^2+Q^2\right) ^2} \langle 0\vert \mathcal {O}_8^{J/\psi }(^3{P}{_0})\vert 0\rangle \nonumber \\&-\frac{8 Q^4}{3M^2(M^2+Q^2)^2} \langle 0\vert \mathcal {O}_8^{J/\psi }(^3{P}{_1})\vert 0\rangle \nonumber \\&+\frac{8 Q^4}{15 M^2 \left( M^2+Q^2\right) ^2} \langle 0\vert \mathcal {O}_8^{J/\psi }(^3{P}{_2})\vert 0\rangle \Bigg \}, \end{aligned}$$

(48)

$$\begin{aligned} \mathcal {B}_1= & {} (2-y)\sqrt{1-y}\frac{2\mathcal {N}Q}{y^2M} \Bigg \{Q^2\langle 0\vert \mathcal {O}_8^{J/\psi }(^1{S}{_0})\vert 0\rangle \nonumber \\&-\frac{2}{3M^2}\frac{ \left( 3 M^2+Q^2\right) ^2 }{M^2+Q^2} \langle 0\vert \mathcal {O}_8^{J/\psi }(^3{P}{_0})\vert 0\rangle \nonumber \\&+\frac{8 Q^4}{3M^2(M^2+Q^2)}\langle 0\vert \mathcal {O}_8^{J/\psi }(^3{P}{_1})\vert 0\rangle \nonumber \\&-\frac{4Q^2}{15M^2}\frac{Q^2-5M^2}{ M^2+Q^2} \langle 0\vert \mathcal {O}_8^{J/\psi }(^3{P}{_2})\vert 0\rangle \Bigg \}\frac{k_\perp }{M^2+Q^2}.\nonumber \\ \end{aligned}$$

(49)

The dependence of the cross section on the azimuthal angle vanishes when the intrinsic parton transverse momentum $k_\perp =0$. The $\cos 2\phi$ asymmetry is defined [58, 59] by

$$\begin{aligned} <\cos 2\phi >=\frac{\int \mathrm{d}\phi _h \cos (2\phi _h)\mathrm{d}\sigma }{\int d\phi _h \mathrm{d}\sigma }. \end{aligned}$$

(50)

To estimate the $\cos 2\phi$ asymmetry the parameterization of TMDs is needed. For the unpolarized TMD the Gaussian parameterization as defined in Eq. (21) is used. The widely used Gaussian parameterization for a linearly polarized gluon distribution function is given by [73]

$$\begin{aligned} h_1^{\perp g}(x,\mathbf{k}^2_{\perp })=\frac{M_p^2f_1^g(x,Q^2)}{\pi \langle k^2_{\perp }\rangle ^2}\frac{2(1-r)}{r}e^{1- \mathbf{k}^2_{\perp }\frac{1}{r\langle k^2_{\perp }\rangle }}, \end{aligned}$$

(51)

where r ($0<r<1$) is the parameter. The upper bound on $h_1^{\perp g}$ is given by [74]

$$\begin{aligned} \frac{\mathbf{k}_{\perp }^2}{2M_p^2}|h^{\perp }_1(x,\mathbf{k}_{\perp }^2)|\le f_1^g(x,\mathbf{k}^2_{\perp }). \end{aligned}$$

(52)

We consider $\langle k^2_{\perp }\rangle =0.25$ GeV$^2$ [73] and $r=\frac{1}{3}$ and $\frac{2}{3}$ [73] for numerical estimations.

5 Numerical results

We have estimated the Sivers and the $\cos 2\phi$ asymmetries, respectively, in the polarized and unpolarized SIDIS processes, using the TMD factorization formalism at $\sqrt{s}=4.7\mathrm {~GeV}$ (JLab), $\sqrt{s}=7.2\mathrm {~GeV}$ (HERMES), $\sqrt{s}=17.33\mathrm {~GeV}$ (COMPASS) and $\sqrt{s}=45.0\mathrm {~GeV}$ (EIC). In this work, the NRQCD color octet model (COM) is used for $J/\psi$ production. The color octet states $^{1}{S}{_0}$, $^{3}{P}{_0}$, $^{3}{P}{_1}$ and $^{3}{P}{_2}$ are taken into account for the LO subprocess $\gamma ^*g\rightarrow c\bar{c}$ of the charmonium production. $M=3.096\mathrm {~GeV}$ and $m_\mathrm{c}=1.4\mathrm {~GeV}$ are considered for $J/\psi$ and charm quark mass, respectively. MSTW2008 [75] is used for collinear PDFs.

The following experimental cuts are imposed on the integration variables in Eq. (14). For COMPASS [76, 77], $0.0001<x_\mathrm{B}<0.65,~0.1<y<0.9~\mathrm {and}~0<P_{hT}<1.0~\mathrm {GeV}$, for HERMES [26], $0.023<x_\mathrm{B}<0.40,~0.35<y<0.95~\mathrm {and}~0<P_{hT}<1.0~\mathrm {GeV}$, for JLab [28], $0.0001<x_\mathrm{B}<0.35,~0.7<y<0.9~\mathrm {and}~0<P_{hT}<0.64~\mathrm {GeV}$, and for EIC, $0.0001<x_\mathrm{B}<0.9,~0.1<y<0.9~\mathrm {and}~0<P_{hT}<1.0~\mathrm {GeV}$. The $\sin (\phi _h-\phi _s)$ weighted Sivers asymmetry for the kinematics of different experiments is shown in Figs. 2, 3, 4 and 5 as a function of $P_{hT}$ and $x_\mathrm{B}$. The SSA is estimated both in the DGLAP and the Collins–Soper–Sterman (CSS) TMD evolution approach, which is shown in Figs. 2, 3, 4 and 5. The figure convention is as follows. “SIDIS1” and “SIDIS2” represent the SSA obtained in the DGLAP evolution approach by considering two sets of the best fit parameters SIDIS1 and SIDIS2 from Eqs. (30) and (31). Similarly, “BV-a” and “BV-b” represent the Sivers asymmetry obtained by using Eq. (28) in DGLAP evolution. The obtained SSA in the TMD evolution approach using two parameterizations from Eq. (28) is denoted “TMD-a” and “TMD-b”.

Fig. 2

Single spin asymmetry in $e+p^{\uparrow }\rightarrow e+J/\psi +X$ process as function of a $x_\mathrm{B}$ (left panel) and b $P_{hT}$ (right panel) at $\sqrt{s}=45.0$ GeV (EIC) using DGLAP (SIDIS1, SIDIS2, BV-a and BV-b) and TMD (TMD-a and TMD-b) evolution approaches. The integration ranges are $0<P_{hT}<1.0$ GeV, $0.1<y<0.9$ and $0.0001<x_\mathrm{B}<0.9$

Fig. 3

Single spin asymmetry in $e+p^{\uparrow }\rightarrow e+J/\psi +X$ process as function of a $x_\mathrm{B}$ (left panel) and b $P_{hT}$ (right panel) at $\sqrt{s}=17.2$ GeV (COMPASS) using DGLAP (SIDIS1, SIDIS2, BV-a and BV-b) and TMD (TMD-a and TMD-b) evolution approaches. The integration ranges are $0<P_{hT}<1.0$ GeV, $0.1<y<0.9$ and $0.0001<x_\mathrm{B}<0.65$

Fig. 4

Single spin asymmetry in $e+p^{\uparrow }\rightarrow e+J/\psi +X$ process as function of a $x_\mathrm{B}$ (left panel) and b $P_{hT}$ (right panel) at $\sqrt{s}=7.2$ GeV (HERMES) using DGLAP (SIDIS1, SIDIS2, BV-a and BV-b) and TMD (TMD-a and TMD-b) evolution approaches. The integration ranges are $0<P_{hT}<1.0$ GeV, $0.35<y<0.95$ and $0.023<x_\mathrm{B}<0.40$

Fig. 5

Single spin asymmetry in $e+p^{\uparrow }\rightarrow e+J/\psi +X$ process as function of a $x_\mathrm{B}$ (left panel) and b $P_{hT}$ (right panel) at $\sqrt{s}=4.7$ GeV (JLab) using DGLAP (SIDIS1, SIDIS2, BV-a and BV-b) and TMD (TMD-a and TMD-b) evolution approaches. The integration ranges are $0<P_{hT}<0.64$ GeV, $0.7<y<0.9$ and $0.0001<x_\mathrm{B}<0.35$

Fig. 6

Single spin asymmetry in $e+p^{\uparrow }\rightarrow e+J/\psi +X$ process at $z=1$ with $\sqrt{s}=17.2$ GeV (COMPASS) using DGLAP (SIDIS1, SIDIS2, BV-a and BV-b) and TMD (TMD-a and TMD-b) evolution approaches. The integration ranges are $0<P_{hT}<1.0$ GeV, $0.1<y<0.9$ and $0.0001<x_\mathrm{B}<0.65$. Data from [77]

Fig. 7

$\cos 2\phi$ asymmetry in $e+p\rightarrow e+J/\psi +X$ process as function of a $x_\mathrm{B}$ (left panel) and b $P_{hT}$ (right panel) at $\sqrt{s}=45.0$ GeV (EIC). The integration ranges are $0<P_{hT}<1.0$ GeV, $0.1<y<0.9$ and $0.0001<x_\mathrm{B}<0.9$

Recently the extracted gluon Sivers function [49] from the RHIC data and the quark’s Sivers function [67] from the latest SIDIS data have been employed in the DGLAP evolution approach. The SSA as a function of $P_{hT}$ is negative and is decreasing as the center of the mass energy of the experiment is increasing. This is maximum around $30\%$ at JLab energy. Moreover, the Sivers asymmetry as a function of the Bjorken variable ($x_\mathrm{B}$) is negative and is maximum for SIDIS1 GSF parameters. Echevarria et al. [70] have extracted the u and d quarks’ Sivers function by fitting data from JLab, HERMES and COMPASS within the TMD evolution formalism.The best fit parameters for the gluon Sivers function as defined in Eq. (28) in the CSS–TMD evolution approach are used. The Sivers asymmetry with respect to $P_{hT}$ obtained from the SIDIS1 parameters is higher at JLab and HERMES whereas the SSA obtained from the BV-b set parameters is dominant at COMPASS and EIC experiments. Basically, the SSA is proportional to the gluon Sivers function, which is considered as an average of the u and d quarks’ x-dependent normalization $\mathcal {N}(x)$ in a TMD-a parameterization. The sign of the asymmetry depends on the relative magnitude of $N_u$ and $N_d$. These have opposite signs, as can be observed in Table  1. Note that our kinematics is different from previous work in [39,40,41], which also affects the sign. The magnitude of $\mathcal {N}_u(x)$ is comparable but slightly dominant compared to $\mathcal {N}_d(x)$ at the EIC $\sqrt{s}$. Therefore, the estimated Sivers asymmetry as a function of $P_{hT}$ using the TMD-a parameters for the EIC experiment is almost zero and positive. For the JLab experiment the estimated Sivers asymmetry by all the parameterizations except the SIDIS1 is close to zero.

The delta function in Eq. (12) implies that $z=1$ (LO). In Fig. 6 the obtained Sivers asymmetry at $z=1$ is compared with the COMPASS data [77]. Interestingly, all the parameter sets give a negative asymmetry. However, the estimated SSA with the BV-b set of parameters is within the error bar of the experiment. In Ref. [76] the negative gluon Sivers asymmetry with more than two standard deviations, $A^{\text {Siv}}_{\text {PGF}}=-0.23\pm 0.08$, is reported in the SIDIS process based on the Monte Carlo simulation analysis. As stated before, it is expected that the Sivers function has a different sign in the DY and the SIDIS process which comes from the gauge link. The Sivers function in SIDIS has been extracted by COMPASS [76, 77], HERMES [26] and JLab [28] Collaborations. However, information about the DY Sivers function has not been explored, since the polarized DY process has never been measured. Only very recently data became available in the DY process $pp^\uparrow \rightarrow W^{\pm }/Z+X$ [78]. Anselmino et al. [67] have for the first time attempted to study the nonuniversality signature, i.e. the sign change of the Sivers function. However, they could not draw a definite conclusion about it, due to poor data, although data for $W^-$ production seem to favor the sign change.

The $\cos 2\phi$ asymmetry is shown in Figs. 7, 8, 9 and 10 as a function of $x_\mathrm{B}$ and $P_{hT}$ for $r=1/3$ and $r=2/3$. To obtain the $\cos 2\phi$ asymmetry the Gaussian parameterizations for the unpolarized and linearly polarized gluon distribution functions are used, as defined in Eqs. (21) and (51). Until today experimental investigation to extract the unknown Boer–Mulders function, $h^{\perp g}_1$, has not been done. In Refs. [45, 46] the effect of $h^{\perp g}_1$ on the unpolarized differential cross section of the $J/\psi$ production in the pp collision is explored. The $J/\psi$ production in the unpolarized ep collision process is also a reliable channel to probe the $h^{\perp g}_1$ by measuring the $\cos 2\phi$ asymmetry. It is obvious from Eq. (48) that the negative $\cos 2\phi$ asymmetry as a function of $x_\mathrm{B}$ and $P_{hT}$ is obtained due to the dominant contribution of the $^{1}{S}{_0}$ state compared to the other states ($^{3}{P}{_0}$, $^{3}{P}{_1}$ and $^{3}{P}{_2}$). The $\cos 2\phi$ asymmetry as a function of $P_{hT}$ is almost the same for all the experiments. However, the maximum value of $<\cos 2\phi>$ decreases with $\sqrt{s}$. The maximum of $26\%$ $\cos 2\phi$ asymmetry as a function of $x_\mathrm{B}$ is observed at the EIC experiment.

Fig. 8

$\cos 2\phi$ asymmetry in $e+p\rightarrow e+J/\psi +X$ process as function of a $x_\mathrm{B}$ (left panel) and b $P_{hT}$ (right panel) at $\sqrt{s}=17.2$ GeV (COMPASS). The integration ranges are $0<P_{hT}<1.0$ GeV, $0.1<y<0.9$ and $0.0001<x_\mathrm{B}<0.65$

Fig. 9

$\cos 2\phi$ asymmetry in $e+p\rightarrow e+J/\psi +X$ process as function of a $x_\mathrm{B}$ (left panel) and b $P_{hT}$ (right panel) at $\sqrt{s}=7.2$ GeV (HERMES). The integration ranges are $0<P_{hT}<1.0$ GeV, $0.35<y<0.95$ and $0.023<x_\mathrm{B}<0.40$

Fig. 10

$\cos 2\phi$ asymmetry in $e+p\rightarrow e+J/\psi +X$ process as function of a $x_\mathrm{B}$ (left panel) and b $P_{hT}$ (right panel) at $\sqrt{s}=4.7$ GeV (JLab). The integration ranges are $0<P_{hT}<0.64$ GeV, $0.7<y<0.9$ and $0.0001<x_\mathrm{B}<0.35$

6 Conclusion

We have calculated the Sivers and the $\cos 2\phi$ asymmetries in the production of the $J/\psi$ in polarized and the unpolarized ep collision, respectively. The $J/\psi$ production process gives direct access to the gluon Sivers function at leading order through the channel $\gamma ^*g \rightarrow c \bar{c}$. The NRQCD-based color octet model and a formalism based on the TMD factorization have been used. A sizable negative Sivers asymmetry is observed in the $J/\psi$ production. The estimated SSA at $z=1$ is compared with the COMPASS data and is in considerable agreement. Also the effect of the TMD evolution on the Sivers asymmetry has been investigated. Moreover, the sizable $\cos 2\phi$ asymmetry is obtained in the unpolarized SIDIS process which allows one to probe the Boer–Mulders function, $h^{\perp g}_1$. Thus the asymmetries in the polarized and the unpolarized SIDIS processes are important observables that give valuable information on the gluon Sivers function and the linearly polarized gluon TMD, respectively. Further work would involve taking into account higher order corrections to the asymmetry. In this case the charmonium production mechanism is likely to play an important role.

Appendix: LO amplitude of \(\gamma ^{*}g\rightarrow J/\psi \)

From Refs. [73, 79] the amplitude of the quarkonium bound state can be written

$$\begin{aligned}&\mathcal {M}^{\mu \nu }\left( \gamma ^{*}g \rightarrow Q\bar{Q}[^{2S+1}{L}{_J}^{(1,8a)}]\right) \nonumber \\&\quad =\sum _{L_zS_z} \int \frac{d^3{\varvec{k}}^{\prime }}{(2\pi )^3}\Psi _{LL_z}({\varvec{k}}^\prime ) \langle LL_z;SS_z|JJ_z\rangle \mathrm {Tr}[O^{\mu \nu }(q,k,P_h,k^\prime )\nonumber \\&\quad \times \,\mathcal {P}_{SS_z}(P_h,k^\prime )], \end{aligned}$$

(A.53)

where $k^\prime$ is the relative momentum of the heavy quark in the quarkonium rest frame. The eigenfunction of the orbital angular momentum L is $\Psi _{LL_z}({\varvec{k}}^\prime )$. A similar calculation as reported in [73] is followed. Only the important steps are presented here. For more details Ref. [73] is preferred. From Fig. 11, the amplitude of the heavy quark pair is given by

(A.54)

Fig. 11

Feynman diagrams for $\gamma ^{*}+g\rightarrow J/\psi$ process

The sum over the SU(3) Clebsch–Gordan coefficients project out the color state of the $Q\bar{Q}$ pair; either it is in a color singlet or in a octet state, and they are defined by $\langle 3i;\bar{3}j|1\rangle =\frac{\delta ^{ij}}{\sqrt{N_c}}, \langle 3i;\bar{3}j|8a\rangle =\sqrt{2}(T^a)^{ij}$ for color singlet and color octet states, respectively. $T^b$ is the SU(3) Gell-Mann matrix. The charm quark and quarkonium bound state masses are denoted $m_\mathrm{c}$ and $M=2m_\mathrm{c}$, respectively. The excluded external legs in Eq. (A.54) are absorbed in the spin projection operator, which is given by

(A.55)

with $\Pi _{SS_z}=\gamma ^{5}$ for the singlet ($S=0$) state and for the triplet ($S=1$) state. Here the spin polarization vector of the $Q\bar{Q}$ system is denoted $\varepsilon _{s_z}(P_h)$. The Taylor expansion around ${\varvec{k}}^\prime =0$ in Eq. (A.53) gives the S-wave and P-wave amplitudes. The first term in the expansion is the S-wave amplitude is

(A.56)

and we have

(A.57)

The derivative term in the expansion of Eq. (A.53) is the P-wave amplitude,

(A.58)

(A.59)

and

(A.60)

The definitions of $O^{\mu \nu }(0)$ and $O^{\mu \nu \alpha }(0)$ are obtained from Eq. (A.54); they are given by

(A.61)

(A.62)

Here $R_0(0)$ and $R_1^\prime (0)$ are the radial wave function and its derivative at the origin. They have the following relation with LDME [80]:

$$\begin{aligned} \langle 0\vert \mathcal {O}_8^{J/\psi }(^1{S}{_J})\vert 0\rangle= & {} \frac{2}{\pi }(2J+1)|R_0(0)|^2, \end{aligned}$$

(A.63)

$$\begin{aligned} \langle 0\vert \mathcal {O}_8^{J/\psi }(^3{P}{_J})\vert 0\rangle= & {} \frac{2N_c}{\pi }(2J+1)|R^\prime _1(0)|^2. \end{aligned}$$

(A.64)

After taking the trace one obtains the following amplitude expressions for the S-wave and the P-wave states:

$$\begin{aligned} \mathcal {M}^{\mu \nu }\left[ ^{1}{S}{_0}^{(8a)}\right]= & {} 2i\frac{\sqrt{2}g_s(ee_c)\delta ^{ab}}{\sqrt{\pi M}(Q^2+M^2)}R_0(0) \epsilon ^{\mu \nu \rho \sigma }k_{\rho }P_{h\sigma }, \end{aligned}$$

(A.65)

$$\begin{aligned} \mathcal {M}^{\mu \nu }\left[ ^{3}{S}{_1}^{(8a)}\right]= & {} \frac{\sqrt{2}g_s(ee_c)\delta ^{ab}}{\sqrt{\pi M}(Q^2+M^2)}R_0(0) 4Mg^{\mu \nu }P_h^\beta \varepsilon _{s_z\beta }(P_h) \nonumber \\= & {} 0, \end{aligned}$$

(A.66)

$$\begin{aligned} \mathcal {M}^{\mu \nu }\left[ ^{3}{P}{_0}^{(8a)}\right]= & {} 2i\frac{\sqrt{2}g_s(ee_c) \delta ^{ab}}{\sqrt{\pi M^3}} R^\prime _1(0)\frac{3M^2+Q^2}{M^2+Q^2}\Big [ g^{\mu \nu } \nonumber \\&-2\frac{k^\nu P^\mu _h}{M^2+Q^2}\Big ], \end{aligned}$$

(A.67)

$$\begin{aligned} \mathcal {M}^{\mu \nu }\left[ ^{3}{P}{_1}^{(8a)}\right]= & {} \sqrt{\frac{3}{8\pi M}}\frac{\sqrt{2}g_s(ee_c)\delta ^{ab}}{Q^2+M^2} R^\prime _1(0)\epsilon _{\rho \sigma \alpha \beta }\frac{P_h^\rho }{M} \varepsilon ^\sigma _{J_z}(P_h) \nonumber \\&\times \frac{4}{M}\Bigg \{g^{\mu \beta }\Big ((M^2-Q^2)\nonumber \\&\times g^{\nu \alpha }+2k^{\alpha }P_h^\nu \Big ) +g^{\nu \beta }\left( (M^2+Q^2)g^{\mu \alpha } \right. \nonumber \\&\left. -2k^{\alpha }P_h^\mu \right) -2g^{\mu \alpha }k^\beta P_h^{\nu }\nonumber \\&-\frac{2k^\beta }{M^2+Q^2}\left( 2M^2g^{\mu \nu } k^\alpha -2M^2g^{\mu \alpha }k^\nu \right. \nonumber \\&\left. +(M^2-Q^2)g^{\nu \alpha }P_h^\mu \right) \Bigg \}, \end{aligned}$$

(A.68)

$$\begin{aligned} \mathcal {M}^{\mu \nu }\left[ ^{3}{P}{_2}^{(8a)}\right]= & {} 2i\sqrt{\frac{3}{\pi M}} \frac{\sqrt{2}g_s(ee_c)\delta ^{ab}M}{(Q^2+M^2)} R^\prime _1(0)\varepsilon _{J_z\alpha \beta }(P_h) \nonumber \\&\times \Big [g^{\alpha \nu }g^{\beta \mu }+g^{\alpha \mu }g^{\beta \nu } \nonumber \\&-\frac{4k^\alpha }{Q^2+M^2}\left( k^\beta g^{\mu \nu } -k^\nu g^{\beta \mu }+P_h^\mu g^{\beta \nu }\right) \Big ].\nonumber \\ \end{aligned}$$

(A.69)