Resonances in positron scattering on a supercritical nucleus and spontaneous production of $e^{+}e^{-}$ pairs

Abstract

We re-examine the physics of supercritical nuclei, specially focusing on the scattering phase $\delta _{\varkappa }$ and its dependence on the energy $\varepsilon$ of the diving electronic level, for which we give both exact and approximate formulas. The Coulomb potential $Z\alpha /r$ is rounded to the constant $Z\alpha /R$ for $r < R$. We confirm the resonant behavior of $\delta _{\varkappa }$ that we investigate in detail. In addition to solving the Dirac equation for an electron, we solve it for a positron, in the field of the same nucleus. This clarifies the interpretation of the resonances. Our results are compared with claims made in previous works.

1 Introduction

The Coulomb problem for a nucleus with charge $Z>Z_\mathrm{cr}$ was recently analyzed [1] by solving the Dirac equation for an electron in the external field of this nucleus. Because of the specificity of the Dirac equation that accounts simultaneously for electrons and positrons this problem gets connected to the scattering of positrons (holes in the Dirac sea) on the nucleus (see below). The behavior of the scattering amplitude was found to be very peculiar: it contains resonances and their energies, obtained from an analytical formula found in [1],

$$\begin{aligned} \varepsilon = -\xi + \frac{i}{2} \gamma , \; \xi> m, \; \gamma > 0, \end{aligned}$$

(1)

correspond to poles of the S matrix located above the left cut, on the second (unphysical) sheet of the energy plane. The resonances in positron scattering were discussed in Refs. [2, 3].

At $Z<Z_\mathrm{cr}$, the width $\gamma$ vanishes, and this equation describes the usual bound states of electrons in the Coulomb field of the nucleus.

When $Z>Z_\mathrm{cr}$, $\gamma \ne 0$ makes these states quasistationary [4, 5].

For electrons, as Z increases, the transition from bound states to resonant states corresponds to the diving of the bound states, which start at $\varepsilon =+\,m$, downwards into the lower continuum.

In the present paper, in order to clarify the situation, we will also study “the Dirac equation for positron”. By this we mean here the standard Dirac equation with the substitution of the electron charge e by $-\,e$.

Now, as Z increases, bound states increase from $\varepsilon =-\,m$ and become resonant in the upper continuum.

For $Z<Z_\mathrm{{cr}}$, the interpretation of these bound states (also noted in [6] Chapt. 4.3) is the following. For obvious reasons they cannot be $(e^{+}N^{+})$ bound states, but are just our previous $(e^{-}N^{+})$ bound states. There is no more information in there.¹

For $Z>Z_\mathrm{cr}$, we find that $(e^{+}N^{+})$ resonances occur at the energies

$$\begin{aligned} \varepsilon _\mathrm{p} = \xi - \frac{i}{2} \gamma , \; \xi> m, \; \gamma > 0, \end{aligned}$$

(2)

which now correspond to poles of the S matrix below the right cut of the energy plane, also, as it should be, on the second, unphysical, sheet. This result confirms the proposal made in [1] that the sign of the energy in (1) should be reversed.

This change of sign we are accustomed to when dealing with holes in the lower continuum: the absence of an electron with energy $-\,\varepsilon$ is then interpreted as the presence of a positron with energy $\varepsilon$. It is now to be operated on the empty states of the energy levels that dive into the lower continuum. Our consideration of the Dirac equation for positrons therefore helps to clarify the nature and position of the resonances.

No physical interpretation for them was suggested in [1]. It was only claimed that spontaneous $e^{+}e^{-}$ pair production by naked nuclei at $Z>Z_\mathrm{{cr}}$, as discussed in [2, 3, 6,7,8,9,10,11,12,13,14,15,16,17,18,19,20], does not occur.

We, however, do not see any sensible objection to the occurrence of this process: an empty state diving into the lower continuum gets filled by one electron of the Dirac sea; the resulting hole in the sea is the positron that gets ejected by the nucleus the charge of which has become $Z-1$. The characteristic time of this emission process is $1/\gamma$, in agreement with the results obtained in [2, 3, 6,7,8,9,10,11,12,13,14,15,16,17,18,19,20].

Furthermore, spontaneous production of $e^+e^-$ pairs was recently observed in the numerical solution of the Dirac equation in the case of heavy ion collisions [21, 22].

The plan of the paper is as follows. In Sect. 2, following [1] and using the Dirac equation, we study the scattering of states of the lower continuum on a supercritical nucleus. In addition to reproducing the approximate results obtained in [1] we get explicit results without using an expansion over the parameter $m\times R$, where R is the nucleus radius. Such an expansion, being good for electrons, does not work for heavy particles, for example, muons [4, 5]. In Sect. 3, we use instead the Dirac equation for positrons (see above) and study the scattering of states of its upper continuum on a supercritical nucleus. We conclude in Sect. 4.

2 Lower continuum wave functions and scattering phases in the Coulomb field of a supercritical nucleus

The radial functions of the Dirac equation $F(r) \equiv rf(r)$ and $G(r) \equiv rg (r)$ are determined by the following differential equations [23,24,25]:

$$\begin{aligned} \left\{ \begin{aligned}&\frac{\mathrm{d}F}{\mathrm{d}r} + \frac{\varkappa }{r}F - (\varepsilon + m - V(r))G = 0,\\&\frac{\mathrm{d}G}{\mathrm{d}r} - \frac{\varkappa }{r}G + (\varepsilon - m - V(r))F = 0, \end{aligned} \right. \end{aligned}$$

(3)

where $\varkappa = -(j+1/2) = -1, -2,\ldots$ for $j = l + 1/2$ and $\varkappa = (j +1/2)= 1,2,3\ldots$ for $j = l-1/2$ and the ground state corresponds to $\varkappa = -1$ (let us note that in [1] the Dirac equation with the substitution $F\Rightarrow -F$ is used).

In order to deal with the case $Z\alpha >1$ the Coulomb potential should be regularised at $r=0$ [26]. To do this we shall approximate the nucleus as a homogeneous charged sphere with radius R (the so-called rectangular cutoff). Thus, the potential in which the Dirac equation should be solved looks like:

At small distances $r< R$, substituting Eq. (4a) into (3), we obtain the Dirac equation with a constant potential, the solution of which is expressed through Bessel functions. In order to obtain finite f and g at $r=0$ among the two sets of solutions the one with a positive index of the Bessel function should be selected²:

$$\begin{aligned} \left( \begin{array}{l} {F} \\ {G}\\ \end{array}\right) = {\mathrm{const}}\cdot \sqrt{\beta r}\cdot \left( \begin{array}{l} {\mp } J_{{\mp }(1/2 + \varkappa )} (\beta r)\\ J_{{\pm }(1/2 - \varkappa )} (\beta r) \frac{\beta }{\varepsilon +m+\frac{Z\alpha }{R}} \end{array} \right) ,\; r < R, \end{aligned}$$

(5)

where $\beta = \sqrt{(\varepsilon + Z\alpha /R)^2 - m^2}$. The upper (lower) signs should be taken for $\varkappa < 0$ ($\varkappa > 0$).

For $r>R$, we need the solution of the Dirac equation for the Coulomb potential. We introduce the standard quantity $\lambda$ which, for $-m< \varepsilon < m$, equals $\lambda = \sqrt{(m-\varepsilon )(m+\varepsilon )} \equiv -ik$, where k is the electron momentum. Here we have to make an important remark. Since later we are going to look for resonances in the complex $\varepsilon$ plane, we must carefully define the square roots used here. Each of them, $\sqrt{m-\varepsilon }$ and $\sqrt{m+\varepsilon }$, are defined on two Riemann sheets of the complex $\varepsilon$ plane. To avoid ambiguous expressions let us introduce a uniquely defined function $\mathrm{sqrt(z)}$ as follows:

$$\begin{aligned} \mathrm{{sqrt}} (|z|e^{i\mathrm{{Arg}}(z)})=\sqrt{|z|}e^{i\mathrm{{Arg}}(z)/2},\text { for } \mathrm{{Arg}}(z)\in (-\pi ;\pi ]. \end{aligned}$$

(6)

For example

$$\begin{aligned} \mathrm{sqrt}\left( z\right) = {\left\{ \begin{array}{ll} i&{} \text {for }z=-1+i\cdot 0,\\ i&{} \text {for }z=-1,\\ -i&{} \text {for }z=-1-i\cdot 0. \end{array}\right. } \end{aligned}$$

(7)

It is therefore the first branch of the function $\sqrt{z}$ with the cut $(-\infty ;0)$. The second branch is given by $-\mathrm{sqrt}(z)$. This definition is also very convenient because the square root is defined in this way in many numerical tools for computers.

Switching branches of both square roots, $\sqrt{m-\varepsilon }$ and $\sqrt{m+\varepsilon }$, leads to the same value of $\lambda$. Therefore, $\lambda$ is defined on the two Riemann sheets according to

$$\begin{aligned} \lambda = {\left\{ \begin{array}{ll} \mathrm{sqrt} (m-\varepsilon )\cdot \mathrm{sqrt} (m+\varepsilon )&{} \text {on the physical sheet,}\\ -\mathrm{sqrt} (m-\varepsilon )\cdot \mathrm{sqrt} (m+\varepsilon )&{} \text {on the unphysical sheet,} \end{array}\right. } \end{aligned}$$

(8)

with two cuts originating, respectively, from each of the square roots (see Fig. 1).³ From general arguments of scattering theory, we know that electron bound states are located at real $\varepsilon$ in the interval $-m< \varepsilon < m$. Unbound electron states are located above the right cut and unbound positron states below the left cut.

Fig. 1

The plane of complex energy $\varepsilon$

In what follows we shall use the following conventions for the “” symbol:

$$\begin{aligned} \sqrt{m+\varepsilon }&= {\left\{ \begin{array}{ll} \mathrm{sqrt}(m+\varepsilon )&{}\text {on the physical sheet,}\\ -\mathrm{sqrt}(m+\varepsilon )&{}\text {on the unphysical sheet,} \end{array}\right. } \end{aligned}$$

(9)

$$\begin{aligned} \sqrt{m-\varepsilon }&=\mathrm{sqrt} (m-\varepsilon )\,\,\text { on both sheets.} \end{aligned}$$

(10)

It does not matter which root changes sign when we go to the second sheet since we can always also change the signs of both.

We are looking for solution written in the standard form [25]⁴:

$$\begin{aligned} \left( \begin{array}{c} F \\ G \end{array} \right) = \left( \begin{array}{c} \sqrt{m+\varepsilon } \\ -\sqrt{m-\varepsilon } \end{array} \right) \mathrm{exp} (-\rho /2)\rho ^{i\tau } \left( \begin{array}{c} Q_1 + Q_2 \\ Q_1 - Q_2 \end{array} \right) , \end{aligned}$$

(11)

where $\tau =\sqrt{(Z\alpha )^{2}-\varkappa ^{2}}$, $\rho = 2\lambda r = -2ikr$, $Q_1$ and $Q_2$ are determined by differential equations, the solutions of which are Kummer confluent hypergeometric functions $_1F_1(\alpha ,\beta ,z)$ (also sometimes noted $F(\alpha ,\gamma ,z)$ like in [25]). In textbooks dealing with the case $Z \alpha <1$, $R=0$, only solutions regular at $r=0$ are considered. We must instead here take into account both type of solutions of the equations for $Q_1$ and $Q_2$. The formulas for the $Q_i$ are derived in Appendix A. From (A6) to (A8) we get

$$\begin{aligned} \left\{ \begin{aligned}&Q_1 = C\cdot \frac{-\frac{iZ\alpha m}{k}+\varkappa }{-i\tau +\frac{iZ\alpha \varepsilon }{k}} \cdot {_1F_{1}}\left( i\tau -\frac{iZ\alpha \varepsilon }{k},2i\tau +1,\rho \right) \\&+D\cdot \frac{-\frac{iZ\alpha m}{k} +\varkappa }{i\tau +\frac{iZ\alpha \varepsilon }{k}} \rho ^{-2i\tau }{_{1}F_{1}}\left( -i\tau - \frac{iZ\alpha \varepsilon }{k}, -2i\tau +1, \rho \right) ,\\&Q_2 = C\cdot {_{1}F_{1}}\left( 1+i\tau - \frac{iZ\alpha \varepsilon }{k}, 2i\tau +1, \rho \right) \\&+ \, D\rho ^{-2i\tau }{_{1}F_{1}}\left( 1-i\tau - \frac{iZ\alpha \varepsilon }{k}, -2i\tau +1, \rho \right) , \end{aligned}\right. \end{aligned}$$

(12)

where C and D are arbitrary coefficients.⁵

The scattering phase $\delta _{\varkappa }(\varepsilon ,Z)$ is determined by investigating the behavior of the wave function at large r. To this purpose, the asymptotic expansion of $_1F_1$ at large |z|

$$\begin{aligned} _{1}F_{1}(\alpha , \gamma , z)\Big |_{|z| \rightarrow \infty }= & {} \frac{\Gamma (\gamma )}{\Gamma (\gamma -\alpha )}(-z)^{-\alpha } [1+ O(1/z)] \nonumber \\&+ \frac{\Gamma (\gamma )}{\Gamma (\alpha )} e^z z^{\alpha -\gamma } [1+O(1/z)] \end{aligned}$$

(13)

is very useful.

Using the asymptotic expansion (13) for the Kummer functions occurring in (12) gives

$$\begin{aligned} \left. \left( \begin{array}{l} F \\ G \end{array} \right) \right| _{r\rightarrow \infty }&= A\cdot \left( \begin{array}{c} \sqrt{m+\varepsilon } \\ -\sqrt{m-\varepsilon } \end{array} \right) \end{aligned}$$

(14)

$$\begin{aligned}&\quad \times \left( C \left[ e^{-\frac{\rho }{2}}\frac{\Gamma \left( 2i\tau +1\right) }{\Gamma \left( 1+i\tau +\frac{iZ\alpha \varepsilon }{k}\right) } \frac{\frac{iZ\alpha m}{k}-\varkappa }{i\tau -\frac{iZ\alpha \varepsilon }{k}} \rho ^{i\tau }\right. \right. \nonumber \\ {}&\quad \times \left. \left. \left( -\rho \right) ^{-i\tau } \left( -\rho \right) ^{\frac{iZ\alpha \varepsilon }{k}} \pm e^{\frac{\rho }{2}}\frac{\Gamma \left( 2i\tau +1\right) }{\Gamma \left( 1+i\tau -\frac{iZ\alpha \varepsilon }{k}\right) } \rho ^{-\frac{iZ\alpha \varepsilon }{k}} \right] \right. \end{aligned}$$

(15)

$$\begin{aligned}&\quad \left. +D \left[ e^{-\frac{\rho }{2}}\frac{\Gamma \left( -2i\tau +1\right) }{\Gamma \left( 1-i\tau +\frac{iZ\alpha \varepsilon }{k}\right) } \frac{\frac{iZ\alpha m}{k}-\varkappa }{-i\tau -\frac{iZ\alpha \varepsilon }{k}} \rho ^{-i\tau }\left( -\rho \right) ^{i\tau }\right. \right. \nonumber \\ {}&\quad \times \left. \left. (-\rho )^{\frac{iZ\alpha \varepsilon }{k}} \pm e^{\frac{\rho }{2}}\frac{\Gamma \left( -2i\tau +1\right) }{\Gamma \left( 1-i\tau -\frac{iZ\alpha \varepsilon }{k}\right) } \rho ^{-\frac{iZ\alpha \varepsilon }{k}} \right] \right) , \end{aligned}$$

(16)

where the upper sign corresponds to F and the lower sign corresponds to G.

The ratio

$$\begin{aligned} \frac{\left( -\rho \right) ^{\frac{iZ\alpha \varepsilon }{k}}}{\rho ^{-\frac{iZ\alpha \varepsilon }{k}}} \end{aligned}$$

(17)

yields the Coulomb logarithm (for real $\varepsilon$ below the left cut it gives $\exp \left[ \frac{2iZ\alpha \varepsilon }{k}\ln \left( 2kr\right) \right]$). Since the latter does not contribute to the differential scattering cross section at nonzero angle $\theta$, we will omit this term in our further calculations.

From the general formula

$$\begin{aligned} \left. \left( \begin{array}{c} F \\ G \end{array} \right) \right| _{r\rightarrow \infty }&\propto \left( \begin{array}{c} \sqrt{m+\varepsilon } \\ -\sqrt{m-\varepsilon } \end{array} \right) \nonumber \\&\times \quad \{e^{i(kr+\frac{Z\alpha \varepsilon }{k}\ln (2kr))} e^{2i\delta } \pm e^{-i(kr+\frac{Z\alpha \varepsilon }{k}\ln (2kr))}\} \end{aligned}$$

(18)

it follows that the ratio of the remaining coefficients define the scattering phase $\delta _{\varkappa }$ (on the real axis below the left cut $e^{-\rho /2}\equiv e^{ikr}$ corresponds to the outgoing wave and $e^{\rho /2}\equiv e^{-ikr}$ corresponds to the incoming wave):

$$\begin{aligned} e^{2i\delta _{\varkappa }}&=-\frac{1}{\varkappa +\frac{iZ\alpha m}{k}}\nonumber \\&\quad \cdot \frac{\frac{C}{D}\cdot \frac{\Gamma (2i\tau )}{\Gamma \left( i\tau +\frac{iZ\alpha \varepsilon }{k}\right) } \rho ^{i\tau }(-\rho )^{-i\tau } - \frac{\Gamma (-2i\tau )}{\Gamma \left( -i\tau +\frac{iZ\alpha \varepsilon }{k}\right) } \rho ^{-i\tau }(-\rho )^{i\tau }}{\frac{C}{D}\cdot \frac{\Gamma (2i\tau )}{\Gamma \left( 1+i\tau -\frac{iZ\alpha \varepsilon }{k}\right) } - \frac{\Gamma (-2i\tau )}{\Gamma \left( 1-i\tau -\frac{iZ\alpha \varepsilon }{k}\right) }}, \end{aligned}$$

(19)

where

$$\begin{aligned} \rho ^{i\tau }\left( -\rho \right) ^{-i\tau }&= \exp \left[ i\tau \ln \left( \rho \right) -i\tau \ln \left( -\rho \right) \right] \nonumber \\&=\exp \left[ -\tau \left( \mathrm{Arg}\left[ \rho \right] -\mathrm{Arg}\left[ -\rho \right] \right) \right] \nonumber \\&=e^{-\pi \tau \cdot \mathrm{sign}\left[ \mathrm{Arg}\left[ \rho \right] \right] }. \end{aligned}$$

(20)

The resonance of the scattering amplitude corresponds to the pole of the S-matrix element $S\equiv e^{2i\delta }$ and from (19) we immediately get an equation for the position of this pole in the $\varepsilon$-plane:

$$\begin{aligned} \frac{C}{D}\cdot \frac{\Gamma (2i\tau )}{\Gamma \left( 1+i\tau -\frac{iZ\alpha \varepsilon }{k}\right) } - \frac{\Gamma (-2i\tau )}{\Gamma \left( 1-i\tau -\frac{iZ\alpha \varepsilon }{k}\right) }=0. \end{aligned}$$

(21)

In what follows we will match the solutions at $r<R$ and $r>R$ to obtain the ratio C / D, such that we can calculate the phase $\delta _{\varkappa }$ and find the poles of the S matrix which correspond to the energy levels. This procedure can be performed both exactly and approximately.

2.1 Exact results

With the help of the exact formulas (5), (11), and (12) we get the ratio C / D from matching F / G at $r=R+0$ and $r=R-0$:

$$\begin{aligned} \frac{C}{D}= -\rho _{0}^{-2i\tau }\cdot \frac{F_{g}^{-}-MF_{f}^{-}}{F_{g}^{+}-MF_{f}^{+}}, \end{aligned}$$

(22)

where

$$\begin{aligned} M&=\pm \frac{\sqrt{m+\varepsilon }}{\sqrt{m-\varepsilon }} \cdot \frac{J_{\pm \left( 1/2-\varkappa \right) }(\beta R)}{J_{\mp \left( 1/2+\varkappa \right) }(\beta R)} \cdot \frac{\beta }{\varepsilon +m+\frac{Z\alpha }{R}}, \end{aligned}$$

(23)

$$\begin{aligned} F_{f}^{\pm }&= {_{1}F_{1}} (\alpha _{1}^{\pm },\gamma ^{\pm },\rho _{0}) \frac{\frac{iZ\alpha m}{k}-\varkappa }{\alpha _{1}^{\pm }} +{_{1}F_{1}} (\alpha _{2}^{\pm },\gamma ^{\pm },\rho _{0}), \end{aligned}$$

(24)

$$\begin{aligned} F_{g}^{\pm }&= {_{1}F_{1}} (\alpha _{1}^{\pm },\gamma ^{\pm },\rho _{0}) \frac{\frac{iZ\alpha m}{k}-\varkappa }{\alpha _{1}^{\pm }} -{_{1}F_{1}} (\alpha _{2}^{\pm },\gamma ^{\pm },\rho _{0}), \end{aligned}$$

(25)

and

$$\begin{aligned} \alpha _{1}^{\pm }= & {} \pm i\tau -\frac{iZ\alpha \varepsilon }{k},\nonumber \\ \alpha _{2}^{\pm }= & {} 1\pm i\tau -\frac{iZ\alpha \varepsilon }{k}, \gamma ^{\pm }=\pm 2i\tau +1, \rho _{0}=-2ikR. \end{aligned}$$

(26)

The numerical evaluation of the square roots in (23) and of k in (26) for real $\varepsilon$ is somewhat tricky since one should carefully choose the side of the cut to use. Due to the definition (6)–(7) of the $\mathrm{sqrt}()$ function the expression $\mathrm{sqrt}\left( m+\varepsilon \right)$ gives, for real $\varepsilon$, the values above the cut such that $-\mathrm{sqrt}\left( m+\varepsilon \right)$ should be used. It corresponds formally to calculating the scattering phase on the second (unphysical) sheet. The same holds for k. For any real $\varepsilon$ it is also possible to use $k=\mathrm{sqrt}\left( \varepsilon ^{2}-m^{2}\right)$, which chooses the correct side of the cut; then $\sqrt{m+\varepsilon }/\sqrt{m-\varepsilon }=-ik/\left( m-\varepsilon \right)$.

With the help of (22) we can calculate the scattering phase $\delta _{\varkappa }$ defined by (19).

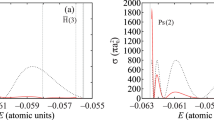
In the domain $\varepsilon <-m$, $\delta _{\varkappa }(\varepsilon ,Z)$ gives the scattering phase of a positron with energy $\varepsilon _\mathrm{p}=-\varepsilon >m$ on the nucleus (for real $\varepsilon <-m$ we get $\mathrm{Arg}\left[ \rho \right] <0$). Its dependence on $\varepsilon _\mathrm{p}$ for $\varkappa = -1$ and $Z = 232$ is shown in Fig. 2 (compare with Fig. 3 of [1]). The scattering phase $\delta _{\varkappa }$ exhibits a resonance behavior; it goes through $\pi /2$ at $\varepsilon _\mathrm{p}/m\approx 5.06$.

We obtain the equation for the position of the poles by substituting (22) into (21)

$$\begin{aligned} \frac{\Gamma \left( -2i\tau \right) }{\Gamma \left( 2i\tau \right) }\cdot \frac{\Gamma \left( 1+i\tau -\frac{iZ\alpha \varepsilon }{k}\right) }{\Gamma \left( 1-i\tau -\frac{iZ\alpha \varepsilon }{k}\right) }= -\rho _{0}^{-2i\tau }\cdot \frac{F_{g}^{-}-MF_{f}^{-}}{F_{g}^{+}-MF_{f}^{+}}. \end{aligned}$$

(27)

The solutions of (27) can be found by scanning the complex $\varepsilon$ plane. This is the method that we used to find the exact positions⁶ of the S-matrix poles (see Fig. 3 and Table 1). The energies $\varepsilon$ of the quasistationary states are located above the left cut on the second sheet of the complex $\varepsilon$ plane⁷:

$$\begin{aligned} \varepsilon = -\xi + \frac{i}{2}\gamma ,~\xi>m,~\gamma >0. \end{aligned}$$

(28)

Fig. 2

Dependence on $\varepsilon _\mathrm{p}$ of the scattering phase $\delta _{-1}(\varepsilon _\mathrm{p}, 232)$ ($Z=232$ and $\varkappa =-1$) for a nucleus with radius $R=0.031/m$. The blue solid line corresponds to the exact phase, the green dashed line corresponds to the approximate one

2.2 Approximate results

In [1] the approximation $1/R\gg \varepsilon ,m$ was used. In this section we are going to reproduce their results and compare them to the exact ones.

Being interested in the case $Z\alpha \gtrsim 1$ and taking into account the smallness of the nucleus radius in comparison with the electron Compton wavelength 1 / m we obtain $\beta \approx Z\alpha /R$ in (5).

The solution of the system (3) at $r > R$ should match (5) at $r=R$, in particular the ratio F / G of both solutions at $r=R$ should coincide. Substituting (4b) in (3) at $r\rightarrow 0$ we easily get

$$\begin{aligned} \left. \left( \begin{array}{l} F \\ G \end{array}\right) \right| _{r \rightarrow 0} = \eta _\sigma r^\sigma \left( \begin{array}{c} -1 \\ \frac{Z\alpha }{\sigma - \varkappa } \end{array} \right) + \eta _{-\sigma } r^{-\sigma } \left( \begin{array}{c} -1 \\ \frac{Z\alpha }{-\sigma - \varkappa } \end{array} \right) , \end{aligned}$$

(29)

where $\sigma = \sqrt{\varkappa ^2 - Z^2\alpha ^2}$ and $\eta _\sigma$ and $\eta _{-\sigma }$ are arbitrary constants. Matching the ratios F / G from (29) and (5) at $r=R$ we obtain

$$\begin{aligned} \frac{\eta _\sigma }{\eta _{-\sigma }}= & {} \frac{\sigma -\varkappa }{\sigma +\varkappa }\nonumber \\&\cdot \frac{Z\alpha J_{\mp (1/2 +\varkappa )}(Z\alpha ) \pm (\sigma + \varkappa )J_{\pm (1/2 -\varkappa )}(Z\alpha )}{Z\alpha J_{\mp (1/2 +\varkappa )}(Z\alpha ) \mp (\sigma - \varkappa ) J_{\pm (1/2 -\varkappa )}(Z\alpha )}\nonumber \\&\cdot \frac{R^{-\sigma }}{R^\sigma }=\tan \theta , \end{aligned}$$

(30)

which coincides with Eq. (13) from [1]. In the case $Z\alpha > |\varkappa |$ one should substitute $\sigma$ by $i\tau$ (where, as before, $\tau = \sqrt{Z^2\alpha ^2 - \varkappa ^2}$):

$$\begin{aligned} \frac{\eta _\tau }{\eta _{-\tau }}= & {} \frac{i\tau -\varkappa }{i\tau +\varkappa }\nonumber \\&\cdot \frac{Z\alpha J_{\mp (1/2 +\varkappa )}(Z\alpha ) \pm (i\tau + \varkappa ) J_{\pm (1/2 -\varkappa )}(Z\alpha )}{Z\alpha J_{\mp (1/2 +\varkappa )}(Z\alpha ) \mp (i\tau - \varkappa ) J_{\pm (1/2 -\varkappa )}(Z\alpha )} \nonumber \\&\cdot \frac{R^{-i\tau }}{R^{i\tau }}= e^{2i\theta }. \end{aligned}$$

(31)

The modulus of the r.h.s. of (31) can easily be checked to be unity, this is why we can rewrite it as an $\exp {\left( 2i\theta \right) }$ with real $\theta$.

The expansion of (11) at small $\rho$ contains terms $\sim \rho ^{i\tau }$ and $\rho ^{-i\tau }$. Comparing this expansion with (29) and substituting $\sigma \rightarrow i\tau$, $\eta _\sigma \rightarrow \eta _\tau$, $\eta _{-\sigma }\rightarrow \eta _{-\tau }$ yields

$$\begin{aligned} \eta _\tau= & {} C\cdot (-2ik)^{i\tau } \frac{i\tau - \varkappa + Z\alpha \sqrt{\frac{m-\varepsilon }{m+\varepsilon }}}{i\tau - \frac{iZ\alpha \varepsilon }{k}}, \nonumber \\ \eta _{-\tau }= & {} D\cdot (-2ik)^{-i\tau } \frac{-i\tau - \varkappa + Z\alpha \sqrt{\frac{m-\varepsilon }{m+\varepsilon }}}{-i\tau - \frac{iZ\alpha \varepsilon }{k}}. \end{aligned}$$

(32)

Getting an equation for C / D needs matching (31) with $\eta _{\tau }/\eta _{-\tau }$ obtained from (32):

$$\begin{aligned} \frac{C}{D}&=e^{2i\theta }\cdot \frac{(-2ik)^{-i\tau }}{(-2ik)^{i\tau }}\nonumber \\&\quad \cdot \frac{Z\alpha \sqrt{m-\varepsilon }+(-i\tau -\varkappa )\sqrt{m+\varepsilon }}{Z\alpha \sqrt{m-\varepsilon }+(i\tau -\varkappa )\sqrt{m+\varepsilon }}\nonumber \\&\quad \cdot \frac{i\tau -\frac{iZ\alpha \varepsilon }{k}}{-i\tau -\frac{iZ\alpha \varepsilon }{k}}. \end{aligned}$$

(33)

Two sets of approximations were made in deriving (33): (i) to get $\eta _\tau /\eta _{-\tau }$ at $r=R-0$ we replaced $\beta R$ with $Z \alpha$ and used (29) which was itself derived for $Z \alpha /r \gg \varepsilon ,m$; (ii) to get $\eta _\tau /\eta _{-\tau }$ at $r=R+0$ we expanded (11) and (12) at $\rho \ll 1$. For $m\cdot R = 0.031$ one cannot expect an accuracy better than 3% and, with growing $|\varepsilon |$ it can even get worse. The accuracy of the final result is not easy to guess from the start, and the best way is to compare it with the exact solution which was found in the previous section. Note that all results in [1] are based on the asymptotic behavior (29) and are therefore approximate by default.

Substituting (33) into (19) we obtain the approximate expression for the scattering phase $\delta _{\varkappa }$. Its dependence on $\varepsilon _\mathrm{p}\equiv -\varepsilon$ for $\varkappa = -1$ and $Z = 232$ is shown in Fig. 2 (compare with Fig. 3 of [1]). The scattering phase $\delta _{\varkappa }$ exhibits a resonance behavior; it goes through $\pi /2$ at $\varepsilon _\mathrm{p}/m\approx 4.88$.

Let us note that on the real axis of $\varepsilon$ the expression for the scattering phase $\delta _{\varkappa }$ can be written in the same form as in [1] (see Appendix B).

The positions of the S matrix poles are defined by the same equality (21) with C / D given by (33):

$$\begin{aligned} e^{2i\theta }&= \frac{(-2ik)^{i\tau }}{(-2ik)^{-i\tau }}\cdot \frac{\Gamma (-2i\tau )}{\Gamma (2i\tau )}\nonumber \\&\quad \cdot \frac{\Gamma \left( 1+i\tau -\frac{iZ\alpha \varepsilon }{k}\right) }{\Gamma \left( 1-i\tau -\frac{iZ\alpha \varepsilon }{k}\right) }\nonumber \\&\quad \cdot \frac{Z\alpha \sqrt{m-\varepsilon }+ (-i\tau +\varkappa )\sqrt{m+\varepsilon }}{Z\alpha \sqrt{m-\varepsilon }+(i\tau +\varkappa )\sqrt{m+\varepsilon }}, \end{aligned}$$

(34)

where the l.h.s. is defined by (31). The r.h.s. coincides with Eq. (26) from [1]. The exact expression (27) is, of course, more complicated, but, anyhow, special functions have to be evaluated numerically in both cases.

The accuracy of $\mathrm{Re}[\varepsilon ]$ obtained by the approximate procedure is quite reasonable (see Fig. 3 and Table 1); however, it is much worse for $\mathrm{Im}[\varepsilon ]$, for example $\approx 15\%$ at $Z=186$. This is why it is worth getting the exact values of the energies $\varepsilon$.

The question that we want to address now is the origin of the resonance and how it transforms for $Z < Z_\mathrm{cr}$.

At $Z < Z_\mathrm{cr}$ the resonances become bound states, the energies of which are determined by the same type of matching at $r=R$ as before (it is convenient to replace now, in (34), k by $i\lambda$, since on the real axis, for $-m<\varepsilon <+m$, $\lambda$ is real positive):

$$\begin{aligned} \mathrm{exp}(2i\theta )= & {} \frac{(2\lambda )^{i\tau }}{(2\lambda )^{-i\tau }}\cdot \frac{\Gamma (-2i\tau )}{\Gamma (2i\tau )}\cdot \frac{\Gamma (1+i\tau -\frac{Z\alpha \varepsilon }{\lambda })}{\Gamma (1-i\tau -\frac{Z\alpha \varepsilon }{\lambda })}\nonumber \\&\cdot \frac{Z\alpha \sqrt{m-\varepsilon }+(\varkappa -i\tau )\sqrt{m+\varepsilon }}{Z\alpha \sqrt{m-\varepsilon }+(\varkappa +i\tau )\sqrt{m+\varepsilon }}. \end{aligned}$$

(35)

Last, for $Z\alpha < |\varkappa |$ we must change $i\tau$ into $\sigma = \sqrt{\varkappa ^2 - Z^2\alpha ^2}$:

$$\begin{aligned} \tan \theta= & {} \frac{(2\lambda )^\sigma }{(2\lambda )^{-\sigma }}\cdot \frac{\Gamma (-2\sigma )}{\Gamma (2\sigma )}\cdot \frac{\Gamma \left( 1+\sigma -\frac{Z\alpha \varepsilon }{\lambda }\right) }{\Gamma \left( 1-\sigma -\frac{Z\alpha \varepsilon }{\lambda }\right) }\nonumber \\&\cdot \frac{Z\alpha \sqrt{m-\varepsilon }+(\varkappa -\sigma )\sqrt{m+\varepsilon }}{Z\alpha \sqrt{m-\varepsilon }+(\varkappa +\sigma )\sqrt{m+\varepsilon }}. \end{aligned}$$

(36)

Fig. 3

The dependence of the ground state energy on Z. The square markers are for the exact values of the energy (see (27)) and the round markers are for the approximate ones calculated with the help of (34). The correspondence between color and Z is shown in the legend (the real part of the energy is monotonically decreasing). At $Z=Z_\mathrm{cr}$ the bound states become resonances with positive $\mathrm{Im}[\varepsilon ]$

Let us consider for example $Z\alpha <1$, for which taking a point-like nucleus is reliable. At the limit $R\rightarrow 0$, the r.h.s. of (30) becomes infinite. Therefore, the spectrum of the Dirac equation is given by the poles of (36). They are given by the poles of $\Gamma \left( 1+\sigma - \frac{Z\alpha \varepsilon }{\lambda }\right)$:

$$\begin{aligned} \sqrt{\varkappa ^2-Z^2\alpha ^2} - \frac{Z\alpha \varepsilon }{\sqrt{m^2-\varepsilon ^2}} = -1, -2, \ldots \equiv -n_r, \end{aligned}$$

(37)

to which must be added, for $\varkappa <0$, the zero of the last term in the denominator of (36)⁸:

$$\begin{aligned}&Z\alpha \sqrt{m-\varepsilon }+(\varkappa +\sigma )\sqrt{m+\varepsilon }=0\nonumber \\&\;\Rightarrow \;\sqrt{\varkappa ^2-Z^2\alpha ^2} - \frac{Z\alpha \varepsilon }{\sqrt{m^2 -\varepsilon ^2}} = 0 \equiv n_{r}. \end{aligned}$$

(38)

The electron bound states at $Z < Z_\mathrm{cr}$ become therefore resonances at $Z > Z_\mathrm{cr}$; the poles of the S matrix corresponding to the latter describe positron–nucleus scattering. The trajectory of the ground state energy with growing Z is shown in Fig. 3 (see also Table 1).

Table 1 The dependence of the ground state energy on Z for $m\cdot R= 0.031$. The ground energy level enters the lower continuum at $Z=178$ (though the imaginary part of $\varepsilon$ is much smaller than the accuracy of the calculation). We see that for $Z=232$ the accuracy of the approximate formula is about 10% for the $\mathrm{Im}[\varepsilon ]$

Let us notice the unusual signs of both real and imaginary parts of the resonance energy. It was suggested in [1] that the sign of the energy should be reversed, under the claim that the corresponding state is a resonance in the positron–nucleus system. Such a sign reversal is usual for holes in the lower continuum of the Dirac equation: the absence of an electron of energy $-\,\varepsilon$ is equivalent to the presence of a positron with energy $\varepsilon$. Advocating for the same procedure in the case at hands looks a priori suspicious since the resonances that we found originate from electron bound energy levels (however, also empty) that dive from $\varepsilon =+\,m$ downwards into the lower continuum (and will return upwards to $+\,m$ if Z decreases). An interpretation of the phenomenon in terms of electrons looks therefore more intuitive. In order to resolve this (apparent) puzzle, we shall solve in the next section the Dirac equation for positrons, which describes the scattering of a positron in the upper continuum on a nucleus.

3 The Dirac equation for positrons: upper continuum wave functions and scattering phases in the Coulomb field of a supercritical nucleus

Changing the sign of $Z\alpha$ in (4), we get instead of (3)

$$\begin{aligned} \left\{ \begin{aligned}&\frac{\mathrm{d}\tilde{F}}{\mathrm{d}r} + \frac{\varkappa }{r} \tilde{F} - (\varepsilon +m -\tilde{V}(r)) \tilde{G} = 0,\\&\frac{\mathrm{d}\tilde{G}}{\mathrm{d}r} - \frac{\varkappa }{r} \tilde{G} + (\varepsilon -m -\tilde{V}(r)) \tilde{F} = 0, \end{aligned} \right. \end{aligned}$$

(39)

where

Notice that (3) gives (39) by the set of transformations $\varkappa \rightarrow -\varkappa$, $\varepsilon \rightarrow -\varepsilon$, $F\rightarrow \tilde{G}$ and $G\rightarrow \tilde{F}$.

The states in the upper continuum ($\varepsilon > m$) describe positron scattering on a nucleus. Since a positron cannot form a bound state with a positively charged nucleus, one could think that no resonance at $Z > Z_\mathrm{cr}$ will occur, nor the resonant behavior of the scattering phase found in [1] and reproduced in Sect. 2.

The central issue is therefore to investigate whether bound states and resonances arise or not in the Dirac equation for positrons (39).

Solving (39) at $r < R$ we obtain

$$\begin{aligned} \left( \begin{array}{l} {\tilde{F}} \\ {\tilde{G}} \end{array}\right) = {\mathrm{const}}\cdot \sqrt{\tilde{\beta } r}\cdot \left( \begin{array}{l} {\pm } J_{\mp (1/2 + \varkappa )} (\tilde{\beta } r) \\ J_{{\pm }(1/2 - \varkappa )} (\tilde{\beta } r) \frac{\tilde{\beta }}{\varepsilon +m-\frac{Z\alpha }{R}} \end{array} \right) ,\; r < R, \end{aligned}$$

(41)

where $\tilde{\beta } = \sqrt{(\varepsilon - Z\alpha /R)^2 - m^2}$ and, at small distances, where the solution (41) will be used, $\tilde{\beta } \approx \beta \approx Z\alpha /R$. The upper (lower) signs in (41) should be taken for $\varkappa < 0$ ($\varkappa > 0$). Note that the sign of $\tilde{F}$ is opposite to that of F in (5), while the signs of $\tilde{G}$ and G coincide.

Substituting in (39) the Coulomb potential (40a) and going to the limit $r \rightarrow 0$ we get

$$\begin{aligned} \left. \left( \begin{array}{l} \tilde{F} \\ \tilde{G} \end{array} \right) \right| _{r \rightarrow 0} = \tilde{\eta }_\sigma r^\sigma \left( \begin{array}{c} -1 \\ \frac{-Z\alpha }{\sigma -\varkappa } \end{array} \right) + \tilde{\eta }_{-\sigma } r^{-\sigma } \left( \begin{array}{c} -1 \\ \frac{-Z\alpha }{-\sigma -\varkappa } \end{array} \right) . \end{aligned}$$

(42)

Note that the sign of $\tilde{G}$ is opposite to that of G in (29), while the signs of $\tilde{F}$ and F coincide. Thus, when matching the ratios of $\tilde{F}/\tilde{G}$ from (41) and (42) at $r=R$ we obtain equations identical to (30), (31) with the change $\eta \rightarrow \tilde{\eta }$.

Like in (11), we look for solutions of the form

$$\begin{aligned} \left( \begin{array}{l} \tilde{F} \\ \tilde{G} \end{array} \right) = \left( \begin{array}{c} \sqrt{m+\varepsilon } \\ -\sqrt{m-\varepsilon } \end{array} \right) \mathrm{exp}(-\rho /2) \rho ^{i\tau } \left( \begin{array}{c} \tilde{Q}_1 + \tilde{Q}_2 \\ \tilde{Q}_1 - \tilde{Q}_2 \end{array} \right) , \end{aligned}$$

(43)

where as before $\rho = 2\lambda r = -2ikr$. The expressions for $\tilde{Q}_1$ and $\tilde{Q}_2$ are given by (12), where $Z\alpha$ should be substituted by $-Z\alpha$:

$$\begin{aligned} \left\{ \begin{aligned} \tilde{Q}_1&= C\cdot \frac{\frac{iZ\alpha m}{k} + \varkappa }{-i\tau -\frac{iZ\alpha \varepsilon }{k}}\cdot {_{1}F_{1}}\left( i\tau + \frac{iZ \alpha \varepsilon }{k}, 2i\tau + 1, \rho \right) \\&\quad + D\cdot \frac{\frac{iZ\alpha m}{k} + \varkappa }{i\tau -\frac{iZ\alpha \varepsilon }{k}}\cdot \rho ^{-2i\tau }\cdot {_{1}F_{1}}\left( -i\tau + \frac{iZ\alpha \varepsilon }{k}, -2i\tau +1, \rho \right) , \\ \tilde{Q}_2&= C\cdot {_{1}F_{1}}\left( 1+i\tau + \frac{iZ\alpha \varepsilon }{k}, 2i\tau + 1, \rho \right) \\&\quad + D\rho ^{-2i\tau }\cdot {_{1}F_{1}}\left( 1-i\tau + \frac{iZ\alpha \varepsilon }{k}, -2i\tau +1, \rho \right) . \end{aligned} \right. \end{aligned}$$

(44)

Since we are interested in resonant states, we demand that only terms $\propto \exp [ikr]$ (outgoing waves) survive at $r\rightarrow \infty$. For $\varepsilon <m$, $\exp [ikr]$ becomes $\exp [-\lambda r]$, which describes bound states. In $\tilde{Q}_1$, the coefficient of the $\exp [-ikr]$ term, being damped by an extra 1 / r, does not contribute, and the condition for the terms proportional to $\exp [-ikr]$ to be absent in $\tilde{Q}_2$ is

$$\begin{aligned} C\cdot \frac{\Gamma (2i\tau )}{\Gamma \left( 1+i\tau +\frac{iZ\alpha \varepsilon }{k}\right) } - D\cdot \frac{\Gamma (-2i\tau )}{\Gamma \left( 1-i\tau +\frac{iZ\alpha \varepsilon }{k}\right) } = 0. \end{aligned}$$

(45)

Substituting (44) into (43) at the limit $r\rightarrow 0$, we reproduce (42) for

$$\begin{aligned} \frac{\tilde{\eta }_\tau }{\tilde{\eta }_{-\tau }}= & {} \frac{(-2ik)^{i\tau }}{(-2ik)^{-i\tau }}\cdot \frac{\Gamma (-2i\tau )}{\Gamma (2i\tau )}\cdot \frac{\Gamma \left( 1+i\tau +\frac{iZ\alpha \varepsilon }{k}\right) }{\Gamma \left( 1-i\tau +\frac{iZ\alpha \varepsilon }{k}\right) }\nonumber \\&\cdot \frac{Z\alpha \sqrt{m-\varepsilon } -(-i\tau +\varkappa )\sqrt{m+\varepsilon }}{Z\alpha \sqrt{m-\varepsilon } -(i\tau +\varkappa )\sqrt{m+\varepsilon }}. \end{aligned}$$

(46)

Matching Eqs. (46) and (31) yields an equation for the energies of the resonant states. After the substitution of ($\varkappa , \varepsilon$) by ($-\varkappa , -\varepsilon$), it coincides with a similar equation that we obtained in Sect. 2. Thus, resonances also arise as solutions of the Dirac equation for positrons, at energies $\varepsilon =\xi -\frac{i}{2}\gamma ,~\xi>m,~\gamma >0$.⁹

After making the same substitutions as in Sect. 2, we get equations that coincide with (35), (36)). This clears the mystery concerning the resonances that we have found there. Positrons states of negative energies should be interpreted in terms of electrons. At $Z < Z_\mathrm{cr}$ we just found electron–nucleus bound states—with growing Z, the energy of the bound particle moves from $-m$ (at $Z=0$) to $+m$ (see also footnote 1) and, at $Z > Z_\mathrm{cr}$ it becomes complex and located on the second sheet below the right cut.

Equations for the scattering phase $\delta _{\varkappa }$ analogous to (19), (31), (33) in Sect. 2 can be written. They coincide with these equations after changing $\varkappa \rightarrow -\varkappa$ and $\varepsilon \rightarrow -\varepsilon$.

It is therefore not necessary to solve the Dirac equation for positrons as we did in this section. It is enough to note that, after substitution of $\varepsilon$ by $-\varepsilon$, $\varkappa$ by $-\varkappa$, F by $\tilde{G}$ and G by $\tilde{F}$, Eq. (3) becomes (39) with V(r) converted to $\tilde{V}(r)$. In this way, the formulas of Sect. 3 can be directly deduced from the ones of Sect. 2.

4 Conclusions

In Sects. 2 and 3, the scattering of positrons on a supercritical nucleus was studied. It has the spectacular resonance behavior discovered in [1,2,3]. In the present paper, results with an exact dependence on the parameter $m\times R$ have been obtained on both sheets of the complex energy plane in the form convenient for numerical evaluation. However, one can hardly hope to study this phenomenon experimentally: even if a supercritical nucleus can be produced in heavy ions collisions, its life time will be so short that one cannot scatter a positron on it, not to mention the still bigger challenge of making a target with supercritical nuclei. Let us note that since the elastic scattering matrix was found to be unitary (the scattering phase is real) there are no inelastic processes in the positron scattering on supercritical nucleus.

More realistic is the hope to detect the emission of positrons from a short-lived supercritical nucleus eventually produced in heavy ions collisions. Indeed we do not agree with the claim made in the abstract of [1] (and in contradiction with [16] in particular) that the spontaneous production of $e^+e^-$ pairs from a supercritical nucleus does not occur. On the contrary, we believe that the resonance found in [1] in the system positron—supercritical nucleus is precisely the signal for pair production. It occurs when, as Z grows, an empty electron level dives into the lower continuum of the Dirac equation. In the absence of the nucleus, this empty state in the lower continuum would just mean the presence of a positron. The presence of the nucleus makes the energy of this state complex, and its lifetime is precisely $1/\gamma$. In this lapse of time, an electron from the sea with the same energy $-\xi$ located far from the nucleus can penetrate in its vicinity. It partially screens the charge of the nucleus and, at the same time, an empty electron state arises in the Dirac sea. This is the positron which gets repulsed to infinity by the nucleus.

Let us suppose that solutions of the Dirac equation we get are approximately valid also when an electron screens nuclear potential, being embedded in the lower continuum. It means our solutions for the resonance energy and width are almost valid. It well can be so, since electric charge of one electron is small and it is situated far from nucleus, $r \approx 1/m$. So, the obtained width (imaginary part of energy) is the lifetime of positron in the vicinity of nucleus, which is already surrounded by diving electron. Therefore this is the lifetime of the system of nucleus, electron and positron with respect to positron emission to infinity, so it is an average time of $e^{+}e^{-}$ pair production (in reality two independent pairs are produced because of electron spin degeneracy).

The potential barrier which holds the positron in the vicinity of the nucleus is shown in Fig. 2 of [16]; its penetration time is given by the analytical formulas (4.14, 4.15), and the results of numerical calculations are shown in Fig. 13 of the same review paper. We reproduced the curve shown in Fig. 13 from the dependence $\gamma (Z)$ that we obtained in Sect. 2 for the energy of the Gamov (quasistationary) state.

Let us finally mention that we agree with the description of the stable states of a supercritical nucleus made in Sect. 6 of [1]: empty states in the upper continuum, empty discrete levels, and occupied states in the lower continuum. The levels of the lower continuum that get occupied by electrons after the diving process form the so-called “charged vacuum”; it has charge $-n$, where n is the number of these levels. The n positrons that get emitted compensate for this negative charge. A supercritical nucleus is no longer naked and its electric charge is partially screened by these electrons.

Indirect evidence of such a phenomenon is found in graphene physics [27, 28].

We thank O.V. Kancheli, V.D. Mur, V.A. Novikov, and M.I. Eides for useful discussions. We are grateful to V.M. Shabaev who provided us with references [21, 22]. S.G. is supported by RFBR under grants 16-32-60115 and 16-32-00241, by the Grant of President of Russian Federation for the leading scientific Schools of Russian Federation, NSh-9022-2016, and by the “Dynasty Foundation”. M.V. is supported by RFBR under grant 16-02-00342. M.V. is grateful to LPTHE, CNRS and Sorbonne Univesité for hospitality and funding during the first steps (projet IDEX PACHA OTP-53897) and the last steps of this work.

Appendices

Appendix A: Functions $Q_1$ and $Q_2$

Substituting (11) into the Dirac equations (3) we get

$$\begin{aligned} \begin{aligned}&\rho (Q_1^\prime + Q_2^\prime ) + (i\tau +\varkappa )(Q_1 +Q_2)-\rho Q_2\\&\quad + Z\alpha \sqrt{\frac{m-\varepsilon }{m+\varepsilon }} (Q_1 - Q_2)= 0,\\&\rho (Q_1^\prime - Q_2^\prime ) + (i\tau -\varkappa )(Q_1 - Q_2)+\rho Q_2 \\&\quad -Z\alpha \sqrt{\frac{m+\varepsilon }{m-\varepsilon }} (Q_1 + Q_2) = 0, \end{aligned} \end{aligned}$$

(A1)

where a prime means the derivative with respect to $\rho$.

The sum and difference of the two equations (A1) give (compare with Eq. (36.5) from [25])

$$\begin{aligned} \begin{aligned}&\rho Q_1^\prime + \left( i\tau - \frac{iZ\alpha \varepsilon }{k}\right) Q_1 + \left( \varkappa - \frac{iZ\alpha m}{k}\right) Q_2 = 0,\\&\rho Q_2^\prime + \left( i\tau - \rho +\frac{iZ\alpha \varepsilon }{k}\right) Q_2 + \left( \varkappa + \frac{iZ\alpha m}{k}\right) Q_1 = 0. \end{aligned} \end{aligned}$$

(A2)

Eliminating $Q_1$ or $Q_2$ gives

$$\begin{aligned} \begin{aligned}&\rho Q_1^{\prime \prime } + (2 i\tau +1 -\rho )Q_1^\prime + \left( \frac{iZ\alpha \varepsilon }{k} - i\tau \right) Q_1 = 0,\\&\rho Q_2^{\prime \prime } + (2 i\tau +1 - \rho )Q_2^\prime + \left( \frac{iZ\alpha \varepsilon }{k} - 1 - i\tau \right) Q_2=0. \end{aligned} \end{aligned}$$

(A3)

Unlike in the case of a point-like nucleus, we do not demand here that the solutions of (A3) be regular at $\rho =0$. We accordingly consider linear superpositions of the two independent solutions of the second order differential equations (A3) with arbitrary coefficients.

First let us recall that the general solution of the equation

$$\begin{aligned} zu^{\prime \prime } + (\gamma - z)u^\prime -\alpha u = 0 \end{aligned}$$

(A4)

is

$$\begin{aligned} u = C_1\cdot {_{1}F_{1}}(\alpha , \gamma , z) + C_2\cdot z^{1-\gamma }{_{1}F_{1}}(\alpha -\gamma +1, 2-\gamma , z) , \end{aligned}$$

(A5)

where $C_1$ and $C_2$ are arbitrary coefficients while the $_1F_1$ are the Kummer confluent hypergeometric functions. Thus for the solutions of (A3) we obtain

$$\begin{aligned} \begin{aligned} Q_1&= A\cdot {_{1}F_{1}}\left( i\tau - \frac{iZ\alpha \varepsilon }{k}, 2i\tau + 1, \rho \right) \\&\quad + B\cdot \rho ^{-2i\tau } {_{1}F_{1}}\left( -i\tau -\frac{iZ\alpha \varepsilon }{k}, -2i\tau +1, \rho \right) ,\\ Q_2&= C\cdot {_{1}F_{1}}\left( 1 +i\tau - \frac{iZ\alpha \varepsilon }{k}, 2i\tau + 1, \rho \right) \\&\quad + D\cdot \rho ^{-2i\tau }{_{1}F_{1}}\left( 1 -i\tau -\frac{iZ\alpha \varepsilon }{k}, -2i\tau +1, \rho \right) , \end{aligned} \end{aligned}$$

(A6)

where A, B, C, and D are arbitrary coefficients.

At small z, $_1F_1=1+\mathcal {O}(z)$. Substituting the expansions of (A6) at small $\rho$ into the first equation in (A2) determines A and B, respectively, in terms of C and D:

$$\begin{aligned}&\left( i\tau - \frac{iZ\alpha \varepsilon }{k}\right) A + \left( \varkappa - \frac{iZ\alpha m}{k}\right) C = 0, \end{aligned}$$

(A7)

$$\begin{aligned}&\left( -i\tau - \frac{iZ\alpha \varepsilon }{k}\right) B + \left( \varkappa - \frac{iZ\alpha m}{k}\right) D = 0. \end{aligned}$$

(A8)

Plugging A and B obtained from (A7) and (A8) into (A6) yields (12).

Appendix B: The scattering phase according to [1]

Considering real $\varepsilon <-m$ below the left cut we can rewrite the expression for the scattering phase in a more compact form.

Let us introduce the following notations equivalent to those used in [1]:

$$\begin{aligned} \exp (i\varphi )&= e^{2i\theta }\frac{(2k)^{-i\tau }\Gamma (2i\tau )}{(2k)^{i\tau }\Gamma (-2i\tau )}, \end{aligned}$$

(B1)

$$\begin{aligned} a&= \frac{Z\alpha \sqrt{m-\varepsilon } +(-i\tau +\varkappa )\sqrt{m+\varepsilon }}{\Gamma \left( 1-i\tau - \frac{iZ\alpha \varepsilon }{k}\right) }, \end{aligned}$$

(B2)

$$\begin{aligned} b&= \frac{Z\alpha \sqrt{m-\varepsilon } -(-i\tau +\varkappa )\sqrt{m+\varepsilon }}{\Gamma \left( 1-i\tau + \frac{iZ\alpha \varepsilon }{k}\right) }. \end{aligned}$$

(B3)

With these notations the approximate ratio C / D defined by (33) can be written in the following way:

$$\begin{aligned} C/D&=e^{i\varphi -\pi \tau }\cdot \frac{a^{*}}{b}\cdot \frac{\Gamma \left( -2i\tau \right) }{\Gamma \left( 2i\tau \right) }\cdot \frac{\Gamma \left( i\tau +\frac{iZ\alpha \varepsilon }{k}\right) }{\Gamma \left( -i\tau +\frac{iZ\alpha \varepsilon }{k}\right) } \end{aligned}$$

(B4)

$$\begin{aligned}&=e^{i\varphi -\pi \tau }\cdot \frac{b^{*}}{a}\cdot \frac{\Gamma \left( -2i\tau \right) }{\Gamma \left( 2i\tau \right) }\cdot \frac{\Gamma \left( 1+i\tau -\frac{iZ\alpha \varepsilon }{k}\right) }{\Gamma \left( 1-i\tau -\frac{iZ\alpha \varepsilon }{k}\right) }, \end{aligned}$$

(B5)

where we used

$$\begin{aligned} \frac{\left( -i\right) ^{-i\tau }}{\left( -i\right) ^{i\tau }}=e^{-\pi \tau } \end{aligned}$$

(B6)

and

$$\begin{aligned}&\left( -i\tau -\frac{iZ\alpha \varepsilon }{k}\right) \left( Z\alpha \sqrt{m-\varepsilon }+ \left( i\tau -\varkappa \right) \sqrt{m+\varepsilon }\right) \nonumber \\&\quad =-i\tau \left( Z\alpha \sqrt{m-\varepsilon } +\left( i\tau -\varkappa \right) \sqrt{m+\varepsilon }\right) \nonumber \\ {}&\qquad -iZ\alpha \varepsilon \left( \frac{Z\alpha }{i\sqrt{m+\varepsilon }} +\frac{i\tau -\varkappa }{i\sqrt{m-\varepsilon }}\right) \nonumber \\&\quad =\frac{-i\tau \left( i\tau -\varkappa \right) \left( m+\varepsilon \right) -\left( Z\alpha \right) ^{2}\varepsilon }{\sqrt{m+\varepsilon }}\nonumber \\ {}&\qquad +\frac{-i\tau \left( Z\alpha \right) \left( m-\varepsilon \right) -Z\alpha \varepsilon \left( i\tau -\varkappa \right) }{\sqrt{m-\varepsilon }}\nonumber \\&\quad =\frac{\left( Z\alpha \right) ^{2}m +\varkappa \left( i\tau -\varkappa \right) \left( m+\varepsilon \right) }{\sqrt{m+\varepsilon }}\nonumber \\ {}&\qquad +\frac{-\left( i\tau -\varkappa \right) Z\alpha m-\varkappa Z\alpha \left( m-\varepsilon \right) }{\sqrt{m-\varepsilon }} \nonumber \\&\quad =Z\alpha m\left( \frac{Z\alpha }{\sqrt{m+\varepsilon }}+ \frac{-i\tau +\varkappa }{\sqrt{m-\varepsilon }}\right) \nonumber \\ {}&\qquad -\varkappa \left( Z\alpha \sqrt{m-\varepsilon } +\left( -i\tau +\varkappa \right) \sqrt{m+\varepsilon }\right) =\nonumber \\&\quad =\left( Z\alpha \sqrt{m-\varepsilon }+ \left( -i\tau +\varkappa \right) \sqrt{m+\varepsilon }\right) \left( \frac{iZ\alpha m}{k}-\varkappa \right) , \end{aligned}$$

(B7)

where we used the relation

$$\begin{aligned} \left( -i\tau -\varkappa \right) \left( i\tau -\varkappa \right) = \tau ^{2}+\varkappa ^{2}=\left( Z\alpha \right) ^{2}. \end{aligned}$$

(B8)

Then the scattering phase $\delta _{\varkappa }$ can be written as follows (by substituting (B4) and (B5) into the numerator and the denominator of (19), respectively):

$$\begin{aligned} e^{2i\delta _{\varkappa }} = -\frac{\mathrm{exp}\left( \frac{\pi \tau }{2}+\frac{i\varphi }{2}\right) a^* -\mathrm{exp}\left( -\frac{\pi \tau }{2}-\frac{i\varphi }{2}\right) b}{\mathrm{exp}\left( \frac{\pi \tau }{2}-\frac{i\varphi }{2}\right) a -\mathrm{exp}\left( -\frac{\pi \tau }{2} +\frac{i\varphi }{2}\right) b^*}. \end{aligned}$$

(B9)

In Eq. (22) of [1] the phase $\delta _{\varkappa }$ is expressed through the ratio $f^*/f$, where f is the Jost function. Our result differs from eq. (23) of [1] by the substitution $\varphi \rightarrow \varphi /2$ (it seems that there is a misprint in [1]).

Appendix C: Qualitative explanation of the resonance phenomenon in the $e^+ N^+$ system

The effective potential for an electron in the field of a supercritical nucleus is derived in [16] from the Dirac equation, for $\varepsilon \approx -m$. It is attractive at short distances, repulsive at large distances, with a Coulomb barrier in between. We derive below, in a similar way, the effective potential for a positron in the field of a similar nucleus, in the vicinity of $\varepsilon =+\,m$.

As already noticed at the beginning of Sect. 3, the Dirac equation (3) for electrons becomes (39) for positrons after the following substitutions:

$$\begin{aligned}&\varkappa \rightarrow -\varkappa , \;\; \varepsilon \rightarrow -\varepsilon , \;\; F \nonumber \\&\quad \rightarrow \tilde{G}, \;\; G \rightarrow \tilde{F}, \;\; V(r) \rightarrow \tilde{V}(r) = -V(r). \end{aligned}$$

(C1)

To proceed like in [16], we deduce the second order differential equation satisfied by $\tilde{G}$ from (39), which is

$$\begin{aligned}&\tilde{G}'' +\frac{\tilde{V}'}{\varepsilon -m-\tilde{V}}\left( \tilde{G}'-\frac{\varkappa }{r}\tilde{G}\right) \nonumber \\&\quad +\left( \left( \varepsilon -\tilde{V}\right) ^{2}-m^{2} +\frac{\varkappa \left( 1-\varkappa \right) }{r^{2}}\right) \tilde{G}=0, \end{aligned}$$

(C2)

in which “$~'~$” means here derivation with respect to r. In order to transform this equation into a Schrödinger-like equation, the following change of variables must be performed:

$$\begin{aligned} \tilde{G}=\chi \sqrt{m-\varepsilon +\tilde{V}}. \end{aligned}$$

(C3)

Thus, we get

$$\begin{aligned} \chi ''+ k^{2}\chi =0, \end{aligned}$$

(C4)

where $k^{2}=2m\left( E-U\right)$, $E=\frac{\varepsilon ^{2}-m^{2}}{2m}$. The effective potential is seen to be made of two terms: $U=U_{1}+U_{2}$, where

$$\begin{aligned} U_{1}=\frac{\varepsilon }{m}\tilde{V}-\frac{1}{2m}\tilde{V}^{2} -\frac{\varkappa \left( 1-\varkappa \right) }{2mr^{2}} \end{aligned}$$

(C5)

and

$$\begin{aligned} U_{2}= & {} \frac{\tilde{V}''}{4m\left( \varepsilon -m-\tilde{V}\right) }\nonumber \\&+\frac{3}{8m}\frac{\left( \tilde{V}'\right) ^{2}}{\left( \varepsilon -m-\tilde{V}\right) ^{2}} +\frac{\varkappa \tilde{V}'}{2mr\left( \varepsilon -m-\tilde{V}\right) }. \end{aligned}$$

(C6)

It coincides with the equation obtained in [16] after the substitution $\varepsilon \rightarrow -\varepsilon$, $\varkappa \rightarrow -\varkappa$ and $\tilde{V}\rightarrow -V$.

We are interested in positrons with $\varepsilon \approx m$. At large distances the first term in $U_1$ dominates, and describes the repulsion of the positron by the nucleus. For the ground state $\varkappa =1$ the centrifugal term in $U_1$ vanishes. Finally, for $\varepsilon =m$ and $\varkappa =1$, we get from (C5) and (C6)

$$\begin{aligned} U = \frac{Z\alpha }{r} + \frac{3-4(Z\alpha )^2}{8mr^{2}}. \end{aligned}$$

(C7)

At short distances the terms $\propto 1/r^2$ dominates and, for a supercritical nucleus, they lead to attraction, while the Coulomb term dominates at $r\ge 1/m$. This attractive force explains the existence of resonances in the $e^{+}N^{+}$ system, while a bound state cannot exist due to the narrowness of the well.

Let us note that the fall to the center occurs only for $Z\alpha >1$ when the coefficient in front of the term $\propto -1/r^2$ becomes larger than 1 / 8m (see [29], eq. (35.10)). We are grateful to V.A. Novikov who brought our attention to this feature. In the problem under consideration the finite nucleus size prevents the fall to the center.