Emerging anisotropic compact stars in $f(\mathcal {G},T)$ gravity

Abstract

The possible emergence of compact stars has been investigated in the recently introduced modified Gauss–Bonnet $f(\mathcal {G},T)$ gravity, where $\mathcal {G}$ is the Gauss–Bonnet term and T is the trace of the energy-momentum tensor (Sharif and Ikram, Eur Phys J C 76:640, 2016). Specifically, for this modified $f(\mathcal {G}, T)$ theory, the analytic solutions of Krori and Barua have been applied to an anisotropic matter distribution. To determine the unknown constants appearing in the Krori and Barua metric, the well-known three models of the compact stars, namely 4U1820-30, Her X-I, and SAX J 1808.4-3658 have been used. The analysis of the physical behaviour of the compact stars has been presented and the physical features like energy density and pressure, energy conditions, static equilibrium, stability, measure of anisotropy, and regularity of the compact stars, have been discussed.

1 Introduction

In astrophysics, compact stars are generally referred to as white dwarfs, neutron stars (including the hybrid and quark stars), and black holes. White dwarfs and neutron stars originate due to the degeneracy pressure produced by the fundamental particles responsible for their formation. These stars are massive but volumetrically smaller objects, and therefore they come with high densities. Usually, the exact nature of these compact stars is not known to us, but they are believed to be the massive objects with a small radius. Excluding black holes, all the other types of compact stars are sometimes also known as degenerate stars. In general relativity (GR), an analysis of configured equilibrium is essential due to the reason of compact stars having huge mass and density. This can be started in a general relativistic way by considering the Oppenheimer–Volkoff equations [2] for static spherically symmetric and hydrostatic equilibrium, given as

$$\begin{aligned} \frac{\mathrm{d}p}{\mathrm{d}r}=-G\frac{(mc^2+4p\pi {r^3})(\rho {c^2}+p)}{r^2c^4-2Gmc^2r}~~\text {and}~~\frac{\mathrm{d}m}{\mathrm{d}r}=4\rho {\pi }r^2, \end{aligned}$$

(1)

where p, $\rho$, and m is the pressure, density, and mass of the star, respectively, varying with radial coordinate r. At $r=R$ (the coordinate radius of the compact star), the total mass of the compact star is determined as

$$\begin{aligned} M(R)=\int _{0}^{R}4\pi {r^2}\rho \mathrm{d}{r}. \end{aligned}$$

(2)

The combination of these Oppenheimer–Volkoff equations with the equation of the sate (EoS) parameter $\omega =\frac{p}{\rho }$ when solved numerically results in different configurations of the compact stars with divisions of low and high densities [3, 4].

Schwarzschild [5] was the pioneer to present the spherically symmetric exact solutions of the Einstein field equations. The outcome of the first solution was the exploration of the space-time singularity which gave the idea of a black hole. The second non-trivial solution predicted the bounded compactness parameter i.e., $\mu {(R)}=\frac{2M(R)}{R}<\frac{8}{9}$ in hydrostatic equilibrium for some static and spherically symmetric configured structure [6]. The investigation of compact stars (neutron stars, dark stars, quarks, gravastars, and black holes) has become now an interesting research pursuit in astrophysics despite not being a new one. Baade and Zwicky [7] studied the compact stellar objects and argued that the supernova may turn into a smaller dense compact object, which came true later on after the discovery of pulsars, which are highly magnetized rotating neutrons [8, 9]. Ruderman [10] was first to explore that, at the core of the compact stars, the nuclear density turns anisotropic. A number of investigations have been made to find the solutions of the field equations for spherically symmetric anisotropic configurations in different contexts [11,12,13]. The pressure of the fluid sphere splits into tangential and radial pressures in anisotropic configurations. Different investigations reveal that the repulsive forces, which are determining for compact stars, are produced due to anisotropy. Kalam et al. [14] showed that the Krori and Barua metric [15] establishes the necessary conditions for the advocacy of an effective and stable approach in modelling the compact objects. From an integrated Tolman–Oppenheimer–Volkoff (TOV) equation, the numerical simulations may be used to study the nature of the compact stars, using the EoS parameter. Rahaman et al. [16, 17] used the EoS of the Chaplygin gas to explore their physical characteristics by extending the Krori and Barua models. Mak and Harko [18] used some standard models for spherically symmetric compact objects and explored exact solutions to find the physical parameters such as the energy density, radial and tangential pressures, thereby concluding that inside these stars, the parameters would remain positive and finite. Hossein et al. [19] studied the effects on anisotropic stars due to the cosmological constant. Various physical properties, such as mass, radius, and moment of inertia, of neutron stars have been investigated and a comprehensive comparison has been established with GR and modified theories of gravity [20]. Some interesting investigations related to the structure of slowly rotating neutron stars in $R^2$ gravity have been accomplished by making use of two distinct hadronic and a strange matter EOS parameters [21]. For a comprehensive study, some fascinating results can be found in [22,23,24,25,26,27,28].

As an alternative to the theory of GR, modified theories of gravity have played an important and pivotal role in revealing the hidden facts as regards the accelerating expansion of the universe. After being motivated by the original theory and using the complex Lagrangian, modified theories of gravity like f(R), f(R, T), $f(\mathcal {G})$, and $f(R,\mathcal {G})$ have been structured, where R is the Ricci scalar, $\mathcal {G}$ is the Gauss–Bonnet invariant term, and T is the trace of the energy-momentum tensor. Some reviews and important discussions relating to different modified theories of gravity have been published by different researchers [29,30,31,32,33,34,35,36,37,38,39,40,41,42]. Das et al. [43] presented exact conformal solutions to describe the interior of a star in modified teleparallel gravity. In another work, Das et al. [44] explored several physical features of the model admitting conformal motion to describe the behaviour of the compact stars using modified f(R, T) gravity. Sharif and Yousuf [45] investigated the stability conditions of collapsing object by considering the non-static and spherically symmetric space-time. The field equations of f(R, T) modified theory have been explored by implementing the perturbation approach [46]. The possible formation of compacts stars in a modified theory of gravity by using the Krori and Barua metric for spherically symmetric anisotropic compact stars has been discussed [47, 48]. In a recently published paper [1], Sharif and Ikram presented a new modified $f(\mathcal {G},T)$ theory of gravity and studied various energy conditions for the Friedmann–Robertson–Walker (FRW) universe. They found that the massive test particles follow non-geodesic geometry lines due to the presence of an extra force. It is expected that the theory may describe the late-time cosmic acceleration for some special choices of $f(\mathcal {G},T)$ gravity models. We discussed the Noether symmetry approach to find the exact solutions of the field equations in an $f(\mathcal {G},T)$ theory of gravity [49]. In Ref. [50], we investigated the same modified Gauss–Bonnet $f(\mathcal {G},T)$ gravity and used the Noether symmetry methodology to discuss some cosmologically important $f(\mathcal {G},T)$ gravity models with anisotropic background reported for a locally rotationally symmetric Bianchi type I universe. We used two models to explore the exact solutions and found that the specific models of modified Gauss–Bonnet gravity may be used to reconstruct $\Lambda$CDM cosmology without involving any cosmological constant. Thus it seems interesting to further explore the universe in this theory.

This paper aims to investigate the possible emergence of compact stars by constructing some viable stellar solutions in a $f(\mathcal {G},T)$ theory of gravity by choosing some specific models. The plan of our present study is as follows: In Sect. 2, we give the fundamental formalism of $f(\mathcal {G},T)$ gravity with an anisotropic matter distribution. Section 3 is dedicated to the matching of the metric conditions. Some physical features of the present study in the context of the $f(\mathcal {G},T)$ gravity model under consideration are given in Sect. 4. Lastly, we present some conclusive discussions.

2 Anisotropic matter distribution in $f(\mathcal {G},T)$ gravity

The general action for the modified $f(\mathcal {G},T)$ model is [1]

$$\begin{aligned} \mathcal {A}= \frac{1}{2{\kappa }^{2}}\int \mathrm{d}^{4}x \sqrt{-g}[R+f(\mathcal {G},\mathrm {\textit{T}})]+\int \mathrm{d}^{4}x\sqrt{-g}\mathcal {L}_\mathrm{M}, \end{aligned}$$

(3)

where the function $f( \mathcal {G},T)$ contains the Gauss–Bonnet term $\mathcal {G}$ and the trace of the energy-momentum tensor T, $\kappa$ denotes the coupling constant, g is for the determinant of the metric tensor, R is the Ricci scalar, and $\mathcal {L}_\mathrm{M}$ represents the matter part of the Lagrangian. The Gauss–Bonnet term $\mathcal {G}$ is defined as

$$\begin{aligned} \mathcal {G}=R^{2}-4R_{\zeta \eta }R^{\zeta \eta }+R_{\zeta \eta \mu \nu }R^{\zeta \eta \mu \nu }, \end{aligned}$$

(4)

where $R_{\zeta \eta \mu \nu }$, and $R_{\zeta \eta }$ is for the Riemann and Ricci tensors, respectively. The variation of Eq. (3) with respect to $g_{\zeta \eta }$, and by setting $\kappa =1$, gives the following fourth order non-linear field equations:

$$\begin{aligned} G_{\zeta \eta }= & {} [2Rg_{\zeta \eta }\nabla ^{2}+ 2R\nabla _{\zeta }\nabla _{\eta }+4g_{\zeta \eta }R^{\mu \nu }\nabla _{\mu }\nabla _{\nu }\nonumber \\&+\, 4R_{\zeta \eta }\nabla ^{2}-4R^{\mu }_{\zeta }\nabla _{\eta }\nabla _{\mu }-4R^{\mu }_{\eta }\nabla _{\zeta }\nabla _{\mu }\nonumber \\&-\,4R_{\zeta \mu \eta \nu }\nabla ^{\mu }\nabla ^{\nu }]f_{\mathcal {G}}+ \frac{1}{2}g_{\zeta \eta }f-[\mathrm {\textit{T}}_{\zeta \eta }+\Theta _{\zeta \eta }]\nonumber \\&\times \, f_{\mathrm {\textit{T}}}-[2RR_{\zeta \eta }-4R^{\mu }_{\zeta }R_{\mu \eta }-4R_{\zeta \mu \eta \nu }R^{\mu \nu }\nonumber \\&+\,2R^{\mu \nu \delta }_{\zeta }R_{\eta \mu \nu \delta }] f_{\mathcal {G}}+\kappa ^{2}\mathrm {\textit{T}}_{\zeta \eta }, \end{aligned}$$

(5)

where $\Box =\nabla ^{2}=\nabla _{\zeta }\nabla ^{\zeta }$ is the d’Alembertian operator, ${G}_{\zeta \eta }=R_{\zeta \eta }-\frac{1}{2}g_{\zeta \eta }R$ is the Einstein tensor, $\Theta _{\zeta \eta }= g^{\mu \nu }\frac{\delta \mathrm {\textit{T}}_{\mu \nu }}{\delta g_{\zeta \eta }}$, $f\equiv f(\mathcal {G},T)$, $f_{\mathcal {G}}\equiv \frac{\partial f (\mathcal {G},\mathrm {\textit{T}})}{\partial \mathcal {G}}$, and $f_{\mathrm {\textit{T}}}\equiv \frac{\partial f(\mathcal {G},\mathrm {\textit{T}})}{\partial \mathrm {\textit{T}}}$. The Einstein equations can be recovered by putting simply $f(\mathcal {G},\mathrm {\textit{T}})=0$, whereas the field equations for $f(\mathcal {G})$ are reproduced by replacing $f(\mathcal {G},\mathrm {\textit{T}})$ with $f(\mathcal {G})$ in Eq. (5). The energy-momentum tensor, denoted by $\mathrm {\textit{T}}_{\zeta \eta }$, can be defined as

$$\begin{aligned} \mathrm {\textit{T}}_{\zeta \eta }=-\frac{2}{\sqrt{-g}}\frac{\delta (\sqrt{-g}\mathcal {L}_\mathrm{M})}{\delta g^{\zeta \eta }}. \end{aligned}$$

(6)

Moreover, the metric dependent energy-momentum tensor may have the form

$$\begin{aligned} \mathrm {\textit{T}}_{\zeta \eta }=g_{\zeta \eta }\mathcal {L}_\mathrm{M}-2\frac{\partial \mathcal {L}_\mathrm{M}}{\partial g^{\zeta \eta }}. \end{aligned}$$

(7)

The usual anisotropic energy-momentum tensor $T_{\zeta \eta }$ is given as

$$\begin{aligned} T_{\zeta \eta }=(\rho +p_\mathrm{t})V_{\zeta }V_{\eta }-p_\mathrm{t}g_{\zeta \eta }+(p_\mathrm{r}-p_\mathrm{t})\xi _{\zeta }\xi _{\eta }, \end{aligned}$$

(8)

where $p_\mathrm{t}$ and $p_\mathrm{r}$ represent the tangential and radial pressures, respectively, while $\rho$ denotes the energy density. The four velocity is denoted by $V_{\zeta }$ and the radial four vector by $\xi _{\alpha }$; they satisfy

$$\begin{aligned} V^{\alpha }=e^{\frac{-a}{2}}\delta ^{\alpha }_{0},~~~V^{\alpha }V_{\alpha }=1,~~~\xi ^{\alpha }=e^{\frac{-b}{2}}\delta ^{\alpha }_{1},~~~\xi ^{\alpha }\xi _{\alpha }=-1. \end{aligned}$$

(9)

In this paper, we have chosen specifically the following $f(\mathcal {G},T)$ model [49]:

$$\begin{aligned} f(\mathcal {G},T)=f_{1}(\mathcal {G})+f_{2}(T), \end{aligned}$$

(10)

where $f_{1}(\mathcal {G})$ is an analytic function comprised of a Gauss–Bonnet term. In particular, we consider $f_{1}(\mathcal {G})=\alpha \mathcal {G}^n$, a power law model of $f(\mathcal {G})$ gravity proposed by Cognola et al. [51] with $\alpha$ being an arbitrary real constant, and n a positive real number. Here we take $f_{2}({T})=\lambda \textit{T}$, with $\lambda$ being some positive real number. Further, for the investigations of compact stars we take the static, spherically symmetric space-time as

$$\begin{aligned} \mathrm{d}s^{2}=e^{a(r)}\mathrm{d}t^{2}-e^{b(r)}\mathrm{d}r^2-r^{2}\mathrm{d}\theta ^{2}-r^2{\text {sin}}^{2}\theta \mathrm{d}\phi ^{2}. \end{aligned}$$

(11)

We parameterize metric (11) by taking $a(r)=Br^{2}+C$ and $b(r)=Ar^{2}$, given by Krori and Barua [15] and with the help of some physical assumptions, the arbitrary constants A, B and C will be calculated. The above set of functions are established to reach a singularity free structure for compact stars. Therefore, our main concern is to present these functions to the metric in a way so as to achieve the structure for the compact star in this extended model, free of the singularities in the neighbourhood of r. To investigate the existence of the compact stars for the model $f(\mathcal {G},T)=\alpha \mathcal {G}^{n}+\lambda \textit{T}$, we have considered $\alpha =1$, $\lambda =2$, and $n=2$. For these parametric values, the energy density and all the energy conditions remain positive for the model under investigation. It is worth mentioning here that one may opt for some other choices of these values for further analysis. The explicit expressions for the energy density $\rho$, the radial pressure $p_\mathrm{r}$, and the tangential pressure $p_\mathrm{t}$ are obtained:

$$\begin{aligned}&\rho =\frac{e^{-2b}}{8r^4(1+\lambda )(1+2\lambda )}\Big [8e^b(-1+e^b)r^2(1+2\lambda )\nonumber \\&-\,4e^{2b}r^4(1+\lambda )f_1+f_\mathcal {G}\Big \{-16(-1+e^b)^2\lambda \nonumber \\&+\,r^2\Big \{r^2(1+2\lambda )a'^4-2r^2(1+2\lambda )a'^3b'\nonumber \\&-\,4a'b'\Big \{2(-3+e^b)(1+\lambda )+r^2(1+2\lambda )a''\nonumber \\&+\,a'^2\Big \{8(\lambda +e^b(1+\lambda ))\Big \}\nonumber \\&+\,r^2(1+2\lambda )(b'^2+4a'')\Big \}+4\Big \{-2\lambda b'^2\nonumber \\&+\,a''\{4(-1+e^b)(1+\lambda )\}\Big \}\nonumber \\&+\,r^2(1+2\lambda )a''\Big \}\Big \}+2r\Big \{4f_\mathcal {G}'\{-8(2+5\lambda )\nonumber \\&+\,r\{b'(10+27\lambda -2r\lambda b')\}\nonumber \\&-\,r\{8+18\lambda +r(2+3\lambda )b'\}a''\}\nonumber \\&-\,8r(2+5\lambda )(1-2rb'+r^2a'')f_\mathcal {G}''\nonumber \\&+\,r^2a'^2\Big \{e^{b}r\lambda -2(8+18\lambda +r(2+3\lambda )b')f_\mathcal {G}'\nonumber \\&-\,4r(2+5\lambda )f_\mathcal {G}''\Big \}\nonumber \\&+\,2e^b\Big \{16(2+5\lambda )f_\mathcal {G}'+2rb'\{r+2r\lambda \nonumber \\&+\,(2+3\lambda )f_\mathcal {G}'\}+r^3\lambda a''+4r(2+5\lambda )f_\mathcal {G}''\Big \}\nonumber \\&+\,ra'\Big \{2(-32-74\lambda +rb'(2\lambda +r(2+3\lambda )b'))\Big \}f_\mathcal {G}'\nonumber \\&-\,e^b\lambda \Big \{r(-4+r b')+4f_\mathcal {G}'\Big \}\nonumber \\&+\,4r\Big \{-2(4+9\lambda )+r(2+5\lambda )b'f_\mathcal {G}''\Big \}\Big \}\Big ], \end{aligned}$$

(12)

$$\begin{aligned} p_\mathrm{r}= & {} \frac{e^{-2b}}{8r^4(1+\lambda )(1+2\lambda )}\Big [-4e^{2b}r^4(1+\lambda )f_{1}\nonumber \\&+\,f_\mathcal {G}\Big \{-16(-1+e^b)^2\lambda \nonumber \\&+\,r^2\Big (r^2(1+2\lambda )a'^4-2r^2(1+2\lambda )a'^{3}b'\nonumber \\&-\,4a'b'\{2(-3+e^b)(1+\lambda )\nonumber \\&+\,r^2(1+2\lambda )a''\}+a'^2\Big \{8(-1+e^b)(1+\lambda )\nonumber \\&+\,r^2(1+2\lambda )(b'^2+4a'')\Big \}\nonumber \\&+\,4\Big \{2(1+\lambda )b'^2+a''\{4(-1+e^b)(1+\lambda )\nonumber \\&+\,r^2(1+2\lambda )a''\}\Big \}\Big )\Big \}\nonumber \\&+\,2r\{4e^b(-1+e^b)\}r(1+2\lambda )\nonumber \\&+\,4f_\mathcal {G}'\Big \{-8\lambda +r\Big \{-b'(4+\lambda +2r\lambda b')\nonumber \\&+\,r\lambda (-2+r b'a'')+r^2\lambda a'^2\{2(-2+rb')f_\mathcal {G}'\nonumber \\&+\,r(e^b-4f_\mathcal {G}'')\}-8r\lambda (1-2rb'\nonumber \\&+\,r^2a'')f_\mathcal {G}''+ra'\Big \{-2\{12+34\lambda \nonumber \\&+\,rb'(8+14\lambda +r\lambda b')\}f_\mathcal {G}'\nonumber \\&+\,e^b\Big \{-r(4+4\lambda +r\lambda b')+4(2+3\lambda )f_\mathcal {G}'\Big \}\nonumber \\&+\,4r\lambda (-2+rb')f_\mathcal {G}''\Big \}\nonumber \\&+\,2e^b[2\{8\lambda +r(4+7\lambda )b'\}f_\mathcal {G}'\nonumber \\&+\,r\lambda (r^2a''+4f_\mathcal {G}'')]\Big \}\Big \}\Big ], \end{aligned}$$

(13)

$$\begin{aligned} p_\mathrm{t}= & {} \frac{e^{-2b}}{4r^4(1+\lambda )(1+2\lambda )}\Big [-2e^{2b}r^4(1+\lambda )f_1\nonumber \\&+\,2f_\mathcal {G}\Big \{4(-1+e^b)^2(1+\lambda )\nonumber \\&+\,r^2\Big \{\{-1+2e^b(1+\lambda )\}a'^2\nonumber \\&-\,2(-3+e^b)(1+\lambda )a'b'+b'^2+4(-1+e^b)(1\nonumber \\&+\,\lambda )a''\Big \}\Big \}-r\Big \{4f_\mathcal {G}'[8\lambda \nonumber \\&+\,r\{b'(-7\lambda -2r(1+\lambda )b')+r(2+6\lambda \nonumber \\&+\,r(2+3\lambda )b')a''\}]+8r\lambda (1-2rb'+r^2a'')f_\mathcal {G}''\nonumber \\&+\,2e^b\{-16\lambda f_\mathcal {G}'-rb'(r+2r\lambda -\,2\lambda f_\mathcal {G}')\nonumber \\&+r^3(1+\lambda )a''-4r\lambda f_\mathcal {G}''\}+r^2a'^2\Big \{e^br(1+\lambda )\nonumber \\&+\,2\Big \{2+6\lambda +r(2+3\lambda )b'\Big \}f_\mathcal {G}'+4r\lambda f_\mathcal {G}''\Big \}\nonumber \\&+\,ra'-2[-10\lambda +rb'\{2+6\lambda \nonumber \\&+\,r(2+3\lambda )b'\}]f_\mathcal {G}'+e^b[-r\{-2+r(1+\lambda )b'\}\nonumber \\&+\,4\lambda f_\mathcal {G}']+4r(2+6\lambda -r\lambda b')f_\mathcal {G}''\Big \}\Big ], \end{aligned}$$

(14)

where a prime denotes the radial derivative.

3 Matching with Schwarzschild’s exterior metric

Whatever the geometry of the star is, either derived internally or externally, the intrinsic boundary metric remains the same. Thus, one confirms that the components of the metric tensor irrespective of the coordinate system across the surface of the boundary will remain continuous. No doubt, in GR, the Schwarzschild solutions have been the lead in guiding us to choose from the diverse possibilities of the matching conditions while investigating the stellar compact objects. Now when we come to the case of modified theories of gravity, modified TOV equations with zero pressure and energy density, the solution outside the star can differ from Schwarzschild’s solution. However, it is expected that the solutions of the modified TOV equations with energy density and pressure (maybe non-zero) may accommodate Schwarzschild’s solution with some specific choice of the $f(\mathcal {G},T)$ gravity model. Perhaps this is the reason that Birkhoff’s theorem may not hold in modified gravity. A detailed investigation of the issue in the context of $f(\mathcal {G},T)$ gravity can be an interesting task. Many authors have considered the Schwarzschild solution for this purpose, giving some interesting results [52,53,54,55]. Now to solve the field equations under the restricted boundary conditions at $r=R$, the pressure $p_\mathrm{r}=0$, the interior metric (11) requires these matching conditions. This can be done by taking a smooth match at $r=R$ to Schwarzschild’s exterior metric, given by

$$\begin{aligned} \mathrm{d}s^{2}=\Big (1-\frac{2M}{r}\Big )\mathrm{d}t^{2}-\Big (1-\frac{2M}{r}\Big )^{-1}\mathrm{d}r^{2}-r^{2}(\mathrm{d}\theta ^{2}+{\text {sin}}^{2}\theta \mathrm{d}\phi ^{2}), \end{aligned}$$

(15)

yielding

$$\begin{aligned} g^{-}_{tt}=g^{+}_{\alpha },~~~g^{-}_{rr}=g^{+}_{rr},~~~\frac{\partial g^{-}_{\alpha }}{\partial r}=\frac{\partial g^{+}_{\alpha }}{\partial r}, \end{aligned}$$

(16)

where $(+)$ corresponds to the exterior solution and $(-)$ to the interior solution. Now from a comparison of exterior and interior metrics, the constants A, B, and C are obtained:

$$\begin{aligned} A= & {} \frac{-1}{R^{2}}{\text {ln}}\Big (1-\frac{2M}{R}\Big ), \end{aligned}$$

(17)

$$\begin{aligned} B= & {} \frac{M}{R^{3}}\Big (1-\frac{2M}{R}\Big ), \end{aligned}$$

(18)

$$\begin{aligned} C= & {} {\text {ln}}\Big (1-\frac{2M}{R}\Big )-\frac{M}{R}\Big (1-\frac{2M}{R}\Big ). \end{aligned}$$

(19)

The approximated values of the mass M and radius R of the compact stars Her X-1, SAX J1808.4-3658 and 4U1820-30 are used to calculate the values of constants A and B [56, 57]. The result $\mu =\frac{M(R)}{R}$ defines the compactness of the star and the expression $Z_\mathrm{s}=(1-2\mu )^{-1/2}-1$ determines the surface redshift $Z_\mathrm{s}$. For the compact stars under consideration, the values of $Z_\mathrm{s}$ are given in Table 1.

Table 1 The approximate values of the masses M, radii R, compactness $\mu$, and the constants A, and B for the compact stars Her X-1, SAXJ 1808.4-3658, and 4U 1820-30

Now making use of the Krori and Barua metric, Eqs. (12)–(14) take the form

$$\begin{aligned} \rho= & {} \frac{e^{-2Ar^{2}}}{2r^{4}(1+\lambda )(1+2\lambda )}\Big [4\Big \{-\lambda -e^{2Ar^{2}}\lambda \nonumber \\&+\,2e^{Ar^{2}}\{\lambda +Br^{2}(1+(-A+B)r^{2})(1+\lambda )\nonumber \\&+\,r^{2}\{-2A^{2}r^{2}\lambda +\,2B(-1+3Ar^{2})(1+\lambda )\nonumber \\&+\,B^{4}r^{6}(1+2\lambda )-2B^{3}r^{4}(-1+Ar^{2})(1+2\lambda )\nonumber \\&+\,B^{2}r^{2}(1+4\lambda +Ar^{2}(-2+Ar^{2})(1+2\lambda ))\}\}\Big \}f_{\mathcal {G}}\nonumber \\&+\,r\Big \{-4(2+5\lambda )+r^{2}(10A-24B\nonumber \\&-\,4B(A+2B)r^{2}+4A(A-B)Br^{4}+\{27A\nonumber \\&-\,55B-2(2A^2+2AB+9B^{2})r^{2}\nonumber \\&+\,6A(A-B)Br^{4}\}\lambda )\nonumber \\&+\,e^{Ar^{2}}[8+20\lambda +r^{2}(-B\lambda +A(2+3\lambda ))]f_{\mathcal {G}}'\nonumber \\&+\,r(e^{Ar^{2}}(-2+4Ar^{2}-4\lambda +2r^{2}(4A+3B\nonumber \\&+\,B(-A+B)r^{2})\lambda +e^{Ar^{2}}(2+4\lambda -8^{n}r^{2}\nonumber \\&\times \,\frac{1}{r^{2n}}\Big (Be^{-2Ar^{2}}(1+(-3A+B)r^{2}\nonumber \\&+\,e^{Ar^{2}}(-1+(A-B)r^{2}))\Big )^{n}\nonumber \\&\times \,\alpha (1+\lambda )))+4(-2-5\lambda +e^{Ar^{2}}(2+5\lambda )\nonumber \\&+\,2r^{2}(A(2+Br^{2})(2+5\lambda )\nonumber \\&-\,B(6+14\lambda +Br^{2}(2+5\lambda ))))f_{\mathcal {G}}'')\Big \}\Big ], \end{aligned}$$

(20)

$$\begin{aligned} \ p_\mathrm{r}= & {} \frac{e^{-2Ar^{2}}}{2r^{4}(1+\lambda )(1+2\lambda )}\Big [4\Big \{-(-1\nonumber \\&+\,e^{Ar^{2}})^{2}\lambda +2A^{2}r^{4}(1+\lambda )\nonumber \\&-\,2Br^{2}(1-3Ar^{2}+e^{Ar^{2}}(-1+Ar^{2}))(1+\lambda )\nonumber \\&+\,B^{4}r^{8}(1+2\lambda )-2B^{3}r^{6}(-1+Ar^{2})(1+2\lambda )\nonumber \\&+\,B^{2}r^{4}(-1+2e^{Ar^{2}}(1+\lambda )\nonumber \\&+\,Ar^{2}(-2+Ar^{2})(1+2\lambda ))\Big \}f_\mathcal {G}\nonumber \\&+\,r(e^{Ar^{2}}r(e^{Ar^{2}}(2+4\lambda -8^{n}r^{2}\nonumber \\&\times \,\frac{1}{r^{2n}}\Big (Be^{-2Ar^{2}}(1+(-3A+B)r^{2}\nonumber \\&+\,e^{Ar^{2}}(-1+(A-B)r^{2}))\Big )^{n}\nonumber \\&\times \,\alpha (1+\lambda ))-2(1+2\lambda \nonumber \\&+\,Br^{2}(2+(1+(A-B)r^{2})\lambda )))\nonumber \\&+\,4(-4\lambda -r^{2}(4A+6B+8ABr^{2}\nonumber \\&+\,(A+19B+2(2A^{2}+6AB+B^{2})r^{2}\nonumber \\&+\,2A(A-B)Br^{4})\lambda )+e^{Ar^{2}}(4\lambda +r^{2}(B(2\nonumber \\&+\,3\lambda )+A(4+7\lambda ))))f_\mathcal {G}'\nonumber \\&+\,4r(-1+e^{Ar^{2}}+2(A-B)r^{2}(2+Br^{2}))\lambda f_\mathcal {G}'')\Big ],\nonumber \\ \end{aligned}$$

(21)

$$\begin{aligned} p_\mathrm{t}= & {} \frac{e^{-2Ar^{2}}}{2r^{4}(1+\lambda )(1+2\lambda )}\Big [4(1+A^{2}r^{4}\nonumber \\&-\,B^{2}r^{4}+\lambda +e^{2Ar^{2}}(1+\lambda )\nonumber \\&+\,2Br^{2}(-1+3Ar^{2})(1+\lambda )+2e^{Ar^{2}}(-1\nonumber \\&+\,Br^{2}+B(-A+B)r^{4})\nonumber \\&\times \,(1+\lambda ))f_\mathcal {G}+r(e^{Ar^{2}}r^{3}(-8^{n}e^{Ar^{2}}\nonumber \\&\times \,\frac{1}{r^{2n}}\Big (Be^{-2Ar^{2}}(1+(-3A+B)r^{2}\nonumber \\&+\,e^{Ar^{2}}(-1+(A-B)r^{2}))\Big )^{n}\alpha (1+\lambda )\nonumber \\&-\,2B(2+\lambda +Br^{2}(1+\lambda ))+2A\nonumber \\&\times \,(1+2\lambda +Br^{2}(1+\lambda )))+4(4(-1+e^{Ar^{2}})\lambda \nonumber \\&+\,r^{2}(A(-(-7+e^{Ar^{2}})\lambda \nonumber \\&+\,4Ar^{2}(1+\lambda ))-2B^{2}r^{2}(1+3\lambda \nonumber \\&+\,Ar^{2}(2+3\lambda ))+B(-2-(11+e^{Ar^{2}}))\lambda \nonumber \\&+\,2Ar^{2}(-1+Ar^{2}(2+3\lambda )))))f_\mathcal {G}'\nonumber \\&-\,4r(\lambda -e^{Ar^{2}}\lambda +2r^{2}(B-2A\lambda \nonumber \\&+\,B(4+(-A+B)r^{2})\lambda ))f_\mathcal {G}'')\Big ], \end{aligned}$$

(22)

where

Fig. 1

Plot of the density evolution of the strange star candidate Her X-1, SAX J 1808.4-3658, and 4U 1820-30; represented by (left to right) the first, second, and third graphs, respectively

Fig. 2

Plots of the radial pressure evolution of the strange star candidates Her X-1, SAX J 1808.4-3658, and 4U 1820-30; represented by (left to right) the first, second, and third graphs, respectively

Fig. 3

Plots of the transverse pressure evolution of the strange star candidates Her X-1, SAX J 1808.4-3658, and 4U 1820-30; represented by (left to right) the first, second, and third graphs, respectively

$$\begin{aligned} f_{1}= & {} \alpha \Big [\frac{e^{-2Ar^{2}} (-16ABr^{2}+2(1-e^{Ar^{2}})(4B-4ABr^{2}+4B^{2} r^{2}))}{r^{2}}\Big ]^{n},\nonumber \\ \end{aligned}$$

(23)

$$\begin{aligned} f_{\mathcal {G}}'= & {} \frac{1}{r^{3}}\Big [2^{-2+3n}Be^{-2Ar^{2}}(-1\nonumber \\&+\,n)n(Be^{-2Ar^{2}}(1+(-3A+B)r^{2}\nonumber \\&+\,e^{Ar^{2}}(-1+(A-B)r^{2}))){r^{2}}^{-2+n}(-1\nonumber \\&+\,6A^{2}r^{4}-2A(r^{2}+Br^{4})\nonumber \\&+\,e^{Ar^{2}}(1+Ar^{2}+A(-A+B)r^{4}))\alpha \Big ], \end{aligned}$$

(24)

$$\begin{aligned} f_{\mathcal {G}}''= & {} \frac{4^{-1+2n}e^{3Ar^{2}}(-1+n)n\alpha }{B(-1+(3A-B)r^{2}+e^{Ar^{2}}(1+(-A+B)r^{2}))^{3}}\nonumber \\&\times \frac{1}{r^{2n}}\Big (-Be^{-\frac{3Ar^{2}}{2}}\left( Ar^{2}{\text {cosh}}\left( \frac{Ar^{2}}{2}\right) \right) \nonumber \\&+\,(1+(2A+B)r^{2}){\text {sinh}}\left. \left( \frac{Ar^{2}}{2}\right) \right) \Big )^{n}\nonumber \\&\times \,(2-4n-3(2B+A(-9+4n))r^{2}\nonumber \\&+\,2A(9B-6Bn+A(-21+10n))r^{4}\nonumber \\&+\,A(3B^2-16ABn+A^{2}(-15+32n))r^{6}\nonumber \\&-\,2A^{2}(3A^{2}-4AB+B^{2})\nonumber \\&\times (-3+4n)r^{8}+(-2+4n+3(2B\nonumber \\&+\,A(-9+4n))r^{2}+2A(16A-9B\nonumber \\&-\,9An+6Bn)r^{4}+A(-3B^{2}+A^{2}(33-52n)\nonumber \\&+\,2AB(-3+10n))r^{6}\nonumber \\&+\,2A^{2}(37A^{2}-26AB+5B^{2})(-1\nonumber \\&+\,n)r^{8}){\text {cosh}}(Ar^{2})+Ar^{2}(11-4n\nonumber \\&+\,2(B(3-2n)+A(-12+7n))r^{2}+(B^{2}\nonumber \\&+\,2AB(1-6n)+A^{2}(-27\nonumber \\&+\,44n))r^{4}-2A(7A-3B)(5A-B)(-1\nonumber \\&+\,n)r^6){\text {sinh}}(Ar^2)). \end{aligned}$$

(25)

Now we investigate the nature and some interesting features of the compact star, specifically for the assumed model of $f(\mathcal {G},T)$ gravity.

4 Physical aspects of $f(\mathcal {G},T)$ gravity model

In this section, some interesting physical aspects of compact stars, such as the energy density and pressure evolutions, energy conditions, equilibrium conditions, stability and adiabatic index analysis, compactness, and redshift analysis, shall be discussed.

4.1 Energy density and pressure evolutions

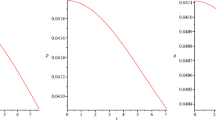
The plot of the energy density for the strange star candidate Her X-1 (Fig. 1) shows that as $r\rightarrow 0$, $\rho$ goes to maximum, and this in fact indicates the high compactness of the core of the star, validating that our model under investigation is viable for the outer region of the core. The other two graphs in the same row provide us with a similar sort of conclusions. Furthermore, from the other plots of the anisotropic radial pressure $p_\mathrm{r}$ (Fig. 2), it is evident that the radius of the star for this model is $R=10$ km, which further gives us a density of $1.5828\times 10^{15}$ g cm$^{-3}$, a high value with a small radius of 10 km, showing that our $f(\mathcal {G},T)$ model is compatible with the structure of the ultra-compact star [10, 59]. A comparison of this with the already existing data labels this compact star as quark/strange star [60]. All the three plots in Fig. 3 indicate that the tangential pressure $p_\mathrm{t}$ remains positive and finite and show their decreasing behaviour, which is required for the viability of the compact star model.

Fig. 4

Plots of $\frac{\mathrm{d}\rho }{\mathrm{d}r}$ with increasing radius of the strange star candidates Her X-1, SAX J 1808.4-3658, and 4U 1820-30; represented by (left to right) the first, second, and third graphs, respectively

Fig. 5

Variations of $\frac{\mathrm{d}p_\mathrm{r}}{\mathrm{d}r}$ with increasing radius of the strange star candidate Her X-1, SAX J 1808.4-3658, and 4U 1820-30; represented by (left to right) the first, second, and third graphs, respectively

The variations of the radial derivatives of the density and radial pressure are shown in Figs. 4 and 5, respectively. One can see the decreasing evolution of the first r-derivatives, i.e. $\frac{\mathrm{d}\rho }{\mathrm{d}r}<0$ and $\frac{\mathrm{d}p_\mathrm{r}}{\mathrm{d}r}<0$. It may be noted here that at $r=0$, these derivatives just disappear except for the radial pressure for the SAX J 1808.4-3658 candidate. The mathematical calculations for the second derivative test both for $\rho$ and $p_\mathrm{r}$ tell us that $\frac{\mathrm{d}^{2}\rho }{\mathrm{d}r^{2}}<0$ and $\frac{\mathrm{d}^{2}p_\mathrm{r}}{\mathrm{d}r^{2}}<0$, indicating the maximum values of the density and radial pressure at the centre. This further suggests the compact nature of the star.

4.2 Energy conditions

For the viability of the model, the energy bounds must be satisfied due to their significant importance in analysing the theoretical data. NEC (null energy conditions), WEC (weak energy conditions), SEC (strong energy conditions), and DEC (dominant energy conditions) are given as

$$\begin{aligned} \mathbf{NEC }:&\rho +p_\mathrm{r}\ge 0,~~~~\rho +p_\mathrm{t}\ge 0,\\ \mathbf{WEC }:&\rho \ge 0,~~~~\rho +p_\mathrm{r}\ge 0,~~~~\rho +p_\mathrm{t}\ge 0,\\ \mathbf{SEC }:&\rho +p_\mathrm{r}\ge 0,~~~~\rho +p_\mathrm{t}\ge 0,~~~~\rho +p_\mathrm{r}+2p_\mathrm{t}\ge 0,\\ \mathbf{DEC }:&\rho>|p_\mathrm{r}|,~~~~\rho >|p_\mathrm{t}|. \end{aligned}$$

The evolution of all these energy conditions have been well satisfied as represented graphically for the strange star candidate Her X-1 in Fig. 6. Hence our solutions are physically viable.

4.3 Tolman–Oppenheimer–Volkoff (TOV) equation

In anisotropic case, the generalized TOV equation is given as

$$\begin{aligned} \frac{M_\mathrm{G}(r)(\rho +p_\mathrm{r})}{r^{2}}e^{\frac{b-a}{2}} +\frac{\mathrm{d}p_\mathrm{r}}{\mathrm{d}r}-\frac{2}{r}(p_\mathrm{t}-p_\mathrm{r})= & {} 0, \end{aligned}$$

(26)

where

$$\begin{aligned} M_\mathrm{G}(r)= & {} \frac{1}{2}r^{2}e^{\frac{a-b}{2}}a' \end{aligned}$$

(27)

is the gravitational mass of a sphere of radius r. Now putting Eq. (27) into Eq. (26), it follows

$$\begin{aligned} -\frac{a'}{2}(\rho +p_\mathrm{r})-\frac{\mathrm{d}p_\mathrm{r}}{\mathrm{d}r}+\frac{2}{r}(p_\mathrm{t}-p_\mathrm{r})= & {} 0. \end{aligned}$$

(28)

Equation (28) gives the information as regards the stellar configuration equilibrium under the combined effect of different forces, like the anisotropic force $F_\mathrm{a}$, the hydrostatic force $F_\mathrm{h}$, and the gravitational force $F_\mathrm{g}$. Their summation to zero eventually describes the equilibrium condition of the form

$$\begin{aligned} F_\mathrm{g}+F_\mathrm{h}+F_\mathrm{a}= & {} 0, \end{aligned}$$

(29)

where

Fig. 6

Plots of energy conditions with respect to radius r (km) of the strange star candidate Her X-1

Fig. 7

The plot of gravitational force $(F_\mathrm{g})$, hydrostatic force $(F_\mathrm{h})$ and anisotropic force $(F_\mathrm{a})$ for the strange star candidate Her X-1 with respect to the radial coordinate r (km)

$$\begin{aligned} F_\mathrm{g}= & {} -\frac{a'}{2}(\rho +p_\mathrm{r}),\nonumber \\ F_\mathrm{h}= & {} -\frac{\mathrm{d}p_\mathrm{r}}{\mathrm{d}r},\nonumber \\ F_\mathrm{a}= & {} \frac{2}{r}(p_\mathrm{t}-p_\mathrm{r}). \end{aligned}$$

(30)

From Fig. 7, it can be noticed that under the mutual effect of the three forces $F_\mathrm{g}$, $F_\mathrm{h}$ and $F_\mathrm{a}$, the static equilibrium might be achieved. It is mentioned here that at some point if $p_\mathrm{r}=p_\mathrm{t}$ then $F_\mathrm{a}=0$, which suggests that the equilibrium becomes independent of the anisotropic force $F_\mathrm{a}$.

Fig. 8

Variations of $v^{2}_{\text {sr}}$ with respect radius r (km) of the strange star candidate Her X-1, SAX J 1808.4-3658, and 4U 1820-30; represented by (left to right) the first, second, and third graphs, respectively

Fig. 9

Variations of $v^{2}_{\text {st}}$ with respect radius r (km) of the strange star candidate Her X-1, SAX J 1808.4-3658, and 4U 1820-30; represented by (left to right) the first, second, and third graphs, respectively

4.4 Stability analysis

For the stability, the radial and transversal sound speeds denoted by $v^{2}_{\text {sr}}$ and $v^{2}_{\text {st}}$, respectively, should satisfy the bounds, $0\le {v^{2}_{\text {sr}}}\le 1$ and $0\le {v^{2}_{\text {st}}}\le 1$ [61], where $\frac{\mathrm{d}p_\mathrm{r}}{\mathrm{d}\rho }=v^{2}_{\text {sr}}$ and $\frac{\mathrm{d}p_\mathrm{t}}{\mathrm{d}\rho }=v^{2}_{\text {st}}$. It can be seen from Figs. 8 and 9 that the evolution of the radial and transversal sound speeds for the strange star candidate Her X-1 are within the bounds of stability as discussed, but in the case of SAX J 1808.4-3658, and 4U 1820-30 strange star candidates, the radial sound speeds evolution expressed in the radial coordinate r temporarily violates these stability conditions. However, for the same candidates the requirements for the transversal sound speeds are satisfied. Within the matter distribution, the estimation of the potentially stable and unstable eras can be obtained from the difference of the sound propagation speeds, found by the expression $v^{2}_{\text {st}}-v^{2}_{\text {sr}}$, satisfying the inequality $0<|v^{2}_{\text {st}}-v^{2}_{\text {sr}}|<1$. This can be seen clearly from the plots of Fig. 10. Thus, overall the stability may be attained for compact stars in the $f(\mathcal {G},T)$ gravity model, particularly for the strange star candidate Her X-1.

Fig. 10

Variations of $v^{2}_{\text {st}}-v^{2}_{\text {sr}}$ with respect to radius r (km) of the strange star candidate Her X-1, SAX J 1808.4-3658, and 4U 1820-30; represented by (left to right) the first, second, and third graphs, respectively

4.5 Adiabatic index analysis

For the case of an anisotropic fluid spherical star, as proposed in [62, 63], the stability depends on the adiabatic index $\gamma$, and for the radial and tangential cases, we, respectively, have

$$\begin{aligned} \gamma _{r}=\frac{\rho +p_\mathrm{r}}{p_\mathrm{r}}\frac{\mathrm{d}p_\mathrm{r}}{\mathrm{d}\rho }~~\text {and}~~\gamma _{t}=\frac{\rho +p_\mathrm{t}}{p_\mathrm{t}}\frac{\mathrm{d}p_\mathrm{t}}{\mathrm{d}\rho }. \end{aligned}$$

(31)

The stability of a Newtonian sphere should be satisfied if $\gamma >\frac{4}{3}$, and $\gamma =\frac{4}{3}$ is the condition for the occurrence of neutral equilibrium [64]. Due to the presence of the effective pressure, the anisotropic relativistic sphere obeys the more complicated stability condition given by

$$\begin{aligned} \gamma > \frac{4}{3}+\Big [\frac{4}{3}\frac{p_{\mathrm{t}_{0}}-p_{\mathrm{r}0}}{|p'_{\mathrm{r}_{0}}|r}+\frac{8\pi }{3}\frac{\rho _{0}p_{\mathrm{r}_{0}}r}{|p'_{\mathrm{r}_{0}}|}\Big ]_{\text {max}}, \end{aligned}$$

(32)

where $\rho _{0}$, $p_{\mathrm{t}_{0}}$, and $p_{\mathrm{r}_{0}}$ are the initial energy density, tangential pressure, and radial pressure in static equilibrium, respectively, satisfying Eq. (26). In our case, the adiabatic index has been calculated analytically for the strange star candidate Her X-1, giving us $\gamma _\mathrm{r}=1.3757$ and $\gamma _\mathrm{t}=1.0597$, which shows the complete stability in the radial case but some deviation in the tangential case.

4.6 Mass–radius relationship

The mass of the compact star as a function of radius r is given as

$$\begin{aligned} M(r)=4\int _{0}^{r}\pi {\acute{r}}^2\rho \mathrm{d}{\acute{r}}. \end{aligned}$$

(33)

It can be seen clearly from the profile of the mass function given in Fig. 11 that the mass of the star is directly proportional to the radius, and $M(r)\rightarrow 0$ as $r\rightarrow 0$, which shows that the mass function is regular at the centre of the star. Moreover, for the spherically symmetric anisotropic perfect fluid case, the ratio of the mass to the radius, according to Buchdahl [6], should be bounded like $\frac{2M}{r}\le \frac{8}{9}$. In our case, the situation is very good as we get $\frac{2M}{r}=0.4987$ and the condition is clearly satisfied.

Fig. 11

Evolution of the mass function M(r) for the strange star candidate Her X-1 with respect to the radial coordinate r (km)

Fig. 12

Plots of the compactness $\mu (r)$ and surface redshift $(Z_\mathrm{s})$ of the strange star candidate Her X-1 with respect to the radial coordinate r (km)

Fig. 13

Variations of the radial EoS parameter with respect to the radial coordinate r(km) of the strange star candidate Her X-1, SAX J 1808.4-3658, and 4U 1820-30; represented by (left to right) the first, second, and third graphs, respectively

Fig. 14

Variations of the tangential EoS parameter with respect to the radial coordinate r (km) of the strange star candidate Her X-1, SAX J 1808.4-3658, and 4U 1820-30; represented by (left to right) the first, second, and third graphs, respectively

Fig. 15

Variations of anisotropic measure $\Delta$ with respect to the radial coordinate r (km) of the strange star candidate Her X-1, SAX J 1808.4-3658, and 4U 1820-30; represented by (left to right) the first, second, and third graphs, respectively

4.7 Compactness and redshift analysis

Compactness $\mu (r)$ of the star is expressed as

$$\begin{aligned} \mu (r)=\frac{4}{r}\int _{0}^{r}\pi \acute{r^2}\rho \mathrm{d}\acute{r}. \end{aligned}$$

(34)

Therefore, the redshift $Z_\mathrm{S}$ is determined as

$$\begin{aligned} Z_\mathrm{S}+1=[-2\mu (r)+1]^{\frac{-1}{2}}. \end{aligned}$$

(35)

The graphical evolution of the surface redshift is given in Fig. 12. The value of the function $Z_{S}$ for the case of the strange star candidate Her X-1 is calculated as $Z_\mathrm{S}\approx 0.22$, which is within the desired bound of $Z_\mathrm{S}\le 2$.

4.8 EoS parameter and the measurement of anisotropy

Now for the anisotropic case, the radial and transversal forms of the EoS parameter can be written as

$$\begin{aligned} \omega _\mathrm{r}=\frac{p_\mathrm{r}}{\rho }~~\text {and}~~\omega _\mathrm{t}=\frac{p_\mathrm{t}}{\rho }. \end{aligned}$$

(36)

The evolution of these EoS parameters with the increasing radius is shown in Figs. 13 and 14, which clearly demonstrates that all the six plots satisfy the inequalities $0<\omega _\mathrm{r}<1$ and $0<\omega _\mathrm{t}<1$. This further advocates the effectiveness of the considered model.

The measurement of the anisotropy denoted by $\Delta$ is given by

$$\begin{aligned} \Delta =\frac{2}{r}{(p_\mathrm{t}-p_\mathrm{r})}, \end{aligned}$$

(37)

which gives the information as regards the anisotropic behaviour of the model. $\Delta$ remains positive if $p_\mathrm{t}>p_\mathrm{r}$, suggesting the anisotropy being drawn outward, and for the reverted situation, i.e., $p_\mathrm{t}<p_\mathrm{r}$, the anisotropy $\Delta$ turns negative, which corresponds to being directed inward. For our situation, the variations of the anisotropic measurement $\Delta$ with respect to the radial coordinate r show the decreasing negative behaviour for the strange star candidate Her X-1 and SAX J 1808.4-3658 suggesting that $p_\mathrm{t}<p_\mathrm{r}$. For the 4U 1820-30 candidate, it remains positive for a fraction of the radius r where some repulsive anisotropic force followed by the massive matter distribution appears, and very soon it gets negative after $r=0.25$ (Fig. 15).

5 Concluding discussion

In this paper, we have presented some useful discussions related to the emergence of compact stars in the newly introduced $f(\mathcal {G},T)$ theory of gravity by considering the model $f(\mathcal {G},T)=\alpha \mathcal {G}^n+\lambda {T}$. We have tested this model for the strange star candidates Her X-1, SAX J 1808.4-3658, and 4U 1820-30 for an anisotropic case by using the Krori and Barua approach of the metric function [15], that is, $a=Br^2+C,~b=Ar^2$. The arbitrary constants A, B, and C are calculated by smoothly matching the interior metric conditions with Schwarzschild’s exterior metric conditions. This phenomenon makes us understand the nature of the compact stars by expressing their masses and radii in terms of the arbitrary constants.

By using these constants in our investigation for the strange star candidates Her X-1, SAX J 1808.4-3658, and 4U 1820-30 the energy density, and radial and tangential pressures have been plotted with respect to the radial coordinate r indicating that when r approaches zero, the density goes to its maximum for all the three strange star candidates. The same is the situation for the tangential pressure but different behaviour in the case of the radial pressure for the 4U 1820-30 candidate. Mainly, this situation admits the theory that the core of compact stars under consideration is intensely compact, particularly in the case of the strange star candidate Her X-1. We have succeeded to determine the density of the emerging compact star $(\approx 1.5828\times 10^{15}~{\text {g~cm}}^{-3})$ after estimating the radius of the star $(R\approx 10)$ from the evolution of the radial pressure. The evolution of the EoS parameters with the increasing radius satisfies the inequalities $0<\omega _\mathrm{r}<1$ and $0<\omega _\mathrm{t}<1$ for the radial and tangential EoS parameters, respectively, which favours the acceptance of the model of our study. We have also shown through the graphical representation that all the energy conditions, namely NEC, WEC, SEC, and DEC, are satisfied for the proposed $f(\mathcal {G},T)$ gravity model in the case of Her X-1, favouring the physical viability of the model.

The static equilibrium, to some extent, has been established by plotting the three forces $F_\mathrm{g}$, $F_\mathrm{h}$, and $F_\mathrm{a}$ comprised in the TOV equation. The evolution of the radial and transversal sound speeds, denoted by $v^{2}_{\text {sr}}$ and $v^{2}_{\text {st}}$, respectively, for the strange star candidate Her X-1 are within the bounds of stability [61], but in the case of the strange star candidates SAX J 1808.4-3658, and 4U 1820-30, the radial sound speed $v^{2}_{\text {sr}}$ evolutions temporarily violate these stability conditions. However, for the same candidates the requirements for the transversal sound speeds $v^{2}_{\text {st}}$ are satisfied. Within the matter distribution, the estimation of the strongly stable and unstable eras from the difference of the propagations of the sound speeds satisfies the inequality $0<|v^{2}_{\text {st}}-v^{2}_{\text {sr}}|<1$ for all the candidates as shown in Fig. 11. Thus, overall the stability is attained for the compact star $f(\mathcal {G},T)$ model, particularly for the strange star candidate Her X-1.

We have also investigated the dynamical stability by analytically calculating the adiabatic index $\gamma$ of the model both for the radial and tangential pressures for the strange star candidate Her X-1, giving us $\gamma _\mathrm{r}=1.3757>4/3$ and $\gamma _\mathrm{t}=1.0597$, which shows the complete stability in radial case but a slight deviation in the tangential case. We have found the direct proportionality of the mass function to the radius, and $M(r)\rightarrow 0$ as $r\rightarrow 0$, suggesting that the mass function is regular at the centre of the star. Moreover, for the spherically symmetric anisotropic fluid case, the ratio of the mass to the radius has been calculated as $\frac{2M}{r}=0.4987$, satisfying $\frac{2M}{r}\le \frac{8}{9}$ as proposed by Buchdahl [6]. The evolution of the compactness of the star for Her X-1 favours the model. The values of the surface redshift function $Z_\mathrm{S}$ are within the bound of $Z_\mathrm{S}\le 2$ and, for the case of the strange star candidate Her X-1, the redshift value is calculated as $Z_\mathrm{S}\approx 0.22$, which satisfies the upper bound $Z_\mathrm{S}\le 2$. This further indicates the stability of the model of our study. Conclusively, for the case of the strange star candidate Her X-1, all the physical parameters have been more consistent to favour the $f(\mathcal {G},T)$ gravity model of our study as compared to the other two candidates SAX J 1808.4-3658 and 4U 1820-30. The overall consistency for the model may be improved by considering some more suitable choices of the physical parameters.