1 Introduction

The experimental data on azimuthal angular correlations (see Refs. [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22] show surprizing similarities between different processes: nucleus-nucleus, hadron–nucleus and hadron–hadron collisions. The popular explanation is related to elliptic flow, and stems from the interaction in the final state. In the framework of such an approach, we have to assume that the proton interactions are similar to nucleus scattering, at least for events with large multiplicity. However, the ATLAS data [17, 18] show that \(v_{2,2}\), \(v_{3,3}\) and \(v_{4,4}\) do not depend on multiplicity at \(W=13\) TeV and at \(W= 2.76\) TeV.

In this paper we will discuss these correlations from a different point of view. We believe that the general origin of the azimuthal angular correlations in all reactions, stems from the Bose–Einstein correlations (BEC) of the produced gluons, which originate from the gluon wave function in the initial state [23,24,25,26,27,28,29,30,31,32,33,34]. The attractive feature of this idea is that BECs have a general source that characterizes the volume of the interaction [35,36,37,38]. Therefore, the main dimensional parameters of the interaction that manifest themselves in diffraction scattering, and in inclusive production, should determine the BEC. In other words, in spite of the embryonic stage of our understanding of the confinement of quarks and gluons, we can develop a quantitative approach for the BEC in the framework of a model for soft interactions at high energy. To accomplish this, we need to construct such a model which will allow us to discuss soft and hard processes on the same footing.

The main goal of this paper is to develop such model. Fortunately, we have built a model which provides a good description of all the soft data [39,40,41,42,43,44], including, total, inelastic, elastic and diffractive cross sections, the t-dependence of these cross sections, as well as the inclusive production and rapidity correlations. In this paper we expand this model to include the hard interactions mostly using the geometric scaling behavior of the scattering amplitude [45,46,47,48] for the hard kinematic region in the Color Glass Condensate (CGC)/saturation approach [49].

The idea of BEC being the main source of the azimuthal angular correlations is marred by the observation [27,28,29] that the process of the central diffractive production of colorless gluon dijets gives a contribution which is equal to that of the BEC.Footnote 1 In this case \(v_{n,n}\) with odd n are equal to zero, while \(v_{n,n}\) with even n, are twice larger. We will not discuss this problem here. Our main goal is to obtain reliable quantitative estimates for \(v_{n,n}\). However, we believe that due to the Sudakov suppression in the double log approximation of perturbative QCD, the dijet contribution is negligibly small [50].

The paper is organized as follows. In the next section we give a brief review of our model which is based on the CGC/saturation approach. We discuss what we have taken from the theory in our approach, and what we have considered from a pure phenomenological approach. We will attempt to clarify the physical meaning of the introduced phenomenological parameters, and show how we include three dimensional sizes, which have been used to describe the scattering amplitude. In the language of the constituent quark model these three sizes are the hadron radius, the size of the constituent quark, and the saturation momentum, which is a typical scale for the high energy amplitude.

In Sect. 3 we generalize our model including the construction of an amplitude at short distances, which is able to describe the deep inelastic scattering (DIS). We compare our amplitude with HERA experimental data [51, 52]. In Sect. 4 we calculate the inclusive cross section, and show that we obtain good agreement with the experimental data. This is very important for our calculation, since it demonstrates that we are able to describe the experimental data for inclusive production not only at short distances, but also at long distances.

In Sect. 5 we calculate the value of BE correlations, its energy and multiplicity dependence. We obtain the values of \(v_n\) which are a bit larger than the experimental ones, with a mild dependence on energy and multiplicity. We consider these estimates as the first quantitative prediction for \(v_n\) in proton–proton scattering, which are in agreement with the values of the inclusive cross sections, and the cross sections for the hard processes.

In Sect. 6 we draw our conclusions and outline the problems for future investigations.

2 The model

2.1 Theoretical input from the CGC/saturation approach

In this section we generalize our model for soft interactions at high energy [39,40,41,42,43,44] to include a description of hard processes. This model incorporates two ingredients: the achievements of the CGC/saturation approach, which is an effective theory for QCD at high energy; and the pure phenomenological treatment of the long distance non-perturbative physics, due to the lack of the theoretical understanding of confinement of quark and gluons.

We wish to stress that most of this section does not contain new results; it reviews our approach, and it is included in the paper only for the sake of completeness of presentation. One can find more details in Refs. [39,40,41,42,43,44].

Fig. 1
figure 1

a Shows the set of diagrams in the BFKL Pomeron calculus that produce the resulting (dressed) Green function of the Pomeron in the framework of high energy QCD. The red blobs denote the amplitude for the dipole–dipole interaction at low energy. In b the net diagrams, which include the interaction of the BFKL Pomerons with colliding hadrons, are shown. The sum of the diagrams after integration over the positions of \(G_{3 I\!\!P}\) in rapidity reduces to c

Full size image

The effective theory for QCD at high energies exists in two different formulations: the CGC/saturation approach [53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69], and the BFKL Pomeron calculus [70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97]. In building our model we rely on the BFKL Pomeron calculus, as the relation with diffractive physics and soft processes in general, is more transparent in this approach. However, we believe the CGC/saturation approach produces a more general pattern [93,94,95,96] for the treatment of high energy QCD. Fortunately, in Refs. [95, 96] it was shown that these two approaches are equivalent for

$$\begin{aligned} Y \,\le \,\frac{2}{\Delta _{\mathrm{BFKL}}}\,\ln \left( \frac{1}{\Delta ^2_{\mathrm{BFKL}}}\right) \end{aligned}$$
(2.1)

where \(\Delta _{\mathrm{BFKL}}\) denotes the intercept of the BFKL Pomeron. As we will see, in our model \( \Delta _{\mathrm{BFKL}}\, \approx \,0.2 - 0.25\) leading to \(Y_{\max } = 20 \)–30, which covers all accessible energies.

The main ingredient that we need to find is the resulting (dressed) BFKL Pomeron Green function, which can be calculated using t-channel unitarity constraints:

(2.2)

where \( N( Y- Y', r, \{ r_i,b - b_i\})\) denotes the amplitude for the production in the t-channel of the set of dipoles with \(Y=Y'\) and with the size \(r_i\), at the impact parameters \(b_i\). \(A^{BA}_{\mathrm{dipole-dipole}}\) denotes the dipole–dipole scattering amplitude in the Born approximation of perturbative QCD, which are indicated by red circles in Fig. 1a. In addition, in Refs. [95, 96] it is shown that, for such Y, we can safely use the Mueller–Patel–Salam–Iancu (MPSI) approach [77, 98,99,100,101]. In this approximation we estimate the amplitudes N in Eq. (2.2), using BFKL Pomeron ‘fan’ diagrams (see Fig. 1a for examples of such diagrams). In other words, we can use the parton cascade of the Balitsky–Kovchegov [59,60,61] equation, to find the amplitude for the production of dipoles of size \(r_i\) at impact parameters \(b_i\). This amplitude can be written as (see Fig. 1c)

(2.3)

denotes the Green function of the BFKL Pomeron. In the last equation we used the fact that in the saturation region this Green function has geometric scaling behavior, and so it depends on one variable: \(z_i \,=\,\ln ( Q^2_s(Y') r^2_i)\), where \(Q_s( Y')\), is the saturation scale. In the vicinity of the saturation scale [102]Footnote 2

(2.4)

where \(\gamma _{\mathrm{cr}}=0.37\).

Table 1 Fitted parameters of the model. Fit I: parameters for the soft interaction at high energy are taken from Ref. [40]. The additional parameters for DIS were found by fitting to the \(F_2\) structure function (see below). Fit II: joint fit to the soft interaction data at high energy and the DIS data
Full size table

In Ref. [97], it was shown that the solution to the non-linear BK equation has the following general form:

(2.5)

Comparing Eq. (2.3) with Eq. (2.5) we see

$$\begin{aligned} \widetilde{C}_n( r)=C_n( \phi _0). \end{aligned}$$
(2.6)

Coefficients \(C_n\) can be determined from the solution to the Balitsky–Kovchegov equation [59,60,61], in the saturation region. The numerical solution has been found in Ref. [97] for the simplified BFKL kernel in which only the leading twist contribution was taken into account:

(2.7)

with \(a = 0.65.\) Equation (2.7) is a convenient parameterization of the numerical solution, with an accuracy of better than 5%. Having \(C_n\) we can calculate the Green function of the dressed BFKL Pomeron using Eq. (2.2), and the property of the BFKL Pomeron exchange:

(2.8)

Carrying out the integrations in Eq. (2.2), we obtain the Green function of the dressed Pomeron in the following form:

$$\begin{aligned}&G^{\mathrm{dressed}}( T)=a^2 (1 - \exp ( -T) ) + 2 a (1 - a)\frac{T}{1 + T}\nonumber \\&\quad +\, (1 - a)^2 G( T)\nonumber \\&\quad \mathrm{with}\ G( T) = 1 - \frac{1}{T} \exp \left( \frac{1}{T}\right) \Gamma \left( 0, \frac{1}{T}\right) \end{aligned}$$
(2.9)

where \(\Gamma \left( s, z\right) \) is the upper incomplete gamma function (see Ref. [103], Eq. 8.35), and T denotes the BFKL Pomeron in the vicinity of the saturation scale (see Eq. (2.4)),

$$\begin{aligned} T\left( r_\bot , Y\,=\,\ln \left( s/s_0\right) , b\right) \,\,=\,\,\phi _0 \left( r^2_\bot Q^2_s\left( Y, b\right) \right) ^{\bar{\gamma }}. \end{aligned}$$
(2.10)

The Green function of Eq. (2.9) depends on the size of the dipoles, and we will use it when discussing the hard processes. In our analysis of the soft interaction we fixed \(r = 1/m\), m is a fitting parameter, whose value is the same in all formulas in this paper.

2.2 Phenomenology: assumptions and new small parameters

Unfortunately, due to the embryonic stage of theoretical understanding of the confinement of quarks and gluons, it is necessary to use pure phenomenological ideas to fix two major problems in high energy scattering: the structure of hadrons, and the large impact parameter behavior of the scattering amplitude [104, 105]. The main idea to correct the large impact parameter behavior, is to assume that the saturation momentum has the following dependence on the impact parameter b:

$$\begin{aligned} Q^2_s( b, Y)=Q^2_{0s}( b, Y_0)\,\mathrm{e}^{\lambda \,(Y - Y_0)} \end{aligned}$$
(2.11)

with

$$\begin{aligned}&Q^2_{0s}( b, Y_0)=( m^2)^{1 - 1/\bar{\gamma }}\,( S( b, m))^{1/\bar{\gamma }},\nonumber \\&\quad S( b, m )=\frac{m^2}{2 \pi } \mathrm{e}^{ - m b}\quad \mathrm{and}\quad \bar{\gamma }=0.63. \end{aligned}$$
(2.12)

We have introduced a new phenomenological parameter m to describe the large b behavior. The Y dependence, as well as \(r^2\) dependence, can be found from CGC/saturation approach [49], since \(\phi _0\) and \(\lambda \) can be calculated in the leading order of perturbative QCD. However, since the higher order corrections turn out to be large [106, 107], we treat them as parameters to be fitted. m is a non-perturbative parameter, which determines the typical sizes of dipoles within the hadrons. In Table 1, we show that, from the fit, \(m = 5.25\) GeV, supporting our main assumption that we can apply the BFKL Pomeron calculus, based on perturbative QCD, to the soft interaction, since \(m \,\gg \,\mu _{\mathrm{soft}}\), where \(\mu _{\mathrm{soft}}\) is the scale of soft interaction, which is of the order of the mass of the pion or \(\Lambda _\mathrm{QCD}\).

The idea to absorb the non-perturbative b dependence into the saturation scale stems both from the success of this idea in the description of the hard processes in the framework of the saturation model [108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132], and from the semi-classical solution to the BK equation [133], as well as from the analytical solution deep in the saturation domain [47].

The second unsolved problem for which we need a phenomenological input, is the structure of the scattering hadrons. We use a two channel model, which allows us to calculate the diffractive production in the region of small masses. In this model, we replace the rich structure of the diffractively produced states by a single state with the wave function \(\psi _D\), a la Good–Walker [134]. The observed physical hadronic and diffractive states are written in the form

$$\begin{aligned}&\psi _h=\alpha \,\Psi _1+\beta \,\Psi _2;\quad \psi _D=-\beta \,\Psi _1+\alpha \,\Psi _2;\nonumber \\&\quad \mathrm{where}\ \alpha ^2+\beta ^2=1. \end{aligned}$$
(2.13)

The functions \(\psi _1\) and \(\psi _2\) form a complete set of orthogonal functions \(\{ \psi _i \}\) which diagonalize the interaction matrix T,

$$\begin{aligned} A^{i'k'}_{i,k}=\langle \psi _i\,\psi _k|{\mathbf {T}}|\psi _{i'}\,\psi _{k'}\rangle = A_{i,k}\,\delta _{i,i'}\,\delta _{k,k'}. \end{aligned}$$
(2.14)

The unitarity constraints take the form

$$\begin{aligned} 2\,\mathrm{Im}\,A_{i,k}\left( s,b\right) =|A_{i,k}\left( s,b\right) |^2 +G^{\mathrm{in}}_{i,k}(s,b), \end{aligned}$$
(2.15)

where \(G^{\mathrm{in}}_{i,k}\) denotes the contribution of all non-diffractive inelastic processes, i.e. it is the summed probability for these final states to be produced in the scattering of a state i off a state k. In Eq. (2.15) \(\sqrt{s}=W\) denotes the energy of the colliding hadrons and b the impact parameter. A simple solution to Eq. (2.15) at high energies has the eikonal form with an arbitrary opacity \(\Omega _{ik}\), where the real part of the amplitude is much smaller than the imaginary part. We have

$$\begin{aligned}&A_{i,k}(s,b)=i ( 1 -\exp ( - \Omega _{i,k}(s,b))),\end{aligned}$$
(2.16)
$$\begin{aligned}&G^{\mathrm{in}}_{i,k}(s,b)=1-\exp ( - 2\,\Omega _{i,k}(s,b)). \end{aligned}$$
(2.17)

Equation (2.17) implies that \(P^S_{i,k}=\exp ( - 2\,\Omega _{i,k}(s,b))\) is the probability that the initial projectiles (i, k) reach the final state interaction unchanged, regardless of the initial state re-scatterings.

The first approach is to use the eikonal approximation for \(\Omega \) in which

$$\begin{aligned}&\Omega _{i,k}(r_\bot , Y - Y_0,b)=\int \mathrm{d}^2 b'\,\mathrm{d}^2 b''\, g_i(\vec {b}',m_i) \,G^{\mathrm{dressed}}\nonumber \\&\quad \times \,( T( r_\bot , Y - Y_0, \vec {b}''))\,g_k( \vec {b} - \vec {b}'\ - \vec {b}'',m_k) \end{aligned}$$
(2.18)

where the \(m_i\) denote the masses, which are introduced phenomenologically to determine the b dependence of \(g_i\) (see below).

We propose a more general approach, which takes into account the new small parameters that are determined by fitting to the experimental data (see Table 1 and Fig. 1 for notation):

(2.19)

The second equation in Eq. (2.19) leads to the fact that \(b''\) in Eq. (2.18) is much smaller than b and \( b'\); therefore, Eq. (2.18) can be re-written in the simpler form

$$\begin{aligned}&\Omega _{i,k}(r_\bot , Y - Y_0, b)\nonumber \\&\quad =\left( \int \mathrm{d}^2 b''\, G^{\mathrm{dressed}}( T( r_\bot , Y - Y_0, \vec {b}''))\right) \nonumber \\&\qquad \times \int \mathrm{d}^2 b' g_i(\vec {b}')\,g_k( \vec {b} - \vec {b}') \,\nonumber \\&\quad =\tilde{G}^{\mathrm{dressed}}( r_\bot , Y - Y_0)\,\, \int \mathrm{d}^2 b' g_i(\vec {b}') \,g_k(\vec {b} - \vec {b}'). \end{aligned}$$
(2.20)
Table 2 The values of cross sections versus energy. \(\sigma ^\mathrm{smd}_\mathrm{sd}\) and \(\sigma ^\mathrm{smd }_\mathrm{dd}\) denote the cross sections for diffraction dissociation in the small mass region, for single and double diffraction, which stem from the Good–Walker mechanism. \(\sigma ^\mathrm{lmd}_\mathrm{sd}\) and \(\sigma ^\mathrm{lmd}_\mathrm{dd}\) denote high mass diffraction, coming from the dressed Pomeron contributions. The predictions of fit II are shown in brackets
Full size table

Using the first small parameter of Eq. (2.19), we see that the main contribution stems from the net diagrams shown in Fig. 1b. The sum of these diagrams [40] leads to the following expression for \( \Omega _{i,k}(s,b)\):

(2.21)
(2.22)

where

0

$$\begin{aligned}&S_p( b,m_i)=\frac{1}{4 \pi } m^3_i \,b \,K_1( m_i b )\ \xrightarrow {\mathrm{Fourier\,image}}\ \frac{1}{( 1 + Q^2_T/m^2_i)^2},\nonumber \\ \end{aligned}$$
(2.23)
$$\begin{aligned}&\tilde{G}^{\mathrm{dressed}}( r, Y -Y_0)=\int \mathrm{d}^2 b \,\,G^{\mathrm{dressed}}( T( r, Y - Y_0, b)), \end{aligned}$$
(2.24)

where \( T( r, Y - Y_0, b)\) is given by Eq. (2.10).

Table 3 Fitted parameters for DIS. The description of fit I and fit II is given in Sect. 2.3, and in the caption of Table 1
Full size table

The impact parameter dependence of \(S_p( b,m_i)\) is purely phenomenological, however, Eq. (2.23), which has the form of an electromagnetic proton form factor, leads to the correct (\(\exp ( - \mu b)\)) behavior at large b [135, 136], and it shows the correct behavior at large \(Q_T\), which has been calculated in the framework of perturbative QCD [137, 138]. We wish to draw the reader’s attention to the fact that \(m_1\) and \(m_2\) are the two dimensional scales in a hadron, which characterize elastic (\(m_1\)) and diffractive (\(m_2\)) scattering. Both have a very simple meaning in the constituent quark model: the size of the hadron (\(R_h \propto 1/m_1\)), and the size of the constituent quark (\(R_Q \propto 1/m_2\)).

Note that \(\tilde{G}^{\mathrm{dressed}}( Y - Y_0)\) does not depend on b. In all previous formulas, the value of the triple BFKL Pomeron vertex is known: . This value is extracted from the numerical solution to the Balitsky–Kovchegov equation (see Eq. (2.9)), calculating the probability for the production of two parton showers, in the framework of non-linear evolution [97].

For further discussion, we introduce the notation

(2.25)

with \(a = 0.65\). Equation (2.25) is an analytical approximation to the numerical solution for the BK equation [97]. . We recall that the BK equation sums the ‘fan’ diagrams.

2.3 Results of the fit

In this paper we make two fits. In the first one (fit I in Tables 1, 3) we do not change the parameters that govern the soft interactions in our model, and that are shown in Table 1. The additional parameters that we need for the description of the deep inelastic data, and which we will discuss in the next section (see Table 3), were fitted using the HERA data on the deep inelastic structure function \(F_2\). The second fit is a joint fit to the soft strong interaction data and the DIS data. In Fig. 2 we show the results of our model compared with the HERA data. The model predictions are in accord with the data for \(0.85 \le Q^{2} \le 27~\hbox {GeV}^{2}\), while for higher values of \(Q^{2}\) and of x the model values are slightly larger than the data.

In Table 2 we present our predictions for the soft interaction observables, in general the values obtained in the model for the soft interactions agree with the published LHC data, as well as the new preliminary TOTEM values at \(W =2.7,\) 7, 8, and 13 TeV (see Ref. [139]). We have good agreement with the data for \(\sigma _{\mathrm{tot}}\), \(\sigma _{\mathrm{el}}\) and \(B_{\mathrm{el}}\). For these three quantities we obtain a \(\chi ^{2}\)/d.o.f. of 1.02 for fit I and 1.28 for fit II. Regarding \(\sigma _{sd}\) and \(\sigma _{dd}\), a problem exists when attempting to compare with the experimental results. This is due to the difficulties of measuring diffractive events at LHC energies, the different experiments have different cuts on the values of the diffractive mass measured, making it problematic when attempting to compare the model predictions with the experimental results.

In Table 2 we show the results of the two fits; the results are close to one another, the main difference shows up only at high energies. Indeed, in fit I the cross section for single diffraction is equal to 14.9 mb, while in fit II this value is smaller (13.1 mb). The smaller value of the diffraction cross sections is closer to TOTEM and CMS data.

Fig. 2
figure 2

\(F_2\) versus x at fixed Q. The red curve corresponds to fit I, while the blue one describes fit II. Data is taken from Refs. [51, 52]

Full size image

3 Deep inelastic scattering

3.1 Generalities

In this section, we compare our amplitude with the experimental data on deep inelastic scattering (DIS). In the framework of our approach, the observables of DIS can be re-written using

$$\begin{aligned} N_{T,L}( Q, Y; b)=\int \frac{\mathrm{d}^2 r}{4\,\pi } \int ^1_0 \mathrm{d} z \,|\Psi ^{\gamma ^*}_{T,L}( Q, r, z)|^2 \,N( r, Y; b)\nonumber \\ \end{aligned}$$
(3.1)

where \(Y =\ln (1/x_{Bj})\) and \(x_{Bj}\) is the Bjorken x. z is the fraction of energy carried by quark. Q is the photon virtuality. b denotes the impact parameter for the scattering of the colorless dipole of size r with the proton. N(r, Y; b) is the scattering amplitude of this dipole, which in our model can be written in the following form:

(3.2)

In Eq. (3.1) \(|\Psi ^{\gamma ^*}_{T,L}( Q, r, z)|^2\) is the probability to find a dipole of size r in a photon with the virtuality Q, and with transverse or longitudinal polarization. The wave functions are known (see Ref. [49] and the references therein) and they are equal to the following expressions:

$$\begin{aligned} (\Psi ^*\Psi )_{T}^{\gamma ^*}= & {} \frac{2N_c}{\pi }\alpha _{\mathrm {em}}\sum _f e_f^2\{[z^2+(1-z)^2]\nonumber \\&\times \,\epsilon ^2 K_1^2(\epsilon r) + m_f^2 K_0^2(\epsilon r)\},\end{aligned}$$
(3.3)
$$\begin{aligned} (\Psi ^*\Psi )_{L}^{\gamma ^*}= & {} \frac{8N_c}{\pi }\alpha _{\mathrm {em}} \sum _f e_f^2 Q^2 z^2(1-z)^2 K_0^2(\epsilon r), \end{aligned}$$
(3.4)

where \(\epsilon ^2=m^2_f + z(1-z) Q^2\).

Finally, the physical observables take the form

$$\begin{aligned}&\sigma _{T,L}( Q,Y)=2\int \mathrm{d}^2 b \,\, N_{T,L}( Q, Y; b),\end{aligned}$$
(3.5)
$$\begin{aligned}&F_2( Q, Y)=\frac{Q^2}{ 4 \pi ^2 \alpha _\mathrm{\mathrm{e.m.}}}\{ \sigma _T\,+\,\sigma _L\}. \end{aligned}$$
(3.6)

3.2 Modification to include DIS

First we need to include the mild violation of the geometric scaling behavior of the scattering amplitude. We use the same procedure as has been suggested in Refs. [108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132]: we change \(\bar{\gamma } \) in Eq. (2.10),

$$\begin{aligned} \bar{\gamma }= & {} 1 -\gamma _{\mathrm{cr}}\rightarrow 1 -\gamma _{\mathrm{cr}}-\frac{1}{2\,\kappa \,\lambda \,Y} \,\ln \ (r^2 \,Q^2_s(b))\nonumber \\= & {} 0.63-\frac{1}{2\,\kappa \,\lambda \,Y} \,\ln \ ( r^2 \,Q^2_s(b)) \end{aligned}$$
(3.7)

where \(\kappa =\chi ''(\gamma _{\mathrm{cr}})/\chi '(\gamma _{\mathrm{cr}})=9.8\). \(\chi (\gamma )\) is the BFKL kernel, which has the following form:

$$\begin{aligned}&\chi (\gamma )=2 \psi (1) - \psi (\gamma ) - \psi ( 1 - \gamma )\nonumber \\&\quad \mathrm{while } \; \frac{\chi (\gamma _{\mathrm{cr}})}{1 - \gamma _{\mathrm{cr}}} = \frac{\mathrm{d}\chi (\gamma )}{\mathrm{d} \gamma }{|}_{\gamma = \gamma _{\mathrm{cr}}} \end{aligned}$$
(3.8)

where \(\psi (z) = \mathrm{d}\Gamma (z)/\mathrm{d}z\) is the Euler \(\psi \)-function (see Ref. [103], Eq. 8.360).

Since we take into account the contribution of the heavy c-quark we introduce a correction due to the large mass of this quark:

$$\begin{aligned} x_{Bj}\rightarrow x_{Bj}\,\left( \frac{1}{1+ \frac{4 m^2_c}{Q^2}}\right) \quad \mathrm{or}\quad Y_c = Y - \ln (1 + 4\,m^2_c/Q^2).\nonumber \\ \end{aligned}$$
(3.9)

In describing the saturation phenomena and fitting the strong interaction data, we assumed that the QCD coupling is frozen at some value of the momentum \(\mu _\mathrm{soft}\). However, for DIS we take into account the running QCD coupling, replacing Eq. (3.6) by the following expression:

$$\begin{aligned} F_2(Q,Y)= & {} \frac{Q^2}{ 4 \pi ^2 \alpha _\mathrm{\mathrm{e.m.}}}\left\{ \frac{\bar{\alpha }_S(Q^2)}{\bar{\alpha }_S(\mu ^2)} \, \sigma ^\mathrm{light \,q}(Q, Y)\right. \nonumber \\&\left. +\,\frac{\bar{\alpha }_S(Q^2 + 4m^2_c )}{\bar{\alpha }_S(\mu ^2)}\sigma ^\mathrm{charm \,q}(Q, Y_c)\right\} \end{aligned}$$
(3.10)

where \(\mu \) denotes the typical mass of the soft strong interaction \(\mu \sim 1\,\hbox {GeV}\) and

$$\begin{aligned} \frac{\bar{\alpha }_S(Q^2)}{\bar{\alpha }_S(\mu ^2)} =\frac{1}{1+\beta \bar{\alpha }_S( \mu ^2)\,\ln ( Q^2/\mu ^2)} \end{aligned}$$
(3.11)

with \(\beta =3/4\).

Fig. 3
figure 3

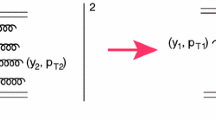
The generic Mueller diagrams [142] for single inclusive (a) and for double inclusive (b, c) production. b Double inclusive cross section, c interference diagram for the Bose–Einstein correlation. For ease of drawing we take \(y_1=y_2\)

Full size image

We consider the strong interaction data for energies \(W \ge 0.546\,\hbox {TeV}\), while the experimental data from HERA were measured for lower energies. Therefore, we need to include the contribution of the secondary Reggeons which give a substantial contribution [140]. We have

$$\begin{aligned} \sigma _{{I\!\!R}}(Q, Y)= & {} \int \frac{\mathrm{d}^2 r}{4\,\pi } \left\{ (\Psi ^*\Psi )_{T}^{\gamma ^*}+ (\Psi ^*\Psi )_{L}^{\gamma ^*} \right\} \nonumber \\&\times \,A_{I\!\!R}\,r^2 \,\left( \frac{Q^2}{x_{Bj}\,Q^2_0} \right) ^{ \alpha _{I\!\!R}( 0 ) - 1} \end{aligned}$$
(3.12)

with \(Q_0 = 1 \,\hbox {GeV}\).

The final equation for \(F_2\) takes the form

$$\begin{aligned}&F_2( Q,Y)=\frac{Q^2}{ 4 \pi ^2 \alpha _\mathrm{\mathrm{e.m.}}}\left\{ \frac{\bar{\alpha }_S(Q^2)}{\bar{\alpha }_S(\mu ^2)} \, \sigma ^\mathrm{light \,q}(Q, Y)\right. \nonumber \\&\quad \left. +\,\frac{\bar{\alpha }_S( Q^2 + 4m^2_c )}{\bar{\alpha }_S(\mu ^2)} \sigma ^\mathrm{charm \,q}( Q, Y_c)+\sigma _{{I\!\!R}}( Q, Y)\right\} .\nonumber \\ \end{aligned}$$
(3.13)

3.3 The description of the HERA data

We introduce in Eq. (3.13) a set of new parameters for DIS: \(m_q\), the mass of the light quark, which we hope will be of the order of the constituent quark mass (\({\sim } 300\,\hbox {MeV}\)), the mass of the charm quark (\(m_c = 1.2 \div 1.5 \,\hbox {GeV}\)), \(\mu \), which we believe will be of the order of 1 GeV, and we introduce two new parameters \(A_{I\!\!R}\) and \(\alpha _{I\!\!R}(0 )\) for the secondary Reggeon contribution. From fitting the experimental data on soft interactions at low energies (see Ref. [141]) it has been estimated that at \(x_{Bj} = 4 \,10^{-6}\) we have \( \sigma ^\mathrm{light \,q}_{{I\!\!R}} \le 0.02 \sigma _{\mathrm{tot}}\), for \( \alpha _{I\!\!R}( 0 )= 0.4 \div 0.6\). This leads to some restriction on the value of \(A_{I\!\!R}\).

In Table 3 we display the parameters that were determined by fitting to the data, Fig. 2 shows the quality of our fit to the DIS HERA data. As one can see fit I (red curve) and fit II (blue curve) are close to one another, but fit II has lower \(\chi ^2/\hbox {d.o.f}.\)

We consider the fit shown in Fig. 2 to be in very good agreement with the experimental data, and to demonstrate that our model is able to describe the hard processes to within an accuracy of 5%.

4 Inclusive production

The cross section of the inclusive production is a very important observable for our estimates, since it indicates how well we can describe the multi-particle generation processes in our model. We have described the experimental data in our soft interaction model [41]; we now recalculate using our generalization of the model, which we have discussed above. Reference [117] showed that the CGC/saturation approach is able to describe the LHC data on inclusive production. In this section we re-visit these calculations, using our model, which we can now apply both to soft and to hard processes.

The expression for the inclusive cross section takes the form [49, 117, 143] (see Fig. 3 for notation)

$$\begin{aligned}&\frac{\mathrm{d} \sigma }{\mathrm{d} y \,\mathrm{d}^2 p_{T}}\,\, \frac{2C_F}{\alpha _s (2\pi )^4}\,\frac{1}{p^2_T}\int \mathrm{d}^2 {\vec {b}} \,\mathrm{d}^2 {\vec {B}} \,\mathrm{d}^2 r \,\mathrm{e}^{i \vec {p}_T\cdot \vec {r}}\nonumber \\&\quad \times \,\nabla ^2_T\,N^{h_1}_G( Y - y; r; b )\,\,\nabla ^2_T\,N^{h_2}_G( y; r; |{\vec {b}}-{\vec {B}}|), \end{aligned}$$
(4.1)

where the scattering amplitudes \(N^{h_i}_G\) can be found from the dipole amplitude [143]

$$\begin{aligned} N^{h_i}_G( y_i ; r; b )=2 \,N( y_i ; r; b )-N^2( y_i ; r; b ), \end{aligned}$$
(4.2)

and r denotes the dipole size. \(C_F = (N^2_c-1)/2N_c\). For further discussion it is convenient to introduce two more observables

$$\begin{aligned}&\frac{\mathrm{d} \sigma _{i,j}}{\mathrm{d}y \,\mathrm{d}^2 p_{T}\,\mathrm{d}^2B }= \frac{2C_F}{\alpha _s (2\pi )^4}\,\frac{1}{p^2_T}\int \mathrm{d}^2 b \, \,\mathrm{d}^2 r \,\mathrm{e}^{i \vec {p}_T\cdot \vec {r}}\,\,\nabla ^2_T\,N^{i}_G\nonumber \\&\quad \times ( Y - y; r; b )\,\,\nabla ^2_T\,N^{j}_G( y; r; |{\vec {b}}-{\vec {B}}| );\nonumber \\&\frac{\mathrm{d} \sigma _{i,j}}{\mathrm{d}y \,\mathrm{d}^2 p_{T}\,\mathrm{d}^2 B\,\mathrm{d}^2 b }\,\,= \frac{2C_F}{\alpha _s (2\pi )^4}\,\frac{1}{p^2_T}\int \,\mathrm{d}^2 r \,\mathrm{e}^{i \vec {p}_T\cdot \vec {r}}\,\,\nabla ^2_T\,N^{i}_G\nonumber \\&\quad \times \,( Y - y; r; b )\,\,\nabla ^2_T\,N^{j}_G( y; r; |{\vec {b}}-{\vec {B}}| ) \end{aligned}$$
(4.3)

where

(4.4)

Taking for \(N(y_i; r; b)\) in Eq. (4.2) the amplitude of Eq. (3.2) we obtain

$$\begin{aligned} \frac{\mathrm{d}N}{\mathrm{d}y}\Bigg {|}_{y = 0}=\frac{1}{\sigma _\mathrm{NSD}}\int \mathrm{d}^2 p_T \frac{\mathrm{d} \sigma }{\mathrm{d}y \,\mathrm{d}^2 p_{T}}. \end{aligned}$$
(4.5)

We take the values of \(\sigma _\mathrm{NSD} =\sigma _\mathrm{tot} - \sigma _\mathrm{el} - \sigma _\mathrm{single\,diffraction}\) from the description of the total and diffraction cross section in our model [40]. One can see that the integral over \(p_T\) is logarithmically divergent at small \(p_T\). As shown in Ref. [144] this divergence is regularized by the mass of the produced gluon jet at \(y=0\). In Fig. 4 we plot our estimates for \(\frac{\mathrm{d}N}{\mathrm{d}y}{|}_{y = 0}\) using the value of this mass as was taken in Ref. [117] \(m_\mathrm{jet} = 350~\hbox {MeV}\). The agreement with the experimental data is good and it gives us confidence that our model is able to discuss the typical process of many particle production. We do not discuss the rapidity and \(p_T\) distribution of the single inclusive cross section, since this has been discussed in Refs. [41, 117], where it is shown that this distribution agrees with the experimental data.

Fig. 4
figure 4

\(\frac{\mathrm{d}N}{\mathrm{d}y}{|}_{y = 0}\) versus energy W. The experimental data are taken from Refs. [145,146,147,148,149,150,151]

Full size image

5 Azimuthal angular correlations

5.1 Double inclusive cross section

The Mueller diagram [142] for double inclusive cross section is shown in Fig. 3b. Using Eq. (4.3) this cross section can be written in the form

$$\begin{aligned} \Sigma _{i,j}\equiv & {} \frac{\mathrm{d}^2 \sigma _{i,j}}{\mathrm{d}y_1 \,\mathrm{d}^2 p_{1,T}\,\mathrm{d}y_2 \,\mathrm{d}^2 p_{2,T}} \nonumber \\= & {} \int \mathrm{d}^2 B \frac{\mathrm{d} \sigma }{\mathrm{d}y_1 \,\mathrm{d}^2 p_{1,T}\,\mathrm{d}^2B } \,\frac{\mathrm{d} \sigma }{\mathrm{d}y_2 \,\mathrm{d}^2 p_{2,T}\,\mathrm{d}^2B } \end{aligned}$$
(5.1)
$$\begin{aligned}&\times \;\frac{\mathrm{d}^2 \sigma }{\mathrm{d}y_1 \,\mathrm{d}^2 p_{1,T}\,\mathrm{d}y_2 \,\mathrm{d}^2 p_{2,T}} \nonumber \\= & {} \alpha ^4\, \Sigma _{1,1}+2\,\alpha ^2\,\beta ^2\, \Sigma _{1,2}+\beta ^4\,\Sigma _{2,2} . \end{aligned}$$
(5.2)

Equation (5.1) stems from the AGK cutting rules [152, 153], which are violated in perturbative QCD, as has been proven in Ref. [154]. Nevertheless, we assume these rules, since their violation originated from the structure of the triple Pomeron vertex in QCD, and this violation is not important when \(y_1 = y_2\), as we have no triple Pomeron vertices in rapidities between \(y_1\) and \(y_2\) (see Fig. 9 of Ref. [154]). Recall that in all our estimates we assume that \(\bar{\alpha }_Sy_{12} \ll 1\). In addition, in our model all integrations over the position of the triple Pomeron vertices lead to new probabilities (see Eq. (2.5) and Fig. 1c) for two parton shower production, for which we can use the AGK cutting rules.

We can re-write Eq. (5.1) in a different form if we introduce

$$\begin{aligned} I^G_{i}( y, r, Q_T)=\int \mathrm{d}^2 b \,\mathrm{e}^{i \vec {Q}_T \cdot \vec {r}}\,\nabla ^2_T\,N^{i}_G(Y - y; r; b ). \end{aligned}$$
(5.3)

Note that \(\vec {Q}_T\) denotes the transverse momentum carried by the BFKL Pomeron, which emits gluons with momentum \(\vec {p}_{1,T}\) or \(\vec {p}_{2,T}\).

Plugging Eq. (5.3) in Eq. (5.1), the expression for the double inclusive cross section takes the form

$$\begin{aligned}&\frac{\mathrm{d}^2 \sigma _{i,j}}{\mathrm{d}y_1 \,\mathrm{d}^2 p_{1,T}\,\mathrm{d}y_2 \,\mathrm{d}^2 p_{2,T}} =\frac{2C_F}{\alpha _s (2\pi )^4}\,\frac{1}{p^2_{1,T}}\, \frac{2C_F}{\alpha _s (2\pi )^4}\,\frac{1}{p^2_{2,T}}\nonumber \\&\qquad \times \int \mathrm{d}^2 r_1\, \mathrm{e}^{ \vec {p}_{1,T} \cdot \vec {r}_1}\,\int \mathrm{d}^2 r_2 \, \mathrm{e}^{ \vec {p}_{2,T} \cdot \vec {r}_2}\nonumber \\&\qquad \times \,\,\int \frac{\mathrm{d}^2 Q_T}{(2 \pi )^2} I^G_{i}( Y - y_1, r_1, Q_T)\, I^G_{i}\nonumber \\&\qquad \times ( Y - y_2, r_2, Q_T) I^G_{j}( y_1, r_1, Q_T)\, I^G_{j}( y_2, r_2, Q_T).\nonumber \\ \end{aligned}$$
(5.4)

Therefore, using either Eq. (5.1) or Eq. (5.4) and the decomposition of Eq. (5.2), one can calculate the double inclusive cross section.

Fig. 5
figure 5

Correlation function \(C\left( L_c |\vec {p}_{T2} - \vec {p}_{T1}|\right) \) versus \( \vec {p}_{12,T} \,\equiv \,\vec {p}_{1,T} \,-\,\vec {p}_{2,T}\) at different values of \(p_{1,T}\) and energies \(W = 7 \,\hbox {TeV}\) (a) and \(W=13\,\hbox {TeV}\) (b)

Full size image

5.2 Bose–Einstein correlation: energy dependence

The double inclusive cross section of two identical gluons has the following general form:

$$\begin{aligned}&\frac{\mathrm{d}^2 \sigma }{\mathrm{d}y_1 \,\mathrm{d}y_2 \mathrm{d}^2 p_{T1} \mathrm{d}^2 p_{T2}}(\hbox {identical gluons})\nonumber \\&\quad =\frac{\mathrm{d}^2 \sigma }{\mathrm{d}y_1 \,\mathrm{d}y_2 \mathrm{d}^2 p_{T1} \mathrm{d}^2 p_{T2}}(\hbox {different gluons})\nonumber \\&\qquad \times ( 1 +C( L_c |\vec {p}_{T2} - \vec {p}_{T1}|)) \end{aligned}$$
(5.5)

where \(C( L_c |\vec {p}_{T2} - \vec {p}_{T1}|)\) denotes the correlation function, and \(L_c\) the correlation length. The first term in Eq. (5.5) is given by Eq. (5.1) or Eq. (5.4), while the second term describes the interference diagram for the identical gluons (see Fig. 3c and Refs. [30, 50] for details). The expression for the interference term is more transparent in the momentum representation, where it has the form

$$\begin{aligned}&\frac{\mathrm{d}^2 \sigma _{i,j}(\hbox {interference contribution})}{\mathrm{d}y_1 \,\mathrm{d}y_2 \mathrm{d}^2 p_{T1} \mathrm{d}^2 p_{T2}}=\frac{1}{N^2_c - 1}\,\frac{2C_F}{\alpha _s (2\pi )^4}\,\frac{1}{p^2_{1,T}}\nonumber \\&\qquad \times \frac{2C_F}{\alpha _s (2\pi )^4}\,\frac{1}{p^2_{2,T}}\int \mathrm{d}^2 r_1\, \mathrm{e}^{ \vec {p}_{1,T} \cdot \vec {r}_1}\,\int \mathrm{d}^2 r_2 \, \mathrm{e}^{ \vec {p}_{2,T} \cdot \vec {r}_2}\nonumber \\&\qquad \times \left\{ \int \frac{\mathrm{d}^2 Q_T}{(2 \pi )^2} I^G_{i}( Y - y_1, r_1, Q_T)\, I^G_{i}( Y - y_2, r_2, Q_T) I^G_{j}\right. \nonumber \\&\qquad \times ( y_1, r_1, \vec {Q}_T - \vec {p}_{12,T} )\, I^G_{j}( y_2, r_2,\vec { Q}_T - \vec {p}_{12,T}) \nonumber \\&\quad =\int \frac{\mathrm{d}^2 Q'_T}{(2 \pi )^2} I^G_{i}\left( Y - y_1, r_1, \vec {Q'}_T + \frac{1}{2}\vec {p}_{12,T}\right) \,\nonumber \\&\qquad \times I^G_{i}\left( Y - y_2, r_2, \vec {Q'}_T + \frac{1}{2}\vec {p}_{12,T}\right) \nonumber \\&\qquad \left. \times I^G_{j}\left( y_1, r_1, \vec {Q}_T -\frac{1}{2}\vec {p}_{12,T} \right) \, I^G_{j}\left( y_2, r_2,\vec { Q}_T -\frac{1}{2}\vec {p}_{12,T}\right) \right\} .\nonumber \\ \end{aligned}$$
(5.6)

Equation (5.6) takes into account that the lower BFKL Pomerons in Fig. 3c carry momenta \(\vec {Q}_T - \vec {p}_{12,T}\), where \( \vec {p}_{12,T} \,\equiv \,\vec {p}_{1,T} \,-\,\vec {p}_{2,T}\).

Equation (5.6) can be re-written in the impact parameter representation using Eq. (4.3)

$$\begin{aligned}&\frac{\mathrm{d}^2 \sigma _{i,j}}{\mathrm{d}y_1 \,\mathrm{d}y_2 \mathrm{d}^2 p_{T1} \mathrm{d}^2 p_{T2}} (\hbox {interference contribution})\nonumber \\&\quad =\frac{1}{N^2_c - 1}\int \mathrm{d}^2 \tilde{b} \,\mathrm{e}^{i \vec {p}_{12,T} \cdot \vec {\tilde{b}}}\int \mathrm{d}^2 B' \mathrm{d}^2 b \, \frac{\mathrm{d} \sigma _{i,j}}{\mathrm{d}y \,\mathrm{d}^2 p_{T}\,\mathrm{d}^2 B\,\mathrm{d}^2 b } \nonumber \\&\qquad \times \left( \vec {b} + \frac{1}{2}\vec {\tilde{b}}, \vec {B'} + \frac{1}{2}\vec {\tilde{b}} \right) \,\frac{\mathrm{d} \sigma _{i,j}}{\mathrm{d}y \,\mathrm{d}^2 p_{T}\,\mathrm{d}^2 B\,\mathrm{d}^2 b } \nonumber \\&\qquad \times \left( \vec {b} - \frac{1}{2}\vec {\tilde{b}}, \vec {B'} - \frac{1}{2}\vec {\tilde{b}} \right) . \end{aligned}$$
(5.7)

Finally, using the decomposition of Eq. (5.2), we can calculate the correlation function. In Fig. 5 we show the calculated correlation function

$$\begin{aligned}&C\left( L_c |\vec {p}_{T2} - \vec {p}_{T1}|\right) \,\,\nonumber \\&\quad =\frac{\frac{\mathrm{d}^2 \sigma }{\mathrm{d}y_1 \,\mathrm{d}y_2 \mathrm{d}^2 p_{T1} \mathrm{d}^2 p_{T2}}\left( {\mathrm{interference\,\, contribution}}\right) }{ \frac{\mathrm{d}^2 \sigma }{\mathrm{d}y_1 \,\mathrm{d}y_2 \mathrm{d}^2 p_{T1} \mathrm{d}^2 p_{T2}}\left( {\mathrm{different \,\, gluons}}\right) }. \end{aligned}$$
(5.8)

From this figure we note that the correlation function does not depend on energy. This is an expected result. Indeed, the production of two parton showers, which is taken into account in Fig. 3b, c, leads to the correlation function, which does not depend on \(y_{12} = |y_1 - y_2|\) (long range rapidity correlations (LRCs)). This happens in our approach where the structure of one parton shower cannot be reduced to the exchange of the one BFKL Pomeron. Figure 5 illustrates that the dependence on energy also cancels in the ratio of Eq. (5.8).

5.3 Bose–Einstein correlation: values of \(v_n\) and its multiplicity dependence

We first introduce \(v_n\), which can be defined it terms of the following representation of the double inclusive cross section:

$$\begin{aligned} \frac{\mathrm{d}^2 \sigma }{\mathrm{d}y_1 \,\mathrm{d}y_2 \mathrm{d}^2 p_{T1} \mathrm{d}^2 p_{T2}}\propto 1+2 \sum _n v_{ n,n } ( p_{T1}, p_{T2}) \,\cos ( n\, \varphi )\nonumber \\ \end{aligned}$$
(5.9)

where \( \varphi \) is the angle between \(\vec {p}_{T1}\) and \( \vec {p}_{T2} \). \(v_n\) is determined from \(v_{n,n} ( p_{T1}, p_{T2}) \),

$$\begin{aligned}&1.\quad v_n( p_T)=\sqrt{v_{n,n}( p_T, p_T)};\nonumber \\&2.\quad v_n( p_T)=\frac{v_{n, n}( p_T, p^\mathrm{Ref}_T)}{\sqrt{v_{n,n}( p^\mathrm{Ref}_T, p^\mathrm{Ref}_T)}}; \end{aligned}$$
(5.10)

Equations (5.10)-1 and (5.10)-2 depict two methods of how the values of \(v_n\) have been extracted from the experimentally measured \(v_{n,n} ( p_{T1}, p_{T2})\). Here \( p^\mathrm{Ref}_T\) denotes the momentum of the reference trigger. These two definitions are equivalent if \(v_{n, n}( p_{T1}, p_{T2}) \) can be factorized as \(v_{n, n}( p_{T1}, p_{T2})\,=\, v_n( p_{T1})\,v_n( p_{T2}) \). In this paper we use the definition in Eq. (5.10)-1.

Taking into account Eq. (5.8) and Eq. (5.9) we obtain

$$\begin{aligned}&v_{n,n}=\frac{\int ^{2 \pi }_0 \mathrm{d} \varphi \,C\left( 2 \,p_T\, \sin ( \frac{1}{2}\varphi )\right) \,\cos (n\,\varphi )}{2\,\pi \,+ \int ^{2 \pi }_0 \mathrm{d} \varphi \,C\left( 2 p_T \sin (\frac{1}{2}\varphi )\right) };\nonumber \\&v_n=\sqrt{v_{n,n}}; \end{aligned}$$
(5.11)

Equation (5.11) gives the prescription for the calculation of \(v_n\) that is measured as a sum of the events with all possible multiplicities of the secondary hadrons. However, in practice, only events with multiplicities larger than \(2 \bar{n}\), where \(\bar{n} \) is the average multiplicity which are measured in single inclusive experiments. Figure 6 shows our calculations for W= 7 TeV.

Fig. 6
figure 6

\(v_n\) versus \(p_T\) for the proton–proton scattering at \(W = 7\,\hbox {TeV}\)

Full size image

The dependence of \(v_n\) on the multiplicity of the event has been discussed in Ref. [50]. Using AGK cutting rules [152, 153], it is shown in this paper that the double inclusive cross section Eq. (5.7) has a different form for measurements that sum all events with multiplicity (N) larger than \(m\,\bar{n}\) (\(N \ge m \bar{n}\)), where \(\bar{n}\) is the average multiplicity:

$$\begin{aligned}&\frac{\mathrm{d}^2 \sigma ^{(m)}}{\mathrm{d}y_1 \,\mathrm{d}y_2 \mathrm{d}^2 p_{T1} \mathrm{d}^2 p_{T2}}(\hbox {interference contribution})\nonumber \\&\quad =\frac{1}{N^2_c - 1}\int \mathrm{d}^2 \tilde{b} \,\mathrm{e}^{i \vec {p}_{12,T} \cdot \vec {\tilde{b}}}\end{aligned}$$
(5.12)
$$\begin{aligned}&\qquad \times \int \mathrm{d}^2 B' \mathrm{d}^2 b \, \frac{\mathrm{d} \sigma }{\mathrm{d}y \,\mathrm{d}^2 p_{T}\,\mathrm{d}^2 B\,\mathrm{d}^2 b } \left( \vec {b} + \frac{1}{2}\vec {\tilde{b}}, \vec {B'} + \frac{1}{2}\vec {\tilde{b}} \right) \nonumber \\&\qquad \times \frac{\mathrm{d} \sigma }{\mathrm{d}y \,\mathrm{d}^2 p_{T}\,\mathrm{d}^2 B\,\mathrm{d}^2 b } \left( \vec {b} - \frac{1}{2}\vec {\tilde{b}}, \vec {B'} - \frac{1}{2}\vec {\tilde{b}} \right) \frac{\sigma ^{(m)}(\vec {b} + \vec {B'})}{\sigma _0}; \nonumber \\&\qquad \mathrm{with}\ \frac{\sigma ^{(m)}(\vec {b} + \vec {B'})}{\sigma _0}=\frac{\Gamma (m - 2, 2 \Omega ( Y, \vec {b} + \vec {B'}))}{\Gamma (m - 2)}, \nonumber \\ \end{aligned}$$
(5.13)

where \(\Omega ( r=1/m Y, b)\) is given by Eq. (2.21).

Fig. 7
figure 7

\(v_2\) versus \(p_T\) for proton–proton scattering at \(W = 7\,\hbox {TeV}\) for the multiplicities \(N \ge \,5 \bar{n}\)

Full size image

To account for the dependence on the multiplicities, we replace the double inclusive cross section in Eq. (5.8) by Eq. (5.12). Recall that we can obtain the double inclusive cross section with \(N \ge m\, \bar{n}\), from Eq. (5.12), by removing the factor \(1/( N^2_c - 1)\), and inserting \(\vec {p}_{T,12} = 0\). Using \(C^{(m)}\), calculated in this way, we insert it in Eq. (5.11) to obtain estimates of \(v_{n,n}\) for the events with the multiplicity \(N \ge m\,\bar{n}\).

Comparing Figs. 6 and 7 one can see that in the framework of our approach, the \(v_n\) do not depend on the multiplicity of the event. This independence is in excellent agreement with the experimental data (see Refs. [17, 18] and Fig. 8). Note that \(v_n\) do not depend on N only for proton–proton scattering, while for hadron–nucleus collisions, such a dependence is considerable.

Fig. 8
figure 8

\(v_n\) versus multiplicities for hadron–hadron and hadron–nucleus interactions

Full size image

Figure 5 shows that the correlation length \(L_c \approx 1/m_1\) (the typical momentum is about \(m_1\)). From Table 1, the technical reason for this is clear: the component with such a characteristic momentum makes the largest contribution. In more general language, the correlation length depends on the non-perturbative hadron structure. In terms of the processes, this typical transverse momentum is responsible for diffractive scattering with the production of hadrons with small masses. Intuitively, we expect that diffractive production of large masses, which depend on the saturation scale, can lead to larger typical momenta (smaller correlation length). We will discuss these processes in the next section.

Fig. 9
figure 9

Semi-enhanced and enhanced diagrams: a, c show the cross sections of double inclusive productions; b, d describe the interference diagram that leads to Bose–Einstein correlations

Full size image
Fig. 10
figure 10

\(v_n\) versus \(p_T\) at \(W = 13\,\hbox {TeV}\) for non-enhanced diagram of Fig. 3 and sum of all contributions

Full size image

5.4 Bose–Einstein correlation: contribution of the semi-enhanced and enhanced diagrams (diffraction production of large masses)

In Fig. 9 we show the diagrams in our model that have not been taken into account. They correspond to single diffraction in the region of large masses (Fig. 9a, b), and to double diffraction in two bunches of particles with large masses (Fig. 9c, d).

One can see from Fig. 9 that all these diagrams contain the integration over \(y'\). This integration is concentrated in the region \(Y - y' \propto 1/\Delta _\mathrm{BFKL}\), where \(\Delta _\mathrm{BFKL} \) is the intercept of the BFKL Pomeron. Performing this integration, we reduce the diagrams of the upper part of Fig. 9 to almost the same expression as was used in the previous section, but instead of \(g_i( b )\) we need to insert the b-dependence of the triple Pomeron vertex, which in our model has the following form:

(5.14)

Bearing this in mind we can re-write \( \frac{\mathrm{d} \sigma }{\mathrm{d}y \,\mathrm{d}^2 p_{T} \,\mathrm{d}^2 B\,\mathrm{d}^2 b }\) of Eq. (4.3) in the form

$$\begin{aligned}&\frac{\mathrm{d} \sigma _{i,j}}{\mathrm{d}y \,\mathrm{d}^2 p_{T}\,\mathrm{d}^2 B\,\mathrm{d}^2 b }=\frac{\mathrm{e}^{-\,m\,b}}{S\left( b, m_i\right) }\,\frac{m^2 }{2 \,\pi \,\sqrt{g_i(0)\,\lambda }}\,\frac{2C_F}{\alpha _s (2\pi )^4}\,\frac{1}{p^2_T}\nonumber \\&\quad \times \int \,\mathrm{d}^2 r \,\mathrm{e}^{i \vec {p}_T\cdot \vec {r}}\,\,\nabla ^2_T\,N^{i}_G( Y - y; r; b)\nonumber \\&\quad \times \nabla ^2_T\,N^{j}_G( y; r; |{\vec {b}}-{\vec {B}}| ). \end{aligned}$$
(5.15)

In Eq. (5.15) we restrict ourselves, by accounting only for an interaction with the state \(|1>\), as \(g_1(0) \,\gg \,g_2(0)\). Since in our model we have \(m \,\gg \,m_1\), we can put \(b=0\) and reduce Eq. (5.15) to

$$\begin{aligned}&\frac{\mathrm{d} \sigma _{i,j}}{\mathrm{d}y \,\mathrm{d}^2 p_{T}\,\mathrm{d}^2 B\,\mathrm{d}^2 b } \nonumber \\&\quad =\frac{\mathrm{e}^{-\,m\,b}}{S( b, m_i)}\,\frac{m^2 }{2 \,\pi \,\sqrt{g_i(0)\,\lambda }}\,\frac{2C_F}{\alpha _s (2\pi )^4}\,\frac{1}{p^2_T}\nonumber \\&\qquad \times \int \,\mathrm{d}^2 r \,\mathrm{e}^{i \vec {p}_T\cdot \vec {r}}\,\,\nabla ^2_T\,N^{i}_G( Y - y; r; 0)\nonumber \\&\qquad \times \nabla ^2_T\,N^{j}_G( y; r; |{\vec {B}}| ) \end{aligned}$$
(5.16)

for diagrams of Fig. 9a, b.

For the diagrams of Fig. 9c, d, which correspond to double diffraction in large masses, we obtain

$$\begin{aligned}&\frac{\mathrm{d} \sigma _{i,j}}{\mathrm{d}y \,\mathrm{d}^2 p_{T}\,\mathrm{d}^2 B\,\mathrm{d}^2 b }\nonumber \\&\quad =\frac{\mathrm{e}^{-\,m\,b - m B}}{S^2( b, m_i)}\,\frac{m }{2 \,\pi \,g_i(0)\,\lambda }\,\frac{2C_F}{\alpha _s (2\pi )^4}\,\frac{1}{p^2_T}\nonumber \\&\qquad \times \int \,\mathrm{d}^2 r \,\mathrm{e}^{i \vec {p}_T\cdot \vec {r}}\,\,\nabla ^2_T\,N^{i}_G(Y - y; r; 0)\nonumber \\&\qquad \times \nabla ^2_T\,N^{j}_G(y; r;0). \end{aligned}$$
(5.17)

Plugging Eqs. (5.16) and (5.17) into Eq. (5.2), we can calculate the double inclusive cross sections. Plugging them in Eqs. (5.7) and (5.8), we obtain the correlation function and \(v_n\). The result of these calculations is shown in Fig. 10. One can see from this figure that contributions of semi-enhanced and enhanced diagrams increase the typical transverse momentum in the \(v_n\) dependence on the transverse momenta. Note that the contributions of these diagrams are closely related to the contribution of the processes of diffractive production of large masses in single diffraction (LMD-SD), and of double diffraction (LMD-DD), to the total cross section.

Such a behavior is a direct consequence of the fact that typical momenta in the LMD contribution are of the order of \(Q_s\), which is larger than \(m_1\) and \(m_2\), which determine the hadron structure (see Fig. 11)

Fig. 11
figure 11

The contribution to \(v_{22}\) versus \(p_T\) at \(W = 13\,\hbox {TeV}\) for large mass diffraction in single (LMD-SD) and in double (LMD-DD)

Full size image
Fig. 12
figure 12

Experimental data for \(v_{nn}\) and \(v_n\) versus \(p_T\) at \(W = 13\,\hbox {TeV}\) [17, 18]

Full size image

In Fig. 10b we plot the values of \(v_n\) that were calculated using Eqs. (5.8) and (5.11), replacing the double inclusive cross sections by sum of contributions which stem from non-enhanced, semi-enhanced and enhanced diagrams shown in Figs. 3 and 9. Comparing Fig. 10a, b shows that the typical momentum for the sum of the diagrams, is larger than for the non-enhanced diagrams. Figure 11 displays the dependence of \(v_{n,n}\) in the semi-enhanced and enhanced diagrams. Comparing this figure with Fig. 10b, we note that the contributions of these diagrams are larger than the non-enhanced one, leading to an explanation of the \(p_T\) dependence in the experimental data of Fig. 12. Therefore, in our model the typical momentum is close to \(Q_s\). Comparing Fig. 11 and Fig. 10b, one can see that at \(p_T >1\,\hbox {GeV}\) the main contribution originates from the semi-enhanced diagrams denoted in Fig. 11 as LMD-SD. Indeed, \(v_2 =\sqrt{v_{2,2}}\) in Fig. 11 turns out to be almost the same as \(v_2\) shown in Fig. 10b.

5.5 Comparison with the experiment

In Figs. 12 and 13 we plot the experimental data [17, 18] and the results of our calculations. One can see that we predict values and \(p_T\) dependence of \(v_n\) in agreement with the experimental data. We wish to stress that we used Eq. (5.9)-1 for the estimates of the values of \(v_{n}\), but one can see that our predictions for \(v_{n,n}\) are also in accord with the data. As we have mentioned, the semi-enhanced and enhanced diagrams are closely related to the processes of large mass diffraction. On the other hand, these processes give only about 30% contributions (see Table 2). Indeed, at \(W = 13\,\hbox {TeV}\) \(R^\mathrm{lmd}_\mathrm{sd} = \sigma ^\mathrm{lmd}_\mathrm{sd}/(\sigma _\mathrm{el} + \sigma ^\mathrm{smd}_\mathrm{sd} + \sigma ^\mathrm{smd}_\mathrm{dd} )\,=\,0.26\) and \(R^\mathrm{lmd}_\mathrm{dd} = \sigma ^\mathrm{lmd}_\mathrm{dd}/(\sigma _\mathrm{el} + \sigma ^\mathrm{smd}_\mathrm{sd} + \sigma ^\mathrm{smd}_\mathrm{dd}) \,=\,0.16\).

Such an essential difference stems from the fact that the cross sections of diffractive production should be multiplied by the survival probability factor \(\exp \left( - 2 \Omega (r, Y - Y_0, b\right) \) (see Eq. (2.21) and Ref. [40]). This factor results in substantial suppression of the diffractive production, however, it is absent in the double inclusive cross sections.

Fig. 13
figure 13

Our model for \(v_{nn}\) and \(v_n\) versus \(p_T\) at \(W=13\,\hbox {TeV}\)

Full size image

6 Conclusions

In this paper we generalized our model to include the hard processes and presented our estimates for \(v_n\) for proton–proton collisions at high energy. Our main result can be briefly formulated thus: the model predicts Bose–Einstein correlations which lead to values of \(v_n\) that are in accord with the experimental values. Our estimates are obtained from a model which is able to describe the typical soft observables for diffractive production, such as total and elastic cross section and cross section of diffraction production, inclusive cross sections, long range rapidity correlations and the deep inelastic \(F_2\) structure function. In spite of being a phenomenological model which parameterizes the data rather than giving a theoretical interpretation, we believe that our model leads to reliable predictions for \(v_n\) at high energies. This belief is based not only on the fact that the model describes both diffractive processes and processes of the multi-particle generation, but also on the fact that it includes all that we know from CGC on the behavior of the scattering amplitude in the saturation region. We showed that the angular correlations do not depend on energy and multiplicity, in accord with the experimental data.

Therefore, before making extreme assumptions on proton–proton collisions, such as the production of quark–gluon plasma in the large multiplicity events, we need to explain what happens to the Bose–Einstein correlations which are so large that they are able to describe the angular correlations in the proton–proton scattering, without taking into account interactions in the final state.