Azimuthal angle correlations at large rapidities: revisiting density variation mechanism

Abstract

We discuss the angular correlation present in hadron–hadron collisions at large rapidity difference ($\bar{\alpha }_S\,y_{12}\gg \,1$). We find that in the CGC/saturation approach the largest contribution stems from the density variation mechanism. Our principal results are that the odd Fourier harmonics ($v_{2n+1}$) decrease substantially as a function of $y_{12}$, while the even harmonics ($v_{2n}$) increase considerably with the growth of $y_{12}$.

1 Introduction

In this paper we address the problem of the azimuthal angle correlations of two hadrons with transverse momenta $\vec {p}_{T1}$ and $\vec {p}_{T2}$ and rapidities $y_1$ and $y_2$, at large values of $y_{12} \equiv | y_1 - y_1| \gg 1/\bar{\alpha }_S$. Our main theoretical assumption is that these correlations stem from interactions in the initial state. We are aware that, unlike rapidity correlations which at large rapidities originate from the initial state interactions due to causality reasons [1], a substantial part of these correlations could be due to the interactions in the final states [2,3,4]. On the other hand, it has been demonstrated that at small rapidity difference $\bar{\alpha }_S\,y_{12} \,<\,1$ the interactions in the initial state [5,6,7,8,9,10,11,12,13,14] yield the value of the correlations, which describe the major part of the experimentally observed correlations [15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37].

Fig. 1

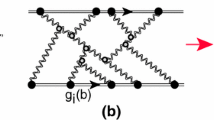
Mueller diagrams[39] for two partonic showers production. a The square of the production amplitudes, while b corresponds to the interference diagram which leads to the Bose–Einstein correlations. The wavy lines show the BFKL Pomeron [40,41,42,43], while the helical lines denote gluons. Figure 1c shows the example of a more complicated structure of the partonic cascades, than the exchange of the BFKL Pomeron. The color of the lines indicates the parton shower

Fig. 2

The generalization of Fig. 1b for $\bar{\alpha }_S\,y_{12}\,\gg \,1$. The wavy lines show the BFKL Pomeron[40,41,42,43], while the helical lines denote gluons. The color (blue and black) of the lines indicates the parton shower

In this paper we concentrate our efforts on calculating the long range rapidity part of angular correlations with large value of the rapidity difference $y_{12}$. All previous calculations assumed that $\bar{\alpha }_Sy_{12}\, < \,1$[5,6,7,8,9,10,11,12,13,14]. It turns out that in this kinematic region, the main source of the azimuthal angle correlations is the Bose–Einstein correlations of identical gluons, corresponding to the interference diagram in the production of two partonic showers. Intuitively, we expect that the correlations in the process, where two different gluons are produced from two different partonic showers, should not depend on the difference of rapidities ($y_{12}$), nor on the values of $y_1$ and $y_2$. Using the AGK cutting rules [38]¹ one can prove that the two gluon correlations can be calculated using the Mueller diagrams [39] of Fig. 1.

The diagrams of Fig. 1 lead to correlations which do not depend on $y_1$ and $y_2$, but only for $\bar{\alpha }_S\,y_{12}\, \ll \,1$. For large $y_{12}$ the contributions of Fig. 1 decrease. The main goal of this paper is to find the contributions which survive at large $y_{12}$ ($\bar{\alpha }_S\, y_{12}\, \gg \,1$).

At large $y_{12}$, we have to take into account the emission gluons, with rapidities $y_2 \,<\,y_i\,<\,y_1$, which transform the Mueller diagram of Fig. 1b to the more general diagrams of Fig. 2. The general feature of Fig. 1b is that the lower Pomerons carry momenta $\vec {Q}_T + \vec {p}_{12}$ and $-\vec {Q}_T - \vec {p}_{12}$ with $\vec {p}_{12} = \vec {p}_{T1} - \vec {p}_{T2}$. $\vec {Q}_T$ denotes the momentum along the BFKL Pomeron. After integration over $Q_T$, we obtain $p_{12} \sim 1/R_h$, where $R_h$ is the size of the target (projectile), which has a non-perturbative origin. Roughly speaking, the correlation function turns out to be proportional to $G\left( p_{12}\right)$, where G denotes the non-perturbative form factor of the target or projectile [12]. This conclusion stems from the value of the typical $Q_T$ for the BFKL Pomeron, which is determined by the size of the largest dipoles in the Pomeron. Figure 2 does not have these features. We will show that the azimuthal angle correlations originate from the integration over $\vec {Q}_T$ (see Fig. 2), due to the structure of the vertices of emission of the gluons with $\vec {p}_{T1}$ and $\vec {p}_{T2}$, which have contributions proportional to $(\vec {p}_{T1}\cdot \vec {Q}_T)^n$ $(\vec {p}_{T2}\cdot \vec {Q}_T)^n$. Recall that these kinds of vertices are the only possibilities to obtain angular correlations in the classical Regge analysis [53]. This mechanism for azimuthal angular correlations was suggested in Ref. [54] (see also Refs. [10, 55,56,57]), and in the review of Ref. [57] it was called the density variation mechanism.

The paper is organized as follows. In the next section we discuss the contribution of the diagram of Fig. 2 in the momentum representation. In the remainder of the paper, we will use the mixed representation: the dipole sizes and momentum transferred ($Q_T$), which will be introduced in Sect. 3 and appendix A. Section 4 is devoted to the discussion of the single inclusive production in the Color Glass Condensate (CGC)/saturation approach. The double inclusive production is considered in Sect. 4, in which the rapidity dependence of the master diagram of Fig. 2 will be calculated. In Sect. 5, we estimate the angular correlation function and Fourier harmonics $v_n$, and we present our prediction for the dependence of $v_n$ on the difference of rapidities ($y_{12}$). In Sect. 6 we draw our conclusions and outline problems for future investigation.

2 Correlations in the momentum representation

The double inclusive cross section of Fig. 2 takes the following form:

$$\begin{aligned}&\frac{\mathrm{d}^2 \sigma }{\mathrm{d} y_1 \mathrm{d}^2 p_{T1}\,\mathrm{d} y_2 \mathrm{d}^2 p_{T2}}\left( \mathrm{Fig}.~2\right) \nonumber \\&\quad =\left( \frac{2 C_F \alpha _S}{(2 \pi )^2 }\right) ^2\int \frac{\mathrm{d}^2 k_T}{( 2 \pi )^2}\,\frac{\mathrm{d}^2 k'_T}{( 2 \pi )^2} \,\frac{\mathrm{d}^2 Q'_T}{( 2 \pi )^2}\,\frac{\mathrm{d}^2 Q_T}{( 2 \pi )^2 }\,\frac{\mathrm{d}^2 Q''_T}{( 2 \pi )^2 } \,k^2_T \,(\vec {k}_T\nonumber \\&\qquad - \vec {Q}_T)^2\times \,\,N\left( Q'_T\right) \, \phi ^G_H\left( -\vec {k}_T + \vec {Q}'_T, \vec {k}_T; Y - y_1\right) \nonumber \\&\qquad \times \phi ^G_H\left( \vec {k}_T - \vec {Q}_T, -\vec {k}_T + \vec {Q}_T - \vec {Q}'_T; Y -y_1\right) \,\,\Gamma _\nu \big ( -\vec {k} \nonumber \\&\qquad + \vec {Q}_T, \vec {p}_{T1}\big )\times \Gamma _\nu \left( \vec {k} - \vec {Q}_T - \vec {Q}'_T, \vec {p}_{T1}\right) \nonumber \\&\qquad \times \,\, \phi \big (-\vec {k}_T , -\vec {k}_T + \vec {Q}_T; \vec {k}'_t + \vec {p}_{T2},-\vec {k}'_T - \vec {p}_{2T} \nonumber \\&\qquad - \vec {Q}_T; y_{12}\big )\times \phi \left( - \vec {k}_T+ \vec {Q}'_T + \vec {p}_{T1}, \vec {k}_T - \vec {p}_{T1} \right. \nonumber \\&\qquad \left. - \vec {Q}_T - \vec {Q}'_T;\vec {k}'_T - \vec {Q}''_T +\vec {Q}_T, \vec {k}'_T- \vec {p}_{T2}; y_{12}\right) \nonumber \\&\qquad \times \,\,N\left( Q''_T\right) \, \phi ^G_H\big ( \vec {k}'_T - \vec {Q}''_T + \vec {Q}_T,- \vec {k}'_T \nonumber \\&\qquad - \vec {Q}_T; y_2\big )\,\phi ^G_H\big ( -\vec {k}'_T - \vec {Q}''_T + \vec {Q}_T , \vec {k}'_T;y_2\big )\,\Gamma _\mu \big ( -\vec {k}'_T \nonumber \\&\qquad -\vec {p}_{T2} + \vec {Q}''_T ,\vec {p}_{T2}\big ) \,\Gamma _\mu \big ( \vec {k}'_T- \vec {p}_{T 2},\vec {p}_{T2}\big ) \end{aligned}$$

(2.1)

where $\phi ^G_H\left( \vec {k}_T,-\vec {k} +\vec {Q}_T'\right)$, as well as all other functions $\phi$ of this type, are the correlation functions, which at $Q'_T=0$ give the probability to find a gluon with transverse momentum $\vec {k}_T$ in the hadron (nucleus) of the projectile (target). $\phi \left( \vec {k}_T,-\vec {k} +\vec {Q}_T; \vec {k}'_T,-\vec {k}'_T +\vec {Q}_T\right)$ describes the interaction of two gluons with momenta $\vec {k}_T$ and $\vec {k}'_T$, which scatter at momentum transferred $Q''_T$. $N\left( Q'_T\right)$ is a pure phenomenological form factor that describes the probability to find two Pomerons in the projectile or target, with transferred moment $\vec {Q}'_T$ and $-\vec {Q}'_T$. $C_F \,=\,\left( N^2_c - 1\right) /2 N_c$ where $N_c$ is the number of colors. The Lipatov vertex $\Gamma _\mu \left( k_T,p_{T1}\right)$ has the following form:

$$\begin{aligned} \Gamma _\mu \left( k_{T}, p_{T1}\right) = \frac{1}{p_{T1}^2}\left( \,k^2_{T}\, p_{T1,\mu } \,-\,{k}_{T,\mu }\,p^2_{T1}\right) . \end{aligned}$$

(2.2)

Using Eq. (2.2) we obtain

$$\begin{aligned}&2\,\Gamma _\nu \left( -\vec {k} + \vec {Q}_T, \vec {p}_{T1}\right) \,\Gamma _\nu \left( \vec {k} - \vec {Q}_T - \vec {Q}'_T, \vec {p}_{T1}\right) \nonumber \\&\quad =\frac{1}{p^2_{T1}}\left( \left( -\vec {k} + \vec {Q}_T \right) ^2\,\left( \vec {k}_T - \vec {p}_{T1} - \vec {Q}_T - \vec {Q}'_T\right) ^2 \right. \nonumber \\&\qquad \left. +\,\left( -\vec {k} +\vec {p}_{T1} - \vec {Q}_T \right) ^2\,\left( \vec {k}_T - \vec {Q}_T - \vec {Q}'_T\right) ^2\right) \,-\,Q'^2_T;\nonumber \\&2\, \Gamma _\mu \left( -\vec {k}'_T -\vec {p}_{T2} + \vec {Q}''_T ,\vec {p}_{T2}\right) \,\Gamma _\mu \left( \vec {k}'_T - \vec {p}_{T 2} - \vec {Q}_T,\vec {p}_{T2}\right) \nonumber \\&\quad =\frac{1}{p^2_{T2}} \left( \left( -\vec {k}'_T -\vec {p}_{T2} + \vec {Q}''_T \right) ^2 \left( \vec {k}'_T - \vec {Q}_T \right) ^2\right. \nonumber \\&\qquad \left. \,+\, \left( -\vec {k}'_T + \vec {Q}''_T + \vec {Q}_T \right) ^2 \left( \vec {k} - \vec {p}_{T 2}- \vec {Q}''_T \right) ^2\right) \,-\,Q''^2_T .\nonumber \\ \end{aligned}$$

(2.3)

We can simplify the master equation (see Eq. (2.1) by observing that the dependence on $Q'_T$ and $Q''_T$ is determined by the non-perturbative scale of the projectile (target) structure, which in Eq. (2.1) is absorbed in the phenomenological form factors $N(Q'_T)$ and $N(Q''_T)$. Therefore, the typical $Q'_T$ and $Q''_T$ turn out to be of the order of the soft scale $\mu _\mathrm{soft}$, which is much smaller that the other typical momenta in Eq. (2.1), assuming that $P_{T1}$ and $P_{T2}$ are larger than $\mu _\mathrm{soft}$. Introducing

$$\begin{aligned} \mu ^2_\mathrm{soft} = \int \frac{\mathrm{d}^2 Q'_T}{(2\,\pi )^2} N\left( Q'_T\right) \end{aligned}$$

(2.4)

we can neglect $Q'_T$ and $Q''_T$ in the BFKL Pomeron Green functions and rewrite Eq. (2.1) in the form

$$\begin{aligned}&\frac{\mathrm{d}^2 \sigma }{\mathrm{d} y_1 \mathrm{d}^2 p_{T1}\,\mathrm{d} y_2 \mathrm{d}^2 p_{T2}}\left( \mathrm{Fig}.~2\right) \nonumber \\&\quad =\,\,\left( \frac{2 C_F \alpha _S\,\mu ^2_\mathrm{soft}}{(2 \pi )^2 }\right) ^2\int \frac{\mathrm{d}^2 k_T}{( 2 \pi )^2}\,\frac{\mathrm{d}^2 k'_T}{( 2 \pi )^2} \,\,\frac{\mathrm{d}^2 Q_T}{( 2 \pi )^2 }\, \,k^2_T \,(\vec {k}_T\nonumber \\&\qquad - \vec {Q}_T)^2\times \,\, \phi ^G_H\left( -\vec {k}_T , \vec {k}_T; Y - y_1\right) \times \phi ^G_H\big ( \vec {k}_T\nonumber \\&\qquad - \vec {Q}_T, -\vec {k}_T + \vec {Q}_T;Y - y_1 \big )\,\,\times \Gamma _\nu \big ( -\vec {k}\nonumber \\&\qquad + \vec {Q}_T, \vec {p}_{T1}\big ) \,\Gamma _\nu \left( \vec {k} - \vec {Q}_T , \vec {p}_{T1}\right) \times \,\, \phi \big (-\vec {k}_T ,\nonumber \\&\qquad -\vec {k}_T + \vec {Q}_T; \vec {k}'_t + \vec {p}_{T2},-\vec {k}'_T - \vec {p}_{2T} - \vec {Q}_T; y_{12}\big )\nonumber \\&\qquad \times \phi \big (- \vec {k}_T + \vec {p}_{T1}, \vec {k}_T - \vec {p}_{T1} - \vec {Q}_T ; \vec {k}'_T +\vec {Q}_T, \vec {k}'_T \nonumber \\&\qquad - \vec {p}_{T2}; y_{12}\big )\times \,\, \phi ^G_H\left( \vec {k}'_T + \vec {Q}_T,- \vec {k}'_T - \vec {Q}_T; y_2\right) \nonumber \\&\qquad \times \phi ^G_H\left( -\vec {k}'_T + \vec {Q}_T , \vec {k}'_T;y_2\right) \times \Gamma _\mu ( -\vec {k}'_T\nonumber \\&\qquad -\vec {p}_{T2}, \vec {p}_{T2}) \,\Gamma _\mu \left( \vec {k}'_T - \vec {p}_{T 2},\vec {p}_{T2}\right) , \end{aligned}$$

(2.5)

with Eq. (2.3), which takes the following form:

$$\begin{aligned}&2\,\Gamma _\nu \left( -\vec {k} + \vec {Q}_T, \vec {p}_{T1}\right) \,\Gamma _\nu \left( \vec {k} - \vec {Q}_T, \vec {p}_{T1}\right) \nonumber \\&\quad =\frac{1}{p^2_{T1}}\left( \left( -\vec {k} + \vec {Q}_T \right) ^2\,\left( \vec {k}_T - \vec {p}_{T1} - \vec {Q}_T \right) ^2\,\right. \nonumber \\&\qquad \left. +\,\left( -\vec {k} +\vec {p}_{T1} - \vec {Q}_T \right) ^2\,\left( \vec {k}_T - \vec {Q}_T \right) ^2\right) \,-\,Q^2_T;\nonumber \\&2\, \Gamma _\mu \left( -\vec {k}'_T -\vec {p}_{T2} ,\vec {p}_{T2}\right) \,\Gamma _\mu \left( \vec {k}'_T - \vec {p}_{T 2}- \vec {Q}_T,\vec {p}_{T2}\right) \nonumber \\&\quad = \frac{1}{p^2_{T2}} \left( \left( -\vec {k}'_T -\vec {p}_{T2} \right) ^2 \left( \vec {k}'_T- \vec {Q}_T \right) ^2 \,\right. \nonumber \\&\qquad \left. +\, \left( -\vec {k}'_T \right) ^2 \left( \vec {k} - \vec {p}_{T 2} - \vec {Q}_T \right) ^2\right) \,-\,Q^2_T. \end{aligned}$$

(2.6)

At high energies the parton densities $\phi ^G_H\big (-\vec {l}_T , \vec {l}_T ; Y - y_{2}\big )$ in Eqs. (2.1) and (2.5) are proportional to $\exp \left( \Delta _\mathrm{BFKL} \,Y - y_2\right)$ for the BFKL Pomeron, where $\Delta _\mathrm{BFKL} = 2.8\, \bar{\alpha }_S$ is the intercept of the BFKL Pomeron. Bearing this in mind, one can see that the interference diagram for the double inclusive cross section does not depend on $y_1, y_2$ or on $y_{12}$.

As $\phi ^G_H\left( -\vec {l}_T , \vec {l}_T ; Y - y_{2}\right) \,\,\propto exp\left( \Delta _\mathrm{BFKL} \,Y - y_2\right)$ the main diagram of Fig. 1a also does not depend on the rapidities $y_1$ and $y_2$, and its expression has the following form:

$$\begin{aligned}&\frac{\mathrm{d}^2 \sigma }{\mathrm{d} y_1 \mathrm{d}^2 p_{T1}\,\mathrm{d} y_2 \mathrm{d}^2 p_{T2}}\left( \mathrm{Fig}.~1\mathrm{a}\right) \,\,\nonumber \\&\quad =\,\,\left( \frac{2 C_F \alpha _S}{(2 \pi )^2 } \int \mathrm{d}^2 Q_T N^2\left( Q_T\right) \right) ^2\int \frac{\mathrm{d}^2 k_T}{( 2 \pi )^2}\,\frac{\mathrm{d}^2 k'_T}{( 2 \pi )^2} \nonumber \\&\qquad \times \,\, \phi ^G_H\left( -\vec {k}_T , \vec {k}_T; Y - y_1\right) \,\phi ^G_H\left( \vec {k}_T - \vec {p}_{T1}, - y_2 \right) \,\,\nonumber \\&\qquad \times \Gamma _\nu \left( -\vec {k} , \vec {p}_{T1}\right) \,\Gamma _\nu \left( \vec {k} , \vec {p}_{T1}\right) \nonumber \\&\qquad \times \varphi ^G_H\left( -\vec {l}_T , \vec {l}_T ; Y - y_{2}\right) \,\varphi ^G_H\big ( \vec {l}_T + \vec {p}_{T2}, -\vec {l}_T \,\nonumber \\&\qquad - \vec {p}_{T2}; y_2\big ) \times \Gamma _\mu \left( \vec {l}_T , \vec {p}_{T2}\right) \,\Gamma _\mu \left( - \vec {l}_T ,\vec {p}_{T2}\right) . \end{aligned}$$

(2.7)

The most economical way of calculating the diagram of Fig. 2, is to use the mixed representation of the BFKL Pomeron Green function, $G\left( \vec {r}, \vec {R},\vec {Q}_T,Y\right)$, where r and R are the sizes of two interacting dipoles, $Q_T$ denotes the momentum transferred by the Pomeron, and Y the rapidity between the two dipoles. This Green function is well known [42, 43], and for the completeness of presentation we discuss it in Appendix A, referring to Refs. [42, 43, 58,59,60] for all details.

3 Single inclusive production in a one parton shower

3.1 BFKL Pomeron: the simplest approach for a one parton shower

The single inclusive cross section resulting from the one BFKL Pomeron is well known, and it is equal to

$$\begin{aligned} \frac{\mathrm{d}^2 \sigma }{\mathrm{d} y \mathrm{d}^2 p_{T}}= & {} \frac{2 C_F \alpha _S}{(2 \pi )^2}\int \frac{ \mathrm{d}^2 k_T}{(2 \pi )^2} \phi ^G_H\left( \vec {k}_T, Q_T=0; Y - y\right) \nonumber \\&\times \phi ^G_H\left( \vec {k}_T - \vec {p}_T, Q_T=0; y \right) \,\Gamma _\nu \left( \vec {k}_T,\vec {p}_T\right) \,\Gamma _\nu \left( -\vec {k}_T,\vec {p}_T \right) .\nonumber \\ \end{aligned}$$

(3.1)

The relation between the parton densities $\phi$ and the Green function of the BFKL Pomeron has been given in Ref. [46]:

$$\begin{aligned}&N^{\tiny {\mathrm{BFKL}}}\left( r, r_1; y, Q_T=0\right) \nonumber \\&\quad = \frac{\alpha _S}{2} \int \mathrm{d}^2 k_T \,\left( 1\,-\,\mathrm{e}^{i \vec {k}_T \cdot \vec {r}}\right) \, \frac{\phi ^G_H\left( \vec {k}_T, Q_T=0; y \right) }{k^2_T}\nonumber \\ \end{aligned}$$

(3.2)

where $N^{\tiny {\mathrm{BFKL}}}\left( r, r_1; Y\right)$ is given by Eq. (A.1) or by Eq. (A.9), in the high energy limit. Equation (3.2) can be rewritten as follows:

$$\begin{aligned}&\phi ^G_H\left( \vec {k}_T , Q_T=0; y \right) \nonumber \\&\quad = \frac{2}{\alpha _S}\int \mathrm{d}^2 r\, \mathrm{e}^{i \vec {k}_T \cdot \vec {r}}\,\nabla ^2_{r} \, N^{\tiny {\mathrm{BFKL}}}\left( r, r_1; y, Q_T=0\right) . \end{aligned}$$

(3.3)

We have

$$\begin{aligned} \Gamma _\nu \left( \vec {k}_T,\vec {p}_T\right) \,\Gamma _\nu \left( -\vec {k}_T,\vec {p}_T\right) = \frac{k^2_T\,\left( \vec {k}_T - \vec {p}_T\right) ^2}{p^2_T}. \end{aligned}$$

(3.4)

Substituting Eq. (3.2) and also Eq. (3.4) into Eq. (3.1) we obtain [46]

$$\begin{aligned} \frac{\mathrm{d}^2 \sigma }{\mathrm{d} y\, \mathrm{d}^2 p_{T}}= & {} \frac{8 C_F }{\alpha _S\,(2 \pi )^2} \frac{1}{p^2_T}\int \mathrm{d}^2 r \,\mathrm{e}^{i \vec {p}_T \cdot \vec {r}}\,\nabla ^2 _r\,N^{\tiny {\mathrm{BFKL}}}_\mathrm{pr}\nonumber \\&\times \left( r, r_1; Y- y, Q_T=0\right) \nabla ^2 _r\,N^{\tiny {\mathrm{BFKL}}}_\mathrm{tr}\nonumber \\&\times \left( r, r_2; y, Q_T=0\right) \end{aligned}$$

(3.5)

where $N_\mathrm{pr}$ and $N_\mathrm{tr}$ denote the probability to find a dipole in the projectile and target, respectively. $r_1$ and $r_2$ are the typical dipoles sizes in the projectile and target.

As can be seen from Eq. (2.1) we need to generalize Eq. (3.5) for the case $Q_T \ne 0$. Equation (3.1) has to be replaced by

$$\begin{aligned}&\frac{\mathrm{d}^2 \sigma }{\mathrm{d} y \mathrm{d}^2 p_{T}}\left( Q_T \ne 0\right) \nonumber \\&\quad =\frac{2 C_F \alpha _S}{(2 \pi )^2}\int \frac{ \mathrm{d}^2 k_T}{(2 \pi )^2} \phi ^G_H\left( \vec {k}_T, Q_T, Y - y\right) \times \phi ^G_H\big ( \vec {k}_T\nonumber \\&\qquad - \vec {p}_T, Q_T; y \big )\Gamma _\nu \left( \vec {k}_T,\vec {p}_T\right) \,\Gamma _\nu \left( -\vec {k}_T + \vec {Q}_T,\vec {p}_T \right) .\nonumber \\ \end{aligned}$$

(3.6)

Taking into account Eq. (3.2) for $Q_T \ne 0$ and

$$\begin{aligned}&\Gamma _\nu \left( \vec {k}_T,\vec {p}_T\right) \,\Gamma _\nu \left( -\vec {k}_T + \vec {Q}_T,\vec {p}_T \right) \nonumber \\&\quad =\frac{1}{2}\left\{ \frac{1}{p^2_T}\Bigg [ \left( \vec {k}_T - \vec {Q}_T\right) ^2 \left( \vec {k}_T - \vec {p}_T\right) ^2 \right. \nonumber \\&\qquad \left. + \left( \vec {k}_T\right) ^2 \left( \vec {k}_T - \vec {p}_T - \vec {Q}_T\right) ^2\Bigg ]\,\,-\,\,Q^2_T\right\} \end{aligned}$$

(3.7)

we rewrite Eq. (3.5) in the form

$$\begin{aligned}&\frac{\mathrm{d}^2 \sigma }{\mathrm{d} y\, \mathrm{d}^2 p_{T}}\left( Q_T \ne 0\right) \nonumber \\&\quad = \frac{4 C_F }{\alpha _S\,(2 \pi )^2} \frac{1}{p^2_T}\int \mathrm{d}^2 r \,\mathrm{e}^{i \vec {p}_T \cdot \vec {r}}\nonumber \\&\qquad \times \Bigg \{-\nabla ^2 _r\,N^{\tiny {\mathrm{BFKL}}}_\mathrm{pr}\,\left( r, r_1; Y - y, Q_T\right) \nonumber \\&\qquad \times ( - i \nabla _r -\vec {Q}_T)^2\,N^{\tiny {\mathrm{BFKL}}}_\mathrm{tr}\,\left( r, r_2; y, Q_T\right) \,\nonumber \\&\qquad +\,( - i \nabla _r\, -\,\vec {Q}_T)^2\,(-\nabla ^2_r)N^{\tiny {\mathrm{BFKL}}}_\mathrm{pr}\nonumber \\&\qquad \times \left( r, r_1; Y- y, Q_T\right) \,\,N^{\tiny {\mathrm{BFKL}}}_\mathrm{tr}\,\left( r, r_2; y, Q_T\right) \Bigg \}\nonumber \\&\qquad - \,\, Q^2_T \frac{4 C_F }{\alpha _S\,(2 \pi )^2} \int \mathrm{d}^2 r \,\mathrm{e}^{i \vec {p}_T \cdot \vec {r}}\,N^{\tiny {\mathrm{BFKL}}}_\mathrm{pr}\,\left( r, r_1; Y \right. \nonumber \\&\qquad \left. - y, Q_T\right) \,N^{\tiny {\mathrm{BFKL}}}_\mathrm{tr}\,\left( r, r_2; y, Q_T\right) . \end{aligned}$$

(3.8)

3.2 General estimates

It should be stressed that the single inclusive production has the form of Eqs. (3.5) and (3.8) for the general structure of the single parton shower, as was shown in Ref. [46]. For example, for the process shown in Fig. 1c. We need only to substitute $N^{G}_\mathrm{tr}\,\left( r, r_2; y, Q_T\right)$ for $2 N^{\tiny {\mathrm{BFKL}}}_\mathrm{tr}\,\left( r, r_2; y, Q_T\right)$ where

$$\begin{aligned}&2 N^{\tiny {\mathrm{BFKL}}}_\mathrm{tr}\,\left( r, r_2; y, Q_T\right) \,\,\rightarrow \,\, N^{G}_\mathrm{tr}\,\left( r, r_2; y, Q_T\right) \nonumber \\&\quad =\,\,2 N_\mathrm{tr}\,\left( r, r_2; y, Q_T\right) - \int \mathrm{d}^2 Q'_T\, N_\mathrm{tr}\,\big ( r, r_2; y, \vec {Q}_T\nonumber \\&\qquad - \vec {Q}'_T\big )\, N_\mathrm{tr}\,\left( r, r_2; y, \vec {Q}'_T\right) ; \end{aligned}$$

(3.9)

$N_\mathrm{tr}\,\left( r, r_2; y, Q_T\right)$ is a solution to the non-linear evolution equation. For the case of inclusive production, we can considerably simplify the estimates noting that

$$\begin{aligned} \nabla ^2_r \,N_\mathrm{tr}\,\left( r, r_2; y, Q_T\right)&\xrightarrow {r^2 Q^2 _s\left( y\right) \ll \,1}&N^\mathrm{BFKL}_\mathrm{tr}\,\left( r, r_2; y, Q_T\right) \ll \,\,1;\nonumber \\ \nabla ^2_r \,N_\mathrm{tr}\,\left( r, r_2; y, Q_T\right)&\xrightarrow {r^2 Q^2_s\left( y\right) \, \gg \,1}&0, \end{aligned}$$

(3.10)

where $Q_s(y)$ denotes the saturation momentum.

In other words, the main contribution to inclusive production comes from the vicinity of the saturation scale, where $r^2 Q^2_s \approx \,1$. Fortunately, the behavior of N in this kinematic region is determined by the linear BFKL evolution equation [62,63,64,65,66,67] and has the following form [68]:

$$\begin{aligned}&N_\mathrm{tr}\,\left( r, r_2; y, Q_T = 0\right) \propto \left( r^2 Q^2_s(y)\right) ^{1 - \gamma _{cr}}~\text{ with }~~ Q^2_s\nonumber \\&\quad = (1/r^2_2)\,\exp \left( \frac{\omega \left( \gamma = \frac{1}{2}+ i \nu = \gamma _{cr}\right) }{1 - \gamma _{cr}}\,y\right) \nonumber \\&\quad = (1/r^2_2)\mathrm{e}^{\kappa \,y} \end{aligned}$$

(3.11)

where $\gamma _{cr}$ = 0.37.

From Eq. (A.8) we see that, for $Q_T \ne 0$, the scattering amplitude decreases at $Q^4_T\, r^2 \,r^2_2\, \gg \,1$. Therefore, we need to consider rather small values of $Q_T$: $Q^4_T\, r^2 \,r^2_2\, \le \,1$. The product of vertices that determines the amplitude has two terms (see Eq. (A.5)) which are proportional to $\left( r^2/r^2_2\right) ^{i \nu }$ and to $\left( Q^4_T\, r^2 \,r^2_2\right) ^{I \nu }$. Therefore, the maximum of $\nabla ^2_r N$ can be reached if $r^2/r^2_2 \mathrm{e}^{\kappa \,y} \,\sim \, 1$ and $Q^4_T\,r^2\,r^2_2 \mathrm{e}^{\kappa \,y} \,\sim \,1$ and the amplitude then has the following form:

$$\begin{aligned}&N_\mathrm{tr}\,\left( r, r_2; y, Q_T\right) \propto c_1 \left( \frac{r^2}{r^2_2} \mathrm{e}^{\kappa \,y}\right) ^{1 - \gamma _{cr}} \nonumber \\&\quad + \, c_2 \left( Q^4_T\, r^2 \,r^2_2\,\mathrm{e}^{\kappa \,y}\right) ^{1 - \gamma _{cr}}. \end{aligned}$$

(3.12)

The first term does not depend on $Q_T$ and, therefore, the upper limit of the integral over $Q_T$, goes up to $\left( Q^{max}_T\right) ^2\,\approx 1/(r\,r_2)$. The second term, both for $Q^2_T \,r\,r_2\,<\,\mathrm{e}^{- \frac{1}{2}\kappa \,y}$ and for $Q^2_T \,r\,r_2\,>\,\mathrm{e}^{- \frac{1}{2}\kappa \,y}$, turns out to be small. Indeed, in the first region the amplitude is small, while in the second region we are deep in the saturation domain where $\nabla ^2_r N \rightarrow 0$. Hence, we expect that in the integral over $Q_T$, the first term gives a larger contribution than the second term, and we will only keep this contribution in our estimates.

4 Double inclusive cross section for two parton shower production

4.1 The simplest diagram

In this section we calculate the simplest diagram of Fig. 2. We need to integrate the product of two BFKL Pomerons over $Q_T$ (see Eq. (2.5)):

$$\begin{aligned} I = \int \mathrm{d}^2 Q_T\,V_{\nu _1}\left( \vec {r}_1,\vec {Q}_T\right) \,V^*_{\nu _1}\left( \vec {r}_2,\vec {Q}_T\right) \, V_{\nu _2}\left( \vec {r}'_1,\vec {Q}_T\right) \,V^*_{\nu _2}\left( \vec {r}'_2,\vec {Q}_T\right) . \end{aligned}$$

(4.1)

From Eq. (2.5) in the momentum representation, we see that $r_1 \ne r'_1$ ($r_2 \ne r'_2$), however, they are close to each other, being determined by the same momentum $k_T$. We assume that $p_{T1} < k_T$, since $k_T \sim Q_s\left( Y - y_1\right) \gg \mu _\mathrm{soft}$. Considering $r_1 \approx r'_1 \,\ll \,r_2 \approx r'_2$ we will show that in the integral over $Q_T$, the typical $Q_T \sim 1/r_2$. In other words, the dependence of $Q_T$ is determined by the largest of interacting dipoles.

From Eq. (A.8) we see that, for large $Q_T$, when $r^2_1 Q^2_T \,\gg \,1$ and $r^2_2\,Q^2_T\,\gg \,1$, the integrand is proportional to $1/Q^4_T$ and converges. The main region of interest is $r^2_2\, Q^2_T \,\gg \,1$ and $r^2_1\,Q^2_T\,\ll \,1$. In this kinematic region for the vertices $V_{\nu _1}\left( \vec {r}_1,\vec {Q}_T\right)$  and $V_{\nu _2}\left( \vec {r}'_1,\vec {Q}_T\right)$, we can use Eq. (A.6), while the conjugated vertices are still in the regime of Eq. (A.8). Eq. (4.1) then takes the form

$$\begin{aligned} I= & {} 2^{6 i (\nu _1 + \nu _2)} \left( - 16\nu _1\,\nu _2\right) \pi \nonumber \\&\times \int _{1/r^2_2}\,\, d Q^2_T\,\left\{ \left( \frac{Q^2\,r^2_1}{2^6}\right) ^{-i \nu _1} - \left( \frac{Q^2\,r^2_1}{2^6}\right) ^{i \nu _1}\right\} \,\nonumber \\&\times \left\{ \left( \frac{Q^2\,r'^2_1}{2^6}\right) ^{-i \nu _2} - \left( \frac{Q^2\,r'^2_1}{2^6}\right) ^{i \nu _2}\right\} \frac{\cos ^2\left( \frac{1}{2}\vec {Q}_T\cdot \vec {r}_1\right) }{Q^2_T \,r^2_2}.\nonumber \\ \end{aligned}$$

(4.2)

Assuming that both $\nu _1$ and $\nu _2$ are small, we see that all four terms are equal to each other, and the integral can be written as follows:

$$\begin{aligned} I = 2^{6 i (\nu _1 + \nu _2)} \left( - 2^6\nu _1\,\nu _2\right) \pi \frac{1}{i\,(\nu _1 + \nu _2)} \left( \frac{r^2_1}{r^2_2}\right) ^{i\,(\nu _1 + \nu _2)}\frac{1}{r^2_2}. \end{aligned}$$

(4.3)

The appearance of the pole $\nu _1=-\nu _2$ indicates that the contribution from this kinematic region is large.

Closing the contour of integration on $\nu _2$ over the pole, we obtain

$$\begin{aligned} I = 2^6 \pi \,\nu ^2_1\frac{1}{r^2_2}. \end{aligned}$$

(4.4)

Actually, the double inclusive cross section depends on $\nabla ^2 N$ as we argued in the previous section. Repeating the procedure for

$$\begin{aligned} \mathcal{I}= & {} \int \mathrm{d}^2 Q_T\,\nabla ^2_{r_1}\left( r_1\,V_{\nu _1}\left( \vec {r}_1,\vec {Q}_T\right) \right) \,\nabla ^2_{r'_1}\left( r'_1\,V^*_{\nu _1}\left( \vec {r}_2,\vec {Q}_T\right) \right) \,\nonumber \\&\quad \times \nabla ^2_{r_2} \left( r_2\,V_{\nu _2}\left( \vec {r}'_1,\vec {Q}_T\right) \right) \,\nabla ^2_{r'_2}\left( r'_2\,V^*_{\nu _2}\left( \vec {r}'_2,\vec {Q}_T\right) \right) ,\nonumber \\ \end{aligned}$$

(4.5)

we obtain for small $\nu _1$ and $\nu _2$

$$\begin{aligned} \mathcal{I} = 2^6 \pi \,\nu ^2_1\frac{1}{r_1\,r'_1\,r^2_2\,r'^2_2}. \end{aligned}$$

(4.6)

Using the method of steepest descent, to integrate over $\nu _1$, we obtain the following contribution:

$$\begin{aligned} \mathcal{I} = 2^5 \,\frac{1}{r_1\,r'_1\,r^2_2\,r'^2_2}\sqrt{\frac{\pi }{\left( 2 \,D\,y_{12}\right) ^3}}\,\,\mathrm{e}^{ 2 \Delta _\mathrm{BFKL} \,y_{12}} \end{aligned}$$

(4.7)

where $\Delta _\mathrm{BFKL}$ and D are defined in Eq. (A.2).

Rewriting Eq. (2.5) in the coordinate representation we obtain

$$\begin{aligned}&\frac{\mathrm{d}^2 \sigma }{d y_1 \mathrm{d}^2 p_{T1}\,\mathrm{d} y_2 \mathrm{d}^2 p_{T2}}\left( \mathrm{Fig}.~2\right) \nonumber \\&\quad = \left( \frac{2 C_F \,\mu ^2_\mathrm{soft}}{\alpha _S\,(2 \pi )^2}\right) ^2\,\,\frac{1}{p^2_{T1}\,p^2_{T2}}\,\int \frac{\mathrm{d}^2 Q_T}{(2\,\pi )^2}\nonumber \\&\qquad \times \,\,\int \mathrm{d}^2 r_1\,\mathrm{d}^2 r'_1\, \mathrm{d}^2 \tilde{r} _1\,\mathrm{d}^2 \tilde{r}'_1 \,\mathrm{e}^{-i\, \vec {p}_{T1} \cdot \vec {\tilde{r}}'_1}\delta ^{(2)}\left( \vec {r}_1 + \vec {r}'_1 - \vec {\tilde{r}}_1 - \vec {\tilde{r}}'_1\right) \,\nonumber \\&\qquad \times \nabla ^2_{r_1} N_\mathrm{pr}\left( r_1; Y - y_1\right) \,\mathrm{e}^{i \vec {Q}_T \cdot \vec {\tilde{r}'}_1}\,\nabla ^2_{\tilde{r}'_1} N_\mathrm{pr}\left( \tilde{r}'_1; Y - y_1\right) \nonumber \\&\qquad \times \,\, \nabla ^2_{\tilde{r}_1} \nabla ^2_{\tilde{r}_2} N\left( \tilde{r}_1; \tilde{r}_2, Q_T; y _{12}\right) \nabla ^2_{\tilde{r}'_1} \nabla ^2_{\tilde{r}'_2} N\left( \tilde{r}'_1; \tilde{r}'_2, Q_T; y_{12}\right) \nonumber \\&\qquad \times \,\,\int \, \mathrm{d}^2 r_2\,\mathrm{d}^2 r'_2\, \mathrm{d}^2 \tilde{r} _2\,\mathrm{d}^2 \tilde{r}'_2\,\mathrm{e}^{- i\,\vec {p}_{T2} \cdot \vec {\tilde{r}}_2} \,\delta ^{(2)}\left( \vec {r}_2 + \vec {r}'_2 - \vec {\tilde{r}}_2 - \vec {\tilde{r}}'_2\right) \,\nonumber \\&\qquad \times \nabla ^2_{r_2} N_\mathrm{tr}\left( r_2; y_2\right) \,\mathrm{e}^{i \vec {Q}_T \cdot \vec {\tilde{r}'}_2}\,\nabla ^2_{\tilde{r}'_2} N_\mathrm{tr}\left( \tilde{r}'_2; y_2\right) . \end{aligned}$$

(4.8)

In Eq. (4.8) we have neglected the terms which are proportional to $Q^2_T$ (see Eq. (2.5)), since, as we have argued, the typical $Q_T$ are small, and because these terms do not lead to additional correlations in the azimuthal angles. In Appendix B we calculate this integral and obtain the final expression for the double inclusive cross section:

$$\begin{aligned}&\frac{\mathrm{d}^2 \sigma }{\mathrm{d} y_1 \mathrm{d}^2 p_{T1}\,\mathrm{d} y_2 \mathrm{d}^2 p_{T2}}\left( \mathrm{Fig}.~2\right) \,\,\nonumber \\&\quad = 4 \pi \left( \frac{2 C_F}{\alpha _S\,(2 \pi )^2 }\right) ^2\frac{1}{p^2_{T1}\,p^4_{T2}} \, \sqrt{\frac{1}{2 \,D\,(Y - y_1)}}\sqrt{\frac{1}{\left( 2 \,D\,y_{12}\right) ^3}}\, \frac{1}{\,D\,y_2}\,\mathrm{e}^{ 2 \Delta _\mathrm{BFKL }\,Y}.\nonumber \\ \end{aligned}$$

(4.9)

4.2 The CGC/saturation approach

The integral over $k'_T$ in Eq. (B.6) has an infrared singularity with a cutoff at $p_{T2}$, since we assume that $p_{T2}$ is the smallest momentum. This reflects the principal feature of the BFKL Pomeron parton cascade, which has diffusion, both in the region of small and large transverse momenta. On the other hand, we know that the CGC/saturation approach suppressed the diffusion in the small momenta [44], providing the natural cutoff for the infrared divergency. We expect that such a cutoff will be the value of the smallest saturation momenta: $Q_s( Y - y_1)$ or $Q_s( y_2)$, which will replace one of the $p^2_{T2}$ in the dominator of Eq. (4.9). Therefore, we anticipate that for a realistic structure of the one parton shower cascade, (see Fig. 1c for example), the contribution for the double inclusive cross section will be different.

We need to specify the behavior of the scattering amplitude in the vicinity of the saturation scale. We have discussed the basic formulas [68] of Eq. (3.11), but for integration over the dipole sizes we need to know the size of this region. The scattering amplitude can be written in the form

$$\begin{aligned} N\left( r_1,r_2; Y\right) = \int ^{\epsilon + i \infty }_{\epsilon - i \infty }\frac{\mathrm{d} \gamma }{2 \pi }\,n_{in}\left( \gamma \right) \mathrm{e}^{ \omega \left( \gamma , 0\right) Y - ( 1 - \gamma ) \xi } \end{aligned}$$

(4.10)

where $\omega (\gamma ,0)$ is given by Eq. (A.2), replacing $\frac{1}{2}+ i \nu \equiv \gamma$ and $\xi = \ln \left( r^2_1/r^2_2\right)$. The saturation scale is determined by the line on which the amplitude is a constant (C), of the order one. This leads to the following equation for the saturation scale [62, 68]:

$$\begin{aligned} \omega \left( \gamma _{cr}, 0\right) Y - ( 1 - \gamma _{cr}) \xi _s\,=\,0;\quad \omega '_\gamma \left( \gamma , 0\right) Y - \xi _s\,=\,0, \end{aligned}$$

(4.11)

which results in the value of $\gamma _{cr}$ given by the equation

$$\begin{aligned} \frac{ \omega \left( \gamma _{cr}, 0\right) }{1 - \gamma _{cr}} = \omega '_\gamma \left( \gamma , 0\right) \end{aligned}$$

(4.12)

and gives $\gamma _{cr}= 0.37$, with the equation for the saturation momentum:

$$\begin{aligned} \xi _s\,\,\equiv \,\,\ln \left( Q^2_s\,r^2_2\right) \,=\,\kappa Y\,=\,\frac{\omega \left( \gamma _{cr}\right) }{1 - \gamma _{cr}}\,Y. \end{aligned}$$

(4.13)

Fig. 3

a $-\,\Delta N\left( \tau \right) = -\,\nabla ^2$ $N\left( \tau \right) \, =\, -\,4\,\tau \frac{1}{\tau } \frac{\mathrm{d}}{\mathrm{d} \tau } \tau \frac{\mathrm{d}}{\mathrm{d} \tau }N\left( \tau \right)$ versus $\tau$ for the behavior of the scattering amplitude deep in the saturation domain[72]. b The example of a more complicated structure of the partonic cascades than the exchange of the BFKL Pomeron, which are shown in Fig. 2. The color of the lines indicates the parton shower

Expanding the phase $\omega \left( \gamma , 0\right) Y - ( 1 - \gamma ) \xi$ in the vicinity $\Delta \xi = \xi - \xi _s$ and $\Delta \gamma = \gamma - \gamma _{cr}$ we obtain

$$\begin{aligned}&N\left( r_1,r_2; Y\right) \,\,\nonumber \\&\quad = \text{ C }\,\int ^{\epsilon + i \infty }_{\epsilon - i \infty }\frac{\mathrm{d} \gamma }{2 \pi }\,\left( r^2_1\,Q^2_s\right) ^{1 - \gamma _{cr}}\int \frac{\mathrm{d} \Delta \gamma }{2 \pi i} \mathrm{e}^{ \frac{1}{2}\omega ''_{\gamma \gamma }\left( \gamma , 0\right) Y(\Delta \gamma )^2 + \Delta \gamma \Delta \xi }\, \nonumber \\&\quad = \left( r^2_1\,Q^2_s\right) ^{1 - \gamma _{cr}}\text{ C }\sqrt{\frac{\pi }{D Y}}\,\mathrm{e}^{ - \frac{(\Delta \xi )^2}{4 D Y}}. \end{aligned}$$

(4.14)

At first sight, Eq. (4.14) shows that the amplitude has a maximum at $\tau = r^2_1 \,Q^2_s=1$. However, this is not correct. Equation (4.14) gives the correct behavior for $\tau < 1$, while for $\tau >1$ we need to take into account the interaction of the BFKL Pomerons and the non-linear evolution, generated by these interactions. The general result of this evolution is the fact that the amplitude depends on one variable [69,70,71,72] $\tau$, i.e. $N\left( \tau \right)$ (as it shows geometric scaling behavior). The peak at $\tau =1$ appears in

(4.15)

From Eq. (4.15) we can conclude that the width of the distribution in $r^2_1$ is of the order of $Q^2_s$, but it depends crucially on the model for the Pomeron interaction. In Fig. 3a we plot this value for the behavior of the scattering amplitude deep in the saturation domain (see Ref. [72]).

This approach is not correct for $\tau \rightarrow 1$ and $- \nabla ^2 N = 1.58$ at $\tau =1$, but it starts to be small at $\tau > 2$, which could be large enough to trust the formulas of Ref. [72]. At least such a conclusion can be justified considering the fit of the DIS data in the saturation model of Refs. [73, 74], which is based on the idea of Ref. [75], and which has the correct behavior of the scattering amplitude, both deep in the saturation domain, and near $\tau = 1$. Hence, we expect that $\nabla ^2 N$ decreases faster than we can see from Eq. (4.14). Bearing these conclusions in mind, we will calculate the contribution of Fig. 2, keeping all N in Eq. (4.8) in the vicinities of the saturation scales, by replacing $\int ^\infty _0 d \tau (-\nabla ^2 N)= -\int ^1_0 \mathrm{d} \tau (-\nabla ^2 N)$.

We will show in the following that we cannot integrate over the dipole sizes, so that all six Pomerons will be in the vicinity of the saturation scale. At least two of the Pomerons occur either deep in the saturation domain, or in the perturbative QCD region. We believe that the largest contribution stems from the exchange of two Pomerons between rapidities $y_1$ and $y_2$ (see Fig. 3b), which are in the perturbative QCD region. Unfortunately, we cannot use the AGK cutting rules [38], which state that these Pomerons will not be affected by the Pomeron interaction, and the contributions of these interactions (see the red Pomeron in Fig. 3b) are canceled. Indeed, it has been proven that for the double inclusive production [47] they are not applicable in perturbative QCD. On the other hand, these Pomerons carry transverse momentum $Q_T$, unlike the others in the diagram, which is larger than the saturation scale $Q_s\left( y_2\right)$; hence, their contributions are suppressed in comparison with the other Pomerons in Fig. 2. In addition our choice leads to the natural matching with the region $\bar{\alpha }_S\,y_{12}\, <\,1$.

The integration over $Q_T$ will produce the same result as Eq. (4.7), as in the previous section. In Appendix C we discuss making estimates for the integrals over the dipole sizes which lead for $p_{T1}\, \ll \,Q^2_s\left( y_1\right)$ to the following cross section:

$$\begin{aligned}&\frac{\mathrm{d}^2 \sigma }{\mathrm{d} y_1 \mathrm{d}^2 p_{T1}} \left( Q_T = 0; Eq.~(3.5)\right) \nonumber \\&\quad = \frac{8 C_F }{\alpha _S\,(2 \pi )^2} \frac{1}{p^2_T}\int \mathrm{d}^2 r \,\mathrm{e}^{i \vec {p}_T \cdot \vec {r}}\,\nabla ^2 _r\,N^{\tiny {\mathrm{BFKL}}}_\mathrm{pr}\,\left( r, r_1; Y- y, Q_T=0\right) \nonumber \\&\qquad \times \nabla ^2 _r\,N^{\tiny {\mathrm{BFKL}}}_\mathrm{tr}\,\left( r, r_2; y, Q_T=0\right) \nonumber \\&\quad =\frac{8 C_F }{\alpha _S\,(2 \pi )^2} \frac{1}{p^2_T} \text{ C }^2\,(4\bar{\gamma }^2)^2 \,\exp \left( - \frac{ \ln ^2\left( Q^2_s\left( Y - y\right) /Q^2\left( y \right) \right) }{4 D \,y}\right) .\nonumber \\ \end{aligned}$$

(4.16)

In Eq. (4.16) we used backward evolution from the saturation boundary where $N = \text{ C }$.

Fig. 4

The ratio of Eq. (4.17) at W=13 TeV versus $y_{12}$, assuming that the experiment has a symmetric pattern with $Y - y_1 = y_2 = \frac{1}{2}(Y - y_{12})$. The dotted line in a is for the estimates for the $y_{12}$ dependence of the Bose–Einstein contribution at small $y_{12}$ [11, 76]. a and b The estimates in the leading order of perturbative QCD with $\bar{\alpha }_S= 0.25$. In c we take $\Delta _\mathrm{BFKL} = 0.25$ and $Q^2_s(Y) \propto \exp \left( \lambda Y\right)$ with $\lambda = 0.25$. These numbers correspond to the BFKL phenomenology

The ratio of the two contributions takes the following form:

$$\begin{aligned} R= & {} \frac{\frac{\mathrm{d}^2 \sigma }{\mathrm{d} y_1 \mathrm{d}^2 p_{T1}\,\mathrm{d} y_2 \mathrm{d}^2 p_{T2}}\left( \mathrm{Fig}.~3\mathrm{b}\right) }{\frac{\mathrm{d}^2 \sigma }{\mathrm{d} y_1 \mathrm{d}^2 p_{T1}\,\mathrm{d} y_2 \mathrm{d}^2 p_{T2}}\left( \mathrm{Fig}.~1\mathrm{a}\right) }\nonumber \\= & {} \frac{1}{N^2_c - 1} \frac{\tilde{\mu }^2_\mathrm{soft}}{Q^2_s\left( y_2\right) }\,8\,\pi ^5\,\left( 2\,\bar{\gamma }\right) ^4 \,\,0.18\,\,3.5 \nonumber \\&\times \sqrt{\frac{\pi }{\left( 2 \,D\,y_{12}\right) ^3}}\,\,\mathrm{e}^{ 2 \Delta _\mathrm{BFKL} \,y_{12}}\,\,\nonumber \\&\times \exp \left( \frac{ \ln ^2\left( Q^2_s\left( Y - y_1\right) /Q^2\left( y_1 \right) \right) }{4 D \,y_1}\right) \nonumber \\&\times \exp \left( \frac{ \ln ^2\left( Q^2_s\left( Y - y_2\right) /Q^2\left( y_2 \right) \right) }{4 D \,y_2}\right) . \end{aligned}$$

(4.17)

One can see that Eq. (4.17) demonstrates the additional suppression due to the infrared cutoff at $Q_s\left( y_2\right)$ instead of at $p_{T2}$, as taken in the calculation of the simplest diagram. The factor $\exp \left( 2 \Delta _\mathrm{BFKL} \,y_{12} \right)$ reflects the fact that two BFKL Pomerons between rapidities $y_1$ and $y_2$ are taken in the perturbative QCD region. It should be stressed that we can only trust our estimates for values of $y_{12}$ at which the exchange of the BFKL Pomeron with rapidity $y_{12}$ give a contribution smaller than $\mathrm{C}$. This condition means that

$$\begin{aligned} \frac{1}{\left( 2 \,D\,y_{12}\right) }\,\,\mathrm{e}^{ 2 \Delta _\mathrm{BFKL} \,y_{12}} \,\,<\,\,\mathrm{C}. \end{aligned}$$

(4.18)

Taking $\Delta _\mathrm{BFKL} = 0.25$ and $Q^2_s(Y) \propto \exp \left( \lambda Y\right)$ with $\lambda = 0.25$ (these values correspond to the BFKL phenomenology) we see that the l.h.s. of Eq. (4.18) is smaller than 0.15 for $y_{12}\, \le \,7$. Therefore, we can trust our estimates shown in Fig. 4 for $\mathrm{C}\, > \,0.15$. We take $\mathrm{C}=0.3$, which leads to the contribution of the shadowing corrections of the order of 30%.

The two last factors in Eq. (4.17) stem from the perturbative QCD nature of two Pomerons in Eq. (C.8) (see Eq. (4.16)).

In Fig. 4 we plot the ratio R as a function of $y_{12}$ for $y_{12} \le 7$ (see Eq. (4.18). One can see that the ratio increases for large $y_{12}$.

5 Azimuthal angle correlations

The azimuthal angle correlations stem from terms $( \vec {Q}_T \cdot \vec {r}_i)^n$ in the vertices (see Eqs. (A.5), (A.6)). Indeed, after integrating over $r_i$ these terms transform to expressions of the following type [54]: $\left( \vec {Q}_T \cdot \vec {p}_{T1}\right) ^{m_1}\, \left( \vec {Q}_T \cdot \vec {p}_{T2}\right) ^{m_2}$, which lead to the term $\left( \vec {p}_{T1} \cdot \vec {p}_{T2}\right) ^m$. We have illustrated in Eqs. (A.5) and (A.6) how these originate from the general form of the BFKL Pomeron vertices in the coordinate representation. From Eqs. (A.5) and (A.6) only terms proportional to $\left( \vec {Q}_T \cdot \vec {r}_{i}\right) ^n$ with even n appear in the expansion. Therefore, the azimuthal angle ($\phi$) correlation function contains only terms $\cos ^{2 n}\left( \phi \right)$, and it is invariant with respect to $\phi \rightarrow \pi - \phi$. In other words, $v_n$ with odd n turn out to be zero. Hence, we have the first prediction: the value $v_n$ with odd n should decrease with $y_{12}$, and their dependence should follow the dotted lines in Fig. 4a.

We return to Eq. (4.1) and integrate over $Q_T$, collecting terms that depend on the angles between $\vec {Q}_T$ and $\vec {r}_i$, which we have neglected in the previous section. As we have learned, the typical values of $Q_T \propto 1/r_2 \sim 1/r'_2$ where $r_2$ and $r'_2$ are larger than $r_1$ and $r'_1$. In other words, we showed that the main contributions stem from the kinematic regions $r^2_1 Q^2_s\left( Y - y_1\right) \sim 1$ ( $r'^2_1 Q^2_s\left( Y - y_1\right) \sim 1$) and $r^2_2 Q^2_s\left( y_2\right) \sim 1$ ( $r'^2_2 Q^2_s\left( y_2\right) \sim 1$). Assuming that $Q_s\left( Y - y_1\right) \gg Q_s\left( y_2\right)$ we conclude that $r_1(r'_1) \ll r_2(r'_2)$. The typical $Q_T$ is determined by the largest dipoles and, therefore, we expect $Q_T \approx 1/r_2 (1/r'_2)$, as has been demonstrated above. Bearing these estimates in mind, we can replace vertices $V_{\nu _1}\left( \vec {r}_1, \vec {Q}_T\right)$ and $V_{\nu _2}\left( \vec {r}'_1, \vec {Q}_T\right)$ in Eq. (4.1) by Eq. (A.6) in which we put $Q_T = 1/r_2$ and $Q_T = 1/r'_2$, respectively. Taking into account that $r_1/r_2\,\ll \,1 (r'_1/r'_2\,\ll \,1)$, we obtain

$$\begin{aligned}&V_{\nu _1}\left( \vec {r}_1, \vec {Q}_T\right) \,V_{\nu _2}\left( \vec {r}'_1, \vec {Q}_T\right) \nonumber \\&\quad = \left\{ \left( \frac{r^2_1}{2^6}\right) ^{-i \nu _1 } - \left( \frac{Q^4_T r^2_1}{2^{6}}\right) ^{ i \nu _1}\right\} \,\left( 1 \,-\,\frac{1}{2^4} \left( \vec {Q}_T \cdot \vec {r}_1\right) ^2\right. \nonumber \\&\qquad \left. \,+\,\frac{1}{2^8} \left( \vec {Q}_T \cdot \vec {r}_1\right) ^4 \right) \nonumber \\&\qquad \times \, \left\{ \left( \frac{r'^2}{2^6}\right) ^{-i \nu _2 } - \left( \frac{Q^4_T r'^2_1}{2^{6}}\right) ^{ i \nu _2}\right\} \,\left( 1 \,-\,\frac{1}{2^4} \left( \vec {Q}_T \cdot \vec {r}'_1\right) ^2\right. \nonumber \\&\qquad \left. \,+\,\frac{1}{2^8} \left( \vec {Q}_T \cdot \vec {r}'_1\right) ^4 \right) . \end{aligned}$$

(5.1)

At first sight Eq. (5.1) should enter two angles between $\vec {Q}_T$ and $\vec {r}_1$ and $\vec {r}'_1$, respectively. However, in the integrand for integration over $r_i$ (see Eq. (B.1)) it depends only on one vector $\vec {p}_{T1}$. Therefore, after integration over all angles, we find that the angle $\phi$ in Eq. (5.1) is the angle between $\vec {Q}_T$ and $\vec {p}_{T1}$.

For vertices $V^*_{\nu _1}\left( \vec {r}_2, \vec {Q}_T\right)$ and $V^*_{\nu _2}\left( \vec {r}'_2, \vec {Q}_T\right)$ in Eq. (4.1) we use Eq. (A.8). Finally, we need to evaluate the integral

$$\begin{aligned} I_Q= & {} -16 \,\nu _1\,\nu _2 \int Q_T d Q_T \Bigg \{V_{\nu _1}\left( \vec {r}_1, \vec {Q}_T\right) \,V_{\nu _2}\left( \vec {r}'_1, \vec {Q}_T\right) \Bigg \}^{r_1\,=\,r'_1=1/Q_s\left( Y - y_1\right) }_{Eq.~(5.1)}\nonumber \\&\times \left( Q^2_T\right) ^{ -i (\nu _1 + \nu _2)} \frac{\cos ^2\left( \frac{1}{2}\vec {Q}_T\cdot \vec {r}_2\right) }{Q^2_T \,r^2_2} \,\cos \left( \vec {Q}_T\cdot \vec {r}_2\right) \end{aligned}$$

(5.2)

with better accuracy that we did in Sect. 5.1, keeping the dependence on the angle between $\vec {Q}_T$ and $\vec {r}_2$. Note that the factor $\cos \left( \vec {Q}_T\cdot \vec {r}_2\right)$ comes from $\exp \left( i \, \vec {Q}_T\cdot \vec {r}_2\right)$ in Eq. (4.8). Taking this integral we substitute for the terms in parentheses in Eq. (5.1), $|Q_T| = 1/r^2_2 (1/r'^2_2)$.

The integral is equal to

$$\begin{aligned} I_Q= & {} 2^{6 i (\nu _1 + \nu _2)} \left( - 2^7\nu _1\,\nu _2\right) \ \left( \frac{r^2_1}{r^2_2}\right) ^{i\,(\nu _1 + \nu _2)}\frac{1}{r^2_2} \nonumber \\&\times \,\left( 1 \,-\,\frac{1}{2^4} \frac{ \left( \vec {n} \cdot \vec {r}_1\right) ^2 }{r^2_2} \,+\,\frac{1}{2^8}\frac{ \left( \vec {n} \cdot \vec {r}_1\right) ^4 }{r^4_2}\right) \, \nonumber \\&\times \left( 1 \,-\,\frac{1}{2^4} \frac{ \left( \vec {n} \cdot \vec {r}'_1\right) ^2 }{r'^2_2} \,+\,88,\frac{1}{2^8}\frac{ \left( \vec {n} \cdot \vec {r}'_1\right) ^4 }{r'^4_2}\right) \nonumber \\&\times \Bigg \{ \frac{1}{ i (\nu _1 + \nu _2)} \,-\,\frac{9}{32} \,\cos \left( 2 \phi _2\right) \,+\,\frac{3}{16} \cos \left( 4 \,\phi _2\right) \Bigg \}\nonumber \\ \end{aligned}$$

(5.3)

where $\vec {n} = \vec {Q}_T/Q_T$, and $\phi _2$ is the angle between $\vec {n}$ and $\vec {n}_2 = \vec {r}_2/r_2$. In Eq. (5.3) the terms in $\left( \dots \right) \left( \dots \right)$ stem from the expansion with respect to $r^2_1/r^2_2 \,\ll \,1$. However, for the terms in $\{\dots \}$ there are no such small parameters, and we expand the function of $\phi _2$ in a Fourier series.

Integrating over $\vec {n}$ one obtains

$$\begin{aligned} \left( \dots \right) \left( \dots \right) \left\{ \dots \right\}= & {} \frac{1}{ i (\nu _1 + \nu _2)} \,+\,\frac{3}{ 2^{10}} \frac{r^2_1}{r^2_2}\nonumber \\&\times \left( \left( \vec {n}_1 \cdot \vec {n}_2\right) ^2 +\left( \vec {n}'_1 \cdot \vec {n}_2\right) ^2\right) \nonumber \\&+\frac{3}{2^{12}} \frac{r^4_1}{r^4_2} \left( \left( \vec {n}_1 \cdot \vec {n}_2\right) ^4 \,+\,\left( \vec {n}'_1 \cdot \vec {n}_2\right) ^4 \right) \nonumber \\ \end{aligned}$$

(5.4)

where $\vec {n}_1 = \vec {r}_1/r_1,\vec {n}'_1 = \vec {r}_1/r_1$ and $\vec {n}_2 = \vec {r}_2/r_2$. Deriving Eq. (5.4) we neglected the extra powers of $r^2_1/r^2_2$, which are small. Finally

$$\begin{aligned} I_Q\left( \vec {r}_1, \vec {r}',\vec {r}_2; \nu _1, \nu _2\right)= & {} 2^{6 i (\nu _1 + \nu _2)} \left( - 2^7\nu _1\,\nu _2\right) \ \left( \frac{r^2_1}{r^2_2}\right) ^{i\,(\nu _1 + \nu _2)}\frac{1}{r^2_2} \nonumber \\&\times \, \Bigg \{\frac{1}{ i (\nu _1 + \nu _2)} \,+\,\frac{9}{ 2^{10}} \frac{r^2_1}{r^2_2}\nonumber \\&\times \, \left( \left( \vec {n}_1 \cdot \vec {n}_2\right) ^2 \,+\left( \vec {n}'_1 \cdot \vec {n} _2\right) ^2\right) \nonumber \\&\,+\,\frac{3}{2^{12}} \frac{r^4_1}{r^4_2} \left( \left( \vec {n}_1 \cdot \vec {n}_2\right) ^4 \,+\,\left( \vec {n}'_1 \cdot \vec {n}_2\right) ^4 \right) \Bigg \}.\nonumber \\ \end{aligned}$$

(5.5)

From Eq. (4.8) we can see that the integration over $r_i$ can be written in the form

$$\begin{aligned}&\frac{\mathrm{d}^2 \sigma }{\mathrm{d} y_1 \mathrm{d}^2 p_{T1}\,\mathrm{d} y_2 \mathrm{d}^2 p_{T2}}\left( \mathrm{Fig}.~2\right) \nonumber \\&\quad = \left( \frac{2 C_F \,\mu ^2_{\mathrm{soft}}}{\alpha _S\,(2 \pi )^2 }\right) ^2\,\,\frac{1}{p^2_{T1}\,p^2_{T2}}\,\nonumber \\&\qquad \times \,\,\int \mathrm{d}^2 r_1\,\mathrm{d}^2 r'_1\, \mathrm{d}^2 \tilde{r} _1\,\mathrm{d}^2 \tilde{r}'_1 \,\mathrm{e}^{-i\, \vec {p}_{T1} \cdot \vec {{r}}_1}\delta ^{(2)}\nonumber \\&\qquad \times \left( \vec {r}_1 + \vec {r}'_1 - \vec {\tilde{r}}_1 - \vec {\tilde{r}}'_1\right) \nabla ^2_{\tilde{r}_1} \tilde{r}_1 V_\mathrm{pr}\left( \tilde{r}_1\right) \,\,\nabla ^2_{\tilde{r}'_1}\tilde{ r}'_1 V_\mathrm{pr}\left( \tilde{r}'_1\right) \nonumber \\&\qquad \times \,\int \mathrm{d}^2 r_2\,\mathrm{d}^2 r'_2\, \mathrm{d}^2 \tilde{r} _2\,\mathrm{d}^2 \tilde{r}'_2 \,\mathrm{e}^{-i\, \vec {p}_{T2} \cdot \vec {{r}}_2}\delta ^{(2)}\nonumber \\&\qquad \times \left( \vec {r}_2 + \vec {r}'_2 - \vec {\tilde{r}}_2 - \vec {\tilde{r}}'_2\right) \nabla ^2_{\tilde{r}_2} r_2 V_\mathrm{tr}\left( \tilde{ r}_2\right) \,\, \nabla ^2_{\tilde{r}'_2} \tilde{r}'_2 V_\mathrm{tr}\left( \tilde{r}'_2\right) \nonumber \\&\qquad \times \,\, \nabla ^2_{{r}_1} \nabla ^2_{{r}_2} \nabla ^2_{{r}'_1} \nabla ^2_{{r}'_2} \,\Bigg ({r}_1\,{r}_2\, {r}'_1\, {r}'_2\, I_Q\left( \vec {r}_1, \vec {r}',\vec {r}_2; \nu _1, \nu _2\right) \Bigg )\nonumber \\&\qquad \times \,2 \pi \left\{ \frac{1}{ i (\nu _1 + \nu _2)} \,+\,\, \frac{9}{ 2^{10}}\frac{r^2_1}{r^2_2}\left( \left( \vec {n}_1 \cdot \vec {n}_2\right) ^2 \,+\left( \vec {n}'_1 \cdot \vec {n}_2\right) ^2\right) \right. \nonumber \\&\qquad \left. +\,\frac{3}{2^{12}} \frac{r^4_1}{r^4_2} \left( \left( \vec {n}_1 \cdot \vec {n}_2\right) ^4 \,+\,\left( \vec {n}'_1 \cdot \vec {n}_2\right) ^4 \right) \right\} . \end{aligned}$$

(5.6)

The tedious calculations of the integral over the dipole sizes in Eq. (5.6) are collected in Appendix D.

The values of $v_2$ and $v_4$ can be determined from the following representation of the double inclusive cross section:

$$\begin{aligned} \frac{\mathrm{d}^2 \sigma }{\mathrm{d} y_1 \,\mathrm{d} y_2 \mathrm{d}^2 p_{T1} \mathrm{d}^2 p_{T2}}\,\,\propto \,\,1 \,\,+\,\,2 \sum _n v_{ n,n } \left( p_{T1}, p_{T2}\right) \,\cos \left( n\, \varphi \right) \end{aligned}$$

(5.7)

where $\varphi$ is the angle between $\vec {p}_{T1}$ and $\vec {p}_{T2}$. $v_n$ is calculated from $v_{n,n} \left( p_{T1}, p_{T2}\right)$,

$$\begin{aligned}&1.~~ v_n\left( p_T\right) = \sqrt{v_{n,n}\left( p_T, p_T\right) }; \nonumber \\&2.~~ v_n\left( p_T\right) = \frac{v_{n, n}\left( p_T, p^\mathrm{Ref}_T\right) }{\sqrt{v_{n,n}\left( p^\mathrm{Ref}_T, p^\mathrm{Ref}_T\right) }}. \end{aligned}$$

(5.8)

Equations (5.8)-1 and (5.8)-2 depict two methods of how the values of $v_n$ have been extracted from the experimentally measured $v_{n,n} \left( p_{T1}, p_{T2}\right)$, where $p^\mathrm{Ref}_T$ denotes the momentum of the reference trigger. These two definitions are equivalent if $v_{n, n}\left( p_{T1}, p_{T2}\right)$ can be factorized as $v_{n, n}\left( p_{T1}, p_{T2}\right) \,=\, v_n\left( p_{T1}\right) \,v_n\left( p_{T2}\right)$. In this paper we use the definition in Eq. (5.8)-1.

Introducing the angular correlation function as

$$\begin{aligned} C\left( p_T, \phi \right) \,\,\equiv \,\,\frac{\frac{\mathrm{d}^2 \sigma }{\mathrm{d} y_1 \mathrm{d}^2 p_{T1}\,\mathrm{d} y_2 \mathrm{d}^2 p_{T2}}\left( \mathrm{Fig}.~3\mathrm{b}\right) }{\frac{\mathrm{d}^2 \sigma }{\mathrm{d} y_1 \mathrm{d}^2 p_{T1}\,\mathrm{d} y_2 \mathrm{d}^2 p_{T2}}\left( \mathrm{Fig}.~1\mathrm{a}\right) } \end{aligned}$$

(5.9)

we obtain

$$\begin{aligned} v_{n,n} = \frac{\int ^{2 \pi }_0 \mathrm{d} \phi \,C\Big ( \,p_T,\,\phi \Big )\,\cos \left( n\,\phi \right) }{2\,\pi \,+\, \int ^{2 \pi }_0 \mathrm{d} \phi \,C\Big ( p_T, \phi \Big )}; \quad v_n\,=\,\sqrt{v_{n,n}}\,; \end{aligned}$$

(5.10)

In Eq. (4.17) we have calculated the part of $C\left( p_{T}, \phi \right)$ which does not depend on $\phi$, which coincides with $C( p_{T}, \phi =0)$ = R of Eq. (4.17) for $Q_s\left( Y - y_1\right) \,\gg \, Q_s\left( y_2\right)$. To calculate the contribution to C, which depends on $\phi$, we need to take the separate integrals over $\nu _1$ and $\nu _2$, since the terms, which are proportional to $\cos ^2\left( \phi \right)$ and $\cos ^4\left( \phi \right)$ do not have a pole at $\nu _1 = -\nu _2$ (see Eq. (5.5)). These integrations lead to the following extra factor in $C\left( p_T,\phi \right) \,-\,C\left( p_T, \phi =0\right)$:

$$\begin{aligned}&C\left( p_T,\phi \right) \,-\,C\left( p_T, \phi =0\right) \,\,\nonumber \\&\quad \propto \,\,\,\mathcal{R}\,\frac{p^2_T}{Q^2_s\left( Y-y_1\right) }\,\frac{p^2_T}{Q^2_s\left( Y-y_1\right) }\,\,C\left( p_T, \phi =0\right) ;\nonumber \\&\mathcal{R}\,=\,2\,\xi ^2\,\,\sqrt{\frac{1}{\left( 2\,D\,y_{12}\right) ^3}}\,\exp \left( - 2 \xi ^2/\left( 4 \,D\,y_{12}\right) \right) \end{aligned}$$

(5.11)

where $\xi \,=\,\ln \left( Q^2_s\left( Y - y_1\right) /Q^2_s\left( y_2\right) \right)$. We took factors proportional to $p_T$ from the expression for $A\left( k_T, p_{T1}\right)$ and $A^{(4)}\left( k_T, p_{T1}\right)$ putting $p_{T1} = p_{T2} = p_T$. To find the final correlation function and $v_{2,2}$ and $v_{4,4}$, we need to collect all numerical factors that come from $A\left( k_T, p_{T1}\right)$, $A^{(4)}\left( k_T, p_{T1}\right)$ and Eq. (5.6), and to integrate over $\phi$, as given in Eq. (5.9).

Note that in the case of symmetric kinematics, where $Y - y_1 = y_2 = \frac{1}{2}\left( Y - y_{12}\right)$, $\xi = 0$ and Eq. (5.11 vanishes. In this case, we have to use Eq. (A.5) instead of Eq. (A.6), keeping track of the corrections, which are proportional to $\nu _i$. As a result, we can consider $\xi = 0$ in Eq. (D.7), but we need to replace the factor $\xi ^2$ by 1.

Equations (4.17) and (5.11) contain numerical uncertainties, which stem both from the values of the soft parameters $\tilde{\mu }_\mathrm{soft}$ and $\mu _\mathrm{soft}$, as well as the values of the saturation scale at low energies, and from the integration in Eqs. (C.3) and (C.5), which were taken neglecting contribution from the region $\tau ' \,<\,1$. On the other hand, the contribution to the double inclusive cross sections of the diagram of Fig. 2 at $\bar{\alpha }_S\,y_{12}\,\ll \,1$ coincides with the contribution of Fig. 1b,

$$\begin{aligned} \frac{\mathrm{d}^2 \sigma \left( \mathrm{Fig}.~2\right) }{\mathrm{d} y_1 \,\mathrm{d} y_2 \mathrm{d}^2 p_{T1} \mathrm{d}^2 p_{T2}}\,\,\,\xrightarrow {\bar{\alpha }_S\,y_{12} \rightarrow \,1} \,\,\,\,\,\frac{\mathrm{d}^2 \sigma \left( \mathrm{Fig}.~1b\right) }{\mathrm{d} y_1 \,\mathrm{d} y_2 \mathrm{d}^2 p_{T1} \mathrm{d}^2 p_{T2}}. \end{aligned}$$

(5.12)

Therefore, to obtain the realistic estimate we use the following procedure of matching:

$$\begin{aligned} v_2\left( p_T = 5 \,GeV, y_{12} = 2\right) |_{\mathrm{Fig}.~2} \,\,= & {} \,\, v_2\left( p_T = 5 \,GeV \right) |_{\mathrm{Fig}.~1\mathrm{b} };\nonumber \\ v_4\left( p_T = 5 \,GeV, y_{12} = 2\right) |_{\mathrm{Fig}.~2} \,\,= & {} \,\, v_4\left( p_T = 5 \,GeV \right) |_{\mathrm{Fig}.~1\mathrm{b} },\nonumber \\ \end{aligned}$$

(5.13)

where $v_2\left( p_T = 5 \,\mathrm{GeV} \right) |_{\mathrm{Fig}.~1\mathrm{b} }$ and $v_4\left( p_T = 5 \,\mathrm{GeV} \right) |_{\mathrm{Fig}.~1\mathrm{b} }$ are taken from Ref. [14] where the estimates were performed based on the model for soft interaction which describes all features of the soft interaction at high energy and provides an interface with the hard processes.

Fig. 5

$v_n$ versus $p_T$ (a, c) and versus y (b, d) at W $=$ 13 TeV assuming that the experiment has a symmetric pattern with $Y - y_1 = y_2 = \frac{1}{2}(Y - y_{12})$. In all these figures we use Eq. (5.12) for normalization and we take $\Delta _\mathrm{BFKL} = 0.25$ and $Q^2_s(Y) \propto \exp \left( \lambda Y\right)$ with $\lambda = 0.25$. These numbers correspond to the BFKL phenomenology

Figure 5 shows the $p_T$ and y dependence of the $v_2$ and $v_4$ using Eq. (5.13) for normalization. In addition we take $\Delta _\mathrm{BFKL}$ = 0.25 and $Q^2_s( y)\, \propto \, \exp \left( \lambda \,y\right)$ with $\lambda = 0.25$. These values correspond to the BFKL Pomeron phenomenology. We believe that this figure illustrates the scale of rapidity dependence and will be instructive for future experimental observations.

6 Conclusions

In this paper we generalize the interference diagram that described the Bose–Einstein correlation for small rapidity difference $\bar{\alpha }_Sy_{12}\,\ll \,1$, to include the emission of the gluons with rapidities ($y_i$) between $y_1$ and $y_2$ ($y_1\,,\,y_i\,<\,y_2$). We calculate the resulting diagram in the CGC/saturation approach and make two observations, which we consider as the main result of this paper. The first one is a substantial decrease of the odd Fourier harmonics $v_{2 n + 1}$ as a function of the rapidity difference $y_{12}$ ( see Fig. 4c). The second result is that even Fourier harmonics $v_{2 n}$ have a rather strong dependence on $y_{12}$, showing a considerable increase in the region of large $y_{12}$ (see Fig. 5). We believe that our calculations, which have been performed both for the simplest diagrams and for the CGC/saturation approach, will be instructive for further development of the approach especially in the part that is related to the integration of the momenta transferred by the BFKL Pomerons.

We demonstrated in this paper the general origin of the density variation mechanism, whose nature does not depend on the technique that has been used. This mechanism has to be taken into account, since it leads to the values of the Fourier harmonics that are large and of the order of $v_n$, which have been observed experimentally.

We hope that the paper will be useful in the clarification of the origin of the angular correlation, especially for hadron–hadron scattering at high energy. We firmly believe that the experimental observation of both phenomena, the sharp decrease of $v_n$ with odd n and the substantial increase of $v_n$ with even n as a function of $y_{12}$, will be a strong argument for the CGC/saturation nature of the angular correlations.

Appendices

Appendix A: BFKL Pomeron in the mixed representation

In this appendix we discuss the BFKL Pomeron Green function $G\left( \vec {r}, \vec {R},\vec {Q}_T,Y\right)$ in the mixed representation, where r and R are the sizes of two interacting dipoles, $Q_T$ denotes the momentum transferred by the Pomeron, and Y the rapidity between the two dipoles. This Green function has the following form [42, 43, 58,59,60]:

$$\begin{aligned}&G\left( \vec {r}, \vec {R},\vec {Q}_T; Y\right) \nonumber \\&\quad = \frac{r \,R}{16}\sum ^{\infty }_{n= - \infty }\int ^{\infty }_{-\infty } d \nu \frac{1}{\left( \nu ^2 + \frac{1}{4}(n-1)^2\right) \,\left( \nu ^2 + \frac{1}{4}(n+1)\right) }\nonumber \\&\qquad \times V_{\nu ,n}\left( \vec {r},\vec {Q}_T\right) \,V^*_{\nu ,n}\left( \vec {R},\vec {Q}_T\right) \,\mathrm{e}^{ \omega \left( \nu ,n\right) \,Y} \end{aligned}$$

(A.1)

where

$$\begin{aligned} \omega \left( \nu ,n\right) \,\,= & {} \,\,2\,\bar{\alpha }_S\mathrm{Re}\left( \psi \left( \frac{1}{2}+ \frac{1}{2}|n| + \nu \right) - \psi \left( 1 \right) \right) ;\nonumber \\ \omega \left( \nu ,0\right) \,\,= & {} \,\,2\,\bar{\alpha }_S\mathrm{Re}\left( \psi \left( \frac{1}{2}+ \nu \right) - \psi \left( 1 \right) \right) \nonumber \\&\,\,\xrightarrow {\nu \ll 1}\,\,\Delta _\mathrm{BFKL} \,\,-\,\,D\,\nu ^2, \end{aligned}$$

(A.2)

where $\psi (z)$ is the Euler $\psi$-function (see Ref. [61] formulas 8.36) and $\Delta _\mathrm{BFKL} = \bar{\alpha }_S4 \ln 2 , D = \bar{\alpha }_S14 \zeta (3), \xi = \ln \left( r^2_1/r^2_2\right)$.

Each term in Eq. (A.1) has a very simple structure, being the typical contribution of the Regge-pole exchange: the product of two vertices and Regge-pole propagator. From Eq. (A.2) one can see that at large Y the main contribution comes from the term with $n = 0,$ and in what follows we will concentrate on this particular term. The vertices with $n=0$ have been determined in Refs. [42, 43, 58,59,60], and they have an elegant form in the complex number representation for the point on the two dimensional plane, viz.,

$$\begin{aligned}&\text{ For } \vec {r}(x,y) : \,\, \rho = x + i y; \,\, \rho ^*= x - i y;\nonumber \\&\quad \text{ For } \vec {Q}_T(Q_x, Q_y) : \,\, q = Q_x + i Q_y;\,\, q^*= Q_x - i Q_y.\nonumber \\ \end{aligned}$$

(A.3)

Using this notation the vertices have the following structure:

$$\begin{aligned} V_{\nu }\left( \vec {r},\vec {Q}_T\right)= & {} \left( Q^2_T\right) ^{i \nu }\,\Gamma ^2\left( 1 - i \nu \right) \nonumber \\&\times \Bigg \{ J_{-i \nu }\left( \frac{1}{4}q^* \rho \right) \,J_{- i \nu }\left( \frac{1}{4}q \rho ^*\right) \nonumber \\&- J_{i \nu }\left( \frac{1}{4}q^* \rho \right) \,J_{ i \nu }\left( \frac{1}{4}q \rho ^*\right) \Bigg \}. \end{aligned}$$

(A.4)

At $Q_T \rightarrow 0$ this vertex takes the form

$$\begin{aligned}&2^{6 i \nu }\,V_{\nu }\left( \vec {r},\vec {Q}_T\right) \xrightarrow {Q_T r\,\ll \,1}\left( \frac{r^2}{2^6}\right) ^{-i \nu }\nonumber \\&\quad \times \left( \frac{(\nu +i) \left( 8 (\vec {Q}_T\cdot \vec {r})^4 - 8(\vec {Q}_T\cdot \vec {r})^2 Q^2_T r^2 + 5\frac{1}{2}Q^4_T r^4\right) +(2 i + \nu )Q^4_T r^4 )}{64^2 (\nu +2 i) (1-i \nu )^2}\right. \nonumber \\&\quad \left. +\frac{i (\nu +i)\left( (2 ( \vec {Q}_T\cdot \vec {r})^2 - Q^2_T r^2\right) }{32 (1-i \nu )^2} +1\right) + \left( Q^2\right) ^{i \nu } \left( \frac{Q^2 r^2}{2^6}\right) ^{i \nu }\nonumber \\&\quad \times \left( \frac{(\nu -2 i)\left( 8 (\vec {Q}_T\cdot \vec {r})^4 - 8(\vec {Q}_T\cdot \vec {r})^2 Q^2_T r^2 + 5\frac{1}{2}Q^4_T r^4\right) )}{2^{12} ((2+i \nu ) (1+i \nu ))^2}\right. \nonumber \\&\quad \left. +\frac{2 (1+i \nu ) \left( (2 ( \vec {Q}_T\cdot \vec {r})^2 - Q^2_T r^2\right) }{2^6 (1+i \nu )^2}-1\right) . \end{aligned}$$

(A.5)

For small values of $\nu$ (which are related to the region of large $\bar{\alpha }_SY \,\gg \,1$), Eq. (A.5) can be simplified and reduced to the form

$$\begin{aligned}&2^{6 i \nu } V_{\nu }\left( \vec {r},\vec {Q}_T\right) \, \nonumber \\&\quad \xrightarrow {Q_T r\,\ll \,1} \left( \frac{r^2}{2^6}\right) ^{-i \nu } \left( \frac{ (\vec {Q}_T\cdot \vec {r})^4 - (\vec {Q}_T\cdot \vec {r})^2 Q^2_T r^2 + \frac{9}{16} Q^4_T r^4 )}{2^8 }\right. \nonumber \\&\quad \left. -\frac{2 ( \vec {Q}_T\cdot \vec {r})^2 - Q^2_T r^2}{2^5 } +1\right) \nonumber \\&\quad - \, \left( Q^2\right) ^{i \nu } \left( \frac{Q^2 r^2}{2^6}\right) ^{i \nu } \left( \frac{ (\vec {Q}_T\cdot \vec {r})^4 - (\vec {Q}_T\cdot \vec {r})^2 Q^2_T r^2 + \frac{9}{16} Q^4_T r^4)}{2^{8} } \right. \nonumber \\&\quad \left. - \frac{ 2 ( \vec {Q}_T\cdot \vec {r})^2 - Q^2_T r^2}{2^5 } + 1\right) . \end{aligned}$$

(A.6)

Using

$$\begin{aligned} J_{-i \nu }\left( z \right) \,\,\xrightarrow {z\,\gg \,1}\,\,\sin \left( \frac{1}{4}\pi + z + \frac{1}{2}i \pi \nu \right) \sqrt{\frac{2}{\pi }} \sqrt{\frac{1}{z}} \end{aligned}$$

(A.7)

at $\nu \ll 1$ we obtain for $Q^2_T r^2 \gg 1$

$$\begin{aligned}&V_{\nu }\left( \vec {r},\vec {Q}_T\right) \,\,\nonumber \\&\quad \xrightarrow {Q_T r\,\gg \,1} \,\, \left( Q^2_T\right) ^{i \nu }\, \Gamma ^2\left( 1 - i \nu \right) \, \,\cos \left( \frac{1}{2}\vec {Q}_T\cdot \vec {r}\right) \, \frac{4 \,i\, \nu }{Q_T\, r}.\nonumber \\ \end{aligned}$$

(A.8)

The contribution of the first term in Eq. (A.1) can be reduced to the following form for the scattering amplitude of two dipoles with sizes $r_1$ and $r_2$:

$$\begin{aligned} N\left( r_1,r_2; Y\right)= & {} \frac{r_1\,r_2}{16}\int \mathrm{d} \nu \frac{1}{\left( \nu ^2 + 1/4\right) ^2}\,V_\nu \left( r_1,Q_t \right. \nonumber \\&\left. \rightarrow 0\right) V^*_{\nu }\left( r_2,Q_T \rightarrow 0\right) \,\mathrm{e}^{\omega \left( \nu ,0\right) Y}\nonumber \\= & {} \frac{r_1\,r_2}{16}\int \mathrm{d} \nu \frac{1}{\left( \nu ^2 + 1/4\right) ^2}\,\mathrm{e}^{\omega \left( \nu ,0\right) Y} \nonumber \\&\times \left\{ (r^2_1)^{- i \nu } - \left( \frac{Q^4_T r^2_1}{2^{12}}\right) ^{ i \nu }\right\} \nonumber \\&\times \left\{ (r^2_2)^{ i \nu }- \left( \frac{Q^4_T r^2_2}{2^{12}}\right) ^{ - i \nu }\right\} \nonumber \\= & {} \frac{r_1\,r_2}{16}\int \mathrm{d} \nu \frac{1}{\left( \nu ^2 + 1/4\right) ^2}\,\mathrm{e}^{\omega \left( \nu ,0\right) Y} 2 \left( \frac{r^2_2}{r^2_1} \right) ^{i \nu }\nonumber \\&\xrightarrow {Y \gg 1; \nu \ll 1}\,\,2\, r_1\,r_2 \int \mathrm{d} \nu \exp \left( \left( \bar{\alpha }_S\,4 \ln 2 \,\right. \right. \nonumber \\&\left. \left. - \bar{\alpha }_S14 \zeta (3) \nu ^2\right) Y\right) \left( \frac{r^2_2}{r^2_1} \right) ^{i \nu } \nonumber \\= & {} r_1\, r_2 \sqrt{\frac{2 \pi }{ D Y}}\exp \left( \Delta _\mathrm{BFKL} Y - \frac{\xi ^2}{4 D Y}\right) \end{aligned}$$

(A.9)

where $\Delta _\mathrm{BFKL}$ and D are defined in Eq. (A.2).

In the derivation of Eq. (A.9) we neglected the contributions that are proportional to $\left( \frac{Q^4_T r^2_2 \,r^2_1}{2^{12}}\right) ^{ - i \nu }$, since this contribution will be the same as in Eq. (A.9), but with $\xi = \ln \left( \frac{Q^4_T r^2_2 \,r^2_1}{2^{12}}\right) \,\gg \,1$. To integrate over $\nu$, we use the method of steepest descent, and the expansion of $\omega \left( \nu ,0\right)$ at small $\nu$ (diffusion approximation; see the second equation in Eq. (A.2)).

$N\left( r_1,r_2; Y\right)$ denotes the imaginary part of the dipole-dipole sacttering amplitude at $Q_T=0$, which is related to the cross section. One can check that Eq. (A.9) has the correct dimension.

Appendix B: Calculation of the integrals for the contribution of the simplest diagram

In this appendix we discuss the integrations in Eq. (2.5). The integral over $Q_T$ has been considered in Sect. 4.1 and it has the form of Eq. (4.7). The extra $\mathrm{e}^{i \vec {r}'_1 \cdot \vec {Q}_T}$ give an additional numerical factor, replacing $2^5$ by $2^7$ in Eq. (4.7). To integrate over $k_T$ and $k'_T$ we replace

$$\begin{aligned}&\int \prod \mathrm{d} \phi _i\,\mathrm{e}^{-i\, \vec {p}_{T1} \cdot \vec {\tilde{r}}'_1}\delta ^{(2)}\left( \vec {r}_1 + \vec {r}'_1 - \vec {\tilde{r}}_1 - \vec {\tilde{r}}'_1\right) \nonumber \\&\quad \,\rightarrow \, \left( 2 \pi \right) ^4 \int k_T d k_T\,J_0\left( k_T r_1\right) \,J_0\left( |\vec {k}_T\right. \nonumber \\&\quad \left. + \vec {p}_{T1}|\,\tilde{r}'_1\right) \,J_0\left( k_T \tilde{r}_1\right) \,J_0\left( k_T \tilde{r}_1\right) .\nonumber \\ \end{aligned}$$

(B.1)

Now we can take the integrals over $r_i$ bearing in mind Eq. (4.7) and

$$\begin{aligned} N_{pr}\left( r_i, Y - y_1\right) = \int \frac{\mathrm{d} \nu }{2 \pi } \left( \mu ^2_\mathrm{soft}\,r^2_i\right) ^{\frac{1}{2}+ i \nu _i}\,\mathrm{e}^{\omega \left( \nu _i,0\right) \left( Y - y_1\right) }. \end{aligned}$$

(B.2)

The integrals over $\tilde{r}_1$and $\tilde{r}'_1$ have the following form (see Ref. [61], Eq. 6.511(6)):

$$\begin{aligned}&\int ^{\tilde{r}_2}_0 J_0\left( k_T \tilde{r}_1\right) \,d \tilde{r}_1 = \tilde{r}_2\,J_0\left( k \tilde{r}_2\right) + \frac{1}{2}\pi \tilde{r}_2 \Big ( J_1\left( k \tilde{r}_2\right) \,\mathbf{H}_0\left( k \tilde{r}_2\right) \nonumber \\&\quad \,-\, J_0\left( k \tilde{r}_2\right) \,\mathbf{H}_1\left( k \tilde{r}_2\right) \Big ) = \left\{ \begin{array}{ll} \tilde{r}_2 &{}\quad \text {if } k \tilde{r}_2\,\ll \, 1,\\ \frac{1}{k} &{} \quad \text {if } k \tilde{r}_2\,\gg \, 1.\\ \end{array} \right. \end{aligned}$$

(B.3)

Using Eq. (B.2) we obtain

$$\begin{aligned}&\int ^{\infty }_0\,r_i\,\mathrm{d} r_i\,J_0\left( k_T \,r_i\right) ,\nabla ^2_{r_i} N_{pr}\left( r_i, Y - y_1\right) \nonumber \\&\quad = \frac{1}{k} \left( \frac{4 \mu ^2_\mathrm{soft}}{k^2}\right) ^{i \,\nu _i} \,\mathrm{e}^{\omega \left( \nu _i,0\right) \, \left( Y - y_1\right) }. \end{aligned}$$

(B.4)

Collecting Eqs. (B.2), (B.3) and (B.4) we see that the main contribution stems from the region $k \tilde{r}_2\,\ll \, 1$ and the integral over $k_T$ has the form

$$\begin{aligned}&\tilde{r}_2 \tilde{r'}_2 \int ^{1/\tilde{r}_2^2}_{p^2_{T1}} \frac{d k^2_T}{k^2_T} \left( \frac{4 \mu ^2_\mathrm{soft}}{k^2}\right) ^{i \,(\nu _1 +\nu '_1)}\,\mathrm{e}^{(\omega \left( \nu _i, 0\right) \,+\omega \left( 0,\nu '_1\right) ) \left( Y - y_1\right) }\nonumber \\&\quad =\tilde{r}_2 \tilde{r'}_2\frac{1}{i \,(\nu _1 +\nu '_1)} \left( \frac{1}{ \tilde{r}_2^2 \, p^2_{T1}}\right) ^{i \,(\nu _1 +\nu '_1)} \mathrm{e}^{(\omega \left( \nu _i, 0\right) \,+\omega \left( 0,\nu '_1\right) ) \left( Y - y_1\right) } \,\nonumber \\&\quad \xrightarrow {\text{ after } \text{ integration } \text{ over } \nu _1, \nu _2}\,\,\frac{1}{2}\, \sqrt{\frac{\pi }{2 \,D\,(Y - y_1)}}\,\mathrm{e}^{ 2 \Delta _\mathrm{BFKL} \left( Y - y_1\right) }.\nonumber \\ \end{aligned}$$

(B.5)

The integral over $k'_T$ has the same structure while the integration in Eq. (B.3) goes to infinity. As a result we can reduce the integral to the form

$$\begin{aligned}&\int _{p^2_{T2}} \frac{\mathrm{d} k^2_T}{k^4_T} \left( \frac{4 \mu ^2_\mathrm{soft}}{k^2}\right) ^{i \,(\nu _1 +\nu '_1)}\,\mathrm{e}^{(\omega \left( \nu _i, 0\right) \,+\omega \left( 0,\nu '_1\right) ) \left( Y - y_1\right) } \,\,\nonumber \\&\quad =\,\,\frac{1}{1 + i (\nu _1+\nu '_1)}\frac{1}{4 \mu ^2_\mathrm{soft}}\left( \frac{4 \mu ^2_\mathrm{soft}}{p^2_{T2}}\right) ^{1+i \,(\nu _1 +\nu '_1)}\,\mathrm{e}^{(\omega \left( \nu _i, 0\right) \,+\omega \left( 0,\nu '_1\right) ) \left( Y - y_1\right) }\nonumber \\&\quad \xrightarrow {\text{ after } \text{ integration } \text{ over } \nu _1, \nu '_1} \,\,\, \frac{1}{2}\frac{\pi }{\,D\,y_2}\,\frac{1}{p^2_{T2}}. \end{aligned}$$

(B.6)

Finally, we obtain Eq. (4.9).

Appendix C: Integration over dipole sizes in the CGC/saturation approach

The integration over $Q_T$ will produce the same result as Eq. (4.7), as in the previous section. We rewrite the integration over $\phi _i$ (see Eq. (B.1)) in the following way:

$$\begin{aligned}&\int \prod d \phi _i\,\mathrm{e}^{-i\, \vec {p}_{T1} \cdot \vec {\tilde{r}}'_1}\delta ^{(2)}\left( \vec {r}_1 + \vec {r}'_1 - \vec {\tilde{r}}_1 - \vec {\tilde{r}}'_1\right) \nonumber \\&\quad \,\rightarrow \, \left( 2 \pi \right) ^4 \int \mathrm{d} \phi \,\mathrm{e}^{i \vec {p}_{T1} \cdot \vec {r}} \int k_T d k_T\,J_0\left( k_T r\right) \,J_0\left( k_T r_1\right) \,J_0\left( k_T \tilde{r}_1\right) \,J_0\left( k_T \tilde{r}'_1\right) .\nonumber \\ \end{aligned}$$

(C.1)

We see that the integrals over $r'_1$ and $r'_1$ lead to $r_1 \sim 1/Q_s(Y - y_1)$ and $r'_1 \sim 1/Q_s(Y - y_1)$. The same holds for the integrals over $r'_2$ and $r'_2,$ leading to $r_2 \sim 1/Q_s(y_2)$ and $r'_2 \sim 1/Q_s(y_2)$. Assuming that $Q_s\left( Y - y_1\right) \,>\,Q_s\left( y_2\right)$ we conclude that $r_i$ and $r'_i$ are much smaller than $r_2$ and $r'_2$. Replacing

$$\begin{aligned}&\nabla ^2_{r_1} N_\mathrm{pr}\left( r_1; Y - y_1\right) \,\mathrm{e}^{i \vec {Q}_T \cdot \vec {\tilde{r}'}_1}\,\nabla ^2_{\tilde{r}'_1} N_\mathrm{pr}\left( \tilde{r}'_1; Y - y_1\right) \nonumber \\&\quad \,\rightarrow \,\frac{2^8\,\bar{\gamma }^4}{r_1\,r'_1} \left( r^2_1\,Q^2_s\left( Y - y_1\right) \right) ^{\bar{\gamma }} \left( r'^2_1\,Q^2_s\left( Y - y_1\right) \right) ^{\bar{\gamma }} \end{aligned}$$

(C.2)

where $\bar{\gamma } = 1 - \gamma _{cr}$, we see from Eq. (C.1) that integration over r takes the form

$$\begin{aligned}&\frac{1}{Q_s} \frac{1}{1 + 2\bar{\gamma }}\,\int ^1_0 \mathrm{d} \tau \, J_0\left( \frac{k_T}{Q_s}\sqrt{\tau }\right) \,\tau ^{\bar{\gamma }}\frac{d \tau }{2 \sqrt{\tau }}\nonumber \\&\quad \,=\, \frac{1}{Q_s} \frac{1}{1 + 2\bar{\gamma }}\, {}_1F_2\left( \left\{ \frac{1}{2}+ \bar{\gamma }\right\} ,\left\{ 1, \frac{3}{2} + \bar{\gamma }\right\} , - \frac{k^2_T }{4 \,Q^2_s}\right) .\nonumber \\ \end{aligned}$$

(C.3)

Recall that we consider $Q_s = Q_s(Y - Y_1)$ in Eq. (C.3). For $p_{T1} \ll \,Q_s\left( Y - y_1\right)$ we can replace $\mathrm{e}^{-i\, \vec {p}_{T1} \cdot \vec {\tilde{r}}'_1}\,=\,1$ in Eq. (C.1). In this case the integral has the form

$$\begin{aligned}&\frac{1}{Q^2_s} \frac{1}{(1 + 2\bar{\gamma })^2}\,\int ^1_0 \mathrm{d} \tau '\,\Bigg ( \frac{1}{Q_s} \frac{1}{1 + 2\bar{\gamma }}\, {}_1\nonumber \\&\quad \times \, F_2\left( \left\{ \frac{1}{2}+ \bar{\gamma }\right\} ,\left\{ 1, \frac{3}{2}+ \bar{\gamma }\right\} , - \frac{1 }{4 \,\tau '}\right) \Bigg )^2\frac{\mathrm{d} \tau '}{\tau '}\,=\,0.18/Q^2_s\nonumber \\ \end{aligned}$$

(C.4)

where $\tau ' = k^2/Q^2_s$.

The integral over r in the lower part of the diagram takes the form

$$\begin{aligned} \int \frac{\mathrm{d}^2 r'}{r'^2} \,J_0\left( k_T \, r\right) \,=\, \pi \,\ln \left( k^2_T/(4 \mu ^2_\mathrm{soft})\right) . \end{aligned}$$

(C.5)

Using Eq. (C.5) for $p_{T2} \ll Q_s\left( y_2\right)$ the integral over $k'_T$ can be reduced to

$$\begin{aligned}&\frac{1}{(1 + 2\bar{\gamma })^2}\,\int ^1_0 \mathrm{d} \tau ''\,\Bigg ( \, {}_1F_2\left( \left\{ \frac{1}{2}+ \bar{\gamma }\right\} ,\left\{ 1, \frac{3}{2} + \bar{\gamma }\right\} , - \frac{1 }{4 \,\tau ''}\right) \Bigg )^2\nonumber \\&\quad \times \left( \frac{\ln \left( \tau ''\right) }{\tau ''}\right) ^2\,=\,3.50. \end{aligned}$$

(C.6)

Finally, collecting all numerical coefficients, we obtain

$$\begin{aligned}&\frac{\mathrm{d}^2 \sigma }{\mathrm{d} y_1 \mathrm{d}^2 p_{T1}\,\mathrm{d} y_2 \mathrm{d}^2 p_{T2}}\left( \mathrm{Fig.}~3\mathrm{b}\right) \,\,= \nonumber \\&\quad =\text{ C }^4\,2^3 \pi ^3 \left( \frac{2 C_F }{\alpha _S\,(2 \pi )^2 }\right) ^2\,\,\frac{1}{p^2_{T1}\,p^2_{T2}}\nonumber \\&\qquad \times \frac{0.18\,3.5}{Q^2_s\left( Y - y_1\right) } \left( 2 \bar{\gamma }\right) ^8 \, \sqrt{\frac{1}{\left( 2 \,D\,y_{12}\right) ^3}}\,\,\mathrm{e}^{ 2 \Delta _\mathrm{BFKL} \,y_{12}}\, \end{aligned}$$

(C.7)

where the constant C is the value of the amplitude at $\tau =1$.

This contribution is proportional to

$$\begin{aligned} \propto ~~~\mathrm{e}^{ 2 \Delta _{\mathrm{BFKL}} \,y_{12}}{/} Q^2_s\left( Y- y_1\right) \end{aligned}$$

for $p_{T1} \ll Q_s\left( Y - y_1\right)$ and $p_{T2} \ll Q_s\left( y_2\right)$. Note that $Q^2_s\left( Y - y_1\right) \,>\, Q^2_s\left( y_2\right)$.

We need to estimate the diagram of Fig. 1a (see Eq. (2.7)). This diagram can be rewritten as

$$\begin{aligned}&\frac{\mathrm{d}^2 \sigma }{\mathrm{d} y_1 \mathrm{d}^2 p_{T1}\,\mathrm{d} y_2 \mathrm{d}^2 p_{T2}}\left( Fig.~1{\text {-}}a\right) \nonumber \\&\quad = \tilde{\mu }^2_{\mathrm{soft}} \frac{\mathrm{d}^2 \sigma }{\mathrm{d} y_1 \mathrm{d}^2 p_{T1}} \left( Q_T = 0; Eq.~(3.5)\right) \nonumber \\&\qquad \times \frac{\mathrm{d}^2 \sigma }{\mathrm{d} y_2 \mathrm{d}^2 p_{T2}} \left( Q_T = 0; Eq.~(3.5)\right) \nonumber \\&\quad \text{ where } ~~~~\tilde{ \mu }^2_\mathrm{soft}\,=\,\int \mathrm{d}^2 Q_T\, N^2\left( Q_T\right) . \end{aligned}$$

(C.8)

Examining Eq. (3.5), one can see that in the general case when $Y - y_1 \ne y_1$ and $Y - y_2 \ne y_2$ all four Pomerons cannot be in the vicinity of the saturation scale. Actually we have two kinematic regions which give the maximal contributions (assuming $Q_s\left( Y - y_1\right) \,>\,Q^2_s\left( y_1\right)$):

• 1. $r^2 \,Q^2_s\left( Y - y_1\right) \,\approx \,1$ but $r^2 Q^2_s\left( y_1\right) \rightarrow Q^2_s\left( Y - y_1\right) {/} Q^2_s\left( y_1\right) \,\ll \,1$;

• 2. $r^2 \,Q^2_s\left( y_1\right) \,\approx \,1$ but $r^2 Q^2_s\left( y_1\right) \rightarrow Q^2_s\left( y_1\right) {/} Q^2_s\left( Y - y_1\right) \gg \,1$.

In region 1 the upper Pomeron is in the vicinity of the saturation scale, while the lower Pomeron is in the perturbative QCD region. In region 2 the lower Pomeron is in the vicinity of the saturation scale, and the upper Pomeron is deep inside the saturation domain. As we have discussed (see Fig. 3a) $\nabla ^2 N$ decreases in the saturation region much faster than in the perturbation QCD region and, therefore, we assume that the kinematic region 1 gives the largest contribution. Hence, for $p_{T1}\, \ll \,Q^2_s\left( y_1\right)$ we obtain Eq. (4.16).

Appendix D: Integration over dipole sizes in the angle correlation function

In this appendix we collect tedious integration over the dipole sizes in Eq. (5.6).

Each term in this equation can be factorized as a product of two functions which depend on $r^i_1$ and on $r^i_2$. Bearing this feature in mind we calculate each term going to the momentum representation using Eq. (C.1). We obtain a product of functions of $k_T$. Each of these functions has the following general form:

$$\begin{aligned}&\int \mathrm{d}^2 r \,\mathrm{e}^{ i \vec {k}_T \cdot \vec {r}}\,\prod _{i=1}^j\, r_{\mu _i}\,F\left( r\right) \nonumber \\&\quad =(- i \vec { \nabla }_{k_T})^j \,\int \mathrm{d}^2 r \,\mathrm{e}^{ i \vec {k}_T \cdot \vec {r}}\,\,F\left( r\right) \nonumber \\&\quad = 2 \pi \,(-i \vec { \nabla }_{k_T})^j \,\int \mathrm{d}^2 r \,J_0\left( k_T\,r\right) \,\,F\left( r\right) . \end{aligned}$$

(D.1)

As we have seen the dependence on $\vec {r}_i$ stems from the integration over $Q_T$ or, in other words, from ($I_Q$). In $I_Q$ the dependence on $r_1$ and $r'_1$ can be extracted explicitly, leading to $F\left( r\right) \propto 1/r$. Hence the momentum image for Eq. (D.1) has a simple form:

$$\begin{aligned} \int \mathrm{d}^2 r \,\mathrm{e}^{ i \vec {k}_T \cdot \vec {r}}\,\prod _{i=1}^j\, r_{\mu _i}\,F\left( r\right) = \,2 \pi \,(-i \vec { \nabla }_{k_T})^j \frac{1}{k_T}. \end{aligned}$$

(D.2)

For $j =2$ and $j=4$, which we need to calculate considering Eq. (5.6), we have

$$\begin{aligned} (-i \vec { \nabla }_{k_T})^2 \frac{1}{k_T}= & {} \left\{ \frac{3}{k^5_T} \, k_{T,i} \, k_{T,i'} \, -\,\frac{1}{k^3_T} \delta _{i,i'}\right\} ;\\ (-i \vec { \nabla }_{k_T})^4 \frac{1}{k_T}= & {} \left\{ \frac{105}{k^9_T} \, k_{T,i} \, k_{T,i'} \, k_{T,j} \, k_{T,j'}\right. \\&\left. -\,\frac{15}{k^7_T} \left( \delta _{i j} \, k_{T,i'} \, k_{T,j'} \,+\,\delta _{i i'} \, k_{T,j} \, k_{T,j'} \right. \right. \nonumber \\&+\,\delta _{i' j} \, k_{T,i} \, k_{T,j'}+\,\delta _{j i'} \, k_{T,i} \, k_{T,j'} \, \\&\left. \left. \,+\,\delta _{i' j'} \, k_{T,j} \, k_{T,i} \,+\,\delta _{j j'} \, k_{T,i} \, k_{T,i'}\right) \right. \,\\&\left. + \,\frac{3}{k^5} \left( \delta _{i i'} \delta _{j j'}\,+\, \delta _{i j} \delta _{i' j'}\,+\,\delta _{i j} \delta _{i' j'}\right) \right\} . \end{aligned}$$

Note that, for integration over $\vec {r}_1$, Eq. (D.2) takes the form

$$\begin{aligned}&\int \mathrm{d}^2 r_1 \,\mathrm{e}^{ i (\vec {k}_T + \vec {p}_{T1}) \cdot \vec {r}_1}\,\prod _{i=1}^j\, r_{1,\mu _i}\,F\left( r_1\right) \nonumber \\&\quad = \,2 \pi \,\left( -i \vec { \nabla }_{\vec {k}_T + \vec {p}_{T1}}\right) ^j \frac{1}{\sqrt{(\vec {k}_T\,+\,\vec {p}_{T1} )^2}}. \end{aligned}$$

(D.3)

The term $\left( r^2_1\left( \vec {n}_1 \cdot \vec {n}_2\right) ^2 \,+ r'^2_1\left( \vec {n}'_1 \cdot \vec {n}_2\right) ^2\right)$ can be rewritten as $\left( r_{1,\mu }\,r_{1,\nu }\,+\,r'_{1,\mu } \,r'_{1,\nu }\right) r_{2,\mu }\,r_{2,\nu }$ and in the momentum representation it is

$$\begin{aligned}&\int \mathrm{d} \phi \left\{ \Big (\frac{3}{k^5_T} \, k_{T,i} \, k_{T,i'} \,-\,\frac{\delta _{i i'}}{k^3_T}\Big ) \frac{1}{\sqrt{k^2_T + p^2_{T1} + 2\cos \left( \phi \right) k_T p_{T1}}}\right. \nonumber \\&\qquad \left. +\left( \frac{3}{\left( \sqrt{k^2_T + p^2_{T1} + 2\cos \left( \phi \right) k_T p_{T1}}\right) ^{5}} \, ( \vec {k}_{T} + \vec {p}_{T1})_i \,( \vec {k}_{T} \right. \right. \nonumber \\&\qquad \left. \left. + \vec {p}_{T1})_{i'}-\,\frac{\delta _{i i'}}{\left( \sqrt{k^2_T + p^2_{T1} + 2\cos \left( \phi \right) k_T p_{T1}}\right) ^3}\right) \frac{1}{k_T}\right\} \nonumber \\&\quad =\,\,A \,\frac{p_{T1, i}\,p_{T1, i'}}{p^2_{T1}}\,+\, B\,\,\delta _{i i'}. \end{aligned}$$

(D.4)

The expressions for A and B can be written in a general form. Assuming that both $p_{T1}$ and $p_{T2}$ are smaller than $Q_s\left( y_2\right)$, we can expand the answer, taking into account only terms that are proportional to $p^2_{T1}/k^2_T$ and $p_{T2}^2/k'^2_T$. We obtain

$$\begin{aligned} A\left( k_T, p_{T1}\right) \,= & {} \,\frac{3 p^2_{T1}}{4\,k^8_T}\left( -13 k^2_T\,+\,50 \,p^2_{T1}\right) ;\nonumber \\ B\left( k_T, p_{T1}\right) \,= & {} \,\frac{1}{8\,k^4_T}\left( 8 k^4_T + 65 k^2_T p^2_{T1} - 150 p^4_{T1}\right) . \end{aligned}$$

(D.5)

The integrations over $r'_2$ and $r_2$ differ from the integrations over $r_1$ and $r'_1$, due to the extra factor $1/r^2_2$, which comes from the integration over $Q_T$ in Eqs. (4.2) and (4.3). Since $r^2_2 \approx \,1/Q^2_s(y_2)$ we replace it by $1/r^2_2 = Q^2_s\left( y_2\right)$. In the case the integral over $k'_T$ takes the same form as the integral over $k_T$, leading to the following expression, which is proportional to $\cos ^2\left( \phi \right)$, where $\phi$ is the angle between $\vec {p}_{T1}$ and $\vec {p}_{T2}$:

$$\begin{aligned}&\frac{\mathrm{d}^2 \sigma }{\mathrm{d} y_1 \mathrm{d}^2 p_{T1}\,\mathrm{d} y_2 \mathrm{d}^2 p_{T2}}\left( Fig.~2\right) \nonumber \\&\quad \, \,\propto \,\,\,Q^2_s\left( y_2\right) \,\,A\left( k_T,p_{T1}\right) \,A\left( k'_T,p_{T2}\right) \, \cos ^2\left( \phi \right) , \end{aligned}$$

(D.6)

which is responsible for the appearance of $v_{2,2}$ and $v_2$.

Using the second expression in Eq. (D.5) we can calculate the term which is proportional to $\cos ^4\left( \phi \right)$ and has the form

$$\begin{aligned}&\frac{\mathrm{d}^2 \sigma }{\mathrm{d} y_1 \mathrm{d}^2 p_{T1}\,\mathrm{d} y_2 \mathrm{d}^2 p_{T2}}\left( Fig.~2\right) \nonumber \\&\quad \,\,\propto \,\,\,Q^2_s\left( y_2\right) \,\,A^{(4)}\left( k_T,p_{T1}\right) \,A^{(4)}\left( k'_T,p_{T2}\right) \, \cos ^4\left( \phi \right) \nonumber \\ \end{aligned}$$

(D.7)

with

$$\begin{aligned} A^{(4)}\left( k_T,p_{T1}\right) = 15\,\frac{573}{8}\frac{1}{k^6_T}\,\frac{p^2_{T1}}{k^2_T}. \end{aligned}$$

(D.8)