Branching ratios, CP asymmetries and polarizations of $B\rightarrow \psi (2S) V$ decays

Abstract

We analyze the non-leptonic decays $B/B_s\rightarrow \psi (2S) V$ with $V=(\rho , \omega , K^{*}, \phi )$ by employing the perturbative QCD (pQCD) factorization approach. Here the branching ratios, the CP asymmetries and the complete set of polarization observables are investigated systematically. Besides the traditional contributions from the factorizable and non-factorizable diagrams at the leading order, the next-to-leading order (NLO) vertex corrections could also provide considerable contributions. The pQCD predictions for the branching ratios of the $B_{(s)}\rightarrow \psi (2S)K^{*}, \psi (2S)\phi$ decays are consistent with the measured values within errors. As for $B\rightarrow \psi (2S) \rho , \psi (2S) \omega$ decays, the branching ratios can reach the order of $10^{-5}$ and could be measured in the LHCb and Belle-II experiments. The numerical results show that the direct CP asymmetries of the considered decays are very small. Thus the observation of any large direct CP asymmetry for these decays will be a signal for new physics. The mixing-induced CP asymmetries in the neutral modes are very close to $\sin 2\beta _{(s)}$, which suggests that these channels can give a cross-check on the measurement of the Cabbibo–Kobayashi–Maskawa (CKM) angle $\beta$ and $\beta _s$. We find that the longitudinal polarization fractions $f_0$ are suppressed to $\sim 50\%$ due to the large non-factorizable contributions. The magnitudes and phases of the two transverse amplitudes $\mathcal {A}_{\parallel }$ and $\mathcal {A}_{\perp }$ are roughly equal, which is an indication for the approximate light-quark helicity conservation in these decays. The overall polarization observables of $B\rightarrow \psi (2S) K^{*0}$ and $B_s\rightarrow \psi (2S) \phi$ channels are also in good agreement with the experimental measurements as reported by LHCb and BaBar. Other results can also be tested by the LHCb and Belle-II experiments.

1 Introduction

Studies of the decays of B mesons into a charmonium meson plus a light vector meson contribute a lot to our knowledge about the CP violation and mixing in the B meson system [1], and also provide a particularly important place to look for the physics beyond the standard model (SM). For example, the mode $B^0_s\rightarrow J/\psi \phi$ is the so-called “golden mode” for measuring $\beta _s$, which is extracted from the angular analysis of the time-dependent differential decay rate [2,3,4]. The counterpart phase $\beta$ in the B meson system can also be extracted in $B^0\rightarrow J/\psi K^*$ decay [5]. The decay $B^0\rightarrow J/\psi \phi$, which would proceed mainly via a Cabibbo-suppressed and color-suppressed transition ($\bar{b}d\rightarrow \bar{c}c\bar{d}d$) with rescattering of $d\bar{d}$ into $s\bar{s}$, provide useful information for understanding rescattering mechanisms [6,7,8]. In addition, combining the decays $B^0\rightarrow J/\psi \phi$ and $B^0\rightarrow J/\psi \omega$ can be helpful to study the $\omega -\phi$ mixing [9]. These decays are dominated by tree diagrams and the contributions from penguin diagrams are expected to be small. With continuously increasing high-precision measurements, the penguin effects, which play an important role in the extraction of the above phases, can be measured by means of an analysis of the angular distribution of $B^0\rightarrow J/\psi \rho ^0$ [10] and $B^0_s\rightarrow J/\psi \bar{K}^{*0}$ [11].

In the framework of SM, these decay modes are induced by transitions $b\rightarrow q c \bar{c}$ with $q=d,s$. In principle, any mode involving various excitations of the $c\bar{c}$ mesons such as $B\rightarrow \psi (2S) V$ decays could be an alternative to that for $J/\psi$ analogues, and they could give additional and complementary information. Experimentally, the $\psi (2S)$ meson can be reconstructed in the decay channels $\psi (2S)\rightarrow \mu ^+\mu ^-$ and $\psi (2S)\rightarrow J/\psi \pi ^+\pi ^-$, with the $J/\psi$ meson decaying into two muons [12]. Nowadays, several experimental Collaborations have measured the decays $B_s^0\rightarrow \psi (2S) \phi$ [13], $B\rightarrow \psi (2S) K^*(892)$ [14,15,16,17,18], $B^0 \rightarrow \psi (2S) \pi ^0$ [19], $B^+ \rightarrow \psi (2S) \pi ^+$ [20], $B_s \rightarrow \psi (2S) \eta ^{(')}$ [21, 22]. Some relative ratios of the branching ratios for B meson decays into $\psi (2S)$ and $J/\psi$ mesons are also measured by several experiments [23,24,25,26].

On the theory side, these $B \rightarrow \psi (2S)V$ modes do have some special properties. Since there are three possible values of the total angular momentum with different CP eigenvalues ($L=1$ is odd, while $L=0,2$ are even), the angular analysis is needed to separate the contributions from the CP-even and CP-odd partial waves. Therefore the final state can be decomposed into three helicity amplitudes (one longitudinal and two transverse components ). The information about the phases of the transverse decay amplitudes provides a test of the factorization hypothesis [27]. Furthermore, $B \rightarrow \psi (2S)V$ are the color-suppressed modes and therefore a significant impact of non-factorizable contributions is expected. Both improvements in the accuracy of the experimental measurements and the observation of new modes, especially involving $\psi (2S)$ in the final states, can be helpful in understanding the role of any non-factorizable corrections [28,29,30] and differentiating various theory approaches. Nowadays there exist several theoretical approaches as described in Refs. [31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46] which shed more light on the S-wave ground state charmonium decays of B mesons. The non-leptonic B decays with radially excited charmonium mesons in final state, however, have received less attention in the literature.

Based on the $k_T$ factorization theorem, The perturbative QCD (pQCD) approach [47, 48] is suitable for describing different types of heavy hadron decays. After including the parton transverse momentum $k_T$, which is not negligible in the end-point region, both factorizable and non-factorizable contributions are calculable without end-point singularity. The Sudakov resummation has also been introduced to suppress the long-distance contributions effectively. Therefore, the pQCD approach is a self-consistent framework and has a good predictive power. In our previous works [49,50,51], the semi-leptonic, two-body and three-body non-leptonic decays of the $B_c(B)$ mesons to $\psi (2S)$ are studied in the pQCD framework. Here, furthermore, we will extend our previous analysis to the $B \rightarrow \psi (2S)V$ decays. In a recent work [52], The authors applied the pQCD approach to the study of $B\rightarrow J/\psi V$ decays and also obtained the theoretical predictions in good agreement with currently available data. Therefore we have good reasons to believe that it is appropriate to analyze $B\rightarrow \psi (2S) V$ in this framework.

This work is organized as follows. In Sect. 2 we present some basic formulas such as the effective Hamiltonian and kinetic conventions, then briefly review the pQCD approach. The technical formulas of the calculation and the non-perturbative meson wave functions are summarised in Appendices A and B, respectively. Section 3 devoted to a numerical calculation and discussion. Our conclusions are left for Sect. 4.

2 Analytic formulas and perturbative calculations

For non-leptonic charmonium B decays, both the tree operators and the penguin operators of the standard effective weak Hamiltonian contribute, which is given by [53]

$$\begin{aligned} \mathcal {H}_\mathrm{eff}= & {} \frac{G_F}{\sqrt{2}}\Bigg \{\xi _c[C_1(\mu )O^c_1(\mu )+C_2(\mu )O^c_2(\mu )]\nonumber \\&-\xi _t\sum _{i=3}^{10}C_i(\mu )O_i(\mu )\Bigg \}, \end{aligned}$$

(1)

with the CKM matrix element $\xi _{c(t)}=V^*_{c(t)b}V_{c(t)q}$. $O_i(\mu )$ and $C_i(\mu )$ are the effective four quark operators and their QCD corrected Wilson coefficients at the renormalization scale $\mu$, respectively. Their explicit form can be found in Ref. [53].

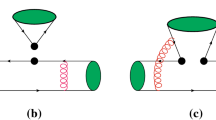
At quark level, when the $\bar{b}\rightarrow \bar{q}c\bar{c}$ decay occurs through the four quark operators, a $c\bar{c}$ state $\psi (2S)$ is created while the other light anti-quark $\bar{q}$ is flying away. Since the heavy b quark in B meson carry most of the energy of B meson, the spectator quark of the B meson is soft. A hard gluon is exchanged so that the spectator quark gets energy from the four quark operator and then form a fast moving vector meson with its partner anti-quark. This renders the perturbative calculations in a six-quark interaction form, which involves the four quark operator and the spectator quark connected by a hard gluon. The relevant Feynman diagrams are shown in Fig. 1.

Fig. 1

The typical leading-order Feynman diagrams for the decay $B \rightarrow \psi (2S)V$. a, b The factorizable diagrams, and c, d the non-factorizable diagrams

In the pQCD approach, the decay amplitudes are expressed as the convolution of the hard kernels H with the relevant meson wave functions $\Phi _i$

$$\begin{aligned} \mathcal {A}(B\rightarrow \psi (2S) V)= & {} \int \mathrm{d}^4k_1\mathrm{d}^4k_2\mathrm{d}^4k_3 Tr[C(t)\Phi _B(k_1)\nonumber \\&\times \Phi _{\phi (2S)}(k_2)\Psi _V(k_3) H(k_1,k_2,k_3,t)],\nonumber \\ \end{aligned}$$

(2)

where $k_i$ are the momentum of the quark in each meson, and “Tr” denotes the trace over all Dirac structure and color indices. C(t) is the short distance Wilson coefficients at the hard scale t. The meson wave functions $\Phi$, including all non-perturbative components in the $k_T$ factorization, can be extracted from experimental data or other non-perturbative methods. The hard kernel $H(k_i,t)$ describes the four quark operator and the spectator quark connected by a hard gluon, which can be perturbatively calculated including all possible Feynman diagrams without end-point singularity. In the following, we start to compute the decay amplitudes of $B\rightarrow \psi (2S) V$ decay.

We will work in the B meson rest frame and employ the light-cone coordinates for momentum variables. The B meson momentum $P_1$, the $\psi (2S)$ meson momentum $P_2$, the vector-meson momentum $P_3$ and the quark momenta $k_i$ in each meson are chosen as

$$\begin{aligned} P_1= & {} \frac{M}{\sqrt{2}}(1,1,\mathbf 0 _\mathrm{T}),\quad P_2=\frac{M}{\sqrt{2}}(1-r_v^2,r^2,\mathbf 0 _\mathrm{T}),\nonumber \\ P_3= & {} \frac{M}{\sqrt{2}}(r_v^2,1-r^2,\mathbf 0 _\mathrm{T}),\nonumber \\ k_1= & {} \left( \frac{M}{\sqrt{2}}x_1,0,\mathbf k _\mathrm{1T}\right) ,\nonumber \\ k_2= & {} \left( \frac{M}{\sqrt{2}}x_2(1-r_v^2),\frac{M}{\sqrt{2}}x_2r^2,\mathbf k _{2\mathrm T}\right) ,\nonumber \\ k_3= & {} \left( \frac{M}{\sqrt{2}}x_3r_v^2,\frac{M}{\sqrt{2}}x_3(1-r^2),\mathbf k _\mathrm{3T}\right) , \end{aligned}$$

(3)

with the mass ratio $r_{(v)}=m_{\psi (2S)}(m_V)/M$ and $m_{\psi (2S)},m_V,$ M are the masses of the charmonium, vector meson and B meson, respectively. The $k_{iT}$, $x_i$ represent the transverse momentum and longitudinal momentum fraction of the quark inside the meson. Since the final state consists of two spin-1 particles, to extract the helicity amplitudes, the following parametrizations for the longitudinal and transverse polarization vectors are useful:

$$\begin{aligned} \epsilon _2^L= & {} \frac{1}{\sqrt{2(1-r_v^2)}r}(1-r_v^2,-r^2,\mathbf 0 _\mathrm{T}),\nonumber \\&\times \epsilon _2^T=(0,0,\mathbf 1 _\mathrm{T}),\nonumber \\ \epsilon _3^L= & {} \frac{1}{\sqrt{2(1-r^2)}r_v}(-r_v^2,1-r^2,\mathbf 0 _\mathrm{T}),\nonumber \\&\times \epsilon _3^T=(0,0,\mathbf 1 _\mathrm{T}); \end{aligned}$$

(4)

they satisfy the normalization $(\epsilon _{2,3}^{L})^2= (\epsilon _{2,3}^{T})^2=-1$ and the orthogonality $\epsilon _2^L \cdot P_2=\epsilon _3^L \cdot P_3=0$.

The decay amplitude can be decomposed into three parts of the polarizations amplitudes as follows:

$$\begin{aligned} \mathcal {A}(B\rightarrow \psi (2S) V)= & {} \mathcal {A}_L+\mathcal {A}_N\epsilon _2^T\cdot \epsilon _3^T\nonumber \\&+i\mathcal {A}_T\epsilon _{\alpha \beta \rho \sigma }n^{\alpha }v^{\beta }\epsilon _2^{T\rho }\epsilon _3^{T\sigma }, \end{aligned}$$

(5)

with the null vectors $n=(1,0,\mathbf 0 _\mathrm{T})$ and $v=(0,1,\mathbf 0 _\mathrm{T})$. The subscript L, N, T correspond to the longitudinal, normal and transverse polarization states, respectively. According to Eq. (1), the three different polarization amplitudes have the following expressions:

$$\begin{aligned}&\mathcal {A}_{L,N,T}(B\rightarrow \psi (2S) V)\nonumber \\&\quad =\xi _c\Big [(C_1+\frac{1}{3}C_2)\mathcal {F}_{L,N,T}^{LL}+C_2\mathcal {M}_{L,N,T}^{LL} \Big ]\nonumber \\&\quad -\xi _t\Big [(C_3+\frac{1}{3}C_4+C_9+\frac{1}{3}C_{10})\mathcal {F}_{L,N,T}^{LL}\nonumber \\&\quad +(C_5+\frac{1}{3}C_6+C_7+\frac{1}{3}C_{8})\mathcal {F}_{L,N,T}^{LR}\nonumber \\&\quad +(C_4+C_{10})\mathcal {M}_{L,N,T}^{LL}+(C_6+C_8)\mathcal {M}_{L,N,T}^{SP}\Big ], \end{aligned}$$

(6)

where $\mathcal {F}(\mathcal {M})$ describes the contributions from the factorizable (non-factorizable) diagrams. The superscripts LL, LR, and SP refer to the contributions from $(V-A)\otimes (V-A)$, $(V-A)\otimes (V+A)$ and $(S-P)\otimes (S+P)$ operators, respectively. These explicit factorization formulas are all listed in Appendix A. In this work, we also consider the vertex corrections to the factorizable amplitudes $\mathcal {F}$ at the current known next-to-leading order (NLO) level. Their effects can be combined in the Wilson coefficients as usual [54,55,56]. In the NDR scheme, the vertex corrections are included by the modifications to the combinations $a_i$ ¹ of the Wilson coefficients $C_i$ associated with the factorizable amplitudes in Eq. (6):

$$\begin{aligned} a_2\rightarrow & {} a_2 +\frac{\alpha _s}{9\pi }C_2 \left[ -18-12\text {ln}(\frac{\mu }{m_b})+f^h_I\right] ,\nonumber \\ a_3+a_9\rightarrow & {} a_3+a_9+\frac{\alpha _s}{9\pi }(C_4+C_{10})\nonumber \\&\quad \times \left[ -18-12\text {ln}(\frac{\mu }{m_b})+f^h_I \right] ,\nonumber \\ a_5+a_7\rightarrow & {} a_5+a_7+\frac{\alpha _s}{9\pi }( C_6+C_{8})\nonumber \\&\quad \times \left[ 6+12\text {ln}(\frac{\mu }{m_b})-f^h_I\right] . \end{aligned}$$

(7)

The functions $f^h_I$ arise from the vertex corrections, which are given in Ref. [31].

3 Numerical results

Meant to be used in our numerical calculations, parameters such as the meson mass, the Wolfenstein parameters, the decay constants, and the lifetime of $B_{(s)}$ mesons [57] are given in Table 1, while the input wave functions and various parameters of the light vectors are shown in Appendix B.

Table 1 The decay constants of $\psi (2S)$ meson is from [49], while the other parameters are adopted in PDG [57] in our numerical calculations

We now use the method previously illustrated to estimate the physical observables (such as the CP averaged branching ratios, direct and mixing CP violations, polarization fractions, and relative phases) of the considered decays.

3.1 The CP averaged branching ratios

For $B\rightarrow \psi (2S) V$ decays, the branching ratios can be written as

$$\begin{aligned} \mathcal {B}(B\rightarrow \psi (2S) V)=\frac{G_F^2\tau _{B}}{32\pi M}(1-r^2)\sum _{i=0,\parallel ,\perp }|\mathcal {A}_i|^2, \end{aligned}$$

(8)

where the terms $\mathcal {A}_0, \mathcal {A}_{\parallel },\mathcal {A}_{\perp }$ denote the longitudinal, parallel, and perpendicular polarization amplitude in the transversity basis, respectively, which are related to $\mathcal {A}_{L,N,T}$ of Eq. (6) via

$$\begin{aligned} \mathcal {A}_0=-\mathcal {A}_L, \quad \mathcal {A}_{\parallel }=\sqrt{2}\mathcal {A}_{N}, \quad \mathcal {A}_{\perp }=\sqrt{2}\mathcal {A}_{T}. \end{aligned}$$

(9)

Here $\mathcal {A}_0$ and $\mathcal {A}_{\parallel }$ are the CP even amplitudes whereas $\mathcal {A}_{\perp }$ corresponds to CP odd ones. Note that an additional minus sign in $\mathcal {A}_0$ (see Ref. [58]) make our definitions of the relative phase between $\mathcal {A}_{\parallel (\perp )}$ and $\mathcal {A}_{0}$ takes the value of $\pi$ in the heavy-quark limit. The CP averaged branching ratios for the $B\rightarrow \psi (2S) V$ decays are shown in Table 2 together with some of the experimental measurements. Some dominant uncertainties are considered in our calculations. The first error in these entries is caused by the hadronic parameters in the $B_{(s)}$ meson wave function: (1) the shape parameters, $\omega _b=0.40\pm 0.04$ for the B meson, and $\omega _b=0.50\pm 0.05$ for the $B_s$ meson; (2) the decay constants, which are given in Table 1. The second error is from the uncertainty of the heavy-quark masses. In the evaluation, we vary the values of $m_{c(b)}$ within a $10\%$ range. The last one is caused by the variation of the hard scale from 0.8t to 1.2t, which characterizes the size of the NLO QCD contributions. It is found that the main uncertainties in our approach come from the B meson wave function, which can reach 20–$30\%$ in magnitude. The scale-dependent uncertainty is less than $20\%$ due to the inclusion of the NLO vertex corrections. We have checked the sensitivity of our results to the choice of the shape parameter $\omega _c$ (see Eq. (B7)) in the charmonia meson wave function. The variation of $\omega _c$ in the range $0.18\sim 0.22$ will result in a small change of the branching ratio, say less than $10\%$. In addition, the uncertainties related to the light vector mesons, such as the vector-meson decay constants and the Gegenbauer moments shown in Table 6, are only several percent. Therefore they have been neglected in our calculations.

Table 2 The pQCD predictions for the CP-averaged branching ratios for the $B\rightarrow \psi (2S) V$ decays (in units of $10^{-5}$). For comparison, experimental results from BaBar [17], Belle [59, 60], or the world average from HFAG 2016 [61] and PDG 2016 [57] are also listed

For the color-suppressed decays, it is expected that the factorizable diagram contribution is suppressed due to the cancellation of Wilson coefficients $C_1+C_2/3$. After the inclusion of the vertex corrections, the factorizable diagram contributions become comparable with the non-factorizable ones. Some important features of the numerical results collected in Table 2 are of the following forms:

• (I) The $b\rightarrow s$ transition processes $B^{+(0)}\rightarrow \psi (2S) K^{*+(0)}$ and $B_s\rightarrow \psi (2S) \phi$ have a comparatively large branching ratio $10^{-4}$; while the branching ratios of those $b\rightarrow d$ channels $B^{+(0)}\rightarrow \psi (2S)\rho ^{+(0)}$, $B^{0}\rightarrow \psi (2S)\omega ^{0}$ and $B_s\rightarrow \psi (2S) \bar{K}^{*0}$ are relatively small ($\sim 10^{-5}$) owing to the CKM factor suppression: $|V^*_{cb}V_{cd}|\sim \lambda ^3$.

• (II) In the quark model, the difference between $B^0 \rightarrow \psi (2S)\omega$ and $B^0 \rightarrow \psi (2S)\rho ^0$ decays comes from the sign of $d\bar{d}$ component, which only appears in penguin operators, so their difference should be relatively small. The branching ratio $\mathcal{B}(B^0 \rightarrow \psi (2S)\omega )$ is indeed slightly smaller than $\mathcal{B}(B^0 \rightarrow \psi (2S)\rho ^0)$. This is a consequence of the fact that the $\omega$ vector and tensor decay constants are smaller than those of the $\rho ^0$ according to Table 6;

• (III) The value of $\mathcal {B}(B_s \rightarrow \psi (2S) \bar{K}^{*0})$ have a tendency to be smaller than 2$\mathcal {B}(B^0 \rightarrow \psi (2S) \rho ^{0})$. Although the $K^*$ and $B_s$ meson decay constants are larger than those of the $\rho ^0$ and $B^0$ meson, the SU(3) breaking effects in the twist-2 distribution amplitudes, parametrized by the first Gegenbauer moment $a_{1K^*}$ (see Eq. (B10)), gives a negative contribution to the $B_s \rightarrow \psi (2S) \bar{K}^{*0}$ decay, which induces the smaller branching ratio.

• (IV) For the first four $B_{(s)}\rightarrow \psi (2S) V$ decays as listed in Table 2, one can see that the pQCD predictions for their branching ratios agree well with the world averaged values given in HFAG 2016 and PDG 2016 [57, 61] within one standard deviation. For $B_s \rightarrow \psi (2S) \bar{K}^{*0}$ decay, the central value of our theoretical prediction for its branching ratio is slightly smaller than that of the PDG number [57]. But we know that the PDG result is obtained by multiplying the best value $\mathcal {B}(B^{0}\rightarrow \psi (2S) K^{*0})$ with the measured ratio $\mathcal {B}(\bar{B}_s^{0}\rightarrow \psi (2S) K^{*0})/\mathcal {B}(B^{0}\rightarrow \psi (2S) K^{*0})$ from the LHCb [62]. We hope the future experiment will provide a direct measurement to this mode.

• (V) As for the channels with $\rho$ and $\omega$ as the final-state V meson, they have not been measured yet. The pQCD predictions for the decay rates of these three channels are at the order of $10^{-5}$, measurable in the future LHCb and Belle-II experiments.

For a more direct comparison with the available experimental measurements of the relative rates of $B_{(s)}$ meson decays into $\psi (2S)$ and $J/\psi$ mesons, we recalculated the corresponding $B_{(s)}$ decays to $J/\psi V$ by using the same input parameters as in this paper but with the replacement $\psi (2S)\rightarrow J/\psi$, and we found numerically that

$$\begin{aligned}&\mathcal {B}(B_s \rightarrow J/\psi \bar{K}^{*0} )=(4.2^{+1.2+0.6+0.6}_{-0.8-0.3-0.1})\times 10^{-5}, \nonumber \\&\mathcal {B}(B_s \rightarrow J/\psi \phi )=(9.3^{+2.6+1.0+1.5}_{-1.9-0.7-0.8})\times 10^{-4},\nonumber \\&\mathcal {B}(B^+ \rightarrow J/\psi K^{*+} )=(11.2^{+2.5+1.4+1.5}_{-2.2-1.2-0.9})\times 10^{-4}, \nonumber \\&\mathcal {B}(B^0 \rightarrow J/\psi K^{*0} )=(10.4^{+2.2+1.3+1.3}_{-2.0-1.1-0.8})\times 10^{-4},\nonumber \\&\mathcal {B}(B^+ \rightarrow J/\psi \rho ^+ )=(5.1^{+1.2+0.6+0.8}_{-1.0-0.5-0.3})\times 10^{-5},\nonumber \\&\mathcal {B}(B^0 \rightarrow J/\psi \rho ^0 )=(2.4^{+0.6+0.3+0.4}_{-0.5-0.3-0.2})\times 10^{-5}, \nonumber \\&\mathcal {B}(B^0 \rightarrow J/\psi \omega )=(1.8^{+0.4+0.2+0.3}_{-0.4-0.1-0.1})\times 10^{-5}, \end{aligned}$$

(10)

where the errors have the same meaning as those for $B_{(s)}\rightarrow \psi (2S) V$ decays. The above results are well consistent with the previous pQCD calculations [52] and also with the present data [57].

Finally, as a cross-check, using the pQCD predictions as given in Table 2 and Eq. (10) we can estimate the relative ratios $\mathcal {R}_V=\mathcal {B}(B\rightarrow \psi (2S)V)/\mathcal {B}(B\rightarrow J/\psi V)$ as below,

$$\begin{aligned} \mathcal {R}_{\phi }= & {} 0.51^{+0.02}_{-0.01}, \, \mathcal {R}_{K^{*0(+)}}=0.53^{+0.00}_{-0.02}, \, \mathcal {R}_{\rho ^{0(+)}}=0.53^{+0.00}_{-0.03},\nonumber \\ \mathcal {R}_{\omega }= & {} 0.56^{+0.01}_{-0.04}, \, \mathcal {R}_{\bar{K}^{*0}}=0.52^{+0.01}_{-0.04}, \end{aligned}$$

(11)

where all uncertainties are added in quadrature. Since the parameter dependences of the pQCD predictions for the branching ratios are largely canceled in their relative ratios, the total theoretical error of $R_{V}$ are only a few percent, much smaller than those for the branching ratios. Fortunately, two of these five ratios have been measured by LHCb [24] D0 [25], and CDF [14, 26] experiments:

$$\begin{aligned}&\mathcal {R}_{\phi }=\left\{ \begin{aligned} 0.489&\pm 0.026(\text {stat})\pm 0.021(\text {syst})\pm 0.012(R_{\psi })\quad \quad \quad \text {LHCb}, \nonumber \\ 0.53&\pm 0.10(\text {stat})\pm 0.07(\text {syst})\pm 0.06(R_{\psi })\quad \qquad \qquad \quad \text {D0}, \\ 0.52&\pm 0.13(\text {stat})\pm 0.04(\text {syst})\pm 0.06(R_{\psi })\quad \quad \quad \quad \quad \text { CDF}, \end{aligned}\right. \nonumber \\&\mathcal {R}_{K^{*0}}=\left\{ \begin{aligned} 0.476&\pm 0.014(\text {stat})\pm 0.010(\text {syst})\pm 0.012(R_{\psi })\quad \quad \text {LHCb} ,\\0.515&\pm 0.113(\text {stat})\pm 0.052(\text {syst}) \quad \qquad \qquad \qquad \quad \quad \text { CDF}, \end{aligned}\right. \nonumber \\ \end{aligned}$$

(12)

where the third uncertainty is from the ratio of the $\psi (2S)$ and $J/\psi$ branching fractions to $\mu ^+\mu ^-$. It is easy to see that our pQCD predictions for both $R_\phi$ and $R_{K^{*0}}$ agree very well with the measured values.

3.2 CP Asymmetries

Studying CP asymmetries is an important task in B physics. For the charged B decays, the CP asymmetries arise from the interference between the penguin diagrams and tree diagrams. The direct CP violation asymmetry including three polarization are defined by

$$\begin{aligned} A^{\text {dir}}_{0,\parallel ,\perp }=\frac{|\mathcal {\bar{A}}_{0,\parallel ,\perp }|^2-|\mathcal {A}_{0,\parallel ,\perp }|^2}{|\mathcal {\bar{A}}_{0,\parallel ,\perp }|^2+|\mathcal {A}_{0,\parallel ,\perp }|^2}, \end{aligned}$$

(13)

where $\mathcal {\bar{A}}_{0,\parallel ,\perp }$ is the CP-conjugate amplitude of $\mathcal {A}_{0,\parallel ,\perp }$.

For the neutral $B^0_{(s)}$ decays, because of the $B^0_{(s)}$–$\bar{B}^0_{(s)}$ mixing, it is required to include time-dependent measurements in CP violation asymmetries. If the final states are CP eigenstates, the time-dependent CP asymmetry is defined as

$$\begin{aligned} A^{0,\parallel ,\perp }_f(t)=-C^{0,\parallel ,\perp }_f \text {cos}(\Delta m t)+S^{0,\parallel ,\perp }_f \text {sin}(\Delta m t), \end{aligned}$$

(14)

where $\Delta m$ is the mass difference of the two mass eigenstates of the neutral B meson and f is a two-body final state. The direct CP asymmetry $C^{0,\parallel ,\perp }_f$ and mixing-induced CP asymmetry $S^{0,\parallel ,\perp }_f$ are referred to as

$$\begin{aligned} C^{0,\parallel ,\perp }_f=\frac{1-|\lambda ^{0,\parallel ,\perp }_f|^2}{1+|\lambda ^{0,\parallel ,\perp }_f|^2},\quad S_f=\frac{2\text {Im}(\lambda ^{0,\parallel ,\perp }_f)}{1+|\lambda ^{0,\parallel ,\perp }_f|^2}. \end{aligned}$$

(15)

The parameter $\lambda ^{0,\parallel ,\perp }_f=\eta _f e^{-2i\beta _{(s)}}\frac{\mathcal {\bar{A}}_{0,\parallel ,\perp }}{\mathcal {A}_{0,\parallel ,\perp }}$ describes CP violation in the interference between mixing and decay. $\eta _f$ is the CP eigenvalue $(\pm 1)$ of the polarization state. $\beta _{(s)}$ is the CKM angle defined as usual [57]. Note that the final states of $\psi (2S) K^{*0}$ and its CP conjugate are flavor-specific, for example, the kaon and pion charges of $K^{*0}\rightarrow K^+\pi ^-$ and $\bar{K}^{*0}\rightarrow K^-\pi ^+$ depend on whether we had a B and $\bar{B}$ meson in the initial state, and the time-dependent angular distributions do not show CP violation due to interference between mixing and decay. Therefore, we only calculate the direct CP asymmetry for $B^0_s\rightarrow \psi (2S) \bar{K}^{*0}$ and $B^0\rightarrow \psi (2S) K^{*0}$ decays.

The pQCD predictions for the CP asymmetry parameters $A^{\text {dir}}_{0,\parallel ,\perp }$ are listed in Table 3 and 4. Unlike the branching ratios, the direct CP asymmetry is not sensitive to the wave function parameters and heavy-quark masses, but suffer from large uncertainties due to the hard scale t. In order to reduce the large scale dependence effectively, one has to know the complete NLO corrections, which are in fact not yet available now, thus beyond the scope of this paper.

Since the direct CP asymmetry is proportional to the interference between the tree and penguin contributions, while the Wilson coefficients of the penguin diagram are loop suppressed when compared with those tree contributions. Therefore, the direct CP asymmetry parameters of these processes are rather small (only $10^{-3}\sim 10^{-4}$), and the mixing-induced CP asymmetry for neutral B decays is almost proportional to the $\sin 2\beta _{(s)}$ from Eq. (15). The mixing-induced CP asymmetry parameters $S_{\psi (2S)\rho ^0(\omega )}$ and $S_{\psi (2S)\phi }$ in Table 4 are very close to the current world average values $-\sin {2\beta }=-0.691\pm 0.017$ and $-2\beta _s=-0.0376^{+0.0008}_{-0.0007}$ [61], respectively. That is to say, these modes can serve as an alternative places to extract CKM angle $\beta _{(s)}$. Furthermore, the large mixing-induced CP asymmetry $S_f$ for $b\rightarrow d$ transition can confront with future experimental results. It can also be seen that the CP asymmetry parameters for three polarization states are slightly different because the strong phases coming from the non-factorizable diagrams and vertex corrections are polarization-dependent [31]. On the experimental side, so far only the charge asymmetries of $B^+\rightarrow \psi (2S) K^{*+}$ process was measured by the BaBar Collaboration [57]:

$$\begin{aligned} A^{\text {dir}}_{CP}(B^+\rightarrow \psi (2S) K^{*+})=0.08\pm 0.21. \end{aligned}$$

(16)

Of course, the statistical uncertainty is too large to make any statement. Any observation of large direct CP asymmetry for the considered decays $B_{(s)}\rightarrow \psi (2S) V$ decays will be a signal for new physics. Besides, the precise measurements of these mixing-induced CP asymmetries serve to determine the CP phases related to the $B^0$–$\bar{B^0}$ and $B^0_s$–$\bar{B^0_s}$ mixing amplitudes.

Table 3 The pQCD predictions for $A^{\text {dir}}_{0,\parallel ,\perp }(10^{-3})$ in the $B\rightarrow \psi (2S) (\rho ^+,K^*, \bar{K}^*)$ decays. The error arises from the hard scale t

Table 4 The pQCD predictions for the CP asymmetry parameters $C_f^{0,\parallel ,\perp }$ and $S_f^{0,\parallel ,\perp }$ in the $B^0\rightarrow \psi (2S) (\rho ^0, \omega , \phi )$ decays. The error arises from the hard scale t

3.3 Polarization fractions and relative phases

In experimental analyses, we usually define five observables corresponding to three polarization fractions $f_0, f_{\parallel }, f_{\perp }$, and two relative phases $\phi _{\parallel }, \phi _{\perp }$, where

$$\begin{aligned} f_{0,\parallel ,\perp }=\frac{|\mathcal {A}_{0,\parallel ,\perp }|^2}{|\mathcal {A}_0|^2+|\mathcal {A}_{\parallel }|^2+|\mathcal {A}_{\perp }|^2},\quad \phi _{\parallel ,\perp }=\text {arg}\frac{\mathcal {A}_{\parallel ,\perp }}{\mathcal {A}_{0}},\nonumber \\ \end{aligned}$$

(17)

with normalization such that $f_0+f_{\parallel }+f_{\perp }=1$. The polarization fractions as well as the relative phases are shown in Table 5, where the sources of the errors in the numerical estimates have the same origin as in the discussion of the branching ratios in Table 2. It is easy to see that the most important theoretical uncertainties are caused by the heavy-quark masses. From Eqs. (7) and (A10), we can see the mass terms $m_b$ and $m_c$ associated vertex corrections and non-factorizable amplitudes, respectively. It can numerically change the real and imaginary parts of these contributions and have a significant effect on the polarization fractions, especially for the relative phases. The uncertainties from the wave function parameters are very small because they mainly give an overall change of all polarization amplitudes and the parameter dependence can be canceled out in Eq. (17).

Table 5 The pQCD predictions for the CP-averaged polarization fractions, relative phases in the $B\rightarrow \psi (2S) V$ decays. The errors correspond to the combined uncertainty in the hadronic parameters, heavy-quark masses and the hard scale t

From Table 5, both the $B^+\rightarrow \psi (2S) (K^{*+},\rho ^+)$ and $B^0\rightarrow \psi (2S) (K^{*0}, \rho ^0)$ modes have the same polarization fractions and relative phases, since they differ only in the lifetimes or isospin factor in our formalism. Comparing the three polarization fractions, the perpendicular polarization fractions $f_{\perp }$ are less than $25\%$ shows that the CP even component dominates in these decays. According to the power counting rules in the factorization assumption, the longitudinal polarization dominates the decay ratios and the transverse polarizations are suppressed [63, 64] due to the helicity flips of the quark in the final-state hadrons. However, the situation is very different for the color-suppressed decays, where the contributions from the non-factorizable tree diagrams in Fig. 1c, d are comparable with those of the color-suppressed tree diagrams although the latter are enhanced by the involving vertex corrections. With an additional gluon, the transverse polarization in the non-factorizable diagrams does not encounter helicity flip suppression, therefore numerically we get a longitudinal polarization fraction ($f_0$) smaller than $50\%$, which are compatible with those currently available data. The fact that the non-factorizable diagrams can give a large transverse polarization contribution is also observed in the $B_c\rightarrow J/\psi D_{(s)}^{*+}$ decays [65]. There are another equivalent set of helicity amplitudes $(\mathcal {A}_{0},\mathcal {A}_{+},\mathcal {A}_{-})$, which are related to the spin amplitudes $(\mathcal {A}_{0},\mathcal {A}_{\parallel },\mathcal {A}_{\perp })$ introduced in Eq. (9) by

$$\begin{aligned} \mathcal {A}_{\pm }=\frac{\mathcal {A}_{\parallel }\pm \mathcal {A}_{\perp }}{\sqrt{2}}, \end{aligned}$$

(18)

while $\mathcal {A}_{0}$ is common to both bases.

It is expected that $|\mathcal {A}_{0}|^2>|\mathcal {A}_{+}|^2>|\mathcal {A}_{-}|^2$ if the two final states are both light vector mesons. The larger the mass of the vector-meson daughters, the weaker the inequality. In $B\rightarrow \psi (2S) V$ decays with light V being a recoiled meson and heavy $\psi (2S)$ an ejected one. The positive-helicity amplitude is suppressed by $m_{\psi (2S)}/M$ (almost of order unity) due to one of the quark helicities in $\psi (2S)$ has to be flipped, while the negative-helicity one is subject to a further chirality suppression of order $m_V/M$ [63, 64]. Therefore, $\mathcal {A}_{+}$ and $\mathcal {A}_{0}$ may be comparable and larger than $\mathcal {A}_{-}$. Using values of Table 5 and Eq. (18), the pQCD predictions do favor the hierarchy pattern $|\mathcal {A}_{0}|^2\sim |\mathcal {A}_{+}|^2>|\mathcal {A}_{-}|^2$.

The angular analysis of $B^0\rightarrow \psi (2S) K^{*0}$ and $B_s^0\rightarrow \psi (2S) \phi$ has been carried out by BaBar [18] and LHCb [13], respectively. The obtained polarization observables are also summarized in Table 5. As expected under SU(3)-flavor symmetry, both decay modes have similar magnitudes and phases of the amplitudes. Our results of polarization fractions can accommodate the data well within uncertainties, while the predicted relative phases are a bit smaller than the data. One can find a shift from $\pi$ at the 6–$7\sigma$ level in $\phi _{\parallel }$ and $\phi _{\perp }$ shows the existence of final-state interaction. However, the $f_{\parallel }-f_{\perp }$ is about $5\%$ and the difference between $\phi _{\parallel }$ and $\phi _{\perp }$ does not exceed 0.3 radians, which suggests that our solutions are consistent with approximate s-quark helicity conservation despite substantial strong phases.

For the $B^0_s \rightarrow \psi (2S)\bar{K}^{*0}$ channel, the LHCb Collaboration [62] has reported the longitudinal polarization fraction $f_0$ as $0.524\pm 0.056\pm 0.029$, but a thorough angular analysis is still missing. As for other modes, we obtain reasonably accurate results, which could be tested by future experimental measurements.

4 Conclusion

In this paper we have investigated the seven $B\rightarrow \psi (2S) V$ decay modes carefully by employing the pQCD factorization approach. Besides the color-suppressed factorizable diagrams, the non-factorizable diagrams and the vertex correction diagrams can also be evaluated in this approach.

The predicted branching ratios and the relative rates of B meson decays into $\psi (2S)$ and $J/\psi$ mesons are compared with experiments wherever available. Our results indicate that the direct CP asymmetries in these channels are very small due to the suppressed penguin contributions as we mentioned above. The mixing-induced CP asymmetries are not far away from $\sin 2\beta _{(s)}$, these channels can therefore play an important role in the extraction of the CKM angle $\beta _{(s)}$.

Finally, we made a comprehensive polarization analysis of the considered decays. The predicted polarization fractions and relative phases of $B^0\rightarrow \psi (2S) K^{*0}$ and $B^0_s\rightarrow \psi (2S) \phi$ decays are consistent with data. Due to the large mass of $\psi (2S)$ and the dominant contributions from the non-factorizable diagrams, we obtain an equal amount of transverse and longitudinal polarization. The pattern of $f_{\parallel }\approx f_{\perp }$, $\phi _{\parallel }\approx \phi _{\perp }$ favor the conservation of light-quark helicity. The deviations from $\pi$ at several standard deviations in $\phi _{\parallel }$ and $\phi _{\perp }$ indicate the existence of the still unknown final-state interaction.

We also discussed theoretical uncertainties arising from the hadronic parameters in B meson wave function, heavy-quark masses and hard scale t. The total uncertainties are acceptable, around $30\%$ in magnitude. The uncertainties from the hadronic parameters can give sizable effects on the pQCD predictions for branching ratios, while the CP asymmetries suffer a large error from the hard scale t. Further studies at the completely NLO level are certainly required to improve the accuracy of the theoretical predictions. Furthermore, the polarization observables $f_{0,\parallel ,\perp }$ and $\phi _{\parallel ,\perp }$ are more sensitive to the heavy-quark masses, which suggest that the color-suppressed type decays may be more sensitive to the vertex corrections and non-factorizable contributions. Our results and findings will be further tested by the LHCb and Belle-II experiments in the near future.

Appendices

The decay amplitudes

Following the derivation of the factorization formula of Eq. (2), we get the analytic formulas of the (non)factorizable amplitude for each helicity state listed:

$$\begin{aligned} \mathcal {F}^{LL}_L= & {} -8\pi C_f f_{\psi } M^4\int _0^1\mathrm{d}x_1\mathrm{d}x_3\nonumber \\&\times \int _0^{\infty }b_1b_3db_1db_3 \phi _B(x_1,b_1)\nonumber \\&\times \{\sqrt{1-r^2}[\phi _V(x_3)((r^2-1)x_3-1)\nonumber \\&+\phi _V^s(x_3)\sqrt{1-r^2}r_v(2x_3-1)\nonumber \\&+\phi _V^t(x_3)r_v(2x_3-1-r^2(1+2x_3))]\nonumber \\&\times \alpha _s(t_a)S_{ab}(t_a)h(\alpha _e,\beta _a,b_1,b_3)S_t(x_1)\nonumber \\&-2r_{v}(1-r^2)\phi _V^s(x_3)\alpha _s(t_b)S_{ab}\nonumber \\&\times (t_b)h(\alpha _e,\beta _b,b_1,b_3)S_t(x_3)\}, \end{aligned}$$

(A1)

$$\begin{aligned} \mathcal {F}^{LL}_N= & {} 8\pi C_f f_{\psi } M^4r\int _0^1dx_1dx_3\nonumber \\&\times \int _0^{\infty }b_1b_3db_1db_3 \phi _B(x_1,b_1)\nonumber \\&\times \{[(r^2-1)(\phi _V^a(x_3)r_vx_3-\phi _V^T(x_3))\nonumber \\&+r_v\phi _V^v(2+(1-r^2)x_3)]\nonumber \\&\times \alpha _s(t_a)S_{ab}(t_a)h(\alpha _e,\beta _a,b_1,b_3)S_t(x_1)\nonumber \\&+r_v(1-r^2)(\phi _V^a(x_3)+\phi _V^v(x_3))\alpha _s(t_b)S_{ab}\nonumber \\&\times (t_b)h(\alpha _e,\beta _b,b_1,b_3)S_t(x_3) \}, \end{aligned}$$

(A2)

$$\begin{aligned} \mathcal {F}^{LL}_T= & {} \mathcal {F}^{LL}_N|_{\phi _V^a\leftrightarrow \phi _V^v}, \end{aligned}$$

(A3)

$$\begin{aligned} \mathcal {F}^{LR}_{L,N,T}= & {} \mathcal {F}^{LL}_{L,N,T}, \end{aligned}$$

(A4)

$$\begin{aligned} \mathcal {M}^{LL}_L= & {} -16\sqrt{\frac{2}{3}}\pi C_f M^4\int _0^1dx_1dx_2dx_3\nonumber \\&\times \int _0^{\infty }b_1b_2db_1db_2 \phi _B(x_1,b_1)\nonumber \\&\times \{\sqrt{1-r^2}[\psi ^L(x_2,b_2)r_v(\phi _V^s(x_3)\sqrt{1-r^2}\nonumber \\&+\phi _V^t(x_3)(r^2(2x_2+x_3-2)-x_3))\nonumber \\&-\phi _V(x_3)(\psi ^L(x_2,b_2)(r^2-1)(x_2-1)\nonumber \\&+\psi ^t(x_2,b_2)r_cr]\nonumber \\&\times \alpha _s(t_c)S_{cd}(t_c)h(\alpha _e,\beta _c,b_1,b_2)\nonumber \\&+[\psi ^L(x_2,b_2)(x_2(\phi _V(x_3)(r^2+1)\nonumber \\&-2r^2r_v\phi _V^t(x_3))\nonumber \\&-(r^2-1)x_3(\phi _V(x_3)-r_v\phi _V^t(x_3))\nonumber \\&-\phi _V^s(x_3)\sqrt{1-r^2}r_vx_3)-\psi ^t(x_2,b_2)r_cr(\phi _V(x_3)\nonumber \\&-4r_v\phi _V^t(x_3))]\alpha _s(t_d)S_{cd}(t_d)h(\alpha _e,\beta _d,b_1,b_2) \},\nonumber \\ \end{aligned}$$

(A5)

$$\begin{aligned} \mathcal {M}^{LL}_N= & {} 16\sqrt{\frac{2}{3}}\pi C_f M^4 \int _0^1dx_1dx_2dx_3\nonumber \\&\times \int _0^{\infty }b_1b_2db_1db_2 \phi _B(x_1,b_1)\nonumber \\&\times \{[(r^2-1)(r_cr_v\psi ^T(x_2,b_2)\phi _V^a(x_3)\nonumber \\&+r(x_2-1)\psi ^V(x_2,b_2)\phi _V^T(x_3))\nonumber \\&+\psi ^T(x_2,b_2)\phi _V^v(x_3)r_cr_v(1+r^2)]\nonumber \\&\times \alpha _s(t_c)S_{cd}(t_c)h(\alpha _e,\beta _c,b_1,b_2)\nonumber \\&+[\phi _V^v(x_3)r_v(\psi ^T(x_2,b_2)r_c(1+r^2)\nonumber \\&-2\psi ^V(x_2,b_2)r(x_2(1+r^2)+x_3(1-r^2)))\nonumber \\&-(r^2-1)(\phi _V^T(x_3)(\psi ^V(x_2,b_2)rx_2\nonumber \\&-2\psi ^T(x_2,b_2)r_c)+r_cr_v\phi _V^a(x_3) \psi ^T(x_2,b_2)]\nonumber \\&\times \alpha _s(t_d)S_{cd}(t_d)h(\alpha _e,\beta _d,b_1,b_2)\}, \end{aligned}$$

(A6)

$$\begin{aligned} \mathcal {M}^{LL}_T= & {} \mathcal {M}^{LL}_N|_{\phi _V^a\leftrightarrow \phi _V^v}, \end{aligned}$$

(A7)

$$\begin{aligned} \mathcal {M}^{SP}_{L,N,T}= & {} -\mathcal {M}^{LL}_{L,N,T}, \end{aligned}$$

(A8)

with $r_c=m_c/M$ and $m_c$ is the charm quark mass; $C_f=4/3$ is a color factor; $f_{\psi }$ is the decay constant of the $\psi (2S)$ meson. The coefficient $(-)\frac{1}{\sqrt{2}}$ appears for $B\rightarrow \psi (2S)(\rho ^0) \omega$ decay, because only the d quark component of the $(\rho ^0)\omega$ meson is involved. We neglect terms higher than $r^2_v$ orders, since the vector light cone wave functions derived from sum rules are expanded to this order [66,67,68]. The functions h come from the Fourier transform of virtual quark and gluon propagators. They are defined by

$$\begin{aligned}&h(\alpha ,\beta ,b_1,b_2)=h_1(\alpha ,b_1)\times h_2(\beta ,b_1,b_2),\nonumber \\&h_1(\alpha ,b_1)=\left\{ \begin{array}{ll} K_0(\sqrt{\alpha }b_1), &{} \quad \alpha>0,\\ K_0(i\sqrt{-\alpha }b_1),&{} \quad \alpha<0, \end{array} \right. \nonumber \\&h_2(\beta ,b_1,b_2)\nonumber \\&\quad =\left\{ \begin{array}{ll} \theta (b_1-b_2)I_0(\sqrt{\beta }b_2)K_0(\sqrt{\beta }b_1)+(b_1\leftrightarrow b_2), &{} \quad \beta >0,\\ \theta (b_1-b_2)J_0(\sqrt{-\beta }b_2)K_0(i\sqrt{-\beta }b_1)+(b_1\leftrightarrow b_2),&{} \quad \beta <0, \end{array} \right. \nonumber \\ \end{aligned}$$

(A9)

where $J_0$ is the Bessel function and $K_0$, $I_0$ are modified Bessel function with $K_0(ix)=\frac{\pi }{2}(-N_0(x)+i J_0(x))$. $\alpha _e$ and $\beta _{a,b,c,d}$ are the virtuality of the internal gluon and quark, respectively. Their expressions are

$$\begin{aligned} \alpha _e= & {} x_1x_3(1-r^2)M^2, \quad \beta _a=x_3(1-r^2)M^2,\nonumber \\ \beta _b= & {} x_1(1-r^2)M^2, \nonumber \\ \beta _c= & {} [(x_1+x_2-1)(x_3+r^2(1-x_2-x_3))+r_c^2]M^2, \nonumber \\ \beta _d= & {} [(x_1-x_2)(x_3+r^2(x_2-x_3))+r_c^2]M^2. \end{aligned}$$

(A10)

The hard scale t is chosen as the maximum of the virtuality of the internal momentum transition in the hard amplitudes, including $1/b_i(i=1,2,3)$:

$$\begin{aligned} t_{a,b}= & {} \max (\sqrt{\beta _{a,b}},1/b_1,1/b_3),\nonumber \\ t_{c,d}= & {} \max (\sqrt{\alpha _e},\sqrt{\beta _{c,d}},1/b_1,1/b_2). \end{aligned}$$

(A11)

The Sudakov factors can be written as

$$\begin{aligned} S_{ab}(t)= & {} s\left( \frac{M_B}{\sqrt{2}}x_1,b_1\right) +s\left( \frac{M_B}{\sqrt{2}}x_3(1-r^2),b_3\right) \nonumber \\&+s\left( \frac{M_B}{\sqrt{2}}(1-x_3)(1-r^2),b_3\right) \nonumber \\&+\frac{5}{3}\int _{1/b_1}^t\frac{\mathrm{d}\mu }{\mu }\gamma _q(\mu )+2\int _{1/b_3}^t\frac{\mathrm{d}\mu }{\mu }\gamma _q(\mu ),\nonumber \\ S_{cd}(t)= & {} s\left( \frac{M_B}{\sqrt{2}}x_1,b_1\right) \nonumber \\&+s\left( \frac{M_B}{\sqrt{2}}x_2,b_2\right) +s\left( \frac{M_B}{\sqrt{2}}(1-x_2),b_2\right) \nonumber \\&+s\left( \frac{M_B}{\sqrt{2}}x_3(1-r^2),b_1\right) \nonumber \\&+s\left( \frac{M_B}{\sqrt{2}}(1-x_3)(1-r^2),b_1\right) \nonumber \\&+\frac{11}{3}\int _{1/b_1}^t\frac{\mathrm{d}\mu }{\mu }\gamma _q(\mu )+2\int _{1/b_2}^t\frac{\mathrm{d}\mu }{\mu }\gamma _q(\mu ), \end{aligned}$$

(A12)

where the function s(Q, b) is given in [69]. $\gamma _q=-\alpha _s/\pi$ is the anomalous dimension of the quark. The threshold resummation factor $S_t(x)$ is adopted from [70],

$$\begin{aligned} S_t(x)=\frac{2^{1+2c}\Gamma (3/2+c)}{\sqrt{\pi }\Gamma (1+c)}[x(1-x)]^c, \end{aligned}$$

(A13)

with a running parameter $c(Q^2)=0.04Q^2-0.51Q+1.87$ [71] and $Q^2=M^2(1-r^2)$ [72].

Table 6 Input values of the decay constants and the Gegenbauer moments [75] of the light vector mesons

The wave functions

In the pQCD approach, the necessary inputs contain the light-cone distribution amplitudes (LCDAs), which are constructed by the nonlocal matrix elements. The $B_{u,d,s}$ meson light-cone matrix element are decomposed into the following two Lorentz structures [54,55,56]:

$$\begin{aligned}&\int \mathrm{d}^4 z e^{ik_1 \cdot z}\langle 0|q_{\alpha }(z)\bar{b}(0)_{\beta }|B_q(P_1)\rangle \nonumber \\&\quad =\frac{i}{\sqrt{2N_c}} \left\{ ({/}{P_1}+M)\gamma _5\left[ \Phi _{B_q}(k_1)-\frac{{/}{n}-{/}{v}}{\sqrt{2}} \bar{\Phi }_{B_q}(k_1)\right] \right\} _{\alpha \beta },\nonumber \\ \end{aligned}$$

(B1)

with the color factor $N_c$. As usual the former Lorentz structure in above equation is the dominant contribution in the numerical calculations, while the latter Lorentz structure is negligible [73]. In impact coordinate space the B meson wave function can be expressed by [70, 74]

$$\begin{aligned} \Phi _{B}(x,b)=\frac{i}{\sqrt{2N_c}}({/}{P_1}+M)\gamma _5\phi _{B}(x,b), \end{aligned}$$

(B2)

where b is the conjugate variable of the transverse momentum of the valence quark of the meson. The distribution amplitude $\phi _B(x,b)$ as being used in Refs. [58, 70] is adopted here,

$$\begin{aligned} \phi _{B}(x,b)=N x^2(1-x)^2\exp \left[ -\frac{x^2M^2}{2\omega ^2_b}-\frac{\omega ^2_bb^2}{2}\right] , \end{aligned}$$

(B3)

with the shape parameter $\omega _b$ and the normalization constant N being related to the decay constant $f_B$ by the normalization

$$\begin{aligned} \int _0^1\phi _{B}(x,b=0)\mathrm{d} x=\frac{f_{B}}{2\sqrt{2N_c}}. \end{aligned}$$

(B4)

The shape parameter $\omega _b=0.40\pm 0.04$ GeV for the $B_{u,d}$ mesons and $\omega _b=0.50\pm 0.05$ GeV for the $B_s$ meson.

For the $\psi (2S)$ meson, the longitudinally and transversely polarized LCDAs up to twist-3 are defined by [49, 50]

$$\begin{aligned}&\langle \psi (2S) (P_2, \epsilon ^L_2)|\bar{c}(z)_{\alpha }c(0)_{\beta }|0\rangle \nonumber \\&\quad = \frac{1}{\sqrt{2N_c}}\int _0^1 \mathrm{d}xe^{ixP_2\cdot z} [m_{\psi (2S)}{/}{\epsilon ^L_2}_{\alpha \beta }\psi ^L(x,b)\nonumber \\&\qquad +({/}{\epsilon ^L_2}{/}{P_2})_{\alpha \beta }\psi ^t(x,b)], \nonumber \\&\langle \psi (2S) (P_2, \epsilon ^T_2)|\bar{c}(z)_{\alpha }c(0)_{\beta }|0\rangle \nonumber \\&\quad = \frac{1}{\sqrt{2N_c}}\int _0^1 \mathrm{d}xe^{ixP_2\cdot z} [m_{\psi (2S)}{/}{\epsilon ^T_2}_{\alpha \beta }\psi ^V(x,b)\nonumber \\&\qquad +({/}{\epsilon ^T_2}{/}{P_2})_{\alpha \beta }\psi ^T(x,b)]. \end{aligned}$$

(B5)

The asymptotic models for the twist-2 distribution amplitudes $\psi ^{L,T}$ and the twist-3 distribution amplitudes $\psi ^{V,t}$ are extracted from the correspond Schrödinger states for the harmonic-oscillator potential. Their expressions have been derived [49]:

$$\begin{aligned} \psi ^{L,T}(x,b)= & {} \frac{f_{\psi }}{2\sqrt{2N_c}}N^{L,T} x\bar{x}\mathcal {T}(x) e^{-x\bar{x}\frac{m_c}{\omega _c}[\omega ^2_cb^2+(\frac{x-\bar{x}}{2x\bar{x}})^2]},\nonumber \\ \psi ^t(x,b)= & {} \frac{f_{\psi }}{2\sqrt{2N_c}}N^t (x-\bar{x})^2\mathcal {T}(x) e^{-x\bar{x}\frac{m_c}{\omega _c}[\omega ^2_cb^2+(\frac{x-\bar{x}}{2x\bar{x}})^2]},\nonumber \\ \psi ^V(x,b)= & {} \frac{f_{\psi }}{2\sqrt{2N_c}}N^V [1\nonumber \\&+(x-\bar{x})^2]\mathcal {T}(x) e^{-x\bar{x}\frac{m_c}{\omega _c}[\omega _c^2b^2+(\frac{x-\bar{x}}{2x\bar{x}})^2]}, \end{aligned}$$

(B6)

with

$$\begin{aligned} \mathcal {T}(x)=1-4b^2m_c\omega _c x\bar{x}+\frac{m_c(x-\bar{x})^2}{\omega _c x\bar{x}}, \end{aligned}$$

(B7)

where the parameter $\omega _c=0.20\pm 0.02$ GeV. $N^i(i=L,T,t,V)$ are the normalization constants and we have the normalization conditions

$$\begin{aligned} \int _0^1\psi ^{i}(x,0)d x= & {} \frac{f_{\psi }}{2\sqrt{2N_c}}. \end{aligned}$$

(B8)

For a light vector meson, the light-cone wave function for longitudinal (L) and transverse (T) polarization are written as [66,67,68]

$$\begin{aligned} \Phi _V^L(x_3)= & {} \frac{1}{\sqrt{2N_c}}\left[ m_V{/}{\epsilon ^L_3}\phi _V(x_3)\right. \nonumber \\&\left. +{/}{\epsilon ^L_3}{/}{P_3}\phi _V^t(x_3)+m_V\phi _V^s(x_3)\right] ,\nonumber \\ \Phi _V^T(x_3)= & {} \frac{1}{\sqrt{2N_c}}\left[ m_V{/}{\epsilon ^T_3}\phi _V^v(x_3) +{/}{\epsilon ^T_3}{/}{P_3}\phi _V^T(x_3)\right. \nonumber \\&\left. +im_V\epsilon _{\mu \nu \rho \sigma } \gamma _5\gamma ^{\mu }\epsilon ^{T\nu }_3v^{\rho }n^{\sigma }\phi _V^a(x_3)\right] , \end{aligned}$$

(B9)

respectively, where $\epsilon _{0123}=1$ in our convention. Note that v is the moving direction of the vector particle. The twist-2 distribution amplitudes are given by

$$\begin{aligned} \phi _V(x)= & {} \frac{f_V}{\sqrt{2N_c}}3x(1-x)[1+a_{1V}^{\parallel }3t+a_{2V}^{\parallel }3(5t^2-1)/2],\nonumber \\ \phi _V^T(x)= & {} \frac{f_V^T}{\sqrt{2N_c}}3x(1-x)[1+a_{1V}^{\perp }3t+a_{2V}^{\perp }3(5t^2-1)/2],\nonumber \\ \end{aligned}$$

(B10)

and those of twist-3 are

$$\begin{aligned} \phi _V^t(x)= & {} \frac{3f_V^T}{2\sqrt{2N_c}}t^2,\quad \phi _V^s(x)=-\frac{3f_V^T}{2\sqrt{2N_c}}t,\nonumber \\ \phi _V^v(x)= & {} \frac{3f_V}{8\sqrt{2N_c}}(1+t^2),\quad \phi _V^a(x)=-\frac{3f_V}{4\sqrt{2N_c}}t, \end{aligned}$$

(B11)

with $t=2x-1$. The vector (tensor) decay constants $f_V(f_V^T)$ together with the Gegenbauer moments [75] are shown numerically in Table 6. Note that positive $a_{1}^{\parallel ,\perp }$ refer to a $\bar{K}^{*0}$ containing an s quark, while, for a $K^{*+}(K^{*0})$ with an $\bar{s}$ quark, $a_{1}^{\parallel ,\perp }$ changes sign [76].