1 Introduction

The investigation of the transport properties of strongly coupled field theories using the tool of the gauge/gravity correspondence [1] has been a prominent area of research in theoretical physics. One of the most interesting developments in this field has been the finding of the universal value \(\frac{1}{4\pi }\) for the ratio of the shear viscosity to the entropy density. The dual gravity descriptions in which the computation was carried out have been a variety of theories described by Einstein gravity [2,3,4,5,6,7,8,9,10,11], Gauss–Bonnet (GB) gravity [12,13,14], GB gravity coupled to Maxwell electrodynamics [15] and theories taking into account the presence of \(F^4 \) corrections [16]. The calculations were performed at a finite temperature for which the singularity structures of the black holes are different from those at zero temperature. These black holes with a non-zero Hawking temperature are known as non-extremal black holes. The result for the desired ratio has been shown to get both positive and negative corrections to the universal value of \(\frac{1}{4\pi }\) for non-extremal black holes.

In the case of extremal black holes for which the Hawking temperature vanishes, the ratio of the shear viscosity to the entropy density has been shown to be \(\frac{1}{4\pi }\) from investigations carried out in the background of AdS RN black holes [17], GB gravity with non-zero chemical potentials [18] and more generally in [19].

In this paper, we first compute the ratio of the shear viscosity to the entropy density (\(\eta /s\)) for non-extremal black holes in D dimensions with arbitrary forms of the matter Lagrangian for which the space-time metric takes a particular form. We then calculate this ratio for field theories in the background of GB gravity coupled to BI electrodynamics at non-zero temperature. The importance of looking at this theory is that BI electrodynamics is the only non-linear theory of electrodynamics invariant under electromagnetic duality. It is also the most important non-linear electromagnetic theory free of infinite self-energies of charged point particles that arises in Maxwell theory [20]. The motivation for carrying out this investigation is in looking for non-linear effects on the value of this ratio.

This paper is organized as follows. In Sect. 2, we provide the general set up to study the shear viscosity for non-extremal black hole which is coupled to Born–Infeld electrodynamics. In Sect. 3, we compute the shear viscosity to entropy ratio for non-extremal black holes in D dimensions. In Sect. 4, we analytically calculate the shear viscosity to entropy ratio for GB gravity coupled to BI electrodynamics. We conclude finally in Sect. 5.

2 General set up

In this section, we present the basic set up which would be needed to compute the shear viscosity in the background of non-extremal Gauss–Bonnet black hole in D dimensions. The action for Gauss–Bonnet gravity with a generic matter Lagrangian density is given by

$$\begin{aligned} S= & {} \frac{1}{16\pi G_D}\int \mathrm{d}^{D}x \sqrt{-g}\times \left( R-2\Lambda \phantom {\frac{\lambda l^2}{2}}\right. \nonumber \\&+\,\frac{\lambda l^2}{2}(R_{\mu \nu \rho \sigma }R^{\mu \nu \rho \sigma } -4R_{\mu \nu }R^{\mu \nu }+R^2)\nonumber \\&\left. +16\pi G_D {\mathcal {L}}_M\phantom {\frac{\lambda l^2}{2}}\right) \end{aligned}$$
(1)

where \(\lambda \) is the dimensionless Gauss–Bonnet parameter, l is the radius of curvature of AdS space, \({\mathcal {L}}_M\) denotes the generic matter Lagrangian density and \(\Lambda =-\frac{(D-1)(D-2)}{2 l^2}\) is the cosmological constant. Throughout this work, we shall consider the matter Lagrangian density \({\mathcal {L}}_M\) to be electromagnetic in nature, that is,

$$\begin{aligned} {\mathcal {L}}_M={\mathcal {L}}(F^2) \end{aligned}$$
(2)

where \(F^2=g^{\mu \rho }g^{\nu \sigma }F_{\mu \nu }F_{\rho \sigma }\) and \(F_{\alpha \beta }=\partial _\alpha A_\beta - \partial _\beta A_\alpha \).

The equations of motion following from the above action admit solutions for the metric of the form

$$\begin{aligned} \mathrm{d}s^2= & {} -H(r)N^2\mathrm{d}t^2+\frac{\mathrm{d}r^2}{H(r)}\nonumber \\&+\,\frac{r^2}{l^2}\left( \mathrm{d}x_{1}^2 +\mathrm{d}x_{2}^2+\cdots +\mathrm{d}x_{D-2}^2\right) . \end{aligned}$$
(3)

The constant \(N^2\) in the metric gets fixed at the boundary by the requirement that the geometry reduces to the flat Minkowski metric conformally.

In this paper, we restrict our discussions to those particular forms of \({\mathcal {L}}_{M}\) for which H(r) can be written as

$$\begin{aligned} H(r)=\frac{r^2}{l^2}G(r) \end{aligned}$$
(4)

where G(r) is regular at \(r=\infty \). Note that theories like matter-free Gauss–Bonnet gravity [13], Maxwell Gauss–Bonnet gravity [15] and the case in which we are interested, namely, Born–Infeld Gauss–Bonnet gravity [21] satisfies the above condition. We now make a change of variable to simplify the subsequent calculations. This reads

$$\begin{aligned} u=r_+^2/r^2 \end{aligned}$$
(5)

where \(r_+\) denotes the radius of the outer horizon. The metric in these new coordinates takes the form

$$\begin{aligned} \mathrm{d}s^2=\frac{1}{l^2a^2u}(-f(u)N^2\mathrm{d}t^2+\mathrm{d}{\vec {x}}^2) +\frac{l^2}{4u^2f(u)}\mathrm{d}u^2 \end{aligned}$$
(6)

where \(\mathrm{d}{\vec {x}}^2=(\mathrm{d}x_{1}^2+\mathrm{d}x_{2}^2+\cdots +\mathrm{d}x_{D-2}^2)\), \(a=1/r_+\) and \(f(u)=G(r)\). Thermodynamic quantities in the new coordinates are given by

$$\begin{aligned} T= & {} -\frac{Nr_+}{2\pi l^2}f'(1) \end{aligned}$$
(7)
$$\begin{aligned} s= & {} \frac{1}{4G_D}\left( \frac{r_+}{l}\right) ^{D-2} \end{aligned}$$
(8)

where \(\prime \) denotes the derivative with respect to u.

3 Shear viscosity to entropy ratio for non-extremal black holes

Kubo’s formalism involving retarded Green’s functions give a way to compute the shear viscosity of the conformal field theory living on the boundary of the AdS black holes. The shear viscosity is given by

$$\begin{aligned} \eta = \lim _{\omega \rightarrow 0} - \frac{\hbox {Im}[G^{R}_{x_{1}x_2, x_{1}x_2} (\omega , 0)]}{\omega }. \end{aligned}$$
(9)

The retarded Green’s function of the energy-momentum tensor of the boundary field theory dual to the bulk theory is calculated by making a small tensor perturbation of the background metric denoted by

$$\begin{aligned} \phi (t,x_{D-2},u)=h^{~x_2}_{x_{1}}(t,x_{D-2},u). \end{aligned}$$
(10)

The perturbed metric therefore takes the form

$$\begin{aligned} \mathrm{d}s^2= & {} \frac{1}{l^2a^2u}(-f(u)N^2\mathrm{d}t^2\!+\!\mathrm{d}{\vec {x}}^2 \!+\!2\phi (t,x_{D-2},u)\mathrm{d}x_{1}\mathrm{d}x_{2})\nonumber \\&+\,\frac{l^2}{4u^2f(u)}\mathrm{d}u^2. \end{aligned}$$
(11)

We now introduce the Fourier transform of \(\phi (t,x_{D-2},u)\):

$$\begin{aligned} \phi (t,x_{D-2},u)=\int \frac{\mathrm{d}^{D-1}k}{(2\pi )^{D-1}} \mathrm{e}^{-i\omega t+ik_{D-2} x_{D-2}}\phi (k,u) \end{aligned}$$
(12)

where \(k=(\omega , 0, 0, 0,\ldots , k_{D-2})\) and \(\phi (-k, u) = \phi ^{*} (k, u)\). Plugging this form into the action (1) and using Eq. (11), we compute the effective graviton action up to second order in \(\phi (k,u)\). This reads

$$\begin{aligned} S_{\mathrm{eff}}[\phi (k,u)]= & {} -\frac{r_+^{D-1}N}{16\pi G_Dl^D}\int \frac{\mathrm{d}^{D-1} k}{(2\pi )^{D-1}}\mathrm{d}u\nonumber \\&\times \,[v(u)\phi '^2(u)-v_2(u)\phi ^2(u)] \end{aligned}$$
(13)

up to terms involving total derivatives. The functions v(u) and \(v_2(u)\) read

$$\begin{aligned} v(u)= & {} u^{-\frac{D-3}{2}}f(u) \left[ 1-\frac{2\lambda }{D-3}\left( -2u^2 \left[ \frac{f(u)}{u}\right] '\right. \right. \nonumber \\&\left. \left. +(D-5)f(u)\phantom {\frac{2\lambda }{D-3}}\right) \right] ,\end{aligned}$$
(14)
$$\begin{aligned} v_2(u)= & {} v(u)\frac{\overline{\omega }^2}{u N^2f^2(u)} -\overline{k}_{D-2}^2 u^{-\frac{D-1}{2}}\nonumber \\&\times \left[ 1-\frac{2\lambda }{(D-3)(D-4)}(2u^2 [2u(u^{-1}f(u))''\right. \nonumber \\&+3(u^{-1}f(u))']-(D-5)[4u^2(u^{-1}f(u))'\nonumber \\&\left. -(D-6)f(u)])\phantom {\frac{2\lambda }{(D-3)(D-4)}}\right] , \end{aligned}$$
(15)

where \(\overline{\omega }=\frac{l^2a}{2}\omega \) and \(\overline{k}_{D-2}=\frac{l^2a}{2}k_{D-2}\).

Since the calculation of the shear viscosity involves taking the zero momentum limit, we can set \(k_{D-2}=0\). The equation of motion for \(\phi (u)\) in the zero momentum limit then reads

$$\begin{aligned} \phi ''(u)+\frac{v'(u)}{v(u)}\phi '(u)+\frac{\overline{\omega }^2}{uN^2f^2(u)}\phi (u)=0. \end{aligned}$$
(16)

We now proceed to solve this equation of motion for the case of the non-extremal black hole, for which \(T \ne 0 \), and hence \(f^{\prime }(1) \ne 0\) by assuming the solution to be of the form [15]

$$\begin{aligned} \phi (u)=(1-u)^{\nu }F(u) \end{aligned}$$
(17)

where F(u) is regular at \(u=1\). Putting this in Eq. (16) and looking at the asymptotic behavior of this equation near \(u=1\) yields the value of \(\nu \):

$$\begin{aligned} \nu =\pm \frac{i\omega }{4\pi T}. \end{aligned}$$
(18)

Since we are interested in the incoming wave, we consider only the negative root \(\nu = -\frac{i\omega }{4\pi T}\). Substituting Eq. (17) in Eq. (16) and keeping terms up to linear order in \(\nu \), we get

$$\begin{aligned}{}[v(u)F'(u)]' -\frac{2\nu }{1-u}v(u)F^{\prime }(u) -\nu \left( \frac{v(u)}{1-u}\right) ' F(u)=0.\nonumber \\ \end{aligned}$$
(19)

We now expand F(u) around \(\omega =0\) since we require only the low frequency behavior of the solution to calculate the shear viscosity

$$\begin{aligned} F(u)=F^{(0)}(u)+\nu F^{(1)}(u)+\cdots \end{aligned}$$
(20)

Equation (19) is solved recursively by substituting Eq. (20) in Eq. (19) to find \(F^{(0)}(u)\) and \(F^{(1)}(u)\). The regularity condition of F(u) [15] leads to

$$\begin{aligned} F^{(0)}(u)= & {} C =\hbox {constant} , \end{aligned}$$
(21)
$$\begin{aligned} F^{(1)\prime }(u)= & {} \frac{C}{1-u}+\frac{C f'(1)\left[ 1+\frac{4\lambda }{D-3} f'(1)\right] }{v(u)} , \end{aligned}$$
(22)

which can be integrated to yield

$$\begin{aligned} F^{(1)}(u)= & {} -C\ln (1-u)+C f'(1)\left[ 1+\frac{4\lambda }{D-3}f'(1)\right] \nonumber \\&\times \int \frac{\mathrm{d}u}{v(u)}+D. \end{aligned}$$
(23)

The constant C can be determined in terms of the value of the field \(\phi (u)\) at the boundary \(u=0\),

$$\begin{aligned} \lim _{u\rightarrow 0} \phi (u) = \phi ^{(0)}(u). \end{aligned}$$
(24)

This implies

$$\begin{aligned} \Rightarrow \,C = \phi ^{(0)}(u)[1+O(\nu )]. \end{aligned}$$
(25)

The on-shell graviton action can now computed by using the equation of motion (16) in the effective graviton action (13). This yields

$$\begin{aligned}&S_{\mathrm{on}\text {-}\mathrm{shell}}[\phi (k,u)]=- \frac{r_{+}^{D-1} N}{16\pi G_D l^D}\nonumber \\&\quad \times \int \frac{\mathrm{d}^{D-1}k}{(2\pi )^{D-1}}[v(u)\phi (u) \phi '(u)]\Bigg |_{u=0}. \end{aligned}$$
(26)

Substituting the expression for \(\phi (u)\) from Eq. (17) in Eq. (26) and using Eqs. (18), (21), and (22), the on-shell action (26) takes the form

$$\begin{aligned} S_{\mathrm{on}\text {-}\mathrm{shell}}\!=\!\int \frac{\mathrm{d}^{D-1}k}{(2\pi )^{D-1}}\phi ^{(0)}(k) {{\mathcal {G}}}_{x_{1}x_2, x_{1}x_2}(k,u)\phi ^{(0)}(-k)\Bigg |_{u=0}\nonumber \\ \end{aligned}$$
(27)

where

$$\begin{aligned} {{\mathcal {G}}}_{x_{1}x_2, x_{1}x_2}(k,u)= & {} \frac{-i\omega }{2} \frac{1}{16 \pi G_D}\left( \frac{r_+}{l}\right) ^{D-2}\nonumber \\&\times \left[ 1+\frac{4\lambda }{D-3} f'(1)\right] +O(\omega ^2). \end{aligned}$$
(28)

The retarded Green’s function can be calculated from this on-shell action from the expression [22]

$$\begin{aligned} G^R_{x_{1}x_2, x_{1}x_2}=\lim _{u\rightarrow 0}2{\mathcal {G}}_{x_{1}x_2, x_{1}x_2}(k,u). \end{aligned}$$
(29)

From this we obtain the expression for the retarded Green’s function to be

$$\begin{aligned} G^R_{x_{1}x_2, x_{1}x_2}(\omega ,0)= & {} -i\omega \frac{1}{16 \pi G_D}\left( \frac{r_+}{l}\right) ^{D-2}\nonumber \\&\times \left[ 1+\frac{4\lambda }{D-3} f'(1)\right] +O(\omega ^2). \end{aligned}$$
(30)

The shear viscosity can now be calculated using Eq. (9) and it reads

$$\begin{aligned} \eta = \frac{1}{16 \pi G_D}\left( \frac{r_+}{l}\right) ^{D-2}\left[ 1+ \frac{4\lambda }{D-3} f'(1)\right] . \end{aligned}$$
(31)

Hence the ratio of the shear viscosity to entropy is given by

$$\begin{aligned} \frac{\eta }{s}=\frac{1}{4\pi }\left[ 1+\frac{4\lambda }{D-3} f'(1)\right] . \end{aligned}$$
(32)

This is the most general form for the \(\eta /s\) ratio for non-extremal black holes in D dimensions. The above expression in \(D=5\) dimensions takes the form

$$\begin{aligned} \frac{\eta }{s}=\frac{1}{4\pi }\left[ 1+2\lambda f'(1)\right] . \end{aligned}$$
(33)

It is reassuring that our analytical result for \(\eta /s\) matches with specific cases for matter-free Gauss–Bonnet black hole [13] and Gauss–Bonnet black hole with Maxwell electrodynamics [15].

For the AdS-GB black hole in five dimensions

$$\begin{aligned} f(u)=\frac{1}{2\lambda }\left[ 1-\sqrt{1-4\lambda (1-u^2)}\right] , \end{aligned}$$
(34)

which yields

$$\begin{aligned} f'(1)=-2. \end{aligned}$$
(35)

Putting this value for \(f'(1)\) in Eq. (33) gives [14]

$$\begin{aligned} \frac{\eta }{s}=\frac{1}{4\pi }(1-4\lambda ). \end{aligned}$$
(36)

For the AdS-GB black hole in Maxwell electrodynamics

$$\begin{aligned} f(u)=\frac{1}{2\lambda }\left[ 1-\sqrt{1-4\lambda (1-u)(1+a-au^2)}\right] \end{aligned}$$
(37)

where \(a=\frac{q^2l^2}{r_+^6}\). This gives

$$\begin{aligned} f'(1)=-(2-a), \end{aligned}$$
(38)

which finally leads to [15]

$$\begin{aligned} \frac{\eta }{s}=\frac{1}{4\pi }\left[ 1-4\lambda \left( 1-\frac{a}{2}\right) \right] . \end{aligned}$$
(39)

4 Gauss–Bonnet black hole in Born–Infeld electrodynamics

In this section, we calculate the \(\eta /s\) ratio for the non-extremal Gauss–Bonnet black hole in the presence of Born–Infeld electrodynamics. The Lagrangian density for Born–Infeld electrodynamics reads

$$\begin{aligned} {\mathcal {L}}_M={\mathcal {L}}_{BI}(F^2)=4b^2\left( 1-\sqrt{1+\frac{F^2}{2b^2}}\right) \end{aligned}$$
(40)

where b is the Born–Infeld parameter. In the limit \(b\rightarrow \infty \) one recovers Maxwell electrodynamics. Here we shall first present the analysis in 5 dimensions and then generalize to D dimensions. In 5 dimensions, H(r) is given by [15]

$$\begin{aligned} H(r) = \frac{r^2}{2\lambda l^2} \times \left[ 1- \sqrt{1-4\lambda \left\{ 1-\frac{\mu l^2}{r^4} +\frac{16}{3}\pi Gb^2l^2\left( 1-\sqrt{1+\frac{q^2}{b^2r^6}} \right) +8\pi Gl^2\frac{q^2}{r^6} {}_2F_1\left[ \frac{1}{3}, \frac{1}{2},\frac{4}{3},-\frac{q^2}{b^2r^6}\right] \right\} }\right] \end{aligned}$$
(41)

where \(F_1[.,.,.,.]\) denotes the Gauss hypergeometric function, \(\mu \) is an integration constant and q is another integration constant related to the charge. Defining the new parameters

$$\begin{aligned} a_1=\frac{\mu l^2}{r_+^4},\quad a_2=\frac{16\pi Gl^2q^2}{3r_+^6},\quad c_1=\frac{16}{3}\pi Gl^2, \end{aligned}$$
(42)

the function f(u) takes the form

$$\begin{aligned} f(u)=\frac{1}{2\lambda } \left[ 1- \sqrt{1-4\lambda \left( 1-a_1u^2+c_1b^2 \left( 1-\sqrt{1+\frac{a_2u^3}{c_1b^2}}\right) +\frac{3}{2}a_2u^3{}_2F_1\left[ \frac{1}{3},\frac{1}{2}, \frac{4}{3},-\frac{a_2u^3}{c_1b^2}\right] \right) }\right] . \end{aligned}$$
(43)

Since \(f(1) = 0 \), the parameters \(a_1\) and \(a_2\) are related by

$$\begin{aligned}&a_1-c_1b^2+c_1b^2\sqrt{1+\frac{a_2}{c_1b^2}}\nonumber \\&\quad -\frac{3a_2}{2}{}_2F_1\left[ \frac{1}{3},\frac{1}{2},\frac{4}{3}, -\frac{a_2}{c_1b^2}\right] =1. \end{aligned}$$
(44)

Using this relation in Eq. (43), we obtain

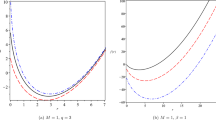
$$\begin{aligned} f'(1)= & {} -\left[ 2a_1+\frac{3a_2}{2\sqrt{1+\frac{a_2}{c_1b^2}}}\right. \nonumber \\&-\frac{9a_2}{2}{}_2F_1\left[ \frac{1}{3},\frac{1}{2},\frac{4}{3}, -\frac{a_2}{c_1b^2}\right] \nonumber \\&\left. +\frac{9a_2^2}{36c_1b^2}{}_2F_1\left[ \frac{4}{3},\frac{3}{2}, \frac{7}{3},-\frac{a_2}{c_1b^2}\right] \phantom {2a_1+\frac{3a_2}{2\sqrt{1+\frac{a_2}{c_1b^2}}}}\right] .~ \end{aligned}$$
(45)

The ratio \(\eta /s\) is now fully determined from Eqs. (33) and (45). The above equation indicates that the viscosity to entropy density ratio of a 5-dimensional AdS-GB black hole in BI electrodynamics is always less than \(\frac{1}{4\pi }\). The ratio approaches the standard Maxwell GB value [15] in the \(b\rightarrow \infty \) limit. This is evident from Figs. 3 and 4). Figure 2 shows that it approaches the free GB value [13] in the \(b\rightarrow 0\) limit. Figure 1 shows that the viscosity to entropy density ratio for AdS-GB black hole coupled to BI electrodynamics is smaller than that for an AdS-GB black hole coupled to Maxwell electrodynamics for a small value of the BI parameter; then there is a switch over and finally, for high values of the BI parameter, the ratios become identical.

We now simplify our results by looking at the leading order contribution of the Born–Infeld parameter b in the metric H(r). For this purpose we expand H(r) and take only the leading order term in 1 / b. This yields

$$\begin{aligned} H(r)= & {} \frac{r^2}{2\lambda l^2}\left( 1-\sqrt{1-4\lambda -\frac{64\pi Gl^2\lambda q^2}{3r^6}+\frac{4\mu l^2\lambda }{r^4}}\right) \nonumber \\&-\,\frac{G\pi q^4}{\left( 3r^{10}\sqrt{1-4\lambda -\frac{64\pi Gl^2\lambda q^2}{3r^6}+\frac{4\mu l^2\lambda }{r^4}}\right) b^2}. \end{aligned}$$
(46)
Fig. 1
figure 1

Viscosity to entropy ratio for small value of BI parameter

Full size image
Fig. 2
figure 2

Viscosity to entropy ratio in the limit of zero charge

Full size image
Fig. 3
figure 3

Viscosity to entropy ratio for small charge regime

Full size image
Fig. 4
figure 4

Viscosity to entropy ratio in large charge regime

Full size image

Defining a new parameter

$$\begin{aligned} c_2=\frac{3}{128\pi Gl^2}, \end{aligned}$$
(47)

the functional form of f(u) up to order \(1/b^2\) takes the form

$$\begin{aligned} f(u)= & {} \frac{1}{2\lambda }\left[ 1-\sqrt{1-4\lambda \left( 1-a_1u^2+a_2u^3\right) }\phantom {\frac{c_2\lambda a_2^2u^6}{b^2\sqrt{1-4\lambda \left( 1-a_1u^2+a_2u^3\right) }}}\right. \nonumber \\&\left. -\frac{c_2\lambda a_2^2u^6}{b^2\sqrt{1-4\lambda \left( 1-a_1u^2+a_2u^3\right) }}\right] . \end{aligned}$$
(48)

As \(f(1)=0\), the constants \(a_1\) and \(a_2\) are related by

$$\begin{aligned} \sqrt{1-4\lambda \left( 1-a_1+a_2\right) }+\frac{a_2^2c_2}{b^2\sqrt{1-4\lambda \left( 1-a_1+a_2\right) }}=1.\nonumber \\ \end{aligned}$$
(49)

Equations (48) and (49) yield

$$\begin{aligned} f'(1)= & {} \frac{3a_2-2a_1}{\sqrt{1-4\lambda \left( 1-a_1+a_2\right) }}\nonumber \\&+\,\frac{a_2^2c_2}{b^2}\left( \frac{12\lambda (1\!-\!a_1\!+\!a_2) \!-\![3\!+\!\lambda (3a_2\!-\!2a_1)]}{\left( 1-4\lambda \left( 1-a_1+a_2\right) \right) ^3}\right) .\nonumber \\ \end{aligned}$$
(50)

It is reassuring to note that the exact result (45) when expanded up to leading order in \(\frac{1}{b}\) yields Eq. (50).

We now move on to calculate the ratio \(\eta /s\) for the D-dimensional AdS-GB black hole coupled to BI electrodynamics.

The black hole metric in D dimensions reads

$$\begin{aligned} H(r)= & {} \frac{r^2}{2\lambda l^2} \left( 1\!-\!\left[ 1\!-\!4\lambda \left( 1-\frac{\mu l^2}{r^{D-1}}\!+\!\frac{64\pi Gl^2b^2}{(D-1)(D\!-\!2)}\right. \right. \right. \nonumber \\&\times \left. \left. \left. \left( 1-\sqrt{1+\frac{q^2}{b^2r^{2D-4}}}\right) \right. \right. \right. \nonumber \\&+\frac{64\pi Gl^2q^2}{(D-1)(D-3)r^{2D-4}}{}_2F_1\nonumber \\&\left. \left. \left. \times \left[ \frac{1}{2},\frac{D\!-\!3}{2D\!-\!4}, \frac{3D\!-\!7}{2D\!-\!4},-\frac{q^2}{b^2r^{2D-4}}\right] \right) \right] ^{\frac{1}{2}}\right) ~.\nonumber \\ \end{aligned}$$
(51)

Defining

$$\begin{aligned} a_{1D}=\frac{\mu l^2}{r_+^{D-1}},\quad a_{2D}=\frac{16\pi Gl^2q^2}{3r_+^{2D-4}},\quad c_1=\frac{16}{3}\pi Gl^2, \end{aligned}$$
(52)

we have

$$\begin{aligned} f(u)= & {} \frac{1}{2\lambda }\times \left( 1-\left[ 1-4\lambda \left( 1-a_{1D}u^{\frac{D-1}{2}} \right. \right. \right. \nonumber \\&+\frac{12c_1b^2}{(D-1)(D-2)}\left( 1-\sqrt{1+\frac{a_{2D}u^{D-2}}{c_1b^2}}\right) \nonumber \\&+\frac{12a_{2D}u^{D-2}}{(D-1)(D-3)}{}_2F_1\nonumber \\&\left. \left. \left. \times \left[ \frac{1}{2},\frac{D-3}{2D-4},\frac{3D-7}{2D-4}, -\frac{a_{2D}u^{D-2}}{c_1b^2}\right] \right) \right] ^{\frac{1}{2}}\right) .\nonumber \\ \end{aligned}$$
(53)

Since \(f(1)=0\), the constants \(a_{1D}\) and \(a_{2D}\) are not independent and they are related by

$$\begin{aligned} a_{1D}= & {} 1+\frac{12c_1b^2}{(D-1)(D-2)} \left( 1-\sqrt{1+\frac{a_{2D}}{c_1b^2}}\right) \nonumber \\&+\frac{12a_{2D}}{(D-1)(D-3)}{}_2F_1\nonumber \\&\times \left[ \frac{1}{2},\frac{D-3}{2D-4},\frac{3D-7}{2D-4}, -\frac{a_{2D}}{c_1b^2}\right] . \end{aligned}$$
(54)

Equations (53) and (54) finally give

$$\begin{aligned} f'(1)= & {} -\frac{(D-1)a_{1D}}{2}-\frac{6a_{2D}}{(D-1)}{}_2F_1\nonumber \\&\times \left[ \frac{1}{2},\frac{D-3}{2D-4},\frac{3D-7}{2D-4}, -\frac{a_{2D}}{c_1b^2}\right] \nonumber \\&+\frac{12a_{2D}(D-2)}{(D-3)(D-1)}{}_2F_1\nonumber \\&\times \left[ \frac{1}{2}, \frac{D-3}{2D-4},\frac{3D-7}{2D-4}, -\frac{a_{2D}}{c_1b^2}\right] . \end{aligned}$$
(55)

The viscosity to entropy density ratio for an AdS-GB black hole coupled to D-dimensional space-time is completely specified by Eqs. (32) and (55).

Figure 5 shows that the viscosity to entropy density ratio for a fixed value of the extremality parameter (that is, \(\frac{q^2}{r_+^{2D-4}}\)) increases with the dimension of the space-time, but it always stays below the extremal limit of \(1/(4\pi )\).

Fig. 5
figure 5

Figure representing viscosity to entropy density ratio for different dimensions

Full size image

5 Conclusions

In this paper, the ratio of the shear viscosity to the entropy density (\(\eta /s\)) is evaluated for non-extremal black holes in D dimensions with arbitrary forms of the matter Lagrangian for which the space-time metric takes a particular form. The computation of this ratio is then carried out for field theories in the background of GB black holes (at non-zero temperature) coupled to BI electrodynamics. We find that the ratio gets corrections due to the BI coupling parameter.

We observe that the \(\eta /s\) ratio is always less than \(1/(4\pi )\). The result reduces to the standard Maxwell GB value in the \(b\rightarrow \infty \) limit and to the GB value in the \(b\rightarrow 0\) limit. We then extend our computations to the case of the D-dimensional AdS-GB black hole coupled to BI electrodynamics. We also find that the \(\eta /s\) ratio gets corrected due to the BI parameter and also depends upon the dimension D of the black hole space-time. In particular we observe that the ratio \(\eta /s\) for a fixed value of the extremality parameter increases with increase in the dimension of the black hole space-time, but it always remains lower than the value \(1/(4\pi )\).