1 Introduction

A large lepton number asymmetry of neutrinos is an intriguing possibility with respect to its capability of resolving several non-trivial issues of cosmology (see for example [1,2,3]), but it has been known to be constrained tightly by Big Bang Nucleosynthesis (BBN) [4, 5]. Interestingly, recently [6] it has been shown that, even if BBN constrains the lepton number asymmetry of the electron-neutrino very tightly, such as \(L_e \lesssim \mathcal {O}(10^{-3})\), much larger muon- and tau-neutrino asymmetries of \(\mathcal {O}(0.1\)–1) are still allowed as long as the total lepton number asymmetry is sizable. Such large asymmetries are expected to be constrained mainly by cosmic microwave background (CMB) via the extra neutrino species \(\Delta N_\mathrm{eff}\) [7].

Fig. 1
figure 1

Evolutions of \(\mathbf {L}_\mathrm{f}\) for \(\theta =(\theta _{12},\theta _{13},\theta _{23})\) with \(\theta _{ij}\) being the mixing angles in PMNS matrix, and \((\xi _e,\xi _\mu ,\xi _\tau ) = (-1.0,1.6,0.3)\). Left/Right diagonal/off-diagonal entries

Full size image

If asymmetric neutrinos have a thermal distribution, their contribution to \(\Delta N_\mathrm{eff}\) is expressed as

$$\begin{aligned} \Delta N_\mathrm{eff} = \frac{15}{7} \sum _\alpha \left( \frac{\xi _\alpha }{\pi } \right)^2 \left[ 2 + \left( \frac{\xi _\alpha }{\pi } \right)^2 \right] \end{aligned}$$
(1)

where \(\xi _\alpha \equiv \mu _\alpha /T\) is the neutrino degeneracy parameter. Conventionally, the summation in Eq. (1) has been done with neutrino flavors (\(\nu _{e,\mu ,\tau }\) in the case of only three active neutrinos). An implicit assumption here is that the extra radiation energy coming from asymmetric neutrinos are solely from flavor eigenstates. However, due to neutrino flavor oscillations [9,10,11,12], the equilibrium density matrix is not diagonal in the flavor basis (as one naively expects, flavor eigenstates not being asymptotic states of the Hamiltonian) and their description in terms of only diagonal components (a more or less hidden assumption when assuming thermal distribution for flavors) cannot capture all the contributions to the extra radiation energy density [8]. On the other hand, well after their decoupling from a thermal bath, free-streaming neutrinos should be described as incoherent mass eigenstates only. Hence, the appropriate estimation of \(\Delta N_\mathrm{eff}\) should be done exclusively with neutrino mass eigenstates instead of flavor eigenstates in Eq. (1).

In this letter, we argue that the equilibrium lepton number asymmetry matrix reached by the BBN epoch is diagonal in the mass-eigenstate basis and related to the one in the flavor-eigenstate basis simply by the Pontecorvo–Maki–Nakagawa–Sakata (PMNS) matrix, and we show that the lepton number asymmetries of the mass eigenstates are different from those of flavors. A numerical demonstration is provided. Also, we discuss implications of a lepton number asymmetry on cosmological data such as CMB + SNIa.

2 Lepton number asymmetries of neutrino flavor vs. mass eigenstates

The lepton number asymmetries of neutrinos in flavor basis can be defined as a matrix such as

$$\begin{aligned} \mathbf {L}_\mathrm{f} = \frac{\rho -\bar{\rho }}{n_\gamma } \end{aligned}$$
(2)

where \(\rho /\bar{\rho }\) and \(n_\gamma \) are the (mode-integrated) density matrices of neutrinos/antineutrinos and the photon number density. In the very early universe, it is natural to assume that neutrinos are in interaction eigenstates (i.e., flavor eigenstates), since their kinematic phases are very small and collisional interactions to thermal bath are large enough to block flavor oscillations. Hence, if it were generated at very high energy, \(\mathbf {L}_\mathrm{f}\) is likely to be diagonal and to remain constant. While oscillations are blocked, individual flavor lepton numbers are conserved. However, due to the fact that neutrinos are not massless and mix (according to the values of the mixing parameters and mass differences measured by a variety of experiments [13]), as the temperature of the radiation dominated universe drops below around \(T \sim 15 {\mathrm {MeV}}\), flavor oscillations become active. \(\mathbf {L}_\mathrm{f}\) starts evolving at this epoch, and it settles down to an equilibrium state finally at \(T \sim 2\)–\(5\, {\mathrm {MeV}}\) before BBN starts [4, 14,15,16,17,18], depending on the neutrino mass hierarchy. Here, we consider the case of the normal mass hierarchy with zero CP-violating phase.

Fig. 2
figure 2

Comparisons of lepton number asymmetries of both mass eigenstates (\(L_i ; \ i=1,2,3\)) and flavor eigenstates (\(L_\alpha ; \ \alpha = e,\mu ,\tau \)) for \(\theta =(\theta _{12},\theta _{13},\theta _{23})\). Solid/dashed lines are the asymmetries of flavor/mass eigenstates. Left and right panels are showing two examples of \(\mathbf {L}_\mathrm{m}\) leading to \(L_e \approx 0\) satisfying BBN constraint. Left \(\mathbf {L}_\mathrm{m} = \mathrm{diag}(L_1,L_2,L_3)=(-t_{12}^2 L_0, L_0, 0)\). Right \(\mathbf {L}_\mathrm{m} = \mathrm{diag}(-(t_{12}^2+t_{13}^2/c_{12}^2) L_0, L_0, L_0)\)

Full size image

Once it reaches its final equilibrium value, \(\mathbf {L}_\mathrm{f}\) becomes time-independent. The shape of \(\mathbf {L}_\mathrm{f}\) at the final equilibrium is determined by various effects including vacuum oscillations, MSW-like effects coming from charged lepton backgrounds, neutrino self-interactions, and collisional damping. So, it is difficult to predict analytically, and in practice it is only accessible via numerical methods. However, all these effects except vacuum oscillations are active in particular windows in temperature and eventually disappear. Hence, the final shape of \(\mathbf {L}_\mathrm{f}\) should be determined by vacuum oscillation parameters only. Note that the flavor states mixed by vacuum oscillation parameters are nothing but mass eigenstates in the flavor basis. Therefore, the statistical equilibrium state of \(\mathbf {L}_\mathrm{f}\) should be that of mass eigenstates expressed in the flavor basis.

Since in vacuum the mass and flavor eigenstates are related to each other by the PMNS matrix, \(U_\mathrm{PMNS}\) [19,20,21], our argument implies that, for a diagonalization matrix D, the matrix \(\mathbf {L}_\mathrm{m}\) of asymmetries in the mass basis is given by

$$\begin{aligned} \mathbf {L}_\mathrm{m} = D^{-1} \mathbf {L}_\mathrm{f} D = U_\mathrm{PMNS}^{-1} \mathbf {L}_\mathrm{f} U_\mathrm{PMNS}, \end{aligned}$$
(3)

implying

$$\begin{aligned} D=U_\mathrm{PMNS}. \end{aligned}$$
(4)

On general grounds, at late times we do not expect \(\mathbf {L}_\mathrm{f}\) to be diagonal. The operator responsible for the evolution of the density matrix is not diagonal, so that a diagonal density matrix will not be the asymptotic solution of those equations unless it is proportional to the identity matrix. Hence, generically the asymmetries of the neutrino mass eigenstates differ from those of the flavor, and this fact should be taken into account when observational constraints on the lepton number asymmetries are considered.

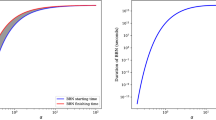
In order to verify our argument, we solved numerically the quantum kinetic equations of neutrino/antineutrino density matrices [22, 23] in a simplified way as done in Ref. [6], in which the dynamics of a typical mode mimicking the collective behavior of all modes was analyzed. An example is shown in Fig. 1, where one finds the evolutions of \(L_{\alpha \beta }\), the (real) entries of \(\mathbf {L}_\mathrm{f}\) for the neutrino’s normal mass hierarchy with [13]

$$\begin{aligned} \Delta m_{21}^2= & {} 7.53 \times 10^{-5} \mathrm{eV}^2 ,\end{aligned}$$
(5)
$$\begin{aligned} \Delta m_{31}^2\simeq & {} \Delta m_{32}^2 = 2.67 \times 10^{-3} \mathrm{eV}^2, \end{aligned}$$
(6)

and the mixing angle \(\theta _{ij}\) shown in the figure [13, 24]. As shown in the right panel of the figure, the off-diagonal entries of \(\mathbf {L}_\mathrm{f}\) do not disappear, making \(\mathbf {L}_\mathrm{m}\) different from \(\mathbf {L}_\mathrm{f}\). Also, we found that the numerical simulation reproduces the relation of Eq. (4) quite precisely within errors of \(\mathcal {O}(0.1) \%\) even at \(x=1\).

The differences between diagonal entries of \(\mathbf {L}_\mathrm{f}\) and \(\mathbf {L}_\mathrm{m}\) can be seen by expressing the former in terms of the latter. First, \(L_e\) is given by

$$\begin{aligned} L_e = c_{13}^2 \left( c_{12}^2 L_1 + s_{12}^2 L_2 \right) + s_{13}^2 L_3, \end{aligned}$$
(7)

where \(c_{ij}/s_{ij}/t_{ij} = \cos \theta _{ij}/ \sin \theta _{ij}/\tan \theta _{ij}\) with \(\theta _{ij}\) being the mixing angle in the PMNS matrix. Since BBN requires \(|L_e| \lesssim \mathcal {O}(10^{-3})\), we may set \(L_e=0\) for an illustration when \(|L_e| \lll |L_i|\) in Eq. (7). In this case, \(L_\mu \) and \(L_\tau \) are given by

$$\begin{aligned} L_\mu= & {} c_{23} \left[ (1-t_{12}^2) c_{23} - 2 s_{13} s_{23} t_{12} \right] L_2 \nonumber \\&+ \left[ (1-t_{13}^2) s_{23}^2 - t_{12} t_{13}^2 c_{23} (2 s_{13} s_{23} + t_{12} c_{23}) \right] L_3, \end{aligned}$$
(8)
$$\begin{aligned} L_\tau= & {} s_{23} \left[ (1-t_{12}^2) s_{23} + 2 s_{13} c_{23} t_{12} \right] L_2 \nonumber \\&+ \left[ (1-t_{13}^2) c_{23}^2 + t_{12} t_{13}^2 s_{23} (2 s_{13} c_{23} - t_{12} s_{23}) \right] L_3. \nonumber \\ \end{aligned}$$
(9)

From Eqs. (8) and (9) with measured values of mixing angles [13], we find that \(L_\mu \sim L_\tau \) for \(|L_3| \lesssim |L_2|\), as shown in Fig. 2. One may think that it is also possible to have \(|L_{\mu ,\tau }| \ll |L_{2,3}|\) if \(L_2 \sim - L_3\). However, our numerical testing showed that generically \(\mathbf{Max}[\{ |L_{\alpha \beta }|_{\alpha \ne \beta } \}] \lesssim \mathbf{Max}[\{ |L_{\alpha \alpha }| \}]\). Hence, on general grounds one expects to have

$$\begin{aligned} \mathcal {O}(0.1) \lesssim \mathbf{Max}[\{ |L_i| \}]/\mathbf{Max}[\{ |L_{\alpha \alpha }| \}] \lesssim \mathcal {O}(1), \end{aligned}$$
(10)

showing that it is critical to know at least two of the \(L_i\) in order to constrain \(L_\mu \) and \(L_\tau \).

3 Cosmological constraints

A large lepton number asymmetry in one or more neutrino species creates an extra radiation density in the universe relative to the standard contributions of photons and CP-symmetric active neutrinos, a form of so-called “dark radiation”. Extra relativistic degrees of freedom in cosmology have attracted considerable recent attention as a way to resolve the apparent discrepancy in measurement of the Hubble parameter from CMB data and type-Ia supernovae [7, 28, 29, 34,35,36,37,38,39]. In this section, we investigate the possibility that a primordial lepton asymmetry may provide a dark radiation density which can reconcile CMB and SNIa values for the Hubble parameter.

We consider two basic cases. The first is an eight-parameter \(\Lambda \)CDM + \(\xi \) version of cosmology without contribution from primordial tensor fluctuations, with parameters:

  • Baryon density \(\Omega _\mathrm{b} h^2\).

  • Dark matter density \(\Omega _\mathrm{C} h^2\).

  • Angular scale of acoustic horizon \(\theta \).

  • Reionization optical depth \(\tau \).

  • Helium fraction \(Y_P\).

  • Power spectrum normalization \(A_s\).

  • Scalar spectral index \(n_\mathrm{S}\).

  • Lepton asymmetry \(\xi \).

In the second case, motivated by models of early-universe inflation, we include the tensor/scalar ratio r as a ninth parameter to the fit. \(H_0\) is a derived parameter. We assume a normal mass hierarchy for neutrinos, with one massive neutrino with mass \(m_\nu = 0.06\ \mathrm{eV}\). Since the BBN constraint on \(L_e\) should be satisfied, we are not free to choose \(|L_i| \gg |L_e|\) in an arbitrary way, but constrained to satisfy approximately

$$\begin{aligned} c_{12}^2 L_1 + s_{12}^2 L_2 + t_{13}^2 L_3 = \frac{L_e}{c_{13}^2} \approx 0, \end{aligned}$$
(11)

from Eq. (7). As the simplest possibility, we may set \(L_3=0\) leading to \(L_1 \approx - t_{12}^2 L_2\). Then, for thermal distributions of two light mass eigenstates,Footnote 1

$$\begin{aligned} \Delta N_\mathrm{eff}= & {} \frac{15}{7} \sum _{i=1,2} \left( \frac{\xi _i}{\pi } \right)^2 \left[ 2 + \left( \frac{\xi _i}{\pi } \right)^2 \right] \nonumber \\\approx & {} \frac{15}{7} \left( \frac{\xi _2}{\pi } \right)^2\nonumber \\&\times \left\{ (1+t_{12}^4) 2 + \left[ 1 + (4+t_{12}^4) t_{12}^4 \right] \left( \frac{\xi _2}{\pi } \right)^2 \right\} ,\nonumber \\ \end{aligned}$$
(12)

where \(\xi _i\)s are degeneracy parameters of each mass eigenstate, and \(|\xi _i| \lesssim 1\) and \(t_{12}^2 \ll 1\) were assumed. (See also Refs. [30,31,32,33] for a discussion of joint constraints on \(N_{eff}\) and \(Y_P\).)

Strictly speaking, the late-time free-streaming neutrino mass eigenstates are not in thermal distribution since they are linear combinations of thermal distributions of flavor eigenstates. Hence, the \(\xi _i\) in Eq. (12) should be understood as effective degeneracy parameters. The error in \(\Delta N_\mathrm{eff}\) depends on the initial configuration of the lepton number asymmetries in flavor basis, but it is expected to be of \(\mathcal {O}(10)\)% or smaller for \(|\xi _i| \lesssim 1\). We constrain the parameter space with: (a) Planck 2015 TT/TE/EE + lowTEB temperature and polarization data [7, 41], and the Bicep/Keck 2014 combined polarization data [42], and (b) CMB data combined with the Riess et al. supernova data [34]. The allowed contours are calculated numerically using a Markov chain Monte Carlo method with the cosmomc software package [43], using the CAMB Boltzmann code modified according to Eq. (12).Footnote 2 The curvature \(\Omega _\mathrm{k}\) is set to zero, and the dark energy equation of state is fixed at \(w = -1\). For these constraints, we run eight parallel chains with Metropolis-Hastings sampling, and use a convergence criterion of the Gelman and Ruben R parameter of \(R - 1 < 0.05\).

3.1 Case 1: \(\Lambda \)CDM + \(\xi \)

Fig. 3
figure 3

Constraints on \(H_0\) and \(\xi \) for the eight-parameter \(\Lambda \)CDM + \(\xi \) case. Filled contours show the 68% (dark red) and 95% (light red) constraints from Planck + BICEP/Keck alone. Dashed contours show the corresponding constraints with the addition of the Riess et al. supernova data. The constraint on \(H_0\) from the supernova data alone, \(H_0 = 73.24 \pm 1.74\) [34], is shown by the filled regions, with \(1\sigma \) limits in lavender, and \(2\sigma \) limits in gray

Full size image
Fig. 4
figure 4

CMB constraints on lepton number asymmetries for the nine-parameter model including tensor perturbations. Contours are 68 and 95% uncertainties from CMB-only (red-shaded regions), and CMB + supernovae (dashed lines). Left constraint as a function of \(\xi \) and \(H_0\). The filled region is the Riess et al. constraint on \(H_0\) from supernovae. Right constraint on the spectral index \(n_\mathrm{S}\) and tensor-to-scalar ratio r, plotted with the predictions of representative choices of inflationary scalar-field potential. Dotted contours for \(\Lambda \)CDM + r, with fixed \(\xi = 0\). This can be compared to Fig. 1 of Tram et al. [39]

Full size image

Figure 3 shows constraints on \(H_0\) and \(\xi \) for the case of the eight-parameter \(\Lambda \)CDM + \(\xi \) fit. We plot constraints from Planck + BICEP/Keck only (filled contours), and Planck + BICEP/Keck + Riess et al. (dashed contours). The CMB data alone show no evidence for non-zero neutrino chemical potential, with a 95%-confidence upper bound of \(|\xi | < 0.77\) (corresponding to \(\Delta N_\mathrm{eff} \lesssim 0.30\) or \((L_1,L_2) \lesssim (-0.19,0.56)\) for \(\theta _{12}=\pi /6\)), with \(H_0 = 67.71 \pm 0.95\). For combined CMB and supernova data, there is weak evidence for a non-zero chemical potential, with \(|\xi | = 0.63 \pm 0.27\) (corresponds to \(\Delta N_\mathrm{eff} \approx 0.20^{+0.21}_{-0.14}\) or \((L_1,L_2) \approx (-0.15^{+0.07}_{-0.07},0.45^{+0.22}_{-0.20})\) for \(\theta _{12}=\pi /6\)) at 68% confidence, with \(H_0 = 69.25 \pm 1.18\). The combined CMB + supernova data, however, should be interpreted with caution: as the filled contours illustrate, the CMB data and supernova data taken separately are barely compatible, with only a small overlap in the 95% confidence regions, even when dark radiation from a neutrino asymmetry is included as a parameter. Combining two fundamentally incompatible data sets in a Bayesian analysis is likely to give a biased fit, which is reflected in the best-fit values for the two cases, with the best-fit to CMB alone having \(-\ln ({\mathcal L}) = 6794.38\), while the best-fit for the combined CMB + supernova data is measurably worse, with \(-\ln ({\mathcal L}) = 6798.21\). For the CMB data alone, including lepton asymmetry, the 95%-confidence upper bound on the Hubble parameter is \(H_0 < 69.7\). This can be compared with a 95%-confidence lower bound from Type-Ia supernovae of \(H_0 > 69.8\). Other parameters are consistent with their best-fit \(\Lambda \)CDM values. We therefore conclude, contrary to existing claims in the literature [25,26,27,28,29], that inclusion of dark radiation does not provide a consistent mechanism for reconciling the discrepancy between CMB and supernova data. Furthermore, there is no evidence for a non-zero lepton asymmetry from current data.

3.2 Case 2: \(\Lambda \)CDM + \(\xi \) + r: constraints on inflation

Figure 4 shows parameter constraints on the nine-parameter case, with tensor perturbations included, consistent with generic expectations from inflation. Constraints in the \(H_0\), \(\xi \) parameter space are extremely similar to the case of no tensors, which is reasonable considering the upper bound of \(r < 0.07\) obtained from Planck + BICEP/Keck data [44]. In this case we obtain a 95%-confidence upper bound on the lepton asymmetry of \(|\xi | < 0.77\), and \(|\xi | = 0.63 \pm 0.29\) for Planck + BICEP/Keck + SNIa at 68%-confidence. The best-fit to CMB alone is \(-\ln ({\mathcal L}) = 6793.52\), and CMB + SNIa is \(-\ln ({\mathcal L}) = 6798.14\), nearly identical to the no-tensor case. As in the no-tensor case, we conclude that here is no evidence for dark radiation from a lepton asymmetry. Constraints on inflationary potentials are shown in the right-hand panel of Fig. 4, which can be compared to Fig. 1 of Tram et al. [39]. Our constraints here are considerably tighter. The difference is that here we include the BICEP/Keck polarization data, which results in a considerably stronger constraint on the parameter space than that provided by Planck alone. Of particular note, our constraint rules out power-law inflation, with \(V\left( \phi \right) \propto e^{\phi / \mu }\), even in the presence of dark radiation, which is allowed by the constraints of Tram et al. Reference [45] reaches a similar conclusion based on constraints from Planck on \(\sigma _8\) and the reionization optical depth \(\tau _\mathrm{reio}\).

4 Conclusions

In this letter, we argued that, when lepton number asymmetries of neutrinos in flavor basis are mixed among themselves due to neutrino oscillation in the early universe before BBN, the eventual asymmetries after reaching the final equilibrium of flavor mixings are well described in the basis of mass eigenstates, which are related to flavor eigenstates by the Pontecorvo–Maki–Nakagawa–Sakata (PMNS) matrix. That is, the matrices of lepton number asymmetries in mass and flavor basis (\(\mathbf {L}_\mathrm{m}\) and \(\mathbf {L}_\mathrm{f}\), respectively) are related as

$$\begin{aligned} \mathbf {L}_\mathrm{m} = U_\mathrm{PMNS}^{-1} \mathbf {L}_\mathrm{f} U_\mathrm{PMNS}, \end{aligned}$$
(13)

where \(U_\mathrm{PMNS}\) is the PMNS matrix, and \(\mathbf {L}_\mathrm{m}\) appears to be diagonal. We demonstrated this argument by a numerical simulation, and we showed analytically that the asymmetries of mass eigenstates can be even larger than those of flavor eigenstates.

Conventionally, the constraint on the lepton number asymmetries of neutrino flavors has been associated with neutrino flavor eigenstates, counting their contributions to the extra radiation energy density \(\Delta N_\mathrm{eff}\). However, our finding showed that, when neutrino flavor eigenstates have large lepton number asymmetries at temperatures well above \(\mathcal {O}(10) {\mathrm {MeV}}\), neutrino flavor mixings cause not only re-distribution of asymmetries among flavor eigenstates but also sizable amounts of asymmetries of flavor-mixed states. Hence, an appropriate estimation of \(\Delta N_\mathrm{eff}\) should take into account the contributions from flavor-mixed states too. Such an estimation can be performed in either a flavor basis or a mass basis, but the mass basis provides a simpler way since the asymmetries are diagonal in the basis. The resulting \(\Delta N_\mathrm{eff}\) can be larger than the one estimated with flavor eigenstates only. This implies that the constraint on the lepton number asymmetries of neutrino flavor eigenstates becomes stronger than conventional expectation (or the asymmetries of neutrino flavor eigenstates are more constrained than those of mass eigenstates).

As shown in Ref. [6] and in this work, in principle \(\Delta N_\mathrm{eff}\) can be of \(\mathcal {O}(0.1\)–1) just from asymmetric neutrinos without resorting to an unknown “dark radiation”. Such a large \(\Delta N_\mathrm{eff}\) has been considered in the literature as a possible solution to the discrepancy of the measured expansion rate \(H_0\) in CMB and SNIa data. In analyses of cosmological data, typically, if \(\Delta N_\mathrm{eff}\) is from asymmetric neutrinos, the neutrino degeneracy parameters have been taken in an arbitrary way without distinguishing mass and flavor eigenstates, although implicitly the lepton number asymmetry (\(L_e\)) of electron-neutrinos must be assumed to be small to satisfy BBN constraint. We showed that this approach is inconsistent unless the lepton number asymmetries (\(L_i\)) of mass eigenstates which are relevant for CMB data for example are constrained to satisfy

$$\begin{aligned} L_e = c_{12}^2 L_1 + s_{12}^2 L_2 + t_{13}^2 L_3 \approx 0, \end{aligned}$$
(14)

for \(|L_e| \lll |L_i|\). Also, analyzing cosmological data (CMB only or CMB + SNIa), we found that CMB data alone show no evidence for non-zero neutrino lepton number asymmetries, with 95% CL upper bound of \(|\xi | \le 0.77\) at 95% CL as the degeneracy parameter of the dominant mass eigenstate. For combined CMB and SNIa data, there is weak evidence for non-zero lepton number asymmetries, with \(|\xi | = 0.63 \pm 0.27\) at 68% CL, but the fit becomes worse relative to the case of CMB data alone. So, even if large lepton number asymmetries may fit the data, it does not look preferred.

As the final remark, because of the degeneracy of \(\mathbf {L}_\mathrm{m}\) for a given \(\Delta N_\mathrm{eff}\), the bound on \(\Delta N_\mathrm{eff}\) cannot be uniquely interpreted in terms of the asymmetries of neutrino flavors (specifically \(L_\mu \) and \(L_\tau \) of muon- and tau-neutrinos), unless the impact on small scale power spectrum is sensitive enough to distinguish at least the contribution of the heaviest neutrinos.