Physical attributes of anisotropic compact stars in f(R, G) gravity

Abstract

Modified gravity is one of the potential candidates to explain the accelerated expansion of the universe. Current study highlights the materialization of anisotropic compact stars in the context of f(R, G) theory of gravity. In particular, to gain insight in the physical behavior of three stars namely, Her X1, SAX J 1808-3658 and 4U 1820-30, energy density, and radial and tangential pressures are calculated. The f(R, G) gravity model is split into a Starobinsky like f(R) model and a power law f(G) model. The main feature of the work is a 3-dimensional graphical analysis in which, anisotropic measurements, energy conditions and stability attributes of these stars are discussed. It is shown that all three stars behave as usual for positive values of the f(G) model parameter n.

1 Introduction

The spatial behavior of constituents of the universe is a complex phenomenon. Visual observation of the remote universe enlightens us about its continuous expansion, and it accentuates the need to find alternative descriptions which may be helpful to explain the phenomenon of expansion of the universe [1]. So, these alternative models are known currently as modified theories of general relativity (GR), some of which are f(R), f(G), f(R, T), f(G, T) and f(R, G) theories of gravity, where R, G, and T denotes the Ricci scalar, the Gauss–Bonnet invariant and the trace of the energy-momentum tensor, respectively. The theory of GR explains the cosmological phenomena in weak field regimes, while some modifications are required to address the strong fields in the scenario of continuous expansion of universe. The same thought occurred Buchdahl in 1970 and one of the modified theories, f(R) gravity, was proposed [2]. Hydrostatic equilibrium and the stellar structure in f(R) gravity have been investigated by considering the Lane–Emden equation [3]. Some finite time future singularities in modified gravity were described with their solution using the addition of higher derivative gravitational invariants [4]. Harko [5] presented modified f(R, T) theory in 2011 by invoking both matter and curvature terms. Furthermore, the next modification to the GR was Gauss–Bonnet gravity [6], also known as Einstein–Gauss–Bonnet gravity, which includes the Gauss–Bonnet term

$$\begin{aligned} G\equiv R^2-4R_{\mu \nu }R^{\mu \nu }+R_{\mu \nu \theta \phi }R^{\mu \nu \theta \phi }, \end{aligned}$$

(1)

where $R_{\mu \nu }$ and $R_{\mu \nu \theta \phi }$ are the Ricci tensor and the Riemann tensor, respectively. f(G) gravity [7] is the further generalization of Gauss–Bonnet gravity. It has been shown that this kind of generalization may naturally approach an operative cosmological constant, quintessence and phantom cosmic acceleration [8]. Recently, another alternative theory with the title of f(G, T) gravity has been proposed by Sharif and Ikram [9]. They studied the energy conditions for the well-known Friedmann–Robertson–Walker space time. So far some interesting work has been done in this modified theory [10,11,12,13]. Similarly, $f(\mathcal {T})$ gravity is also a modified theory, which has attracted the attention of theoretical physicists gain insight in acceleration and regular thermal expansion of the late-time universe by assuming an alternative for the cosmological constant, where $f(\mathcal {T})$ is a function of the torsion scalar [14]. An endeavor was made by combining R and G in a bivariate function f(R, G) [15,16,17,18,19,20,21,22]. The function f(R, G) provides a foundation for the double inflationary scenario [23]. It has been shown that f(R, G) theory is consistent with the observational data [24, 25]. Besides its stability, this theory is perfectly suitable to explain the accelerating waves of the celestial bodies as well as the phantom divide line crossing and the transition from acceleration to deceleration phases. An important feature of f(R, G) gravity is that it reduces the risk of ghost contributions and the gravitational action is regularized because of the term G [26, 27]. Thus, modified theories of gravity seem interesting in exploring the universe in different cosmological contexts [28].

The study of compact stars has always been a strong topic of research [29,30,31,32,33,34,35,36,37,38,39,40]. Different properties like mass, radius and moment of inertia of neutron stars are studied and a comparison has been developed with GR and alternative theories of gravity [41]. Some investigations of the structure of slowly rotating neutron stars in $R^2$ gravity have been done using two different hadronic parameters and a strange matter equation of state (EOS) parameter [42]. The mass ratio for compact objects in the presence of a cosmological constant has been derived [43]. In this article, we are interested in the compact stars and in examining their physical behavior using standard models of a spherically symmetric space time by finding exact solution of the field equations. We study the stability of the anisotropic compact stars using a generalized modified Gauss–Bonnet f(R, G) gravity.

The arrangement of this paper is as follows: In the second section, we find the expressions for energy density, radial pressure and tangential pressure for an anisotropic matter source using a spherically symmetric metric in f(R, G) gravity. Section 3 comprises the analysis of the behavior of EOS parameters, anisotropy measure, the matching conditions, the energy bounds, the Tolman–Oppenheimer–Volkoff (TOV) equation and a stability analysis of three compact stars, namely Her X1, SAX J 1808-3658 and 4U 1820-30. The last section is for the conclusion and a summary of the paper.

2 Anisotropic matter configuration in f(R, G) gravity

We start with the action of modified Gauss–Bonnet gravity [44],

$$\begin{aligned} S=\frac{1}{2K}\int \mathrm{d}^4x\sqrt{-g}f(R,G)+S_M(g^{\mu \nu },\psi ). \end{aligned}$$

(2)

Varying the action (2) with respect to the metric tensor yields the following modified field equations [25]:

$$\begin{aligned} R_{\mu \nu }-\frac{1}{2}g_{\mu \nu }R= & {} \kappa T^{(\mathrm{matt})}_{\mu \nu }+\nabla _\mu \nabla _\nu f_R-g_{\mu \nu }\Box f_R\nonumber \\&+2R\nabla _\mu \nabla _\nu f_G-2g_{\mu \nu }R\Box f_G\nonumber \\&-4R^\alpha _\mu \nabla _\alpha \nabla _\nu f_G -4R^\alpha _\nu \nabla _\alpha \nabla _\mu f_G\nonumber \\&+4R_{\mu \nu }\Box f_G+4g_{\mu \nu }R^{\theta \phi }\nabla _\theta \nabla _\phi f_G\nonumber \\&+4R_{\mu \theta \phi \nu }\nabla ^\theta \nabla ^\phi f_G-\frac{1}{2}g_{\mu \nu }V\nonumber \\&+(1-f_R)G_{\mu \nu }, \end{aligned}$$

(3)

where $f_R$ and $f_G$ are partial derivatives with respect to R and G, respectively,

$$\begin{aligned} V\equiv f_RR+f_GG-f(R,G), \end{aligned}$$

(4)

and $T_{\mu \nu }^{(\mathrm{matt})}$ describes the ordinary matter. The most general spherically symmetric space time is [45]

$$\begin{aligned} \mathrm{d}s^{2}=e^{a(r)}\mathrm{d}t^{2}-e^{b(r)}\mathrm{d}r^{2}-r^{2}{\left( \mathrm{d}\theta ^{2}+\sin ^{2}\theta \mathrm{d}\phi ^{2}\right) }. \end{aligned}$$

(5)

The energy-momentum tensor in the case of an anisotropic fluid is given by

$$\begin{aligned} T_{\alpha \beta }^{m}=(\rho +p_\mathrm{t})u_\alpha u_\beta -p_\mathrm{t}g_{\alpha \beta }+(p_\mathrm{r}-p_\mathrm{t})v_\alpha v_\beta , \end{aligned}$$

(6)

where $u_\alpha =e^{a/2} \delta _\alpha ^0$, $v_\alpha =e^{b/2}\delta _\alpha ^1$ are four velocities. The radial pressure and tangential pressure are $p_\mathrm{r}$ and $p_\mathrm{t}$, respectively, and the energy density is denoted by $\rho$. Using Eqs. (5) and (6) in the field equation (3), and after some manipulations, we obtain

$$\begin{aligned} \rho= & {} -e^{-b} f''_{1R}-\frac{4e^{-2b}}{r^2}(a'r-b'r-e^b+4)f''_{2G}\nonumber \\&-e^{-b}\left( \frac{b'}{2}+ \frac{2}{r}\right) f'_{1R}+e^{-2b}\Bigg (a''a'\nonumber \\&+a''b'-a''-a'^2+a'b'+\frac{a'^3}{2}-\frac{4a'}{r}\nonumber \\&-\frac{4b'e^b}{r^2}+\frac{8a''}{r}+\frac{6a'^2}{r} -\frac{13b'}{r^2}-\frac{2b'^2}{r}\nonumber \\&-\frac{17a'}{r^2}-\frac{18e^b}{r^3}+\frac{18}{r^3}\Bigg )f'_{2G}+ \frac{e^{-b}}{r^2}\Bigg (\frac{a''r^2}{2}\nonumber \\&+\frac{a'^2r^2}{2}-\frac{a'b'r^2}{4}+a'r\Bigg )f_{1R}+\frac{e^{-2b}}{r^2}\nonumber \\&\times \left\{ (1-e^b)(a'^2+2a''-a'b')-2a'b')\right\} f_{2G}-\frac{f}{2},\nonumber \\ \end{aligned}$$

(7)

$$\begin{aligned} p_\mathrm{r}= & {} e^{-b}\bigg (\frac{a'}{2}+b'+\frac{2}{r}\bigg )f'_{1R}+e^{-2b}\left\{ \Bigg (2a''b'\right. \nonumber \\&\left. +a'^2b'-a'b'^2+ \frac{4a'b'}{r}+\frac{8a'}{r^2}-\frac{4b'^2}{r}\right. \nonumber \\&\left. -\frac{4a'e^b}{r^2}-\frac{4b'e^b}{r^2} -\frac{8e^b}{r^3}+\frac{2a'}{r^2}+\frac{4b'}{r^2}+\frac{8}{r^3}\Bigg )\right. \nonumber \\&\left. -r\Bigg (2a''b'+a'^2b'-a'b'^2- \frac{4b'^2}{r}\Bigg )\right\} f'_{2G}\nonumber \\&-\frac{e^{-b}}{r^2}\Bigg (\frac{a''r^2}{2}+\frac{a'^2r^2}{4}- \frac{a'b'r^2}{4}-b'r\Bigg )f_{1R}\nonumber \\&-\frac{e^{-2b}}{r^2}\left\{ (1-e^b)(a'^2+2a''-a'b')-2a'b'\right\} f_{2G}\nonumber \\&+\frac{f}{2}, \end{aligned}$$

(8)

$$\begin{aligned} p_\mathrm{t}= & {} e^{-b} f''_{1R}+e^{-2b}\Bigg (2a''+a'^2-a'b'\nonumber \\&+\frac{2a'}{r}-\frac{2b'}{r}\Bigg )f''_{2G}+e^{-b}\bigg (\frac{a'}{2}+ \frac{b'}{2}+\frac{1}{r}\bigg )f'_{1R}\nonumber \\&-\frac{1}{2r^3}\left\{ e^{-b}\Bigg (2b'^2r^2+4b'r-4a'^2r^2-16a'r\right. \nonumber \\&\left. -24-2a'a''r^3+a'^2b'r^3-a'^3r^3\Bigg )+32-8e^b\right\} \nonumber \\&f'_{2G}-\frac{e^{-b}}{r^2}\Bigg (\frac{a'r}{2}-\frac{b'r}{2}-e^b+1\Bigg )f_{1R}\nonumber \\&-\frac{e^{-2b}}{r^2}\left\{ (1-e^b)(a'^2{+}2a''-a'b'){-}2a'b'\right\} f_{2G}+\frac{f}{2}.\nonumber \\ \end{aligned}$$

(9)

The set of three equations (7)–(9) involve five unknown functions $\rho , p_\mathrm{r}, p_\mathrm{t}, a, b$. Moreover, the equations are too complicated and highly non-linear due to the involved bivariate function f(R, G). So following Krori and Barua [45], we choose $a(r)=Br^{2}+C$, $b(r)=Ar^{2}$, A, B, and C are constants. These constants will be determined by using some physical assumptions. For the present analysis, we propose $f(R,G)=f_1(R)+f_2(G)$. We further consider the Starobinsky like model $f_1(R)=R+\lambda R^2$, where $\lambda$ is an arbitrary constant, and we take $f_2(G)=G^n$, $n\ne 0$. Also $f_{1R}=\frac{\mathrm{d}f_1}{\mathrm{d}R}$, $f_{2G}=\frac{\mathrm{d}f_2}{\mathrm{d}G}$ and a prime denotes the derivatives with respect to the radial coordinate. Using these assumptions, Eqs. (7)–(9) take the form

$$\begin{aligned}&\rho =\frac{1}{2r^4}\bigg [-8^nr^4\nonumber \\&\quad \times \,\bigg (-\frac{Be^{-2Ar^2}(-1+3Ar^2-Br^2+e^{Ar^2}(1-Ar^2+Br^2))}{r^2}\bigg )^n\nonumber \\&\quad +8^nr^4\nonumber \\&\quad \times \,\bigg (-\frac{Be^{-2Ar^2}(-1+3Ar^2-Br^2+e^{Ar^2}(1-Ar^2+Br^2))}{r^2}\bigg )^n\nonumber \\&\quad +\frac{8^n(-1+n)nr^2}{\left( -1+3Ar^2-Br^2+e^{Ar^2}(1-Ar^2+Br^2)\right) ^2}\nonumber \\&\quad \times \bigg (-\frac{Be^{-2Ar^2}\left( -1+3Ar^2-Br^2+e^{Ar^2}(1-Ar^2+Br^2)\right) }{r^2}\bigg )^n\nonumber \\&\quad \times (-1+6A^2r^4-2A(r^2+Br^4)+e^{Ar^2}(1-A^2r^4\nonumber \\&\quad +A(r^2+Br^4)))(-e^{Ar^2}(9+4Ar^2)\nonumber \\&\quad +r^2(-4A^2r^2+B(-9-5r+14Br^2\nonumber \\&\quad -2Br^3+2B^2r^4)+A(-13+2Br^2(1+r))))\nonumber \\&\quad +\frac{2^{1+3n}(-1+n)nr^2(-4+e^{Ar^2}+2Ar^2-2Br^2)}{B(-1+3Ar^2-Br^2+e^{Ar^2}(1-Ar^2+Br^2))^3}\nonumber \\&\quad \times \bigg (-\frac{Be^{-2Ar^2}(-1+3Ar^2-Br^2+e^{Ar^2}(1-Ar^2+Br^2))}{r^2}\bigg )^n\nonumber \\&\quad \times (-1-19Ar^2+3Br^2+28A^2r^4-12ABr^4\nonumber \\&\quad +30A^3r^6-4A^2Br^6-72A^4r^8+48A^3Br^8 \nonumber \\&\quad -8A^2B^2r^8+2n(1-6A^2r^4+2A(r^2+Br^4))^2\nonumber \\&\quad +e^{2Ar^2}(-1+3Br^2-2A^4r^8+A^3r^6\nonumber \\&\quad \times (3+4Br^2)-2A^2r^4(-2+Br^2+B^2r^4)\nonumber \\&\quad -Ar^2(8+6Br^2+B^2r^4)+2n(1-A^2r^4\nonumber \\&\quad +A+(r^2+Br^4))^2+e^{Ar^2}(2-6Br^2+18A^4r^8\nonumber \\&\quad +3Ar^2(3+Br^2)^2-3A^3r^6(5+8Br^2)\nonumber \\&\quad +6A^2r^4(-7+B^2r^4)-4n(1+6A^4r^8\nonumber \\&\quad +3A(r^2+Br^4)+A^2r^4(-5+4Br^2+2B^2r^4)\nonumber \\&\quad -8A^3(r^6+Br^8))))+16e^{-2Ar^2}(-3+3e^{Ar^2}\nonumber \\&\quad -B^2r^4+2A^3r^6(2+Br^2) -A^2r^4(4+11Br^2+2B^2r^4)\nonumber \\&\quad +Ar^2(-3+4Br^2+5B^2r^4))\lambda \nonumber \\&\quad -16e^{-2Ar^2}(2+Ar^2)(-1+e^{Ar^2}\nonumber \\&\quad +B^2r^4(2+Br^2)-A(r^2+4Br^4+B^2r^6))\lambda \nonumber \\&\quad +2e^{-2Ar^2}(-1+e^{Ar^2}-3Br^2-B^2r^4\nonumber \\&\quad +Ar^2(2+Br^2)) (e^{Ar^2}(r^2-2\lambda )+2(1+3Br^2+B^2r^4\nonumber \\&\quad -Ar^2(2+Br^2))\lambda )+2Be^{-2Ar^2}r^2\nonumber \\&\quad \times (3-Ar^2+2Br^2)\big (e^{Ar^2}(r^2-4\lambda )\nonumber \\&\quad +4(1+3Br^2+B62r^4-Ar^2(2+Br^2))\lambda \big )\bigg ], \end{aligned}$$

(10)

$$\begin{aligned}&p_\mathrm{r}=\frac{1}{2}\bigg [8^n\bigg (-\frac{Be^{-2Ar^2}(-1+3Ar^2-Br^2+e^{Ar^2}(1-Ar^2+Br^2))}{r^2}\bigg )^n\nonumber \\&\quad -8^nn\bigg (-\frac{Be^{-2Ar^2}(-1+3Ar^2-Br^2+e^{Ar^2}(1-Ar^2+Br^2))}{r^2}\bigg )^n\nonumber \\&\quad -(2^{1+3n}(-1+n)n\bigg (-\frac{Be^{-2Ar^2}(-1+3Ar^2-Br^2+e^{Ar^2}(1-Ar^2+Br^2))}{r^2}\bigg )^n\nonumber \\&\quad \times (-2-5Br^2-2A^2(-1+r)r^4(2+Br^2)+2e^{Ar^2}(1+Ar^2+Br^2)\nonumber \\&\quad +2Ar^2(-1+B(-3+r)r^2+B^2(-1+r)r^4))(-1+6A^2r^4-2A(r^2+Br^4)+e^{Ar^2}\nonumber \\&\quad \times (1-A^2r^4+A(r^2+Br^4)))) \frac{1}{(Br^2(1-3Ar^2+Br^2+e^{Ar^2}(-1+Ar^2-Br^2))^2}\nonumber \\&\quad +\frac{16e^{-2Ar^2}}{r^4}\times (2+2Ar^2+Br^2)(-1+e^{Ar^2}+B^2r^4+A^2r^4(2+Br^2)\nonumber \\&\quad -A(r^2+4Br^4+B^2r^6))\lambda -\frac{2}{r^4}e^{-2Ar^2}(-1+e^{Ar^2}-3Br^2-B^2r^4+Ar^2(2+Br^2))\nonumber \\&\quad \times (e^{Ar^2}(r^2-2\lambda )+2(1+3Br^2+B^2r^4-Ar^2(2+Br^2))\lambda )+2e^{-2Ar^2}\nonumber \\&\quad \times \frac{(-B(1+Br^2)+A(2+Br^2))(e^{Ar^2}(r^2-4\lambda )+4(1+3Br^2+B^2r^4-Ar^2(2+Br^2))\lambda }{r^2}\bigg ], \end{aligned}$$

(11)

$$\begin{aligned}&p_\mathrm{t}=\frac{1}{r^6}\bigg [2^{-1+3n}r^6\bigg (-\frac{Be^{-2Ar^2}(-1+3Ar^2-Br^2+e^{Ar^2}(1-Ar^2+Br^2))}{r^2}\bigg )^n\nonumber \\&\quad -2^{-1+3n}nr^6\bigg (-\frac{Be^{-2Ar^2}(-1+3Ar^2-Br^2+e^{Ar^2}(1-Ar^2+Br^2))}{r^2}\bigg )^n\nonumber \\&\quad +\frac{8^ne^{Ar^2}(-1+n)nr^4}{B(1-3Ar^2+Br^2+e^{Ar^2}(-1+Ar^2-Br^2))^2}\bigg (-\frac{Be^{-2Ar^2}(-1+3Ar^2-Br^2+e^{Ar^2}(1-Ar^2+Br^2))}{r^2}\bigg )^n\nonumber \\&\quad -(3-4e^{Ar^2}+e^{2Ar^2}+4Br^2-A^2r^4 +3B^2r^4+B^3r^6-A(r^2+B^2r^6)) (-1+6A^2r^4-2A(r^2+Br^4)\nonumber \\&\quad +e^{Ar^2}(1-A^2r^4+A(r^2+Br^4))) +\frac{8^n(-1+n)nr^6(A+ABr^2-B(2+Br^2))}{B(-1+3Ar^2-Br^2+e^{Ar^2}(1-Ar^2+Br^2))^3}\nonumber \\&\quad \times \bigg (-\frac{Be^{-2Ar^2}(-1+3Ar^2-Br^2+e^{Ar^2}(1-Ar^2+Br^2))}{r^2}\bigg )^n\nonumber \\&\quad \times (-1-19Ar^2+3Br^2+28A^2r^4-12ABr^4 +30A^3r^6-4A^2Br^6-2AB^2r^6-72A^4r^8\nonumber \\&\quad +48A^3Br^8-8A^2B^2r^8+2n(1-6A^2r^4 +2A(r^2+Br^4))^2+e^{2Ar^2}(-1+3Br^2-2A^4r^8\nonumber \\&\quad +A^3r^6(3+4Br^2)-2A^2r^4(-2+Br^2+B^2r^4)-Ar^2(8+6Br^2+B^2r^4) +2n(1-A^2r^4+A(r^2+Br^4))^2)+e^{Ar^2}\nonumber \\&\quad \times (2-6Br^2+18A^4r^8+3Ar^2(3+Br^2)^2 -3A^3r^6(5+8Br^2)+6A^2r^4(-7+B^2r^4)\nonumber \\&\quad -4n(1+6A^4r^8+3A(r^2+Br^4) +A^2r^4(-5+4Br^2+2B^2r^4)-8A^3(r^6+Br^8))))\nonumber \\&\quad -8e^{-2Ar^2}r^2(-3+3e^{Ar^2}-B^2r^4 +2A^3r^6(2+Br^2)-A^2r^4(4+11Br^2+2B^2r^4)\nonumber \\&\quad +Ar^2(-3+4Br^2+5B^2r^4))\lambda +8e^{-2Ar^2}r^2 \times (1+Ar^2+Br^2)(-1+e^{Ar^2}+B^2r^4\nonumber \\&\quad +A^2r^4(2+Br^2)-A(r^2+4Br^4+B^2r^6))\lambda +e^{-2Ar^2}r^2(-1+e^{Ar^2}-3Br^2-B^2r^4\nonumber \\&\quad +Ar^2(2+Br^2)) (-e^{Ar^2}(r^2-2\lambda )-2(1+3Br^2+B^2r^4\nonumber \\&\quad -Ar^2(2+Br^2))\lambda )+e^{-2Ar^2}r^2 (-1+e^{Ar^2}+Ar^2-Br^2)(e^{Ar^2}(r^2-4\lambda )\nonumber \\&\quad +4(1+3Br^2+B^2r^4-Ar^2(2+Br^2))\lambda )\bigg ]. \end{aligned}$$

(12)

Fig. 1

Variation of EOS parameter $\omega _\mathrm{r}$ with radial coordinate r (km) and model parameter n

Fig. 2

Variation of EOS parameter $\omega _\mathrm{t}$ with radial coordinate r (km) and model parameter n

3 Physical analysis and graphical representation

This section presents the physical properties of the solutions regarding EOS, anisotropic behavior, energy conditions, TOV and matching conditions along with a stability analysis of three different compact stars, Her X1, SAX J 1808-3658 and 4U 1820-30. Many EOS parameters have been considered in the literature in different cosmological contexts. Staykov et al. [42] used two different hadronic parameters and a strange matter EOS parameter to study the structure of rotating neutron stars. Quadratic EOS parameters have been used to study the properties of compact stars [46, 47]. For the sake of simplicity, in this work we assume a linear EOS [48]:

$$\begin{aligned} p_\mathrm{r}={w}_\mathrm{r}\rho ,\quad p_\mathrm{t}={w}_\mathrm{t}\rho . \end{aligned}$$

(13)

It is important to note that the EOS parameters are dependent on radius rather than a constant quantity as in an ordinary matter distribution. The non-constant behavior is due to the usual matter and exotic matter contributions. Figures 1 and 2 show the variation of the EOS parameters $\omega _\mathrm{r}$ and $\omega _\mathrm{t}$, respectively. It is obvious from the figures that the effective EOS in our model is the same as in the normal matter distribution [49], i.e.

$$\begin{aligned} 0<\omega _\mathrm{r}<1,\quad 0<\omega _\mathrm{t}<1. \end{aligned}$$

(14)

Fig. 3

Behavior of energy density $\rho$ with radial coordinate r (km) and model parameter n

Fig. 4

Behavior of radial pressure $p_\mathrm{r}$ with radial coordinate r (km) and model parameter n

Fig. 5

Behavior of transverse pressure $p_\mathrm{t}$ with radial coordinate r(km) and model parameter n

Fig. 6

Behavior of $\frac{\mathrm{d}\rho }{\mathrm{d}r}$ with radial coordinate r (km) and model parameter n

Fig. 7

Behavior of $\frac{\mathrm{d}p_\mathrm{r}}{\mathrm{d}r}$ with radial coordinate r (km) and model parameter n

3.1 Anisotropy measure of the compact stars

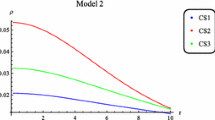
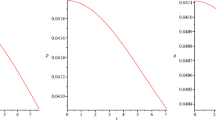
The variation of energy density $\rho$, radial pressure $p_\mathrm{r}$ and tangential pressure $p_\mathrm{t}$ can be observed in Figs. 3, 4 and 5. The behavior of $\frac{\mathrm{d}\rho }{\mathrm{d}r}$ and $\frac{\mathrm{d}p_\mathrm{r}}{\mathrm{d}r}$ in Figs. 6 and 7 reveals that $\frac{\mathrm{d}\rho }{\mathrm{d}r}<0$ and $\frac{\mathrm{d}p_\mathrm{r}}{\mathrm{d}r}<0$. It shows that with the increase in radius of the compact star, both energy density and radial pressure decrease. We analyze the variation of $\frac{\mathrm{d}\rho }{\mathrm{d}r}$ and $\frac{\mathrm{d}p_\mathrm{r}}{\mathrm{d}r}$ at the center of the compact star $r=0$ and found that

$$\begin{aligned} \frac{\mathrm{d}\rho }{\mathrm{d}r}=0,\quad \frac{\mathrm{d}p_\mathrm{r}}{\mathrm{d}r}=0,\quad \frac{\mathrm{d}^2\rho }{\mathrm{d}r^2}<0,\quad \frac{\mathrm{d}^2p_\mathrm{r}}{\mathrm{d}r^2}<0. \end{aligned}$$

(15)

Equation (15) gives the maximum value of $\rho$ and $p_\mathrm{r}$ at center $r=0$. The anisotropy measurement $\triangle =\frac{2}{r}(p_\mathrm{t}-p_\mathrm{r})$ has been shown graphically in Fig. 14. The anisotropy measurement is directed outward when $p_\mathrm{t} > p_\mathrm{r}$, which results as $\triangle >0$, and directed inward when $p_\mathrm{t} < p_\mathrm{r}$, which results as $\triangle <0$. It is depicted in Fig. 14 that for the large values of r, $\triangle >0$ for all stars implying that the anisotropic force permits the construction of great massive configurations. It is worthy to mention that anisotropy measurement vanishes at the center of the star.

3.2 The matching conditions with Schwarzchild exterior metric

The interior metric of the boundary surface remains same in the interior and exterior geometry of the compact star. It justifies the continuity of the metric components for the boundary surface of the star. Many choices for the matching conditions are possible and one can consider the vacuum outside a general spherically symmetric space time with suitable boundary conditions [50]. For the present analysis, we consider Schwarzchild solution for describing the exterior geometry. Many authors have considered the Schwarzchild solution for this purpose giving some interesting results [51,52,53]. Therefore, the exterior metric given by Schwarzchild is

$$\begin{aligned}&\mathrm{d}s^2=\left( 1-\frac{2M}{r}\right) \mathrm{d}t^2-\left( 1-\frac{2M}{r}\right) ^{-1}\mathrm{d}r^2\nonumber \\&\quad -r^2(\mathrm{d}\theta ^2+\sin ^2\mathrm{d}\varphi ^2). \end{aligned}$$

(16)

The intrinsic metric (5) for the smooth match at the boundary surface $r=R$ with Schwarzchild exterior metric produces

$$\begin{aligned} g^-_{tt}=g^+_{tt},\quad g^-_{rr}=g^+_{rr},\quad \frac{\partial g^-_{tt}}{\partial r}=\frac{\partial g^+_{tt}}{\partial r}, \end{aligned}$$

(17)

where interior solutions and exterior solutions are represented by (−) and (+). By the matching of interior and exterior metrics, we obtain

$$\begin{aligned} A= & {} -\frac{1}{R^2}\ln \left( 1-\frac{2M}{R}\right) ,\end{aligned}$$

(18)

$$\begin{aligned} B= & {} \frac{M}{R^3}\left( 1-\frac{2M}{R}\right) ^{-1},\end{aligned}$$

(19)

$$\begin{aligned} C= & {} \ln \left( 1-\frac{2M}{R}\right) -\frac{M}{R}\left( 1-\frac{2M}{R}\right) ^{-1}. \end{aligned}$$

(20)

Using the approximate values of M and R for the compact stars under observation, the constants A and B are given in the following table [49].

Models	M	R (km)	$\alpha =\frac{M}{R}$	$A\,(\mathrm{km}^{-2})$	$B\,(\mathrm{km}^{-2})$	$Z_{\mathrm{s}}$
Her XI	0.88$M_{\odot }$	7.7	0.168	0.0069062764281	0.0042673646183	0.23
SAX J	1.435$M_{\odot }$	7.07	0.299	0.018231569740	0.014880115692	0.57
4U	2.25$M_{\odot }$	10.0	0.332	0.010906441192	0.0098809523811	0.073

3.3 The energy bounds

The energy bounds have gained much importance in the discussion of some important issues in cosmology. In fact, one can investigate the validity of the second law of black hole thermodynamics and Hawking–Penrose singularity theorems using energy conditions [54]. Many interesting results have been reported in cosmology using the energy bounds [55,56,57,58,59,60]. These energy conditions are defined as

$$\begin{aligned}&\mathrm{NEC{:}}\quad \rho +p _\mathrm{r}\ge 0,\quad \rho +p _\mathrm{t}\ge 0,\\&\mathrm{WEC{:}}\quad \rho \ge 0,\quad \rho +p _\mathrm{r}\ge 0,\quad \rho +p _\mathrm{t}\ge 0,\\&\mathrm{SEC{:}}\quad \rho +p _\mathrm{r}\ge 0,\quad \rho +p _\mathrm{t}\ge 0,\quad \rho +p _\mathrm{r}+2p _\mathrm{t}\ge 0,\\&\mathrm{DEC{:}}\quad \rho>\mid p _\mathrm{r}\mid ,\quad \rho >\mid p _\mathrm{t}\mid , \end{aligned}$$

where the null energy conditions, weak energy conditions, strong energy conditions and dominant energy conditions are denoted by NEC, WEC, SEC and DEC, respectively. In Fig. 8, it is evident that all energy conditions are satisfied for Her X1. The energy conditions are also satisfied for the other two stars but the graphs are not shown here.

Fig. 8

Energy conditions for compact star Her X1 with radial coordinate r (km) and model parameter n

Fig. 9

Behavior of three different forces namely, gravitating, hydrostatic and pressure anisotropic forces in compact star candidate 4U

3.4 Implementation of Tolman–Oppenheimer–Volkoff equation

The TOV equation is expressed in the following generalized form:

$$\begin{aligned} \frac{\mathrm{d}p_\mathrm{r}}{\mathrm{d}r}+\frac{\nu \acute{} (\rho +p_\mathrm{r})}{2}+\frac{2(p_\mathrm{r}-p_\mathrm{t})}{r}=0. \end{aligned}$$

(21)

It follows from Eq. (21) that

$$\begin{aligned} F_\mathrm{g}+F_\mathrm{h}+F_\mathrm{a}=0, \end{aligned}$$

(22)

where

$$\begin{aligned} F_\mathrm{g}=-Br(\rho +p_\mathrm{r}),\quad F_\mathrm{h}=-\frac{\mathrm{d}p_\mathrm{r}}{\mathrm{d}r},\quad F_\mathrm{a}=\frac{2(p_\mathrm{t}-p_\mathrm{r})}{r}. \end{aligned}$$

(23)

Here $F_\mathrm{g}$, $F_\mathrm{h}$ and $F_\mathrm{a}$ are the gravitating force, hydrostatic force and anisotropic pressure force for compact stars. Using the values of $\rho$, $p_\mathrm{r}$ and $p_\mathrm{t}$ from Eqs. (10)–(12), for compact star 4U, Fig. 9 shows the behavior of these forces. Figure 10 depicts that the TOV equation is satisfied for the compact star 4U. The TOV equation is satisfied for the other two stars as well and graphical analysis is not presented here.

Fig. 10

Plot of TOV equation for compact star candidate 4U

3.5 Stability analysis

Now we find the radial sound speed $\upsilon _{\mathrm{sr}}$ and transverse sound speed $\upsilon _{\mathrm{st}}$ to determine the stability of our model where

$$\begin{aligned} \upsilon _{\mathrm{sr}}=\frac{\mathrm{d}p_\mathrm{r}}{\mathrm{d}\rho },\quad \upsilon _{\mathrm{st}}=\frac{\mathrm{d}p_\mathrm{t}}{\mathrm{d}\rho }. \end{aligned}$$

(24)

For a stable model the following conditions must hold:

$$\begin{aligned} 0\le \upsilon _{\mathrm{sr}}^2\le 1,\quad 0\le \upsilon _{\mathrm{st}}^2\le 1. \end{aligned}$$

(25)

The conditions (25) are exhibited graphically in Figs. 11 and 12 and it is shown that these conditions are true for the compact stars considered. In 1992, Herrera presented the important concept that for a potentially stable region $\upsilon _{\mathrm{sr}}$ is greater than $\upsilon _{\mathrm{st}}$ [61]. Therefore, the behavior of $\upsilon _{\mathrm{sr}}^2-\upsilon _{\mathrm{st}}^2$ is shown in Fig. 13. It can be observed that $\mid \upsilon _{\mathrm{sr}}^2-\upsilon _{\mathrm{st}}^2\mid <1$. So, the proposed models of compact stars are stable (Fig. 13).

Fig. 11

Behavior of $\upsilon ^2_{\mathrm{sr}}$ with radial coordinate r (km) and model parameter n in different compact stars

Fig. 12

Behavior of $\upsilon ^2_{\mathrm{st}}$ with radial coordinate r (km) and model parameter n in different compact stars

Fig. 13

Behavior of $\upsilon ^2_{\mathrm{st}}-\upsilon ^2_{\mathrm{sr}}$ with radial coordinate r (km) and model parameter n in different compact stars

Fig. 14

Variation of $\triangle$ with radial coordinate r (km) and model parameter n in different compact stars

4 Final remarks

The current study deals with the physical attributes of the compact stars in the scenario of f(R, G) gravity. In this regard, interior solutions are figured out for three compact stars namely, Her X1, SAX J 1808-3658 and 4U 1820-30, with the assumption that they have anisotropic internal structure. The analytic solutions of the interior metric in f(R, G) are smoothly matched with Schwarzchild exterior metric. This matching has provided the values of the unknown constants A, B, and C in the form of observed values of radii and masses of the model compact stars. The nature of the stars has been discussed using the values of these constants. The analysis of the physical attributes leads one to conclude to the following results as regards the anisotropic compact stars in f(R, G) gravity:

• The EOS parameters for compact stars are true as in the case of an ordinary matter distribution in f(R, G) gravity which shows that the compact stars are composed of ordinary matter. The matter density, and radial and tangential pressures get the maximum values at the center of the star and they are also decreasing functions. It confirms the fact that the matter components of compact stars are positive and remain finite in the interior of stars. Thus, all three compact stars in this present study are singularity free.

• It is also noticed that anisotropic force is directed outward for $p_\mathrm{t}> p_\mathrm{r}$, which means $\triangle >0$, while on the other hand the anisotropic force is directed inward for $p_\mathrm{t}< p_\mathrm{r}$, which shows that $\triangle <0$. The graphical description of $\triangle >0$ for three different compact stars is revealed in Fig. 14.

• The energy conditions and the TOV are analyzed for all three compact stars under consideration. The behavior of energy conditions and TOV are shown in Figs. 8 and 10 for the stars Her X1 and 4U, respectively. These are verified for the remaining two stars as well. Furthermore, the inequality $\mid \upsilon _{\mathrm{sr}}^2-\upsilon _{\mathrm{st}}^2\mid <1$ is satisfied as shown in Fig. 13 for the considered compact stars. So these models of the stars show them to be stable.

The important feature of the present study is the 3-dimensional analysis and all the results show that the compact stars behave as usual for the f(G) model parameter $0<n<200$. Thus it is conjectured that the stars behave in the same way for a polynomial form of f(G), $n\ge 200$. Also the behavior of the stars can be checked for negative values of n as well and considering some other forms of f(R) gravity model. It is worth mentioning that the findings of the current study are in conformity with the results in [62] for $n=2$ and $f_1(R)=0$.