1 Introduction

General relativity (GR) laid down the foundations of modern cosmology. The observational ingredients of \(\Lambda \)-cold dark matter model are found to be compatible with all cosmological outcomes but suffers some discrepancies like cosmic coincidence and fine-tuning [1,2,3]. The accelerated expansion of the universe has become clearly manifest after the discovery of an unexpected reduction in the detected energy fluxes coming from cosmic microwave background radiations, large-scale structures, redshift and supernovae Type Ia surveys [4,5,6]. These observations have referred to dark energy (DE) (an enigmatic force), as the reason behind this interesting and puzzling phenomenon. Various techniques have been proposed in order to modify Einstein gravity in these directions. Qadir et al. [7] discussed various aspects of modified relativistic dynamics and proposed that GR may need to be modified to resolve various cosmological issues, like quantum gravity and the dark matter problem.

The modified theories of gravity are generalized models; they came into being by modifying only the gravitational portion of the GR action (for further reviews on DE and modified gravity, see, for instance, [8,9,10,11,12,13,14,15,16,17,18,19,20,21,22]). The first theoretical and observationally viable possibility of our accelerating cosmos from f(R) gravity was proposed by Nojiri and Odintsov [23]. There has been interesting discussion of dark cosmic contents on the structure formation and the dynamics of various celestial bodies in Einstein-\(\Lambda \) [24], f(R) [25,26,27,28], f(R, T) [29,30,31,32] (T is the trace of energy-momentum tensor) and \(f(R,T,R_{\mu \nu }T^{\mu \nu })\) gravity [33,34,35,36]. Recently, Nojiri et al. [37] have studied a variety of cosmic issues, like early-time, late-time cosmic acceleration, bouncing cosmology. They emphasized that some extended gravity theories such as f(R),  f(G) (where G is the Gauss–Bonnet term) and \(f(\mathcal {T})\) (where \(\mathcal {T}\) is the torsion scalar) can be modeled to unveil various interesting cosmic scenarios.

The search for the effects of anisotropicity in the matter configurations of compact objects is the basic key leading to various captivating phenomena, like transitions of phase of different types [38], condensation of pions [39], the existence of a solid as well as a Minkowskian core [40,41,42,43,44], etc. One can write all possible exact solutions of a static isotropic relativistic collapsing cylinder in terms of scalar expressions in GR [45] as well as in f(R) gravity [46, 47]. Sussman and Jaime [48] analyzed a class of irregular spherical solutions in the presence of a specific traceless anisotropic pressure tensor for the choice of a model with \(f(R)\propto \sqrt{R}\). Shabani and Ziaie [49] used dynamical and numerical techniques to analyze the effects of a particular f(R, T) gravity model on the stability of an emergent Einstein universe. Garattini and Mandanici [50] examined some stable configurations of various anisotropic relativistic compact objects and concluded that extra curvature gravitational terms coming from rainbow’s gravity are likely to support various patterns of compact stars. Sahoo et al. [51, 52] explored various cosmological aspects in the context of anisotropic relativistic backgrounds.

Gravitational collapse (GC) is an interesting process, due to which the stellar bodies could gravitate continuously to move towards their central points. In this regard, the singularity theorem [53] states that during this implosion process of massive relativistic structures, spacetime singularities may appear in the realm of Einstein’s gravity. The investigation of the final stellar phase has been a focus of great interest for many relativistic astrophysicists and gravitational theorists. In this respect, various authors [54,55,56,57] explored the problem of GC by taking some realistic configurations of matter and geometry. In the context of f(R) gravity, various results have been found in the literature as regards collapsing stellar interiors and black holes [58,59,60,61].

Capozziello et al. [62, 63] studied the GC of non-interacting particles by evaluating dispersion expressions through a perturbation approach and found some unstable regime of the collapsing object under certain limits. Cembranos et al. [64] examined GC of non-static inhomogeneous gravitational sources and studied the large-scale structure formation for an early-time cosmos in different f(R) gravity theories. Modified gravity theories are likely to host massive celestial objects with smaller radii as compared to GR [65,66,67,68,69,70]. Guo and Joshi [71] discussed a scalar GC of spherically symmetric spacetime and inferred that a relativistic sphere could give rise to black hole configurations, if the source field is strong.

The concept of energy conditions (ECs) could be considered a viable approach for better understanding of the well-known singularity theorem. Santos et al. [72] developed viability bounds coming from ECs on a generic f(R) formalism. Their approach could be considered to constrain various possible f(R) gravity models with proper physical backgrounds. Wang et al. [73] evaluated some generic expressions for ECs in the f(R) gravity and employed them on a class of cosmological models to obtain some viability constraints.

Shiravand et al. [74] evaluated ECs for f(R) gravity and obtained some stability constraints against a Dolgov–Kawasaki instability. They found special ranges of some f(R) model parameters under which the theory would satisfy WECs. The investigation of ECs in modified theories has been carried out regarding a variety of cosmological issues like, f(R) gravity [75], \(f(R,L_m)\) gravity [76], f(R, T) gravity [77], f(R, G) gravity [78], and f(G) gravity [79, 80]. The stability of compact objects and their ECs have been analyzed in detail by various researchers [81,82,83,84].

The main goal of this paper is to investigate the role of f(R) models as well as the anisotropic pressure in the modeling of realistic compact stellar structures. We study various structural properties, like the distributions of the density and pressure anisotropicity, the Tolman–Oppenheimer–Volkoff (TOV) equation, energy conditions, stability as well as the equation of state parameter, for three different observational data of stellar structures. The paper is outlined as follows. In the next section, we briefly review f(R) gravity for anisotropic configurations of the static spherical geometry. Section 3 is devoted to a demonstration of some f(R) gravity models along with their physical viability. In Sect. 4, we check the physical viability of three well-known stellar structures. At the end, we conclude with a summary of our main findings.

2 Anisotropic relativistic spheres in f(R) gravity

The standard Einstein–Hilbert action in f(R) gravity can be modified as follows:

$$\begin{aligned} S_{f(R)}=\frac{1}{2\kappa }\int \mathrm{{d}}^4x\sqrt{-g}f(R)+S_M, \end{aligned}$$
(1)

where \(g,~\kappa ,~S_M\) stand for the determinant of the tensor, the coupling constant and matter field action. The basic motivation of this theory is to introduce a generic algebraic expression of the Ricci scalar rather than a cosmological constant in the GR action. By giving a variation in the above equation with respect to \(g_{\mu \nu }\), the field equations for f(R) gravity can be found to be

$$\begin{aligned} R_{\alpha \beta }f_R-\frac{1}{2}f(R)g_{\alpha \beta }+\left( g_{\alpha \beta }{\Box } -\nabla _{\alpha }\nabla _{\beta }\right) f_R={\kappa }T_{\alpha \beta }, \end{aligned}$$
(2)

where \(T_{\alpha \beta }\) is the standard energy-momentum tensor, while \(\nabla _{\beta }\) is an covariant derivative operator, \(\Box \equiv \nabla ^{\beta }\nabla _{\beta }\) and \(f_R\equiv \mathrm{{d}}f/\mathrm{{d}}R\). The quantity \(f_R\) comprises the corresponding second derivatives of the metric variables, which is often termed a scalaron; it propagates new scalar freedom degrees. The trace of Eq. (2) specifies the scalaron equation of motion:

$$\begin{aligned} 3\Box {f_R}+Rf_R-2f(R)={\kappa }T, \end{aligned}$$
(3)

where \(T\equiv T^\beta _{~\beta }\). It has been noticed that the above equation is a second order differential equation in \(f_R\), unlike GR, in which the trace of the Einstein field equations boils down to \(R=-\kappa T\). This points to \(f_R\) as a source of producing scalar degrees of freedom in f(R) theory. The condition \(T=0\) does not necessarily implies the vanishing (or constant value) of the Ricci scalar in the dynamics. This shows Eq. (3) to be a useful mathematical tool in discussing many hidden and interesting cosmic arenas, like the Newtonian limit, stability etc. The constraints, constant Ricci scalar as well as \(T_{\alpha \beta }=0\), boil down via Eq. (3) to

$$\begin{aligned} Rf_R-2f(R)=0, \end{aligned}$$
(4)

which is the Ricci algebraic equation after choosing any viable formulations of the f(R) model. If someone finds a constant root of the above equation, i.e., \(R=\Lambda \) (say), then Eq. (3) yields

$$\begin{aligned} R_{\alpha \beta }=\frac{g_{\alpha \beta }\Lambda }{4}, \end{aligned}$$
(5)

thereby indicating the (anti) de Sitter model as the maximally symmetric solution. Equation (2) can be manipulated:

$$\begin{aligned} G_{\alpha \beta }=\frac{\kappa }{f_R}(\overset{(D)}{T_{\alpha \beta }}+T_{\alpha \beta })\equiv {T_{\alpha \beta }^{\text {eff}}}, \end{aligned}$$
(6)

where \(G_{\alpha \beta }\) is the Einstein tensor and \(\overset{(D)}{T_{\alpha \beta }}\) is termed an effective form of the energy-momentum tensor. Its expression is given by

$$\begin{aligned} \overset{(D)}{T_{\alpha \beta }}=\frac{1}{\kappa }\left\{ \nabla _{\alpha }\nabla _{\beta }f_R-\Box f_Rg_{\alpha \beta }+(f-Rf_R)\frac{g_{\alpha \beta }}{2}\right\} . \end{aligned}$$

We consider a general form of a static spherically symmetric line element as

$$\begin{aligned} \mathrm{{d}}{s^2} = e^{a}\mathrm{{d}}{t^2} -e^{b}\mathrm{{d}}{r^2}-{r^2}( {\mathrm{{d}}{\theta ^2} + {{r^2}{\sin }^2}\theta \mathrm{{d}}{\phi ^2}}), \end{aligned}$$
(7)

where a and b are radially dependent metric coefficients. We assume that our spherical self-gravitating system is filled with locally anisotropic relativistic fluid distributions. The energy-momentum tensor of this matter is given by

$$\begin{aligned} {T_{\mu \nu }} = (\rho + p_t){U_\mu }{U_\nu } - {p_t}{g_{\mu \nu }} + ({p_r} - {p_t}){V_\mu }{V_\nu }, \end{aligned}$$
(8)

where \(p_r,~p_t\) are the radial and tangential components of pressure and \(\rho \) is the fluid energy density. The four-vectors \(U_\mu \) and \(V_\mu \), in a non-tilted coordinate frame, obey the relations \(U_\mu U^\mu =1\) and \(V_\mu V^\mu =-1\). The f(R) field equations (6) for the metric (7) and fluid (8) can be given as

$$\begin{aligned} \rho= & {} \frac{{{e^{ - b}}}}{{2{r^2}}}\left( {r^2}b'{f_R}^\prime + 2{f_R}rb' + f( - {r^2}{e^{b}}) + {f_R}{r^2}{e^{b}}R \right. \nonumber \\&\left. + \, 2{f_R}{e^{b}} - 2{r^2}{f_R}^{\prime \prime }- 4r{f_R}^\prime - 2{f_R}\right) , \end{aligned}$$
(9)
$$\begin{aligned} {p_r}= & {} - \frac{{{\mathrm{{e}}^{ - b}}}}{{2{r^2}}} \left( - 2{f_R} + 2{\mathrm{{e}}^b}{f_R} - {\mathrm{{e}}^b}f{r^2}\nonumber \right. \\&\left. + \,{\mathrm{{e}}^b}{f_R}{r^2}R- 2{f_R}ra' - 4r{f_R}^\prime - {r^2}a'{f_R}^\prime \right) , \end{aligned}$$
(10)
$$\begin{aligned} {p_t}= & {} \frac{{{e^{ - b}}}}{{4r}}\left( 2{f_R}ra'' - {f_R}ra'b' + 2ra'{f_R}^\prime + {f_R}r{{a'}^2} \nonumber \right. \\&+\, 2{f_R}a' - 2rb'{f_R}^\prime - 2{f_R}b'\nonumber \\&\left. +\, 2rf{e^b} - 2r{f_R}{e^b}R + 4r{f_R}^{\prime \prime } + 4{f_R}^\prime \right) . \end{aligned}$$
(11)

The corresponding Ricci scalar is given by

$$\begin{aligned} R = \frac{{{\mathrm{{e}}^{ - b}}}}{{2{r^2}}}\left[ 4 - 4{\mathrm{{e}}^b} + {r^2}{a'^2} - 4rb' + ra'\left( {4 - rb'} \right) + 2{r^2}{a^{\prime \prime }}\right] .\nonumber \\ \end{aligned}$$
(12)

In order to achieve some realistic results for the modeling of an anisotropic compact stellar structure, we use a specific combination of metric variables, i.e., \(a(r) =B r^2 +C\) and \(b(r)=A r^2\), as suggested by Krori and Barua [85]. Here, A,  B and C are constants and can be found by imposing some viable physical requirements. Making use of these expressions, the f(R) field equations can be recast as

$$\begin{aligned} \rho= & {} \frac{1}{{2{r^2}}}{\mathrm{{e}}^{ - {r^2}A}} \Bigg ( - 2{f_R} + 2{\mathrm{{e}}^{{r^2}A}}{f_R} - {\mathrm{{e}}^{{r^2}A}}f{r^2} + 4{f_R}{r^2}A\nonumber \\&+\,{\mathrm{{e}}^{{r^2}A}}{f_R}{r^2}R +2{f_R}{r^3}A' - 4r{f_R}^\prime \nonumber \\&+\, 2{r^3}A{f_R}^\prime + {r^4}A'{f_R}^\prime - 2{r^2}{f_R}^{\prime \prime }\Bigg ), \end{aligned}$$
(13)
$$\begin{aligned} {p_r}= & {} - \frac{1}{{2{r^2}}}{\mathrm{{e}}^{ - {r^2}A}} \Bigg ( - 2{f_R} +\, 2{\mathrm{{e}}^{{r^2}A}}{f_R} - {\mathrm{{e}}^{{r^2}A}}f{r^2} \nonumber \\&- 4{f_R}{r^2}B + {\mathrm{{e}}^{{r^2}A}}{f_R}{r^2}R - 2{f_R}{r^3}B' \nonumber \\&-\, 4r{f_R}^\prime - 2{r^3}B{f_R}^\prime - {r^4}B'{f_R}^\prime \Bigg ), \end{aligned}$$
(14)
$$\begin{aligned} {p_t}= & {} \frac{1}{{4r}}{\mathrm{{e}}^{ - {r^2}A}}\Bigg (2{\mathrm{{e}}^{{r^2}A}}fr - 4{f_R}rA+ \,8{f_R}rB - 4{f_R}{r^3}AB \nonumber \\&+\, 4{f_R}{r^3}{B^2} - 2{\mathrm{{e}}^{{r^2}A}}{f_R}rR - 2{f_R}{r^2}\times \, A'- 2{f_R}{r^4}BA' \nonumber \\&+\, 10{f_R}{r^2}B' - 2{f_R}{r^4}AB'+ 4{f_R}{r^4}BB' - {f_R}{r^5}A'B' \nonumber \\&+\, {f_R}{r^5}{{B'}^2} + 4{f_R}^\prime - 4{r^2} A{f_R}^\prime + 4{r^2}B{f_R}^\prime \nonumber \\&-\, 2{r^3}A'{f_R}^\prime + 2{r^3}B'{f_R}^\prime + 2{f_R}{r^3}{B^{\prime \prime }} + 4r{f_R}^{\prime \prime }\Bigg ). \end{aligned}$$
(15)

Now, we consider a three-dimensional hypersurface, \(\Sigma \), that differentiates our system into interior and exterior regions. The spacetime for the description of exterior geometry is given by the following vacuum solution:

$$\begin{aligned} \mathrm{{d}}{s^2}= & {} \left( {1 - \frac{{2M}}{r}} \right) \mathrm{{d}}{t^2} - {\left( {1 - \frac{{2M}}{r}} \right) ^{ - 1}}\mathrm{{d}}{r^2}\nonumber \\&-\, {r^2}\left( {\mathrm{{d}}{\theta ^2} + {\mathrm{sin}} {\theta ^2}\mathrm{{d}}{\varphi ^2}} \right) , \end{aligned}$$
(16)

where M is the gravitating mass of the black hole. The continuity of the structural variables, i.e., \(g_{ii},~i=1,2\) and derivatives \(\frac{\partial g_{tt}}{\partial r}\) over the hypersurface, i.e., \(r=R\), provide some equations. On solving these equations simultaneously, one can obtain

$$\begin{aligned} A&= \frac{{ - 1}}{{{R^2}}}\ln \left( {1 - \frac{{2M}}{r}} \right) ,\quad B = \frac{M}{{{R^3}}}{\left( {1 - \frac{{2M}}{r}} \right) ^{ - 1}}, \end{aligned}$$
(17)
$$\begin{aligned} C&= \ln \left( {1 - \frac{{2M}}{r}} \right) - \frac{M}{R}{\left( {1 - \frac{{2M}}{r}} \right) ^{ - 1}}. \end{aligned}$$
(18)

After selecting some particular values of M and R, the corresponding values of metric coefficients A and B can be found. Some possibilities of such types are mentioned in Table 1.

Table 1 The approximate values of the masses M, radii R, compactness \(\mu \), and the constants A and B for the compact stars, Her X-1, SAX J 1808.4-3658, and 4U 1820-30
Full size table

3 Physical aspects of f(R) gravity models

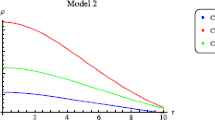
In this section, we consider some well-known viable f(R) models of gravity for the description of some physical environment of compact stellar interiors. We shall check the evolution of the energy density, pressure, the equation of state parameter, the TOV equation and energy conditions for some particular stars with the three above mentioned f(R) models. We use three configurations of stellar bodies, i.e., Her X-1, SAX J 1808.4-3658, and 4U 1820-30 of masses \(0.88M_{\odot },~1.435M_{\odot }\) and \(2.25M_{\odot }\), respectively. We use three f(R) models in Eqs. (13)–(15) to obtain \(\rho ,~p_r\) and \(p_t\). These equations would assist us to investigate various stability features of compact stellar structures (shown in Table 1). We shall also check the corresponding behavior of stellar interiors by drawing plots. In the diagrams, the stellar structures Her X-1, SAX J 1808.4-3658, and 4U 1820-30 are labeled CS1, CS2 and CS3, respectively.

The strange stars are widely known as those quark structures that are filled with strange quark matter contents. There has been interesting theoretical evidence to indicate that quark stars could come into existence from the remnant of neutron stars and violent supernovas [86]. Surveys suggested the possible existence of such structures in the early epochs of cosmic history followed by the Big Bang [87]. On the other hand, the evolution of stellar structure could end up with white dwarfs, neutron stars or black holes, depending upon their initial mass configurations. Such structures are collectively dubbed compact stars.

The maximum permitted mass–radius ratio for the case of a static background of spherical relativistic structures coupled with ideal matter distributions should be \(2M/R< \frac{8}{9}\). This result has gained a certain attraction among relativistic astrophysicists in order to address the existence of compact structures and is widely known as the Buchdahl–Bondi bound [88,89,90]. In this paper, we consider the radial and transverse sound speed in order to perform a stability analysis. However, in order to investigate the equilibrium conditions, we shall study the impact of hydrostatic, gravitational and anisotropic forces, in the possible modeling of compact stars.

Fig. 1
figure 1

Density evolution of the strange star candidates with three different f(R) models

Full size image
Fig. 2
figure 2

Radial pressure evolution of the strange stars

Full size image
Fig. 3
figure 3

Transverse pressure evolution of the strange stars

Full size image

3.1 Model 1

Firstly, we assume a model with power-law form of the Ricci scalar given by [91]

$$\begin{aligned} f(R) = R + \alpha {R^2}, \end{aligned}$$
(19)

where \(\alpha \) is a constant number. Starobinsky presented this model for highlighting the exponential growth of early-time cosmic expansion. This Ricci scalar formulation, in most publications, is introduced as a possible candidate of DE. Einstein gravity can be retrieved, in the limit \(f(R)\rightarrow R\).

3.2 Model 2

Next, we consider the Ricci scalar exponential gravity given by [92]

$$\begin{aligned} f = R + \beta R\left( {{e^{\left( { - R/\tilde{R} } \right) }} - 1} \right) , \end{aligned}$$
(20)

where \(\beta \) and \(\tilde{R}\) are constants. The models of such configurations have been studied in the field of cosmology by [93]. The consideration of this model could provide an active platform for the investigation of a late-time accelerating universe complying with matter-dominated eras.

3.3 Model 3

It would be interesting to consider f(R) corrections of the form

$$\begin{aligned} f = R + \alpha {R^2}\left( {1 + \gamma R} \right) , \end{aligned}$$
(21)

in which \(\alpha \) and \(\gamma \) are arbitrary constants. The constraint \(\gamma R\sim \mathcal {O}(1)\) specifies this model to become relatively interesting as one can compare the analysis of cubic Ricci scalar corrections with that of a quadratic Ricci term.

3.4 Energy density and pressure evolutions

Here, we analyze the domination of star matter as well as the anisotropic pressure at the center with f(R) models. The corresponding changes in the profiles of energy density, radial and transverse pressures are shown in Figs. 4, 5 and 6, respectively. We see that \(\frac{\mathrm{{d}}\rho }{{\mathrm{{d}}r}}<0\), \(\frac{\mathrm{{d}}p_r}{{\mathrm{{d}}r}}<0\) and \(\frac{\mathrm{{d}}p_t}{{\mathrm{{d}}r}}<0\) for all three models and strange stars. For \(r=0\), we obtain

$$\begin{aligned} \frac{\mathrm{{d}}\rho }{{\mathrm{{d}}r}}=0,\quad \frac{\mathrm{{d}}p_r}{{\mathrm{{d}}r}}=0, \end{aligned}$$

which is expected because these are monotonically decreasing functions. One can observe a maximum impact of the density (star core density \(\rho (0)=\rho _c\)) for small r. The plots of the density for the strange star candidates Her X-1, SAX J 1808.4-3658, and 4U 1820-30 are drawn. Figure 1 shows that, as \(r\rightarrow 0\), the profile of the density \(\rho \) keeps on increasing, thereby indicating \(\rho \) as a monotonically decreasing function of r. This suggests that \(\rho \) would decrease its effects on increasing r, which indicates high compactness at the stellar core. This leads one to propose that our chosen f(R) models may provide viable results at the outer region of the core. The other two plots, shown in Figs. 2 and 3, indicate the variations of the anisotropic radial and transverse pressure, \(p_r\) and \(p_t\).

Fig. 4
figure 4

Behavior of \(\mathrm{{d}}\rho /\mathrm{{d}}r\) with respect to r with three different f(R) models

Full size image
Fig. 5
figure 5

Behavior of \(\mathrm{{d}}p_r/\mathrm{{d}}r\) with respect to r

Full size image
Fig. 6
figure 6

Behavior of \(\mathrm{{d}}p_t/\mathrm{{d}}r\) with increasing r

Full size image

3.5 Energy conditions

For the mathematical expressions of the stress-energy tensors to represent physically acceptable matter fields, they should obey some particular constraints, widely known as ECs. These ECs have the very important property that they are coordinate-invariant (independent of symmetry). Recently, Yousaf [94] explored various analytical models of the stellar filaments with dark source terms coming from the cosmological constant and checked the validity regimes of ECs in order to make them physically viable. Bamba et al. [95] presented a general formalism for checking the viability of ECs in modified gravity. In f(R) gravity (having effective density and anisotropic pressure), the NEC and WEC are formulated as

$$\begin{aligned}&\text {NEC}\Leftrightarrow {\rho ^{\text {eff}}} + {p_i^{\text {eff}}} \ge 0,\\&\text {WEC}\Leftrightarrow {\rho ^{\text {eff}}} \ge 0 \text { and } {\rho ^{\text {eff}}} + {p_i^{\text {eff}}} \ge 0, \end{aligned}$$

while the SEC and the dominant energy condition (DEC) yield

$$\begin{aligned}&\text {SEC}\Leftrightarrow {\rho ^{\text {eff}}+ 3{p_r^{\text {eff}}}}+2{p_t^{\text {eff}}} \ge 0 \text { and } {\rho ^{\text {eff}}} + {p_i^{\text {eff}}} \ge 0,\\&\text {DEC} \Leftrightarrow {\rho ^{\text {eff}}} \ge 0 \text { and } {\rho ^{\text {eff}}} \pm {p_i^{\text {eff}}} \ge 0. \end{aligned}$$

The evolution of all these ECs for three different compact structures are well satisfied for all of our chosen f(R) models. These are graphically shown in Figs. 7, 8 and 9.

Fig. 7
figure 7

Viability of energy conditions for three different strange stars with dark source terms coming from \(f(R) = R + \alpha {R^2}\)

Full size image
Fig. 8
figure 8

Viability of energy conditions for three different strange stars with \(f(R) = R + \beta R( {{e^{( { - R/\tilde{R} })}} - 1})\) model

Full size image
Fig. 9
figure 9

Viability of energy conditions for three different strange stars in the presence of \(f(R) = R + \alpha {R^2}\left( {1 + \gamma R} \right) \) corrections

Full size image

3.6 TOV equation

The TOV equation for the spherical anisotropic stellar interior is given by

$$\begin{aligned} \frac{{\mathrm{{d}}{p_r}}}{{\mathrm{{d}}r}} + \frac{{a'(\rho + {p_r})}}{2} + \frac{{2({p_r} - {p_t})}}{r} = 0. \end{aligned}$$
(22)

The quantity \(a'\) is the radial derivative of the function appearing in the first metric coefficient of the line element (7). However, the quantity a, in general, is directly in correspondence with the scalar associated with the four-acceleration (\(a_\beta =aV_\beta \)) of the anisotropic fluid and is defined as

$$\begin{aligned} a^2=a_\beta a^\beta . \end{aligned}$$

Equation (22) can be relabeled in terms of gravitational \((F_g)\), hydrostatic \((F_h)\) and anisotropic \((F_a)\) forces as

$$\begin{aligned} F_g + F_h + F_a= 0. \end{aligned}$$
(23)

The values of these forces for our anisotropic spherical matter distribution have been found as follows:

$$\begin{aligned} F_g=-B r (\rho +p_r), \quad F_h=-\frac{{\mathrm{{d}}{p_r}}}{{\mathrm{{d}}r}},\quad F_a= \frac{{2({p_r} - {p_t})}}{r}. \end{aligned}$$

By making use of these definitions, the behavior of these forces for the onset of hydrostatic equilibrium is shown for three strange compact stars in Fig. 10. In the graphs, we have continued our analysis with different f(R) theories. In Fig. 10, the left plot is showing variations due to model 1, the middle is for model 2 and the right plot is describing the corresponding changes for the principal forces due to model 3.

Fig. 10
figure 10

The plot of gravitational force (\(F_g\)), hydrostatic force (\(F_h\)) and anisotropic force \((F_a)\) with respect to the radial coordinate r(km) and three different models

Full size image
Fig. 11
figure 11

Variations of \(v_{st}^2 - v_{sr}^2\) with respect radius, r (km)

Full size image
Fig. 12
figure 12

Variations of the radial EoS parameter, \(\omega _r\) with respect to the radial coordinate

Full size image

3.7 Stability analysis

Here, we check the stability of our stars by adopting the scheme presented by Herrera [96], which was based on the concept of cracking (or overturning). This approach states that \(v^2_{sr}\) as well as \(v^2_{st}\) must belong to the closed interval [0, 1], where \(v_{sr}\) indicates the radial sound speed, while \(v_{st}\) denotes the transverse sound speed defined by

$$\begin{aligned} \frac{{\mathrm{{d}}{p_r}}}{{\mathrm{{d}}\rho }} = v_{sr}^2,\quad \frac{{\mathrm{{d}}{p_t}}}{{\mathrm{{d}}\rho }} = v_{st}^2. \end{aligned}$$

The system will be dynamically stable, if \(v^2_{st}>v^2_{sr}\). It has been observed that the evolution of the radial and transversal sound speeds for all three types of strange stars are within the bounds of stability for some regions. It can be seen from Fig. 11 that all of our stellar structures (within the background of all f(R) models) obey the following constraint:

$$\begin{aligned} 0< |v_{st}^2-v_{sr}^2|<1. \end{aligned}$$

Therefore, we infer that all of our proposed models are stable in this theory. Such kinds of results have been proposed by Sharif and Yousaf [97,98,99] by employing a different mathematical strategy on compact stellar objects.

Fig. 13
figure 13

Variations of anisotropicity, \(\Delta \), with respect to r

Full size image

3.8 Equation of state parameter

The parameter corresponding to the equation of state (EoS) is a dimensionless term that illustrates the matter state under some specific physical grounds. This parameter has as its range the open interval (0, 1). In that case, it represents a radiation dominated cosmic era. For an anisotropic relativistic interior, the EoS can be defined as

$$\begin{aligned} p_r=\omega _r \rho , \quad p_t=\omega _t \rho . \end{aligned}$$

The behavior of \(\omega _r\) for our compact structures is shown graphically in Fig. 12. However, a similar behavior of \(\omega _t\) can be very easily observed for all of our observed compact structures. It has been observed that the maximum radius of compact objects to achieve the limit \(0<\omega _r<1\) is \(r\sim (\le 7)\), while the constraint \(0<\omega _t<1\) is valid for any large value of r. This means that \(\omega _i>1\) near its central point. The spherically symmetric self-gravitating system would be in a radiation window at the corresponding hypersurfaces. From this, we conclude that our relativistic bodies have a compact interior.

3.9 The measurement of anisotropy

Here, we measure the extent of anisotropy in the modeling of relativistic interiors. It is well known that anisotropicity in the stellar system can be measured with the help of the following formula:

$$\begin{aligned} \Delta = \frac{2}{r}({p_t} - {p_r}), \end{aligned}$$
(24)

The quantity \(\Delta \) is directly related to the difference \(p_t-p_r\). The positivity of \(\Delta \) indicates the positivity of \(p_t-p_r\). Such a background suggests an outwardly drawn behavior of anisotropic pressure. However, the resultant pressure will be directly inward once \(\Delta \) is less than zero. We have drawn the anisotropic factor for our systems and obtain \(\Delta >0\), thereby giving \(p_t > p_r\). All these results are mentioned through plots as shown in Fig. 13.

4 Summary

This paper is devoted to a discussion of some physical aspects of spherically symmetric compact stars in the background of metric f(R) theory. We have used the Krori–Barua solutions for the metric functions of a spherical star whose arbitrary constants are explored over the boundary surface by matching it with a suitable exterior. The arbitrary constants of the Krori–Barua solutions can be written in the form of the mass and the radius for any compact star. We have used the observational data of three particular star models to explore the influence of extra degrees of freedom on compact stars. For this purpose, three different physically viable f(R) models are used. By using the values of these star and gravity models, we have plotted the material variables like the energy density and anisotropic stresses against radial distance. It is found that as the radius of the star increases, the density tends to decrease, thereby indicating the maximally dense configurations of the stellar interiors. A similar behavior is found by analysis of the evolutionary phases of the tangential and radial pressures.

It is seen that r-derivatives of these material variables remain negative with increasing radius for all three models, while only the r-derivative of the tangential pressure for compact star Her X-1 has some positive value till \(r=4.8\) and then becomes negative. It is also significant to note that the first derivatives of these material variables vanish at \(r=0\) for all the compact stars. It is found that our spherically symmetric anisotropic systems obey NECs, WECs, SECs and DECs; hence the compact stars under the effects of extra degrees of freedom of fourth order gravity are physically valid. We have seen that the gravitational forces overcome the corresponding repulsive forces, thus indicating the collapsing nature of compact relativistic structures. It is well known that a stellar system would be stable against fluctuations, if it satisfies the bounds of [0, 1] for radial and tangential sound speeds. We have found that the compact star Her X-1 under the effects of the second gravity model does not remain in [0, 1], but Fig. 11 indicates that all of our stellar models are stable (i.e., \(v_{st}^2>v_{sr}^2\)). Further, we have observed that the equation of state parameter lies in the interval (0, 1) for all the compact stars. The anisotropic parameter remains positive which is necessary for a realistic stellar configurations. We can conclude our discussion as follows.

  • The anisotropic stresses and energy density are positive throughout the star configurations.

  • The r-derivatives of density and anisotropic stresses (i.e., density and pressure gradients) remain negative.

  • All types of ECs are valid.

  • The sound speeds remain within the bounds of [0, 1] (i.e., compact stars are stable).

  • The equation of state parameter lies between 0 and 1 for each star radius.

  • The measure of anisotropy remains positive at the star core.