Spectra of heavy–light mesons in a relativistic model

Abstract

The spectra and wave functions of heavy–light mesons are calculated within a relativistic quark model which is based on a heavy-quark expansion of the instantaneous Bethe–Salpeter equation by applying the Foldy–Wouthuysen transformation. The kernel we choose is the standard combination of linear scalar and Coulombic vector. The effective Hamiltonian for heavy–light quark–antiquark system is calculated up to order $1/m_Q^2$. Our results are in good agreement with available experimental data except for the anomalous $D_{s0}^*(2317)$ and $D_{s1}(2460)$ states. The newly observed heavy–light meson states can be accommodated successfully in the relativistic quark model with their assignments presented. The $D_{sJ}^*(2860)$ can be interpreted as the $|1^{3/2}D_1\rangle$ and $|1^{5/2}D_3\rangle$ states being members of the 1D family with $J^P=1^-$ and $3^-$.

1 Introduction

Great experimental progress has been achieved in studying the spectroscopy of heavy–light mesons in the last decades [1,2,3,4,5,6,7,8]. In the charm sector several new excited charmed meson states were discovered in addition to the low-lying states. For $D_J$ mesons, the excited resonances $D(2740)^0$, $D^*(2760)$ [1], $D_J(2580)^0$, $D^*(2650)$ and $D^*(3000)$ [2] were found in the $D^{(*)}\pi$ invariant mass spectrum by the BaBar and LHCb Collaborations. For $D_{sJ}$ mesons, besides the well-established 1S and 1P charmed-strange states, the excited resonances $D_{sJ}(2632)$ [3], $D_{sJ}(2860)$ [4], $D_{sJ}(2700)$ [5] and $D_{sJ}(3040)$ [6] were observed in the $D^{(*)}K$ invariant mass distribution by the two collaborations. In the b-flavored meson sector, several excited states were studied in experiment as well as the ground B and $B_s$ meson states [9]. The strangeless resonances $B_J(5840)^0$ and $B(5970)^0$ were found in the $B\pi$ invariant mass spectrum by the LHCb and CDF Collaborations, respectively [10, 11]. The stranged $B^*_{sJ}(5850)$ were observed in the $B^{(*)}K$ invariant mass distribution by the OPAL Collaboration [12].

The heavy–light meson spectroscopy plays an important role in understanding the strong interactions between quark and antiquark. Meanwhile, it provides a powerful test of the various phenomenological quark models inspired by QCD. Heavy–light mesons have been investigated extensively in relativistic quark models [13,14,15,16,17,18,19], where many relativistic potential models are constructed by modifying or relativizing nonrelativistic quark potential models and additional phenomenological parameters are employed. For the heavy–light system one needs a model that can retain the relativistic effects of the light quark. In this work we resort to the originally relativistic Bethe–Salpeter equation [20]. The Bethe–Salpeter approach was widely used in studying mesons so as to embody the relativistic dynamics [21,22,23,24,25,26]. It is rather difficult to solve the Bethe–Salpeter equation for meson states, especially when considering states with large angular momentum quantum number. In order to study the spectrum of heavy–light mesons systematically, we choose to reduce the Bethe–Salpeter equation in the first place.

In our previous work [27], we apply the instantaneous approximation and obtain an equation equivalent to the Bethe–Salpeter equation. The Hamiltonian for the heavy–light quark–antiquark system is expanded to order $1/m_Q$ by applying the Foldy–Wouthuysen transformation to the equivalent equation. We find that the leading Hamiltonian is actually not Dirac-like. The interaction we derive is essentially different from the Breit interaction [28,29,30]. In this paper we extend and improve our study of the spectrum of the heavy–light mesons D, $D_{s}$, B and $B_{s}$. The running of the coupling constant is considered. Moreover, the $1/m_Q^2$ correction is calculated. Many papers have only considered the leading $1/m_Q$ term in the heavy-quark expansion [27, 31,32,33,34]. Our calculation shows that the $1/m_Q^2$ corrections to the masses of the mesons are around 50 MeV, which is too large to be neglected. The parameters in the equations are determined by fitting the masses of the 1S and 1P meson states presented by particle data group (PDG) [9], while the states beyond 1P are calculated as a prediction. We find that in the Bethe–Salpeter formalism the linear confining parameter, i.e. the string tension, actually depends on the masses of the constituent quark and antiquark in mesons. The large discrepancy between experimental data and our previous work is decreased in this work. The newly observed heavy–light meson states can be accommodated successfully in our predicted spectra.

This paper is organized as follows. In the next section, we have a brief review of the relativistic quark model. Section 3 is for the solution of the wave equation and the perturbative corrections. In Sect. 4 we have numerical results and discussions. The last section is for a brief summary.

2 The model

According to the conventional constituent-quark model, the mesons can be seen as a composition of a quark and an antiquark. In the Bethe–Salpeter formalism, the eigenequation for quark–antiquark systems has the general form [20]

$$\begin{aligned}&(p\!\!\!/_1-m_1)\chi (p_1, p_2)(p\!\!\!/_2+m_2)\nonumber \\&\quad =\frac{1}{(2\pi )^4} \int \!\mathrm{d}^4p'_1 d^4p'_2 \overline{K}(p_1, p_2; p'_1, p'_2)\chi (p'_1, p'_2), \end{aligned}$$

(1)

where $p_1$ and $p_2$ relate to the total momentum P and the relative momentum p, as follows:

$$\begin{aligned} p_1= & {} \alpha _1 P-p,\quad \alpha _1=\frac{m_1}{m_1+m_2},\end{aligned}$$

(2)

$$\begin{aligned} p_2= & {} \alpha _2 P+p,\quad \alpha _2=\frac{m_2}{m_1+m_2}. \end{aligned}$$

(3)

Using the energy-momentum conservation, i.e. $p'_1+p'_2=p_1+p_2$, Eq. (1) can be simplified as

$$\begin{aligned}&(p\!\!\!/_1-m_1)\chi (p,P)(p\!\!\!/_2+m_2)\nonumber \\&\quad =\int \!\frac{\mathrm{d}^4p^\prime }{(2\pi )^4}\overline{K}(p,p^\prime ,P)\chi (p^\prime ,P). \end{aligned}$$

(4)

Here we choose the interaction kernel as the standard Coulomb-plus-linear form, which is one-gluon-exchange (OGE) dominant at short distances with linear confinement at long distances. If one applies the instantaneous approximation, i.e. neglecting the frequency dependence, the kernel can be written as

$$\begin{aligned} \overline{K}(p,p^\prime ,P)=\gamma ^{(1)}\cdot \gamma ^{(2)}V_v(-\varvec{k}^2)+V_\mathrm{s}(-\varvec{k}^2), \end{aligned}$$

(5)

where the transferred momentum $\varvec{k}$ is defined as

$$\begin{aligned} \varvec{k}=\varvec{p}-\varvec{p}^\prime . \end{aligned}$$

(6)

Since the interaction kernel $\overline{K}(\varvec{p},\varvec{p}^\prime ,P)$ is no longer dependent on $p^{\prime 0}$, we can perform the integration over $p^{\prime 0}$ in Eq. (4). After transforming the instantaneous Bethe–Salpeter equation into coordinate space, the wave function of the eigenequation decouples from the time coordinate [35,36,37].

In our previous work [27], with the help of projection operators for the wave function we found that the instantaneous Bethe–Salpeter equation is equivalent to the following equation:

$$\begin{aligned} \left( \omega _1\!+\!\omega _2\!+\!\frac{1}{2}(h_1\!+\!h_2)U(\varvec{r})\frac{1}{2}(h_1\!+\!h_2)-h_1E\right) \phi (\varvec{r})=0, \end{aligned}$$

(7)

where the superscript “1” and “2” stand for the heavy quark Q and the light antiquark $\bar{q}$ in the $Q\bar{q}$ meson, respectively. The operators in the above equation are defined as

$$\begin{aligned} \omega _i(\varvec{p})= & {} \sqrt{\varvec{p}^2+m_i^2},\quad i=1,2 , \end{aligned}$$

(8)

$$\begin{aligned} h_i(\varvec{p})= & {} \frac{H_i(\varvec{p})}{\omega _i(\varvec{p})},\quad i=1,2, \end{aligned}$$

(9)

with the free Dirac Hamiltonians

$$\begin{aligned} H_1(\varvec{p})= & {} {\beta }^{(1)}m_1-{\varvec{\alpha }}^{(1)}\cdot \varvec{p},\end{aligned}$$

(10)

$$\begin{aligned} H_2(\varvec{p})= & {} {\beta }^{(2)}m_2+{\varvec{\alpha }}^{(2)}\cdot \varvec{p}. \end{aligned}$$

(11)

Inserting Eqs. (10) and (11) into (9), we can verify the relation

$$\begin{aligned} h_i^2(\varvec{p})=1,\quad i=1,2. \end{aligned}$$

(12)

The interaction potential $U(\varvec{r})$ in Eq. (7) is directly derived from the instantaneous Bethe–Salpeter equation and closely related to the interaction form we assumed in the kernel. It can be written as

$$\begin{aligned} U(\varvec{r})=U_1(\varvec{r})+U_2(\varvec{r}) \end{aligned}$$

(13)

with

$$\begin{aligned} U_1(\varvec{r})= & {} \beta ^{(1)}\beta ^{(2)}V_s(r)+V_v(r),\end{aligned}$$

(14)

$$\begin{aligned} U_2(\varvec{r})= & {} -\frac{1}{2}\left[ {\varvec{\alpha }}^{(1)}\cdot {\varvec{\alpha }}^ {(2)}\!+\!({\varvec{\alpha }}^{(1)}\cdot \hat{\varvec{r}}) ({\varvec{\alpha }}^{(2)}\cdot \hat{\varvec{r}})\right] V_v(r),\nonumber \\ \end{aligned}$$

(15)

where V(r) and $V(-\varvec{k}^2)$ are related to each other according to Fourier transformation.

The instantaneous Bethe–Salpeter equation as an integral equation is equivalent to a less complicated differential equation shown in Eq. (7) but it is still difficult to solve. For heavy–light systems, the heavy-quark effective theory is applied. It is reasonable to consider the heavy-quark expansion, i.e. the $1/m_Q$ expansion. One can reduce the equivalent eigenequation by calculating the interactions of the heavy–light quark–antiquark meson order by order.

Our goal can be achieved by employing the Foldy–Wouthuysen transformation [38]. The operators involved in Eq. (7) can be divided into two sets: the “odd” $\mathcal {O}$ and the “even” $\mathcal {E}$. The name “odd” denotes the operators couple the large and small components of the Dirac spinor, while the “even” operators are diagonal with respect to the large and small components. The main idea of the Foldy–Wouthuysen transformation is to apply a unitary transformation U which retains the “even” operators and eliminates the “odd” operators. If one writes the original Hamiltonian as

$$\begin{aligned} H=\beta \, m+\mathcal {E}+\mathcal {O}, \end{aligned}$$

(16)

according to Foldy and Wouthuysen, one obtains the transformed Hamiltonian:

$$\begin{aligned} \tilde{H}= & {} U^{-1}H\, U\nonumber \\= & {} \beta m+\mathcal {E}+\frac{\beta }{2m}\mathcal {O}^2+\frac{1}{8m^2}[\, [ \mathcal {O},\,\mathcal {E} ],\, \mathcal {O}\, ]+\cdots \end{aligned}$$

(17)

The reduction by performing the Foldy–Wouthuysen transformation on Eq. (7) has been detailed in our previous work [27]. Instead of $\beta m$ being the main term in the common Dirac Hamiltonian shown in Eq. (16), the dominant term is $\beta E$ in our case:

$$\begin{aligned} -h_1 E= & {} \frac{{\varvec{\alpha }}^{(1)}\cdot \varvec{p}-{\beta }^{(1)}m_1}{\omega _1}E \nonumber \\= & {} -\beta ^{(1)} E+\frac{\varvec{\alpha }^{(1)}\cdot \varvec{p} }{\omega _1}E -\beta ^{(1)}\left( \frac{m_1}{\omega _1}-1\right) E.\nonumber \\ \end{aligned}$$

(18)

The reduction result is calculated to order $1/m_Q$ in our previous work [27]. With the similar procedure, here we extend the result to order $1/m_Q^2$. By inserting the “odd” and “even” operators of Eq. (7) into Eq. (17), we obtain the Hamiltonian expansion. After the Foldy–Wouthuysen transformation, we have

$$\begin{aligned} \tilde{H}= & {} \tilde{H}_0+\tilde{H}^{\prime } \end{aligned}$$

(19)

with

$$\begin{aligned} \tilde{H}_0= & {} \omega _1+\omega _2 +\frac{1}{2}\left( 1+h_2\right) U_1\frac{1}{2}\left( 1+h_2\right) . \end{aligned}$$

(20)

The perturbative term $\tilde{H}^{\prime }$ consists of various terms of order $1/m_Q$ and $1/m^2_Q$. We divide it into three parts:

$$\begin{aligned} \tilde{H}^{\prime }=\tilde{H}_1^{\prime }+\tilde{H}_{a}^{\prime }+\tilde{H}_{b}^{\prime }, \end{aligned}$$

(21)

where

$$\begin{aligned} \tilde{H}_1^{\prime }= & {} \frac{1}{2}\left( 1+h_2\right) \left\{ -\frac{{\varvec{\alpha }}^{(1)}\cdot \varvec{p}}{2 m_1},\;U_2\right\} \frac{1}{2}\left( 1+h_2\right) , \end{aligned}$$

(22)

$$\begin{aligned} \tilde{H}_{a}^{\prime }= & {} \frac{1}{2}\left( 1+h_2\right) \frac{{\varvec{\alpha }}^{(1)}\cdot \varvec{p}}{2m_1}U_1 \frac{{\varvec{\alpha }}^{(1)}\cdot \varvec{p}}{2m_1}\frac{1}{2}\left( 1+h_2\right) \nonumber \\&- \frac{1}{2}\left( -3+h_2\right) \frac{{\varvec{p}}^2}{8m_1^2} U_1 \frac{1}{2}\left( 1+h_2\right) +h.c. , \end{aligned}$$

(23)

$$\begin{aligned} \tilde{H}_{b}^{\prime }= & {} \frac{1}{2}\left( 1+h_2\right) U_2\frac{1}{2}(1+\beta ^{(1)}h_2)U_1\frac{{\varvec{\alpha }}^{(1)}\cdot \varvec{p}}{4Em_1}+h.c. \nonumber \\&+\frac{1}{2}\left( 1+h_2\right) U_2\frac{1}{2}(\beta ^{(1)}+h_2)\frac{{\varvec{\alpha }}^{(1)}\cdot \varvec{p}}{4Em_1}U_1\frac{1}{2}\left( 1+h_2\right) \nonumber \\&+\, h.c. \end{aligned}$$

(24)

We can simplify the above equations by inserting an identity matrix $(\gamma ^{(1)}_5)^2=1$ between two odd operators of the heavy quark, with the help of the relations $\{\gamma _5,\;\beta \}=0$, $[\gamma _5,\;\varvec{\alpha }]=0$, $\gamma _5\varvec{\alpha }=\varvec{\Sigma }$ and the substitutions $\beta ^{(1)}\rightarrow 1$, $\varvec{\Sigma }^{(1)}\rightarrow \varvec{\sigma }^{(1)}$. Moreover, we can take the substitution $h_2\rightarrow 1$ if $h_2$ appears at the ends of the expression of $\tilde{H}^{\prime }$ as in Eqs. (22–20), since the corrections of $\tilde{H}^{\prime }$ are calculated as a perturbation to $\tilde{H}_0^{\prime }$.

With the considerations above, we obtain our final Hamiltonian

$$\begin{aligned} H= & {} H_0+H^{\prime }, \end{aligned}$$

(25)

where the leading order Hamiltonian $H_0$ has the form

$$\begin{aligned} H_0= & {} \omega _1+\omega _2 +\frac{1}{2}\left( 1+h_2\right) \overline{U}_1\frac{1}{2}\left( 1+h_2\right) , \end{aligned}$$

(26)

and the subleading Hamiltonian $H^{\prime }$ to order $1/m^2_Q$ can be written as

$$\begin{aligned} H^{\prime }=H_1^{\prime }+H_a^{\prime }+H_b^{\prime }, \end{aligned}$$

(27)

with

$$\begin{aligned} H_1^{\prime }= & {} -\frac{1}{2}\left\{ \frac{{\varvec{\sigma }}^{(1)}\cdot \varvec{p}}{m_1},\;\widetilde{U}_2\right\} ,\end{aligned}$$

(28)

$$\begin{aligned} H_a^{\prime }= & {} \frac{1}{4}\frac{{\varvec{\sigma }}^{(1)}\cdot \varvec{p}}{m_1}\widetilde{U}_1\frac{{\varvec{\sigma }}^{(1)}\cdot \varvec{p}}{m_1} +\frac{1}{8}\left\{ \frac{{\varvec{p}}^2}{m_1},\;\overline{U}_1\right\} ,\end{aligned}$$

(29)

$$\begin{aligned} H_b^{\prime }= & {} \frac{1}{4E}\left( \widetilde{U}_2\frac{1}{2}(1-h_2)\widetilde{U}_1\frac{{\varvec{\sigma }}^{(1)}\cdot \varvec{p}}{m_1}+h.c.\right) \nonumber \\&-\frac{1}{4E}\left( \widetilde{U}_2\frac{1}{2}(1-h_2)\frac{{\varvec{\sigma }}^{(1)}\cdot \varvec{p}}{m_1}\overline{U}_1+h.c.\right) , \end{aligned}$$

(30)

the interaction potentials $\overline{U}_1(\varvec{r})$, $\widetilde{U}_1(\varvec{r})$ and $\widetilde{U}_2(\varvec{r})$ in the above equations are defined as

$$\begin{aligned} \overline{U}_1(\varvec{r})= & {} V_v(r)+\beta ^{(2)}V_s(r),\end{aligned}$$

(31)

$$\begin{aligned} \widetilde{U}_1(\varvec{r})= & {} V_v(r)-\beta ^{(2)}V_s(r),\end{aligned}$$

(32)

$$\begin{aligned} \widetilde{U}_2(\varvec{r})= & {} -\frac{1}{2}\left[ {\varvec{\sigma }}^{(1)}\cdot {\varvec{\alpha }}^ {(2)}+({\varvec{\sigma }}^{(1)}\cdot \hat{\varvec{r}}) ({\varvec{\alpha }}^{(2)}\cdot \hat{\varvec{r}})\right] V_v(r).\nonumber \\ \end{aligned}$$

(33)

The leading order Hamiltonian $H_0$ we obtain for the heavy–light quark–antiquark system in Eq. (26) is not Dirac-like as in Refs. [33, 39]. We have

$$\begin{aligned} H_0^\mathrm{{Dirac}}=\omega _1+ H_2(\varvec{p}) +V_v(r)+ \beta ^{(2)}V_s(r). \end{aligned}$$

(34)

Its form is more like the form used in relativized quark models [13, 40, 41]. As for the double-heavy system, we have $h_2\rightarrow 1$ and $\beta ^{(2)}\rightarrow 1$, then Eq. (26) can be reduced to

$$\begin{aligned} H_0^\mathrm{{Schr}}=\omega _1+\omega _2+V_v(r)+V_s(r), \end{aligned}$$

(35)

which is the Schrödinger formalism extensively used in nonrelativistic or semirelativistic quark models.

3 Solution of the wave equation

In this section we solve the eigenequation of the leading order Hamiltonian $H_0$ in Eq. (26). Before doing this we would like to discuss the properties of the solution of the eigenequation associated with $H_0$.

The eigenequation of $H_0$ can be written as

$$\begin{aligned} \left( \omega _1+\omega _2 +\frac{1}{2}\left( 1+h_2\right) \overline{U}_1\frac{1}{2}\left( 1+h_2\right) -E\right) \psi =0; \end{aligned}$$

(36)

the above equation is equivalent to

$$\begin{aligned} h_2\left( \omega _1+\omega _2 +\frac{1}{2}\left( 1+h_2\right) \overline{U}_1\frac{1}{2}\left( 1+h_2\right) -E\right) \psi =0, \end{aligned}$$

(37)

which is equivalent to

$$\begin{aligned} \left( \omega _1+\omega _2 +\frac{1}{2}\left( 1+h_2\right) \overline{U}_1\frac{1}{2}\left( 1+h_2\right) -E\right) h_2\psi =0. \end{aligned}$$

(38)

From Eqs. (36) and (38), we have

$$\begin{aligned} h_2\psi =c\psi , \end{aligned}$$

(39)

and since $(h_2)^2=1$,

$$\begin{aligned} c=\pm 1. \end{aligned}$$

(40)

When we take $c=-1$, Eq. (36) is transformed to

$$\begin{aligned} (\omega _1+\omega _2-E)\psi =0, \end{aligned}$$

(41)

which is not the correct eigenequation for the bound systems we are interested in. Thus we only have $c=+1$. This is the reason for the substitution $h_2\rightarrow 1$ we use in the last section.

If all the eigenfunctions of $H_0$ for bound states satisfy the relation

$$\begin{aligned} h_2\psi =\psi , \end{aligned}$$

(42)

the eigenfunction set of $H_0$ is not complete.

A complete set is needed to construct the identity operator $1=\sum _{i}|\psi _i> <\psi _i|$ in order to calculate the perturbative correction of $H_b^{\prime }$. Thus we construct a new Hamiltonian. Inspired by the relation $h_2\psi =\psi$ we transform the potential term in Eq. (36) as

$$\begin{aligned}&\frac{1}{2}\left( 1+h_2\right) \overline{U}_1\frac{1}{2}\left( 1+h_2\right) \\&\quad =\frac{1}{4}\left( \overline{U}_1+h_2\overline{U}_1+\overline{U}_1h_2+h_2\overline{U}_1h_2\right) \\&\quad \Rightarrow \frac{1}{4}\left( \overline{U}_1h_2+h_2\overline{U}_1+\overline{U}_1h_2+h_2\overline{U}_1\right) \\&\quad =\frac{1}{2}\{h_2,\;\overline{U}_1\}, \end{aligned}$$

then the new Hamiltonian we construct can be written as

$$\begin{aligned} H_0=\omega _1+\omega _2 +\frac{1}{2}\{h_2,\;\overline{U}_1\}. \end{aligned}$$

(43)

It is easy to verify that the eigenfunction set of the new Hamiltonian includes both subsets:

$$\begin{aligned} h_2\psi ^+=\psi ^+\quad \mathrm{and}\quad h_2\psi ^-=-\psi ^-, \end{aligned}$$

(44)

where the subset $\{\psi ^+\}$ is identical to the eigenfunction set associated with the original Hamiltonian $H_0$ in Eq. (36).

Now we turn to solving the eigenequation associated with the new Hamiltonian $H_0$, that is,

$$\begin{aligned} \left( \omega _1+\omega _2 +\frac{1}{2}\{h_2,\;\overline{U}_1\}-E\right) \psi (\varvec{r})=0. \end{aligned}$$

(45)

In the heavy–light quark–antiquark system, we treat the heavy quark as a static source, while the light one is described relativistically by a Dirac spinor. It is easy to verify that $H_0$ commutes with all the elements of the standard operator set $\{ {\varvec{j}}^2,j_z,K, S_z \}$ associated with the free Dirac Hamiltonian. Then the eigenstates of $H_0$ can be labeled by the quantum number set $\{n,j,m_j,k,s\}$ corresponding to the operator set.

The quantum number k can have two opposite values for an eigenstate with quantum number j:

$$\begin{aligned} k=\pm (j+1/2), \quad \mathrm{for}\quad l=j\pm 1/2. \end{aligned}$$

(46)

The leading order invariant mass $E^{(0)}$ can be determined by quantum numbers n, j and k, or equivalently by n, j and l. The parity of the bound states is determined by $P=(-1)^{l+1}$.

The Dirac spinor with quantum numbers j $m_j$ and l can be written as

$$\begin{aligned} \Psi (\varvec{r}) =\left( \begin{array}{cc} g(r)\;y_{j,l_A}^{m_j}(\theta ,\varphi )\\ i f(r)\;y_{j,l_B}^{m_j}(\theta ,\varphi )\end{array}\right) , \end{aligned}$$

(47)

where the subscripts $l_A$ and $l_B$ stand for l and $2j-l$, respectively. The complete expression of $y_{j,l}^{m_j}(\theta ,\varphi )$ can be found in Ref. [34].

For a bound state of a quark and an antiquark the wave function will effectively vanish when the distance between them is large enough. We designate such a large typical distance as L. Then the heavy quark and light antiquark bounded in the meson can be viewed as restricted in a limited space, $0< r < L$. Thus we can expand the radial functions f(r) and g(r) by spherical Bessel functions associated with the distance L:

$$\begin{aligned} g(r)= & {} \sum _{i=1}^N\frac{g_i}{N_i^A}j_{l_A}\left( \frac{a_i^Ar}{L}\right) ,\end{aligned}$$

(48)

$$\begin{aligned} f(r)= & {} \sum _{\alpha =1}^N\frac{f_\alpha }{N_\alpha ^B}j_{l_B}\left( \frac{a_\alpha ^Br}{L}\right) , \end{aligned}$$

(49)

where $N_n$ and $a_n$ are the module and the nth root of the spherical Bessel function $j_l(r)$, respectively.

Inserting Eqs. (9) and (11) into (43), we can rewrite $H_0$ in the matrix form

$$\begin{aligned} H_0= & {} \left( \begin{array}{cc} \omega _1+\omega _2&{} \\ &{} \omega _1+\omega _2 \end{array}\right) + \frac{1}{2}\left( \begin{array}{cc} H_a &{}H_b\\ H_c &{} H_d \end{array}\right) +h.c., \end{aligned}$$

(50)

where h.c. stands for Hermitian conjugate and the operator elements are

$$\begin{aligned} H_a= & {} \frac{m_2}{\omega _2}(V_\mathrm{v}+V_\mathrm{s}),\end{aligned}$$

(51)

$$\begin{aligned} H_b= & {} \frac{\varvec{\sigma }\cdot \varvec{p}}{\omega _2} (V_\mathrm{v}-V_\mathrm{s}),\end{aligned}$$

(52)

$$\begin{aligned} H_c= & {} \frac{\varvec{\sigma }\cdot \varvec{p}}{\omega _2} (V_\mathrm{v}+V_\mathrm{s}),\end{aligned}$$

(53)

$$\begin{aligned} H_d= & {} \frac{m_2}{\omega _2}(V_\mathrm{s}-V_\mathrm{v}). \end{aligned}$$

(54)

According to Eqs. (48) and (49) we can rewrite the eigenequation of $H_0$ in the representation of the state basis constructed from spherical Bessel functions. In this representation the operator $H_0$ can be written in its matrix form:

$$\begin{aligned} H_0= & {} \left( \begin{array}{cc}<\omega _1+\omega _2>_{ij}&{} \\ &{}<\omega _1+\omega _2>_{\alpha \beta } \end{array}\right) \nonumber \\&+\frac{1}{2}\left( \begin{array}{cc}<H_a>_{ij}&{}<H_b>_{i\beta }\\<H_c>_{\alpha j} &{} <H_d>_{\alpha \beta } \end{array}\right) +h.c. \end{aligned}$$

(55)

The matrix elements of $H_0$ in the above equation can be calculated by applying the relation

$$\begin{aligned}&(\varvec{\sigma }\cdot \varvec{p}) \;y_{j,l_{\pm }}^{m_j}=\pm i\left( \frac{k\pm 1}{r}\pm \frac{\mathrm{d}}{\mathrm{d}r}\right) \;y_{j,l_{\mp }}^{m_j},\end{aligned}$$

(56)

$$\begin{aligned}&l_{A}=l_{+},\quad l_{B}=l_{-}, \end{aligned}$$

(57)

and the eigenequation [27]

$$\begin{aligned} \Omega (p) \; j_l(k r)Y_{lm}(\hat{\varvec{r}}) =\Omega (k) \; j_l(k r)Y_{lm}(\hat{\varvec{r}}), \end{aligned}$$

(58)

where $\Omega (p)$ is a pseudo-differential operator function and $\Omega (k)$ is a normal function, p and k stand for the modules of momentum operator $\varvec{p}$ and momentum $\varvec{k}$, respectively.

With the normalization condition we easily obtain the matrix elements of $H_0$. For the operators regarding the energy of the motion, we have

$$\begin{aligned} \left<\omega _1(\varvec{p})+\omega _2(\varvec{p})\right>_{ij}= & {} \left[ \;\omega _1\left( \frac{a_i^A}{L}\right) +\omega _2\left( \frac{a_i^A}{L}\right) \;\right] \delta _{ij},\nonumber \\ \end{aligned}$$

(59)

$$\begin{aligned} \left<\omega _1(\varvec{p})+\omega _2(\varvec{p})\right>_{\alpha \beta }= & {} \left[ \;\omega _1\left( \frac{a_\alpha ^B}{L}\right) +\omega _2\left( \frac{a_\alpha ^B}{L}\right) \;\right] \delta _{\alpha \beta }.\nonumber \\ \end{aligned}$$

(60)

In order to write down the expressions of the elements associated with the interaction potential in a compact form we introduce a symbolic notation:

$$\begin{aligned} \left<\,\hat{O}\,\right>_{m,l_A;n,l_B}=\int _0^L \mathrm{d}r\,r^2 \; j_{l_A}\left( \frac{a_m^Ar}{L}\right) \;\hat{O} \; j_{l_B}\left( \frac{a_n^Br}{L}\right) .\nonumber \\ \end{aligned}$$

(61)

Then we have

$$\begin{aligned} \left<H_a\right>_{ij}= & {} \frac{1}{N_i^AN_j^A}\frac{m_2}{\omega _2\left( \frac{a_i^A}{L}\right) }<V_\mathrm{v}+V_\mathrm{s}>_{i,l_A;j,l_A},\end{aligned}$$

(62)

$$\begin{aligned} \left<H_b\right>_{i\beta }= & {} \frac{1}{N_i^AN_\beta ^B}\frac{1}{\omega _2\left( \frac{a_i^A}{L}\right) }\nonumber \\&\times \left<\left( \frac{k-1}{r}-\frac{\mathrm{d}}{\mathrm{d}r}\right) (V_\mathrm{v}-V_\mathrm{s})\right>_{i,l_A;\beta ,l_B},\end{aligned}$$

(63)

$$\begin{aligned} \left<H_c\right>_{\alpha j}= & {} \frac{1}{N_\alpha ^BN_j^A}\frac{1}{\omega _2\left( \frac{a_\alpha ^B}{L}\right) }\nonumber \\&\times \left<\left( \frac{k+1}{r}+\frac{\mathrm{d}}{\mathrm{d}r}\right) (V_\mathrm{v}+V_\mathrm{s})\right>_{\alpha ,l_B;j,l_A},\end{aligned}$$

(64)

$$\begin{aligned} \left<H_d\right>_{\alpha \beta }= & {} \frac{1}{N_\alpha ^B N_\beta ^B}\frac{m_2}{\omega _2\left( \frac{a_\alpha ^B}{L}\right) }\left<V_\mathrm{s}-V_\mathrm{v}\right>_{\alpha ,l_B;\beta ,l_B}. \end{aligned}$$

(65)

After calculating every element of the Hermitian matrix of $H_0$ we diagonalize the Hermitian matrix and obtain eigenvalues and eigenvectors. The eigenvalue of the matrix is the eigenenergy of $H_0$, while the eigenvector is associated with the coefficients $g_i,f_\alpha$, which are defined in Eqs. (48) and (49). That is to say, the eigenequation shown in Eq. (45) is solved and the corresponding eigenenergy and eigenfunction are obtained.

Here we turn to discussing the perturbative corrections of $H^\prime$ defined in Eq. (27). The perturbative term $H^\prime$ does not commute with the standard operators introduced for the free Dirac Hamiltonian, but it still commutes with the total angular momentum operator $\varvec{J}=\varvec{j}+\varvec{S}$ and the parity operator $\mathcal {P}$ of the bound state.

Thus the quantum number set associated with the total Hamiltonian $H=H_0+H^\prime$ can be denoted by $\{n,J,M_J,P\}$. By using Clebsch–Gordan coefficients the total wave function of the heavy–light quark–antiquark bound state can be decomposed as follows:

$$\begin{aligned} \Psi ^{(0)}_{n,k,j;J,M_J}(\varvec{r})= & {} \sum _{m_j,s} C^{J,M_J}_{j,m_j;1/2,s} \nonumber \\&\times \left( \begin{array}{cc} g_{n,k,j}(r)\;y_{j,l_A}^{m_j}(\theta ,\varphi )\\ i f_{n,k,j}(r)\;y_{j,l_B}^{m_j}(\theta ,\varphi ) \end{array}\right) \otimes \chi _s, \end{aligned}$$

(66)

with which the corrections and mixings caused by $H^\prime$ can be calculated perturbatively. The $1/m_Q$ and $1/m^2_Q$ perturbative terms are given in Eqs. (28)–(30).

The properties of the eigenfunctions of $H_0$ are of great help in calculating the perturbative corrections. We have already used $h_2\rightarrow 1$ to get rid of the $h_2$ at the ends of the perturbative terms. As for the $h_2$ sandwiched in $H_b^\prime$, $h_2\rightarrow \pm 1$ can be applied due to Eq. (44). $H_b^\prime$ can be rewritten as

$$\begin{aligned} H_b^{\prime }= & {} \frac{1}{4E}\widetilde{U}_2\frac{1}{2}(1-h_2)\left( \widetilde{U}_1\frac{{\varvec{\sigma }}^{(1)}\cdot \varvec{p}}{m_1} -\frac{{\varvec{\sigma }}^{(1)}\cdot \varvec{p}}{m_1}\overline{U}_1\right) +h.c.\nonumber \\ \end{aligned}$$

(67)

Here we define two operators:

$$\begin{aligned} \hat{A}= & {} \widetilde{U}_2, \\ \hat{B}= & {} \widetilde{U}_1({\varvec{\sigma }}^{(1)}\cdot \varvec{p}) -({\varvec{\sigma }}^{(1)}\cdot \varvec{p})\overline{U}_1. \end{aligned}$$

Then we have

$$\begin{aligned} H_b^{\prime }=\frac{1}{4m_1E}\hat{A}\frac{1}{2}(1-h_2)\hat{B}+h.c. \end{aligned}$$

(68)

As discussed at the beginning of this section the eigenfunction set of $H_0$ can be divided into two parts $\{\psi ^+,\,\psi ^-\}$, where $\psi ^+$ and $\psi ^-$ represent the physical and unphysical states, respectively. Inserting the identity operator consisting of the complete set of $H_0$ in Eq. (68) we obtain

$$\begin{aligned} H_b^{\prime }= & {} \frac{1}{4m_1E}\hat{A}\frac{1}{2}(1-h_2)\sum _{i}|\psi _i> <\psi _i|\hat{B}+h.c.\nonumber \\= & {} \frac{1}{4m_1E}\sum _{m}\hat{A}|\psi ^-_m> <\psi ^-_m|\hat{B}+h.c. \end{aligned}$$

(69)

The correction in first order perturbation can be written as

$$\begin{aligned} E_{n,l,j,J}=E^{(0)}_{n,l,j}+\delta E^{(1)}_{n,l,j,J}+\delta E^{(2)}_{n,l,j,J}, \end{aligned}$$

(70)

where

$$\begin{aligned} \delta E^{(2)}_{n,l,j,J}=\delta E^{(a)}_{n,l,j,J}+\delta E^{(b)}_{n,l,j,J}. \end{aligned}$$

(71)

From Eq. (69), the correction of $H_b^{\prime }$ for $\psi ^+_n$ can be written as

$$\begin{aligned} \delta E^{(b)}_{n,l,j,J}= & {} \frac{1}{2m_1E_{n,l,j}^{(0)}}\sum _m<\psi ^+_n|\hat{A}|\psi ^-_m> <\psi ^-_m|\hat{B}|\psi ^+_n>\nonumber \\= & {} \frac{1}{2m_1E_{n,l,j}^{(0)}}\sum _m A_{nm}B_{mn}. \end{aligned}$$

(72)

With the eigenfunctions we obtain the $1/m_Q$ and $1/m^2_Q$ corrections can be calculated. Then the masses of all the different $J^P$ states are determined.

4 Numerical results and discussions

The vector and scalar potentials are chosen to have a Coulombic behavior at short distance and a linear confining behavior at long distance. They can be written in a simple form:

$$\begin{aligned} V_\mathrm{v}(r)= & {} -\frac{4\alpha _\mathrm{s}(r)}{3r},\end{aligned}$$

(73)

$$\begin{aligned} V_\mathrm{s}(r)= & {} b\;r+c. \end{aligned}$$

(74)

The running coupling constant $\alpha _\mathrm{s}(r)$ in the vector potential is derived from the coupling constant $\alpha _\mathrm{s}(Q^2)$ in momentum space via Fourier transformation. It can be parametrized in a more convenient form [13]:

$$\begin{aligned} \alpha _\mathrm{s}(r)=\sum _i\alpha _i\frac{2}{\sqrt{\pi }}\int _0^{\gamma _i r}e^{-x^2}\mathrm{d}x, \end{aligned}$$

(75)

where $\alpha _i$ and $\gamma _i$ are parameters which can be fitted according to the behavior of the running coupling constant at short distance predicted by QCD. The behavior of $\alpha _\mathrm{s}(r)$ is depicted in Fig. 1. In this work we use the same $\alpha _\mathrm{s}(r)$ given in Ref. [13], where the $\alpha _i$ and $\gamma _i$ parameters have the values $\alpha _1=0.25$, $\alpha _2=0.15$, $\alpha _3=0.20$, and $\gamma _1=1/2$, $\gamma _2=\sqrt{10}/2$, $\gamma _3=\sqrt{1000}/2$.

Fig. 1

The behavior of the running coupling constant $\alpha _\mathrm{s}(r)$ with the critical value $\alpha _\mathrm{s}^\mathrm{{critical}}=0.6$

There are two free parameters in the scalar potential. One is the string tensor constant b which characterizes the confinement of the quark–antiquark system. The other is a phenomenological constant c which is adjusted to give the correct ground state energy level of the heavy–light meson state. The behavior of the parameters b in our model is quite different from those in usual quark models. The slope parameter b is the most essential parameter in all the different kinds of phenomenological quark models where the linear confinement is assumed. The parameter b determines the structure of the calculated spectrum, more specifically, it determines the Regge trajectories and the energy gaps between radial excitations. But unlike the Dirac Hamiltonian in Eq. (34) or the Schrödinger Hamiltonian in Eq. (35), the Hamiltonian for the heavy–light meson states in the Bethe–Salpeter formalism has a different form for the interaction potential, that is,

$$\begin{aligned} \frac{1}{2}\left( 1+h_2\right) \left( V_v(r)+\beta ^{(2)}V_s(r)\right) \frac{1}{2}\left( 1+h_2\right) , \end{aligned}$$

where $h_2$ has the form

$$\begin{aligned} h_2=\frac{m_1}{\omega _2}{\beta }^{(2)}+\frac{{\varvec{\alpha }}^{(2)}\cdot \varvec{p}}{\omega _2}. \end{aligned}$$

(76)

In the above equation the diagonal part, i.e. the “even” operator, is the chief contributor to the eigenvalue of the eigenequation. If $m_2$ tends to infinity the Hamiltonian degenerates into the nonrelativistic case. But if $m_2$ tends to 0 an additional factor 1 / 4 will appear and it weakens the ability of the confinement parameter b in $V_\mathrm{s}(r)$ to elevate the energy levels of the excitations. That is to say, in the Bethe–Salpeter formalism the energy level is also sensitive to the light-quark mass $m_q$. The experimental data shows that the mass splitting is similar in the D and $D_{s}$ mesons. For example, the energy gaps between $1^{3/2}P_2$ and $1^{1/2}S_0$ states are

$$\begin{aligned} m_D(1^{3/2}P_2)-m_D(1^{1/2}S_0)= 595 \;\mathrm{MeV},\\ m_{D_{s}}(1^{3/2}P_2)-m_{D_s}(1^{1/2}S_0)= 603 \; \mathrm{MeV}. \end{aligned}$$

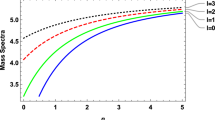
Thus in the Bethe–Salpeter formalism different slope parameters are required to coordinate with different constituent-quark masses in order to recover the structure of the heavy–light meson spectra. This is also true for the radial excitations. In Fig. 2, the energy gap $\Delta E$ between the first radial excitation and the ground state is depicted as a function of $m_q$. We take the D meson as an example to illustrate the dependence on the quark mass. The values of the parameters, which are fitted for the D meson spectrum, are fixed except for the light-quark mass of the D meson.

Fig. 2

The energy gap $\Delta E$ as a function of the light-quark mass in the D meson. The dashed, dotted and solid lines stand for the Schrödinger, Dirac and Bethe–Salpeter formalisms, respectively

From the different shapes of the dashed, dotted and solid lines according to the three schemes, i.e. the Schrödinger, Dirac and Bethe–Salpeter formalisms, one can find:

• When $m_q$ is taken large enough the three schemes tend to give the same value for the energy gap $\Delta E$. It indicates the equivalence of the three schemes when dealing with double-heavy mesons.

• In the region $m_q < 1\, \mathrm{GeV}$, which is the case for heavy–light mesons, the three schemes give quite different values for the energy gap. It has the pattern $\Delta E^{\mathrm{Schr}}> \Delta E^{\mathrm{Dirac}} > \Delta E^{B-S}$. In order to give the same energy gap for a specific meson the confinement parameter should be chosen as $b^{\mathrm{Schr}}< b^{\mathrm{Dirac}} < b^{B-S}$. The literature supports this sequence. For instance, $b^{\mathrm{Schr}}$ is taken as $0.175\;\mathrm{GeV}^2$ [41], $0.180\;\mathrm{GeV}^2$ [13], $b^{\mathrm{Dirac}}$ is taken as $0.257\;\mathrm{GeV}^2$ [34], $0.309\;\mathrm{GeV}^2$ [28], while $b^{B-S}$ can be taken up to $0.400\;\mathrm{GeV}^2$ in this work.

• In the Schrödinger and Dirac schemes the energy gap changes slowly over $m_q$. This is especially true when $m_q$ is less than 1 GeV. $\Delta E^{\mathrm{Schr}}$ and $\Delta E^{\mathrm{Dirac}}$ can be viewed as constants. In the Bethe–Salpeter scheme, $\Delta E^{B-S}$ changes drastically over $m_q$. From the experimental data we know that the $\Delta E$ are not sensitive to their light quark masses. For example, the $\Delta E$ for both D and $D_s$ mesons are around $0.7\;\mathrm{GeV}$. Thus $b^{\mathrm{Schr}}$ and $b^{\mathrm{Dirac}}$ can be taken as a constant, while $b^{B-S}$ varies with the quark mass.

Our analysis suggests that in the Bethe–Salpeter formalism the string tension b depends on the masses of the quark and antiquark, especially the light ones. Besides the potential parameters four quark mass parameters are employed to fit the heavy–light meson spectra. With all the considerations above our best fitting of the parameters gives the following values:

$$\begin{aligned} m_{u,d}= & {} 0.398\; \mathrm{GeV},\\ m_s= & {} 0.598\;\mathrm{GeV},\\ m_c= & {} 1.450\; \mathrm{GeV},\\ m_b= & {} 4.765\; \mathrm{GeV},\\ b= & {} \left\{ \begin{array}{llll} 0.390\;\mathrm{GeV}^2&{}\quad \mathrm{for}\; c\bar{q}\; \mathrm{system}, \\ 0.421\;\mathrm{GeV}^2&{}\quad \mathrm{for}\; b\bar{q}\; \mathrm{system}, \\ 0.300\;\mathrm{GeV}^2&{}\quad \mathrm{for}\; c\bar{s}\; \mathrm{system}, \\ 0.316\;\mathrm{GeV}^2&{}\quad \mathrm{for}\; b\bar{s}\; \mathrm{system}, \end{array}\right. \\ c= & {} -0.320\; \mathrm{GeV}. \end{aligned}$$

In Sect. 3 two numerical parameters L and N are introduced in our calculation. In principle, if the distance L and the size of the expansion basis N are taken to $\infty$, we can obtain the exact solution of the wave equation. Our calculation shows the solution is stable when $L>5$ fm, $N>50$. In this work they are taken as $L=10$ fm, $N=150$. The size of the matrix of $H_0$ in Eq. (55) is $300\times 300$. Since a lot of integrals are involved the Gauss–Legendre quadrature is widely used in our numerical calculation. The spectra of the heavy–light D, $D_{s}$, B, $B_{s}$ mesons are fitted based on the data given by PDG [9]. In this work we take the masses of the well-established 1S and 1P heavy–light meson states as our input for fitting the parameters. After the fitting the highly excited states beyond 1P are also calculated in the spectra and we identify the newly observed highly excited meson states in our model. The numerical results for the spectra of D, $D_{s}$ mesons are presented in Table 1, while the B and $B_{s}$ mesons are presented in Table 2. The calculated spectra are in good agreement with the experimental data. Our results are compared with the results of two other relativistic models [34, 39]. One is derived by a quasipotential approach and the other is obtained by reducing the Bethe–Salpeter vertex function. The result in this work is improved compared with our previous work [27]. Taking the mass difference between the pseudoscalar state and the vector state for example, as shown in Table 1, in our previous work, we have

$$\begin{aligned} m_{D^*}-m_{D}= & {} 167\;\mathrm{MeV}, \\ m_{D_{s}^*}-m_{D_{s}}= & {} 161\;\mathrm{MeV}, \end{aligned}$$

while in this work we have

$$\begin{aligned} m_{D^*}-m_{D}= & {} 137\;\mathrm{MeV}, \\ m_{D_{s}^*}-m_{D_{s}}= & {} 143\;\mathrm{MeV}, \end{aligned}$$

the discrepancy from experimental data is decreased for D, $D^*$, $D_{s}$ and $D_{s}^*$ states as well as other states.

Theoretical deviations from experimental data mainly occur in the $D_{s}$ meson sector, specifically, the $D_{{s0}}^*(2317)$ and $D_{{s1}}(2460)$ resonances. Our calculations for the two resonances are about $100\;\mathrm{GeV}$ higher than their masses measured in the experiment. The discrepancy may be ascribed to the instantaneous approximation, the naive assumption of the kernel or the $\alpha ^2_\mathrm{s}(r)$ contributions, i.e. the loop corrections. However, it is more likely to find an explanation beyond the naive quark model [42]. The masses of the two resonances predicted by the constituent-quark model are generally 100–200 MeV higher than experiments [33, 34, 43,44,45]. The mass of $D_0^*$, $2318 \pm 29\;\mathrm{MeV}$ is almost identical to the mass of $D_{{s0}}^*$, $2317.8\pm 0.6\;\mathrm{MeV}$. It cannot be explained in the conventional quark model if the difference between the two anomalous resonances in the model is merely their light-quark masses $m_s$ and $m_{u,d}$. In this work the confinement parameter b takes different values for different systems but it still is not capable to explain the small mass difference of the two resonances.

As $D_{{s0}}^*$ and $D_{{s1}}$ lie just below the DK and $D^*K$ threshold, respectively, the authors in Ref. [46] have suggested that the two resonances may be $D_{{s0}}^*(DK)$ and $D_{{s1}}(D^*K)$ molecular states, while in Refs. [47,48,49], $D_{{s0}}^*$ and $D_{{s1}}$ are considered as $c\bar{s}$ states which are significantly affected by mixing with the DK and $D^*K$ continua. In Ref. [50], the authors suggest that the discrepancy of the calculated masses in quark models can be qualitatively understood as a consequence of self-energy effects due to strong coupled channels. In Refs. [51,52,53] the interpretation of the heavy $J^P (0^+, 1^+)$ spin multiplet as the parity partner of the ground-state $(0^-, 1^-)$ multiplet is proposed. Both theoretical and experimental efforts are required in order to fully understand the nature of the anomalous $D_{s0}^*(2317)$ and $D_{s1}(2460)$ states.

Table 1 Spectra for D and $D_s$ mesons. The comparison of the result in this work with our previous work and other theoretical results in Refs. [34, 39] is presented. All units are in MeV

Table 2 Spectra for B and $B_s$ mesons. The comparison of the result in this work with our previous work and other theoretical results in Refs. [34, 39] is presented. All units are in MeV

As for the D mesons, in the mass region 2500–3000 MeV several resonances are measured by the LHCb Collaboration [2]. The assignments of these states are listed in the upper part of Table 1, where the resonances $D_J(2740)$, $D_J^*(2760)$, $D_J(3000)$ are identified as $n=1$ states and the resonances $D_J(2580)$, $D_J^*(2650)$, $D_J^*(3000)$ are identified as radially exited states with $n=2$. In our predicted spectrum for D meson, $D_J(2740)$ and $D_J^*(2760)$ are identified as the $|1^{5/2}D_2\rangle$ state with $J=2^-$ and the $|1^{5/2}D_3\rangle$ state with $J=3^-$, respectively. Our best assignment for $D_J^* (3000)$ is the $|1^{7/2}F_3\rangle$ state and $D_J(3000)$ the $|2^{3/2}P_2\rangle$ state, although in Ref. [2] they favor the natural and unnatural parity, respectively. The last two resonances $D_J(2580)$ and $D_J^*(2650)$ are identified as the first radial excitations of the ground D and $D^*$ states. Recently, the LHCb Collaboration observed $D_J^*(2650)$ and $D_J^*(2760)$. Their masses and widths were measured as [56]

$$\begin{aligned}&M(D_{1}^*(2680)^0)=2681.1\pm 5.6\pm 4.9\pm 13.1\;\text{ MeV },\\&\Gamma (D_{1}^*(2680)^0)=186.7\pm 8.5\pm 8.6\pm 8.2\;\text{ MeV },\\&M(D_{3}^*(2760)^0)=2775.5\pm 4.5\pm 4.5\pm 4.7\;\text{ MeV },\\&\Gamma (D_{3}^*(2760)^0)=95.3\pm 9.6\pm 7.9\pm 33.1\;\text{ MeV }. \end{aligned}$$

From Table 1 one can see our results favor the measurements.

As for the $D_s$ mesons, several states beyond the 1P state have been observed. Their masses and identifications are presented in the lower part of Table 1. Recently, the LHCb Collaboration identified $D_{sJ}^*(2860)$ as an admixture of two resonances: $D_{s3}^*(2860)^-$ and $D_{s1}^*(2860)^-$ [7, 8], with their masses measured as $2859\pm 12\pm 6\pm 23\;\text{ MeV }$ and $2860.5\pm 2.6\pm 2.5\pm 6.0\;\text{ MeV }$, respectively. In Refs. [34, 39] cited in Table 1, their predictions do not favor this identification, with their calculations generally 60 MeV higher than the measured masses. While our results for both $|1^{3/2}D_1\rangle$ and $|1^{5/2}D_3\rangle$ are around 2860 MeV, the two resonances can be interpreted as members of the 1D family with $J^P=1^-$ and $3^-$. The resonances $D_{sJ}(2632)$ , $D_{s1}^*(2710)$ and $D_{sJ}(3040)$ are identified as radially exited states with $n=2$ in our model. The $D_{sJ}(2632)$ was firstly observed by SELEX Collaboration at a mass of $2632.5\pm 1.7$ MeV, it can be assigned as the $|2^{1/2}S_0\rangle$. The assignment for $D_{s1}^*(2710)$ is proposed as $J^P=1^-$ in Refs. [54, 55], which agree with our prediction as our calculated mass for $|2^{1/2}S_1\rangle$ is close to its experimental mass $2708\pm 9^{+11}_{-10}$ MeV [5]. The $D_{sJ}(3040)$ resonance is observed in the $D^*K$ mass spectrum at a mass of $3044\pm 8_{-5}^{+30}$ MeV by the BABAR Collaboration [6]. Here we assign it as $|2^{1/2}P_1\rangle$ in our predicted $D_s$ meson spectrum.

In the b-flavored meson sector, experimental data for excited B meson states are limited for now. But still several b-flavored mesons are observed [57]. The strangeless resonances $B_J(5840)^0$ and $B(5970)^0$ were measured by the LHCb and CDF Collaborations, respectively [10, 11]. The stranged $B^*_{sJ}(5850)$ was observed by the OPAL Collaboration [12]. Their masses were measured as

$$\begin{aligned}&M(B_J(5840))= 5862.9\pm 5.0\pm 6.7\pm 0.2\;\text{ MeV },\\&M(B(5970)^0)= 5978\pm 5\pm 12\;\text{ MeV },\\&M(B^*_{sJ}(5850))= 5853\pm 15\;\text{ MeV }. \end{aligned}$$

In Table 2, we can identify $B_J(5840)^0$ and $B(5970)^0$ as $|1^{1/2}P_1\rangle$ and $|2^{1/2}S_1\rangle$, respectively, in the spectrum of B meson, while $B^*_{sJ}(5850)$ can be assigned as $|1^{1/2}P_1\rangle$ in the spectrum of $B_s$ meson.

Finally, after solving the wave equation one can obtain not only the eigenenergy of each bound state but also their wave functions. The radial wave functions $g_{n,l,j}(r)$ and $f_{n,l,j}(r)$ for physical and unphysical D meson states are depicted as an example in Figs. 3 and 4, respectively. We stress that the solution of the eigenequation associated with the original $H_0$ in Eq. (26) gives only the wave functions of the physical states depicted in Fig. 3. In Sect. 3 we construct a new $H_0$ for the heavy–light systems in Eq. (43), the unphysical states depicted in Fig. 4 are due to the new $H_0$ for which the original one is substituted.

Fig. 3

The radial wave functions $g_{n,l,j}(r)$ and $f_{n,l,j}(r)$ for physical D meson states as an example. The wave functions are the radial part of the solution of the eigenequation associated with $H_0$

Fig. 4

The radial wave functions $g_{n,l,j}(r)$ and $f_{n,l,j}(r)$ for unphysical D meson states as an example. The wave functions are the radial part of the solution of the eigenequation associated with $H_0$

5 Summary

The spectra of heavy–light mesons are restudied in a relativistic model, which is derived by reducing the instantaneous Bethe–Salpeter equation. The kernel is chosen to be the standard combination of linear scalar and Coulombic vector. By applying the Foldy–Wouthuysen transformation on the heavy quark, the Hamiltonian for the heavy–light quark–antiquark system is calculated up to order $1/m_Q^2$. We find that in the framework of an instantaneous Bethe–Salpeter equation the string tension b in the confinement potential is sensitive to the masses of the constituent quarks in the meson. The spectra of the D, $D_s$, B and $B_s$ mesons are calculated in the relativistic model. Most of the heavy–light meson states can be accommodated successfully in our model except for the anomalous $D_{s0}^*(2317)$ and $D_{s1}(2460)$ resonances. In the Bethe–Salpeter formalism, the assumption of the interaction kernel for mesons is rather a priori; kernels with other spin structures can also be studied. In this work, we only restrict our calculations to the spectra of heavy–light mesons. With the wave functions obtained when solving the wave equation, B and D decays can be studied in further research.