1 Introduction

Black holes have been used as the laboratory of many kinds of theories, specially the thermodynamics of the black hole plays an important role. It has been found that a black hole possesses not only standard thermodynamic quantities but also abundant phase structures and critical phenomena, such as the Hawking–Page phase transition [1], similar to a general thermodynamic system. Even more interesting is that the studies on the charged black holes show that they may have an analogous phase transition to that of van der Walls–Maxwell’s liquid-gas [2, 3]. In recent years, the idea of including the variation of the cosmological constant \(\Lambda \) in the first law of the black hole thermodynamics has attracted increasing attention [2,3,4,5,6]. In the case of an asymptotical AdS and dS black hole in n dimensions, one identifies the pressure of the black hole with the cosmological constant \(\Lambda \) [4],

$$\begin{aligned} P=-\frac{1}{8 \pi } \Lambda =\frac{n(n-1)}{16 \pi l^2} \end{aligned}$$
(1.1)

and the corresponding conjugate quantity, the thermodynamic volume [5],

$$\begin{aligned} V=\left( {\frac{\partial M}{\partial P}} \right) _{S,Q_i ,J_k}. \end{aligned}$$
(1.2)

It may seem a little surprising that one elevate \(\Lambda \) to the status of a thermodynamic variable. \(\Lambda \) is usually thought of as an energy in the Einstein action. However, there are some physical reasons to view the cosmological constant as a variable of pressure. For example, one may suppose that there exist several more fundamental theories where some physical constants such as Yukawa coupling, gauge coupling constants, Newton’s constant, and/or cosmological constant may not be fixed values but dynamical ones arising from the vacuum expectation values. In that case, it is natural to add these variations of “constants” into the first law of black hole thermodynamics [3,4,5,6]. The \((P\sim V)\) critical behaviors in AdS and dS black holes have been extensively studied [7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58]. A completely simulated gas–liquid system has been put forward.

Using the Ehrenfest scheme, Refs. [39,40,41,42,43] studied the critical phenomena in a series of black holes in AdS spacetime, and proved the phase transition at the critical point is second order, which has also been confirmed in Refs. [5, 59,60,61] by studying thermodynamics and state space geometry of black holes. Although some encouraging results about black hole thermodynamic properties in AdS and dS spacetimes have been achieved and the problems about phase transition of black holes have been extensively discussed, a unified recognition about the phase transition of the black hole has not been put forward. It is significant to further explore phase equilibrium and phase structure in black holes, which can help to recognize the evolution of black holes.

The motivation for studying higher dimensional black holes comes from developments in string/M-theory, which is believed to be the most consistent approach to a quantum theory of gravity. It was argued that black holes may play a crucial role in the analysis of the dynamics in higher dimensions as well as in the compactification mechanisms. In particular, to test novel predictions of string/M-theory, black holes may serve as good theoretical laboratories. It has been thought that the statistical-mechanical calculation of the Bekenstein–Hawking entropy for a class of supersymmetric black holes in five dimensions is one of the remarkable results in string theory [62, 63]. Another motivation for studying higher dimensional black holes originates from the braneworld scenarios, as a new fundamental scale of quantum gravity. An interesting consequence of these models is the possibility of mini black hole production at future accelerating colliders [64]. It is nontrivial to study the higher dimensional spacetime, because the dimension of spacetime will affect the thermodynamical properties of the black hole [65,66,67,68].

The theory of nonlinear electrodynamics was first introduced in 1930s by Born and Infeld to obtain a classical theory of charged particles with finite self-energy [69]. Born–Infeld (BI) theory has received a lot of attention since it turns out to play an important role in string theory. The BI action, including a dilaton and an axion field, appears in the coupling of an open superstring and an Abelian gauge field theory [70]. Here we would like to consider another type of nonlinear electrodynamics, namely, the exponential form of the nonlinear electrodynamics in the setup of dilaton gravity. These are our main motivations to explore the effects of dilaton field on the properties of higher dimensional charged black holes with a nonlinear source.

The isotherms in P–v diagrams of charged topological dilaton AdS black holes in Ref. [15] show that there exists a thermodynamically unstable region with \(\partial P/\partial v>0\) when the temperature is below the critical temperature and the negative pressure emerges when temperature is below a certain value. This situation also exists in van der Waals–Maxwell gas–liquid system, which has been resolved by Maxwell’s equal area law. In this paper, using the Maxwell’s equal area law, we establish a phase transition process in charged topological dilaton AdS black holes, where the issues about unstable states and negative pressure are resolved. By studying the phase transition process, we acquire the two-phase equilibrium properties including the P–T phase diagram, Clapeyron equation and latent heat of the phase change. The results show the phase transition below the critical temperature is of the first order but phase transition at the critical point belongs to the continuous one, i.e., the second order phase transition.

Outline of this paper is as follows: the higher dimensional charged topological dilaton AdS black hole as a thermodynamic system is briefly introduced in Sect. 2. In Sect. 3, by the Maxwell equal area law the phase transition processes at certain temperatures are obtained and the boundary of two-phase equilibrium region are depicted in the P–v diagram for a higher dimensional charged topological dilaton AdS black hole. Then some parameters of the black hole are analyzed to find the relevance with the two-phase equilibrium. In Sect. 4, the P–T phase diagrams are plotted and the Clapeyron equation and latent heat of the phase change are derived. We present some discussions and conclusions in Sect. 5 (we use the units \(G_d =\hbar =k_B=c=1\) in this paper).

2 The thermodynamic quantities of higher-dimensional charged dilaton black holes

We consider the n-dimensional \((n\ge 4)\) action in which gravity is coupled to the dilaton and nonlinear electrodynamic field. The motivation for choosing the model includes: First, the solution of this model might lead to possible extensions of the AdS/CFT correspondence. Second, such solutions of this model may be used to extend the range of validity of methods and tools originally developed for asymptotically flat or asymptotically (A)dS black holes. The Einstein–Maxwell–Dilaton (EMD) action in n-dimensional spacetime is [71]

$$\begin{aligned} S= & {} \frac{1}{16\pi }\int {\mathrm{d}^{n}} x\sqrt{-g} \nonumber \\&\times \left( {R-\frac{4}{n-2}(\nabla \Phi )^2-V(\Phi )-L(F, \Phi )} \right) , \end{aligned}$$
(2.1)

where the dilaton potential contains two Liouville terms:

$$\begin{aligned} V(\Phi ) =2\Lambda _0 e^{2 \varsigma _0 \Phi } + 2\Lambda e^{2 \varsigma \Phi } \end{aligned}$$
(2.2)

and

$$\begin{aligned} L(F,\Phi )=4 \beta ^2 e^{4\alpha \Phi /(n-2)}\left[ \mathrm{exp}\left( -\frac{e^{-8\alpha \Phi /(n-2)}F^2}{4\beta ^2}-1 \right) \right] \nonumber \\ \end{aligned}$$
(2.3)

where R is the Ricci scalar curvature, \(\Phi \) is the dilaton field and \(V(\Phi )\) is a potential for \(\Phi \), \(\Lambda _0 \), \(\Lambda \), \(\varsigma _0 \) and \(\varsigma \) are parameters. \(\alpha \) is a parameter determining the strength of the coupling of the scalar and electromagnetic field. This kind of potential was previously investigated in the context of BI–dilaton (BId) black holes [20, 21] as well as EMD gravity [41,42,43,44,45,46]. In the limit \(\beta \rightarrow \infty \), the Lagrangian of the exponential nonlinear electrodynamics coupled to the dilaton field recovers the standard linear Maxwell Lagrangian coupled to the dilaton field. The obtained solutions fully satisfy the system of Eq. (2.1) provided we take

$$\begin{aligned} \varsigma _0=1/\alpha ,\quad \varsigma =\alpha ,\quad \Lambda _0=b^{-2} \alpha ^2/(\alpha ^2-1). \end{aligned}$$
(2.4)

Notice that \(\Lambda \) remains as a free parameter, which plays the role of the cosmological constant [71].

Fig. 1
figure 1

Isotherms in the P–v diagrams of higher-dimensional charged topological dilaton black holes in n dimensional AdS spacetime

Full size image

The metric of such a spacetime can be written

$$\begin{aligned} \mathrm{d}s^2=-f(r)\mathrm{d}t^2+\frac{\mathrm{d}r^2}{f(r)}+r^2R^2(r)\mathrm{d}\Omega _{n-2}^2. \end{aligned}$$
(2.5)

More details of the metric function f(r) can be found in Appendix A. The location of the black horizon satisfies the equation \(f(r_+)=0\), from which we obtain

$$\begin{aligned} m= & {} - \frac{(n - 3)(\alpha ^2 + 1)^2b^{ - \gamma }}{(\alpha ^2 - 1)(\alpha ^2 + n - 3)}r_+^{n - 3 - (n - 4)\gamma / 2} \nonumber \\&+\;\frac{2\Lambda (\alpha ^2 + 1)^2b^\gamma }{(n - 2)(\alpha ^2 - n + 1)}r_+^{n - 1 - n\gamma / 2}\nonumber \\&+\;\frac{2q^2(\alpha ^2 + 1)^2b^{ - (n - 3)\gamma }}{(n - 2)(\alpha ^2 + n - 3)r_+^{ - (n - 4)\gamma / 2 + n - 3}}\nonumber \\&-\;\frac{q^4(\alpha ^2 + 1)^2b^{ - (2n - 5)\gamma }}{2\beta ^2(n - 2)(\alpha ^2 + 3n - 7)r_+^{3n - 7 + (8 - 3n)\gamma / 2}} \nonumber \\&+\; o\left( {\frac{1}{\beta ^4}} \right) . \end{aligned}$$
(2.6)

In (2.6), m serves as an integration constant. According to the definition of mass due to Abbott and Deser [72], the ADM (Arnowitt–Deser–Misner) mass of the solution (A8) is

$$\begin{aligned} M(S,Q,P)= & {} \frac{b^{(n - 2)\gamma / 2}(n - 2)\omega _{n - 2} }{16\pi (\alpha ^2 + 1)}m \nonumber \\= & {} - \frac{(n - 3)(n - 2)\omega _{n - 2} (\alpha ^2 + 1)b^{(n - 4)\gamma / 2}}{16\pi (\alpha ^2 - 1)(\alpha ^2 + n - 3)}\nonumber \\&\times \; r^{n - 3 - (n - 4)\gamma / 2} \nonumber \\&+\, \frac{2\Lambda (\alpha ^2 + 1)\omega _{n - 2} b^{n\gamma / 2}}{16\pi (\alpha ^2 - n + 1)}r^{n - 1 - n\gamma / 2} \nonumber \\&+\, \frac{2q^2(\alpha ^2 + 1)\omega _{n - 2} b^{ - (n - 4)\gamma / 2}}{16\pi (\alpha ^2 + n - 3)r^{ - (n - 4)\gamma / 2 + n - 3}} \nonumber \\&-\, \frac{q^4(\alpha ^2 + 1)\omega _{n - 2} b^{ - (3n - 8)\gamma / 2}}{32\pi \beta ^2(\alpha ^2 + 3n - 7)r^{3n - 7 + (8 - 3n)\gamma / 2}} \nonumber \\&+\, o\left( {\frac{1}{\beta ^4}} \right) . \end{aligned}$$
(2.7)

The entropy of the EMD black hole still satisfies the so-called area law of the entropy, which states that the entropy of the black hole is a quarter of the event horizon area [73]. This universal law applies to almost all kinds of black holes, including dilaton black holes, in Einstein gravity [74, 75]. It is easy to show

$$\begin{aligned} S = \frac{b^{(n - 2)\gamma / 2}\omega _{n - 2} r_ + ^{(n - 2)(1 - \gamma / 2)} }{4}. \end{aligned}$$
(2.8)

One may then regard the parameters S, Q and P as a complete set of parameters for the mass M(S, Q, P) and define the parameters conjugate to S, Q and P. These quantities are the temperature, the electric potential and the volume,

$$\begin{aligned} T = \left( {\frac{\partial M}{\partial S}} \right) _{Q,P} , \quad U = \left( {\frac{\partial M}{\partial Q}} \right) _{S,P} , \quad V = \left( {\frac{\partial M}{\partial P}} \right) _{Q,S} ,\nonumber \\ \end{aligned}$$
(2.9)

where the temperature of Hawking radiation is

$$\begin{aligned} T= & {} - \frac{(n - 3)(1 + \alpha ^2)b^{ - \gamma }}{4\pi (\alpha ^2 - 1)}r_ + ^{\gamma - 1} - \frac{\Lambda (1 + \alpha ^2)b^\gamma }{2\pi (n - 2)}r_ + ^{1 - \gamma } \nonumber \\&-\;\frac{q^2(1 + \alpha ^2)b^{ - (n - 3)\gamma }}{2\pi (n - 2)}r_ + ^{(n\gamma + 5 - 3\gamma - 2n)} \nonumber \\&+\;\frac{q^4(1 + \alpha ^2)b^{ - (2n - 5)\gamma }}{8\pi (n - 2)\beta ^2}r_ + ^{9 + 2n\gamma - 4n - 5\gamma } + o\left( {\frac{1}{\beta ^4}} \right) ,\nonumber \\ \end{aligned}$$
(2.10)

the electric potential is

$$\begin{aligned} U= & {} \frac{4\pi Q(\alpha ^2 + 1)b^{(4 - n)\gamma / 2}}{(\alpha ^2 + n - 3)\omega _{n - 2} r_ + ^{n - 3 + 2\gamma - n\gamma / 2} }\nonumber \\&-\;\frac{(4\pi )^3Q^3(\alpha ^2 + 1)b^{ - (3n - 8)\gamma / 2}}{2\beta ^2\omega _{n - 2}^3 (\alpha ^2 + 3n - 7)r^{3n - 7 + (8 - 3n)\gamma / 2}} + o\left( {\frac{1}{\beta ^4}} \right) ,\nonumber \\ \end{aligned}$$
(2.11)

and the volume is

$$\begin{aligned} V = - \frac{(\alpha ^2 + 1)b^{\gamma n / 2}\omega _{n - 2} }{(\alpha ^2 - n + 1)}r_ + ^{n - 1 - \gamma n / 2} . \end{aligned}$$
(2.12)

Note that in the limit \(\beta \rightarrow \infty \), Eq. (2.10) reduces to the temperature of higher dimensional EMD black holes [43]. Thus, the thermodynamics quantities satisfy the first law of thermodynamics

$$\begin{aligned} \mathrm{d}M = T\mathrm{d}S + U\mathrm{d}Q + V\mathrm{d}P. \end{aligned}$$
(2.13)

For the electric potential satisfies the superposition principle, we can rewrite Eq. (2.11),

$$\begin{aligned} U = U_1 + U_2 , \end{aligned}$$
(2.14)

where

$$\begin{aligned} U_1 = \frac{4\pi Q(\alpha ^2 + 1)b^{(4 - n)\gamma / 2}}{(\alpha ^2 + n - 3)\omega _{n - 2} r_ + ^{n - 3 + 2\gamma - n\gamma / 2} }, \end{aligned}$$
$$\begin{aligned} U_2= & {} - \frac{(4\pi )^3Q^3(\alpha ^2 + 1)b^{ - (3n - 8)\gamma / 2}}{2\beta ^2\omega _{n - 2}^3 (\alpha ^2 + 3n - 7)r^{3n - 7 + (8 - 3n)\gamma / 2}} + o\left( {\frac{1}{\beta ^4}} \right) .\nonumber \\ \end{aligned}$$
(2.15)

So we have the Smarr formula,

$$\begin{aligned} M= & {} \frac{(n - 2)}{\alpha ^2 + n - 3}TS + U_1 Q + \frac{(\alpha ^2 + 2n - 5)}{2(\alpha ^2 + n - 3)}U_2 Q \nonumber \\&+\;\frac{2(\alpha ^2 - 1)}{\alpha ^2 + n - 3}VP. \end{aligned}$$
(2.16)

Notice that Eqs. (2.13) and (2.16) satisfy the given family of solutions. We can rewrite Eq. (2.10),

$$\begin{aligned} P= & {} \frac{T}{v} + \frac{k(n - 2)(\alpha ^2 + 1)^2}{\pi (n - 1)(\alpha ^2 - 1)v^2} \nonumber \\&+\;\frac{Q^2b^{2(1 - n)\gamma }2\pi }{\omega _{n - 1}^2 }\left( {\frac{v(n - 1)}{4(\alpha ^2 + 1)b^{2\gamma }}} \right) ^{\textstyle {{(2 - n)(2 - \gamma )} \over {1 - 2\gamma }}} \nonumber \\&-\;\frac{Q^4(4\pi )^3(1 + \alpha ^2)b^{ - (2n - 5)\gamma }}{2\omega _{n - 2}^4 (n - 2)\beta ^2}r_ + ^{9 + 2n\gamma - 4n - 5\gamma } \nonumber \\= & {} \frac{T}{v} - \frac{A}{v^2} + \frac{BQ^2}{v^d} - \frac{CQ^4}{v^{2d}}, \end{aligned}$$
(2.17)

with the specific volume [15]

$$\begin{aligned} v = \frac{4(\alpha ^2 + 1)b^\gamma }{(n - 2)}r_ + ^{1 - \gamma } , \end{aligned}$$
(2.18)

and with

$$\begin{aligned} d = \frac{(n - 2)(2 - \gamma )}{1 - \gamma }, \quad A = \frac{(n - 3)(\alpha ^2 + 1)^2}{\pi (n - 2)(1 - \alpha ^2)}, \end{aligned}$$
$$\begin{aligned} B = \frac{b^{(2 - n)\gamma }2\pi }{\omega _{n - 1}^2 }\left( {\frac{4(\alpha ^2 + 1)b^{2\gamma }}{(n - 2)}} \right) ^{(n - 2)(2 - \gamma ) / (1 - \gamma )}, \end{aligned}$$
$$\begin{aligned} C = \frac{b^{2(2 - n)\gamma }(4\pi )^3}{8\omega _{n - 1}^4 \beta ^2}\left( {\frac{4(\alpha ^2 + 1)b^{2\gamma }}{(n - 2)}} \right) ^{2(n - 2)(2 - \gamma ) / (1 - \gamma )}.\nonumber \\ \end{aligned}$$
(2.19)

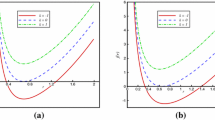
In Fig. 1 we plot the isotherms in the P–v diagrams in terms of the state equation (2.17) at different dimension n, charge Q, and parameters b and \(\alpha \). One can see from Fig. 1 that there are thermodynamically unstable regimes with \(\partial P/\partial v>0\) on the isotherms when the temperature \(T<T_c \), where \(T_c \) is the critical temperature. When the temperature \(T=T_0\), there is a point of intersection between the isotherms and the horizontal v axis. The negative pressure emerges when the temperature is below a certain value \(T_0\). \(T_0\) and the corresponding specific volume \(v_0\) can be derived,

$$\begin{aligned} \begin{aligned}&Av_0^{2d - 1} = BQ^2(d - 1)v_0^d - CQ^4(2d - 1), \\&T_0 = \frac{A}{v_0 } - \frac{BQ^2}{v_0^{d - 1} } + \frac{CQ^4}{v_0^{2d - 1} }. \end{aligned} \end{aligned}$$
(2.20)

3 Two-phase equilibrium and Maxwell’s equal area law

The equation of state of the charged topological black hole is exhibited by the isotherms in Fig. 1, in which the thermodynamic unstable states with \(\partial P/\partial v>0\) will lead to the system automatically expand or contract unrestrictedly. The cases occur also in the van der Waals equation but they have been resolved by Maxwell’s equal area law.

We extend the Maxwell equal area law to n-dimensional charged topological dilaton AdS black hole to establish a phase transition process of the black hole as a thermodynamic system. On the isotherm with temperature \(T_0 \) in the P–v diagram, the two points \(\left( {P_0 ,\;v_1 } \right) \) and \(\left( {P_0 ,\;v_2 } \right) \) meet Maxwell’s equal area law,

$$\begin{aligned} P_0 (v_2 -v_1 )=\int \limits _{v_1 }^{v_2 } {P\mathrm{d}v} , \end{aligned}$$
(3.1)

which results in

$$\begin{aligned} P_0 (v_2 - v_1 )= & {} T_0 \ln \left( {\frac{v_2 }{v_1 }} \right) - A\left( {\frac{1}{v_1 } - \frac{1}{v_2 }} \right) \nonumber \\&+\;\frac{BQ^2}{d - 1}\left( {\frac{1}{v_1^{d - 1} } - \frac{1}{v_2^{d - 1} }} \right) \nonumber \\&-\;\frac{CQ^4}{2d - 1}\left( {\frac{1}{v_1^{2d - 1} } - \frac{1}{v_2^{2d - 1} }} \right) , \end{aligned}$$
(3.2)

where the two points \(\left( {P_0 ,\;v_1 } \right) \) and \(\left( {P_0 ,\;v_2 } \right) \) are seen as endpoints of an isothermal phase transition. Considering

$$\begin{aligned} \begin{aligned}&P_0 = \frac{T_0 }{v_1 } - \frac{A}{v_1^2 } + \frac{BQ^2}{v_1^d } - \frac{CQ^4}{v_1^{2d} }, \\&P_0 = \frac{T_0 }{v_2 } - \frac{A}{v_2^2 } + \frac{B}{v_2^d } - \frac{CQ^4}{v_2^{2d} }, \end{aligned} \end{aligned}$$
(3.3)

we can get

$$\begin{aligned} 0= & {} T_0 \left( {\frac{1}{v_1 } - \frac{1}{v_2 }} \right) - A\left( {\frac{1}{v_1^2 } - \frac{1}{v_2^2 }} \right) + BQ^2\left( {\frac{1}{v_1^d } - \frac{1}{v_2^d }} \right) \nonumber \\&- \,CQ^4\left( {\frac{1}{v_1^{2d} } - \frac{1}{v_2^{2d} }} \right) , \end{aligned}$$
(3.4)
$$\begin{aligned} 2P_0= & {} T_0 \left( {\frac{1}{v_1 } + \frac{1}{v_2 }} \right) - A\left( {\frac{1}{v_1^2 } + \frac{1}{v_2^2 }} \right) \nonumber \\&+\; BQ^2\left( {\frac{1}{v_1^d } + \frac{1}{v_2^d }} \right) - CQ^4\left( {\frac{1}{v_1^{2d} } + \frac{1}{v_2^{2d} }} \right) . \end{aligned}$$
(3.5)

Using Eqs. (3.2), (3.3) and (3.4), we get

$$\begin{aligned}&Av_2^{2d - 2} x^{2d - 2}\left( {2(1 - x) + (1 + x)\ln x} \right) \nonumber \\&\quad = BQ^2v_2^d x^d\left( {\frac{d(1 - x^{d - 1})}{(d - 1)} + \frac{(1 - x^d)\ln x}{(1 - x)}} \right) \nonumber \\&\qquad -\;CQ^4\left( {\frac{2d(1 - x^{2d - 1})}{(2d - 1)} + \frac{(1 - x^{2d})\ln x}{(1 - x)}} \right) , \end{aligned}$$
(3.6)

with \(x=v_1 /v_2 \) \((0<x<1)\). When x is given, we can obtain \(v_2\) and \(v_1\) corresponding to x from (3.6).

For small C, taking the zeroth order approximation, we obtain

$$\begin{aligned} v_{2;0}^{d - 2}= & {} \frac{B}{A}\frac{d(1 - x^{d - 1})(1 - x) + (d - 1)(1 - x^d)\ln x}{x^{d - 2}(d - 1)(1 - x)\left( {2(1 - x) + (1 + x)\ln x} \right) }\nonumber \\= & {} f^{d - 2}(x). \end{aligned}$$
(3.7)

Therefore, we can obtain the first order approximation solution \(v_{2;1}^{d - 2}\) by substituting \(v_{2;0}^{d - 2}\) into Eq. (3.6). Similarly, we can obtain the second order approximation solution \(v_{2;2}^{d - 2}\) by substituting \(v_{2;2}^{d - 2}\) into Eq. (3.6). Thus proceeding, we can obtain the arbitrary order approximation solution. For convenience, we take

$$\begin{aligned} v_2 = F(x). \end{aligned}$$
(3.8)

In the first order approximation, we have

$$\begin{aligned} v_{2;1}^{2d - 2}= & {} \left( {\frac{d(1 - x^{d - 1})}{(d - 1)} + \frac{(1 - x^d)\ln x}{(1 - x)}} \right) \nonumber \\&\times \frac{BQ^2f^{d}(x)}{Ax^{d - 2}\left( {2(1 - x) + (1 + x)\ln x} \right) } \nonumber \\&-\;\frac{CQ^4}{Ax^{2d - 2}\left( {2(1 - x) + (1 + x)\ln x} \right) }\nonumber \\&\times \left( {\frac{2d(1 - x^{2d - 1})}{(2d - 1)} + \frac{(1 - x^{2d})\ln x}{(1 - x)}} \right) \nonumber \\\approx & {} F^{2d - 2}(x). \end{aligned}$$
(3.9)

When \(x\rightarrow 1\), the corresponding state is a critical point state. From (3.7) and (3.9), we can obtain

$$\begin{aligned} v_c^{2d - 2}= & {} v_c^d \mathop {\lim }\limits _{x \rightarrow 1} \frac{BQ^2}{Ax^{d - 2}\left( {2(1 - x) + (1 + x)\ln x} \right) } \nonumber \\&\times \left( {\frac{d(1 - x^{d - 1})}{(d - 1)} + \frac{(1 - x^d)\ln x}{(1 - x)}} \right) \nonumber \\&- \mathop {\lim }\limits _{x \rightarrow 1} \frac{CQ^4}{Ax^{2d - 2}\left( {2(1 - x) + (1 + x)\ln x} \right) }\nonumber \\&\times \left( {\frac{2d(1 - x^{2d - 1})}{(2d - 1)} + \frac{(1 - x^{2d})\ln x}{(1 - x)}} \right) . \end{aligned}$$
(3.10)

From (3.4), we obtain

$$\begin{aligned} Tv_2^{2d - 1} x^{2d - 1}= & {} Av_2^{2d - 2} x^{2d - 2}(1 + x) - BQ^2\frac{v_2^d x^d(1 - x^d)}{1 - x} \nonumber \\&+ \,CQ^4\frac{(1 - x^{2d})}{1 - x}. \end{aligned}$$
(3.11)

Substituting (3.8) into (3.11), we can obtain

$$\begin{aligned}&\chi T_c x^{2d - 1}F^{2d - 1}(x) \nonumber \\&\quad = Ax^{2d - 2}F^{2d - 2}(x)(1 + x)- BQ^2\frac{x^dF^d(x)(1 - x^d)}{1 - x} \nonumber \\&\quad \quad +\, CQ^4\frac{(1 - x^{2d})}{1 - x}, \end{aligned}$$
(3.12)

with \(T=\chi T_c\). Because we take account of the case that the temperature T below the critical temperature \(T_c\), the value of \(\chi =\frac{T}{T_c}\) is from 0 to 1. When \(x\rightarrow 1\) and \(\chi \rightarrow 1\), the corresponding state is critical state. For a fixed \(\chi \), i.e. a fixed \(T_0 \), we can get a certain x from Eq. (3.12), and then according to Eqs. (3.3) and (3.6), \(v_2 \) and \(P_0 \) are solved.

Fig. 2
figure 2

The simulated isothermal phase transition by isobars and the boundary of two-phase coexistence region for the topological dilaton black hole as \(n=5\), \(b=1.2\), \(Q=1.2\), \(\alpha =\frac{1}{\sqrt{3}}\)

Full size image
Fig. 3
figure 3

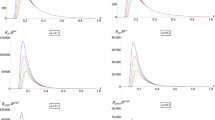
Two-phase equilibrium coexistence curves in the P–T diagrams for the topological dilaton black hole in 5-dimensional AdS spacetime. In the diagram, we have the first line with \(b=0.8\), the second line with \(b=1.0\), the final line with \(b=1.2\) and the first column with \(Q=1.0\), the second column with \(Q=1.2\), the final column with \(Q=1.5\)

Full size image
Fig. 4
figure 4

L–x curves for the topological dilaton black hole in n-dimensional AdS spacetime as \(n=4,5,6\). In each diagram, the coupling coefficient \(\alpha =\frac{1}{\sqrt{3}}\) and the arbitrary constant \(b=1.2\)

Full size image
Fig. 5
figure 5

L–T curves for the topological dilaton black hole in n-dimensional AdS spacetime as \(n=5\). In the diagram, we have the first line with \(b=0.8\), the second line with \(b=1.0\), the final line with \(b=1.2\) and the first column with \(Q=1.0\), the second column with \(Q=1.2\), the final column with \(Q=1.5\)

Full size image

4 Two-phase coexistent curves and the phase change latent

Due to the lack of knowledge of the chemical potential, the P–T curves of two-phase equilibrium coexistence for a general thermodynamic system are usually obtained by experiment. However, the slope of the curves can be calculated by the Clapeyron equation in theory,

$$\begin{aligned} \frac{\mathrm{d}P}{\mathrm{d}T}=\frac{L}{T(v^\beta -v^\alpha )}, \end{aligned}$$
(4.1)

where the latent heat of the phase change \(L=T(s^\beta -s^\alpha )\), \(v^\alpha \), \(s^\alpha \) and \(v^\beta \), \(s^\beta \) are the molar volumes and molar entropy of phase \(\alpha \) and phase \(\beta \), respectively. So the Clapeyron equation provides a direct experimental verification for some phase transition theories.

Here we investigate the two-phase equilibrium coexistence P–T curves and the slope of them for the topological dilaton AdS black hole. From (3.12), we can obtain the temperature

$$\begin{aligned} T= & {} A\frac{(1 + x)}{xF(x)} - BQ^2\frac{(1 - x^d)}{(1 - x)x^{d - 1}F^{d - 1}(x)}\nonumber \\&+\, CQ^4\frac{(1 - x^{2d})}{1 - x} + CQ^4\frac{(1 - x^{2d})}{(1 - x)x^{2d - 1}F^{2d - 1}(x)} \nonumber \\= & {} G(x). \end{aligned}$$
(4.2)

Meanwhile, from Eq. (2.17), we obtain

$$\begin{aligned} P = \frac{T}{F(x)} - \frac{A}{F^2(x)} + \frac{BQ^2}{F^d(x)} - \frac{CQ^4}{F^{2d}(x)}. \end{aligned}$$
(4.3)

Substituting Eq. (4.2) into Eq. (4.3), we can obtain

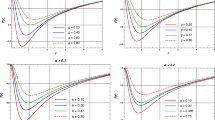
$$\begin{aligned} P = \frac{G(x)}{F(x)} - \frac{A}{F^2(x)} + \frac{BQ^2}{F^d(x)} - \frac{CQ^4}{F^{2d}(x)} = H(x). \end{aligned}$$
(4.4)

We plot the P–T curves with \(0<x\le 1\) in Fig. 3 when the parameter b, coupling parameter \(\alpha \), and charge Q take different values, respectively. The curves represent the two-phase equilibrium condition for the topological dilaton AdS black hole and the terminal points of the curves represent the corresponding critical points. Figure 3 shows that, for fixed parameter b and charge Q, both the critical temperature and the critical pressure increase as the coupling parameter \(\alpha \) increases. Both the critical temperature and the critical pressure increase with coupling parameter \(\alpha \), but the two-phase equilibrium pressure decreases with increasing parameter b at a certain temperature. The change of the two-phase equilibrium curve with charge Q is similar to that with parameter b. As the charge Q becomes larger the critical pressure and critical temperature become smaller.

From Eq. (4.4), we obtain

$$\begin{aligned} \frac{\mathrm{d}P}{\mathrm{d}T}=\frac{H '(x)}{G'(x)}, \end{aligned}$$
(4.5)

where \(H'(x)=\frac{\mathrm{d}H}{\mathrm{d}x}\). Equation (4.5) represents the slope of two-phase equilibrium P–T curve as a function of x. From Eqs. (4.1) and (4.5), we can get the latent heat of the phase change as a function of x for the n-dimensional charged topological dilaton AdS black hole,

$$\begin{aligned} L=T(1-x)\frac{H '(x)}{G '(x)}F(x)=(1-x)\frac{H '(x)}{G '(x)}G (x)F(x).\nonumber \\ \end{aligned}$$
(4.6)

We plot the L–x curves with \(0<x\le 1\) in Fig. 4, as the parameter b, coupling parameter \(\alpha \) and charge Q take certain values. From Fig. 5 we can see that the effects of x and the spacetime dimension n and charge Q on phase change latent heat L.

The change rate of latent heat of the phase change with temperature for some usual thermodynamic systems

$$\begin{aligned} \frac{\mathrm{d}L}{\mathrm{d}T}= & {} C_P^\beta -C_P^\alpha +\frac{L}{T}\nonumber \\&-\left[ {\left( {\frac{\partial v^\beta }{\partial T}} \right) _P -\left( {\frac{\partial v^\alpha }{\partial T}} \right) _P } \right] \frac{L}{v^\beta -v^\alpha }, \end{aligned}$$
(4.7)

where \(C_P^\beta \) and \(C_P^\alpha \) are the molar heat capacities of phase \(\beta \) and phase \(\alpha \). For \(n+1\)-dimensional charged topological dilaton AdS black hole, the change rate of the latent heat of the phase transition with temperature can be obtained from Eqs. (4.6) and (4.2),

$$\begin{aligned} \frac{\mathrm{d}L}{\mathrm{d}T}=\frac{\mathrm{d}L}{\mathrm{d}x}\frac{\mathrm{d}x}{\mathrm{d}T}=\frac{\mathrm{d}L}{\mathrm{d}x}\frac{1}{G '(x)}. \end{aligned}$$
(4.8)

Using Eqs. (4.6) and (4.2) we plot the latent heat and the temperature curves in Fig. 5 as the parameter b, coupling parameter \(\alpha \) and charge Q take certain values. From Fig. 5 we can see that the effects of the temperature T and the coupling parameters \(\alpha \), parameter b, and charge Q on the latent heat L of the phase change. When T increases, the latent heat L is not monotonous but increases firstly and then decreases to zero as \(T\rightarrow T_c \). The latent heat L decreases with increasing coupling parameter \(\alpha \) as the other parameters, b and charge Q, are fixed. Similarly the latent heat L decreases with increasing charge Q for fixed parameter b and coupling parameter \(\alpha \).

5 Concluding remarks

Investigation of the phase transition of the black holes is important and necessary. On the one hand, it is helpful for us to understand the structure and nature of spacetime. On the other hand, it may uncover some phase transitions of the realistic physics in the conformal field theory according to the AdS/CFT correspondence. The higher-dimensional charged topological dilaton AdS black hole with a nonlinear source is regarded as a thermodynamic system, and its equation of state has been derived. But when the temperature is below the critical temperature, a thermodynamically unstable situation appears on the isotherms, and when the temperature reduces to a certain value a negative pressure emerges, which can be seen in Figs. 1 and 2. However, by Maxwell’s equal area law we established a phase transition process and the problems can be resolved. The phase transition process at a defined temperature happens at a constant pressure, where the system specific volume changes along with the ratio of the two coexistent phases. According to the Ehrenfest scheme the phase transition is of first order. We draw the isothermal phase transition process and depict the boundary of the two-phase coexistence region in Fig. 2. In this paper we have plotted the two-phase equilibrium curves in the P–T diagrams, derived the slope of the curves, and acquired information on the latent heat of the phase change by the Clapeyron equation, which could create conditions for finding some usual thermodynamic systems similar to black holes as regards thermodynamic properties and provide a theoretical basis for experimental research on analogous black holes.

In this paper, we have extended the study of the exponential nonlinear electrodynamics by taking into account the dilaton scalar field in the action. It is important to mention that one can see the influences of the nonlinear parameter on the thermodynamic properties of the black hole system from Figs. 3 and 5. For fixed Q, \(\alpha \), and temperature, the pressure of the two-phase coexistence decreases as the parameter b decreases. Besides, the latent heat L also decreases as the parameter b increases. Analyzing these data, it is found that the phase transition of black hole thermodynamics become harder if the coupled coefficient \(\alpha \) grows or the parameter b increases. From Fig. 4 one can find that the latent heat L increases as the spacetime dimension n increases. The latent heat L is more different in higher dimensions than 4-dimensional spacetime. Meanwhile, we find that the dimension n have an effect on the simulated phase transition process. The phase transition will be harder when the dimension n is large.

An appropriate theoretical interpretation to the phase structure of the AdS black hole thermodynamic system can help to learn about the black hole thermodynamic properties, such as entropy, temperature, heat capacity and so on, of the black hole, and that is significant for improving a self-consistent thermodynamic theory of black holes. The Clapeyron equation of usual thermodynamic systems agrees well with the experimental result. The thermodynamics of higher order gravity remains to be further explored. It is quite possible that these objects may also exhibit interesting thermodynamic behavior by Maxwell’s equal area laws.