1 Moments of net-baryon distributions and quasi-particle model of QGP

Lattice QCD calculations indicate that at baryon chemical potential \(\mu _\mathrm{B}=0\), the transition from the quark–gluon plasma (QGP) to a hadron gas is a smooth crossover, while at large \(\mu _\mathrm{B}\), the phase transition is of first order. The end point of the first order phase transition boundary is the so-called the critical point (CP). The fluctuations of the net-proton number measured by the STAR experiment at RHIC suggest that a possible CP is unlikely below \(\mu _\mathrm{B}=200\) MeV [1]. The moments of the conserved quantities distributions, for example the net-baryon number, in the relativistic heavy ion collisions are sensitive to the correlation length \(\xi \) of the system [2, 3], and they are believed to be good signatures of the QCD phase transition and CP. Typically variances (\(\sigma ^2=\left<(N-\left<N\right>)^2\right>\)) of the distributions are related to \(\xi \) by \(\sigma ^2\sim \xi ^2\). The numerator in the skewness (\(S=\left<(N-\left<N\right>)^3\right>/\sigma ^3\)) goes as \(\xi ^{4.5}\) and the kurtosis (\(\kappa =\left<(N-\left<N\right>)^4\right>/\sigma ^4-3\)) goes as \(\xi ^7\).

On the other hand, the moments of the baryon number are related to the various order baryon number susceptibilities [4]. In order to cancel the volume, the products of the moments, \(S\sigma \) and \(\kappa \sigma ^2\), are constructed as the experimental observables. The results in RHIC of these observables show a centrality and energy dependence [5], which are not reproduced by a non-CP transport and hadron resonance gas model calculations. The deviations of \(S\sigma \) and \(\kappa \sigma ^2\) below the Skellam expectation are qualitatively consistent with a QCD-based model which includes a CP [6]. The energy dependence of the \(\kappa \sigma ^2\) of net-proton distributions in Au+Au collisions show non-monotonic behavior, which is consistent with being close to the CP [7, 8].

In this paper we apply the quasi-particle model (qQGP) of the quark–gluon plasma (QGP) to calculate the moments of the net-baryon distributions. The qQGP model was first proposed by Peshier et al. [9] to study the non-ideal equation of state (EoS) by lattice QCD results. Instead of real quarks and gluons with QCD interactions, the system is considered to be made up of non-interacting quasi-quarks and quasi-gluons with thermal masses. Quasi-particles are thought to be quanta of plasma collective modes excited by quarks and gluons through QCD interactions.

By now, some approaches have been proposed to study the qQGP model. The effective mass methods [9,10,11,12,13,14], the approaches based on the Polyakov loop [15,16,17,18,19], the approach based on Fermi liquids theory [20,21,22,23,24] and so on. Compared with the first and second approach, the third one is fundamentally different and powerful. Besides reproducing the EoS accurately, it is also successful in predicting the bulk and transport properties of QGP [20,21,22,23,24].

Gorenstein and Yang pointed out that the initial quasi-particle model was thermodynamically inconsistent and then reformulated the statistical mechanics (SM) to solve the inconsistency [25]. But then the expressions of pressure and energy density end up with extra undetermined, temperature dependent terms, which need to be phenomenologically chosen. One should pay attention to this reformulation, which in fact is based on mathematical identities involving derivatives with respect to temperature and chemical potentials, used to redefine the average energy density and the number density, respectively. The qQGP model with reformulated SM by Gorenstein and Yang has been studied by various groups [10,11,12, 26,27,28,29,30,31]. On the other hand Bannur put forward another method, which skips the thermodynamic inconsistency by avoiding derivatives and instead uses the original definition of all thermodynamic quantities [32]. By doing this, the parameters of qQGP model are reduced. The results of the qQGP model EoS, no matter which SM is adopted, are widely compared with lattice data [27,28,29, 32, 33]. The results fit the lattice data well if the parameters are chosen properly.

Besides the EoS and the bulk and transport properties of QGP, quark-number susceptibilities are another important tool to test the reliability of qQGP model [36, 37]. The second order quark-number susceptibility of finite chemical potential and zero temperature [31] and of finite chemical potential and finite temperature [38, 39] are studied. But there are few works on the qQGP model for the higher order susceptibilities associated with the results in RHIC so far. Therefore, in this paper, we will calculate the moments of the baryon distributions of proton and anti-proton in RHIC. By doing this, the study of qQGP model will be improved.

2 Moments by quasi-particle model

As mentioned in Ref. [25], since the thermal mass of quasi-particle is temperature and chemical potential related, derivatives of the partition function with respect to temperature and chemical potentials destroy the thermodynamic consistence in the qQGP model. Then we have to redefine the average energy density and number density, respectively, by introducing extra undetermined, temperature dependent terms. Since the common method to obtain the susceptibilities of the baryon number involves derivatives of the partition function with respect to baryon chemical potentials, an extra term must be introduced in the calculation to maintain thermodynamic consistence. To avoid it, we adopt the same method as Bannur has done. In Ref. [32], Bannur gets the expectation of particle number,

$$\begin{aligned} \left<N\right>=\sum _{k}\frac{z\epsilon _ke^{-\beta \epsilon _k}}{1\mp z\epsilon _ke^{-\beta \epsilon _k}}, \end{aligned}$$
(1)

instead of working with the derivatives of the partition function,

$$\begin{aligned} \left<N\right>=T\frac{\partial {Ln Z}}{\partial \mu }, \end{aligned}$$
(2)

where z is the fugacity, \(\epsilon _\mathrm{k}\) is the single particle energy and Z is the partition function of particles (more details can be found in Ref. [32]). Similarly, in this paper we obtain the quark-number susceptibilities thermodynamic consistently by avoiding to use the derivatives of the partition function. It should be emphasized that, rather than the method of Eq. (1), we calculate the mathematical expectations of \(\left<N\right>\) and \(\left<N^n\right>\) directly by the field theory at finite temperature and the chemical potential according to the Lagrangian of quasi-quarks.

For simplicity of the calculation, we adopt the quasi-particle model of QGP here. In this model, the interaction of quarks and gluons is treated as an effective mass term [32]. The effective mass of a quark is made up of the rest mass and the thermal mass,

$$\begin{aligned} m^2=m_{q0}^2+\sqrt{2}m_{q0}m_{\mathrm{th}}+m_{\mathrm{th}}^2, \end{aligned}$$
(3)

where \(m_{q0}\) is the rest mass of up or down quark, and in this paper \(m_{q0}=6.5\) MeV. The temperature and chemical potential dependent quark mass \(m_{\mathrm{th}}\) is

$$\begin{aligned} m_{\mathrm{th}}^2(\mu ,T)=\frac{g^2T^2}{18}\mathcal {N}_{\mathrm{f}}\left( 1+\frac{\mu ^2}{\pi ^2T^2}\right) , \end{aligned}$$
(4)

and \(g^2\) is related to the two-loop order running coupling constant,

$$\begin{aligned} \alpha _\mathrm{s}= & {} \frac{6\pi }{(33-2\mathcal {N}_{\mathrm{f}})\ln \frac{T}{\Lambda _T}\sqrt{1+a\frac{\mu ^2}{T^2}}}\nonumber \\&\times \left( 1-\frac{3(153-19\mathcal {N}_{\mathrm{f}})}{(33-2\mathcal {N}_{\mathrm{f}})^2}\frac{\ln \left( 2\ln {\frac{T}{\Lambda _T}\sqrt{1+a\frac{\mu ^2}{T^2}}}\right) }{\ln {\frac{T}{\Lambda _T}\sqrt{1+a\frac{\mu ^2}{T^2}}}}\right) ,\nonumber \\ \end{aligned}$$
(5)

where \(\alpha _\mathrm{s}=g^2/4\pi \). In this paper, only up and down quarks are considered, so \(\mathcal {N}_{\mathrm{f}}=2\). For the parameter a one mainly has two options. One is taking it equal to \((1.91/2.91)^2\) in the calculation of Schneider [34] and the other is taking \((1/\pi )^2\) in the phenomenological model of Letessier and Rafelski [35].

The expectation of the quark number is

$$\begin{aligned} \left<N_{\mathrm{q}}\right>=\left<N_{\mathrm{u}}\right>+\left<N_{\mathrm{d}}\right>=\mathcal {N}_{\mathrm{c}}\mathcal {N}_{\mathrm{f}}\left<N\right>, \end{aligned}$$
(6)

where \(\left<N\right>\) is the quark-number expectation of one single color and flavor. And the expectation of the baryon number is \(\left<N_{\mathrm{B}}\right>=\frac{1}{3}\left<N_{\mathrm{q}}\right>\). The variance of the quark number is

$$\begin{aligned} \left<(N_{q}-\left<N_{q}\right>)^2\right>= & {} \left<[(N_{u}+N_{d})-\left<N_{u}+N_{d}\right>]^2\right>\nonumber \\= & {} \left<(N_{u}-\left<N_{u}\right>)^2\right>+\left<(N_{d}-\left<N_{d}\right>)^2\right>\nonumber \\&+2\left<(N_{u}-\left<N_{u}\right>)(N_{d}-\left<N_{d}\right>)\right>\nonumber \\= & {} \left<(N_{u}-\left<N_{u}\right>)^2\right>+\left<(N_{d}-\left<N_{d}\right>)^2\right>\nonumber \\= & {} {\mathcal {N}_{c}}^2\mathcal {N}_{f}\left<(N-\left<N\right>)^2\right>, \end{aligned}$$
(7)

since the up quarks and down quarks are independent, we have \(\left<(N_{\mathrm{u}}-\left<N_{\mathrm{u}}\right>)(N_{\mathrm{d}}-\left<N_{\mathrm{d}}\right>)\right>=0\). Then the variance of the baryon number is

$$\begin{aligned} \begin{array}{ll} \sigma ^2 &{}=\left<(N_{\mathrm{B}}-\left<N_{\mathrm{B}}\right>)^2\right>\\ &{}=\displaystyle \frac{1}{{\mathcal {N}_{c}}^2}\left<(N_{\mathrm{q}}-\left<N_{\mathrm{q}}\right>)^2\right>=\mathcal {N}_{\mathrm{f}}\left<(N-\left<N\right>)^2\right>.\\ \end{array} \end{aligned}$$
(8)

The skewness of the baryon number is

$$\begin{aligned} S=\frac{\left<(N_{\mathrm{B}}-\left<N_{\mathrm{B}}\right>)^3\right>}{[\sigma ^2]^{3/2}}=\frac{\mathcal {N}_{\mathrm{f}}\left<(N-\left<N\right>)^3\right>}{[\mathcal {N}_{\mathrm{f}}\left<(N-\left<N\right>)^2\right>]^{3/2}}, \end{aligned}$$
(9)

and the kurtosis of the baryon number is

$$\begin{aligned} \kappa= & {} \frac{\left<(N_{\mathrm{B}}-\left<N_{\mathrm{B}}\right>)^4\right>}{[\sigma ^2]^2}-3\nonumber \\= & {} \frac{\mathcal {N}_{\mathrm{f}}(\left<(N-\left<N\right>)^4\right>+3\left<(N-\left<N\right>)^2\right>^2)}{[\mathcal {N}_{\mathrm{f}}\left<(N-\left<N\right>)^2\right>]^{2}}-3\nonumber \\= & {} \frac{\mathcal {N}_{\mathrm{f}}(\left<(N-\left<N\right>)^4\right>-3\left<(N-\left<N\right>)^2\right>^2)}{[\mathcal {N}_{\mathrm{f}}\left<(N-\left<N\right>)^2\right>]^{2}}\ ; \end{aligned}$$
(10)

then the products of the moments constructed as the experimental observables, \(S\sigma \) and \(\kappa \sigma ^2\), are

$$\begin{aligned} S\sigma =\frac{\left<(N-\left<N\right>)^3\right>}{\left<(N-\left<N\right>)^2\right>}\ , \end{aligned}$$
(11)
$$\begin{aligned} \kappa \sigma ^2=\frac{\left<(N-\left<N\right>)^4\right>-3\left<(N-\left<N\right>)^2\right>^2}{\left<(N-\left<N\right>)^2\right>}\ . \end{aligned}$$
(12)

Since the quarks are treated as the free quasi-particle with thermal masses, it can be written as

$$\begin{aligned}&-\beta (H-\mu N)\nonumber \\&\quad =\int _{0}^{\beta }\mathrm{d}\tau \int \mathrm{d}^3x \overline{\psi }_{\mathrm{q}}\left( -\gamma _{4}\frac{\partial }{\partial \tau }+i\overrightarrow{\gamma }\cdot \overrightarrow{\nabla }-m+\mu \gamma _{4}\right) \psi _{\mathrm{q}},\nonumber \\ \end{aligned}$$
(13)

where \(\psi _{\mathrm{q}}\) is the quark field and \(\mu \) is the chemical potential of quarks (\(\mu ={\mu }_\mathrm{u}={\mu }_d=\frac{1}{3}{\mu }_\mathrm{B}\)), then the quark number N is

$$\begin{aligned} \beta N=\int _{0}^{\beta }\mathrm{d}\tau \int \mathrm{d}^3x \overline{\psi }_{\mathrm{q}} \gamma _{4}\psi _{\mathrm{q}}, \end{aligned}$$
(14)

and the quark-number expectation \(\left<N\right>\) is

$$\begin{aligned} \left<N\right>= & {} \frac{\int \mathcal {D}\overline{\psi }_{\mathrm{q}}\int \mathcal {D}\psi _{\mathrm{q}}\int _{0}^{\beta }\mathrm{d}\tau \int \mathrm{d}^3x \overline{\psi }_{\mathrm{q}}(\overrightarrow{x},\tau )\gamma _{4}\psi _{\mathrm{q}}(\overrightarrow{x},\tau )\exp {(-\beta (H-\mu N))}}{\beta \int \mathcal {D}\overline{\psi }_{\mathrm{q}}\int \mathcal {D}\psi _{\mathrm{q}}\exp {(-\beta (H-\mu N))}}\nonumber \\= & {} -VT\displaystyle \sum _{k=-\infty }^{+\infty }\int \frac{\mathrm{d}^3p}{(2\pi )^3}Tr[G(\widetilde{p}_k)\gamma _4]\nonumber \\= & {} VT\displaystyle \sum _{k=-\infty }^{+\infty }\int \frac{\mathrm{d}^3p}{(2\pi )^3}\frac{4i\widetilde{\omega }_{k}}{\overrightarrow{p}^2+m^2+\widetilde{\omega }^2_{k}}, \end{aligned}$$
(15)

and this expression of the quark number is the same as that widely used in other work [40, 41], where \(\widetilde{p}_k=(\vec {p},\widetilde{\omega }_k)=(\vec {p},i\mu +\omega _k)\), \(\omega _k=(2k+1)\pi T\). \(\overline{\psi }_{\mathrm{q}} \gamma _{4}\psi _{\mathrm{q}}\) can be analogized as the interaction term.Then the Feynman rules are as follows [42].

  1. 1.

    The vertex is \(\gamma _{4}\);

  2. 2.

    the fermion line is \(T\sum _{k}\int \frac{\mathrm{d}^3p}{(2\pi )^3}G(\widetilde{p}_k)\);

  3. 3.

    we have \(-Tr\) for each closed fermion loop;

  4. 4.

    we have \(\beta (2\pi )^3\delta (\overrightarrow{p}_{\mathrm{in}}-\overrightarrow{p}_{\mathrm{out}})\delta _{\omega _{\mathrm{in}},\omega _{\mathrm{out}}}\) for each vertex, corresponding to energy-momentum conservation; also \(\beta (2\pi )^3\delta (0)=\beta V\).

Similarly, the expectation of \(N^2\) can be expressed as

$$\begin{aligned}&\left<N^{2}\right>=\frac{\int \mathcal {D}\overline{\psi }_{\mathrm{q}}\int \mathcal {D}\psi _{\mathrm{q}}\int _{0}^{\beta }\mathrm{d}\tau _{1}\int \mathrm{d}^3x_1 \overline{\psi }_{q1}\gamma _{4}\psi _{q1}\int _{0}^{\beta }\mathrm{d}\tau _{2}\int \mathrm{d}^3x_2 \overline{\psi }_{q2}\gamma _{4}\psi _{q2}\exp {(-\beta (H-\mu N))}}{\beta ^2*\int \mathcal {D}\overline{\psi }_{\mathrm{q}}\int \mathcal {D}\psi _{\mathrm{q}}\exp {(-\beta (H-\mu N))}}, \end{aligned}$$
(16)

and the Feynman diagram for

\(\frac{\int \mathcal {D}\overline{\psi }_{\mathrm{q}}\int \mathcal {D}\psi _{\mathrm{q}}\int _{0}^{\beta }\mathrm{d}\tau _{1}\int \mathrm{d}^3x_1 \overline{\psi }_{q1}\gamma _{4}\psi _{q1}\int _{0}^{\beta }\mathrm{d}\tau _{2}\int \mathrm{d}^3x_2 \overline{\psi }_{q2}\gamma _{4}\psi _{q2}\exp {(-\beta (H-\mu N))}}{(\int \mathcal {D}\overline{\psi }_{\mathrm{q}}\int \mathcal {D}\psi _{\mathrm{q}}\exp {(-\beta (H-\mu N))}}\) is shown in Fig. 1. Then the variance of N is

$$\begin{aligned} \left<(N-\left<N\right>)^2\right>= & {} \left<N^2\right>-\left<N\right>^2\nonumber \\= & {} -VT^2\displaystyle \sum _{k=-\infty }^{+\infty }\int \frac{\mathrm{d}^3p}{(2\pi )^3}Tr[G(\widetilde{p}_k)\gamma _4G(\widetilde{p}_k)\gamma _4]\nonumber \\= & {} -VT^2\displaystyle \sum _{k=-\infty }^{+\infty }\int \frac{\mathrm{d}^3p}{(2\pi )^3}\frac{4(\overrightarrow{p}^2+m^2-\widetilde{\omega }^2_{k})}{(\overrightarrow{p}^2+m^2+\widetilde{\omega }^2_{k})^2}\ .\nonumber \\ \end{aligned}$$
(17)

The Feynman diagram for \(\left<N^3\right>\) is shown in Fig. 2 and the third moment of N is

$$\begin{aligned}&\left<(N-\left<N\right>)^3\right>=\left<N^3\right>-3\left<N\right>\left<N^2\right>+2\left<N\right>^3\nonumber \\&\quad =-2VT^3\displaystyle \sum _{k=-\infty }^{+\infty }\int \frac{\mathrm{d}^3p}{(2\pi )^3}Tr[G(\widetilde{p}_k)\gamma _4G(\widetilde{p}_k)\gamma _4G(\widetilde{p}_k)\gamma _4]\nonumber \\&\quad =2VT^3\displaystyle \sum _{k=-\infty }^{+\infty }\int \frac{\mathrm{d}^3p}{(2\pi )^3}\frac{4i\widetilde{\omega }_{k}(3\overrightarrow{p}^2+3m^2-\widetilde{\omega }^2_{k})}{(\overrightarrow{p}^2+m^2+\widetilde{\omega }^2_{k})^3}. \end{aligned}$$
(18)
Fig. 1
figure 1

Feynman diagram for \(\left<N^2\right>\). The point represents the vertex and the line represents the quark propagator

Full size image
Fig. 2
figure 2

Feynman diagram for \(\left<N^3\right>\). The point represents the vertex and the line represents the quark propagator

Full size image
Fig. 3
figure 3

Feynman diagram for \(\left<N^4\right>\). The point represents the vertex and the line represents the quark propagator

Full size image

The Feynman diagram for \(\left<N^4\right>\) is shown in Fig. 3 and the numerator of \(\kappa \sigma ^2\) is

$$\begin{aligned}&\left<(N-\left<N\right>)^4\right>-3\left<(N-\left<N\right>)^2\right>^2\nonumber \\&\quad =-6VT^4\nonumber \\&\qquad \times \sum _{k=-\infty }^{+\infty }\int \frac{\mathrm{d}^3p}{(2\pi )^3}Tr[G(\widetilde{p}_k)\gamma _4G(\widetilde{p}_k)\gamma _4G(\widetilde{p}_k)\gamma _4G(\widetilde{p}_k)\gamma _4]\nonumber \\&\quad =-6VT^4\nonumber \\&\qquad \times \sum _{k=-\infty }^{+\infty }\int \frac{\mathrm{d}^3p}{(2\pi )^3}\frac{4((\overrightarrow{p}^2+m^2)^2-6\widetilde{\omega }^2_{k}(\overrightarrow{p}^2+m^2)+\widetilde{\omega }^4_{k})}{(\overrightarrow{p}^2+m^2+\widetilde{\omega }^2_{k})^4}.\nonumber \\ \end{aligned}$$
(19)

Putting the results of Eqs. (17) and (18) into (11), we get the value of \(S\sigma \),

$$\begin{aligned} S\sigma =\frac{2T\sum _{k=-\infty }^{+\infty }\int \frac{\mathrm{d}^3p}{(2\pi )^3}Tr[G(\widetilde{p}_k)\gamma _4G(\widetilde{p}_k)\gamma _4G(\widetilde{p}_k)\gamma _4]}{\sum _{k=-\infty }^{+\infty }\int \frac{\mathrm{d}^3p}{(2\pi )^3}Tr[G(\widetilde{p}_k)\gamma _4G(\widetilde{p}_k)\gamma _4]}, \end{aligned}$$
(20)

and putting the results of Eqs. (18) and (19) into (12), we get \(\kappa \sigma ^2\),

$$\begin{aligned} \kappa \sigma ^2=\frac{3T^2\sum _{k=-\infty }^{+\infty }\int \frac{\mathrm{d}^3p}{(2\pi )^3}Tr[G(\widetilde{p}_k)\gamma _4G(\widetilde{p}_k)\gamma _4G(\widetilde{p}_k)\gamma _4G(\widetilde{p}_k)\gamma _4]}{\sum _{k=-\infty }^{+\infty }\int \frac{d^3p}{(2\pi )^3}Tr[G(\widetilde{p}_k)\gamma _4G(\widetilde{p}_k)\gamma _4]}\ . \end{aligned}$$
(21)
Fig. 4
figure 4

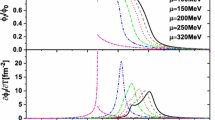
The top three lines are \(S\sigma \) results from Eq. (11) as a function of \(\sqrt{S_{NN}}\) for \(\Lambda _T/T_\mathrm{c}=0.85,0.7,0.6\) at \(a=(1.91/2.91)^2\). The bottom three lines are \(S\sigma \) for \(\Lambda _T/T_\mathrm{c}=0.7,0.63,0.58\) at \(a=(1/\pi )^2\). Data points from Ref. [7, 8] are \(S\sigma \) results for 0–5%, 30–40% and 70–80% Au+Au collisions, respectively

Full size image

3 Results

The experimental results for the \(S\sigma \) and \(\kappa \sigma ^2\) of net-proton multiplicity distributions are shown in Figs. 4 and 5, respectively. In Fig. 4, the top three lines are \(S\sigma \) results from Eq. (11) as a function of \(\sqrt{S_{NN}}\) for \(\Lambda _T/T_\mathrm{c}=0.85,0.7,0.6\) at \(a=(1.91/2.91)^2\) and the bottom three lines are for \(\Lambda _T/T_\mathrm{c}=0.7,0.63,0.58\) at \(a=(1/\pi )^2\), where \(T_\mathrm{c}=175\) MeV is from Ref. [4]. The temperature and baryon chemical potential parameters for each energy are determined from the chemical freeze-out parameterization in heavy-ion collisions [43]. Data points are the experimental results of \(S\sigma \) from Ref. [7, 8]. In Fig. 5, the top three lines are \(\kappa \sigma ^2\) results from Eq. (12) as a function of \(\sqrt{S_{NN}}\) for \(\Lambda _T/T_\mathrm{c}=0.85,0.7,0.6\) at \(a=(1.91/2.91)^2\) and the bottom three lines are for \(\Lambda _T/T_\mathrm{c}=0.7,0.63,0.57\) at \(a=(1/\pi )^2\). Data points from Ref. [7, 8] are \(\kappa \sigma ^2\) results of Au+Au collisions at different centrality bins.

Fig. 5
figure 5

The top three lines are \(\kappa \sigma ^2\) results from Eq. (12) as a function of \(\sqrt{S_{NN}}\) for \(\Lambda _T/T_\mathrm{c}=0.85,0.7,0.6\) at \(a=(1.91/2.91)^2\). The bottom three lines are \(\kappa \sigma ^2\) for \(\Lambda _T/T_\mathrm{c}=0.7,0.63,0.57\) at \(a=(1/\pi )^2\). Data points from Ref. [7, 8] are \(\kappa \sigma ^2\) results of Au+Au collisions at different centrality bins

Full size image

There are two parameters a and \(\Lambda _T\) in our calculation. The parameter a is introduced to take account of the finite quark chemical potential \(\mu \) [34, 35]. As mentioned above, there are mainly two options: \(a=(1.91/2.91)^2\) [34] and \(a=(1/\pi )^2\) [35]. \(\Lambda _T\) is related to the QCD scale parameter. Since the second order quark-number susceptibility is studied at \(\Lambda _T/T_\mathrm{c}=0.7\) [38], \(S\sigma \) and \(\kappa \sigma ^2\) are calculated with \(\Lambda _T/T_\mathrm{c}\) around 0.7. When the parameter a is fixed, the values of \(S\sigma \) and \(\kappa \sigma ^2\) are reduced with the reduction of \(\Lambda _T\). In Fig. 4 the difference between the results of \(S\sigma \) calculated from different \(\Lambda _T\) are smaller at high energies than low energies. For \(\kappa \sigma ^2\) in Fig. 5 the results at different \(\Lambda _T\) are almost parallel with each other at large \(\sqrt{S_{NN}}\) and they have with bigger discrepancies at small \(\sqrt{S_{NN}}\).

Particularly, the results for \(\Lambda _T/T_\mathrm{c}=0.7\) are shown as solid lines in Figs. 4 and 5. Comparing the two solid lines in Fig. 4, we find that the values with \(a=(1.91/2.91)^2\) are lower than the one with \(a=(1/\pi )^2\) at small \(\sqrt{S_{NN}}\) and the difference gets smaller and smaller with increasing \(\sqrt{S_{NN}}\). As for \(\kappa \sigma ^2\) in Fig. 5, at small \(\sqrt{S_{NN}}\) the two lines have different trends. The one with \(a=(1.91/2.91)^2\) increases with increasing \(\sqrt{S_{NN}}\) and the other one shows an opposite trend. The results of the qQGP model are more sensitive to the parameters at small colliding energies.

The experimental results in Figs. 4 and 5 demonstrate that both \(S\sigma \) and \(\kappa \sigma ^2\) clearly show a non-monotonic variation for 0–5% centrality when \(\sqrt{S_{NN}}\) is below 30 GeV. Above 30 GeV the results of different centralities are close to each other. The experimental results indicate that the corresponding chemical freeze-out T and \(\mu \) around 20 GeV may be close to the critical point [7, 8]. In Figs. 4 and 5, it is shown that our results with different parameters show similar trends to the experimental data for the colliding energies above 30 GeV. In this region, for \(S\sigma \) our results is approximately 0.1 less than the experimental data at the maximum deviation, and for \(\kappa \sigma ^2\) our results describe the experimental data well. But below 30 GeV, our results have significant discrepancies from the experimental data of 0–5% centrality.

4 Summary

Baryon number fluctuations are sensitive to the QCD phase transition and QCD critical point. We calculated various order moments of the baryon number distributions in the quasi-particle model of QGP. To avoid an extra undetermined term in calculating susceptibilities in the quasi-particle model we try to directly calculate the various order of moments of the quark-number distributions. Since the term of the quark number in the Lagrangian is analogized as the interaction term, we can obtain the moments of the quark number based on the Feynman rules of finite-temperature field theory. Finally, we compare our calculations with the latest experimental data. It is found that the results of qQGP model are more sensitive to the parameters at small colliding energies. For energies above 30 GeV, our results with different parameters show similar trends to the experimental data. We found that the \(S\sigma \) are smaller than the experimental data, while \(\kappa \sigma ^2\) fits the experimental data well. However, at energies below 30 GeV, our results have large discrepancies from the experimental data of 0–5% centrality. These comparisons suggest that, at low energies, the experimental data may contain other physics effects, for e.g. the critical point, which is not included in the qQGP model. It also indicates that the future low energy heavy-ion collisions experiment is much more important for the QCD critical point search.