Radial excitations of the decuplet baryons

Abstract

The ground and first excited states of the decuplet baryons are studied using the two-point QCD sum rule approach. The mass and residue of these states are computed and compared with the existing experimental data and other theoretical predictions. The results for the masses of the ground state particles as well as the excited $\Delta$ and $\Sigma ^{*}$ states are in good consistency with experimental data. Our results on the excited $\Xi ^{*}$ and $\Omega ^{-}$ states reveal that the experimentally poorly known $\Xi (1950)$ and $\Omega ^{-}(2250)$ can be assigned to the first excited states in $\Xi ^{*}$ and $\Omega ^{-}$ channels, respectively.

1 Introduction

In recent years, the spectroscopy of hadrons is living its renaissance period due to the discovery of many new particles. The study of the spectroscopy and internal structure of hadrons is one of the main problems in hadron physics. Investigation of the properties of hadrons will give a clear picture for understanding the dynamics of their excited states. The experimental study of the spectrum of excited baryons is one of the central elements of the physics programs of many accelerators. During the last years, there has been made significant progress in collecting data on excited state hadrons at JLAB, MIT-Bates, LEGS, MAMI, ELSA, etc. In experiments, radial excitations of hadrons having the same quantum numbers as the ground states were discovered [1].

The analysis of the properties of excited hadrons represents a formidable task due to the fact that they can interact with many hadrons and it leads to the difficulty in their identification. For studying the properties of ground state hadrons the QCD sum rule approach [2, 3] has occupied a special place and has been very successful. It is based on the fundamental QCD Lagrangian and all non-perturbative effects are parametrized in terms of quark and gluon condensates. Now, the question is: how successful is this method in the study of the radially excited baryons, which carry the same quantum numbers as the ground states? In the present letter we apply this method to a study of the excitations of decuplet baryons. It should be noted that the radial excitations of light–heavy mesons, the mass of first radial excitations of mesons and nucleon by using the least square method within the QCD sum rules method were analyzed in [4, 5], respectively. Recently, this method has been applied to an estimation of the mass and residue of the first radial excitations of octet baryons in [6] and it has been found that the method is very predictive for radial excitations of the baryons as well. The excited baryons have also been studied using lattice QCD in [7, 8]. For a theoretical study on the excited baryons see for instance [9] and the references therein.

This paper is organized as follows. In Sect. 2, the mass sum rules for decuplet baryons including their first radial excitations are calculated. In Sect. 3, the numerical analysis of the obtained sum rules is presented. The last section is devoted to our summary and conclusions.

2 QCD sum rules for the mass and residue of decuplet baryons including their radial excitations

In order to derive the two-point QCD sum rules required for obtaining the mass and residue of the radially excited decuplet baryons, we consider the following correlation function:

$$\begin{aligned} \Pi _{\mu \nu }(q)=i\int \mathrm{d}^{4}xe^{iq\cdot x}\langle 0|\mathcal {T}\{\eta _{\mu }^{D}(x)\bar{\eta }_{\nu }^{D}(0)\}|0\rangle , \end{aligned}$$

(1)

where $\eta _{\mu }^{D}(x)$ is the interpolating current of the decuplet baryon and q is its four momentum. The interpolating current of the decuplet baryons coupled to the ground and excited states with the same quantum numbers can be written as

$$\begin{aligned} \eta _{\mu }^{D}= & {} A \epsilon ^{abc} \Big \{(q_{1}^{aT}C\gamma _\mu q_{2}^{b})q_{3}^{c} + (q_{2}^{aT}C\gamma _\mu q_{3}^{b})q_{1}^{c} \nonumber \\&+ (q_{3}^{aT}C\gamma _\mu q_{1}^{b})q_{2}^{c} \Big \}, \end{aligned}$$

(2)

where a, b, c are color indices, C is the charge conjugation operator and A is the normalization constant. The light quark fields $q_1$, $q_2$, $q_3$ and the normalization constant for different members of decuplet baryons are collected in Table 1 (for details see for instance [3, 10,11,12]). We shall also remark that the above current couples to both the spin-1/2 and the spin-3/2 baryons with both the negative and the positive parities (see for instance [13, 14]). In the present study, we consider only the positive parity baryons. As we consider both the ground states and the first excited states, taking into account the negative parity baryons requires implementing both the negative parity ground states and the negative parity first excited states. This will require either additional sum rules obtained by applying derivatives to those obtained from the two Dirac structures entering the calculations or experimental knowledge of the ground state negative parity and the first excited state positive/negative parity baryons. This brings about more uncertainties, which makes a reliable estimation of the masses difficult, especially in the case of first excited states.

Table 1 The value of the normalization constant A and the quark fields $q_1$, $q_2$, $q_3$ for the decuplet baryons

To derive the aimed QCD sum rules for the mass and residue of the considered baryons, the above correlation function has to be calculated using both the hadronic and the OPE (operator product expansion) languages. By equating these two representations, one can get the QCD sum rules for the physical quantities of the considered baryons.

2.1 Hadronic representation

The correlation function in the hadronic side is calculated in terms of the hadronic degrees of freedom which contains the physical parameters of the decuplet baryons. After insertion of a complete set of baryonic state with the same quantum numbers as the interpolating current, we get

$$\begin{aligned} \Pi _{\mu \nu }^{\mathrm {Had}}(q)= & {} \frac{\langle 0|\eta _{\mu }^D |D(q,s)\rangle \langle D(q,s)|\bar{\eta }_{\nu }|0\rangle }{m_{D}^{2}-q^{2}} \nonumber \\&+\frac{\langle 0|\eta _{\mu }^D |D^{\prime }(q,s)\rangle \langle D^{\prime }(q,s)|\bar{\eta }_{\nu }|0\rangle }{m_{D^{\prime }}^{2}-q^{2}}+\cdots , \end{aligned}$$

(3)

with $m_{D}$ and $m_{D^{\prime }}$ being the mass of the ground state and the first excited states of the decuplet baryons, respectively. The dots indicates the contributions coming from the higher states and continuum. Since the ground state and the first radial excitations of decuplet baryons have the same quantum numbers, their matrix elements between vacuum and one particle states are defined in a similar manner, i.e.,

$$\begin{aligned} \langle 0|\eta _{\mu }^D |D(q,s)\rangle= & {} \lambda _{D}u_{\mu }(q,s), \nonumber \\ \langle 0|\eta _{\mu }^D |D^{\prime }(q,s)\rangle= & {} \lambda _{D^{\prime }}u_{\mu }^{\prime }(q,s), \end{aligned}$$

(4)

where $\lambda _{D^{(\prime )}}$ is the residue of the corresponding baryon. By using summations over the spins of the Rarita–Schwinger spinor,

(5)

for the physical part we get

(6)

As we previously mentioned the current $\eta _{\mu }$ couples not only to the spin-3/2 particles but also to the spin-1/2 states. Hence, the unwanted spin-1/2 contributions should be removed. To this end, we try to make the entering structures independent of each other by a special ordering of the Dirac matrices and separate the spin-1/2 contributions, which can easily be removed from the correlation function. The matrix element of $\eta _{\mu }$ between vacuum and spin-1/2 states can be parametrized as

$$\begin{aligned} \left\langle 0 |\eta _{\mu }^D|\frac{1}{2}(q)\right\rangle =\left( C_1q_{\mu }+C_2\gamma _{\mu }\right) u(q), \end{aligned}$$

(7)

where $C_1$ and $C_2$ are some constants and u(q) is the Dirac spinor of momentum q. By imposing the condition $\eta _{\mu }^D \gamma _{\mu }=0$, one immediately finds $C_1$ in terms of $C_2$,

$$\begin{aligned} \left\langle 0 |\eta _{\mu }^D|\frac{1}{2}(q)\right\rangle = C_2 \left( -\frac{4}{m_{\frac{1}{2}}}q_{\mu }+\gamma _{\mu }\right) u(q), \end{aligned}$$

(8)

where $m_{\frac{1}{2}}$ is the spin-1/2 mass. It is clear from this formula that the unwanted spin-1/2 contributions are proportional to either $q_{\mu }$ or $\gamma _{\mu }$. After insertion of this equation into the correlation function and ordering of the corresponding Dirac matrices, , we remove the terms with the $\gamma _{\mu }$ in the beginning, $\gamma _{\nu }$ at the end and those proportional to $q_{\mu }$ or $q_{\nu }$ in order to get rid of the spin-1/2 contributions. Note that in the results only two structures, and $g_{\mu \nu }$, contain contributions from spin-3/2 states. Hence, for the hadronic part of the correlation function, we get

(9)

The Borel transformation with respect to $q^{2}$, with the aim of suppressing the contributions of the higher states and continuum, leads to the final form of the hadronic representation:

(10)

Here we remark that we perform our analysis in the zero width approximation since the resonance widths of the first radial excitations are not known yet. Taking into account these widths can bring about additional uncertainties to the sum rules.

2.2 OPE representation

The OPE side of the correlation function is calculated at large space-like region, where $q^{2}\ll 0$ in terms of quark–gluon degrees of freedom. For this purpose, we substitute the interpolating current given by Eqs. (2) into (1), and contract the relevant quark fields. As a result, we get

$$\begin{aligned} \Pi _{\mu \nu }^{\mathrm {OPE},\Delta }(q)= & {} \frac{i}{3}\epsilon _{abc}\epsilon _{a'b'c'}\int \mathrm{d}^4 x e^{iqx} \nonumber \\&\times \Bigg \langle 0|\left\{ 2S^{ca'}_{d}(x)\gamma _{\nu }\widetilde{S}^{ab'}_{d}(x)\gamma _{\mu }S^{bc'}_{u}(x) \right. \nonumber \\&\left. -2S^{cb'}_{d}(x)\gamma _{\nu }\widetilde{S}^{aa'}_{d}(x)\gamma _{\mu }S^{bc'}_{u}(x)\right. \nonumber \\&\left. +4S^{cb'}_{d}(x)\gamma _{\nu }\widetilde{S}^{ba'}_{u}(x)\gamma _{\mu }S^{ac'}_{d}(x)\right. \nonumber \\&\left. +2S^{ca'}_{u}(x)\gamma _{\nu }\widetilde{S}^{ab'}_{d}(x)\gamma _{\mu }S^{bc'}_{d}(x)\right. \nonumber \\&\left. -2S^{ca'}_{u}(x)\gamma _{\nu }\widetilde{S}^{bb'}_{d}(x)\gamma _{\mu }S^{ac'}_{d}(x)\right. \nonumber \\&\left. -S^{cc'}_{u}(x)Tr\left[ S^{ba'}_{d}(x)\gamma _{\nu }\widetilde{S}^{ab'}_{d}(x)\gamma _{\mu }\right] \right. \nonumber \\&+\left. S^{cc'}_{u}(x)Tr\left[ S^{bb'}_{d}(x)\gamma _{\nu }\widetilde{S}^{aa'}_{d}(x)\gamma _{\mu }\right] \right. \nonumber \\&\left. -4S^{cc'}_{d}(x)Tr\left[ S^{ba'}_{u}(x)\gamma _{\nu }\widetilde{S}^{ab'}_{d}(x)\gamma _{\mu }\right] \right\} |0 \Bigg \rangle ,\nonumber \\ \end{aligned}$$

(11)

$$\begin{aligned} \Pi _{\mu \nu }^{\mathrm {OPE},\Sigma ^{*}}(q)= & {} -\frac{2i}{3}\epsilon _{abc}\epsilon _{a'b'c'}\nonumber \\&\times \int \mathrm{d}^4 x e^{iqx} \Bigg \langle 0 | \left\{ S^{ca'}_{d}(x)\gamma _{\nu }\widetilde{S}^{bb'}_{u}(x)\gamma _{\mu }S^{ac'}_{s}(x)\right. \nonumber \\&\left. +S^{cb'}_{d}(x)\gamma _{\nu }\widetilde{S}^{aa'}_{s}(x)\gamma _{\mu }S^{bc'}_{u}(x)\right. \nonumber \\&\left. +S^{ca'}_{s}(x)\gamma _{\nu }\widetilde{S}^{bb'}_{d}(x)\gamma _{\mu }S^{ac'}_{u}(x)\right. \nonumber \\&\left. +S^{cb'}_{s}(x)\gamma _{\nu }\widetilde{S}^{aa'}_{u}(x)\gamma _{\mu }S^{bc'}_{d}(x)\right. \nonumber \\&\left. +S^{ca'}_{u}(x)\gamma _{\nu }\widetilde{S}^{bb'}_{s}(x)\gamma _{\mu }S^{ac'}_{d}(x)\right. \nonumber \\&\left. +S^{cb'}_{u}(x)\gamma _{\nu }\widetilde{S}^{aa'}_{d}(x)\gamma _{\mu }S^{bc'}_{s}(x)\right. \nonumber \\&\left. +S^{cc'}_{s}(x)Tr\left[ S^{ba'}_{d}(x)\gamma _{\nu }\widetilde{S}^{ab'}_{u}(x)\gamma _{\mu }\right] \right. \nonumber \\&+\left. S^{cc'}_{u}(x)Tr\left[ S^{ba'}_{s}(x)\gamma _{\nu }\widetilde{S}^{ab'}_{d}(x)\gamma _{\mu }\right] \right. \nonumber \\&+\left. S^{cc'}_{d}(x)Tr\left[ S^{ba'}_{u}(x)\gamma _{\nu }\widetilde{S}^{ab'}_{s}(x)\gamma _{\mu }\right] \right\} |0\Bigg \rangle ,\nonumber \\ \end{aligned}$$

(12)

$$\begin{aligned} \Pi _{\mu \nu }^{\mathrm {OPE},\Xi ^{*}}(q)= & {} \frac{i}{3}\epsilon _{abc}\epsilon _{a'b'c'}\nonumber \\&\times \int \mathrm{d}^4 x e^{iqx}\Bigg \langle 0 |\left\{ 2S^{ca'}_{s}(x)\gamma _{\nu }\widetilde{S}^{ab'}_{s}(x)\gamma _{\mu }S^{bc'}_{u}(x)\right. \nonumber \\&\left. -\,2S^{cb'}_{s}(x)\gamma _{\nu }\widetilde{S}^{aa'}_{s}(x)\gamma _{\mu }S^{bc'}_{u}(x)\right. \nonumber \\&\left. +\,4S^{cb'}_{s}(x)\gamma _{\nu }\widetilde{S}^{ba'}_{u}(x)\gamma _{\mu }S^{ac'}_{s}(x)\right. \nonumber \\&\left. +\,2S^{ca'}_{u}(x)\gamma _{\nu }\widetilde{S}^{ab'}_{s}(x)\gamma _{\mu }S^{bc'}_{s}(x)\right. \nonumber \\&\left. -\,2S^{ca'}_{u}(x)\gamma _{\nu }\widetilde{S}^{bb'}_{s}(x)\gamma _{\mu }S^{ac'}_{s}(x)\right. \nonumber \\&\left. -\,S^{cc'}_{u}(x)Tr\left[ S^{ba'}_{s}(x)\gamma _{\nu }\widetilde{S}^{ab'}_{s}(x)\gamma _{\mu }\right] \right. \nonumber \\&+\,S^{cc'}_{u}(x)Tr\left[ S^{bb'}_{s}(x)\gamma _{\nu }\widetilde{S}^{aa'}_{s}(x)\gamma _{\mu }\right] \nonumber \\&-\,\left. 4S^{cc'}_{s}(x)Tr\left[ S^{ba'}_{u}(x)\gamma _{\nu }\widetilde{S}^{ab'}_{s}(x)\gamma _{\mu }\right] \right\} |0\Bigg \rangle ,\nonumber \\ \end{aligned}$$

(13)

and

$$\begin{aligned} \Pi _{\mu \nu }^{\mathrm {OPE},\Omega ^{-}}(q)= & {} \epsilon _{abc}\epsilon _{a'b'c'}\nonumber \\&\times \int d^4 x e^{iqx} \Bigg \langle 0 |\left\{ S^{ca'}_{s}(x)\gamma _{\nu }\widetilde{S}^{ab'}_{s}(x)\gamma _{\mu }S^{bc'}_{s}(x)\right. \nonumber \\&\left. -\,S^{ca'}_{s}(x)\gamma _{\nu }\widetilde{S}^{bb'}_{s}(x)\gamma _{\mu }S^{ac'}_{s}(x)\right. \nonumber \\&\left. -\,S^{cb'}_{s}(x)\gamma _{\nu }\widetilde{S}^{aa'}_{s}(x)\gamma _{\mu }S^{bc'}_{s}(x)\right. \nonumber \\&\left. +\,S^{cb'}_{s}(x)\gamma _{\nu }\widetilde{S}^{ba'}_{s}(x)\gamma _{\mu }S^{ac'}_{s}(x)\right. \nonumber \\&\left. -\,S^{cc'}_{s}(x)Tr\left[ S^{ba'}_{s}(x)\gamma _{\nu }\widetilde{S}^{ab'}_{s}(x)\gamma _{\mu }\right] \right. \nonumber \\&+\left. S^{cc'}_{s}(x)Tr\left[ S^{bb'}_{s}(x)\gamma _{\nu }\widetilde{S}^{aa'}_{s}(x)\gamma _{\mu }\right] \right\} |0\Bigg \rangle ,\nonumber \\ \end{aligned}$$

(14)

where $\widetilde{S}(x)=CS^{T}(x)C$ and the quantity $S_{q}^{ab}(x)$ with $q=u, d, s$ appearing in Eqs. (11)–(14) is the light quark propagator. The explicit expression for the light quark propagator in $x-$space has the following form:

$$\begin{aligned} S_\mathrm{q}(x)= & {} {i /x\over 2\pi ^2 x^4} - {m_q\over 4 \pi ^2 x^2} - {\langle \bar{q} q \rangle \over 12} \left( 1 - i {m_q\over 4} /x \right) \nonumber \\&- {x^2\over 192} m_0^2 \langle \bar{q} q \rangle \left( 1 - i {m_q\over 6}/x \right) \nonumber \\&- i g_s \int _0^1 du \Bigg [{/x\over 16 \pi ^2 x^2} G_{\mu \nu } (ux) \sigma _{\mu \nu } \nonumber \\&- {i\over 4 \pi ^2 x^2} u x^\mu G_{\mu \nu } (ux) \gamma ^\nu \nonumber \\&- i {m_q\over 32 \pi ^2} G_{\mu \nu } \sigma ^{\mu \nu } \left( \ln \left( {-x^2 \Lambda ^2\over 4} \right) + 2 \gamma _\mathrm{E} \right) \Bigg ]~,\nonumber \\ \end{aligned}$$

(15)

where $\gamma _\mathrm{E} \simeq 0.577$ is the Euler constant and $\Lambda$ is a scale parameter.

By using this propagator in Eqs. (11)–(14) and performing the Fourier and Borel transformations as well as applying the continuum subtraction, after very lengthy calculations, we get

(16)

where the functions $\widetilde{\Pi }_{1}$ and $\widetilde{\Pi }_{2}$, for instance for $\Sigma ^{*}$, are obtained as

$$\begin{aligned} \widetilde{\Pi }_{1}^{\Sigma ^{*}}= & {} \frac{1}{\pi ^{2}}\nonumber \\&\times \int _0^{s_{0}} ds e^{-\frac{s}{M^2}} \bigg \lbrace \frac{s^2}{5\times 2^{5}\pi ^{2}} \nonumber \\&\left. + \frac{1}{3\times 2^{2}} \left[ \langle \bar{d} d\rangle \left( m_\mathrm{d}-2m_\mathrm{u}-2m_\mathrm{s} \right) \right. \right. \nonumber \\&\left. \left. + \langle \bar{u} u\rangle \left( m_\mathrm{u}-2m_\mathrm{d}-2m_\mathrm{s} \right) \right. \right. \nonumber \\&+ \left. \langle \bar{s} s\rangle \left( m_\mathrm{s}-2m_\mathrm{u}-2m_\mathrm{d} \right) \right] -\frac{5 \langle g_s^2 G^2\rangle }{3^2\times 2^7 \pi ^2}\nonumber \\&+\frac{7 \langle g_s^2 G^2\rangle }{3^3\times 2^4 M^4}\left[ \langle \bar{d} d\rangle \left( m_\mathrm{u}+m_\mathrm{s} \right) +\langle \bar{u} u\rangle \left( m_\mathrm{d}+m_\mathrm{s}\right) \right. \nonumber \\&+ \left. \langle \bar{s} s\rangle \left( m_\mathrm{u}+m_\mathrm{d}\right) \right] \mathrm {Log}\left[ \frac{s}{\Lambda ^{2}} \right] \bigg \rbrace \nonumber \\&+ \frac{m_0^{2}\langle \bar{d} d\rangle }{3^2\times 2^3 \pi ^2} \left( 7m_\mathrm{u}+7m_\mathrm{s}-5m_\mathrm{d} \right) \nonumber \\&+ \frac{m_0^{2}\langle \bar{u} u\rangle }{3^2\times 2^3 \pi ^2} \left( 7m_\mathrm{d}+7m_\mathrm{s}-5m_\mathrm{u} \right) \nonumber \\&+ \frac{m_0^{2}\langle \bar{s} s\rangle }{3^2\times 2^3 \pi ^2} \left( 7m_\mathrm{u}+7m_\mathrm{d}-5m_\mathrm{s} \right) \nonumber \\&+\frac{4}{3^2} \left( \langle \bar{u} u\rangle \langle \bar{d} d\rangle +\langle \bar{u} u\rangle \langle \bar{s} s\rangle +\langle \bar{d} d\rangle \langle \bar{s} s\rangle \right) \nonumber \\&-\frac{7}{3^3 M^2} m_0^2\left( \langle \bar{u} u\rangle \langle \bar{d} d\rangle +\langle \bar{u} u\rangle \langle \bar{s} s\rangle +\langle \bar{d} d\rangle \langle \bar{s} s\rangle \right) \nonumber \\&+\frac{\langle g_\mathrm{s}^2 G^2\rangle }{3^3\times 2^4 \pi ^2 M^2} \left\{ \langle \bar{d} d\rangle \left[ 4(m_\mathrm{u}+m_\mathrm{s})-m_\mathrm{d} \right] \right. \nonumber \\&+ \langle \bar{u} u\rangle \left[ 4(m_\mathrm{d}+m_\mathrm{s})-m_\mathrm{u} \right] \nonumber \\&\left. +\langle \bar{s} s\rangle \left[ 4(m_\mathrm{u}+m_\mathrm{d})-m_\mathrm{s} \right] \right\} \nonumber \\&+\frac{\langle g_\mathrm{s}^2 G^2\rangle }{3^4\times 2^7 \pi ^2 M^4}m_0^2\left\{ \langle \bar{d} d\rangle \left[ m_\mathrm{d}-48(m_\mathrm{u}+m_\mathrm{s})\right] \right. \nonumber \\&+ \langle \bar{u} u\rangle \left[ m_\mathrm{u}- 48(m_\mathrm{d}+m_\mathrm{s}) \right] \nonumber \\&\left. +\langle \bar{s} s\rangle \left[ m_\mathrm{s}- 48(m_\mathrm{u}+m_\mathrm{d}) \right] \right\} \nonumber \\&+\frac{7 \langle g_\mathrm{s}^2 G^2\rangle }{3^3\times 2^4 \pi ^2 s_0 M^2}\bigg \lbrace \langle \bar{d} d\rangle (m_\mathrm{u}{+}m_\mathrm{s}){+}\langle \bar{u} u\rangle (m_\mathrm{d}{+}m_\mathrm{s}) \nonumber \\&+\langle \bar{s} s\rangle (m_\mathrm{d}+m_\mathrm{u}) \bigg \rbrace \left[ M^2+s_0 \mathrm {Log}\left[ \frac{s}{\Lambda ^{2}} \right] \right] e^{-\frac{s_0}{M^2}} \end{aligned}$$

(17)

and

$$\begin{aligned}&\widetilde{\Pi }_{2}^{\Sigma ^{*}}=\frac{1}{\pi ^{2}}\int _0^{s_{0}} ds e^{-\frac{s}{M^2}} \left\{ \frac{s^2 \left( m_\mathrm{u}+m_\mathrm{d}+m_\mathrm{s}\right) }{2^{6} \pi ^{2}}\right. \nonumber \\&\quad \left. - \frac{\left( \langle \bar{u} u\rangle + \langle \bar{d} d\rangle + \langle \bar{s} s\rangle \right) s}{3^2}-\frac{m_{0}^{2}\left( \langle \bar{u} u\rangle + \langle \bar{d} d\rangle + \langle \bar{s} s\rangle \right) }{3^2\times 2} \right. \nonumber \\&\quad +\left. \frac{\langle g_{s}^{2}G^{2}\rangle \left( m_\mathrm{u}+m_\mathrm{d}+m_\mathrm{s} \right) }{3^2\times 2^7 \pi ^2}\left[ \left( 8\gamma _{\mathrm{E}}-3 \right) -8 \mathrm {Log}\left[ \frac{s}{\Lambda ^{2}} \right] \right] \right. \nonumber \\&\quad +\left. \frac{\langle g_{s}^{2}G^{2}\rangle ^{2} \left( m_\mathrm{u}+m_\mathrm{d}+m_\mathrm{s} \right) }{3^3\times 2^9 \pi ^2 M^4}\mathrm {Log}\left[ \frac{s}{\Lambda ^{2}}\right] \right\} \nonumber \\&\quad + \frac{2}{3} \left[ \langle \bar{d} d\rangle \langle \bar{s}s\rangle m_\mathrm{u}+\langle \bar{d} d\rangle \langle \bar{u}u\rangle m_\mathrm{s}+\langle \bar{d} d\rangle \langle \bar{u}u\rangle m_\mathrm{d} \right] \nonumber \\&\quad \left. -\frac{m_0^2}{3^3\times 2^2 M^2}\left[ \langle \bar{d} d\rangle \langle \bar{s}s\rangle \left( 4m_\mathrm{u}+9m_\mathrm{d}+9m_\mathrm{s}\right) \right. \right. \nonumber \\&\quad +\left. \langle \bar{d} d\rangle \langle \bar{u}u\rangle \left( 9m_\mathrm{u}+9m_\mathrm{d}+4m_\mathrm{s}\right) \right. \nonumber \\&\quad \left. + \langle \bar{d} d\rangle \langle \bar{u}u\rangle \left( 9m_\mathrm{u}+4m_\mathrm{d}+9m_\mathrm{s}\right) \right] \nonumber \\&\quad - \frac{\langle g_\mathrm{s}^2G^2\rangle }{3^2\times 2^4 \pi ^{4}}M^2 \left( m_\mathrm{u}+m_\mathrm{d}+m_\mathrm{s}\right) \gamma _{\mathrm{E}} \left( 1-e^{-\frac{s_0}{M^2}} \right) \nonumber \\&\quad + \frac{\langle g_\mathrm{s}^2G^2\rangle ^{2}\left( m_\mathrm{u}+m_\mathrm{d}+m_\mathrm{s} \right) }{3^4\times 2^9 \pi ^{4} M^2 s_0}\nonumber \\&\quad \times \left( 5s_0+3M^2 e^{-\frac{s_0}{M^2}} + 3s_0 \mathrm {Log}\left[ \frac{s_0}{\Lambda ^{2}}\right] e^{-\frac{s_0}{M^2} } \right) \nonumber \\&\quad + \frac{\langle g_\mathrm{s}^2G^2\rangle }{3^3\times 2^3 \pi ^{2}}\left( \langle \bar{u} u\rangle +\langle \bar{d} d\rangle +\langle \bar{s} s\rangle \right) \nonumber \\&\quad +\frac{\langle g_\mathrm{s}^2G^2\rangle }{3^2\times 2 M^4}\left( m_\mathrm{u} \langle \bar{d} d\rangle \langle \bar{s} s\rangle + m_\mathrm{s} \langle \bar{d} d\rangle \langle \bar{u} u\rangle + m_\mathrm{d} \langle \bar{u} u\rangle \langle \bar{s} s\rangle \right) \nonumber \\&\quad - \frac{\langle g_\mathrm{s}^2G^2\rangle }{3^3\times 2^6 \pi ^2 M^2}\left( m_0^2 \langle \bar{d} d\rangle + m_0^2 \langle \bar{u} u\rangle + m_0^2 \langle \bar{s} s\rangle \right) \nonumber \\&\quad + \frac{\langle g_\mathrm{s}^2G^2\rangle }{3^{2}\times 2 \pi ^{2} M^6} \left( m_\mathrm{u} m_0^2 \langle \bar{d} d\rangle \langle \bar{s} s\rangle \right. \nonumber \\&\quad \left. +m_\mathrm{d} m_0^2 \langle \bar{u} u\rangle \langle \bar{s} s\rangle + m_\mathrm{s} m_0^2 \langle \bar{u} u\rangle \langle \bar{d} d\rangle \right) . \end{aligned}$$

(18)

The results for the $\Delta$, $\Xi ^{*}$ and $\Omega ^{-}$ baryons can be obtained from Eqs. (17) and (18) with the help of the following replacements:

$$\begin{aligned} \widetilde{\Pi }_{1,2}^{\Delta }= & {} \widetilde{\Pi }_{1,2}^{\Sigma ^{*}}\left( u\rightarrow d, s \rightarrow u \right) , \nonumber \\ \widetilde{\Pi }_{1,2}^{\Xi ^{*}}= & {} \widetilde{\Pi }_{1,2}^{\Sigma ^{*}}\left( u\rightarrow s, d \rightarrow s, s \rightarrow u \right) , \nonumber \\ \widetilde{\Pi }_{1,2}^{\Omega ^{-}}= & {} \widetilde{\Pi }_{1,2}^{\Sigma ^{*}}\left( u\rightarrow s, d \rightarrow s \right) . \end{aligned}$$

(19)

Having calculated both the hadronic and the OPE sides of the correlation function, we match the coefficients of the structures and $g_{\mu \nu }$ from these two sides and obtain the following sum rules, which will be used to extract the masses and residues of the ground and first excited states:

$$\begin{aligned} \lambda _{D}^2 e^{-\frac{m_{D}^{2}}{M^{2}}}+\lambda _{D^{\prime }}^2 e^{-\frac{m_{D^{\prime }}^{2}}{M^{2}}}= & {} \widetilde{\Pi }_{1}^{D}, \nonumber \\ m_D \lambda _{D}^2 e^{-\frac{m_{D}^{2}}{M^{2}}}+m_{D^{\prime }} \lambda _{D^{\prime }}^2 e^{-\frac{m_{D^{\prime }}^{2}}{M^{2}}}= & {} \widetilde{\Pi }_{2}^{D}. \end{aligned}$$

(20)

3 Numerical results

As is seen from Eq. (20), in order to obtain the numerical values of the mass and residue of the radial excitations of the decuplet baryons, we need to have the values of the mass and residue of the ground states. Because of this, first of all we calculate the mass and residue of the ground state particles by choosing an appropriate threshold $s_0$ according to the standard prescriptions. The working region of the threshold parameter is found requiring that the sum rules show a good convergence of the OPE and lead to a maximum possible pole contribution. Besides, the physical quantities are required to demonstrate relatively weak dependencies on this parameter in its working interval. The sum rules contain numerous parameters, i.e. quark, gluon and mixed condensates and mass of the light quarks, the values of which are shown in Table 2.

Table 2 Some input parameters

In addition to the input parameters, the auxiliary parameter $M^2$ should also be fixed. We find the working region of $M^2$ such that the physical quantities weakly depend on it as much as possible. This is achieved requiring that not only the contributions of the higher states and continuum should be small compared to the ground and first excited states contributions, but also the higher dimensional operators should have small contributions and the series of sum rules should converge.

Using the above procedures, the working regions of $M^2$ for different channels are obtained. These intervals together with the working regions of $s_0$ for the ground states are given in Table 3. After standard analysis of the sum rules, we extract the values of the mass and residue of the ground state decuplet baryons as presented in Table 4. Note that the presented values are obtained taking the average of the corresponding values obtained via two different sum rules presented in Eq. (20). The two some rules’ predictions differ by an amount of maximally $5\%$ from each other; this we have included in the errors. We also compare our results with the existing experimental data and other theoretical predictions in this table. From this table, we see that our predictions on the ground state mass of the decuplet baryons are well consistent with the average experimental data presented in PDG [15]. In the case of the residues, our predictions for the residues of ground states are overall comparable with those obtained in [10, 17].

Table 3 The working regions of $M^2$ and $s_0$ for the ground state $\Delta$, $\Sigma ^{*}$, $\Xi ^{*}$ and $\Omega ^{-}$ baryons

Table 4 The numerical values of masses and residues of the ground state $\Delta$, $\Sigma ^{*}$, $\Xi ^{*}$ and $\Omega ^{-}$ baryons. In [17] the numerical values of $\widetilde{\lambda }^{2}=4\pi ^{2}\lambda ^{2}$ are given in chiral-odd and chiral-even sum rules approaches. To compare with our results, we calculate the average $\lambda$ from those results and do not show the uncertainties of the results

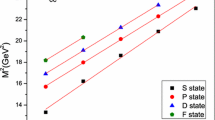
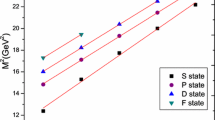
At this stage, we proceed to find the values of the masses and residues of the radially excited baryons considering the values of the masses and residues of the corresponding ground state baryons as inputs. For this purpose the sum rules in Eq. (20) are used. When taking into account the contributions of the radial excitations, the continuum threshold should be changed compared to the previous case. Using the standard criteria, the continuum threshold $(s^{\prime }_{0})$ including the first excited states is found as presented in Table 5. Our analyses show that by the above intervals for $M^{2}$, $s_0$ and $s^{\prime }_{0}$, the OPE nicely converges and the pole ground and the first excited states constitute the main part of the total result and the effects of higher states and continuum are relatively small. Taking the average of the values in the channels under consideration, the pole and first excited state contribution is found to be $59\%$ of the total contribution. The mass and residue of the excited $D^{\prime }$ baryons versus $M^{2}$ at different values of the new continuum threshold are shown in Figs. 1, 2, 3 and 4. Extracted from our analysis, we depict the numerical values of the masses and residues of $D^{\prime }$ baryons in Table 6.

A quick glance at Table 6 leads to the following results:

• The values of the masses obtained for the radially excited $\Delta '$ and $\Sigma ^{*'}$ baryons are well consistent with the experimentally well-known $\Delta (1600)$ and $\Sigma (1730)$ baryons masses.

• Our result on the mass of the radially excited $\Xi ^{*'}$ baryon is in nice consistency with the experimentally observed $\Xi (1950)$ state presented in PDG [15]. The quantum numbers of this state have not been established yet from the experiment. This consistency suggests that the $\Xi (1950)$ state can be assigned to the first excited state of the ground state $\Xi (1530)$. For more information as regards the $\Xi (1950)$ state, see for instance [18,19,20,21,22,23,24] and the references therein.

• In the $\Omega ^{-}$ channel, our prediction for the excited state is also consistent with the mass of the experimentally observed (but unknown quantum numbers) $\Omega (2250)^{-}$ state within the errors. Therefore our analyses show that the $\Omega (2250)^{-}$ listed in the PDG [15] at $\Omega ^{-}$ channel can be assigned to the first excited state of the ground state $\Omega ^{-}$ with quantum numbers $J^{P}=\frac{3}{2}^{+}$. For more information as regards the $\Omega (2250)^{-}$ state, see for instance [25, 26] and the references therein.

Table 5 The working regions of $s^{\prime }_0$ for the radially excited $\Delta '$, $\Sigma ^{*'}$, $\Xi ^{*'}$ and $\Omega ^{-'}$ baryons

Fig. 1

Left the mass of the radially excited $\Delta '$ baryon vs. Borel parameter $M^2$. Right the residue of the radially excited $\Delta '$ baryon vs Borel parameter $M^2$

Fig. 2

The same as Fig. 1, but for the radially excited $\Sigma ^{*'}$ baryon

Fig. 3

The same as Fig. 1, but for the radially excited $\Xi ^{*'}$ baryon

Fig. 4

The same as Fig. 1, but for the radially excited $\Omega ^{-'}$ baryon

Table 6 The numerical values of masses and residues of the radially excited $\Delta '$, $\Sigma ^{*'}$, $\Xi ^{*'}$ and $\Omega ^{-'}$ baryons

4 Conclusion

We have studied the spin-3/2, $\Delta$, $\Sigma ^{*}$, $\Xi ^{*}$ and $\Omega ^{-}$ baryons and calculated the mass and residue of the corresponding ground and first excited states in the framework of two-point QCD sum rules. First, we extracted the mass and residue of the ground state baryons by choosing an appropriate threshold from the obtained sum rules. We then used those values as inputs to obtain the mass and residue of the first excited state in each channels. Our results for the ground states are in nice agreement with the experimental data and the existing theoretical predictions. In the case of excited states, our predictions for the mass of the excited $\Delta '$ and $\Sigma ^{*'}$ states are in good consistency with the experimentally known $\Delta (1600)$ and $\Sigma (1730)$ states’ masses. In the case of excited $\Xi ^{*'}$ and $\Omega ^{-'}$ baryons, our results suggest that the experimentally poorly known $\Xi (1950)$ and $\Omega (2250)^{-}$ states can be assigned to the first excited states in $\Xi ^{*}$ and $\Omega ^{-}$ channels with $J^{P}=\frac{3}{2}^{+}$. Our results for the residues can be verified via different theoretical approaches.