No-scale $\mu$-term hybrid inflation

Abstract

To solve the fine-tuning problem in $\mu$-term hybrid inflation, we will realize the supersymmetry scenario with the TeV-scale supersymmetric particles and intermediate-scale gravitino from anomaly mediation, which can be consistent with the WMAP and Planck experiments. Moreover, we for the first time propose the $\mu$-term hybrid inflation in no-scale supergravity. With four scenarios for the $SU(3)_C\times SU(2)_L\times SU(2)_R\times U(1)_{B-L}$ model, we show that the correct scalar spectral index $n_s$ can be obtained, while the tensor-to-scalar ratio r is predicted to be tiny, about $10^{-10}$–$10^{-8}$. Also, the $SU(2)_R\times U(1)_{B-L}$ symmetry breaking scale is around $10^{14}$ GeV, and all the supersymmetric particles except gravitino are around the TeV scale, while the gravitino mass is around $10^{9}$–$10^{10}$ GeV. Considering the complete potential terms linear in S, we for the first time show that the tadpole term, which is the key for such kind of inflationary models to be consistent with the observed scalar spectral index, vanishes after inflation. Thus, to obtain the $\mu$ term, we need to generate the supersymmetry breaking soft term $A^{S \Phi \Phi '}_{\kappa } \kappa S \Phi \Phi '$ due to $A^{S \Phi \Phi '}_{\kappa }=0$ in no-scale supergravity, where $\Phi$ and $\Phi '$ are vector-like Higgs fields at high energy. We show that the proper $A^{S \Phi \Phi '}_{\kappa } \kappa S \Phi \Phi '$ term can be obtained in the M-theory inspired no-scale supergravity. We also point out that $A^{S \Phi \Phi '}_{\kappa }$ around 700 GeV can be generated via the renormalization group equation running from string scale. We briefly comment on the supersymmetry phenomenological consequences as well.

It is well known that our Universe may experience an accelerated expansion, i.e., inflation [1,2,3,4], at a very early stage of evolution, as suggested by the observed temperature fluctuations in the cosmic microwave background radiation (CMB). From the particle physics point of view, supersymmetry is the most promising extension for the Standard Model (SM). In particular, the scalar masses can be stabilized, and the superpotential is non-renormalized. Because gravity is also very important in the early Universe, it seems to us that supergravity theory is a natural framework for the inflationary model building [5, 6].

The F-term hybrid inflation in a supersymmetric high energy model with gauge symmetry G has a renormalizable superpotential W and a canonical Kähler potential K [7, 8]. In particular, the $Z_2$ R-parity in the supersymmetric SMs (SSMs) is extended to a continuous $U(1)_R$ symmetry, which determines superpotential. With the minimal W and K, the gauge symmetry G is broken down to a subgroup H at the end of inflation. For the supersymmetric high energy model, in general, we can consider either a left–right model with gauge symmetry $SU(3)_C\times SU(2)_L\times SU(2)_R\times U(1)_{B-L}$, or a Grand Unified Theory (GUT) such as the SU(5) model, the flipped $SU(5)\times U(1)_X$ model, or the Pati–Salam $SU(4)_c \times SU(2)_L \times SU(2)_R$ model [9, 10]. H can be the SM or SM-like gauge group, etc.

In the supersymmetric hybrid inflation [7],¹ the quantum corrections arising from supersymmetry breaking drive inflation, and the scalar spectral index was predicted to be $n_s = 1 - 1/N \simeq 0.98$, where $N= 60$ denotes the number of e-foldings necessary to resolve the horizon and flatness problems in Big Bang cosmology. Interestingly, with a class of linear supersymmetry breaking soft terms in the inflationary potential [14,15,16,17,18], such a kind of models can be highly consistent with the observed scalar spectral index values of $n_s=0.96-0.97$ from the WMAP [19] and Planck satellite experiments [20, 21] as well. In particular, the corresponding supersymmetry breaking A-term for the linear superpotential term can be around the TeV scale [14,15,16,17,18].

As we know, in the Minimal SSM (MSSM), there exists a well-known $\mu$ problem. However, the $\mu H_d H_u$ term is forbidden by $U(1)_R$ symmetry, where $H_u$ and $H_u$ are one pair of Higgs fields in the SSMs. With the linear supersymmetry breaking soft term after inflation, the inflaton field S acquires a Vacuum Expectation Value (VEV). Thus, the $\mu$ problem can be solved if there exists a superpotential term $\lambda S H_d H_u$, as proposed by Dvali, Lazarides and Shafi (DLS) [22, 23]. Assuming the minimal K, the magnitude of $\mu$ is typically around the gravitino mass $m_G$ [22, 23]. Recently, such scenario has been studied in detail [13]. With the reheating and cosmological gravitino constraints, it was found that a consistent inflationary scenario gives rather concrete predictions regarding supersymmetric dark matter and Large Hadron Collider (LHC) phenomenology. Especially, the gravitino must be sufficiently heavy ($m_G \gtrsim 5 \times 10^7$ GeV) so that it decays before the freeze out of the lightest supersymmetric particle (LSP) neutralino, which is the dark matter candidate. Moreover, the wino with mass $\simeq 2$ TeV becomes a compelling dark matter candidate. The supersymmetry breaking scalar mass $M_0$ is expected to be of the same order as $m_G$ or larger, which can reproduce a SM-like Higgs boson mass $\simeq 125$ GeV for suitable $\tan \beta$ values, where $\tan \beta$ is the ratio of the VEVs for $H_u$ and $H_d$. Depending on the underlying gauge symmetry G associated with the inflationary scenario, the observed baryon asymmetry in the Universe can be explained via leptogenesis [24, 25]. The compelling examples of G, in which the DLS mechanism can be successfully merged with inflation, contain $U(1)_{B-L}$, $SU(2)_L \times SU(2)_R \times U(1)_{B-L}$, and flipped $SU(5)\times U(1)_X$. The other examples of G are SU(5) and $SU(4)_C \times SU(2)_L \times SU(2)_R$ [9, 10], but there may exist a monopole problem.

In short, in the recent study [13], to solve the gravitino problem in the $\mu$-term hybrid inflation, Okada and Shafi showed that the sfermions, Higgsinos, and gravitino are heavy around $10^7$ GeV, while the gauginos are light around TeV, which are similar to the split supersymmetry [26,27,28,29,30].² Thus, the supersymmetry solution to gauge hierarchy problem is at least partly gone, i.e., there exists big fine-tuning around $10^{-10}$. On the other hand, even if the corresponding supersymmetry breaking A-term for the linear superpotential term is around TeV scale [14,15,16,17,18], we can still obtain the observed scalar spectral index values of $n_s=0.96-0.97$ from the WMAP [19] and Planck satellite experiments [20, 21]. Therefore, to solve this problem, we do need the supersymmetry scenario, which can have the TeV-scale supersymmetric particles (sparticles) in the SSMs, together with the intermediate-scale heavy gravitino. The well-known example is no-scale supergravity [33,34,35,36,37] or its generalization. In this paper, we shall realize such a supersymmetry scenario via anomaly mediation [30]. In addition, we for the first time propose the $\mu$-term hybrid inflation in no-scale supergravity.³ We discuss it in detail, and we find some interesting results different from the previous study of the $\mu$-term hybrid inflation. Also, we briefly discuss the supersymmetry phenomenological consequences.

First, with anomaly mediation, we will derive the supersymmetry scenario, where the sparticles are light, while the gravitino is heavy [30]. We consider the Kähler potential and superpotential as follows:

$$\begin{aligned} K= & {} -3 M_\mathrm{Pl}^2 \left( z+{\bar{z}}+\epsilon f(z, {\bar{z}})\right) {\bar{X}} X +\sum _Y {\bar{Y}} Y,\, \end{aligned}$$

(1)

$$\begin{aligned} W= & {} X^3 W_0 + S (\kappa X^2 M^2 - \kappa \Phi ' \Phi + \lambda H_d H_u ),~\, \end{aligned}$$

(2)

where $M_\mathrm{Pl}$ is the reduced Planck scale, z and X are respectively a hidden sector superfield and a compensator multiplet ($X=1+F_X$), Y denotes all the other superfields, $\epsilon$ is a small parameter, $W_0$ is a constant superpotential, and $\Phi '$ and $\Phi$ are the Higgs fields which breaks the high-scale gauge symmetry in the F-term hybrid inflation [7, 8]. Similar to the no-scale supergravity, the scalar potential vanishes in the limit $\epsilon \rightarrow 0$. Considering the equations of motion for the auxiliary fields, we obtain

$$\begin{aligned} F_X \!\simeq \!-\!\frac{W_0^{\dagger }}{M_\mathrm{Pl}^2} \epsilon f_{{\bar{z}}z} \!=\! -\! \epsilon m_G f_{{\bar{z}}z},\quad ~~~ F_z \simeq \frac{W_0^{\dagger }}{M_\mathrm{Pl}^2}~=~m_G,~ \end{aligned}$$

(3)

for small $\epsilon$. Here, we define $f_{{\bar{z}}z} \equiv \partial ^2 f(z, {\bar{z}})/ \partial {\bar{z}} \partial z$, and $m_G$ is the gravitino mass. So the scalar potential becomes

$$\begin{aligned} V =-3 F_X W_0 \simeq 3\frac{|W_0|^2}{M_\mathrm{Pl}^2} \epsilon f_{{\bar{z}}z} = 3 \epsilon m^2_G M_\mathrm{Pl}^2 f_{{\bar{z}}z}.~ \end{aligned}$$

(4)

For example, assuming $f_{{\bar{z}}z} = (|z|^2-1/4)^2-1$, we get the minimum for the scalar potential at $\langle z\rangle =1/2$

$$\begin{aligned} V_\mathrm{min} \simeq -3 \epsilon m^2_G M_\mathrm{Pl}^2,~ \end{aligned}$$

(5)

which is an AdS vacuum. Thus, we have $F_X\simeq \epsilon m_G<< m_G$. Because the supersymmetry breaking soft terms in the SSMs are proportional to $F_X$ via anomaly mediation, we obtain the supersymmetry breaking scenario which has TeV-scale sparticles and an intermediate-scale gravitino. In particular, the supersymmetry breaking linear term for S is given by

$$\begin{aligned} V= & {} -4 \kappa F_X M^2 S + \mathrm{H.C} \simeq -4 \kappa \epsilon m_G M^2 S + \mathrm{H.C}.~\, \end{aligned}$$

(6)

From the numerical studies in Refs. [14,15,16,17,18], we can still obtain the observed scalar spectral index values of $n_s=0.96-0.97$ from the WMAP [19] and Planck satellite experiments [20, 21] as well. By the way, the AdS vacuum given by Eq. (5) can be lifted to the Minkowski vacuum by considering the F-term and D-term contributions in the anomalous U(1) theory inspired from string models [30].

In the following, we shall embed the previous $\mu$-term hybrid inflation scenario into no-scale supergravity framework, i.e., we propose the $\mu$-term hybrid inflation in no-scale supergravity where $\mu$ term is generated via the VEV of inflaton field after inflation. We introduce a conjugate pair of vector-like Higgs fields $\Phi$ and $\Phi '$, which breaks G down to the SM or SM-like gauge symmetry. Considering four scenarios for the $SU(3)_C\times SU(2)_L\times SU(2)_R\times U(1)_{B-L}$ model, we show that the correct scalar spectral index $n_s$ can be obtained, while the tensor-to-scalar ratio r is predicted to be tiny, about $10^{-10}$–$10^{-8}$. Thus, the $\eta$ problem is solved as well. Also, the $SU(2)_R\times U(1)_{B-L}$ symmetry breaking scale is around $10^{14}$ GeV, and all the supersymmetric particles except the gravitino are around the TeV scale, while the gravitino mass is around $10^{9}$–$10^{10}$ GeV. We present the complete potential terms that are linear in S, and for the first time we show that the tadpole term, which is the key for such kind of inflationary models to be consistent with the observed scalar spectral index, vanishes after inflation or say gauge symmetry G breaking. Thus, to reproduce the $\mu$ term, we need to generate the supersymmetry breaking soft term $A^{S \Phi \Phi '}_{\kappa } \kappa S \Phi \Phi '$ since we have $A^{S \Phi \Phi '}_{\kappa }=0$ in no-scale supergravity. We show that the supersymmetry breaking soft term $A^{S \Phi \Phi '}_{\kappa } \kappa S \Phi \Phi '$ can be generated properly in the M-theory inspired no-scale supergravity which has no-scale supergravity at the leading or lowest order [39,40,41,42,43]. We also point out that the $A^{S \Phi \Phi '}_{\kappa } \kappa S \Phi \Phi '$ term with $A^{S \Phi \Phi '}_{\kappa }$ around 700 GeV can be obtained via the renormalization group equation (RGE) running from string scale [44,45,46,47]. Therefore, we solve the fine-tuning problem in the previous $\mu$-term hybrid inflation, and propose the no-scale $\mu$-term hybrid inflation models where the sparticles in the SSMs are around TeV scale, while the gravitino is around $10^{9}$–$10^{10}$ GeV.

Let us present our model in the following. The Kähler potential is

$$\begin{aligned} K= & {} \overline{S} S - 3 \mathrm{ln}(T+\overline{T}-2\overline{C_i} C_i ),~\, \end{aligned}$$

(7)

where T is a modulus, and $C_i$ are matter/Higgs fields in the supersymmetric SMs which include $\Phi$, $\Phi '$, $H_u$, and $H_d$. To simplify the discussions, we will assume $\langle T \rangle =1/2$ in the following study.

Fig. 1

The allowed numerical values for M, $m_{G}$ and $\kappa$ to get $0.955 \le n_s \le 0.977$ and $50 \le N \le 60$ for the potential in Eq. (11) with $m_\phi \simeq m_G$

Assuming S and superpotential have charge 2, while the $\Phi$, $\Phi '$, $H_u$ and $H_d$ are neutral under the $U(1)_R$ R-symmetry, we obtain the $U(1)_R$ invariant inflaton superpotential [22, 23]

$$\begin{aligned} W = S ( \kappa \Phi ' \Phi - \kappa M^2 + \lambda H_d H_u ).\, \end{aligned}$$

(8)

To realize the correct symmetry breaking pattern after inflation, we require $\lambda > \kappa$ [22, 23]. In particular, the $\mu H_d H_u$ term is forbidden by the $U(1)_R$ R-symmetry, and then such term can be generated only after $U(1)_R$ R-symmetry is broken down to a $Z_2$ symmetry, for example, by the VEV of S.

Assuming that the F-term of T breaks supersymmetry, we obtain the following scalar potential which is linear in S:

$$\begin{aligned} V&\supset&m_G S ( \kappa \Phi ' \Phi - \kappa M^2 + \lambda H_d H_u )+\mathrm{H.C.}.~\, \end{aligned}$$

(9)

As a side remark, for the Polonyi model, we will have an extra ($-2$) factor in the above tadpole term due to the $-3|W|^2$ contribution. During inflation, we have $\langle \Phi \rangle = \langle \Phi ' \rangle =0$, as well as a tadpole term for S,

$$\begin{aligned} V&\supset&- \kappa m_G M^2 S + \mathrm{H.C.}.~\, \end{aligned}$$

(10)

After inflation (or say after gauge symmetry G breaking) and neglecting the VEVs of $H_u$ and $H_d$, we have $\langle \Phi \rangle = \langle \Phi ' \rangle =M$, and then the above tadpole term vanishes. To obtain the $\mu$ term which is forbidden by $U(1)_R$ symmetry, we need to generate the tadpole term of S, which will be discussed below.

With the supersymmetry breaking soft mass term as well as the radiative and supergravity corrections, we obtain the inflationary potential as follows:

$$\begin{aligned} V(\phi )= & {} \frac{1}{2} m_\phi ^2 \phi ^2 + m^4 \left( 1+ \alpha \ln \left[ \frac{\phi }{\phi _0}\right] + \frac{3 \phi ^2}{2M^2_\mathrm{Pl}} + \frac{7\phi ^4}{8M^4_\mathrm{Pl}}\right) \nonumber \\&- \sqrt{2} m_G m^2 \phi ,~ \end{aligned}$$

(11)

where $m = \sqrt{\kappa } M$, $\phi$ is the real part of S, $m_\phi$ is the supersymmetry breaking soft mass, $M_\mathrm{Pl}$ is the reduced Planck scale, the renormalization scale (Q) is chosen to be equal to the initial inflaton VEV $\phi _0$, and the coefficient $\alpha \ll 1$ is given by

$$\begin{aligned} \alpha = \frac{1}{4 \pi ^2} \left( \lambda ^2 + \frac{N_{\Phi }}{2} \kappa ^2 \right) .~\, \end{aligned}$$

(12)

In particular, the negative sign of the linear term is essential to generate the correct value for the spectral index. Without this linear term, the scalar spectral index $n_s$ is predicted to lie close to 0.98, as shown in Ref. [7]. The imaginary part of S is assumed to stay constant during inflation (for a more complete discussion of this last point, see Refs. [15,16,17,18]). Because $\phi$ is around 0.1, we find that the $\phi ^4$ term is much smaller than the other terms in general and can be neglected.

In the following discussions, to be concrete, we consider the left–right model with gauge symmetry $SU(3)_C\times SU(2)_L\times SU(2)_R\times U(1)_{B-L}$. Because $\Phi$ and $\Phi '$, respectively, have quantum numbers $(\mathbf {1}, \mathbf {1}, \mathbf {2}, \mathbf {1/2})$ and $(\mathbf {1}, \mathbf {1}, \mathbf {2}, \mathbf {-1/2})$, we get $N_{\Phi }=2$. For simplicity, we set $\gamma \equiv \lambda /\kappa =2$, and then have $\tilde{\gamma } \equiv \sqrt{\gamma ^2+N_{\Phi }/2} = \sqrt{5}$.

We will study the scenario for the potential in Eq. (11) with $m_\phi \simeq m_G$. The parameters in Eq. (11) are chosen so that the power spectrum $\Delta _R^2=2.20 \times 10^{-9}$ from the Planck 2015 results [20, 21] can be explained simultaneously. The well-known slow-roll parameters are given by

$$\begin{aligned} \epsilon =\frac{M^2_\mathrm{Pl}}{2} \left( \dfrac{V'}{V}\right) ^2, \quad ~ \eta =M^2_\mathrm{Pl}~\dfrac{V''}{V}.~ \end{aligned}$$

(13)

Then the scalar spectral index and tensor-to-scalar ratio are calculated as

$$\begin{aligned} n_s=1-6\epsilon (\phi _0)+2\eta (\phi _0), \quad ~ r=16\epsilon (\phi _0) ,~ \end{aligned}$$

(14)

and e-folding number is

$$\begin{aligned} N=-\frac{1}{M^2_\mathrm{Pl}}\int _{\phi _0}^{\phi _e} \mathrm {d}\phi ~ \dfrac{V}{V'},~ \end{aligned}$$

(15)

where $\phi _0$ is the value of field when the interesting mode $k_*$ crossed outside the horizon, and $\phi _e$ is the field value at the end of inflation. This coincides with either the critical point $\phi _c=\sqrt{2}M$ or the value for which one of the slow-roll parameters exceeds unity. In our scenario, we find inflation ends at $|\eta |=1$. For convenience of the calculation, we will redefine the parameter as follows:

$$\begin{aligned} B= \dfrac{\sqrt{2}m_G}{m^2}.~ \end{aligned}$$

(16)

To obtain $0.955 \le n_s \le 0.977$ within about $1\sigma$ range of the Planck 2015 results [20, 21] and the e-folding number $50 \le N \le 60$, we present the numerical values of M, $m_{G}$ and $\kappa$ for the viable points in Fig. 1, where the mass parameters M and $m_{G}$ are normalized by the reduced Planck scale $M_\mathrm{Pl}=2.43 \times 10^{18}~\mathrm{GeV}$. Thus, we find that the range of $\kappa$ is from 0.35 to 1.05, the tensor-to-scalar ratio r is tiny, from $4\times 10^{-10}$ to $5\times 10^{-9}$, the gravitino mass $M_G$ is from $5\times 10^{-10}~M_\mathrm{Pl}$ to $1.05\times 10^{-8}~M_\mathrm{Pl}$ or from $1.215\times 10^9$ to $2.5515\times 10^{10}$ GeV, and M is from $8\times 10^{-5}~M_\mathrm{Pl}$ to $1.5\times 10^{-4}~M_\mathrm{Pl}$ or from $1.944\times 10^{14}$ to $3.645\times 10^{14}$ GeV.

Fig. 2

$\epsilon /\eta$ and V versus $\phi$ for the best fit point. The black and red dashed lines correspond to $\phi _0$ or the inflation end point $\phi _e$, respectively

Fig. 3

$\epsilon /\eta$ and V versus $\phi$ for the minimal value of M. The black and red dashed lines correspond to $\phi _0$ or the inflation end point $\phi _e$

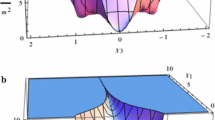
From Fig. 1, the best fit point consistent with the Planck results has $n_{s}=0.964677$, $r=1.32516\times 10^{-9}$, and $N=54.1$, which can be obtained by choosing $\alpha =0.0276$, and $B=0.5950 ~M^{-1}_\mathrm{Pl}$. Thus, we have $m_{G}=2.8227024 \times 10^{-9} ~M_\mathrm{Pl}\approx 6.85917\times 10^{9}~\mathrm{GeV}$, $M=1.1988279 \times 10^{-4}~M_\mathrm{Pl}\approx 2.91315\times 10^{14}~\mathrm{GeV}$, $\kappa =0.46682$ and $m=8.1909\times 10^{-5} ~M_\mathrm{Pl}$ determined by the power spectrum $\Delta _R^2$. Also, we present $\epsilon /\eta$ and V versus $\phi$ in Fig. 2. Inflation begins at $\phi _0=0.0917 ~M_\mathrm{Pl}$ and ends with $\phi _e=0.08102 ~M_\mathrm{Pl}$. During inflation, the magnitude of each term in potential Eq. (11) is given as follows:

$$\begin{aligned}&\frac{7 m^4 }{8 ~M_\mathrm{Pl}^4}\phi ^4 \sim 1.7\times 10^{-21}M^4_\mathrm{Pl} ,\nonumber \\&\frac{1}{2}m^2_{\phi } \phi ^2 \sim 2.6\times 10^{-20}~M_\mathrm{Pl}^4,~\nonumber \\&\frac{3 m^4 }{2 ~M_\mathrm{Pl}^2}\phi ^2\sim 4.4\times 10^{-19}~M_\mathrm{Pl}^4 ,\nonumber \\&m^4 \alpha \ln \left[ \frac{\phi }{\phi _0}\right] \sim -1.5\times 10^{-19}~M_\mathrm{Pl}^4~,~\\&-\sqrt{2}m_G m^2\phi \sim -2.2\times 10^{-18}~M_\mathrm{Pl}^4 ,\nonumber \\&m^4 \sim 4.5\times 10^{-17}~M_\mathrm{Pl}^4.~\nonumber \end{aligned}$$

(17)

As we expected, we find that the $\phi ^4$ term is much smaller than all the other terms, and it can indeed be neglected. The $\frac{1}{2}m^2_{\phi } \phi ^2$ term is small as well.

Fig. 4

$\epsilon /\eta$ and V versus $\phi$ for the minimal value of $m_G$. The black and red dashed lines correspond to $\phi _0$ or the inflation end point $\phi _e$

Next, we give the benchmark point with the minimal value of M, which has $\alpha =0.1261$, $B=1.4469 ~M^{-1}_\mathrm{Pl}$. So we have $m_ G= 7.1897574\times 10^{-9} ~M_\mathrm{Pl} \approx 1.74711\times 10^{10}~\mathrm{GeV}$, $M=8.392071\times 10^{-5}~M_\mathrm{Pl}\approx 2.03927\times 10^{14}~\mathrm{GeV}$, $\kappa =0.99782$ and $m=8.38292\times 10^{-5} ~M_\mathrm{Pl}$ determined by the power spectrum $\Delta _R^2$. The corresponding inflationary observables and number of e-foldings are $n_{s}=0.961001$, $r=1.23311\times 10^{-9}$, and $N=57.1$, respectively. Also, we present $\epsilon /\eta$ and V versus $\phi$ in Fig. 3. Inflation begins at $\phi _0=0.16995 ~M_\mathrm{Pl}$ and ends with $\phi _e=0.156956 ~M_\mathrm{Pl}$. Similarly, during inflation, the $\phi ^4$ term is much smaller than the other terms,

$$\begin{aligned}&\frac{7 m^4 }{8 ~M_\mathrm{Pl}^4}\phi ^4 \sim 2.6\times 10^{-20}M^4_\mathrm{Pl} ,\nonumber \\&\frac{1}{2}m^2_{\phi } \phi ^2 \sim 6.4\times 10^{-19}~M_\mathrm{Pl}^4~,~\nonumber \\&\frac{3 m^4 }{2 ~M_\mathrm{Pl}^2}\phi ^2\sim 1.8\times 10^{-18}~M_\mathrm{Pl}^4 , \nonumber \\&m^4 \alpha \ln \left[ \frac{\phi }{\phi _0}\right] \sim -5.0 \times 10^{-19}~M_\mathrm{Pl}^4~,~\\&-\sqrt{2}m_G m^2\phi \sim -1.1\times 10^{-17}~M_\mathrm{Pl}^4 ,\nonumber \\&m^4 \sim 5.0\times 10^{-17}~M_\mathrm{Pl}^4~.~\nonumber \end{aligned}$$

(18)

Moreover, we present the benchmark point with the minimal $m_G$, which has $\alpha =0.0172$, $B=0.4638 ~M^{-1}_\mathrm{Pl}$. So we have $m_G=1.50442\times 10^{-9}~M_\mathrm{Pl} \approx 3.61061\times 10^{9}~\mathrm{GeV}$, $M=1.1156992 \times 10^{-4}~M_\mathrm{Pl}\approx 2.71115\times 10^{14}~\mathrm{GeV}$, $\kappa =0.368518$, and $m=6.7729\times 10^{-5} ~M_\mathrm{Pl}$ determined by the power spectrum $\Delta _R^2$. The corresponding inflationary observables and number of e-foldings are $n_{s}=0.959809$, $r=6.29505\times 10^{-10}$, and $N=57.4$, respectively. Also, we present $\epsilon /\eta$ and V versus $\phi$ in Fig. 4. Inflation begins at $\phi _0=0.0735 ~M_\mathrm{Pl}$ and ends with $\phi _e=0.064568 ~M_\mathrm{Pl}$. During inflation, the $\phi ^4$ and $\phi ^{2}$ terms are much smaller than the other terms,

$$\begin{aligned}&\frac{7 m^4 }{8 ~M_\mathrm{Pl}^4}\phi ^4\sim 3.2\times 10^{-22}M^4_\mathrm{Pl} ,\nonumber \\&\frac{1}{2}m^2_{\phi } \phi ^2 \sim 4.7\times 10^{-21}~M_\mathrm{Pl}^4,~\nonumber \\&\frac{3 m^4 }{2 ~M_\mathrm{Pl}^2}\phi ^2\sim 1.3\times 10^{-19}~M_\mathrm{Pl}^4 ,\nonumber \\&m^4 \alpha \ln \left[ \frac{\phi }{\phi _0}\right] \sim -4.7\times 10^{-20}~M_\mathrm{Pl}^4,~\\&-\sqrt{2}m_G m^2\phi \sim -6.3 \times 10^{-19}~M_\mathrm{Pl}^4 ,\nonumber \\&m^4\sim 2.1\times 10^{-17}~M_\mathrm{Pl}^4.~\nonumber \end{aligned}$$

(19)

In short, from the above numerical studies, we find that the observed scalar spectral index $n_s$ can be realized, but the tensor-to-scalar ratio r is predicted to be tiny, about $10^{-10}$–$10^{-8}$. Also, the $SU(2)_R\times U(1)_{B-L}$ symmetry breaking scale is around $10^{14}$ GeV, and the gravitino mass is around $10^{9}$–$10^{10}$ GeV. Thus, we do need the no-scale supergravity to realize the light sparticle spectrum.

Because the gravitino is heavy and thus unstable, we encounter the cosmological gravitino problem [48, 49], which originates from the gravitino lifetime,

$$\begin{aligned} \tau _G \simeq 10^{4} \; \mathrm{sec} \times \left( \frac{1\; \mathrm{TeV}}{m_G}\right) ^3. \end{aligned}$$

(20)

To avoid the constraint on the neutralino abundance from gravitino decay, we assume that the LSP neutralino is still in thermal equilibrium when gravitino decays. So the LSP neutralino abundance is not related to the gravitino yield. Using a typical value of the ratio $x_F\equiv m_{{\tilde{\chi }}^0}/T_F \simeq 20$, where $T_F$ is the freeze out temperature of the LSP neutralino, this occurs for a gravitino lifetime of

$$\begin{aligned} \tau _G \lesssim 4 \times 10^{-10} \left( \frac{1 \text { TeV}}{m_{{\tilde{\chi }}^0}} \right) ^2. \end{aligned}$$

(21)

Combining this with Eq. (20), we find

$$\begin{aligned} m_G \gtrsim 4.6 \times 10^7 \text { GeV} \left( \frac{m_{{\tilde{\chi }}^0}}{2 \text { TeV}} \right) ^{2/3}. \end{aligned}$$

(22)

Therefore, such cosmological scenario favors a gravitino mass at an intermediate scale above $10^7$ GeV, and the gravitino mass in our model satisfies this bound clearly.

Furthermore, after $SU(2)_R\times U(1)_{B-L}$ gauge symmetry breaking, the leading tadpole term for S in Eq. (9) vanishes. Thus, to obtain the $\mu$ term which is forbidden by $U(1)_R$ symmetry, we need to generate the supersymmetry breaking soft term $A^{S \Phi \Phi '}_{\kappa } \kappa S \Phi \Phi '$. With it, we get the VEV of S,

$$\begin{aligned} \langle S \rangle= & {} \frac{A^{S \Phi \Phi '}_{\kappa }}{2\kappa }.~\, \end{aligned}$$

(23)

The $\mu$ term is given by

$$\begin{aligned} \mu= & {} \frac{\lambda }{2\kappa }A^{S \Phi \Phi '}_{\kappa }.~\, \end{aligned}$$

(24)

For $\lambda =2 \kappa$, we have

$$\begin{aligned} \mu= & {} A^{S \Phi \Phi '}_{\kappa }.~\, \end{aligned}$$

(25)

However, in no-scale supergravity, we have $A^{S \Phi \Phi '}_{\kappa }=0$. To solve this problem, first, we consider M-theory on $S^1/Z_2$ [39]. For the standard Calabi–Yau compactification at the leading order or lowest order, we can realize no-scale supergravity [40], and there exists next to leading order corrections [41,42,43]. In particular, we can have the non-zero supersymmetry breaking soft term $A^{S \Phi \Phi '}_{\kappa } \kappa S \Phi \Phi '$. To compare with no-scale supergravity, we consider moduli dominant supersymmetry breaking, whose the supersymmetry breaking soft terms for universal gaugino mass, scalar mass and trilinear soft term are [43]

$$\begin{aligned} M_{1/2}= & {} \frac{x}{1+x} m_G,~ \, \end{aligned}$$

(26)

$$\begin{aligned} M_0= & {} \frac{x}{3+x} m_G,~\, \end{aligned}$$

(27)

$$\begin{aligned} A= & {} - \frac{3x}{3+x} m_G,~\, \end{aligned}$$

(28)

where $0< x < 1$. For $x \sim 10^{-6}-10^{-7}$, we can indeed have the TeV-scale supersymmetry breaking soft terms in the SSMs, while the gravitino mass is around $10^{9}$–$10^{10}$ GeV. Also, we obtain the approximate relation among the supersymmetry breaking soft terms $M_{1/2} \simeq 3 M_0 \simeq 3 A$. Of course, there exists some fine-tuning for x. In this paper, for simplicity, we assume that the anomaly mediation is forbidden, i.e., the compensator field in superconformal field theory does not have a non-zero F-term.

Another way to generate the $A^{S \Phi \Phi '}_{\kappa } \kappa S \Phi \Phi '$ term is from the RGE running in no-scale supergravity [44,45,46,47]. Because of $A=0$ from the no-scale boundary condition, we can neglect the Yukawa contributions and the RGE for $A^{S \Phi \Phi '}_{\kappa }$ is

$$\begin{aligned} 16\pi ^2 \frac{\mathrm{d}A^{S \Phi \Phi '}_{\kappa }}{\mathrm{d}t}= & {} -2(g_{B-L}^2 M_{B-L}+3 g_{2R}^2 M_{2R}) \end{aligned}$$

(29)

before the $SU(2)_R\times U(1)_{B-L}$ gauge symmetry breaking, and

$$\begin{aligned} 16\pi ^2 \frac{\mathrm{d}A^{S \Phi \Phi '}_{\kappa }}{\mathrm{d}t}= & {} -4 g_{1}^2 M_{1} \end{aligned}$$

(30)

after the $SU(2)_R\times U(1)_{B-L}$ gauge symmetry breaking. Here, $t=\mathrm{ln} \mu$, $g_{B-L}$, $g_{2R}$, and $g_1$ are, respectively, gauge couplings for $U(1)_{B-L}$, $SU(2)_R$, and $U(1)_Y$, and $M_{B-L}$, $M_{2R}$, and $M_{1}$ are the corresponding gaugino masses. The boundary condition for the gauge couplings at the $SU(2)_R\times U(1)_{B-L}$ gauge symmetry breaking scale is

$$\begin{aligned} \frac{1}{g_1^2}= & {} \frac{1}{g_{B-L}^2} + \frac{1}{g_{2R}^2}.~\, \end{aligned}$$

(31)

Because we do not present a complete model here, let us consider the simple case. For no-scale supergravity, we should run the RGEs from the string scale; otherwise, the light stau will be the LSP [44,45,46,47]. Thus, we run the RGE from the string scale to the scale around the masses of S, $\Phi$, and $\Phi '$. For $g_{B-L}=g_{2R}=1$ and $M_{B-L}= M_{2R}=2$ TeV, assuming the constant gauge couplings and gaugino masses, we get $\mu = A^{S \Phi \Phi '}_{\kappa }\simeq -700$ GeV for order one $\kappa$. Of course, in such a kind of left–right models, we generically need to introduce more particles, and the complete RGE study is much more complicated. Note that if we have more particles above the $SU(2)_R\times U(1)_{B-L}$ symmetry breaking scale, their gauge couplings will become larger at higher scale and then the magnitude of $A^{S \Phi \Phi '}_{\kappa }$ will be larger, which can give us a larger $\mu$ term if we want. Therefore, we can indeed obtain the SSMs with TeV-scale supersymmetry and the intermediate-scale heavy gravitino.

Let us briefly comment on the phenomenological consequences of the no-scale supergravity and M-theory supergravity. From the LHC supersymmetry search constraints, it is well known that there exists a supersymmetric electroweak fine-tuning problem in the SSMs. With the Giudice–Masiero mechanism [50], we have shown that the fine-tuning measure defined by Ellis, Enqvist, Nanopoulos, and Zwirner (EENZ) [51] as well as Barbieri and Giudice (BG) [52] is automatically at the order one for the no-scale supergravity and M-theory supergravity, and then the supersymmetric electroweak fine-tuning problem is solved naturally [53,54,55,56]. This is called super-natural supersymmetry. If we do not introduce the additional vector-like particles, to obtain the correct SM-like Higgs boson mass, the sparticle spectra except the light sleptons will be too heavy and thus out of the LHC reaches. The light sleptons, especially the light stau, may be probed at the LHC in the future. For example, see Table 1 in Ref. [55]. This explains the (so far) non-detection of supersymmetry at the LHC. On the other hand, if we introduce the vector-like particles, the SM-like Higgs boson mass can be lifted via the Yukawa couplings between the Higgs bosons and vector-like particles at one loop. Thus, the sparticle spectra can be light and within the reaches of the LHC supersymmetry searches. In particular, the light stop is lighter than the gluino, and they are lighter than all the other squarks. The prediction is the ultra-high jet multiplicity signals at the LHC, which can be tested as well. For example, see the no-scale $\mathcal{F}-SU(5)$ case in Ref. [57].

In summary, to solve the problem in the $\mu$-term hybrid inflation with a canonical Kähler potential, we obtained the supersymmetry scenario which has the TeV-scale supersymmetric particles and intermediate-scale gravitino from anomaly mediation. Moreover, we for the first time proposed the $\mu$-term hybrid inflation in no-scale supergravity where the $\mu$ term is generated via the VEV of the inflaton field after inflation. Considering four scenarios for the $SU(3)_C\times SU(2)_L\times SU(2)_R\times U(1)_{B-L}$ model, we showed that the correct scalar spectral index $n_s$ can be obtained, while the tensor-to-scalar ratio r is predicted to be tiny, about $10^{-10}$–$10^{-8}$. Also, the $SU(2)_R\times U(1)_{B-L}$ symmetry breaking scale is around $10^{14}$ GeV, and all the supersymmetric particles except gravitino are around the TeV scale, while the gravitino mass is around $10^{9}$–$10^{10}$ GeV. With the complete potential terms linear in S, we for the first time showed that the tadpole term, which is the key for such kind of inflationary models to be consistent with the observed scalar spectral index, vanishes after inflation or, say, gauge symmetry G breaking. Thus, to obtain the $\mu$ term, we need to generate the supersymmetry breaking soft term $A^{S \Phi \Phi '}_{\kappa } \kappa S \Phi \Phi '$, since we have $A^{S \Phi \Phi '}_{\kappa }=0$ in no-scale supergravity. We showed that the supersymmetry breaking soft term $A^{S \Phi \Phi '}_{\kappa } \kappa S \Phi \Phi '$ can be realized properly in the M-theory inspired no-scale supergravity which has no-scale supergravity at the leading or lowest order. Also, we pointed out that the $A^{S \Phi \Phi '}_{\kappa } \kappa S \Phi \Phi '$ term with $A^{S \Phi \Phi '}_{\kappa }$ around a few hundred GeVs can be reproduced via the RGE running from string scale. Therefore, we proposed the no-scale $\mu$-term hybrid inflation models where the sparticles in the SSMs are around the TeV scale, while the gravitino is around $10^{9}$–$10^{10}$ GeV. We briefly explained the supersymmetry phenomenological consequences as well.