The renormalizable three-term polynomial inflation with large tensor-to-scalar ratio

Abstract

We systematically study the renormalizable three-term polynomial inflation in the supersymmetric and non-supersymmetric models. The supersymmetric inflaton potentials can be realized in supergravity theory, and only have two independent parameters. We show that the general renormalizable supergravity model is equivalent to one kind of our supersymmetric models. We find that the spectral index and tensor-to-scalar ratio can be consistent with the Planck and BICEP2 results, but the running of spectral index is always out of the $2\sigma$ range. If we do not consider the BICEP2 experiment, these inflationary models can be highly consistent with the Planck observations and saturate its upper bound on the tensor-to-scalar ratio ($r \le 0.11$). Thus, our models can be tested at the future Planck and QUBIC experiments.

1 Introduction

It is well-known that the standard big bang cosmology has some problems, for instance, the flatness, horizon, and monopole problems, etc., which can be solved naturally by inflation [1–4]. Also, the observed temperature fluctuations in the cosmic microwave background radiation (CMB) strongly suggests an accelerated expansion at a very early stage of our Universe evolution, i.e., inflation. Moreover, the inflationary models predict the cosmological perturbations in the matter density and spatial curvature from the vacuum fluctuations of the inflaton, which can explain the primordial power spectrum elegantly. Besides the scalar perturbation, the tensor perturbation is produced as well, which has special features in the B-mode of the CMB polarization data as a signature of the primordial inflation.

The Planck satellite measured the CMB temperature anisotropy with an unprecedented accuracy. From its first-year observational data [5] in combination with the 9 years of Wilkinson Microwave Anisotropy Probe polarization low-multipole likelihood data [6] and the high-multipole spectra data from the Atacama Cosmology Telescope [7] and the South Pole Telescope [8] (Planck $+$ WP $+$ highL), the scalar spectral index $n_s$, the running of the scalar spectral index $n_s' \equiv \mathrm{d} n_s/\mathrm{d}\ln k$, the tensor-to-scalar ratio r, and the scalar amplitude $A_s$ for the power spectrum of the curvature perturbations are, respectively, constrained to be [9, 10]

$$\begin{aligned} n_s= & {} 0.9603 \pm 0.0073,\quad n_s'=-0.0134\pm 0.0090,\nonumber \\ r\le & {} 0.11,\quad A^{1/2}_s = 4.6856^{+0.0566}_{-0.0628} \times 10^{-5}. \end{aligned}$$

(1)

As given by the Planck Collaboration, we also quote 68 % errors on the measured parameters and 95 % upper limits on the other parameters.

Recently, the BICEP2 experiment announced the discovery of the gravitational waves or primordial tensor perturbations in the B-mode power spectrum around $\ell \sim 80$ [11]. If confirmed by future experiments, it will definitely be a huge progress in fundamental physics. The measured tensor-to-scalar ratio is

$$\begin{aligned} r = 0.20^{+0.07}_{-0.05}. \end{aligned}$$

(2)

Subtracting the various dust models and re-deriving the r constraint still results in high significance of detection, we have

$$\begin{aligned} r = 0.16^{+0.06}_{-0.05}. \end{aligned}$$

(3)

Thus, the BICEP2 results are in tension with the Planck results. To be consistent with both experiments, one can consider the running of the spectral index. With it, we have the following results from the Planck+WP+highL data [9]

$$\begin{aligned} n_s= & {} 0.9570\pm 0.0075 , \quad n'_s=-0.022\pm 0.010 ,\nonumber \\ r< & {} 0.26\quad (95\,\%\,\mathrm{CL}) . \end{aligned}$$

(4)

And the combined Planck $+$ WP $+$ highL $+$ BICEP2 data give

$$\begin{aligned} n_s= & {} 0.9574^{+0.0073}_{-0.0074},\quad n'_s= -0.0292\pm 0.0096 ,\nonumber \\ r= & {} 0.21^{+0.05}_{-0.06} . \end{aligned}$$

(5)

Therefore, we must at least require the running of the spectral index $n'_s$ to be smaller than 0.0004 at 3$\sigma$ level for any viable inflationary model. However, there might exist the foreground subtleties in the BICEP2 experiment such as dust effects, etc. As we know, the recent observations from the Planck and BICEP2/Keck Array Collaborations provided strong constraints on the primordial tensor fluctuations [12–14], $r < 0.11$ ($r < 0.12$ from BICEP2/Keck Array) at 95 % confidence level (CL). Because these results were announced seven months after we submitted our paper to arXiv, we will not consider them here.

Obviously, such a large tensor-to-scalar ratio r from the BICEP2 measurement does impose a strong constraint on the inflationary models. For example, most inflationary models from string theory predict a small r, far below 0.01, and then contradict the BICEP2 results [15]. With $r=0.16$ or 0.20, we find that the Hubble scale during inflation is about $1.0\times 10^{14}$ GeV, and the inflaton potential is around the Grand Unified Theory (GUT) scale $2\times 10^{16}$ GeV which might have some connections with GUTs. From the naive analysis of Lyth bound [16], we will have large field inflation, and then the effective field theory might not be valid, since the high-dimensional operators are suppressed by the reduced Planck scale. The inflationary models, which can realize $n_s\simeq 0.96$ and $r\simeq 0.16/0.20$, have been studied extensively [17–50]. Especially, the simple chaotic and natural inflation models are favored.

From the particle physics point of view, supersymmetry is the most promising new physics beyond the Standard Model (SM). Especially, it can stabilize the scalar masses and has a non-renormalized superpotential. Moreover, gravity is very important in the early Universe. Thus, a natural framework for inflationary model building is supergravity theory [51, 52]. However, supersymmetry breaking scalar masses in a generic supergravity theory are of the same order as gravitino mass, giving rise to the so-called $\eta$ problem [53–58], where all the scalar masses are at the order of the Hubble scale due to the large vacuum energy density during inflation [59]. Two elegant solutions were proposed: no-scale supergravity [60–71], and shift symmetry in the Kähler potential [72–81].

The Planck satellite experiment might measure the tensor-to-scalar ratio r down to 0.03–0.05 in one or 2 years. The target of future QUBIC experiment is to constrain the tensor-to-scalar ratio of 0.01 at the 90 % CL with 1 year of data taking from the Concordia Station at Dôme C, Antarctica [82]. Thus, even if the BICEP2 results on the tensor-to-scalar ratio r were too large, as long as r is not smaller than 0.01, for example, $r=0.05$ or 0.1, how to construct inflationary models which highly agree with the Planck results and have a large tensor-to-scalar ratio is still a very important question, since these models can be tested in the near future.

The simple inflationary models have one parameter, for example, the monomial inflaton potentials. So the next to the simple inflationary models have two parameters. In the supergravity models with two parameters, we will generically have three terms due to the square of the F-term. In particular, we show that the general renormalizable supergravity model is equivalent to one kind of our supersymmetric models. Thus, in this paper, we will classify the renormalizable three-term polynomial inflationary models for both supersymmetric and non-supersymmetric models. The supersymmetric inflaton potentials can be obtained from supergravity theory. We find that their spectral indices and tensor-to-scalar ratios can be consistent with the Planck and BICEP2 experiments. However, $n'_s$ is always out of the $2\sigma$ range. In addition, even if we do not consider the BICEP2 results, we find that the three-term polynomial inflationary models can be consistent with the Planck observations. Especially, the tensor-to-scalar ratio cannot only be larger than 0.01 in the $1\sigma$ region, above the well-known Lyth bound [16], but it also saturates the Planck upper bound 0.11 in the $1\sigma$ region. Thus, these models produce the typical large field inflation, and they can be tested at the future Planck and QUBIC experiments.

This paper is organized as follows. In Sect. 2, we briefly review the slow-roll inflation. In Sect. 3, we construct the supersymmetric models from the supergravity theory. In Sect. 4, we systematically study the three-term polynomial inflation. Our conclusion is given in Sect. 5.

2 Brief review of slow-roll inflation

In the inflation, the slow-roll parameters are defined as

$$\begin{aligned} \epsilon= & {} \frac{M_\mathrm{Pl}^2V_\phi ^2}{2V^2},\end{aligned}$$

(6)

$$\begin{aligned} \eta= & {} \frac{M_\mathrm{Pl}^2V_{\phi \phi }}{V},\end{aligned}$$

(7)

$$\begin{aligned} \xi ^2= & {} \frac{M_\mathrm{Pl}^4V_\phi V_{\phi \phi \phi }}{V^2}, \end{aligned}$$

(8)

where $M^2_\mathrm{Pl}=(8\pi G)^{-1}$ is the reduced Planck scale, $V_\phi \equiv \partial V(\phi )/\partial \phi$, $V_{\phi \phi } \equiv \partial ^2V(\phi )/\partial \phi ^2$, and $V_{\phi \phi \phi } \equiv \partial ^3V(\phi )/\partial \phi ^3$. Also, the scalar power spectrum in the single field inflation is

$$\begin{aligned} \mathcal {P}_{\mathcal {R}}=A_s\left( \frac{k}{k_*}\right) ^{n_s-1+n_s'\ln (k/k_*)/2}, \end{aligned}$$

(9)

where the subscript “*” means the value at the horizon crossing, and the scalar amplitude is

$$\begin{aligned} A_s\approx \frac{1}{24\pi ^2M^4_\mathrm{Pl}}\frac{\Lambda ^4}{\epsilon }. \end{aligned}$$

(10)

The scalar spectral index and its running at the second order are [83, 84]

$$\begin{aligned} n_s= & {} 1+2\eta -6\epsilon +2\left[ \frac{1}{3}\eta ^2+(8C-1)\epsilon \eta \right. \nonumber \\&-\left. \left( \frac{5}{3}+12C\right) \epsilon ^2-\left( C-\frac{1}{3}\right) \xi ^2\right] , \end{aligned}$$

(11)

$$\begin{aligned} n_s'= & {} 16\epsilon \eta -24\epsilon ^2-2\xi ^2, \end{aligned}$$

(12)

where $C=-2+\ln 2+\gamma \simeq -0.73$ with $\gamma$ the Euler–Mascheroni constant. Moreover, the tensor power spectrum is

$$\begin{aligned} \mathcal {P}_{T}=A_T\left( \frac{k}{k_*}\right) ^{n_t}, \end{aligned}$$

(13)

where the tensor spectral index is [83, 84]

$$\begin{aligned} n_t=-2\epsilon \left[ 1+\left( 4C+\frac{11}{3}\right) \epsilon -2\left( \frac{2}{3}+C\right) \eta \right] . \end{aligned}$$

(14)

Thus, the tensor-to-scalar ratio is given by [83, 84]

$$\begin{aligned} r\equiv \frac{A_T}{A_s}=16 \epsilon \left[ 1+8\left( C+\frac{2}{3}\right) (2\epsilon -\eta ) \right] . \end{aligned}$$

(15)

Because $8(C+\frac{2}{3})\simeq -0.506667$, we can safely neglect the term $8 (C+\frac{2}{3})(2\epsilon -\eta )$ at the next leading order in the above equation. Thus, we will take the next leading order approximation $r=16 \epsilon$ for simplicity. Therefore, with the BICEP2 result $r=0.16/0.20$, we obtain the inflation scale about $2\times 10^{16}$ GeV and the Hubble scale around $1.0\times 10^{14}$ GeV.

The number of e-foldings before the end of inflation is

$$\begin{aligned} N(\phi )&= \int _{t_i}^{t_e}H\mathrm{d}t\approx \frac{1}{M_\mathrm{Pl}^2}\int _{\phi _e}^{\phi _i}\frac{V(\phi )}{V_\phi (\phi )}\mathrm{d}\phi \nonumber \\&=\frac{1}{\sqrt{2} \,M_\mathrm{Pl}}\int _{\phi _e}^{\phi _i}\frac{\mathrm{d}\phi }{\sqrt{\epsilon (\phi )}}, \end{aligned}$$

(16)

where the value $\phi _i$ of the inflaton at the beginning of the inflation is the value at the horizon crossing, and the value $\phi _e$ of the inflaton at the end of inflation is defined by either $\epsilon (\phi _e)=1$ or $\eta (\phi _e)=1$. From the above equation, we get the Lyth bound [16]

$$\begin{aligned} \Delta \phi \equiv |\phi _i-\phi _e| > {\sqrt{2\epsilon _\mathrm{min}}} N(\phi ) M_\mathrm{Pl}, \end{aligned}$$

(17)

where $\epsilon _\mathrm{min}$ is the minimal $\epsilon$ during inflation. If $\epsilon (\phi )$ is a monotonic function of $\phi$, we have $\epsilon _\mathrm{min}=\epsilon (\phi _i)\equiv \epsilon$. Thus, for $r=0.01$, 0.05, 0.1, 0.16, and 0.21, we obtain the large field inflation due to $\Delta \phi > 1.77 M_\mathrm{Pl}$, $4.0 M_\mathrm{Pl}$, $5.6 M_\mathrm{Pl}$, $7.1 M_\mathrm{Pl}$, and $8.1 M_\mathrm{Pl}$ for $N(\phi )=50$, respectively. Moreover, to violate the Lyth bound and have a magnitude of $\phi$ smaller than the reduced Planck scale during inflation, we require that $\epsilon (\phi )$ be not a monotonic function and have a minimum between $\phi _i$ and $\phi _e$.

In this paper, we will consider the renormalizable three-term polynomial inflation with a large tensor-to-scalar ratio. Under the slow-roll condition, each term in the polynomial potential will be around $10^{-8}M^4_\mathrm{Pl}$ or smaller. However, without the slow-roll condition and with fine-tuning, each term could be much larger than $10^{-8}M^4_\mathrm{Pl}$ and there exist large cancelations among the three terms. Thus, the quantum corrections can be very large and then get out of control during large field inflation.

3 Supergravity model building

In this paper, to simplify the discussions, we take $M_\mathrm{Pl}=1$. In the non-supersymmetric inflationary models, we will consider the following polynomial potentials at the renormalizable level:

$$\begin{aligned} V= & {} a_0 + a_1 \phi + a_2 \phi ^2 + a_3 \phi ^3 + a_4 \phi ^4 , \end{aligned}$$

(18)

where $\phi$ is the inflaton, and the $a_i$ are couplings. In the supersymmetric inflationary models from the supergravity theory, there are some relations among the $a_i$. Before we construct the concrete models, let us briefly review the supergravity model building.

In the supergravity theory with a Kähler potential K and a superpotential W, the scalar potential is

$$\begin{aligned} V=e^K((K^{-1})^{i}_{\bar{j}}D_i W D^{\bar{j}} \overline{W}-3|W|^2 ), \end{aligned}$$

(19)

where $(K^{-1})^{i}_{\bar{j}}$ is the inverse of the Kähler metric $K_{i}^{\bar{j}}=\partial ^2 K/\partial \Phi ^i\partial {\bar{\Phi }}_{\bar{j}}$, and $D_iW=W_i+K_iW$. Moreover, the kinetic term for a scalar field is

$$\begin{aligned} \mathcal{L} = K_{i}^{\bar{j}} \partial _{\mu } \Phi ^i \partial ^{\mu } {\bar{\Phi }}_{\bar{j}}. \end{aligned}$$

(20)

We first briefly review the generic model building. Introducing two superfields $\Phi$ and X, we consider the following Kähler potential and superpotential:

$$\begin{aligned} K= & {} -\frac{1}{2}(\Phi -{\bar{\Phi }})^2+X{\bar{X}}-\delta (X{\bar{X}})^2,\end{aligned}$$

(21)

$$\begin{aligned} W= & {} Xf(\Phi ). \end{aligned}$$

(22)

Thus, the above Kähler potential K is invariant under the following shift symmetry [72–81]:

$$\begin{aligned} \Phi \rightarrow \Phi +CM_\mathrm{Pl}, \end{aligned}$$

(23)

with C a dimensionless real parameter. In general, the Kähler potential K is a function of $\Phi -{\bar{\Phi }}$ and independent on the real part of $\Phi$. Before we proceed with further discussions, we shall present a few comments on the Kähler potential and superpotential.

• If shift symmetry is a global symmetry, it will be violated by quantum gravity effects, i.e., one might add high-dimensional operators suppressed by the reduced Planck scale. To solve this problem, one can consider a gauged discrete symmetry from the anomalous $U(1)_X$ gauge symmetry inspired by string models, and then quantum gravity violating effects can be forbidden.

• Shift symmetry is violated by the superpotential in Eq. (25). In principle, we can break the shift symmetry spontaneously by introducing a spurion field S and extending the shift symmetry as follows [85]:

  $$\begin{aligned} \Phi \rightarrow \Phi +CM_\mathrm{Pl},\quad S \rightarrow \frac{S\Phi }{\Phi +CM_\mathrm{Pl}}. \end{aligned}$$

  (24)

  Also we consider the following superpotential:

  $$\begin{aligned} W = Xf(S\Phi /M_\mathrm{Pl}), \end{aligned}$$

  (25)

  which is clearly invariant under the extended shift symmetry. After S obtains a non-zero vacuum expectation value, we obtain the superpotential in Eq. (25). The effects from spontaneous shift symmetry breaking have been studied in Ref. [86].

• In a supersymmetric theory, the superpotential is non-renormalized, while there indeed exist quantum corrections to the Kähler potential in general. In the renormalizable three-term polynomial inflation which we shall study in the following, the inflaton value is about $10M_\mathrm{Pl}$, and each term in the scalar potential is about $10^{-8}M^4_\mathrm{Pl}$ or smaller during inflation. The Kähler potential for $\Phi$ in Eq. (21) is about $100M^2_\mathrm{Pl}$, and the quantum corrections will be around $10^{-6}M^2_\mathrm{Pl}$ as we see from the naive dimensional analysis with a loop factor. Thus, such quantum corrections are under control and negligible.

  In addition, supersymmetry is violated during inflation. Thus, the masses for the scalar and fermionic components of any superfield may be split. Then we might have an additional one-loop effective scalar potential, which may affect the inflation and is beyond the scope of our current paper.

From the above Kähler potential and superpotential, the scalar potential is given by

$$\begin{aligned} V= & {} e^K\left[ |(\Phi - {\bar{\Phi }})Xf(\Phi )+X \frac{\partial f(\Phi )}{\partial \Phi }|^2+|({\bar{X}}-2\delta X{\bar{X}}^2) \right. \nonumber \\&\times Xf(\Phi )+f(\Phi )|^2 -\left. 3|Xf(\Phi )|^2\right] . \end{aligned}$$

(26)

Because there is no real component $\mathrm{Re} [\Phi ]$ of $\Phi$ in the Kähler potential due to the shift symmetry, this scalar potential along $\mathrm{Re} [\Phi ]$ is very flat and then $\mathrm{Re} [\Phi ]$ is a natural inflaton candidate. From the previous studies [76, 77, 81], we can stabilize the imaginary component $\mathrm{Im} [\Phi ]$ of $\Phi$ and X at the origin during inflation, i.e., $\mathrm{Im} [\Phi ]=0$ and $X=0$. Therefore, with $\mathrm{Re} [\Phi ]=\phi /{\sqrt{2}}$, we get the inflaton potential

$$\begin{aligned} V = |f(\phi /{\sqrt{2}})|^2. \end{aligned}$$

(27)

For a renormalizable superpotential, we have

$$\begin{aligned} f(\Phi ) = a'_0 + a'_1 {\sqrt{2}} \Phi + 2 a'_2 \Phi ^2 , \end{aligned}$$

(28)

where we choose $a_i$ as real numbers. Then the polynomial inflaton potential is

$$\begin{aligned} V= & {} |a'_0+a'_1 \phi + a'_2 \phi ^2|^2. \end{aligned}$$

(29)

The polynomial inflations from supergravity model building have been considered before. At the renormalizable level, only the case with $a_1'\not =0$ and $a_2'\not =0$ has been studied in the literature [43, 78, 79]. In this paper, we also consider the following three cases with $a_0'\not =0$: (1) $a_0'\not =0$ and $a_1'\not =0$; (2) $a_0'\not =0$ and $a_2'\not =0$; (3) the most general case with $a_0'\not =0$, $a_1'\not =0$, and $a_2'\not =0$. Moreover, we study the three-term polynomial inflations whose coefficients for the lowest and highest order terms in the inflaton potential can be negative. These inflations cannot be realized in supergravity model building where the coefficients for the lowest and highest order terms must be positive.

4 The renormalizable three-term polynomial inflation

To classify the three-term polynomial inflation at renormalizable level, we consider the following inflaton potential:

$$\begin{aligned} V= & {} a_j \phi ^j + a_k \phi ^k + a_l \phi ^l , \end{aligned}$$

(30)

where $0\le j<k<l\le 4$. With (j, k, l), we will study all the renormalizable non-supersymmetric and supersymmetric three-term polynomial inflations with a large tensor-to-scalar ratio r, which can be consistent with the Planck and/or BICEP2 experiments. For simplicity, we denote the maximum and minimum of the inflaton potential as $\phi _M$ and $\phi _m$, respectively. Because we shall consider the super-Planckian inflation, our inflation around the maxima and minima of the inflaton potentials is similar to the inflection point inflation [87–90].

4.1 Inflaton potential with $(j,k,l)=(0, 1, 2)$

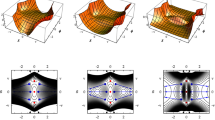
First, we consider the non-supersymmetric models with the inflaton potential $V=a_0+a_1 \phi + a_2 \phi ^2$. For $a_2<0$, there exists a maximum at $\phi _M=-\frac{a_1}{2a_2}$. Independent of whether the slow-roll inflation occurs at the right or left of this maximum (which is the same because of symmetry), we cannot find any r within the $2\sigma$ range of the BICEP2 data. The numerical results for r versus $n_s$ is given in Fig. 1. When $n_s$ is within the $1\sigma$ range $0.9603\pm 0.0073$, the range of r is [0.0132, 0.0534].

Fig. 1

r versus $n_s$ for the inflaton potential with $(j,k,l)=(0, 1, 2)$ and $a_2<0$. The inner and outer circles are the $1\sigma$ and $2\sigma$ regions, respectively

Fig. 2

r versus $n_s$ for the inflaton potential with $(j,k,l)=(0, 1, 2)$, $a_1<0$, and $a_2>0$

Moreover, for $a_2>0$ and $a_1<0$, we have a minimum at $\phi _m=-\frac{a_1}{2a_2}$. We present the numerical results for r versus $n_s$ in Fig. 2, where the inner and outer circles are the $1\sigma$ and $2\sigma$ regions, respectively. For $n_s$ in the $1\sigma$ range $0.9603\pm 0.0073$, the range of r is [0.0132, 0.16160], which can be consistent with the BICEP2 experiment. In addition, for the number of e-foldings $N_e=50$, $n_s$ and r are within the $1\sigma$ and $2\sigma$ regions of the BICEP2 experiment for $a_1>-30a_2$ and $a_0<\frac{a_1^2+2a_2^2}{4a_2}$ and for $a_1>-10a_2$ and $a_0<\frac{a_1^2+2a_2^2}{4a_2}$, respectively. Also, for $N_e=60$, $n_s$ and r are within the $2\sigma$ region for $a_1>-10a_2$ and $a_0<\frac{a_1^2+2a_2^2}{4a_2}$, but there is no viable parameter space for the $1\sigma$ region. In particular, the best fit point with $n_s=0.96$ and $r=0.16$ for the BICEP2 data can be obtained for $N_e=50$, $a_2\approx -a_1$ and $a_2 \approx -3 a_0$. For example, $a_0=3, a_1=-10$, and $a_2=10$, and the corresponding $\phi _i, \phi _e$, and $\phi _{m}$, respectively, are $-13.621, 0.464$, and 0.5. Thus, we obtain $\Delta \phi =14.085$, which satisfies the Lyth bound. In the following discussions, we will not comment on $\Delta \phi$, since the Lyth bound is always satisfied in our models.

Fig. 3

r versus $n_s$ for the inflaton potential with $(j,k,l)=(0, 1, 3)$, $a_1>0$, and $a_3<0$, where the inflationary trajectories are at the left and right of the minimum

Second, we consider the supersymmetric model with inflaton potential $V=a^2+2ab\phi + b^2 \phi ^2$, which has a minimum at $-a/b$. We find that for $\phi = -a/b\pm \sqrt{2}$, both $\epsilon$ and $\eta$ are equal to 1, and then the slow-roll inflation ends. Also, we find that independent of whether the slow-roll inflation occurs at the left or right of the minimum, $n_s$ and r can be written as functions of the e-folding number $N_e$:

$$\begin{aligned} n_s = 1-\frac{8}{4N_e+2},\quad r = \frac{32}{4N_e+2}. \end{aligned}$$

(31)

Thus, for $N_e=50$, we get $n_s=0.9604$ and $r=0.1584$. For $N_e=60$, we get $n_s=0.9669$ and $r=0.1322$. In fact, this is similar to the chaotic inflation with inflaton potential $\phi ^2$.

4.2 Inflaton potential with $(j,k,l)=(0, 1,3)$

The inflaton potential is $V=a_0+a_1 \phi + a_3 \phi ^3$. First, we consider $a_1>0$ and $a_3<0$. Because there is a minimum at $\phi _m=-\sqrt{-\frac{a_1}{3a_3}}$ and a maximum at $\phi _M=\sqrt{-\frac{a_1}{3a_3}}$, we have three inflationary trajectories, and let us discuss them one by one. For the slow-roll inflation occurring at the left of the minimum, the numerical results for r versus $n_s$ are given in Fig. 3. The range of r is about [0.1231, 0.2237] for $n_s$ within its $1\sigma$ range $0.9603\pm 0.0073$, which is consistent with the BICEP2 results. In the viable parameter space, we generically have $a_0 < a_1$. For the number of e-foldings $N_e=50$, $n_s$ and r are within the $1\sigma$ and $2\sigma$ regions of the BICEP2 experiment for $-11a_3 < a_1<-1000a_3$ and $-11a_3 < a_1<-5000a_3$, respectively. For the number of e-foldings $N_e=60$, $n_s$ and r are within the $1\sigma$ and $2\sigma$ regions of the BICEP2 experiment for $a_1<-125a_3$ and $a_1<-600a_3$, respectively. To be concrete, we will present two best fit points for the BICEP2 data. The best fit point with $n_s=0.963$ and $r=0.16$ can be realized for $N_e=50$, $a_0\thickapprox a_1 \thickapprox -230 a_3$, for example, $a_0=1, a_1=1$, and $a_3=-0.00436$, and the corresponding $\phi _i, \phi _f, \phi _{m}$, and $\phi _{M}$ are, respectively, $-27.1459, -15.3793, -8.74372$, and 8.74372. Another best fit point with $n_s=0.959$ and $r=0.196$ can be obtained for $N_e=60$, $a_0\thickapprox a_1 \thickapprox -2 a_3$, for example, $a_0=1, a_1=1$, and $a_3=-0.5$, and the corresponding $\phi _i, \phi _f, \phi _{m}$, and $\phi _{M}$ are $-19.2289, -2.35496, -0.816497$, and 0.816497, respectively. In addition, when slow-roll inflation occurs at the right of the minimum, we also present the numerical results for r versus $n_s$ in Fig. 3. The range of r is about [0.0337, 0.0669] for $n_s$ within its $1\sigma$ range $0.9603\pm 0.0073$. Although we cannot fit the BICEP2 data, we still have a large enough tensor-to-scalar ratio, which can be tested at the future Planck and QUBIT experiments.

Furthermore, for the slow-roll inflation at the right of the maximum, the numerical results for r versus $n_s$ is given in Fig. 4. For $n_s$ in the $1\sigma$ range $0.9603\pm 0.0073$, the range of r is [0.0085, 0.0482], which is within the reach of the future Planck and QUBIT experiments.

Fig. 4

r versus $n_s$ for the inflaton potential with $(j,k,l)=(0, 1, 3)$, $a_1>0$, and $a_3<0$, where the inflationary trajectory is at the right of the maximum

Second, we consider $a_1<0$ and $a_3<0$, the potential will decrease monotonically, and the curves for r versus $n_s$ are given in Fig. 5. The range of r is about [0.1670, 0.2427] for $n_s$ within its $1\sigma$ range $0.9603\pm 0.0073$, which is consistent with the BICEP2 results. In the viable parameter space, we generically have $a_0\thickapprox 1$. For the number of e-foldings $N_e=50$, $n_s$ and r are within the $1\sigma$ and $2\sigma$ regions of the BICEP2 experiment for $-90a_3 < -a_1<-300a_3$ and $-a_1<-1000a_3$, respectively. For the number of e-foldings $N_e=60$, $n_s$ and r are within the $1\sigma$ and $2\sigma$ regions of the BICEP2 experiment for $-a_1<-210a_3$ and $-a_1<-300a_3$, respectively. The best fit point with $n_s=0.96$ and $r=0.206$ can be realized for $N_e=60$, $a_0\thickapprox 1$, and $- a_1\thickapprox -90 a_3$, for example, $a_0=1, a_1=-90$, and $a_3=-1$, and the corresponding $\phi _i$ and $\phi _f$ are, respectively, $-15.2061$ and $-0.7038$.

Fig. 5

r versus $n_s$ for the inflaton potential with $(j,k,l)=(0, 1, 3)$, $a_1<0$, and $a_3<0$

Fig. 6

r versus $n_s$ for the inflaton potential with $(j,k,l)=(0, 1, 4)$, $a_1>0$, and $a_4<0$ for inflation at the left of the maximum

4.3 Inflaton potential with $(j,k,l)=(0, 1, 4)$

We consider the non-supersymmetric inflation models with $V=a_0+a_1 \phi + a_4 \phi ^4$. First, we consider $a_1>0$ and $a_4<0$. There is a maximum at $\phi _M=\left( -\frac{a_1}{4a_4}\right) ^{1/3}$. When slow-roll inflation occurs at the left and right of the maximum, we present the numerical results for r versus $n_s$ in Figs. 6 and 7, respectively. For $n_s$ in the $1\sigma$ range $0.9603\pm 0.0073$, the corresponding ranges of r are [0.0250, 0.0732] and [0.0077, 0.0459], respectively, which is large enough to be tested at the future Planck and QUBIT experiments.

Fig. 7

r versus $n_s$ for the inflaton potential with $(j, k, l)=(0, 1, 4)$, $a_1>0$, and $a_4<0$ for inflation at the right of the maximum

Second, we consider $a_1<0$ and $a_4>0$. There exists a minimum at $\phi _m=\left( -\frac{a_1}{4a_4}\right) ^{1/3}$. If the slow-roll inflation occurs at the left of the minimum, we obtain $n_s \le 0.94$ and $r>0.3$, which is not consistent with the Planck and BICEP2 data. For the slow-roll inflation occurring at the right of the minimum, the numerical results for r versus $n_s$ are given in Fig. 8. With $n_s$ in the $1\sigma$ range $0.9603\pm 0.0073$, the range of r is about [0.1288, 0.2498], which agrees with the BICEP2 experiment. Moreover, for the number of e-foldings $N_e=50$, $n_s$ and r are within the $1\sigma$ and $2\sigma$ regions of the BICEP2 experiment for $-5 \times 10^4 a_4<a_1<-1000a_4$ and $-1 \times 10^6a_4<a_1<-3000a_4$, respectively. For $N_e=60$, $n_s$ and r are within the $1\sigma$ and $2\sigma$ regions of the BICEP2 experiment for $-1\times 10^4 a_4<a_1<-100 a_4$ and $-5\times 10^4 a_4<a_1$, respectively. To be concrete, we will present the best fit point for the BICEP2 data. The best fit point with $n_s=0.9607$ and $r=0.2035$ can be realized for $N_e=60$, $a_1<-100a_0$, and $a_1\thickapprox -1000 a_4$, for example, $a_0=1, a_1=-1000$, and $a_4=1$, and the corresponding $\phi _i, \phi _f$, and $\phi _{m}$ are, respectively, 26.1887, 10.8134, and 6.29961.

Fig. 8

r versus $n_s$ for the inflaton potential with $(j, k, l)=(0, 1, 4)$, $a_1<0$, and $a_4>0$

Fig. 9

r versus $n_s$ for the inflaton potential with $(j, k, l)=(0, 2, 3)$ where the inflationary trajectories are at the left and right of the minimum

4.4 Inflaton potential with $(j,k,l)=(0, 2, 3)$

We consider the inflationary model with potential $V=a_0+a_2\phi ^2+a_3\phi ^3$. First, for $a_2>0$ and $a_3<0$, there exist a minimum at $\phi _m=0$ and a maximum at $\phi _M=-\frac{2a_2}{3a_3}$. So we have three inflationary trajectories, and let us discuss them one by one. For the slow-roll inflation occurring at the left of the minimum, we present the numerical results for r versus $n_s$ in Fig. 9. For $n_s$ within its $1\sigma$ range $0.9603\pm 0.0073$, the range of r is about [0.1363, 0.2206], which agrees with the BICEP2 results. For the number of e-foldings $N_e=50$, $n_s$ and r are within the $1\sigma$ and $2\sigma$ regions of the BICEP2 experiment for $a_2>-5a_3$ and $a_0<\mathrm{Max}(a_2/2,-2a_3)$ and for $a_0<\mathrm{Max}(a_2/2,-2a_3)$, respectively. Also, for $N_e=60$, $n_s$ and r are within the $1\sigma$ and $2\sigma$ regions of the BICEP2 experiment for $a_0<\mathrm{Max}(a_2/2,-2a_3)$. To be concrete, we will present two best fit points for the BICEP2 data. The best fit point with $n_s=0.96$ and $r=0.16$ can be realized for $N_e=50$, $a_2>10a_0$ and $a_2\thickapprox 10^3 a_3$, for instance, $a_0=1, a_2=10$, and $a_3=-0.01$, and the corresponding $\phi _i, \phi _f$, and $\phi _{m}$ are, respectively, $-14.2222, -1.34067$, and 0. Another best fit point with $n_s=0.958$ and $r=0.199$ can be obtained for $N_e=59$, $a_2\approx 40a_0$, and $a_2\thickapprox -2 a_3$, for example, $a_0=1, a_2=10$, and $a_3=-0.01$, and the corresponding $\phi _i, \phi _f$, and $\phi _{m}$ are, respectively, $-18.3869, -1.73496$, and 0.

In addition, when slow-roll inflation occurs at the right of the minimum, the numerical results for r versus $n_s$ are given in Fig. 9 as well. The range of r is about [0.0645, 0.160] for $n_s$ within its $1\sigma$ range $0.9603\pm 0.0073$. In the viable parameter space, we have $a_0<a_2/2$ in general. For the number of e-foldings $N_e=50$, $n_s$ and r are within the $1\sigma$ and $2\sigma$ regions of the BICEP2 experiment for $a_2>-50a_3$ and $a_2>-30a_3$, respectively. For the number of e-foldings $N_e=60$, $n_s$ and r are out of the $1\sigma$ region of the BICEP2 experiment and are within the $2\sigma$ region for $a_2>-50a_3$. The best fit point with $n_s=0.96$ and $r=0.158$ for the BICEP2 data can be realized for $N_e=50$, $a_2>10a_0$, and $a_2>-10^4 a_3$, for instance, $a_0=0.1, a_2=1$, and $a_3=-10^{-4}$, and the corresponding $\phi _i, \phi _f, \phi _{m}$, and $\phi _M$ are, respectively, 14.1854, 1.33945, 0.0, and 6666.67.

Furthermore, for the slow-roll inflation at the right of the maximum, the numerical results for r versus $n_s$ are given in Fig. 10. For $n_s$ in the $1\sigma$ range $0.9603\pm 0.0073$, the range of r is [0.0097, 0.0431], which can be tested at the future Planck and QUBIT experiments.

Fig. 10

r versus $n_s$ for the inflaton potential with $(j, k, l)=(0, 2, 3)$ where the inflationary trajectory is at the right of the maximum

Fig. 11

r versus $n_s$ for the inflaton potential with $(j, k, l)=(0, 2, 3)$ where the inflationary trajectory is at the left of the minimum

Second, for $a_2<0$ and $a_3<0$, there exist a minimum at $\phi _m=-\frac{2a_2}{3a_3}$ and a maximum at $\phi _M=0$. Similar to the above discussions, there exist three inflationary trajectories, and we will discuss them one by one. For the slow-roll inflation occurring at the left of the minimum, we present the numerical results for r versus $n_s$ in Fig. 11. For $n_s$ within its $1\sigma$ range $0.9603\pm 0.0073$, the range of r is about [0.1249, 0.2242], which can be consistent with the BICEP2 experiment. Generically, we have $a_0\thickapprox 1$. For the number of e-foldings $N_e=50$, $n_s$ and r are within the $1\sigma$ and $2\sigma$ regions of the BICEP2 experiment for $-a_2<-30a_3$ and $-a_2<-100a_3$, respectively. Also, for $N_e=60$, $n_s$ and r are within the $1\sigma$ and $2\sigma$ regions of the BICEP2 experiment, respectively, for $-a_2<-15a_3$ and $-a_2<-35a_3$. To be concrete, we will present two best fit points for the BICEP2 data. The best fit point with $n_s=0.959$ and $r=0.196$ can be realized for $N_e=60$, $a_0=1$, and $-a_2\thickapprox -2 a_3$, for instance, $a_0=1, a_2=-2$, and $a_3=-1$, and the corresponding $\phi _i, \phi _f$, and $\phi _{m}$ are, respectively, $-19.8863, -3.10761$, and $-1.33333$.

In addition, for the slow-roll inflations occurring at the right of the minimum and maximum, we present the numerical results for r versus $n_s$ in Figs. 12 and 13. For $n_s$ within its $1\sigma$ range $0.9603\pm 0.0073$, the corresponding ranges of r are, respectively [0.0104, 0.0512] and [0.0099, 0.0505], which are within the reach of the future Planck and BICEP2 experiments.

Fig. 12

r versus $n_s$ for the inflaton potential with $(j, k, l)=(0, 2, 3)$ where the inflationary trajectory is at the right of the minimum

Fig. 13

r versus $n_s$ for the inflaton potential with $(j, k, l)=(0, 2, 3)$ where the inflationary trajectory is at the right of the maximum

Third, for $a_2<0$ and $a_3>0$, there exist a maximum at $\phi _M=0$ and a minimum at $\phi _m=-\frac{2a_2}{3a_3}$. Similarly, we have three inflationary trajectories, and we will discuss them one by one as well. For the slow-roll inflations occurring at the left and right of the maximum, we present the numerical results for r versus $n_s$ in Figs. 14 and 15, respectively. For $n_s$ within its $1\sigma$ range $0.9603\pm 0.0073$, the corresponding ranges of r are [0.0099, 0.0485] and [0.0097, 0.0515], which can be tested at the future Planck and BICEP2 experiments.

Fig. 14

r versus $n_s$ for the inflaton potential with $(j, k, l)=(0, 2, 3)$ where the inflationary trajectory is at the left of the maximum

Fig. 15

r versus $n_s$ for the inflaton potential with $(j, k, l)=(0, 2, 3)$ where the inflationary trajectory is at the right of the maximum

Fig. 16

r versus $n_s$ for the inflaton potential with $(j, k, l)=(0, 2, 3)$ where the inflationary trajectory is at the right of the minimum

Furthermore, for the slow-roll inflation at the right of the minimum, the numerical results for r versus $n_s$ are given in Fig. 16. For $n_s$ in the $1\sigma$ range $0.9603\pm 0.0073$, the range of r is [0.1232, 0.2253], which can be consistent with the BICEP2 experiment. In general, we can take $a_0\thickapprox 1$. For the number of e-foldings $N_e=50$, $n_s$ and r are within the $1\sigma$ and $2\sigma$ regions of the BICEP2 experiment for $-a_2<30a_3$ and $-a_2<100a_3$ respectively. Also, for $N_e=60$, $n_s$ and r are within the $1\sigma$ and $2\sigma$ regions of the BICEP2 experiment, respectively, for $-a_2<15a_3$ and $-a_2<35a_3$. The best fit point with $n_s=0.959$ and $r=0.196$ can be realized for $N_e=60$, $a_0=1$, and $-a_2\thickapprox -2 a_3$, for instance, $a_0=1, a_2=-2$, and $a_3=1$, and the corresponding $\phi _i, \phi _f$, and $\phi _{m}$ are, respectively, 19.8863, 3.10761, and 1.33333.

4.5 Inflaton potential with $(j,k,l)=(0, 2, 4)$

First, we consider the non-supersymmetric inflation models with potential $V=a_0+a_2\phi ^2+a_4\phi ^4$. For simplicity, we only study the hill-top scenario with $a_0>0$, $a_2>0$, and $a_4<0$. Thus, there is a maximum at $\phi =\phi _M=\sqrt{-\frac{a_2}{2a_4}}$. For the slow-roll inflation occurring at the left of the maximum with $0<\phi _f<\phi _i<\phi _M$, to achieve a proper r, we require $|a_4|\ll a_2$ to get a relatively large $\phi _M$, and thus, the $\phi ^2$ term dominates the potential. We present the numerical results for r versus $n_s$ in Fig. 17. For $n_s$ in the $1\sigma$ range $0.9603\pm 0.0073$, the range of r is [0.0480, 0.1565], which can be consistent with the BICEP2 experiment. In the viable parameter space, we always have $a_2>10a_0$. Moreover, for the number of e-foldings $N_e=50$, $n_s$ and r are within the $1\sigma$ and $2\sigma$ regions of the BICEP2 experiment for $a_2>-1000a_4$ and $a_2>-700a_4$, respectively. Also, for $N_e=60$, $n_s$ and r are within the $2\sigma$ region for $a_2>-1200a_4$, but there is no viable parameter space for the $1\sigma$ region. The best fit point with $n_s=0.96$ and $r=0.158$ for the BICEP2 data can be obtained for $N_e=50$, $a_2>10^5 a_4$, and $a_2>10a_0$. For example, $a_0=1$, $a_2=10$, and $a_4=-10^{-4}$, and the corresponding $\phi _i$, $\phi _f$, and $\phi _M$ are, respectively, 14.1817, 1.33953, and 223.607.

Fig. 17

r versus $n_s$ for the non-supersymmetric inflaton potential with $(j, k, l)=(0, 2, 4)$, $a_0>0$, $a_2>0$, and $a_4<0$, where the inflationary trajectory is at the left of the maximum

In addition, when slow-roll inflation occurs at the right of the maximum, i.e., $\phi _M<\phi _i<\phi _f$, the numerical results for r versus $n_s$ are given in Fig. 18. For $n_s$ within its $1\sigma$ range $0.9603\pm 0.0073$, the range of r is about [0.0072, 0.0444], which is within the reach of the future Planck and QUBIT experiments.

Fig. 18

r versus $n_s$ for the non-supersymmetric inflaton potential with $(j, k, l)=(0, 2, 4)$, $a_0>0$, $a_2>0$, and $a_4<0$, where the inflationary trajectory is at the right of the maximum

Fig. 19

r versus $n_s$ for the supersymmetric inflaton potential with $(j, k, l)=(0, 2, 4)$

Second, we consider the supersymmetric inflationary model with potential $V=|a+b\phi ^2|^2=a^2+2ab\phi ^2+b^2\phi ^4$. For simplicity, we assume $a>0$ and $b<0$. So the potential has two minima at $\phi =\phi _m=\pm \sqrt{-\frac{a}{b}}$. Without loss of generality, we only consider the positive branch of the field $\phi =\phi _m= \sqrt{-\frac{a}{b}}$. The inflationary process can occur at either the left or right of the minimum. For the slow-roll inflation occurring at the left of the minimum, i.e., $\phi _i<\phi _f<\phi _m$, we present the numerical results for r versus $n_s$ in Fig. 19. For $n_s$ in its $1\sigma$ range $0.9603\pm 0.0073$, the range of r is [0.0254, 0.1585]. In addition, for the number of e-foldings $N_e=50$, $n_s$ and r are within the $1\sigma$ and $2\sigma$ regions of the BICEP2 experiment for $a>-1650b$ and $a>-550b$, respectively. Also, for $N_e=60$, $n_s$ and r are within the $2\sigma$ region for $a>-1650b$, but there is no viable parameter space for the $1\sigma$ region. Also, the best fit point with $n_s=0.96$ and $r=0.158$ for the BICEP2 data can be obtained for $N_e=50$ and $a>-3 \times 10^7 b$. For example, $a=1$ and $b=-3 \times 10^{-7}$, and the corresponding $\phi _i, \phi _e$, and $\phi _{m}$ are, respectively, 3148.08, 3160.86, and 3162.28.

Furthermore, for the slow-roll inflation occurring at the right of the minimum, i.e., $\phi _m<\phi _f<\phi _i$, the numerical results for r versus $n_s$ are given in Fig. 19. Interestingly, we will always get a larger r than the above case for any value of a or b. With $n_s$ in its $1\sigma$ range $0.9603\pm 0.0073$, the range of r is about [0.1319, 0.2484]. In addition, for the number of e-foldings $N_e=50$, $n_s$ and r are within the $1\sigma$ and $2\sigma$ regions of the BICEP2 experiment for $a>-165b$ and $a>-33b$, respectively. Also, for $N_e=60$, $n_s$ and r are within the $1\sigma$ region for $a>-17b$ and the $2\sigma$ region for the viable parameter space. Let us present two best fit points for the BICEP2 data. The best fit point with $n_s=0.96$ and $r=0.16$ can be realized for $N_e=50$ and $a\thickapprox -1\times 10^6 b$. For example, $a=1$ and $b=-1\times 10^{-6}$, and the corresponding $\phi _i, \phi _f$, and $\phi _{m}$ are, respectively, 1014.25, 1001.42, and 1000.0. Another best fit point with $n_s=0.96$ and $r=0.2$ can be obtained for $a=165$ and $b=-1$. For example, $a=165$ and $b=-1$, and the corresponding $\phi _i, \phi _f$, and $\phi _{m}$ are 30.5877, 14.3371, and 12.8452, respectively.

4.6 Inflaton potential with $(j,k,l)=(0, 3, 4)$

We consider the inflaton potential $V=a_0+a_3\phi ^3+a_4\phi ^4$. First, we study the hill-top scenario with $a_0>0$, $a_3>0$, and $a_4<0$. So there is a maximum at $\phi _M=-\frac{3 a_3}{4 a_4}$. For the slow-roll inflation occurring at the left of the maximum, i.e., $\phi _f<\phi _i<\phi _M$, we present the numerical results for r versus $n_s$ in Fig. 20. The range of r is about [0.0742, 0.1956] for $n_s$ within its $1\sigma$ range $0.9603\pm 0.0073$, which can be consistent with the BICEP2 results. In the viable parameter space, we generically have $a_0 < a_3$. For the number of e-foldings $N_e=50$, $n_s$ and r are within the $1\sigma$ and $2\sigma$ regions of the BICEP2 experiment for $a_3>-33a_4$ and $a_3>-26a_4$, respectively. For $N_e=60$, $n_s$ and r are within the $1\sigma$ and $2\sigma$ regions of the BICEP2 experiment for $a_3>-40a_4$ and $a_3>-29a_4$, respectively. Let us present two best fit points for the BICEP2 data. The best fit point with $n_s=0.96$ and $r=0.16$ can be realized for $N_e=59$, $a_3> 10a_0$, and $a_3\thickapprox -58.4a_4$, for example, $a_0=10, a_3=100$, and $a_4=-1.71$, and the corresponding $\phi _i, \phi _f$, and $\phi _{M}$ are, respectively, 18.0429, 2.07119, and 43.8596. Another best fit point with $n_s=0.959$ and $r=0.196$ can be obtained for $N_e=60$, $a_3\approx 5a_0$, and $a_3\thickapprox -1000a_4$, for instance, $a_0=20, a_3=100$, and $a_4=-0.1$, and the corresponding $\phi _i, \phi _f$, and $\phi _{M}$ are 19.0411, 2.07322, and 750.0, respectively.

Fig. 20

r versus $n_s$ for the inflaton potential with $(j, k, l)=(0, 3, 4)$ where the inflationary trajectory is at the left of the maximum

Moreover, we consider the slow-roll inflation occurs at the right of the maximum, i.e., $\phi _M<\phi _i<\phi _f$. The numerical results for r versus $n_s$ is given in Fig. 21. For $n_s$ within the $1\sigma$ range $0.9603\pm 0.0073$, the range of r is [0.0067, 0.0454], which is large enough to be tested at the future Planck and QUBIT experiments.

Fig. 21

r versus $n_s$ for the inflaton potential with $(j, k, l)=(0, 3, 4)$ where the inflationary trajectory is at the right of the maximum

Second, we consider the other case with $a_0>0$, $a_3<0$, and $a_4>0$, which has a minimum at $\phi _m=-\frac{3 a_3}{4 a_4}$. When the slow-roll inflation occurs at the left of the minimum, i.e., $\phi _i<\phi _f<\phi _m$, we present the numerical results for r versus $n_s$ in Fig. 22. The range of r is about [0.1995, 0.2473] for $n_s$ within its $1\sigma$ range $0.9603\pm 0.0073$, which can be consistent with the BICEP2 results. In the viable parameter space, we generically have $a_0 \thickapprox 1$. For the number of e-foldings $N_e=50$, $n_s$ and r are within the $2\sigma$ region of the BICEP2 experiment for $-a_3>50a_4$, but there is no viable parameter space for the $1\sigma$ region. For $N_e=60$, $n_s$ and r are within the $1\sigma$ region of the BICEP2 experiment for $-a_3>15a_4$, and they will always lie in the $2\sigma$ region for any values of $a_3$ and $a_4$. The best fit point with $n_s=0.958$ and $r=0.199$ can be realized for $N_e=60$, $a_0\thickapprox 1$, and $a_3\thickapprox -1000a_4$, for example, $a_0=1, a_3=-1000$, and $a_4=1$, and the corresponding $\phi _i, \phi _f$, and $\phi _{m}$ are, respectively, $-19.1319, -2.1226$, and 750.

In addition, let us consider the slow-roll inflation, which occurs at the right of the minimum, i.e., $\phi _m<\phi _f<\phi _i$. We present the numerical results for r versus $n_s$ in Fig. 23. The range of r is about [0.1311, 0.2512] for $n_s$ within its $1\sigma$ range $0.9603\pm 0.0073$, which can be consistent with the BICEP2 results. In the viable parameter space, we have $a_0 \thickapprox 1$ in general. For the number of e-foldings $N_e=50$, $n_s$ and r are within the $1\sigma$ and $2\sigma$ regions of the BICEP2 experiment for $10a_4<-a_3<150a_4$ and $15a_4<-a_3<60a_4$, respectively. For $N_e=60$, $n_s$ and r are within the $1\sigma$ and $2\sigma$ regions of the BICEP2 experiment for $-a_3<55a_4$ and $8a_4<-a_3<32a_4$, respectively. The best fit point with $n_s=0.96$ and $r=0.2$ can be obtained for $N_e=54$, $a_0=1$, and $-a_3\thickapprox -19a_4$, for instance, $a_0=1, a_3=-19$, and $a_4=1$, and the corresponding $\phi _i, \phi _f$, and $\phi _{m}$ are 33.5051, 19.7918, and 14.25, respectively.

Fig. 22

r versus $n_s$ for the inflaton potential with $(j, k, l)=(0, 3, 4)$ and $a_3<0$, where the inflationary trajectory is at the left of the minimum

Fig. 23

r versus $n_s$ for the inflaton potential with $(j, k, l)=(0, 3, 4)$ and $a_3<0$, where the inflationary trajectory is at the right of the minimum

Fig. 24

r versus $n_s$ for the inflaton potential with $(j, k, l)=(1, 2, 3)$ where the inflationary trajectories are at the left and right of the minimum

4.7 Inflaton potential with $(j,k,l)=(1, 2, 3)$

We consider the inflaton potential $V=a_1\phi +a_2\phi ^2+a_3\phi ^3$. For simplicity, we only study the hill-top scenario with $a_1>0$, $a_2>0$, and $a_3<0$. So, there exist a minimum at $\phi _m=-\frac{a_2}{3 a_3}-\frac{1}{3} \sqrt{\frac{a_2^2-3 a_1 a_3}{a_3^2}}$ and a maximum at $\phi _M=-\frac{a_2}{3 a_3}+\frac{1}{3} \sqrt{\frac{a_2^2-3 a_1 a_3}{a_3^2}}$. We find that only the inflationary processes near the minimum will give us a proper r. First, for the slow-roll inflation at the left of the minimum, we present the numerical results for r versus $n_s$ in Fig. 24. With $n_s$ in its $1\sigma$ range $0.9603\pm 0.0073$, the range of r is about [0.1234, 0.2207], which can be consistent with the BICEP2 results. Moreover, for the number of e-foldings $N_e=50$, $n_s$ and r are within the $1\sigma$ and $2\sigma$ regions of the BICEP2 experiment for $-20a_3<a_1<-1000a_3$ and $a_1<1000 ~\mathrm{Max}(a_2,-a_3)$, respectively. Also, for $N_e=60$, $n_s$ and r are within the $1\sigma$ and $2\sigma$ regions for $a_1<-100a_3$ and $a_1<-1000a_3$, respectively. Let us present two best fit points for the BICEP2 data. The best fit point with $n_s=0.963$ and $r=0.16$ can be realized for $N_e=50$, $a_2>10a_1$, and $a_2\thickapprox -10^3 a_3$, for example, $a_1=0.1, a_2=1$, and $a_3=-10^{-3}$, and the corresponding $\phi _i, \phi _f, \phi _{m}$, and $\phi _{M}$ are, respectively, $-14.2966, -1.46697, -0.0499963$, and 666.717. Another best fit point with $n_s=0.958$ and $r=0.2$ can be obtained for $N_e=58$, $a_2>10a_1$, and $a_2\thickapprox -3.3 a_3$, for example, $a_1=0.1, a_2=1$, and $a_3=-0.3$, and the corresponding $\phi _i, \phi _f, \phi _{m}$, and $\phi _{M}$ are $-17.9616, -1.64821, -0.0000499989$, and 2.22227, respectively.

Second, we consider the slow-roll inflation at the right of the minimum. The numerical results for r versus $n_s$ are given in Fig. 24 as well. The range of r is about [0.0337, 0.158] for $n_s$ in its $1\sigma$ range $0.9603\pm 0.0073$, which can be consistent with the BICEP2 results. In addition, for the number of e-foldings $N_e=50$, $n_s$ and r are within the $1\sigma$ and $2\sigma$ regions of the BICEP2 experiment for $a_2>-50a_3$ and $a_1< a_2 (1+\ln { -\frac{a_2}{50a_3} })$ and for $a_2>-32a_3$ and $a_1<8 [a_2 (1+\ln {-\frac{a_2}{32a_3} })]$, respectively. Also, for $N_e=60$, $n_s$ and r are within the $2\sigma$ region for $a_2>-50a_3$ and $a_1<2 [a_2 (1+\ln {-\frac{a_2}{50a_3} })]$, but there is no viable parameter space for the $1\sigma$ region. Especially, the best fit point with $n_s=0.96$ and $r=0.158$ for the BICEP2 data can be obtained for $N_e=50$, $a_2>10a_1$, and $a_2>-10^4 a_3$. For example, $a_1=0.1, a_2=1$, and $a_3=-10^{-4}$, and the corresponding $\phi _i, \phi _f, \phi _{m}$, and $\phi _{M}$, respectively, are $14.1599, 1.36588, -0.0499996$, and 6666.72.

Third, for the slow-roll inflation at the right of the maximum, we present the numerical results for r versus $n_s$ in Fig. 25. So we cannot find the proper parameter space which can give a large enough r in the $2\sigma$ region of the BICEP2 data. For $n_s$ within the $1\sigma$ range $0.9603\pm 0.0073$, the range of r is [0.0083, 0.0471], which can still be tested at the future Planck and QUBIT experiments.

Fig. 25

r versus $n_s$ for the inflaton potential with $(j, k, l)=(1, 2, 3)$ where the inflationary trajectory is at the right of the maximum

4.8 Inflaton potential with $(j,k, l)=(1, 2,4)$

For the inflaton potential $V=a_1 \phi + a_2 \phi ^2 +a_4 \phi ^4$, we consider the hill-top scenario with $a_4<0$. Thus, either we have only one maximum at

$$\begin{aligned} \phi _m= & {} \frac{(1-i \sqrt{3}) a_2}{2 \root 3 \of {3} \root 3 \of {\sqrt{3} \sqrt{27 a_1^2 a_4^4+8 a_2^3 a_4^3}-9 a_1 a_4^2}}\nonumber \\&-\frac{(1+i \sqrt{3}) \root 3 \of {\sqrt{3} \sqrt{27 a_1^2 a_4^4+8 a_2^3 a_4^3}-9 a_1 a_4^2}}{4\ 3^{2/3} a_4}, \end{aligned}$$

(32)

or we have one minimum given by Eq. (32) and two maxima at

$$\begin{aligned} \phi _{M1}= & {} \frac{1}{2} \left( \frac{\root 3 \of {\sqrt{3} \sqrt{27 a_1^2 a_4^4+8 a_2^3 a_4^3}-9 a_1 a_4^2}}{3^{2/3} a_4} \right. \nonumber \\&-\left. \frac{2 a_2}{\root 3 \of {3} \root 3 \of {\sqrt{3} \sqrt{27 a_1^2 a_4^4+8 a_2^3 a_4^3}-9 a_1 a_4^2}}\right) , \end{aligned}$$

(33)

and

$$\begin{aligned} \phi _{M2}= & {} \frac{(1+i \sqrt{3}) a_2}{2 \root 3 \of {3} \root 3 \of {\sqrt{3} \sqrt{27 a_1^2 a_4^4+8 a_2^3 a_4^3}-9 a_1 a_4^2}}\nonumber \\&-\frac{(1-i \sqrt{3}) \root 3 \of {\sqrt{3} \sqrt{27 a_1^2 a_4^4+8 a_2^3 a_4^3}-9 a_1 a_4^2}}{4\ 3^{2/3} a_4},\nonumber \\ \end{aligned}$$

(34)

with $\phi _{M1}<\phi _{M2}$. For the former case with $\phi _m$ as a maximum, because the parameters can only be considered in a very restricted way, we cannot get a proper r. Therefore, we will consider the latter case with $\phi _m$ a minimum.

First, we consider the inflation at the left of the maximum, i.e., $\phi _f<\phi _i<\phi _{M1}$. We present the numerical results for r versus $n_s$ in Fig. 26. So we cannot find the viable parameter space which can generate a large enough r. For $n_s$ in the $1\sigma$ range $0.9603\pm 0.0073$, the range of r is [0.0084, 0.0449]. Interestingly, such r can still be within the reach of the future Planck and QUBIT experiments.

Fig. 26

r versus $n_s$ for the inflaton potential with $(j, k, l)=(1, 2, 4)$ where the inflationary trajectory is at the left of the maximum $\phi _{M1}$

Second, we consider the inflationary trajectory between $\phi _{M1}$ and $\phi _m$, i.e., $\phi _{M1}<\phi _i<\phi _f<\phi _m$. We present the numerical results for r versus $n_s$ in Fig. 27. For $n_s$ within the $1\sigma$ range $0.9603\pm 0.0073$, the range of r is [0.0487, 0.1585], which can be consistent with the BICEP2 experiment. In addition, for the number of e-foldings $N_e=50$, $n_s$ and r are within the $1\sigma$ and $2\sigma$ regions of the BICEP2 experiment for $a_2>-1250a_4$ and $a_1<[a_2 (1+20\ln {\frac{a_2}{-1250a_4}})]/10$ and for $a_2>-660a_4$ and $a_1<[a_2 (1+20\ln {\frac{a_2}{-660a_4}})]/10$, respectively. Also, for $N_e=60$, $n_s$ and r are within the $2\sigma$ region for $a_2>-1100a_4$ and $a_1<[a_2 (1+20\ln { \frac{a_2}{-1100a_4} })]/10$, but there is no viable parameter space for the $1\sigma$ region. The best fit point with $n_s=0.96$ and $r=0.158$ for the BICEP2 data can be obtained for $N_e=50$, $a_2>10a_1$, and $a_2>-10^6 a_4$. For example, $a_1=0.1, a_2=1$, and $a_4=-10^{-6}$, and the corresponding $\phi _i, \phi _f, \phi _{M1}$, and $\phi _{m}$ are respectively $-14.2625, -1.46598, -707.082$, and $-0.05$.

Third, we consider the inflationary trajectory between $\phi _{m}$ and $\phi _{M2}$, i.e., $\phi _{m}<\phi _f<\phi _i<\phi _{M2}$. We present the numerical results for r versus $n_s$ in Fig. 28. For $n_s$ in the $1\sigma$ range $0.9603\pm 0.0073$, the range of r is [0.0487, 0.1585]. This case is similar to the above second case with $\phi _{M1}<\phi _i<\phi _f<\phi _m$, so we will not present benchmark point here.

Fig. 27

r versus $n_s$ for the inflaton potential with $(j, k, l)=(1, 2, 4)$ where the inflationary trajectory is between $\phi _{M1}$ and $\phi _m$

Fig. 28

r versus $n_s$ for the inflaton potential with $(j, k, l)=(1, 2, 4)$ where the inflationary trajectory is between $\phi _m$ and $\phi _{M2}$

Fourth, we consider the inflation at the right of the maximum $\phi _{M2}$, i.e., $\phi _{M2}<\phi _i<\phi _f$. The numerical results for r versus $n_s$ are given in Fig. 29. With $n_s$ in its $1\sigma$ range $0.9603\pm 0.0073$, the range of r is about [0.0084, 0.0449]. Similar to the first case, r is not large enough, but it can still be tested at the future Planck and QUBIT experiments.

Fig. 29

r versus $n_s$ for the inflaton potential with $(j, k, l)=(1, 2, 4)$ where the inflationary trajectory is at the right of the maximum $\phi _{M2}$

Fig. 30

r versus $n_s$ for the inflaton potential with $(j, k, l)=(1, 3, 4)$ where the inflationary trajectory is at the left of the maximum

4.9 Inflaton potential with $(j,k,l)=(1, 3, 4)$

We consider the inflaton potential $V=a_1\phi +a_3\phi ^3+a_4\phi ^4$. For simplicity, we focus on the hill-top scenario with $a_1>0$ and $a_3>0$, while $a_4<0$. So, there exists a maximum as follows:

$$\begin{aligned} \phi= & {} \phi _M=\frac{1}{4} \left( \frac{a_3^2}{a_4 \root 3 \of {-a_3^3-8 a_1 a_4^2+4 \sqrt{4 a_1^2 a_4^4+a_1 a_3^3 a_4^2}}} \right. \nonumber \\&-\left. \frac{a_3}{a_4}+\frac{\root 3 \of {-a_3^3-8 a_1 a_4^2+4 \sqrt{4 a_1^2 a_4^4+a_1 a_3^3 a_4^2}}}{a_4}\right) .\nonumber \\ \end{aligned}$$

(35)

First, for the inflation at the left of the maximum with $\phi _f<\phi _i<\phi _M$, we present the numerical results for r versus $n_s$ in Fig. 30. For $n_s$ within the $1\sigma$ range $0.9603\,\pm \,0.0073$, the range of r is [0.0556, 0.2328], which can be consistent with the BICEP2 experiment. In addition, for the number of e-foldings $N_e=50$, $n_s$ and r are within the $1\sigma$ and $2\sigma$ regions of the BICEP2 experiment for $a_3>-30a_4$ and $100a_3<a_1<100[3\tan {(\sec ^{-1}{(-a_3/10a_4+3)}-2.5)}+7] a_3$ and for $a_3>-25a_4$ and $a_1<100[3\tan (\sec ^{-1} (-a_3/10a_4+0.8)-2.5) +13] a_3$, respectively. Also, for $N_e=60$, $n_s$ and r are within the $1\sigma$ and $2\sigma$ regions for $a_3>-35a_4$ and $a_1<100[3\tan {(\sec ^{-1}{(-a_3/10a_4+6.5)}-2.5)}+6] a_3$ and for $a_3>-30a_4$ and $a_1<100[3\tan {(\sec ^{-1}{(-a_3/10a_4+1.7)}}-2.5)+8] a_3$, respectively. Let us present two best fit points for the BICEP2 data. The best fit point with $n_s=0.96$ and $r=0.16$ can be realized for $N_e=50$, $a_1\thickapprox 100a_3$, and $a_3\thickapprox -36.5a_4$, for example, $a_1=10000, a_3=100$, and $a_4=-2.74$, and the corresponding $\phi _i, \phi _f$, and $\phi _{M}$ are, respectively, 12.3513, 0.714071, and 28.4959. Another best fit point with $n_s=0.96$ and $r=0.2$ can be obtained for $N_e=60$, $a_1\thickapprox 90a_3$, and $a_3\thickapprox -1000a_4$, for example, $a_1=9000, a_3=100$, and $a_4=-0.1$, and the corresponding $\phi _i, \phi _f$, and $\phi _{M}$ are 15.1757, 0.715088, and 750.04, respectively.

Second, we consider the inflation at the right of the maximum with $\phi _M<\phi _f<\phi _i$, and we present the numerical results for r versus $n_s$ in Fig. 31. For $n_s$ within the $1\sigma$ range $0.9603\pm 0.0073$, the range of r is [0.0081, 0.0458], which is still within the reach of the future Planck and QUBIT experiments.

Fig. 31

r versus $n_s$ for the inflaton potential with $(j, k, l)=(1, 3, 4)$ where the inflationary trajectory is at the right of the maximum

4.10 Inflaton potential with $(j,k,l)=(2, 3, 4)$

First, we consider the non-supersymmetric models with inflaton potential $V=a_2\phi ^2+a_3\phi ^3+a_4\phi ^4$. For simplicity, we assume $a_2>0$ and $a_3>0$, while $a_4<0$. Thus, there exists a minimum at $\phi _m=0$ as well as two maxima at $\phi _{M1}=\frac{-3 a_3-\sqrt{9 a_3^2-32 a_2 a_4}}{8 a_4}$ and $\phi _{M2}=\frac{-3 a_3+\sqrt{9 a_3^2-32 a_2 a_4}}{8 a_4}$. Thus, we shall discuss four cases as follows:

Fig. 32

r versus $n_s$ for the non-supersymmetric inflaton potential with $(j, k, l)=(2, 3, 4)$ where the inflationary trajectory is at the left of the maximum $\phi _{M1}$

Fig. 33

r versus $n_s$ for the non-supersymmetric inflaton potential with $(j, k, l)=(2, 3, 4)$ where the inflationary trajectory is at the right of the maximum $\phi _{M1}$

• 1. When the slow-roll inflation occurs at the left of the maximum $\phi _{M1}$, i.e., $\phi _f<\phi _i<\phi _{M1}$, $a_2$ must be large enough to get a $\phi _f$ with a relatively large absolute value, and we present the numerical results for r versus $n_s$ in Fig. 32. For $n_s$ in the $1\sigma$ range $0.9603\pm 0.0073$, the range of r is [0.0073, 0.0472], which is out of the $2\sigma$ region for the BICEP2 data. Interestingly, we still have a large enough tensor-to-scalar ratio within the reach of the future Planck and QUBIT experiments.

• 2. For the slow-roll inflation occurring at the right of $\phi _{M1}$, i.e., $\phi _{M1}<\phi _i<\phi _f<\phi _{m}$, we can obtain a large r via chaotic inflation by requiring $a_3\ll a_2$ and $a_4\ll a_2$. The numerical results for r versus $n_s$ are given in Fig. 33. With $n_s$ in the $1\sigma$ range $0.9603\pm 0.0073$, the range of r is [0.0496, 0.1585], which can be consistent with the BICEP2 experiment. In the viable parameter space, we generically have $a_2>1000a_3$. Moreover, for the number of e-foldings $N_e=50$, $n_s$ and r are within the $1\sigma$ and $2\sigma$ regions of the BICEP2 experiment for $a_2>-1250a_4$ and $a_2>-660a_4$, respectively. Also, for $N_e=60$, $n_s$ and r are within the $2\sigma$ region for $a_2>-1000a_4$, but there is no viable parameter space for the $1\sigma$ region. The best fit point with $n_s=0.96$ and $r=0.158$ for the BICEP2 data can be obtained for $N_e=50$, $a_2>10^4 a_3$, and $a_2>-10^6a_4$. For instance, $a_2=10000, a_3=1$, and $a_4=-0.01$, and the corresponding $\phi _i, \phi _e$, and $\phi _{M1}$ are, respectively, $-14.2086, -1.41411$, and $-670.6$.

• 3. For the slow-roll inflation occurring at the left of the maximum $\phi _{M2}$, i.e., $\phi _{m}<\phi _f<\phi _i<\phi _{M2}$, we present the numerical results for r versus $n_s$ in Fig. 34. For $n_s$ in the $1\sigma$ range $0.9603\pm 0.0073$, the range of r is [0.0490, 0.2228], which can be consistent with the BICEP2 experiment. For the number of e-foldings $N_e=50$, $n_s$ and r are within the $1\sigma$ and $2\sigma$ regions of the BICEP2 experiment for $a_2>-1000a_4$ and $a_3>-150a_4$ and for $a_2>-660a_4$ and $a_3>-100a_4$, respectively. For the number of e-foldings $N_e=60$, $n_s$ and r are within the $1\sigma$ and $2\sigma$ regions of the BICEP2 experiment for $a_2>-1550a_4$ and $a_3>-150a_4$ and for $a_2>-1250a_4$ and $a_3>-100a_4$, respectively. Let us give two best fit points for the BICEP2 data. The best fit point with $n_s=0.96$ and $r=0.16$ can be realized for $N_e=50$, $a_2\approx 900 a_3$, and $a_3>-10^3a_4$, for example, $a_2=90, a_3=0.1$, and $a_4=-0.0001$, and the corresponding $\phi _i, \phi _f$, and $\phi _{M2}$ are respectively 14.249, 1.41532, and 1143.52. Another best fit point with $n_s=0.959$ and $r=0.1953$ can be obtained for $N_e=60$, $a_2\approx a_3$, and $a_3\approx -10^3a_4$, for instance, $a_2=1, a_3=1$, and $a_4=-0.001$, and the corresponding $\phi _i, \phi _f$, and $\phi _{M2}$ are 18.7512, 1.87413, and 750.666, respectively.

• 4. The case that the slow-roll inflation occurs at the right of the maximum $\phi _{M2}$, i.e., $\phi _{M2}<\phi _i<\phi _{f}$, we will not study here, since it is the same as the above case (1).

Fig. 34

r versus $n_s$ for the non-supersymmetric inflaton potential with $(j, k, l)=(2, 3, 4)$ where the inflationary trajectory is at the left of the maximum $\phi _{M2}$

Fig. 35

r versus $n_s$ for the supersymmetric inflaton potential with $(j, k, l)=(2, 3, 4)$ where the inflationary trajectories are at the left and right of the minimum $\phi _{m1}$

Second, we study the supersymmetric models with inflaton potential $V=|a\phi +b\phi ^2|^2=a^2\phi ^2+2ab\phi ^3+b^2\phi ^4$. For simplicity, we assume $a>0$, while $b<0$. Thus, there exist a maximum at $\phi _M=-\frac{a}{2b}$ and two minima at $\phi _{m1}=0$ and $\phi _{m2}=-\frac{a}{b}$. We shall consider the following four cases:

• 1. For the slow-roll inflation occurring at the left of the minimum $\phi _{m1}$, i.e., $\phi _i<\phi _f<\phi _{m1}$, we present the numerical results for r versus $n_s$ in Fig. 35. With $n_s$ in the $1\sigma$ range $0.9603\,\pm \,0.0073$, the range of r is [0.1369, 0.2490], which can be consistent with the BICEP2 experiment. Moreover, for the number of e-foldings $N_e=50$, $n_s$ and r are within the $1\sigma$ and $2\sigma$ regions of the BICEP2 experiment for $a>-30b$ and $a>-15b$, respectively. For the number of e-foldings $N_e=60$, $n_s$ and r are within the $1\sigma$ region of the BICEP2 experiment for $a>-8b$ and are generically in the $2\sigma$ region. Let us give two best fit points for the BICEP2 data. The best fit point with $n_s=0.96$ and $r=0.16$ can be realized for $N_e=50$ and $a\thickapprox -2000 b$, for example, $a=2000$ and $b=-1$, and the corresponding $\phi _i, \phi _f$, and $\phi _{m1}$ are respectively $-14.2462, -1.41521$, and 0. Another best fit point with $n_s=0.959$ and $r=0.20$ can be obtained for $N_e=60$, and $a\thickapprox -26 b$, for instance, $a=26$ and $b=-1$, and the corresponding $\phi _i, \phi _f$, and $\phi _{m1}$ are $-17.7247, -1.49091$, and 0, respectively.

• 2. When the slow-roll inflation occurs at the right of the minimum $\phi _{m1}$ and the left of the maximum $\phi _{M}$, i.e., $\phi _{m1}<\phi _f<\phi _i<\phi _M$, to have relatively large r, we find that |b| cannot be equal to or larger than a. The numerical results for r versus $n_s$ are also given in Fig. 35. For $n_s$ in the $1\sigma$ range $0.9603\pm 0.0073$, the range of r is [0.0254, 0.1584], which can be consistent with the BICEP2 experiment. In addition, for the number of e-foldings $N_e=50$, $n_s$ and r are within the $1\sigma$ and $2\sigma$ regions of the BICEP2 experiment for $a>-85b$ and $a>-47b$, respectively. For the number of e-foldings $N_e=60$, $n_s$ and r are within the $2\sigma$ region for $a>-85b$, while there is no viable parameter space for the $1\sigma$ region. Especially, the best fit point with $n_s=0.96$ and $r=0.158$ for the BICEP2 data can be obtained for $N_e=50$, and $a>-10^4 b$. For example, $a=1$ and $b=-10^{-4}$, and the corresponding $\phi _i, \phi _e$, and $\phi _{M}$, respectively, are 14.2025, 1.41391, and 3333.33.

• 3. The case that slow-roll inflation occurs at the right of the maximum $\phi _{M}$, i.e., $\phi _{M}<\phi _i<\phi _f<\phi _{m2}$, is the same as the above case (2) and thus we will not discuss it here.

• 4. The case that the slow-roll inflation occurs at the right of the minimum $\phi _{m2}$, i.e., $\phi _{m2} < \phi _f <\phi _i$, we will not study here, since it is the same as the above case (1).

4.11 The most general renormalizable supersymmetric inflationary models

We briefly comment on the most general renormalizable supersymmetric inflationary models with the following inflaton potential:

$$\begin{aligned} V= & {} (a'+b'\phi '+c'\phi ^{\prime 2})^2, \end{aligned}$$

(36)

where $a'$, $b'$, and $c'$ are all non-zero. Redefining the inflaton field and parameters as follows:

$$\begin{aligned} \phi \equiv \phi '+\frac{b'}{2c'},\quad a \equiv a'-\frac{b^{\prime 2}}{4c'}, b \equiv c', \end{aligned}$$

(37)

we obtain the inflaton potential

$$\begin{aligned} V= & {} (a+b\phi ^{ 2})^2. \end{aligned}$$

(38)

This is the same as the supersymmetric inflaton potential which is studied in the Sect. 4.5. Thus, we will not repeat it here.

4.12 Numerical result summary

To summarize the above results for $n_s$ within its $1\sigma$ range $0.9603\pm 0.0073$, we present the ranges of r for different signs of parameters in the non-supersymmetric and supersymmetric models respectively in Tables 1 and 2. Interestingly, we always have large enough tensor-to-scalar ratios, which are within the reach of the future Planck and QUBIT experiments.

Table 1 The ranges of r for different signs of parameters and $n_s$ within its $1\sigma$ range $0.9603\pm 0.0073$ in the non-supersymmetric models

Table 2 The ranges of r for different signs of parameters and $n_s$ within its $1\sigma$ range $0.9603\pm 0.0073$ in the supersymmetric models

5 Conclusion

We have systematically studied the renormalizable three-term polynomial inflation in the supersymmetric and non-supersymmetric models. We can construct the supersymmetric inflaton potentials via the supergravity theory, and we showed that the general renormalizable supergravity model is equivalent to one kind of our supersymmetric models. Although the running of the spectral index is out of the $2\sigma$ range for all the models, we found that the spectral index and tensor-to-scalar ratio can be consistent with the Planck and BICEP2 results. Even if we do not consider the BICEP2 experiment, our inflationary models cannot only highly agree with the Planck observations, but they also saturate its upper bound on the tensor-to-scalar ratio ($r \le 0.11$). In short, our models can be tested at the future Planck and QUBIC experiments.