Excited state mass spectra of doubly heavy $\Xi$ baryons

Abstract

In this paper, the mass spectra are obtained for doubly heavy $\Xi$ baryons, namely, $\Xi _{cc}^{+}$, $\Xi _{cc}^{++}$, $\Xi _{bb}^{-}$, $\Xi _{bb}^{0}$, $\Xi _{bc}^{0}$ and $\Xi _{bc}^{+}$. These baryons consist of two heavy quarks (cc, bb, and bc) with a light (d or u) quark. The ground, radial, and orbital states are calculated in the framework of the hypercentral constituent quark model with Coulomb plus linear potential. Our results are also compared with other predictions, thus, the average possible range of excited states masses of these $\Xi$ baryons can be determined. The study of the Regge trajectories is performed in (n, $M^{2}$) and (J, $M^{2}$) planes and their slopes and intercepts are also determined. Lastly, the ground state magnetic moments of these doubly heavy baryons are also calculated.

1 Introduction

Doubly heavy baryons have two families: $\Xi$ and $\Omega$. $\Omega$ has a light strange quark, while $\Xi$ has up or down quark(s) with two heavy quarks (c and b). Our previous work [1] exhibited the mass spectra, magnetic moments, and Regge trajectories of doubly heavy $\Omega$ baryons, while in the present paper, we established the $\Xi$ baryon family with six members. The only experimental evidence comes for $\Xi _{cc}^{+}$ by the SELEX experiment. One reported a ground state at 3520 MeV containing two charm quarks and a down quark [2,3,4]. It is yet to be confirmed from the other experiments [5,6,7,8]. Recently, the Hamiltonian model [9], Regge phenomenology [10, 11], lattice QCD [12,13,14,15], QCD sum rules [16, 17], the variational approach [18], and many more [19,20,21,22,23,24,25,26,27,28,29,30,31,32,33] have provided new results in the field of doubly heavy baryons. Many of them have only calculated the ground state masses, while some of them have also shown the excited states.

We have used the QCD inspired hypercentral constituent quark model (hCQM) with Coloumb plus linear potential. The first order correction is also taken into account to the potential and calculation has been performed by solving the six-dimensional hyperradial Schrödinger equation numerically [1, 34, 35]. We have calculated the mass spectra of radial excited states up to 5S and orbital excited states for 1P–5P, 1D–4D, and 1F–2F states. To the best of our knowledge, all the theoretical approaches have considered the $m_{u}=m_{d}$ case so far but the light quark masses are different in our model. Thus, we have obtained the mass spectra with u and d quarks combinations for these baryons. The obtained masses were used in the formation of Regge trajectories in the (n, $M^{2}$) and (J, $M^{2}$) planes. The determination of the slope and intercept of the Regge trajectories of these baryons is very important as it provides a better understanding of the dynamics of strong interactions in the production of charmed and bottom baryons at high energies.

The paper is organized as follows. We give a brief introduction in Sect. 1 and explain our hypercentral constituent quark model in Sect. 2. We present our mass spectra results of all doubly heavy $\Xi$ baryons in Sect. 3. Regge trajectories and magnetic moments are discussed in Sect. 4. Finally, our conclusion is in Sect. 5.

Table 1 Ground state masses of $\Xi$ baryons are listed and compared. Our work shows the ground state masses of all baryons with both light quark combination as $\Xi _{cc}^{+}$/$\Xi _{cc}^{++}$, $\Xi _{bb}^{-}$/$\Xi _{bb}^{0}$ and $\Xi _{bc}^{0}$/$\Xi _{bc}^{+}$ (in GeV)

2 The model

The methodology for the determination of the excited masses follows the same pattern as in our previous work; see [1] and the references therein. Therefore, we discuss the model very briefly in the present paper. We start with the Jacobi coordinates of three quark baryons that are given in terms of mass ($m_i$) and coordinates ($\mathbf {r_i}$) below [36]. The quark masses are taken in the calculations as $m_{u} = 0.338$, $m_{d} = 0.350$, $m_{c} = 1.275$, and $m_{b} = 4.67$ (in GeV). The coordinates $\mathbf {\rho }$ and $\mathbf {\lambda }$ with the respective reduced masses are given by

$$\begin{aligned}&m_{\rho }=\frac{2 m_{1} m_{2}}{m_{1}+ m_{2}}, \end{aligned}$$

(1)

$$\begin{aligned}&m_{\lambda }=\frac{2 m_{3} (m_{1}^2 + m_{2}^2+m_1m_2)}{(m_1+m_2)(m_{1}+ m_{2}+ m_{3})}. \end{aligned}$$

(2)

The Hamiltonian of the three-body baryonic system in the hCQM is then expressed as

$$\begin{aligned} H=\frac{P_{x}^{2}}{2m} +V(x). \end{aligned}$$

(3)

The hyperradius $x= \sqrt{\rho ^{2} + \lambda ^{2}}$ is a collective coordinate and therefore the hypercentral potential contains also the three-body effects. Here $m=\frac{2 m_{\rho } m_{\lambda }}{m_{\rho } + m_{\lambda }}$ is the reduced mass and x is the six-dimensional radial hyper central coordinate of the three-body system. In the present paper, the confining three-body potential is chosen within a string-like picture, where the quarks are connected by gluonic strings and the potential strings increase linearly with a collective radius $r_{3q}$ as mentioned in [37]. Accordingly the effective two-body interactions can be written as

Table 2 Radial excited states of doubly heavy $\Xi$ baryons(in GeV). Columns 4 and 5 show the masses with light quark d combination whereas Columns 6 and 7 show the masses with light quark u

$$\begin{aligned} \sum _{i<j}V(r_{ij})=V(x)+\cdots . \end{aligned}$$

(4)

In the hypercentral approximation, the potential is only depends on hyper radius(x). More details can be found in the references [37, 38]. We consider a reduced hypercentral radial function, $\phi _{\gamma }(x) = x^{\frac{5}{2}}\Psi _{ \gamma }(x)$ where $\Psi _{\gamma }$(x) is the hypercentral wave function and $\gamma$ is the grand angular quantum number. Thus, the six dimensional hyperradial Schrödinger equation reduces to

$$\begin{aligned} \left[ \frac{-1}{2m}\frac{\mathrm{d}^{2}}{\mathrm{d} x^{2}} + \frac{\frac{15}{4}+ \gamma (\gamma +4)}{2mx^{2}}+ V(x)\right] \phi _{ \gamma }(x)= E\phi _{\gamma }(x).\nonumber \\ \end{aligned}$$

(5)

For the present study we consider the hypercentral potential V(x) as the color Coulomb plus linear potential with first order correction [39,40,41] given by

$$\begin{aligned} V(x) = V^{0}(x) + \left( \frac{1}{m_{\rho }}+ \frac{1}{m_{\lambda }}\right) V^{(1)}(x)+V_{SD}(x), \end{aligned}$$

(6)

$$\begin{aligned} V^{(0)}(x)= \frac{\tau }{x}+ \beta x \quad \hbox {and}\quad V^{(1)}(x)= - C_{F}C_{A} \frac{\alpha _{s}^{2}}{4 x^{2}}, \end{aligned}$$

(7)

$$\begin{aligned} V_{SD}(x)= & {} V_{SS}(x)(\mathbf {S_{\rho }}.\mathbf {S_\lambda }) + V_{\gamma S}(x) (\mathbf {\gamma } \cdot \mathbf {S}) \nonumber \\&+\, V_{T} (x) \left[ S^2-\frac{3(\mathbf {S }\cdot \mathbf {x})(\mathbf {S} \cdot \mathbf {x})}{x^{2}} \right] . \end{aligned}$$

(8)

Here, $\tau$ is the hyper-Coulomb strength corresponding to the strong running coupling constant $\alpha _{s}$. $\beta$ is the string tension of the confinement part of potential. $C_{F}$ and $C_{A}$ are the Casimir charges of the fundamental and adjoint representation with values $\frac{2}{3}$ and 3. The spin-dependent part, $V_{SD}(x)$ contains three types of the interaction terms [42]: the spin–spin term $V_{SS} (x)$, the spin–orbit term $V_{\gamma S}(x)$, and the tensor term $V_{T}(x)$. The details of the terms are given in [34]. We solve the six dimensional Schrodinger equation using Mathematica notebook [43].

Table 3 P and D state masses of $\Xi _{cc}$ baryon (in GeV)

Table 4 P and D state masses of $\Xi _{bb}$ (in GeV)

Table 5 P and D state masses of $\Xi _{bc}$ (in GeV)

Table 6 F state masses of $\Xi _{cc}$, $\Xi _{bb}$, and $\Xi _{bc}$ baryons (in GeV)

3 Mass spectroscopy: $\Xi _{cc}$, $\Xi _{bb}$, and $\Xi _{bc}$

We begin with calculating the ground state masses of doubly heavy $\Xi _{cc}$, $\Xi _{bb}$ and $\Xi _{bc}$ baryons¹. The masses are computed for both parities $\frac{1}{2}^{+}$ and $\frac{3}{2}^{+}$ mentioned in Table 1. As is well known, the ground state of $\Xi _{cc}^{+}$ is found experimentally as $\Xi _{cc}(3520)^{+}$; but its $J^{P}$ value is still undefined. Our prediction suggests that it would be $J^{P}= \frac{1}{2}^+$; a similar suggestion is given by Refs. [10, 11, 25, 27]. The other ground state, with $J^{P}= \frac{3}{2}^+$, is found as 3.695 GeV by us. The value is closer to other predictions [10, 11, 24, 26] and lattice [12, 13] calculations. In the case of $\Xi _{bb}$ baryon, our ground state results (both parities) are matched (with [9, 18]) very well. Our predicted ground states of $\Xi _{bc}$ are very close to Refs. [13, 22, 26]. We have also calculated the ground state spectra of the ccu, bbu, and bcu baryons. They are close to the results of d quark combinations (8, 5, and 6 MeV differences, respectively).

Moving toward the excited states, the radial excited states are calculated from 2S–5S for $J^{P}$=$\frac{1}{2}^{+}$ and $\frac{3}{2}^{+}$. These radial excited states of $\Xi _{cc}$, $\Xi _{bb}$, and $\Xi _{bc}$ are mentioned in Table 2. P, D, and F states with their different isospin splittings are computed and the excited state masses from 1P–5P, 1D–4D, and 1F–2F are shown in Tables 3, 4, 5, and 6. One can observe that the B masses are a few MeV higher than the A masses in each case of every baryonic system. The results of different theoretical approaches for all the systems are also compared in the respective tables. Notice that the heavy quark combination (cc, bb, and bc) with light quarks (u and d) for all three baryons are represented individually in Table 1, 2, 3, 4, 5, and 6.

The excited states of the doubly heavy $\Xi$ family are unknown experimentally. Starting from radial excited states mentioned in Table 2, we have compared our results with Refs. [9, 18,19,20,21,22]. For the 2S state of the system $\Xi _{cc}$ with $J^{P}$ values $\frac{1}{2}^{+}(\frac{3}{2}^{+})$ we have a lowest prediction of 3.910 (4.027) (by [22]) and a highest of 4.183(4.282) (by [20]). Specifically, our 2S predictions are close to [22]. In a similar way, while analyzing the 2S state of the $\Xi _{bb} (\frac{1}{2}^{+})$ and $\Xi _{bb} (\frac{3}{2}^{+})$ baryons, the lowest to highest ranges of the masses are found to be (10441–10751) MeV and (10482–10770) MeV, respectively, whereas our model suggested masses that are close to the result of Ref. [19]. The next baryon is $\Xi _{bc}$ and the 2S states with both isospins show more than 100 MeV difference with others ([18, 20]. Though Refs. [9, 20, 22] have computed the 3S state (with $\frac{1}{2}^{+}$ and $\frac{3}{2}^{+}$) for $\Xi _{cc}$ and $\Xi _{bb}$ baryons and only [20] has computed for $\Xi _{bc}$ baryon, the mass difference from ours they obtained is large (except [9] for $\Xi _{cc}$).

In the case of $\Xi _{cc}$, our 1P state $J^{P}=\frac{1}{2}^{-}$ shows a difference of 57 MeV (with [19]), 27 MeV (with [21]), 12 MeV (with [22]) and 39 MeV (with [12]), while $J^{P}=\frac{3}{2}^{-}$ shows 87 MeV (with [19]) and 0 MeV (with [23]).

For $\Xi _{bb}$, our 1P states $J^{P}=\frac{1}{2}^{-}$ and $J^{P}=\frac{3}{2}^{-}$ are only 14 and 7 MeV higher than those of Ref. [19] whereas Ref. [9] has masses for $J^{P}=\frac{1}{2}^{-}$ and $J^{P}=\frac{3}{2}^{-}$ that are 31, 26 MeV lower than our prediction. Our 2P state is a few MeV higher than that of [9, 19]. Our 1D–2D states have $\approx$35 MeV and $\approx$178 MeV difference with [19]. The P and D states of the $\Xi _{bc}^{0}$ baryons are given in Table 5 and it follows the same description as mentioned in [1] and the references therein. We have compared our results with recent papers [10, 11] for 1P and 1D. Their values are higher than ours. The rest of the spectra (2P–5P and 2D–4D) is addressed by us for completeness.

The F state masses for all three doubly heavy baryons are given in Table 6. Apart from our work, Ref. [10, 11] has also calculated the 1F state of $\Xi _{cc}$ and $\Xi _{bb}$ for $J^{P}$= $\frac{7}{2}^{-}$ and $\frac{9}{2}^{-}$. For $\Xi _{cc}$, their masses are 73 and 280 MeV higher, while for the other system we have values 212 and 328 MeV higher than our predictions. We did not find any other F state calculations for the $\Xi _{bc}$ systems.

4 Regge trajectories and magnetic moments

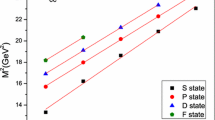
As discussed in Sect. 3, we have calculated the 1S–5S, 1P–5P, 1D–4D, and 1F–2F state masses for all doubly heavy $\Xi$ baryons. The obtained masses were very much useful in constructing the Regge trajectories in the (n, $M^{2}$) and (J, $M^{2}$) planes. Here n is the principal quantum number and J is the total spin. The Regge trajectories are presented in Figs. 1, 2, 3, 4, and 5 for the $\Xi _{cc}(ccd)$, $\Xi _{bb}(bbd)$ and $\Xi _{bc}(bcd)$ baryons. Similar trajectories can also be plotted for the rest of the baryons. Straight lines were obtained by the linear fitting in all figures. The ground and radial excited S states ($J^{P}=\frac{1}{2}^{+}$) and the orbital excited P ($J^{P}= \frac{1}{2}^{-}$), D ($J^{P}= \frac{5}{2}^{+}$) and F ($J^{P}= \frac{7}{2}^{-}$) states are plotted in Fig 1, 2, and 3 from bottom to top. We use

$$\begin{aligned} n=\beta M^2+ \beta _{0}. \end{aligned}$$

(9)

Here $\beta$ and $\beta _{0}$ are the slope and intercept, respectively. The fitted slopes and intercepts are given in Table 7. We use the natural parity $J^{P}=\frac{1}{2}^{+}$, $J^{P}=\frac{3}{2}^{-}$, $J^{P}=\frac{5}{2}^{+}$, $J^{P}=\frac{7}{2}^{-}$ and the unnatural ($J^{P}=\frac{3}{2}^{+}$, $J^{P}=\frac{5}{2}^{-}$, $J^{P}=\frac{7}{2}^{+}$, $J^{P}=\frac{9}{2}^{-}$) parity masses and plot the graphs for the $\Xi _{cc}$ and $\Xi _{bb}$ baryon states (see Figs. 4, 5). For that we use,

Fig. 1

Regge trajectory ($M^{2} \rightarrow n$) for $\Xi _{cc}$ baryon

Fig. 2

Regge trajectory ($M^{2} \rightarrow n$) for $\Xi _{bb}$ baryon

Fig. 3

Regge trajectory ($M^{2} \rightarrow n$) for $\Xi _{bc}$ baryon

$$\begin{aligned} J=\alpha M^2+ \alpha _{0}. \end{aligned}$$

(10)

Here $\alpha$ and $\alpha _{0}$ are the slope and intercept, respectively. The fitted slopes and intercepts are given in Table 8. We observe that the square of the calculated masses fit very well to the linear trajectory and are almost parallel and equidistant in S, P, D, and F states. We can determine the possible quantum numbers and prescribe them to a particular Regge trajectory with the help of our obtained results.

To obtain the magnetic moments of the $\Xi$ family, we need to calculate their effective masses first. As the combination of quarks in baryons changes, its binding interaction affects the situation and $m_{i}^{eff}$ differs. The effective mass for each of the constituting quark $m_{i}^{eff}$ can be defined as

$$\begin{aligned} m_{i}^{eff}= m_i\left( 1+ \frac{\langle H \rangle }{\sum _{i} m_i} \right) \end{aligned}$$

(11)

where $\langle H \rangle$ = E + $\langle V_{\mathrm{spin}} \rangle$. Thus, the magnetic moment of baryons with bound quarks are given as [1] and the references therein]

$$\begin{aligned} \mu _{B}=\sum _{i}\langle \phi _{sf}\vert \mu _{iz}\vert \phi _{sf}\rangle ) \end{aligned}$$

(12)

where

$$\begin{aligned} \mu _{i}=\frac{e_i \sigma _i}{2m_{i}^{eff}}. \end{aligned}$$

(13)

Fig. 4

Regge trajectory ($M^{2} \rightarrow J$) for $\Xi _{cc}$ baryon

Fig. 5

Regge trajectory ($M^{2} \rightarrow J$) for $\Xi _{bb}$ baryon

Table 7 Fitted slopes and intercepts of the Regge trajectories in (n, $M^{2}$) plane

$e_i$ is a charge and $\sigma _i$ is the spin of the respective constituent quark corresponding to the spin flavor wave function of the baryonic state. Using these equations and our obtained ground state masses (mentioned in Table 1), we calculated the magnetic moments of all six $\Xi$ baryons. The spin flavor wave function and magnetic moments are given in Table 9. Our obtained ground state magnetic moments are also compared with others, as shown in Table  9.

5 Conclusion

The hypercentral constituent quark model is used to construct the mass spectra of doubly heavy $\Xi$ baryons. Ground states as well as excited state masses are obtained successfully. The mass difference between the light quarks (u and d) is 12 MeV in our model. So, it is obvious that when we move toward the calculations of the excited states the baryon masses would also have a very small mass difference. For the sake of completeness we calculated whole mass spectrum for all six doubly heavy baryon and noticed that it hardly differs less than $\approx$10 MeV, which can be observed in Tables 1, 2, 3, 4, 5, and 6. The ground state of $\Xi _{cc}$ is experimentally known and while comparing our ground states of the $\Xi _{cc}^{++}$, $\Xi _{cc}^{+}$ baryons we define the state with parity $J^{P}$= $\frac{1}{2}^{+}$.

Table 8 Fitted parameters $\alpha$ and $\alpha _0$ are slope and intercept of parent and daughter Regge trajectories

Table 9 Magnetic moment (in nuclear magnetons) of $J^{P}$  $\frac{1}{2}^{+}$ and $\frac{3}{2}^{+}$ doubly heavy baryons

We successfully plotted Regge trajectories of present work in both (n, $M^{2}$) and (J,$M^{2}$) planes and fortunately assigned the quantum number for each cases of six $\Xi$ baryons. The magnetic moments of the ground states are also calculated using obtained masses. We can observe that our obtained results are close to other predictions (except $\Xi _{cc}^{++}$, $\Xi _{cc}^{+ *}$, $\Xi _{bb}^{0 *}$ baryons).

This study will definitely help future experiments and other theoretical models to identify the baryonic states from resonances. We would like to extend this model to calculate the mass spectra and other properties of triply heavy baryons.