Abstract
A non-diagonal vielbein ansatz is applied to the N-dimension field equations of f(T) gravity. An analytical vacuum solution is derived for the quadratic polynomial \(f(T)=T+\epsilon T^2\) and an inverse relation between the coupling constant \(\epsilon \) and the cosmological constant \(\Lambda \). Since the induced metric has off-diagonal components, it cannot be removed by a mere coordinate transformation, the solution has a rotating parameter. The curvature and torsion scalars invariants are calculated to study the singularities and horizons of the solution. In contrast to general relativity, the Cauchy horizon differs from the horizon which shows the effect of the higher order torsion. The general expression of the energy-momentum vector of f(T) gravity is used to calculate the energy of the system. Finally, we have shown that this kind of solution satisfies the first law of thermodynamics in the framework of f(T) gravitational theories.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
General relativity is constructed in Riemann geometry, which reduces to Minkowski spacetime in the absence of a gravitational field. In the Riemannian geometry, the differentiable manifold is described by a metric tensor which measures the distances between different space points. However, gravitation in this theory is a manifestation of the curvature of the spacetime, where the Riemann Christoffel tensor is responsible for this curvature. All quantities in this manifold can be defined in terms of the metric tensor [1]. At present time, to extend GR to include torsion is considered as an urgent issue because many questions depend on whether the spacetime connection is symmetric or not. General relativity is an orthodox theory that does not allow quantum effects. However, these effects should be taken into account in any theory that accompanies gravity. Changing geometry from \(V_4\) (4-dimensional Riemannian manifolds) to \(U_4\) (4-dimensional Weitzenböck manifolds) is considered as a first direct extension that attempts to incorporate the spin fields of matter into the same geometrical scheme of GR. As an example of this, we have the mass-energy in which curvature is the source of gravity, while the spin of torsion. Einstein–Cartan–Sciama–Kibble theory is considered as one of the most significant trails in this direction. Nevertheless, the task of spin-matter fields does not explain the function of the torsion tensor that seems to play important tasks in any fundamental theory.
The accelerated expansion of our Universe is confirmed by many separated cosmological experiments [3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21]. This expansion can be explained in GR by taking into account the dark energy component in the total energy of our Universe. It is widely accepted, without real justifications, to interpret these components by inserting a cosmological constant \(\Lambda \) into Einstein’s field equation which is called \(\Lambda \)CDM model [2]. Also, this model can be extended by adding a speculated dynamical fluid with a negative pressure, e.g. quintessence fluid. Therefore, we can consider the accelerated expansion of our Universe as an indicator of the failure of our information to the principles of gravitational field, and thus a modification of GR is necessary. This modification can be done by making the action a function of the curvature scalar R, i.e., f(R) [22,23,24].
Using a different processor we can set up another method and use the Weitzenböck connection, which includes torsion as an alternative to curvature. This process was suggested by Einstein who called it a “teleparallel equivalent of general relativity” (TEGR) [1, 25,26,27,28,29,30]. This theory, TEGR, is closely related to GR and differs only by a total derivative term in the action. The dynamical objects in such geometry are the four linearly independent vierbeinsFootnote 1 \(b^{a}{_{\mu }}\). The advantage of this framework is that the torsion tensor is formed solely from the products of first derivatives of the vielbein. In the TEGR formalism, the features of a gravitational field are described in the torsion scalar [25, 26]. Therefore, guided by the construction of f(R) gravitational theory we are allowed to postulate the Lagrangian of the amended Einstein–Hilbert action as a function of the torsion scalar to extend TEGR in a natural way. This extension is called f(T), where T is the teleparallelism scalar torsion, gravitational theory [31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48]. It is necessary to note that in f(T) theory the field equations are of second order while the field equations of f(R) are of fourth order. Different aspects of cosmology in f(T) theory have been discussed in the literature [49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67].
A black-hole solution [45] has been investigated in the quadratic polynomial f(T) gravity using a diagonal vielbein as a first approach to the study of the features of the theory. As is well known, the diagonal relation between vielbein and the metric is always allowed in the linear teleparallel gravity. However, the non-diagonal relation in the generalized theories, e.g. f(T) gravity is essential. The aim of the present study to derive a rotating N-dimensional black-hole solution for a quadratic polynomial f(T) gravitational theory using a non-diagonal vielbein and discuss its relevant physics. This study is arranged as follows: in Sect. 2, the installation of teleparallel space and the f(T) gravitational theory is provided. In Sect. 3, a vielbein fieldFootnote 2 is applied to the N-dimension field equations of \(f(T)=T+\epsilon T^{2}\) and an exact rotating solution is obtained. This solution is asymptotically de Sitter or anti de Sitter (dS/AdS). The main merit of this solution is that its scalar torsion is constant. In Sect. 4, some relevant physics, singularities, energy, and the first law of thermodynamics, are discussed. The final section is reserved for the discussion.
2 Installing f(T) gravitational theories
We are going, in this section, to briefly review f(T) gravitational theory. Then we apply the field equations of a quadratic polynomial \(f(T)=T+\epsilon T^2\) to a non-diagonal vielbein field with a spherical symmetry aiming to find a new black-hole solution.
2.1 Teleparallel space
In this subsection, we give a brief survey of the teleparallel space. In the literature, this space has many names, e.g. distant parallelism, Weitzenböck, absolute parallelism (AP), vielbein, parallelizable etc. For more details, we refer the reader to [68,69,70,71]. A teleparallel space is a pair \((M,\,b_{a})\), where M is an N-dimensional manifold and \(b_{a}\) (\(a=1,\ldots , N\)) are N independent vector fields defined globally on M. The vector fields \(b_{a}\) are known as the parallelization vector fields or vielbein fields.
Let \(b_{a}{^{\mu }}\) \((\mu = 1, \ldots , N)\) be the coordinate components of the ath vector field \(b_{a}\). The Einstein summation convention is applied on both Greek (world) and Latin (mesh) indices. The covariant components \(b^{a}{_{\mu }}\) of the vector \(b_{a}\) and its contravariant ones satisfy the following orthogonal condition:
with \(\delta \) being the Kronecker tensor. Due to the linear independence of the vector \(b_{a}\), the determinant \(b:=\det (b_{a}{^{\mu }})\) must be nonzero.
On a teleparallel spacetime, \((M,\,b_{a})\), there uniquely exists a non-symmetric linear (Weitzenböck) connection, which is constructed from the vielbein fields as
This connection identifies the important property
which is known as the AP condition. So the connection (2) sometimes can be called the canonical connection. Associated to it, the covariant differential operator \(\nabla ^{(\Gamma )}_{\nu }\) is given as (3).
The curvature tensor \(R^{\alpha }{_{\epsilon \mu \nu }}\) and the torsion tensor \(T^{\epsilon }{_{\nu \mu }}\) of the canonical connection can be calculated using the non-commutation relation of an arbitrary vector fields \(V_{a}\) given by
Combining the above non-commutation relation and the AP condition (3), the curvature tensor \(R^{\alpha }_{~~\mu \nu \sigma }\) of the canonical connection \(\Gamma ^{\alpha }_{~\mu \nu }\) must be null identically [68]. Moreover, we can induce the metric tensor corresponding to a given vielbein field as
and the contravariant one
Also, we can construct the symmetric linear (Levi-Civita) connection from the metric tensor \(g_{\mu \nu }\) as
Using Eqs. (3) and (6), it is easy to check that both the canonical connection \(\Gamma {^\alpha }{_{\mu \nu }}\) (2) and the Leivi-Civita connection are metric ones, i.e.
where the operator \(\nabla ^{(\mathring{\Gamma })}_{\sigma }\) is the covariant derivative associated with the Levi-Civita connection \(\mathring{\Gamma }\). For the non-symmetric connection (2), we define the torsion tensor
Also, we define the contortion tensor \(K^{\alpha }_{~\mu \nu }\) as the difference between the Weitzenböck and Levi-Civita connections as
Due to the symmetrization of the connection \(\mathring{\Gamma }{^{\alpha }}{_{\mu \nu }}\), the torsion and contortion tensors are related by
Alternatively, one can write the torsion in terms of contortion as
where \(T_{\sigma \mu \nu } = g_{\epsilon \sigma }\,T^{\epsilon }_{~\mu \nu }\) and \(K_{\mu \nu \sigma } = g_{\epsilon \mu }\,K^{\epsilon }_{~\nu \sigma }\). The torsion \(T_{\sigma \mu \nu }\) (contortion \(K_{\mu \nu \sigma }\)) tensor is skew-symmetric in the last (first) pair of indices. Moreover, Eqs. (9) and (10) show that the torsion tensor vanishes if and only if the contortion tensor vanishes.
2.2 f(T) gravitational theory
In f(T) gravity, and similar to all torsional formulations, we use the vierbein fields \(b^{i}{_{\mu }}\) which form an orthonormal base. The Lagrangian of TEGR, i.e. the torsion scalar T, is constructed by contractions of the torsion tensor as [72]
Similar to the f(R) extensions of GR we can extend T to a function f(T), constructing the action of f(T) gravity [32, 33]:
where \(\kappa \) is the N-dimensional gravitational constant given by \(\kappa =2(N-3)\Omega _{N-1} G_N\), \(G_N\) being Newton’s constant in N dimensions and \(\Omega _{N-1}\) the volume of an \((N-1)\)-dimensional unit sphere, which is given by the expression \(\Omega _{N-1} = \frac{2\pi ^{(N-1)/2}}{\Gamma ((N-1)/2)}\) (with the \(\Gamma \)-function of the argument that depends on the dimension of spacetime).Footnote 3 \( |b|=\sqrt{-g}=\det \left( {b^a}_\mu \right) \) and \( \mathcal{L}_\mathrm{Matter}\) is the Lagrangian matter. The variation of Eq. (12) with respect to the vielbein field \({b^i}_\mu \) and its first derivative gives the following field equations [33]:
with \(f := f(T)\), \(f_{T}:=\frac{\partial f(T)}{\partial T}\), \(f_{TT}:=\frac{\partial ^2 f(T)}{\partial T^2}\), and \(\mathcal{T}^\nu {}_\mu \) is the energy–momentum tensor.
Equation (13) can rewritten as
where \(t^{\nu \mu }\) is defined as
Due to the anti- symmetrization of the tensor \({S}^{a \nu \lambda }\) we get
Equation (16) yields the continuity equation in the form
where the integration is on the (\(N-1\)) volume V bounded by the surface \(\Sigma \). This recommends one to represent the quantity \(t^{\lambda \mu }\), the energy-momentum tensor of the gravitational field, in the frame of f(T) gravitational theories [73]. Therefore, the total energy-momentum tensor of f(T) gravitational theory is defined as
Equation (18) is the generalization of the energy-momentum tensor that can be used to calculate energy and spatial momentum. It is clear that the TEGR case [74] is recovered by setting \(f(T)=T\).
3 Rotating solution in f(T) gravitational theories
For an N-dimensional spacetime having spherical symmetry with a flat horizon, we write the following vielbein ansatz in cylindrical coordinates (t, r, \(\phi _1\), \(\phi _2\) \(\ldots \) \(\phi _{N-3}\), z) [45]:
where \(\lambda \equiv \sqrt{\frac{-(N-1)(N-2)}{2\Lambda }}\), \(S_i(r), \; i=1\cdots 3\), are three unknown functions of the radial coordinate r, while \(c_1\) and \(c_2\) are some constants.Footnote 4 It is clear that, if the two constants \(c_1=1\), \(c_2=0\), and the function \(S_{2}(r)=0\), then the vielbein (19) reduces to the previous diagonal vielbein case studied in [45]. The line element of (19) takes the form
Equation (20) arises from the vielbein ansatz (19) using Eq. (4). Substituting (19) into (11) we evaluate the torsion scalar in the formFootnote 5
where \(S'_i=\displaystyle \frac{\mathrm{d} S_i(r)}{\mathrm{d} r}\). Inserting the vielbein (19) into the field equations (13), and assuming the vacuum case, we get the following non-vanishing components:
We constrain the system by the following:
Here the second constraint is to simplify the results. However, the vacuum solution can be found in general. For more details as regards the second constraint, one may consult [45]. Substituting Eq. (23) into Eq. (22), the black-hole solution is given as
where \(c_3\) and \(c_4\) are constants of integration. Equation (24) shows that when the constants \(c_1=1\) and \(c_2=0\), the solution reproduces the static black-hole solution of [45]. We note that the null value of the constant \(c_{2}\) implies the vanishing of the function \(S_{2}(r)\). So we need not to impose the vanishing of \(S_{2}(r)\) as an extra condition to reduce to the static black-hole solution. To understand the characteristics of the above derived solution and its relevant physics, we are going to study the singularities, horizon, energy, and the first law of thermodynamics in the following section.
4 Relevant physics
In this section, we are going to study some physical quantities of the analytical solution at hand.
4.1 Singularities
We start with studying one of the fundamental concepts in any gravitational theory, that is, the singularity. Substituting solution (24) into the metric (20), the spacetime configuration takes the form
Equation (25) shows that the spacetime metric has a cross term that cannot be removed by a coordinate transformation. This cross term is responsible for the rotation similar to the cross term that appears in GR which creates a Kerr black hole. Equation (25) shows that when \(c_1=1\) and \(c_2=0\), we get
which represents the gravitational field of a static black hole [45].
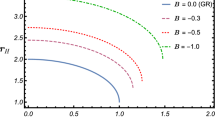
To study spacetime singularities of the solution at hand, first we find the radial distance r at which the functions \(S_1\), \(S_2\), and \(S_3\) become null or infinitely large. Since these functions are coordinate dependent quantities, we would like to make sure that the singular points are real and not a reflection of a bad choice of the coordinate system. In order to distinguish real singularities from coordinate ones, we study various invariants. These invariants do not change under coordinate transformation. If they are not defined at a specific spacetime point, they will be undefined at that point in any other coordinate choice. Then the singular point will be a physical singularity. In GR, we usually study some invariants, e.g. the Ricci scalar, the Kretschmann scalar, etc, but all invariants are constructed from the Riemann tensor and its contractions. However, in TEGR, there are two ways to calculate invariants. In the first, one uses the obtained solution to calculate the torsion invariants, e.g. the torsion scalar T. In the second, one employs the solution to obtain the induced metric, then to calculate the curvature invariants. The comparison between these two ways is an interesting topic of this study which may shed light on the differences between the curvature-based gravity and the torsion one. More specifically, one can use the vielbeins, Weitzenböck’s connection, to construct all torsion-based invariants, or to use the metric, the Levi-Civita connection, and construct all the curvature-based invariants. Since particles follow geodesics defined by the Levi-Civita connection, some prefer to study the curvature invariants instead of the torsion ones. However, we can say that the two ways (invariants constructed from metric and those constructed from vielbeins) are equivalent only when a suitable choice of vielbeins and metric is selected. Therefore, classically, the above two ways might be alternatives; however, on the quantization level, it would be important to discover which is more fundamental field: the metric or the vielbein? We calculate some curvature and torsion invariants corresponding to the solution (24) as given below, using the symmetric connection of Eq. (6) for curvature invariants and the non-symmetric one given by Eq. (3) for torsion invariants, and we get
From the above calculations, we have the following comparison:
-
(i)
The invariants \(R^{\mu \nu \lambda \rho }R_{\mu \nu \lambda \rho }\), \( T^{\mu \nu \lambda }T_{\mu \nu \lambda }\), and \( T^{\mu }T_{\mu }\) have a singularity at \(r=0\).
-
(ii)
The invariants \( T^{\mu \nu \lambda }T_{\mu \nu \lambda }\) and \( T^{\mu }T_{\mu }\) have one more singularity at \(c_3=c_4r^{N-1}\).
-
(iii)
The scalars \(R^{\mu \nu }R_{\mu \nu }\), R, and T have no singularities and the black-hole solution is regular even at \(r=0\). We see that the limit \(\epsilon =0\) is not valid to keep a regular black-hole solution.
-
(iv)
All the above invariants are not defined when \(\epsilon \rightarrow 0\). This means that solution (24) has no analogy in GR and cannot reduce to GR (or TEGR). Indeed, this result depends on the constraint \(\Lambda =\frac{1}{24 \epsilon }\). This constraint facilitates the calculations and makes the above differential equations solvable.
-
(v)
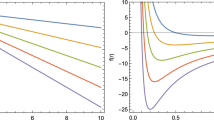
Equation (27) shows that the Cauchy horizon of \(g_{tt}=0\) and the horizons constructed from \(g^{rr}=0\) are the same, which is familiar in GR (TEGR). However, this condition is not satisfied for Eq. (27). We may say that this is due to the contribution of the higher order torsion. This contribution appears in a non-trivial black hole, like a rotating one. This point still needs more study which will be performed elsewhere.
4.2 Energy
We next study the energy of the system according to the solutionFootnote 6 (24). Using Eq. (18) we calculate the necessary components needed to study the evaluation of the energy:
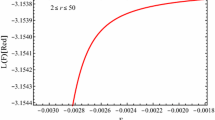
where the value of \(\kappa \) has been used in the second equation of Eq. (29). The value of the energy of the above equation is not a finite value; therefore, we must use the regularized method to get a finite value of the energy. This regularized expression takes the form

Using (30) in solution (24) we get
which is a finite value.
4.3 First law of thermodynamics
There is a great deal of work in analyzing the behavior of the horizon thermodynamics in modified theories of GR. In a wide category of these theories, one gets solutions with horizons and can connect the temperature and entropy with horizons. Since the temperature T can be determined from the periodicity of the Euclidean time, determining the right form of the entropy is a most non-trivial issue. Here we shall briefly describe how these results arise in a class of theories which are natural modifications of TEGR. A fundamental law in need to be studied in a modification of TEGR gravity is the fulfillment of the first law of thermodynamics. Miao et al. [75] have discussed whether the first law of thermodynamics is satisfied within f(T) gravitational theories or not. They split the non-symmetric field equations (13) into symmetric and skew symmetric parts to have the forms

Assuming an exact Killing vector they have shown that for a heat flux \(\delta Q\) passing through the black-hole horizon and by using the symmetric part of Eq. (32) they show
where H stands for the black-hole horizon, which in this study is equal to an \((N - 2)\)-dimensional boundary of the hypersurface at infinity. It is shown that the first term in Eq. (33) can be rewritten as \(T\delta S\) [75]. Therefore, when the second term in Eq. (33) is not vanishing there will be a violation of the first law of thermodynamics. Miao et al. [75] have shown that the second term cannot be equal to zero. Therefore, if we need to satisfy the first law we must either have \(f_{TT}=0\), which gives the TEGR (GR) theory, or have \(T=\mathrm{constant}\). Indeed, solution (24) enforces the torsion scalar to be a constant. Therefore, the black-hole solution (24) satisfies the first law of thermodynamics.
5 Concluding remarks
We show that finding an exact solution in modified theories of gravity, e.g. f(R) or f(T), is not an easy task. In this work we derived an exact rotating black-hole solution in the f(T) gravity framework. Indeed, the authors of [45], have found a static black-hole solution using a diagonal vielbein. However, studying non-diagonal vielbein in f(T) theories is necessary. In this work, we have employed a non-diagonal vielbein field, with three unknown functions, to the quadratic \(f(T)=T+\epsilon T^2\) field equations to study the non-charged case. We obtained an exact solution by taking the useful constraint \(\Lambda =\frac{1}{24 \epsilon }\) into account. The derived analytical solution containing two constants of integration. This solution coincides with what derived in [45] when the off-diagonal components are set equal to zero, i.e., \(c_2=S_2=0\).
The solution of the non-diagonal vielbein is a new one and has no analog in GR due to the appearance of the dimensional parameter, \(\epsilon \), which is the coefficient of the higher order torsion tensor. This coefficient is not allowed to be zero; otherwise, the torsion scalar and the metric will be singular. The torsion scalar of this solution is constant, i.e. \(T=\frac{-1}{6\epsilon }\).
The issue of singularities is discussed by calculating the scalars constructed from curvature and torsion. We have shown that all the scalars will have a singularity at \(\epsilon =0\), which ensures that this parameter must not be equal to zero and ensure that our derived solution is a novel one. Moreover, we have shown that there are more singularities for the scalars constructed from torsion than those constructed from curvature. This addition singularity may be due to the divergence term, which makes the torsion scalar different from the Ricci one. One more interesting property of solution (24) is that its Cauchy horizon is not identical to the horizon. This property shows the accumulation of the higher order torsion.
To investigate the physics of Eq. (24) in a deeper way we have calculated the energy and shown that it depends on the parameter \(\epsilon \). Equation (31) cannot give the known form of energy due to the dimension parameter \(\epsilon \), which demonstrates the effect of the higher torsion scalar. Furthermore, Eq. (31) shows that, in the case of four dimensions, \(\sqrt{c_4}=\frac{4\sqrt{2}}{27}\) and \(c_1{}^2-c_2{}^2=1\), which gives \(c_1=\sqrt{1+c_2{}^2}\) and \(E=\frac{c_3}{\epsilon }\). From this analysis we can assume \(c_2\) to be the rotation parameter.
Then we have discussed if solution (24) satisfies the first law of thermodynamics. We have shown that solution (24), which is an exact one to the non-trivial case \(f(T)=T+\epsilon T^2\), satisfied the first law of thermodynamics. This satisfaction comes from the fact that solution (24) gave a constant torsion. In general Miao et al. [75] have shown that for non-constant scalar torsion and when \(f_{TT}\ne 0\) we get a violation of the first law of thermodynamics.
Finally, we want to make a comparison between our solution in which the Cauchy horizon of \(g_{tt}=0\) and the horizons constructed from \(g^{rr}=0\) are not the same. However, in orthodox GR the Cauchy horizon of \(g_{tt}=0\) and the horizons constructed from \(g^{rr}=0\) are the same [76]. This difference between the horizons of \(g_{00}\) and \(g^{rr}\) in higher order torsion at the present time is not clear and its needs more study, which will be done elsewhere.
Notes
In this study Greek indices and Latin ones refer to the coordinate and tangent spaces, respectively.
In the 4-dimensional spacetime case, we call the vielbein a vierbein or tetrad.
When \(N = 4\), one can show that \(2(N-3)\Omega _{N-1} = 8 \pi \).
The vielbein (19) is not the most general non-diagonal one. However, we use it to facilitate the calculations.
For abbreviation we will write \(S_i(r)\equiv S_i\), \(S'_i\equiv \frac{dS_i}{dr}\).
In this study we take the Newtonian constant to be an effective constant in which \(G_\mathrm{eff.}=\frac{G_{N}}{f_T} \) [59].
References
A. Einstein, Prussian Academy of Sciences, 414 (1925). arXiv:physics/0503046 [physics.hist-ph]
S. Capozziello, G. Lambiase, N. Adv. Phys. 7, 13 (2013)
A.G. Riess, A.V. Filippenko, P. Challis et al., Astronom. J. 116, 1009 (1998)
S. Perlmutter, G. Aldering, G. Goldhaber et al., Astrophys. J. 517, 565 (1999)
M. Kowalski, D. Rubin, G. Aldering et al., Astrophys. J. 686, 749 (2008)
E. Komatsu, J. Dunkley, M.R. Nolta et al., Astrophys. J. 180, 330 (2009)
E. Komatsu, K.M. Smith, J. Dunkley et al., Astrophys. J. Sup. 192, 18 (2011)
N. Jarosik, C.L. Bennett, J. Dunkley, B. Gold, M.R. Greason, M. Halpern, R.S. Hill, G. Hinshaw, A. Kogut, E. Komatsu et al., Astrophys. J. Sup. 192, 14 (2011)
P.A.R. Ade et al., Astronomy Astrophys. 594, 63 (2016)
W.J. Percival, B.A. Reid, D.J. Eisenstein et al., MNRAS 401, 2148 (2010)
M. Tegmark et al., SDSS Collaboration, Phys. Rev. D 69, 103501 (2004)
S. Cole et al., FGRS Collaboration, MNRAS 362, 505 (2005)
D.J. Eisenstein et al., SDSS Collaboration, Astrophys. J. 633, 560 (2005)
B.A. Reid, L. Samushia, M. White, W.J. Percival, M. Manera et al., MNRAS 426, 2719 (2012)
C. Blake, S. Brough, M. Colless, C. Contreras, W. Couch et al., MNRAS 415, 2876 (2011)
J.S. Alcaniz, Phys. Rev. D 69, 083521 (2004)
S.W. Allen, R.W. Schmidt, H. Ebeling, A.C. Fabian, L. van Speybroeck, MNRAS 353, 457 (2004)
L. Wang, P.J. Steinhardt, Astrophys. J. 508, 483 (1998)
J. Benjamin, C. Heymans, E. Semboloni, L. Van Waer- beke, H. Hoekstra, T. Erben, M. D. Gladders, M. Hetterscheidt, Y. Mellier, H. K. C. Yee, MNRAS 381, 702 (2007)
L. Amendola, M. Kunz, D. Sapone, JCAP 0804, 013 (2008)
L. Fu et al., Astron. Astrophys. 479, 9 (2008)
S. Capozziello, M. Francaviglia, Gen. Rel. Grav. 40, 357 (2008)
S. Nojiri, S.D. Odintsov, Phys. Rept. 505, 59 (2011)
T.P. Sotiriou, V. Faraoni, Rev. Mod. Phys. 82, 451 (2010)
K. Hayashi, T. Shirafuji, Phys. Rev. D 19, 3524 (1979)
J.W. Maluf, J. Math. Phys. 36, 4242 (1995)
W. El Hanafy, G.G.L. Nashed, Astrophys. Space Sci. 361, 68 (2016)
R. Aldrovandi, J.G. Pereira, K.H. Vu, Braz. J. Phys. 34, 1374 (2004)
G.G.L. Nashed, Chaos. Solitons Fract. 15, 841 (2003)
J.W. Maluf, Annalen Phys. 525, 339 (2013)
G.G.L. Nashed, Chin. Phys. B 19, 020401 (2010)
R. Ferraro, F. Fiorini, Phys. Rev. D 78, 124019 (2008)
G.R. Bengochea, R. Ferraro, Phys. Rev. D 79, 124019 (2009)
E.V. Linder, Phys. Rev. D 81, 127301 (2010)
R. Myrzakulov, Eur. Phys. J. C 71, 1752 (2011)
J.B. Dent, S. Dutta, E.N. Saridakis, JCAP 1101, 009 (2011)
Y. Zhang, H. Li, Y. Gong, Z.-H. Zhu, JCAP 1107, 015 (2011)
S. Capozziello, V.F. Cardone, H. Farajollahi, A. Ravanpak, Phys. Rev. D 84, 043527 (2011)
C.-Q. Geng, C.-C. Lee, E.N. Saridakis, Y.-P. Wu, Phys. Lett. B 704, 384 (2011)
K. Bamba, R. Myrzakulov, S. Nojiri, S.D. Odintsov, Phys. Rev. D 85, 104036 (2012)
K. Bamba, C.-Q. Geng, C.-C. Lee, L.-W. Luo, J. Cosmol. Astropart. Phys. 01, 021 (2011)
P. Wu, H. Yu, Eur. Phys. J. C 71, 1552 (2011)
A. de la Cruz-Dombriz, P.K.S. Dunsby, D. Saez-Gomez, JCAP 1412, 048 (2014)
G.G.L. Nashed, Phys. Rev. D 88, 104034 (2013)
S. Capozziello, P. A. González, D. E. N. Saridakis, Y. Vásquez, JHEP 1302, 039 (2013)
G.G.L. Nashed, Gen. Relat. Grav. 45, 1878 (2013)
P. Wu, H.W. Yu, Phys. Lett. B 692, 176 (2010)
H. Wei, Phys. Lett. B 712, 430 (2012)
B. Li, T.P. Sotiriou, J.D. Barrow, Phys. Rev. D 83, 104017 (2011)
B. Li, T.P. Sotiriou, J.D. Barrow, Phys. Rev. D 83, 064035 (2011)
K. Karami, A. Abdolmaleki, S. Asadzadeh, Z. Safari, Eur. Phys. J. C 73, 2565 (2013)
P. Wu, H.W. Yu, Phys. Lett. B 693, 415 (2010)
R.C. Nunes, S. Pan, E.N. Saridakis, JCAP 1608, 011 (2016)
D. Saez-Gomez, C.S. Carvalho, F.S.N. Lobo, I. Tereno, Phys. Rev. D 94, 024034 (2016)
G.G.L. Nashed, W. El Hanafy, Eur. Phys. J. C 74, 3099 (2014)
G.G.L. Nashed, Chin. Phys. Lett. 29, 050402 (2011)
K. Bamba, G. G. L. Nashed, W. El Hanafy, Sh. K. Ibraheem, Phys. Rev. D 94, 083513 (2016)
C.-Q. Geng, C.-C. Lee, E.N. Saridakis, JCAP 1201, 002 (2012)
H. Wei, H.-Y. Qi, X.-P. Ma, Eur. Phys. J. C 72, 2117 (2012)
V.F. Cardone, N. Radicella, S. Camera, Phys. Rev. D 85, 124007 (2012)
L. Iorio, N. Radicella, M.L. Ruggiero, JCAP 1508, 021 (2015)
R. Zheng, Q.-G. Huang, JCAP 1103, 002 (2011)
Y.-P. Wu, C.-Q. Geng, Phys. Rev. D 86, 104058 (2012)
W. El Hanafy, G.G.L. Nashed, Astrophys. Space Sci. 361, 266 (2016)
Y.-P. Wu, C.-Q. Geng, JHEP 11, 142 (2012)
K. Izumi, Y.C. Ong, JCAP 1306, 029 (2013)
C.-Q. Geng, Y.-P. Wu, JCAP 1304, 033 (2013)
F.I. Mikhail, Ain Shams Bull. 6, 87 (1962)
M.I. Wanas, Stud. Cercet. Stiin. Ser. Mat. 10, 297 (2011)
N.L. Youssef, W.A. Elsayed, Rep. Math. Phys. 2, 1 (2013)
J.W. Maluf, Annalen der Physik 525, 339 (2013)
W. El Hanafy, G.G.L. Nashed, Astrophys. Space Sci. 361, 68 (2016)
S.C. Ulhoa, E.P. Spaniol, IJMP D22, 1350069 (2013)
J.W. Maluf, J.F. da Rocha-neto, T.M.L. Toribio, K.H. Castello-Branco, Phys. Rev. D 65, 124001 (2002)
R.-X Miao, M. Li, Y.-G Miao, JCAP 11, 033 (2011)
G.W. Gibbons, M.J. Perry, C.N. Pope, Class. Quant. Grav. 22, 1503 (2005)
Acknowledgements
The authors would like to thank the referee for her/his useful comments which indeed improved the presentation of the paper, and also we would like to thank Prof. A. Awad for fruitful discussion. This work is partially supported by the Egyptian Ministry of Scientific Research under project No. 24-2-12.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
Funded by SCOAP3
About this article
Cite this article
Nashed, G.G.L., El Hanafy, W. Analytic rotating black-hole solutions in N-dimensional f(T) gravity. Eur. Phys. J. C 77, 90 (2017). https://doi.org/10.1140/epjc/s10052-017-4663-6
Received:
Accepted:
Published:
DOI: https://doi.org/10.1140/epjc/s10052-017-4663-6