Jet azimuthal angle correlations in the production of a Higgs boson pair plus two jets at hadron colliders

Abstract

Azimuthal angle correlations of two jets in the process $pp\rightarrow HHjj$ are studied. The loop induced $\mathcal {O}(\alpha _\mathrm{s}^4 \alpha _{}^2)$ gluon fusion (GF) sub-process and the $\mathcal {O}(\alpha _{}^4)$ weak boson fusion (WBF) sub-process are considered. The GF sub-process exhibits strong correlations in the azimuthal angles $\phi _{1,2}^{}$ of the two jets measured from the production plane of the Higgs boson pair and the difference between these two angles $\phi _1^{}-\phi _2^{}$, and a very small correlation in their sum $\phi _1^{}+\phi _2^{}$. Using a finite value for the mass of the loop running top quark in the amplitude is crucial for the correlations. The impact of a non-standard value for the triple Higgs self-coupling on the correlations is found small. The peak shifts of the azimuthal angle distributions reflect the magnitude of parity violation in the $gg\rightarrow HH$ amplitude and the dependence of the distributions on parity violating phases is analytically clarified. The normalised distributions and the peak positions of the correlations are stable against the variation of factorisation and renormalisation scales. The WBF sub-process also produces correlated distributions and it is found that they are not induced by the quantum effect of the intermediate weak bosons but mainly by a kinematic effect. This kinematic effect is a characteristic feature of the WBF sub-process and is not observed in the GF sub-process. It is found that the correlations are different in the GF and in the WBF sub-processes. As part of the process dependent information, they will be helpful in the analyses of the process $pp\rightarrow HHjj$ at the LHC.

1 Introduction

The discovery of a Higgs boson with a mass around 125 GeV in 2012 is the main discovery of Run I of the Large Hadron Collider (LHC) [1, 2]. The study of its properties has started and until now they are compatible with the standard model (SM) hypothesis [3,4,5]. To probe the mechanism of electroweak symmetry breaking [6,7,8,9] directly one would want to measure the triple Higgs self-coupling that is one of the key parameters of the scalar potential. This is one of the main goals of the future high-luminosity LHC and the future circular collider (FCC) in hadron–hadron mode, a potential 100 TeV proton–proton collider following the LHC at CERN (for reviews of the FCC physics potential, see Refs. [10, 11]). In this view the production of a pair of Higgs bosons needs to be observed and has been extensively studied over the last years [12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32] (see also Refs. [33,34,35] for studies at the FCC). The gluon fusion (GF) sub-process [36,37,38,39] and the weak boson fusion (WBF) sub-process [40, 36, 41, 42] are the two main sub-processes; see e.g. Ref. [43] for a review of SM studies. Both of the two sub-processes are sensitive to the triple Higgs self-coupling. In the WBF sub-process, we have access to the coupling between the two Higgs bosons and the two weak bosons, too. In Refs. [23, 30] studies using the production of a pair of Higgs bosons plus two hadronic jets has been conducted, using both the GF and the WBF sub-processes. The main advantage of the latter sub-process is the fact that the theoretical uncertainties are under control [19, 27], but the phenomenological studies suffer from the difficulty to separate the GF contributions from that of the WBF.

Azimuthal angle correlations of two jets produced together with heavy particles have been actively studied as a provider of important information as regards the heavy particles [44,45,46,47,48,49,50]. The correlations are induced by only a certain type of sub-processes, called vector boson fusion (VBF) sub-processes,¹ in which a heavy object is produced by a fusion of two vector bosons emitted from incoming two coloured particles. The correlations arise from the quantum effect of the two fusing intermediate vector bosons [42, 47].² A set of cuts on the rapidity $y_{1,2}^{}$ of the two jets, $y_2^{}< 0 < y_1^{}$ and $y_1^{}-y_2^{}\gtrsim 3$ and an upper cut on the transverse momentum $p_\mathrm{T}^{}$ of the two jets are therefore crucial for the two jets to show strong correlations if any, since they enhance contributions from VBF sub-processes [47]. These rapidity cuts are often called VBF cuts.

The azimuthal angle correlations of the two jets both in the GF sub-process and in the WBF sub-process of the single Higgs boson plus two jets production process $pp\rightarrow Hjj$ [42, 52, 44,45,46,47] are nowadays a common knowledge, have been studied in detail [53,54,55,56,57,58,59,60,61,62,63,64,65] and applied in many phenomenological studies. However, the azimuthal angle correlations of the two jets in the Higgs boson pair plus two jets production process $pp\rightarrow HHjj$ have not been studied thoroughly. To our knowledge, the correlations in the GF sub-process, which is an one-loop induced $\mathcal {O}(\alpha _\mathrm{s}^4 \alpha _{}^2)$ process at leading order (LO), have not been studied in the literature. One of the reasons may be that event generations are still challenging even with an advanced calculation technique. For the GF sub-process in the process $pp\rightarrow Hjj$, the approach of using the effective interactions between the Higgs boson and gluons is known to work quite well as long as the $p_\mathrm{T}^{}$ of the jets are small enough [66, 67]. The azimuthal angle correlation after the VBF cuts is also described correctly [67]. Therefore event generations can be easily performed with a tree-level event generator which implements the effective interactions. In contrast, for the GF sub-process in the process $pp\rightarrow HHjj$, the effective interaction approach is known not to work well in describing the distributions of several observables [23, 30]. It is naively expected that this observation is the same for the azimuthal angle correlations. The process $pp\rightarrow HHjj$ at LO with the exact one-loop amplitude has been calculated for the first time in Ref. [23] and subsequently phenomenology is studied in Ref. [30]. The fully automated event generation for one-loop induced processes is now available in MadGraph5_aMC@NLO [68, 69]. This achievement will activate further phenomenological studies of the process $pp\rightarrow HHjj$ including studies which use the azimuthal angle correlations. The azimuthal angle correlations of the two jets in the WBF sub-process, which is an $\mathcal {O}(\alpha _{}^4)$ process at LO, have been studied in [42]. There, only the azimuthal angle difference of the two jets is studied as an azimuthal angle observable.

Fig. 1

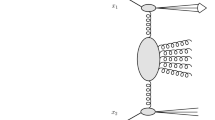
Feynman diagrams calculated in this paper. Here $V^*$ stands for either an off-shell weak boson W / Z or an off-shell gluon g. The second and third diagrams only contribute in the case $V=g$. The circles denote all the Feynman diagrams contributing to the process $V^*_{}V^*_{} \rightarrow HH$ at LO

In this paper, we study the azimuthal angle correlations of the two jets in the process $pp \rightarrow HHjj$. Instead of considering all of the sub-processes contributing to the process $pp \rightarrow HHjj$, we consider only the VBF sub-processes:

$$\begin{aligned}&qq \rightarrow qq V^*_{}V^*_{} \rightarrow qq HH\quad ( V = W, Z, g ), \end{aligned}$$

(1.1a)

$$\begin{aligned}&qg \rightarrow qg V^*_{}V^*_{} \rightarrow qg HH\quad ( V = g ), \end{aligned}$$

(1.1b)

$$\begin{aligned}&gg \rightarrow gg V^*_{}V^*_{} \rightarrow gg HH\quad ( V = g ), \end{aligned}$$

(1.1c)

where q denotes a light quark or a light antiquark, g denotes a gluon and $V^*_{}$ denotes an intermediate off-shell vector boson. The two Higgs bosons are produced by a fusion of two vector bosons emitted from incoming two coloured particles. More precisely, we calculate the amplitudes contributed from only t-channel Feynman diagrams shown in Fig. 1 ³ and obtain the approximate analytic cross section formula. We call them VBF amplitudes and VBF diagrams, respectively, in this paper. The circles denote all the Feynman diagrams contributing to the process $V^*_{}V^*_{} \rightarrow HH$ at LO. When the two virtual vector bosons are weak bosons (WBF sub-process), there are four tree-level Feynman diagrams. When the two virtual vector bosons are gluons (GF sub-process), there are eight one-loop Feynman diagrams in which heavy quarks run. We calculate these LO diagrams exactly.

Our calculations give not the exact LO results but approximate ones, since diagrams other than the VBF diagrams are not considered. In a kinematic region where the virtualities of the intermediate vector bosons are small (this is achieved by the VBF cuts and the $p_\mathrm{T}^{}$ upper cut), the VBF amplitudes dominate and thus our approximate analytic cross section gives a valid approximation to the exact LO result. We call it the VBF kinematic region. For the WBF sub-process, we explicitly compare our approximate result with the exact LO result and find good agreement between the two results. For the GF sub-process, in order to make our discussion clearer, we list the calculation methods which we discuss:

• Calc.1 Our approximate analytic cross section, to which only the VBF diagrams contribute. The mass of the loop running top quark $m_\mathrm{t}^{}$ in the $gg\rightarrow HH$ amplitude is set finite.

• Calc.2 Our approximate analytic cross section, to which only the VBF diagrams contribute. The mass of the loop running top quark $m_\mathrm{t}^{}$ in the $gg\rightarrow HH$ amplitude is set extremely large.

• Calc.3 The LO cross section, to which all LO diagrams contribute. The mass of the loop running top quark $m_\mathrm{t}^{}$ in the full amplitude is set extremely large.

• Calc.4 The LO cross section, to which all LO diagrams contribute. The mass of the loop running top quark $m_\mathrm{t}^{}$ in the full amplitude is set finite.

We note that the full amplitude in Calc.3 and Calc.4 contains contributions from diagrams with a triangle, box, pentagon or hexagon loop. Calc.3 is equivalent to the calculation that is performed by a tree-level event generator which implements the effective interactions between gluons and the Higgs bosons (we use MadGraph5_aMC@NLO [68] to generate the Calc.3 result). Calc.4 is the one that was performed in Ref. [23]. In the VBF kinematic region, we expect that Calc.1 reproduces the Calc.4 result and Calc.2 reproduces the Calc.3 result. In this paper, we compare the Calc.2 result with the Calc.3 result and find good agreement between the two results in the inclusive cross section and the azimuthal angle correlations. We do not perform Calc.4 and thus do not compare the Calc.1 result with the Calc.4 result. We stress that, if it is confirmed that Calc.2 reproduces the Calc.3 result, then we can be confident that Calc.1 is able to reproduce the Calc.4 result. This is because the dominance of the VBF amplitudes in the VBF kinematic region is solely due to the propagator factors of the intermediate gluons and the details of the core process $gg \rightarrow HH$ in Calc.1 and Calc.2, which are represented by the circles in Fig. 1, have nothing to do with the validity of the approximation. We mention that the validity of the approximation has been demonstrated in other processes, too. Ref. [47] studies the processes $pp\rightarrow \Phi jj$, where $\Phi = H, A, G$ denotes the Higgs boson, a parity-odd Higgs boson and a spin-2 massive graviton, respectively. In Ref. [50], the processes $pp\rightarrow Q\bar{Q}jj$, where Q denotes the top quark or the bottom quark, are studied. In the both studies, it has been shown that the approximate cross sections reproduce the exact LO results in the VBF kinematic region.

In order to measure the azimuthal angle correlations, we study four observables: $\phi _1^{}$, $\phi _2^{}$, $\Delta \phi = \phi _1^{} - \phi _2^{}$ and $\phi _+^{} = \phi _1^{} + \phi _2^{}$, where $\phi _{1,2}^{}$ are azimuthal angles of the two jets measured from the production plane of the Higgs boson pair ($\Delta \phi$ is irrelevant to the production plane as is clear from its definition). $\Delta \phi$ is the observable which is sensitive to the property of the Higgs boson in the process $pp\rightarrow Hjj$ [44,45,46,47, 49] and thus has been the subject of many studies. The processes $pp\rightarrow Gjj$ [47] and $pp\rightarrow Q\bar{Q}jj$ [50] exhibit strong correlations in $\phi _+^{}$. To our knowledge, correlations in $\phi _{1,2}^{}$ have not been addressed in any hadronic process in the literature. Our explicit findings can be summarised as follows. The GF sub-process has strong correlations in $\Delta \phi$ and $\phi _{1,2}^{}$, and the $p_\mathrm{T}^{}$ of the Higgs boson can be an useful measure to enhance or suppress these correlations. Using the finite $m_\mathrm{t}^{}$ value is important to produce the correlations correctly. Violation of the parity invariance of the $gg\rightarrow HH$ amplitude appears as the peak shifts of the correlations. The impact of a non-standard value for the triple Higgs self-coupling on the correlations is smaller than that on other observables, such as the invariant mass of the two Higgs bosons, of the inclusive process $pp\rightarrow HH$. The correlation in $\phi _+^{}$ is negligibly small in most every case. The normalised distributions of and the peak positions of the correlations are stable against scale variations in the parton distribution functions and the strong couplings. The WBF sub-process produces correlated distributions in all of the azimuthal angle observables and they are not induced by the quantum effect of the intermediate weak bosons but mainly by a kinematic effect. This kinematic effect is a characteristic feature of the WBF sub-process and is not observed in the GF sub-process. The impact of a non-standard value for the triple Higgs self-coupling on the correlations is not significant in the WBF sub-process, too. The correlations in the GF and WBF sub-processes are found to be different.

The paper is organised as follows. In Sect. 2, we perform a calculation of the VBF amplitudes. Since it can be shown that the azimuthal angle correlations arise from the interference of amplitudes with various helicities of the two intermediate vector bosons [42, 47], we employ a helicity amplitude technique. Our calculation is performed based on the method presented in Ref. [47]. A full analytic set of helicity amplitudes is presented. Since the material in Sect. 2 is rather technical, the reader who is interested in only the results may skip this section. In Sect. 3, a detailed study of the azimuthal angle correlations is presented. First, we discuss the GF sub-process in Sect. 3.1. The squared VBF amplitude for the four sub-processes Eq. (1.1) is given in a compact form. This analytic formula is found to be quite useful in making expectations of the correlations. The correlations in different kinematic regions of the two Higgs bosons and those in non-standard values for the Higgs triple self-coupling are studied. The impact of parity violation in the $gg\rightarrow HH$ amplitude on the correlations is also studied. Next, we discuss the WBF sub-process in Sect. 3.2. The squared VBF amplitude is given in a simple form by keeping only the dominant terms. The correlations in non-standard values for the Higgs triple self-coupling are studied. In Sect. 4 we summarise our findings and give some comments.

2 Helicity amplitudes for the process $\varvec{pp \rightarrow V^*_{}V^*_{}jj}$ $\varvec{\rightarrow HHjj}$

In this section we present a full analytic set of helicity amplitudes contributed from the vector boson fusion (VBF) diagrams. Our calculation is based on the method presented in Ref. [47]. We present a more complete discussion on the treatment of the intermediate off-shell gluons in the VBF diagrams. In addition, we discuss the importance of an appropriate choice of gauge-fixing vectors for the polarisation vectors of the external gluons. We believe that the above two remarks provide sufficient justification for repeating some of the calculations of Ref. [47].

2.1 VBF amplitudes

We first introduce a common set of kinematic variables

$$\begin{aligned}&a_1^{}\bigl (k_1^{}, \sigma _1^{}\bigr ) + a_2^{}\bigl (k_2^{}, \sigma _2^{}\bigr )\nonumber \\&\quad \rightarrow a_3^{}\bigl (k_3^{}, \sigma _3^{}\bigr ) + a_4^{}\bigl (k_4^{}, \sigma _4^{}\bigr ) + V_1^{}\bigl (q_1^{}, \lambda _1^{}\bigr ) + V_2^{}\bigl (q_2^{}, \lambda _2^{}\bigr ) \nonumber \\&\quad \rightarrow a_3^{}\bigl (k_3^{}, \sigma _3^{}\bigr ) + a_4^{}\bigl (k_4^{}, \sigma _4^{}\bigr ) + H\bigl (q_3^{}\bigr ) + H\bigl (q_4^{}\bigr ), \end{aligned}$$

(2.1)

where $a_{1,2,3,4}^{}$ can be quarks, antiquarks or gluons, $V_{1,2}^{}$ are intermediate off-shell vector bosons, H denotes the Higgs boson and the four-momentum $k_i^{}$ and helicity $\sigma _i^{}$ of each particle are shown. This assignment for the VBF sub-processes is more apparent in Fig. 2.

Fig. 2

The assignment of the four-momenta and helicities of each particle for the VBF sub-processes

The external particles take helicities $\sigma _i^{}=\pm 1$ ⁴ and the intermediate vector bosons take helicities $\lambda _i^{}=\pm 1, 0$. Colour indices are suppressed. The VBF helicity amplitude can be expressed as follows:

$$\begin{aligned} \mathcal{M}_{\sigma _1^{} \sigma _2^{}}^{\sigma _3^{} \sigma _4^{}}&= J_{V_1^{}a_1^{}a_3^{}}^{\mu _1^{\prime }}\bigl ( k_1^{}, k_3^{}; \sigma _1^{}, \sigma _3^{}\bigl ) J_{V_2^{}a_2^{}a_4^{}}^{\mu _2^{\prime }}\bigl ( k_2^{}, k_4^{}; \sigma _2^{}, \sigma _4^{}\bigl )\nonumber \\&\quad \times D_{\mu _1^{\prime }\mu _1^{}}^{V_1^{}}\bigl ( q_1^{} \bigr ) D_{\mu _2^{\prime }\mu _2^{}}^{V_2^{}}\bigl ( q_2^{} \bigr ) \Gamma ^{\mu _1^{}\mu _2^{}}_{HHV_1^{}V_2^{}}\bigl (q_1^{},q_2^{},q_3^{},q_4^{}\bigr ), \end{aligned}$$

(2.2)

where $J_{V_i^{}a_i^{}a_{i+2}^{}}^{\mu _i^{\prime }}( k_i^{}, k_{i+2}^{}; \sigma _i^{}, \sigma _{i+2}^{})$ is a current involving the off-shell vector boson $V_i^{}$ and the two external quarks, antiquarks or gluons, $D_{\mu _i^{\prime }\mu _i^{}}^{V_i^{}}( q_i^{})$ is the $V_i^{}$ propagator and $\Gamma ^{\mu _1^{}\mu _2^{}}_{HHV_1^{}V_2^{}}\bigl (q_1^{},q_2^{},q_3^{},q_4^{}\bigr )$ is the tensor amplitude for the process $V_1^{}V_2^{} \rightarrow HH$. When we denote a helicity amplitude in this paper, we show only helicity indices.

For the weak boson fusion (WBF) sub-process, we have $(V_1^{}, V_2^{})=(W^+_{}, W^-_{})$, $(W^-_{}, W^+_{})$ and (Z, Z), and only the VBF diagram shown in Fig. 1 (left) contributes to the VBF amplitude. The VBF amplitude is gauge invariant on its own. This is apparent from the fact that only the VBF diagram exists in some of the WBF sub-processes, for instance there are no other diagrams describing the sub-process $u d\rightarrow u d H H$. We choose the unitary gauge for the weak boson propagator,

$$\begin{aligned} D_{\mu _{}^{\prime }\mu }^{V}\bigl ( q \bigr )&= \biggl ( - g_{\mu _{}^{\prime }\mu }^{} + \frac{ q_{\mu _{}^{\prime }}^{} q_{\mu }^{} }{m_{V}^2} \biggr ) D_{V}^{}\bigl ( q \bigr ), \end{aligned}$$

(2.3a)

$$\begin{aligned} D_{V}^{}\bigl ( q \bigr )&= \bigl ( q_{}^2 - m_{V}^2 \bigr )^{-1}_{}. \end{aligned}$$

(2.3b)

We express the projector part of the above propagator in terms of polarisation vectors in the helicity basis $(\lambda =\pm 1, 0, s)$:

$$\begin{aligned} - g^{\mu _{}^{\prime }\mu }_{} + \frac{ q_{}^{\mu _{}^{\prime }} q_{}^{\mu } }{m_{V}^2}&= - g^{\mu _{}^{\prime }\mu }_{} + \frac{ q_{}^{\mu _{}^{\prime }} q_{}^{\mu } }{q_{}^2} \nonumber \\&\quad - \biggl ( 1 - \frac{q_{}^2}{m_{V}^2} \biggr ) \frac{ q_{}^{\mu _{}^{\prime }} }{ \sqrt{-q_{}^2} } \frac{ q_{}^{\mu } }{ \sqrt{-q_{}^2} } \nonumber \\&= \sum _{\lambda =\pm 1, 0} \bigl (-1\bigr )^{\lambda +1}_{} \epsilon ^{\mu _{}^{\prime }}_{}\bigl (q, \lambda \bigr )^*_{} \epsilon ^{\mu }_{}\bigl (q, \lambda \bigr )\nonumber \\&\quad - \biggl ( 1 - \frac{q_{}^2}{m_{V}^2} \biggr ) \epsilon ^{\mu _{}^{\prime }}_{}\bigl (q, \lambda =s \bigr )^*_{} \epsilon ^{\mu }_{}\bigl (q, \lambda =s \bigr ). \end{aligned}$$

(2.4)

The $\lambda =s$ component $\epsilon ^{\mu }_{}(q, \lambda =s) = q_{}^{\mu } / \sqrt{-q_{}^2}$ is the scalar part of a virtual weak boson and vanishes when it couples with a light quark current. As a result, the following replacement is possible when the external quarks are assumed to be massless:

$$\begin{aligned} - g^{\mu _{}^{\prime }\mu }_{} + \frac{ q_{}^{\mu _{}^{\prime }} q_{}^{\mu } }{m_{V}^2} \rightarrow \sum _{\lambda =\pm 1, 0} \bigl (-1\bigr )^{\lambda +1}_{} \epsilon ^{\mu _{}^{\prime }}_{}\bigl (q, \lambda \bigr )^*_{} \epsilon ^{\mu }_{}\bigl (q, \lambda \bigr ). \end{aligned}$$

(2.5)

The polarisation vectors $\epsilon ^{\mu }_{}(q_i^{}, \lambda _i^{}=\pm ,0)$ will be defined later once the kinematics of the weak bosons is fixed. After that, one can confirm Eq. (2.4) explicitly. By inserting the identity Eq. (2.5) into the VBF helicity amplitude in Eq. (2.2), it can be expressed as a product of three helicity amplitudes:

$$\begin{aligned} \mathcal{M}_{\sigma _1^{} \sigma _2^{}}^{\sigma _3^{} \sigma _4^{}}&= D_{V_1^{}}^{}\bigl ( q_1^{} \bigr ) D_{V_2^{}}^{}\bigl ( q_2^{} \bigr )\nonumber \\&\quad \times \sum _{\lambda _1^{}=\pm , 0} \sum _{\lambda _2^{}=\pm , 0} \bigl ( \mathcal{J}_{a_1^{}a_3^{}}^{V_1^{}} \bigr )_{\sigma _1^{} \sigma _3^{}}^{\lambda _1^{}} \bigl ( \mathcal{J}_{a_2^{}a_4^{}}^{V_2^{}} \bigr )_{\sigma _2^{} \sigma _4^{}}^{\lambda _2^{}} \bigl ( \mathcal{M}_{V_1^{}V_2^{}}^{HH} \bigr )_{\lambda _1^{} \lambda _2^{}}^{} \end{aligned}$$

(2.6)

with

$$\begin{aligned}&\bigl ( \mathcal{J}_{a_i^{}a_{i+2}^{}}^{V_i^{}} \bigr )_{\sigma _i^{} \sigma _{i+2}^{}}^{\lambda _i^{}} \nonumber \\&\quad = \bigl (-1\bigr )^{\lambda _i^{}+1}_{} J_{V_i^{}a_i^{}a_{i+2}^{}}^{\mu _i^{\prime }}\bigl ( k_i^{}, k_{i+2}^{}; \sigma _i^{}, \sigma _{i+2}^{}\bigl ) \epsilon _{\mu _i^{\prime }}^{}\bigl (q_i^{}, \lambda _i^{}\bigr )^*_{}, \end{aligned}$$

(2.7a)

$$\begin{aligned}&\bigl ( \mathcal{M}_{V_1^{}V_2^{}}^{HH} \bigr )_{\lambda _1^{} \lambda _2^{}}^{} \nonumber \\&\quad = \epsilon _{\mu _1^{}}^{}\bigl (q_1^{}, \lambda _1^{}\bigr ) \epsilon _{\mu _2^{}}^{}\bigl (q_2^{}, \lambda _2^{}\bigr ) \Gamma ^{\mu _1^{}\mu _2^{}}_{HHV_1^{}V_2^{}}\bigl (q_1^{},q_2^{},q_3^{},q_4^{}\bigr ). \end{aligned}$$

(2.7b)

Equation (2.7a) represents a helicity amplitude for the splitting process $a_i^{} \rightarrow a_{i+2}^{} V_i^{}$, where $V_i^{}$ is off-shell. This will be derived in Sect. 2.2. Equation (2.7b) represents a helicity amplitude for the process $V_1^{} V_2^{} \rightarrow HH$, where $V_1^{}$ and $V_2^{}$ are off-shell. This will be presented in Sect. 2.3.

The gluon fusion (GF) sub-process $(V_1^{}, V_2^{})=(g, g)$ is more complicated than the WBF sub-process. The VBF amplitude for the qq initiated sub-process $(a_1^{}, a_2^{})=(q, q)$ is gauge invariant on its own, the reason being the same as for the WBF amplitude. If we choose the Feynman–’t Hooft gauge for a gluon propagator, the projector part of the propagator is:

$$\begin{aligned} - g^{\mu _{}^{\prime }\mu }_{}&= - g^{\mu _{}^{\prime }\mu }_{} + \frac{ q_{}^{\mu _{}^{\prime }} q_{}^{\mu } }{q_{}^2} - \frac{ q_{}^{\mu _{}^{\prime }} }{ \sqrt{-q_{}^2} } \frac{ q_{}^{\mu } }{ \sqrt{-q_{}^2} } \nonumber \\&= \sum _{\lambda =\pm 1, 0} \bigl (-1\bigr )^{\lambda +1}_{} \epsilon ^{\mu _{}^{\prime }}_{}\bigl (q, \lambda \bigr )^*_{} \epsilon ^{\mu }_{}\bigl (q, \lambda \bigr )\nonumber \\&\quad \,\, - \epsilon ^{\mu _{}^{\prime }}_{}\bigl (q, \lambda =s \bigr )^*_{} \epsilon ^{\mu }_{}\bigl (q, \lambda =s \bigr ). \end{aligned}$$

(2.8)

The $\lambda =s$ component $\epsilon ^{\mu }_{}(q, \lambda =s) = q_{}^{\mu } / \sqrt{-q_{}^2}$ again vanishes when it couples with a quark current. As a result, the following replacement is possible without any approximation:

$$\begin{aligned} - g^{\mu _{}^{\prime }\mu }_{} \rightarrow \sum _{\lambda =\pm 1, 0} \bigl (-1\bigr )^{\lambda +1}_{} \epsilon ^{\mu _{}^{\prime }}_{}\bigl (q, \lambda \bigr )^*_{} \epsilon ^{\mu }_{}\bigl (q, \lambda \bigr ). \end{aligned}$$

(2.9)

Therefore, for the qq initiated sub-process, we can arrive at the same expression as in Eq. (2.6). In Ref. [47], the above procedure and thus the expression Eq. (2.6) is used not only for the qq initiated sub-process but also for the qg and gg initiated sub-processes $(a_1^{}, a_2^{})=(q, g), (g, g)$.⁵ We point out that this approach does not necessarily calculate the off-shell effects of the intermediate gluons correctly for the qg and gg initiated sub-processes and only introduces unnecessary complications in the amplitude calculation. Since the off-shell gluon amplitude $( \mathcal{M}_{gg}^{HH} )_{\lambda _1^{} \lambda _2^{}}^{}$ is not enhanced in the on-shell limit of the gluons, we can always expand the off-shell gluon amplitude around the on-shell limit. To make our discussion simpler, let us consider an amplitude which involves only one off-shell gluon. The off-shell gluon amplitude can be expanded as

$$\begin{aligned} \mathcal{M}_g^{}\bigl (Q \bigr )&= \mathcal{M}_g^{}\bigl (Q=0 \bigr ) + c_1^{} Q + c_2^{} Q^2_{} + \cdots , \nonumber \\ c_n^{}&= \frac{1}{n!}\frac{d^n_{} \mathcal{M}_g^{}\bigl (Q\bigr ) }{(dQ)^n_{}}\biggr |_{Q \rightarrow 0}^{}, \end{aligned}$$

(2.10)

where Q is the virtuality of the gluon and the first term in the right hand side (RHS) of the first equation is the on-shell amplitude, which is gauge invariant. As we will see in Sect. 2.2, the amplitude for the splitting process in Eq. (2.7a), where an off-shell gluon with virtuality Q is emitted, has an overall factor of Q. By considering this factor and $Q^{-2}$ in the propagator factor of the off-shell gluon, we find the following term in a VBF amplitude:

$$\begin{aligned} Q \times \frac{1}{Q^2_{}} \times \mathcal{M}_g^{}\bigl (Q \bigr ) = \frac{\mathcal{M}_g^{}\bigl (Q=0 \bigr )}{Q} + c_1^{} + c_2^{} Q + \cdots . \end{aligned}$$

(2.11)

While the first term in the RHS of the above equation is gauge invariant, the rest terms are generally dependent on a gauge-fixing choice for the off-shell gluon. As we have mentioned above, for the qq initiated sub-process, the VBF amplitude is gauge invariant on its own and hence not only the first term in the RHS of Eq. (2.11) but also the other terms as a whole are gauge invariant. This is not the case for the qg and gg initiated sub-processes. For the qg and gg initiated sub-processes, the second and higher terms in the RHS of Eq. (2.11), which are not enhanced in the on-shell limit, become gauge invariant only after contributions from other diagrams are also included. Therefore, in our method where only the VBF diagrams are calculated, we can calculate the off-shell effect of the intermediate gluons correctly only for the qq initiated sub-process. For the qg and gg initiated sub-processes, therefore, we take the following approach: Completely ignore the off-shell effect of the intermediate gluons and look at only a kinematic region where the virtualities of the gluons are small ($Q\rightarrow 0$). This is possible because the off-shell effect in the amplitude will not be essential as long as we look at the small virtuality region, as is clear from Eq. (2.11). The unitarity condition gives the following equation for a gluon propagator in its on-shell limit $q_{}^2 \rightarrow 0$:

$$\begin{aligned} D_{\mu _{}^{\prime }\mu }^{g}\bigl ( q \bigr )&= D_{g}^{}\bigl ( q \bigr ) \sum _{\lambda =\pm } \epsilon _{\mu _{}^{\prime }}^{}\bigl (q, \lambda \bigr )^*_{} \epsilon _{\mu }^{}\bigl (q, \lambda \bigr ), \end{aligned}$$

(2.12a)

$$\begin{aligned} D_{g}^{}\bigl ( q \bigr )&= \bigl ( q_{}^2 \bigr )^{-1}_{}. \end{aligned}$$

(2.12b)

By using this, we can express the VBF amplitude for the GF sub-process as a product of three helicity amplitudes in the same way that we do for the WBF sub-process and the qq initiated GF sub-process in Eq. (2.6). The differences from the qq initiated GF sub-process are (1) the $\lambda =0$ component $\epsilon ^{\mu }_{}(q, \lambda =0)$ in Eq. (2.6) is neglected, (2) the off-shell gluon amplitude $( \mathcal{M}_{V_1^{}V_2^{}}^{HH} )_{\lambda _1^{} \lambda _2^{}}^{}$ is replaced by the on-shell gluon amplitude in which $q_1^2 = 0$ and $q_2^2 = 0$. Note that these two approximations are nothing less than the two fundamental ingredients of the equivalent photon approximation (EPA) [71, 72]. As a rule of using the EPA, we should clarify the kinematic region where the approximated VBF amplitude is a good approximation to the exact VBF amplitude. For the process $pp \rightarrow HHjj$, it should be $-q_1^2 < \hat{s}$ and $-q_2^2 < \hat{s}$, where $\hat{s} =M_{HH}^2$. We use the EPA not only for the qg and gg initiated sub-processes but also for the qq initiated sub-process, so that we can consistently use the on-shell gluon amplitude $( \mathcal{M}_{V_1^{}V_2^{}}^{HH} )_{\lambda _1^{} \lambda _2^{}}^{}$. It should be noted that, while we use the on-shell gluon amplitude for the process $gg\rightarrow HH$, the amplitude for an off-shell gluon emission in Eq. (2.7a) is still calculated without ignoring the off-shell effect of the gluon ($q_{1,2}^2 \ne 0$), as in other applications of the EPA.

Fig. 3

The coordinate systems in the $q_1^{}$ Breit frame (left), the c.m. frame of the two colliding vector bosons (middle) and the $q_2^{}$ Breit frame (right). The y-axis points to us. The directions of the z-axis in the three coordinate systems are chosen common, so that the coordinate system in one of the frames can coincide with that in the other of the frames by a single boost along the z-axis

2.2 Helicity amplitudes for the splitting processes

We derive the helicity amplitude (2.7a) for the splitting processes. We use the chiral representation for Dirac matrices. Since we neglect the mass of the external quarks, the helicity of the quark is equal to its chirality and the helicity of the antiquark is opposite to its chirality. As a result, the helicity of $a_i^{}$ is always equal to that of $a_{i+2}^{}$ ($\sigma _i^{}=\sigma _{i+2}^{}$) for the quark and antiquark splitting processes. Otherwise, the amplitude vanishes. By introducing one common current $\hat{J}_i^{\mu }$, we can express the quark and antiquark currents $J_{V_i^{}a_i^{}a_{i+2}^{}}^{\mu }\bigl ( k_i^{}, k_{i+2}^{}; \sigma _i^{}, \sigma _{i+2}^{}\bigl )$ in a compact manner:

$$\begin{aligned} J_{V_i^{}a_i^{}a_{i+2}^{}}^{\mu } \bigl ( k_i^{}, k_{i+2}^{}; \sigma _i^{}, \sigma _{i+2}^{} \bigr )&= g_{\sigma _i^{}}^{V_i^{}a_i^{}a_{i+2}^{}} \hat{J}_i^{\mu } \bigl ( k_i^{}, k_{i+2}^{}; \sigma _i^{}, \sigma _{i+2}^{} \bigr ), \end{aligned}$$

(2.13a)

$$\begin{aligned} \hat{J}_i^{\mu } \bigl ( k_i^{}, k_{i+2}^{}; \sigma _i^{}, \sigma _{i+2}^{} \bigr )&= u^{\dagger }_{} \bigl ( k_{i+2}^{}, \sigma _{i+2}^{} \bigr )_{\alpha } \sigma ^{\mu }_{\alpha } \nonumber \\&\quad u\bigl (k_{i}^{}, \sigma _i^{}\bigr )_{\alpha }^{} \ \delta _{\sigma _i^{} \sigma _{i+2}^{}}^{} \ \delta _{\sigma _i^{} \alpha }^{} , \end{aligned}$$

(2.13b)

where $u(k,\sigma )_{\alpha }^{}$ represents the two-component Weyl u-spinor with its four-momentum k, helicity $\sigma$ and chirality $\alpha$ ($=\pm 1$), and $\sigma ^{\mu }_{\pm } = (1, \pm \vec {\sigma })$ with the Pauli matrices $\vec {\sigma }$. Note that we can use the above $\hat{J}_i^{\mu }$ for the antiquark current, too, since

$$\begin{aligned} v^{\dagger }_{}\bigl (k_{i}^{}, \sigma _i^{}\bigr )_{\alpha } \sigma ^{\mu }_{\alpha } v\bigl (k_{i+2}^{}, \sigma _{i+2}^{}\bigr )_{\alpha }^{}= u^{\dagger }_{}\bigl (k_{i+2}^{}, \sigma _{i+2}^{}\bigr )_{-\alpha } \sigma ^{\mu }_{-\alpha } u\bigl (k_{i}^{}, \sigma _i^{}\bigr )_{-\alpha }^{}. \end{aligned}$$

(2.14)

The couplings between quarks and vector bosons relevant to our study are summarised as follows:

$$\begin{aligned} g_{\pm }^{gqq}&= g_{\pm }^{g\bar{q}\bar{q}} = g_\mathrm{s}^{} t^{a}_{}, \nonumber \\ g_{-}^{W^+_{}ud}&= g_{+}^{W^+_{}\bar{d}\bar{u}} = \frac{g_\mathrm{w}^{}}{\sqrt{2}} \bigl ( V_{ud}^{} \bigr )^*_{}, \nonumber \\ g_{-}^{W^-_{}du}&= g_{+}^{W^-_{}\bar{u}\bar{d}} = \frac{g_\mathrm{w}^{}}{\sqrt{2}} V_{ud}^{}, \nonumber \\ g_{+}^{Zqq}&= g_{-}^{Z\bar{q}\bar{q}} = g_\mathrm{z}^{} \bigl ( - Q_q^{} \sin ^2{\theta _\mathrm{w}} \bigr ), \nonumber \\ g_{+}^{Z\bar{q}\bar{q}}&= g_{-}^{Zqq} = g_\mathrm{z}^{} \bigl ( T_{q}^3 - Q_q^{} \sin ^2{\theta _\mathrm{w}} \bigr ), \end{aligned}$$

(2.15)

where $g_\mathrm{s}^{}$ is the QCD coupling, $t^\mathrm{a}_{}$ is the generator of the SU(3) group, $g_\mathrm{w}^{} = e / \sin {\theta _\mathrm{w}^{}}$, $g_\mathrm{z}^{} = e /(\sin {\theta _w^{}}\cos {\theta _w^{}})$ with $\theta _\mathrm{w}^{}$ being the Weinberg mixing angle and e being the proton charge, $V_{ud}^{}$ is an element of the CKM matrix, $Q_q^{}$ is the electric charge of the quark in units of e, $T^3_u=1/2$ and $T^3_d=-1/2$. The gluon current involving three gluons is also expressed by Eq. (2.13a) with

$$\begin{aligned}&g^{ggg}_{\pm } = g_\mathrm{s}^{} f^{abc}_{}, \end{aligned}$$

(2.16a)

$$\begin{aligned}&\hat{J}_i^{\mu } \bigl ( k_i^{}, k_{i+2}^{}; \sigma _i^{}, \sigma _{i+2}^{} \bigr ) = \bigl ( k_i^{} + q_i^{} \bigr ) \cdot \epsilon ( k_{i+2}^{}, \sigma _{i+2}^{} )^*_{} \ \epsilon ^{\mu }_{}\bigl ( k_i^{}, \sigma _i^{} \bigr ) \nonumber \\&\quad + \bigl ( - q_i^{} + k_{i+2}^{} \bigr ) \cdot \epsilon \bigl ( k_{i}^{}, \sigma _{i}^{} \bigr ) \ \epsilon ^{\mu }\bigl ( k_{i+2}^{}, \sigma _{i+2}^{} \bigr )^*_{} \nonumber \\&\quad + \epsilon \bigl ( k_{i}^{}, \sigma _{i}^{} \bigr ) \cdot \epsilon \bigl ( k_{i+2}^{}, \sigma _{i+2}^{} \bigr )^*_{} \ \bigl ( - k_{i+2}^{} - k_i^{} \bigr )^{\mu }_{}, \end{aligned}$$

(2.16b)

where $f^{abc}_{}$ is the structure constant of the SU(3) group.

Generally speaking, helicities are frame dependent and so are helicity amplitudes. When we calculate the VBF helicity amplitude $\mathcal{M}_{\sigma _1^{} \sigma _2^{}}^{\sigma _3^{} \sigma _4^{}}$ in Eq. (2.6), we must choose one frame at first and then define the four-momenta and the helicities of all the external particles in this particular frame. For our calculation we choose the centre-of-mass (c.m.) frame of the two intermediate vector bosons moving along the z-axis, which is shown in the middle of Fig. 3. We call it the VBF frame. Note that the production plane of the two Higgs bosons coincides with the plane of the x–z axes. All of the three helicity amplitudes in the VBF helicity amplitude must be evaluated in the VBF frame. However, by using a property of helicities, we can justify a calculation of the helicity amplitude $( \mathcal{J}_{a_i^{}a_{i+2}^{}}^{V_i^{}} )_{\sigma _i^{} \sigma _{i+2}^{}}^{\lambda _i^{}}$ for the splitting processes in a different frame. Because the helicity of a massless quark is frame independent and furthermore the helicity of a massive vector boson is invariant under Lorentz boosts along its momentum direction as long as the boosts do not change the sign of its three-momentum,⁶ the helicity amplitude $( \mathcal{J}_{a_i^{}a_{i+2}^{}}^{V_i^{}})_{\sigma _i^{} \sigma _{i+2}^{}}^{\lambda _i^{}}$ for the quark splitting processes is invariant under Lorentz boosts along the z-axis from the VBF frame, as long as the boosts do not change the sign of the three-momentum of $V_i^{}$. By this property, it is justified to calculate the helicity amplitude $( \mathcal{J}_{a_1^{}a_{3}^{}}^{V_1^{}})_{\sigma _1^{} \sigma _{3}^{}}^{\lambda _1^{}}$ for the quark splitting process in the $q_1^{}$ Breit frame, to which $k_{1,3}^{}$ and $q_1^{}$ in the VBF frame can move by a single Lorentz boost along the negative direction of the z-axis. Similarly, it is justified to calculate the helicity amplitude $( \mathcal{J}_{a_2^{}a_{4}^{}}^{V_2^{}})_{\sigma _2^{} \sigma _{4}^{}}^{\lambda _2^{}}$ for the quark splitting process in the $q_2^{}$ Breit frame, to which $k_{2,4}^{}$ and $q_2^{}$ in the VBF frame can move by a single Lorentz boost along the positive direction of the z-axis. The $q_1^{}$ and $q_2^{}$ Breit frames are illustrated in the left and right of Fig. 3, respectively. A calculation of the helicity amplitude $( \mathcal{J}_{a_i^{}a_{i+2}^{}}^{V_i^{}})_{\sigma _i^{} \sigma _{i+2}^{}}^{\lambda _i^{}}$ for the gluon splitting process in the $q_i^{}$ Breit frame is also justified by appropriately choosing gauge-fixing vectors for the polarisation vectors of the external gluons. Although the helicity of a gluon is frame independent, the polarisation vectors of the gluon are dependent on their gauge-fixing vectors and hence the helicity amplitude for the gluon splitting process is in general frame dependent. However, if we choose the gauge-fixing vectors in a way that their directions are invariant under Lorentz boosts along the z-axis, the helicity amplitude for the gluon splitting process also becomes invariant under the same boosts, again as long as the boosts do not change the sign of the three-momentum of the intermediate off-shell gluon. This can be simply achieved by choosing all the gauge-fixing vectors along the z-axis.

We parametrise the four-momenta $k_1^{}$, $k_3^{}$ and $q_1^{}$ in the $q_1^{}$ Breit frame as

$$\begin{aligned} q_1^{\mu }&= k_1^{\mu } - k_3^{\mu } = \bigl ( 0, \ 0,\ 0,\ Q_1^{} \bigr ), \nonumber \\ k_1^{\mu }&= \frac{Q_1^{}}{2\cos {\theta _1^{}}} \bigl ( 1,\ \sin {\theta _1^{}} \cos {\phi _1^{}},\ \sin {\theta _1^{}} \sin {\phi _1^{}}, \ \cos {\theta _1^{}} \bigr ), \nonumber \\ k_3^{\mu }&= \frac{Q_1^{}}{2\cos {\theta _1^{}}} \bigl ( 1,\ \sin {\theta _1^{}} \cos {\phi _1^{}},\ \sin {\theta _1^{}} \sin {\phi _1^{}},\ - \cos {\theta _1^{}} \bigr ), \end{aligned}$$

(2.17)

where $Q_1^{} = \sqrt{- (q_1^{})^2_{}} > 0$, $0< \theta _1^{} < \pi /2$ and $0< \phi _1^{} < 2\pi$, and the four-momenta $k_2^{}$, $k_4^{}$ and $q_2^{}$ in the $q_2^{}$ Breit frame as

$$\begin{aligned} q_2^{\mu }&= k_2^{\mu } - k_4^{\mu } = \bigl ( 0, \ 0,\ 0,\ -Q_2^{} \bigr ), \nonumber \\ k_2^{\mu }&= -\frac{Q_2^{}}{2\cos {\theta _2^{}}} \bigl ( 1,\ \sin {\theta _2^{}} \cos {\phi _2^{}},\ \sin {\theta _2^{}} \sin {\phi _2^{}}, \ \cos {\theta _2^{}} \bigr ), \nonumber \\ k_4^{\mu }&= -\frac{Q_2^{}}{2\cos {\theta _2^{}}} \bigl ( 1,\ \sin {\theta _2^{}} \cos {\phi _2^{}},\ \sin {\theta _2^{}} \sin {\phi _2^{}},\ - \cos {\theta _2^{}} \bigr ), \end{aligned}$$

(2.18)

where $Q_2^{} = \sqrt{- (q_2^{})^2_{}} > 0$, $\pi /2< \theta _2^{} < \pi$ and $0< \phi _2^{} < 2\pi$. We define polarisation vectors for the intermediate vector boson $V_1^{}$ in the $q_1^{}$ Breit frame by

$$\begin{aligned} \epsilon ^{\mu }_{} \bigl ( q_1^{}, \lambda _1^{}= \pm \bigr )&= \frac{1}{\sqrt{2}} \bigl ( 0,\ - \lambda _1^{},\ -i,\ 0 \bigr ),\nonumber \\ \epsilon ^{\mu }_{} \bigl ( q_1^{}, \lambda _1^{}= 0 \bigr )&= \bigl ( 1,\ 0,\ 0,\ 0 \bigr ), \end{aligned}$$

(2.19)

and those for the intermediate vector boson $V_2^{}$ in the $q_2^{}$ Breit frame by

$$\begin{aligned} \epsilon ^{\mu }_{} \bigl ( q_2^{}, \lambda _2^{}= \pm \bigr )&= \frac{1}{\sqrt{2}} \bigl ( 0,\ - \lambda _2^{},\ i,\ 0 \bigr ),\nonumber \\ \epsilon ^{\mu }_{} \bigl ( q_2^{}, \lambda _2^{}= 0 \bigr )&= \bigl ( 1,\ 0,\ 0,\ 0 \bigr ). \end{aligned}$$

(2.20)

It is easy to explicitly confirm that the above sets of the polarisation vectors satisfy the identity for the propagator of a weak boson in Eq. (2.4). We use the same polarisation vectors $\epsilon ^{\mu }_{} ( q_i^{}, \lambda _i^{}= \pm )$ for the intermediate weak bosons ($V_i^{}=W, Z$) and gluons ($V_i^{}=g$). As a result, the $\lambda _i^{}=\pm$ helicity amplitudes $( \mathcal{J}_{a_i^{}a_{i+2}^{}}^{V_i^{}})_{\sigma _i^{} \sigma _{i+2}^{}}^{\pm }$ for a weak boson emission from a quark and those for a gluon emission from a quark are the same, except for couplings. (Let us recall that the $\lambda =0$ components of the intermediate gluons are neglected.)

As we have discussed above, the gauge-fixing vectors for polarisation vectors of the external gluons should be chosen along the z-axis. For the polarisation vectors of the two external gluons in the $q_1^{}$ Breit frame, we choose a common vector $n_1^{\mu } = ( 1, 0, 0, -1)$, i.e. the light-cone axial gauge. With this choice, the polarisation vectors in the $q_1^{}$ Breit frame are

$$\begin{aligned}&\epsilon ^{\mu }_{}( k_1^{}, \sigma _1^{} ) = \frac{-\sigma _1^{}}{\sqrt{1+\cos {\theta _1^{}}}}\nonumber \\&\quad \times \biggl ( \sin {\frac{\theta _1^{}}{2}} e^{i\sigma _1^{}\phi _1^{}}_{}, \ \cos {\frac{\theta _1^{}}{2}}, \ i \sigma _1^{} \cos {\frac{\theta _1^{}}{2}}, \ - \sin {\frac{\theta _1^{}}{2}} e^{i\sigma _1^{}\phi _1^{}}_{} \biggr ), \end{aligned}$$

(2.21a)

$$\begin{aligned}&\epsilon ^{\mu }_{}( k_3^{}, \sigma _3^{} ) = \frac{-\sigma _3^{}}{\sqrt{1-\cos {\theta _1^{}}}} \nonumber \\&\quad \times \biggl ( \cos {\frac{\theta _1^{}}{2}} e^{i\sigma _3^{}\phi _1^{}}_{}, \ \sin {\frac{\theta _1^{}}{2}}, \ i \sigma _3^{} \sin {\frac{\theta _1^{}}{2}}, \ - \cos {\frac{\theta _1^{}}{2}} e^{i\sigma _3^{}\phi _1^{}}_{} \biggr ). \end{aligned}$$

(2.21b)

Similarly, a vector $n_2^{\mu } = ( 1, 0, 0, 1)$ is commonly chosen for the polarisation vectors of the two external gluons in the $q_2^{}$ Breit frame, then the polarisation vectors in the $q_2^{}$ Breit frame are

$$\begin{aligned}&\epsilon ^{\mu }_{}( k_2^{}, \sigma _2^{} ) = \frac{\sigma _2^{}}{\sqrt{1-\cos {\theta _2^{}}}}\nonumber \\&\quad \times \biggl ( \cos {\frac{\theta _2^{}}{2}}, \ \sin {\frac{\theta _2^{}}{2}} e^{i\sigma _2^{}\phi _2^{}}_{}, \ -i \sigma _2^{} \sin {\frac{\theta _2^{}}{2}} e^{i\sigma _2^{}\phi _2^{}}_{}, \ \cos {\frac{\theta _2^{}}{2}} \biggr ), \end{aligned}$$

(2.22a)

$$\begin{aligned}&\epsilon ^{\mu }_{}( k_4^{}, \sigma _4^{} ) = \frac{\sigma _4^{}}{\sqrt{1+\cos {\theta _2^{}}}} \nonumber \\&\quad \times \biggl ( \sin {\frac{\theta _2^{}}{2}}, \ \cos {\frac{\theta _2^{}}{2}} e^{i\sigma _4^{}\phi _2^{}}_{}, \ -i \sigma _4^{} \cos {\frac{\theta _2^{}}{2}} e^{i\sigma _4^{}\phi _2^{}}_{}, \ \sin {\frac{\theta _2^{}}{2}} \biggr ). \end{aligned}$$

(2.22b)

It is easy to confirm that the above polarisation vectors with their gauge-fixing vectors satisfy the unitarity condition for an on-shell gluon:

$$\begin{aligned} -g^{\mu \nu }_{}+\frac{k^{\mu }_{} n^{\nu }_{} + n^{\mu }_{} k^{\nu }_{} }{k \cdot n} = \sum _{\sigma = \pm 1} \epsilon ^{\mu }_{}\bigl (k, \sigma \bigr )^*_{} \epsilon ^{\nu }_{}\bigl (k, \sigma \bigr ). \end{aligned}$$

(2.23)

With our preparations up to now, we can easily derive the helicity amplitude $( \mathcal{J}_{a_i^{}a_{i+2}^{}}^{V_i^{}})_{\sigma _i^{} \sigma _{i+2}^{}}^{\lambda _i^{}}$ for the quark splitting process and that for the gluon splitting process in the Breit frames. Following Ref. [47], we write the amplitudes as

$$\begin{aligned} \bigl ( \mathcal{J}_{a_i^{}a_{i+2}^{}}^{V_i^{}} \bigr )_{\sigma _i^{} \sigma _{i+2}^{}}^{\lambda _i^{}} = \sqrt{2}\ g_{\sigma _i^{}}^{V_i^{}a_i^{}a_{i+2}^{}}\ Q_i^{}\ \mathcal{\hat{J}}_{i\ \sigma _i^{} \sigma _{i+2}^{}}^{\ \lambda _i^{}}. \end{aligned}$$

(2.24)

The coupling factor is already defined in Eq. (2.13a). The common amplitude $\mathcal{\hat{J}}_{i\ \sigma _i^{} \sigma _{i+2}^{}}^{\ \lambda _i^{}}$ is summarised in Table 1. Note that we adopt the phase convention for the two-component Weyl spinors developed in refs. [73, 74]. Since we use the same phase convention for the spinors and the same gauge-fixing vectors for the external gluons with Ref. [47], the amplitudes in Table 1 are consistent with those in Tables 1 and 2 of Ref. [47] including the common overall phase.

Table 1 The helicity amplitudes $\mathcal{\hat{J}}_{i\ \sigma _i^{} \sigma _{i+2}^{}}^{\ \lambda _i^{}}$ defined in Eq. (2.24) in the $q_1^{}$ Breit frame (left row) and the $q_2^{}$ Breit frame (right row). The amplitudes of an off-shell vector boson (weak boson or gluon) emission from a quark are given in the upper part and those of an off-shell gluon emission from a gluon are given in the lower part

Table 2 Functions $F_i^{}[a_1^{}a_2^{}]$ in Eq. (3.1) for the qq initiated sub-process $(a_1^{}, a_2^{})=(q, q)$ (upper left), the qg initiated sub-process $(a_1^{}, a_2^{})=(q, g)$ (upper right), the gq initiated sub-process $(a_1^{}, a_2^{})=(g, q)$ (lower left) and the gg initiated sub-process $(a_1^{}, a_2^{})=(g, g)$ (lower right). $\theta _{1,2}^{}$ are defined in the $q_{1,2}^{}$ Breit frames Eqs. (2.17) and (2.18)

2.3 Helicity amplitudes for the processes $VV \rightarrow HH$

Finally we present the helicity amplitudes for the processes $V_1^{} V_2^{} \rightarrow HH$, $( \mathcal{M}_{V_1^{}V_2^{}}^{HH} )_{\lambda _1^{} \lambda _2^{}}^{}$ defined in Eq. (2.7b). As we have mentioned in Sect. 2.2, we evaluate the amplitudes in the VBF frame. We parametrise the four-momenta $q_1^{}$, $q_2^{}$, $q_3^{}$ and $q_4^{}$ in the VBF frame as

$$\begin{aligned} q_1^{\mu }&= \biggl ( \frac{1}{2\sqrt{\hat{s}}}\bigl (\hat{s} - Q_1^2 + Q_2^2\bigr ),\ 0,\ 0,\ \sqrt{\frac{1}{4\hat{s}}\bigl (\hat{s} - Q_1^2 + Q_2^2\bigr )^2_{} + Q_1^2}\ \biggr ), \nonumber \\ q_2^{\mu }&= \biggl ( \frac{1}{2\sqrt{\hat{s}}}\bigl (\hat{s} + Q_1^2 - Q_2^2\bigr ),\ 0,\ 0,\ -\sqrt{\frac{1}{4\hat{s}}\bigl (\hat{s} - Q_1^2 + Q_2^2\bigr )^2_{} + Q_1^2}\ \biggr ),\nonumber \\ q_3^{\mu }&= \frac{\sqrt{\hat{s}}}{2} \bigl (1,\ \beta \sin {\theta },\ 0,\ \beta \cos {\theta } \bigr ), \nonumber \\ q_4^{\mu }&= \frac{\sqrt{\hat{s}}}{2} \bigl (1,\ -\beta \sin {\theta },\ 0,\ -\beta \cos {\theta } \bigr ), \end{aligned}$$

(2.25)

where $\hat{s}$ is the c.m. energy squared $\hat{s}=(q_1^{}+q_2^{})^2_{}$ and $\beta = \sqrt{1-4m_\mathrm{H}^2/\hat{s}}$ with $m_\mathrm{H}^{}$ being the Higgs boson mass. The polarisation vectors for the vector bosons $V_{1,2}^{}$ in the VBF frame can be simply obtained by boosting those in the $q_{1,2}^{}$ Breit frames [Eqs. (2.19), (2.20)] to the VBF frame along the z-axis:

$$\begin{aligned} \epsilon ^{\mu }_{} \bigl ( q_1^{}, \lambda _1^{}= \pm \bigr )&= \frac{1}{\sqrt{2}} \bigl ( 0,\ - \lambda _1^{},\ -i,\ 0 \bigr ), \nonumber \\ \epsilon ^{\mu }_{} \bigl ( q_1^{}, \lambda _1^{}= 0 \bigr )&= \frac{1}{Q_1^{}} \bigl (\ q_1^3,\ 0,\ 0,\ q_1^0\ \bigr ), \end{aligned}$$

(2.26)

and

$$\begin{aligned} \epsilon ^{\mu }_{} \bigl ( q_2^{}, \lambda _2^{}= \pm \bigr )&= \frac{1}{\sqrt{2}} \bigl ( 0,\ - \lambda _2^{},\ i,\ 0 \bigr ),\nonumber \\ \epsilon ^{\mu }_{} \bigl ( q_2^{}, \lambda _2^{}= 0 \bigr )&= \frac{1}{Q_2^{}} \bigl (\ -q_2^3,\ 0,\ 0,\ -q_2^0\ \bigr ). \end{aligned}$$

(2.27)

Needless to say, the $\lambda _{1,2}^{} = \pm 1$ components remain the same after the boost. The helicity amplitude for the WBF process $V_1^{}V_2^{}\rightarrow HH$, where $(V_1^{}, V_2^{}) = (W^+_{}, W^-_{})$, $(W^-_{}, W^+_{})$ or (Z, Z), is given by [42]

$$\begin{aligned} \bigl ( \mathcal{M}_{V_1^{}V_2^{}}^{HH} \bigr )_{\lambda _1^{} \lambda _2^{}}^{}&= \frac{4}{\sqrt{2}} G_\mathrm{F}^{} m_{V_1^{}}^2 \epsilon ^{\mu _1^{}}_{}\bigl (q_1^{}, \lambda _1^{}\bigr ) \epsilon ^{\mu _2^{}}_{}\bigl (q_2^{}, \lambda _2^{}\bigr )\nonumber \\&\quad \times \biggl \{ g_{\mu _1^{}\mu _2^{}}^{} + 3 m_\mathrm{H}^2 \lambda _h^{} D_\mathrm{H}^{} \bigl ( q_1^{} + q_2^{} \bigr ) g_{\mu _1^{}\mu _2^{}}^{} \nonumber \\&\quad - 2 m_{V_1^{}}^2 \Bigl [ D_{\mu _1^{}\mu _2^{}}^{V_1^{}}\bigl ( q_1^{} - q_3^{} \bigr ) + D_{\mu _1^{}\mu _2^{}}^{V_1^{}}\bigl ( q_1^{} - q_4^{} \bigr ) \Bigr ] \biggr \}, \end{aligned}$$

(2.28)

where $G_\mathrm{F}^{}$ is the Fermi constant and $\lambda _h^{}$ is the factor re-scaling the triple Higgs self-coupling: $\lambda _{\mathrm{HHH}}^{}=\lambda _h^{} \lambda _{\mathrm{HHH}}^{\mathrm{SM}}$, where $\lambda _{\mathrm{HHH}}^{\mathrm{SM}}=3m_\mathrm{H}^2/v$ with $v^{-2}_{}=\sqrt{2}G_\mathrm{F}^{}$. The standard model predicts $\lambda _h^{}=1$. The notation for the propagators is defined in Eq. (2.3). By using the four-momenta and the polarisation vectors defined above, we can obtain the off-shell weak boson amplitude.

As we have discussed in Sect. 2.1, we use the on-shell gluon amplitude for the GF process $gg \rightarrow HH$. Using the notation given in the appendix of Ref. [39], we write the amplitude as

$$\begin{aligned} \bigl ( \mathcal{M}_{gg}^{HH} \bigr )_{\lambda _1^{} \lambda _2^{}}^{}&= \frac{G_\mathrm{F}^{}\alpha _\mathrm{s}^{} \hat{s} }{2\sqrt{2}\pi } \delta _{b_1^{} b_2^{}}^{} \epsilon ^{\mu _1^{}}_{}\bigl (q_1^{}, \lambda _1^{}\bigr ) \epsilon ^{\mu _2^{}}_{}\bigl (q_2^{}, \lambda _2^{}\bigr )\nonumber \\&\quad \times \biggl \{ \Bigl [ 3m_\mathrm{H}^2 \lambda _h^{} D_\mathrm{H}^{} \bigl ( q_1^{} + q_2^{} \bigr ) F_{\triangle }^{} + F_{\square } \Bigr ] A_{1 \mu _1^{} \mu _2^{}}^{}\nonumber \\&\quad + G_{\square }^{} A_{2 \mu _1^{} \mu _2^{}}^{} \biggr \}, \end{aligned}$$

(2.29)

where $b_{1,2}^{}$ are the colour indices of the gluons, and $F_{\triangle }^{}$, $F_{\square }^{}$ and $G_{\square }^{}$ are form factors [39] consisting of the scalar loop functions after tensor reduction and $A_{i \mu _1 \mu _2}$ are the tensor structures of the process. Not only we neglect the $\lambda _{1,2}^{}=0$ components of the gluons, but we also set $Q_1^{}=Q_2^{}=0$ in the four-momenta in Eq. (2.25). Our definitions of the polarisation vectors $\epsilon ^{\mu }_{} ( q_{i}^{}, \lambda _{i}^{}= \pm )$ in Eqs. (2.26) and (2.27) actually correspond to an axial gauge $n_{}^{\mu } = ( 1, 0, 0, -1)$ for an on-shell gluon $q_1^{\mu } \propto (1, 0, 0, 1)$ and to an axial gauge $n_{}^{\mu } = ( 1, 0, 0, 1)$ for an on-shell gluon $q_2^{\mu } \propto (1, 0, 0, -1)$, respectively.

In order to simplify further analyses, we introduce the following amplitude:

$$\begin{aligned} \mathcal{\hat{N}}_{i \lambda _1^{} \lambda _2^{} }^{} = \epsilon ^{\mu _1^{}}_{}\bigl (q_1^{}, \lambda _1^{}\bigr ) \epsilon ^{\mu _2^{}}_{}\bigl (q_2^{}, \lambda _2^{}\bigr ) A_{i \mu _1^{} \mu _2^{}}^{}. \end{aligned}$$

(2.30)

Then the amplitude Eq. (2.29) has a simpler form,

$$\begin{aligned} \bigl ( \mathcal{M}_{gg}^{HH} \bigr )_{\lambda _1^{} \lambda _2^{}}^{}&= \frac{G_\mathrm{F}^{}\alpha _\mathrm{s}^{} \hat{s} }{2\sqrt{2}\pi } \delta _{b_1^{} b_2^{}}^{} \biggl \{ \Bigl [ 3 m_\mathrm{H}^2 \lambda _h^{} D_\mathrm{H}^{} \bigl ( q_1^{} + q_2^{} \bigr ) F_{\triangle }^{}\nonumber \\&\quad + F_{\square } \Bigr ] \mathcal{\hat{N}}_{1 \lambda _1^{} \lambda _2^{} }^{} + G_{\square }^{} \mathcal{\hat{N}}_{2 \lambda _1^{} \lambda _2^{} }^{} \biggr \}. \end{aligned}$$

(2.31)

After a simple manipulation in the VBF frame, we find

$$\begin{aligned} \mathcal{\hat{N}}_{1 \lambda _1^{} \lambda _2^{} }^{}&= - \delta _{ \lambda _1^{}, \lambda _2^{} }^{}, \end{aligned}$$

(2.32a)

$$\begin{aligned} \mathcal{\hat{N}}_{2 \lambda _1^{} \lambda _2^{} }^{}&= - \delta _{ \lambda _1^{}, -\lambda _2^{} }^{}. \end{aligned}$$

(2.32b)

The parity invariance of the amplitude is apparent, $( \mathcal{M}_{gg}^{HH} )_{++}^{} = ( \mathcal{M}_{gg}^{HH} )_{--}^{}$ and $( \mathcal{M}_{gg}^{HH} )_{+-}^{} = ( \mathcal{M}_{gg}^{HH} )_{-+}^{}$. Up to now we have assumed the Higgs sector of the standard model. In this paper, we study the impact of parity symmetry violation in the GF process $gg\rightarrow HH$.⁷ We can read off parity violating phases from a parity-odd process $gg \rightarrow HA$, where A is a parity-odd Higgs boson. By using the tensor $A_{i \mu _1^{} \mu _2^{}}^{}$ for the process $gg \rightarrow HA$ [39], we find the amplitude in the VBF frame:

$$\begin{aligned} \mathcal{\hat{N}}_{1 \lambda _1^{} \lambda _2^{} }^{\text {P-odd}}&= - i \lambda _1^{} \delta _{ \lambda _1^{}, \lambda _2^{} }^{}, \end{aligned}$$

(2.33a)

$$\begin{aligned} \mathcal{\hat{N}}_{2 \lambda _1^{} \lambda _2^{} }^{\text {P-odd}}&= - i \lambda _1^{} \delta _{ \lambda _1^{}, -\lambda _2^{} }^{}. \end{aligned}$$

(2.33b)

In order to evaluate the impact of parity violation, we introduce two angles (or phases) $\xi _{1,2}^{}$ ($-\pi /2 \le \xi _{1,2}^{} \le \pi /2$) and write the amplitude as

$$\begin{aligned} \mathcal{\hat{N}}_{1 \lambda _1^{} \lambda _2^{} }^{}&= - \delta _{ \lambda _1^{}, \lambda _2^{} }^{} e^{+i \lambda _1^{} \xi _1^{}}_{}, \end{aligned}$$

(2.34a)

$$\begin{aligned} \mathcal{\hat{N}}_{2 \lambda _1^{} \lambda _2^{} }^{}&= - \delta _{ \lambda _1^{}, -\lambda _2^{} }^{} e^{+i \lambda _1^{} \xi _2^{}}_{}. \end{aligned}$$

(2.34b)

The two phases $\xi _{1,2}^{}$ parametrise the magnitude of parity violation in the process $gg \rightarrow HH$ and independently affect the $\Delta \lambda = \lambda _1^{} - \lambda _2^{} = 0$ helicity states and $\Delta \lambda = \pm 2$ helicity states, respectively. We believe that this simplified introduction of parity violating phases is enough for studying the impact of parity violation on the azimuthal angle correlations.

3 Azimuthal angle correlations

In this section we present a detailed study of the azimuthal angle correlations of the two jets by using the helicity amplitudes presented in Sect. 2.

3.1 The gluon fusion process

The azimuthal angle correlations of the two jets can be analytically apparent, once we obtain the squared VBF amplitude. There are four gluon fusion (GF) sub-processes $(V_1^{}, V_2^{})=(g, g)$, namely the qq initiated sub-process $(a_1^{}, a_2^{})=(q, q)$, the qg initiated sub-processes $(a_1^{}, a_2^{})=(q, g), (g, q)$ and the gg initiated sub-process $(a_1^{}, a_2^{})=(g, g)$. The squared VBF amplitude for the four GF sub-processes has the following compact form, after averaging over the initial state colours and helicities and summing over the final state colours and helicities:

$$\begin{aligned}&\overline{\sum _{\mathrm {col.}}}\ \overline{\sum _{\sigma _i^{}=\pm }} \bigl | \mathcal{M}_{\sigma _1^{} \sigma _2^{}}^{\sigma _3^{} \sigma _4^{}} \bigr |^2_{}\nonumber \\&\quad = \frac{( 4\pi \alpha _\mathrm{s})^2_{} C_{a_1^{}a_2^{}}^{} }{ Q_1^2 Q_2^2 } \overline{\sum _{b_1^{},b_2^{}}} \biggl \{ F_0^{}[a_1^{}a_2^{}] \Bigl ( |\hat{\mathcal{M}}_{++}^{}|^2_{}\nonumber \\&\qquad + |\hat{\mathcal{M}}_{+-}^{}|^2_{} + |\hat{\mathcal{M}}_{-+}^{}|^2_{} + |\hat{\mathcal{M}}_{--}^{}|^2_{} \Bigr ) \nonumber \\&\qquad - 2 F_1^{}[a_1^{}a_2^{}] \Bigl [ \mathrm{Re}\bigl ( \hat{\mathcal{M}}_{++}^{} \hat{\mathcal{M}}_{-+}^* \bigr ) + \mathrm{Re}\bigl ( \hat{\mathcal{M}}_{+-}^{} \hat{\mathcal{M}}_{--}^* \bigr ) \Bigr ] \cos {2\phi _1^{}} \nonumber \\&\qquad - 2 F_2^{}[a_1^{}a_2^{}] \Bigl [ \mathrm{Re}\bigl ( \hat{\mathcal{M}}_{+-}^{} \hat{\mathcal{M}}_{++}^* \bigr ) + \mathrm{Re}\bigl ( \hat{\mathcal{M}}_{--}^{} \hat{\mathcal{M}}_{-+}^* \bigr ) \Bigr ] \cos {2\phi _2^{}} \nonumber \\&\qquad + 2 F_3^{}[a_1^{}a_2^{}] \mathrm{Re}\bigl ( \hat{\mathcal{M}}_{++}^{} \hat{\mathcal{M}}_{--}^* \bigr ) \cos {2(\phi _1^{}-\phi _2^{})} \nonumber \\&\qquad + 2 F_3^{}[a_1^{}a_2^{}] \mathrm{Re}\bigl ( \hat{\mathcal{M}}_{+-}^{} \hat{\mathcal{M}}_{-+}^* \bigr ) \cos {2(\phi _1^{}+\phi _2^{})} \nonumber \\&\qquad + \bigl ( \mathrm{Re} \rightarrow \mathrm{Im}, \cos {} \rightarrow \sin {} \bigr ) \biggr \}. \end{aligned}$$

(3.1)

In order to simplify our writing, we introduce the notation $\hat{\mathcal{M}}_{\lambda _1^{} \lambda _2^{}}^{}$, which denotes the helicity amplitude $( \mathcal{M}_{gg}^{HH} )_{\lambda _1^{} \lambda _2^{}}^{}$. $C_{a_1^{} a_2^{}}^{}$ are the colour factors from the splitting processes $a_1^{} \rightarrow a_{3}^{} + g_1^*$ and $a_2^{} \rightarrow a_{4}^{} + g_2^*$, and they take values $C_{qq}^{} = 16/9$, $C_{qg}^{} = C_{gq}^{} = 4$ and $C_{gg}^{}=9$. $F_i^{}[a_1^{}a_2^{}]$ are functions of the kinematic variables $\theta _{1,2}^{}$ defined in the $q_{1,2}^{}$ Breit frames Eqs. (2.17) and (2.18), and summarised in Table 2. The azimuthal angles $\phi _{1,2}^{}$ are also defined in the Breit frames. $b_{1,2}^{}$ are the colour indices of the intermediate gluons and the average over $b_{1,2}^{}$ gives 1 / 8; see Eq. (2.29). The colour factors $C_{a_1^{} a_2^{}}^{}$ and the functions $F_i^{}[a_1^{}a_2^{}]$ for antiquarks are the same as those for quarks, since the QCD interaction does not distinguish quarks and antiquarks.

The first term in the right hand side (RHS) of Eq. (3.1) contributes to the inclusive cross section after a phase space integration, while the other terms give the azimuthal angle distributions of the two jets. The azimuthal angles $\phi _{1,2}^{}$ of the two jets are defined in the $q_{1,2}^{}$ Breit frames, respectively, and they remain the same in the VBF frame. In the limit that each of the two jets in the proton–proton (pp) frame is collinear to the incoming parton that emits it (collinear limit), the emitted two intermediate vector bosons also move on the z-axis. After rotating the two jets and the two Higgs bosons around the z-axis in such a way that the two Higgs bosons have zero azimuthal angle [Let us recall that the two Higgs bosons have zero azimuthal angle in the VBF frame; see Eq. (2.25)] and after a single boost along the z-axis, all of these particles can be studied in the VBF frame. Therefore, in the collinear limit, the azimuthal angles of the two jets after the single rotation around the z-axis are identical to $\phi _1^{}$ and $\phi _2^{}$. We apply the VBF cuts and an upper transverse momentum $p_\mathrm{T}^{}$ cut on the jets in the pp frame and these cuts reproduce the collinear limit to some extent. Hence the azimuthal angles of the two jets in the pp frame after the rotation around the z-axis should not be very different from $\phi _{1,2}^{}$ defined in the $q_{1,2}^{}$ Breit frames. We perform the rotation of the two jets and the two Higgs bosons around the z-axis in the following way:

• 1. Go to the centre-of-mass (c.m.) frame of the two Higgs bosons and then rotate the two Higgs bosons around the z-axis by $\tilde{\phi }$ in a way that the two Higgs bosons have zero azimuthal angle.

• 2. Rotate the two jets in the pp frame around the z-axis by $\tilde{\phi }$.

• 3. Measure the azimuthal angles of the two jets.

In the collinear limit, it is clear that the azimuthal angles of the two jets measured after this rotation coincide with $\phi _{1,2}^{}$. Note that this rotation is necessary for the azimuthal angles and the sum of them to show meaningful distributions, because the process $pp \rightarrow HHjj$ in the pp frame is completely symmetric around the z-axis. This rotation is, however, not needed for the difference of the two azimuthal angles. Before we show numerical results, we point out characteristic features of the GF sub-process in the standard model (SM) already expected from the analytic formula Eq. (3.1):

• The azimuthal angles of the two jets show the same distribution due to the parity invariance of the amplitude $\hat{\mathcal{M}}_{\lambda _1^{} \lambda _2^{}}^{}$; see Eq. (2.32).

• All of the azimuthal angle observables show cosine distributions, again due to the parity invariance of the amplitude.

Violation of the parity invariance of the amplitude should appear as a deviation from the above expectations. This case will be studied at the end of this subsection.

Fig. 4

The normalised differential cross section of the GF process as a function of $\phi _1^{}$ (upper left), $\phi _2^{}$ (upper right), $\Delta \phi$ (lower left) and $\phi _+^{}$ (lower right). The correspondence between curves and simulation methods is shown inside the upper left panel. The simulation methods are explained in text

We show numerical results for the 14 TeV LHC. We do not study decays of the two Higgs bosons and assume that they can be reconstructed. An outgoing quark, antiquark or gluon is identified as a jet. The following set of parameters are chosen: $m_\mathrm{H}^{}=125.5$ GeV, $m_\mathrm{t}^{}=173.5$ GeV and $\alpha _\mathrm{s}^{}(m_\mathrm{Z}^{})=0.13$. We use the CTEQ6L1 [75] set for the parton distribution functions (PDFs) and have chosen the input value for the strong coupling constant accordingly. For the factorisation scales in the PDFs, we choose a fixed value of 25 GeV, which corresponds to the lower cutoff on the transverse momentum $p_\mathrm{T}^{}$ of the jets (see below). The renormalisation scales in the strong couplings are chosen as $\alpha _\mathrm{s}^{}(\sqrt{\hat{s}})^2_{} \alpha _\mathrm{s}^{}(150 \mathrm {GeV})^2_{}$, where $\sqrt{\hat{s}}$ is the invariant mass of the two Higgs bosons. Using the two different scales in the strong couplings can be considered as a better choice, since we look at only a kinematic region where the virtualities of the gluons are small ($Q_{1,2}^{}\rightarrow 0$) and this separates the two splitting processes from the process $gg\rightarrow HH$ in time-scale. The renormalisation scales in the strong couplings of the splitting processes correspond to the upper cutoff on the $p_\mathrm{T}^{}$ of the jets. Different choices for the factorisation and renormalisation scales are also studied, when we discuss the uncertainties about scale choices. The following cuts are applied on the rapidity y and $p_\mathrm{T}^{}$ of the two jets in the pp frame:

$$\begin{aligned}&-5< y_2^{}< 0< y_1^{}< 5,\,\, y_1^{} - y_2^{} > 5,\nonumber \\&\quad 25\ \mathrm {GeV}< p_\mathrm{T}^{} < 150\ \mathrm {GeV}. \end{aligned}$$

(3.2)

The above rapidity cuts are the VBF cuts. As we have already mentioned in Sect. 1, the VBF cuts and the upper $p_\mathrm{T}^{}$ cut enhance the contributions from the VBF sub-processes. This can be understood as follows. The virtuality $Q_1^{}$ of the intermediate vector boson $V_1^{}$ is

$$\begin{aligned} Q_1^2&= - \bigl (k_1^{}-k_{3}^{}\bigr )^2_{} \nonumber \\&= 2 E_1^{} E_{3}^{} \bigl ( 1 - \cos {\theta _{13}^{}} \bigr ) \nonumber \\&= E_1^{} E_{3}^{} \theta _{13}^2 + \mathcal {O}( \theta _{13}^4 ), \end{aligned}$$

(3.3)

where the momentum assignment given in Eq. (2.1) is used and $\theta _{13}^{}$ is the angle between $\vec {k}_1^{}$ and $\vec {k}_{3}^{}$. The VBF cuts make $\vec {k}_{3}^{}$ collinear to $\vec {k}_1^{}$ ($\theta _{13}^{}\rightarrow 0$), then $Q_1^{}$ is decreased and the VBF amplitude is enhanced. The upper $p_\mathrm{T}^{}$ cut additionally enhances the VBF amplitude. In a collinear case ($\theta _{13}^{}\rightarrow 0$), the $p_\mathrm{T}^{}$ of $k_3^{}$ is

$$\begin{aligned} p_\mathrm{T}^2&= E_{3}^2 \sin ^2{\theta _{13}^{}} \nonumber \\&= E_{3}^2 \theta _{13}^2 + \mathcal {O}( \theta _{13}^4 ), \end{aligned}$$

(3.4)

so the upper $p_\mathrm{T}^{}$ cut reasonably implies the upper cut on $Q_1^{}$. Only the VBF cuts may be enough to enhance contributions from the VBF sub-processes. However, we need to impose the upper $p_\mathrm{T}^{}$ cut, too, because we perform the further two approximations in calculating the VBF amplitude for the GF sub-process and these approximations are justified only when $Q_1^2 < \hat{s}$ and $Q_2^2 < \hat{s}$ (see Sect. 2.1). Throughout our analyses, the four-momentum of the jet which has a positive rapidity $y_1^{}$ in the pp frame is used for calculating its azimuthal angle labelled $\phi _1^{}$ and that of the other jet which has a negative rapidity $y_2^{}$ in the pp frame is used for calculating its azimuthal angle labelled $\phi _2^{}$. Azimuthal angles labelled $\phi _{1,2}^{}$ in our numerical results shown below are not those defined in the $q_{1,2}^{}$ Breit frames anymore. The phase space integration and event generations are performed with the programs BASES and SPRING [76]. The scalar loop functions are calculated with the program FF [77].

We show the normalised differential cross section as a function of $\phi _1^{}$ (upper left), $\phi _2^{}$ (upper right), $\Delta \phi = \phi _1^{} - \phi _2^{}$ (lower left) and $\phi _+^{} = \phi _1^{} + \phi _2^{}$ (lower right) in Fig. 4 and the inclusive cross sections of qqHH, ggHH, qgHH final states and the sum of these final states in pp collisions in Table 3. The calculation methods are the following:

Table 3 The inclusive cross sections in units of femtobarn for various final states in pp collisions, produced by the three different methods which are the same as those used in Fig. 4 and explained in text. The statistical uncertainty for the last digit is shown in the parentheses

• Calc.1 Our approximate analytic cross section, to which only the VBF diagrams contribute. The mass of the loop running top quark in the $gg\rightarrow HH$ amplitude [$\hat{\mathcal{M}}_{\lambda _1^{} \lambda _2^{}}^{}$ in Eq. (3.1)] is set finite (173.5 GeV).

• Calc.2 Our approximate analytic cross section, to which only the VBF diagrams contribute. The mass of the loop running top quark in the $gg\rightarrow HH$ amplitude [$\hat{\mathcal{M}}_{\lambda _1^{} \lambda _2^{}}^{}$ in Eq. (3.1)] is set extremely large (14 TeV).

• Calc.3 The LO cross section, to which all LO diagrams contribute. The mass of the loop running top quark in the full amplitude is set extremely large.

• Calc.4 The LO cross section, to which all LO diagrams contribute. The mass of the loop running top quark in the full amplitude is set finite.

The above methods are already explained in Sect. 1. Although we do not perform Calc.4, it is listed above for the sake of our discussion. In Fig. 4, the blue solid curve, the red solid curve and the black dashed curve represent the Calc.1 result, the Calc.2 result and the Calc.3 result, respectively. Calc.3 is performed by implementing the following effective Lagrangian density [78] into an UFO file [79] with the help of FeynRule [80] version 1.6.18 and subsequently using the UFO file in MadGraph5_aMC@NLO[68] version 5.2.2.1:

$$\begin{aligned} \mathcal{L} = \frac{\alpha _\mathrm{s}^{}}{12\pi } \bigl (\sqrt{2}G_\mathrm{F}^{}\bigr )^{1/2}_{} F_{\mu \nu }^a F_{}^{a, \mu \nu }H - \frac{\alpha _\mathrm{s}^{}}{24\pi } \sqrt{2}G_\mathrm{F}^{} F_{\mu \nu }^a F_{}^{a, \mu \nu }HH, \end{aligned}$$

(3.5)

where $F_{\mu \nu }^a$ is the gluon field strength tensor and H is the Higgs boson field. The good agreement between the Calc.2 result and the Calc.3 result in all of the panels of Fig. 4 and in the inclusive cross sections of Table 3 (within 5%) shows that Calc.2 successfully reproduces the Calc.3 result. We stress that this observation indicates that Calc.1 is able to reproduce the Calc.4 result, for the following reason. Our approximate analytic cross section in Calc.1 and Calc.2 relies only on the fact that the VBF diagrams dominate in a kinematic region where the virtualities of the intermediate gluons are small [this kinematic region is achieved by the cuts in Eq. (3.2)]. This fact is solely due to the propagator factors of the intermediate gluons and the details of the core process $gg \rightarrow HH$ have nothing to do with the validity of the approximation. Therefore, once it is observed that Calc.2 reproduces the Calc.3 result, then we can be confident that Calc.1 is also able to reproduce the Calc.4 result. The large discrepancies between the Calc.1 result and the Calc.2 (or Calc.3) result in Fig. 4 and Table 3 show the importance of using a finite value for the mass $m_\mathrm{t}^{}$ of the loop running top quark in the amplitude. In Calc.4, the diagrams other than the VBF diagrams should also include some effects of finite $m_\mathrm{t}^{}$. However, only the VBF diagrams dominate, after all, in the kinematic region at which we are looking. Therefore, we are able to deny the possibility that the effects of finite $m_\mathrm{t}^{}$ we have found are washed out by some effects of finite $m_\mathrm{t}^{}$ existing in the diagrams other than the VBF diagrams.

Fig. 5

The differential cross section in units of femtobarn as a function of $\phi _{1,2}^{}$ (left), $\Delta \phi$ (middle) and $\phi _+^{}$ (right), contributed by different GF sub-processes. All of the sub-processes contribute to the black curve, the qg and gq initiated sub-processes to the blue curve, the gg initiated sub-process to the red curve and the qq initiated sub-process to the green curve

The reason why we do not find correlated distributions in $\phi _{1,2}^{}$ in the Calc.2 (or Calc.3) result can be understood from the squared VBF amplitude in Eq. (3.1). The second and third terms in the RHS shows that the correlations in $\phi _{1,2}^{}$ arise from the interference of the amplitudes $\hat{\mathcal{M}}_{\lambda _1^{} \lambda _2^{}}^{}$ for $\Delta \lambda = 0$ and $\Delta \lambda = \pm 2$ states, where $\Delta \lambda = \lambda _1^{}-\lambda _2^{}$. In the large $m_\mathrm{t}^{}$ limit, the amplitude for $\Delta \lambda = \pm 2$ states vanishes and hence the correlations also vanish. The GF sub-process exhibits the largest correlation in $\Delta \phi$ and an almost zero correlation in $\phi _+^{}$. The squared VBF amplitude in Eq. (3.1) tells us that the correlation in $\Delta \phi$ arises from the interference of the amplitudes $\hat{\mathcal{M}}_{\lambda _1^{} \lambda _2^{}}^{}$ for $\Delta \lambda = 0$ states (the fourth term in the RHS) and the correlation in $\phi _+^{}$ arises from the interference of the amplitudes for $\Delta \lambda = \pm 2$ states (the fifth term in the RHS). The reason of the large correlation in $\Delta \phi$ and the small correlation in $\phi _+^{}$ is because the amplitudes for $\Delta \lambda = 0$ states are much larger than those for $\Delta \lambda = \pm 2$ states in a large part of the phase space (this will be confirmed explicitly below soon). We briefly mention differences in the correlations between the processes $pp\rightarrow HHjj$ and $pp\rightarrow Hjj$. The process $gg\rightarrow H$ has non-zero amplitudes $\hat{\mathcal{M}}_{\lambda _1^{} \lambda _2^{}}^{}$ only for $\Delta \lambda = 0$ states. Therefore, the process $pp\rightarrow Hjj$ exhibits a large correlation in $\Delta \phi$ [44,45,46,47] but no correlations in $\phi _{1,2}^{}$ and $\phi _+^{}$.

Fig. 6

Left: the differential cross sections of the GF sub-process in units of femtobarn as a function of $\Delta \phi$, with different factorisation scales. The renormalisation scales are fixed to our default choice. The solid curve shows the result for our default choice and $\triangledown$, $\diamond$ and $\times$ points give the $\alpha =1$, $\alpha =2$ and $\alpha =1/2$ results in Eq. (3.6), respectively. The ratios with respect to the solid curve result are shown in the lower part. Right: the differential cross sections of the GF sub-process in units of femtobarn as a function of $\Delta \phi$, with different renormalisation scales. The factorisation scales are fixed to our default value. The solid curve shows the result for our default choice and $\triangledown$, $\diamond$ and $\times$ points give the $\beta =1$, $\beta =2$ and $\beta =1/2$ results in Eq. (3.7), respectively. The ratios with respect to the solid curve result are shown in the lower part

In Fig. 5 we show the differential cross section as a function of $\phi _{1,2}^{}$ (left), $\Delta \phi = \phi _1^{} - \phi _2^{}$ (middle) and $\phi _+^{} = \phi _1^{} + \phi _2^{}$ (right), contributed by all of the sub-processes (black curve, labelled (1) pp), by the qg and gq initiated sub-processes (blue curve, labelled (2) $qg+gq$), by the gg initiated sub-process (red curve, labelled (3) gg) and by the qq initiated sub-process (green curve, labelled (4) qq). Calc.1 is used to produce all of the numerical results hereafter in this subsection. As we have already discussed before showing the numerical results and have actually confirmed in Fig. 4, $\phi _1^{}$ and $\phi _2^{}$ show the same distribution due to the parity invariance of the amplitude in the SM. Therefore, we show only the $\phi _1^{}$ distribution and label it $\phi _{1,2}^{}$ instead of showing the two distributions, until we study parity violation.

Fig. 7

List plots of $CR_{2\phi _{1,2}^{}}^{}$ (left), $CR_{2\Delta \phi }^{}$ (middle) and $CR_{2\phi _+^{}}^{}$ (right) defined in Eq. (3.8) with the $p_\mathrm{T}^{}$ of the Higgs boson (in GeV) in the c.m. frame of the two Higgs bosons

We now study the uncertainties stemming from the choice of the factorisation scales in the PDFs and the renormalisation scales in the strong couplings. We set the notations for the factorisation scales as follows: $\mu _{F 1}^{}$ denotes the factorisation scale in the PDF of the proton that moves along the positive direction of the z-axis, $\mu _{F 2}^{}$ denotes that in the PDF of the proton that moves along the negative direction of the z-axis. Let us remind that our default setting is $\mu _{F 1}^{}=\mu _{F 2}^{}=25$ GeV. We write $\mu _{F 1,2}^{}$ as

$$\begin{aligned} \mu _{F 1}^{} = \alpha \times p_{T 1}^{},\ \ \mu _{F 2}^{} = \alpha \times p_{T 2}^{}, \end{aligned}$$

(3.6)

where $p_{\mathrm{T} 1}^{}$ is the $p_\mathrm{T}^{}$ of the jet with a positive rapidity, $p_{\mathrm{T} 2}^{}$ is the $p_\mathrm{T}^{}$ of the jet with a negative rapidity, and $\alpha$ is a constant factor. We use the following expression for the renormalisation scales in the strong couplings, $\alpha _\mathrm{s}^{}(\mu _{gg\rightarrow HH}^{})^2_{} \alpha _\mathrm{s}^{}(\mu _{R 1}^{}) \alpha _\mathrm{s}^{}(\mu _{R 2}^{})$:

$$\begin{aligned} \mu _{gg\rightarrow HH}^{} = \beta \times \sqrt{\hat{s}},\ \ \mu _{\mathrm{R} 1}^{} = \beta \times p_{\mathrm{T} 1}^{},\ \ \mu _{\mathrm{R} 2}^{} = \beta \times p_{\mathrm{T} 2}^{}, \end{aligned}$$

(3.7)

where $\beta$ is a constant factor. Let us remind that out default setting is $\mu _{gg\rightarrow HH}^{} = \sqrt{\hat{s}}$, $\mu _{\mathrm{R} 1}^{}=\mu _{\mathrm{R} 2}^{}=150$ GeV. In the left panel of Fig. 6, we show the differential cross sections as a function of $\Delta \phi$, with different $\alpha$ values. The renormalisation scales are fixed to our default choice. The solid curve shows the result for our default choice and $\triangledown$, $\diamond$ and $\times$ points give the $\alpha =1$, $\alpha =2$, $\alpha =1/2$ results, respectively. In the right panel of Fig. 6, we show the differential cross sections as a function of $\Delta \phi$, with different $\beta$ values. The factorisation scales $\mu _{F 1,2}^{}$ are fixed to our default choice. The solid curve shows the result for our default choice and $\triangledown$, $\diamond$ and $\times$ points give the $\beta =1$, $\beta =2$, $\beta =1/2$ results, respectively. The ratios with respect to the solid curve result are shown in the lower part of each panel. The panels show the large differences between the different scale choice results in the differential cross section. This is due to the fact that the scale dependence in the inclusive cross section is large. Nevertheless, the important observation is that the ratios with respect to the calculation with our default choice of scales are almost flat, as shown in the lower part of each panel. This means that the normalised differential cross section is robust against the scale variations and the correlation in $\Delta \phi$ is not washed out by this theoretical uncertainty. We note that the same is confirmed for the other observables $\phi _{1,2}^{}$ and $\phi _+^{}$, too.

Fig. 8

The normalised differential cross section of the GF process as a function of $\phi _{1,2}^{}$ (left), $\Delta \phi$ (middle) and $\phi _+^{}$ (right), with three different values for lower cutoff on $p_\mathrm{T}^{}$ of the Higgs boson in the c.m. frame of the two Higgs bosons. The correspondence between the curves and the cutoff values is shown inside the left panel

In order to study how the azimuthal angle correlations depend on the kinematics of the two Higgs bosons, we introduce the following three quantities:

$$\begin{aligned} \mathrm{CR}_{2\phi _{1,2}^{}}^{} = - 2 \frac{ \mathrm{Re}\bigl ( \hat{\mathcal{M}}_{++}^{} \hat{\mathcal{M}}_{-+}^* \bigr ) + \mathrm{Re}\bigl ( \hat{\mathcal{M}}_{+-}^{} \hat{\mathcal{M}}_{--}^* \bigr ) }{ |\hat{\mathcal{M}}_{++}^{}|^2_{} + |\hat{\mathcal{M}}_{+-}^{}|^2_{} + |\hat{\mathcal{M}}_{-+}^{}|^2_{} + |\hat{\mathcal{M}}_{--}^{}|^2_{} }, \end{aligned}$$

(3.8a)

$$\begin{aligned} \mathrm{CR}_{2\Delta \phi }^{} = +2 \frac{ \mathrm{Re}\bigl ( \hat{\mathcal{M}}_{++}^{} \hat{\mathcal{M}}_{--}^* \bigr ) }{ |\hat{\mathcal{M}}_{++}^{}|^2_{} + |\hat{\mathcal{M}}_{+-}^{}|^2_{} + |\hat{\mathcal{M}}_{-+}^{}|^2_{} + |\hat{\mathcal{M}}_{--}^{}|^2_{} }, \end{aligned}$$

(3.8b)

$$\begin{aligned} \mathrm{CR}_{2\phi _+^{}}^{} = +2 \frac{ \mathrm{Re}\bigl ( \hat{\mathcal{M}}_{+-}^{} \hat{\mathcal{M}}_{-+}^* \bigr ) }{ |\hat{\mathcal{M}}_{++}^{}|^2_{} + |\hat{\mathcal{M}}_{+-}^{}|^2_{} + |\hat{\mathcal{M}}_{-+}^{}|^2_{} + |\hat{\mathcal{M}}_{--}^{}|^2_{} }. \end{aligned}$$

(3.8c)

These are simply the coefficients of the azimuthal angle dependent terms divided by the coefficient of the azimuthal angle independent term in Eq. (3.1). Although the functions $F_i^{}[a_1^{}a_2^{}]$ are omitted, these quantities are useful in that an azimuthal angle observable should show a strong correlation in a kinematic region where the corresponding quantity $CR_i^{}$ is enhanced. We find that all of the quantities $CR_i^{}$ are well correlated with the $p_\mathrm{T}^{}$ of the Higgs boson in the c.m. frame of the two Higgs bosons, as shown in Fig. 7. Figure 7 presents list plots of $CR_{2\phi _{1,2}^{}}^{}$ (left), $CR_{2\Delta \phi }^{}$ (middle) and $CR_{2\phi _+^{}}^{}$ (right) with the $p_\mathrm{T}^{}$ of the Higgs boson in the c.m. frame of the two Higgs bosons. The large value of $CR_{2\Delta \phi }^{}$ and the small value of $CR_{2\phi _+^{}}^{}$ in the most part of the phase space explain the large correlation in $\Delta \phi$ and the small correlation in $\phi _+^{}$ observed in Fig. 4. The plots indicate that the correlation in $\Delta \phi$ is enhanced as the $p_\mathrm{T}^{}$ of the Higgs boson is decreased, while the correlations in $\phi _{1,2}^{}$ and $\phi _+^{}$ are enhanced as the $p_\mathrm{T}^{}$ of the Higgs boson is increased. This is confirmed in Fig. 8. In Fig. 8, we show the normalised differential cross section as a function of $\phi _{1,2}^{}$ (left), $\Delta \phi = \phi _1^{} - \phi _2^{}$ (middle) and $\phi _+^{} = \phi _1^{} + \phi _2^{}$ (right) with different values for the lower cutoff on the $p_\mathrm{T}^{}$ of the Higgs boson in the c.m. frame of the two Higgs bosons, blue solid curve: $p_T^{}>0$ GeV (no cut), black dashed curve: $p_T^{}>150$ GeV, and red solid curve: $p_\mathrm{T}^{}>250$ GeV.

Next, we study how the azimuthal angle correlations depend on the triple Higgs self-coupling. Equations (2.31) and (2.32) tell us that $\lambda _h^{}$, which is the factor re-scaling the triple Higgs self-coupling, affects only the amplitude $\hat{\mathcal{M}}_{\lambda _1^{} \lambda _2^{}}^{}$ for $\Delta \lambda = 0$ states. However, as is clear from the quantities in Eq. (3.8), $\lambda _h^{}$ affects all of the correlations. For an extreme example, if we could make the amplitude for $\Delta \lambda = 0$ states to be identically zero (this is actually not possible because the amplitude depend not only on $\lambda _h^{}$ but also on the kinematic of the process $gg\rightarrow HH$), we would observe a large correlation only in $\phi _+^{}$. In Fig. 9, we study the correlations with three different values for $\lambda _h^{}$, the blue solid curve: $\lambda _h^{}=0$, the black dashed curve: $\lambda _\mathrm{h}^{}=1$ (the SM prediction), and the red solid curve: $\lambda _\mathrm{h}^{}=2$. The impact of a non-standard value for $\lambda _\mathrm{h}^{}$ ($\lambda _\mathrm{h}^{}\ne 1$) in the distributions is visible but not large. Actually this is much smaller than that in other observables, such as the $p_\mathrm{T}^{}$ of the Higgs boson [18, 19] or the invariant mass of the two Higgs bosons [19, 22], of the inclusive process $pp\rightarrow HH$. The azimuthal angle correlations may not be useful to probe $\lambda _h^{}$.

Fig. 9

The normalised differential cross section of the GF process as a function of $\phi _{1,2}^{}$ (left), $\Delta \phi$ (middle) and $\phi _+^{}$ (right), with three different values for the triple Higgs self-coupling re-scaling factor $\lambda _h^{}$. The correspondence between the curves and the values for $\lambda _h^{}$ is shown inside the left panel

Fig. 10

The normalised differential cross section of the GF process as a function of $\phi _{1}^{}$ (left column), $\phi _{2}^{}$ (middle column) and $\Delta \phi$ (right column), with different values for the parity violating phases $\xi _{1,2}^{}$. In all of the panels, the SM prediction is shown by the black dashed curve. The correspondence between the curves and values for $\xi _{1,2}^{}$ is shown inside each panel. A cutoff on the $p_\mathrm{T}^{}$ of the Higgs boson $p_T^{}>200$ GeV is imposed in the $\phi _{1}^{}$ and $\phi _{2}^{}$ panels. Each row has the same set of the parity violating phases

Finally, we study the impact of parity symmetry violation on the azimuthal angle correlations. Let us remind that we have introduced two phases $\xi _{1,2}^{}$ in Eq. (2.34) and these phases parametrise the magnitude of parity violation in the process $gg\rightarrow HH$. If they are non-zero, the $gg\rightarrow HH$ amplitude $\hat{\mathcal{M}}_{\lambda _1^{} \lambda _2^{}}^{}$ is not parity invariant anymore: $\hat{\mathcal{M}}_{++}^{} \ne \hat{\mathcal{M}}_{--}^{}$ if $\xi _1^{}\ne 0$, $\hat{\mathcal{M}}_{+-}^{} \ne \hat{\mathcal{M}}_{-+}^{}$ if $\xi _2^{}\ne 0$. The squared VBF amplitude Eq. (3.1) tells us that violation of the parity invariance of the amplitude appears as the following deviations from the standard model predictions: (1) the $\phi _1^{}$ and $\phi _2^{}$ distributions are not necessarily equal to each other, (2) the azimuthal angle observables do not necessarily show cosine distributions. In order to make these expectations more explicit, we write the amplitude $\hat{\mathcal{M}}_{\lambda _1^{} \lambda _2^{}}^{}$ with the phases $\xi _{1,2}^{}$ in the following way:

$$\begin{aligned} \hat{\mathcal{M}}_{\lambda , \lambda }^{}&= A\ e^{+i \lambda \xi _1^{}}_{}, \end{aligned}$$

(3.9)

$$\begin{aligned} \hat{\mathcal{M}}_{\lambda , -\lambda }^{}&= B\ e^{+i \lambda \xi _2^{}}_{}. \end{aligned}$$

(3.10)

These are simply obtained by putting Eq. (2.34) into the amplitude in Eq. (2.31) and substituting the terms including the form factors with A and B. By inserting the above amplitudes into the azimuthal angle dependent terms in Eq. (3.1), each term becomes

$$\begin{aligned} -2 \bigl [&\mathrm{Re}\bigl ( \hat{\mathcal{M}}_{++}^{} \hat{\mathcal{M}}_{-+}^* \bigr ) + \mathrm{Re}\bigl ( \hat{\mathcal{M}}_{+-}^{} \hat{\mathcal{M}}_{--}^* \bigr ) \bigr ] \cos {2\phi _1^{}}\nonumber \\&\qquad + ( \mathrm{Re} \rightarrow \mathrm{Im}, \cos {} \rightarrow \sin {} ) \nonumber \\&\quad = -2\bigl ( AB^*_{} + A^*_{}B \bigr ) \cos {(2\phi _1^{} - \xi _1^{} - \xi _2^{})}, \end{aligned}$$

(3.11a)

$$\begin{aligned} \nonumber \\ - 2 \bigl [&\mathrm{Re}\bigl ( \hat{\mathcal{M}}_{+-}^{} \hat{\mathcal{M}}_{++}^* \bigr ) + \mathrm{Re}\bigl ( \hat{\mathcal{M}}_{--}^{} \hat{\mathcal{M}}_{-+}^* \bigr ) \bigr ]\cos {2\phi _2^{}}\nonumber \\&\qquad + ( \mathrm{Re} \rightarrow \mathrm{Im}, \cos {} \rightarrow \sin {} ) \nonumber \\&\quad = -2\bigl ( AB^*_{} + A^*_{}B \bigr ) \cos {(2\phi _2^{} + \xi _1^{} - \xi _2^{})}, \end{aligned}$$

(3.11b)

$$\begin{aligned} \nonumber \\ 2 \mathrm{Re}&\bigl ( \hat{\mathcal{M}}_{++}^{} \hat{\mathcal{M}}_{--}^* \bigr ) \cos {2(\phi _1^{}-\phi _2^{})} + ( \mathrm{Re} \rightarrow \mathrm{Im}, \cos {} \rightarrow \sin {} )\nonumber \\&\quad = 2 |A|^2_{} \cos {2(\phi _1^{}-\phi _2^{}-\xi _1^{})}, \end{aligned}$$

(3.11c)

$$\begin{aligned} 2 \mathrm{Re}&\bigl ( \hat{\mathcal{M}}_{+-}^{} \hat{\mathcal{M}}_{-+}^* \bigr ) \cos {2(\phi _1^{}+\phi _2^{})} + ( \mathrm{Re} \rightarrow \mathrm{Im}, \cos {} \rightarrow \sin {} ) \nonumber \\&\quad = 2 |B|^2_{} \cos {2(\phi _1^{}+\phi _2^{}-\xi _2^{})}. \end{aligned}$$

(3.11d)

These results show that parity violation appears as peak shifts of the azimuthal angle distributions. The results also tell us an important fact that the peak shifts of the distributions reflect only the magnitude of parity violation (recall that $\xi _{1,2}^{}$ parametrise the magnitude of parity violation in our study). It is an easy exercise to confirm that this is true no matter how parity violating phases are introduced. From the above analytic results, it is also apparent how each observable depends on the phases $\xi _{1,2}^{}$. $\Delta \phi$ is sensitive to $\xi _{1}^{}$ and $\phi _+^{}$ is sensitive to $\xi _{2}^{}$. $\phi _{1}^{}$ and $\phi _{2}^{}$ are sensitive to both $\xi _{1}^{}$ and $\xi _{2}^{}$. Although we are far less likely to be able to measure $\xi _{2}^{}$ in the $\phi _+^{}$ distribution because of the very small correlation in $\phi _+^{}$, we may use $\phi _{1}^{}$ and $\phi _{2}^{}$ to probe $\xi _{2}^{}$ instead.

Fig. 11

The differential cross sections of the GF sub-process in units of femtobarn as a function of $\Delta \phi$ (left panel) and $\phi _1^{}$ (right panel), with different factorisation and renormalisation scale choices. The set of the parity violating phases is chosen as $(\xi _1^{},\xi _2^{})=(30^{\circ }_{}, 60^{\circ }_{})$. By using the notations in Eqs. (3.6) and (3.7), the solid curves show the $\alpha =\beta =1$ results and $\diamond$ and $\times$ points give the $\alpha =\beta =2$ and $\alpha =\beta =1/2$ results, respectively. The ratios with respect to the solid curve result are shown in the lower part of each panel

We note in passing the impact of parity violation in the process $pp\rightarrow Hjj$, which can be considered as a simpler case. Since the process $gg\rightarrow H$ has non-zero amplitudes $\hat{\mathcal{M}}_{\lambda _1^{} \lambda _2^{}}^{}$ only for $\Delta \lambda = \lambda _1^{}-\lambda _2^{} = 0$ states, the process $pp\rightarrow Hjj$ has only Eq. (3.11c) in its cross section formula. Therefore, parity violation in the process $gg\rightarrow H$ appears as a peak shift only in the $\Delta \phi$ distribution [45, 46].

While the phase dependence on the correlations is apparent from Eq. (3.11), we present numerical results, too. In Fig. 10 we show the normalised differential cross section as a function of $\phi _{1}^{}$ (left column), $\phi _{2}^{}$ (middle column) and $\Delta \phi =\phi _1^{}-\phi _2^{}$ (right column) with different values for $\xi _{1,2}^{}$. The correspondence between the curves and values for $\xi _{1,2}^{}$ is shown inside each panel. In all of the panels, the SM prediction is shown by the black dashed curve. A cutoff, $p_\mathrm{T}^{}>200$ GeV, is imposed on the $p_\mathrm{T}^{}$ of the Higgs boson in the c.m. frame of the two Higgs bosons, when we produce the $\phi _{1}^{}$ and $\phi _{2}^{}$ plots, in order to enhance the correlations in $\phi _{1,2}^{}$; see Fig. 8. The distributions of $\phi _+^{}=\phi _1^{}+\phi _2^{}$ are not shown anymore, since we have found that the correlation in $\phi _+^{}$ is very small in most every case; see Figs. 8 and 9.

In Fig. 11, we study the uncertainties about the scale choices in the case of parity violation. The differential cross sections as a function of $\Delta \phi$ are shown in the left panel and that as a function of $\phi _1^{}$ is shown in the right panel. The phase $(\xi _1^{},\xi _2^{})=(30^{\circ }_{}, 60^{\circ }_{})$ is chosen. A cutoff, $p_\mathrm{T}^{}>200$ GeV, is imposed on the $p_T^{}$ of the Higgs boson in the c.m. frame of the two Higgs bosons, for the results in the right panel. The notations in Eqs. (3.6) and (3.7) are used. The solid curves show the $\alpha =\beta =1$ results and $\diamond$ and $\times$ points give the $\alpha =\beta =2$ and $\alpha =\beta =1/2$ results, respectively. The ratios with respect to the solid curve result are shown in the lower part of each panel. An important observation is that the peak positions which are shifted by the parity violation, namely the $\Delta \phi$ or $\phi _{1,2}^{}$ values that give the highest cross sections, do not depend on the scale choices. This fact is important from the point of view of parity violation measurements.

3.2 The weak boson fusion process

The weak boson fusion (WBF) sub-process $(V_1^{}, V_2^{})=(W^+_{}, W^-_{})$, $(W^-_{}, W^+_{})$ and (Z, Z) consists of only the qq initiated sub-process $(a_1^{}, a_2^{})=(q, q)$. However, the squared VBF amplitude for the WBF sub-process takes a more complicated form than that for the GF sub-process in Eq. (3.1) because of the following two reasons: (1) the helicity $\lambda _{1,2}^{}=0$ components of the intermediate weak bosons additionally induce 16 azimuthal angle dependent terms, such as $\cos {(\phi _1^{}-\phi _2^{})}$, (2) we cannot simply take averages for the initial helicities and take summations for the final helicities, since the electroweak interactions distinguish different helicity states. The squared VBF amplitude for four sets of the helicities of the external quarks must be prepared: $(\sigma _1^{}, \sigma _3^{}, \sigma _2^{}, \sigma _4^{})=(+,+,+,+), (+,+,-,-), (-,-,+,+), (-,-,-,-)$.

The amplitude $( \mathcal{M}_{V_1^{}V_2^{}}^{HH} )_{\lambda _1^{} \lambda _2^{}}^{}$ for helicity $\lambda _{1,2}^{}=0$ weak bosons gives a dominant contribution in the WBF sub-process and the amplitudes for other helicities are much smaller than the above amplitude. Thus we can expect that all of the azimuthal angle correlations are small, because the correlations arise from the interference of the amplitudes for various helicities; see Eq. (3.1). If we keep only terms which contain at least one $( \mathcal{M}_{V_1^{}V_2^{}}^{HH} )_{0 0}^{}$, the squared VBF amplitude for $(\sigma _1^{}, \sigma _3^{}, \sigma _2^{}, \sigma _4^{})=(+,+,+,+)$ has the following form:

$$\begin{aligned} \bigl | \mathcal{M}_{+ +}^{+ +} \bigr |^2_{}&= \frac{ 4 \bigl |g^{V_1^{}a_1^{}a_3^{}}_{+}\bigr |^2_{} \bigl |g^{V_2^{}a_2^{}a_4^{}}_{+}\bigr |^2_{} Q_1^2 Q_2^2 }{ \bigl ( Q_1^2+m_{V_1^{}}^2 \bigr )^2_{} \bigl ( Q_2^2+m_{V_2^{}}^2 \bigr )^2_{} }\Bigl \{s_0^{} t_0^{} |\hat{\mathcal{M}}_{00}^{}|^2_{} \nonumber \\&\quad + 2 \Bigl [ s_1^{} t_1^{} \mathrm{Re}\bigl ( \hat{\mathcal{M}}_{++}^{} \hat{\mathcal{M}}_{00}^* \bigr ) + s_2^{} t_2^{} \mathrm{Re}\bigl ( \hat{\mathcal{M}}_{00}^{} \hat{\mathcal{M}}_{--}^* \bigr ) \Bigr ] \nonumber \\&\quad \times \cos {(\phi _1^{}-\phi _2^{})} \nonumber \\&\quad - 2 \Bigl [ s_1^{} t_2^{} \mathrm{Re}\bigl ( \hat{\mathcal{M}}_{+-}^{} \hat{\mathcal{M}}_{00}^* \bigr ) + s_2^{} t_1^{} \mathrm{Re}\bigl ( \hat{\mathcal{M}}_{00}^{} \hat{\mathcal{M}}_{-+}^* \bigr ) \Bigr ]\nonumber \\&\quad \times \cos {(\phi _1^{}+\phi _2^{})} \nonumber \\&\quad + \bigl ( \mathrm{Re} \rightarrow \mathrm{Im}, \cos {} \rightarrow \sin {} \bigr ) \Bigr \}, \end{aligned}$$

(3.12)

where we introduce a notation $\hat{\mathcal{M}}_{\lambda _1^{} \lambda _2^{}}^{}$ which denotes the amplitude $( \mathcal{M}_{V_1^{}V_2^{}}^{HH} )_{\lambda _1^{} \lambda _2^{}}^{}$. $s_{0,1,2}^{}$ and $t_{0,1,2}^{}$ are functions of $\theta _{1,2}^{}$ defined in the $q_{1,2}^{}$ Breit frames Eqs. (2.17) and (2.18) and given by

$$\begin{aligned}&s_0^{} = \frac{ \sin ^2_{}{\theta _1^{}} }{2 \cos ^2_{}{\theta _1^{}} },\quad s_1^{} = \frac{ \sqrt{2} \sin {\theta _1^{}} (1+\cos {\theta _1^{}}) }{4 \cos ^2_{}{\theta _1^{}} },\ \nonumber \\&s_2^{} = \frac{ \sqrt{2} \sin {\theta _1^{}} (1-\cos {\theta _1^{}}) }{4 \cos ^2_{}{\theta _1^{}} }, \end{aligned}$$

(3.13a)

$$\begin{aligned}&t_0^{} = \frac{ \sin ^2_{}{\theta _2^{}} }{2 \cos ^2_{}{\theta _2^{}} },\quad t_1^{} = \frac{ \sqrt{2} \sin {\theta _2^{}} (1-\cos {\theta _2^{}}) }{4 \cos ^2_{}{\theta _2^{}} },\ \nonumber \\&t_2^{} = \frac{ \sqrt{2} \sin {\theta _2^{}} (1+\cos {\theta _2^{}}) }{4 \cos ^2_{}{\theta _2^{}} }. \end{aligned}$$

(3.13b)

The squared VBF amplitude for the other three helicity states can be simply obtained by exchanging $s_{1,2}^{}$ and $t_{1,2}^{}$ in $| \mathcal{M}_{+ +}^{+ +} |^2_{}$ in the following ways:

$$\begin{aligned} | \mathcal{M}_{+ +}^{+ +} |^2_{} \rightarrow | \mathcal{M}_{- +}^{- +} |^2_{} \ \&\text {by}~ s_1^{} \leftrightarrow s_2^{},\,\nonumber \\ | \mathcal{M}_{+ +}^{+ +} |^2_{} \rightarrow | \mathcal{M}_{+ -}^{+ -} |^2_{} \ \&\text {by}~ t_1^{} \leftrightarrow t_2^{},\,\nonumber \\ | \mathcal{M}_{+ +}^{+ +} |^2_{} \rightarrow | \mathcal{M}_{- -}^{- -} |^2_{} \ \&\text {by}~ s_1^{} \leftrightarrow s_2^{}~\text {and}~t_1^{} \leftrightarrow t_2^{}. \end{aligned}$$

(3.14)

The couplings should also be changed accordingly. The coefficients of $\cos {\phi _{1,2}^{}}$ terms actually contain one $\hat{\mathcal{M}}_{00}^{}$, too. However, the $\cos {\phi _{1,2}^{}}$ terms cannot give correlated distributions in the process $pp\rightarrow HHjj$, because we cannot distinguish the two Higgs bosons. More practically, an azimuthal angle dependent term which changes its overall sign under the transformations $\phi _1^{} \rightarrow \phi _1^{}+\pi$ and $\phi _2^{} \rightarrow \phi _2^{}+\pi$ gives only a flat distribution after the phase space integration. The first term in the right hand side (RHS) of Eq. (3.12) contributes to the inclusive cross section after the phase space integration and the other terms give the correlations in $\Delta \phi =\phi _1^{}-\phi _2^{}$ and $\phi _+^{}=\phi _1^{}-\phi _2^{}$. An interesting difference from the GF sub-process is that the sine terms do not vanish even when the amplitude is parity invariant ($\hat{\mathcal{M}}_{++}^{} = \hat{\mathcal{M}}_{--}^{}$ and $\hat{\mathcal{M}}_{+-}^{} = \hat{\mathcal{M}}_{-+}^{}$), if the amplitude contains an imaginary part. This is because the interaction between the external quarks and the intermediate weak boson already violates the parity symmetry. In our tree-level calculation, the amplitude is purely real and we will observe only cosine distributions.

Fig. 12

The normalised differential cross section of the WBF process as a function of $\phi _1^{}$ (upper left), $\phi _2^{}$ (upper right), $\Delta \phi$ (lower left) and $\phi _+^{}$ (lower right). The correspondence between curves and simulation methods is shown inside the upper left panel: (1) The blue solid curve represents the result according to our approximate analytic cross section, (2) The black dashed curve represents the exact LO result, (3) The red solid curve represents the result according to our approximate analytic cross section from which the quantum effects of the intermediate weak bosons are removed on purpose

We show numerical results for the 14 TeV LHC. The setup and phase space cuts are the same as in the GF study in Sect. 3.1. Therefore the numerical results in this Section can be directly compared with those in Sect. 3.1. The only difference is the scale choice in the PDFs. The $p_\mathrm{T}^{}$ of the jet with a positive rapidity is used for the scale in the PDF of the incoming parton which moves along the positive direction of the z-axis, and the $p_\mathrm{T}^{}$ of the jet with a negative rapidity is used for the scale in the PDF of the other incoming parton. In Fig. 12, we show the normalised differential cross section as a function of $\phi _1^{}$ (upper left), $\phi _2^{}$ (upper right), $\Delta \phi = \phi _1^{} - \phi _2^{}$ (lower left) and $\phi _+^{} = \phi _1^{} + \phi _2^{}$ (lower right). The blue solid curve, labelled (1) VBF, represents the result according to our approximate analytic cross section, to which only the VBF diagrams contribute. The black dashed curve, labelled (2) MG, represents the result according to the exact LO cross section, to which not only the VBF diagrams but also the s-channel and u-channel diagrams contribute, generated by MadGraph5_aMC@NLO [68] version 5.2.2.1. The red solid curve, labelled (3) VBF w/o QE, represents the result according to our approximate analytic cross section from which the azimuthal angle dependent terms are removed on purpose, that is, the quantum effects of the intermediate weak bosons expressed as the interference of the amplitudes for different helicities are killed. Therefore, the differences between the result (1) and the result (3) in the distributions visualise the contribution from the azimuthal angle dependent terms. The good agreement between the result (1) and the result (2) confirms the validity of our approximate analytic cross section. The $\phi _1^{}$ and $\phi _2^{}$ plots show correlated distributions. However, the agreement between the result (1) and the result (3) reveals that the correlated distributions are not induced by the quantum effects of the intermediate weak bosons but by a kinematic effect. The small discrepancies between the result (1) and the result (3) in the $\Delta \phi$ and $\phi _+^{}$ plots come from the $\cos {\Delta \phi }$ and the $\cos {\phi _+^{}}$ terms in Eq. (3.12), respectively. The smallness of the discrepancies is as expected [see the discussion above Eq. (3.12)]. In the $\Delta \phi$ and $\phi _+^{}$ plots, the result (3) again shows correlated distributions, which must be induced by a kinematic effect. Therefore, the WBF sub-process produces the correlated distributions in all of the azimuthal angle observables; however, they are mainly induced by a kinematic effect. We note that the GF sub-process produces only flat distributions in all of the azimuthal angle observables, when the quantum effects of the intermediate gluons are killed in the same way as above. It can be concluded that the non-flat distributions induced by a kinematic effect are a characteristic feature of the WBF sub-process.

We study how the azimuthal angle distributions depend on the triple Higgs self-coupling. We have observed the kinematic effect on the distributions in non-standard cases $\lambda _h^{} \ne 1$, too, where $\lambda _h^{}$ is the factor re-scaling the triple Higgs self-coupling. The three cases $\lambda _h^{}=0, 1, 2$ produce the similar distributions in the azimuthal angle observables, when the quantum effects of the intermediate weak bosons are killed. In Fig. 13 we show the normalised differential cross section as a function of $\phi _{1,2}^{}$ (left), $\Delta \phi = \phi _1^{} - \phi _2^{}$ (middle) and $\phi _+^{} = \phi _1^{} + \phi _2^{}$ (right) with three different values of $\lambda _h^{}$, the blue solid curve: $\lambda _h^{}=0$, the black dashed curve: $\lambda _h^{}=1$ (the SM prediction), and the red solid curve: $\lambda _h^{}=2$. The correlated distributions in the $\phi _{1,2}^{}$ plot are completely induced by a kinematic effect. We find that, when $\lambda _h^{}=2$, the coefficient of the $\cos {(\phi _1^{}-\phi _2^{})}$ term [the second term in the RHS of Eq. (3.12)] is large enough to flip the $\Delta \phi$ distribution. The impact of a non-standard value for $\lambda _h^{}$ ($\lambda _h^{} \ne 1$) is again not so significant. However, differently from the GF sub-process which is actually the $\mathcal {O}(\alpha _\mathrm{s}^2)$ correction to the inclusive GF sub-process $gg\rightarrow HH$, the WBF sub-process is a LO tree-level process and so the correlations should be used together with other observables, such as the invariant mass of the Higgs boson pair, to probe $\lambda _h^{}$.

4 Summary and discussion

In this paper, we have studied the azimuthal angle correlations of two jets in the production of a Higgs boson pair plus two jets $pp\rightarrow HHjj$. Based on the known fact that the azimuthal angle correlations are induced by the quantum effects of the two intermediate vector bosons in vector boson fusion (VBF) sub-processes, we have calculated the amplitudes contributed from only VBF Feynman diagrams. As VBF sub-processes, we have considered the gluon fusion (GF) sub-process, which is an one-loop $\mathcal {O}(\alpha _\mathrm{s}^4 \alpha _{}^2)$ process at leading order (LO), and the weak boson fusion (WBF) sub-process, which is an $\mathcal {O}(\alpha _{}^4)$ process at LO. We have used a helicity amplitude technique for evaluating the VBF amplitudes. Based on the method presented in Ref. [47], we have divided a VBF amplitude into two amplitudes for off-shell vector boson emissions ($q\rightarrow qV^*_{}$ or $g\rightarrow gV^*_{}$) and one amplitude for the Higgs boson pair production by a fusion of the two off-shell vector bosons ($V_{}^*V_{}^* \rightarrow HH$), and presented each of the three amplitudes in the helicity basis. The quantum effects of the intermediate vector bosons are still included correctly and are expressed as the interference of the $V_{}^*V_{}^* \rightarrow HH$ amplitudes with various helicities of the vector bosons. With this method, we have obtained the squared VBF amplitude in a compact form, from which we can easily make an expectation on the azimuthal angle correlations, both for the GF sub-process and for the WBF sub-process. We have numerically compared our approximate analytic cross sections with the exact LO results and have observed the good agreement between the two results both in the inclusive cross sections and in azimuthal angle distributions, after the VBF cuts and the upper transverse momentum $p_\mathrm{T}^{}$ cut on the jets are imposed (for the GF sub-process, the comparison is performed only in the large $m_\mathrm{t}^{}$ limit). As azimuthal angle observables, we have studied four observables: $\phi _1^{}$, $\phi _2^{}$, $\Delta \phi = \phi _1^{} - \phi _2^{}$ and $\phi _+^{} = \phi _1^{} + \phi _2^{}$, where $\phi _{1,2}^{}$ are the azimuthal angles of the two jets measured from the production plane of the Higgs boson pair.

Fig. 13

The normalised differential cross section of the WBF process as a function of $\phi _{1,2}^{}$ (left), $\Delta \phi$ (middle) and $\phi _+^{}$ (right), with three different values for the triple Higgs self-coupling re-scaling factor $\lambda _h^{}$. The correspondence between the curves and values for $\lambda _\mathrm{h}^{}$ is shown inside the left panel

Fig. 14

The normalised differential cross section as a function of $\phi _{1,2}^{}$ (left), $\Delta \phi$ (middle) and $\phi _+^{}$ (right) for the GF process (red solid curve) and the WBF process (black dashed curve)

In the GF sub-process, using a finite $m_\mathrm{t}^{}$ value is found to be important to produce the azimuthal angle correlations correctly. The GF sub-process exhibits large correlations in $\phi _{1,2}^{}$ and $\Delta \phi$. The $p_\mathrm{T}^{}$ of the Higgs boson is found to be useful in controlling these correlations. The correlation in $\Delta \phi$ is enhanced when the $p_\mathrm{T}^{}$ of the Higgs boson is decreased and the correlations in $\phi _{1,2}^{}$ are enhanced when the $p_\mathrm{T}^{}$ of the Higgs boson is increased. We have found that the correlation in $\phi _+^{}$ is very small in most every case. The impact of a non-standard value for the triple Higgs self-coupling on the correlations is found to be much smaller than that in other observables, such as the invariant mass of the Higgs boson pair, of the inclusive process $pp\rightarrow HH$. In order to study the impact of parity violation on the correlations, we have introduced two independent phases $\xi _{1,2}^{}$ which parametrise the magnitude of parity violation in the process $gg \rightarrow HH$. They are introduced in a way that $\xi _{1}^{}$ affects the $gg \rightarrow HH$ amplitude for $\Delta \lambda =\lambda _1^{}-\lambda _2^{}=0$ helicity states, where $\lambda _{1,2}^{}$ are helicities of the gluons, and $\xi _{2}^{}$ affects the amplitude for $\Delta \lambda =\pm 2$ helicity states. We have analytically shown that parity violation appears as peak shifts of the correlations and that the peak shifts reflect only the magnitude of parity violation. We have also shown that $\Delta \phi$ is sensitive to $\xi _1^{}$, $\phi _+^{}$ is sensitive to $\xi _2^{}$, and $\phi _{1,2}^{}$ are sensitive to both $\xi _1^{}$ and $\xi _2^{}$. Although we are far less likely to be able to measure $\xi _{2}^{}$ in the $\phi _+^{}$ distribution because of the very small correlation in $\phi _+^{}$, we may use $\phi _{1}^{}$ and $\phi _{2}^{}$ to probe $\xi _{2}^{}$ instead. The scale uncertainties in the GF sub-process are large in the inclusive cross section, as expected from the study of the GF sub-process in the process $pp\rightarrow Hjj$ [67] or $pp\rightarrow HH$. However, the uncertainties in the normalised distributions of the correlations are found very small. Therefore, the prediction of the correlations is stable and thus useful, as long as the normalised distributions are discussed. The peak positions of the correlations, namely the $\Delta \phi$ or $\phi _{1,2}^{}$ values that give the highest cross sections, are also found robust against the scale choices. This fact further motivates us to measure parity violation by using the correlations. While we can naively expect that the azimuthal angle distributions in the WBF sub-process are almost flat, we have actually observed correlated (non-flat) distributions. We have found that they are not induced by the quantum effects of the intermediate weak bosons but by a kinematic effect. Since we do not find a similar kinematic effect in the GF sub-process, we conclude that this is a characteristic feature of the WBF sub-process. The impact of a non-standard value for the triple Higgs self-coupling is not so significant in the WBF sub-process, too.

The parton level event samples of the process $pp\rightarrow HHjj$ are exclusively generated and each of the two outgoing partons is identified as a jet in our numerical studies. When more realistic event generations are intended to be performed, merging the parton level event samples with the leading logarithmic parton shower [81,82,83] and subsequently proceeding to a hadronisation procedure will be a promising approach. However, a careful merging procedure is required for correctly reproducing the azimuthal angle correlations after the merging procedure, because the correlations studied in this paper are completely process dependent ($pp\rightarrow HHjj$) and those process dependent angular correlations are not described correctly by the parton shower. Contamination from the parton shower may lead to a wrong prediction [84].

The azimuthal angle correlations revealed in this paper will help the analyses of the process $pp\rightarrow HHjj$ at the LHC. Since the production cross section of the process $pp\rightarrow HHjj$ is small, we should use as much process dependent information as possible to extract the events of the process. The azimuthal angle correlations are obviously a part of the process dependent information. It is a known issue that separating the contributions coming from the GF sub-process and those coming from the WBF sub-process is difficult in the production of a Higgs boson pair plus two jets [23]. One possible application of the correlations is to help disentangling the GF sub-process and the WBF sub-process by using the fact that these two sub-processes exhibit different correlations, as shown in Fig. 14. We have studied only the signal processes in this paper and so the impact of the correlations in a realistic situation is not so clear yet. The fully automated event generation for loop induced processes is now available in MadGraph5_aMC@NLO [68, 69]. This achievement will activate phenomenological studies of the process. We hope that further phenomenological studies including the uses of the azimuthal angle correlations will be performed both by theorists and by experimentalists.