1 Introduction

The recent detection of gravitational waves ([3] and references therein) carried implicit evidence for the existence of black holes since the cataclysmic event generating the wave carried the expected signature of a coalescing binary black hole system. Nevertheless, the question of what the final fate of gravitational collapse is remains open. Black holes are one possibility but this does not preclude others. The gravastar (gravitational vacuum star) model has been proposed by Mazur and Mottola [5, 6], and it has attracted attention as an alternative model to the black hole. The general idea is preventing horizon (and singularity) formation, by stopping the collapse of matter at or near where the event horizon is expected to form i.e., alternative configurations of black holes could be formed by gravitational collapse of a massive star. The quasi-normal modes of thin-shell non-rotating gravastars were studied by Pani et al. [4] and they also considered the gravitational wave signatures when no horizon is present such as in the case of gravastars. To the best of the knowledge of the authors no investigations into the wave signature from coalescing gravastars have been made to date. It has been speculated that the gravastars and black holes emit the same gravitational wave signatures.

In the gravastar model, the interior consists of a segment of the de Sitter geometry, enclosed by a shell of Bose–Einstein condensate, all of which is surrounded by a Schwarzschild vacuum but without encountering a horizon. The de Sitter interior with negative pressure favoring expansion is necessary to provide a mechanism to counterbalance the gravitational collapse of the ultra-compact Bose–Einstein condensate (BEC), which itself is assumed to have the most extreme equation of state permissible by causality – that of stiff matter (\(p = \rho \)). Therefore the gravastar is a multilayered structure consisting of three different regions with three different equations of state (EOS):

  1. (I)

    an internal core (de Sitter) with an EOS: \(p+\rho = 0\),

  2. (II)

    a thin shell of ultra-stiff matter (BEC) with an EOS: \(p = +\rho \),

  3. (III)

    an outer vacuum Schwarzschild solution with EOS: \(p = \rho =0\),

In practice, the Mazur–Mottola model is a static spherically symmetric model with a five-layer solution of the Einstein equations including two infinitesimally thin shells endowed with surface densities \(\sigma _{\pm }\) and surface pressure \( p_{\pm }\).

Motivated by the work Visser and Wiltshire [7], one analyzed the dynamic stability against spherically symmetric perturbations using the Israel thin-shell formalism while Carter in [8] has extended gravastar stability with generalized exteriors (Reissner–Nordstrom). In Ref. [9] gravastar solutions have been studied within the context of nonlinear electrodynamics. Later some simplifications and important aspects of the gravastar have been studied in-depth in [10,11,12,13,14]. Moreover, the limits on gravastars and how an external observer can distinguish it from a black hole have been studied in [15, 16].

After the theoretical discovery of radiating black holes by Hawking [17, 18], based on quantum field theory, the thermodynamical properties of black holes have been studied extensively. Since this theoretical effort first disclosed the mysteries of quantum gravity, considerable interest in this problem has developed in theoretical physics. It is generally believed that spacetime as a manifold of points breaks down at very short distances of the order of the Planck length. In these circumstances noncommutative geometry [19, 20] plays a key attribute in unraveling the properties of nature at the Planck scale. From the fundamental point of view of noncommutative geometry there is an interesting interplay between mathematics, high energy physics as well as cosmology and astrophysics. In a noncommutative spacetime the coordinate operators on a D-brane [20, 21] can be encoded by the commutator \([\hat{x}^{\mu }, \hat{x}^{\nu }]\) = \(i\vartheta ^{\mu \nu }\), where \(\hat{x}\) and \(i\vartheta ^{\mu \nu }\) are the coordinate operators and an antisymmetric tensor of dimension (length)\(^2\), which determines the fundamental cell discretization of spacetime. As Smailagic et al. have shown [22] that noncommutativity replaces point-like structures by smeared objects in flat spacetime. Thus it is reasonable to believe that noncommutativity could eliminate the divergences that normally appear in general relativity that appears in various form. As discussed in Ref. [23] the smearing effect is mathematically implemented as a substitution rule: position Dirac delta function is substituted everywhere using a Gaussian distribution of minimal length \(\sqrt{\alpha }\).

In the same spirit, Nicolini et al. [23,24,25] have investigated the behavior of a noncommutative radiating Schwarzschild black hole. There is a lot of noncommutative effects have been performed to extend the solution for higher dimensional black hole [26], charged black hole solutions [27, 28] and charged rotating black hole solution [29, 30]. A number of studies have been performed in these directions where spacetime is commutative [31,32,33,34]. In the same context wormhole solutions have been studied in [35,36,37]. Recently, Lobo and Garattini [38] showed that a noncommutative geometry background is able to account for exact gravastar solutions and studied the linearized stability. Gravastar solutions in lower dimensional gravity have been studied in [39, 40] in an anti-de Sitter background spacetime.

It is well known that general relativity and its modified counterparts are highly non-trivial systems to investigate in the physically realistic four spacetime dimensions. It is therefore interesting to reduce the number of spatial dimensions by 1 and to study general relativity in the simpler context of (\(2+1\)) dimensions in the hope that it has the potential to generate non-trivial and valuable insight into some of the conceptual issues that arise in the (\(3+1\)) dimensional case, especially in regard to the question of quantizing gravity. Seminal contributions in this regard were made by Witten [41,42,43] who showed an equivalence between (\(2+1\)) gravity theory and Chern–Simons theory. The usefulness of (\(2+1\))-dimensional gravity motivated us to show that neutral gravastars solutions do exist to avoid the event horizon formation, which may be considered as an alternative to BTZ in the context of noncommutative geometry.

The motivation for this investigation is clear from the above summary on the aspect of an exact gravastar solution in the context of NC in (\(2+1\))-dimension. Our paper is organized as follows. In Sect. 2 we construct BTZ black hole solution from an exact solution of the Einstein field equations in the context of noncommutative geometry and specifying the mass function we present the structural equations of gravastar. In Sect. 3 we discuss the matching conditions at the junction interface and determine the surface stresses. In Sects. 4 and 5 we investigate the linearized stability of gravastars and determine the stability regions of the transition layer. Finally, in Sect. 6 we draw the conclusions.

2 Interior geometry

We will be concerned here the interior spacetime described by the line element for a static spherically symmetry and time independent metric in (\(2+1\)) dimensions in the following form:

$$\begin{aligned} {\text {d}}s^2=-e^{2\varPhi (r)}{\text {d}}t^2 + \frac{{\text {d}}r^2}{1-2m(r)/r} +r^2 {\text {d}}\theta ^2 , \end{aligned}$$
(1)

where \(\varPhi (r)\) and m(r) are arbitrary functions of the radial coordinate, r. Here the “gravity profile” factor \(\varPhi (r)\) is related with the relationship \(\mathcal {A}\) = \(\sqrt{1-m(r)/r }\varPhi ^{\prime }(r)\), which represents the locally measured acceleration due to gravity [44, 45]. The convention used is that \(\varPhi ^{\prime }(r)\) is positive or negative for an inwardly gravitational attraction or an outward gravitational repulsion and m(r) can be interpreted as the mass function.

We take the matter distribution to be anisotropic in nature and therefore the stress-energy tensor for an anisotropic matter distribution is provided by

$$\begin{aligned} T_{ij}=(\rho +p_{\perp })u_iu_j+p_{\perp }g_{ij}+(p_r-p_{\perp })\mathcal {X}_i\mathcal {X}_j, \end{aligned}$$
(2)

where \(u^i\) is the 3-velocity of the fluid and \(\mathcal {X}_i\) is the unit spacelike vector in the radial direction. \(\rho (r)\), \(p_r(r)\), and \(p_{\perp }(r)\) represent the energy density, radial pressure and tangential pressure, respectively.

The Einstein field equations \(G_{\mu \nu } + \Lambda \) \(g_{\mu \nu }\) = 8\(\pi T_{\mu \nu }\), for the spacetime given in Eq. (1) together with the energy-momentum tensor given in Eq. (2), rendering G = c = 1, provides the following relationships:

$$\begin{aligned}&8\pi \rho +\Lambda = \frac{rm'-m}{r^3},\end{aligned}$$
(3)
$$\begin{aligned}&8\pi p_r - \Lambda =\frac{\varPhi ^ {'}}{r}\left( 1-\frac{2m}{r}\right) ,\end{aligned}$$
(4)
$$\begin{aligned}&8\pi p_{\perp } - \Lambda = \left( 1-\frac{2m}{r}\right) \left( \varPhi ^ {'2}+\varPhi ^ {''}-\varPhi ^ {'}\frac{(rm'-m)}{r^2}\right) ,\nonumber \\ \end{aligned}$$
(5)

In addition, we have the conservation equation in (\(2+1\)) dimensions:

$$\begin{aligned} \left( \rho +p_r\right) \varPhi ^{\prime }+p_r^{\prime }+\frac{1}{r}\left( p_r-p_{\perp }\right) =0, \end{aligned}$$
(6)

where \(\Lambda \) is the cosmological constant and \(\varPhi \) are arbitrary functions of the radial coordinate r. Here \(\prime \) denotes differentiation with respect to the radial parameter r. Although we shall not invoke isotropic particle pressure, it is interesting to note that the isotropy Eq. (4) = (5)

$$\begin{aligned} \varPhi '' + \varPhi '^2 - \frac{\varPhi '}{r^2}\left( r(m' - 1) - m\right) = 0, \end{aligned}$$
(7)

ostensibly nonlinear in \(\varPhi \), may be reduced to the linear form

$$\begin{aligned} y'' -\frac{1}{r^2} \left( r(m'-1)-m\right) y'=0 \end{aligned}$$
(8)

by making the change of variables \(e^{2\varPhi (r)} = y^2(r)\). Equation (8) may be solved explicitly by

$$\begin{aligned} y=c_1 \int \exp \left( \int {\left( \frac{m'-1}{r} - \frac{m}{r^2}\right) {\text {d}}r}\right) + c_2 \end{aligned}$$
(9)

where \(c_1\) and \(c_2\) are integration constants that may be settled by considering the boundary conditions. For stellar distributions \(\Lambda \) is ignored and so (9) provides an algorithm to detect all static isotropic perfect fluid solutions in (\(2+1\)) dimensions. Once a suitable form for m(r) is selected, \(\varPhi \) can be determined (theoretically) and hence the density and pressure may be obtained to complete the model. But we shall not pursue these ideas here as we shall require anisotropic particle pressure for our model.

We are going to solve the resulting Einstein’s equations, for static spherically symmetric perfect fluids in (\(2+1\)) dimensions, with a maximally localized source of energy having the minimal width, Gaussian, mass/energy distribution

$$\begin{aligned} \rho =\frac{M}{4\pi \alpha }~ \text{ exp }\left( -\frac{r^2}{4\alpha }\right) , \end{aligned}$$
(10)

where M is the total mass of the source. This is due to the coordinate coherent states approach to noncommutative geometry with the noncommutative parameter \(\theta \) being a small (\(\sim \)Planck length\(^2\)) positive number.

By solving the Einstein equations with an EOS \(p_r= - \rho \), as a matter source, we have the following relationship (see Ref. [2]):

$$\begin{aligned} e^{2\varPhi }= -A+2Me^{-\frac{r^2}{4\alpha }}-\Lambda r^2, \end{aligned}$$
(11)

where A is an integration constant. In the limit \(\frac{r}{\sqrt{\alpha }}\rightarrow ~\infty \), Eq. (11) is reduced to the BTZ black hole where the constant term A plays the role of the mass of the BTZ black hole, i.e., \(A = M\).

In order to proceed with our investigation, we choose a specific mass function m(r), for closing the system. For this purpose, we are now interested in the noncommutative geometry inspired mass function (see Refs. [46, 47]) in the following form:

$$\begin{aligned} m=\frac{M}{\pi ^{(\tilde{m}-2)/2}}\gamma \left[ \frac{\tilde{m}}{2}, \chi ^2 \left( \frac{r}{2M}\right) ^2\right] , \end{aligned}$$
(12)

where \(\chi ^2= M^2/\alpha \) and \(\gamma \left( \frac{a}{b}; x\right) \) is the Euler lower Gamma function defined by

$$\begin{aligned} \gamma \left( \frac{a}{b}; x\right) \equiv \int ^x_0 u^{a/b} e^{-u}\frac{{\text {d}}u}{u}. \end{aligned}$$
(13)

For a BTZ black hole, \(\tilde{m}=2\), we obtain the following expression for the mass function:

$$\begin{aligned} m(r)= M\int ^{r^2/4\theta }_0 e^{-t}{\text {d}}t= M \left[ 1-\text{ exp }\left( -\frac{r^2}{4\alpha }\right) \right] . \end{aligned}$$
(14)

At the origin, \(m(0) = 0\), which is consistent with the solution of Eq. (12) and we notice that the parameter \(\chi \) plays a critical role in determining the horizons.

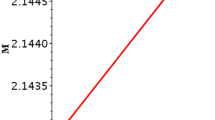
An interesting feature of the solution is the horizon. Corresponding to \(A= M\) given in Eq. (11), and letting the function \(g_{tt}(r_h) =0\), gives the event horizon(s) which is depicted in Fig. 1 for different values of \(\chi \). Thus we find three possible cases [2]:

  1. (i)

    for \(M>\) \(M_0=0.214 \sqrt{\alpha }\) there are two horizons i.e., when \(\chi > 0.214 \);

  2. (ii)

    for \(M =\) \(M_0 = 0.214 \sqrt{\alpha }\) with one degenerate horizon i.e., when \(\chi = 0.214 \);

  3. (iii)

    for 0< \(M<\) \(M_0\) no horizon for \(\chi < 0.214 \),

where \(M_0\) is the existence of a lower bound for a black hole mass and represents its final state at the end of Hawking evaporation process. It is also clear from Fig. 1 that below the minimal mass there is no black hole.

Fig. 1
figure 1

The function \(g_{tt}\) cuts the r-axis gives the event horizons for different values of \(\chi \) = 0.8, \(\chi \) = 0.214 and \(\chi \) = 0.1, respectively

Full size image

3 Matching at junction interface and surface stresses

For the specific gravastar model we match the interior gravastar geometry, given in Eq. (1), with an exterior geometry associated with the BTZ solution,

$$\begin{aligned} {\text {d}}s ^2=- \left( -M-\Lambda r^2\right) {\text {d}}t^2{+}\left( -M-\Lambda r^2\right) ^{-1} {\text {d}}r^2 + r^2 {\text {d}}\theta ^2,\nonumber \\ \end{aligned}$$
(15)

both interior and exterior matched at the junction surface \(\Sigma \), situated outside the event horizon, \(a > r_h\). As the gravastar solution does not possess a singularity at the origin and has no event horizon, we are interested in the case \(\chi < 0.214 \) and there is no event horizon yielding a solution.

Since the outer solutions have a zero stress-energy, while at the junction surface \(\Sigma \), both will have a non-zero stress-energy. The junction hypersurface is a timelike hypersurface defined by the parametric equation \(f(x^{\mu }(\xi ^i)) = 0\), where \(\xi ^i\) = (\(\tau , ~\theta \)) represents the intrinsic coordinates on the hypersurface and \(\tau \) is the proper time, respectively.

In order to proceed one can write the line element for intrinsic metric to \(\Sigma \) as

$$\begin{aligned} {\text {d}}s ^2_{\Sigma } = - {\text {d}}\tau ^2 + a^2 {\text {d}}\theta ^2. \end{aligned}$$
(16)

For the purpose of this paper we matched our interior geometry by the exterior BTZ solution; the three velocity of a piece of stress energy at the junction surface is given by \(\xi ^{\mu } (\tau , \theta )\) = \((t(\tau ), a(\tau ), \theta )\)

$$\begin{aligned} U^{\mu }_{\pm } = \left( \frac{{\text {d}}t}{{\text {d}}\tau }, \frac{{\text {d}}a}{{\text {d}}\tau }, 0\right) = \left( \frac{\sqrt{1-\frac{2m_{\pm }}{a}+\dot{a}^2}}{1-\frac{2m_{\pm }}{a}}, \dot{a},0\right) , \end{aligned}$$
(17)

where the \((\pm )\) correspond to the exterior and interior spacetimes, with \(m_{\pm }\) defined as interior and exterior mass, respectively.

Also the normal unit vector (\(n^{\pm }_{\mu }\)) to the boundary can be defined as (with \(n^{\mu }n_{\mu }= 1\) and \(U^{\mu }n_{\mu }=0\))

$$\begin{aligned} n^{\pm }_{\mu } = \left( - \dot{a},\frac{\sqrt{1-\frac{2m_{\pm }}{a}+\dot{a}^2}}{1-\frac{2m_{\pm }}{a}}, 0\right) . \end{aligned}$$
(18)

At the junction surface the components of the extrinsic curvature tensor read

$$\begin{aligned} K^{\pm }_{ij} = -n_{\nu }\left( \frac{\partial ^2 x^{\nu }}{\partial \xi ^i \partial \xi ^j}+\Gamma ^{\nu \pm }_{\alpha \beta }\frac{\partial x^{\alpha }}{\partial \xi ^{i}}\frac{\partial x^{\beta }}{\partial \xi ^{j}}\right) , \end{aligned}$$
(19)

where \(\xi ^i\) = (\(\tau , ~\theta \)) represent the coordinates on the shell. Here, in general \(K_{ij}\) is discontinuous at the junction surface, the discontinuity in the second fundamental forms is defined as

$$\begin{aligned} \mathcal {K} _{ij} = K^+_{ij}-K^-_{ij}. \end{aligned}$$
(20)

Then using the Lanczos equation the Einstein equations lead to the following form:

$$\begin{aligned} \mathcal {S}^{i} _{~j} = -\frac{1}{8\pi } \left( \mathcal {K}^{i} _{~j}-\delta ^{i} _{~j}\mathcal {K}^{k} _{~k} \right) , \end{aligned}$$
(21)

where \(\mathcal {S}^{i} _{~j}\) is the surface stress-energy tensor on \(\Sigma \), with the discontinuity of the extrinsic curvature defined by \(\mathcal {K}^{i} _{~j}\).

Now, let us calculate the non-trivial components of the extrinsic curvature for the interior spacetime (1) and the exterior BTZ solution (15), given by

$$\begin{aligned} K^{\tau +} _{~\tau } = \frac{-\Lambda a+\ddot{a}}{\sqrt{-M-\Lambda a^2+\dot{a}^2}}, \end{aligned}$$
(22)
$$\begin{aligned} K^{\tau -} _{~\tau } = \frac{\frac{m}{a^2}-\frac{m'}{a}+\ddot{a}}{\sqrt{1-\frac{2m(a)}{a}+\dot{a}^2}}, \end{aligned}$$
(23)

and

$$\begin{aligned} K^{\theta +} _{~\theta } = \frac{1}{a} {\sqrt{-M-\Lambda a^2+\dot{a}^2}}, \end{aligned}$$
(24)
$$\begin{aligned} K^{\theta -} _{~\theta } = \frac{1}{a} {\sqrt{1-\frac{2m(a)}{a}+\dot{a}^2}}, \end{aligned}$$
(25)

where the prime denotes a derivative with respect to r and a dot stands for \({\text {d}}/{\text {d}}\tau \). Therefore, the stress-energy tensor (21) in the most general form of the surface energy density \(\sigma \) and the surface pressure \(\mathcal {P}\) is \(\mathcal {S}^{i} _{~j}\) = diag \(\left( -\sigma , \mathcal {P}\right) \).

After some algebraic manipulation and using the Lanczos equation, we obtain the energy density and the surface pressures given by

$$\begin{aligned} \sigma = -\frac{1}{8\pi a}\left( {\sqrt{-M-\Lambda a^2+\dot{a}^2}}- {\sqrt{1-\frac{2m(a)}{a}+\dot{a}^2}}\right) , \end{aligned}$$
(26)
$$\begin{aligned} \mathcal {P}= & {} \frac{1}{8\pi a}\left[ \phantom {\frac{1-\frac{m}{a}-m'+\dot{a}^2+\ddot{a}}{\sqrt{1-\frac{2m(a)}{a}+\dot{a}^2}}}\frac{-M-2\Lambda a^2+\dot{a}^2+\ddot{a}}{\sqrt{-M-\Lambda a^2+\dot{a}^2}}\right. \nonumber \\&\left. - \frac{1-\frac{m}{a}-m'+\dot{a}^2+\ddot{a}}{\sqrt{1-\frac{2m(a)}{a}+\dot{a}^2}}\right] . \end{aligned}$$
(27)

Note that by definition the surface tension \(\sigma \) has the opposite sign to the surface pressure \(\mathcal {P}\). Now, we shall also use the conservation identity in the form \(\mathcal {S}^{i} _{~j|i} =[T_{\mu \nu }e^{\mu }_{j}n^{\nu }]^{+}_{-}\), where \([X]^{+}_{-}\) represents the discontinuity across the surface interface. The method is developed in Refs. [44, 45]. To study the stability of the solutions under perturbations we encroach on the momentum flux term \(F_{\mu }=T_{\mu \nu }U^{\nu }\) in the right hand side corresponding to the net discontinuity. With the definitions of the conservation identity one can convert this into conserved energy and momentum of the surface stresses at the junction interface.

It is useful to introduce the conservation equation in a form that relates the surface energy and surface pressure with the work done by the pressure and the energy flux on the shell given by the equation \(\mathcal {S}^{i} _{~\tau |i} = -\left[ \dot{\sigma }+\frac{\dot{a}}{a}(\sigma +\mathcal {P})\right] \). Then the conservation identity provides the following relationship:

$$\begin{aligned} \sigma ^{\prime } = -\frac{1}{a}\left( \sigma +\mathcal {P}\right) , \end{aligned}$$
(28)

where \(\sigma ^{\prime }= \frac{\dot{\sigma }}{\dot{a}}\). Now taking into account Eqs. (26) and (27), Eq. (28) has the form

$$\begin{aligned} \sigma ^{\prime } {=}\frac{1}{8\pi a^2}\left[ \frac{-M+\dot{a}^2-\ddot{a}}{\sqrt{-M-\Lambda a^2 {+}\dot{a}^2}}{-} \frac{1-\frac{3m}{a}+m^{\prime }+\dot{a}^2-\ddot{a}}{\sqrt{1-\frac{2m}{a} +\dot{a}^2}}\right] , \end{aligned}$$
(29)

and at the static solution \(a_0\) it reduces to

$$\begin{aligned} \sigma ^{\prime }(a_0) = \frac{1}{8\pi a_0^2}\left[ \frac{-M}{\sqrt{-M-\Lambda a_0^2}}- \frac{1-\frac{3m}{a_0}+m^{\prime }(a_0)}{\sqrt{1-\frac{2m}{a_0}}}\right] , \end{aligned}$$
(30)

which plays a crucial role in determining the stability regions as we consider below.

4 Stability analysis

In this section, we investigate the stability of the gravastar solution in a perturbative treatment of the shell dynamics, more precisely: by linearized stability of the solutions. For that we rearrange Eq. (26) to obtain the thin-shell equation of motion,

$$\begin{aligned} \dot{a}^{2}+V(a) =0, \end{aligned}$$
(31)

where the potential V(a) is given by

$$\begin{aligned} V(a) =\frac{\mathcal {G}_{1}(a)+\mathcal {G}_{2}(a)}{2}-\left[ \frac{\mathcal {G}_{1}(a)-\mathcal {G}_{2}(a)}{16\pi a \sigma (a)}\right] ^2-\left[ 4\pi a \sigma (a)\right] ^2, \end{aligned}$$
(32)

where we have used the notation \(\mathcal {G}_{1}(a)= {\sqrt{1-\frac{2m(a)}{a}+\dot{a}^2}}\) and \(\mathcal {G}_{2}(a)={\sqrt{-M-\Lambda a^2+\dot{a}^2}}\), respectively.

Now using the surface mass of the thin shell, \(m_s = 2\pi a \sigma \), allows one to write the potential in the form

$$\begin{aligned} V(a) = \mathcal {S}-\left( \frac{\mathcal {T}}{4m_s}\right) ^2-(2m_s)^2, \end{aligned}$$
(33)

with

$$\begin{aligned} \mathcal {S}=\frac{\mathcal {G}_{1}(a)+\mathcal {G}_{2}(a)}{2} \quad \text {and} \quad \mathcal {T}= \frac{\mathcal {G}_{1}(a)-\mathcal {G}_{2}(a)}{2}. \end{aligned}$$
(34)

For the stability analysis of the static solutions at \(a_0\) under the radial perturbations, we consider the Taylor expansion of the potential function V(a) around \(a_0\) up to second order, given by

(35)

where the prime denotes the derivative with respect to a. The existence and stability of the static solutions depend upon the inequalities that \(V(a_0)\) has local minimum at \(a_0\) and \(V^{\prime \prime }(a_0)>0\). The first derivative of the potential is given by

$$\begin{aligned} V^{\prime }(a) =\mathcal {S}^{\prime }-8m_s m_s^{\prime }-\frac{\mathcal {T}}{8m_s}\left( \frac{\mathcal {T}}{m_s}\right) ^{\prime }, \end{aligned}$$
(36)

using the conditions \(V^{\prime }(a_0) =0\), we can write the equilibrium relationship as

$$\begin{aligned} \varvec{X}\equiv m_s^{\prime }=\frac{1}{8m_s}\left[ \mathcal {S}^{\prime }-\frac{\mathcal {T}}{8m_s}\left( \frac{\mathcal {T}}{m_s}\right) ^{\prime }\right] . \end{aligned}$$
(37)

Finally, the second derivative of the potential reads

$$\begin{aligned} V^{\prime \prime }(a)= & {} \mathcal {S}^{\prime \prime }-8m_s m_s^{\prime \prime }-8 m_s^{\prime 2}\nonumber \\&-\frac{1}{8} \left[ \left( \frac{\mathcal {T}}{m_s}\right) \left( \frac{\mathcal {T}}{m_s}\right) ^{\prime \prime }+\left( \frac{\mathcal {T}}{m_s}\right) ^{\prime 2}\right] . \end{aligned}$$
(38)

To evaluate a static equilibrium configuration as regards the stability, we rewrite the conservation of the surface stress-energy tensor as \(a\sigma ^{\prime } = -\left( \sigma +\mathcal {P} \right) \), and taking into account the new parameter \(\eta =\frac{\mathcal {P}^{\prime }}{\sigma ^{\prime }}\), the surface mass of the thin shell is given by

$$\begin{aligned} m_s^{\prime \prime } =\frac{2\pi }{a}\left( \sigma +\mathcal {P}\right) \eta . \end{aligned}$$
(39)

Here the parameter \(\eta \), which is interpreted as the subluminal speed of sound, has been used to present the stability regions without using the surface equation of state.

Now, evaluated for a static equilibrium configuration for the stability and taking into account Eq. (38), with \(V^{\prime \prime }(a_0) > 0\), we have

$$\begin{aligned} \eta _{0}\frac{{\text {d}}\sigma ^{2}}{{\text {d}}a} \Bigl |_{a=a_0} > \Pi , \end{aligned}$$
(40)

by using Eq. (39), where \(\eta _{0}\) = \(\eta (a_0)\) and \(\Pi \), for notational simplicity, we define a simply behaving function of the form

$$\begin{aligned} \Pi \equiv \frac{1}{2\pi ^2 a_0}\left( \varvec{X^2-{Y}}\right) , \end{aligned}$$
(41)

where

$$\begin{aligned} \varvec{Y}=\frac{\mathcal {S}^{\prime \prime }}{8}-\frac{1}{64} \left[ \left( \frac{\mathcal {T}}{m_s}\right) \left( \frac{\mathcal {T}}{m_s}\right) ^{\prime \prime }+\left( \frac{\mathcal {T}}{m_s}\right) ^{\prime 2}\right] . \end{aligned}$$
(42)

In order to analyze the stable equilibrium regions of the solution we adopt the following inequalities:

$$\begin{aligned} \eta _{0}> \mathfrak {I},~~~ \text {if}~~~ \frac{{\text {d}}\sigma ^{2}}{{\text {d}}a}\Bigl |_{a=a_0}>~0, \end{aligned}$$
(43)
$$\begin{aligned} \eta _{0}< \mathfrak {I},~~~ \text {if}~~~ \frac{{\text {d}}\sigma ^{2}}{{\text {d}}a}\Bigl |_{a=a_0}<~0, \end{aligned}$$
(44)

with the definition

$$\begin{aligned} \mathfrak {I}\equiv \Pi \left( \frac{{\text {d}}\sigma ^{2}}{{\text {d}}a}\Bigl |_{a=a_0}\right) ^{-1}. \end{aligned}$$
(45)
Fig. 2
figure 2

The dimensionless parameter \(L= {\text {d}}{\sigma ^2}/ {\text {d}}a |_{a_0}\) corresponding to the value of \(\chi \) = 0.16 with \(\Lambda \sqrt{\alpha }\) = −0.02. The figure is shown for the specific case when m(a) < M/2

Full size image
Fig. 3
figure 3

The stability region for \(\chi \) = 0.16 and \(\Lambda \sqrt{\alpha }\) = −0.02. The stability region is depicted below the surfaces, which is sufficient close to the event horizon

Full size image

5 Region of stability

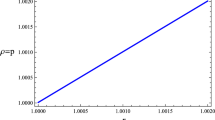
We shall in this section consider the static solution for the stability analysis and deduce the stability region by considering the inequalities Eqs. (43) and ( 44). For this purpose we shall impose a positive surface energy density \(\sigma >0\), which indicates \(m(a) < M\). For the case of m(a) \(< M\) and using the condition \(\chi < 0.214\), one can prove that \({\text {d}}\sigma ^{2}/{\text {d}}a\Bigl |_{a_0} < 0\). Therefore the stability region is constrained by the inequality (44). To justify our assumption we use a graphical representation due to the complexity of the expression \(\mathfrak {I}\), which is plotted in Fig. 2 for the specific case of m(a) = M/2 and when \(\chi \) = 0.16 with \(\Lambda \sqrt{\theta } = - 0.02\). From Fig. 2 it is clear that the solution does not correspond to any horizon.

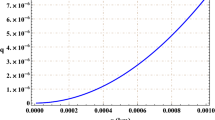
In order to study the stability region we use the graphical representation (Fig. 3) for the case when \(\chi \) = 0.16. We have examined the stability of the model based on the speed of sound which should lie within the limit (0, 1]. According to Fig. 3, the above stability region is sufficiently close to the event horizon, which decreases for increasing a, and increases again as a increases.

6 Conclusions

In this paper, we have studied the stability of the gravastar solution in a (2+1)-dimensional anti-de Sitter space given in a context of noncommutative geometry. At first we derive a BTZ solution assuming the source of energy density to be compared with point-like structures in favor of smeared objects, where the particle mass is diffused throughout a region of linear size \(\sqrt{\alpha }\) and is described by a Gaussian function of finite width rather than a Dirac delta function. In Fig. 1, it was shown that depending on the values of \(\chi \) the metric displays a different causal structure: we have the existence of two horizons, one horizon or no horizons.

To search for a gravastar solution we matched the interior geometry for a specific mass function, with an exterior BTZ solution at a junction interface situated outside the event horizon. However, to obtain a realistic picture, we explored the linearized stability analysis of the surface layer, which is sufficient close to the event horizon. Considering the static solution to find the stability region we use the graphical representation (Fig. 3) based on a speed of sound which lies within the limit (0, 1]. At this point we would like to mention that a large stability region exists and is sufficiently close to the event horizon. Therefore, considering the model one could state that it is difficult to distinguish the exterior geometry of the gravastar from a black hole.